SUMMARY
DNA sequencing data continue to progress toward longer reads with increasingly lower sequencing error rates. Here, we define an algorithmic approach, mdBG, that makes use of minimizer-space de Bruijn graphs to enable long-read genome assembly. mdBG achieves orders-of-magnitude improvement in both speed and memory usage over existing methods without compromising accuracy. A human genome is assembled in under 10 min using 8 cores and 10 GB RAM, and 60 Gbp of metagenome reads are assembled in 4 min using 1 GB RAM. In addition, we constructed a minimizer-space de Bruijn graph-based representation of 661,405 bacterial genomes, comprising 16 million nodes and 45 million edges, and successfully search it for anti-microbial resistance (AMR) genes in 12 min. We expect our advances to be essential to sequence analysis, given the rise of long-read sequencing in genomics, metagenomics, and pangenomics. Code for constructing mdBGs is freely available for download at https://github.com/ekimb/rust-mdbg/.
In brief
DNA sequencing continues to progress toward longer and more accurate reads. Yet, primary analyses, such as genome assembly and pangenome graph construction, remain challenging and energy-inefficient. Here, we introduce the concept of minimizer-space sequencing analysis, expanding the alphabet of DNA sequences to atomic tokens made of fixed-length words. This leads to ordersof-magnitude improvements in speed and memory usage for human genome assembly and metagenome assembly and enables for the first time a representation of a pangenome made of 661,405 bacterial genomes.
Graphical Abstract
INTRODUCTION
DNA sequencing data continue to improve from long reads of poor quality (Batzoglou et al., 2002), used to assemble the first human genomes and Illumina short reads with low error rates (≤1%) to longer reads with low error rates. For instance, recent Pacific Biosciences (PacBio) instruments can sequence 10to 25-Kbp-long (HiFi) reads at ≤1% error rate (Wenger et al., 2019). The R10.3 pore of the Oxford Nanopore produces reads of hundreds of Kbps in length at a ~ 5% error rate. A tantalizing possibility is that DNA sequencing will eventually converge to long, nearly perfect reads. These new technologies require algorithms that are both efficient and accurate for important sequence analysis tasks such as genome assembly (Logsdon et al., 2020).
Efficient algorithms for sequence analysis have played a central role in the era of high-throughput DNA sequencing. Many analyses, such as read mapping (Yorukoglu et al., 2016; Shajii et al., 2021), genome assembly (Pevzner et al., 2004), and taxonomic profiling (Lu and Salzberg, 2020; Nazeen et al., 2020), have benefited from milestone advances that effectively compress, or sketch, the data (Loh et al., 2012), for e.g., fast full-text search with the Burrows-Wheeler transform (BWT) (Burrows and Wheeler, 1994), space-efficient graph representations with succinct de Bruijn graphs (Chikhi et al., 2019), and light-weight databases with MinHash sketches (Ondov et al., 2016). Large-scale data re-analysis initiatives (Edgar et al., 2020; Lachmann et al., 2018) further incentivize the development of efficient algorithms, as they aim to re-analyze petabases of existing public data.
However, there has traditionally been a trade-off between algorithmic efficiency and loss of information, at least during the initial sequence-processing steps. Consider short-read genome assembly: the non-trivial insight of chopping up reads into k-mers, thereby bypassing the ordering of k-mers within each read, has unlocked fast and memory-efficient approaches using de Bruijn graphs; yet, the short k-mers—chosen for efficiency—lead to fragmented assemblies (Berger et al., 2013). In modern sequence similarity estimation and read mapping approaches, (Yorukoglu et al., 2016) information loss is even more drastic, as large genomic windows are sketched down to comparatively tiny sets of minimizers—which index a sequence (window) by its lexicographically smallest k-mer (Ondov et al., 2016) and enable efficient but sometimes inaccurate comparisons between gigabase-scale sets of sequences (Jain et al., 2020).
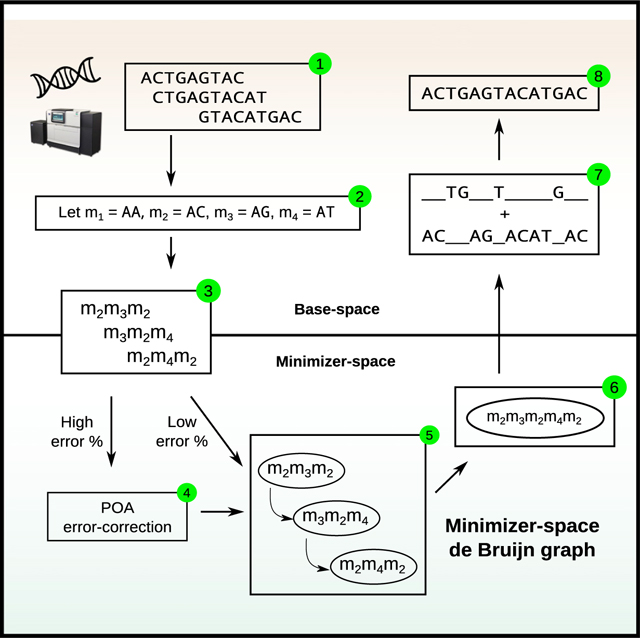
Here, we provide a highly efficient genome assembly tool for state-of-the-art and low-error long-read data (for a high-level summary, see Box 1: Progress and Potential). We introduce minimizer-space de Bruijn graphs, mdBGs, which instead of building an assembly over sequence bases—the standard approach that for clarity we refer to as base space—newly performs assembly in minimizer space (Figure 1A) and later converts it back to base-space assemblies. Specifically, each read is initially converted to an ordered sequence of its minimizers (Roberts et al., 2004; Li and Yan 2015). The order of the minimizers is important, as our aim is to reconstruct the entire genome as an ordered list. Our method differs from the classical MinHash technique, which converts sequences into unordered sets of minimizers to detect pairwise similarities between them (Broder, 1997). To aid in assembly of higher-error-rate data, we also introduce a variant of the partial order alignment (POA) algorithm that operates in minimizer space instead of base space and effectively corrects only the bases corresponding to minimizers in the reads. Sequencing errors that occur outside minimizers do not affect our representation. Those within minimizers cause substitutions or indels in minimizer space (Figure 4), which can be identified and subsequently corrected in minimizer space using POA (Figure 1C).
Box 1. Progress and potential.
Progress: third generation sequencing technologies, such as PacBio and Oxford Nanopore (ONT), can now yield terabytes of long read genomic sequences (contiguous sequences typically on the order of tens of thousands of base pairs) of higher quality (1%–4% error rate) to analyze genomes. With these evolving technologies, several important computational challenges have emerged. A fundamental problem among these is genome assembly, which is the computational task of assembling (stitching together) sequencing reads into a single genomic sequence per chromosome. The prevailing approach, de novo assembly, is naively resource intensive since it requires pairwise comparisons between all possible pairs of reads. Although the coverage and quality of sequencing technologies have vastly advanced over the past several years, genome assembly from sequencing data remains a challenging task due to the size and scope of genomic data being generated across the tree of life.
More efficient de novo assemblers use graph based data structures, most frequently de Bruijn graphs, which conceptually encode a set of sequence fragments found in the reads, as well as their overlaps. The sequence of each complete chromosome corresponds to a path in this graph. While de Bruijn graphs theoretically scale linearly in the size of the target genome instead of the number of reads and are, therefore, more efficient, sequencing errors can cause branching and, thus, increase their size and runtime to search. Moreover, all k-mers (sequences of length k) that appear in the reads need to be stored, which is memory intensive. A key insight of language models, which have emerged as an effective way to model natural languages, is that words (or sentence fragments), instead of letters, can be used as tokens (small building blocks) in the computational model of the natural language. Taking inspiration from this concept, our key conceptual advance is a data structure we call a minimizer-space de Bruijn graph (mdBG), where, instead of single nucleotides as tokens of the de Bruijn graph, we use short sequences of nucleotides known as minimizers, which allow for an even more compact representation of the genome in what we call minimizer space. Minimizer space de Bruijn graphs store only a small fraction of the nucleotides from the input data while preserving the overall graph structure, enabling them to be orders of magnitude more efficient than classical de Bruijn graphs. By doing so, we can reconstruct whole genomes from accurate long read data in minutes—about a hundred times faster than state-of-the-art approaches—on a personal computer, while using significantly less memory and achieving similar accuracy.
To enable assembly of reads with up to a 4% error rate (e.g., from emerging Oxford Nanopore data, which offers high sequencing throughput, low cost and ultra-long read lengths), we newly correct for read errors by performing minimizer-space partial order alignment (POA), in which sequencing errors in a query read are corrected by aligning other reads from the same genomic region to the query in minimizer space.
We also show that we can build very large minimizer-space de Bruijn graphs that can be queried for biologically useful questions by constructing a graphical pangenome of a large and diverse collection of 661,405 bacterial genomes. This collection of several terabytes has never before been represented as a pangenome graph (a graph that represents multiple genomes simultaneously). Such a task is computationally nearly impossible using state-of-the-art methods, which would take weeks and terabytes of RAM to complete. We show that our method completes the construction in roughly 3 h with low memory usage, and the connected components in the mdBG distinguish species, allowing us to quickly search for anti-microbial resistance genes inside the entire pangenome.
Potential: as long-read sequencing technologies mature, they offer the promise of genome reconstruction with unprecedented accuracy and contiguity. However, the assembly of these genomes can be memory-intensive and time-consuming (taking days). This precludes any but the largest centers with nearly unlimited computing power to assemble metagenomes, large bacterial pangenomes, and the growing number of human genomes for personalized medicine. If personalized medicine is expected to be effective and available to everyone in the near future, processing raw data needs to be done both cheaply and at ultra-fast rates. Consequently, cloud computing for genome assembly and analysis will likely underpin future large-scale genomics collaborations and efforts to re-analyze archived data. Our method, mdBG, significantly reduces the computational resources required for performing whole-genome assembly, making such analyses possible on desktop computers. We specifically demonstrate its use through three examples: human genome assembly, metagenome assembly, and the construction of large pangenome graphs. For microbiome and pangenome analyses, our approach offers the possibility of constructing graphical pangenomes at the scale of the largest existing collections quickly and accurately, enabling us to simultaneously analyze the myriad of genomes available in databases. Given the rise of next-generation sequencing technologies and faster and less expensive genome assembly, we expect our advances to be essential to the convergence among next-generation sequencing (NGS), cloud computing, and precision and personalized medicine, and beneficial in creating the infrastructure necessary to formulate and test disease mechanisms and develop new treatments at scale.
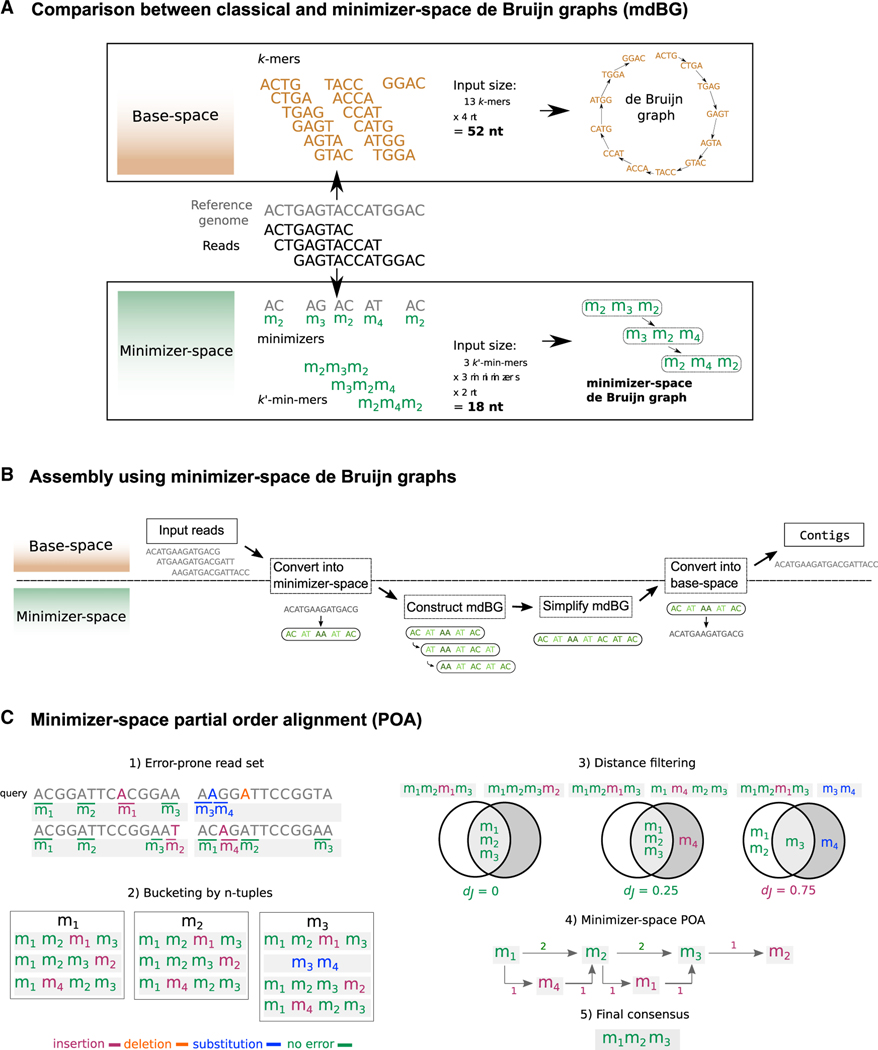
Figure 1. Overview of our methods.
(A) An efficient assembly method for state-of-the-art genome sequencing (e.g., PacBio HiFi data). Illustration of our minimizer-space de Bruijn graph (mdBG, bottom) compared with the original de Bruijn graph (top) commonly used for genome assembly. Center horizontal section shows a toy reference genome, along with a collection of sequencing reads. Top box shows k-mers (k = 4) collected from the reads, which are the nodes of the classical de Bruijn graph. The input size of 52 nucleotides (nt) is depicted in boldface. Bottom box shows the position of minimizers in the reads for = 2, and any -mer starting with nucleotide “A” is chosen as a minimizer. k′-min-mers (using notation k′ = 3 here to differentiate from classical k-mers) are tuples of k′ minimizers as ordered in reads, which constitute the nodes of the minimizer-space de Bruijn graph. Creating k′-min-mers from the minimizer-space representation of reads allows for a reduction in input size, since the only bases stored in a k′-min-mer are the bases of the chosen minimizers. The reduced input size to 18 nucleotides (nt) is depicted in boldface. The minimizer-space representation accelerates the construction and traversal of the de Bruijn graph while reducing memory consumption.
(B) Overview of the assembly pipeline using mdBG. The region of the figure above (respectively, below) the dotted line corresponds to analyses taking place in base space (respectively, minimizer space). The input reads are scanned sequentially, and all [-mers that belong to a pre-selected set of universe minimizers (see STAR Methods) are identified. Each read is then represented as an ordered list of the selected minimizers, and k-min-mers are collected from the minimizer-space representation of reads using a sliding window of length k. A minimizer-space de Bruijn graph (mdBG) is then constructed from the set of all k-min-mers and simplified in order to reduce ambiguity and remove errors. The mdBG is then converted back into base space by concatenating the base-space sequences spanned by the minimizers in the mdBG, and a set of contigs is reported.
(C) Overview of the minimizer-space partial order alignment (POA) procedure with a toy dataset of 4 reads. (1) Error-prone reads and their ordered lists of minimizers ( = 2) are shown, with sequencing errors and the minimizers that are created as a result of errors denoted in colors (insertion as red, deletion as orange, substitution in blue, no errors in green). (2) Before minimizer-space error-correction, the ordered lists of minimizers are bucketed using their n-tuples (n = 1). (3) For a query ordered list (the first read in the read set in the figure), all ordered lists that share an n-tuple with the query are obtained, and the final list of query neighbors are obtained by applying a heuristically determined distance filter dj (Jaccard distance threshold of φ = 0.5). (4) A POA graph in minimizer space is constructed by initializing the graph with the query and aligning each ordered list that passed the filter to the graph iteratively (weights of poorlya supported edges are shown in red). (5) By taking a consensus path of the graph, the error in the query is corrected.
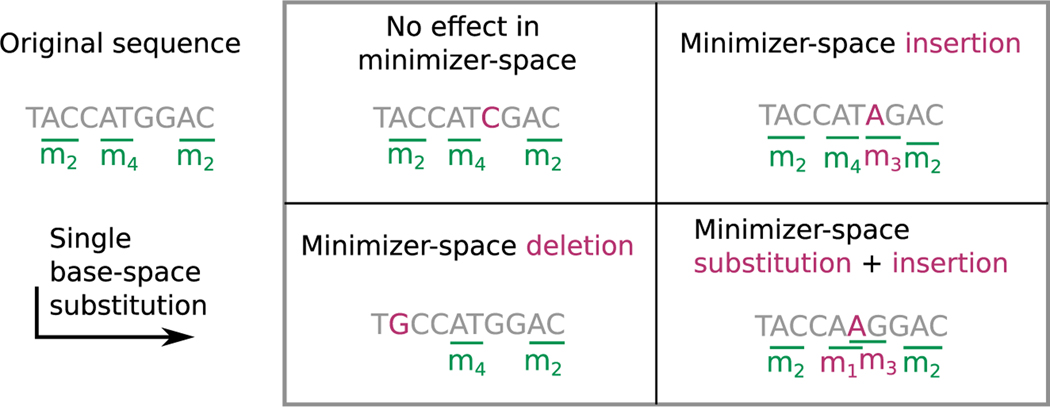
Figure 4. Propagation of sequencing errors in base space to minimizer space.
We consider a sequence along with its minimizers (left of the box). Each panel inside the box depicts the effect of a different mutation on this sequence. Top left panel: G → C (in purple) leads to no change in the minimizer-space representation as the mutation did not change or create any minimizer. Bottom left: A → G led to the disappearance of m2. Top right: C → A made the m3 minimizer appear. Bottom right: T → A affected two minimizers: m4 was substituted for m1, and m3 was inserted.
Our key conceptual advance is that minimizers can themselves make up atomic tokens of an extended alphabet, which enables efficient long-read assembly that, along with error correction, leads to preserved accuracy. By performing assembly using a minimizer-space de Bruijn graph, we drastically reduce the amount of data input to the assembler, preserving accuracy, lowering running time, and decreasing memory usage by 1 to 2 orders of magnitude compared with current assemblers. Setting adequate parameters for the order of the de Bruijn graph and the density of our minimizer scheme allows us to overcome stochastic variations in sequencing depth and read length, in a similar fashion to traditional base-space assembly. To handle higher sequencing error rates, we correct for base errors by introducing the concept of minimizer-space partial order alignment (POA).
With error-prone data, we study two regimes: real PacBio HiFi read data (<1% error rate) for Drosophila melanogaster and Human, which turn out to require little adjustment for errors due to the very low rate, and synthetic 1 to 10% error-rate data, which correspond to the range of error rates of Oxford Nanopore’s recent technology. We also demonstrate that despite data reduction, running our rust-mdbg software on synthetic error-free and 4% error rate data results in near-perfect reconstruction of a genome, the latter entirely due to our application of POA in minimizer space.
To further demonstrate rust-mdbg’s capabilities, we used it to assemble two PacBio HiFi metagenomes, achieving runtimes of minutes as opposed to days, and memory usage two orders of magnitude lower than the current state-of-the-art hifiasm-meta, with comparable assembly completeness yet lower contiguity. As a versatile use case of minimizer-space analysis, we construct, to the best of our knowledge, the largest pangenome graph to date of 661K bacterial genomes and perform minimizer-space queries of anti-microbial resistance (AMR) genes within this graph, identifying nearly all those with high sequence similarity to original bacterial genomes. Rapidly detecting AMR genes in a large collection of samples would facilitate real-time AMR surveillance (Ellington et al., 2017), and mdBG provides a space-efficient alternative to indexed k-mer searches.
Remarkably, our approach is equivalent to examining a tunable fraction (e.g., only 1%) of the input bases in the data and should generalize to emerging sequencing technologies.
Comparison with related work
This work is at the confluence of three core ideas that were recently proposed in three different genome assemblers: Shasta (Shafin et al., 2020), wtdbg2 (Ruan and Li, 2020), and Peregrine (Chin and Khalak, 2019). (1) Shasta transforms ordered lists of reads into minimizers (Shasta used the term markers) to produce an efficiently reduced representation of sequences that facilitates quick detection of overlaps between reads. A similar idea was previously used for read mapping and assembly in minimap/miniasm (Li, 2016, 2018) and edit distance calculation with Order Min Hash (OMH) (Març ais et al., 2019). (2) The wtdbg2 idea extends the usual ∑ = {A, C, T, G} alphabet, which forms the basis of traditional genome de Bruijn graphs, to 256 bp windows: a “fuzzy” de Bruijn graph is constructed by “zooming out” of read sequences and considering batches of 256 bps at a time. (3) The Peregrine idea can be broken down into two parts: (1) pairs of consecutive minimizers can be indexed—and they are naturally less often repeated across a genome than isolated minimizers, and (2) a hierarchy of minimizers can be constructed so that fewer minimizers are selected than in classical methods, thus increasing the distance between minimizers.
In distantly related independent work, a very recent pre-print (Rautiainen and Marschall, 2020) (MBG) demonstrates a similar idea as Peregrine, performing assembly by finding pairs of consecutive minimizers on reads. Although MBG does combine the concepts of minimizers and de Bruijn graphs, it is fundamentally different from the work presented here. Nodes in the MBG are classical k-mers over the DNA alphabet, whereas nodes in our representation are k-mers over an alphabet of minimizers. Two other related concepts to MBG are sparse de Bruijn graphs (Ye et al., 2012) and A-Bruijn graphs (Kolmogorov et al., 2019; Lin et al., 2016), in which the nodes are a subset of the original de Bruijn graph nodes and the edge condition is relaxed so that overlaps may be shorter than (k −1) when pairs of nodes are seen consecutively in a read.
Conceptually, our advance is in tightly combining both de Bruijn graphs and minimizers, introducing a non-trivial mix of previously known ingredients (see Box 2). The concept of a de Bruijn graph was not considered in either the Shasta or the Peregrine assemblers; whereas in the wtdbg2 assembler, de Bruijn graphs were considered, but not minimizers. Moreover, reducing the three aforementioned genome assemblers into a single idea for each of them, in terms of how they achieve algorithmic efficiency, is a contribution in itself and simplifies our presentation greatly. What we offer is essentially an ultrafast variation of de Bruijn graphs for long reads.
Box 2. A primer on minimizers and de Bruijn graphs.
The variable σ is used as a placeholder for an unspecified alphabet (a non-empty set of characters). We define ∑DNA = {A, C, T, G} as the alphabet containing the four DNA bases. Given an integer >0, ∑ is the alphabet consisting of all possible strings on ∑DNA of length . To avoid confusion, we stress that ∑ is an unusual alphabet: any “character” of ∑ is itself a string of length over the DNA-alphabet.
Given an alphabet σ,a string is a finite ordered list of characters from σ. Note that our strings will sometimes be on alphabets where each character cannot be represented by a single alphanumeric symbol. Given a string x over some alphabet σ and some integer n>0, the prefix (respectively, the suffix) of x of length n is the string formed by the first (respectively, the last) n characters of x. We now introduce the concept of a minimizer. In this paragraph, we consider strings over the alphabet ∑DNA. We consider two types of minimizers: universe and window. Consider a function f that takes as input a string of length and outputs a numeric value within range [0,H], where H>0. Usually, f is a 4-bit encoding of DNA or a random hash function (it does not matter whether the values of f are integers or whether H is an integer). Given an integer >1 and a coefficient 0<δ<1, a universe (, δ)-minimizer is any string m of length such that f(m)<δ•H. We define M,δ to be the set of all universe (,δ)-minimizers, and we refer to d as the density of Mδ.This definition of a minimizer is in contrast with the classical one (Roberts et al., 2004), which we recall here, although we will not use it. Consider a string x of any length and a substring (window) y of length w of x. A window -minimizer of x given window y is a substring m of length of y that has the smallest value f(m) among all other such substrings in y. Observe that universe minimizers are defined independently of a reference string, unlike window minimizers. They have been recently independently termed mincode syncmers (Edgar, 2021). We also performed experiments with an alternative concept to minimizers, Locally Consistent Parsing (LCP) (Șahinalp and Vishkin, 1994), which replaces universal minimizers with core substrings: substrings that can be pre-computed for any given alphabet such that any sequence of length n includes ~n/ substrings of length on average (see “locally consistent parsing [LCP]“).
We recall the definition of de Bruijn graphs. Given an alphabet σ and an integer k≥2, a de Bruijn graph of order k is a directed graph where nodes are strings of length k over σ (k-mers), and two nodes x, y are linked by an edge if the suffix of x of length k −1 is equal to the prefix of y of length k − 1. This definition corresponds to the node-centric de Bruijn graph (Chikhi et al., 2014) generalized to any alphabet.
RESULTS
An overview of our pipeline, implemented in Rust (rust-mdbg), is shown in Figure 1B. We compared rust-mdbg with three recent assemblers optimized for low-error rate long reads: Peregrine, HiCanu (Nurk et al., 2020), and hifiasm (Cheng et al., 2020) (see “genome assembly tools, versions, and parameters“ for versions and parameters).
Ultra-fast, memory-efficient, and highly contiguous assembly of real HiFi reads using rust-mdbg
We evaluated our software, rust-mdbg, on real PacBio HiFi reads from D. melanogaster, at 100X coverage, and HiFi reads for human (HG002) at ~ 50× coverage, both taken from the HiCanu publication (https://obj.umiacs.umd.edu/marbl_publications/hicanu/index.html) (Nurk et al., 2020).
Since our method does not resolve both haplotypes in diploid organisms, we compared against the primary contigs of HiCanu and hifiasm. In our tests with D. melanogaster, the reference genome consists of all nuclear chromosomes from the RefSeq accession (GenBank: GCA_000001215.4). Assembly evaluations were performed using QUAST (Gurevich et al., 2013) v5.0.2 and run with parameters recommended in HiCanu’s article (Nurk et al., 2020). QUAST aligns contigs to a reference genome, allowing to compute contiguity and completeness statistics that are corrected for misassemblies (NGA50 and Genome fraction metrics respectively in Table 3). Assemblies were all run using 8 threads on a Xeon 2.60 GHz CPU. For rust-mdbg assemblies, contigs shorter than 50 Kbp were filtered out similar to as shown in Nurk et al. (2020). We did not report the running time of the base-space conversion step and graph simplifications, as they are under 15% of the running CPU time and run on a single thread, taking no more memory than the final assembly size, which is also less memory than the mdBG.
Table 3.
Comparison of assembly statistics between original universe minimizers and universe minimizers with LCP
| D. mel 100x real HiFi reads | D. mel 50x simulated perfect reads | Human real HiFi reads | ||||
|---|---|---|---|---|---|---|
| Minimizers scheme | Universe | Universe + LCP | Universe | Universe + LCP | Universe | Universe + LCP |
| Time | 1 m 9 s | 1 m 13 s | 21 s | 22 s | 10 m 23 s | 10 m 31 s |
| Memory | 1.5 GB | 1 GB | <1 GB | <1 GB | 10 GB | 10 GB |
| # contigs | 93 | 106 | 34 | 35 | 805 | 807 |
| NGA50 (M) | 6.0 | 5.4 | 15.4 | 15.4 | 16.1* | 13.9* |
| Complete (%) | 90.8% | 91.1% | 96.2% | 96.3% | 95.5% | 95.5% |
| # misasm. | 0 | 0 | 1 | 2 | N/A* | N/A* |
Assembly statistics using both universe minimizers (denoted by “Universe,” same datasets as in Table 1) and universe minimizers with LCP (denoted by “Universe + LCP”) of D. melanogaster real HiFi reads (left), simulated perfect reads (center), and Human real HiFi reads (right), evaluated using the same metrics in Table 1. Parameters for both schemes were k = 35, = 12, and δ = 0.002 for D. melanogaster, and k = 21, = 14, and δ = 0.003 for Human.
For the Human assemblies, NG50 is reported instead of NGA50, and misassemblies are not reported due to structural differences between HG002 and the hg38 reference.
Table 1 (leftmost) shows assembly statistics for D. melanogaster HiFi reads. Our software rust-mdbg uses ~ 33× less wall-clock time and 8× less RAM than all other assemblers. In terms of assembly quality, all tools yielded high-quality results. HiCanu had 66% higher NGA50 statistics than rust-mdbg, at the cost of making more misassemblies, 385× longer runtime, and 8× higher memory usage. rust-mdbg reported the lowest Genome fraction statistics, likely due, in part, to an aggressive tip-clipping graph simplification strategy, also removing true genomic sequences.
Table 1.
Assembly statistics of D. melanogaster real HiFi reads (left), simulated perfect reads (center), and Human real HiFi reads (right), all evaluated using the commonly used QUAST program
|
|
D. mel 100x real HiFi reads |
D. mel 50x simulated perfect reads |
Human real HiFi reads |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Tool | Peregrine | HiCanu | Hifiasm | Rust-mdbg | Peregrine | HiCanu | Hifiasm | Rust-mdbg | Peregrine | Hifiasm | Rust-mdbg |
| Time | 40 min 11s | 7 h 43min | 5 h 17min | 1 min 9 s | 23 min 31 s | 8 h 12 min | 19 h 38 min | 21 s | 14 h 8 min | 58 h 41min | 10 min 23 s |
| Memory | 12 GB | 12 GB | 21 GB | 1.5 GB | 16 GB | 18 GB | 51 GB | <1 GB | 188 GB | 195 GB | 10 GB |
| # Contigs | 682 | 928 | 538 | 93 | 63 | 45 | 48 | 34 | 8,109 | 431 | 805 |
| NGA50 (M) | 5.2 | 10.1 | 4.8 | 6.0 | 6.3 | 19.4 | 21.5 | 15.4 | 18.2* | 88.0* | 16.1* |
| Complete (%) | 93.9% | 96.6% | 96.6% | 90.8% | 98.2% | 98.1% | 98.2% | 96.2% | 97.0% | 94.2% | 95.5% |
| # Misasm. | 10 | 5 | 0 | 0 | 3 | 5 | 0 | 1 | N/A* | N/A* | N/A* |
All assemblies were homopolymer compressed. Wall-clock time is reported for 8 threads. NGA50 is a contiguity metric reported in megabases (Mbp) by QUAST as the longest contig alignment to the reference genome so that shorter contig alignments collectively make up 50% of the genome length. The number of misassemblies is reported by QUAST. NGA50/NG50 and Genome fraction (Complete%) should be maximized, whereas all other metrics should be minimized. Only Peregrine, hifiasm, and our method rust-mdbg were evaluated on Human assemblies, since HiCanu requires around an order of magnitude more running time.
For the Human assemblies, NG50 is reported instead of NGA50, and misassemblies are not reported due to structural differences between HG002 and the hg38 reference.
Table 1 (rightmost) shows assembly statistics for Human HiFi (HG002) reads. rust-mdbg performed assembly 81x faster with 18× less memory usage than Peregrine, at the cost of a 22% lower contiguity and 1.5% lower completeness. Compared with hifiasm, rust-mdbg performed 338× faster with 19× lower memory, resulting in a less contiguous assembly (NG50 of 16.1 Mbp versus 88.0 Mbp for hifiasm) and 1.3% higher completeness.
Remarkably, the initial unsimplified mdBG for the Human assembly only had ~12 million k-min-mers (seen at least twice in the reads, out of 40 million seen in total) and 24 million edges, which should be compared with the 2.2 Gbp length of the (homopolymer compressed) assembly and the 100-GB total length of input reads in the uncompressed FASTA format. This highlights that the mdBG allows very efficient storage and simplification operations over the initial assembly graph in minimizer space.
Minimizer-space POA enables correction of reads with higher sequencing error rates
We introduce minimizer-space partial order alignment (POA) to tackle sequencing errors. To determine the efficacy of minimizer-space POA and the limits of minimizer-space de Bruijn graph assembly with higher read error rates, we performed experiments on a smaller dataset. In a nutshell, we simulated reads for a single Drosophila chromosome at various error rates and performed mdBG assembly with and without POA (see STAR Methods for more details).
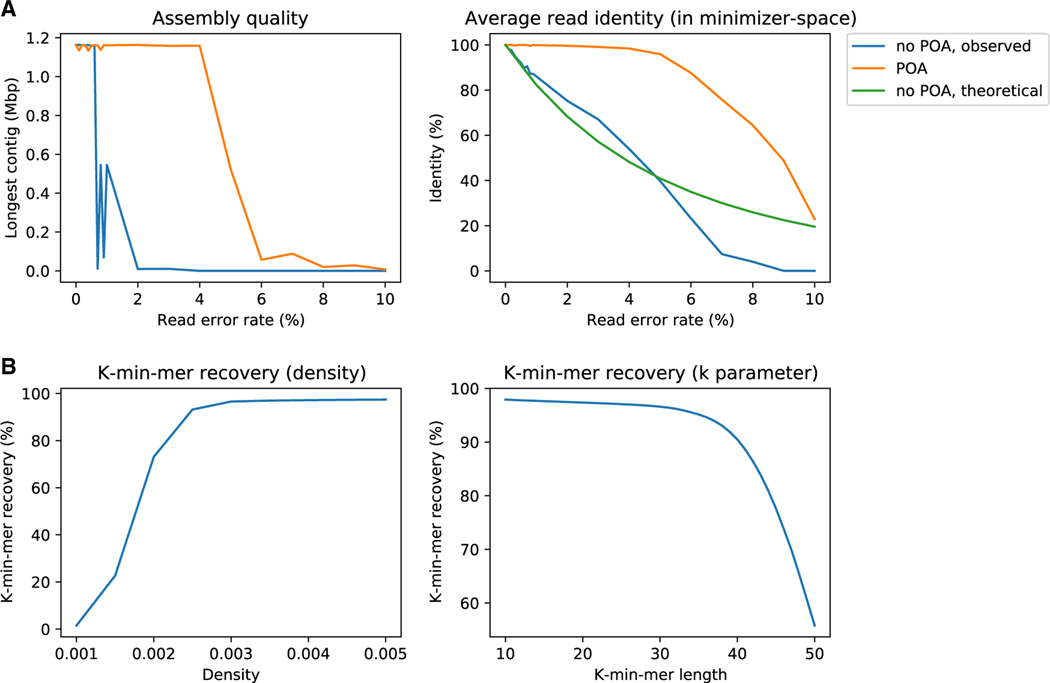
Figure 2A (left) shows that the original implementation without POA is only able to reconstruct the complete chromosome into a single contig up to error rates of 1%, after which the chromosome is assembled into ≥2 contigs. With POA, an accurate reconstruction as a single contig is obtained with error rates up to 4%. We further verified that, up to a 3% error rate, the reconstructed contig corresponds structurally exactly to the reference, apart from the base errors in the reads. At a 4% error rate, a single uncorrected indel in minimizer space introduces a ~1 Kbp artificial insertion in the assembly.
Figure 2. Evaluation of minimizer-space POA correction.
(A) Effect of our minimizer-space POA correction on mdBG assembly and reads. Reads from D. melanogaster chromosome 4 were simulated with base error rates ranging from 0%, 1%, …, up to 10%. Assemblies were run with and without minimizer-space POA correction. Left panel depicts the length of the longest contig for each assembly (uncorrected in blue, minimizer-space POA-corrected in orange). Right panel depicts the average read identity to the reference, computed in minimizer space, for raw reads (observed in blue, and predicted by Equation 1 in green), and reads corrected by POA in minimizer space (in orange).
(B) Robustness of rust-mdbg assemblies by varying the k and δ parameters, on whole-genome D. melanogaster simulated perfect reads. The proportion of recovered k-min-mer values is reported in both plots. Left panel shows recovery rates for k = 30, = 12, and varying δ from 0.001 to 0.005, with good recovery (≥ 90%) occurring with δ≥0.0025). Right panel shows recovery rates for = 12, δ = 0.003, and varying k from 10 to 50, again with good recovery with k ≥ 40.
Figure 2A (right) indicates that the minimizer-space identity of raw reads linearly decreases with increasing error rate. With POA, near-perfect correction can be achieved up to a ~ 4% error rate, with a sharp decrease at >5% error rates but still with an improvement in identity over uncorrected reads.
This highlights the importance of accurate POA correction: to put these results in perspective, mdBGs appear to be suitable to HiFi-grade data (< 1% error rates) without POA and our POA implementation is almost, but not quite yet, able to cope with the error rate of ONT data (5%).
With POA, the runtime of our implementation was around 45 σ and 0.4 GB of memory, compared with under 1 σ and < 30 MB of memory without POA. Note that we did not use an optimized POA implementation; thus, we anticipate that further engineering efforts would significantly lower the runtime and possibly also improve the quality of correction.
Pangenome mdBG of a collection of 661,405 bacterial genomes allows efficient large-scale search of AMR genes
We applied mdBG to represent a recent collection of 661,405 assembled bacterial genomes (Blackwell et al., 2021). To the best of our knowledge, this is the first de Bruijn graph construction of such a large collection of bacterial genomes. Previously only approximate sketches were created for this collection: a COBS index (Bingmann et al., 2019), allowing probabilistic membership queries of short k-mers (k = 31) (Blackwell et al., 2021), and sequence signatures (MinHash) using sourmash (Pierce et al., 2019) and pp-sketch (Lees et al., 2019), none of which are graph representations.
The mdBG construction with parameters k = 10, = 12, and δ = 0.001 took 3 h 50 m wall-clock running time using 8 threads, totaling 8 h CPU time (largely IO-bound). The memory consumption was 58 GB and the total disk usage was under 150 GB. Increasing δ to 0.01 yields a finer-resolution mdBG but increases the wall-clock running time to 13h30m, the memory usage to 481 GB, and the disk usage to 200 GB.
To compare the performance of mdBG with existing state-of-the-art tools for building de Bruijn graphs, we executed KMC3 (Kokot et al., 2017) to count 63-mers and Cuttlefish (Khan and Patro, 2020) to construct a de Bruijn graph from the counted k-mers. KMC3 took 22 wall-clock h and 191 GB memory using 8 threads, 2 TB of temporary disk usage, and 758 GB of output (56 billion distinct k-mers). Cuttlefish (Khan and Patro, 2020) did not terminate within three weeks of execution time. Hence, constructing the mdBG is at least two orders of magnitude more efficient in running time and one order of magnitude in disk usage and memory usage.
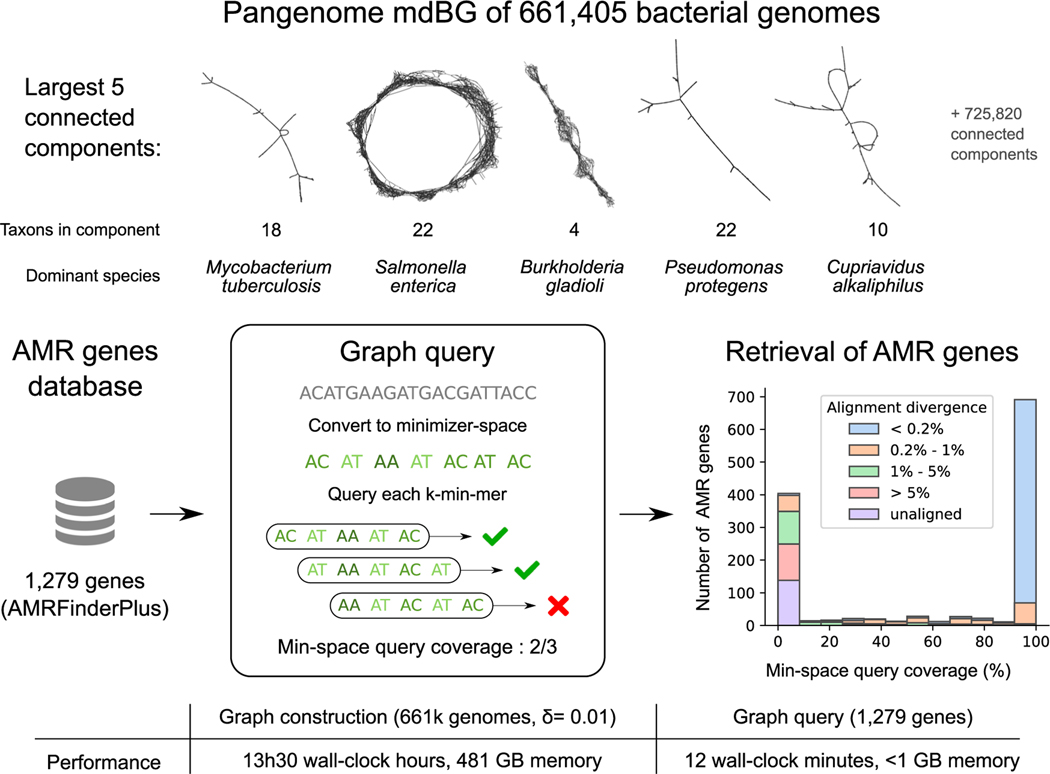
Figure 3 shows the largest 5 connected components of the δ = 0.001 bacterial pangenome mdBG. As expected, several similar species are represented within each connected component. The entire graph consists of 16 million nodes and 45 million edges (5.3 GB compressed GFA), i.e., too large to be rendered, yet much smaller than the original sequences (1.4 TB lz4-compressed).
Figure 3. Pangenome mdBG of 661,405 bacterial genomes and retrieval of anti-microbial resistance genes.
Top panel: a complete δ = 0.001 pangenome mdBG is constructed for the whole 661,405 bacterial collection and the first five connected components are displayed here (using Gephi software). Each node is a k-min-mer, and edges are exact overlaps of k − 1 minimizers between k-min-mers. Middle panel: a collection of anti-microbial resistance gene targets was converted into minimizer space, then each k-min-mer is queried in a 661,405 bacterial pangenome graph (δ = 0.01) yielding a bimodal distribution of gene retrieval: genes with high identity (99%+) to those in the pangenome are found, while those with lower identity are not found. The histogram is annotated by the minimal sequence divergence of each gene as aligned by minimap2 to the pangenome over 90% of its length. Bottom panel: runtime and memory usage for the δ = 0.01 graph construction and query. Note that the graph need only be constructed once in a preprocessing step.
To illustrate a possible application of this pangenome graph, we performed queries for the presence of AMR genes in the δ = 0.01 mdBG. We retrieved 1,502 targets from the NCBI AMR-FinderPlus “core” database (the whole amr_targets.fa file as of May 2021) and converted each gene into minimizer space, using parameters k = 10, = 12, and δ = 0.01. Of these, 1,279 genes were long enough to have at least one k-min-mer (on average 10 k-min-mers per gene). Querying those k-min-mers on the mdBG, we successfully retrieved on average 61.2% of the k-min-mers per gene; however, the retrieval distribution is bimodal: 53% of the genes have ≥99% k-min-mers found, and 31% of the genes have ≤10% k-min-mers found.
Further investigation of the genes missing from the mdBG was done by aligning the 661,405 genomes collection to the genes (in base space) using minimap2 (7 h running time over 8 cores). We found that a significant portion of genes (141, 11%) could not be aligned to the collection. Also, k-min-mers of genes with aligned sequence divergence of 1% or more (267, 20%) did not match k-min-mers from the collection and, therefore, had zero minimizer-space query coverage. Finally, although we performed sequence queries on a text representation of the pangenome graph, in principle, the graph could be indexed in memory to enable instantaneous queries at the expense of higher memory usage.
This experiment illustrates the ability of mdBG to construct pangenomes larger than supported by any other method, and those pangenomes record biologically useful information such as AMR genes. Long sequences, such as genes (containing at least 1 k-min-mer), can be quickly searched using k-min-mers as a proxy. There is nevertheless a trade-off of minimizer-space analysis that is akin to classical k-mer analysis: graph construction and queries are extremely efficient; however, they do not capture sequence similarity below a certain identity threshold (in this experiment, around 99%). Yet, the ability of the mdBG to quickly enumerate which bacterial genomes possess any AMR gene with high similarity could provide a significant boost to AMR studies.
Highly efficient assembly of real HiFi metagenomes using mdBG
We performed an assembly of two real HiFi metagenome datasets (mock communities Zymo D6331 and ATCC MSA-1003, accessions GenBank: SRX9569057 and GenBank: SRX8173258). Rust-mdbg was run with the same parameters as in the human genome assembly for the ATCC dataset, with slightly tuned parameters for the Zymo dataset (see “genome assembly tools, versions, and parameters“).
Table 2 shows the results of rust-mdbg assemblies in comparison with hifiasm-meta, a metagenome-specific flavor of hifiasm. In a nutshell, rust-mdbg achieves roughly two orders of magnitude faster and more memory-efficient assemblies, while retaining similar completeness of the assembled genomes. Although rust-mdbg metagenome assemblies are consistently more fragmented than hifiasm-meta assemblies, the ability of rust-mdbg to very quickly assemble a metagenome enables instant quality control and preliminary exploration of gene content of microbiomes at a fraction of the computing costs of current tools.
Table 2.
Metagenome assembly statistics of the Zymo D6331 dataset (left) and the ATCC MSA-1003 dataset (right) using hifiasm-meta and rust-mdbg
| Zymo D6331 Species | Abundance | hifiasm | rust-mdbg | ATCC MSA-1003 Species | Abundance | hifiasm | rust-mdbg |
|---|---|---|---|---|---|---|---|
| A. muciniphila | 1.36% | 100.00% | 100.00% | A. baumannii | 0.18% | 99.84% | 99.96% |
| B. fragilis | 13.13% | 99.99% | 100.00% | B. pacificus | 1.80% | 100.00% | 100.00% |
| B. adolescentis | 1.34% | 100.00% | 99.73% | B. vulgatus | 0.02% | 81.85% | 70.90% |
| C. albicans | 1.61% | 67.83% | 39.82% | B. adolescentis | 0.02% | 5.24% | 0.64% |
| C. difficile | 1.83% | 100.00% | 99.98% | C. beijerinckii | 1.80% | 99.99% | 99.99% |
| C. perfringens | 0.00% | 0.01% | 0.01% | C. acnes | 0.18% | 100.00% | 100.00% |
| E. faecalis | 0.00% | 0.01% | 0.01% | D. radiodurans | 0.02% | 82.50% | 53.66% |
| E. coli B1109 | 8.44% | 100.00% | 97.92% | E. faecalis | 0.02% | 54.98% | 21.05% |
| E. coli b2207 | 8.32% | 100.00% | 98.66% | E. coli | 18.00% | 100.00% | 100.00% |
| E. coli B3008 | 8.25% | 100.00% | 99.56% | H. pylori | 0.18% | 100.00% | 100.00% |
| E. coli B766 | 7.83% | 96.91% | 96.27% | L. gasseri | 0.18% | 97.78% | 98.14% |
| E. coli JM109 | 8.37% | 100.00% | 97.85% | N. meningitidis | 0.18% | 98.59% | 99.03% |
| F. prausnitzii | 14.39% | 100.00% | 100.00% | P. gingivalis | 18.00% | 91.74% | 99.94% |
| F. nucleatum | 3.78% | 100.00% | 99.96% | P. aeruginosa | 1.80% | 99.71% | 99.73% |
| L. fermentum | 0.86% | 100.00% | 100.00% | R. sphaeroides | 18.00% | 99.75% | 100.00% |
| M. smithii | 0.04% | 99.84% | 87.18% | S. odontolytica | 0.02% | 8.18% | 1.05% |
| P. corporis | 5.37% | 99.56% | 99.56% | S. aureus | 1.80% | 100.00% | 100.00% |
| R. hominis | 3.88% | 100.00% | 100.00% | S. epidermidis | 18.00% | 100.00% | 100.00% |
| S. cerevisiae | 0.18% | 69.52% | 39.56% | S. agalactiae | 1.80% | 99.50% | 99.98% |
| S. enterica | 0.02% | 6.23% | 4.62% | S. mutans | 18.00% | 100.00% | 100.00% |
| V. rogosae | 11.02% | 100.00% | 100.00% | – | – | – | – |
| Running time | – | 34 h 29 min | 55s | – | – | 59 h 16 min | 3 min 51 s |
| Memory usage | – | 83 GB | 0.9 GB | – | – | 313 GB | 1.3 GB |
The Abundance column shows the relative abundance of the species in the sample. The two rightmost columns show the species completeness of the assemblies as reported by metaQUAST.
DISCUSSION
Three areas we hope to tackle in our assembly implementation are: (1) its reliance on setting adequate assembly parameters, (2) lack of base-level polishing, and (3) haplotype separation. Regarding (1), we are experimenting with automatic selection of parameters , k, and δ. A heuristic formula is presented along with its implementation and results in the GitHub repository of rust-mdbg; however, it leads to lower-quality results (e.g., 1 Mbp N50 for the HG002 assembly versus 14 Mbp in Table 3). We also provide a preliminary multi-k assembly script inspired by IDBA (Peng et al., 2010). While automatically setting mdBG parameters is fundamentally a more complex task than just determining a single parameter (k) in classical de Bruijn graphs, we anticipate that similar techniques to KmerGenie (Chikhi and Medvedev, 2014) could be applicable, where optimal values of (, k, δ) would be found as a function of the k-min-mer abundance histogram.
Regarding directions (2) and (3), polishing could be performed as an additional step by feeding the reads and the unpolished assembly to a base-space polishing tool such as racon (Vaser et al., 2017). Haplotype separation might prove more difficult to incorporate in mdBGs: unlike HiFi assemblers that use overlap graphs with near-perfect overlaps, minimizer-space de Bruijn graphs cannot differentiate between exact and inexact overlaps in bases that are not captured by a minimizer. However, an immediate workaround is to perform haplotype phasing on resulting contigs, using tools such as HapCut2 (Edge et al., 2017) or HapTree-X (Berger et al., 2020).
We anticipate that k-min-mers could become a drop-in replacement for ubiquitously adopted k-mers for the comparison and indexing of long, highly similar sequences, e.g., in genome assembly, transcriptome assembly, and taxonomic profiling.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact Rayan Chikhi (rchikhi@pasteur.fr)
Materials availability
This study did not generate new materials.
Data and code availability
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
All original code has been deposited at https://github.com/ekimb/rust-mdbg/ and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Biological samples | ||
|
| ||
| D. melanogaster and H. sapiens HiFi reads | Nurk et al., 2020 | Table 1; https://doi.org/10.1101/gr.263566.120 |
| ATCC MSA-1003 and Zymo D6331 HiFi reads | N/A | Table 2; SRA identifiers SRX9569057 and SRX8173258 |
|
| ||
| Software and algorithms | ||
|
| ||
| mdBG code | This paper | https://doi.org/10.5281/zenodo.5145931; https://github.com/ekimb/rust-mdbg |
METHOD DETAILS
Minimizer-space de Bruijn graphs
We say that an algorithm or a data structure operates in minimizer-space when its operations are done on strings over the ∑ alphabet, with characters from M,δ. Conversely, it operates in base-space when the strings are over the usual DNA alphabet ∑DNA.
We introduce the concept of (k, , δ)-min-mer, or just k-min-mer when clear from the context, defined as an ordered list of k minimizers from M,δ. We use this term to avoid confusion with k-mers over the DNA alphabet. Indeed, a k-min-mer can be seen as a k-mer over the alphabet ∑, i.e. a k-mer in minimizer-space. For an integer k>2 and an integer >1, we define a minimizer-space de Bruijn graph (mdBG) of order k as de Bruijn graph of order k over the ∑ alphabet. As per the definition in the previous section, nodes are k-min-mers, and edges correspond of identical suffix-prefix overlaps of length k − 1 between k-min-mers. Figure 1A shows an example.
We present our procedure for constructing mdBGs as follows. First, a set M of minimizers are pre-selected using the universe minimizer scheme from the previous section. Then, reads are scanned sequentially, and positions of elements in M are identified. A multiset V of k-min-mers is created by inserting all tuples of k successive elements in M,δ found in the reads into a hash table. Each of those tuples is a k-min-mer, i.e., a node of the mdBG. Edges of the mdBG are discovered through an index of all (k − 1)-min-mers present in the k-min-mers.
mdBGs can be simplified and compacted similarly to base-space de Bruijn graphs, using similar rules for removing likely artefactual nodes (tips and bubbles), and performing path compaction. They are also bidirected, though we present them as directed here for simplicity. See ‘implementation details‘ for more details on reverse complements and simplification.
By itself the mdBG is insufficient to fully reconstruct a genome in base-space, as in the best case it can only provide a sketch consisting of the ordered list of minimizers present in each chromosome. To reconstruct a genome in base-space, we associate to each k-min-mer the substring of a read corresponding to that k-min-mer. The substring likely contains base-space sequencing errors, which we address at the end of this paragraph. To deal with overlaps, we also keep track of the positions of the second and second-to-last minimizers in each k-min-mer. After performing compaction, the base sequence of a compacted mdBG can be reconstructed by concatenating the sequences associated to k-min-mers, making sure to discard overlaps. Note that in the presence of sequencing errors, or when the same k-min-mer corresponds to several locations in the genome, the resulting assembled sequence will be imperfect (similar to the output of miniasm (Li, 2016)) which can be fixed by additional base-level polishing (not performed here).
How sequencing errors in base-space propagate to minimizer-space
In order to clarify the difference between base-space and minimizer-space in the presence of sequencing errors, we newly derive an expression of the expected error rate in minimizer-space (parameterized by k, , and δ), using a Poisson process model of random site mutations that was invoked by Mash (Ondov et al., 2016). Given the probability d of a single base substitution, the probability that no mutation will occur in a given -mer is e−d under a Poisson model.
To estimate the number of erroneous k-min-mers in a read, we define for a given read R, the expected number nR of universe (,δ)-minimizers (described in Box 2) in the read as . Since a k-min-mer is erroneous whenever at least one of k universe (,δ)-minimizers within the k-min-mer is erroneous, the probability that a given k-min-mer is erroneous is then 1 − e−dk. The number of k-min-mers obtained from the read is nR − k + 1. Thus, the expected number of erroneous k-min-mers in a read is
For instance, for a base-space mutation rate of d = 0.01, minimizer-space parameters = 12, k = 10, and δ = 0.01, and a read length of |R| = 20000, 70% of the k-min-mers in the read are erroneous. However, lowering the base-space mutation rate to d = 0.001 and keeping other values of k and identical renders only 10% of the k-min-mers erroneous within a read.
To estimate the average -mer identity of a read, we provide an approximation of the minimizer-space error rate given the base-space error rate. As seen above, an -mer that was selected as a universe minimizer has probability e−d to be mutated. Mutations that occur outside of universe minimizers may now still affect the minimizer-space representation by turning a non-minimizer -mer into a universe minimizer (see Figure 4). Under the simplifying assumption that this effect occurs independently at each position in a read, the probability that an -mer turns into a universe minimizer is the probability of a mutation within that -mer times the probability δ that a random -mer is a universe minimizer, i.e., (1 − e−d)δ. For a universe minimizer m, there are approximately 1 / δ neighboring -mers that are candidates for turning into universe minimizers themselves due to a base error. We will conceptually attach those -mers to m, and consider that an error in any of those -mers leads to an insertion error next to m.
Combining the above terms leads to the following minimizer-space error rate approximation:
| (Equation 1) |
For an error rate of d = 5%, i.e. close to that of the Oxford Nanopore R10.3 chemistry, = 12, and δ = 0.01, the minimizer-space error rate is 65.1%, dropping to 2.3% when d = 0.1%. This analysis indicates that parameters , k, δ and the base error rate d together play an essential role in the performance of a mdBG-guided assembly.
Error correction using minimizer-space partial order alignment (POA)
Long-read sequencing technologies from Pacific Biosciences (PacBio) and Oxford Nanopore (ONT) recently enabled the production of genome assemblies with high contiguity, albeit with a relatively high error rate (≥%5) in the reads, requiring either read error correction and/or assembly polishing, which are both resource-intensive steps (Chin et al., 2013; Loman et al., 2015). We will demonstrate that our minimizer-space representation is applicable to error-free sequencing reads and PacBio HiFi reads, which boast error rates lower than %1; however, in order to work with long reads with a higher error rate such as PacBio CLR and ONT, we present a resource-frugal error correction step that uses partial order alignment (POA) (Lee et al., 2002), a graph representation of a multiple sequence alignment (MSA), in order to rapidly correct sequencing errors that occur in the minimizer-space representation of reads. Stand-alone error correction modules such as racon (Vaser et al., 2017) and Nanopolish (Loman et al., 2015) have also relied on POA for error correction of long reads; however, these methods work in base-space, and as such, are still resource-intensive. We present an error correction module that uses POA in minimizer-space that can correct errors in minimizer-space, requiring only the minimizer-space representation of reads as input.
An overview of the minimizer-space POA procedure is shown in Figure 1C, and the detailed processes for the stages of the error-correction procedure are shown in Section “Minimizer-space partial order alignment”. The input for the procedure is the collection of ordered lists of minimizers obtained from all reads in the dataset (one ordered list per read). As seen earlier, the ordered list of minimizers obtained from a read containing sequencing errors will likely differ from that of an error-free read. However, provided the dataset has enough coverage, the content of other ordered lists of minimizers in the same genomic region can be used to correct errors in the query read in minimizer-space. To this end, we first perform a bucketing procedure for all ordered lists of minimizers using each of their n-tuples, where n is a user-specified parameter.
After bucketing, in order to initiate the error-correction of a query we collect its neighbors: other ordered lists likely corresponding to the same genomic region. We use a distance metric (Jaccard or Mash (Ondov et al., 2016) distance) to pick sufficiently similar neighbors. Once we obtain the final set of neighbors that will be used to error-correct the query, we run the partial order alignment (POA) procedure as described in (Lee et al., 2002), with the modification that a node in the POA graph is now a minimizer instead of an individual base, directed edges now represent whether two minimizers are adjacent in any of the neighbors, and edge weights represent the multiplicity of the edge in all of the neighbor ordered lists. After constructing the minimizer-space POA by aligning all neighbors to the graph, we generate a consensus (the best-supported traversal through the graph). Once the consensus is obtained in minimizer-space, we replace the query ordered list of minimizers with the consensus, and repeat until all reads are error-corrected. In order to recover the base-space sequence of the obtained consensus after POA, we store the sequence spanned by each pair of nodes in the edges, and generate the base-space consensus by concatenating the sequences stored in the edges of the consensus.
Implementation details
Reverse complementation is handled in our method in a natural way that is similar to classical base-space de Bruijn graphs. Each -mer is identified with its reverse complement, and a representative canonical -mer is chosen as the lexicographically smaller of the two alternatives. In turn, k-min-mers are identified with their reverse; no complementation is performed in minimizer-space, as the complement of a canonical -mer is itself. Similarly to base-space assembly, any k-min-mer appearing only once in the multiset V is removed from V due to the likelihood that it is artefactual. Assembly graph simplifications are performed using gfatools (https://github.com/lh3/gfatools), with alternating rounds of tip clipping and bubble removal (see “gfatools command line” Section), except for simulated perfect reads, which were only compacted into base-space unitigs.
In order to reduce memory usage, we write k-min-mers and the base-space sequences spanned by k-min-mers on disk, and retrieve them once the contigs are generated in minimizer-space. rust-mdbg includes a binary program (to_basespace) that transforms a simplified minimizer-space assembly into a base-space assembly.
Minimizer-space partial order alignment
POA bucketing and preprocessing
In Algorithm 1, all tuples of length n of an ordered list of minimizers are computed using a sliding window (lines 4–6), and the ordered list of minimizers itself is stored in the buckets labeled by each n-tuple (line 7). We use bucketing as a proxy for set similarity, since each pair of reads in the same bucket will have an n-tuple (the label of the bucket), and will be more likely to come from the same genomic region.
Algorithm 1.
Bucketing procedure for all ordered lists of minimizers
| Input Set of ordered list of minimizers S, bucket index length n | ||
| 1: | procedure: BUCKET(S, n) | |
| 2: | B ← {} | ▹ Empty hash table of buckets |
| 3: | for s∈S do | |
| 4: | for i = 0 to i = |s| − n + 1 do | |
| 5: | t ← s[i : i + n] | ▹ n-tuple of s starting at position i |
| 6: | B[t] ← B[t] ∪ s | |
| 7: | end for | |
| 8: | end for | |
| 9: | return B | |
| 10: | end procedure | |
The overview of the collection of neighbors for error-correcting a query ordered list of minimizers is shown in Algorithm 2. We obtain all n-tuples of a query ordered list, and collect the ordered lists in the previously populated buckets indexed by its n-tuples (lines 10–15). These ordered lists are viable candidates for neighbors, since they share a tuple of length at least n with the query ordered list; however, since a query n-tuple may not uniquely identify a genomic region, we apply a similarity filter to further eliminate candidates unrelated to the query. Using either Jaccard or Mash distance (Ondov et al., 2016) as a similarity metric, for a user-specified threshold φ, we filter out all candidates that have distance ≥ φ to the query ordered list to obtain the final set of neighbors that will be used for error-correcting the query (lines 1–9).
Algorithm 2.
Collection of neighbors for a given query ordered list
| Input: A query ordered list of minimizers q to be error-corrected, collection of buckets B, bucket index length n, distance function d, distance threshold φ | ||
| 1: | function FILTER(q,C,d,φ) | |
| 2: | F ← {} | ▹ Empty set of candidates that pass the filter |
| 3: | for c∈C do | |
| 4: | if d(q,c)<φ | ▹ Apply distance threshold of φ to a candidate then |
| 5: | F ← F∪c | |
| 6: | end if | |
| 7: | end for | |
| 8: | return F | |
| 9: | end function | |
| 10: | procedure COLLECT(q, B, n, d, φ) | |
| 11: | C ← {} | ▹ Empty set of candidate neighbors |
| 12: | for i = 0 to i = |q| − n + 1 do | |
| 13: | t ← q[i : i + n] | ▹ n-tuple of q starting at position i |
| 14: | C ← C ∪ B[t] | |
| 15: | end for | |
| 16: | F ← FILTER(q, C, d, φ) | |
| 17: | return F | |
| 18: | end procedure | |
POA graph construction and consensus generation
Algorithm 3.
Minimizer-space POA graph construction and consensus generation
| Input: A query ordered list of minimizers q to be error-corrected, collection of query neighbors N | ||
| 1: | procedure POA(q, N) | |
| 2: | G = (V,E) ← initializeGraph(q) | ▹ As described in (Lee et al., 2002) |
| 3: | for n∈N do | |
| 4: | G ← semiGlobalAlign(G,n) | ▹ As described in (Lee et al., 2002) |
| 5: | end for | |
| 6: | λ ← {} | ▹ Scoring table for nodes |
| 7: | P ← {} | ▹ Predecessor table for nodes |
| 8: | topologicalSort(G) | ▹ Topological sorting of nodes |
| 9: | for v∈V do | |
| 10: | e = (u, v) ← max(inEdges(v)) | ▹ Find the maximum-weighted incoming edge to v |
| 11: | λ[v] ← We + λ[u] | |
| 12: | P[v] ← u | |
| 13: | end for | |
| 14: | C ← CONSENSUS(V, λ; P) | ▹ Described in the “Minimizer-space POA” |
| Section | ||
| 15: | return C | |
| 16: | end procedure | |
Algorithm 4 describes a canonical POA consensus generation procedure, similar to racon (Vaser et al., 2017), except that here consensus is performed in minimizer-space.
Algorithm 4.
Consensus generation on POA graph
| Input: The node set V of the POA graph, scoring array λ, predecessor array P | ||
| 1: | function CONSENSUS(V, λ, P) | |
| 2: | C ← [] | ▹ Consensus path to be |
| obtained | ||
| 3: | vmax ← Ø | ▹ Initialize the highest-scoring node |
| 4: | for v ∈ V do | |
| 5: | if λ[v]>λ[vmax] then | |
| 6: | vmax ← v | |
| 7: | end if | |
| 8: | end for | |
| 9: | vcurr ← vmax | ▹ Start traceback from highest-scoring node |
| 10: | while vcurr ≠ Ø do | |
| 11: | C ← C + [vcurr] | |
| 12: | vcurr)←P[vcurr] | ▹ Move to predecessor of current node |
| 13: | end while | |
| 14: | return C | |
| 15: | end function | |
The minimizer-space POA error-correction procedure is shown in Algorithm 3. For each neighbor of the query, we perform semi-global alignment between a neighbor ordered list and the graph, where for two minimizers mi and mj, a match is defined as mi = mj, and a mismatch is defined as (lines 17–19). After building the POA graph G = (V, E) by aligning all neighbors in minimizer space, we generate a consensus to obtain the best-supported traversal through the graph. We first initialize a scoring λ, and set λ[v] = 0 for all v∈V. Then, we perform a topological sort of the nodes in the graph, and iterate through the sorted nodes. For each node v, we select the highest-weighted incoming edge e = (u, v) with weight we, and set λ[v] = we + λ(u). The node u is then marked as a predecessor of v (lines 21–28).
Minimizer-space POA evaluation set-up
We extracted chromosome 4 (~ 1.2 Mbp) of the D. melanogaster reference genome, and simulated reads using the command randomreads.sh pacbio=t of BBMap (Bushnell, 2014). We generated one dataset per error rate value from 0% to 10%, keeping other parameters identical (24 Kbp mean read length and 70X coverage). Reads were then assembled using our implementation with and without POA, using parameters = 10, k = 7, and δ = 0.0008 experimentally determined to yield a perfect assembly with error-free reads. We evaluated the average read identity in minimizer-space using semi-global Smith-Waterman alignment between the sequence of minimizers of a read and the sequence of minimizers of the reference, taking BLAST-like identity (number of minimize matches divided by the number of alignment columns). We also evaluated the length of the longest reconstructed contig in basespace as a proxy for assembly quality.
Exploration of rust-mdbg parameter space on simulated perfect reads
In order to demonstrate the efficacy of our approach in terms of results quality in an ideal setting, we simulated error-free reads of length 100 Kbp at 50X coverage of the D. melanogaster genome. The parameters for the assembly were k = 30, = 12, and δ = 0.005. Table 3 (center) shows that rust-mdbg is able to assemble these error-free reads nearly as well as HiCanu and hifiasm, within lower but similar NGA50 (~ 25% lower) and genome fraction (< 1% lower) values. However, rust-mdbg is 2–3 orders of magnitudes faster and uses an order of magnitude less memory.
For a base-space de Bruijn graph assembler, the quality of the assembly depends on a single parameter (k), whereas in a rust-mdbg assembly, there are three parameters (, k, δ) that can affect assembly quality independently (see STAR Methods). We investigated the effect of changing k for given and δ, and changing d for given k and on the performance of rust-mdbg on perfect reads. For = 12 and k = 30, we tested different values for d from 0.001 to 0.005 (increased by 0.0005 in each iteration). For = 12 and δ = 0.003, we tested different values of k from 10 to 50 (increased by 1 in each iteration). For each iteration, we computed the k-min-mer recovery rate (the percentage of k-min-mers obtained from the reads that also exist in the set of k-min-mers from the reference) as a means of quantifying the quality of a minimizer-space assembly through a completeness metric.
Figure 2B shows the results of this investigation. For fixed values of k = 30 and = 12, k-min-mer recovery rate is insufficiently low for δ<0.0025: Since the ordered lists of minimizers obtained from the reads need to have length >k in order to not be discarded, a very low density value causes a higher fraction of reads to be skipped, decreasing k-min-mer recovery rate. For δ≥0.0025, an increasingly smaller portion of the reads are discarded, consistently yielding k-min-mer recovery rates of >90%. We further observe that for fixed values of δ = 0.003 and = 12, k-min-mer recovery rate is consistently above 95% for k-min-mer lengths of 10 to 35. Since δ = 0.003, a sufficient portion of the reads are transformed into k-min-mers at this k-min-mer length, and higher values of k will result in a larger portion of the reads to be discarded.
gfatools command lines
The following (relatively aggressive) GFA assembly graph simplifications rounds were performed for all mdBG assemblies, using https://github.com/lh3/gfatools/. Rounds are of two types: -t x,y removes tips having at most x segments and of maximal length y bp, and -b z removes bubbles of maximal radius z bp. In addition, gfa_break_loops.py is a custom script (available in the rust-mdbg GitHub repository) that removes self-loops in the assembly graph, as well as an arbitrary edge in cycles.
gfatools asm -t 10,50000 -t 10,50000 -b 100000 -b 100000 -t 10,50000 \
-b 100000 -b 100000 -b 100000 -t 10,50000 -b 100000 \
-t 10,50000 -b 1000000 -t 10,150000 -b 1000000 -u > $base.tmp1.gfa
gfa_break_loops.py $base.tmp1.gfa > $base.tmp2.gfa
gfatools asm $base.tmp2.gfa -t 10,50000 -b 100000 -t 10,100000 \
-b 1000000 -t 10,150000 -b 1000000 -u > $base.tmp3.gfa
gfa_break_loops.py $base.tmp3.gfa > $base.tmp4.gfa
gfatools asm $base.tmp4.gfa -t 10,50000 -b 100000 -t 10,100000 \
-b 1000000 -t 10,200000 -b 1000000 -u > $base.msimpl.gfa
Genome assembly tools, versions, and parameters
HiCanu (v2.1) was run with default parameters, hifiasm (commit 8cb131d) with parameters -l0 -f0, and Peregrine (commit 008082a) with command line: 8 8 8 8 8 8 8 8 8 –with-consensus –shimmer-r 3 –best_n_ovlp 8. rust-mdbg was run with parameters k = 35, = 12, and δ = 0.002 for D. melanogaster, and k = 21, = 14, δ = 0.003 for HG002.
For metagenomes, rust-mdbg was run with parameters k = 21, = 14, δ = 0.003 for the ATCC MSA-1003 dataset (same parameters as the human dataset), and k = 40, = 12, δ = 0.004 for the Zymo D6331 dataset. Hifiasm-meta (commit cda13b8) was run with parameters -S -lowq-10 50 for ATCC MSA-1003 and default for Zymo.
Locally Consistent Parsing (LCP)
Locally Consistent Parsing (LCP) describes sets of evenly spaced core substrings of a given length that cover any string of length n for any alphabet (Şahinalp and Vishkin, 1994). The set of core substrings can be pre-computed such that a string of length n is covered by ~ n/ core substrings on average. LCP and the concept of core substrings were used in the first linear-time algorithm for approximate string matching (Şahinalp and Vishkin, 1994), for string indexing under block edit distance (Muthukrishnan and Şahinalp, 2000), and for almost linear-time approximate string alignment (Batu et al., 2006).
SCALCE (Hach et al., 2012) introduced LCP to genome compression, and used the longest core substring(s) in each read as representatives to group together similar reads, which are then reordered lexicographically for compression without the need of a reference genome. In preliminary testing of LCPs as an alternative to minimizers in our pipeline, we integrated the pre-computed set of core substrings described in SCALCE into the universe (,δ)-minimizers scheme in rust-mdbg, where we selected an -mer m as a minimizer if m is a universe (,δ)-minimizer and also appears in the set of core substrings. We evaluated both minimizer schemes on simulated perfect reads from D. melanogaster at 50X coverage, real Pacific Biosciences HiFi reads from D. melanogaster at 100X coverage, and HiFi reads for human (HG002) at ~ 50X coverage, taken from the HiCanu publication (https://obj.umiacs.umd.edu/marbl_publications/hicanu/index.html) (Nurk et al., 2020). We did not notice a major difference using LCP versus only universe minimizers, but our implementation should be seen as a baseline for future optimizations.
Highlights.
We propose a novel graph representation for highly accurate and long sequencing reads
It improves the efficiency of genome assembly and pangenome graph construction
We construct for the first time a pangenome of 661,405 bacterial genomes
ACKNOWLEDGMENTS
B.E. was partially funded by grant NIH R01HG010959 (to B.B.) and B.B. by NIH R35GM141861. R.C. was funded by grants ANR Inception (ANR-16-CONV-0005), PRAIRIE (ANR-19-P3IA-0001), and PANGAIA (H2020 MSCA RISE 872539). The authors are grateful to A. Limasset, P. Peterlongo, B. Hie, and R. Singh for remarks on the manuscript and to Simon Barnett for inspiration for the Graphical Abstract.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Batu T, Ergun F, and Şahinalp C. (2006). Oblivious string embeddings and edit distance approximations. In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms’, SODA ‘06, Society for Industrial and Applied Mathematics), pp. 792–801. [Google Scholar]
- Batzoglou S, Jaffe DB, Stanley K, Butler J, Gnerre S, Mauceli E, Berger B, Mesirov JP, and Lander ES (2002). ARACHNE: a whole-genome shotgun assembler. Genome Res. 12, 177–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger B, Peng J, and Singh M. (2013). Computational solutions for omics data. Nat. Rev. Genet 14, 333–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger E, Yorukoglu D, Zhang L, Nyquist SK, Shalek AK, Kellis M, Numanagić I, and Berger B. (2020). Improved haplotype inference by exploiting long-range linking and allelic imbalance in RNA-seq datasets. Nat. Commun 11, 4662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bingmann T, Bradley P, Gauger F, and Iqbal Z. (2019). COBS: a compact bit-sliced signature index. In 26th International Conference on String Processing and Information Retrieval (SPIRE), pp. 285–303. arXiv:1905. 09624v2. [Google Scholar]
- Blackwell GA, Hunt M, Malone KM, Lima L, Horesh G, Alako BT, Thomson NR, and Iqbal Z. (2021). Exploring bacterial diversity via a curated and searchable snapshot of archived DNA sequences. bioRxiv. 10.1101/2021.03.02.433662. [DOI] [PMC free article] [PubMed]
- Broder AZ (1997). On the resemblance and containment of documents. In Proceedings. Compression and Complexity of SEQUENCES 1997 (Cat. No.97TB100171), pp. 21–29. https://www.cs.princeton.edu/courses/archive/spring13/cos598C/broder97resemblance.pdf. [Google Scholar]
- Burrows M, and Wheeler D. (1994). A block-sorting lossless data compres sion algorithm. In Digital SRC Research Report (Citeseer). [Google Scholar]
- Bushnell B. (2014). BBMap: a fast, accurate, splice-aware aligner. (Lawrence Berkeley National Laboratory). https://www.osti.gov/servlets/purl/1241166.
- Cheng H, Concepcion GT, Feng X, Zhang H, and Li H. (2020). Haplotype-resolved de novo assembly with phased assembly graphs. arXiv arXiv:2008.01237. [DOI] [PMC free article] [PubMed]
- Chikhi R, Holub J, and Medvedev P. (2019). Data structures to represent sets of k-long DNA sequences. arXiv, arXiv:1903.12312.
- Chikhi R, Limasset A, Jackman S, Simpson JT, and Medvedev P. (2014). On the representation of de Bruijn graphs. In International Conference on Research in Computational Molecular Biology (Springer; ), pp. 35–55. [DOI] [PubMed] [Google Scholar]
- Chikhi R, and Medvedev P. (2014). Informed and automated k-mer size selection for genome assembly. Bioinformatics 30, 31–37. [DOI] [PubMed] [Google Scholar]
- Chin CS, Alexander DH, Marks P, Klammer AA, Drake J, Heiner C, Clum A, Copeland A, Huddleston J, Eichler EE, et al. (2013). Nonhybrid, finished microbial genome assemblies from long-read SMRT sequencing data. Nat. Methods 10, 563–569. [DOI] [PubMed] [Google Scholar]
- Chin C-S, and Khalak A. (2019). Human genome assembly in 100 minutes. bioRxiv. 10.1101/705616. [DOI]
- Edgar R. (2021). Syncmers are more sensitive than minimizers for selecting conserved k-mers in biological sequences. PeerJ 9, e10805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC, Taylor J, Altman T, Barbera P, Meleshko D, Lin V, Lohr D, Novakovsky G, Al-Shayeb B, Banfield JF, et al. (2020). Petabase-scale sequence alignment catalyses viral discovery. bioRxiv. 10.1101/2020.08.07.241729. [DOI] [PubMed]
- Edge P, Bafna V, and Bansal V. (2017). HapCUT2: robust and accurate haplotype assembly for diverse sequencing technologies. Genome Res. 27, 801–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellington MJ, Ekelund O, Aarestrup FM, Canton R, Doumith M, Giske C, Grundman H, Hasman H, Holden MTG, Hopkins KL, et al. (2017). The role of whole genome sequencing in antimicrobial susceptibility testing of bacteria: report from the eucast subcommittee. Clin. Microbiol. Infect 23, 2–22. [DOI] [PubMed] [Google Scholar]
- Gurevich A, Saveliev V, Vyahhi N, and Tesler G. (2013). QUAST: quality assessment tool for genome assemblies. Bioinformatics 29, 1072–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hach F, Numanagićc I, Alkan C, and Şahinalp SC. (2012). SCALCE: boosting sequence compression algorithms using locally consistent encoding. Bioinformatics 28, 3051–3057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain C, Rhie A, Zhang H, Chu C, Koren S, and Phillippy A. (2020). Weighted minimizer sampling improves long read mapping. bioRxiv https://www.biorxiv.org/content/10.1101/2020.02.11.943241v1.full. [DOI] [PMC free article] [PubMed]
- Khan J, and Patro R. (2020). Cuttlefish: fast, parallel, and low-memory compaction of de Bruijn graphs from large-scale genome collections. bioRxiv. 10.1101/2020.10.21.349605. [DOI] [PMC free article] [PubMed]
- Kokot M, D1ugosz M, and Deorowicz S. (2017). KMC 3: counting and manipulating k-mer statistics. Bioinformatics 33, 2759–2761. [DOI] [PubMed] [Google Scholar]
- Kolmogorov M, Yuan J, Lin Y, and Pevzner PA (2019). Assembly of long, error-prone reads using repeat graphs. Nat. Biotechnol 37, 540–546. [DOI] [PubMed] [Google Scholar]
- Lachmann A, Torre D, Keenan AB, Jagodnik KM, Lee HJ, Wang L, Silverstein MC, and Ma’ayan A. (2018). Massive mining of publicly available RNA-seq data from human and mouse. Nat. Commun 9, 1366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C, Grasso C, and Sharlow MF (2002). Multiple sequence alignment using partial order graphs. Bioinformatics 18, 452–464. [DOI] [PubMed] [Google Scholar]
- Lees JA, Harris SR, Tonkin-Hill G, Gladstone RA, Lo SW, Weiser JN, Corander J, Bentley SD, and Croucher NJ (2019). Fast and flexible bacterial genomic epidemiology with PopPUNK. Genome Res. 29, 304–316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2016). Minimap and miniasm: fast mapping and de novo assembly for noisy long sequences. Bioinformatics 32, 2103–2110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. (2018). Minimap2: pairwise alignment for nucleotide sequences. Bioinformatics 34, 3094–3100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, and Yan X. (2015). MSPKmerCounter: a fast and memory efficient approach for k-mer counting. arXiv https://arxiv.org/pdf/1505.06550.pdf.
- Lin Y, Yuan J, Kolmogorov M, Shen MW, Chaisson M, and Pevzner PA (2016). Assembly of long error-prone reads using de Bruijn graphs. Proc. Natl. Acad. Sci. USA 113, E8396–E8405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logsdon GA, Vollger MR, and Eichler EE (2020). Long-read human genome sequencing and its applications. Nat. Rev. Genet 21, 597–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loh PR, Baym M, and Berger B. (2012). Compressive genomics. Nat. Biotechnol 30, 627–630. [DOI] [PubMed] [Google Scholar]
- Loman NJ, Quick J, and Simpson JT (2015). A complete bacterial genome assembled de novo using only nanopore sequencing data. Nat. Methods 12, 733–735. [DOI] [PubMed] [Google Scholar]
- Lu J, and Salzberg S. (2020). Ultrafast and accurate 16S microbial community analysis using Kraken 2. bioRxiv. 10.1101/2020.03.27.012047. [DOI] [PMC free article] [PubMed]
- Marçais G, DeBlasio D, Pandey P, and Kingsford C. (2019). Locality-sensitive hashing for the edit distance. Bioinformatics 35, i127–i135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthukrishnan S, and Şahinalp SC (2000). Approximate nearest neighbors and sequence comparison with block operations. In STOC ‘00. Proceedings of the thirty-second annual ACM symposium on Theory of computing, pp. 416–424. 10.1145/335305.335353. [DOI]
- Nazeen S, Yu YW, and Berger B. (2020). Carnelian uncovers hidden functional patterns across diverse study populations from whole metagenome sequencing reads. Genome Biol. 21, 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nurk S, Walenz BP, Rhie A, Vollger MR, Logsdon GA, Grothe R, Miga KH, Eichler EE, Phillippy AM, and Koren S. (2020). HiCanu: accurate assembly of segmental duplications, satellites, and allelic variants from high-fidelity long reads. Genome Res. 30, 1291–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ondov BD, Treangen TJ, Melsted P, Mallonee AB, Bergman NH, Koren S, and Phillippy AM (2016). Mash: fast genome and metagenome distance estimation using MinHash. Genome Biol. 17, 132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Y, Leung HCM, Yiu SM, and Chin FYL (2010). IDBA–A practical iterative de Bruijn graph de novo assembler. In Annual International Conference on Research in Computational Molecular Biology (Springer; ), pp. 426–440. [Google Scholar]
- Pevzner PA, Tang H, and Tesler G. (2004). De novo repeat classification and fragment assembly. Genome Res. 14, 1786–1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce NT, Irber L, Reiter T, Brooks P, and Brown CT (2019). Large-scale sequence comparisons with sourmash. F1000Res. 8, 1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rautiainen M, and Marschall T. (2020). MBG: minimizer-based sparse de Bruijn graph construction. bioRxiv https://www.biorxiv.org/content/10.1101/2020.09.18.303156v1.full. [DOI] [PMC free article] [PubMed]
- Roberts M, Hayes W, Hunt BR, Mount SM, and Yorke JA (2004). Reducing storage requirements for biological sequence comparison. Bioinformatics 20, 3363–3369. [DOI] [PubMed] [Google Scholar]
- Ruan J, and Li H. (2020). Fast and accurate long-read assembly with wtdbg2. Nat. Methods 17, 155–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Şahinalp SC, and Vishkin U. (1994). Symmetry breaking for suffix tree construction. In Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing’, STOC ‘94 (Association for Computing Machinery), pp. 300–309. 10.1145/195058.195164. [DOI] [Google Scholar]
- Shafin K, Pesout T, Lorig-Roach R, Haukness M, Olsen HE, Bosworth C, Armstrong J, Tigyi K, Maurer N, Koren S, et al. (2020). Nanopore sequencing and the Shasta toolkit enable efficient de novo assembly of eleven human genomes. Nat. Biotechnol 38, 1044–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shajii A, Numanagić I, Leighton AT, Greenyer H, Amarasinghe S, and Berger B. (2021). A python-based programming language for high-performance computational genomics. Nat. Biotechnol 10.1038/s41587-021-00985-6. [DOI] [PMC free article] [PubMed]
- Vaser R, Sović I, Nagarajan N, and Šikić M. (2017). Fast and accurate de novo genome assembly from long uncorrected reads. Genome Res. 27, 737–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wenger AM, Peluso P, Rowell WJ, Chang PC, Hall RJ, Concepcion GT, Ebler J, Fungtammasan A, Kolesnikov A, Olson ND, et al. (2019). Accurate circular consensus long-read sequencing improves variant detection and assembly of a human genome. Nat. Biotechnol 37, 1155–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye C, Ma ZS, Cannon CH, Pop M, and Yu DW (2012). Exploiting sparseness in de novo genome assembly. BMC Bioinformatics 13 (Supplement 6), S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yorukoglu D, Yu YW, Peng J, and Berger B. (2016). Compressive mapping for next-generation sequencing. Nat. Biotechnol 34, 374–376. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
All original code has been deposited at https://github.com/ekimb/rust-mdbg/ and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Biological samples | ||
|
| ||
| D. melanogaster and H. sapiens HiFi reads | Nurk et al., 2020 | Table 1; https://doi.org/10.1101/gr.263566.120 |
| ATCC MSA-1003 and Zymo D6331 HiFi reads | N/A | Table 2; SRA identifiers SRX9569057 and SRX8173258 |
|
| ||
| Software and algorithms | ||
|
| ||
| mdBG code | This paper | https://doi.org/10.5281/zenodo.5145931; https://github.com/ekimb/rust-mdbg |