Abstract
Resting-state functional magnetic resonance imaging (rs-fMRI) studies have focused primarily on characterizing functional or effective connectivity of discrete brain regions. A major drawback of this approach is that it does not provide a mechanistic understanding of brain cognitive function or dysfunction at cellular and circuit levels. To overcome this limitation, we combined the methods of computational neuroscience with traditional macroscale connectomic analysis and developed a Multiscale Neural Model Inversion (MNMI) framework that links microscale circuit interaction with macroscale network dynamics and estimates both local coupling and inter-regional connections via stochastic optimization based on blood oxygen-level dependent (BOLD) rs-fMRI. We applied this method to the rs-fMRI data of 66 normal healthy subjects and 66 individuals with major depressive disorder (MDD) to identify potential biomarkers at both local circuit and global network level. Results suggest that the recurrent excitation and inhibition within the dorsal lateral prefrontal cortex (dlPFC) might be disrupted in MDD, consistent with the commonly accepted hypothetical model of MDD. In addition, recurrent excitation in the thalamus was found to be abnormally elevated, which may be responsible to abnormal thalamocortical oscillations often observed in MDD. Overall, our modeling approach holds the promise to overcome the limitation of traditional large-scale connectome modeling by providing hidden mechanistic insights into neuroanatomy, circuit dynamics and pathophysiology.
Keywords: Neural mass model, Functional connectivity, Resting-state fMRI, Major depressive disorder, Stochastic optimization
1. Introduction
Brain cognitive functions depend on the complex interplay among distributed brain regions and networks [1] characterized by functional magnetic resonance imaging (fMRI) [2]. To delineate brain network interactions for both healthy and patient cohorts, such fMRI analysis has predominately focused on macroscale systemic modeling of inter-regional interactions including undirected functional connectivity [3] and directed effective connectivity [4]. Despite the great success of macroscopic connectome modeling with resting-state fMRI (rs-fMRI) in charactering the interaction of the large-scale functional systems, their applications to fundamental neuroscience problems and clinical translation are still limited. This is because such connectivity analysis is largely descriptive and superficial, and therefore cannot offer a deep mechanistic understanding of neural circuit functions or dysfunction. Addressing this limitation is a key to unlocking the power of computational neuroscience modeling for the macroscale systemic neuroscience studies.
Recent development in computational neuroimaging has started to deal with this problem. Dynamic causal modeling (DCM) is one of them, which was recently redesigned to incorporate a two-state model for each brain region [5] and the latest DCM used a standard neural mass model of neuronal dynamics within a canonical microcircuit [6]. Nevertheless, the two-state model is an only simple extension of the one-state model without modeling realistic neural dynamics (e.g., oscillations), and the DCM with the neural mass model currently only applies to task-based fMRI. More recently, Wang et al. [7] inverted a large-scale circuit model of the cerebral cortex using dynamic mean field modeling of rs-fMRI to study macroscale cortical hierarchy. Despite its applicability to rs-fMRI, the computational model they used is oversimplified with only a single type (excitatory) of the neural population modeled for each brain region and the inter-regional connection weights were only allowed to be scaled by a factor homogenously for all connections, making it less realistic in real applications. Moreover, to the best of our knowledge, no rs-fMRI based neural mass model has been applied to study abnormal circuit dynamics in brain disease populations.
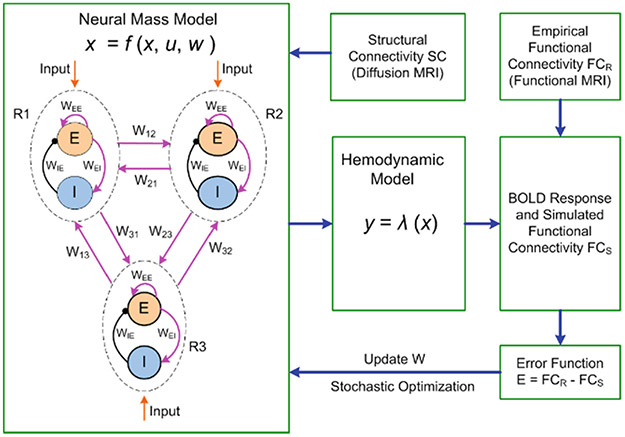
To advance our understanding of the underlying circuit mechanisms of the functional interactions among remote brain regions and promote clinically-orientated studies, built upon the previous modeling work [4, 6, 7], we developed a Multiscale Neural Model Inversion (MNMI) framework (Fig. 1) that links microscale intra-regional circuit interactions with macroscale inter-network dynamics. Specifically, we used biologically plausible Wilson-Cowan oscillators [8] to model the oscillatory dynamics of local neural circuits consisting of excitatory and inhibitory neural populations (E, I) coupled with reciprocal interactions (Fig. 1, Neural Mass Model). Different brain regions are connected through inter-network connectivities initialized based on diffusion MRI. The neural activity is converted into BOLD signals through a hemodynamic model to generate the conventional functional connectivity (FC) matrix. By computing the difference between the simulated (FCS) and empirical FC matrices (FCR), both local coupling weights (WEI, WIE) and inter-region connection strength (W12, W13, …; Fig. 1) can be estimated using a stochastic optimization.
Fig. 1.
A multiscale neural modeling framework to study pathophysiological mechanisms of MDD.
We applied this modeling framework to solve a real clinical problem, i.e., identification of potentially abnormal intra-regional and inter-network interactions in major depressive disorder (MDD), a devastating mental disorder without clear neuropathological mechanism but causing severe personal distress and tremendous cost to the society. Results indicate that the MDD patients might have disrupted recurrent excitation/inhibition in the dorsal lateral prefrontal cortex (dlPFC) as well as abnormally elevated excitation in the thalamus, consistent with experimental/clinical observations and the hypothetical MDD models [9, 10]. Our method offers a new multiscale modeling approach to understand brain cognitive functions and their deteriorations in various neurological and psychiatric disorders.
2. Methods
2.1. Data Acquisition and Pre-processing
Structural Connectivity.
The structural connectivity (SC) matrix was derived based on the probabilistic tractography with the diffusion MRI data from the Human Connectome Project. Tissue segmentation was performed using the T1-weighted image (aligned with the diffusion MRI data) based on Freesurfer using the pipeline described in [11]. After preprocessing, the probabilistic tractography [12] was employed in the diffusion MRI’s native space using the 2nd order integration over fiber orientation distributions (iFOD2) algorithm (considering fiber crossing) to reconstruct two million streamlines within the whole brain with random seeds and the output fiber tracks were cropped at the grey matter-white matter interface. Finally, based on the tractography result and the Desikan-Killiany atlas that includes 84 regions of interest (ROIs) [13], we calculated an 84 × 84 structural connectivity matrix as a prior of the inter-network connectivity. The SC matrix was normalized by the largest streamline number within the matrix.
FMRI Data Acquisition and Pre-processing.
The fMRI data was obtained from a single-center, large-cohort first-episode, treatment-nïve MDD resting-state fMRI database, consisting of 66 MDD adults and 66 matched normal controls (NC) [14]. The data was acquired with a 3.0-T scanner and preprocessed using a widely adopted pipeline (http://rfmri.org/DPARSF). FC between any pair of the selected brain regions were calculated according to the Desikan-Killiany atlas using Pearson’s correlation between regional averaged BOLD rs-fMRI time series.
2.2. Neural Mass Model
As a proof of concept, we included eight pre-defined ROIs selected from the default mode (DMN), executive control (EXE), salience (SAL) and limbic (LIM) networks according to the Desikan-Killiany atlas. They were chosen based on the hypothetical MDD neuropathology [15, 16] and two representative ROIs were chosen for each functional network [DMN: medial prefrontal cortex (mPFC) and posterior cingulate cortex (PCC); EXE: dorsal lateral prefrontal cortex (dlPFC) and superior parietal cortex (sPar); SAL: dorsal anterior cingulate cortex (dACC) and insula; LIM: thalamus (Thal) and amygdala (Amyg)]. It is generally accepted that the functional interactions among these networks are altered in MDD [17]. Of note, more regions could be easily included in the future as a natural extension of our method proposed in a general form.
The regional brain dynamics are modeled by the biologically motivated nonlinear Wilson-Cowan oscillator [8]. The population-level activity of the jth region is governed by the following two equations [18]:
| (1) |
| (2) |
where Ej and Ij are the mean firing rates of the excitatory and inhibitory neuron populations in brain region j, τe and τi are the excitatory and inhibitory time constants (0.01 and 0.02 s, respectively), WEE, WEI and WIE are the local connection strength (3.0), P is a constant external excitatory input (0.3), and ξ(t) is random additive noise following a normal distribution centering at 0 with standard deviation of 0.2. It is important to mention that the constant input P and noisy input ξ(t) represent the extrinsic inputs from other un-modeled brain regions to allow the generalization ability of the model. The long-range connectivity strength from region k to region j is represented by Wkj (and that from region j to k is Wjk, with Wkj = Wjk) that was derived from the empirical structural connectivity and scaled by an inter-network coupling factor CLM (5.0; from network L to network M). The nonlinear response function S is modeled as a sigmoid function (μ = 1.0; σ = 0.25). The default model parameters given above are adapted from previous study [18] and were initial values for recurrent excitation (WEE) and inhibition (WIE) weights and the inter-network coupling factor (CLM); their actual values were estimated using stochastic optimization (Sect. 2.4).
2.3. Hemodynamic Model
The hemodynamic response of each ROI is computed by convolving the mean firing rates of the local excitatory and inhibitory neural populations with the canonical hemodynamic response function (HRF) as defined in Eqs. 3-8 with parameters taken from [4]. Specifically, for each region jth, the neuronal activity xj (Ej and Ij) drives a vasodilatory signal sj that is subject to auto-regulatory feedback. Blood flow fj responds in proportion to the vasodilatory signal and leads to change in blood volume νj and deoxyhemoglobin content qj. The hemodynamic state equations are given by [4]:
| (3) |
| (4) |
| (5) |
| (6) |
The oxygen extraction O is a function of flow:
| (7) |
where ρ is the resting oxygen extraction. The simulated BOLD signal is taken to be a static nonlinear function of volume and deoxyhemoglobin that depends on the relative contribution of intravascular and extravascular components:
| (8) |
where ν0 is the resting blood volume fraction, and k1, k2 and k3 are the intravascular, concentration and extravascular coefficients, respectively. The neural activity from excitatory populations and inhibitory populations are summed up within each region with respective weighting (excitatory: 2/3; inhibitory: 1/3) to obtain the full BOLD time series [19] that will be used to calculate simulated FC matrix.
2.4. Stochastic Optimization of Model Parameters
A total of 22 model parameters were optimized, including 8 recurrent excitation (WEE) and 8 recurrent inhibition (WIE) weights (one for each ROI) as well as six inter-network scaling coupling factors (CLM) among the four functional networks. We used an expectation-maximization (EM) algorithm, a stochastic optimization method, to estimate the model parameters [4, 7]. The initial values of the model parameters were set to be: , which resulted in balanced excitation and inhibition. The optimization is to iteratively update the model parameter sets until they lead to the smallest L2 norm error between the empirical (observable, calculated using rs-fMRI data) and simulated FC matrices for each subject. For more details, see [7]. The maximum iteration steps were set to be 256, but we observed good convergence within 256 steps for all the subjects.
2.5. Numerical Integration
The neural mass model and the hemodynamic model were simulated using the 4th order Runge-Kutta (RK) scheme with an integration step of 5 ms. We simulated the network for a total of 80 s, and the first 20 s of the BOLD signals was discarded to remove transient effects. The optimization procedure with model simulation were coded with MATLAB (R2018b) and run at a high performance computer cluster. Please note that we only simulated 80 s BOLD signals as a proof-of-concept study, but it can be easily extended to longer simulated BOLD signals under the same framework.
2.6. Statistical Test
We used two-sample t-test to compare the estimated model parameters from the NC and MDD groups. The significant level was set to a false discovery rate (FDR) of q < 0.1 (a relatively loose threshold but strictly corrected for multiple comparisons).
3. Experiments and Results
3.1. Simulated Model Responses
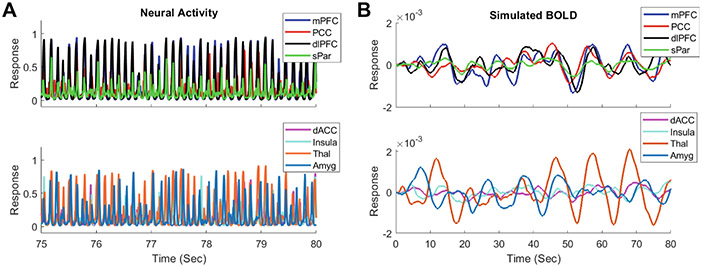
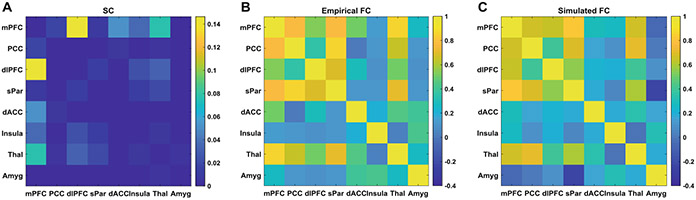
All the 22 parameters in the multiscale neural model were successfully estimated for each of the NCs and MDDs. The average minimal error was similar (p > 0.5) between NC (1.28 ± 0.2) and MDD (1.26 ± 0.22). A segment of activity of the excitatory neural populations within the eight ROIs with corresponding BOLD signals for the best matched subject (similar results for other subjects) are respectively shown in Figs. 2A and B. Both the neural activity and BOLD signals displayed rhythmic fluctuations, and high levels of neural activity led to larger amplitude of BOLD signals (e.g., thalamus). Note that it is the correlation among simulated BOLD signals, rather than the raw time series of BOLD signals determined how the parameters were updated in stochastic optimization. The normalized structural connectivity of the eight ROIs is shown in Fig. 3A. The empirical and simulated FC matrices are shown in Figs. 3B and 3C, respectively, and they are highly similar (Pearson’s correlation: 0.93; L2 norm error: 0.78).
Fig. 2.
Simulated neural activity and BOLD signals. (A) A segment of simulated activity of excitatory neural populations from the eight ROIs for the best matched subject. (B) Simulated BOLD signals from the eight ROIs for the best matched subject.
Fig. 3.
Structural connectivity and functional connectivity. (A) Normalized structural connectivity among the eight ROIs. (B) Empirical functional connectivity (FC) for the best matched subject. (C) Simulated FC for the best matched subject.
3.2. Estimated Parameters of Multiscale Neural Model
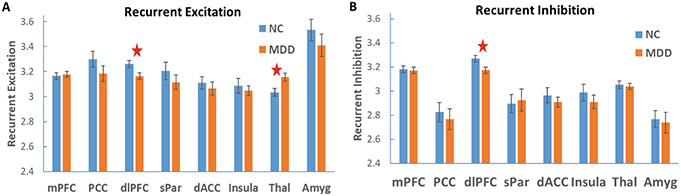
The average recurrent excitation and inhibition weights of the eight ROIs are shown in Figs. 4A and 4B, respectively. We noticed that the amygdala exhibited the largest recurrent excitation with the lowest recurrent inhibition, which may be due to the important role of amygdala in emotion processing and neurochemical control. Among the eight ROIs, the recurrent excitation in the dlPFC was significantly reduced in the MDDs, while the recurrent excitation in the thalamus was abnormally elevated in the MDDs compared to the NCs (Fig. 4A). In addition, the current inhibition weight within the dlPFC was also significantly decreased in the MDDs (Fig. 4B). It is worth noting that we did not observe significant difference in any inter-network connectivities between the two groups (results not shown). Such findings confirm the importance of modeling regional cellular and circuit interactions in detection of imaging biomarkers of mental disorders.
Fig. 4.
Average estimated model parameters for the NC and MDD groups. (A) Average recurrent excitation weight within the eight ROIs. (B) Average recurrent inhibition weight within the eight ROIs. Error bars indicate standard error. Connection weights with significant group difference are denoted with red stars.
4. Discussions
In this study, we developed a Multiscale Neural Model Inversion (MNMI) framework that enabled the integration of microscale cellular/circuit interactions with macroscale network dynamics and estimation of both local coupling weight and inter-regional connection strength using rs-fMRI data. By applying the MNMI framework to rs-fMRI data collected from normal control and depressive subjects, we observed that depression could be associated with reduced excitation and inhibition in the dlPFC as well as increased excitation in the thalamus. Our findings are consistent with decreased glucose metabolism in the dlPFC measured by positron emission tomography (PET, an invasive imaging technique) in MDD [9]. The potential biomarker of imbalanced excitation and inhibition mirrors a common clinical practice for effective MDD treatment using transcranial magnetic stimulation (TMS) targeting at the left dlPFC to persistently increase its excitation [20]. In addition, in an fMRI experiment involving negative picture–caption pairs versus positive picture–caption pairs, the thalamus showed greater responses in MDD patients compared to controls [10], thus supporting the elevated recurrent excitation found by our model. Moreover, due to the essential role of the thalamus in generating cerebral oscillations [21], increased thalamic excitation may be responsible for abnormal thalamocortical oscillations as observed in MDD [22].
Overall, the MNMI framework is able to better characterize potential intra-regional pathophysiological mechanisms of MDD than the traditional FC analysis that only focuses on inter-regional co-activity. In addition, it provides a feasible approach to estimate the parameters of neural mass models based on empirical fMRI data, which contributes to better multiscale neural mass analysis. By using more biophysically realistic neuronal models and circuits in future, this modeling framework holds the promise to provide mechanistic insights into neuroanatomy, circuit dynamics and pathophysiology in neuroimaging studies.
Acknowledgements.
This work was supported in part by NIH grants MH108560, EB022880, AG042599, and AG041721.
References
- 1.Sporns O: Contributions and challenges for network models in cognitive neuroscience. Nat. Neurosci 17(5), 652–660 (2014) [DOI] [PubMed] [Google Scholar]
- 2.van den Heuvel MP, Hulshoff Pol HE: Exploring the brain network: a review on resting-state fMRI functional connectivity. Eur. Neuropsychopharmacol 20(8), 519–534 (2010) [DOI] [PubMed] [Google Scholar]
- 3.Li K, et al. : Review of methods for functional brain connectivity detection using fMRI. Comput. Med. Imaging Graph 33(2), 131–139 (2009) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Friston KJ, Harrison L, Penny W: Dynamic causal modeling. NeuroImage 19(4), 1273–1302 (2003) [DOI] [PubMed] [Google Scholar]
- 5.Marreiros AC, Kiebel SJ, Friston KJ: Dynamic causal modelling for fMRI: a two-state model. NeuroImage 39(1), 269–278 (2008) [DOI] [PubMed] [Google Scholar]
- 6.Friston KJ, et al. : Dynamic causal modelling revisited. NeuroImage 199, 730–744 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang P, Kong R, Kong X, et al. : Inversion of a large-scale circuit model reveals a cortical hierarchy in the dynamic resting human brain. Sci. Adv. 5(1), eaat7854 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wilson HR, Cowan JD: Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J 12(1), 1–24 (1972) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kimbrell TA, et al. : Regional cerebral glucose utilization in patients with a range of severities of unipolar depression. Biol. Psychiatry 51(3), 237–252 (2002) [DOI] [PubMed] [Google Scholar]
- 10.Kumari V, et al. : Neural abnormalities during cognitive generation of affect in treatment-resistant depression. Biol. Psychiatry 54(8), 777–791 (2003) [DOI] [PubMed] [Google Scholar]
- 11.Smith RE, et al. : Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage 62 (3), 1924–1938 (2012) [DOI] [PubMed] [Google Scholar]
- 12.Tournier J, Calamante F, Connelly A: Improved probabilistic streamlines tractography by 2nd order integration over fibre orientation distributions. In: Proceedings of the 18th Annual Meeting of the International Society for Magnetic Resonance in Medicine (ISMRM), Stockholm, Sweden, p. 1670 (2010) [Google Scholar]
- 13.Desikan RS, et al. : An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. NeuroImage 31(3), 968–980 (2006) [DOI] [PubMed] [Google Scholar]
- 14.Zheng Y, et al. : Treatment-nïve first episode depression classification based on high-order brain functional network. J. Affect. Dis 256, 33–41 (2019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Pandya M, et al. : Where in the brain is depression? Curr. Psychiatry Rep 14(6), 634–642 (2012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Price JL, Drevets WC: Neurocircuitry of mood disorders. Neuropsychopharmacology 35 (1), 192–216 (2010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dutta A, McKie S, Deakin JF: Resting state networks in major depressive disorder. Psychiatry Res. Neuroimaging 224(3), 139–151 (2014) [DOI] [PubMed] [Google Scholar]
- 18.Abeysuriya RG, et al. : A biophysical model of dynamic balancing of excitation and inhibition in fast oscillatory large-scale networks. PLoS Comput. Biol 14(2), e1006007 (2018) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Becker R, et al. : Relating alpha power and phase to population firing and hemodynamic activity using a thalamo-cortical neural mass model. PLoS Comput. Biol 11(9), 1–23 (2015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Leuchter AF, et al. : The relationship between brain oscillatory activity and therapeutic effectiveness of transcranial magnetic stimulation in the treatment of major depressive disorder. Front. Hum. Neurosci 7, 37 (2013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li G, Henriquez CS, Fröhlich F: Unified thalamic model generates multiple distinct oscillations with state-dependent entrainment by stimulation. PLoS Comput. Biol 13(10), e1005797 (2017) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Llinás RR, et al. : Thalamocortical dysrhythmia: a neurological and neuropsychiatric syndrome characterized by magnetoencephalography. Proc. Natl. Acad. Sci. U.S.A 96(26), 15222–15227 (1999) [DOI] [PMC free article] [PubMed] [Google Scholar]