Origin of enantioselectivity reversal in Lewis acid-catalysed Michael additions relying on the same chiral source

Abstract

Enantiodivergence is an important concept in asymmetric catalysis that enables access to both enantiomers of a product relying on the same chiral source as reagent. This strategy is particularly appealing as an alternate approach when only one enantiomer of the required chiral ligand is readily accessible but both enantiomers of the product are desired. Despite the potential significance, general catalytic methods to effectively reverse enantioselectivity by changing an achiral reaction parameter remain underdeveloped. Herein we report our studies focused on elucidating the origin of metal-controlled enantioselectivity reversal in Lewis acid-catalysed Michael additions. Rigorous experimental and computational investigations reveal that specific Lewis and Brønsted acid interactions between the substrate and ligand change depending on the ionic radius of the metal catalyst, and are key factors responsible for the observed enantiodivergence. This holds potential to further our understanding of and facilitate the design of future enantiodivergent transformations.

Enantiodivergence is an important concept in asymmetric catalysis that enables access to both enantiomers of a product relying on the same chiral source as reagent.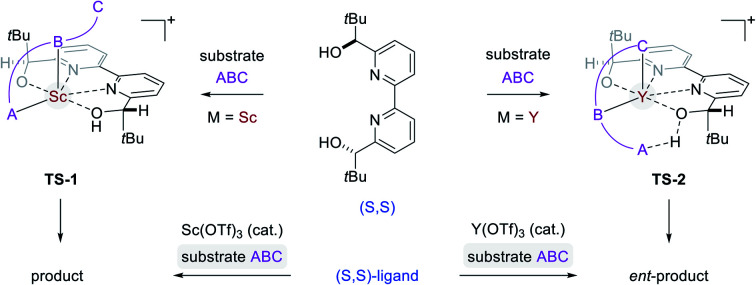

Introduction

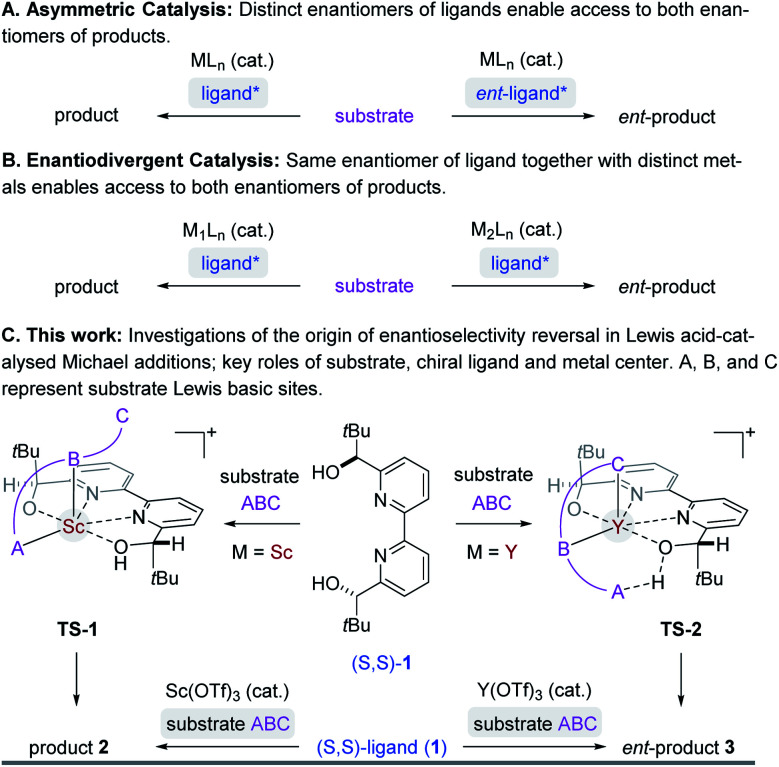
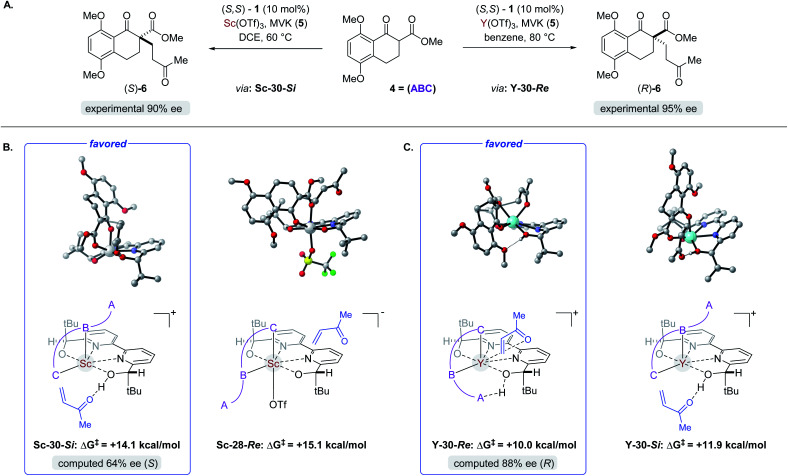
Asymmetric synthesis enables access to enantioenriched complex molecules which is particularly desirable as distinct enantiomers can exhibit different biological activity. In asymmetric catalysis,¹ chiral induction is often conferred by optically active molecules of natural origin that function as ligands² in metal complexes (Fig. 1A). Consequently, the most straightforward synthetic route to both enantiomers of a target structure requires access to both enantiomers of a chiral catalyst. However, many naturally occurring chiral pool reagents³ used to synthesize chiral ligands are often available in only one absolute configuration, which greatly hampers efficient access to both enantiomers.⁴ Enantiodivergent catalytic strategies⁵ can represent intriguing alternatives to overcome this limitation by transferring chirality of a single chiral source to selectively obtain either enantiomer of a product (Fig. 1B). Several reports observing a reversal in enantioselectivity with the same chiral source exist, including the use of distinct metals,⁶ counterions,⁷ the introduction of subtle structural modifications of the catalyst system,⁸ or simply changes in solvent or temperature.⁹ Unfortunately, often only one of the two enantiomers is obtained in high enantiomeric excess since it is difficult to induce large energetic differences between transition states (TS) that lead to the competing products required for effective enantiodivergence. Consequently, the design of general asymmetric methods that allow for complete reversals in enantioselectivity continues to be a challenge while their controlling features remain poorly understood.^5e,f,6 We recently developed an efficient synthetic strategy towards the meroterpenoids (+)- and (−)-lingzhiol¹⁰ that relies on an enantiodivergent Michael addition reaction catalysed by Lewis acid complexes formed between (S,S)-bipyridine 1 and either scandium- or yttrium triflate (Fig. 1C).¹¹ This approach is unique in that both enantiomers of a product (6) are accessible with an enantiomeric excess of ≥90%.^12–16 We herein report detailed studies that integrate experimental and computational tools to understand the origin of this highly efficient reversal of enantioselectivity. Given the prominence of Lewis acids in asymmetric catalysis, we expect that the insights described in this report will enable the design and development of general synthetic strategies to achieve high levels of enantiodivergence in other transformations.

Fig. 1. Select strategies in asymmetric catalysis to access both enantiomers of product.

Results and discussion

Initial reaction optimization

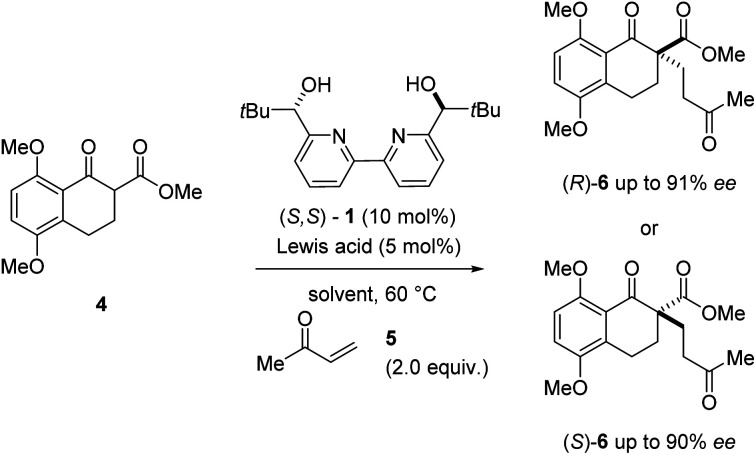
During our efforts towards the enantioselective total synthesis of (+)- and (−)-lingzhiol,¹¹ we investigated the conjugate addition between β-ketoester 4 and methyl vinyl ketone 5 catalysed by Sc(OTf)₃ and bipyridine ligand 1 under conditions initially reported by Kobayashi and coworkers.¹⁷ Although the reaction proceeded with high enantiomeric excess of 90%, product formation advanced slowly and only resulted in the formation of the Michael adduct (S)-6 in 31% yield (entry 1, Table 1). In an effort to improve the conversion of this transformation, we evaluated a variety of metal triflates to identify higher-yielding conditions for the formation of Michael adduct 6. Indeed, higher yields and conversions were observed with Dy(OTf)₃, Y(OTf)₃, and La(OTf)₃ in 88%, 92%, and 93% yield, respectively in shorter overall reaction times while moderate to good enantioselectivities of up to 76% ee were obtained (entries 3, 5, and 7, Table 1). Interestingly, catalytic amounts of Dy(OTf)₃ and Y(OTf)₃ favored the R enantiomer of product 6 when compared to Sc(OTf)₃ (which favored (S)-6) despite relying on the same enantiomer of ligand 1 (S,S-1).¹⁸ In subsequent efforts, we focused on the evaluation of additional solvents and observed improved enantioselectivities for Y(OTf)₃ and Dy(OTf)₃ with 91% ee and 90% ee, respectively when switching to benzene while high yields were maintained (entries 4 and 6, Table 1). In comparison, catalytic amounts of Sc(OTf)₃ in benzene under otherwise identical conditions did not result in the formation of Michael adduct 6 even after extended reaction times (entry 2, Table 1).

Performance of select metal triflates in the enantioselective Michael reaction compared to the individual metals' ionic radii^a.

Entry	Metal ion	r (Å)	Solvent	Time (h)	Yield 6 (%)	ee (%)
1	Sc3+	0.870	DCE	96	31	90 (S)
2			Benzene	96	Trace	—
3	Y3+	1.019	DCE	18	92	71 (R)
4			Benzene	18	91	91 (R)
5	Dy3+	1.027	DCE	17	88	76 (R)
6			Benzene	17	83	90 (R)
7	La3+	1.160	DCE	14	93	60 (S)
8			Benzene	14	97	43 (S)

^aConditions: 10 mol% 1 and 5 mol% M(OTf)₃ were pre-stirred at 60 °C (1 h). Reactions were performed on 0.15 mmol scale in the listed solvent (0.02 M) at 60 °C for the listed time.

Metal ionic radii

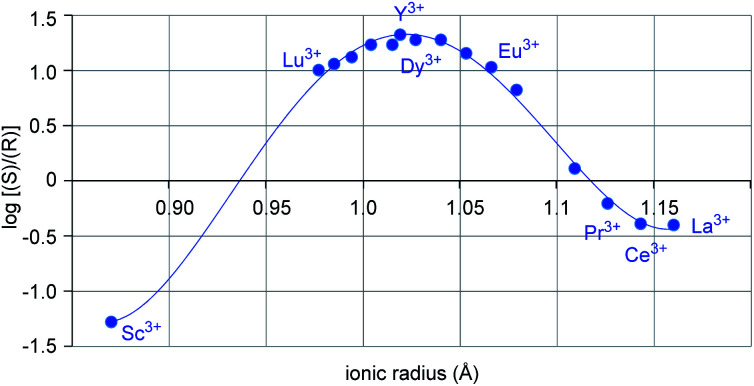
Metal-dependent reversal of enantioselectivity has been previously attributed to the distinct ionic radii of the central metal.⁵ Table S1 (ESI†) correlates the optimal reaction conditions identified for the selective formation of either enantiomer of 6 together with the respective ionic radius of the lanthanide. While dichloroethane proved superior as solvent with the smaller scandium metal centre, no formation of the desired product was observed in benzene, presumably due to the low solubility of the Lewis acid catalyst (entries 1–2, Table 1).¹⁹ In comparison, the larger yttrium-based catalyst displayed superior reactivity in benzene (entries 3–4, Table 1). Moreover, when the log of the enantiomeric ratio of product 6 is plotted against the ionic radius of the metal catalyst, a bell-shaped curve is observed (Fig. 2). This is consistent with previous literature reports correlating ionic radii to enantiomeric excess.^6a–c Interestingly, the formation of the (S)-6 enantiomer is strongly favored with the small scandium metal while increasing the ionic radius to 1.019 Å in yttrium leads to the selective formation of the opposite enantiomer (R-6). However, a further increase in metal ionic radii reverses this trend to favor the formation of the S-enantiomer albeit with lower enantioselectivities. These observations indicate that the choice of central metal significantly changes the chiral environment. Based on these data alone, it cannot be concluded how the choice of metal has such a strong impact on the configuration of product 6, leading us to undertake further studies into this phenomenon.

Fig. 2. Plot of log(e.r.) vs. ionic radii of distinct lanthanides.

Nonlinear effect studies

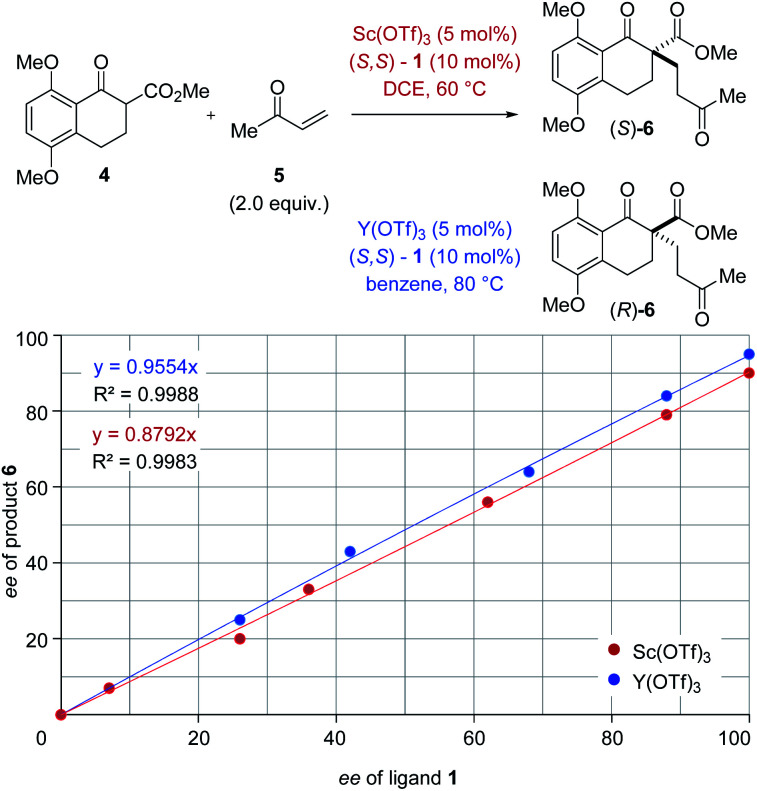
The origin of enantiodivergence in metal-controlled reversals of enantioselectivity is often attributed to distinct coordination modes characteristic of larger and smaller metals.^6a–c,e However, a reversal of enantioselectivity has also been observed due to the formation of metal–ligand aggregates or metal complexes varying in their metal to ligand ratio.²⁰ To gain additional insights into the controlling features of this enantiodivergent Michael addition, we conducted nonlinear effect studies²¹ with scandium- and yttrium-based Lewis acids (Fig. 3). Importantly, both scandium- and yttrium-catalysed reactions show a linear relationship between enantiomeric excess of ligand and enantiomeric excess of the Michael adduct 6 (Fig. 3). This result is consistent with one equivalent of the chiral ligand 1 being incorporated in the catalytically active species in both the scandium- and yttrium-catalysed reaction pathways.

Fig. 3. Nonlinear effect studies of the scandium- and yttrium-catalysed enantiodivergent Michael addition with (S,S)-1 ligand.

Kinetic studies

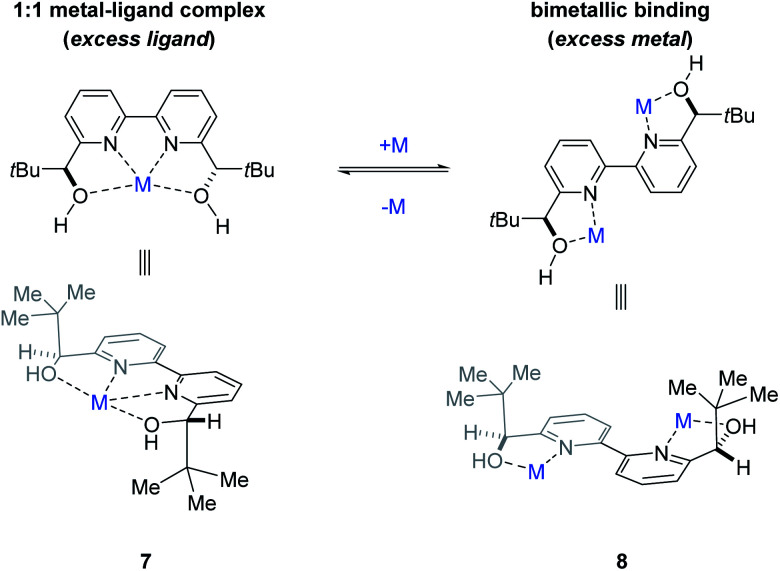
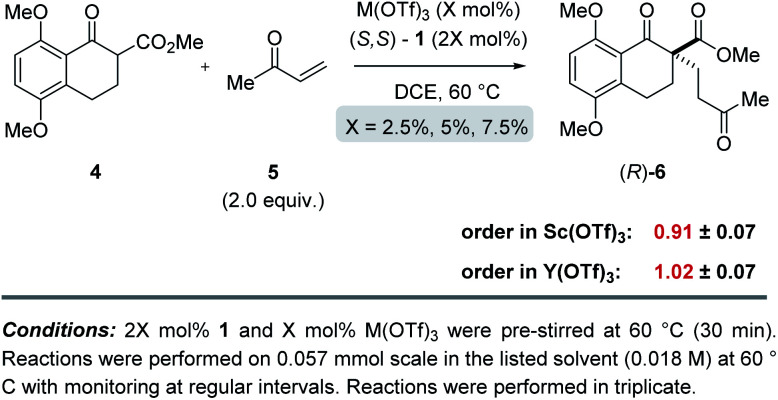
To determine whether more than one equivalent of the Lewis acidic metal is involved in the active catalyst, we conducted kinetic investigations of both the scandium- and yttrium-catalysed transformations. Importantly, previous studies focused on aqueous Mukaiyama aldol reactions relying on bipyridine 1 as chiral ligand and Bi(OTf)₃ as Lewis acid, Kobayashi and coworkers observed that excess ligand was required to maintain high enantioselectivity of the product formed.²² Specifically, their studies showed that a 1 : 1 metal–ligand complex (7) was favoured when excess ligand was present while additional metal promoted a competing bimetallic binding mode 8 (Fig. 4). In comparison, our own initial ¹H-NMR studies that followed the chemical shift of the characteristic methine proton of the ligand are consistent with tetradentate binding mode 7 of the bipyridine 1 to both scandium and yttrium (see ESI† for details). To gain additional support for this hypothesis, we conducted subsequent kinetic investigations of the enantiodivergent Michael addition. Specifically, we opted to study the initial rates of these reactions in dichloroethane at 60 °C as both Lewis acids, Y(OTf)₃ and Sc(OTf)₃ form effective catalysts while maintaining the observed reversal of enantioselectivity (entries 1–4, Table 1) despite the deviation from the optimal solvent and temperature for the Y(OTf)₃-catalysed reaction. In our studies, 2.5%, 5%, and 7.5% loadings of each metal catalyst were investigated and the superior 2 : 1 ligand to metal ratio previously identified during reaction optimization was maintained. For the comparatively fast Y(OTf)₃-catalysed transformation, the yield of product formed was monitored by UPLC analysis in 3 minute intervals over 30 minutes. Based on the results obtained, the order in Y(OTf)₃ was determined to be 1.02 (Fig. 5). In comparison, the scandium-catalysed reaction proceeding with a slower rate was monitored in 30 minute intervals for 7 hours and the order of the reaction in catalyst was determined to be 0.91 (see ESI† for additional details on kinetic studies). Taken together, the ¹H-NMR and first-order kinetics²³ observed in our kinetic studies are consistent with a tetradentate monometallic binding mode 7 for both the scandium- and yttrium-based catalyst systems.

Fig. 4. Potential metal–ligand binding modes between the metal and ligand 1.

Fig. 5. Kinetic investigations of the scandium- and yttrium-catalysed enantiodivergent Michael addition.

Ligand structure

To further understand the structural elements required to maintain high ee and mediate a reversal of enantioselectivity, we next studied various pyridine-derived ligands (Table 2). In comparison to bipyridine 1, bidentate and tridentate ligands 9 and 10 failed to form enantiomerically enriched Michael adduct 6 with either Y(OTf)₃ or Sc(OTf)₃. These results suggest that the tetradentate binding mode of ligand 1 is an important feature for enantioinduction. Similarly, methyl ether ligand 11 resulted in the formation of racemic 6 with both scandium- and yttrium-based Lewis acids, suggesting that the free alcohol moieties are critical for the induction of chirality. More electron-rich methoxy-substituted ligand 12 afforded higher yields and faster reaction times with minimal loss of enantiomeric excess. We attribute this enhanced reactivity to a more electron-rich metal centre upon binding to 12 leading to a more reactive metal enolate¹⁷ in both the scandium- and yttrium-catalysed reactions. Finally, conformationally locked phenanthroline-derived ligand 13 similarly showed a reversal of enantioselectivity for substrate 6. Importantly, unlike ligands 1 and 12, phenanthroline 13 cannot undergo rotation around its central bond and as a result is unable to adopt a twisted conformation for a bimetallic binding mode (8, Fig. 4). Together with the NMR and kinetic studies, these results suggest that (1) a conformational change in the bipyridine ligand is not responsible for the reversal of enantioselectivity and that (2) both scandium and yttrium metal centres interact with the bipyridine ligand to form a 1 : 1 metal–ligand complex.

Evaluation of structural requirements of pyridyl ligands.

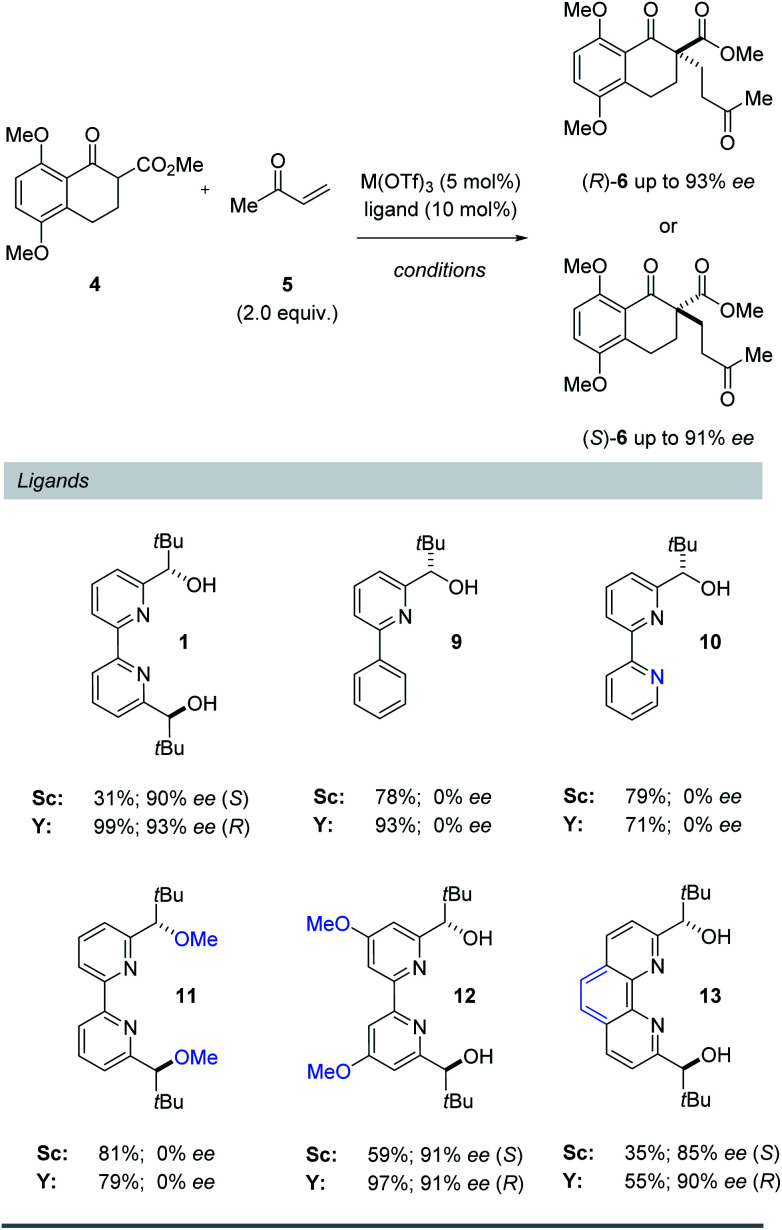
Substrate structure

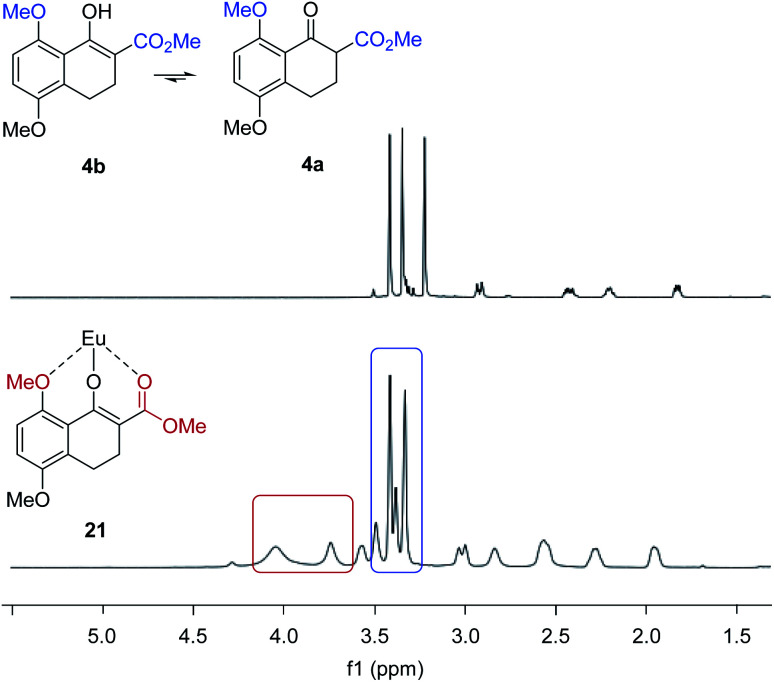
We next evaluated the effect of the substrate on the reversal of enantioselectivity in asymmetric Michael reactions. Specifically, aromatic β-ketoester substrates differing in their aromatic substitution pattern were evaluated (Table 3). Importantly, the scandium-catalysed transformation generally afforded high enantioselectivities (6, 16–20, Table 3) which is consistent with the initial report by Kobayashi and coworkers¹⁷ and demonstrates that the ortho-methoxy substituent is not necessary to achieve high enantioselectivity with this catalyst system. In comparison, the yttrium-catalysed reaction was generally high-yielding, resulting in up to 99% yield of products 6 and 16–20. However, Michael adducts 17 and 19 bearing methoxy substituents in the meta position were formed in low enantiomeric excess of 17% ee and 13% ee, respectively. Similarly, para-methoxy substituted indanone 20 was formed in low enantiomeric excess of 24%, as was the meta, para-substituted dimethoxy product 18 (7% ee). Interestingly, those substrates containing substitution in the ortho position afforded the desired Michael adducts (16, 6, Table 3) in high enantioselectivities of 90% and 95%. Importantly, for all substrates investigated the major enantiomer formed under the Y(OTf)₃-catalysed reaction conditions was opposite to that formed relying on Sc(OTf)₃. To further investigate the unique impact of the ortho substituents, we conducted ¹H-NMR studies on Eu(fod)₃ as an NMR-shift reagent.²⁴ Importantly, Eu³⁺ has an ionic radius of 1.066 Å that is comparable in size to that reported for Y³⁺ with 1.019 Å. Additionally, our initial reaction optimization showed that Eu(OTf)₃ resulted in the formation of product 6 with similar yield and enantiomeric excess compared to Y(OTf)₃ (entries 6 and 15, ESI Table S6†). When substrate 4 was treated with Eu(fod)₃ in d₆-benzene, two new methoxy signals were observed in the ¹H-NMR spectrum, which suggests a three-point binding of the substrate to the europium metal centre (21, Fig. 6). This result is consistent with the hypothesis that the ortho-substituent can also interact with the catalyst. Thus, the substrate structure plays an important role in the observed enantiodivergence.

Evaluation of differentially MeO-substituted aryl β-keto-ester substrates.

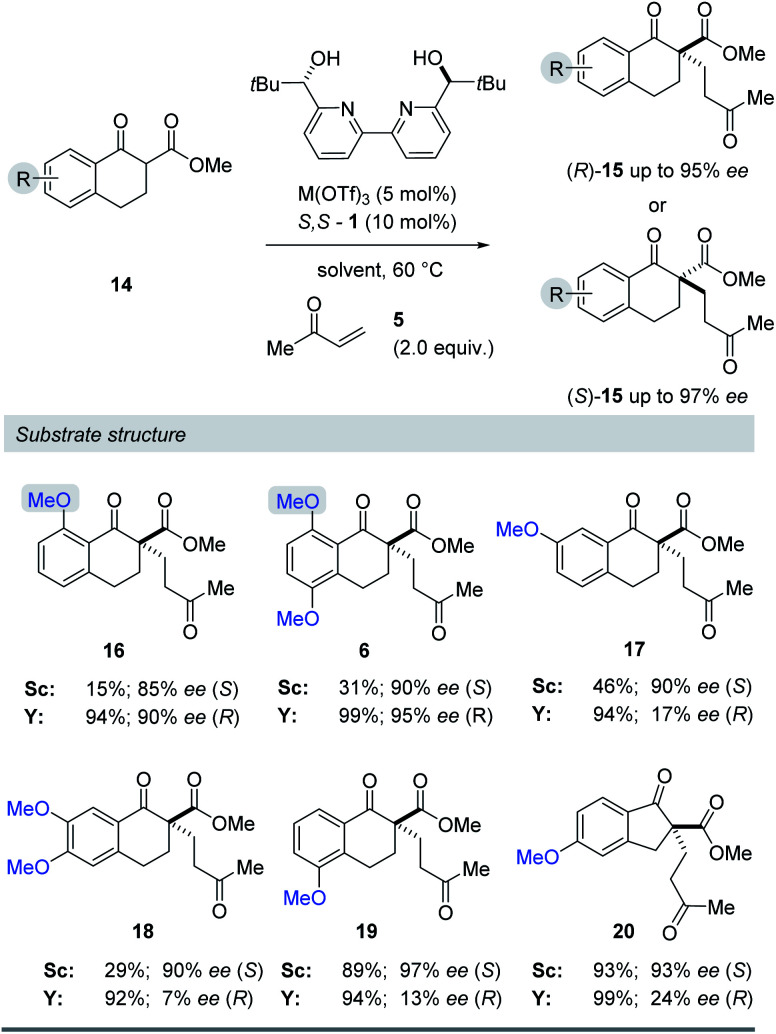
Fig. 6. Eu(fod)₃ NMR shift reagent induces chemical shifts of the methyl groups in β-ketoester substrate 4.

Computational analysis

These mechanistic experiments provided a firm basis for computationally exploring the precise interactions determining the metal dependent selectivity outcomes. Specifically, we employed DFT calculations as such techniques have become powerful tools for the mechanistic interrogation of reactions including those catalysed by Lewis acids.²⁵ However, we anticipated that the investigation of the chiral Lewis acid complexes identified as optimal in this study would entail several additional challenges. Specifically, the possibility of multiple catalytically competent species in solution would render the control and interpretation of experimental outcomes difficult. Thus, we aimed to restrict the computational analysis²⁶ to the expected enantiodetermining step in which the stereogenic centre is formally set during the Michael addition. Stationary points relevant to this step were located using M06 density functional using a mixed basis set of SDD for yttrium and 6-31G(d,p) for all other atoms; for scandium the same functional was deployed with the 6-31G(d,p) basis set. Solvation free energy corrections were computed by means of single point energy calculations at the same level of theory with the IEFPCM model.

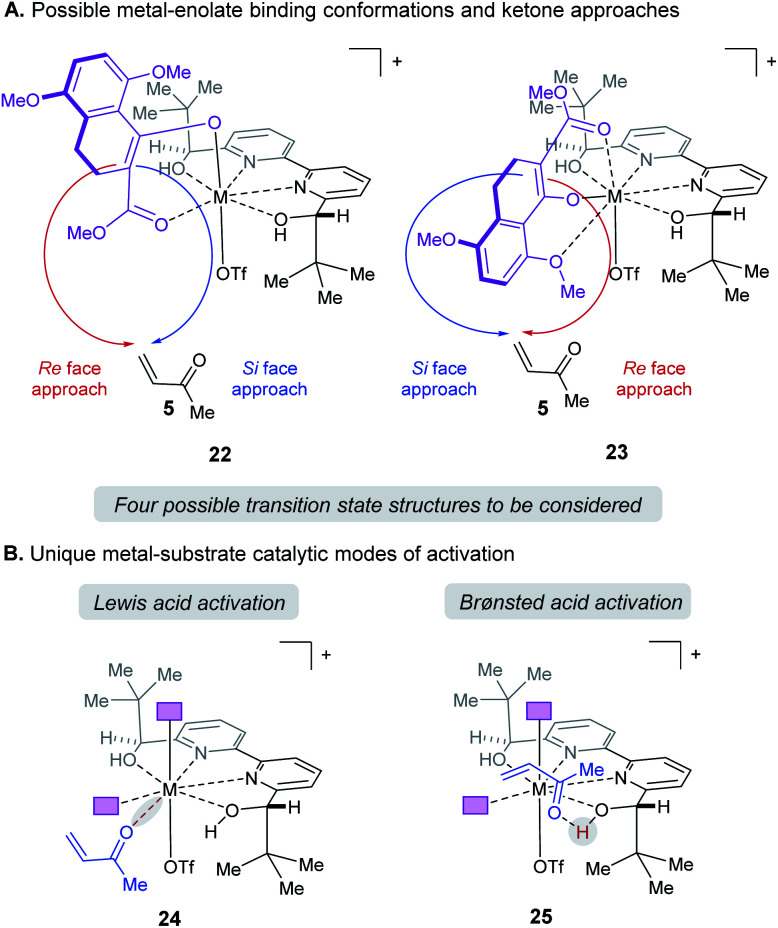
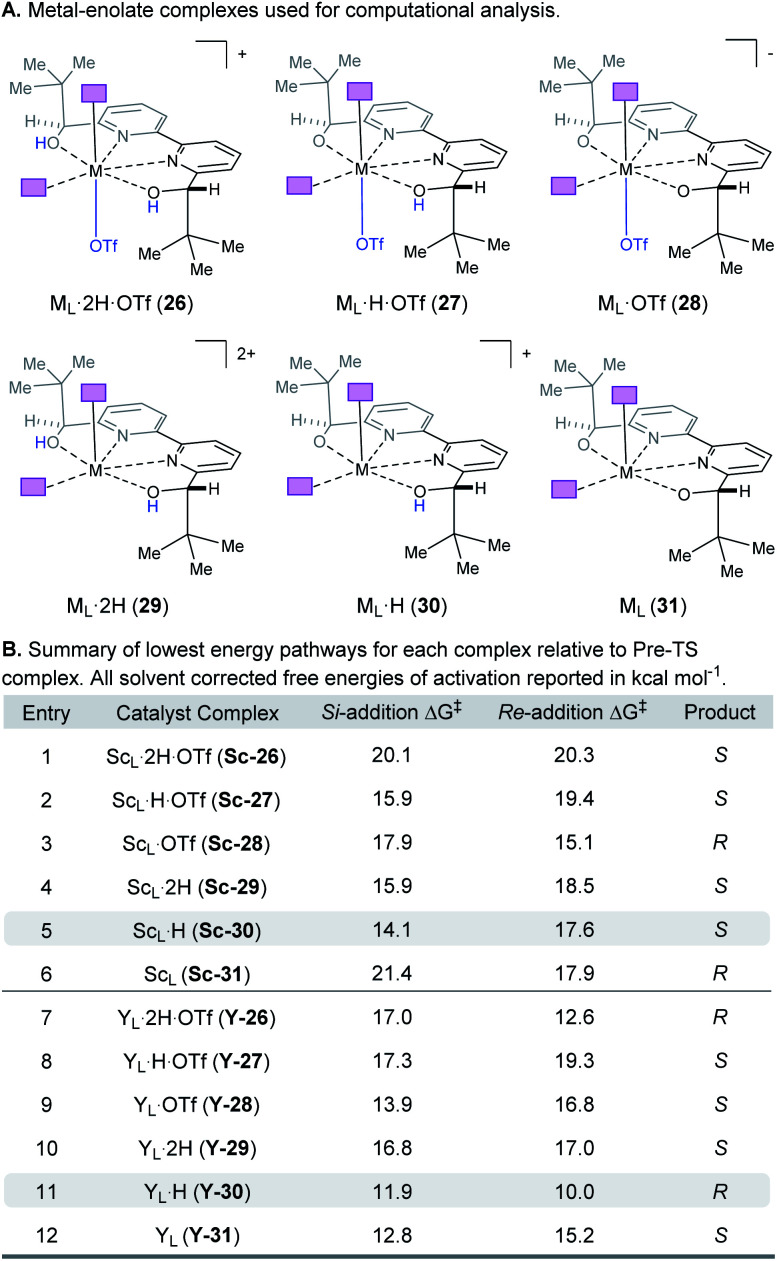
When modeling this enantiodetermining step, we identified two ways in which the enolate could orient itself with respect to the catalyst: the aromatic group can be directed away from the axial triflate ligand (22) or towards it (23) as shown in Fig. 7A. Additionally, the electrophile 5 can approach from either the Re or Si face. Combining these considerations, four classes of TS are formulated for this catalytic species. Furthermore, as part of the exploration of the TS conformations within each of the classes, we identified two possible modes of bifunctional activation (Fig. 7B) in which the catalyst can interact with both the nucleophile (4) and electrophile (5): (1) a Lewis acid mediated mechanism, in which the carbonyl of 5 is activated by direct coordination with the metal centre (24), and (2) a Brønsted acid type mechanism in which substrate 5 is activated by hydrogen bonding between the carbonyl and the hydroxy protons of the metal–ligand complex (25). Further complicating our analysis, ligand exchange between the bipyridine and triflate can lead to a number of catalytically active species which differ in triflate coordination number and ligand protonation state (26–31, Fig. 8). By assuming that the ligand bound Lewis acid species are in equilibrium at 60–80 °C, Curtin–Hammett conditions²⁷ should apply and, therefore, the favored pathway is determined by the absolute energies of the transition state (TS).²⁸ As all species are assumed to be in solution, it is important to note that the lowest-energy transition state leading to the (R)-enantiomer of product 6 may be of a different binding mode, electrophile activation mode, ligand protonation state or triflate binding number than that affording the (S)-enantiomer. The calculated enantioselectivity arises from comparing these two lowest-energy pathways leading to either the (R)- or (S)-enantiomer.

Fig. 7. (A) Enantiomers arise from enolate conformation and substrate facial approach. (B) Illustration of the relevant catalytic modes of activation for protonated ligands. Purple boxes denote enolate substrate.

Fig. 8. (A) Complexes investigated computationally. (B) Lowest energy pathways for each complex relative to the pre-TS complex.

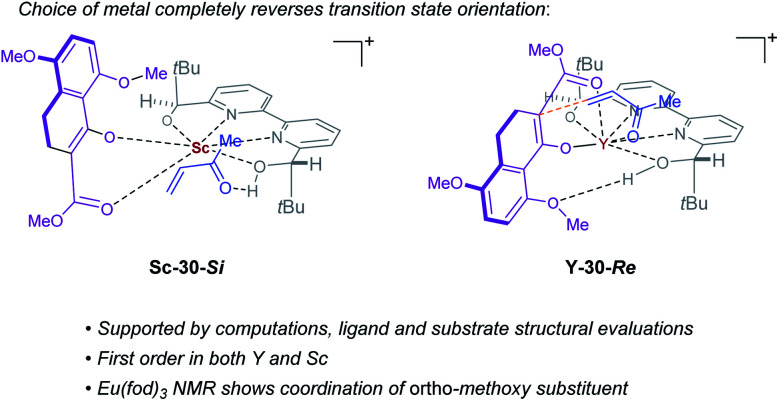
Complex ML·2H·OTf (26), proposed by Kobayashi,¹⁷ was initially investigated as the catalytically active species (Fig. 8). In addition to ML·2H·OTf (26), we considered several catalytic species which varied in triflate coordination number and protonation state (partially or fully deprotonated) of the bound bipyridine ligand (26–31, Fig. 8). Our initial calculations with ScL·2H·OTf (Sc-26) determined the lowest-energy transition state to proceed via Si-face attack of Sc-26 on electrophile 5 (Sc-26-Si), having an activation free energy of 20.1 kcal mol⁻¹ (Fig. 8B, entry 1). This pathway was found to be only 0.2 kcal mol⁻¹ lower in energy than that leading to the competing product, Sc-26-Re. Consequently, the enantioselectivity computed from comparing these two pathways (−15% ee) was found to be significantly lower than that observed (−90% ee) suggesting that this complex is unlikely to be responsible for the experimental outcome. Considering the TS possibilities with ScL·H·OTf (Sc-27) we next identified Sc-27-Si and Sc-27-Re, for which the activation energies were calculated to be 15.9 and 19.4 kcal mol⁻¹ respectively (Fig. 8B, entry 2). While these values are significantly lower than those found for ScL·2H·OTf (Sc-26), it is possible that there are even lower energy pathways. To test this hypothesis, we exhaustively considered the remaining complexes outlined in Fig. 8A. Notably, these calculations determined that the lowest energy TS corresponds to complex Sc-30. In both the Si and Re TS of Sc-30, the reaction proceeds via a Brønsted acid type mechanism in which the electrophile (5) is activated via hydrogen-bonding interactions (Sc-30-Si; Fig. 9B). The combination of reduced steric contacts with the coordinated triflate and stronger H-bonding interactions between the catalyst and electrophile contribute to the low activation barriers observed with ScL·H (Sc-30). The preference for Sc-30-Si over Sc-30-Re (Fig. 8B, entry 5) can be attributed to a steric clash between the catalyst's tert-butyl substituent and the substrate 4 in Sc-30-Re. This lowest energy pathway proceeding through transition state Sc-30-Si has an activation free energy of 14.1 kcal mol⁻¹ and leads to product (S)-6, in agreement with our experimental results (Table 1, entry 1). Additionally, our calculations holistically suggest that the lowest energy pathway leading to the disfavored (R) enantiomer proceeds viaSc-28-Re (Fig. 8B, entry 3) involving a ScL·OTf (Sc-28) complex. Because the catalyst is fully deprotonated, the reaction leading to the minor enantiomer proceeds via a Lewis acid mono-activation mode in which only substrate 4 is activated. Although the activation modes of ScL·OTf (Sc-28; Fig. 8B, entry 3; ΔG^‡ 15.1 kcal mol⁻¹) and ScL (Sc-31; Fig. 8B, entry 6; ΔG^‡ 17.9 kcal mol⁻¹) are similar, the former is noticeably more energetically preferable. This result is unexpected since steric interactions between ligand and triflate would destabilize the TS. However, this can be rationalized by the increased Lewis acidity of ScL·OTf (Sc-28) which compensates for the energetically repulsive contacts. Importantly, our calculations suggest that the Brønsted acid catalysis of ScL·H (Sc-30-Si, Fig. 9B) is more effective than the Lewis acid catalysis of ScL·OTf (Sc-28-Re, Fig. 9B) explaining the high levels and absolute sense (S) of stereoinduction observed (−64% ee computed,²⁹ −90% ee observed at 60 °C). The lack of an interaction between the complex and the substrate's ortho-methoxy substituent implies that selectivity will not be sensitive to structural modifications at this position, which agrees with our structure selectivity analysis (Table 3).

Fig. 9. (A) The two pathways leading to opposite enantiomers of product 6. Relevant structures to the enantiodetermining steps for both the (A) Sc- and (B) Y-catalysed reactions (C).

Next, we computed the possible pathways for the yttrium-catalysed system. Initially, we began by investigating YL·2H·OTf (Y-26; Fig. 8A, entry 7) as the active catalytic species. In these TS, the larger ionic radius of yttrium renders the Lewis acid activation of substrate 5 the lowest energy TS pathway. A comparison of the lowest energy TS, Y-26-Re (17.0 kcal mol⁻¹) and Y-26-Si (12.6 kcal mol⁻¹, Fig. 8B, entry 7), indicates that the reaction is expected to give (R) product in high enantioselectivities. However, after a thorough investigation of all other complexes, we determined that both the major and minor enantiomers arise from YL·H (Y-30; Fig. 8B, entry 11). This energy difference closely matches the experimental observations (88% ee computed, 95% ee experimental at 80 °C) and the reproduction of experimental enantioselectivity trends, namely that yttrium is calculated to promote the reaction with higher levels of enantioselectivity compared to scandium, illustrates the strength of the computational analysis. Additionally, the lower activation barrier computed with YL·H (Y-30; Fig. 8B, entry 11; 10.0 kcal mol⁻¹) compared to ScL·H (Sc-30; Fig. 8B, entry 5; 14.1 kcal mol⁻¹) is consistent with the observed faster reaction for the yttrium-catalysed transformation. The strong preference for the R product is due to the generation of a hydrogen bonding interaction between the ortho-methoxy substituent of 4 and the catalyst hydroxyl group which is not present in Y-30-Si (Fig. 9C). Performing the reaction in a polar solvent such as THF (entry 25, ESI Table S6†) reduces the enantioselectivity induced by the catalyst from 95% to 43% ee. One possible explanation is that coordinating solvents such as THF can compromise this favorable interaction stabilizing Re attack whereas the stronger H-bonding contact with the electrophile in Si face attack remains unaffected. Using the IEFPCM solvation model, single point energy calculations in THF reduced the relative free energy difference between Y-30-Re and Y-30-Si to 0.2 kcal mol⁻¹, in agreement with the trend observed in the experimental data (calculated value 15% ee). The importance of the ortho-methoxy hydrogen-bonding contact with the catalyst in determining the stereochemical outcome of the reaction agrees with the ligand and substrate selectivity trends (Tables 2 and 3). Despite challenges in modeling this reaction, including the possible involvement of multiple catalyst species and a variety of potential coordination modes between substrate and catalyst, and a variety of conformational possibilities, modern DFT methods accurately reproduce the experimental results and reveal how metal-dependent reversal of enantioselectivity is achieved: specifically, a rotation of the substrate 4 is energetically favorable for the larger metal yttrium but not the smaller scandium due to the presence of a favorable hydrogen-bonding interaction between the substrate's ortho-methoxy substituent and the catalyst.

Conclusions

Our observation of metal-dependent reversal of enantioselectivity for this conjugate addition reaction has been optimized for scandium and yttrium with bipyridine ligand 1 and the mechanistic details have been studied extensively to enhance our understanding of enatiodivergent transformations (Fig. 10). Through non-linear effect and kinetic studies, we have determined that the mechanism relies on a 1 : 1 complex of ligand and metal, ruling out bimetallic pathways. Structure-selectivity analysis of substrate and catalyst show the importance of the C₂ symmetry and the free hydroxy groups in ligand 1 for both complexes. Intriguingly, an ortho substituent in the substrate is a requirement to afford high enantioselectivity in the yttrium-catalysed reaction. Focusing on the two most selective Lewis acids (scandium and yttrium), we determined through density functional theory (DFT) calculations that because scandium has a small ionic radius only the enolate can be activated, and the ketone is associated with one of the ligand's protons in the lowest energy TS. Conversely, yttrium is larger rendering Lewis acid dual activation of both the enolate (4) and the ketone (5) possible. Furthermore, these investigations revealed a hydrogen-bonding interaction between the ortho substituent of substrate 4 and the yttrium catalyst, favoring rotation of the substrate and reversal of enantioselectivity when compared to the scandium-catalysed reaction. These studies will serve to aid in the future development of enantiodivergent catalytic methods relying only on a change in the identity of metal catalyst.

Fig. 10. Transition states leading to opposite enantiomers of product 6 when switching between Sc and Y as catalyst.

Data availability

All experimental and computational data associated with the article are incorporated into the ESI.†

Author contributions

P. S. R., A. D. R., T. S. and C. S. S. designed experiments. P. S. R., A. D. R. and T. S. conducted the experiments. J. P. R. designed and conducted all DFT investigations. All authors contributed to the manuscript.

Conflicts of interest

The authors declare no conflicts of interest.