Abstract
Background
If the different transmission risks of respiratory infectious diseases according to the type of confined space and associated factors could be discovered, this kind of information will be an important basis for devising future quarantine policies. However, no comprehensive systematic review or meta-analysis for this topic exists.
Objective
The objective of this study is to analyze different transmission risks of respiratory infectious diseases according to the type of confined space. This information will be an important basis for devising future quarantine policies.
Methods
A medical librarian searched MEDLINE, EMBASE, and the Cochrane Library (until December 01, 2020).
Results
A total of 147 articles were included. The risk of transmission in all types of confined spaces was approximately 3 times higher than in open space (combined RR, 2.95 (95% CI 2.62–3.33)). Among them, school or workplace showed the highest transmission risk (combined RR, 3.94 (95% CI 3.16–4.90)). Notably, in the sub-analysis for SARS-CoV-2, residential space and airplane were the riskiest space (combined RR, 8.30 (95% CI 3.30–20.90) and 7.30 (95% CI 1.15–46.20), respectively).
Discussion
Based on the equation of the total number of contacts, the order of transmission according to the type of confined space was calculated. The calculated order was similar to the observed order in this study. The transmission risks in confined spaces can be lowered by reducing each component of the aforementioned equation. However, as seen in the data for SARS-CoV-2, the closure of one type of confined space could increase the population density in another confined space. The authority of infection control should consider this paradox. Appropriate quarantine measures targeted for specific types of confined spaces with a higher risk of transmission, school or workplace for general pathogens, and residential space/airplane for SARS-CoV-2 can reduce the transmission of respiratory infectious diseases.
Keywords: Transmission risk, Respiratory infectious disease, Confined space, SARS-CoV-2, COVID-19, Meta-analysis
Graphical abstract
1. Introduction
From ancient times until the present day, many types of respiratory infectious diseases have been a major threat to humanity. As a recent representative example, the Spanish flu infected 500 million people and caused over 1 million mortality during the 1918–1919 pandemic (Taubenberger and Morens, 2006). As another example, tuberculosis caused about 10 million morbidities and about 1.4 million mortalities worldwide in only 2019 (World Health Organization, 2020). Most importantly, we are currently struggling amid the upheaval of the COVID-19 pandemic. Despite fierce efforts to overcome this tragic pandemic, this terrible pandemic is still ongoing.
Most respiratory infectious diseases spread via droplets or aerosols, with some cases in which close contact itself plays as a transmission pathway (Musher, 2003). For these respiratory infectious diseases, a pathogen-indoor environment interaction is important for infectivity because the air in confined spaces is shared by all occupants of the space, and the possibility of droplet transmission is increased in a small confined closed space (Fujiyoshi et al., 2017).
Infectious disease outbreaks in various confined spaces were reported many times (Chadwick and McCann, 1994; Distasio and Trump, 1990; Kenyon et al., 1996; Lessa et al., 2009; MacIntyre et al., 1995; Marks et al., 2003). These confined spaces include the residential space (home or dormitory), the workplace, a closed ward in a hospital, a cruise ship, the airplane, and other social gathering sites (bar or restaurant). According to the type of confined space, the social activities conducted are different, and accordingly, factors such as the intensity of mixing, the density of occupants, the staying time, and the total number of occupants are different (Mossong et al., 2008). From this perspective, the transmission risk of respiratory infectious diseases would differ according to the type of confined space.
If the different transmission risks of respiratory infectious diseases according to the type of confined space and associated factors could be discovered, this kind of information will be an important basis for devising future quarantine policies. However, no comprehensive systematic review or meta-analysis for this topic exists.
Therefore, in this study, the author systematically collected and analyzed articles that report transmission risks of respiratory infectious diseases, according to the type of confined space. Considering the remaining risk of COVID-19 and future pandemics, this quantitative study will be of great help for securing the public health of future generations. In addition, this study can provide a concrete evidence base for deciding quarantine policies and devising quarantine measures.
2. Methods
2.1. Literature search
A literature search was conducted by a medical librarian (information specialist, N.K. commented in the Acknowledgement section) in the library of an author's affiliation (Medical library, The Catholic University of Korea, Seoul, Republic of Korea). The medical librarian searched MEDLINE (PubMed), EMBASE, and the Cochrane Library (until December 01, 2020). (Supplementary material A).
2.2. Inclusion criteria and selection of studies
The inclusion criteria were as follows: (ⅰ) The article should deal with the spread of an infectious disease in a confined space. (ⅱ) The route of transmission should be airborne or droplet transmission. (respiratory infection) (ⅲ) Only original research articles were included. (ⅳ) The risk ratio (RR) or odds ratio (OR) for transmission of an infectious disease in a confined space, compared with an open space, should be reported in the article. (ⅴ) Only the articles published since 1990 were included. (ⅵ) Articles written in only English were included.
Primary screening using the title and abstract of each article and final selection of included studies through full-text review was conducted by two authors (J.M. and B.R.) independently. Disagreements between the two authors were resolved by discussion.
2.3. Quality assessment of included studies
The quality assessment of each included study was conducted by two authors (J.M. and B.R.) independently, using the National Institutes of Health (NIH) Quality Assessment tool for observational cohort and cross-sectional studies and case-control studies (https://www.nhlbi.nih.gov/health-topics/study-quality-assessment-tools). The NIH quality assessment tool for observational cohort and cross-sectional studies is composed of 14 questions. Question number 1 deals with a clearly stated research question. Question numbers 2, 3, 4, and 13 deal with the possibility of selection bias. Question numbers 6, 8, 9, and 10 deal with the possibility of exposure misclassification. Question numbers 7, 11, and 12 deal with the possibility of outcome misclassification. Question 14 deals with the possibility of confounding. Question number 5 deals with the adequacy of sample size. The quality rating according to the total score was set as the following: Good for 12–14, Fair for 9–11, and Poor for 0–8. The NIH quality assessment tool for case-control studies is composed of 12 questions. Question number 1 deals with a clearly stated research question. Question numbers 2, 4, 5, 6, 7, and 8 deal with the possibility of selection bias. Question numbers 9, 10, and 11 deal with the possibility of exposure misclassification. Question number 12 deals with the possibility of confounding. Question number 3 deals with the adequacy of sample size. The quality rating according to the total score was set as the following: Good for 11–12, Fair for 9–10, and Poor for 0–8.
2.4. Data extraction and conversion
Relevant data from each included article, including the study period, the study country, the causative pathogen, the infectious disease induced by the pathogen, the type of confined space (environmental setting), route of transmission for the pathogen, the number of persons infected versus total population, the type of risk estimate reported (RR or OR), the risk estimate, the compared baseline status (open space), and used statistical method, were extracted.
For articles that reported ORs as risk estimates, the ORs were converted into RRs using the method in Zhang et al. (1998) (Zhang and Kai, 1998). The prevalence of infection in the non-exposed population (i.e., who had not been in the confined space) reported in each article was used as the non-exposed prevalence for the corresponding OR. If an OR was calculated based on a traditional case-control study context that involves an intentional selection of cases and controls with/without matching, the non-exposed prevalence could not be determined. It is because according to the size of controls determined, the non-exposed prevalence would change. However, if an OR was calculated from a natural experiment/a cross-sectional study context, the non-exposed prevalence for this OR can be acquired. Therefore, the OR in the studies from only this latter group was converted into a RR.
2.5. The examination of publication bias
For the examination of publication bias, the funnel plot for studies with OR risk estimate and the funnel plot for studies with RR risk estimate were plotted separately. Egger's regression test was conducted separately for these two groups of studies. The p-value for publication bias was set at 0.05.
2.6. The main meta-analysis
Between a fixed-effect model and a random-effect model, all meta-analyses in this study applied a random-effect model based on the test of heterogeneity result and conceptual heterogeneity among study conditions (Borenstein et al., 2021; Nikolakopoulou et al., 2014). Numerous study conditions were different among included studies, and this issue will be discussed in the limitation subsection of the Discussion section. A random-effect model was selected to consider the variability of these associated conditions. Higgins I-square statistics above 25% and Cochran's Q test results with a significance level of less than 0.1 were considered as ‘heterogeneous’ and used as a supplement measure.
A meta-analysis for all studies with OR risk estimate, all studies with RR risk estimate, and all studies with RR risk estimate and converted RR risk estimate were conducted to look over the overall effect of confined spaces on the transmission risk of various pathogens.
2.7. Subgroup analyses and meta-ANOVA analyses
For the calculation of transmission risks according to each type of confined space, subgroup analysis according to each type of confined space was conducted: (ⅰ) airplane, (ⅱ) school or workplace, (ⅲ) hospital, (ⅳ) residential space, and (ⅴ) navy ship or cruise ship. This subgroup analysis was conducted for the studies with RR risk estimate, for the studies with OR risk estimate, and for the studies with RR risk estimate and converted RR risk estimate.
For the calculation of transmission risks according to each type of pathogen, subgroup analysis according to each type of pathogen was conducted: Mycobacterium tuberculosis, Middle East Respiratory Syndrome Coronavirus (MERS-CoV), Severe Acute Respiratory Syndrome Coronavirus (SARS-CoV), SARS-CoV-2, Influenza, Measles morbillivirus, Mumps Orthorubulavirus, Adenovirus, Human metapneumovirus, other respiratory viruses, Neisseria meningitides, and Bordetella pertussis.
For a more accurate analysis of transmission risks according to each type of confined space, subgroup analysis according to each type of confined space was conducted for each group of pathogens in which similar types of the pathogen were grouped: (ⅰ) Tuberculosis group: Mycobacterium tuberculosis, (ⅱ) MERS and SARS group: MERS-CoV, SARS-CoV, and SARS-CoV-2, (ⅲ) Viruses group: Influenza, Measles morbillivirus, Adenovirus, Human metapneumovirus, other respiratory viruses, (ⅳ) Bacteria group: Neisseria meningitides, Bordetella pertussis, and (ⅴ) COVID-19 group: SARS-CoV-2.
For comparing the risk of transmission according to the statistical method used, subgroup analysis according to the statistical method used was conducted: (ⅰ) Fisher's exact test, (ⅱ) Chi-square test, (ⅲ)Cochran-Mantel Haenszel test, (ⅳ) McNemar test, (ⅴ) Univariable logistic regression, (ⅵ) Univariable conditional logistic regression, (ⅶ) Multivariable logistic regression, (ⅷ) Multivariable conditional logistic regression, (ⅸ) Log-binomial regression, (ⅹ) Poisson regression.
For all subgroup analyses, a meta-ANOVA analysis was conducted. The p-value for significance was set at 0.1.
2.8. Statistical software
Through all statistical analyses, R software version 4.0.3 was used. The package ‘meta’, ‘dplyr’, and ‘data.table’ were used.
3. Results
3.1. Literature searching and screening
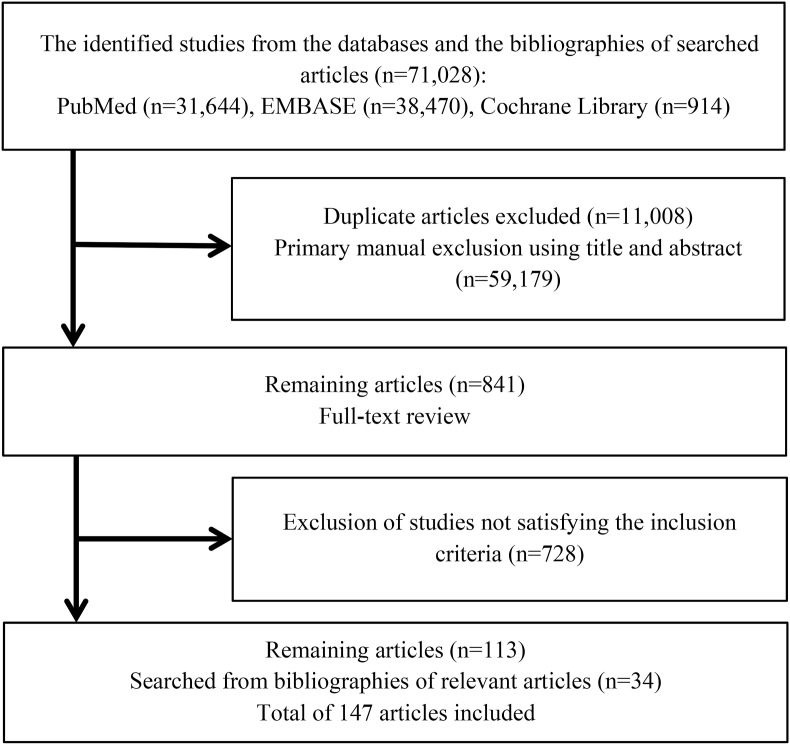
Fig. 1 provides the flowchart for literature searching and screening. In 3 databases (PubMed, EMBASE, and Cochrane Library), a total of 71,028 articles were searched. Among them, 11,008 duplicate articles were excluded. After exclusion, using the title and abstract of searched articles, the primary manual exclusion was conducted. After the exclusion of 59,179 articles, for the remaining 841 articles, a full-text review was conducted. Through the full-text review, 728 articles not satisfying the inclusion criteria were excluded. Finally, the remaining 113 articles and 34 articles searched from bibliographies of relevant articles were selected as the final included articles.
Fig. 1.
The flowchart for literature searching and screening.
3.2. The characteristics of included studies
Supplementary material B provides the characteristics of the final included articles. The study period spread from 1987 to 2020. Study countries were 17 countries for studies with RR risk estimate and were 33 countries for studies with OR risk estimate. For the route of transmission, only Mumps Orthorubulavirus, Neisseria meningitides, and Bordetella pertussis pertain to droplet transmission. Other pathogens pertain to airborne transmission. The point estimate of RR spread from 0.9 to 26.5, and the point estimate of OR spread from 0.18 to 124.
The quality assessment results of included studies are provided in Supplementary material C. For RR studies and OR studies with a natural experiment/a cross-sectional study context, the quality assessment tool for observational cohort and cross-sectional studies was used. For OR studies with a traditional case-control study context, the quality assessment tool for case-control studies was used.
3.3. The examination of publication bias
Each funnel plot for studies with RR risk estimate and for studies with OR risk estimate are provided in Supplementary material D. Egger's p-value for bias was 0.063 for studies with RR risk estimate and was 0.051 for studies with OR risk estimate.
3.4. Non-exposed prevalence and converted RR
Supplementary material E provides the prevalence of the infectious disease in the reference group (non-exposed prevalence) and the converted RRs for the studies with OR risk estimates. For 24 studies, the calculation of non-exposed prevalence was impossible because the studies were conducted in the context of a traditional case-control study. The intentional selection of control subjects could change the non-exposed prevalence according to the number of included control subjects. Therefore, for these studies, the calculation of non-exposed prevalence has no meaning. The point estimate for converted RRs ranged from 0.197 to 34.559.
3.5. Main meta-analysis and subgroup analysis: the type of confined space
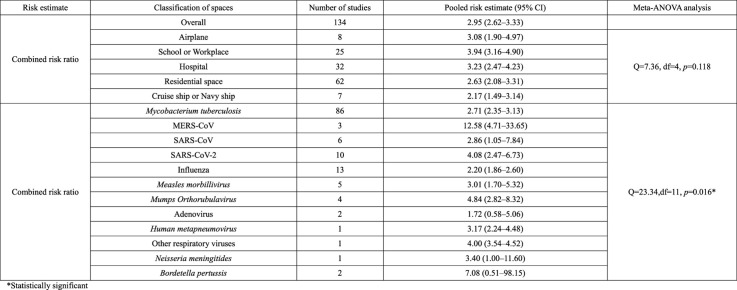
All results for the test of heterogeneity were statistically significant (Supplementary material F). Therefore, the selection of a random-effect model was justified. In Table 1 , the risk of transmission according to the type of confined spaces is provided. For studies with RR risk estimate (RR studies), the pooled RR for overall types of confined space was 4.31 (95% Confidence Interval, CI, 3.51–5.29). For studies with OR risk estimate (OR studies), the pooled OR for overall types of confined space was 3.93 (95% CI 3.31–4.67). For studies with converted RR risk estimate and RR risk estimate (combined RR studies), the pooled RR for overall types of confined space was 2.95 (95% CI 2.62–3.33).
Table 1.
Risk of transmission according to the type of confined spaces and pathogen.
| Risk estimate | Classification of spaces | Number of studies | Pooled risk estimate (95% CI) | Meta-ANOVA analysis |
|---|---|---|---|---|
| Risk ratio | Overall | 52 | 4.31 (3.51–5.29) | |
| Airplane | 8 | 3.08 (1.90–4.97) | Q = 3.38, df = 4, p = 0.497 | |
| School or Workplace | 12 | 5.84 (4.03–8.46) | ||
| Hospital | 12 | 3.86 (2.41–6.16) | ||
| Residential space | 18 | 4.27 (2.88–6.32) | ||
| Cruise ship or Navy ship | 2 | 3.71 (2.45–5.62) | ||
| Odds ratio | Overall | 107 | 3.93 (3.31–4.67) | |
| School or Workplace | 14 | 5.31 (3.74–7.53) | Q = 9.04, df = 4, p = 0.060* | |
| Hospital | 33 | 5.01 (3.57–7.03) | ||
| Residential space | 53 | 3.39 (2.63–4.36) | ||
| Other social gathering sites | 2 | 6.16 (0.95–39.98) | ||
| Cruise ship or Navy ship | 5 | 2.04 (1.27–3.28) | ||
| Combined risk ratio | Overall | 134 | 2.95 (2.62–3.33) | |
| Airplane | 8 | 3.08 (1.90–4.97) | Q = 7.36, df = 4, p = 0.118 | |
| School or Workplace | 25 | 3.94 (3.16–4.90) | ||
| Hospital | 32 | 3.23 (2.47–4.23) | ||
| Residential space | 62 | 2.63 (2.08–3.31) | ||
| Cruise ship or Navy ship | 7 | 2.17 (1.49–3.14) | ||
| Combined risk ratio | Mycobacterium tuberculosis | 86 | 2.71 (2.35–3.13) | Q = 23.34,df = 11, p = 0.016* |
| MERS-CoV | 3 | 12.58 (4.71–33.65) | ||
| SARS-CoV | 6 | 2.86 (1.05–7.84) | ||
| SARS-CoV-2 | 10 | 4.08 (2.47–6.73) | ||
| Influenza | 13 | 2.20 (1.86–2.60) | ||
| Measles morbillivirus | 5 | 3.01 (1.70–5.32) | ||
| Mumps Orthorubulavirus | 4 | 4.84 (2.82–8.32) | ||
| Adenovirus | 2 | 1.72 (0.58–5.06) | ||
| Human metapneumovirus | 1 | 3.17 (2.24–4.48) | ||
| Other respiratory viruses | 1 | 4.00 (3.54–4.52) | ||
| Neisseria meningitides | 1 | 3.40 (1.00–11.60) | ||
| Bordetella pertussis | 2 | 7.08 (0.51–98.15) |
*Statistically significant.
For each type of confined space, the meta-ANOVA analysis did not show any significant difference for the subgroups in RR studies and for the subgroups in combined RR studies. However, for OR studies, the meta-ANOVA analysis showed a significant difference among subgroups (p = 0.060).
Even though the meta-ANOVA analysis result for combined RR studies was insignificant, the p-value showed a borderline value (p = 0.118). Given firstly, that various confounding factors which could affect the transmission risk in a confined space, and secondly, that additional study outcomes could narrow the confidence interval for each subgroup risk estimate, if more studies are added in the future, this meta-ANOVA analysis could show a significant result. Therefore, to look over the pooled risk estimate for each subgroup would have a meaning.
For combined RR studies, the school or workplace showed the highest pooled risk estimate (3.94 (95% CI 3.16–4.90), followed by hospital (3.23 (95% CI 2.47–4.23)) and airplane (3.08 (95% CI 1.90–4.97)). The next was residential space (2.63 (95% CI 2.08–3.31)), and cruise ship or navy ship showed the least pooled risk estimate (2.17 (95% CI 1.49–3.14)).
3.6. Main meta-analysis and subgroup analysis: the type of pathogen
For combined RR studies, the risk of transmission according to the type of pathogen is also provided in Table 1. For 12 pathogens, the lowest RR was for adenovirus (1.72 (95% CI 0.58–5.06)), and the highest RR was for MERS-CoV (12.58 (95% CI 4.71–33.65)). The meta-ANOVA analysis showed a significant difference among 12 pathogens, with a p-value of 0.016.
3.7. Additional subgroup analysis: the type of confined space for each pathogen group
Table 2 provides the risk of transmission for each type of pathogen separately according to the type of confined spaces. For the Tuberculosis group, the pooled RR for overall types of confined space was 2.79 (95% CI 2.40–3.25). For MERS and SARS group, the pooled RR for overall types of confined space was 4.44 (95% CI 2.92–6.73). For the viruses group and the bacteria group, the pooled RR was 2.21 (95% CI 1.75; 2.80) and 5.63 (95% CI 0.75–42.25), respectively.
Table 2.
Risk of transmission for each pathogen according to the type of confined spaces.
| Pathogen | Classification of spaces | Number of studies | Pooled risk ratio | Meta-ANOVA analysis |
|---|---|---|---|---|
| Mycobacterium tuberculosis | Overall | 83 | 2.79 (2.40–3.25) | |
| Airplane | 2 | 3.77 (1.52–9.34) | Q = 8.42, df = 4, p = 0.077* | |
| School or Workplace | 21 | 3.88 (3.04–4.97) | ||
| Hospital | 21 | 2.96 (2.20–3.99) | ||
| Residential space | 35 | 2.19 (1.60–2.98) | ||
| Cruise ship or Navy ship | 4 | 3.21 (2.40–4.30) | ||
| MERS-CoV SARS-CoV-1 SARS-CoV-2 |
Overall | 19 | 4.44 (2.92–6.73) | |
| Airplane | 2 | 3.55 (1.70–7.40) | Q = 1.14, df = 3, p = 0.767 | |
| Hospital | 7 | 4.19 (2.09–8.42) | ||
| Residential space | 9 | 5.14 (2.45–10.8) | ||
| Cruise ship or Navy ship | 1 | 1.80 (1.51–2.14) | ||
| Influenza Measles morbillivirus Adenovirus Human metapneumovirus Other respiratory viruses |
Overall | 18 | 2.21 (1.75–2.80) | |
| Airplane | 4 | 2.58 (0.89–7.50) | Q = 6.90, df = 4, p = 0.141 | |
| School or Workplace | 1 | 2.69 (2.13–3.40) | ||
| Hospital | 2 | 2.56 (1.40–4.71) | ||
| Residential space | 9 | 2.44 (1.86–3.21) | ||
| Cruise ship or Navy ship | 2 | 1.07 (0.80–1.43) | ||
|
Neisseria meningitides Bordetella pertussis |
Overall | 3 | 5.63 (0.75–42.25) | |
| School or Workplace | 2 | 7.08 (0.51–98.15) | Q = 0.09, df = 1, p = 0.760 | |
| Residential space | 1 | 3.40 (1.00–11.60) |
For this table, risk ratios and converted risk ratios from odds ratios were used (combined risk ratios).
*Statistically significant.
For each type of confined space, the meta-ANOVA analysis showed a significant result only for Mycobacterium tuberculosis studies (p = 0.077). However, the order of pooled risk ratios was different from the order of pooled risk estimates for combined RR studies in Table 1. School or workplace showed the highest risk ratio (3.88 (95% CI 3.04–4.97)), followed by airplane (3.77 (95% CI 1.52–9.34)) and cruise ship or navy ship (3.21 (95% CI 2.40–4.30)), respectively. The next was hospital (2.96 (95% CI 2.20–3.99)). Finally, residential space subgroup showed the least risk ratio (2.19 (95% CI 1.60–2.98)).
3.8. Additional subgroup analysis: the COVID-19 group
Table 3 provides the risk of transmission for SARS-CoV-2 according to the type of confined spaces. For combined RR studies, Residential space showed the highest RR (8.30 (95% CI 3.30–20.90)). Airplane showed the second-highest RR (7.30 (95% CI 1.15–46.20). Hospital and navy ship showed a rather lower RR, 1.78 (95% CI 1.09–2.93) and 1.80 (95% CI 1.51–2.14), respectively.
Table 3.
Risk of transmission for SARS-CoV-2 according to the type of confined spaces.
| SARS-CoV-2 | Classification of spaces | Number of studies | Pooled risk ratio | Meta-ANOVA analysis |
|---|---|---|---|---|
| Risk ratio | Overall | 3 | 1.52 (0.96–2.39) | |
| Airplane | 1 | 7.30 (1.15–46.20) | Q = 2.79, df = 1, p = 0.095* | |
| Hospital | 2 | 1.40 (0.96–2.05) | ||
| Odds ratio | Overall | 11 | 7.39 (4.41–12.36) | |
| Hospital | 1 | 5.19 (1.84–14.66) | Q = 1.40, df = 3, p = 0.706 | |
| Residential space | 7 | 9.39 (5.05–17.43) | ||
| Other social gathering site | 2 | 6.16 (0.95–39.98) | ||
| Navy ship | 1 | 3.30 (1.79–6.10) | ||
| Combined risk ratio | Overall | 10 | 4.08 (2.47–6.73) | |
| Airplane | 1 | 7.30 (1.15–46.20) | Q = 8.67, df = 3, p = 0.034* | |
| Hospital | 3 | 1.78 (1.09–2.93) | ||
| Residential space | 5 | 8.30 (3.30–20.90) | ||
| Navy ship | 1 | 1.80 (1.51–2.14) |
*Statistically significant.
For OR studies, other social gathering sites showed a rather high RR, 6.16 (95% CI 0.95–39.98), even though the confidence interval was wide.
For a meta-ANOVA analysis, the RR studies group and the combined RR studies group showed a significant difference among subgroups.
This order of transmission risk according to the type of confined space for SARS-CoV-2 is different from the order of transmission risk observed in combined RR studies in Table 1. This order pattern is also considerably different from the order of transmission risks observed for the Mycobacterium tuberculosis group in Table 2. This different order pattern will be dealt with in the Discussion section in detail.
3.9. Additional subgroup analysis: the statistical method used
Supplementary material G provides the risk of transmission according to the statistical method used. For RR studies and OR studies, 7 and 8 types of statistical methods were applied, respectively. For RR studies, the Chi-square test group showed the highest pooled risk estimate (5.40 (95% CI 3.79–7.69)) and the univariable logistic regression group showed the lowest pooled risk estimate (2.50 (95% CI 1.75–3.57)). For OR studies, the Fisher's exact test group showed the highest pooled risk estimate (10.66 (95% CI 2.29–49.50)), and the Univariable logistic regression group showed the lowest pooled risk estimate (1.7 (95% CI 0.99–2.90)). The meta-ANOVA analysis showed a significant difference among subgroups only for OR studies (p = 0.008).
4. Discussion
In this meta-analysis, the transmission risks of respiratory infectious diseases in various confined spaces are summarized. The risk of transmission in all types of confined spaces was approximately 3 times higher than in open space (combined RR, 2.95 (95% CI 2.62–3.33)). Among them, school or workplace showed the highest transmission risk (combined RR, 3.94 (95% CI 3.16–4.90) (Table 1). Notably, in the sub-analysis for SARS-CoV-2, residential space and airplane were the riskiest space (combined RR, 8.30 (95% CI 3.30–20.90) and 7.30 (95% CI 1.15–46.20), respectively) (Table 3).
4.1. The transmission risk for each type of confined space: the order of risks
The spread of respiratory infection in a confined space is the combination of a number of related factors: the number of persons in the space, the time period of stay, the total number of persons in the space, and the intensity of mixing. The following equations quoted from Rocklov et al. provide how each of these components interact to increase the transmission risk in confined spaces (Rocklöv and Sjödin, 2020).
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
β, the daily reproductive number, τ, transmissibility, c, contact rate, R0, the basic reproduction number, i, the infectious period (the inverse of the recovery rate, γ), m, the intensity of mixing, d, the population density, T(t), the total number of contacts, t, the time period of stay, N, the total number of persons in the space.
For example, if the population density (d) increases by four times, the contact rate (c), the total number of contacts (T(t)), and the basic reproduction number (R 0) will increase by four times. These equations could be applied to explain the overall and subgroup results of this study.
Each included study in this meta-analysis compared the risk of transmission in various confined spaces with the risk of transmission in non-confined spaces. To simplify the discussion, if we assume that other confounding factors are identical, the only determinant of transmission risk is the frequency of exposure to the pathogen for a person. According to equation T(t) = mdtN, the total number of contacts (i.e., the frequency of exposure to the pathogen) is directly proportional to the intensity of mixing (m), the population density (d), the time period of stay (t), and the total number of persons in the space (N).
The order of the aforementioned 4 variables for the 5 types of confined space included in our meta-analysis was estimated in Table 4 .
Table 4.
The calculated and observed order of transmission risk for each type of confined space.
| Type of confined space | m | d | t | N | Calculated order (mean valuea) | Observed orderc (combined RR with 95% CI) |
|---|---|---|---|---|---|---|
| School or workplace | 1st | 2nd | 3rd | 3rd | 1st (2.06th) | 1st (3.94 (3.16–4.90)) |
| Airplane | 4th | 1st | 5th | 1st | 2nd (2.11th) | 3rd (3.08 (1.90–4.97)) |
| Hospital | 3rd | 4th | 2nd | 2nd | 3rd (2.63rd) | 2nd (3.22 (2.47–4.19)) |
| Other social gathering sites | 2nd | 3rd | 4th | 4th | 4th (3.13th) | N/Ab |
| Residential space | 5th | 5th | 1st | 5th | 5th (3.34th) | 4th (2.63 (2.08–3.31)) |
m, the intensity of mixing; d, the population density; t, the time period of stay; N, the total number of persons in the space; RR, risk ratio.
Mean value indicates the geometric mean of the order for each variable. For example, for school or workplace, 2.06th = .
The combined RR for other social gathering sites was not calculated (non-exposed prevalence unavailable).
The meta-ANOVA analysis showed a borderline significance (p = 0.116).
First, for the intensity of mixing (m), school or workplace was regarded as the riskiest space. School students usually participate in a collective physical activity or in a group leisure activity. Office workers are usually densely packed in a small confined office; therefore, the mixing occurs through a form of joint works or meetings (Guclu et al., 2016; Mossong et al., 2008). On the other hand, airplane and residential space were considered as the space with low (m), because persons usually minimize an unnecessary movement in airplanes and do not actively move in the bedroom.
Second, for the population density (d), airplane was regarded as the densest space due to the densely packed seats within an airplane (Graham et al., 1983). Similar reasons with airplane, school or workplace was classified as the second densest space. Usually, in metropolitan cities, because of high rental costs, many workers usually work in a small confined space (Zheng and Kahn, 2008). Following these 2 spaces, the population density (d) was regarded as decreasing in the order of other social gathering sites, hospital, and residential space. Usually, hospital beds are located with a sufficient interval space to prevent possible nosocomial transmission of infection. The bedroom was regarded as the least dense space, because bedroom is occupied by an individual for private purposes.
Third, for the time period of stay (t), residential space was regarded as space with the longest period of stay, followed by the hospital. An ordinary person sleeps 6–8 h per day on average and spends most of the time resting at home on weekends (Lauderdale et al., 2008). In the case of hospitals, standard 8-h shifts of healthcare workers (8 h per day), length of stay in the emergency department (mean 3.3–15 h) (Cho et al., 2016; McCaig and Nawar, 2006), wait time or length of stay in outpatients (mean 98–168 min) (Cao et al., 2011; Mohebbifar et al., 2013; Xie and Or, 2017) and length of stay for inpatients (all day) were considered comprehensively and was regarded as space with the second-longest period of stay. Other spaces were given an appropriate order based on the following reasons: Usually, 6–8 h are spent at school/workplace on weekdays only (3rd for school or workplace), restaurants and bars are occasionally visited (4th for other social gathering sites), and airplane travel rarely occurs in a year (5th for airplane) (Hill et al., 2010).
Fourthly, for the total number of persons in a space (N), the airplane was regarded as having the largest number of persons, based on the average number of passenger seats of commercial airplanes (100–300 seats) (Milne and Kelly, 2014). Hospital was considered to have the second-largest number of persons (N) following airplane. Due to the multiple sub-compartments (ward, inpatient unit, outpatient department, emergency room, etc.), various scales of hospitals (primary, secondary, and tertiary), and variability in the number of visiting patients, we made this decision based on the information from a number of included articles; 30 to 77 healthcare workers (Control and Prevention, 2004a, Control and Prevention, 2004b; Medrano et al., 2014) and 11 to 99 patients (Beck-Sagué et al., 1992; Biribawa et al., 2020; Dooley et al., 1992; Pan et al., 2016; Tasaka et al., 2020) in a single ward; 1 to 5 patients in a single patient room (Leckerman et al., 2010), and 100 to 200 patients in a single emergency room (Cho et al., 2016). School or workplace was regarded to have the third-largest number of persons in space: A typical school classroom is occupied by 16–35 students (Muennig and Woolf, 2007; Skarlatos and Manatakis, 2003). For the office, an average of 58 and 140 people worked in a federal office building in the US and Canada, respectively (Charles and Veitch, 2002; Lindberg et al., 2018). For factories, about 91% of the US factories employed less than 100 workers in 2015 (Levinson, 2017). Other social gathering sites were rated as the next, and residential space was regarded as the space with the least number of persons.
After this estimation of the order of the aforementioned 4 variables for 5 types of confined spaces, the geometric mean of these orders for each type of confined space was calculated. In the order of this geometric mean, the calculated order was rated in Table 4. This calculated order was compared with the observed order (rated using combined RR in Table 1) in this study. Similar orders were observed except for airplane and hospital space: For these 2 spaces, the calculated order is reversed in observed order.
However, simply quantifying and ranking the exposure variables may not be enough to accurately predict the risk of spreading respiratory infectious diseases in confined spaces. According to the traditional Wells-Riley equation (Sze To and Chao, 2010), transmission risk in a confined space is associated with the following factors: i) the number of spreaders, ii) the contagious particles produced by them, iii) the breathing rate of exposed people, and iv) the ventilation rate of the confined space. However, these factors were not sufficiently considered in each study and in this meta-analysis. The effect of these confounding factors will be dealt with in the following limitation section in detail.
4.2. Various strategies for restricting the transmission risks
The transmission risks in confined spaces can be lowered by reducing each component of the aforementioned equation, T(t) = mdtN. Even if radical, the most certain way is to lock a certain region down: by this lock-down, the four components can be definitely reduced. For example, the lock-down of Wuhan city by travel restriction and home quarantine successfully prevented a massive outbreak of COVID-19 in mainland China (Lau et al., 2020). However, this policy is difficult to be enforced except for an exceptional explosive pandemic situation because it would cause fatal drawbacks, including social and economic losses (You et al., 2020).
As another policy option, strict social distancing and a pin-pointed shutdown of specific types of facilities could be adopted. School or workplace was the riskiest space in this study (Table 4). For schools, national school closure in the US led to decreased COVID-19 incidence and mortality (Auger et al., 2020). For workplaces, a recent simulation study suggested that teleworking could be a new standard for reducing COVID-19 transmission (Karako et al., 2020).
For essential facilities that cannot be easily closed like hospitals, the application of additional preventive measures can be an alternative. In the separate analysis for SARS-CoV-2 (Table 3), the pooled combined RR in hospital (1.78 (95% CI 1.09–2.93)) showed the lowest risk when compared with other types of spaces. This demonstrates that by complying with infection control rules and by wearing personal protective equipment, the transmission risk in hospitals can be effectively reduced. Even when persons are directly exposed to COVID-19 patients in hospitals, these preventive measures were effective (Iversen et al., 2020; Lidström et al., 2020).
Singapore's successful containment of COVID-19 without strong social distancing measures, such as school closure, sets another good precedent. They proved that even in confined spaces, simple measures such as regular fever checking, mask-wearing, and physical distancing could reduce the risk of infection significantly (Lee et al., 2020).
4.3. A paradox of social distancing for COVID-19: risky residential spaces
Another noteworthy finding of this study was a relatively high transmission risk of SARS-CoV-2 in residential space. This finding is consistent with previous studies reporting the importance of household transmission in the COVID-19 epidemic (Lei et al., 2020; Madewell et al., 2020). This finding can be attributed to the paradox of social distancing: As social distancing is emphasized, distancing between family members in the home becomes difficult (Curmei et al., 2020). The closure of one type of confined space would inevitably increase the population density in another confined space. The authority of infection control should consider this paradox.
4.4. Limitations of this study
This study has several limitations. The first is the possibility of selective reporting. Not all infectious disease outbreaks are reported and published in academic literature. In addition, some practical reasons can introduce a bias in the reporting of an outbreak. For example, an infectious disease outbreak that occurred in a workplace could not be reported for the disadvantages anticipated by the employer. Outbreaks in a hospital also could not be reported because of similar reasons.
Secondly, confounding is an important factor to be considered. There are numerous factors that can affect the transmission risk of infectious diseases in confined spaces. A recent article (Khan and Meyer, 2020) summarized various factors affecting the transmission risk of SARS-CoV-2 for healthcare workers: (ⅰ) mode of transmission including fomite transmission, (ⅱ) the dose of an infectious pathogen, (ⅲ) duration of exposure, (ⅳ) aerosol-generating behavior, (ⅴ) administrative control measures, (ⅵ) personal protective equipment, (ⅶ) comorbidities of exposed persons including immune status. These various confounding factors should be adjusted for a more accurate analysis.
Thirdly, because the included studies were conducted at different times in various regions of various countries, population heterogeneity could have affected the results of included studies. Different genetic traits of the different populations can affect the susceptibility to an infectious disease (Chapman and Hill, 2012; Mozzi et al., 2018; Segal and Hill, 2003). However, this meta-analysis included studies conducted from 1987 to 2020 and included studies conducted in 39 countries. Considering a rather widely distributed study times and many study countries included, the authors concluded that the effect of population genetic heterogeneity would be small. In future studies, this important factor should be considered.
Fourthly, the statistical method applied in each study was not adjusted in this study. However, for RR studies, the meta-ANOVA analysis did not show a significant difference among subgroups. In addition, for OR studies, the pooled OR from studies with a more advanced statistical method (multivariable logistic regression) showed similar results with the pooled OR for overall types of confined space. This is because of the large fraction of studies that used the multivariable logistic regression method among all OR studies. From these points, the effect of different statistical methods might not change the risk estimate significantly.
4.5. Conclusion
In conclusion, for overall types of confined space, the risk of transmission was about 3 times higher than in open space. Among the types of confined space, school or workplace showed the highest risk of transmission (about 4 times). For SARS-CoV-2, residential space and airplane were the risky space (about 8 and 7 times, respectively). Appropriate quarantine measures targeted for specific types of confined spaces are urgent to reduce the transmission of respiratory infectious diseases.
Credit author statement
1. Jinyoung Moon: Conceptualization, Methodology, Software, Validation, Formal analysis, Writing – Original Draft, Visualization, Project administration. 2. Byung-Han Ryu: Investigation, Resources, Data Curation, Writing –Review & Editing, Supervision.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: This research was supported by the researcher training program (Environmental Medicine) of the Environmental Health Center, which was funded by the Ministry of Environment, Republic of Korea. Only the first author (Jinyoung Moon) received this grant from the funder.
Acknowledgements
The authors appreciate the work of Najin Kim in the Medical Library of the Catholic University of Korea, Seoul, Republic of Korea (ORCID: https://orcid.org/0000-0001-7280-9579), for building the search query, conducting the literature search, and double-checking of included studies.
This research was supported by the researcher training program (Environmental Medicine) of the Environmental Health Center, which was funded by the Ministry of Environment, Republic of Korea.
Footnotes
Supplementary data for this article can be found on https://doi.org/10.1016/j.envres.2021.111679.
Funding
This research was supported by the researcher training program (Environmental Medicine) of the Environmental Health Center, which was funded by the Ministry of Environment, Republic of Korea.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Auger K.A., et al. Association between statewide school closure and COVID-19 incidence and mortality in the US. Jama. 2020;324:859–870. doi: 10.1001/jama.2020.14348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck-Sagué C., et al. Hospital outbreak of multidrug-resistant Mycobacterium tuberculosis infections: factors in transmission to staff and HIV-infected patients. Jama. 1992;268:1280–1286. doi: 10.1001/jama.1992.03490100078031. [DOI] [PubMed] [Google Scholar]
- Biribawa C., et al. Measles outbreak amplified in a pediatric ward: lyantonde District, Uganda, August 2017. BMC Infect. Dis. 2020;20:1–8. doi: 10.1186/s12879-020-05120-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borenstein M., et al. John Wiley & Sons; 2021. Introduction to Meta-Analysis. [Google Scholar]
- Cao W., et al. A web-based appointment system to reduce waiting for outpatients: a retrospective study. BMC Health Serv. Res. 2011;11:318. doi: 10.1186/1472-6963-11-318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chadwick P., McCann R. Transmission of a small round structured virus by vomiting during a hospital outbreak of gastroenteritis. J. Hosp. Infect. 1994;26:251–259. doi: 10.1016/0195-6701(94)90015-9. [DOI] [PubMed] [Google Scholar]
- Chapman S.J., Hill A.V. Human genetic susceptibility to infectious disease. Nat. Rev. Genet. 2012;13:175–188. doi: 10.1038/nrg3114. [DOI] [PubMed] [Google Scholar]
- Charles K.E., Veitch J.A. Institute for Reserch in Construction; 2002. Environmental Satisfaction in Open-Plan Environments: 2. Effects of Workstation Size, Partition Height and Windows. National Reserch Council Canadá. Internal Report No. IRC-IR-845. Recuperado de https://nparc. nrc-cnrc. gc. ca/eng/view/fulltext. [Google Scholar]
- Cho S.Y., et al. MERS-CoV outbreak following a single patient exposure in an emergency room in South Korea: an epidemiological outbreak study. Lancet. 2016;388:994–1001. doi: 10.1016/S0140-6736(16)30623-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention Nosocomial transmission of Mycobacterium tuberculosis found through screening for severe acute respiratory syndrome--Taipei, Taiwan. MMWR. Morbid. Mortal. Weekly Rep. 2004;53:321. 2003. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention Tuberculosis outbreak in a community hospital--District of Columbia, 2002. MMWR. Morbid. Mortal. Weekly Rep. 2004;53:214. [PubMed] [Google Scholar]
- Curmei M., et al. Estimating household transmission of SARS-CoV-2. medRxiv. 2020;23:20111559. 2020 05. [Google Scholar]
- Distasio A.J., Trump D.H. The investigation of a tuberculosis outbreak in the closed environment of a US Navy ship. Mil. Med. 1990;155:347–351. 1987. [PubMed] [Google Scholar]
- Dooley S.W., et al. Nosocomial transmission of tuberculosis in a hospital unit for HIV-infected patients. Jama. 1992;267:2632–2634. [PubMed] [Google Scholar]
- Fujiyoshi S., et al. Transmission of airborne bacteria across built environments and its measurement standards: a review. Front. Microbiol. 2017;8:2336. doi: 10.3389/fmicb.2017.02336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graham D.R., et al. Efficiency and competition in the airline industry. Bell J. Econ. 1983:118–138. [Google Scholar]
- Guclu H., et al. Social contact networks and mixing among students in K-12 schools in Pittsburgh, PA. PloS One. 2016;11 doi: 10.1371/journal.pone.0151139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill E.J., et al. Workplace flexibility, work hours, and work-life conflict: finding an extra day or two. J. Fam. Psychol. 2010;24(3):349–358. doi: 10.1037/a0019282. [DOI] [PubMed] [Google Scholar]
- Iversen K., et al. Risk of COVID-19 in health-care workers in Denmark: an observational cohort study. Lancet Infect. Dis. 2020 doi: 10.1016/S1473-3099(20)30589-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karako K., et al. Shifting work style to teleworking as a new normal in face of COVID-19: analysis with the model introducing intercity movement and behavioral pattern. Ann. Transl. Med. 2020;8:1056. doi: 10.21037/atm-20-5334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenyon T.A., et al. Transmission of multidrug-resistant Mycobacterium tuberculosis during a long airplane flight. N. Engl. J. Med. 1996;334:933–938. doi: 10.1056/NEJM199604113341501. [DOI] [PubMed] [Google Scholar]
- Khan R.F., Meyer J.D. How does the hierarchy of controls integrate with the epidemiologic triangle to help address and understand transmission of SARS-CoV-2? J. Occup. Environ. Med. 2020;62:e665–e668. doi: 10.1097/JOM.0000000000002009. [DOI] [PubMed] [Google Scholar]
- Lau H., et al. The positive impact of lockdown in Wuhan on containing the COVID-19 outbreak in China. J. Trav. Med. 2020;27 doi: 10.1093/jtm/taaa037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauderdale D.S., et al. Self-reported and measured sleep duration: how similar are they? Epidemiology. 2008:838–845. doi: 10.1097/EDE.0b013e318187a7b0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leckerman K.H., et al. Risk factors for healthcare-associated, laboratory-confirmed influenza in hospitalized pediatric patients: a case-control study. Infect. Control Hosp. Epidemiol. 2010;31:421–424. doi: 10.1086/651311. [DOI] [PubMed] [Google Scholar]
- Lee V.J., et al. Interrupting transmission of COVID-19: lessons from containment efforts in Singapore. J. Trav. Med. 2020;27 doi: 10.1093/jtm/taaa039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lei H., et al. Household transmission of COVID-19-a systematic review and meta-analysis. J. Infect. 2020;81:979–997. doi: 10.1016/j.jinf.2020.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lessa F.C., et al. Health care transmission of a newly emergent adenovirus serotype in health care personnel at a military hospital in Texas, 2007. J. Infect. Dis. 2009;200:1759–1765. doi: 10.1086/647987. [DOI] [PubMed] [Google Scholar]
- Levinson M. 2017. Job Creation in the Manufacturing Revival. [Google Scholar]
- Lidström A.-K., et al. Work at inpatient care units is associated with an increased risk of SARS-CoV-2 infection; a cross-sectional study of 8679 healthcare workers in Sweden. Ups. J. Med. Sci. 2020:1–6. doi: 10.1080/03009734.2020.1793039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindberg C.M., et al. Effects of office workstation type on physical activity and stress. Occup. Environ. Med. 2018;75:689–695. doi: 10.1136/oemed-2018-105077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacIntyre C.R., et al. High rate of transmission of tuberculosis in an office: impact of delayed diagnosis. Clin. Infect. Dis. 1995;21:1170–1174. doi: 10.1093/clinids/21.5.1170. [DOI] [PubMed] [Google Scholar]
- Madewell Z.J., et al. Household transmission of SARS-CoV-2. JAMA Network Open. 2020;3 doi: 10.1001/jamanetworkopen.2020.31756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marks P., et al. A school outbreak of Norwalk-like virus: evidence for airborne transmission. Epidemiol. Infect. 2003;131:727–736. doi: 10.1017/s0950268803008689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCaig L.F., Nawar E.W. National hospital ambulatory medical care survey: 2004 emergency department summary. Adv. Data. 2006:1–29. [PubMed] [Google Scholar]
- Medrano B.A., et al. A missed tuberculosis diagnosis resulting in hospital transmission. Infect. Contr. Hosp. Epidemiol. 2014;35:534. doi: 10.1086/675833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milne R.J., Kelly A.R. A new method for boarding passengers onto an airplane. J. Air Transport. Manag. 2014;34:93–100. [Google Scholar]
- Mohebbifar R., et al. Outpatient waiting time in health services and teaching hospitals: a case study in Iran. Global J. Health Sci. 2013;6:172–180. doi: 10.5539/gjhs.v6n1p172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossong J., et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5:e74. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mozzi A., et al. Genetic susceptibility to infectious diseases: current status and future perspectives from genome-wide approaches. Infect. Genet. Evol. 2018;66:286–307. doi: 10.1016/j.meegid.2017.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muennig P., Woolf S.H. Health and economic benefits of reducing the number of students per classroom in US primary schools. Am. J. Publ. Health. 2007;97:2020–2027. doi: 10.2105/AJPH.2006.105478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musher D.M. How contagious are common respiratory tract infections? N. Engl. J. Med. 2003;348:1256–1266. doi: 10.1056/NEJMra021771. [DOI] [PubMed] [Google Scholar]
- Nikolakopoulou A., et al. Demystifying fixed and random effects meta-analysis. Evid. Base Ment. Health. 2014;17:53–57. doi: 10.1136/eb-2014-101795. [DOI] [PubMed] [Google Scholar]
- Pan S.-W., et al. Assessment of latent tuberculosis infection in psychiatric inpatients: a survey after tuberculosis outbreaks. J. Microbiol. Immunol. Infect. 2016;49:575–583. doi: 10.1016/j.jmii.2015.10.005. [DOI] [PubMed] [Google Scholar]
- Rocklöv J., Sjödin H. High population densities catalyse the spread of COVID-19. J. Trav. Med. 2020;27 doi: 10.1093/jtm/taaa038. taaa038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal S., Hill A.V. Genetic susceptibility to infectious disease. Trends Microbiol. 2003;11:445–448. doi: 10.1016/s0966-842x(03)00207-5. [DOI] [PubMed] [Google Scholar]
- Skarlatos D., Manatakis M. Effects of classroom noise on students and teachers in Greece. Percept. Mot. Skills. 2003;96:539–544. doi: 10.2466/pms.2003.96.2.539. [DOI] [PubMed] [Google Scholar]
- Sze To G.N., Chao C.Y.H. Review and comparison between the Wells-Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20:2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tasaka M., et al. A tuberculosis outbreak in a psychiatric hospital: Kanagawa, Japan, 2012. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268819002206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taubenberger J.K., Morens D.M. 1918 Influenza: the mother of all pandemics. Emerg. Infect. Dis. 2006;12:15–22. doi: 10.3201/eid1201.050979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization . Global Tuberculosis Report 2020. World Health Organization; 2020. https://www.who.int/publications/i/item/9789240013131 [Google Scholar]
- Xie Z., Or C. Associations between waiting times, service times, and patient satisfaction in an endocrinology outpatient department: a time study and questionnaire survey. Inquiry. 2017;54 doi: 10.1177/0046958017739527. 46958017739527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You S., et al. Assessment of monthly economic losses in Wuhan under the lockdown against COVID-19. Human. Soc. Sci. Comm. 2020;7:1–12. [Google Scholar]
- Zhang J., Kai F.Y. What's the relative risk?: a method of correcting the odds ratio in cohort studies of common outcomes. Jama. 1998;280:1690–1691. doi: 10.1001/jama.280.19.1690. [DOI] [PubMed] [Google Scholar]
- Zheng S., Kahn M.E. Land and residential property markets in a booming economy: new evidence from Beijing. J. Urban Econ. 2008;63:743–757. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.