Abstract
Coleus (Coleus scutellarioides) is a popular ornamental plant that exhibits a diverse array of foliar color patterns. New cultivars are currently hand selected by both amateur and experienced plant breeders. In this study, we reimagine breeding for color patterning using a quantitative color analysis framework. Despite impressive advances in high-throughput data collection and processing, complex color patterns remain challenging to extract from image datasets. Using a phenotyping approach called “ColourQuant,” we extract and analyze pigmentation patterns from one of the largest coleus breeding populations in the world. Working with this massive dataset, we can analyze quantitative relationships between maternal plants and their progeny, identify features that underlie breeder-selections, and collect and compare public input on trait preferences. This study is one of the most comprehensive explorations into complex color patterning in plant biology and provides insights and tools for exploring the color pallet of the plant kingdom.
Quantitative analysis of color patterning in a large coleus breeding population reveals color features that are associated with aesthetic value.
Introduction
Coleus (Coleus scutellarioides) is a common ornamental bedding plant that is bred for its brilliant and diverse foliar color patterning (Bailey, 1924; Pedley and Pedley, 1974; Paton et al., 2018, 2019). Wild relatives in the Coleus genus harbor a small degree of variegated pigmentation that has been expanded into distinctive new cultivars that harbor complex variegation patterns through successive rounds of hybridization and selection (Suddee et al., 2004). The prevalence of coleus in gardens and urban landscapes around the world is a testament to the unique aesthetic capacity of this species (Rogers, 2008). With over 500 cultivars on the market, and new ones added each year, coleus represents one of the largest and most diverse examples of pigmentation patterning within a single species.
Although the genetic basis for color patterning in coleus is poorly studied, conserved regulatory networks identified in other model plants can provide insight and a fundamental framework for understanding the molecular genetic mechanisms of pigmentation patterning in this horticultural model (Albert et al. 2014). The biochemical deposition of anthocyanins produces the vast majority of red, blue, and purple pigmentation in plants (Forkmann 1991; Holton and Cornish 1995). Anthocyanin biosynthesis pathways can be activated uniformly, creating solid colors, or they can be spatially regulated, producing spots and stripes that give rise to patterned color traits. The spatial regulation of pigment deposition is controlled by an MYB-bHLH-WD40 repeat (MBW) regulon that functions in diverse species to activate the anthocyanin biosynthetic pathway (Paz-Ares et al. 1987; Ludwig et al. 1989; Goodrich et al. 1992; de Vetten et al. 1997; Quattrocchio et al. 1998, 1999; Walker et al. 1999; Spelt et al. 2000; Schwinn et al. 2006; Albert et al. 2011, 2014; Hsu et al. 2015; Ding et al. 2020). A long-standing hypothesis posed by the late computer scientist, Alan Turing (1990), postulates that self-generated pigmentation patterns in nature arise from a reaction–diffusion-based mechanism involving a local activator that self-activates and turns on a mobile inhibitor that represses the activator (Kondo and Miura 2010). Molecular regulators for Turing’s proposed reaction–diffusion model have now been identified in petunia (Petunia hybrida) and monkeyflowers (Mimulus), providing a genetic basis for pigmentation patterning that could likely be extended to the wide diversity of patterning found among coleus cultivars (Albert et al. 2014; Ding et al. 2020).
Advances in plant phenotyping have revolutionized how humans interact with botanical traits (Fahlgren et al., 2015; Gehan et al., 2017; Gehan and Kellogg, 2017; Li et al., 2018b; Amézquita et al., 2020; Prunet and Duncan, 2020). High-throughput data collection has enabled rapid agricultural trait selection (Shakoor et al., 2019; Singh et al., 2019; Ibba et al., 2020), early detection and management of disease (Mutka and Bart, 2014; Shakoor et al., 2017), and large-scale two-dimensional (2D) morphological analyses (Li et al., 2018a). Penetrating high-resolution imaging technologies, such as X-ray CT and laser ablation tomography have also made complex, three-dimensional (3D) topologies accessible (Chitwood et al., 2019; Li et al., 2019b, 2020; Amézquita et al., 2020; Prunet and Duncan, 2020; Vanhees et al., 2020). Despite these enormous advances, rapid phenotyping for complex color patterning remains a major hurdle in high-throughput phenotyping (HTP) analysis. Indeed, the majority of color phenotypes expressed in plants are typically uniformly expressed [e.g. monochromatic leaves (Gehan et al., 2017) and berries (Underhill et al., 2020)], un-patterned in their expression [e.g. lesions (Arnal Barbedo, 2013; Gobalakrishnan et al., 2020; Xie et al., 2020)], or have highly predictable patterns (e.g. nectar guides). These color phenotypes are readily extractable using existing image processing approaches that are not suited for the complex suite of color patterns represented in our coleus population (Arnal Barbedo, 2013; Gobalakrishnan et al., 2020; Xie et al., 2020). Here, we address the need for enhanced tools to extract and analyze complex color patterns. In this study, we map out pigmentation values as 3D point clouds in Lab color space, extract the continuous distribution of color using Gaussian density estimation (Li et al., 2019a), dissect color patterns based on pigmentation position on 2D leaves, quantify bilateral symmetry for shape and color, and separate shape from color using thin-plate spline deformation.
Given the prominence of coleus in the gardening marketplace, and the vast diversity of pigmentation patterns that are exhibited within coleus breeding populations, coleus as a breeding system serves as an ideal platform for testing this quantitative approach for HTP color phenotyping. In this study, we develop a pipeline to extract quantitative descriptors for foliar pigmentation patterns from one of the largest coleus breeding populations in the world (n > 32,800 plants). We can extract the distribution of all existing pigmentation patterns presented within this massive breeding population, quantify maternal plant–progeny pigmentation relationships, and identify aesthetic features that are associated with the increased value from the perspective of the breeder as well as the general public. This work is built on a powerful study system and provides a framework for approaching complex color phenotyping. This work has direct implications for investigating color features in both ornamental plant breeding and ecological systems, where pigmentation patterns play an important role in influencing how plants interact with humans, pollinators, and herbivores.
Results
New coleus breeding population
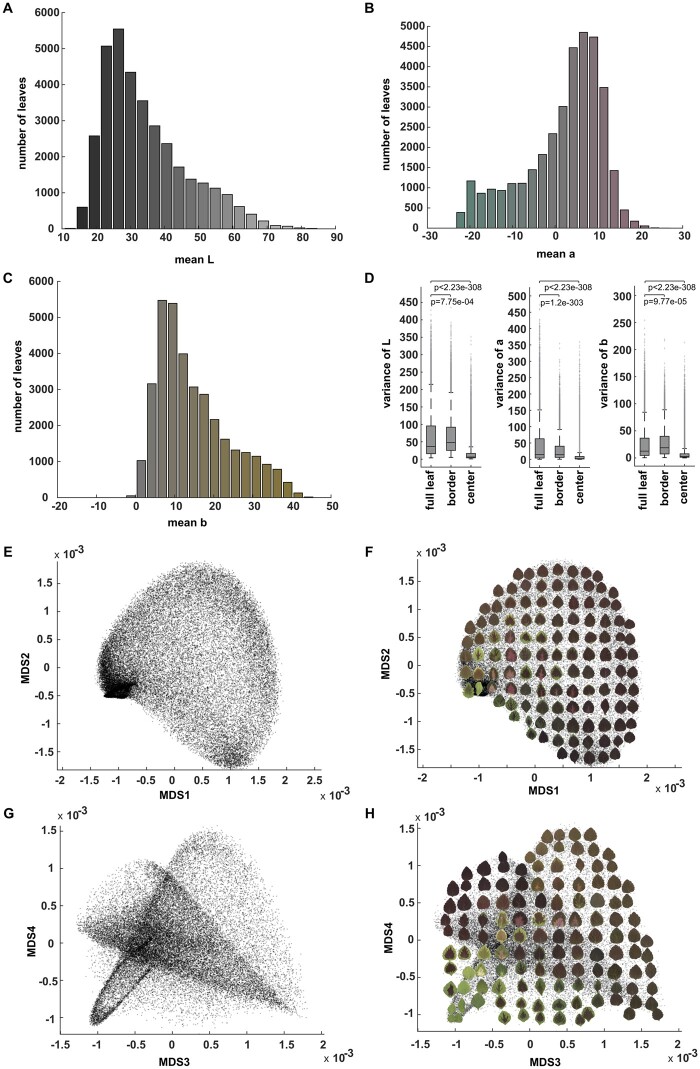
Coleus is one of the most diverse species with regards to leaf pigmentation patterning in the world. Brilliant new coleus cultivars harboring novel leaf color and shape phenotypes can be generated using a recurrent mass selection approach. In this study, we took advantage of a very large coleus breeding population to explore the full spectrum of possible pigmentation patterns and their influence on breeding processes. We used 133 open-pollinated elite coleus lines that exhibit a wide range of existing color and shape phenotypes (Figure 1, A and B) to generate a large population that harbors novel pigmentation combinations. To capture these new combinations, we imaged leaves from 34,825 F1 on high-resolution color scanners (Figure 1, C; Supplemental Figure S1). Color data are typically recorded as a composite of discrete Red, Green, and Blue (RGB) values that range from 0 to 255. We transformed our RGB data into the continuous Lab color space, which we then plotted as a 3D point cloud and extracted quantitative pigmentation data using a Gaussian density estimator function (Figure 1C). A Gaussian density estimator function is a smoothed version of a histogram; it estimates data density by summing all of the normal kernels, which are placed on each of the data points. Higher values are produced from regions with more data points, while lower values are produced from regions with sparse and/or noisy data, thus making the function robust.
Figure 1.
Experimental design, high throughput sampling, and color analysis. A, Total of 133 field-grown parents were randomly mated by pollinators, seeds were collected from each maternal plant, sown in progeny family blocks and grown for 5–6 weeks in a greenhouse. B, One fully expanded leaf was harvested and scanned from each plant in the population. C, Color thresholding was used to isolate binary masks for each leaf. Discrete RGB color matrices were converted to the continuous Lab color space, and color matrices for each leaf were spatially separated into segments: “full”—defined as the entire color matrix, “border”—defined as the outer 15% of pixels from the leaf boundary to the centroid, and “center”—defined as the inner 75% of pixels from the centroid to the boundary.
To visualize the CIELAB (L*a*b*) color space within our breeding population, we plotted the mean L* (lightness), a* (green-to-magenta), and b* (blue-to-yellow) values that were extracted from each leaf. The majority of leaves within the population skewed toward darker (lower) mean L* values (Figure 2A; Supplemental Figure S2). Mean values for a* spanned from magenta-to-green, but were more heavily concentrated toward the magenta/maroon half of the range (Figure 2B; Supplemental Figure S2), and mean values for b* were almost exclusively in the positive range, and were strongly concentrated toward yellow rather than blue values (Figure 2C; Supplemental Figure S2). While this approach provides an estimate of mean color distributions, it fails to capture color patterning within the population. Three discrete regions can be used to generically describe that vast majority of variegation patterns in coleus: the area surrounding the veins, the leaf border, and the leaf center. Importantly, the depth of border and center pigmentation can vary substantially across varieties; we applied a Gaussian density estimator function to three-dimensional point clouds that captured the middle ground between thick and thin border (15% of pixels from the leaf boundary) and center (75% of the pixels from the centroid) regions of the leaf (Figure 1C). Venation varies considerably from leaf-to-leaf, and thus it is challenging to consistently extract this value from a large population, so we did not consider the contribution of variegated venation for this study. Our isolated border and center regions differed significantly from the variance of full L*a*b* values (P-values ranged from 2.12 e-208 to <2.23 e-308 for two-sample Kolmogorov–Smirnov test; P-value ranged from 3.78e-191 to <2.23e-308 in two-sample Levene’s test), indicating that these regions exhibit distinct color patterns (Figure 2D). Full leaves show the largest variance in color patterning, and center regions show the least variance in color patterning. Principal component analysis (PCA) or multidimensional scaling (MDS) can be used to extract the main sources of variance within complex datasets with vector or distance matrix as input, respectively. To investigate the variance in color patterning within our population, we generated PCA plots from the vectorized Lab Gaussian density estimator for the full leaf (Supplemental Figure S3A), border (Supplemental Figure S3B), center (Supplemental Figure S3C), and MDS plots for composite full leaf plus border plus center pixel values (Figure 2E–H). We have superimposed example leaves on top of the plot to illustrate the major color differences that are represented within the population (Figure 2, F and H; Supplemental Figure S3).
Figure 2.
CIELAB (L*a*b*) color distribution. A, The histogram of mean L (lightness) values of the studied coleus population. The color for each bar corresponds to the Lab color with L value at x axis, a = 0 and b = 0. B, Histogram of mean a (green to magenta) values. The color for each bar corresponds to the Lab color with a value at x axis, L = 50 and b = 0. C, Histogram of mean b (blue to yellow) values. The color for each bar corresponds to the Lab color with b value at x axis, L = 50 and a = 0. D, Boxplot of the variance of L, a, and b for full leaf, border, and center. The “+” signs mark outliers that are more than 1.5 interquartile ranges above the upper quartile or below the lower quartile for each box, the central line indicates the median, top and bottom edges of the box indicate 25th and 75th percentiles. Whiskers extend to the most extreme non-outliers of the data. P-values for full leaf versus border, full leaf versus center are also shown using paired sample Levene’s test to show the variances of the distribution are significantly different, E and G. MDS plot (MDS1 vs MDS2 in (E) and MDS3 vs MDS4 in (G)) for the pattern difference defined by the difference of Gaussian density estimator in 3D Lab colorspace across the full leaf, border, and center, F, and (H) The same MDS plots shown in (E) and (G) but with example leaves superimposed to provide visual examples of the data distribution.
The sub-sample border and center plots provided poor separation of the major pattern classes within the population (Supplemental Figure S3, B and C). For example, green bordered leaves with maroon centers are distributed in multiple locations across the border and center PCA plots (Supplemental Figure S3, B and C). The full leaf plot performed much better with regard to pattern separation compared with the sub-sample plots; however, it still failed to produce distinct groupings for detailed pattern differences. For example, pink and maroon center variegation patterns are intermixed with solid maroon leaves in all four dimensions of the full leaf PCA (Supplemental Figure S3A). The composite plot, on the other hand, accounts for both global and isolated center and border pigmentation values, and thus was able to resolve distinct pattern groupings (Figure 2E–H). The first dimension clearly separates the population along the green-to-magenta divide (the a* value of the L*a*b* color space), while the second dimension separates the population from darker (toward the bottom) to lighter L* pixel distributions (Figure 2F). In the third and fourth dimensions, five major patterns are resolved: solid orange in the upper right, solid deep purple in the upper left, solid green in the lower left, solid maroon in the lower right, and several sub-populations of variegated patterns in the lower left and center (Figure 2H). In the lower left corner of MD 3 and MD 4, we were able to resolve most of the variegated patterns into subpopulations based on center and border features, for example, wide maroon centers with thin green borders, light pink centers with green, maroon, or orange borders, yellow/white centers with green borders, and even deep purple venation on green leaves. There are, however, two pigmentation patterns that we failed to isolate in our composite plot. First, the leaves that have both relatively small central pigmentation regions and low contrast between the border and center colors, and second, the leaves with random green and purple sectors whose patterns were most likely generated by active transposons (Tilney-Bassett et al., 1986; Frank and Chitwood, 2016). Overall, this composite MDS approach performed very well with regard to separating the population into major pattern groups.
Maternal phenotypes influence the phenotypic distance of their progeny
The vast majority of brilliant new coleus color patterns result from the spatially regulated production of anthocyanins (purple, red, and blue pigments) and loss of chlorophyll (white and yellow pigments). Classic genetic analyses in coleus indicate that purple pigmentation is controlled by a single dominant allele, while loss of chlorophyll pigmentation resulting in yellow/albino phenotypes results from a recessive allele (Boye and Rife, 1938; Rife, 1948). These studies were carried out in simplified phenotypic and genetic backgrounds that may not reflect the genetic context of our population, which was generated from highly heterozygous allopolyploid parents. Indeed, modern genetic work in diverse model systems demonstrates that anthocyanin production is controlled by a complex of transcription factors, rather than a single gene (Albert et al., 2014). Furthermore, a recent mathematical model for flavonoid biosynthesis demonstrates how purple, blue, and red pigmentation traits are actually under complex metabolic control, involving interactions between multiple alleles (Wheeler and Smith, 2019).
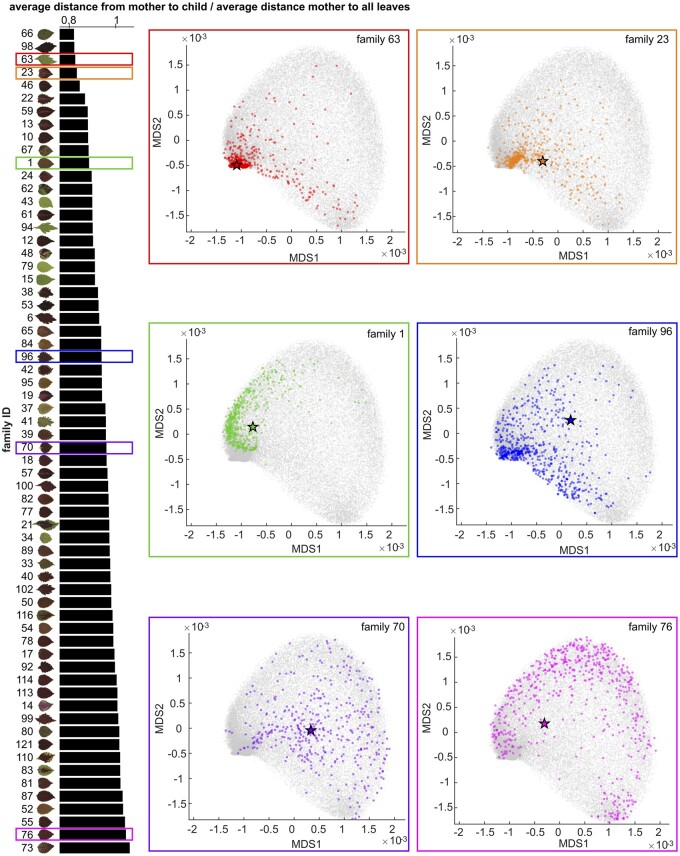
To address patterning relationships within our population of 34,825 individuals, we quantified the relative distance between maternal plants and their progeny and visualized it in MDS space (Figure 3), and then calculated the heritability of these color traits using a mixed effect model. We need to note that our population was generated using an uncontrolled, open-pollination design in which honeybee hives were brought into the field to ensure pollination and promote outcrossing among the maternal plants. In our field setting, it is impossible to track the male half of the parental equation without the developing genotype-specific molecular markers, so we are only analyzing maternal-to-progeny relationships. Additional limitations that we cannot exclude from this experimental design is the potential bias that leaf patterning can have on pollinator behavior, and the bias that may be induced due to beehive position. While we cannot assume true random mating within this context, we have reason to believe that pollination behavior is close to random based on the fact that coleus flowers tend to be highly conserved with respect to their morphology and color. Thus, they are likely equally attractive to our honey bee pollinators.
Figure 3.
Maternal Plant-Progeny relationships. On the left panel, each bar shows the average distance from maternal plants to progeny divided by the average distance from maternal plants to all leaves (x-axis) for each progeny family (y-axis) superimposed upon the scan of the maternal plant. On the right panels, there are six MDS plots (MDS1 vs MDS2) from six progeny families as examples with different colors correspond to the families highlighted in the same colored rectangles on the left panel. On each MDS plot, grey dots show all leaves, colored stars represent the maternal plants, and colored dots are the progeny.
We identified a few clear trends from our mother–child analysis. First, brighter maternal plants (high L*) tend to produce progeny with a greater variance of pixel brightness (Supplemental Figure S4A). This is exemplified by the progeny in families 79 and 43. We also observed that green maternal plants (low a*) tend to produce progeny that exhibit a large variance between green and magenta (Supplemental Figure S4B, e.g. the progeny in families 43 and 94). This is logical, given that purple and magenta pigments have been linked to dominant alleles, and thus would be expressed in F1 crosses with purple/magenta pollen donors. Along similar lines, yellow maternal plants (high b*) tend to produce progeny that express a large variance in the yellow-to-blue color range (Supplemental Figure S4C, e.g. the progeny in families 79 and 29). We also found that maternal plants with complex color patterning (high variance of L*, a*, or b*) tend to produce progeny with larger variance in their complexity (Figure 3; Supplemental Figure S4, D–F, e.g. the progeny in families 22 and 23), which results in more diverse color patterns. Surprisingly, we only saw a minor trend for green versus purple maternal plants being closer versus farther away (respectively) from their progeny in phenotypic space (Figure 3). The majority of green-leafed maternal plants fall on the top half of the phenotypic distance plot (e.g. smaller distance, e.g. the progeny in families 63, 43, 94, 79, and 15), while purple maternal plants are distributed across the phenotypic spectrum (Figure 3). Overall, our measurements of maternal–progeny color relationships agree strongly with our calculation for the heritability of Lab and MDS color traits. All of these traits exhibit moderate to high narrow-sense heritability (L = 0.53, a = 0.60, b = 0.58, MDS1 = 0.57, MDS2 = 0.56, MDS3 = 0.46, and MDS4 = 0.59; Supplemental Tables S1–S4), indicating that these color traits are under strong genetic control in coleus.
Bilateral symmetry for color and shape are associated with the selection of new cultivars
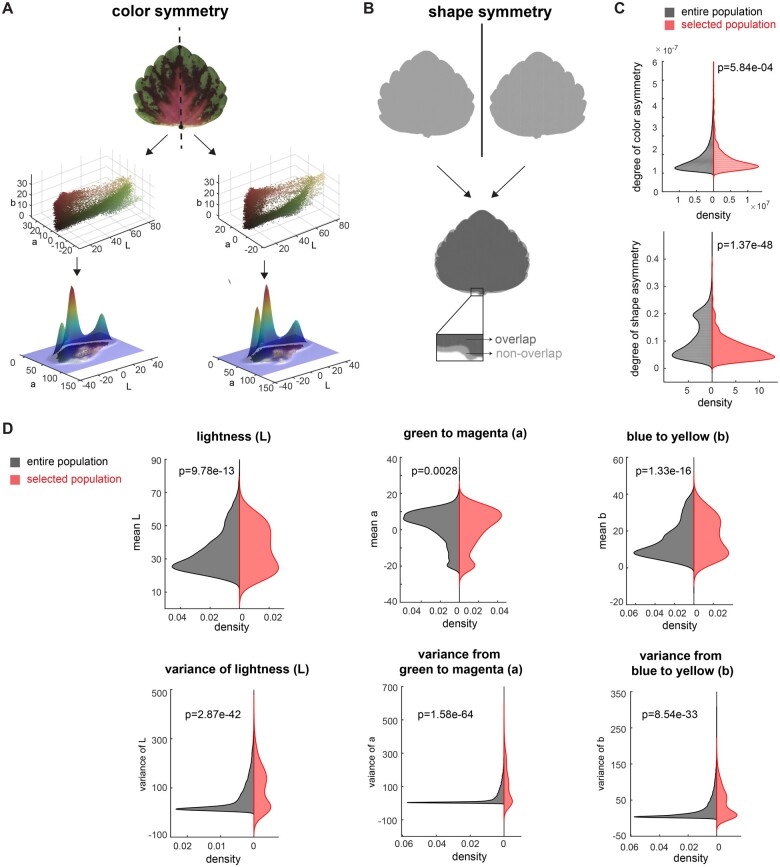
New coleus cultivars are hand selected based on the visual identification of target traits, through a process that is frequently referred to as selection via “the breeder’s eye” (Fasoula et al., 2019). Our experienced coleus breeder identified 697 selected lines from the population to carry forward for potential cultivar development. To investigate the influence of color patterning and symmetry on our breeding process, we tested whether our selected population deviated significantly from the total population with regard to mean Lab distributions, as well as color and shape symmetry (Figure 4).
Figure 4.
Influence of color and shape on cultivar selection. A, Mirror symmetry of color: Partitioning of each leaf into left and right halves (top panel), convert each part into 3D point cloud in Lab color space (middle panel), and calculate the 3D Gaussian density estimator (lower panel, only shows 2D Gaussian density estimator for visualization). B, Mirror symmetry of shape: flip the leaf horizontally (top panel), measure the non-overlapped area (lower panel) and calculate the percentage of a non-overlapped area over the leaf area. C, Distribution of degree of color asymmetry (top panel) and shape asymmetry (bottom panel) for the entire population (in black) and selected population (in red), D, Distribution of mean L (top left), mean a (top middle), mean b (top right), variance of L (bottom left), variance of a (bottom middle), and variance of b (bottom right) for entire population (in black) and selected population (in red). Significance was measured using a two-sample Kolmogorov-Smirnov test for the distribution difference for uneven sample sizes.
To determine if specific color features are associated with cultivar selection, we tested whether the selected pool differed from the total population with regard to independent components of the Lab color space (Figure 4D). Interestingly, the selected pool deviated significantly from the full population with regard to both the mean and variance for each of the three Lab color components (Figure 4D). Comparative plots of mean Lab space for the total population (in gray) and selected pool (in red) clearly show that the source of divergence between these two populations comes from an accentuated bimodal distribution on either end of the spectra within the selected pool, indicating that the breeder is selecting along the extremes of the color space. For example, within the L spectrum (the light-to-dark spectrum), the enriched bimodal distribution reflects strong selection for both bright and dark (deep colored) pixel values (P-value in two-sample Kolmogorov–Smirnov for mean L = 9.78e-13; Figure 4D). Furthermore, our analysis revealed significant divergence in the distribution of selected versus total population values for variance within the Lab space (P-values for L = 2.87e-42, a = 1.58e-64, b = 8.54e-33). Again, graphs for the selected pool have strong bimodal distributions for all three Lab spectra indicating that there was a selection for varieties with either high color contrast or uniform (solid color) patterning (Figure 4D). In contrast, the total population graphs are concentrated around a single mean peak (Figure 4D).
A long-standing theory posits that symmetry is associated with aesthetic value (Birkhoff, 1933). To quantify the degree of mirror symmetry within leaves from the selected versus total population, we manually partitioned every leaf into left and right halves by drawing a line from the tip to the base of the leaf. We then quantified color symmetry by comparing the Lab Gaussian distributions between the left and right halves (Figure 4A), and shape symmetry by folding binary leaf silhouettes along the midline and calculating the percentage of non-overlapped pixels (Figure 4B). Our two-sample Kolmogorov–Smirnov test between the selected and total population showed very strong statistical support for both color and shape symmetry playing a significant role in influencing the selection process (P-value = 5.84e-04 and Cohen’s d effect size 0.6845 for increased color symmetry, and P-value = 1.37e-48 and Cohen’s d effect size 0.1816 for increased shape symmetry in the selected population; Figure 4C).
Taken together, these analyses demonstrate how the “breeder’s eye” reshaped the selected pool to significantly enhance mirror symmetry for both color and shape, and concentrate the cultivars with either high color contrast or complete color uniformity. Notably, this analysis accounts for the first round of selection where a high level of variability concentrated around both commercial targets and novel aesthetic traits are maintained. Approximately 6–8 of the plants from this large selection pool are taken through the commercialization process.
Public survey shows an overlap between public preferences and breeder selection
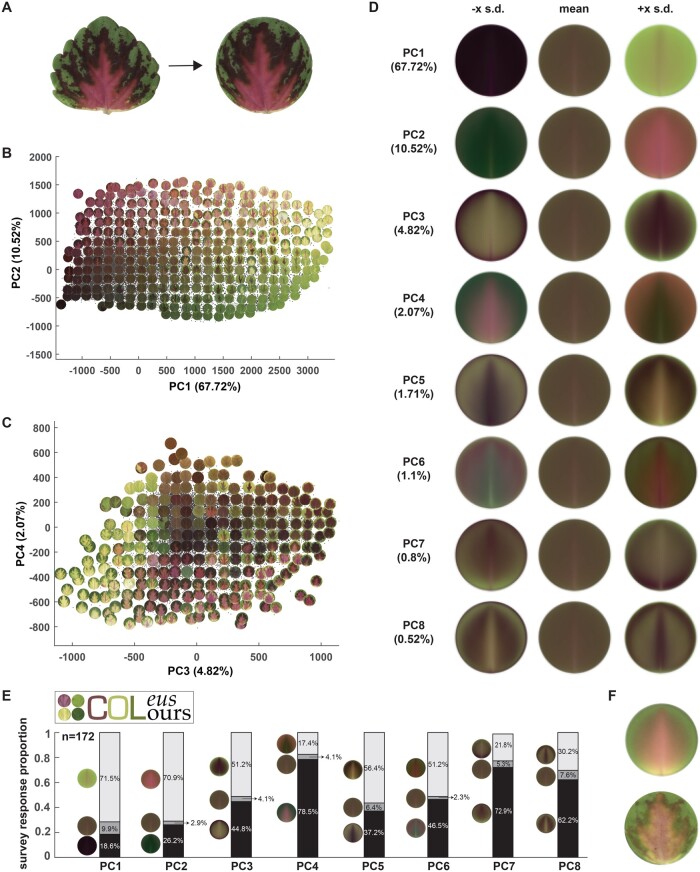
Once we established the quantitative color structure for our breeding population, we explored how the existing coleus color space matched with public color preferences. To do this, we created a pilot survey that was openly distributed using a dedicated Twitter account (@ColeusColours). To avoid the confounding influence of leaf shape on color preference, we standardized the leaf orientation based on the bilateral symmetrical line and deformed our leaf shapes into circles using a thin plate spline interpolation (Figure 5A), this method smoothly transforms the border shape into a uniform edge with minor distortion of the internal color patterning. Next, we performed a PCA with our circularized leaves (Figure 5, B and C) and used the top principal components (PCs) to construct our survey for color preference. Our survey presented eight questions that asked the participants to select their preference from the mean and plus or minus a few standard deviations along PC axis (“eigencolors”) for each of the top 8 PCs (Figure 5D). We gathered data from 172 participants, plotted each of their preferences (Figure 5E), and then reconstructed the ideal leaf based on public preferences for the first eight eigencolors with weighted contributions based on the percentage of variance contained within each PC (Figure 5F). Our results show that participants have a strong preference for very green (responses to PC1 in Figure 5E), very magenta (responses to PC2 in Figure 5E), and leaves with high contrast color patterns (responses to the contrasting standard deviation extremes in PC3–PC8). The resulting ideal leaf that was reconstructed from the survey data has a high contrast bright green border with internal magenta pigmentation and yellow base (Figure 5F). This ideal leaf not only matches an existing variegated pattern that was resolved in the lower left-hand quadrant of MD 3 and MD 4 in our original population analysis (Figure 2H), it is also consistent with the direction of breeding in our selected pool (Figure 4D). This result indicates that even with this small pilot survey, there is an overlap between public preferences and new cultivar development. To provide a quantitative test for whether the public preference and breeder’s selection overlap, we calculated the distance from the ideal leaf to the other leaves using the first 8 PC scores. The average distance from the ideal leaf to selected leaves is 1981–1987. The average distance from the ideal leaf to all the other leaves is 2003–2009, demonstrating that leaves after selection get closer to the ideal leaf in the first 8 PC spaces.
Figure 5.
Public survey for color preferences using shape-transformed leaves. A, Deform each leaflet into a disk by thin-plate spline interpolation—non-linear deformation into a unit circle. B and C, PCA plot superimposed upon some example of leaves [PC1 vs PC2 in (B) and PC3 vs PC4 in (C)] for the pixel Lab values of a deformed leaflet. D, Eigencolors for the first eight PCs and the percentage of variance they explained. For PC k, the eigencolor at −x SD and +x SD along PC axis is shown, where x = 3+(k-1)×0.5 for better visualization. E, Survey logo (top left) and the survey result from 172 responses. White bars = the proportion of responses in favor of positive eigencolors, grey bars = the proportion of responses that selected mean eigencolors, and black bars = the proportion of responses that selected negative eigencolors. F, Reconstructed pattern (top) and closest real leaf (bottom) from first eight eigencolors with weights guided by the survey response proportion. Raw survey data is available in Supplemental Dataset S2.
Discussion
HTP has transformed our ability to select and optimize plant traits (Das et al., 2015; Shakoor et al., 2017; York, 2019; Liu et al., 2020). Relative to morphological and architectural phenotypes, approaches for collecting and analyzing color patterns in plants remain limited. Indeed, existing methods of HTP data analysis are not well-suited for the large suite of patterning phenotypes exhibited in ornamental plants, like coleus. In this article, we use an approach to address the problem of complex color patterning in a large coleus breeding population. We partitioned the 2D leaf into different zones based on morphology and transformed the color data into a continuous, 3D color space, and applied a Gaussian density estimator to extract pixel patterning across the 2D map of the leaf. Using this approach, we were able to successfully resolve the major pigmentation patterns contained within one of the largest and most diverse color patterned breeding populations in the world. Historically, these patterns were discussed using qualitative descriptors. By extracting the quantitative features underlying this pattern space, we were able to mathematically analyze relationships between maternal plants and their progeny, identify how aesthetic preferences reshape the color properties of the breeding population, and independently address whether public preferences align with commercial breeding goals.
Our maternal–offspring color analysis examines the inheritance of pigmentation traits through a quantitative lens. We identified quantitative connections between color variance in maternal plants and their offspring that have direct applications for ornamental breeding. We supplemented this analysis with calculations for trait heritability and found that quantitative color patterns have moderate to high narrow-sense heritability. Breeders and researchers looking to increase the range of brightness within their population can start with a brighter parental population; we show that brighter mothers produce offspring that express a wider variance of brightness. Those aiming to increase overall color variation would want to start with parental plants that exhibit complex color patterning, as these mothers produced offspring with the largest variance in terms of pixel complexity. In line with classic and more recent genetic studies on anthocyanin pigmentation in leaves, showing that purple and red pigmentation is expressed as a dominant trait, while green leaves are recessive, we found that mothers with pixel concentrations on the green end of the spectrum produced offspring that had wider color variation (Rife 1948; Albert et al. 2015; Wang et al. 2021). In essence, recessive color palettes could be considered blank canvases for breeding new pattern variants.
Our analysis of features associated with breeder selection supports long-held theories about aesthetic preferences in humans; aesthetic preference for bilateral symmetry (Birkhoff, 1933) is reflected in the breeding process, where we identified significant enrichment for bilateral color and shape symmetry. Moreover, we found that public preferences for leaves with high color contrast largely agree with the independent selection process for breeding new cultivars. As mentioned previously, new coleus cultivars are currently sight-selected through a process that involves extensive screening by professional and amateur breeders. The strong quantitative agreement between well-established aesthetic preferences and the breeding process opens the possibility for automating this first step of cultivar selection. It is not hard to imagine taking this a step further, transforming the cultivar selection process into a customized system. Simple surveys, like the Coleus Colours pilot survey conducted for this study, could help people identify their ideal patterns and automated population screening would match a novel cultivar from the breeding population with the customer. This reimagined breeding approach offers people the personalized experience of designing and naming their own, unique coleus cultivar.
Pigmentation patterns have fascinated scientists for centuries. These visual cues direct plant–pollinator interactions (Leonard and Papaj, 2011; Whitney et al., 2013), fend off herbivores (Lev-Yadun, 2017), and as shown in this study, influence aesthetic value in ornamentals. A simple, yet elegant model involving a reaction–diffusion based mechanism, was famously put forth by Alan Turing to explain the diversity of pattern formation in nature (Turing, 1952). Recent work in the genus Mimulus uncovered genetic regulators that fit this Turing-based model, and direct the patterning of nectar guides through a reaction–diffusion interaction between an activator NECTAR GUIDE ANTHOCYANIN (NEGAN), and its inhibitor RED TONGUE (RTO) (Ding et al., 2020). Beyond this specific result, significant progress toward mapping the underlying genetic mechanisms that regulate pigment deposition has been made using diverse floral models. In these systems, an R2R3 Myb, bHLH, and WDR “MBW” transcriptional regulon have been identified as a central regulator for color patterning, controlling both orange carotenoid and purple/red anthocyanin deposition (Ludwig et al. 1989; Albert et al. 2014; Sagawa et al. 2016). In contrast to floral systems, relatively little is known about the genetics of color patterning in vegetative organs; however, current knowledge including genetic mapping of pigmentation variants for leaves, roots, and fruits (Albert et al., 2015; Xu et al., 2020; Yan et al., 2020; Yu et al., 2020; Wang et al., 2021) and ectopic expression of floral regulators in vegetative tissue (Albert et al., 2020), indicates that the transcriptional MBW regulon is broadly involved in pigmentation patterning across diverse organs.
Our coleus breeding population expresses a tremendous diversity of pattern combinations. Boye and Rife (1938) recognized the potential of this prized ornamental, and proposed using coleus as a model to dissect genetic regulators for color patterning. This suggestion did not get much traction, and we still know relatively little about color patterning in this unique ornamental. After 80 years of stalled progress, a renewed focus on the genetic regulation of pigmentation production and patterning would not only advance ornamental breeding, it would push the limits of Turing’s reaction–diffusion model, reaching to describe the truly complex pattern variants that have drawn admiration from scientists and gardeners alike.
Materials and methods
Coleus population, sampling, and image processing
We planted 133 open-pollinated coleus (Coleus scutellarioides) plants in Gainesville, FL in early January (2015) to generate our 2015 breeding population. These mothers were selected based on their diverse color traits, desirable branching architectures, and hardiness. We collected and sowed 50,000 seeds from the 133 mothers, of which, 34,825 seedlings germinated. We organized the seedlings into families based on their maternal parents, grew the plants for 5 weeks and then selected 697 individuals as potential new cultivars based on their foliar color patterning and branching architecture in mid-February. coleus produces leaf pairs; we harvested one leaf from the youngest fully expanded leaf pair from each plant between 5 and 6 weeks of age and imaged the leaves on Epson Perfection V550 Scanners with 300 dpi resolution. We included Kodak KOCSGS color separation guides to control for potential color differences across the scanners. During our post-image processing, we found that the calculated values for our color guide were highly consistent across scanners and imaging days (Supplemental Figure 1; data available here: Zenodo.org 10.5281/zenodo.4421754). We performed color analysis using our open-access software program called ColourQuant (Li et al., 2019a); software available on github: github.com/maoli0923/ColourQuant). Briefly, we adjusted the RGB color balance on each scan by a white balance method so that the white swatch in the Kodak KOCSGS color separation guide is pure white, to ensure that scanners were not biasing the color data. Next, we segmented the leaves from the background by converting the RGB matrix into a hue-saturation-value (HSV) format. Since most background pixels become gray in HSV, this was used to set a threshold (e.g. S > 0.15) that separates gray values from true leaf values. We then used the binary leaf silhouettes to extract the leaf color data by setting the background to pure white. We manually adjusted the thresholding for leaves that could not be automatically extracted due to shadows in the scan, and removed outliers from the sample set, including leaves that were overlapping on the scanner, very small, or broken (209 images were removed).
Color pattern analysis
To extract quantitative color distribution information, we converted the leaf color matrices from RGB to CIELAB (L*a*b*) color, which is a continuous color space that consists of three descriptors: L* = “lightness,” a* = “green to magenta,” and b* = “blue to yellow.” Importantly, L*a*b is a device-independent color space that is frequently applied to image processing pipelines (Phung et al. 2005; Jyoti Bora et al. 2015). We used the rgb2lab function in Matlab R2017a to perform the color conversion.
To study the distribution of mean and variance for L*, a*, b* color values across the leaves, we first calculated the average value and variance of L*, a*, and b* for each leaf so that each leaf has six features (“mean L”, “mean a”, “mean b”, “variance of L”, “variance of a”, and “variance of b”) and then plotted histograms and boxplots to show the overall mean and variance distributions for all leaves. Small variance is produced by solid colored leaves, while large variance is produced by leaves with high contrast color patterning. Next, we treated the 3D Lab color matrices as 3D point clouds, which enabled us to extract color distribution and frequency information for each leaf. Here, it is important to emphasize that this method of extracting color patterning using color as a third dimension mapped onto 2D leaves requires a continuous color space, like CIELAB, and would not be possible using standard colorimetric RGB values.
The mean and variance of Lab values roughly describe the color for each leaf. However, to compare the distribution and frequency of Lab values across the leaves, we applied a Gaussian density estimator (GDE) to the Lab point cloud. GDE is a function defined on 3D space, providing a robust and direct density estimate from the point cloud data. To reduce computational complexity, we restricted the domain of the GDE function to a fixed bounded cuboid. The GDE descriptor alone captures statistical color frequency, not spatial patterning. To capture spatial color information, we segmented the leaves into distinct zones based on normalized pixel distances: “border”—defined as the outer 15% of pixels from the leaf boundary to the centroid, “center”—defined as the inner 75% of pixels from the centroid to the boundary, and “full”—defined as the entire color matrix. The distance between any two leaflets is calculated with the following equation, which reweights the contributions from border and center regions where pigmentation patterning is visually distinct:
where represents the L2 distance (the square root of the sum of the squared vector values) between GDE functions for each corresponding zone. With this calculation, the pattern difference between two leaves is determined by their degree of similarity across all three zones. For every two samples, we calculated D between them and then performed MDS on a pairwise matrix in which the element of row i and column j is the distance between sample i and sample j. For these pairwise distances, we used MDS (similar to a PCA) to project the data in a lower dimensional space, which allows us to capture the major features that contribute to pattern variation. These methods and the supporting software for this approach can also be found in the publication by (Li et al., 2019a; https://github.com/maoli0923/ColourQuant).
To quantify the degree of mirror symmetry for each leaf, we first marked a bilaterally symmetric line by placing two landmarks, one at the proximal point (petiole) and another at the distal point (leaf tip). These landmarks were then used to partition the leaf into longitudinal halves that could be directly compared with one another. We used two methods for quantifying mirror symmetry (where smaller values equate to a higher degree of symmetry). First, we performed a general measure by comparing the differences in left and right color distributions (using GDE functions), and second, we measured the degree of bilateral shape symmetry by overlaying the left and right halves of the leaf and computing the percentage of pixels that fail to overlap.
Quantitative analysis of maternal–offspring pigmentation relationships
To calculate the average phenotypic distance between each maternal plant and its progeny, we divided the distance between each maternal leaf and the leaves of its progeny by the distance between the maternal leaf and all of the leaves in the breeding population. To investigate how maternal color and color complexity influence these color traits in the progeny population, we calculated the mean and variance of L*, a*, and b* for the maternal leaves and their offspring and then computed the variance of those traits across the offspring within each family. For example, each family has a trait named “variance of family mean L” which is the variance of “mean L” of all the offspring leaves in this family. Large “variance of family mean L” indicates the offspring leaves in this family have a wide range of color. Similarly, each family has a trait named “variance of family L variance” which is the variance of “variance of L” for all of the offspring leaves in this family. Large “variance of family L variance” indicates that the offspring leaves in this family produced a wild range of color patterns ranging from solid colors to high contrast patterns. Raw data for the family mean and variance of L* a* b* are included in Supplemental Dataset S1.
Calculating the heritability of lab and MDS color space
Multi-trait model for L, a, and b
Given the high phenotypic association between the L, a, b color traits, a multi-trait mixed model was utilized to estimate genetic and residual covariances between traits. The model was fit using ASReml-R (Butler et al., 2017).
| (1) |
where , and are vectors of phenotypes for traits L, a, and b; is a vector of 1’s of length corresponding to the number of observed phenotypes; , , and are the means for each trait; , and are the incidence matrices for each trait; , , and are vectors of the additive genetic effects for each trait; and , and are vectors of the residuals for each trait.
The additive genetic effects, , , , were assumed to be distributed as:
| (2) |
where is the Kronecker product; is the additive pedigree relationship matrix (calculated with male parents treated as unknown and randomly sampled from the population); and is a 3 × 3 unstructured covariance matrix:
| (3) |
where is the additive genetic variance for trait i and is the additive genetic covariance between traits i and j.
The residuals, , , , were assumed to be distributed as:
| (4) |
where is the Kronecker product; is the identity matrix with dimensions corresponding to the number of observations, and is a 3 × 3 unstructured covariance matrix:
| (5) |
where is the residual variance for trait i and is the residual covariance between traits i and j.
Modeling Traits MDS1, MDS2, MDS3, and MDS4
The traits MDS1–4 were assumed to be uncorrelated and analyzed using the following univariate mixed model:
| (6) |
where is a vector of phenotypes for the ith MDS trait; is a vector of 1’s of length corresponding to the number of observed phenotypes; the mean for the ith MDS trait; is the incidence matrix for the ith MDS trait; is a vector of the additive genetic effects for the ith MDS trait; and is a vector of the residuals for the ith MDS trait.
The additive genetic effects were assumed to be distributed as:
| (7) |
where is the additive pedigree relationship matrix, and is the additive genetic variance for the ith MDS trait.
The residuals were assumed to be distributed as:
| (8) |
where is the identity matrix with dimensions corresponding to the number of observations, and is the residual variance for the ith MDS trait.
Heritability
The narrow-sense heritability () for each trait t was calculated as:
| (9) |
where and are the REML estimates of the additive genetic and residual variance for trait t, estimated using Equations 1 and 6
Quantifying aesthetic features of selected plants
We calculated the influence of breeder selection on color and shape symmetry, as well as pigmentation L*, a*, and b* values, by comparing the probability distribution for each value in the entire breeding population with the probability distribution in the selected population. Because the data are not normally distributed, a nonparametric two-sample Kolmogorov–Smirnov test was used to calculate the significance of selection on each color parameter.
Public preferences for coleus colors independent of shape
To investigate color preferences amongst the general public, we created a survey based on the major sources of variation for leaf color patterning. First, we separated shape from color patterning by deforming the leaves into uniform circles using thin-plate-spline interpolation, followed by centering and normalizing the circles into the same position and size. Next, we rotated each circularized leaf so that the first landmark (near the base) is on the negative half of the y axis (x = 0) and the tip is on the positive half. We resized each circular leaf image to be 70×70 dimension and reshaped the pixel L*a*b* colors into a long (12,150 dimension) vector. To calculate the main sources of variance, we performed a PCA on the long vectors of the circularized leaves and created a survey using google forms where public volunteers were asked to select their preference of eigencolors for the top 8 PCs. For kth PC, the eigencolors are represented by ± x standard deviation along the PC axis, where x = 3+(k-1) × 0.5, this produced more distinct color variants for the survey participants. We distributed the survey using a dedicated Twitter account (@ColeusColours), and then plotted the responses from all of the survey participants (N = 172) and reconstructed the composite preferred leaf based on the responses (Supplemental Dataset S2). Unfortunately, we did not randomize the order of the questions, which may have induced some bias in the participant responses.
Supplemental data
The following materials are available in the online version of this article.
Supplemental Figure S1 . Data collection.
Supplemental Figure S2 . Color distribution for mean Lab.
Supplemental Figure S3 . PCA for color in the entire coleus population using segmented or full leaf data sampling.
Supplemental Figure S4 . Maternal plant-progeny relationships based on mean and variance of lab color.
Supplemental Table S1 . Genetic additive relationship matrix.
Supplemental Table S2 . Residuals.
Supplemental Table S3 . Heritability.
Supplemental Table S4 . Heritability of MDS traits.
Supplemental Dataset S1 . Quantitative information for maternal plants and their progeny.
Supplemental Dataset S2 . Public survey result for color preferences.
Supplementary Material
Acknowledgments
We thank the undergraduate researchers who assisted with data collection at the University of Florida, and Joshua Tester for growing the plants. We would also like to thank the participants who took the Twitter survey and two anonymous reviewers whose comments greatly improved this manuscript.
Funding
This work was funded by startup funds from the Donald Danforth Plant Science Center, and royalties from the University of Florida Coleus Breeding Program. This project was also supported by the United States Department of Agriculture National Institute of Food and Agriculture, and by Michigan State University AgBioResearch. M.H.F. was supported by an National Science Foundation Plant Genome Research Program Postdoctoral Fellowship (IOS-1523668).
Conflict of interest statement. None declared.
M.H.F., V.C., and D.H.C. designed the imaging pipeline; D.C. bred the coleus population; K.R.R. calculated heritability for color traits; M.H.F. and V.C. collected the data; and M.L. developed and performed the HTP color analysis. All authors contributed to writing the manuscript.
The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (https://academic.oup.com/plphys/pages/General-Instructions) is: Margaret Frank (mhf47@cornell.edu).
References
- Albert NW, Butelli E, Moss SMA, Piazza P, Waite CN, Schwinn KE, Davies KM, Martin C (2020) Discrete bHLH transcription factors play functionally overlapping roles in pigmentation patterning in flowers of Antirrhinum majus. New Phytol 231: 849–863 doi: 10.1111/nph.17142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert NW, Davies KM, Lewis DH, Zhang H, Montefiori M, Brendolise C, Boase MR, Ngo H, Jameson PE, Schwinn KE (2014) A conserved network of transcriptional activators and repressors regulates anthocyanin pigmentation in eudicots. Plant Cell 26: 962–980 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albert NW, Griffiths AG, Cousins GR, Verry IM, Williams WM (2015) Anthocyanin leaf markings are regulated by a family of R2R3-MYB genes in the genus Trifolium. New Phytol 205: 882–893 [DOI] [PubMed] [Google Scholar]
- Albert NW, Lewis DH, Zhang H, Schwinn KE, Jameson PE, Davies KM (2011) Members of an R2R3-MYB transcription factor family in Petunia are developmentally and environmentally regulated to control complex floral and vegetative pigmentation patterning. Plant J 65: 771–784 [DOI] [PubMed] [Google Scholar]
- Amézquita EJ, Quigley MY, Ophelders T, Munch E, Chitwood DH (2020) The shape of things to come: topological data analysis and biology, from molecules to organisms. Dev Dyn 249: 816–833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnal Barbedo JG (2013) Digital image processing techniques for detecting, quantifying and classifying plant diseases. Springerplus 2: 660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey LH (1924) Manual of Cultivated Plants: a Flora for the Identification of the Most Common of the Most Common Or Significant Species of Plants grown in the Continental United States and Canada for Food, ornament, utility, and general interest, both in the open and under glass. Macmillan Publication, New York [Google Scholar]
- Birkhoff GD (1933) Aesthetic Measure. Cambridge, MA [Google Scholar]
- Boye CL, Rife DC (1938) Genetic studies of coleus I. J Heredity 29: 55–60 [Google Scholar]
- Butler DG, Cullis BR, Gilmour AR, Gogel BG, Thompson R (2017) ASReml-R Reference Manual Version 4. VSN International Ltd, Hemel Hempstead, UK. [Google Scholar]
- Chitwood DH, Eithun M, Munch E, Ophelders T (2019) Topological Mapper for 3D Volumetric Images. In: B Burgeth, A Kleefeld, B Naegel, N Passat, B Perret, eds, Mathematical Morphology and Its Applications to Signal and Image Processing, Vol. 11564. ISMM 2019. Lecture Notes in Computer Science, Springer, Cham, pp ; 84–95 [Google Scholar]
- Das A, Schneider H, Burridge J, Ascanio AKM, Wojciechowski T, Topp CN, Lynch JP, Weitz JS, Bucksch A (2015) Digital imaging of root traits (DIRT): a high-throughput computing and collaboration platform for field-based root phenomics. Plant Methods 11: 51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding B, Patterson EL, Holalu SV, Li J, Johnson GA, Stanley LE, Greenlee AB, Peng F, Bradshaw HD Jr, Blinov ML, et al. (2020) Two myb proteins in a self-organizing activator-inhibitor system produce spotted pigmentation patterns. Curr Biol 30: 802–814.e8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fahlgren N, Gehan MA, Baxter I (2015) Lights, camera, action: high-throughput plant phenotyping is ready for a close-up. Curr Opin Plant Biol 24: 93–99 [DOI] [PubMed] [Google Scholar]
- Fasoula DA, Ioannides IM, Omirou M (2019) Phenotyping and plant breeding: overcoming the barriers. Front Plant Sci 10: 1713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forkmann G (1991) Flavonoids as flower pigments: the formation of the natural spectrum and its extension by genetic engineering. Plant Breed 106: 1–26 [Google Scholar]
- Frank MH, Chitwood DH (2016) Plant chimeras: the good, the bad, and the “Bizzaria.” Dev Biol 419: 41–53 [DOI] [PubMed] [Google Scholar]
- Gehan MA, Fahlgren N, Abbasi A, Berry JC, Callen ST, Chavez L, Doust AN, Feldman MJ, Gilbert KB, Hodge JG, et al. (2017) PlantCV v2: image analysis software for high-throughput plant phenotyping. PeerJ 5: e4088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gehan MA, Kellogg EA (2017) High-throughput phenotyping. Am J Bot 104: 505–508 [DOI] [PubMed] [Google Scholar]
- Gobalakrishnan N, Pradeep K, Raman CJ, Javid Ali L, Gopinath MP (2020) A systematic review on image processing and machine learning techniques for detecting plant diseases. In 2020 International Conference on Communication and Signal Processing (ICCSP), pp. 0465–0468. doi: 10.1109/iccsp48568.2020.9182046
- Goodrich J, Carpenter R, Coen ES (1992) A common gene regulates pigmentation pattern in diverse plant species. Cell 68: 955–964 [DOI] [PubMed] [Google Scholar]
- Holton TA, Cornish EC (1995) Genetics and biochemistry of anthocyanin biosynthesis. Plant Cell 7: 1071–1083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu C-C, Chen Y-Y, Tsai W-C, Chen W-H, Chen H-H (2015) Three R2R3-MYB transcription factors regulate distinct floral pigmentation patterning in Phalaenopsis spp. Plant Physiol 168: 175–191 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ibba MI, Crossa J, Montesinos‐López OA, Montesinos‐López A, Juliana P, Guzman C, Delorean E, Dreisigacker S, Poland J (2020) Genome‐based prediction of multiple wheat quality traits in multiple years. Plant Genome 11: 3. [DOI] [PubMed] [Google Scholar]
- Jyoti Bora D, Gupta AK, Khan FA (2015) Comparing the Performance of LAB and HSV Color Spaces with Respect to Color Image Segmentation. arXiv [e-prints arXiv:1506.01472]
- Kondo S, Miura T (2010) Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329: 1616–1620 [DOI] [PubMed] [Google Scholar]
- Leonard AS, Papaj DR (2011) “X” marks the spot: the possible benefits of nectar guides to bees and plants: nectar guides and bumblebee foraging. Funct Ecol 25: 1293–1301 [Google Scholar]
- Lev-Yadun S (2017) Defensive animal and animal-action mimicry by plants. Israel J Plant Sci 1–31 [Google Scholar]
- Li M, An H, Angelovici R, Bagaza C, Batushansky A, Clark L, Coneva V, Donoghue MJ, Edwards E, Fajardo D, et al. (2018a) Topological data analysis as a morphometric method: using persistent homology to demarcate a leaf morphospace. Front Plant Sci 9: 553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Frank MH, Coneva V, Mio W, Chitwood DH, Topp CN (2018b) The persistent homology mathematical framework provides enhanced genotype-to-phenotype associations for plant morphology. Plant Physiol 177: 1382–1395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Frank MH, Migicovsky Z (2019a) ColourQuant: a high-throughput technique to extract and quantify colour phenotypes from plant images. arXiv [q-bio.QM] [DOI] [PubMed]
- Li M, Klein LL, Duncan KE, Jiang N, Chitwood DH, Londo JP, Miller AJ, Topp CN (2019b) Characterizing 3D inflorescence architecture in grapevine using X-ray imaging and advanced morphometrics: implications for understanding cluster density. J Exp Bot 70: 6261–6276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M, Shao M-R, Zeng D, Ju T, Kellogg EA, Topp CN (2020) Comprehensive 3D phenotyping reveals continuous morphological variation across genetically diverse sorghum inflorescences. New Phytol 226: 1873–1885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu S, Barrow C, Hanlon MT, Lynch J, Bucksch A (2020) DIRT/3D: 3D phenotyping for maize (Zea mays) root architecture in the field. bioRxiv [Google Scholar]
- Ludwig SR, Habera LF, Dellaporta SL, Wessler SR (1989) Lc, a member of the maize R gene family responsible for tissue-specific anthocyanin production, encodes a protein similar to transcriptional activators and contains the myc-homology region. Proceedings of the National Academy of Sciences 86: 7092–7096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutka AM, Bart RS (2014) Image-based phenotyping of plant disease symptoms. Front Plant Sci 5: 734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton AJ, Mwanyambo M, Govaerts RHA, Smitha K, Suddee S, Phillipson PB, Wilson TC, Forster PI, Culham A (2019) Nomenclatural changes in Coleus and Plectranthus (Lamiaceae): a tale of more than two genera. PhytoKeys 129: 1–158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paton A, Mwanyambo M, Culham A (2018) Phylogenetic study of Plectranthus, Coleus and allies (Lamiaceae): taxonomy, distribution and medicinal use. Bot J Linn Soc 188: 355–376 [Google Scholar]
- Paz-Ares J, Ghosal D, Wienand U, Peterson PA, Saedler H (1987) The regulatory c1 locus of Zea mays encodes a protein with homology to myb proto-oncogene products and with structural similarities to transcriptional activators. EMBO J 6: 3553–3558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedley R, Pedley K (1974) Coleus: A Guide to Cultivation and Identification. HarperCollins Distribution Services, J Bartholomew, Edinburgh [Google Scholar]
- Phung SL, Bouzerdoum A, Chai D (2005) Skin segmentation using color pixel classification: analysis and comparison. IEEE Trans Pattern Anal Mach Intell 27: 148–154 [DOI] [PubMed] [Google Scholar]
- Prunet N, Duncan K (2020) Imaging flowers: a guide to current microscopy and tomography techniques to study flower development. J Exp Bot 71: 2898–2909 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quattrocchio F, Wing JF, van der Woude K, Mol JN, Koes R (1998) Analysis of bHLH and MYB domain proteins: species-specific regulatory differences are caused by divergent evolution of target anthocyanin genes. Plant J 13: 475–488 [DOI] [PubMed] [Google Scholar]
- Quattrocchio F, Wing J, van der Woude K, Souer E, de Vetten N, Mol J, Koes R (1999) Molecular analysis of the anthocyanin2 gene of petunia and its role in the evolution of flower color. Plant Cell 11: 1433–1444 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rife DC (1948) Simply inherited variations in Coleus: a résumé. J Hered 39: 85–91 [Google Scholar]
- Rogers R (2008) Coleus: rainbow foliage for containers and gardens. Timber Press, OR [Google Scholar]
- Sagawa JM, Stanley LE, LaFountain AM, Frank HA, Liu C, Yuan Y-W (2016) An R2R3-MYB transcription factor regulates carotenoid pigmentation in Mimulus lewisii flowers. New Phytol 209: 1049–1057 [DOI] [PubMed] [Google Scholar]
- Schwinn K, Venail J, Shang Y, Mackay S, Alm V, Butelli E, Oyama R, Bailey P, Davies K, Martin C (2006) A small family of MYB-regulatory genes controls floral pigmentation intensity and patterning in the genus Antirrhinum. Plant Cell 18: 831–851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shakoor N, Agnew E, Ziegler G, Lee S, Lizárraga C, Fahlgren N, Baxter I, Mockler TC (2019) Genomewide association study reveals transient loci underlying the genetic architecture of biomass accumulation under cold stress in Sorghum. bioRxiv 10.1101/760025 [DOI] [PMC free article] [PubMed]
- Shakoor N, Lee S, Mockler TC (2017) High throughput phenotyping to accelerate crop breeding and monitoring of diseases in the field. Curr Opin Plant Biol 38: 184–192 [DOI] [PubMed] [Google Scholar]
- Singh D, Wang X, Kumar U, Gao L, Noor M, Imtiaz M, Singh RP, Poland J (2019) High-throughput phenotyping enabled genetic dissection of crop lodging in wheat. Front Plant Sci 10: 394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spelt C, Quattrocchio F, Mol JN, Koes R (2000) anthocyanin1 of petunia encodes a basic helix-loop-helix protein that directly activates transcription of structural anthocyanin genes. Plant Cell 12: 1619–1632 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suddee S, Paton A. J., Parnell JAN (2004) A taxonomic revision of tribe Ocimeae dumort (Lamiaceae) in continental South East Asia II. Plectranthinae. Kew Bull 59: 379–414 [Google Scholar]
- Tilney-Bassett RAE (1986) Plant chimeras. Edward Arnold (Publishers) Ltd., London [Google Scholar]
- Turing AM (1990) The chemical basis of morphogenesis. 1953. Bull Math Biol 52: 153–97; discussion 119–52 [DOI] [PubMed] [Google Scholar]
- Turing AM (1952) The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, Vol. 237, pp. 37–72 [Google Scholar]
- Underhill AN, Hirsch CD, Clark MD (2020) Evaluating and mapping grape color using image-based phenotyping. Plant Phenomics 2020:8086309 doi: 10.34133/2020/8086309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanhees DJ, Loades KW, Bengough AG, Mooney SJ, Lynch JP (2020) Root anatomical traits contribute to deeper rooting of maize under compacted field conditions. J Exp Bot 71: 4243–4257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Vetten N, Quattrocchio F, Mol J, Koes R (1997) The an11 locus controlling flower pigmentation in petunia encodes a novel WD-repeat protein conserved in yeast, plants, and animals. Genes Dev 11: 1422–1434 [DOI] [PubMed] [Google Scholar]
- Walker AR, Davison PA, Bolognesi-Winfield AC, James CM, Srinivasan N, Blundell TL, Esch JJ, Marks MD, Gray JC (1999) The transparent testa glabra1 locus, which regulates trichome differentiation and anthocyanin biosynthesis in Arabidopsis, encodes a WD40 repeat protein. Plant Cell 11: 1337–1350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C, Ji W, Liu Y, Zhou P, Meng Y, Zhang P, Wen J, Mysore KS, Zhai J, Young ND, et al. (2021) The antagonistic MYB paralogs RH1 and RH2 govern anthocyanin leaf markings in Medicago truncatula. New Phytol 229: 3330–3344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler LC, Smith SD (2019) Computational modeling of anthocyanin pathway evolution: biases, hotspots, and trade-offs. Integr Compar Biol 59: 585–598 [DOI] [PubMed] [Google Scholar]
- Whitney HM, Milne G, Rands SA, Vignolini S, Martin C, Glover BJ (2013) The influence of pigmentation patterning on bumblebee foraging from flowers of Antirrhinum majus. Naturwissenschaften 100: 249–256 [DOI] [PubMed] [Google Scholar]
- Xie X, Ma Y, Liu B, He J, Li S, Wang H (2020) A deep-learning-based real-time detector for grape leaf diseases using improved convolutional neural networks. Front Plant Sci 11: 751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z-S, Yang Q-Q, Feng K, Yu X, Xiong A-S (2020) DcMYB113, a root-specific R2R3-MYB, conditions anthocyanin biosynthesis and modification in carrot. Plant Biotechnol J 18: 1585–1597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan S, Chen N, Huang Z, Li D, Zhi J, Yu B, Liu X, Cao B, Qiu Z (2020) Anthocyanin fruit encodes an R2R3-MYB transcription factor, SlAN2-like, activating the transcription of SlMYBATV to fine-tune anthocyanin content in tomato fruit. New Phytol 225: 2048–2063 [DOI] [PubMed] [Google Scholar]
- York LM (2019) Functional phenomics: an emerging field integrating high-throughput phenotyping, physiology, and bioinformatics. J Exp Bot 70: 379–386 [DOI] [PubMed] [Google Scholar]
- Yu X, Qin Q, Wu X, Li D, Yang S (2020) Genetic and physical localization of the gene controlling leaf pigmentation pattern in Medicago truncatula. G3 10: 4159–4165 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.