Abstract
The Baltic Dry Index (BDI) is a unique gauge for measuring the marine transportation of major dry bulk shipments. Increased sea freight is a precursor to the increase in economic activities. The volumes of sea trade and freight rates are influenced by import–export dynamics and changes in commodity prices. So, levels of commodity prices are monitored to gain insight into the anticipated demand for bulk shipments. In this study, the causality-in-quantiles (CiQ) model is used to model the causal relationship between BDI spot values and spot price of major dry bulk commodities like iron ore, aluminum, copper, agricultural products by considering 12 years of daily data. CiQ model is superior compared to other linear causality models as it helps in capturing the asymmetry and nonlinearity in causality based on different quantiles or market conditions i.e., bearish, normal, and bullish market conditions. Also, it captures the causality-in-mean as well as variance and helps in exploring the causal relationship in returns as well as volatility transmission between BDI and commodity prices. The finding of the paper throws interesting light on the asymmetric relationship between BDI and commodity prices- commodity prices are causing BDI in all market conditions, but the influence is stronger in normal periods than bearish and bullish periods. The causality from commodity to BDI follows a common pattern across most of the commodities. However, the effect of BDI on commodities considerably varies across the range of commodities and across market conditions. So, this model provides a plethora of information that will help commodity market participants to hedge the risk of variations in commodity price and freight rates effectively.
Keywords: Commodity, BDI, Quantiles, Price, Freight, Causality
Introduction
Seaborne trade constitutes 90% of global trade. Almost all bulk transport of metal and mining raw materials, fertilizers, crude oil, and refined finished products, agri-products, finished manufactured goods, etc., are transported through shipping. In fact, according to the International Chamber of Shipping (2019) report, there are about 50,000 merchant ships registered in over 150 countries and operated by millions of seafarers representing an equal number of countries. According to the UNCTAD (2019) Review of Maritime Transport report, dry bulk cargo constitutes about 30% of total global trade. Baltic Dry Index (BDI) is the composite index based on daily freight rates quoted for major sea routes for dry bulk commodities and is an important barometer of the volume of worldwide trade, manufacturing activity as well as global demand for industrial commodities and finished manufactured products. BDI and demand for raw materials and primary goods tend to comove, as during the period of economic growth, the demand for raw materials increases resulting in higher transportation volume and higher BDI rates. On the other side, demand for raw materials reduces during a financial slowdown, thus affecting global trade volume and simultaneously impacting BDI rates (Radelet and Sachs1998; Stopford 2003; Kilian 2009; Geman and Smith 2012; Papailias et al. 2017; Lin et al. 2019).
Studies by Haigh and Bryant (2000), Yu et al. (2007), Poulakidas and Joutz (2009), Kavussanos et al. (2010, 2014), Bakshi et al.(2011), Raza et al. (2018a), Sun et al. (2020), Apergis and Payne (2013), Chou et al.(2015), and Tsioumas and Papadimitriou (2018) have either explored lead-lag relationship, volatility spillover among freight rates/freight rate indexes and commodity prices or modeled the predictive content of freight rates/freight rate indexes on a wide array of financial and macro-economic parameters such as stock market returns, the interest rate of short-term and long-term bonds, major bulks and oil price, etc. As a common theme, studies mentioned above explore the relationship between different types of freight rates/freight indexes with different commodity prices over a sufficiently long period, but do not segregate the time period based on different market conditions i.e., bullish, bearish, or normal market, and fail to identify the asymmetry in the relationship between freight rates and commodity prices. Very few studies such as (Koch 2014; Bildirici et al. 2015) have explored the relationship between freight rates and commodity prices in different market conditions. Using a multinomial logit model framework, Koch (2014) analyzed extreme energy price changes, in the 10% distribution tails, during the 2006–2012 boom-bust period. Bildirici et al. (2015) modeled BDI and economic growth for the USA using the Markov-switching Granger-causality model in three different regimes i.e., crisis, moderate growth, and high growth period.
As evident from existing research, though the relationship between commodity prices and BDI has been studied to some extent, how the relationship changes during extreme market conditions has remained under focus. Commodity prices and the BDI, like any financial or macroeconomic time series, are affected by structural changes in the economy/business cycle and are frequently accompanied by abnormally high or low periods, thus making it challenging to capture the underlying dynamics using linear models. Nonlinear models, especially quantile-based models, are effective in analyzing the dynamics in extreme market conditions as lower (higher) quantiles of the sample distribution can be intuitively linked to a bearish (bullish) market scenario. Hence, the objective of this study is to explore the heterogeneous relationship between commodity spot prices and BDI in a bearish, normal, and bullish market scenario. The study uses nonparametric causality-in-quantiles (CiQ approach henceforth) by Balcilar et al. (2016a) to identify the causal relationship between BDI and commodity prices in different quantiles.
The insights from this study can help exporters and importers of bulk commodities to monitor the dynamic relationship between commodity price and shipping freight rates and accordingly decide when it is relatively convenient for the business to export or import dry bulks. Simultaneously, the research findings will help shipbrokers to offer competitive charter rates considering the prevailing commodity market conditions. It advances the knowledge of freight market dynamics and commodity prices, while at the same moment supporting decision-making processes in dry bulk chartering and commodity trading through better hedging and investment procedures.
The rest of the paper is organized as follows: a short overview of the BDI is provided in Sect. 2. Section 3 provides a concise evaluation of the literature. The methodology of the assessment is discussed in Sect. 4. Section 5 mentions the stochastic characteristics of the variables. Section 6 presents the empirical outcomes. The conclusion and policy implications are finally presented in Sect. 7.
Baltic Dry Index
The Baltic Dry Index traces back its origin to the Baltic Coffee House where sailors gathered to negotiate the freight rates. The index was officially launched in 1985. Each working day a panel of international shipbrokers submits an assessment of the current freight cost for various sea routes1 to the Baltic Exchange. BDI is a composite index which derives its value from 3 subindices i.e., the Baltic Capesize Index (BCI), Baltic Panamax Index (BPI), and Baltic Supramax Index (BSI).
Economic indicators such as unemployment rate, inflation, and oil prices can be manipulated or influenced by governments and speculators, however, BDI is difficult to manipulate because it is driven by clear forces of supply and demand.
Baltic Dry Index (BDI) calculation formula
(Source: Baltic Exchange, 2019) https://www.balticexchange.com/market-information/indices/BDI/
Supramax, Panamax, and Capesize, etc. indicate the size of the cargo ships measured by deadweight tonnage (DWt). Deadweight is the weight of cargo alone and does not include the weight of the ship. All these cargo ships normally take the voyage on different sea routes. For example, Capesize is the largest vessel so these cannot pass through the Panama or Suez Canal, takes a voyage through the Cape of Good Hope. Panamax ships are the largest ones to pass through the Panama Canal. Interestingly these vessels are also designated for transporting different types of bulk commodities. For example, Panamax and Capesize ships normally carry iron ore and coal. Grains and minor dry bulks commodities such as cotton, corn, soybean, etc., are transported using Supramax vessels.
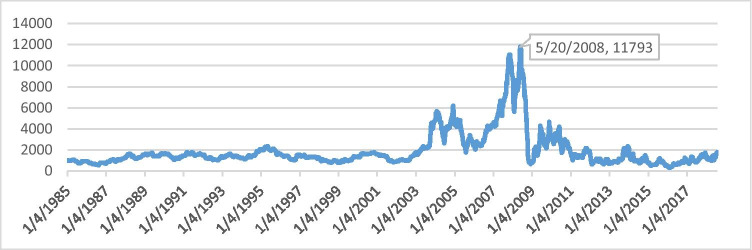
The BDI values have been plotted in Fig. 1. Since its introduction in 1985, from the value of 1000, the BDI reached the highest level of 11,793 on 20-May-2008 but dropped by 94% on 5-Dec-2008 to 663 points coinciding with the period of the 2008 subprime crisis.
Fig. 1.
Historical values of BDI (1985 to 2018
Historically, BDI has experienced significant volatility during major economic events such as the US stock market crisis in 1987, the 1999 dot-com bubble burst, and the 2008 financial crisis.2 In all these crises, commodity prices have also been affected, indicating a plausible causal relationship between BDI and commodity prices.
As BDI is the composite index based on daily freight rates quoted for major sea routes, it essentially reflects the supply–demand situation in the market for major dry bulk commodities. Higher economic activities lead to greater demand for commodities, consequently leading to higher commodity prices and higher BDI rates. Similarly, a decline in economic activities reduces demand for commodities as well as demand for freight transport as shipbrokers compete for the lesser tonnage of the consignment. Though research studies have used other economic indicators such as oil prices, inflation, and unemployment rate, BDI is considered to be a better indicator as it cannot be manipulated by speculators. The scope of speculation in BDI is negligible as only member firms/panelists (international ship-broking firms3) registered with the Baltic exchange provide the quotes. Bildirici et al. (2015) articulates this aspect and mentions that “economic indicators such as unemployment rate, inflation, and oil prices that can be manipulated or influenced by governments and speculators, however, Baltic Dry Index is difficult to manipulate because it is driven by clear forces of supply and demand. One of the reasons for BDI to be difficult to manipulate and influence is the number of ships around the world is limited up to a certain extent therefore in order to manipulate and increase the supply, more ships need to be built which will be very costly.”
Literature review
The BDI and its relationship with various macro-economic parameters have been explored by various researchers. There are mainly three broad areas of research on BDI namely, BDI as an indicator of economic growth and stock market performance, BDI as a predictor of various economic parameters, and the relationship between BDI and commodity markets.
BDI, as an indicator of economic growth and stock market performance, has been explored by many researchers. (Radelet and Sachs 1998; Stopford 2003; Kilian 2009; Bildirici 2016) have identified a positive relationship between the shipping of raw materials, industrial production, and economic growth. Kilian (2009) has used a structural VAR model to develop a global real economic activity index from dry cargo shipping rate, known as Kilian index and it is treated as a good indicator of business cycles in the global economy. Radelet and Sachs (1998) also observed that a country’s economic prosperity has a significant association with its closeness to a seaport. They concluded a clear linkage between the shipping industry growth and economic output, using a regression model. Alizadeh and Muradoglu (2014) analyzed the effect of BDI using regression and the EGARCH model over the sample period 1989–2013 on US stock market returns as well as 28 countries’ stock market indices. The study concluded that freight rates could be used for the prediction of stock market returns globally. Zuccollo (2014) has extensively studied the association of BDI and various indices of the Johannesburg Stock exchange (JSE) like mining, top 40, mid-cap, small-cap, and industry-specific indices. The study identified a high correlation between BDI and the mining index in a lag period of 36 months, which supports the fact that the magnitude of the Mining industry is relatively high in South Africa. Further, they performed an ARIMA regression on BDI and JSE All Share indices (ALSI) and found long-term causality from BDI to ALSI. The study concluded that BDI is statistically significant as a leading economic indicator in the South African economy. Bakshi et al. (2011) have also identified that the BDI growth rate has predictive power for equity and commodity market changes in a global context. Using the sample and out-of-sample regressions, they have concluded that the predictive ability is robust in the presence of alternative predictors such as MSCI World Index returns. Bildirici et al. (2015) identified that BDI influences economic growth positively in a high growth regime. Oomen (2012) also studied the predictive power of BDI using the regression model and concluded that BDI is a better predictor for stock market returns compared to other common predictors. However, this paper also finds that the results are significant in the period before 2008 and performed poorly in the period from 2008–2011. Lin and Sim (2013) identified strong positive co-movement between BDI and trade volume of China, India, Brazil, Russia, and Australia.
Contrary to the positive relationship indicated by the above research studies, few other studies have reported otherwise. Graham et al. (2016) identified that the relation between BDI and the equity market returns is applicable for emerging markets only. Developed market returns are not affected by the BDI, except for the USA. Similarly, Lin and Sim (2013) identified that reduction in BDI has a positive effect on trade and income of the Least Developed Countries (LDC) in Africa, Asia, and Latin America, etc. Baltyn (2016) applied the Bry-Boschan research algorithm to mark the turning points in BDI and USA GDP, but could not find any significant leading indicator role of BDI for the US economy.
Many researchers have studied the predictive property of BDI on various economic aspects. Bakshi et.al. (2011) mention that BDI is most useful as a predictor in the Industrial Raw material sector. Through panel regression studies, they identified that BDI is a good predictor for stock and commodity markets jointly. Oomen (2012) studied the predictive ability of BDI for 23 developed countries and 25 undeveloped countries and 10 different industry sectors for a sample period from 1985–2011. The regression analysis identified that BDI serves as an efficient predictor in the global technology, telecommunications, and consumer services areas. The predictive results have been found valid both in the long as wells as short-term. Jurun et al (2015) find a strong positive correlation between annual BDI values and performance excellence indicators measured by the adjusted Altman z-score for maritime companies. Apergis and Payne (2013) analyzed the information and predictive content of BDI on a wide array of financial assets and macroeconomic parameters such as stock market returns, the interest rate of short-term and long-term bonds, commodity prices, and oil price. Chou (2008) used the VARMA model and identified the predictive capability of BCI for the Asian steel index (ASI). Giannarakis et al. (2017) studied the effect of BDI on the Dow Jones Sustainability Index World (DJSIW) and identified the positive influence of shipping freight rates on DJSIW.
The third aspect is related to the relationship between BDI and commodity markets. Various studies have analyzed the relationship between BDI and demand for various bulk commodities traded internationally. Lun et al. (2010) identified that the most fundamental driver of BDI variation is the demand for the shipment of commodities. If there is a lack of optimism in the market regarding economic growth, producers decrease the production level, and the commodity demand also falls, which results in a drop in freight rates. Various studies such as Radelet and Sachs (1998), Klovland (2002), Stopford (2003), Kilian (2009), Boubaker and Raza (2017) have supported this relationship between raw material demand and economic growth. Radelet and Sachs (1998) concluded from a regression model that manufacturing goods export for countries with lower shipping freight costs had grown rapidly from 1965 to 1990. Bakshi et al. (2011) studied the predictive ability of BDI on Moody’s Commodity Index, Reuter’s commodity index, and CRB spot index and found a statistically significant relationship. Further, the test was repeated on foodgrain and industrial raw material subindexes, but the coefficient for food index failed to be statistically significant. Based on the significance level, they conduced that BDI is a better predictor for industrial raw material prices as compared to food grain. Poulakidas and Joutz (2009) identified a lead-lag relationship between oil prices and West African–US Gulf Tanker rates. Kavussanos et al. (2010) paper explore the cross-market connections between commodity futures contracts on the goods transported by Panamax vessels and forward freight agreements (FFAs) and indicates significant spillover effect between freight and commodity derivatives markets. As an extension to the 2010 paper, Kavussanos et al. (2014) investigated spillovers between freight and commodity derivatives markets by using high-frequency data on commodities and freight rates of different vessels with portfolios (baskets) of commodities that these vessels carry and reported that new information appears first in the returns and volatilities of the commodities futures markets before it is spilled over into the freight derivatives markets. Tsioumas and Papadimitriou (2018) paper explored the lead-lag relationship between the freight rates and prices of “major bulks” such as coal, iron ore, and wheat using Granger causality tests and impulse response analysis. They reported a bidirectional relationship for coal and iron ore, unlike wheat price which leads to BPI. Using two hypothetical countries, Ready et al. (2017) mentioned that BDI, as a proxy for trade costs, can forecast carry trade returns, and carry trade profits are high when transportation cost/BDI is high. Dale and Ulvund (2018) used a regression model between foreign exchange rates and BDI and find that an increase in BDI leads to increase in forwarding premium and carry trade profits in subsequent days, except for JPY/USD. Haigh and Bryant (2000) have identified the linkage between barge and ocean freight prices on international grain market price while Chou et al. (2015) modeled the predictive capability of the BCI for Asian steel index (ASI). Tsouknidis (2016) identified intra-industry volatility spillover for shipping freight markets and also identified co-movement of BCI, BPI, BSI, and BHSI (Baltic Handysize Index). Tsioumas and Papadimitriou (2015) employed VAR–Granger causality tests and identified bi-directional causality between Chinese steel production and freight rates. Some studies indicate this causal link between BDI and commodities has a sufficient impact on the pricing of products. Kavussanos and Nomikos (2003) studied the causal relationship between the spot and futures market for freight rates. The study identified that future price is efficient in price discovery for freight rates, and it has long-term causality on spot prices. In an extended study, Kavussanos et al. (2014) analyzed high-frequency data for 2006–2009 of FFA and commodity future prices for six commodities traded in the Chicago Board of Trade (CBOT). They employed the VECM framework and concluded that new information appears in the commodity futures market, and gets spilled over to the freight futures market. Kärrlander (2010) studied a 2-step regression of stock market returns on metals such as zinc, nickel, copper, and found BDI to be significant only for copper. Further, the study highlighted a statistically significant correlation between BDI and the MSCI metals and mining index. Jung (2015) studied the reason for the collapse of BDI in 2008. The study explored the effect of spot price and volume of iron ore, coal, grains on BDI using multivariate linear regression analysis. It concluded that commodity spot prices are not responsible for the collapse of BDI in 2008. Tsioumas and Papadimitriou (2018) have studied the lead-lag relationship between Chinese steel production and Baltic Exchange indices from 1999 to 2014. The study has applied VAR-Granger causality and identified the significant bi-directional causality between steel productions and BCI. Papailias et al. (2017) studied the effect of BDI on trades of 13 representative countries and found a considerable permanent effect on Australia, Brazil, China, Russia, and the USA, as they are major exporters of iron ore, coal, corn, and tin. The study also identified significant coincidence with BDI annual percent change and price of copper, coal, tin, crude oil, iron ore, and cotton and used these commodities individually to review the forecasting performance for BDI. The results have been compared with the benchmark AR (1) model and identified that beyond a 1-month horizon Iron and Coal model outperforms the benchmark model in forecasting BDI. Ruan et al. (2016) studied cross-correlation between BDI and Crude oil prices and identified cross-correlation is strongly persistent in the short term and weakly anti-persistent in the long-term, which is attributable to volatility and fat-tailed distributions. Wårell (2014) has identified that volatility in the freight rates market triggers price regime change, and iron ore prices are cointegrated with freight rates and GDP growth in China. Lin et al. (2019) used a VAR-BEKK-GARCH-X model to study the relationship between BDI and equity, commodity, and currency markets. The study concludes that BDI is a short-term indicator and identified the spillover effect in the crisis period. Melas and Michail (2021) studied the relationship between commodity price and different dry bulk shipment charter rates and identified a lead-lag relationship, whereby the study suggests that freight rates adjust to falling commodity prices. Angelopoulos et al. (2020) identified a strong economic relationship from commodity to freight markets with commodity markets reacting faster to new information and transferring it to freight markets. In another study, Michail and Melas (2020) study highlight that quantity of seaborne trade also impacts BDI.
Studies discussed above either model BDI’s relationship with economic growth and commodity prices or explore the predictive power of BDI as a leading economic indicator. However, most of the studies are based on linear models and fail to capture the presence of asymmetry in the relationship. Like most variables, BDI and commodity prices are also subject to various economic conditions and so it is hypothesized that their relationship should behave differently in different market conditions. Most of the earlier research works have used either regression models or Granger causality models to explore the relationship with BDI, but the presence of asymmetric aspect in the relationship gets missed out in this process.
In this paper, initially, a modified version of the Granger causality test proposed by Toda and Yamamoto (1995) has been used to investigate the linear model of causality. Further, the nonparametric CiQ, developed by Balcilar et al. (2016a) is applied to examine the causal relationship between BDI and commodity prices. CiQ model being nonparametric also helps in analyzing the causality-in-variance, i.e., high-order dependencies. (Balcilar et al. 2017a, b, c, 2018) for which the CiQ model is gaining popularity recently (Shahbaz et al. 2017; Raza et al. 2018b; Jena et al. 2019). Linear causality test using Toda-Yamamoto method of Granger causality test and CiQ model are discussed in detail in next section.
Methodology
The objective of this study is to explore the dynamics of the relationship between BDI and commodity prices. Most of the studies have discussed the relationship using linear models, whereby effectively ruling out the presence of heterogeneity in a relationship. In reality, the behavior of commodity price and shipping freight rates during normal economic conditions would be vastly different from its behavior during periods of economic crisis or boom. As the CiQ model helps in unraveling the non-linear causal relationship (Balcinar et al. 2017b, 2017c; Raza et al. 2018b) between two variables in different quantiles representing the bearish, normal and bullish market situation, the paper uses CiQ methodology developed by Balcilar et al. (2016a).
The methodology adopted in this study follows a sequential approach, whereby the linear causal relationship between the variables is explored first, followed by tests of nonlinearity. On the indication of existence of nonlinearity in the variables, the CiQ model is implemented. The main objective of this study is to observe CiQ, however, for the sake of completeness and comparability, the linear model of Toda–Yamamoto causality is evaluated between each commodity and BDI. Section 4.1 and Sect. 4.2 briefly discuss the two methods.
Linear causality test: Toda-Yamamoto method of Granger causality test
The linear causal relationship between commodity prices and BDI has been studied using the (Toda and Yamamoto 1995) approach of Granger causality tests. This approach is relatively more efficient as it can be applied to any order of integration of the variables, whereas the Granger causality test requires the same order of integration. Also, unlike Granger causality, it is not required to validate the cointegration relationship before detecting a causal relationship. Hence, it helps in eliminating the bias associated with the unit root test.
In this approach, a vector autoregressive (VAR) model is estimated between BDI and commodity prices at level (p = k + dmax) where k is the lag order of the VAR model with minimum AIC and d represents maximum order of integration of the time series which added as extra lag to compensate the loss of degrees of freedom of the model. The modified Wald (MWALD) statistics is used to study the causality between the dependent and independent variables.
To apply the Toda-Yamamoto causality test, we summarize the BDI-commodity price relationship model in the following VAR system:
| 1 |
where and are the two variables under consideration i.e., BDI and commodity price, ’s are the parameters and ’s are the errors.
In the last step, the Wald test is applied on the coefficients of the lags to determine the causality between the two variables, as follows:
| 2 |
| 3 |
Rejection of the null hypothesis in Eq. 2 means causes i.e., lagged values of can predict . Similarly, if Eq. 3 is rejected, it means causality running from to .
Causality–in–quantiles model
As already mentioned, the CiQ model of Balcilar et al. (2016a) is beneficial for analyzing the relationship between two variables in quantiles, however, the inherent assumption is the presence of asymmetry and the relationship between the variables has potential reasons to deviate from a linear model. As such, the presence of nonlinearity is tested through the BDS test and subsequently, the CiQ model is analyzed. Section 4.2.1 explains the methodology of the BDS test and Sect. 4.2.2 presents the CiQ model.
BDS test for nonlinearity
In order to check the nonlinearity of the BDI-commodity returns relationship we perform the Broock et al. (1996) BDS nonlinearity test on the residuals of BDI-commodity pair regression. The null hypothesis of the BDS test is that the residuals are independent and identically distributed. Let ei be the time series of regression residuals with N-observations. The embedding dimensions are in Eq. 4:
| 4 |
Further, the correlation integral is calculated to measure the spatial correlation between the points, by combining the number of pair of points (i,j), where 1 ≤ i ≤ N and 1 ≤ j ≤ N, in the m-dimensional space within a radius or tolerance of ε of each other. The correlation integral is given in Eq. 5:
| 5 |
where,
= 0 otherwise.
Under the null hypothesis, the likelihood of the distance between a pair of points being less or equal to ε should be constant. Brock et al. (1996) defined that if the time series is independent and identically distributed:
| 6 |
If the ratio of N/m > 200 and the values of m are between 2 and 5 then, the difference has an asymptotic normal distribution with zero mean and a variance defined as
| 7 |
where, ;
The BDS test statistic is stated as in Eq. 8:
| 8 |
It is a two-tailed test and the null hypothesis is rejected if the test statistic is greater than or less than the critical values based on the level of significance.
Causality-in-quantiles model (CiQ)
In this paper, we use the nonparametric CiQ model proposed by Balcilar et al. (2016a, b). This method evaluates Granger causality in specific quantiles between two variables in a nonparametric approach. The application of this model helps in the minimization of misspecification error probabilities as a nonparametric procedure is used to analyze the structure of dependence of the variables on each other. Another advantage is it also calculates causality in higher moments like variance. So, we can measure causality-in-means as well as variance. Balcilar et al. (2016a, b) proposed this methodology following Nishiyama et al. (2011) and Jeong et al. (2012). The null hypothesis states that in the quantile θ with regards to the lag vectors of y if
| 9 |
So, the alternative hypothesis that in the θ quantile is given by
| 10 |
where is the θth quantile of depending on t and
Following Jeong et al. (2012) the Eqs. 9 and 10 can be rewritten as follows:
| 11 |
| 12 |
where {{
The function is the conditional distribution function of on . It is presumed that this function is solely continuous in for approximately all . Further is the conditional distribution function of on . We define and , hence, will have a probability equal to 1. The detail evaluation of this hypothesis follows Jeong et al. (2012).
Jeong et al. (2012) used a distance measure represented by J, as follows:
| 13 |
where is the error term and is the marginal density function of . The error term is generated from the expression of the null hypothesis in Eq. 11:
| 14 |
where 1{.} is the indicator function. Based on this definition the distance measure J can be defined as
| 15 |
So, from Eq. 15 it can be observed that J > 0 for the alternative hypothesis, but J = 0 only when the null hypothesis in Eq. 11 is true. Jeong et al. (2012) have represented J as feasible Kernel form as follows:
| 16 |
where T denotes the sample size, p represents the lag order; h represents the bandwidth for the Kernel function K (.). The can be estimated as
| 17 |
now, is the θ th conditional quantile of given , which can be estimated using a nonparametric kernel method as
| 18 |
where,
Is the Nadarya Watson Kernel estimator of and L (.) is the kernel function with h bandwidth.
Balcilar (2016a) adopted the model of Nishiyama et al. (2011) for the CiQ test in second or higher moments. For explaining the causality in higher moments, the dependent variable is defined as follows:
| 19 |
where and are unknown functions fulfilling stationary conditions. is a white noise process. When is a general non-linear function, this specification can be used to detect the predictive power from to . Hence, the Granger causality-in-variance definition does not require an explicit specification of squares for . Hence, following Nishiyama et al. (2011), Eqs. 11 and 12 can be written for higher moments as follows:
| 20 |
| 21 |
where k = 1,2,…M. For causality-in-variance k = 2.
So, integrating the entire framework, it can be defined that xt Granger causes yt in quantile θ upto the K-th moment utilizing Eq. 21. The causality-in-variance test is conducted replacing in Eq. 13 to Eq. 18 with . Initially, the nonparametric test for causality in the first moment or mean is conducted. However, rejection of causality doesn’t stop the process, the nonparametric test for the second moment or variance is conducted next. The lag length is selected based on Schwarz Information Criteria (SIC) under the VAR model of commodity and BDI returns. The bandwidth for kernel density estimation has been chosen based on the least square cross-validation technique. Gaussian type kernels are employed for K(.) and L(.).
Data
Daily spot prices of BDI and 84 commodities representing major dry bulk commodities have been considered for this study. Historically, BDI has experienced significant volatility during major economic events such stock market crisis in 1987, the East Asian crisis in 1997, the 1999 dot-com bubble burst, the Latin America debt crisis, and the 2008 financial crisis, etc. The study period is from June-2006 to November-2018. Out of the 8 commodities, four commodities i.e., iron ore, aluminum, copper, and coal are from the metal and mining raw material group while wheat, soybean, cotton, and corn are bulk agri-commodities. The commodities have been selected as representative of major dry bulk shipments, which influences the shipping cost and ultimately the BDI. As mentioned earlier, this study covers a time period starting from 2006 to 2018 so as to cover boom and bust periods in global trade as well as to capture the heterogeneity in a relationship in different quantiles of the data using the conditional quantiles-based model. Some of the papers discussed earlier have used daily, monthly, or even quarterly data to model the relationship between BDI and other financial and macroeconomic parameters. As commodity spot prices, as well as BDI, can vary significantly over a short period of time, this paper uses daily data to model the relationship. The data has been collected from the Bloomberg database. All prices are represented in US dollars.
In Table 1, the descriptive statistics for the return series of the variables are presented. The JB-test statistics show that all return series are non-normal. Aluminum, copper, wheat, and cotton returns are positively skewed, and the rest are negatively skewed and all commodity return series exhibit fat-tail. This justifies the presence of asymmetry and use of the CiQ model, as causality in tails will be different than at the center for fat-tailed distribution.
Table 1.
Descriptive Statistics
| Mean | Std. dev | Min | Max | Skewness | Kurtosis | Jarque–Bera | Prob | #obs | |
|---|---|---|---|---|---|---|---|---|---|
| BDI | − 0.0003 | 0.0279 | − 0.2372 | 0.2314 | − 0.1320 | 14.4758 | 15,290.13 | 0.00 | 2785 |
| Iron ore | 0.0001 | 0.0210 | − 0.2778 | 0.2730 | − 0.9859 | 73.8470 | 582,899 | 0.00 | 2785 |
| Aluminum | − 0.0001 | 0.0339 | − 0.3387 | 0.3266 | 0.0519 | 37.6430 | 139,267.2 | 0.00 | 2785 |
| Coal | 0.0000 | 0.0138 | − 0.2436 | 0.2348 | − 0.8977 | 112.140 | 1,382,613 | 0.00 | 2785 |
| Copper | − 0.0001 | 0.0532 | − 0.3665 | 0.3222 | 0.0612 | 14.0464 | 14,161.6 | 0.00 | 2785 |
| Soybean | 0.0001 | 0.0166 | − 0.2331 | 0.0834 | − 1.1407 | 19.2501 | 31,246.49 | 0.00 | 2785 |
| Wheat | 0.0001 | 0.0487 | − 0.4594 | 0.5070 | 0.1677 | 37.2725 | 136,316.1 | 0.00 | 2785 |
| Cotton | 0.0002 | 0.0195 | − 0.1050 | 0.1506 | 0.0950 | 6.6619 | 1560.246 | 0.00 | 2785 |
| Corn | 0.0002 | 0.0287 | − 0.3083 | 0.2402 | − 0.5955 | 19.9291 | 33,421.45 | 0.00 | 2785 |
| MSCI world | 0.0002 | 0.0114 | − 0.1530 | 0.0674 | − 1.2055 | 20.6845 | 36,965.58 | 0.00 | 2785 |
In Table 2 the stationarity test results are presented. The ADF test results indicate all return series are I (0). Zivot and Andrews’s (2002) test statistics indicate the existence of structural break with unit root for all commodities and BDI, which strengthens the assumption of possible nonlinearity in each time series thus amenable to the chosen CiQ model.
Table 2.
Unit root test result
| ADF test | Zivot-Andrews test | Break date | |
|---|---|---|---|
| BDI | − 25.718* | − 14.508* | 11-Jun-08 |
| Iron ore | − 60.054* | − 18.716* | 29-Apr-08 |
| Aluminum | − 81.62* | − 23.53* | 20-Feb-09 |
| Coal | − 59.244* | − 21.66* | 26-Aug-08 |
| Copper | − 85.197* | − 24.463* | 18-Dec-08 |
| Soybean | − 52.052* | − 19.323* | 2-Jul-08 |
| Wheat | − 74.77* | − 21.135* | 8-Sep-09 |
| Cotton | − 51.688* | − 19.702* | 7-Mar-11 |
| Corn | − 65.665* | − 19.984* | 26-Jun-08 |
| MSCI world | − 47.62* | − 25.623* | 9-Mar-09 |
Note: * indicates rejection of null hypothesis at 5% significance level
Results and discussion
Toda-Yamamoto causality test results
For the sake of completeness and comparability, the linear model of Toda–Yamamoto causality has been undertaken between each commodity and BDI (Table 3).
Table 3.
Toda-Yamamoto causality test result
| Panel (a) | Panel (b) | ||||||
|---|---|---|---|---|---|---|---|
| Dependent variable | Causing variable | P-value | Causality | Dependent variable | Causing variable | P-value | Causality |
| BDI | Iron ore | 0.0000 | √ | Iron ore | BDI | 0.0001 | √ |
| BDI | Aluminum | 0.2423 | X | Aluminum | BDI | 0.0010 | √ |
| BDI | Coal | 0.0000 | √ | Coal | BDI | 0.0003 | √ |
| BDI | Copper | 0.4077 | X | Copper | BDI | 0.0007 | √ |
| BDI | Soybean | 0.0000 | √ | Soybean | BDI | 0.1442 | X |
| BDI | Wheat | 0.0000 | √ | Wheat | BDI | 0.0000 | √ |
| BDI | Corn | 0.4846 | X | Corn | BDI | 0.2241 | X |
| BDI | Cotton | 0.7062 | X | Cotton | BDI | 0.6071 | X |
Note: X denotes no causal relationship; √ denotes causal relationship exists
Analysis of panel (a) shows the impact of commodities on BDI. It can be observed that out of the eight commodities only four commodities, i.e., iron ore, coal, soybean, and wheat, are causing BDI. Similarly, panel (b), shows the impact of BDI on commodity prices and indicates BDI is causing iron ore, aluminum, coal, copper, and wheat. Combining the two results, it can be summarized that bidirectional causality exists between BDI and iron ore, coal, wheat while unidirectional causality exists between BDI and copper, aluminum, soybean. To explore the presence of nonlinearity relationship in BDI and commodity prices, the BDS test (Brock et al. 1996) has been used (Table 4).
Table 4.
BDS test for nonlinearity
| BDI vs | Dimension | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Iron ore | BDS statistic | 0.016706 | 0.03339 | 0.046481 | 0.05115 | 0.051135 |
| Std. error | 0.002739 | 0.00438 | 0.005252 | 0.005516 | 0.005362 | |
| z-statistic | 6.099108 | 7.623779 | 8.849286 | 9.272705 | 9.536479 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Aluminum | BDS statistic | 0.034515 | 0.061774 | 0.076626 | 0.084805 | 0.086069 |
| Std. error | 0.002106 | 0.003348 | 0.003989 | 0.004161 | 0.004017 | |
| z-statistic | 16.38846 | 18.45298 | 19.21002 | 20.38111 | 21.42817 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Coal | BDS statistic | 0.088632 | 0.147496 | 0.177183 | 0.189393 | 0.19246 |
| Std. error | 0.002924 | 0.004673 | 0.005602 | 0.005882 | 0.005716 | |
| z-statistic | 30.31044 | 31.56311 | 31.62742 | 32.19931 | 33.66814 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Copper | BDS statistic | 0.065434 | 0.123835 | 0.163889 | 0.189244 | 0.203048 |
| Std. error | 0.002601 | 0.004147 | 0.00496 | 0.005195 | 0.005035 | |
| z-statistic | 25.16069 | 29.85858 | 33.04071 | 36.43065 | 40.32672 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Soybean | BDS statistic | 0.012684 | 0.026181 | 0.035431 | 0.040474 | 0.041909 |
| Std. error | 0.001708 | 0.002718 | 0.003241 | 0.003382 | 0.003266 | |
| z-statistic | 7.424688 | 9.631818 | 10.93239 | 11.96615 | 12.83101 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Wheat | BDS statistic | 0.024181 | 0.046894 | 0.060935 | 0.065768 | 0.06608 |
| Std. error | 0.001942 | 0.003084 | 0.00367 | 0.003823 | 0.003685 | |
| z-statistic | 12.44853 | 15.20571 | 16.60401 | 17.20338 | 17.9317 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Cotton | BDS statistic | 0.022995 | 0.044488 | 0.056686 | 0.061714 | 0.062411 |
| Std. error | 0.001802 | 0.002857 | 0.003396 | 0.003533 | 0.003401 | |
| z-statistic | 12.76213 | 15.56947 | 16.69214 | 17.46835 | 18.35161 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Corn | BDS statistic | 0.029834 | 0.053836 | 0.066059 | 0.070209 | 0.070756 |
| Std. error | 0.001992 | 0.003166 | 0.00377 | 0.003931 | 0.003792 | |
| z-statistic | 14.97427 | 17.00571 | 17.52088 | 17.86091 | 18.65734 | |
| Prob | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
BDS test is conducted on embedding dimensions from 2 to 6 on the residuals of BDI and commodity price regression residuals. The BDS test statistics indicate that the relation between BDI and commodity returns is nonlinear. The result shows the null hypothesis of linearity has been rejected at a 1% significance level. Also, there is evidence of a structural break in the time series. This means the linear models of causality are susceptible to misspecification and should not be relied upon. So, the CiQ test for ascertaining the non-linear relationship has been detailed in the next section.
Causality-in-quantile in mean and variance
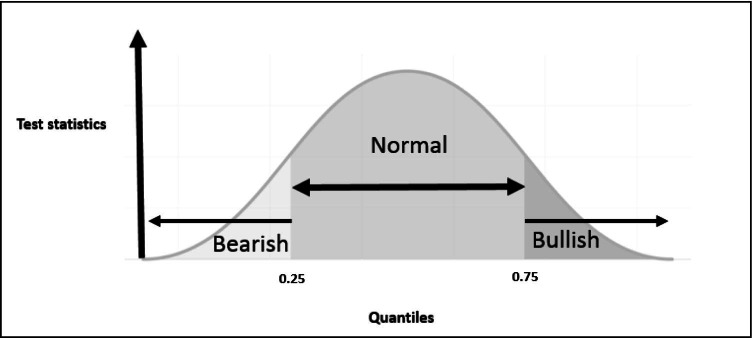
The CiQ approach identifies causality in all possible market conditions, which is advantageous to linear models of causality which provide an average outcome. The test statistics are calculated for all quantiles of the dependent variable. Based on the quantiles, the total study period is to be classified as a bearish period representing lower quantiles (0.1 to 0.25 quantile), normal period (representing 0.25 to 0.75 quantiles), and bullish period (representing 0.75 to 0.99 as higher quantiles) as depicted in Fig. 2.
Fig. 2.
Quantile wise market condition
The results of CiQ (for both mean and variance) can be better interpreted through the graphical output presented in Figs. 3, 4, 5, 6, 7, 8, 9, 10. In general, the shape of the causality curve indicates its strength. If the curve is hump-shaped it means that variable-1 causes variable-2 in normal market conditions, however in the bearish or bullish market condition the causality diminishes. The inverted hump shape curve denotes the opposite.
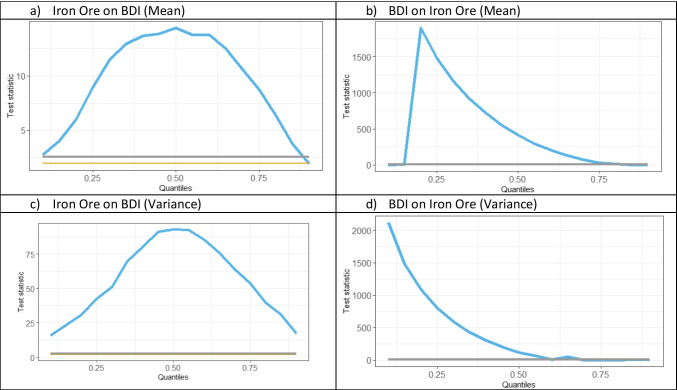
Fig. 3.
CiQ model (BDI vs. iron ore)
Fig. 4.
CiQ model (BDI vs. aluminum)
Fig. 5.
CiQ model (BDI vs. coal)
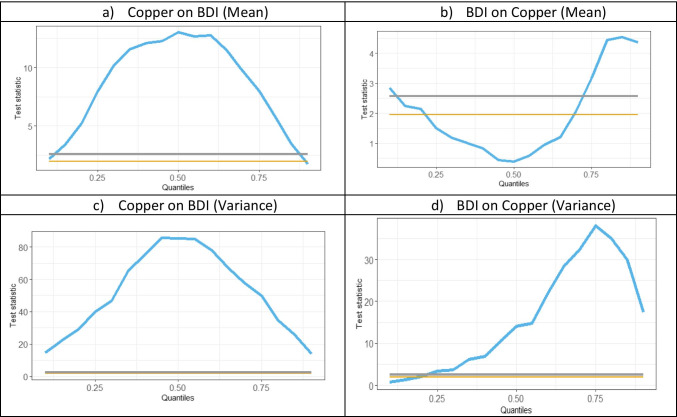
Fig. 6.
CiQ model (BDI vs. copper)
Fig. 7.
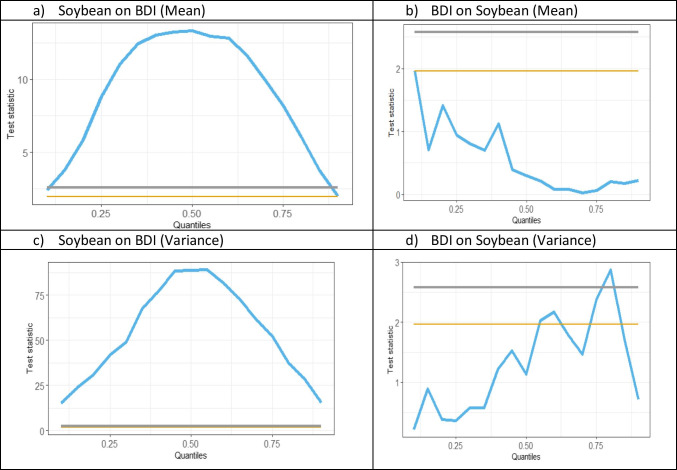
CiQ model (BDI vs. soybean)
Fig. 8.
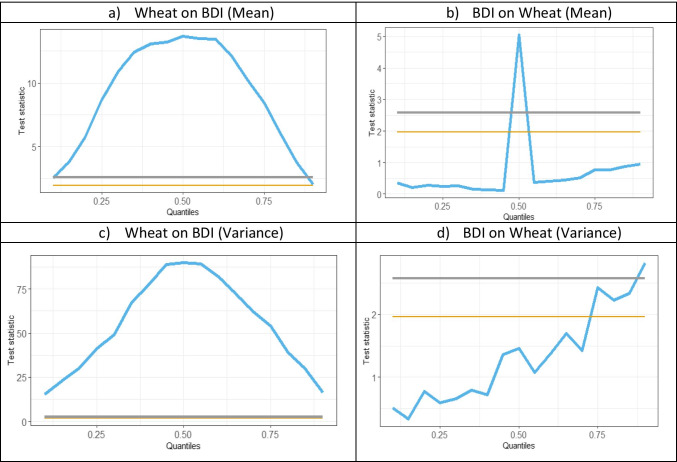
CiQ model (BDI vs. wheat)
Fig. 9.
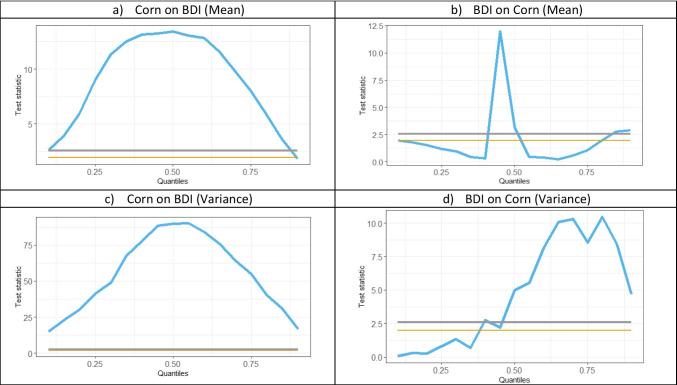
CiQ model (BDI vs. corn)
Fig. 10.
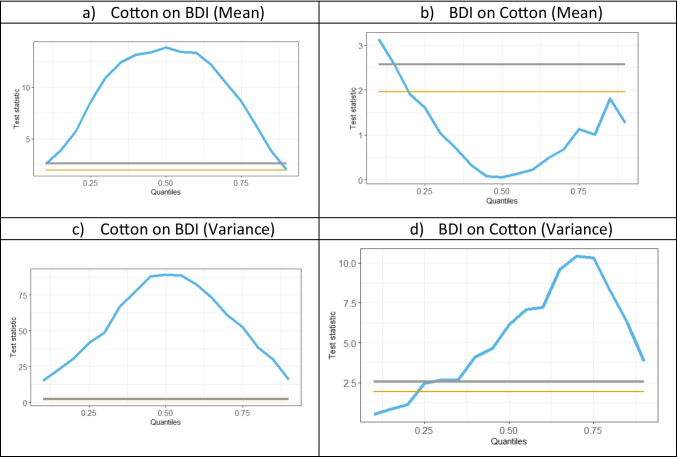
CiQ model (BDI vs. cotton)
Raw material products: iron ore, aluminum, aoal, and copper
Iron ore is the most consumed raw material for industrial usage hence the most transported dry bulk commodity. Fig-3(a) represents causality-in-mean from iron ore to BDI. It can be observed that the causality-in-mean of iron ore causing BDI remains always above the critical values, which means iron ore returns are causing BDI returns. However, the relationship is most prominent under a normal period and gradually diminishes in bearish or bullish market conditions. The relationship is insignificant in extreme bullish markets. Similarly, Fig. 3(b) represents CiQ (in-mean) from BDI to iron ore. From the analysis of Fig. 3(b), it is evident that BDI returns are causing iron ore returns at lower quantiles, i.e., strong causality in a bearish market and it diminishes from normal to bullish market condition. Figures 3(c) and 3(d) models CiQ (in-variance) from BDI to Iron ore and from iron ore to BDI, respectively. Figure 3(c) indicates the CiQ (in-variance) plot from iron ore to BDI, which is significant in all quantiles, but it is most prominent in and around mid-quantile and can be interpreted as most prominent at Normal market condition and gradually diminishes in bearish and bullish market conditions. Similarly, Fig. 3(d) shows CiQ (in-variance) progressively diminishes from bearish markets to a bullish market. Hence, it can be observed that for iron ore, BDI is an effective predictor in bearish market conditions. Combining the results of all four figures, i.e., Fig. 3(a,d), it can be inferred that BDI is a better predictor of iron ore in bearish market conditions, while iron ore is influencing BDI in all market conditions, most prominent being normal market condition.
The reason may be that iron ore is one of the largest transported dry bulk commodities, so if the iron ore market is bearish then higher freight cost leading to higher BDI would result in more expense for iron ore transportation, and it will cause higher volatility spillover from BDI to iron ore. However, the bullish market has no significant impact from freight rates, as higher transportation of raw material is a precursor to future economic growth, so the bullish effect will be visible in a longer time horizon. The discussion on BDI and iron ore can be summarized as follows: bidirectional causal relationship in mean, as well as variance, exists between iron ore prices and BDI in all market conditions. This also indicates feedback loop plays an important role in information transmission between the iron ore price and BDI.
Similar findings have been observed by Tsioumas and Papadimitriou (2018) between iron ore and Capesize index, while Angelopoulos et al.(2020) identified unidirectional causality from iron ore prices to freight rates on an average level. Gu et al. (2019) also identified that iron ore is a key commodity it constitutes the demand side for the shipping market, thereby increase in demand of iron ore pushes the price as well as BDI. At an overarching level, even though the findings of this paper lend support to other studies on iron ore and freight rates (Warell (2014), Wårell (2018), Ma and Zhen (2020)), but the uniqueness of this study emanates from the observed heterogeneous relationship between BDI and Iron Ore in different market conditions.
Figure 4(a) represents CiQ (in-mean) from aluminum to BDI. It can be observed that the causal relationship on conditional mean for aluminum causing BDI always remains above the critical values, which means aluminum returns are causing BDI returns. Similar to iron ore, the relationship is most prominent in the normal market and gradually diminishes in bearish or bullish market conditions. In Fig. 4(b), it can be observed that BDI is causing aluminum returns only in bullish markets condition. There is no causality-in-mean for bearish and normal market conditions, and volatility transfer is also happening in the bullish market (Fig. 4(d)), but it drops subsequently. So, it can be inferred that in the normal market condition, the relation between BDI and aluminum is unidirectional from aluminum to BDI. However, in a bullish market, BDI is causing aluminum.
In Figs. 5(a,c), coal is causing BDI in all quantiles in means as well as variance. However, as shown in Fig. 5(b), the relationship of BDI causing coal is most prominent in the bearish market for mean and it gradually falls in a bullish market. The relationship overall is bidirectional. For variance, in Fig. 5(d), the causality test statistics are very high, both in bearish and bullish market conditions but fall in normal markets. The asymmetric relationship is attributable to the very high consumption of coal in almost all major industries, coal consumption is relatively higher in emerging economies, while developed economies to prefer phase out of coal consumption due to environmental concerns (Lin et al. 2019). When emerging economies face recession, the industrial production is reduced which leads to a fall in demand of coal consumption, while in bullish markets coal demand raises significantly. So, the volatility demand of coal will affect freight rates in bearish and bullish markets, thereby leading to volatility spillover from coal spot prices. The evidence of a strong causal relationship in mean corroborates with the results of Angelopoulos et al. (2020), while Lin et al. (2019) identified that a nonlinear relationship exists between coal prices and all kinds of charter rates.
For Copper, in Fig. 6(b), the causality from BDI to Copper in returns is only significant in bullish market conditions; however, as shown in Fig. 6(d), volatility transmission from BDI to copper is significant in all markets, except some portion in a bearish market. As per Figs. 6(a,c), CiQ (mean), and CiQ (variance) are significant, with most prominent in normal market conditions. The findings are in line with Guzmán and Silva’s (2018) study indicating copper price and stock positions being influenced by BDI. Further, Angelopoulos et al. (2020) identified that copper prices lead to freight rates, whereas Lin et al. (2019) identified a positive relationship between copper price and Handysize and Supramax charter rates.
Overall, the demand for iron ore, aluminum, copper, and coal are sensitive to the business cycle as the raw materials are consumed directly or indirectly by the construction, automotive, power, and consumer durable sectors. These sectors thrive when the economy is growing, and fall into recession when the economy slows (Tilton 2014). Further, different developed economies (e.g., USA) and developing economies (e.g., China) adopt various trade policies related to raw materials from time to time, thereby leading to the fluctuation in demands owing to policy uncertainty which adversely impacts commodity price and freight rates. Our results suggest that BDI and raw material prices are strongly interrelated in bearish market conditions, in line with the outcome of Lin et al. (2019).
Agricultural commodities: wheat, soybean, corn, and cotton
For agricultural commodities given in Figs. 7, 8, 9, 10, the causal relationship from commodity to BDI remains similar to other commodities, however, the causality from BDI to commodity is totally different.
For Soybean, in Fig. 7(b), BDI is not causing Soybean in mean. Also, as per Fig. 7(d), causality-in-variance is also not significant. The results support the findings of Xiong and Hu (2021) of a very low correlation between BDI and Chinese soybean prices. Michail and Melas (2021) also failed to identify strong interaction between soybean price and freight rates. For wheat, BDI causes wheat return for a small portion in the normal market; causality-in-variance is hardly significant in bullish market conditions. For corn, in Fig. 9(b), the CiQ is similar to wheat; however, causality-in-variance is significant in normal to bullish market conditions. For cotton, given in Fig. 10(b), the causality-in-mean is significant for very small quantiles in a bearish market; the causality-in-variance is similar to corn. So, the agricultural commodities are influenced by BDI in normal and bullish markets. The results for wheat support the findings of Michail and Melas (2020, 2021) for normal market conditions.
Agricultural commodities being perishable in nature cannot be stored for long period, thereby agricultural commodities are chartered in the spot market and are transported in Supramax and Panamax vessels (Kavussanos and Alizadeh-M 2001; Michail and Melas 2021). Moreover, certain agricultural commodities display a strong substitution effect and seasonality; thereby the impact of those commodities prices on freight rates is not identical in all market conditions (Angelopoulos et al. 2020; Michail and Melas 2021). In this regard, the analysis presented in this paper considered various quantiles representing different market conditions that unravel the heterogeneous relationship between freight rates and agricultural commodity prices, which is an unique and distinguishable contribution in the extant literature.
Robustness test
The CiQ model has been repeated on commodity and BDI pairs, with conditional on MSCI world index as an alternative indicator of global economic condition. It is observed that the results are the same as before and there is no change in the shape of the causality curves for any of the commodities due to the inclusion of the MSCI world index as a control variable. This proves that the causality in the quantiles model of BDI and commodity spot prices is robust even in presence of other macro-economic variables like the MSCI world index. The outcome is similar to the results of Bakshi et al. (2011).
Result summary
Results of the CiQ tests both at mean and variance level are given in Tables 5, 6, 7, 8, 9. In Table 5, unidirectional causality indicates commodity returns influence BDI return while bidirectional causality indicates when both returns are influencing each other.
Table 5.
Summary of causality in quantiles from commodity to BDI
| Bearish | Normal | Bullish | ||
|---|---|---|---|---|
| Iron ore | Mean | Bidirectional | Bidirectional | Bidirectional |
| Variance | Bidirectional | Bidirectional | Bidirectional | |
| Aluminum | Mean | Unidirectional | Unidirectional | Bidirectional |
| Variance | Unidirectional | Bidirectional | Bidirectional | |
| Coal | Mean | Bidirectional | Bidirectional | Bidirectional |
| Variance | Bidirectional | Bidirectional | Bidirectional | |
| Copper | Mean | Unidirectional | Unidirectional | Bidirectional |
| Variance | Unidirectional | Bidirectional | Bidirectional | |
| Soybean | Mean | Unidirectional | Unidirectional | Unidirectional |
| Variance | Unidirectional | Unidirectional | Unidirectional | |
| Wheat | Mean | Unidirectional | Bidirectional | Unidirectional |
| Variance | Unidirectional | Unidirectional | Bidirectional | |
| Corn | Mean | Unidirectional | Bidirectional | Unidirectional |
| Variance | Unidirectional | Bidirectional | Bidirectional | |
| Cotton | Mean | Unidirectional | Bidirectional | Unidirectional |
| Variance | Unidirectional | Bidirectional | Bidirectional |
Note: A) For mean: unidirectional: causality from commodity to BDI; bidirectional: commodity and BDI causing each other
B) For variance: unidirectional: causality from commodity returns to BDI variance; bidirectional: commodity and BDI returns causing each other variance
Table 6.
Causality-in-quantiles (mean) commodity to BDI
| Causing variable | Dependent variable | Causality in | Bearish | Normal | Bullish |
|---|---|---|---|---|---|
| Iron ore | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Aluminum | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Coal | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Copper | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Soybean | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Wheat | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Corn | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
| Cotton | BDI | Mean | √ (Low) | √ (High) | √ (Low) |
Note: √ denotes causal relationship exists; high and low indicates magnitude of test statistics
Table 7.
Causality-in-quantiles (variance) commodity to BDI
| Causing variable | Dependent variable | Causality | Bearish | Normal | Bullish |
|---|---|---|---|---|---|
| Iron ore | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Aluminum | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Coal | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Copper | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Soybean | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Wheat | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Corn | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
| Cotton | BDI | Variance | √ (Low) | √ (High) | √ (Low) |
Note: √ denotes causal relationship exists; high and low indicates magnitude of test statistics
Table 8.
Causality-in-quantiles (mean)BDI to commodity
| Causing variable | Dependent variable | Causality | Bearish | Normal | Bullish |
|---|---|---|---|---|---|
| BDI | Iron ore | Mean | √ (High) | √ (Mid) | √ (Low) |
| BDI | Aluminum | Mean | X | X | √ (High) |
| BDI | Coal | Mean | √ (High) | √ (Mid) | √ (Low) |
| BDI | Copper | Mean | X | X | √ (High) |
| BDI | Soybean | Mean | X | X | X |
| BDI | Wheat | Mean | X | √ (High) | X |
| BDI | Corn | Mean | X | √ (High) | X |
| BDI | Cotton | Mean | √ (High) | X | X |
Note: √ denotes causal relationship exists; high, mid, and low indicates magnitude of test statistics; X denotes no causal relationship
Table 9.
Causality-in-quantiles (variance) BDI to commodity
| Causing Variable | Dependent Variable | Causality | Bearish | Normal | Bullish |
|---|---|---|---|---|---|
| BDI | Iron Ore | Variance | √ (High) | √ (Mid) | √ (Low) |
| BDI | Aluminum | Variance | X | √ (Low) | √ (High) |
| BDI | Coal | Variance | √ (High) | √ (Low) | √ (High) |
| BDI | Copper | Variance | X | √ (Low) | √ (High) |
| BDI | Soybean | Variance | X | X | X |
| BDI | Wheat | Variance | X | X | X |
| BDI | Corn | Variance | X | √ (Low) | √ (High) |
| BDI | Cotton | Variance | X | √ (Low) | √ (High) |
Note: √ denotes causal relationship exists; high, mid, and low indicates magnitude of test statistics; X denotes no causal relationship
Results given in Table 5 indicate that for a bearish market the relationship in mean and variance is mostly unidirectional while the causality is bidirectional during normal and bullish market conditions.
The magnitude of CiQ in mean and variance for the commodity to BDI are presented in Tables 6 and 7. It is evident from Table 6 and Table 7, that all commodities are causing BDI in mean as well as variance, which means there is stable information transmission and volatility spillover from commodity to BDI.
However, as can be seen from the first-row details in Table 6 and Table 7, the information transmission and volatility spillover from iron ore to BDI is lower in extreme market conditions i.e., bullish and bearish market while the highest information transmission and volatility spillover happen in normal market conditions. The same condition prevails for all commodities given in Table 6 and Table 7. Also, the CiQ in both mean and variance from commodity to BDI is high in normal market condition.
In Table 8 and Table 9, results for information transmission and volatility spillover from BDI to commodities are given. Analysis of details given in row-1 and row-3, it can be observed that BDI is causing iron ore and coal in all market conditions. This result is intuitive because iron ore and coal are the major dry bulks in quantity being transported through shipment. So, BDI is a leading indicator for iron ore and coal returns and there is significant volatility spillover from BDI to iron ore in all market conditions. Results given in row-2 and row-4 indicate that BDI is causing returns for aluminum and copper in bullish market conditions. For wheat and corn, the causality is significant in normal market conditions. For cotton, it is significant in bearish markets. Interestingly BDI has no impact on soybean in any market condition.
As shown in Table 8, BDI to commodity CiQ (in-mean) is high in bearish market conditions for most of the commodities. However, BDI is a strong predictor for Aluminum and copper in bullish market conditions. It can be also observed that BDI is not causing soybean returns in any market condition, but it is a strong predictor for wheat and corn returns in normal market conditions. Further, it can be observed in Table 9, volatility spillover from BDI to aluminum, copper, and coal is high in bullish market conditions. These commodities are major raw materials for power generation and industrial production. When the economy is bullish, high variance in freight rate can affect significantly the prices of raw material shipment, so volatility spillover from freight rates or BDI to commodity is significantly high for bullish market conditions.
Juxtaposing the results of Tables 6, 7, 8, 9, some interesting observations are:
-
i.
Commodity returns and volatility have a significantly higher influence on BDI in normal market conditions as compared to a bearish and bullish market.
-
ii.
High commodity prices (bullish market) do not necessarily correspond to higher BDI, in fact, the influence gets diminished from normal to bullish market conditions.
-
iii.
BDI returns impacts on different commodities vary from one commodity to another. While BDI return is causing iron ore and coal in all market conditions, on the other hand, BDI return has no influence on soybean return.
-
iv.
BDI volatility spillovers also vary from one commodity to another. While there is no volatility spillover for Wheat and Soybean in any market condition, BDI volatility spillover on commodities is high for the rest of the commodities studied in bullish markets.
-
v.
For industrial metals, BDI-commodity relation is mostly bidirectional, less prominent in bullish markets. When BDI rates are high, industrial commodity prices are least affected.
-
vi.
For agricultural products, BDI has a significant effect mostly in bullish markets. When BDI rates are bullish, agricultural commodity prices are most affected.
Overall, the causality from commodity to BDI remains stable for all the commodities, which may be justified as commodity prices are the major factors that determine quantity transportation and freight rates. However, BDI to commodity causal relationships are asymmetric and vary from commodity to commodity. This is also justified as each commodity is defined by its own supply and demand conditions and specific properties, so the impact of freight rate on commodity should be different for different commodities.
Conclusion and policy implications
In this paper, the interaction between BDI and commodity returns has been discussed through linear and nonlinear models in mean as well as variance. This study majorly focuses on the CiQ approach to explore the causal relationship between BDI and 8 dry bulk commodities through causality-in-mean and variance models. The CiQ model helps in exploring causality in different quantiles and identifies the unique relationship between BDI and each of these 8 commodities in bullish, bearish, and normal market conditions. Overall, the causality from commodity to BDI remains stable for all the commodities, which may be justified as commodity prices are the major factors to determine quantity transportation and freight rates. However, BDI to commodity causal relationships are asymmetric and vary from commodity to commodity.
The unique insights from this study can help exporters and importers of bulk commodities to monitor the dynamic relationship between commodity price and shipping freight rates and accordingly decide when it is relatively convenient to export or import dry bulks and hedge freight rates using freight rate derivatives. Simultaneously, the research findings will help shipbrokers to offer competitive charter rates considering the prevailing supply and demand conditions in major dry bulk commodities. This study advances the knowledge of freight market dynamics and commodity prices, while at the same moment supporting decision-making processes in dry bulk chartering and commodity trading through better hedging and investment procedures. Future research can focus on studying the relationship between commodity prices and BDI in different frequency domains using various advanced econometric methodologies to unravel further insights. As a singular event, the impact of the COVID-19 pandemic on triggering a significant decline in global trade in dry bulk commodities which in turn affected the freight rates and freight rate derivatives can also be explored as a case study.
Declarations
Conflict of interest
The authors declare no competing interest.
Footnotes
The representative routes have to be large enough in volume with respect to the overall market. At present, 22 routes are assessed on a daily basis. Details of the routes are available at https://www.balticexchange.com/
A total of 13 international shipbroking firms provide a quotation for the Capsize index while 22 firms provide quotes for Capesize index. More details are available at http://www.imsf.info/media/1039/market-indices-calculations-etc.pdf
MSCI world development index has been modeled as an alternative indicator of global economic condition for robustness test.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Alizadeh AH, Muradoglu G. Stock market efficiency and international shipping-market information. J Int Finan Markets Inst Money. 2014;33:445–461. doi: 10.1016/j.intfin.2014.10.002. [DOI] [Google Scholar]
- Angelopoulos J, Sahoo S, Visvikis ID. Commodity and transportation economic market interactions revisited: new evidence from a dynamic factor model. Transport Res Part E Logist Transport Rev. 2020;133:101836. doi: 10.1016/j.tre.2019.101836. [DOI] [Google Scholar]
- Apergis N, Payne JE. New evidence on the information and predictive content of the Baltic Dry Index. Int Financial Stud. 2013;1:62–80. doi: 10.3390/ijfs1030062. [DOI] [Google Scholar]
- Bakshi G, Panayotov G, Skoulakis G. The Baltic Dry Index as a predictor of global stock returns, commodity returns, and global economic activity. Social Sci Res Network. 2011 doi: 10.2139/ssrn.1787757. [DOI] [Google Scholar]
- Balcilar M, Bekiros S, Gupta R. The role of news-based uncertainty indices in predicting oil markets: a hybrid nonparametric quantile causality method. Empirical Economics. 2016;53:879–889. doi: 10.1007/s00181-016-1150-0. [DOI] [Google Scholar]
- Balcilar M, Gupta R, Pierdzioch C. Does uncertainty move the gold price? New evidence from a nonparametric causality-in-quantiles test. Resour Policy. 2016;49:74–80. doi: 10.1016/j.resourpol.2016.04.004. [DOI] [Google Scholar]
- Balcilar M, Bonato M, Demirer R, Gupta R. The effect of investor sentiment on gold market return dynamics: evidence from a nonparametric causality-in-quantiles approach. Resour Policy. 2017;51:77–84. doi: 10.1016/j.resourpol.2016.11.009. [DOI] [Google Scholar]
- Balcilar M, Cakan E, Gupta R. Does US news impact Asian emerging markets? Evidence from nonparametric causality-in-quantiles test. N Am J Econ Finance. 2017;41:32–43. doi: 10.1016/j.najef.2017.03.009. [DOI] [Google Scholar]
- Balcilar M, Gupta R, Sousa RM, Wohar ME. Do cay and cayMS predict stock and housing returns? Evidence from a nonparametric causality test. Int Rev Econ Financ. 2017;48:269–279. doi: 10.1016/j.iref.2016.12.007. [DOI] [Google Scholar]
- Balcilar M, Hammoudeh S, Toparli EA. On the risk spillover across the oil market, stock market, and the oil related CDS sectors: A volatility impulse response approach. Energy Economics. 2018;74:813–827. doi: 10.1016/j.eneco.2018.07.027. [DOI] [Google Scholar]
- Baltyn P (2016) Baltic Dry Index as economic leading indicator in the United States. In: Managing Innovation and Diversity in Knowledge Society Through Turbulent Time: Proceedings of the MakeLearn and TIIM Joint International Conference 2016. ToKnowPress, pp 205–211 https://ideas.repec.org/h/tkp/mklp16/205-211.html
- Bildirici ME, Kayıkçı F, Onat IŞ. Baltic Dry Index as a major economic policy indicator: the relationship with economic growth. Proc Soc Behav Sci. 2015;210:416–424. doi: 10.1016/j.sbspro.2015.11.389. [DOI] [Google Scholar]
- Bildirici M, Kayıkçı F, Onat IŞ. BDI, gold price and economic growth. Proc Econ Finance. 2016;38:280–286. doi: 10.1016/S2212-5671(16)30200-3. [DOI] [Google Scholar]
- Boubaker H, Raza SA. A wavelet analysis of mean and volatility spillovers between oil and BRICS stock markets. Energy Econ. 2017;64:105–117. doi: 10.1016/j.eneco.2017.01.026. [DOI] [Google Scholar]
- Broock WA, Scheinkman JA, Dechert WD, LeBaron B. A test for independence based on the correlation dimension. Economet Rev. 1996;15:197–235. doi: 10.1080/07474939608800353. [DOI] [Google Scholar]
- Chou M-T, Su Y-L, Chou T-Y, Liang H-U. An analysis of the relationship between Asian Steel Index and the Baltic Capsize Index. Mod Econ. 2015;6:207–216. doi: 10.4236/me.2015.62018. [DOI] [Google Scholar]
- Chou M-T (2008) A fuzzy time series model to forecast the BDI. In: 2008 Fourth International Conference on Networked Computing and Advanced Information Management. pp 50–53 10.4236/me.2015.62018
- Dale F, Ulvund S (2018) An empirical analysis of the unbiasedness hypothesis. Norwegian School of Economics, Masters Thesis. https://openaccess.nhh.no/nhh-xmlui/bitstream/handle/11250/2560016/masterthesis.PDF?sequence=1&isAllowed=y (Last accessed on 15th September 2019)
- Giannarakis G, Lemonakis C, Sormas A, Georganakis C. The effect of Baltic Dry Index, gold, oil and USA trade balance on dow jones sustainability index world. Int J Econ Financ Issues. 2017;7:155–160. [Google Scholar]
- Graham M, Peltomäki J, Piljak V. Global economic activity as an explicator of emerging market equity returns. Res Int Bus Financ. 2016;36:424–435. doi: 10.1016/j.ribaf.2015.09.030. [DOI] [Google Scholar]
- Gu Y, Chen Z, Lien D. Baltic Dry Index and iron ore spot market: dynamics and interactions. Appl Econ. 2019;51:3855–3863. doi: 10.1080/00036846.2019.1584384. [DOI] [Google Scholar]
- Guzmán JI, Silva E. Copper price determination: fundamentals versus non-fundamentals. Miner Econ. 2018;31:283–300. doi: 10.1007/s13563-017-0130-y. [DOI] [Google Scholar]
- Haigh MS, Bryant HL. The effect of barge and ocean freight price volatility in international grain markets. Agric Econ. 2000;25:41–58. doi: 10.1111/j.1574-0862.2001.tb00234.x. [DOI] [Google Scholar]
- Hélyette Geman, Smith William O. Shipping markets and freight rates: an analysis of the Baltic Dry Index. The Journal of Alternative Investments Summer. 2012;15(1):98–109. doi: 10.3905/jai.2012.15.1.098. [DOI] [Google Scholar]
- International Chamber of Shipping (2019) International chamber of shipping annual review 2019. Available at https://www.ics-shipping.org/wp-content/uploads/2019/06/ics-annual-review-2019-min.pdf (last accessed on 02nd October 2021)
- Jena SK, Tiwari AK, Hammoudeh S, Roubaud D. Distributional predictability between commodity spot and futures: evidence from nonparametric causality-in-quantiles tests. Energy Economics. 2019;78:615–628. doi: 10.1016/j.eneco.2018.11.013. [DOI] [Google Scholar]
- Jeong K, Härdle WK, Song S. A consistent nonparametric test for causality in quantile. Economet Theor. 2012;28:861–887. doi: 10.1017/S0266466611000685. [DOI] [Google Scholar]
- Jung S (2015) A study on the reasons for sharp decline on the baltic exchange dry index in 2008. World Maritime University Dissertations. 496. Available at: http://commons.wmu.se/all_dissertations/496
- Jurun E, Ratković N, Moro F. The Baltic Dry Index and performance excellence in a crisis. Croatian Operational Res Rev. 2015;6(2):335–346. doi: 10.17535/crorr.2015.0026. [DOI] [Google Scholar]
- Kärrlander E (2010) Base metals, a base for stock prices. Bachelor thesis, Lund University, Scania (Sweden).Available at: http://lup.lub.lu.se/student-papers/record/1552183
- Kavussanos MG, Alizadeh-M AH. Seasonality patterns in dry bulk shipping spot and time charter freight rates. Transport Res Part E: Logist Transport Rev. 2001;37:443–467. doi: 10.1016/S1366-5545(01)00004-7. [DOI] [Google Scholar]
- Kavussanos MG, Nomikos NK. Price discovery, causality and forecasting in the freight futures market. Rev Deriv Res. 2003;6:203–230. doi: 10.1023/B:REDR.0000004824.99648.73. [DOI] [Google Scholar]
- Kavussanos M, Visvikis I, Dimitrakopoulos D. Information linkages between Panamax freight derivatives and commodity derivatives markets. Marit Econ Logist. 2010;12:91–110. doi: 10.1057/mel.2009.20. [DOI] [Google Scholar]
- Kavussanos MG, Visvikis ID, Dimitrakopoulos DN. Economic spillovers between related derivatives markets: the case of commodity and freight markets. Transport Res Part E Logist Transport Rev. 2014;68:79–102. doi: 10.1016/j.tre.2014.05.003. [DOI] [Google Scholar]
- Kilian L. Not all oil price shocks are alike: disentangling demand and supply shocks in the crude oil market. Am Econ Rev. 2009;99:1053–1069. doi: 10.1257/aer.99.3.1053. [DOI] [Google Scholar]
- Klovland JT (2002) Business cycles, commodity prices and shipping freight rates: some evidence from the pre-WWI period. Paper presented at Workshop on Market Performance and the Welfare Gains of Market Integration in History, Florence, Italy. Available at: https://brage.bibsys.no/xmlui/handle/11250/165223
- Koch N. Tail events: a new approach to understanding extreme energy commodity prices. Energy Economics. 2014;43:195–205. doi: 10.1016/j.eneco.2014.02.015. [DOI] [Google Scholar]
- Lin F, Sim NCS. Trade, income and the Baltic Dry Index. Eur Econ Rev. 2013;59:1–18. doi: 10.1016/j.euroecorev.2012.12.004. [DOI] [Google Scholar]
- Lin AJ, Chang HY, Hsiao JL. Does the Baltic Dry Index drive volatility spillovers in the commodities, currency, or stock markets? Transport Res Part E: Logist Transport Rev. 2019;127:265–283. doi: 10.1016/j.tre.2019.05.013. [DOI] [Google Scholar]
- Lun YH, Lai KH, Cheng TCE. Shipping and logistics management. London: Springer-Verlag; 2010. [Google Scholar]
- Ma Y, Zhen W. Market fundamentals and iron ore spot prices. Economic Record. 2020;96:470–489. doi: 10.1111/1475-4932.12564. [DOI] [Google Scholar]
- Melas KD, Michail NA. The relationship between commodity prices and freight rates in the dry bulk shipping segment: a threshold regression approach. Maritime Transport Research. 2021;2:100025. doi: 10.1016/j.martra.2021.100025. [DOI] [Google Scholar]
- Michail NA, Melas KD. Quantifying the relationship between seaborne trade and shipping freight rates: a bayesian vector autoregressive approach. Maritime Transport Research. 2020;1:100001. doi: 10.1016/j.martra.2020.100001. [DOI] [Google Scholar]
- Michail NA, Melas KD. Market interactions between agricultural commodities and the dry bulk shipping market. Asian J Shipping Logistics. 2021;37:73–81. doi: 10.1016/j.ajsl.2020.07.003. [DOI] [Google Scholar]
- Nishiyama Y, Hitomi K, Kawasaki Y, Jeong K. A consistent nonparametric test for nonlinear causality—specification in time series regression. J Econometr. 2011;165:112–127. doi: 10.1016/j.jeconom.2011.05.010. [DOI] [Google Scholar]
- Oomen J (2012) The Baltic Dry Index: a predictor of stock market returns. Master Thesis, Tilburg, Tilburg University Department of Finance : http://arno.uvt.nl/show.cgi?fid=126903
- Papailias F, Thomakos DD, Liu J. The Baltic Dry Index: cyclicalities, forecasting and hedging strategies. Empir Econ. 2017;52:255–282. doi: 10.1007/s00181-016-1081-9. [DOI] [Google Scholar]
- Poulakidas A, Joutz F. Exploring the link between oil prices and tanker rates. Marit Policy Manag. 2009;36:215–233. doi: 10.1080/03088830902861094. [DOI] [Google Scholar]
- Radelet S, Sachs JD (1998) Shipping costs, manufactured exports, and economic growth. 10.7916/D8J39081
- Raza N, Ali S, Shahzad SJH, Raza SA. Do commodities effectively hedge real estate risk? A multi-scale asymmetric DCC approach. Resour Policy. 2018;57:10–29. doi: 10.1016/j.resourpol.2018.01.001. [DOI] [Google Scholar]
- Raza SA, Shah N, Shahbaz M. Does economic policy uncertainty influence gold prices? Evidence from a nonparametric causality-in-quantiles approach. Resour Policy. 2018;57:61–68. doi: 10.1016/j.resourpol.2018.01.007. [DOI] [Google Scholar]
- Ready R, Roussanov N, Ward C. Commodity trade and the carry trade: a tale of two countries. J Financ. 2017;72:2629–2684. doi: 10.1111/jofi.12546. [DOI] [Google Scholar]
- Ruan Q, Wang Y, Lu X, Qin J. Cross-correlations between Baltic Dry Index and crude oil prices. Physica A. 2016;453:278–289. doi: 10.1016/j.physa.2016.02.018. [DOI] [Google Scholar]
- Shahbaz M, Balcilar M, Abidin Ozdemir Z. Does oil predict gold? A nonparametric causality-in-quantiles approach. Resour Policy. 2017;52:257–265. doi: 10.1016/j.resourpol.2017.03.004. [DOI] [Google Scholar]
- Stopford (2003) Maritime economics. In: Routledge & CRC Press. https://www.routledge.com/Maritime-Economics-3e/Stopford/p/book/9780415275583 Accessed 13 Sep 2021
- Sun X, Liu C, Wang J, Li J. Assessing the extreme risk spillovers of international commodities on maritime markets: a GARCH-Copula-CoVaR approach. Int Rev Financ Anal. 2020;68:101453. doi: 10.1016/j.irfa.2020.101453. [DOI] [Google Scholar]
- Tilton JE. Cyclical and secular determinants of productivity in the copper, aluminum, iron ore, and coal industries. Miner Econ. 2014;27:1–19. doi: 10.1007/s13563-014-0045-9. [DOI] [Google Scholar]
- Toda HY, Yamamoto T. Statistical inference in vector autoregressions with possibly integrated processes. Journal of Econometrics. 1995;66:225–250. doi: 10.1016/0304-4076(94)01616-8. [DOI] [Google Scholar]
- Tsioumas V, Papadimitriou S. Chinese steel production and shipping freight markets: a causality analysis. International Journal of Business and Economic Development. 2015;3(2):116–124. [Google Scholar]
- Tsioumas V, Papadimitriou S. The dynamic relationship between freight markets and commodity prices revealed. Marit Econ Logist. 2018;20:267–279. doi: 10.1057/s41278-016-0005-0. [DOI] [Google Scholar]
- Tsouknidis DA. Dynamic volatility spillovers across shipping freight markets. Transport Res Part E: Logist Transport Rev. 2016;91:90–111. doi: 10.1016/j.tre.2016.04.001. [DOI] [Google Scholar]
- UNCTAD (2019) UNCTAD Review of Maritime Transport Report. Available at https://unctad.org/system/files/official-document/rmt2019_en.pdf (last accessed on 02nd October 2021)
- Wårell L. The effect of a change in pricing regime on iron ore prices. Resour Policy. 2014;41:16–22. doi: 10.1016/j.resourpol.2014.02.002. [DOI] [Google Scholar]
- Wårell L. An analysis of iron ore prices during the latest commodity boom. Miner Econ. 2018;31:203–216. doi: 10.1007/s13563-018-0150-2. [DOI] [Google Scholar]
- Xiong T, Hu Z. Soybean futures price forecasting using dynamic model averaging: do the predictors change over time? Emerg Mark Financ Trade. 2021;57:1198–1214. doi: 10.1080/1540496X.2019.1618265. [DOI] [Google Scholar]
- Yu T-H, Bessler DA, Fuller SW. Price dynamics in U.S. grain and freight markets. Canad J Agricult Econ/Revue canadienne d’agroeconomie. 2007;55:381–397. doi: 10.1111/j.1744-7976.2007.00098.x. [DOI] [Google Scholar]
- Zivot E, Andrews DWK. Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J Bus Econ Stat. 2002;20:25–44. doi: 10.1198/073500102753410372. [DOI] [Google Scholar]
- Zuccollo DR (2014) The Baltic Dry Index: a leading economic indicator and its use in a South African context. Master Thesis, University of the Witwatersrand. Available at: https://pdfs.semanticscholar.org/9e71/e29c9060b6326d8f93457e2d993939bd0e48.pdf