Multivariate Analysis and Modelling of multiple Brain endOphenotypes: Let’s MAMBO!

Abstract

Imaging genetic studies aim to test how genetic information influences brain structure and function by combining neuroimaging-based brain features and genetic data from the same individual.

Most studies focus on individual correlation and association tests between genetic variants and a single measurement of the brain. Despite the great success of univariate approaches, given the capacity of neuroimaging methods to provide a multiplicity of cerebral phenotypes, the development and application of multivariate methods become crucial.

In this article, we review novel methods and strategies focused on the analysis of multiple phenotypes and genetic data. We also discuss relevant aspects of multi-trait modelling in the context of neuroimaging data.

1. Introduction

Genetics plays an important role and provides valuable insights into the etiology of common brain diseases. Genome-wide association studies (GWAS) have identified thousands of genetic variants associated with complex diseases [1]. However, when focusing on brain diseases, mapping genetic associations becomes particularly challenging. Among the possible reasons, their genetic and phenotypic complexity provides inconclusive results, as well as the difficulty assessing clinical diagnosis due to the existence of heterogeneity between individuals with the same diagnosis. This raises the question of using neuroimaging brain-based features as intermediate phenotypes, allowing a biologically more plausible manner to assess these complex associations [2].

Neuroimaging endophenotypes are quantitative measurements of the brain used to disentangle genetic susceptibility for complex neurological diseases and psychiatric [3]. Neuroimaging techniques can provide a wide variety of cerebral phenotypes associated with the brain’s morphology (through structural magnetic resonance imaging (MRI), for instance), presence of lesions (e.g. microbleeds), measurements related to brain function (through functional MRI (fMRI) or fluorodeoxyglucose (FDG)-positron emission tomography (PET) imaging, for example) or the burden of molecular pathology (e.g amyloid and tau PET). Several studies have shown that brain endophenotypes generally seem to be shaped by genetic influences, which suggests that studying genetics and the brain jointly can refine our understanding of the etiology of neurological disease [4], [5], [6].

Neuroimaging data is commonly structured as a matrix, where each endophenotype becomes a single variable (column) for which a number of observations are available (rows). This structure is often maintained regardless of the source (e.g. disease studied), modality (e.g. sMRI, fMRI, DTI), units (e.g. voxels, volumes), number or combination of endophenotypes. Genetic data presents an analogous structure, where each variable is the genotype of a genetic variant (e.g. SNP, structural variant), observed in the same individuals from which neuroimaging data has been collected. In both cases, the variables studied are not independent, due to interconnected brain networks and linkage disequilibrium, respectively.

Imaging genetic (IG) studies started analyzing how candidate genes and genetic variants affected brain endophenotypes, using correlation or linear regression models. Later, IG studies focused on the genome-wide effects through GWAS to leverage high-throughput genetic variant data [7], [8]. In both strategies, neuroimaging traits were modeled as outcome variables. However, despite the increasing availability of brain endophenotype data, most GWAS in the field test associations between genetic variants and a single brain phenotype at a time, that is, in a univariate fashion [9], [10]. Assessing every brain outcome independently ignores the genetic correlation structure (i.e., pleiotropy) among multiple phenotypes, and implies a strict penalization for the significance threshold due to multiple hypothesis testing [11]. Altogether, this translates into reduced statistical power. In addition, since neuroimaging techniques already provide a quantitative measurement of the phenotype of interest across different brain subregions, multivariate approaches are particularly well suited to conduct IG studies.

Nowadays, some studies in the IG field have begun to explore the interplay between genetic variants and multiple phenotypes using multivariate approaches, aiming to identify associations at a genome-wide, whole-brain scale [12], [13], [14]. In these studies, brain features can be used either as outcomes or as independent variables in combination with genetic data, depending on the methodological approach. In contrast to univariate analysis, multivariate methods are able to leverage phenotype correlations due to shared genetic or environmental factors, while reducing the multiple testing burden, resulting in higher statistical power to identify significant associations. In addition, multi-phenotype analysis may reveal pleiotropic variants, providing new insights into the complex genetic architecture of brain endophenotypes and, eventually, helping to clarify their underlying biology.

Our aim with this review is to describe the methods currently employed in IG studies for the analysis of multiple traits, as well as those that are not widely used yet, but may be of great interest for researchers in the field in the near future. We also discuss relevant aspects of multi-trait modelling in the context of neuroimaging data.

2. Methods for the analysis of multiple phenotypes

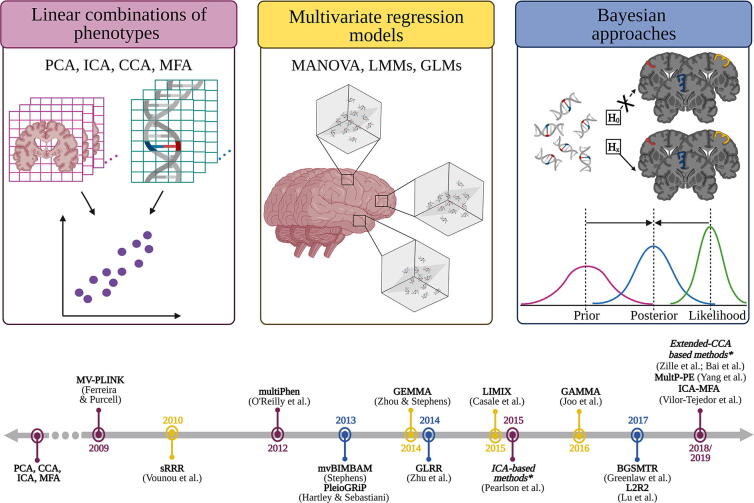
Given the high dimensionality of neuroimaging data, methods for multi-phenotype analysis become a natural choice in IG studies. These approaches can be classified into three main groups: methods based on linear combinations of multiple phenotypes, multivariate regression models and Bayesian strategies [Fig. 1, Table 1]. Overall, they can be applied regardless of the source of the neuroimaging traits.

Fig. 1.

Framework of analytical strategies for multiple phenotype assessment. *Year of these publications corresponds to a literature review describing this family of methods. Legend: BGSMTR: Bayesian group sparse multi-task regression model; CCA: Canonical Correlation Analysis; GLM: General Linear Model; ICA: Independent Component Analysis; ICA-MFA: Independent Multiple Factor Association Analysis for Multiblock Data; L2R2: Bayesian longitudinal low-rank regression; LMM: Linear Mixed Model; MANOVA: Multivariate Analysis of Variance; MFA; Multiple Factor Analysis; PCA: Principal Component Analysis; sRRR: sparse Reduced Rank Regression. This schematic representation was created with Biorender (©BioRender - biorender.com).

Table 1.

Summary of methods and software for multivariate analysis of multiple phenotypes/datasets.

Method	Type	Reference	Description	Pros	Cons	Implementation	R-function{R-package}/ Script
PCA-based methods	Linear Combination Method	Pearlson et al. (2015)	Principal Component Analysis	Computationally faster than other methods.	High dependency of input data. Lack of generalizability. Biologically meaningless.	Matlab	https://trendscenter.org/software/fit/
MV-PLINK	Linear Combination Method	Ferreira and Purcell (2008)	Based on Canonical Correlation Analysis			C++, Command-line	https://genepi.qimr.edu.au/staff/manuelF/multivariate/main.html
MELODIC	Linear Combination Method	Beckman and Smith (2004)	Probabilistic Independent Component Analysis for fMRI			GUI, Command-line	https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/MELODIC#Research_Overview
ICA-MFA	Linear Combination Method	Vilor-Tejedor et al. (2019)	Independent Multiple Factor Association Analysis for Multiblock Data			R/GitHub	{ICA-MFA}
MFA	Linear Combination Method	Lê, Josse and Husson (2008)	Multiple Factor Analysis			R/CRAN	MFA{FactoMineR}
MultiPhen	Linear Combination Method	O’Reilly et al. (2012)	Joint Model of Multiple Phenotypes			R/CRAN	{MultiPhen}
MultP-PE	Linear Combination Method	Yang et al. (2019)	Multiple Phenotypes based on cross-validation Prediction Error			R	https://pages.mtu.edu/~shuzhang/software/MultP-PE.R
GEMMA	Regression-based Approach	Zhou and Stephens (2014)	Genome-wide Efficient Mixed Model Association	Flexibility. Efficiency.	Strong distributional assumptions. Permutations. Requirement of multivariate normality and homoscedasticity. Inflated type I error rates.	C/C++	http://stephenslab.uchicago.edu/software.html
GAMMA	Regression-based Approach	Jo et al. (2016)	Generalized Analysis of Molecular variance for Mixed-model Analysis			R/C	{vegan}; MEMMA{sommer}
mvLMMs	Regression-based Approach	Furlotte and Eskin (2015)	Multivariate Linear Mixed Models			Python	http://genetics.cs.ucla.edu/mvLMM
mtSet	Regression-based Approach	Casale et al. (2015)	multi-trait Set test			Python	https://github.com/limix/limix
SNPtest	Bayesian Modeling	Marchini et al. (2007)	Multipoint method for genome-wide association studies via imputation of genotypes	Interpretability. Adaptability.	Need of specifying a prior probability distribution for the alternative hypothesis. High computational cost.	Java, C++, Command-line	https://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest
PleioGRiP	Bayesian Modeling	Hartley and Sebastiani (2013)	Genetic risk prediction with pleiotropy			Java	http://hdl.handle.net/2144/4367
mvBIMBAM	Bayesian Modeling	Stephens (2013)	Bayesian approach for genetic association analysis of multiple related phenotypes			C/C++	{mvBIMBAM}
GLRR	Bayesian Modeling	Zhu et al. (2014)	Bayesian Generalized Low Rank Regression Models			R/GitHub	{L2R2}
L2R2	Bayesian Modeling	Lu et al. (2017)	Bayesian longitudinal low-rank regression			R/GitHub	{L2R2}
BGSMTR	Bayesian Modeling	Greenlaw et al. (2017)	Bayesian group sparse multi-task regression model for imaging genetics			R/CRAN	{bgsmtr}

2.1. 2.1 Linear combinations of multiple phenotypes

These methods explore the multivariate structure of the data, aiming to select representative components and generate new responses based on combinations of multiple phenotypes.

Principal Component Analysis (PCA) is the traditional method used to reduce the number of phenotypes from large datasets [15], [16]. PCA uses an orthogonal transformation to derive new phenotypes (principal components) that are linear combinations (lower-dimensional representations) of the original phenotypes. The first principal component is the direction in the orthogonal space along which the variance of the multiple phenotypes is maximized, and so on. Thus, PCA can be employed to decompose multiple phenotypes into components that can be used in subsequent univariate regression analyses as dependent variables [17], [18].

The Independent Component Analysis (ICA) [19], [20] and its various related algorithms are an extension of PCA. In ICA, data variables are assumed to be linear or nonlinear mixtures of unknown latent variables. The latent variables are assumed non-gaussian and mutually independent and they are called the independent components of the observed data. ICA is suitable to extract independent components from multiple phenotype measurements and it is extensively used in IG studies [21], [22], [23]. [22] performed a large scale multivariate ICA identifying significant imaging-genetic relationships for Alzheimer’s Disease (AD). [21] used ICA to extract independent component values from connectivity brain measurements to assess their association with genetic variants related with the risk of schizophrenia. More recently, [23] used ICA to extract features from structural brain data, and searched for genetic variants associated with these brain-related features. In addition, multi-modal order methods based on ICA have been proposed to deal with the selection of the optimal number of independent components in neuroimaging studies. For instance, [24] used healthy unrelated subjects from the WU-Minn Human Connectome Project [25] to show the improvement in the selection of components when the method follows a free order model. [26] also proposed a method to capture information at multiple model orders, showing an improvement in classifying brain patterns of schizophrenia individuals vs healthy controls.

The use of ICA-related methods to integrate multimodal data is becoming increasingly widespread. The main objective remains to simultaneously maximize independence and correlation linkage across variables by combining ICA with other methods such as Canonical Correlation Analysis (CCA). For instance, [27] proposed a multi-site canonical correlation analysis fusioned with ICA (MCCAR + jICA), which takes advantage of cross-information among multiple neuroimaging modalities to search for common patterns in brain endophenotypes related to brain disorders. Using this method, similar brain networks were identified in two independent cohorts, suggesting working memory deficits in schizophrenia individuals. More studies applying extended ICA-based methods in IG studies are described in [28], [29].

Regarding CCA, this method allows to derive the relationship between two sets of variables measured in the same individuals (e.g. X and Y). It finds linear combinations of X and Y which have maximum correlation with each other. A comprehensive summary of CCA and its variants is presented in [30]. Specifically in the IG context, several CCA-based methods have been applied, providing higher precision, compared to previous approaches, on assessing the correlation patterns of multiple phenotypes [31], [32], [33]. Most of these methods extract variables co-occurring across imaging phenotypes and modalities together with genomic information. For instance, [32], [33] combined sparse regression and CCA to extract significant sets of fMRI units (voxels) and genetic variants, whereas [31] combined linear regression analysis with CCA to extract features from multiple imaging phenotypes obtained in schizophrenic patients through fMRI and epigenetics. MV-PLINK is also a well known method based on CCA to simultaneously analyze multiple phenotypes. In MV-PLINK, CCA extracts the linear combination of phenotypes that has maximum correlation with a given genetic variant [34]. Although no studies applying MV-PLINK to brain phenotypes were found, interesting related works rely on this approach [35]. Alternatively, MultiPhen [36], uses ordinal regression instead of CCA to test for the association between a linear combination of phenotypes and each genetic variant. In MultiPhen, genetic data is modeled as an ordinal outcome and the multiple phenotypes are treated as the explanatory variables. An extension of MultiPhen was also developed [37], proposing a multiple phenotype procedure based on cross-validation of the prediction error (MultP-PE), which controlled well type I error rates and performed consistently better than MultiPhen.

Multiple Factor Analysis (MFA) is another well known strategy to integrate multiple phenotypes or datasets [38]. By applying MFA, we can evaluate how much the combination of the variables/datasets contributes to the inertia extracted by a unique component. Even with the potential advantages of MFA, few IG studies to date have used this methodological approach [39], [40]. In [39], a sparse MFA framework was proposed. This framework first applied LASSO (least absolute shrinkage and selection operator) procedure to extract relevant genetic and brain features associated with hyperactivity and inattention domains. Then, these features were used as input for the MFA. Moreover, [40], proposed an extension of MFA based on ICA (ICA-MFA). This method implemented an independent component value decomposition of multiple datasets and multiple variables allowing non-normal and non-linear distributions. The application of this method showed the improvement in performance compared to MFA.

All these methods are characterized by being computationally faster than most of the approaches described below. However, several limitations must be considered. First, the loadings of the extracted components depend on the input data, and so slight differences between datasets may yield vastly different loadings. As such, there are constraints in generalizing findings related to the components from one dataset to another [41]. Second, these components maximize the explained (co)variance or correlation, but they may not properly represent the underlying biology. Thus, interpreting the findings can be unintuitive.

2.2. Multivariate regression models

Although multivariate regression models have been less applied to IG studies than the previous group of methods, they are probably the most versatile approaches to identify associations between multiple phenotypes and genetic variants.

These methods generally regress a matrix of m phenotypes measured in n individuals onto a set of covariates, including the genotype at the variant(s) of interest. They include variations from the general linear model, such as multivariate analysis of variance (MANOVA) or multivariate linear mixed models (mvLMMs), as well as multivariate generalized linear models (mvGLMs) and generalized estimating equations (GEEs). Regularized and nonparametric alternatives are also available.

Analogously to its univariate counterpart, MANOVA (equivalently, MANCOVA, when additional covariates need to be accounted for) decomposes the total covariance of the response variables, comparing the covariance explained by the genotype with the residual covariance. MANOVA can be performed using different test statistics (e.g. Wilks’ lambda, Pillai’s trace, etc.). Interestingly, MANOVA (Wilks’ lambda) is equivalent to CCA when the latter is applied using a single variant at time, as in MV-PLINK [42]. This illustrates the close relationship between approaches leveraging multiple phenotypes, even if grouped here in different categories. MANOVA can be considered the direct multivariate equivalent of the univariate GWAS approach, and it has been recently compared with the latter in the context of neuroimaging studies [43].

A nonparametric alternative to MANOVA is PERMANOVA (permutational multivariate analysis of variance, also referred to as multivariate regression analysis of distance matrices) [44], [45]. PERMANOVA computes the similarity (or distance) between pairs of individual samples and performs a covariance decomposition analogous to MANOVA. In contrast to MANOVA, it does not assume errors to follow multivariate normal (MVN) distributions. However, it relies on permutations for significance assessment. This results in a large p-value lower bound (the smallest p-value that can be achieved is approximately 1/(P + 1), where P is the number of permutations) and in running times increasing dramatically with the number of individuals and permutations, hindering its usage in large-scale GWAS studies.

In the context of GWAS studies, population stratification (large-scale, systematic differences in ancestry) and relatedness (either family structure or cryptic relatedness among individuals with no known family relationships) are well known to result in inflated type I errors [46]. Although methods such as MANOVA can account for population stratification by including the top genotype principal components as covariates in the model, they are sensitive to relatedness. In this regard, mvLMMs have become very popular in recent years, given that they can naturally incorporate relatedness as a random effect in the model. However, fitting mvLMMs (often involving restricted maximum likelihood estimation, REML) is computationally intensive and may be slow in large datasets with a large number of individuals and phenotypes, despite continuous implementation enhancements [47], [48], [49]. A widely used mvLMM implementation is available in GEMMA [48]. In GEMMA, the running time per genetic variant increases quadratically with the number of individuals, which makes computationally tractable the analysis of datasets of moderate size (n < 50,000, approximately). Analogously, only a modest number of phenotypes can be studied (e.g., m ∼ 2–10). As a general rule, available mvLMMs implementations scale better with respect to n than with respect to m. An exception is GAMMA [50], which scales linearly with the number of phenotypes, and cubically with the number of individuals. GAMMA combines the LMM and PERMANOVA frameworks. Hence, it requires permutations for significance assessment and presents the limitations pointed out above.

To date, most mvLMM implementations include a single variance component (i.e. relatedness). However, recent advancements have allowed to efficiently incorporate additional variance components. This is the case of mSet [51], which models the sum of the contribution from the variants in the genetic region to be tested (“set component”) as a random factor, in addition to relatedness. mSet scales similarly to GEMMA with respect to n and m, although it does not assess significance of individual genetic variants, but rather of genomic regions of custom size.

MANOVA and mvLMMs assume that the model errors are MVN-distributed. Although they are relatively robust to violations of this assumption, both methods can lead to inflated type I errors in the presence of strong outliers, especially in the case of low minor allele freqüències (MAFs) [36]. As a result, normalization procedures such as rank-based inverse quantile transformation of the phenotypes (a methodology that replaces the sample quantiles by quantiles from the standard normal distribution) are commonly applied. Nevertheless, it is unclear whether these transformations always result in higher power and controlled type I errors compared to modeling the untransformed data [52].

Hence, MANOVA and mvLMMs are sometimes replaced by the more flexible framework provided by multivariate generalized linear models (mvGLMs), which allow error distributions from the exponential family, and therefore discrete outcomes. For instance, for multivariate count data (e.g. microbleed counts across brain subregions), a common choice is the multinomial-logit GLM. Pervasive overdispersion (variance of the phenotypes higher than expected) and complex correlation structures have led to the development of alternative models (boosted by the advent of RNA-seq technologies in the field of transcriptomics), such as Dirichlet-multinomial or negative-multinomial GLMs [53], [54]. Analogously to mvLMMs, mvGLMs can be extended to incorporate random factors. However, mvGL(M)Ms require one to correctly specify the model, including the correlation structure among the multiple phenotypes, which is often difficult, and fitting them is computationally demanding. As a result, they are not routinely used in multivariate GWAS studies. Some of these difficulties may be overcome by generalized estimation equations (GEE), a semi-parametric approach which just assumes marginal phenotype distributions to follow univariate generalized linear error models [55]. GEE require defining the link function and a “working” covariance matrix, being relatively robust to misspecification of the latter [56]. They have been often employed in GWAS, including in the field of IG, although they may not offer a good control of type I error in some scenarios [57].

The multivariate linear regression framework can be also employed to model the joint effect of many genetic variants in multiple phenotypes. However, in this scenario, the number of independent variables of interest could be larger than the number of observations. In addition, due to linkage disequilibrium (LD), multicollinearity may arise. To address these issues, regularized models, such as sparse reduced rank regression (sRRR), have been proposed [58]. For instance, sRRR was employed to identify genetic variants associated with voxel-wise longitudinal changes in the brain of AD patients [59]. Nevertheless, while these approaches allow to select a set of relevant genetic variants, they often lack an appropriate multivariate hypothesis testing setting to assess the significance of each variant’s effect on the multiple phenotypes.

Multivariate regression strategies provide highly flexible and relatively efficient tools to study the genetic architecture of brain imaging endophenotypes. However, they are not exempt from limitations. Overall, they tend to make strong distributional assumptions on the error distributions, which often do not hold. Although nonparametric alternatives are available, they generally rely on permutations for significance assessment, and are thus impractical for large GWAS. In addition to multivariate normality, multivariate homoscedasticity (i.e. homogeneity of covariance matrices) is often required, and the violation of this assumption leads to markedly inflated type I errors, particularly in the case of low minor allele frequencies. Albeit the impact of heteroscedasticity may be reduced in mvGLMs or mixed models, as stated above, these require either defining a priori the variance structure (which can be difficult in large and complex biological datasets), or inferring it from the data (which is slow).

2.3. Bayesian approaches

Bayesian inference approaches have been implemented in the context of multivariate analyses in several genetic software, such as the widely used SNPtest [60], the multivariate version of BIMBAM [61] and, PleioGRiP [62]. All these software calculate a ratio between the probability distribution of the data under two models: the null hypothesis of no association and the alternative hypothesis. This ratio, called Bayes Factor (BF), represents an alternative to the classical use of p-value in frequentist approaches [63]. BFs are specially beneficial in the context of multivariate settings since they can be easily combined into a weighted average measure across different genetic variants, as implemented in SNPtest, or across several models at a given genetic variant, as implemented in mvBIMBAM. Further, mvBIMBAM introduced the idea of dividing the potentially associated genetic variants in two groups: those directly and those indirectly associated with one or more phenotypes. This division increases the interpretability of the multivariate analysis, although it is made according to statistical relationships rather than based on biology [61]. Lately, PleioGRiP introduced the use of Naive Bayesian classifiers to find pleiotropic associations between genetic variants and multiple phenotypes [64].

In the context of IG studies, several Bayesian methods have been also applied to the multivariate analysis of MRI data. [65] proposed a Bayesian generalized low rank regression model (GLRR), able to handle the high-dimensionality of the data which characterizes IG analysis. GLRR also integrates an efficient Markov chain Monte Carlo algorithm for posterior computation. The application of GLRR has led to the description of novel associations between relevant genetic variants associated with AD [66] and brain endophenotypes from the Alzheimer's Disease Neuroimaging Initiative (ADNI) [67]. [68] developed a Bayesian longitudinal low-rank regression (L2R2) model as an adaptation of GLRR for longitudinal designs. L2R2 is characterized by approximating the low-rank matrix including penalized splines that account for overall time effect, and a sparse factor analysis model coupled with random effects to cover the within-subject spatio-temporal correlations of longitudinal imaging endophenotypes. Finally, [69] proposed a novel Bayesian group sparse multi-task regression model (BGSMTR) focused on integrating multiple structural brain endophenotypes with genetic information. This approach adapted a sparse regularization method primarily defined to group genetic variants by genes or LD blocs [70] into a method able to group genetic variants by brain imaging endophenotypes. BGSMTR was applied on the multivariate association analysis of relevant genetic variants for AD. However, the computational complexity of this method makes its application to IG studies infeasible without a previous selection of relevant genetic variants..

Bayesian methods provide interesting advantages compared to frequentist approaches. For instance, in terms of interpretability of the results. They also overcome limitations that are intrinsic to the use of p-values in assessing true associations between genetic variants and multiple phenotypes [71], [72]. Moreover, they provide a setting that can be adapted to a wide range of scenarios (e.g. hierarchical models) and are able to deal with missing data problems. However, some considerations associated with Bayesian models include the need of specifying a prior probability distribution for the alternative hypothesis. The prior distributions will determine the genetic models that will be finally tested by the BF. Thus, they should be cautiously selected according to the scientific question. Additionally, Bayesian analysis often comes with a very high computational cost, especially for models involving a large number of variables [73].

3. Discussion and future perspective

The analysis of neuroimaging and genetic data is highly relevant in elucidating the etiology of neurological diseases. However, despite the intrinsically multivariate nature of neuroimage-derived phenotypes, they are still typically analyzed using univariate strategies. In addition to the increased statistical power offered by multivariate methods, the joint analysis of multiple imaging phenotypes and genetic data can help us to gain new insights on phenomena, such as pleiotropic effects, that are difficult to capture through standard univariate analyses.

In this review, we discussed methods commonly applied -or that can be potentially applied- in IG studies for the analysis of múltiple quantitative phenotypes, as well as examples of their application [Table 2]. Although we have grouped them into three broad categories (i.e. linear combinations of multiple phenotypes and/or datasets, multivariate regression models, and Bayesian approaches), we want to emphasize that the different methods are often related, and in some cases could even be considered complementary views of the same approach. Note also that we focused on quantitative endophenotypes, and that most methods described here may not be suited for the analysis of categorical data. Finally, further considerations that should be taken into account in current and future IG studies are discussed below.

Table 2.

Summary of studies applying multiple phenotype strategies in Imaging genetic studies.

Author	Project/Consortium	Neuroimaging modality	Omics data	Statistical Modelling
Meda et al., (2012)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	ICA
Vounou et al., (2012)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	sRRR
Wang et al., (2012)	Alzheimer's Disease Neuroimaging Initiative	sMRI, FDG-PET	SNPs	sparse multimodal MTL
Mounce et al., (2014)	Mind Clinical Imaging Consortium	DTI	SNPs	ICA
Nazeri et al., (2014)	Alzheimer's Disease Neuroimaging Initiative	TBM, sMRI	Proteomics	PICA
Zhang et al., (2014)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	GEE
Zhu et al., (2014)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	L2R2
Du et al., (2015)	Alzheimer's Disease Neuroimaging Initiative	fMRI	SNPs	CCA
Peng et al., (2016)	Alzheimer's Disease Neuroimaging Initiative	MRI, PET	SNPs	Structured Sparse Kernel Learning
Greenlaw et al., (2017)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	BGSMTR
Liu et al., (2017)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs, Gene expression	SCCA
Lu et al., (2017)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	L2R2
Singanamalli et al., (2017)	Alzheimer's Disease Neuroimaging Initiative	sMRI, FDG-PET	Proteomics	CaMCCo
Yan et al., (2017)	Alzheimer's Disease Neuroimaging Initiative	sMRI	Proteomics	SCCA
Kircher et al., (2018)	FOR2107 Consortium	sMRI, fMRI	Multi-Omics	Multiple methods applied: data reduction; mixed models; machine learning
Ning et al., (2018)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	Neural network
Vilor-Tejedor et al., (2018)	BRain dEvelopment and Air polluTion ultrafine particles in scHool childrEn	sMRI	SNPs	LASSO + MFA
Wachinger et al., (2018)	Alzheimer's Disease Neuroimaging Initiative	sMRI	SNPs	Mixed model
Zille et al., (2018)	Philadelphia Neurodevelopmental Cohort	fMRI	SNPs	CCA
Bai et al., (2019)	Mind Clinical Imaging Consortium	fMRI	Epigenetics	CCA
Vilor-Tejedor et al., (2019)	Rotterdam study	sMRI	SNPs	ICA-MFA
Soheili-Nezhad et al., (2020)	Alzheimer's Disease Neuroimaging Initiative	TBM, sMRI	SNPs	ICA
Vilor-Tejedor et al., (2020)	Rotterdam Study	sMRI	SNPs	Mixed model
Wu et al., (2020)	UK Biobank	sMRI	SNPs	Adaptive multi-trait association test

Legend: BGSMTR: Bayesian group sparse multi-task regression model; CaMCCo: Cascaded Multi-view Canonical Correlation; CCA: Canonical Correlation Analysis; CT: Computed tomography; DTI: Diffusion Tensor Imaging; FDG: fluorodeoxyglucose; fMRI: functional Magnetic Resonance Imaging; GEE: Generalized Estimation Equations; ICA: Independent Component Analysis; ICA-MFA: Independent Multiple Factor Association Analysis for Multiblock Data; ISGC: International Stroke Genetics Consortium; L2R2: Bayesian longitudinal low-rank regression; LASSO: Least Absolute Shrinkage and Selection Operator; MANOVA: Multivariate Analysis of Variance; MFA; Multiple Factor Analysis; MTL: Multi-Task Learning; PET: Positron Emission Tomography; PICA: Parallel Independent Component Analysis; SCCA: Sparse Canonical Correlation Analysis; sMRI: structural Magnetic Resonance Imaging; SNPs: Single Nucleotide Polymorphisms; sRRR: sparse Reduced Rank Regression;TBM: Tensor-Based Morphometry.

3.1. Statistical power

Although the analysis of multiple phenotypes reduces the number of statistical comparisons, large samples are still required to increase statistical power. Statistical power can be boosted through the use of larger sample sizes, particularly by joining global consortia collaborations [74], [75] or by using publicly available data from biobanks and other resources [76]. Nevertheless, it can also be improved by reducing the measurement error in both fields. Moreover, advances in DNA sequencing and reductions in costs associated with its acquisition, will ease the way for obtaining whole genome sequences. For neuroimaging modalities, such as PET data, the problem is to acquire sufficiently large datasets, given the use of ionizing radiation (and associated costs). In addition, improvements on the quality control of neuroimaging data, specifically on increasingly large datasets, could also help to obtain precise MRI-derived quantifications [77]. Finally, we can increase statistical power by using smarter data analysis, and developing more powerful statistical techniques. For instance, the combination of different multivariate approaches has also been proposed as an alternative for increasing significantly association findings [61].

3.2. Multivariate vs meta-analysis (summary-statistic-based) approaches

The multivariate methods described above require individual-level data on phenotypes and genotypes, and estimate the phenotype variances and covariances directly from the observed measurements. Although not discussed here, several methods have been proposed to leverage univariate summary-statistics (estimated effect sizes and standard errors, Z-statistics or association p-values) from published GWAS in a meta-analysis-like approach. Some examples include S_Hom/S_Het [78], metaCCA [79], MTAG [80] or MTAR [81]. They often rely on the assumption that, under the null hypothesis, summary Z-statistics from univariate tests performed on individual phenotypes have an asymptotic multivariate normal distribution with correlation equal to the phenotype correlation matrix. In recent years, this strategy has become very popular, being employed for the analysis of multiple phenotypes in a wide variety of scenarios, including IG studies [82], [83], [84]. The main advantage of these approaches is their ability to carry out fast GWAS analyses across many phenotypes and with very large sample sizes, without requiring complex and time-consuming access to individual-level data. Nevertheless, they are limited by the nature of the univariate analyses upon which they are based (sample size, power, assumptions, data transformations, etc.). In addition, estimating the phenotype correlation matrix from summary statistics is not trivial, and can be affected, among others, by LD or the phenotype heritability, which if not accounted properly may lead to biased estimates [81], [85].

3.3. Longitudinal designs

Much of the existing work in the field, as we previously described, analyzes neuroimaging data cross-sectionally, which does not provide information about changes in the structure and functionality of the brain over time. A better understanding of the longitudinal trajectories of brain endophenotypes would improve our knowledge of the underlying biological characterisation of complex neurological diseases [86], [87], [88]. For example, application of mixed-effect models to longitudinal brain imaging data has helped to identify a large number of significant genetic-multiphenotype associations [89], [90]. Overall, this is an important topic that needs to be further investigated.

3.4. Integration of different types of Omics and Imaging modalities

A critical challenge in IG studies is to model an even greater complexity of genetic effects on the brain. Most neuroimaging studies have examined only two sources of biological data at a time (e.g., genetic variants and structural MRI). However, combining multiple omics would provide a better understanding of the underlying biological mechanisms of neurological diseases [91], [92]. In addition, integrating multiple sources of neuroimaging -beyond than just two modalities- with omics data becomes relevant to amplify the synergistic value of IG studies (e.g., genomics, transcriptomics, proteomics, metabolomics, morphological MRI, DTI, or functional MRI) [93], [94], [95]. In that regard, the implementation of integrated data platforms such as the Brain Imaging Data Structure (BIDS) [96] and the BIDS genetics extension [97] facilitates data search and analytical procedures by aggregating genetic and neuroimaging features across studies.

Some studies have demonstrated the integration of gene expression data and genetic markers to facilitate the detection of markers that are both associated with brain endophenotypes and highly expressed in the brain [98]. Moreover, the integration of genetic neuroimaging methods with epigenetics, known as imaging epigenetics, promises to provide deeper insights into the causative pathways through which genes and environment interact during life and impact human brain development [99], [100]. Other studies have also started to analyse proteomics and neuroimaging-based features as potential biomarkers of the basis for computing essential cell functions to identify the best proteomic model for the diagnosis, monitoring, and prediction of complex neurological disorders [101], [102].

3.5. Imaging gene-environment interaction models

Research focused on multivariate modeling of gene-environment interactions has recently emerged, revealing significant interaction effects between candidate genetic variants and multiple environmental factors [103], [104], [105], [106]. These methods may represent the starting point of designs focused on the integration of multivariate imaging gene-environment interactions open up new sources of analysis by means of which to gain an understanding of the conditional mechanisms through which genes, environment, and brain features interact to predict brain diseases and neurological conditions [107], [108]. Such designs represent an opportunity, not only to integrate different omics and imaging features, but also to incorporate target environmental exposures relevant to the structure and function of the brain.

3.6. Complex prediction models

Machine learning and deep learning strategies represent a powerful alternative, allowing for heterogeneous data integration, and in turn, improving disease classification and prediction in IG studies [109]. However, this family of methods are also computationally expensive and interpretation is not straightforward. Moreover, there is not much literature reported or evidence of their performance yet. Some examples of application of these methods include predicting AD diagnosis and disease conversion [110], [111], [112], [113]. However, more work is still required to use genetics and neuroimaging information to predict complex neurological outcomes and treatment response, as has been accomplished in other areas of psychiatric research [4], [114].

CRediT authorship contribution statement

Natalia Vilor-Tejedor: Conceived the idea presented in the manuscript. Writing - original draft, Writing - review & editing, Visualization. Diego Garrido-Martin: Conceived the idea presented in the manuscript. Writing - original draft, Writing - review & editing, Visualization. Blanca Rodríguez-Fernández: Writing - original draft, Writing - review & editing and Visualization. Sander Lamballais Yu: Writing - review & editing. Roderic Guigó: Writing - review & editing. Juan D Gispert: Writing - review & editing and Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

The authors apologize if relevant publications were not cited.

Author contributions

All the authors made a significant contribution to the preparation of the manuscript. NV-T and DG-M conceived the presented idea and took the lead in writing the manuscript. BR-F contributed to writing and editing the manuscript. SL, RG and JDG contributed to reviewing, and the discussion of the manuscript.

Funding

At the time of writing this review, NV-T is funded by a postdoctoral grant, Juan de la Cierva Programme (FJC2018-038085-I), Ministerio de Ciencia, Innovación y Universidades – Spanish State Research Agency. Her research is also supported by the “la Caixa'' Foundation (LCF/PR/GN17/10300004), the Health Department of the Catalan Government (Health Research and Innovation Strategic Plan (PERIS) 2016–2020 grant #SLT002/16/00201), and the Alzheimer Nederland Project (WE.15–2019-09). DG-M is funded by grant number CZF2019-002436 from the Chan Zuckerberg Initiative. JDG holds a ‘Ramón y Cajal’ fellowship (RYC-2013–13054). All CRG authors acknowledge the support of the Spanish Ministry of Science, Innovation, and Universities to the EMBL partnership, the Centro de Excelencia Severo Ochoa, and the CERCA Programme / Generalitat de Catalunya.