Abstract
Purpose: The study aimed to design and validate computational phantoms (MIRD) using the MCNPX code to assess the impact of shielding on organ doses.
Method: To validate the optimized phantom, the obtained results were compared with experimental results. The validation of the optimized MIRD phantom was provided by using the results of a previous anthropomorphic phantom study. MIRD phantom was designed by considering the parameters used in the anthropomorphic phantom study. A test simulation was performed to compare the dose reduction percentages (%) between the experimental anthropomorphic phantom study and the MCNPX-MIRD phantom. The simulation was performed twice, with and without shielding materials, using the same number and locations of the detector.
Results: The absorbed dose amounts were directly extracted from the required organ and tissue cell parts of output files. Dose reduction percentages between the simulation with shielding and simulation without shielding were compared. The highest dose reduction was noted in the thymus (95%) and breasts (88%). The obtained dose reduction percentages between the anthropomorphic phantom study and the MCNPX-MIRD phantom were highly consistent and correlated values with experimental anthropomorphic data. Both methods showed Relative Difference (%) ranges between 0.88 and 2.22. Moreover, the MCNPX-MIRD optimized phantom provides detailed dose analysis for target and non-target organs and can be used to assess the efficiency of shielding in radiological examination.
Conclusion: Shielding breasts and eyes during cervical radiography reduced the radiation dose to many organs. The decision to not shield patients should be based on research evidence as this approach does not apply to all cases.
Keywords: dose reduction, radiation protection, shielding, monte carlo method, MCNPX
Introduction
Diagnostic radiology is associated with a high collective radiation dose (1), and a patient's exposure to diagnostic ionizing radiation is associated with an increased risk of cancer (2). The International Commission on Radiological Protection (ICRP) recommendation is to optimize and limit exposure to ionizing radiation when possible. Efforts should be made to ensure patient safety and reduce radiation exposure to as low as reasonably achievable (ALARA) while ensuring adequate image quality (3, 4).
Lead (Pb) shields are commonly used to protect patients during radiology procedures (5, 6). The importance of the shielding materials for medical and industrial applications was highlighted by different investigations (7–10). In particular, a remarkable reduction in absorbed radiation dose for testes, ovaries, eyes, and breasts was observed via experimental studies that utilized shielding during radiology procedures. Experimental studies used an anthropomorphic phantom to assess radiation dose for target and non-target organs. Target organs are situated in the primary field of radiation. Even though non-target organs are away from the field of radiation, they were also affected by the scatter radiation (9–13).
Despite these findings, recent studies suggest that shielding patients has no benefits and should be discontinued as the radiation-absorbed dose from a single examination is mostly negligible (14, 15). The major concern is the cumulative risk from multiple radiological examinations, particularly for children and young patients (16), and the decision to not shield patients should be based on research evidence as one size does not fit all (9). Calculation of absorbed radiation doses has an essential place in radiation medical applications to support patient safety and reduce the risk of radiation injuries. Although it is possible to calculate non-target doses in some cases, it is physically very difficult or impossible in many cases. Therefore, the major limitation of using the anthropomorphic phantom in dose measurement studies was to observe the variety of absorbed radiation dose in organs and tissue at micro-scale dosimetry.
In recent years scientists use simulation methods to overcome such situations. One of the most powerful methods used in radiation calculations is Monte Carlo (MC) simulations, which are commonly used in medical radiation physics (17–19). This is a theoretical model in which physical quantities are determined by simulating the transport of X-ray photons. A wide variety of MC codes are available in the literature for various forms of medical radiation application. However, some of them, such as Geant4 (20), PENELOPE (21), MCNPX (22), FLUKA (23), and EGSnrc (24), are even more prominent due to their ease of use, rich libraries, and consistent results. Initial efforts to shape an individual phantom to measure radiation absorbed doses were performed by Cristy et al. (25). Then, different types of human computational phantoms, including the MIRD (Medical Internal Dose) phantom (26, 27), were used for medical radiation measurements by many researchers (28–32).
The literature clearly outlined that MC codes and computational phantoms can model high-precision radiation transport within matter and be implemented to estimate the absorbed radiation dose in medical applications. This has encouraged many authors to perform an extensive organ dose assessment using MCNPX (Monte Carlo N-Particle Transport Code) and MIRD computational phantom (25–33). To the best of our knowledge, no study explored the efficiency of shielding in dose reduction using the computational phantom and MCNPX codes. Optimization of the computational phantoms using the MCNPX code could provide opportunities to simulate the required imaging technique, patient position, radiation sources and direction, and shielding materials. Therefore, it is expected to provide a remarkable contribution to enrich the radiology and medical physics literature about the role of shielding in protecting patients from unnecessary radiation. The current study aimed to design and validate computational phantoms (MIRD) using the MCNPX code to assess the impact of shielding on organ doses during radiology examinations.
Materials and Methods
The study aimed to determine the impact of shielding on organ and tissue dose during radiology examinations using MCNPX code and MIRD Phantom. To address this aim, the study designed a computational phantom (MIRD) using the MCNPX code and then validated it using an anthropomorphic phantom experiment.
Monte Carlo Simulations and MCNPX Code
MCNPX (version 2.7.0) (22) computer simulations were conducted on a voxelized MIRD phantom mentioned in the International Commission on Radiological Protection (ICRP) Publication 110, which describes the features of an adult reference female in ICRP Publication 74 (34). ICRP's phantoms are mathematical representations of the anatomy of the human body, which are used in dosimetry measurements. The advances that have been made to these phantoms, especially in the last few years, represent substantial advances in scientific methods and analytical capacity, along with changing perceptions that the best evidence can be used and shared publicly. The sophisticated models presented in this publication will allow the Commission to be prepared for the potential calculations needed.
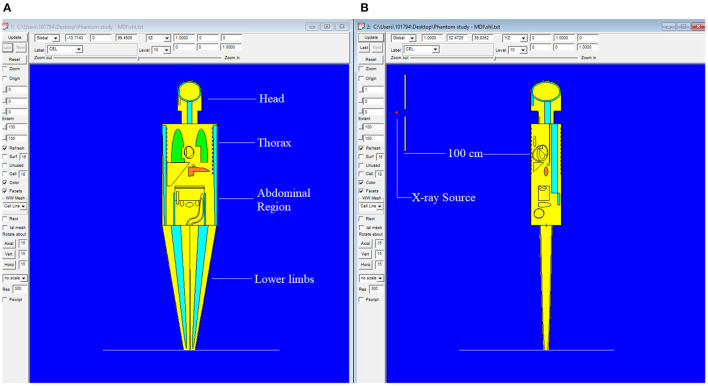
The MIRD, known as a computational phantom, has been defined to represent the structure of a human body with essential properties such as organs, tissues, elemental mass fractions, and densities. The initial heterogeneous MIRD has been published by OAK Ridge National Laboratory (ORNL). During the last few decades, the MIRD phantom has been updated, and many organizations such as NRC (Nuclear Regulatory Commission) used this phantom as a reference for different types of investigations. In the current study, ORNL-MIRD (1996) has been used for extensive organ dose evaluations during radiology examinations. The MIRD phantom has been optimized by considering radiology examination conditions (i.e., patient-source distance, radiation source energy, definitions of body parts, the geometry of shields). The structure of the MIRD phantom with its cell and surface details can be seen in Figure 1A. Figure 1B shows the position of the X-ray source from the lateral view of the MIRD phantom. The phantom represents an adult female body that can be used for many radiology examinations in erect and supine positions. The MIRD surfaces are reconstructed by MCNPX surface and cell definitions. The general appearance of the modified MIRD phantom and CELL numbers of the organs and tissues are seen in Figure 2. Initially, we used the F6 Tally Mesh length estimator to measure the energy deposition, and when they were the same, we use the *f8 tally, which absorbed score doses in terms of MeV in a cell-based on secondary electron dose depositions. No photon and electron energy cutoffs were used in our simulations. As a first step, the MCNPX code was run for 108 histories or NPS (number of particle history) without any shield protection on the MIRD phantom. The uncertainty of MC estimations was <1% in all simulations. The source definition has been done in the sdef (source definition) part of the INPUT file. Accordingly, si (source probability) and sp (source bias) variables were defined by considering the beam distribution of the X-ray from the source. The source consisted of a point source with a directional bias toward the phantom according to realistic geometry used for radiography. The beam size was 18 × 24 cm on the patient surface. The angle of direction bias was 5.14 degrees and was defined in the SDEF card. The photon beam energy spectra of a radiography tube were derived from SpekCalc (version.1) (35–37) considering a 2 mm intrinsic Aluminum filter according, to the tube manufacturer's instructions. The literature review showed that similar investigations were performed using SpeCalc to provide suitable X-ray spectra for the source definition of MCNP code (38–40). The photon beam spectra for 70 kVp are depicted in Figure 3. The obtained normalized spectra were utilized to provide the energy-histogram to define the source definition card (SDEF). It was selected as a point isotropic source with a histogram of energy (Point Isotropic Source with a Histogram of Energies). However, it was collimated onto the MIRD phantom, where X-ray angle was calculated to fit exactly the diameter of the experimental study.
Figure 1.
MIRD phantom utilized in this research using MCNPX general purpose Monte Carlo code (version 2.7.0) (A) Antero-posterior view of MIRD phantom (B) Lateral view of MIRD phantom.
Figure 2.
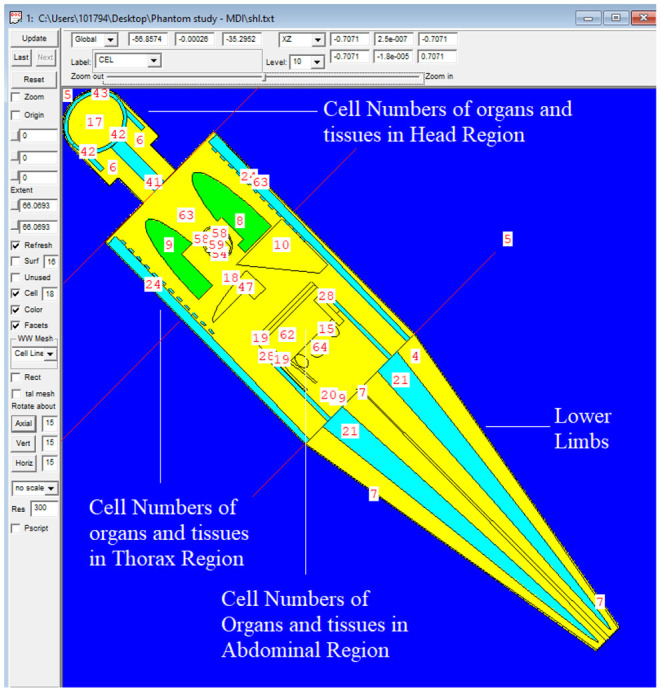
General appearance of the modified MIRD phantom and CELL numbers of the organs and tissues.
Figure 3.
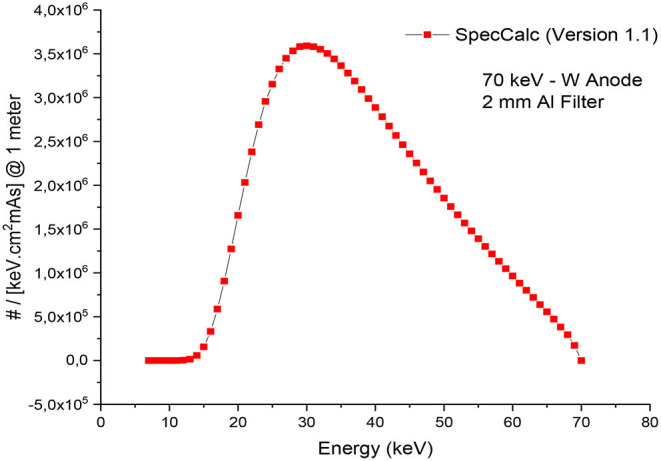
X-ray spectrum obtained from SpecCalc (version 1.1) for 70 kVp tube voltage and 2 mm Al Filter.
Validation of MCNPX Code Through Experimental Data
To validate the outcomes of the MCNPX code and the optimized MIRD phantom, MCNPX-MIRD phantom, previous experimental results from an anthropomorphic phantom study were used. The study assessed the radiation dose absorbed by eyes and breasts during Antero-Posterior (AP) cervical radiography using anthropomorphic phantom (9). In the current study, the technique and exposure parameters used in the anthropomorphic phantom experiment (AP projection, fine focus, kVp = 70, and focus detector distance = 100 cm) were replicated in the MCNPX-MIRD phantom. Similarly, the clinical conditions such as the patient in an erect position, x-ray source, and shielding type, shielding thicknesses, and shielding locations were determined similar to the anthropomorphic phantom study. The definition of shielding materials was implemented in the material definition part of the INPUT file. Moreover, the geometrical properties of shielding materials with their material thicknesses have been defined in the surface cards. Finally, two different lead (Pb) shield materials were defined in the MCNPX-MIRD phantom as the same as in the anthropomorphic study. The MCNPX-MIRD phantom with the added shielding materials. Their locations can be seen in Figure 4.
Figure 4.
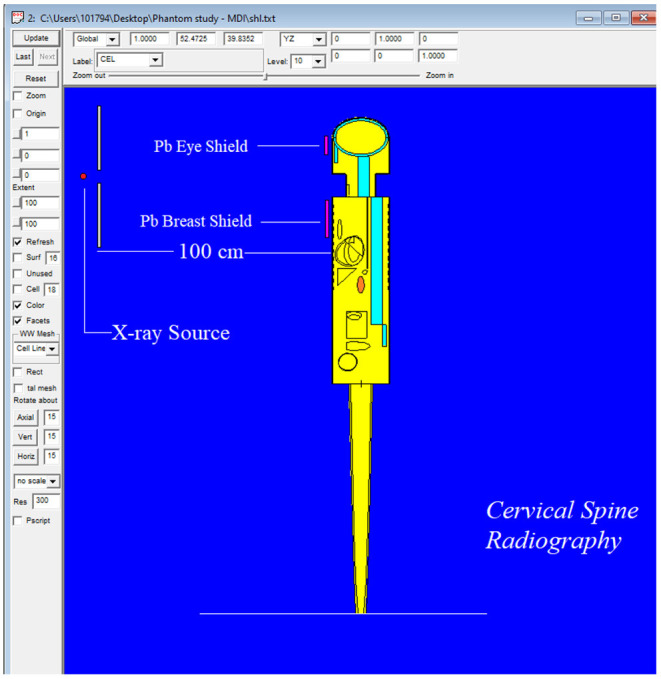
The modified MIRD phantom, shielding materials, and their locations.
A test simulation was performed to compare the dose reduction percentages (%) between the experimental anthropomorphic phantom study and the MCNPX-MIRD phantom. The simulation was performed twice, with and without shielding materials, using the same number and locations of the detector. Accordingly, the energy deposition amounts of each cell (Figure 2) were obtained using the F6 tally mesh of MCNPX. The scored absorbed dose by MCNPX was the averaged dose over cell volume. F6 Tally calculates the dose in terms of MeV/g per initial photon. This type of tally can provide the average energy deposition amount in a certain cell. Finally, the required transformations from recorded data to experimental data were done using verified methods for MCNPX 2.7.0 and MCNP-4C codes (41–43). The results were recorded in the output file, and accordingly, the absorbed dose amount in each pre-defined cell was exported. Table 1 shows the names of organs and their cell number codes.
Table 1.
Energy depositions (MeV/g per initial photon) of some organs and tissues obtained from MCNPX output (F6 Tally Mesh).
| Organ/ | Cell | Without shielding | With shielding |
|---|---|---|---|
| tissue | number | material | material |
| Skin | 7 | 2.8871e-16 | 2.5859e-16 |
| Lung | 8 | 1.7134e-07 | 1.0228e-07 |
| Liver | 10 | 1.8291e-07 | 1.7651e-07 |
| Stomach | 11 | 8.0897e-10 | 7.9340e-10 |
| Urinary bladder | 13 | 4.4353e-10 | 4.4520e-10 |
| Ovaries | 15 | 8.9999e-08 | 9.0950e-08 |
| Brain | 17 | 1.2332e-07 | 8.9033e-08 |
| Esophagus | 18 | 1.0537e-07 | 8.0153e-08 |
| Colon | 19 | 3.4818e-10 | 3.4912e-05 |
| Leg bones | 21 | 3.3325e-08 | 3.3361e-08 |
| Arm bones | 24 | 1.1667e-07 | 9.4818e-08 |
| Clavicles | 25 | 2.6587e-07 | 2.6380e-07 |
| Scapulae | 26 | 4.9649e-08 | 3.4071e-08 |
| Pelvis | 28 | 4.6403e-08 | 4.6487e-08 |
| Rib cage | 29 | 1.7805e-07 | 1.2980e-07 |
| Spine | 41 | 5.2727e-08 | 4.7404e-08 |
| Skull-cranium | 42 | 6.1291e-08 | 2.6767e-08 |
| Facial skeleton | 43 | 3.1124e-07 | 2.5174e-07 |
| Thyroid | 44 | 3.5803e-07 | 3.5542e-07 |
| Kidneys | 45 | 1.2468e-10 | 1.1880e-10 |
| Pancreas | 47 | 3.5941e-10 | 3.3205e-10 |
| Spleen | 48 | 2.1856e-10 | 2.0249e-10 |
| Thymus | 49 | 9.8690e-10 | 3.4890e-10 |
| Adrenals | 50 | 1.4914e-10 | 1.4369e-10 |
| Gall bladder | 52 | 4.3957e-10 | 4.3677e-10 |
| Heart-left ventricle | 54 | 5.9281e-10 | 3.3882e-10 |
| Heart-left ventricle-contents | 55 | 5.9281e-10 | 3.3882e-10 |
| Heart-right ventricle | 56 | 5.9281e-10 | 3.3882e-10 |
| Heart-right ventricle-contents | 57 | 5.9281e-10 | 3.3882e-10 |
| Heart-left atrium | 58 | 5.9281e-10 | 3.3882e-10 |
| Heart- left atrium-contents | 59 | 5.9281e-10 | 3.3882e-10 |
| Heart-right atrium | 60 | 5.9281e-10 | 3.3882e-10 |
| Heart- right atrium-contents | 61 | 5.9281e-10 | 3.3882e-10 |
| Small intestine | 62 | 3.2101e-10 | 3.2094e-10 |
| Uterus | 64 | 2.6720e-10 | 2.6742e-10 |
| Breasts | 65 | 1.0986e-09 | 4.2349e-10 |
Organ Dose Assessment
The radiation doses absorbed by eyes and breasts during AP cervical examination were recorded in two settings (with shielding and without shielding). Finally, a comparison of obtained dose reductions between the anthropomorphic phantom study and the optimized MIRD was performed.
Results
In this study, a computational phantom (MIRD) was optimized using the MCNPX code to assess the impact of shielding on organ doses during radiology examination. A previous anthropomorphic phantom study was used to validate the results of the current study (9). The present study revealed a smooth difference in the variation of organ dose reduction percentages. As shown in Figure 5; Table 2, the obtained dose reduction percentages between the anthropomorphic phantom study and the MCNPX-MIRD phantom were reported for the left eye, right eye, left breast, and right breast. Both methods showed Relative Difference (%) ranges between 0.88 and 2.22. The outcomes obtained from the MCNPX-MIRD phantom can be considered highly consistent and the values correlated with experimental anthropomorphic data.
Figure 5.
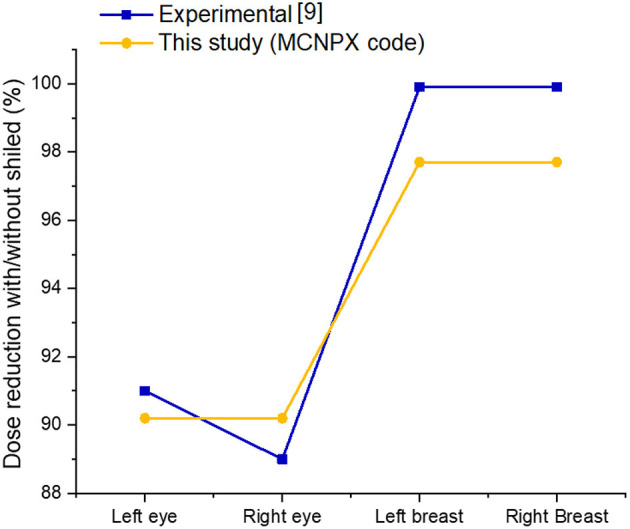
Comparison of dose reductions achieved in experimental and Monte Carlo studies.
Table 2.
Comparison of obtained dose reductions between experimental and Monte Carlo study.
| Organ type | Obtained dose reduction in Experimental study [32] (%) | Obtained dose reduction in this study (MCNPX code) (%) | Relative difference (%) |
|---|---|---|---|
| Left eye | 91 | 90.2 | 0.88 |
| Right eye | 89 | 90.2 | 1.33 |
| Left breast | 99.9 | 97.7 | 2.22 |
| Right Breast | 99.9 | 97.7 | 2.22 |
* Relative difference.
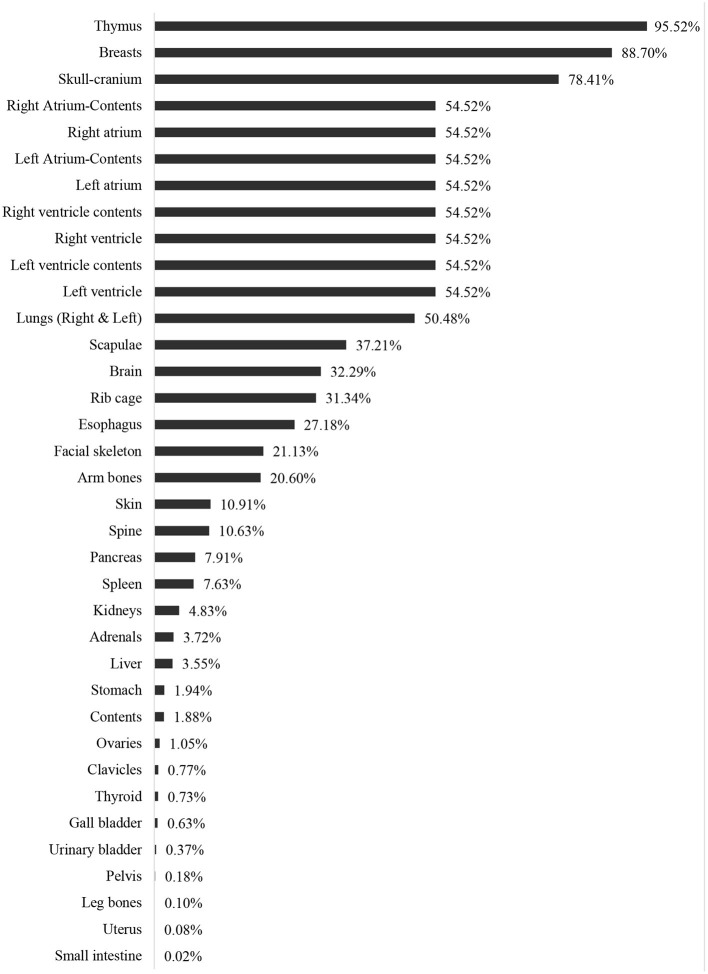
Shielding utilization would significantly decrease the absorbed radiation dose amount in the breasts. Moreover, the use of the MCNPX-MIRD phantom provided detailed information about dose reduction due to the shielding used at the level of the eyes and breasts (Figure 6). It is worth mentioning that it is very difficult to observe such detailed dose measurement for non-target organs using the anthropomorphic phantom.
Figure 6.
The reduction percentages (%) of the absorbed radiation doses in organs and tissues.
Besides the validation, the current study revealed that the highest dose reeducation was observed in the thymus (95.52%) and breasts (88.70%). The majority of the thoracic region showed organ dose reduction such as Heart-Left Ventricle, Heart-Left Ventricle-Contents, Heart-Right Ventricle, Heart-Right Ventricle-Contents Heart-Left Atrium, Heart- Left Atrium-Contents, Heart-Right Atrium Heart- Right Atrium-Contents (Figure 5). Overall, a 54.52% dose reduction was reported with the use of shielding compared to without shielding using the MCNPX-MIRD phantom during AP cervical.
Discussions
The present study designed and validated an MCNPX-MIRD optimized phantom. The result of the current study was compared with a previous study (9) and found that the modified phantom provides highly consistent and correlated radiation dose values with experimental anthropomorphic data. Moreover, it provides a detailed analysis of the role of shielding application in reducing organ dose during radiology examination. In contrast to a previous study investigating the effect of shielding in reducing radiation dose to gonads, breast, and eyes using dosimeters (9), the MCNPX-MIRD phantom makes it possible to assess the radiation dose to other organs and tissues. Our results demonstrate that the application of shielding reduced radiation dose to other organs that are not located in the field of primary radiation. The utilization of shielding benefits the patient by reducing the absorbed dose, and the result of the current study demonstrated a reduction of more than 95.52 and 88.70% in the thymus and breasts, respectively. Exposure of the thymus to low doses of ionizing radiation may lead to changes and disrupt the immune system's function and mechanism (44). Moreover, radiation exposure to the head and neck can result in thyroid dysfunction and may increase the incidence of benign and malignant thyroid nodules (45). Breasts are known as the most radiosensitive organ in the human body (46). In the cervical radiology examination, breasts are exposed to scattered radiation, and the application of shielding reduces the dose by 88% in the current study. Studies highlighted the importance of minimizing radiation exposure to breasts in general radiography (47). Therefore, shielding can be applied if breasts are exposed to scatter radiation and positioned outside the primary field. On the other hand, shielding demonstrated dose reduction by almost 50% and more than 32% for heart and brain tissue, respectively.
Brain tissue is usually not protected due to the misrepresentation of its radio-resistance. Exposure to low doses of ionizing radiation may lead to stochastic effects, including neuro-vascular and neuro-degenerative effects and eye cataracts (48). The United Nations Scientific Committee on the Effects of Atomic Radiation (UNSCEAR) (49) and the International Commission on Radiological Protection (ICRP) (50) recommend particular attention to non-cancer diseases such as cataracts and changes in the cardiovascular system. The current results showed that the radiation dose to the skeletal tissue was reduced in a range from 37.2 to 10.6%. Exposure to ionizing radiation is associated with leukemia and bone cancer (51). Increased fracture risk was observed in bone after exposure to ionizing radiation (52). Nevertheless, the pancreas, spleen, kidneys, adrenal glands, and liver were away from the field of radiation, but the application of shielding reduced their doses by 7.9, 7.6, 4.8, 3.7, and 3.6%, respectively. A previous study showed that the application of lead-rubber inferolateral to the light beam diaphragm during arm radiography reduced radiation dose to the thyroid, left ovary, testes, left breast, and spleen by 13, 9, 6, 3, and 2%, respectively (47). The use of shielding over the organ showed a higher dose reduction in studies using anthropomorphic phantom and radiation dosimeters (9, 53). Nevertheless, the application of shielding in the current study was directly over the organ, leading to a higher radiation dose reduction than previous studies. Moreover, detailed analysis of dose reduction to many organs and tissues was an advantage.
Conclusion
The frequency of radiological diagnostic procedures increased in recent years and will continue to increase every year (53, 54). The cumulative risk from multiple radiological examinations is a major concern, particularly for children and young patients (16). Efforts should be made to ensure patient radiation dose is always kept as low as reasonably achievable. The recommendation of the ICRP, dose optimization should be utilized when appropriate. Therefore, the use of shielding should be based on studies examining the effectiveness of shielding in reducing patient dose for particular radiology examinations as one size does not fit all. The MCNPX-MIRD optimized phantom provides detailed dose analysis for target and non-target organs and can be used to assess the efficiency of shielding in radiological examination.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
Ethics Institutional Review Board approval was not required because our work is based on phantom experimentation. Written informed consent was not required for this study because our work is experiment. No human experimentation was done.
Author Contributions
WE, HT, HZ, and SI were responsible for conceptualization. MA and HT developed the methodology. HT, HZ, MA, and AE contributed software. SI, WE, and AE undertook validation. HZ, WE, and BI performed formal analysis. WE and HT assisted with the investigation. MA and BI resources. HZ, SI, and AE data curation. MA, WE, HT, and BI writing—original draft preparation. HZ, SI, and AE undertook writing—review and editing. WE and MA performed visualization. HT and BI were responsible for supervision. WE, HT, and SI contributed to project administration. AE undertook funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was supported by Dunarea de Jos University of Galati, Romania.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
- 1.Scanff P, Donadieu J, Pirard P, Aubert B. Population exposure to ionizing radiation from medical examinations in France. Br J Radiol. (2008) 81:204–13. 10.1259/bjr/24344062 [DOI] [PubMed] [Google Scholar]
- 2.Han MA, Kim JH. Diagnostic X-ray exposure and thyroid cancer risk: systematic review and meta-analysis. Thyroid. (2018) 28:220–8. 10.1089/thy.2017.0159 [DOI] [PubMed] [Google Scholar]
- 3.Moey SF, Shazli ZA. Optimization of dose and image quality in full-fiand computed radiography systems for common digital radiographic examinations. Iran J Med Phys. (2018) 15:28–38. 10.22038/ijmp.2017.25091.1255 [DOI] [Google Scholar]
- 4.Vano E. ICRP recommendations on “managing patient dose in digital radiology.” Radiat Prot Dosimetry. (2005) 114:126–30. 10.1093/rpd/nch533 [DOI] [PubMed] [Google Scholar]
- 5.Burns KM, Shoag JM, Kahlon SS, Parsons PJ, Bijur PE, Taragin BH, et al. Lead aprons are a lead exposure hazard. J Am Coll Radiol. (2017) 14:641–7. 10.1016/j.jacr.2016.10.024 [DOI] [PubMed] [Google Scholar]
- 6.Clements J, Moirano J, Sherry C, Barr P, Berg J. Best practices for evaluating and tracking protective garments. J Am Coll Radiol. (2015) 12:531–2. 10.1016/j.jacr.2015.02.007 [DOI] [PubMed] [Google Scholar]
- 7.Chen J, Qi S, Hong X, Gu P, Wei R, Tang C, et al. Highly sensitive 3D metamaterial sensor based on diffraction coupling of magnetic plasmon resonances. Results Phys. (2019) 15:102791. 10.1016/j.rinp.2019.102791 [DOI] [Google Scholar]
- 8.Almatari M, Agar O, Altunsoy EE, Kilicoglu O, Sayyed MI, Tekin HO. Photon and neutron shielding characteristics of samarium doped lead alumino borate glasses containing barium, lithium and zinc oxides determined at medical diagnostic energies. Results Phys. (2019) 12:2123–8. 10.1016/j.rinp.2019.01.094 [DOI] [Google Scholar]
- 9.Elshami W, Abuzaid MM, Tekin HO. Effectiveness of breast and eye shielding during cervical spine radiography: an experimental study. Risk Manag Healthc Policy. (2020) 13:697–704. 10.2147/RMHP.S257185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Abuzaid M, Elshami W, Haneef C, Alyafei S. Thyroid shield during brain CT scan: Dose reduction and image quality evaluation. Imaging Med. (2017) 9:45–8. [Google Scholar]
- 11.Clancy CL, O'Reilly G, Brennan PC, McEntee MF. The effect of patient shield position on gonad dose during lumbar spine radiography. Radiography. (2010) 16:131–5. 10.1016/j.radi.2009.10.004 [DOI] [Google Scholar]
- 12.Mekis N, Zontar D, Skrk D. The effect of breast shielding during lumbar spine radiography. Radiol Oncol. (2013) 47:26–31. 10.2478/raon-2013-0004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Davey E, England A. AP versus PA positioning in lumbar spine computed radiography: image quality and individual organ doses. Radiography. (2015) 21:188–96. 10.1016/j.radi.2014.11.003 [DOI] [Google Scholar]
- 14.Jeukens CRLPN, Kütterer G, Kicken PJ, Frantzen MJ, van Engelshoven JMA, Wildberger JE, et al. Gonad shielding in pelvic radiography: modern optimised X-ray systems might allow its discontinuation. Insights Imaging. (2020) 11:1–11. 10.1186/s13244-019-0828-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Marsh RM, Silosky M. Patient shielding in diagnostic imaging: discontinuing a legacy practice. Am J Roentgenol. (2019) 212:755–7. 10.2214/AJR.18.20508 [DOI] [PubMed] [Google Scholar]
- 16.Nievelstein RAJ, Van Ufford HMEQ, Kwee TC, Bierings MB, Ludwig I, Beek FJA, et al. Radiation exposure and mortality risk from CT and PET imaging of patients with malignant lymphoma. Eur Radiol. (2012) 22:1946–54. 10.1007/s00330-012-2447-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Oono T, Araki F, Tsuduki S, Kawasaki K. Monte carlo calculation of patient organ doses from computed tomography. Radiol Phys Technol. (2014) 7:176–82. 10.1007/s12194-013-0250-1 [DOI] [PubMed] [Google Scholar]
- 18.Maria A. Monte carlo simulation in radionuclide therapy dosimetry. Biomed J Sci Tech Res. (2019) 15:11102–7. 10.26717/BJSTR.2019.15.00264722804457 [DOI] [Google Scholar]
- 19.Ay MR, Shahriari M, Sarkar S, Ghafarian P. Measurement of organ dose in abdomen-pelvis CT exam as a function of mA, KV and scanner type by monte carlo method. Iran J Radiat Res. (2004) 1:187–94. Available online at: http://ijrr.com/article-1-28-en.html [Google Scholar]
- 20.Agostinelli S, Allison J, Amako K, Apostolakis J, Araujo H, Arce P, et al. GEANT4 - A simulation toolkit. Nucl Instruments Methods Phys Res Sect A Accel Spectrometers. Detect Assoc Equip. (2003) 506:250–303. 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- 21.Salvat F, Fernández-Vera J, Sempau J. PENELOPE-2008: A Code System for Monte Carlo Simulation of Electron and Photon Transport. (2009). Available online at: http://www.asl-i.com/contents/upload-docs/201466123234.pdf (accessed September 6:2021).
- 22.RSICC Computer Code Collection, MCNPX, User's Manual Version 2,.4.0. MonteCarlo N-Particle Transport Code System for Multiple High Energy Applications. (2002). Available online at: https://www.google.com/search?q=RSICC+Computer+Code+Collection%2C+MCNPX+User%27s+Manual+Version+2.4.0.+MonteCarlo+N-Particle+Transport+Code+System+for+Multiple+and+High+Energy+Applications%2C (2002).&oq=RSICC+Computer+Code+Collection%2C+MCNPX+User%27s+Manu (accessed December 31, 2020).
- 23.Ballarini F, Battistoni G, Brugger M, Campanella M, Carboni M, Cerutti F, et al. The physics of the FLUKA code: recent developments. Adv Sp Res. (2007) 40:1339–49. 10.1016/j.asr.2007.05.031 [DOI] [Google Scholar]
- 24.Walters B, Kawrakow I, Rogers DWO. DOSXYZnrc Users Manual. (2005). Available online at: http://www.irs.inms.nrc.ca/inms/irs/BEAM/beamhome.html (accessed September 6, 2021).
- 25.Cristy M, Eckerman KF. Specific Absorbed Fractions of Energy at Various Ages From Internal Photon Sources,ORNL/TM-8381/V1-V7. (1987). Available online at: http://inis.iaea.org/Search/search.aspx?orig_q=RN:19012902 (accessed September 6, 2021).
- 26.Loevinger R, Berman M. A Revised Schema for Calculating the Absorbed Dose from Biologically Distributed Radionuclides. (1976). Available online at: https://www.scienceopen.com/document?vid=c878124d-7f07-4514-87c2-29f7321c688f (accessed September 6, 2021).
- 27.Cristy M. Mathematical Phantoms Representing Children of Various Ages for Use in Estimates of Internal Dose. (1980). Available online at: https://www.osti.gov/biblio/5308345 (accessed September 6, 2021).
- 28.Badal A, Kyprianou I, Badano A, Sempau J, Myers KJ. Monte Carlo package for simulating radiographic images of realistic anthropomorphic phantoms described by triangle meshes. In: Medical Imaging 2007: Physics of Medical Imaging International Society for Optics Photonics. International Society for Optics and Photonics; (2007). p. 65100Z. [Google Scholar]
- 29.Badal A, Kyprianou I, Badano A, Sempau J. Monte carlo simulation of a realistic anatomical phantom described by triangle meshes: application to prostate brachytherapy imaging. Radiother Oncol. (2008) 86:99–103. 10.1016/j.radonc.2007.11.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Segars WP. Development and application of the new dynamic nurbs-based cadiac-torso (NCAT) phantom (Dissertation). The University of North Carolina at Chapel Hill, Chapel Hill, NC, United States: (2001). [Google Scholar]
- 31.Segars WP, Tsui BMW. MCAT to XCAT: the evolution of 4-D computerized phantoms for imaging research. Proc IEEE. (2009) 97:1954–68. 10.1109/JPROC.2009.2022417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bueno G, Dniz O, Carrascosa CB, Delgado JM, Brualla L. Fast monte carlo simulation on a voxelized human phantom deformed to a patient. Med Phys. (2009) 36:5162–74. 10.1118/1.3245877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.ICRP Publication 23 . Reference Man: Anatomical, Physiological and Metabolic Characteristics. Oxford: Pergamon Press; (1975). p. 5. [Google Scholar]
- 34.ICRP . Conversion Coefficients for Use in Radiological Protection Against External Radiation. Pergamon: ICRP Publication 74; (1996). [Google Scholar]
- 35.Poludniowski G, Landry G, Deblois F, Evans PM, Verhaegen F. SpekCalc: a program to calculate photon spectra from tungsten anode x-ray tubes. Phys Med Biol. (2009) 54:N433. 10.1088/0031-9155/54/19/N01 [DOI] [PubMed] [Google Scholar]
- 36.Poludniowski GG, Evans PM. Calculation of x-ray spectra emerging from an x-ray tube. Part I. Electron penetration characteristics in x-ray targets. Med Phys. (2007) 34:2164–74. 10.1118/1.2734725 [DOI] [PubMed] [Google Scholar]
- 37.Poludniowski GG. Calculation of x-ray spectra emerging from an x-ray tube. Part II. X-ray production and filtration in x-ray targets. Med Phys. (2007) 34:2175–86. 10.1118/1.2734726 [DOI] [PubMed] [Google Scholar]
- 38.Hayati H, Mesbahi A, Nazarpoor M. Monte carlo modeling of a conventional X-ray computed tomography scanner for gel dosimetry purposes. Radiol Phys Technol. (2016) 9:37–43. 10.1007/s12194-015-0331-4 [DOI] [PubMed] [Google Scholar]
- 39.Mesbahi A, Zakariaee SS. Effect of anode angle on photon beam spectra and depth dose characteristics for X-RAD320 orthovoltage unit. Reports Pract Oncol Radiother. (2013) 18:148–52. 10.1016/j.rpor.2012.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hayati H, Mesbahi A. Impact of photon spectra on the sensitivity of polymer gel dosimetry by X-ray computed tomography. Iran J Med Phys. (2019) 16:48–55. 10.22038/ijmp.2018.30042.1334 [DOI] [Google Scholar]
- 41.Malekzadeh R, Mehnati P, Sooteh MY, Mesbahi A. Influence of the size of nano- and microparticles and photon energy on mass attenuation coefficients of bismuth–silicon shields in diagnostic radiology. Radiol Phys Technol. (2019) 12:325–34. 10.1007/s12194-019-00529-3 [DOI] [PubMed] [Google Scholar]
- 42.Taghavi R, Mirzaei HR, Aghamiri SMR, Hajian P. Calculating the absorbed dose by thyroid in breast cancer radiotherapy using MCNP-4C code. Radiat Phys Chem. (2017) 130:12–4. 10.1016/j.radphyschem.2016.06.029 [DOI] [Google Scholar]
- 43.Copeland K, Parker DE, Friedberg W. Fluence to absorbed dose, effective dose and gray equivalent conversion coefficients for iron nuclei from 10 MeV to 1 TeV, calculated using monte carlo radiation transport code MCNPX 2.7.A. Radiat Prot Dosimetry. (2009) 138:353–62. 10.1093/rpd/ncp277 [DOI] [PubMed] [Google Scholar]
- 44.Fabritius G, Brix G, Nekolla E, Klein S, Popp HD, Meyer M, et al. Cumulative radiation exposure from imaging procedures and associated lifetime cancer risk for patients with lymphoma. Sci Rep. (2016) 6:1–9. 10.1038/srep35181 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aldrink JH, Adler B, Haines J, Watkins D, Matthews M, Lubeley L, et al. Patients exposed to diagnostic head and neck radiation for the management of shunted hydrocephalus have a significant risk of developing thyroid nodules. Pediatr Surg Int. (2016) 32:565–9. 10.1007/s00383-016-3894-1 [DOI] [PubMed] [Google Scholar]
- 46.ICRP . Statement on Tissue Reactions and Early and Late Effects of Radiation in Normal Tissues and Organs e Threshold Doses for Tissue Reactions in a Radiation Protection Context. ICRP publication 118 Ann (12012). Available online at: https://scholar.google.ru/scholar?hl=en&as_sdt=0%2C5&as_vis=1&q=ICRP.+Statement+on+tissue+reactions+and+early+and+late+effects+of+radiation+in+normal+tissues+and+organs+e+threshold+doses+for+tissue+reactions+in+a+radiation+protection+context.+ICRP+publica (accessed September 6, 2021). [DOI] [PubMed]
- 47.Hayre C, Bungay H, Jeffery C, Cobb C, Atutornu J. Can placing lead-rubber inferolateral to the light beam diaphragm limit ionising radiation to multiple radiosensitive organs? Radiography. (2018) 24:15–21. 10.1016/j.radi.2017.09.002 [DOI] [PubMed] [Google Scholar]
- 48.Picano E, Vano E, Domenici L, Bottai M, Thierry-Chef I. Cancer and non-cancer brain and eye effects of chronic low-dose ionizing radiation exposure. BMC Cancer 2012 121. (2012) 12:1–13. 10.1186/1471-2407-12-157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.UNSCEAR . Sources and Effects of Ionizing Radiation United Nations Scientific Committee on the Effects of Atomic Radiation. (2008). Available online at: https://www.unscear.org/unscear/en/publications/2008_1.html (accessed September 6, 2021).
- 50.Annals of the ICRP: Early Late Effects of Radiation in Normal Tissues Organs: Threshold Doses for Tissue Reactions Other Non-Cancer Effects of Radiation in a Radiation Protection Context. (2012). Available online at: https://scholar.google.ru/scholar?q=Annals+of+the+ICRP:+Early+and+late+effects+of+radiation+in+normal+tissues+and+organs:+threshold+doses+for+tissue+reactions+and+other+non-cancer+effects+of+radiation+in+a+radiation+protection+context.+2012,+public+draft (accessed September 6, 2021). [DOI] [PubMed]
- 51.Dant JT, Richardson RB, Nie LH. Monte carlo simulation of age-dependent radiation dose from alpha- and beta-emitting radionuclides to critical trabecular bone and bone marrow targets. Phys Med Biol. (2013) 58:3301–19. 10.1088/0031-9155/58/10/3301 [DOI] [PubMed] [Google Scholar]
- 52.Baxter NN, Habermann EB, Tepper JE, Durham SB, Virnig BA. Risk of pelvic fractures in older women following pelvic irradiation. J Am Med Assoc. (2005) 294:2587–93. 10.1001/jama.294.20.2587 [DOI] [PubMed] [Google Scholar]
- 53.Du X, Wang J, Zhu BL. The frequencies of x-ray examinations and CT scans: findings from a sample investigation in Jiangsu, China. Radiat Prot Dosimetry. (2020) 190:38–44. 10.1093/rpd/ncaa076 [DOI] [PubMed] [Google Scholar]
- 54.Liu CX, Niu Z, Zhang JM, Yang SL, Wang Y, Li CY, et al. [An analysis of medical X-ray examination frequency in ten hospitals in Tianjin, China]. Zhonghua Lao Dong Wei Sheng Zhi Ye Bing Za Zhi. (2018) 36:830–3. 10.3760/cma.j.issn.1001-9391.2018.11.008 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.