Assessing the safe haven property of the gold market during COVID-19 pandemic

Abstract

This study examines the safe haven prowess of gold against some exogenous shocks due to the COVID-19 pandemic. We further make a comparison of our findings with those obtained for the period before it. Our results confirm the potential of gold market to serve as a safe haven during the pandemic albeit with a higher effectiveness before the pandemic. Further results suggest that gold consistently offers better safe haven properties than the US stocks as well as other precious metals like Silver, Palladium and Platinum regardless of the period. Finally, we find that the predictive model that accounts for uncertainties outperforms the benchmark model that ignores the same both for the in- and out-of-sample forecast analyses.

1. Motivation

Gold is described as a multifaceted asset due to its many attributes: currency, commodity, and risk aversion (Wu, Tong, Yang, & Derbalic, 2019). Studies have focused more on the last attribute as gold acts as hedging asset in portfolio diversification and safe haven in period of economic uncertainties and turbulent markets environment. More importantly, gold has been found to retain its values during unsettled market episodes. (Salisu, Raheem, & Ndako, 2020; Salisu & Adediran, 2020; Shahzad, Bouri, Roubaud, & Kristoufek, 2020).

The coronavirus (COVID-19) outbreak that started from China, spiralled into a pandemic, and subject the global economic into a shock the world has never witnessed. In an attempt to combat the diseases, health policy guidelines has advised people to practice “stay at home”, a situation that has led to acute drop in production of output. This has triggered sharp disruptions in the demand and supply dynamics. Some countries have already experiencing recession and there are projections many more will follow suit. Assets and equity prices have plummeted, so as internationally traded commodity. For instance, crude oil price collapsed into negative in the second half of April 2020. There has been high volatility in the financial markets, which as further aggravated the intensity of uncertainty. Thus, this pandemic has triggered several exogenous shocks.

Judging by the indicators of COVID-19, it is assumed that we have passed the peak and things are gradually going back to normalcy, as countries are beginning to open up. Evidences have suggested that post-crisis periods are associated with high volatilities and uncertainties in financial markets (Antonakakis, Chatziantonioub, & Filis, 2017), and this can spillover to other sectors of the economy (Summer, Johnson, & Soenen, 2010). In a bid to protect their investments, investors will start to readjustment their portfolios in favour of commodities that are considered to have safe haven property, prominent among which is gold.

Several studies have examined the safe haven property of gold (Bouri, Shahzad, Roubaudd, Kristoufeke, & Lucey, 2020; Shahzad et al., 2020); and other precious metals (Li & Lucey, 2017; Peng, 2019; Sakemoto, 2018). A common feature of these studies is their focus on a specific crisis, such as the financial/stock market crisis (Ciner, Gurdgiev, & Lucey, 2013; Dee, Li, & Zheng, 2013; Gutiérrez, Franco, & Campuzano, 2013; He, He, O'Connor, & Thijssen, 2018; Iqbal, 2017; Shahzad et al., 2020), debt crisis (Agyei-Ampomah, Gounopoulos, & Mazouz, 2014; Boubaker, Cunado, Gil-Alana, & Gupta, 2020; Bredin, Conlon, & Potì, 2015), exchange rate crisis (Joy, 2011; Reboredo, 2013b; Reboredo & Rivera-Castro, 2014a and b; Qureshi, Rehman, & Qureshi, 2018; Bedoui, Guesmi, Kalai, & Porcher, 2019). Some studies have also focused on non-crisis uncertainty such as economic uncertainty (Hood & Malik, 2013; Wu et al., 2019), and commodity price shock (Reboredo, 2013a; Salisu & Adediran, 2020).

Whereas, COVID-19 is a global phenomenon, that has subjected virtually all the countries to various forms of shocks (such as decline in output, stock prices, international reserves, to mention a few). It is argued that the severity of this pandemic is no match to any of the previous crises. The empirical inquiry this study seeks answer to is “does the safe haven property of gold extends to the COVID-19 pandemic induced shock?” To answer this question we built a dataset from 1 Jan. 2020 to 20 May 2020. We further make a comparison about the effectiveness of this safe haven property for pre- and post- announcement of the disease. This comparison becomes germane as studies have shown that the effectiveness of hedging prowess of gold is dependent upon the existing market conditions i.e. bear or bull (Iqbal, 2017). Limiting the scope of the study to COVID-19 era will reveal the true extent of gold hedging capacity. The novel contribution of this study is derived from its objective. No study we are aware of has focused on the safe haven of gold during the current COVID-19 crisis.

Our results confirm the potential of gold market to serve as a safe haven during the pandemic albeit with a higher effectiveness before the pandemic. Further results suggest that gold consistently offers better safe haven properties than the US stocks as well as other precious metals like Silver, Palladium and Platinum regardless of the period. Finally, we find that the predictive model that accounts for uncertainties outperforms the benchmark model that ignores the same both for the in- and out-of-sample forecast analyses.

Our results support the hypothesis set out in this study. Specifically, we show that gold serve as a safe haven during the pandemic albeit with a higher effectiveness before the pandemic. In comparison to other precious metals, gold offers better safe haven properties. The rest of the study is structured as follows. Section 2 provides discussions on methodology. Empirical results are presented in Section 3, while the concluding remark is rendered in Section 4.

2. Methodology

Here, we formulate an empirical model that allows us to assess the safe haven property of gold. The formulation relies on two assumptions: one, that investment in the gold market is expected to retain or increase in value during times of market turbulence (or high market volatility); two and flowing from one, since the COVID-19 pandemic is global, we anticipate a positive correlation between a measure of uncertainty in a competitive market (in this case, stock market) and returns on investment in the gold market. In other words, as the stock market uncertainty increases, investors are tempted to look elsewhere for safe investments and if truly the gold market possesses a safe haven property, it should be a safe destination for investments during the pandemic and by extension its returns should improve as trading in the market improves. The model is specified in such as to control for endogeneity bias (that may result from omitting other predictors of gold returns), conditional heteroscedasticity effect (due to the use of high frequency data) and persistence (which is typical of most financial and economic time series) (see Westerlund and Narayan, 2012, Westerlund and Narayan, 2015):

$$r_t=\alpha +\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}{\mathit{uc}}_{t-i}+\gamma \left({\mathit{uc}}_t-{\rho }_0{\mathit{uc}}_{t-1}\right)+{\eta }_t$$ (1)

where r _t is the log return of gold price; ucis the market uncertainty index using the Chicago Board Options Exchange (CBOE), the Volatility Index, or VIX, as a proxy; the η _t is zero mean idiosyncratic error term gold returns; and the coefficient λ _i ^adj measures the relative impact of market uncertainty on gold returns and we allow for up to five lags given the data frequency (daily five-day of the week) as well as the need to capture more dynamics in the estimation process. Thus, the underlying null hypothesis of no predictability involves a joint (Wald) test - $\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}=0$. Note that the original specification of (1) is given as r _t = α + λuc _t−1 + ε _t  , however, to resolve any probable endogeneity bias resulting from the correlation between uc _t and ε _t as well as any potential persistence effect, we follow the approach of Lewellen (2004) and Westerlund and Narayan, 2012, Westerlund and Narayan, 2015. Thus, the parameter λ ^adj is derived as λ ^adj = λ − γ(1 − ρ ₀) (where ρ ₀ measures the degree of persistence in uc _t) and is described as the bias adjusted OLS estimator of Lewellen (2004) which corrects for any persistence effect in the predictive model. The additional term γ(uc _t − ρ ₀ uc _t−1) corrects for any endogeneity bias resulting from the correlation between uc _t and ε _t as well as any inherent unit root problem in the predictor series. Accounting for endogeneity bias here is important since there could be several determinants of gold returns which are suppressed in Eq. (1). Such omissions could introduce endogeneity bias resulting from probable correlations between uc _t and ε _t. To resolve the conditional heteroscedasticity effect, Westerlund and Narayan, 2012, Westerlund and Narayan, 2015 suggest pre-weighting all the data by $1/{\widehat{\sigma }}_{\eta }$ and estimating the resulting equation with the Ordinary Least Squares (OLS). This modified OLS estimator is described as the Feasible Quasi GLS estimator in Westerlund and Narayan, 2012, Westerlund and Narayan, 2015 and it is technically computed as:

$${\lambda }_{\mathit{adj}}^{\mathit{FQGLS}}=\frac{{\sum }_{t=q_m+2}^T{\tau }_t^2{p}_{t-1}^d{s}_t^d}{\sqrt{{\sum }_{t=q_m+2}^T{\tau }_t^2{\left(p_{t-1}^d\right)}^2}}$$ (2)

where τ _t = 1/σ _{η, t} is used in weighting all the data in Eq. (2) and p _t ^d = p _t − ∑_s=2 ^T p _t/T.1

We further test whether the inclusion of the uncertainty index in the valuation of gold returns will produce better forecast accuracy at least relative to the historical average model which is a typical (baseline) predictive model for most financial and economic series. Since the two models are nested as the historical average is a restricted version of Eq. (1), their forecast performance comparison can easily be implemented using the Clark and West (2007) [CW] test.2 The CW test is used to determine the statistical significance of the difference between the forecast errors of the two nested (restricted and unrestricted) models, with the underlying procedure defined by:

$${\widehat{f}}_{t+h}={\left(r_{t+h}-{\widehat{r}}_{1t,t+h}\right)}^2-\left[{\left(r_{t+h}-{\widehat{r}}_{2t,t+h}\right)}^2-{\left({\widehat{r}}_{1t,t+h}-{\widehat{r}}_{2t,t+h}\right)}^2\right]$$ (3)

where h denotes the forecast period; ${\left(r_{t+h}-{\widehat{r}}_{1t,t+h}\right)}^2$ and ${\left(r_{t+h}-{\widehat{r}}_{2t,t+h}\right)}^2$ are respectively the squared errors for the restricted and the unrestricted models; and ${\left({\widehat{r}}_{1t,t+h}-{\widehat{r}}_{2t,t+h}\right)}^2$ is the adjusted squared error incorporated in the CW test to correct for any noise that may characterize the forecasts of larger models. In Eq. (1), the sample average of ${\widehat{f}}_{t+h}$ can be expressed as MSE ₁ − (MSE ₂ − adj.) where ${\mathit{MSE}}_1=P^{-1}\sum {\left(r_{t+h}-{\widehat{r}}_{1t,t+h}\right)}^2$, ${\mathit{MSE}}_2=P^{-1}\sum {\left(r_{t+h}-{\widehat{r}}_{2t,t+h}\right)}^2$, $\mathrm{adj}.=P^{-1}\sum {\left({\widehat{r}}_{1t,t+h}-{\widehat{r}}_{2t,t+h}\right)}^2$, and P is the number of forecast periods considered in the computation of the averages. In testing for equality of forecast performance between restricted (the historical average) and unrestricted models, the generated${\widehat{f}}_{t+h}$ series is regressed on a constant term only and using the resulting t-statistic for a zero coefficient to determine significance. We reject the hypothesis of a zero coefficient if this statistic is greater than +1.282 (for a one sided 0.10 test) or + 1.645 (for a one sided 0.05 test) (see Clark & West, 2007). The rejection of the null hypothesis implies the preference for the uncertainty-based model for gold returns. We also employ single forecast measures such as the Root Mean Square Error (RMSE), Mean Absolute Deviation (MAD) and Mean Absolute Percentage Error (MAPE) to complement the Clark & West test results.

Since we are confronted with limited data sample between the period COVID-19 was announced (December 31, 2019) and the period of conducting this research (May 28, 2020), we can only use the 75:25 data split for the in-sample and out-of-sample forecast evaluation. Some studies have used 50:50 and 25:75 data splits, however, these cannot be implemented here given the available data scope for our study. We consider two out-of-sample forecast horizons, 10-day and 20-day ahead forecast horizons and the recursive approach to forecasting is adopted.

3. Results

3.1. Preliminary analyses

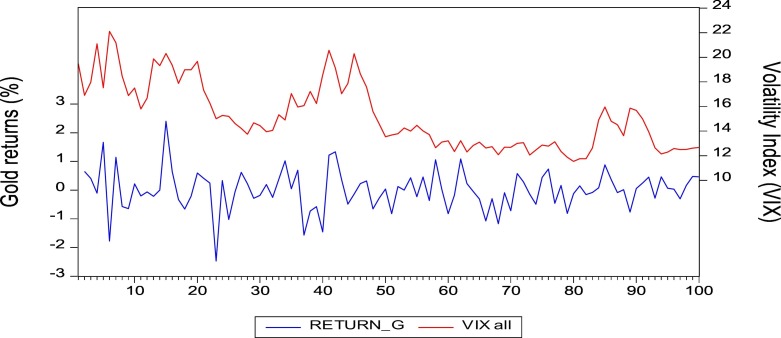
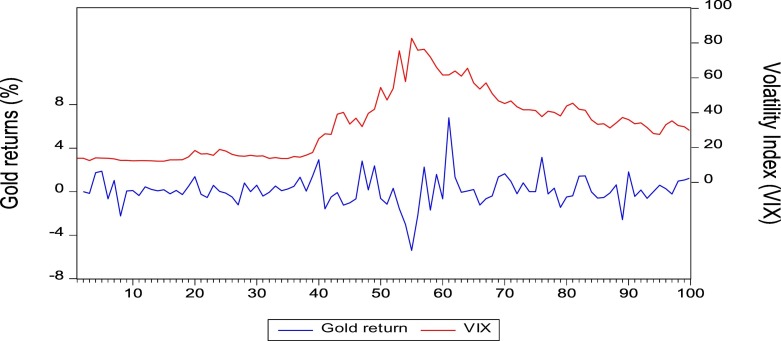
Since this study involves comparative analyses, we dichotomize the sample size into pre- and post-COVID-19 periods. Table 1 presents the results of the descriptive statistics. An overview of the table shows that return on gold is higher in the post-announcement of the COVID-19, as compared to the preceding period. This increase could be explained by the high volatility, as depicted in the standard deviation statistic. This is the first pointer to confirm the hedging property of gold. Expectedly, uncertainty is higher during the turbulent period as compared to the tranquil market condition. There is evidence of conditional heteroscedasticity for VIX, irrespective of the lag-length. There is weak evidence for serial correlation and conditional heteroscedasticity for gold. Fig. 1, Fig. 2 show the trend of gold returns with VIX (pre- and post-announcement, respectively). The figures suggest that both series move in the same direction. While the dispersion between the series is wide in the first half of pre-announcement period, the exact opposite post-announcement period. Result of the unit root test is presented in Table 2 . Irrespective of the period and test, gold is stationary at levels, thus confirming its mean reverting tendencies. On the flip side, VIX is found to be first difference stationary for the post-announcement period, confirming its high level of volatility. Two structural break dates were found: 2020-03-13 and 2020-04-02. The first date could be attributed to World Health Organisation's declaration of COVID-19 a pandemic. The second date could reflect the effect of recording over 5000 and 250,000 deaths and confirmed cases, respectively. Results for persistence and endogeneity, presented in Table 3 , confirm the existence of persistence and absence of endogeneity. The presence of the persistence effect is a necessary condition for the consideration of the bias-adjusted estimator of Lewellen (2004) and Westerlund and Narayan, 2012, Westerlund and Narayan, 2015 used in this study.

Table 1.

Summary statistics and residual based tests.

		Pre-COVID Announcement		Post-COVID Announcement
		Gold return	VIX	Gold return	VIX
Mean		0.0154	15.0844	0.1443	33.1079
Std.		0.6978	2.6298	1.4162	18.5992
Skw		−0.1385	0.7649	0.4901	0.6708
Kurt		5.1160	2.5738	8.8629	2.6207
Autocorrelation	k = 2	0.0056	0.8690	1.7790	17.601***
	k = 4	4.9598	2.6216	2.8022	22.427***
	k = 6	5.1649	4.4544	14.666**	24.633***
Heteroscedasticity	k = 2	0.1592	9.3194***	0.2678	15.9213***
	k = 4	0.1590	4.3412***	0.2089	8.9520***
	k = 6	0.2033	2.0404*	2.6935**	7.1367***

Note: Std is standard deviation, Skw is skewness, Kurt is Kurtosis. For autocorrelation and heteroscedasticity tests, the reported values are the Ljung-Box test Q-statistics for the former and the ARCH-LM test F-statistics in the case of the latter. We consider three different lag lengths (k) of 2, 4, and 6 for robustness. The null hypothesis for the autocorrelation test is that there is no serial correlation, while the null for the ARCH-LM (F distributed) test is that there is no conditional heteroscedasticity. *** and ** & * imply the rejection of the null hypothesis in both cases at 1%, 5% & 10% levels of significance, respectively.

Fig. 1.

Trends in gold returns and VIX index [Pre-COVID Announcement]. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

Trends in gold returns and VIX index [Post-COVID Announcement]. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 2.

Results of Unit root tests.

	ADF		NL		PP		KPSS		ERS		NP
	Pre-COVID Announcement
	Level	FD	Level	FD	Level	FD	Level	FD	Level	FD	Level	FD	Break Dates
Gold return	−10.595a	–	−9.805a	–	−11.810a	–	0.140a	–	2.053a	–	0.099a	–	–
VIX	−3.5360b	–	−3.183b	–	−3.478b	–	0.099a	–	5.082	3.040a	0.152	0.132b	09/04/19
	Post-COVID Announcement
Gold return	−8.690a	–	−12.431	–	−9.129a	–	0.032a	–	1.770a	–	0.098a	–	–
VIX	−1.323	−4.237a	−2.0161	−10.687a	−1.023	−14.12a	0.219	0.119a	15.725	2.065a	0.270	0.118b	13/03/20 02/04/20

Note: ADF test is the Augmented Dickey Fuller test; NL test is the Narayan and Liu (2015) test; PP is the Philips Perron test; KPSS is the Kwiatkowski, Phillips, Schmidt, and Shin (1992) test; ERS is the Elliot, Rothenberg, and Stock (1996) test and NP is the Ng and Perron (2001) test. FD denotes First Difference; “^a” and “^b” indicate the rejection of the null hypothesis of a unit root at 1%, 5% and 10%, respectively; the test regression for all the unit root tests includes intercept and trend; I(d) implies the order of integration, where d is the number of differencing required for a series to become stationary; All the variables are in their log forms. The breaks are determined using the Bai and Perron (2003) test.

Table 3.

Persistence and endogeneity test results for VIX.

	Persistence		Endogeneity
	Pre-COVID	Post-COVID	Pre-COVID	Post-COVID
VIX	0.8741***	0.9572***	−0.0679	−0.0431

Note: ***, **, & * imply statistical significance of coefficients at 1%, 5%, and 10% levels, respectively.

3.2. Main results

Table 4 presents the results of the safe haven prowess of gold due to uncertainties associated with the COVID-19 pandemic as well as those before it. The results confirm the potential of gold market as a safe haven during the pandemic. Confirming the position of the literature, the safe haven effectiveness of financial markets is dependent upon the market condition (see Junttila, Pesonen, & Raatikainen, 2018). We show that the effectiveness is higher for pre-COVID-19 announcement as compared to the post announcement period. Similar results are obtained by previous studies such as (Hood & Malik, 2013) who concluded that safe haven property is weak during period of extreme uncertainty as the 2008 financial crisis, a shock likened to the current pandemic.

Table 4.

Predictability results.

	Pre-COVID Announcement	Post-COVID Announcement
$\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}$	0.0138** (0.0057) [2.4039]	0.0063*** (0.0014) [4.2257]

Note: *** and ** & * imply the rejection of the null hypothesis of no predictability at 1%, 5% & 10% levels of significance, respectively. Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

The forecasting evaluation result is presented in subsequent tables (Table 5, Table 6, Table 7 ). It should be recalled that the data is divided into: in- and out-of-sample sizes using 75% and 25%, respectively. The results of the in-sample are presented in Table 5, which confirm that the uncertainty induced model is our preferred model relative to the historical average model, and the outcome remains the same for both pre- and post-announcement periods particularly judging by the RMSE and MAD where the preferred model reports the least value likewise the Clark and West test shows statistical significance at the 1% level. The out-of-sample forecast evaluation of both the uncertainty-based model and the historical average also produces the same conclusion as the in-sample forecasts irrespective of the period [whether pre-announcement or post-announcement]. Thus, we may conclude that accounting for uncertainties when modelling gold returns will offer better forecast estimates than those that ignore the same.

Table 5.

In-Sample Forecast evaluation.

	Pre-COVID Announcement		Post-COVID Announcement
	Model 1	Model 2	Model 1	Model 2
RMSE	0.3460	0.7565	1.0392	1.4982
MAD	0.5000	0.5570	0.9193	0.9708
MAPE	801.252	2160.096	1255.636	758.942
Clark & West	–	0.2099*** (0.0710) [2.9535]	–	1.2478*** (0.5252) [2.3760]

Note: Model 1 incorporates the Uncertainty (VIX) predictor while Model 2 is the Historical Average model. Thus, the former is the unrestricted model while the latter is the restricted model. RMSE is Root Mean Square Error; MAD is Mean Absolute Deviation & MAPE is Mean Absolute Percentage Error. The results for the Clark & West are reported for the model under the null (i.e. Model 2). The RMSE reported for Model 1 is the version of Clark and West (2007) which adjusts the difference in mean squared prediction errors to account for the additional predictors in the model. *** and ** & * imply the rejection of the null hypothesis of equal forecast accuracy at 1%, 5% & 10% levels of significance, respectively. The null hypothesis of a zero coefficient is rejected if this statistic is greater than +1.282 (for a one sided 0.10 test), +1.645 (for a one sided 0.05 test) and + 2.00 for 0.01 test (for a one sided 0.01 test) (see Clark & West, 2007). Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

Table 6.

Out-of-Sample Forecast evaluation [Pre-COVID Announcement].

	Mode1 1		Model 2
	h = 10	h = 20	h = 10	h = 20
RMSE	0.2954	0.2758	0.7253	0.6966
MAD	0.4685	0.4532	0.5247	0.5031
MAPE	728.076	678.195	2034.644	1950.854
Clark & West	–	0.2140*** (0.0646) [3.3118]	–	0.1928*** (0.0583) [3.3046]

Note: Model 1 incorporates the Uncertainty (VIX) predictor while Model 2 is the Historical Average. Thus, the former is the unrestricted model while the latter is the restricted model. RMSE is Root Mean Square Error; MAD is Mean Absolute Deviation & MAPE is Mean Absolute Percentage Error. The results for the Clark & West are reported for the model under the null (i.e. Model 2). The RMSE reported for Model 1 is the version of Clark and West (2007) which adjusts the difference in mean squared prediction errors to account for the additional predictors in the model. *** and ** & * imply the rejection of the null hypothesis of equal forecast accuracy at 1%, 5% & 10% levels of significance, respectively. The null hypothesis of a zero coefficient is rejected if this statistic is greater than +1.282 (for a one sided 0.10 test), +1.645 (for a one sided 0.05 test) and + 2.00 for 0.01 test (for a one sided 0.01 test) (see Clark & West, 2007). Two out-of-Sample forecast horizons are considered: 10-day & 20-day ahead forecast horizons. Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

Table 7.

Out-of-Sample Forecast evaluation [Post-COVID Announcement].

	Mode1 1		Model 2
	h = 10	h = 20	h = 10	h = 20
RMSE	1.2006	1.1299	1.4706	1.4092
MAD	0.9928	0.9720	0.9717	0.9273
MAPE	1186.005	1073.689	759.618	724.923
Clark & West	–	0.9954*** (0.4697) [2.1193]	–	0.8782*** (0.4227) [2.0779]

Note: Model 1 incorporates the Uncertainty (VIX) predictor while Model 2 is the Historical Average. Thus, the former is the unrestricted model while the latter is the restricted model. RMSE is Root Mean Square Error; MAD is Mean Absolute Deviation & MAPE is Mean Absolute Percentage Error. The results for the Clark & West are reported for the model under the null (i.e. Model 2). The RMSE reported for Model 1 is the version of Clark and West (2007) which adjusts the difference in mean squared prediction errors to account for the additional predictors in the model. *** and ** & * imply the rejection of the null hypothesis of equal forecast accuracy at 1%, 5% & 10% levels of significance, respectively. The null hypothesis of a zero coefficient is rejected if this statistic is greater than +1.282 (for a one sided 0.10 test), +1.645 (for a one sided 0.05 test) and + 2.00 for 0.01 test (for a one sided 0.01 test) (see Clark & West, 2007). Two out-of-Sample forecast horizons are considered: 10-day & 20-day ahead forecast horizons. Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

3.3. Additional results

3.3.1. Safe haven behaviour of stocks during the pandemic

Some robustness checks were conducted. First, we test further whether the US stocks will share the similar safe haven potential with gold by examining how the US stocks respond to uncertainty particularly during turbulent times like the current pandemic. Thus, the Eq. (1) for gold still suffices except that the dependent variable is now replaced with US stock return using S&P 500 index. The results of the predictability analyses are presented in Table 8 . Unlike gold which possesses safe haven properties both for the pre- and post-announcement periods of COVID-19, the ability of US stocks to provide safe investment is noticed during the pandemic albeit with lower magnitude compared to gold. These results replicate those of existing studies (such as He et al., 2018; and Shahzad et al., 2020). The results of the out-of-sample analyses are presented in Table 9 , which confirm the outperformance of the uncertainty-based model over the historical average. In other words, regardless of the choice of market, whether gold or stocks, the consideration of uncertainties is crucial in the valuation of assets. This conclusion is in line with the standard theories of asset pricing such as Capital Asset Pricing Model and Arbitrage Pricing Theory both of which suggest the need to account for one form of risk or the other in the valuation of assets and since the pandemic is associated with global uncertainty, it can serve as one form of systemic risk to financial market.

Table 8.

Predictability results.

	Pre-COVID Announcement	Post-COVID Announcement
$\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}$	−0.0278*** (0.0030) [−9.2979]	0.0039** (0.0015) [2.5397]

Note: *** and ** & * imply the rejection of the null hypothesis of no predictability at 1%, 5% & 10% levels of significance, respectively. Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

Table 9.

Out-of-Sample Forecast evaluation.

	Pre-COVID Announcement		Post-COVID Announcement
	Mode1 1 vs Model 2		Mode1 1 vs Model 2
	h = 10	h = 20	h = 10	h = 20
Clark & West	0.9911*** (0.2410) [4.1132]	0.9052*** (0.2173) [4.1657]	15.9457*** (4.8775) [3.2692]	14.7262*** (4.3784) [3.3633]

Note: Model 1 incorporates the Uncertainty (VIX) predictor while Model 2 is the Historical Average. Thus, the former is the unrestricted model while the latter is the restricted model. *** and ** & * imply the rejection of the null hypothesis of equal forecast accuracy at 1%, 5% & 10% levels of significance, respectively. The null hypothesis of a zero coefficient is rejected if this statistic is greater than +1.282 (for a one sided 0.10 test), +1.645 (for a one sided 0.05 test) and + 2.00 for 0.01 test (for a one sided 0.01 test) (see Clark & West, 2007). Two out-of-Sample forecast horizons are considered: 10-day & 20-day ahead forecast horizons. Values in parentheses – () denote standard errors while those reported in square brackets – [] are for t-statistics.

3.3.2. The safe haven properties of other precious metals

Further analyses are carried out for other precious metals such as Silver, Palladium and Platinum. This consideration is important as most precious metals including gold tend to share some inherent characteristics such as: (i) global acceptance; (ii) no possibility of default risks; (iii) store of value tendencies; and their protection attributes and properties (see Arnold & Auer, 2015), make them (precious metals) have heterogeneous hedging tendencies (Uddin, Shahzad, Boako, Hernandez, & Lucey, 2019). An attempt to isolate gold will only offer biased or partial outcomes if the results are not compared with those from other precious metals. This is the motivation for these additional analyses. The results of the in-sample predictability are rendered in Table 10 while those of out-of-sample forecast evaluation are presented in Table 11 . We can infer two remarks from Table 10: (i) precious metals have different hedging prowess, with silver being the least hedging option; (ii) in comparison with statistics in Table 4, gold offer the best financial assets that could shield investors' portfolio from any exogenous shocks. This confirms position that gold holds a “special position”. Summarizing Table 11, our model, as against the historical average-based model, is more preferred in accurately forecasting the returns of other precious metals except for Palladium during the pre-COVID announcement.

Table 10.

Predictability results.

		Palladium	Platinum	Silver
Pre-COVID Announcement	$\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}$	0.0948*** (0.0065) [14.4949]	−0.2373*** (0.0672) [−3.5318]	0.0068 (0.007768) [0.872976]
Post-COVID Announcement	$\sum _{i=1}^5{\lambda }_i^{\mathit{adj}}$	0.0083 (0.0085) [0.9706]	0.05724*** (0.0041) [14.0426]	−0.0031* (0.0018) [−1.6886]

Note: *** and ** & * imply the rejection of the null hypothesis of no predictability at 1%, 5% & 10% levels of significance, respectively. Values in parentheses - () denote standard errors while those reported in square brackets – [] are for t-statistics.

Table 11.

Out-of-Sample Forecast evaluation.

		Pre-COVID Announcement		Post-COVID Announcement
		Mode1 1 vs Model 2		Mode1 1 vs Model 2
		h = 10	h = 20	h = 10	h = 20
Clark & West	Palladium	0.1309 (0.1059) [1.2357]	0.1206 (0.0953) [1.2660]	2.1448* (1.5472) [1.3862]	1.8567* (1.4013) [1.3250]
	Platinum	48.2419* (30.8232) [1.5651]	44.7887* (27.5875) [1.62352]	55.9379* (36.5221) [1.5316]	52.2739* (32.6786) [1.5996]
	Silver	0.6235*** (0.1811) [3.4428]	0.5313*** (0.1645) [3.2301]	3.4376*** (1.7101) [2.0102]	3.3240*** (1.5398) [2.1587]

Note: Model 1 incorporates the Uncertainty (VIX) predictor while Model 2 is the Historical Average. Thus, the former is the unrestricted model while the latter is the restricted model. *** and ** & * imply the rejection of the null hypothesis of equal forecast accuracy at 1%, 5% & 10% levels of significance, respectively. The null hypothesis of a zero coefficient is rejected if this statistic is greater than +1.282 (for a one sided 0.10 test), +1.645 (for a one sided 0.05 test) and + 2.00 for 0.01 test (for a one sided 0.01 test) (see Clark & West, 2007). Two out-of-Sample forecast horizons are considered: 10-day & 20-day ahead forecast horizons. Values in parentheses – () denote standard errors while those reported in square brackets – [] are for t-statistics.

4. Conclusion

This study aims to examine the safe haven properties of gold on some selected exogenous shocks, such as uncertainty due to the novel virus – COVID-19. For completeness, we further consider the following: (i) we carry out distinct analyses for two sub-periods of pre- and post-COVID announcement periods; (ii) we compare the safe haven potential of gold during the pandemic with that of US stocks and other precious metals; (iii) we evaluate the forecast performance of including uncertainty in the valuation of financial assets. Our results confirm the ability of gold market to safe investment options during the pandemic than other financial assets such as those considered in this study. The results of this exercise further enhance the dexterity of gold as the most useful hedging financial asset that protects investors' portfolios. In other words, investors are better off shielding their investments by diversifying their portfolio to include the acquisition of gold. Finally, for financial analysts and policy makers who constantly confronted with the need to provide accurate forecasts for investment and policy decisions, this study further lends support to the inclusion of uncertainty in the valuation of stocks as well as risk-adjusted returns in order to produce better forecast outcomes. Future studies could extend the frontier of knowledge by conducting similar exercise for other countries, beyond the US market.

CRediT authorship contribution statement

Afees A. Salisu: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Software; Validation; Visualization; Writing - original draft; Writing - review & editing. IIbrahim D. Raheem: Conceptualization; Investigation; Project administration; Validation; Visualization; Writing - original draft; Writing - review & editing. Xuan Vinh Vo: Conceptualization; Funding acquisition; Resources; Visualization; Writing - original draft; Writing - review & editing.