Similarity-based health risk prediction using Domain Fusion and electronic health records data

Abstract

Electronic Health Record (EHR) data represents a valuable resource for individualized prospective prediction of health conditions. Statistical methods have been developed to measure patient similarity using EHR data, mostly using clinical attributes. Only a handful of recent methods have combined clinical analytics with other forms of similarity analytics, and no unified framework exists yet to measure comprehensive patient similarity. Here, we developed a generic framework named Patient similarity based on Domain Fusion (PsDF). PsDF performs patient similarity assessment on each available domain data separately, and then integrate the affinity information over various domains into a comprehensive similarity metric. We used the integrated patient similarity to support outcome prediction by assigning a risk score to each patient. With extensive simulations, we demonstrated that PsDF outperformed existing risk prediction methods including a random forest classifier, a regression-based model, and a naïve similarity method, especially when heterogeneous signals exist across different domains. Using PsDF and EHR data extracted from the data warehouse of Columbia University Irving Medical Center, we developed two different clinical prediction tools for two different clinical outcomes: incident cases of end stage kidney disease (ESKD) and severe aortic stenosis (AS) requiring valve replacement. We demonstrated that our new prediction method is scalable to large datasets, robust to random missingness, and generalizable to diverse clinical outcomes.

1. Introduction

The universal adoption of electronic health records (EHR) provides access to clinical data of unprecedented volume and variety. This rich information awaits utilization for real time clinical decision-support. Conventional approaches in predictive modeling used to build clinical decision-support tools start with feature selection based on domain knowledge, which could be biased. For example, one of the most widely used chronic kidney disease (CKD) progression models uses a simple linear combination of age, sex, estimated glomerular filtration rate (eGFR), and urinary albumin to creatinine ratio (UACR) [1]. This CKD prediction model and other similar existing prediction models were built on a clinically relevant set of features selected either based on clinical expertise, statistical significance, or both. As evidenced from recent scientific research, many human disorders share a complex etiologic basis and exhibit correlated disease progression. Therefore, it is desirable to consider a more comprehensive, agnostic approach that incorporates the entirety of patient data.

One frequently sought goal by using EHR data is to assess patient similarity [2–15]. The objective of patient similarity assessment is to quantify the similarity between any pair of patients according to their retrospective information under a specific clinical context. For example, patients who have “similar” clinical characteristics may have similar disease risk projections or diagnoses. Similarity-based case identification could help stratify patients, enable more efficient diagnoses, and facilitate more effective treatment choices. Despite some successes, current similarity approaches do not use comprehensive patient information, but rather only a fraction of available data, such as only selected clinical characteristics or only genomic information for patient subtyping [9]. A recent approach combined clinical and drug similarity analytics for personalization of drug prescribing [10]. Another recent research developed a disease phenotyping method with tensor factorization using co-occurrence information of diagnoses and medications [16]. Phenotyping algorithms use EHR data to identify patients with specific clinical conditions or events. These include rule-based algorithms to identify patients with chronic kidney disease (CKD) [17], supervised models including logistic regressions and random forest to identify patients with type 2 diabetes [18], and dimensionality-reduction methods such as a tensor factorization approach to identify patients with hypertension and type 2 diabetes [16]. Several recently developed phenotyping methods also consider patient similarities, such as a pipeline that defines patient similarities using concatenated patient concepts in Unified Medical Language System (UMLS) which was applied to ciliopathies phenotyping [19]. However, there are currently few methods that use all available patient data to more comprehensively define “similar patients” for predictive outcome modeling in chronic complex conditions.

A simple way to use comprehensive patient data is to define patient similarity using patient information concatenated. However, the patient information from different domains might be unbalanced. For example, the number of unique drugs, i.e., number of features, in the domain of drug exposures might be very different from the number of unique procedures in the domain of medical procedures. Thus, when using features from these unbalanced domains, simply concatenating all features to calculate patient similarity may be ineffective in capturing signals when these potentially much stronger signal features from a small domain might be diluted.

In this paper, we developed a unified machine learning framework for clinical outcome prediction called Patient similarity based on Domain Fusion (PsDF). PsDF performs patient similarity assessment independently on each available domain data, such as laboratory tests, ICD based diagnoses, drug exposures, medical procedures, and demographic information, and fuses affinity information from all available domains to achieve a comprehensive metric for quantifying patient similarity, which is further used to perform a clinical outcome prediction.

We conducted extensive simulation studies and demonstrated a much-improved prediction performance of the PsDF algorithm over several competing methods including a random forest classifier and a regression-based model both using all features from different domains simultaneously, and a naïve similarity method concatenating all features from different domains.

With EHR data extracted from the data warehouse of Columbia University Irving Medical Center (CUIMC), we demonstrated better performance of PsDF over the competing methods in predicting two independent clinical outcomes, incident end stage kidney disease (ESKD) and incident aortic stenosis (AS) requiring valve replacement. We used comprehensive patient information collected prior to the occurrence of the ESKD and AS outcomes, including 1) laboratory tests, 2) ICD based diagnosis history, 3) drug exposures, 4) medical procedures and 5) demographic information.

Because real-life EHR datasets often have incomplete patient records, we also explored the prediction robustness of PsDF when random missingness was introduced to the test set data. To do so, we randomly masked a percentage of EHR records by setting them to missing, similar to prior studies [20–22]. Our results indicate that when the percentage of randomly masked observations increases, the prediction performance of PsDF is stable while that of the competing methods decreases fast, indicating that one of the major advantages of PsDF is its robustness to data missingness.

2. Methods

2.1. The PsDF algorithm

There are three steps in the PsDF clinical outcome prediction. In Step 1, for each domain of patient data (e.g., laboratory tests, diagnosis history, etc.), a patient similarity matrix with pairwise similarity measures between any given pairs of patients is constructed. In Step 2, patient similarity matrices from different domains of patient data are fused using a nonlinear combination method. In Step 3, the fused patient similarity matrix is served as a clinical outcome prediction tool, through which a patient similarity risk score is assigned to each patient in the test set using a simple logistic regression model that is pretrained on the training set.

Note that all features of a specific domain of patient data are first standard-normalized to have a zero mean and a unit of one standard deviation.

2.1.1. Step 0: EHR patient’s snapshot data

Patients’ EHR data were extracted from the data warehouse of CUIMC. For a specific clinical condition, such as incidence of ESKD between year 2006 and 2016, in order to develop a prospective prediction model, we used a pseudo-prospective study design, where we used a snapshot of patients’ retrospective EHR information from year 2006 and prior. This snapshot of EHR data includes five patient data domains: 1) laboratory tests, 2) ICD based diagnosis history, 3) drug exposures, 4) medical procedures and 5) demographic information.

We next converted EHR snapshot data (2006 and prior) into five data matrices representing information from these five domains. Features in the four clinical domains were coded as binary features with 1 indicating a patient ever had a specific condition in 2006 and prior. Specifically, for one patient domain, e.g., drug exposures, if we have total N patients and total P possible drugs, we generated a drug exposure matrix Y^N×P with each row representing a patient and each column representing a drug exposure. We then considered binary status of each of the P possible drugs. For example, if there is a record in EHR data that a patient had ever taken Aspirin in 2006 and prior, and another record of patient ever taking Ibuprofen in 2006 and prior, then in the drug exposure matrix Y^N×P, there would be one column indicating whether Aspirin had ever been taken (taken will be coded as 1) and another column indicating whether Ibuprofen had ever been taken, in 2006 and prior. We assume that a patient was not on a specific medication if there is no record in the EHR snapshot 2006 and prior. Other three patient domains, ICD based diagnosis history, laboratory tests, and medical procedures were similarly processed to generate corresponding data matrices. In the two clinical applications on incident ESKD and AS, we implemented a random mask procedure which randomly changes a certain percentage of observed records (coded as 1) to missing or unobserved (coded as 0) to explore the robustness of PsDF to missing data. Similar procedures have been applied to evaluate methods when outcomes were randomly changed to be unknown [22]. For the single patient domain, demographic information has two binary variables, gender and race (coded as white or non-white).

2.1.2. Step 1: Constructing a patient similarity matrix for individual patient domain data

Before calculating patient similarities from the data matrix Y^N×P, a normalization procedure is performed to normalize each column to have mean 0 and standard deviation 1. Denote X^N×P as the normalized matrix, for each domain of patient data, we calculate the distance between patients i and j as follows:

$$d\left({\mathit{x}}_i,{\mathit{x}}_j\right)=\Vert {\mathit{x}}_i-{\mathit{x}}_j\Vert =\sqrt{\sum _{p=1}^P{\left(x_{ip}-x_{jp}\right)}^2}.$$ (1)

A similarity matrix of a patient cohort with sample size N is an N by N symmetric matrix S^N×N, where the entry s_ij represents the similarity measure between patients i and j. A similarity measure quantifies the affinity between two patients. For example, a typical similarity measure can be the reciprocal of a Euclidean distance s_ij = −d(x_i, x_j). It can also be a more complex measure of similarity if we use other transformation such as the radial basis function (RBF) kernel:

$$\frac{s_{ij}^{(RBF)}=\frac{1}{\sqrt{2\pi {\eta }_{ij}^2}}\exp \left(\frac{-d^2\left({\mathit{x}}_i,{\mathit{x}}_j\right)}{2{\eta }_{ij}^2}\right)}{{\eta }_{ij}=\frac{\mu }{3}\left[mean\left(d\left({\mathit{x}}_i,N_i\right)\right)+mean\left(d\left({\mathit{x}}_j,N_j\right)\right)+d\left({\mathit{x}}_i,{\mathit{x}}_j\right)\right]},$$ (2)

where μ is a hyperparameter, N_i denotes the set of nearest neighbors of patient i with a pre-fixed size of K, mean(d(x_i, N_i)) is the average distance between patient i and the neighbors N_i, and η_ij is a scaling parameter that adapts to the density of neighbor sets so that a smaller η_ij is used in a denser neighbor set.

The above steps can be similarly applied to each of the individual data domain such as laboratory tests, ICD based diagnosis history, and demographic information etc., and obtain multiple patient similarity matrices. Because there are different numbers of features in different patient domains, the scales of similarity matrices S might be different. Therefore, a normalization on similarity matrices is needed. For similarity measures s_ij between patients i and j, we normalize as follows:

$$\begin{gathered} s_{ij}=\begin{array}{c}\{\frac{s_{ik}^{(RBF)}}{2{\sum }_{k\ne i}^N{s}_{ik}^{(RBF)}},j\ne i\end{array} \\ \frac{\frac{1}{2},j=i}{s_{ij}=\frac{1}{2}(s_{ij}+s_{ji})} \end{gathered}$$ (3)

The normalized similarity measures have a range (0, 1). We denote the normalized similarity matrix as S^N×N. These similarity matrices can be considered as similarity networks for patients whose nodes are patients and edges are similarity measures between any given pair of patients.

2.1.3. Step 2: Fusing patient similarity matrices from multiple patient domains data

The algorithm that fuses networks was originally developed in the field of computer vision [23–25]. For -omics research, the Similarity Network Fusion (SNF) method was recently developed, where individual similarity networks from individual types of omics data were iteratively updated using information from other types of omics data through a nonlinear combination method [25]. We recently developed an annotation boosted SNF to further improve the clustering performance when association signals were used as weights on different types of omics data before fusing them into a fused similarity matrix [26]. Here we applied this nonlinear combination method to integrate patient similarity matrices from different domains of patient data.

Specifically, for the m^th domain of patient data, we first define a global similarity network P^(m) and a local similarity network Q^(m) using the patient similarity network S^(m) defined in Step 1. The entries of the global similarity network P^(m) are defined as the normalized entries in S^(m) introduced in equation (3), and the entries of the local similarity network Q^(m) are defined as the normalized similarities between patient i and his/her neighbors N_i as defined in Step 1, and 0 between patient i and subjects outside of his/her neighbors N_i. This local similarity network Q^(m) is constructed with an assumption that local similarities might be more reliable than remote ones.

The global similarity networks P^(m), m = 1,…, M for M domains of patient data are then smoothened through the parallel interchanging diffusion process [25] that updates the global similarity network P^(m) using the local similarity networks Q^(m) and the global similarity networks of other domains of patient data. Consider the case where there are only two domains of patient data. We have global similarity networks P⁽¹⁾, P⁽²⁾ and local similarity networks Q⁽¹⁾, Q⁽²⁾, respectively. To update P⁽¹⁾, P⁽²⁾ iteratively, let initial condition P⁽¹⁾(t = 0) = P⁽¹⁾ and P⁽²⁾(t = 0) = P⁽²⁾ for the first iteration, the diffusion process is described as follows:

$$P^{(1)}(t+1)=Q^{(1)}\times P^{(2)}(t)\times {\left(Q^{(1)}\right)}^T$$ (4)

$$P^{(2)}(t+1)=Q^{(2)}\times P^{(1)}(t)\times {\left(Q^{(2)}\right)}^T.$$ (5)

After t iterations, the integrated similarity network is calculated as the average of the two updated globe similarity networks P^(fused) = (P⁽¹⁾(t) + P⁽²⁾(t)) /2. When there are more than two domains of patient data, the diffusion process Eqs. (4) and (5) can be expressed as:

$$P^{(m)}=Q^{(m)}\times \frac{{\sum }_{k\ne m}{P}^{(k)}}{M-1}\times {\left(Q^{(m)}\right)}^T,m=1,\cdots ,M.$$ (6)

2.1.4. Step 3: Building a prediction tool

With a training set where samples’ binary outcomes of interest are known (e.g., case vs. control), our goal is to predict the binary outcomes for samples in a test set. To do so, we first calculate the fused patient similarity network P^(fused) with all samples in the training and test sets together. Note that in calculating P^(fused), neighbors for the local similarity network of a test sample are from the training data only. Hence similarity measures of a test sample would not be affected by other test samples.

Using the training set, we assign a similarity t-score to each sample in the training set using the leave-one-out method as follows. For a case sample in a training set with n₁ cases and n₂ controls, this case sample’s similarity t-score is the two-sample t-test statistic comparing its similarity with other n₁ − 1 cases, and its similarity with all n₂ controls. Similarly, for a control sample in a training set with n₁ cases and n₂ controls, this control sample’s similarity t-score is the two-sample t-test statistic comparing its similarity with all n₁ cases, and its similarity with other n₂ − 1 controls. After all samples in the training set are assigned a similarity t-score, we fit a simple logistic regression of the known case-control status on the assigned similarity t-scores. This logistic regression model serves as a similarity-based prediction model, i.e., a classifier that can be used to predict test samples’ case-control status.

To predict case-control status of samples in the test set using the aforementioned similarity-based prediction model, we similarly assign samples in the test set a similarity t-score from a two-sample t-test statistic comparing similarities between a test sample and all n₁ cases in the training set, and similarities between the test sample and all n₂ controls in the training set. After assigning similarity t-scores to the test samples, we can then calculate the probability of each test sample being a case using the fitted logistic regression classifier.

We evaluate our method using receiver operating characteristic (ROC) curve and area under the curve (AUC), as well as the F₁-score, F₂-score, recall and precision. The F_β score is a weighted harmonic mean of recall and precision with the formula:

$$F_{\beta }=\frac{\left(1+{\beta }^2\right)Precision\times Recall}{{\beta }^{2}Precision+Recall},$$ (7)

where β represents relative importance such that recall is considered β times as important as precision. F₁-score considers equal weights for recall and precision while F₂-score considers recall twice as important as precision [27]. The threshold for the probability of being a case is set at 0.5 for F₁-score, F₂-score, recall and precision.

2.2. Simulation studies

We conducted extensive simulation studies to investigate the prediction performance of PsDF and compared to that of the three competing methods.

2.2.1. Simulation settings

In our simulation studies, we considered three different simulated data domains. Domains 1 and 2 have a number of binary features and mimic typical domains based on medical records, e.g., indicating if a drug exposure or a medical procedure is recorded in EHR. Domain 3 has a single continuous feature. We considered a binary outcome. For each simulated binary feature, we generated measures from two different Binomial distributions for cases and controls with probability of success p_case and p_control, respectively. All features in Domain 1 are set to have large signals with the same p_case1 and p_control1. All features in Domain 2 are set to have small signals with the same p_case2 and p_control2. We considered two simulation scenarios.

The first scenario investigates the impact of imbalance among different domains where we fixed the number of features in Domain 1 at 5, and ranged number of features in Domain 2 from 10 to 200. We set p_control1 = 0.1, and p_case1 = 0.4 for features of large effect sizes in Domain 1 and p_control2 = 0.1 and p_case2 = 0.12 for features of small effect sizes in Domain 2. For the continuous feature in Domain 3, we generated measures from a Gaussian distribution with means 0.1 and 0 for cases and controls, and with the standard deviation (SD) 1 for both groups.

The second scenario investigates the influence of nonlinear signals, such as variance signals, where we ranged SD of the single feature in Domain 3 for cases from 0.2 to 1 when the effect sizes of all other features are the same as those in the first scenario. In addition, the number of features in Domain 2 is fixed at 10. In all simulation settings, we set the scaling parameter μ as 0.5, and the size of neighbors K as N/2 in Eq. (2), where N is the sample size of a training set.

The above simulation settings with p_case > p_control mimic data in real EHR domains when cases usually have more records than controls. In order to evaluate PsDF more comprehensively, we also considered parallel scenarios when p_case < p_control, i.e., when binary features are more frequent in controls than in cases, and we set p_control1 = 0.5, p_case1 = 0.2 for features in Domain 1 and p_control2 = 0.5, p_case2 = 0.48 for features in Domain 2.

We simulated a population pool of 5000 cases and 5000 controls. We considered two designs with 1:1 case/control ratio and 1:5 case/control ratio when the latter with more controls is more common in EHR data. With the 1:1 case/control ratio, we randomly selected 200 cases and 200 controls as the training set, and another 100 cases and 100 controls as the test set. Therefore, for the training set, Domain 1 is a data matrix $Y^{400\times p_1}$, Domain 2 is a data matrix $Y^{400\times p_2}$ and Domain 3 is a data matrix Y^400×1. Data matrices of a test set are similar. With the 1:5 case/control ratio, we randomly selected 200 cases and 1000 controls as the training set, and another 100 cases and 500 controls as the test set. We repeated the simulation procedure 100 times and obtained average AUCs, F₁-scores, F₂-scores, recalls and precisions with their 95% confidence intervals (CIs).

2.2.2. Competing methods

We considered three competing methods, a random forest classifier and a logistic regression both using all features in Domains 1, 2 and 3 as predictors to classify case and control groups, and a naïve similarity method where the patient similarity matrix S^N×N is calculated using concatenated features in Domains 1, 2, and 3 with applying Eqs. (1) and (2) and the same prediction step as described in PsDF Step 3.

3. Results

3.1. Simulation studies

We show the average AUCs, F₁-scores, F₂-scores, recalls and precisions when the threshold for the probability of being a case is 0.5 and their corresponding 95% CIs on test sets for the two simulation scenarios, 1) increasing the number of features in Domain 2, and 2) increasing the effect size of the variance signal of the single feature in Domain 3. These two simulation scenarios were done in parallel for two different settings, when cases have more EHR records than controls and when cases have fewer EHR records than controls. Finally, all simulation studies were done for the 1:1 case/control ratio (Fig. 1) and the 1:5 case/control ratio (Fig. 2).

Fig. 1.

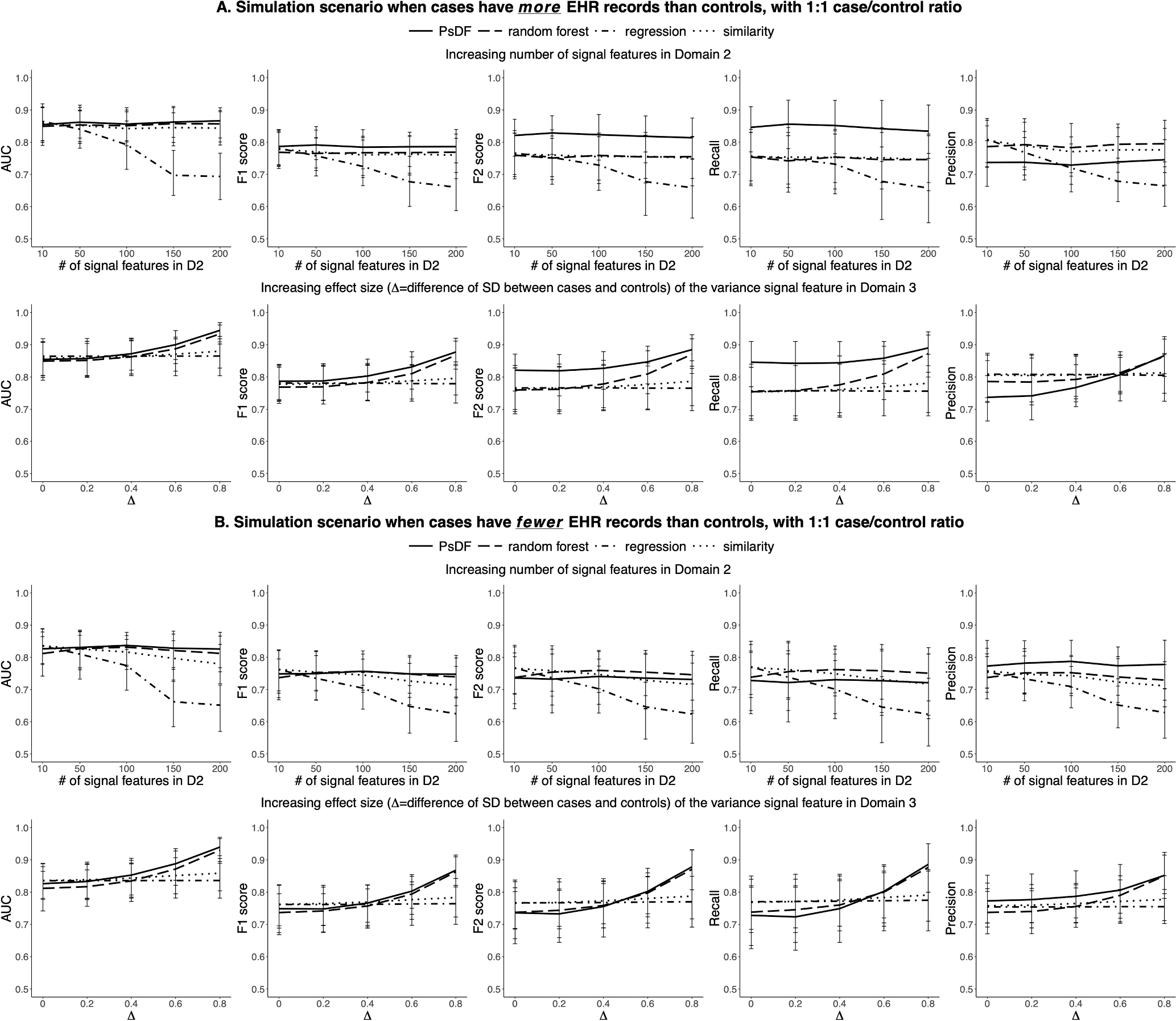
For the 1:1 case/control ratio, simulation results of prediction performance of the PsDF algorithm, the random forest classifier, the logistic regression and the naïve similarity method, under two simulation scenarios: 1) increasing number of signal features in Domain 2, and 2) increasing effect size of the variance signal feature in Domain 3. Part A displays results when cases have more EHR records than controls. Part B displays results when cases have fewer EHR records than controls.

Fig. 2.

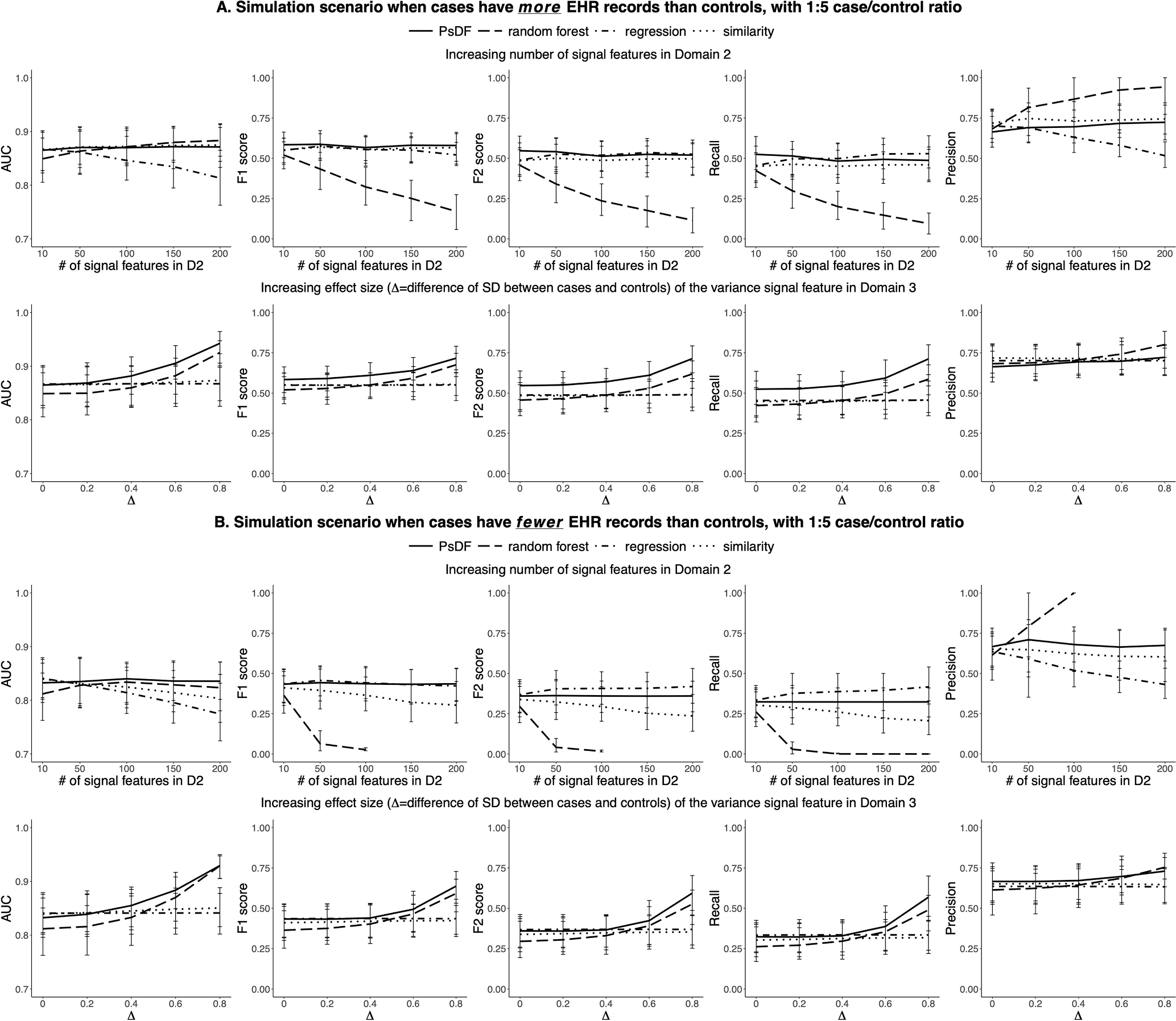
For the 1:5 case/control ratio, simulation results of prediction performance of the PsDF algorithm, the random forest classifier, the logistic regression and the naïve similarity method, under two simulation scenarios: 1) increasing number of signal features in Domain 2, and 2) increasing effect size of the variance signal feature in Domain 3. Part A displays results when cases have more EHR records than controls. Part B displays results when cases have fewer EHR records than controls.

For the 1:1 case/control ratio and when cases have more EHR records than controls (Fig. 1A), when the number of signal features in Domain 2 is comparable (the number of signal features in Domain 2 is 10) to that in Domain 1, all four methods have similar prediction performance in terms of AUCs and F₁-scores, with PsDF having slightly higher F₁-scores. In addition, PsDF has the highest F₂-scores because its recalls are also the highest among four methods and F₂-score weights more on recalls. As the number of signal features in Domain 2 increases from 10 to 200, AUCs, F₁-scores, and F₂-scores of the logistic regression method quickly decrease as expected, while those of the other three methods are hardly affected. This is because regression methods often require certain ratios of sample size to a number of features in models in order to achieve a good model fit. When cases have fewer EHR records than controls (Fig. 1B), AUCs, F₁-scores, and F₂-scores of the naïve similarity method slowly decrease. This is because the effective effect sizes of signal features in Domain 2 (p_control2 = 0.5 and p_case2 = 0.48) in this setting are much smaller than that in the setting of Fig. 1A (p_control2 = 0.1 and p_case2 = 0.12), thus these small signal features become “noise features” to some extent. Therefore, for the naïve similarity method, as Domains 1 and 2 become more imbalanced, the contribution of 5 signal features with strong effect sizes in Domain 1 become weakened with the increasing number of very small effect size features in Domain 2 when the total number of features across all three domains are concatenated. Note that, PsDF and random forest are not affected.

When we increase the effect size of the single continuous feature with variance signal in Domain 3 while keeping the number of features in Domains 1 and 2 at 5 and 10, respectively (Fig. 1A and Fig. 1B), AUCs, F₁-scores and F₂-scores of PsDF and random forest increase rapidly, while those of the logistic regression and the naïve similarity methods do not change much. This is also expected as regression methods cannot capture variance signals and the single variance signal feature in Domain 3 will be similarly diluted in the concatenated pool of signal features across the three domains for the naïve similarity method.

For the 1:5 case/control ratio (Fig. 2), the overall patterns are similar to that of the 1:1 case/control ratio, with two noticeable differences: 1) When increasing the number of signal features in Domain 2, the performance of logistic regression does not decrease too much. This is because the total number of training samples (200 cases and 1000 controls) are large enough. 2) F₁-scores and F₂-scores of random forest decrease quickly when the number of signal features with small effect sizes in Domain 2 increases as random forest tends to classify most samples as controls. When cases have fewer EHR records than controls (Fig. 2B), i.e., when the effective effect sizes of signal features are even smaller, or very close to noises, random forest may classify very few samples or even 0 samples as cases, resulting in a very low recall or even 0 recall, thus and an unavailable precision. The performance of PsDF is not affected by the 1:5 case/control ratio.

3.2. Clinical studies

3.2.1. ESKD prediction tools

More than 47,000 Americans die from chronic kidney disease (CKD) annually [28], yet the disease often has no symptoms in early stages and frequently goes undetected until it is advanced. In fact, less than 10% of patients affected with early CKD (stages 1–3), and only half (52%) of those with severe CKD (stage 4) are aware of having a kidney problem [29]. Kidney disease usually gets worse over time, and although treatment has been shown to delay progression, any preventive strategies are only effective when implemented early. When the kidney dysfunction reaches the level of “failure” (i.e., end stage kidney disease, ESKD), dialysis or kidney transplant are needed for survival. This state is irreversible and associated with accelerated cardiovascular disease and high mortality [30]. This highlights a great need for early diagnosis of CKD and identification of patients at risk of progression to ESKD, motivating our use of CKD as the first case study for PsDF.

We applied the PsDF algorithm and the three competing methods to build ESKD prediction tools and compared their performance. We predicted incident ESKD between 2006 and 2016 using comprehensive EHR data collected in years 2006 and prior. We used two different inclusion criteria to define eligible patients, a less stringent criterion that only requires patients to have demographic domain; and a more stringent criterion that requires patients to have demographic domain as well as records across all four EHR domains (Section 3.2.1.1).

We conducted a sensitivity analysis to evaluate the robustness of PsDF and the three competing methods by randomly masking a percentage of observed EHR records in the test set by setting them to “missing”. We masked 5–50% records in the test set with the increment of 5% to generate new test sets with more missing data than that in the training set.

3.2.1.1. EHR data preprocessing for ESKD prediction.

We defined ESKD as chronic kidney disease (CKD) stage 5 (estimated glomerular filtration rate <15 mL/min/1.73 m²) or CKD requiring kidney transplant, or any form of chronic dialysis. Among all patients in the CUIMC EHR data warehouse as of year 2006, 386,297 patients had sufficient data to define their CKD status. Among those, there were a total of 11,802 cases of ESKD and 374,495 non-ESKD patients (normal renal function or CKD stage 1–4). Among 374,495 non-ESKD patients, as of year 2016, 2080 developed incident ESKD between 2006 and 2016, 353,295 remained non-ESKD, and the remaining 19,120 had status unknown. We considered those 2080 patients who were non-ESKD in 2006 but reached ESKD before 2016 as our incident ESKD cases, and those 353,295 non-ESKD patients who remained non-ESKD between 2006 and 2016 as our controls. Our data processing pipeline is summarized in Fig. 3. The comprehensive patient data included: 1) laboratory tests, 2) ICD based diagnosis history, 3) drug exposures, 4) medical procedures, and 5) demographic information with gender and race (white vs. non-white).

Fig. 3.

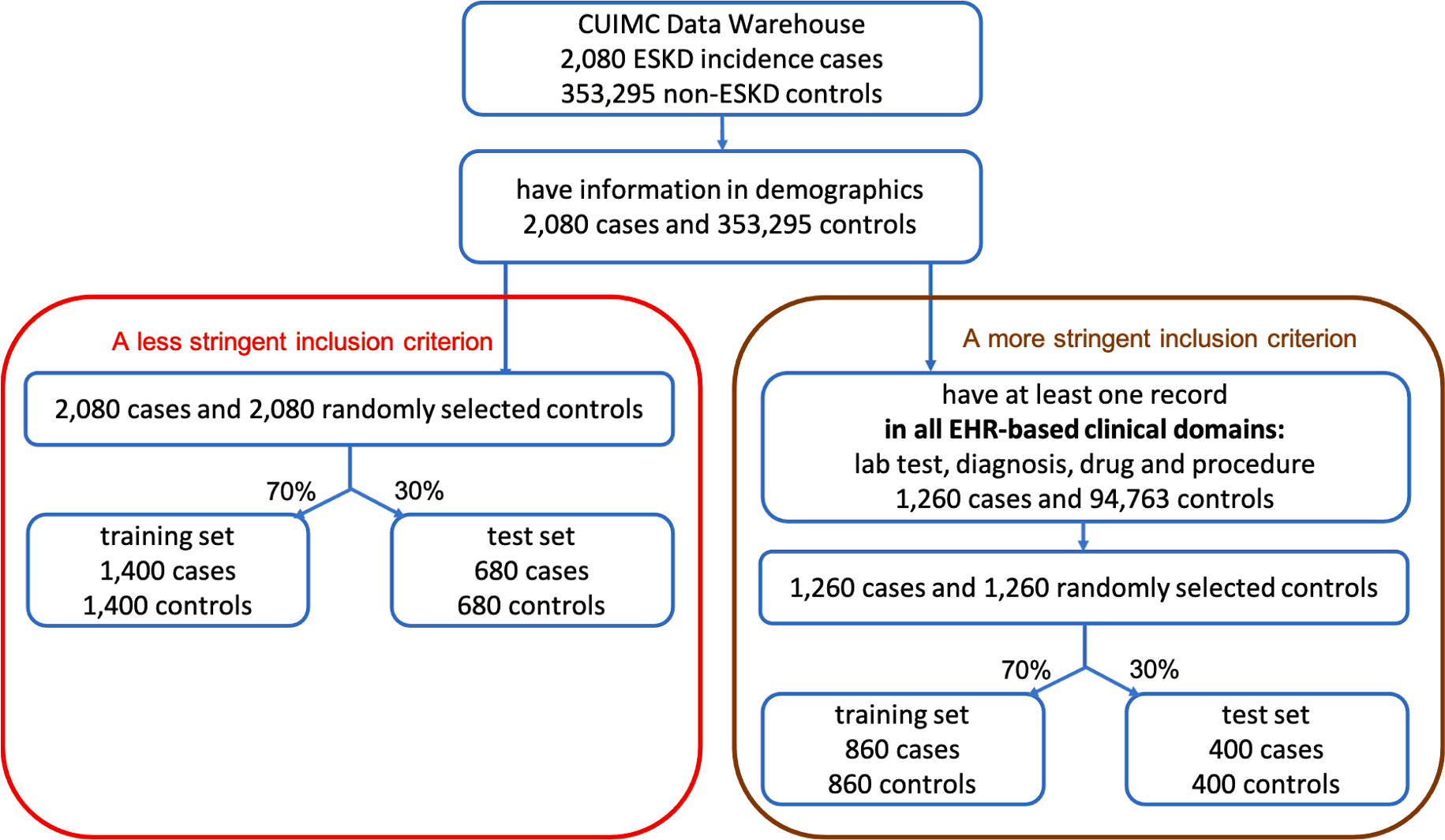
ESKD data preprocessing pipeline with two different inclusion criteria to define eligible patients.

After requiring all patients to have demographic data, we had 2080 ESKD cases and 353,295 non-ESKD controls. We then applied two different inclusion criteria on the four EHR domains to define eligible patients in the study: 1) the less stringent inclusion criterion which does not have any requirement on EHR domains; 2) the more stringent inclusion criterion which requires patients to have records across all four EHR domains. Fig. 3 displays the data preprocessing pipeline and the final sample sizes with the two inclusion criteria.

A less stringent inclusion criterion

Patients were included if they had demographic information, resulting in 2080 ESKD patients and 353,295 non-ESKD controls. We then randomly selected 2080 patients among 353,295 non-ESKD controls to create a balanced case control design, as it is known that a balanced design helps to reduce variances of estimated parameters in logistic regression models [31]. We split 2080 ESKD cases and 2080 non-ESKD controls into two cohorts, one as the training set with 1400 ESKD cases and 1400 non-ESKD controls, the other as the test set with 680 ESKD cases and 680 non-ESKD controls to test the prediction performance of PsDF and the three competing methods.

A more stringent inclusion criterion

Patients were included if they had demographic information as well as records in all four EHR domains, resulting in 1260 ESKD patients and 94,763 non-ESKD controls. We then randomly selected 1260 patients among the 94,763 non-ESKD controls to make a balanced case control design. We similarly split 1260 ESKD cases and 1260 non-ESKD controls into two cohorts, one as the training set with 860 ESKD cases and 860 non-ESKD controls, the other as the test set with 400 ESKD cases and 400 non-ESKD controls.

In order to investigate the model performance under an unbalanced case-control design, we also considered a 1:5 case/control ratio. That is, in addition to the previously selected controls, we randomly selected another 8320 controls (four times of 2080 cases) for the less stringent inclusion criterion, and another 5040 controls (four times of 1260 cases) for the more stringent inclusion criterion. For each criterion, we split these additional control samples into two groups with ratio 70% and 30%, then added them into the training set and test set accordingly.

3.2.1.2. Feature selection using LASSO regression and random forest.

Because of the large number of features in EHR domains, we included a screening step to pre-select potentially relevant features using LASSO regression and random forest in order to capture both linear and nonlinear features for prediction. We used the training set with 1:1 case/control ratio for this step.

We applied the stability selection using LASSO regression on each domain separately. Specifically, we resampled a subset of size N/2 of the training set with sample size N without replacement. We then applied LASSO regression on the subset and obtained a set of selected features of non-zero regression coefficients. We repeated this subsampling 1000 times and obtained the selection probability for each feature out of the 1000 subsampling. We then selected features with selection probability greater than 0.6. With the training set defined by the less stringent inclusion criterion, we selected 19 features out of 1123 laboratory tests, 23 of 7980 diagnostic history features, 18 of 3936 drug exposure features, 34 of 6324 medical procedure features, as well as gender and race out of demographic variables. With the training set defined by the more stringent inclusion criterion, we selected 26 laboratory tests, 26 diagnostic history, 26 drug exposures, 23 medical procedures, as well as gender and race.

We then applied random forest on the training set to select features with nonlinear signals for each domain separately and selected features with high importance, defined as mean decrease accuracy. We used a threshold of greater than 0.1 for the importance measure. With the training set defined by the less stringent inclusion criterion, we selected 23 laboratory tests, 66 diagnostic history, 45 drug exposures, 42 medical procedures, and gender. With the training set defined by the more stringent inclusion criterion, we selected 24 laboratory tests, 31 diagnostic history, 31 drug exposures, 21 medical procedures, as well as gender and race.

We unionized the features selected by LASSO and random forest, which led to 204 features in total for the dataset of less stringent inclusion criterion and 145 features in total for the dataset of more stringent inclusion criterion. The detailed information of selected features is included in the Supplementary Material B.

3.2.1.3. Comparison of the four prediction methods.

To compare the prediction performance of the four methods using the test set, we applied bootstrapping 1000 times on the test set and obtained average AUCs, F₁-scores, F₂-scores, recalls and precisions when the threshold for the probability of being a case is set at 0.5, as well as their 95% CIs. In addition, we conducted a sensitivity analysis where we masked certain percentages of observations to investigate the robustness of PsDF and the three competing methods to missing data, as previously explained. Fig. 4 summarizes prediction performance of the developed ESKD prediction tools from two inclusion criteria for the 1:5 case/control ratio. The results for the 1:1 case/control ratio are included in the Supplementary Material A Figure S1. The results are very similar to that of the 1:5 case/control ratio.

Fig. 4.

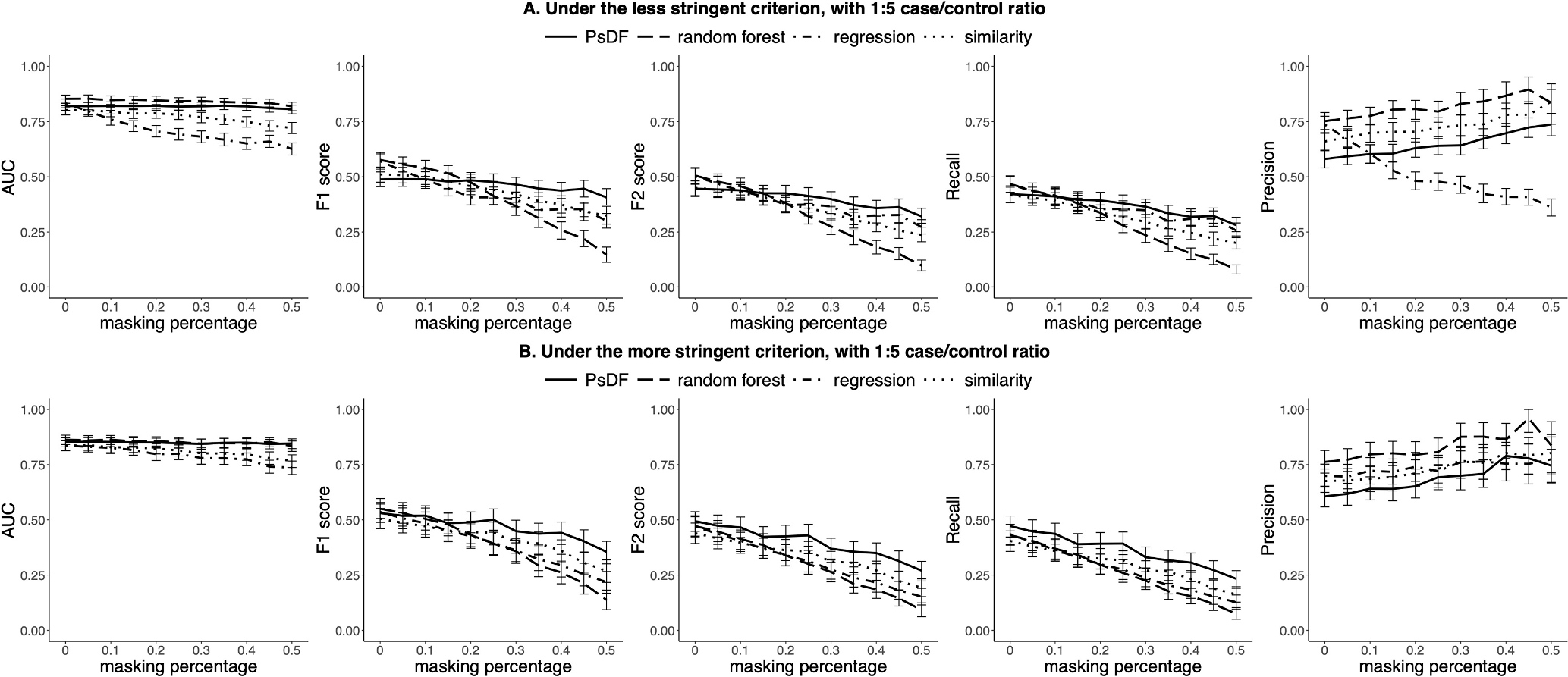
For the 1:5 case/control ratio, prediction performance of the ESKD prediction tools built by the PsDF algorithm, the random forest classifier, the logistic regression and the naïve similarity method when the masking percentage p_mask increases, under two different inclusion criteria: A) the less stringent criterion, and B) the more stringent criterion.

In general, both PsDF and random forest outperform logistic regression and the naïve similarity method in terms of AUCs (Fig. 4). Without missingness (p_mask = 0), AUCs of PsDF, random forest and logistic regression are comparably high, at approximately 0.85 with overlapping 95% CIs. When the robustness of the four methods is tested against the variable degree of missingness, AUCs drop dramatically for the logistic regression and the naïve similarity methods, while F₁-scores and F₂-scores drop quickly for random forest, with increasing masking percentage (p_mask). In contrast, AUCs, F₁-scores and F₂-scores are all relatively stable for the PsDF method, demonstrating a clear advantage of this method over the other three competing methods.

We also note that the ESKD prediction tool developed by PsDF has higher recalls and lower precisions than those of the other three competing methods when the threshold for the probability of being a case is set at 0.5. Because ESKD cases usually have more EHR records than non-ESKD controls, this pattern resembles the one observed in the simulation studies when cases were set to have more EHR records than controls (Fig. 1A). We also observed decrease in recalls with increasing missingness for all four methods, however, the recalls of PsDF decrease much slower than those of the other three methods, while the recalls of random forest decrease dramatically, similar as the patterns observed in simulation studies.

As there are only limited geocoding information available for a small portion of CUIMC patients, to demonstrate that PsDF is designed to fuse all available domains, we repeated the construction of the ESKD prediction tools adding the geocoding domain. We updated the samples selection for the training and test sets accordingly. There are two continuous variables available for the geocoding domain, median household income in dollars and distance to the nearest major road in meters. Other five domains are the same as described in Section 3.2.1. The patterns of AUCs, F₁-scores, F₂-scores, recalls and precisions of the ESKD prediction tools are similar to those with 5 domains. Full description of the construction procedure and results is included in the Supplementary Material A.

3.2.2. AS prediction tools

Similar to kidney disease, the natural history of aortic stenosis (AS) progresses through a prolonged asymptomatic period prior to the development of symptomatic disease that requires valve replacement. Although there is an average rate of reduction of valve area quoted from epidemiologic studies, there are some patients who undergo rapid progression of disease and others who have minimal to no progression over a similar time frame. The targeted use of surveillance ultrasound to monitor progression of AS and to determine when valve replacement should occur could reduce unnecessary medical spending and help direct limited resources to patients who need them most. The application of PsDF to identify patients at high risk of disease progression may further facilitate planning of a valve replacement procedure. We therefore applied PsDF and the three competing methods to build AS prediction tools. The patterns of AUCs, F₁-scores, F₂-scores, recalls and precisions are similar to those observed for the prediction of ESKD. Full description of the methods and results is included in the Supplementary Material A.

4. Discussion and conclusions

We developed Patient similarity based on Domain Fusion (PsDF), a novel framework for clinical outcome prediction using comprehensive patient data. The PsDF method integrates similarity information from multiple data domains into a comprehensive similarity measurement that can be subsequently used to predict important clinical outcomes. In contrast to the similarity-based methods based on concatenated data, our fusion method allows for highly unbalanced data domains to be treated equally, and prevents any domain with a large number of features from dominating the prediction. Moreover, as a similarity-based method, PsDF naturally captures nonlinear signals, such as variance-based signals, and does not require a certain ratio of sample size to the number of features that is required for regression-based models. We demonstrate that PsDF is highly flexible, scalable, and makes use of the entirety of patient’s data (EHR-based as well as non-EHR-based) to define comprehensive similarity.

With extensive simulation studies, we demonstrate an improved prediction performance of PsDF over the competing methods, including random forest, logistic regression and naïve similarity methods. In the presence of nonlinear signals and when domains with unbalanced sizes exist, PsDF outperforms the competing methods through its ability to preserve strong signals, accumulate weak signals, and capture nonlinear effects.

In two clinical application studies, we also demonstrate that PsDF is more robust to random missingness compared to random forest, logistic regression or naïve similarity methods. This is an important advantage, given that missing data is a ubiquitous property of the real life EHR data. This advantage stems from the fact that PsDF integrates similarity information across different domains and performs prediction based on integrated relative similarity between a sample in the test set and all samples in the training set. Even though the masking procedure may change distributions of features in the test set, the relative similarity to the training set may not change much. On the other hand, random forest tends to classify almost all test samples as controls, especially with an unbalanced case-control design with more controls than cases. Logistic regression-based methods rely heavily on parameter estimates for selected features using the training set. When the features’ distributions in the test set are different from that in the training set, it is expected that the prediction performance of logistic regression would rapidly decrease. The naïve similarity method is also not expected to be robust to missingness, because the dilution of signal features with concatenation becomes even more severe when some observations are masked.

We want to emphasize that features used in the two clinical studies were pre-selected by LASSO and random forest, which favor the two competing methods, i.e., logistic regressions and random forest. Close investigation of the selected features for the ESKD prediction tools and the AS prediction tools suggests that they are clinically reasonable (Supplementary Material B). For example, in the ESKD prediction tools, “disorder of kidney and/or ureter”, “biopsy of kidney” and “acute renal failure syndrome” were selected under both less/more stringent inclusion criteria. In the AS prediction tools, “aortic valve disorder”, “cardiac complication” and “diagnostic ultrasound of heart” were selected under both less/more stringent inclusion criteria.

One limitation of the current study is that we coded all features in EHR-based domains to be binary, indicating the presence or absence of a record. We did not use cumulative counts or continuous measures of certain features, which likely led to some information loss. Another limitation is that we did not use longitudinal information embedded in patient records, nor did we consider different visit types (e.g., hospital versus ambulatory). We are currently working on extending the PsDF framework in order to make full usage of such information. We want to emphasize that the prediction performance could be further enhanced if data from more patient domains becomes available in the future, such as genetic or exposome data. The success of our two clinical application studies suggests that the framework of PsDF is highly flexible, scalable, and generalizable, and thus this method has a great potential in developing new patient similarity-based clinical prediction tools.