An agent-based model of the dual causality between individual and collective behaviors in an epidemic

Abstract

The evolution of an epidemic is strongly related to the behavior of individuals, and the consideration of cause and effect of social phenomena can extend epidemiological models and allow for better identification, prediction and control of the impacts of containment and mitigation measures. This work proposes an agent-based model to simulate the double causality that exists between individual behaviors, influenced by the cultural orientation of a population, and the evolution of an epidemic, focusing on recent studies on the COVID-19 pandemic. To do this, concepts from the social sciences are used, such as the theory of planned behavior, as well as Bayesian inference to abstract the decision-making processes involved in human behavior. A set of simulation experiments with different populations was developed to demonstrate the role that the cultural orientation of a population plays in the management of an epidemic. The results agree with the revised theory, showing that in populations that have a greater inclination towards collectivism, epidemiological indicators evolve in a better way than in those populations where the culture is individualistic. This work contributes to the field of computational epidemiology by providing a new way of including the social aspects of studied populations in agent-based models to help develop better interventions.

1. Introduction

On March 11th, the World Health Organization (WHO) declared the COVID-19 epidemic a pandemic. This disease is caused by the SARS-CoV-2 virus (Severe Acute Respiratory Syndrome). By October 2021, there were more than 242 million confirmed cases of COVID-19, including more than 4.9 million deaths, according to WHO [1]. Today, as many of the affected countries go through new waves of infections and others advance in the vaccination process, the analysis of the best measures and policies for the “new normal” becomes crucial. Actions recommended by many authorities focus on washing hands, maintaining physical distance, and taking precautions when sneezing and coughing.

Before strategies are implemented to mitigate an epidemic, it is important to consider the dual causal influences between how the disease is spreading and how people are behaving in terms of social distancing, mask-wearing, etc. [2]. Social scientists have been studying such interactions using a variety of methods [3,4], and the formulation of this agent-based model drew on this prior research.

Historically, analytical tools such as mathematical models have been published to help decision-makers understand the possible scenario effects of interventions to quell the epidemic. Some of them include the model of the theoretical behavior of an infectious disease, using the Susceptible-Infected-Susceptible (SIS) model proposed by Kermack and McKendrick [5], and the Susceptible-Infected-Recovered (SIR) model proposed by Bailey [6]. Some variations of these models have been widely used to address the behavior of epidemics, particularly in the study of COVID-19. One of them is the case of the Susceptible-Exposed-Infected-Recovered (SEIR) model, used by Yang et al. [7], Hou et al. [8], and He et al. [9].

Explicit expressions have recently been proposed to model specific aspects of an epidemic, such as the TM model presented by Turkyilmazoglu in Ref. [10] for the peak time of the fraction of infected people based on the susceptible–infectious–recovered/removed (SIR) model. In a comparison analysis, the TM model proved to have a better performance for small populations with fewer than hundreds of individuals than other approximants such as those proposed in Refs. [11,12], according to Ref. [13] while the latter showed better results for large populations. Schlickeiser and Kröger in Ref. [11] proposed an extension of the SIR model to describe the temporal evolution of subsequent waves in the particular case where a large part of the population was infected in the first wave.

In [14], the authors use and analyze an extension of the classic SEIR model that incorporates additional compartments, such as the group of vaccinated people, to simulate the COVID-19 epidemic. In this work, the authors considered a total of 7 possible compartments: S (susceptible), E (exposed), I (infectious), Q (quarantined), R (recovered), D (dead), and V (vaccinated). In a similar work, in Ref. [15], the authors extend a SEIR-based model by adding two additional compartments corresponding to the two doses required for the COVID-19 vaccine.

The above models are very useful for explaining the global dynamics of an epidemic, using a large-scale top-down approach and population-level variables. However, the evolution of an epidemic is strongly related to the behavior of individuals. In this sense, it is believed that the cause-effect consideration of social variables such as cultural orientation [16,17], risk management in decision-making [18], inequity [3], segregation and informal settlements [19], violence and the social fabric of cities [20] can enhance epidemiological models and allow for better identification, prediction and control of the impacts of containment and mitigation measures. In this work, social aspects are modeled as networks of many interacting elements or components, showing non-linear dynamics. For the study of complex systems, a variety of techniques and modeling tools from different fields can be used, including Agent-Based Modeling (ABM), a type of Computational Social Science.

ABMs use autonomous “agents” (entities) that represent individuals whose behaviors can be influenced by interactions with other agents and their environment [21]. This type of modeling has been widely used for the study of complex systems, partly thanks to the possibility of simulating aggregate behaviors that emerge from local interactions between individuals.

In the social and behavioral sciences, ABM has been applied to study different phenomena such as dynamic segregation [22], criminal justice [23], criminal gang formation [24], and the formation of ethnic and cultural patterns of violence [25]. In the area of urban studies, ABM has been used to study cities’ complexity [26], their social fabric [27] and new modes of mobility [28]. The integration of concepts and theories from the social and behavioral sciences into the study of epidemics can help to find factors that explain the phenomena that emerge during them. One of the factors that is explored in the present work is the cultural orientation of a population.

This factor describes an individual's intention to prioritize collective needs or the individual's needs. In collective societies, priority is given to the tasks that lead to the fulfillment of group objectives [29], while in individualistic societies, there is a tendency to promote the freedom of the individual instead of collective objectives [30]. Following social norms is considered a good way to respond to a crisis [31] as in the context of the current COVID-19 pandemic. Studies have shown that countries with an individualistic culture recorded higher rates of infections and deaths than those where collectivism predominates [17,32,33].

In this work, an agent-based model is proposed for the study of the dynamics of an epidemic, taking into account the cultural orientation of the population. This proposal integrates three main sub-models: (1) a model of contagion and spread of the disease in which the behavior of infections between people is described taking into account their interaction, (2) a mobility model to incorporate people's travel habits, and (3) a decision-making model based on cultural orientation where the theory of planned behavior is used to represent decision-making and implemented using Bayesian inference. Each of the sub-models is based on previous studies and together they make it possible to simulate the dynamics of an epidemic and observe the effects of individuals' preferences to comply with or ignore –according to their individual interest– the established epidemiological intervention measures. The objective is to provide a tool with which the possible effect of mitigation measures can be evaluated based on the population studied.

The sections are organized as follows: Section 2 presents a study of the state of the art of agent-based modeling for epidemics. Then section 3 includes the modeling proposal. The process of experimentation through computer simulations is shown in section 4. In section 5, the findings obtained from the simulations are discussed. Finally, the conclusions of the work are presented in section 6.

2. State of the art

2.1. Agent-based epidemiological models

Recently, due to the current health emergency, a large number of agent-based models have emerged for the specific study of COVID-19. In Ref. [34], an ABM is presented for the study of epidemic dynamics using simple behavioral rules and theoretical scenarios of population. In this work, the modeling and simulation of different scenarios for the COVID-19 evolution is well addressed; however, the author does not introduce the geographical aspects of agents and just considers homogeneous populations. In contrast, in Ref. [35] the authors use a methodology that integrates two categories of data: (1) location-specific data, which refer to the specific locations where agents can move from/to, percentage of individuals having different professions, education-related data, life expectancy, transportation, and family size; and (2) physiological data, which include the probability of a person coughing and sneezing, touching contaminated objects, hand washing, and other parameters that differ when the agent is at home, at work, or hospitalized. In Ref. [36] the authors propose a model that addresses heterogeneity in individual characteristics (sex, age, household), a method to calculate daily routines (agendas), social relationships, and behaviors. In this work, the authors present their model as a combination of five sub-models: (1) individual clinical dynamics and epidemiological status agents, (2) agent-to-agent direct transmission of the infection, (3) environmental transmission through the built environment, (4) policy design and implementation, and (5) agenda-based model of people's activities. Hackl and Dubernet in Ref. [37] propose a model that brings together two sub-models: an agent-based transport model and a basic disease dispersal model, all in the context of an urban area. In this work, the authors introduce a path to be followed by each agent on a daily basis in order to obtain information on contacts between individuals. This model is capable of capturing the agent's interactions and simulating the spread of the disease in scenarios using different transportation modes. In Ref. [38] the authors propose an ABM approach that integrates geographic information systems (GIS) to simulate the spread of a disease in an urban environment.

2.2. Cultural orientation and epidemics

In the literature, works that address the correlation between the cultural orientation of a population and the epidemiological behavior it presents can be found. A comprehensive analysis of COVID-19 data collected from 69 countries was conducted in Ref. [17]. In this study, it was found that people with an individualistic profile had a greater probability of not adhering to epidemiological prevention measures. The study in Ref. [16] considers a more detailed classification of cultural profiles; they place individuals into one of four different categories: horizontal individualist, vertical individualist, horizontal collectivist, and vertical collectivist. The study concludes by suggesting that promoting collectivism could be a way to increase commitment to efforts to reduce the spread of the disease.

2.3. Decision-making and the theory of planned behavior

Conceptualizing human decisions and behaviors is not trivial. To address this, the theory of planned behavior (TPB) is used, which can be expressed through three components: the attitude toward behavior, subjective norms, and perceived behavioral control. Attitude is related to behavior through consequences. In this sense, favorable or unfavorable attitudes are formed depending on the consequences of a given behavior. The subjective norms concept is the decision-maker's beliefs about other individuals' approval of a specific behavior. This can be the result of evaluating the normative beliefs and the motivation to behave under such norms. Normative beliefs are behavioral approvals associated with important referent individuals. The perceived behavioral control is related to the individual's confidence in his or her capability to engage in a behavior – it can be seen as the likelihood that the individual will carry out an action taking into account external factors and the individual's perception of control over them–. Finally, a value of intention is the level of individual motivation to try to engage in a specific behavior, and it can be considered as a function of the three previous TPB components. The theory of planned behavior has proven to be very useful mainly to explain decision-making related to a large number of behaviors, such as addictive behavior [[39], [40], [41], [42]], eating behavior [[43], [44], [45]], and exercising behavior [46,47]. In Ref. [18] a TPB agent-based decision-making model, Bayesian Inference (BI) and a cost-loss model are used to analyze risk perception for water management decisions.

3. Proposal

In order to provide scenarios that take into account people's individual behavior, this proposal can be described as the integration of different specific models in which each one addresses an important aspect in the dynamics of infections in a population. The incorporation of these sub-models can be seen as a way to extend the current epidemiological agent-based model, where the culture of the people is not taken into account, which, as explained previously, is very important in the management of an epidemic. While each of these sub-models in the current section is described, their combination into a single ABM is described in Appendix 8.1 using the ODD format [48], commonly used to describe and compare ABMs.

3.1. Sub-model 1: Epidemiological behavior

Modeling the behavior of a contagious disease in a community is a nontrivial task that can be approached from different points of view. However, there are two elements that will always be involved in the process of the spread of an infectious disease: (1) a population and (2) exposure to infectious material [49].

A first approach to modeling a contagious disease is to use compartments. Individuals can be classified into three basic groups or compartments: (a) susceptibles (individuals who can become infected through contact with infectious material), (b) infected (infected population that hosts the infectious material), and (c) removed (individuals removed for any of several reasons, such as death or immunity). The epidemiological process can be described through a series of time-dependent steps. A susceptible individual is exposed to infectious material through direct contact with an infected individual or through a contaminated object. The individual who has been exposed could be resistant to the invading organism, in which case it is rejected and the individual does not become infected. If s/he is not resistant, the individual becomes infected and the invading organism evolves. In a given time interval, the invading organism develops and transitions the host to the infectious state. This time is called the latency period or incubation period. This model, known as the SIR model, was originally proposed by Ref. [5], and can be represented by equation (1) showing that:

• 1.A part of the population has sufficient contact with other βN individuals every time step, transmitting the disease to them (N is the total population).
• 2.Those infected individuals leave the infected class with a rate of αI per time step.
• 3.The population is not considered to vary, except in the case where an individual dies.

$$S^{\prime }=-\beta SI$$

$$I^{\prime }=\beta SI-\alpha I$$

$$R^{\prime }=\alpha I$$ (1)

This model assumes that the disease incubation period is negligible, in such a way that an individual instantaneously becomes infected, then recovers with permanent or temporary immunity. However, it is relevant for this work to consider the time it takes for an individual to make a transition from one epidemiological state to another (transition time). In the case of the COVID-19 pandemic, it has been observed that, once the virus enters the recipient organism, an incubation period of approximately five days elapses, after which that person becomes potentially infectious [50]. Using the compartmental approach, we can assume that an individual first goes to an exposed compartment for a time equal to the incubation period before becoming infectious [51], resulting in a SEIR-type model.

The SEIR model has proven to be widely used to model epidemics. However, given that the objective of this work is to characterize the dual causal relationship between the emerging phenomenon (the epidemic) and the behaviors of individuals given their cultural orientation, we propose this modeling at an agent scale where the epidemiological compartments taken from SEIR describe the individual health status. Each agent will be in one epidemiological state at a time and will switch between them according to a set of simple rules. This description is made as follows:

We consider the agent $a_i\in A$, where A is the set of all agents. The epidemiological behavior of a _i can be expressed through a Probabilistic Timed Automaton (PTA) [52].

$$G=(S,s_{init},trap,C,E,F,A,\omega )$$

where:

• •S is a finite set that contains the states that the agent can adopt. The model presented in this work considers the states

$$S=\{S,E,I_s,I_a,Q,H,R,D,I\}$$

• •$s_{init}$ is the initial state, such that $s\in \{S,I_a,I_s\}$.
• •$trap\in S$ is a trap state. In the present work $trap=D$.
• •C is a finite set of clocks. Specifically, a total of 4 clocks are considered $t_{1:4}\in C$
• •
  $E\subset S\times S\times 2^c\times guard\left(C\right)$ is the set of edges between two states. For the edge $(s,s’,X,\delta )\in E$ that goes from s to s’, the set $X\subset C$ is the set of clocks that will be reset to zero and δ is a clock constraint in guard(C) that must be satisfied when this transition is used. In this case, $guard\left(C\right)$ is a set made up of true, false, and a set of logical constraints of the form$t\varrho n$ in which $t\in C,n\in N$ and $\varrho \in \{>,<,=\}$.

  • ▪
    $t_1>6$. This corresponds to the average incubation time reported in the literature [53].
  • ▪
    $t_2>25$. This period indicates the number of days that the infectious state lasts when symptoms occur.
  • ▪
    $t_3>15$. Time period of the asymptomatic infectious state.
  • ▪
    $t_4>180$. Once recovered from the disease, a person acquires immunity; t₄ indicates how many days this immunity will last.
• •$F\subset S$ is the set of final states. In our model the only final state is D.
• •A_s is the set of actions that can be performed when the automaton is in the s state. The sets A _s are disjoint.
• •$\sigma :A\times E\to \left[\mathrm{0,1}\right]$ is the transition probability function, such that for all s ∈ S and a ∈ A _s it is true that ${\text{Σ}}_{e\in E_s}\sigma \left(a,e\right)=1.$

The diagram that graphically represents the described automaton is presented in Fig. 1 .

Fig. 1.

Epidemiological model conception for COVID-19.

3.2. Sub-model 2: Human behavior

The relationship between individual behaviors and emerging collective behaviors is a problem that has been constantly addressed in the area of complex systems [[54], [55], [56]], and one of the objectives is to know how the feedback process develops between these two levels. An example of this relationship is that between human behavior and social and epidemiological phenomena, in which people's individual behavior is largely the result of a set of decisions previously made [57,58]. By conducting an analysis individually, a person performs actions that help them carry out their daily activities. They also make decisions about the way in which they will carry out these activities: the means of transport, the path to take, the sanitary measures to be followed, the number of activities they will carry out, etc.

Decisions have a motivator that can be based on an analysis of the risk that each situation entails. In the context of an epidemic, the risk is to become seriously ill or even die.

In order to implement TPB using an agent approach, it is necessary to take all three components into account. In this work, the idea of conceptualized decision-making through Bayesian inference (BI) mapping is used, as has been done in Refs. [18,[59], [60], [61]], determining the probabilities for certain decisions and behaviors to be carried out, built on the basis of Bayesian probability theory and cognitive mapping. As new external information arrives, beliefs of preceding factors are updated. The Bayesian approach has been applied in a number of works in the literature to investigate the influence of incomplete/ambiguous information on decision-making processes to simulate complex social-ecological systems [62].

If we consider f a preceding factor, and B a certain behavior, an agent's belief about engaging in such behavior can be represented as a probability:

$$\pi \left(B\right)=\pi (B\left|f\right)\pi \left(f\right)+\pi \left(B\right|\neg f)\pi (\neg f)$$ (2)

The probability that the agent will engage in behavior $B$ when the factor $f$ happens is given by:

$$\pi \left(B|f\right)=\frac{\pi \left(f\right|B\left)\pi \right(B)}{\pi \left(f|B\right)\pi \left(B\right)+\pi \left(f\right|\neg B\left)\pi \right(\neg B)}$$ (3)

$P\left(f\right|B)$ is called the likelihood in Bayesian theory, and says that if $B$ is known, so are the likely values of $f$. In the same manner, the probability that the agent will engage in behavior B when f does not happen can be expressed as follows:

$$\pi \left(B|\neg f\right)=\frac{\pi (\neg f|B\left)\pi \right(B)}{\pi (\neg f|B)\pi \left(B\right)+\pi (\neg f|\neg B)\pi (\neg B)}$$ (4)

Following the same process described in Ref. [18], in order to incorporate the temporal variable and the influence of external social pressures (related to cultural orientation) Eq. (2), Eq. (3), and Eq. (4) are used to build Eq. (5):

$${\beta }^t=\frac{\delta {\beta }^{t-1}}{\delta {\beta }^{t-1}+(1-\delta )(1-{\beta }^{t-1})}{\epsilon }^t+\frac{\left(1-\delta \right){\beta }^{t-1}}{\left(1-\delta \right){\beta }^{t-1}+\delta \left(1-{\beta }^{t-1}\right)}(1-{\epsilon }^t)$$ (5)

In Eq. (5), the individual's perception of behavior at time $t$, ${\beta }^t$, is calculated based on the perception at time $t-1$, ${\beta }^{t-1}$; a cultural orientation coefficient, δ; and a variable, $\epsilon$, that represents new external information.

3.2.1. Mobility

The proposed model considers two different categories of activities: recreational (visiting friends or family and exercising) and economic (face-to-face work for essential workers). In all cases, they involve mobility from one place to another. Mobility has been shown to play a very important role in the evolution of an epidemic. In fact, in the case of COVID-19, a strong correlation has been found between mobility and cases of viral disease [[63], [64], [65], [66]]. For this reason, an agenda-based mobility sub-model is included. For each simulated day, an agent will plan a series of activities (represented in Fig. 2 as home, activity 1, activity 2, etc.), which will take place at a specific place and time, thus representing a person's agenda. Once agents finish their agenda, they head to a place designated as their home. The incorporation of this sub-model makes it possible to consider the infections generated by the encounters between people who carry out their activities on a daily basis.

Fig. 2.

Conceptual representation of a daily agenda.

In the literature it can be found that mobility has been used to explain up to 92% of the initial spread of COVID-19 in countries of the European Union [63]. In the case of China, it has been found that there is a relationship between the mobility of people and the number of new cases and the growth rate, both before and after restrictions on mobility are established [64]. In the United States, a strong correlation has been found between mobility patterns and the increase or decrease in COVID-19 cases, using anonymous data from cell phones [65]. We can find a similar case for the UK [66].

3.2.2. Society, culture, and behavior

The effectiveness of the actions implemented in the face of the threat of a pandemic tends to vary from one society to another, even though the protocols used have been the same, and this is a consequence of cultural differences. In the literature, a variety of cultural factors can be found that determine the behavior of individuals in a crisis such as that caused by COVID-19.

Individualism-collectivism. The behavioral sciences, specifically social psychology, have explained that a person's cultural orientation and actions have consequences reflected in large-scale emergent phenomena. One measure of a person's cultural orientation is the level of individualism. An individualistic orientation promotes personal freedom over harmony, while in collectivist societies it is ideal to fulfill social duties and obligations in order to maintain harmony [16]. Cultural orientation is important because positive causality has been observed between collectivist-oriented societies and the intention to take actions that help reduce the spread of COVID-19. It has been found that promoting collectivism in a community can be a way to increase participation in efforts to reduce the spread of COVID-19.

4. Experimental work

As part of the experimental work, three simulation scenarios were prepared. The first focused on demonstrating and measuring the variation in the epidemic indicators among populations with different cultural profiles. For this, three parallel simulations were carried out with three different population profiles: totally individualistic, totally collectivist, and a population with equal parts of both profiles. In the second simulation scenario, the parameters of the model were initialized in two communities that contrasted in cultural orientation (one of them in a country with an individualist orientation, and the other in a country with a collectivist orientation). The country cultural profile values were taken from Ref. [17]. The objective was to compare the behavior of the epidemic resulting from the two different cultural profile values. Finally, scenario 3 was a case study in which the parameters of the model were calibrated to study the municipality of El Arenal, Jalisco, Mexico. In this last scenario, the results of the model were validated by contrasting them with the data reported by the government.

The model was implemented on the GAMA Platform [67]. The first two simulation scenarios were geographically located in the Lomas del Centinela polygon in the metropolitan area of Guadalajara, Mexico, through geographically referenced data. The code, supplemental material, and resources can be found in the project repository [68]. An overview of the model implementation is provided in Fig. 3 . Using a graphic and interactive interface, stakeholders and decision-makers are allowed to use the tool. In addition to the scenarios of interest mentioned in this work, readers can experiment with their own assumptions, changing the parameters to adapt the tool to a specific case study. Finally, the results can be exported to be used as input in subsequent data analysis processes.

Fig. 3.

Model implementation using GAMA Platform.

4.1. Epidemiological sub-model parameters

The parameters used in the epidemiological behavior model incorporated in the agents were based on COVID-19 studies reported in the literature [50,69], and are shown in Table 1 .

Table 1.

Epidemiological parameters used in the simulation of the scenarios.

$\beta$	$\rho$	${\delta }_s$	${\delta }_a$	$\gamma$	$\lambda$
0.01	0.86834	0.13266	0.5	0.1	0.8

4.2. Scenario 1

4.2.1. Assumptions

• •A total of 180 days were simulated.
• •Agents carried out a random number of daily activities following the decision-making model explained in the previous section.
• •It was assumed that the disease had been imported by agents who returned to the community without taking precautionary measures.

4.2.2. Parametrization

4.2.2.1. Cultural orientation

Cultural orientation was divided into two subtypes, so that in this scenario there were four types of profiles: vertical individualist (VI), horizontal individualist (HI), vertical collectivist (VC), and horizontal collectivist (HC). The value that changed between each type was the cultural orientation coefficient, such that for each profile a proportional value was assigned: 0.5, 0.67, 0.83, and 1.0 respectively.

4.2.2.2. Population

A total of 400 people agents were used for each population, segmented as follows:

• •Individualistic population. For the individualistic population, 398 agents were placed and divided between types VI and HI; in addition, we placed 1 HC agent and 1 VC agent.
• •Collectivist population. Similarly, the collectivist population was a population that contained 398 collectivist agents (both VC and HC), as well as 1 VI agent, and 1 HI agent.
• •Balanced population. The total agents were divided in half: 50% individualists (both VI and HI), and the other 50% collectivist agents (VC and HC).

The initial number of people exposed to the virus was 10.

4.2.3. Simulation results

4.2.3.1. Compliance with prevention measures by the population

Fig. 4a, b, and 4c show the response shown by the population to the prevention measures recommended by the authorities. It can be observed that the number of people in the collectivist population who follow the recommendations constantly increases, while the individualistic population shows a low response to the measures. In the case of the balanced population, the graph seems to have a lower growth rate than that of the collectivist population; however, on approximately day 100 of the simulation, this rate increases. One possible explanation is that as the number of infections increases, the collectivist population is motivated to comply with the measures.

Fig. 4.

Results of the simulation of scenario 1. The number of agents that adopted each of the contagion prevention measures is shown. The results show that adoption of the measures increased linearly over time in the collectivist population (a). On the other hand, the balanced population showed a low adoption at the beginning (b); however, once the external information indicated an increase in the epidemic, they adopted the measures. It is also shown that in the proposed model, the individualistic population very rarely adopted the measures.

4.2.3.2. Basic reproduction number (R₀)

The basic reproduction number was observed for the three populations (Fig. 5 ).

Fig. 5.

Result of observing the basic reproduction number ($R_0$). The collectivist population (green) shows a decrease in its average infections that is faster than the balanced population's (red). We can also observe a decrease in the value for the individualistic population; however, this is because the large number of infections led to a decrease in the susceptible population, which is reflected in the fact that fewer agents are infected.

4.2.3.3. Epidemiological indicators

In order to distinguish the results, they are classified by study variable: susceptible agents (Fig. 6 a), exposed (Fig. 6b), infected with symptoms (Fig. 6c), infected without symptoms (Fig. 6d), immune (Fig. 6e), deceased (Fig. 6f), quarantined with symptoms (Fig. 7 a), quarantined without symptoms (Fig. 7b), hospitalized (Fig. 7c). Each of these variables is evaluated in three different scenarios: (1) Population divided between individualistic and collectivist people, (2) 100% individualistic population, and (3) 100% collectivist population.

Fig. 6.

The results obtained from the simulation of the model using the configuration of scenario 1 are shown, classified by estimated epidemiological indicator, although it should be noted that the user of this simulation tool can create new population configurations to create scenarios that simulate realistic case studies.

Fig. 7.

The quarantine case estimates for the simulation of scenario 1 are shown. The model allows output data to be generated for user-defined populations. In (a) the cases of infections with symptoms are compared, in (b) the comparison is made with the asymptomatic cases, and in (c) the estimates of hospitalized people are shown.

4.3. Scenario 2

In this scenario, a comparison was made of two populations with the cultural orientation parameters for the US and Mexico, as found in the literature [17].

4.3.1. Assumptions

• •A total of 180 days were simulated.
• •400 agents representing people were used.
• •Agents carried out a random number of daily activities following the decision-making model explained in the previous section.
• •It was assumed that the disease had been imported by agents who returned to the community without taking precautionary measures.

4.3.2. Parametrization

4.3.2.1. Cultural orientation

The cultural parameters used in this simulation scenario were obtained from the literature on the cultural orientation of both countries [17]. In that study, a correlation was made between the cultural orientation of 69 countries with each of their epidemiological behaviors. The individuality index (used in this work as cultural orientation coefficient) reported for Mexico is 0.35 (where the minimum is 0 and the maximum is 1). The second population considered corresponded to the United States, whose individuality value, according to the study, is 0.9 on the same scale.

4.3.2.2. Population

Each of the populations contained the same number of agents (400) in order to more accurately compare both populations. The initial number of people exposed to the virus was 10.

4.4. Simulation results

4.4.1. Compliance with prevention measures by the population

Fig. 8a,b,8c show the evolution of the number of people who adopted the recommended prevention measures in each population studied.

Fig. 8.

Using a configuration of two populations with the cultural parameters reported in the literature, the simulation of scenario 2 shows an estimate of the number of people in each population who adopt each of the prevention measures.

4.4.2. Epidemiological indicators

The results corresponding to the epidemiological variables are shown in Fig. 9a, b, 9c, 9d, 9e, and 9 f. Likewise, the results regarding people in quarantine or hospitalized are shown in Fig. 10 a, b, and 10c.

Fig. 9.

Simulation of two populations with contrasting cultural orientation. The indicators in red belong to the individualistic population, while the indicators in black belong to the collectivist population.

Fig. 10.

Observed results of cases of infected people with symptoms, without symptoms and hospitalized for simulation scenario 3.

4.4.3. Basic reproduction number $\left(R_0\right)$

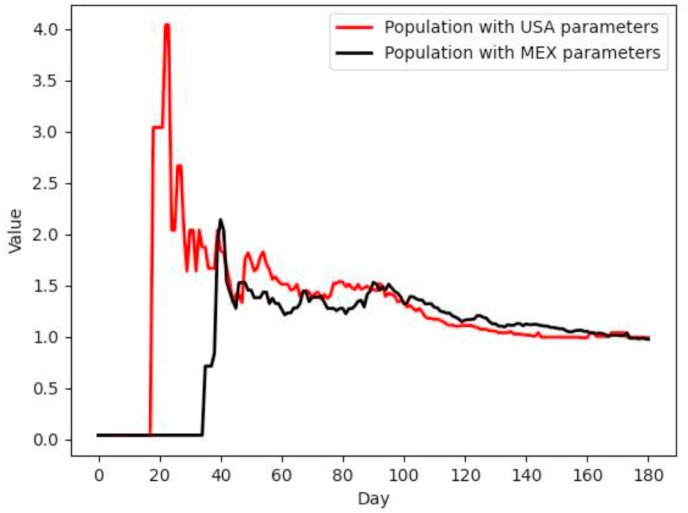
The basic reproduction number $\left(R_0\right)$ was compared for the two populations. The result after 180 days is seen in Fig. 11 .

Fig. 11.

Evolution of the basic reproduction number (R₀) reported by the simulation of scenario 2.

4.5. Scenario 3

In addition to the two scenarios proposed and simulated above, there was a third scenario where calibrated input parameters were used according to the data found in official reports and in the literature. The main objective was to demonstrate that the model can be adjusted and used for scenarios with real data and population.

4.5.1. Assumptions

To implement this scenario, the available data on infections and hospitalizations from the municipality of El Arenal, in the state of Jalisco, Mexico were used. El Arenal is located approximately 38 km west of the Guadalajara metropolitan area (GMA) in Mexico, and it was selected as a case study.

for the following reasons: its population, according to the latest population census published by INEGI [70] (government institution that conducts the population census in Mexico), in 2020 was 21,115; thus, it is not a municipality with a large number of inhabitants (unlike the GMA with more than 8 million residents). This allowed for the validation of the model in a simple way in terms of computational power. Another reason for selecting this scenario was the epidemiological information available, since data on infections and hospitalizations are reported at the municipal level on a daily basis, which allowed direct validation of the simulation. The available data made it possible to segment the population into age ranges and the approximate location of their home, and thus to estimate the number of agents who worked, who did not work but carried out leisure activities, and who stayed home (for example children and older adults). Below, the considerations taken into account are described:

• •Epidemiological traffic light. On June 1, 2020, the government of Mexico implemented a system to impose activity restrictions in accordance with the latest epidemiological indicators [71]. In this case study, the restriction on mobility is determined based on the levels of hospital occupancy, and the daily activities are restricted in accordance with the rules described in Table 2 .
• •Infections outside the municipality. This case study considered that a number of workers carried out their activities within the study area (this information was imported from INEGI). Those who worked outside the municipality were transferred to a common point and were considered to return to the municipality infected, with a probability that this study called infected_outside. This probability served to detect infections that did not occur within the municipality and that could lead to the appearance of waves of infections.
• •Time period. The case study considered a total of 60 days starting on May 23, 2020, the date on which the first confirmed infection was reported in the municipality of El Arenal.
• •Number of experiments. Ten simulations were run in the specified time period.

Table 2.

Rules of operation of the epidemiological traffic light implemented in the case study.

Occupancy level	Traffic Light	Restrictions on Activities
0% to 30%	Green	Essential and non-essential activities are allowed in their entirety on a regular basis.
31% to 50%	Yellow	Essential activities are maintained on a regular basis and non-essential activities are reduced by 75%.
51% to 70%	Orange	Essential activities are maintained with a maximum capacity of 75% and non-essential activities are reduced to 50%.
More than 70%	Red	Essential activities are kept at 50% and non-essential activities are fully restricted.

4.5.2. Parametrization

4.5.2.1. Cultural orientation

A value of 0.35, the cultural orientation value for Mexico reported in Ref. [17], was used.

4.5.2.2. Population

A total of 21,115 agents were used corresponding to the total population according to the most recent population census in Mexico [70]. The rest of the parameters used in this scenario are shown in Table 3 .

Table 3.

List of parameters used to simulate the epidemic in the municipality of El Arenal.

Parameter	Value
β	0.0001
ρ	0.86834
δs	0.13266
δa	0.5
γ	0.1
λ	0.95
essential workers percentage	25%
distance for contact	2 m
infected outside	0.0001

4.5.3. Simulation results

The results of the experiments are shown in Fig. 12 . It can be observed that the real data on the accumulated cases (blue triangles in Fig. 12a), obtained from official sources of the government of the state of Jalisco, Mexico, follow a behavior similar to that estimated by the twenty repetitions of the model with the cultural and population parameters of El Arenal (gray lines). Likewise, the estimated number of hospitalizations (gray lines in Fig. 12b) maintains a similar trend after the first 60 days of simulation, compared to real data (blue triangles). A subsequent analysis was performed to measure the precision of the simulation estimates. The RMSE value for the cumulative real and simulated cases was 2.94, and for the real and simulated hospitalization cases it was 0.84. As part of the validation, we carried out a comparison process using a statistical technique known as the Tukey mean difference plot, which serves to measure the variation between two data sets; the results are shown in Fig. 13 .

Fig. 12.

Demonstration of the use of the proposed model to study the evolution of the coronavirus epidemic in the municipality of El Arenal in the period from May 23, 2020 to July 21, 2020 (60 days). The model was configured to run ten simulations (shown in gray lines) in that time period. The parameters used were the result of a calibration process using data from the municipality of El Arenal. The data used were the accumulated cases and the hospitalizations (blue triangles).

Fig. 13.

Tukey mean difference plots.

5. Discussion

As part of the experimental work, three different scenarios were presented in order to verify the correct functioning of the model and to compare simulations with parameters reported in the literature. The first scenario consisted of 3 populations of agents with generic profiles of different cultural orientation: a population with an individualistic profile, another with a collectivist profile, and one more with a balanced profile. In this scenario, the configuration settings did not correspond to any given specific region or population. The results in this scenario showed that, consistent with previous studies on cultural orientation and COVID-19, the collectivist population generally achieved better control of the epidemic. The basic reproduction number ($R_0$) was compared and during the simulation period, an average of $R_0=0.87$ was observed in the collectivist population, while the individualistic and balanced populations showed $R_0=1.14$ and $R_0=1.16$, respectively. From the analysis of Table 4 , which contains the average values of each output variable for each population, it was found that on average, a totally collectivist population had a better response to the epidemic, managing to keep contagion levels low due to the positive response to the prevention measures proposed by the authorities.

Table 4.

Average value of each of the epidemiological and behavioral variables resulting from simulation scenario 1 for each type of population.

Variable	Individualist	Balanced	Collectivist
Susceptible	244.02	248.13	316.48
Exposed	7.48	7.73	4.28
Infectious Symptomatic	29.94	33.08	16.23
Infectious Asymptomatic	3.07	2.81	1.80
Recovered	4.10	4.34	2.15
Immune	27.38	23.73	12.23
Symptomatic in Quarantine	15.09	16.10	8.07
Asymptomatic in Quarantine	0.83	0.45	0.48
Hospitalized	1.01	1.55	0.81
Dead	84.01	80.18	46.83
Using Mask	8.64	56.21	65.78
Hand Washing	8.45	55.98	65.76
Practicing Social Distance	8.42	56.36	65.16

As specified in Section 4.3, the second scenario considered two specific cultural profiles: Mexico and the United States. From the analysis of the results of the simulation of this scenario as shown in Table 5 , it was found that the behavior of the epidemic in both populations coincided with the empirical results reported in the literature. The mean value of the basic reproduction number for the population with US parameters was $R_0=1.27$, while for the population based on the parameters for Mexico it was $R_0=1.00$. It was observed that, like in simulation scenario 1, the behavior of the epidemic was better in the population that had a population with a profile oriented to collectivism, as is the case of the population with parameters for Mexico. On the other hand, infections and other epidemiological indicators were on average higher for the population based on the US parameters.

Table 5.

Average value of each of the epidemiological and behavioral variables resulting from simulation scenario 2 for each type of population, where population 1 was initialized with parameters from the USA and population 2 with parameters from Mexico, according to the literature.

Variable	Population 1	Population 2
Susceptible	203.60	255.06
Exposed	8.36	6.84
Infectious Symptomatic	37.54	32.44
Infectious Asymptomatic	2.38	1.76
Recovered	4.94	4.07
Immune	28.16	17.49
Symptomatic in Quarantine	16.36	15.81
Asymptomatic in Quarantine	0.68	0.57
Hospitalized	1.67	1.48
Dead	115.02	82.32
Using Mask	101.0	49.05
Hand Washing	100.80	49.16
Practicing Social Distance	101.20	49.044

In the third scenario, a comparison was made of the data reported by the authorities and the results obtained from the model. It is important to consider that the results obtained from the simulations of the scenarios were not expected to fully match the data reported by the authorities. Multiple external factors can help explain this; one of the most important is the fact that official reports are based on the direct results of tests applied to the population daily, and do not take into account the estimate of positive cases that have not been tested. However, it has been shown that the estimates provided by the simulations of the proposed model can help to plan better interventions by considering important aspects such as culture and adherence to prevention measures. A verification of the decision-making model was also carried out by evaluating the correct update of the intention value produced. In this sense, unit testing was performed for the decision-making sub-model corresponding to equation (5). For this, the simulation of this sub-model was run with a list of 11 different parameters for $\delta \in \{0.0,0.1,0.2,\mathrm{...},1.0\}$, representing different cultural orientation indices. Using each of the test indices, a total of 180 simulation cycles were run using different incoming information ranging from 0.0 to 1.0. The results are shown in Fig. 14 a and Fig. 14b. There are two special cases presented in equation (5). The first case is when $\delta =1.0$; the expression is reduced to ${\beta }^t={\epsilon }^t$, which means that the agent takes into account only the external information to obtain its value of intention to perform a behavior. This can be seen in Fig. 14b where the line corresponding to the intention value for δ = 1.0 increases linearly to the incoming information. The second special case occurs when the value of δ = 0.5, for which the expression is reduced to $\beta t={\beta }^{t-1}$. This indicates that the intention value to perform a behavior will depend exclusively on the β value of the previous decision taken. In Fig. 14b, it can be observed that the intention value remains constant for $\delta =0.5$. This means that the same decision is made throughout the 180 simulation cycles. These tests indicate that the decision sub-model behaves correctly and in accordance with the theoretical analysis.

Fig. 14.

Intention value, result of evaluating equation (5) with the set of values for $\delta :\{0.0,0.1,\mathrm{...},0.9,1.0\}$, with 180 incoming information values from 0.0 to 1.0.

Additionally, a one-at-a-time sensitivity validation analysis was performed. The objective of this type of analysis is to obtain a sensitivity value, by increasing each parameter by a given percentage while the others are left constant, and quantifying the change in the output of the model [72,73]. An analysis was performed in which the variation in three dependent variables was observed (basic reproduction number (R ₀), infectious symptomatic people, and number of deaths). The independent variable that was varied was the cultural orientation. The simulation analysis considered 180 days from the first contagion and ran 11 times corresponding to each of the δ values. The results of this variation for each output variable are presented in a boxplot format. Fig. 15 a shows the variation of the basic reproduction number (R ₀) registered in the dependent variable. Fig. 15b shows the variation.

Fig. 15.

Sensitivity analysis of the dependent variables when the independent variable is varied.

observed for the variable infectious symptomatic people, and finally, Fig. 15c shows the variation registered in the variable deaths. It can be seen that the worst control of the epidemic and greatest variation in all cases occurs for the values of the cultural profile δ that range from 0.6 to 1 (individualist cultural profile).

Further validation will be done as future work using local cultural profiling data as they become available. It is important to mention that these cultural profiling studies are still needed at the local or community level at this time in the context of the COVID-19 pandemic.

6. Conclusion

In this work, an agent-based model was proposed to study the evolution of the COVID-19 epidemic considering different simulation scenarios. For this, a set of theories from the social sciences were applied: the theory of planned behavior and cultural orientation. The first scenario that was studied consisted of three generic population profiles with different coefficients of cultural orientation (a measure proposed to incorporate the agents’ level of individualism): an individualistic population, another collectivist, and a more balanced one. The results of the simulation showed, in general terms, a better management of the epidemic in the collectivist population, due to the positive response of the individuals to the prevention measures. A second simulation.

scenario consisted of two populations from two different countries with coefficients of cultural orientation taken from the literature; in this simulation a better control of the epidemic was again demonstrated in the population with a less individualistic orientation. The worst control and greatest variation for the basic reproduction number (R ₀), infectious symptomatic people, and number of deaths were obtained for the cultural profile values of δ ranging from 0.6 to 1.

Local non-pharmaceutical interventions for pandemic mitigation are derived from the recommendations of the WHO and national health authorities. However, the results confirm that the socio-cultural profile is relevant in the individual agents’ response, from which the general behavior of the epidemic arises.

This work has shown that it is possible to model both contagious diseases and social phenomena to study the associated emergence and the general effects on the evolution of an epidemic. This would allow for more precise or better adjusted epidemic interventions according to the specific characteristics of a given modeled community.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix.

8.1. ODD description for the proposed agent-based model

8.1.1. Purpose

This model aims to explain and simulate some behavior of societies living in cities and regions and the affectations caused by COVID-19 mitigation and control measures.

8.1.2. Entities, state variables and scales

Scales. As the purpose of the model is to simulate scenarios at the scale of a community, it is necessary to consider data and behavior according to this scale. The time scale used is 2 min for every time step. The authors of this study believe that this scale is enough to capture the movement and contacts between people. Although these were the parameters chosen for the model, they can be modified in the implementation to be able to test other scenarios and scales.

Entities. People are the most intuitive kind of agent, as they represent each person that is part of the community. Each individual has a series of characteristics: age, sex, household, agenda, medical profile, social profile, professional profile. They also incorporate different behavioral parameters that influence their interactions and how they follow indications and recommendations from authorities. Although the epidemiological state is included in the medical profile, it is important to highlight that people agents have a finite internal state machine which determines the agent's current state in terms of diseases, not only COVID-19, but also other medical situations to be considered. People agents can move, not only from/to buildings, but also inside them to perform daily activities. Therefore, building as a kind of agent is included. As each people agent has an agenda, their daily behavior is guided by activities. Activity agents are used to describe the activities of people agents using information such as the location (where an activity will take place), the scheduled time to perform the activity, and the type of activity. An activity must be implemented based on the profile of each people agent. A list of activities conforms an agenda. Policy agents are designed to implement interventions on the behavior of individuals in the public space, such as restricted mobility, permitted but essential kinds of activities, etc.

8.1.3. Process overview and scheduling

This model describes the double causality between human behavior in pandemic situations and in an urban environment, and the dynamics of an epidemic. For this reason, different levels of dynamics need to be simulated: the agent's agenda, the evolution of the epidemics, and the implementation of the prevention measures by the population. It is considered that during the simulation of a scenario, each time an agent needs to make a decision, it will do so by executing the Bayesian inference proposed in section 3.2, obtaining a value in the range [0,1]. This value is used to decide between taking an action or not, such as wearing a mask or not, going outside or not, etc.

People perform daily activities according to an agenda. The agenda of each agent is randomly generated considering the cultural profile, and it is unique in this sense, although some similarities can be observed. A scheduling function belonging to the people agent manages the activities to be performed according to the hour of the day. A common example is the basic agenda consisting of activities such as going from home to work/school, then going out for lunch or for a leisure activity, and finally, in the afternoon, going back home. (See Fig. 16).

Rule 1: Decision-making about agenda. The agent decides the activities to be performed, taking into account belief and risk analysis. Each time a people agent needs to perform a new activity, a function determines the kind of social behavior according to a level of awareness about the epidemic.

Rule 2. Decision-making about behavior. The agent decides the manner in which to perform the activities. This involves the wearing of a face mask, washing hands and keeping social distance. The three behaviors described above are taken into account since they have been found to be the most important measures in reducing the risk of contagion between people [74,75]. For this purpose, each agent calculates and updates the individual.

Fig. 16.

People agents' daily routine process.

Fig. 17.

Agents' decision-making process.

belief about performing a specific behavior, using the Bayesian inference model presented in Eq. (5). This process is shown in Fig. 17.

Rule 3: Epidemic dynamics. The epidemiological behavior of a _i can be expressed through a Probabilistic Timed Automaton (PTA) and it has been explained in Section 3.1. At the same time activities are performed, people's internal health state changes. The transition from Susceptible to Exposed can occur only if the agent has had contact with the virus, either by transmission from an infected agent or by infected places with a given probability. The described Probabilistic Timed Automaton can be observed in Fig. 1. Fig. 18 shows the class diagram that makes up the implementation of the model described above is shown.

Fig. 18.

Description of agent classes and their relationships.