WEAK SINDY FOR PARTIAL DIFFERENTIAL EQUATIONS

Abstract

Sparse Identification of Nonlinear Dynamics (SINDy) is a method of system discovery that has been shown to successfully recover governing dynamical systems from data [6, 39]. Recently, several groups have independently discovered that the weak formulation provides orders of magnitude better robustness to noise. Here we extend our Weak SINDy (WSINDy) framework introduced in [28] to the setting of partial differential equations (PDEs). The elimination of pointwise derivative approximations via the weak form enables effective machine-precision recovery of model coefficients from noise-free data (i.e. below the tolerance of the simulation scheme) as well as robust identification of PDEs in the large noise regime (with signal-to-noise ratio approaching one in many well-known cases). This is accomplished by discretizing a convolutional weak form of the PDE and exploiting separability of test functions for efficient model identification using the Fast Fourier Transform. The resulting WSINDy algorithm for PDEs has a worst-case computational complexity of $\mathcal{O}\left(N^{D+1}\text{log}(N)\right)$ for datasets with N points in each of D + 1 dimensions. Furthermore, our Fourier-based implementation reveals a connection between robustness to noise and the spectra of test functions, which we utilize in an a priori selection algorithm for test functions. Finally, we introduce a learning algorithm for the threshold in sequential-thresholding least-squares (STLS) that enables model identification from large libraries, and we utilize scale invariance at the continuum level to identify PDEs from poorly-scaled datasets. We demonstrate WSINDy’s robustness, speed and accuracy on several challenging PDEs. Code is publicly available on GitHub at https://github.com/MathBioCU/WSINDy_PDE.

1. Introduction

Stemming from Akaike’s seminal work in the 1970’s [1, 2], research into the automatic creation of accurate mathematical models from data has progressed dramatically. In the last 20 years, substantial developments have been made at the interface of applied mathematics and statistics to design data-driven model selection algorithms that are both statistically rigorous and computationally efficient (see [5, 22, 23, 48, 55, 56] for both theory and applications). An important achievement in this field was the formulation and subsequent discretization of the system discovery problem in terms of a candidate basis of nonlinear functions evaluated at the given dataset, together with a sparsification measure to avoid overfitting [9]. In [50] the authors extended this framework to the context of catastrophe prediction and used compressed sensing techniques to enforce sparsity. More recently, this approach has been generalized as the SINDy algorithm (Sparse Identification of Nonlinear Dynamics) [6] and successfully used to identify a variety of discrete and continuous dynamical systems.

The wide applicability, computational efficiency, and interpretability of the SINDy algorithm has spurred an explosion of interest in the problem of identifying nonlinear dynamical systems from data [8, 34, 10, 11, 15, 49, 27]. In addition to the sparse regression approach adopted in SINDy, some of the primary techniques include Gaussian process regression [31, 36], deep neural networks [26, 25, 24, 40, 51, 22], Bayesian inference [61, 62, 54] and classical methods from numerical analysis [16, 19, 57]. The variety of approaches for model discovery from data qualitatively differ in the interpretability of the resulting data-driven dynamical system, the computational efficiency of the algorithm, and the robustness to noise, scale separation, etc. For instance, a neural-network based data-driven dynamical system does not easily lend itself to physical interpretation¹. The SINDy algorithm allows for direct interpretations of the dynamics from identified differential equations and uses sequential-thresholding least-squares (STLS) to enforce a sparse solution $x\in {ℝ}^n$ to a linear system Ax = b. STLS has been proven to converge to a local minimizer of the non-convex functional $F(x)=\parallel Ax-b{\parallel }_2^2+{\lambda }^2\parallel x{\parallel }_0$ in at-most n iterations [60].

The aim of the present article is to extend the Weak SINDy method (WSINDy) for recovering ordinary differential equations (ODEs) from data to the context of partial differential equations (PDEs) [28]. WSINDy is a Galerkin-based data-driven model selection algorithm that utilizes the weak form of the dynamics in a sparse regression framework. By integrating in time against compactly-supported test functions, WSINDy avoids approximation of pointwise derivatives which are known to result in low robustness to noise [39]. In [28] we showed that by integrating against a suitable choice of test functions, correct ODE model terms can be identified together with machine-precision recovery of coefficients (i.e. below the tolerance of the data simulation scheme) from noise-free synthetic data, and for datasets with large noise, WSINDy successfully recovers the correct model terms without explicit data denoising. The use of integral equations for system identification was proposed as early as the 1980’s [9] and was carried out in a sparse regression framework in [42] in the context of ODEs, however neither works utilized the full generality of the weak form.

Sparse regression approaches for learning PDEs from data have seen a tremendous spike in activity in the years since 2016. Pioneering works include [41], [39], and [43], where the Douglas-Rachford algorithm, sequential-thresholding least squares (STLS), and basis pursuit with denoising, respectively, are used to regularize the NP-hard problem of finding an optimal sparse solution. Many other predominant approaches for learning dynamical systems (Gaussian processes, deep learning, Bayesian inference, etc.) have since been extended to the discovery of PDEs [7, 30, 21, 22, 52, 53, 59, 58, 45, 55]. A significant disadvantage for the vast majority of PDE discovery methods is the requirement of pointwise derivative approximations. Steps to alleviate this are taken by the authors of [35] and [58], where neural network-based recovery schemes are combined with integral and abstract evolution equations to recover PDEs, and in [53], where the finite element-based method Variational System Identification (VSI) is introduced to identify reaction-diffusion systems and uses backward Euler to approximate the time derivative.

WSINDy is a method for discovering PDEs without the use of any pointwise derivative approximations, black-box routines or conventional noise filtering. Through integration by parts in both space and time against smooth compactly-supported test functions, WSINDy is able to recover PDEs from datasets with much higher noise levels, and from truly weak solutions (see Figure 3 in Section 5). This works suprisingly well even as the signal-to-noise ratio approaches one. Furthermore, as in the ODE setting, WSINDy achieves high-accuracy recovery in the low-noise regime. These overwhelming improvements resulting from a fully weak² identification method have also been discovered independently by other groups [37, 13]. WSINDy offers several advantages over these alternative frameworks. Firstly, we use a convolutional weak form which enables efficient model identification using the Fast Fourier Transform (FFT). For measurement data with N points in each of the D + 1 space-time dimensions (N^{D + 1} total data points), the resulting algorithmic complexity of WSINDy in the PDE setting is at worst $\mathcal{O}\left(N^{D+1}\text{log}(N)\right)$, in other words $\mathcal{O}(\text{log}(N))$ floating point operations per data-point. Subsampling further reduces the cost. Furthermore, our FFT-based approach reveals a key mechanism behind the observed robustness to noise, namely that spectral decay properties of test functions can be tuned to damp noise-dominated modes in the data, and we develop a learning algorithm for test function hyperparameters based on this mechanism. WSINDy also utilizes scale invariance of the PDE and a modified STLS algorithm with automatic threshold selection to recover models from (i) poorly-scaled data and (ii) large candidate model libraries.

Figure 3.

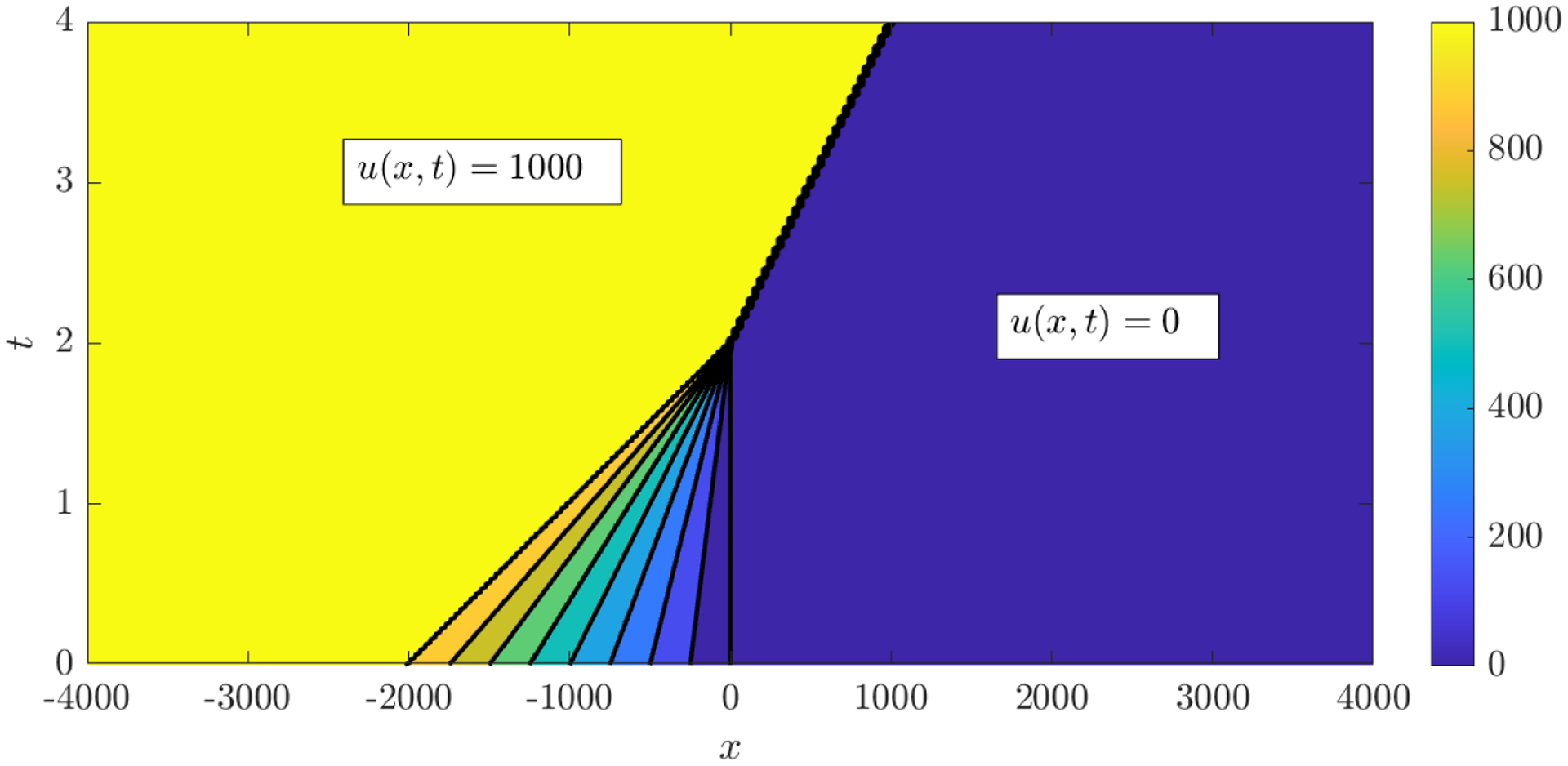
Characteristics of the shock-forming solution (B.2) used to identify the inviscid Burgers equation. A shock forms at time t = 2 and travels along the line x = 500(t − 2).

The outline of the article is as follows. In Section 2 we define the system discovery problem that we aim to solve and the notation to be used throughout. We then introduce the convolutional weak formulation along with our FFT-based discretization in Section 3. Key ingredients of the WSINDy algorithm for PDEs (Algorithm 4.2) are covered in Section 4, including a discussion of spectral properties of test functions and robustness to noise (4.1), our modified sequential thresholding scheme (4.2), and regularization using scale invariance of the underlying PDE (4.3). Section 5 contains numerical model discovery results for a range of nonlinear PDEs, including several vast improvements on existing results in the literature. We conclude the main text in Section 6 which summarizes the exposition and includes natural next directions for this line of research. Lastly, additional numerical details are included in the Appendix.

2. Problem Statement and Notation

Let U be a spatiotemporal dataset given on the spatial grid $X\subset \overline{\Omega }$ over timepoints t ⊂ [0, T] where Ω is an open, bounded subset in ${ℝ}^D$, D ≥ 1. In the cases we consider here, Ω is rectangular and the spatial grid is given by a tensor product of one-dimensional grids X = X₁ ⊗⋯⊗X_D, where each $X_d\in {ℝ}^{N_d}$ for 1 ≤ d ≤ D has equal spacing Δx, and the time grid $t\in {ℝ}^{N_{D+1}}$ has equal spacing Δt. The dataset U is then a (D + 1)-dimensional array with dimensions N₁ × ⋯ × N_{D + 1}. We write h(X, t) to denote the (D + 1)-dimensional array obtained by evaluating the function $h:{ℝ}^D\times ℝ\to ℂ$ at each of the points in the computational grid (X, t). Individual points in (X, t) will often be denoted by (x_k, t_k) ∈ (X, t) where

$$\left(x_k,t_k\right)=\left(X_{k_1,\dots ,k_D},t_{k_{D+1}}\right)=\left(x_{k_1},\dots ,x_{k_D},t_{k_{D+1}}\right)\in {ℝ}^D\times ℝ.$$

In a mild abuse of notation, for a collection of points {(x_k, t_k)}_k∈[K] ⊂ (X, t), the index k plays a double role as a single index in the range [K] := {1, …, K} referencing the point (x_k, t_k) ∈ {(x_k, t_k)}_k∈[K] and as a multi-index on $\left(x_k,t_k\right)=\left(X_{k_1,\dots ,k_D},t_{k_{D+1}}\right)$, where k_d references the dth coordinate. This is particularly useful for defining a matrix $G\in {ℂ}^{K\times J}$ of the form

$$G_{k,j}=h_j\left(x_k,t_k\right)$$

(as in equation (3.6) below) where (h_j)_j∈[J] is a collection of J functions $h_j:{ℝ}^D\times ℝ\to ℂ$ evaluated at the set of K points {(x_k, t_k)}_k∈[K] ⊂ (X, t).

We assume that the data satisfies U = u(X, t) + ϵ for i.i.d. noise³ ϵ and weak solution u of the PDE

$$D^{{\alpha }^0}u(x,t)=D^{{\alpha }^1}{g}_1(u(x,t))+D^{{\alpha }^2}{g}_2(u(x,t))+\cdots +D^{{\alpha }^S}gs(u(x,t)),\hspace{1em}x\in \Omega ,t\in (0,T).$$ (2.1)

The problem we aim to solve is the identification of functions (g_s)_s∈[S] and corresponding differential operators ${\left(D^{{\alpha }^s}\right)}_{s\in [S]}$ that govern the evolution⁴ of u according to $D^{{\alpha }^0}u$ given the dataset U and computational grid (X, t). Here and throughout we use the multi-index notation ${\alpha }^s=\left({\alpha }_1^s,\dots ,{\alpha }_D^s,{\alpha }_{D+1}^s\right)\in {\mathbb{N}}^{D+1}$ to denote partial differentiation⁵ with respect to x = (x₁, … , x_D) and t, so that

$$D^{{\alpha }^s}u(x,t)=\frac{{\partial }^{{\alpha }_1^s+\cdots +{\alpha }_D^s+{\alpha }_{D+1}^s}}{\partial x_1^{{\alpha }_1^s}\dots \partial x_D^{{\alpha }_D^s}\partial t^{{\alpha }_{D+1}^s}}u(x,t).$$

We emphasize that a wide variety of PDEs can be written in the form (2.1). In particular, in this paper we demonstrate our method of system identification on inviscid Burgers, Korteweg-de Vries, Kuramoto-Sivashinsky, nonlinear Schrödinger’s, Sine-Gordon, a reaction-diffusion system and Navier-Stokes. The list of admissable PDEs that can be transformed into a weak form without any derivatives on the state variables includes many other well-known PDEs (Allen-Cahn, Cahn-Hilliard, Boussinesq,…).

3. Weak Formulation

To arrive at a computatonally tractable model recovery problem, we assume that the set of multi-indices (α^s)_s∈[S] together with α⁰ enumerates the set of possible true differential operators that govern the evolution of u and that (g_s)_s∈[S] ⊂ span(f_j)_j∈[J] where the family of functions (f_j)_j∈[J] (referred to as the trial functions) is known beforehand. This enables us to rewrite (2.1) as

$$D^{{\alpha }^0}u=\sum _{s=1}^S\sum _{j=1}^J{w}_{(s-1)J+j}^{\star }{D}^{{\alpha }^s}{f}_j(u),$$ (3.1)

so that discovery of the correct PDE is reduced to a finite-dimensional problem of recovering the true vector of coefficients $w^{\star }\in {ℝ}^{SJ}$, which is assumed to be sparse.

To convert the PDE into its weak form, we multiply equation (3.1) by a smooth test function ψ(x, t), compactly-supported in Ω × (0, T), and integrate over the spacetime domain,

$$\langle \psi ,D^{{\alpha }^0}u\rangle =\sum _{s=1}^S\sum _{j=1}^J{w}_{(s-1)J+j}^{\star }\langle \psi ,D^{{\alpha }^s}{f}_j(u)\rangle ,$$

where the L²-inner product is defined $\langle \psi ,f\rangle ≔{\int }_0^T{\int }_{\Omega }{\psi }^{\ast }(x,t)f(x,t)\mathit{\text{dxdt}}$ and ψ* denotes the complex conjugate of ψ, although in what follows we integrate against only real-valued test functions and will omit the complex conjugation. Using the compact support of ψ and Fubini’s theorem, we then integrate by parts as many times as necessary to arrive at the following weak form of the dynamics:

$$\langle {(-1)}^{|{\alpha }^0|}{D}^{{\alpha }^0}\psi ,u\rangle =\sum _{s=1}^S\sum _{j=1}^J{w}_{(s-1)J+j}^{\star }\langle {(-1)}^{|{\alpha }^s|}{D}^{{\alpha }^s}\psi ,f_j(u)\rangle ,$$ (3.2)

where $|{\alpha }^s|≔{\sum }_{d=1}^{D+1}{\alpha }_d^s$ is the order of the multi-index⁶. Using an ensemble of test functions (ψ_k)_k∈[K], we then discretize the integrals in (3.2) with f_j(u) replaced by f_j(U) (i.e. evaluated at the observed data U) to arrive at the linear system

$$b=G{w}^{\star }$$

defined by

$$\{\begin{array}{c}{b}_k=\langle {(-1)}^{|{\alpha }^0|}{D}^{{\alpha }^0}{\psi }_k,U\rangle ,\\ G_{k,(s-1)J+j}=\langle {(-1)}^{|{\alpha }^s|}{D}^{{\alpha }^s}{\psi }_k,f_j(U)\rangle ,\end{array}$$ (3.3)

where $b\in {ℝ}^K$, $G\in {ℝ}^{K\times SJ}$ and $w^{\star }\in {ℝ}^{SJ}$ are referred to throughout as the left-hand side, Gram matrix and model coefficients, respectively. In a mild abuse of notation, we use the inner product both in the sense of a continuous and exact integral in (3.2) and a numerical approximation in (3.3) which depends on a chosen quadrature rule. Building off of its success in the ODE setting, we use the trapezoidal rule throughout, as it has been shown to yield nearly negligible quadrature error with the test functions employed below (see Section 4.1 and [28]). In this way, solving b = Gw^★ for the model coefficients w^★ allows for recovery of the PDE (3.1) without pointwise derivative approximations. The Gram matrix $G\in {ℝ}^{K\times SJ}$ and left-hand side $b\in {ℝ}^K$ defined in (3.3) conveniently take the same form regardless of the spatial dimension D, as their dimensions only depend on the number of test functions K and the size SJ of the model library, composed of J trial functions (f_j)_j∈[J] and S candidate differential operators enumerated by the multi-index set α := (α^s)_1≤s≤S.

3.1. Convolutional Weak Form and Discretization.

We now restrict to the case of each test function ψ_k being a translation of a reference test function ψ, i.e. ψ_k(x, t) = ψ(x_k − x, t_k − t) for some collection of points {(x_k, t_k)}_k∈[K] ⊂ (X, t) (referred to as the query points). The weak form of the dynamics (3.2) over the test function basis (ψ_k)_k∈[K] then takes the form of a convolution:

$$\left(D^{{\alpha }^0}\psi \right)\ast u\left(x_k,t_k\right)=\sum _{s=1}^S\sum _{i=1}^J{w}_{(s-1)J+j}^{\star }\left(D^{{\alpha }^s}\psi \right)\ast f_j(u)\left(x_k,t_k\right).$$ (3.4)

The sign factor ${(-1)}^{|{\alpha }^s|}$ appearing in (3.2) after integrating by parts is eliminated in (3.4) due to the sign convention in the integrand of the space-time convolution, which is defined by

$$\psi \ast u(x,t)≔{\int }_0^T{\int }_{\Omega }\psi (x-y,t-s)u(y,s)\mathit{\text{dyds}}=\langle \psi (x-\cdot ,t-\cdot ),u(\cdot ,\cdot )\rangle .$$

Construction of the linear system b = Gw^★ as a discretization of the convolutional weak form (3.4) over the query points (x_k, t_k)_k∈[K] can then be carried out efficiently using the FFT as we describe below.

To relate the continuous and discrete convolutions, we assume that the support of ψ is contained within some rectangular domain

$${\Omega }_R≔\left[-b_1,b_1\right]\times \cdots \times \left[-b_D,b_D\right]\times \left[-b_{D+1},b_{D+1}\right]\subset {ℝ}^D\times ℝ$$

where b_d = m_dΔx for d ∈ [D] and b_{D + 1} = m_{D + 1}Δt. We then define a reference computational grid $(Y,\mathfrak{t})\subset {ℝ}^D\times ℝ$ for ψ centered at the origin and having the same sampling rates (Δx, Δt) as the data U, where Y = Y₁ ⊗·⋯·⊗Y_D for $Y_d={(n\Delta x)}_{-m_d\le n\le m_d}$ and $\mathfrak{t}={(n\Delta t)}_{-m_{D+1}\le n\le m_{D+1}}$. In this way Y contains 2m_d + 1 points along each dimension d ∈ [D], with equal spacing Δx, and t contains 2m_{D + 1} + 1 points with equal spacing Δt. As with (X, t), points in (y_k, t_k) ∈ (Y, t) take the form

$$\left(y_k,{\mathfrak{t}}_k\right)=\left(Y_{k_1,\dots ,k_D},{\mathfrak{t}}_{k_{D+1}}\right)$$

where each index k_d for d ∈ [D + 1] takes values in the range {−m_d, … , 0, … , m_d}, and for valid indices k − j, the two grids (X, t) and (Y, t) are related by

$$\left({\text{x}}_k-{\text{x}}_j,t_k-t_j\right)=\left(y_{k-j},{\mathfrak{t}}_{k-j}\right).$$ (3.5)

We stress that (Y, t) is completely defined by the integers m = (m_d)_{d∈[D + 1]}, specified by the user, and that the values of m have a significant impact on the algorithm. For this reason we develop an automatic selection algorithm for m using spectral properties of the data U (see Appendix A).

The linear system (3.3) can now be rewritten

$$\{\begin{array}{c}{b}_k={\Psi }^0\ast U\left(x_k,t_k\right),\\ G_{k,(s-1)J+j}={\Psi }^s\ast f_j(U)\left(x_k,t_k\right),\end{array}$$ (3.6)

where ${\Psi }^s≔D^{{\alpha }^s}\psi (Y,\mathfrak{t})\Delta x^D\Delta t$ and the factor Δx^DΔt characterizes the trapezoidal rule. We define the discrete (D + 1)-dimensional convolution between Ψ^s and f_j(U) at a point $\left(x_k,t_k\right)=\left(X_{k_1,\dots ,k_D},t_{k_{D+1}}\right)\in (X,t)$ by

$${\Psi }^s\ast f_j(U)\left(x_k,t_k\right)≔\sum _{{\ell }_1=1}^{N_1}\cdots \sum _{{\ell }_{D+1}=1}^{N_{D+1}}{\Psi }_{k_1-{\ell }_1,\dots ,k_{D+1}-{\ell }_{D+1}}^s{f}_j\left(U_{{\ell }_1,\dots ,{\ell }_{D+1}}\right),$$

which, substituting the definition of Ψ^s,

$$≔\sum _{{\ell }_1=1}^{N_1}\cdots \sum _{{\ell }_{D+1}=1}^{N_{D+1}}{D}^{{\alpha }^s}\psi \left(Y_{k_1-{\ell }_1,\dots ,k_D-{\ell }_D},{\mathfrak{t}}_{k_{D+1}-{\ell }_{D+1}}\right)f_j\left(U_{{\ell }_1,\dots ,{\ell }_{D+1}}\right)\Delta x^D\Delta t$$ (3.7)

truncating indices appropriately and using (3.5),

$$=\sum _{{\ell }_1=k_1-m_1}^{k_1+m_1}\cdots \sum _{{\ell }_{D+1}=k_{D+1}-m_{D+1}}^{k_{D+1}+m_{D+1}}{D}^{{\alpha }^s}\psi \left(Y_{k_1-{\ell }_1,\dots ,k_D-{\ell }_D},{\mathfrak{t}}_{k_{D+1}-{\ell }_{D+1}}\right)f_j\left(U_{{\ell }_1,\dots ,{\ell }_{D+1}}\right)\Delta x^D\Delta t$$ (3.8)

$$=\sum _{{\ell }_1=k_1-m_1}^{k_1+m_1}\cdots \sum _{{\ell }_{D+1}=k_{D+1}-m_{D+1}}^{k_{D+1}+m_{D+1}}{D}^{{\alpha }^s}\psi \left(x_k-x_{\ell },t_k-t_{\ell }\right)f_j\left(U_{{\ell }_1,\dots ,{\ell }_{D+1}}\right)\Delta x^D\Delta t$$ (3.9)

$$\approx {\int }_0^T{\int }_{\Omega }{D}^{{\alpha }^s}\psi \left(x_k-x,t_k-t\right)f_j(u(x,t))dxdt.$$ (3.10)

3.2. FFT-based Implementation and Computational Complexity for Separable ψ.

Convolutions in the linear system (3.6) may be computed rapidly if the reference test function ψ is separable over the given coordinates, i.e.

$$\psi (x,t)={\varphi }_1\left(x_1\right)\cdots {\varphi }_2\left(x_D\right){\varphi }_{D+1}(t)$$

for univariate functions (ϕ_d)_{d∈[D + 1]}. In this case,

$$D^{{\alpha }^s}\psi (Y,\mathfrak{t})={\varphi }_1^{\left({\alpha }_1^s\right)}\left(Y_1\right)\otimes \cdots \otimes {\varphi }_D^{\left({\alpha }_D^s\right)}\left(Y_D\right)\otimes {\varphi }_{D+1}^{\left({\alpha }_{D+1}^s\right)}(\mathfrak{t}),$$

so that only the vectors

$${\varphi }_d^{\left({\alpha }_d^s\right)}\left(Y_d\right)\in {ℝ}^{2m_d+1},\hspace{1em}d\in [D]\hspace{1em}\text{ and }\hspace{1em}{\varphi }_{D+1}^{\left({\alpha }_{D+1}^s\right)}(\mathfrak{t})\in {ℝ}^{2m_{D+1}+1},$$

need to be computed for each 0 ≤ s ≤ S and the multi-dimensional arrays (Ψ^s)_{s=0, …, S} are never directly constructed. Convolutions can be carried out sequentially in each coordinate⁷, so that the overall cost of computing each column Ψ^s * f_j (U) of G is

$$T_I(N,n,D)≔CN\text{log}(N)\sum _{d=1}^{D+1}{N}^{D+1-d}{(N-n+1)}^{d-1},$$ (3.11)

if the computational grid (X, t) and reference grid (Y, t) have N and n ≤ N points along each of the D + 1 dimensions, respectively. Here CN log(N) is the cost of computing the 1D convolution between vectors vectors $x=\left(x_1,\dots ,x_n\right)\in {ℝ}^n$ and $y=\left(y_1,\dots ,y_N\right)\in {ℝ}^N$ using the FFT,

$$x\ast y=\mathcal{P}{\mathcal{F}}^{-1}\left(\mathcal{F}\left(x^0\right)\odot \mathcal{F}(y)\right),$$ (3.12)

where $x^0=\left(0,\dots ,0,x_1,\dots ,x_n\right)\in {ℝ}^N$, ⊙ denotes element-wise multiplication and $\mathcal{P}$ projects onto the first N − n + 1 components. The discrete Fourier transform $\mathcal{F}$ is defined

$${\mathcal{F}}_k(y)=\sum _{j=1}^N{y}_j{e}^{-2\pi i(j-1)(k-1)}$$

with inverse

$${\mathcal{F}}_k^{-1}(z)=\frac{1}{N}\sum _{j=1}^N{z}_j{e}^{2\pi i(j-1)(k-1)}.$$

The projection $\mathcal{P}$ ensures that the convolution only includes points that correspond to integrating over test functions ψ that are compactly supported in (X, t), which is necessary for integration by parts to hold in the weak form. The spectra of the test functions ${\varphi }_d^{\left({\alpha }_d^s\right)}\left(Y_d\right)$ can be precomputed and in principle each convolution Ψ^s * f_j(U) can be carried out in parallel⁸, making the total cost of the WSINDy Algorithm (4.2) in the PDE setting equal to (3.11) (ignoring the cost of the least-squares solves which are negligible in comparison to computing (G, b)). In addition, subsampling reduces the term (N − n + 1) in (3.11) to (N − n + 1)/s where s ≥ 1 is the subsampling rate such that (N − n + 1)/s points are kept along each dimension.

For most practical combinations of n and N, (say n > N/10 and N > 150) using the FFT and separability provides a considerable reduction in computational cost. See Figure 1 for a comparison between T_I and the naive cost T_II of an (N + 1)-dimensional convolution:

$$T_{II}(N,n,D)≔\left(2n^{D+1}-1\right){(N-n+1)}^{D+1}.$$ (3.13)

For example, with n = N/4 (a typical value) we have $T_{II}=\mathcal{O}\left(N^{2D+2}\right)$ and $T_I=\mathcal{O}\left(N^{D+1}\text{log}(N)\right)$, hence exploiting separability reduces the computational complexity by a factor of N^{D + 1}/log(N).

Figure 1.

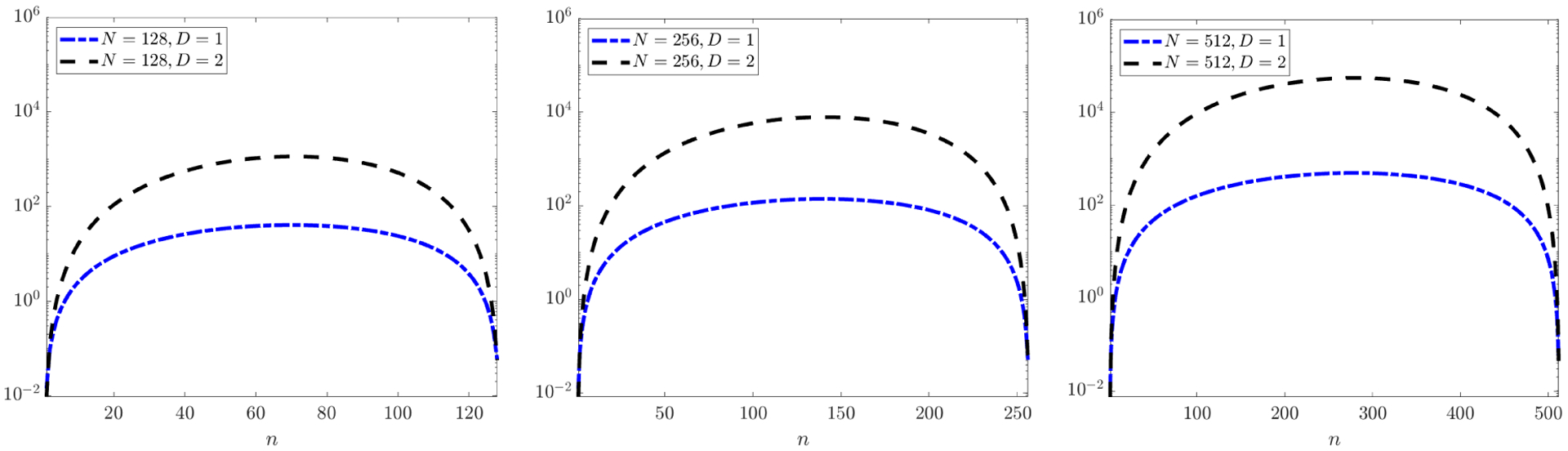
Reduction in computational cost of multi-dimensional convolution Ψ^s * f_j (U) when Ψ^s and f_j(U) have n and N points in each of D + 1 dimensions, respectively. Each plot shows the ratio T_II/T_I (equations (3.13) and (3.11)), i.e. the factor by which the separable FFT-based convolution reduces the cost of the naive convolution, for D + 1 = 2 and D + 1 = 3 space-time dimensions and n ∈ [N]. The right-most plot shows that when N = 512 and D + 1 = 3, the separable FFT-based convolution is 10⁴ times faster for 100 ≤ n ≤ 450.

4. WSINDy Algorithm for PDEs and Hyperparameter Selection

WSINDy for PDE discovery is given in Algorithm 4.2, where the user must specify each of the hyperparameters in Table 1. The key pieces of the algorithm are (i) the choice of reference test function ψ, (ii) the method of a sparsification, (iii) the method of regularization, (iv) selection of convolution query points {(x_k, t_k)}_k∈K, and (v) the model library. At first glance, the number of hyperparameters is quite large. We now discuss several simplifications that either reduce the number of hyperparameters or provide methods of choosing them automatically. In Section 4.1 we discuss connections between the convolutional weak form and spectral properties of ψ that determine the scheme’s robustness to noise and inform the selection of test function hyperparameters. In Section 4.2 we introduce a modified sequential-thresholding least-squares algorithm (MSTLS) which includes automatic selection of the threshold λ and allows for PDE discovery from large libraries. In Section 4.3 we describe how scale invariance of the PDE is used to rescale the data and coordinates in order to regularize the model recovery problem in the case of poorly-scaled data. In Sections 4.4 and 4.5 we briefly discuss selection of query points and an appropriate model library, however these components of the algorithm will be investigated more thoroughly in future research.

Table 1.

Hyperparameters for the WSINDy Algorithm 4.2. Note that f_j piecewise continuous is sufficient (we just need convergence of the trapezoidal rule), m may be replaced by a spectral-decay tolerance $\widehat{\tau }>0$ if test functions are automatically selected from the data using the method in Appendix A, and K is determined from m and s using (4.10).

Hyperparameter	Domain	Description
(fj)j∈[J]	$C(ℝ)$	trial function library
α = (αs)s=0,…,S	${\mathbb{N}}^{(S+1)\times (D+1)}$	partial derivative multi-indices
m = (md)d∈[D + 1]	${\mathbb{N}}^{D+1}$	discrete support lengths of 1D test functions (ϕd)d∈[D + 1]
s = (sd)d∈[D + 1]	${\mathbb{N}}^{D+1}$	subsampling frequencies for query points {(xk, tk)}k∈[K]
λ	[0, ∞)	search space for sparsity threshold $\widehat{\lambda }$
τ	(0, 1]	ψ real-space decay tolerance

4.1. Selecting a Reference Test Function ψ.

4.1.1. Convolutional Weak Form and Fourier Analysis.

Computation of G and b in (3.6) with ψ separable requires the selection of appropriate 1D coordinate test functions (ϕ_d)_{d∈[D + 1]}. Computing convolutions using the FFT (3.12) suggests a mechanism for choosing appropriate test functions. Define the Fourier coefficients of a function u ∈ L²([0, T]) by

$$\widehat{u}(k)=\frac{1}{\sqrt{T}}{\int }_0^{T}u(t)e^{-\frac{2\pi ik}{T}t}dt,\hspace{1em}k\in \mathbb{Z}.$$

Consider data $U=u(t)+ϵ\in {ℝ}^N$ for a T-periodic function u, $t_k=k\frac{T}{N}=k\Delta t$, and i.i.d. noise $ϵ~\mathcal{N}\left(0,{\sigma }^{2}I\right)$. The discrete Fourier transform of the noise $\mathcal{F}(ϵ)≔{ϵ}_R+i{ϵ}_I$ is then distributed ${ϵ}_R,{ϵ}_I~\mathcal{N}\left(0,\left(N{\sigma }^2/2\right)I\right)$. In addition, there exist constants C > 0 and ℓ > 1/2 such that $|{\widehat{u}}_k|\le C|k{|}^{-\ell }$ for each $k\in \mathbb{Z}$. There then exists a noise-dominated region of the spectrum $\mathcal{F}(U)$ determined by the noise-to-signal ratio

$$NS{R}_k≔\mathbb{E}\left[\frac{{|{\mathcal{F}}_k(ϵ)|}^2}{{|{\mathcal{F}}_k(u(t))|}^2}\right]=\frac{N{\sigma }^2}{{|{\mathcal{F}}_k(u(t))|}^2}\approx \frac{T{\sigma }^2}{N|\widehat{u}(k){|}^2}\ge \frac{1}{C^2}\Delta t{\sigma }^2{k}^{2\ell },$$

where ‘≈’ corresponds to omitting the aliasing error. For NSR_k ≥ 1 the kth Fourier mode is by definition noise-dominated, which corresponds to wavenumbers

$$|k|\ge k^{\ast }\approx {\left(\frac{C}{\sigma \sqrt{\Delta t}}\right)}^{1/\ell }.$$ (4.1)

If the critical wavenumber k* between the noise dominated (NSR_k ≥ 1) and signal-dominated (NSR_k ≤ 1) modes can be estimated from the dataset U, then it is possible to design test functions ψ such that the noise-dominated region of $\mathcal{F}(U)$ lies in the tail of $\widehat{\psi }$. The convolutional weak form (3.6) can then be interpreted as an approximate low-pass filter on the noisy dataset, offering robustness to noise without altering the frequency content of the data⁹.

In summary, spectral decay properties of the reference test function ψ serve to damp high-frequency noise in the convolutional weak form, which acts together with the natural variance-reducing effect of integration, as described in [13], to allow for quantification and control of the scheme’s robustness to noise. Specifically, coordinate test functions ϕ_d with wide support in real space (larger m_d) will reduce more variance, but will have a faster-decaying spectrum ${\widehat{\varphi }}_d$, so that signal-dominated modes may not be resolved, leading to model misidentification. On the other hand, if ϕ_d decays too swiftly in real space (smaller m_d), then the spectrum ${\widehat{\varphi }}_d$ will decay more slowly and may put too much weight on noise-dominated frequencies. In addition, smaller m_d may not sufficiently reduce variance. A balance must be struck between (a) effectively reducing variance, which is ultimately determined by the decay of ψ in physical space, and (b) resolving the underlying dynamics, determined by the decay of $\widehat{\psi }$ in Fourier space.

4.1.2. Piecewise-Polynomial Test Functions.

Many test functions achieve the necessary balance between decay in real space and decay in Fourier space in order to offer both variance reduction and resolution of signal-dominated modes (defined by (4.1)). For simplicity, in this article we use the same test function space used in the ODE setting [28] and leave an investigation of the performance of different test functions to future work. Define $\mathcal{S}$ to be the space of functions

$$\varphi (v)=\{\begin{array}{ll}C{(v-a)}^p{(b-v)}^q\hfill & a<v<b,\hfill \\ 0\hfill & \text{otherwise,}\hfill \end{array}$$ (4.2)

where p, q ≥ 1 and v is a variable in time or space. The normalization

$$C=\frac{1}{p^p{q}^q}{\left(\frac{p+q}{b-a}\right)}^{p+q}$$

ensures that ‖ϕ‖_∞ = 1. Functions $\varphi \in \mathcal{S}$ are non-negative, unimodal, compactly-supported in [a, b], and have ⌊min{p, q}⌋ weak derivatives¹⁰. Larger p and q imply faster decay towards the endpoints (a, b) and for p = q we refer to p as the degree of ϕ. See Figure 2 for a visualization of ψ and partial derivatives $D^{{\alpha }^s}\psi$ constructed from tensor products of functions from $\mathcal{S}$. In addition to having nice integration properties combined with the trapezoidal rule (see Lemma 1 of [28]), (a, b, p, q) can be chosen to localize $\widehat{\varphi }$ around signal-dominated frequencies in $\mathcal{F}(U)$ using the fact that for any reference domain length L ≥ |b − a|,

$$|\widehat{\varphi }(k)|=o\left({\left(\frac{|b-a|}{L}|k|\right)}^{-\lfloor \text{min}\{p,q\}\rfloor -1/2}\right).$$

Figure 2.

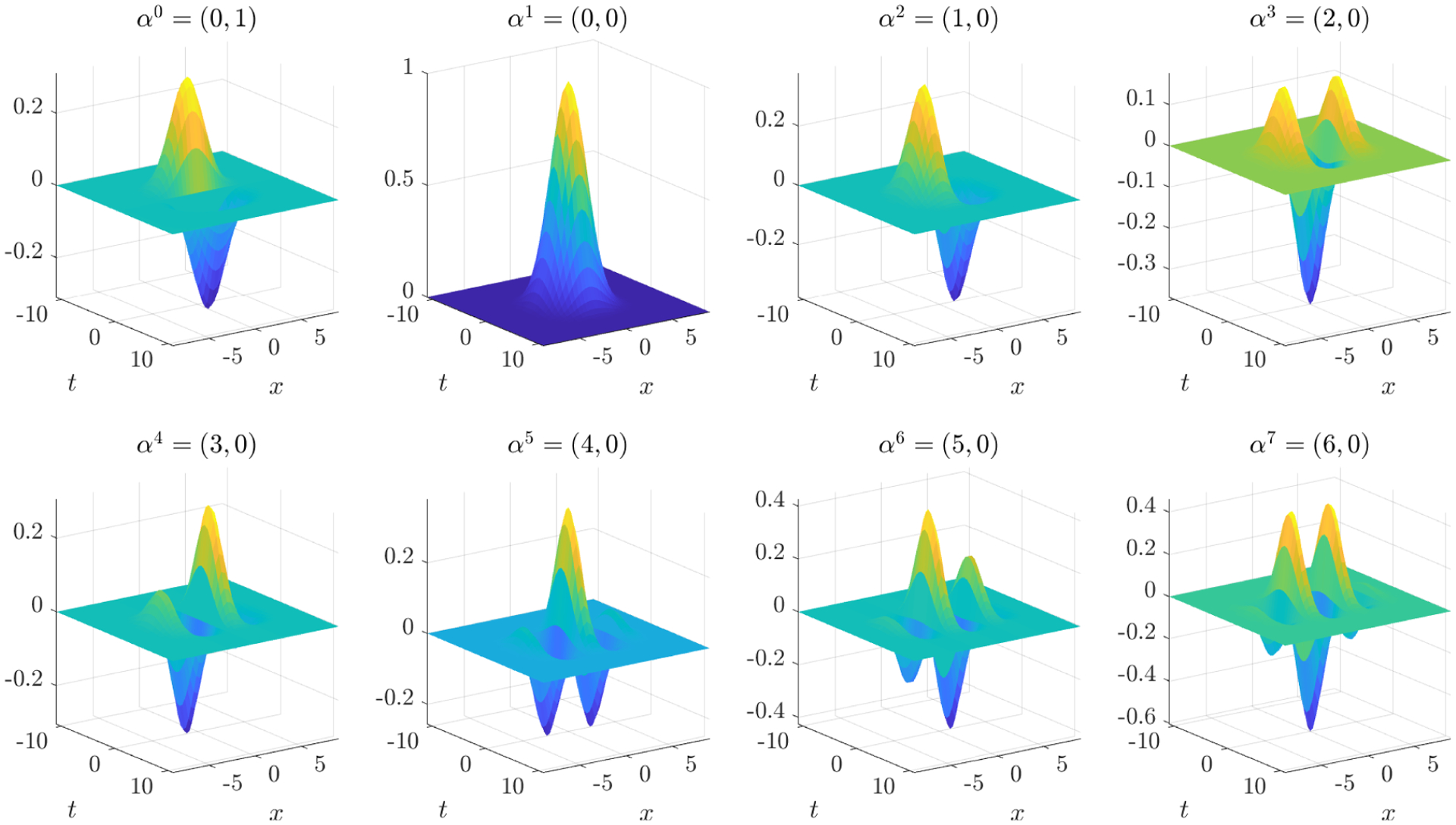
Plots of reference test function ψ and partial derivatives $D^{{\alpha }^s}\psi$ used for identification of the Kuramoto-Sivashinsky equation. The upper left plot shows ∂_tψ, the bottom right shows ${\partial }_x^6\psi$. See Tables 2–4 for more details.

To assemble the reference test function ψ from one-dimensional test functions ${\left({\varphi }_d\right)}_{d\in [D+1]}\subset \mathcal{S}$ along each coordinate, we must determine the parameters (a_d, b_d, p_d, q_d) in the formula (4.2) for each ϕ_d. For convenience we center (Y, t) at the origin so that each ϕ_d is supported on a centered interval [a_d, b_d] = [−b_d, b_d], where b_d = m_dΔx for d ∈ [D] and b_{D + 1} = m_{D + 1}Δt, and set p_d = q_d so that ψ is symmetric¹¹. In this way only m ≔ (m_d)_{d∈[D + 1]} and degrees p ≔ (p_d)_{d∈[D + 1]} need to be specified, hence the vectors ${\left({\varphi }_d^{\left({\alpha }_d^s\right)}\left(Y_d\right)\right)}_{0\le s\le S}$ can be computed from an analogous function ${\overline{\varphi }}_{p_d}$ with support [−1, 1],

$${\overline{\varphi }}_{p_d}(v)≔\{\begin{array}{ll}{\left(1-v^2\right)}^{p_d},\hfill & -1<v<1\hfill \\ 0,\hfill & \text{otherwise,}\hfill \end{array}$$

using

$${\varphi }_d^{\left({\alpha }_d^s\right)}\left(Y_d\right)=\frac{1}{b_d^{{\alpha }_d^s}}{\overline{\varphi }}_{p_d}^{\left({\alpha }_d^s\right)}\left(\frac{Y_d}{b_d}\right)=\frac{1}{{\left(m_d\Delta \right)}^{{\alpha }_d^s}}{\overline{\varphi }}_{p_d}^{\left({\alpha }_d^s\right)}\left(n_d\right),$$

where $n_d≔\left\{-1+\frac{n}{m_d}:n\in \left\{0,\dots ,2m_d\right\}\right\}$ is an associated scaled grid and Δ ∈ {Δx, Δt}.

The discrete support lengths m and degrees p determine the smoothness of ψ, as well as its decay in real and in Fourier space, hence are critical to the method’s performance. The degrees p can be chosen from m to ensure necessary smoothness and decay in real space using

$$p_d=\text{min }\left\{p\ge {\overline{\alpha }}_d+1:{\overline{\varphi }}_p\left(1-\frac{1}{m_d}\right)\le \tau \right\},$$ (4.3)

where ${\overline{\alpha }}_d≔{\text{max}}_{0\le s\le S}\left({\alpha }_d^s\right)$ is the maximum derivative along the dth coordinate and τ is a chosen (real-space) decay tolerance. By enforcing that ϕ_d decays to τ at the first interior gridpoint of its support, (4.3) controls the integration error (specifically, $\tau \le {\left(\frac{2m_d-1}{m_d^2}\right)}^q$ ensures $\mathcal{O}\left(\Delta x^{q+1}\right)$ integration error for noise-free data), while $p\ge {\overline{\alpha }}_d+1$ ensures that ${\varphi }_d\in C^{{\overline{\alpha }}_d}(ℝ)$, which is necessary to integrate by parts as many times as required by the multi-index set α. The steps for arriving at the test function values on the reference grid ${\left({\varphi }_d^{\left({\alpha }_d^s\right)}\left(Y_d\right)\right)}_{0\le s\le S}$ are contained in Algorithm 4.1.

In the examples below, we set τ = 10⁻¹⁰ throughout¹² and we use the method introduced in Appendix A to choose m, which involves estimating the critical wavenumber k* (defined in (4.1)) between noise-dominated and signal-dominated modes of $\mathcal{F}(U)$. We also simplify things by choosing a single test function for all spatial coordinates, ϕ_x = ϕ₁ = ϕ₂ = ⋯ = ϕ_D where ϕ_x has degree p_x and support m_x, and a (possibly different) test function ϕ_t = ϕ_{D + 1} for the time axis with degree p_t and support m_t (recall that subscripts x and t are indices, not partial derivatives). This convention is used in the following sections.

4.2. Sparsification.

To enforce a sparse solution we present a modified sequential-thresholding least-squares algorithm MSTLS(G, b; λ), defined in (4.6), which accounts for terms that are outside of the dominant balance physics of the data, as determined by the left-hand side b, as well as terms with small coefficients. We then utilize the loss function

$$\mathcal{L}(\lambda )=\frac{{\Vert G\left(w^{\lambda }-w^{LS}\right)\Vert }_2}{{\Vert G{w}^{LS}\Vert }_2}+\frac{\text{\#}\left\{{\mathcal{I}}^{\lambda }\right\}}{SJ}$$ (4.4)

to select an optimal threshold $\widehat{\lambda }$, where w^λ is the output of MSTLS(G, b; λ) defined in equation (4.6), #{·} denotes cardinality, ${\mathcal{I}}^{\lambda }≔\left\{1\le i\le SJ:{\text{w}}_i^{\lambda }\ne 0\right\}$ is the index set of non-zero coefficients of w^λ, w^LS ≔ (G^TG)⁻¹G^Tb is the least squares solution, and SJ is the total number of terms in the library (S differential operators and J functions of the data). The first term in $\mathcal{L}$ penalize the distance between Gw^LS (the projection of b onto the range of G) and Gw^λ (the projection of b onto the columns of G restricted to ${\mathcal{I}}^{\lambda }$), while the second term penalizes the number of nonzero terms in the resulting model. The normalization simply enforces $\mathcal{L}(0)=\mathcal{L}(\infty )=1$.

The MSTLS(G, b; λ) iteration is as follows. For a given λ ≥ 0, define the set of lower bounds L^λ and upper bound U^λ by

$$\{\begin{array}{l}{L}_i^{\lambda }=\lambda \text{max}\left\{1,\frac{\parallel b\parallel }{\Vert G_i\Vert }\right\}\hfill \\ U_i^{\lambda }=\frac{1}{\lambda }\text{min}\left\{1,\frac{\parallel b\parallel }{\Vert G_i\Vert }\right\}\hfill \end{array},\hspace{1em}1\le i\le SJ.$$ (4.5)

Then with w⁰ = w^LS, define the iterates

$$\text{MSTLS}(G,b;\lambda )\{\begin{array}{c}{\mathcal{I}}^{\ell }=\left\{1\le i\le SJ:L_i^{\lambda }\le |w_i^{\ell }|\le U_i^{\lambda }\right\}\\ w^{\ell +1}={\text{argmin}}_{\text{supp}(w)\subset {\mathcal{I}}^{\ell }}\parallel Gw-b{\parallel }_2^2.\end{array}$$ (4.6)

The constraint $L_i^{\lambda }\le |w_i^{\ell }|\le U_i^{\lambda }$ is clearly more restrictive than standard sequential thresholding, but it enforces two desired qualities of the model: (i) that the coefficients w^λ do not differ too much from 1, since 1 is the coefficient of the “evolution” term $D^{{\alpha }^0}u$ (assumed known), and (ii) that the ratio ‖w_iG_i‖₂/‖b‖₂ lies in [λ, λ⁻¹], enforcing an empirical dominant balance rule (e.g. λ = 0.01 allows terms in the model to be at most two orders of magnitude from $D^{{\alpha }^0}u$. Using previous results on the convergence of STLS [60], for MSTLS(G, b; λ) we employ the stopping criteria ${\mathcal{I}}^{\ell }\backslash {\mathcal{I}}^{\ell +1}=\cancel{0}$, which must occur for some ℓ ≤ SJ. The overall sparsification algorithm MSTLS(G, b; $\mathcal{L}$, λ) is

$$\text{MSTLS}(G,b;\mathcal{L},\mathbf{\lambda })\hspace{1em}\{\begin{array}{l}\widehat{\lambda }=\text{min }\left\{\lambda \in \mathbf{\lambda }:\mathcal{L}(\lambda )=\underset{\lambda \in \mathbf{\lambda }}{\text{min }}\mathcal{L}(\lambda )\right\}\hfill \\ \widehat{w}=\text{MSTLS}(G,b;\widehat{\lambda }),\hfill \end{array}$$ (4.7)

where λ is a finite set of candidate thresholds¹³. The learned threshold $\widehat{\lambda }$ is the smallest minimizer of $\mathcal{L}$ over the range λ and hence marks the boundary between identification and misidentification of the minimum-cost model, such that $\{\lambda \in \mathbf{\lambda }:\lambda <\widehat{\lambda }\}$ results in overfitting. A similar learning method for $\widehat{\lambda }$ combining STLS and Tikhonov regularization (or ridge regression) was developed in [39]. We have found that our approach of combining MSTLS(G, b; $\mathcal{L}$, λ) with rescaling, as introduced in the next section, regularizes the sparse regression problem in the case of large model libraries without adding hyperparameters¹⁴ and definitely deserves further study.

4.3. Regularization through Rescaling.

Construction of the linear system b = Gw involves taking nonlinear transformations of the data f_j(U) and then integrating against $D^{{\alpha }^s}\psi$, which oscillates for large |α^s|. This can lead to a large condition number κ(G) and prevent accurate inference of the true model coefficients w^★, especially when the underlying data is poorly scaled¹⁵. In particular, identification of polynomial terms such as ∂_x(u²) from a large library of polynomial terms is ill-conditioned for large (or small) amplitude data. Naively rescaling the data can easily lead to unreliable inference of model coefficients, since characteristic scales often effect the dynamics in nontrivial ways. For example, solution amplitude determines the wavespeed in the inviscid Burgers and Korteweg-de Vries equations, hence the solution and space-time coordinates must be rescaled in a principled manner in order to preserve the dynamics. To overcome this problem we propose to rescale the data using scale invariance of the PDE and choose scales that achieve a lower condition number, as described below. This approach allows for reliable identification of the Burgers and KdV equations from highly-corrupted large-amplitude data $(U~\mathcal{O}\left({10}^3\right)$, see Section 5.4).

First, we note that the true model is scale invariant in the following way. If u solves (3.1), then for any scales γ_x, γ_t, γ_u > 0, the rescaled function

$$\tilde{u}(\tilde{x},\tilde{t})≔{\gamma }_{u}u\left(\frac{\tilde{x}}{{\gamma }_x},\frac{\tilde{t}}{{\gamma }_t}\right)≔{\gamma }_{u}u(x,t)$$

solves

$${\tilde{D}}^{{\alpha }^0}\tilde{u}=\sum _{s=1}^S\sum _{j=1}^J{\tilde{w}}_{(s-1)J+j}{\tilde{D}}^{{\alpha }^s}{\tilde{f}}_j(\tilde{u})$$

where ${\tilde{D}}^{{\alpha }^s}$ denotes differentiation with respect to $(\tilde{x},\tilde{t})=\left({\gamma }_{x}x,{\gamma }_{t}t\right)$. For homogeneous functions f_j with power β_j, we have ${\tilde{f}}_j(\tilde{u})=f_j(\tilde{u})={\gamma }_u^{{\beta }_j}{f}_j(u)$, otherwise ${\tilde{f}}_j(\tilde{u})=f_j\left(\frac{\tilde{u}}{{\gamma }_u}\right)=f_j(u)$ (in which case we set β_j = 0). The linear system in the rescaled coordinates $\tilde{b}=\tilde{G}\tilde{w}$ is constructed by discretizing the convolutional weak form as before but with a reference test function $\tilde{\psi }$ on the rescaled grid ${\tilde{\Omega }}_R$. We recover the coefficients¹⁶ $\widehat{w}$ at the original scales by setting $\widehat{w}=M\tilde{w}$, where M = diag(μ) is the diagonal matrix with entries

$${\mu }_{(s-1)J+j}≔{\gamma }_u^{-\left({\beta }_j-1\right)}{\gamma }_x^{{\sum }_{d=1}^D\left({\alpha }_d^s-{\alpha }_d^0\right)}{\gamma }_t^{\left({\alpha }_{D+1}^s-{\alpha }_{D+1}^0\right)}.$$ (4.8)

There is flexibility in choosing the scales γ_u, γ_x, γ_t, and a natural choice is to enforce that the columns of $\tilde{G}$ are similar in norm. Motivated by this, we find that for polynomial and trigonometric libraries, the scales¹⁷

$${\gamma }_u={\left(\frac{\Vert U{\Vert }_{2^{\prime }}}{{\Vert U^{\overline{\beta }}\Vert }_{2^{\prime }}}\right)}^{1/\overline{\beta }},\hspace{1em}{\gamma }_x=\frac{1}{m_x\Delta x}{\left(\left(\frac{\underset{{\overline{\alpha }}_x}{p_x}}{2}\right){\overline{\alpha }}_x!\right)}^{1/{\overline{\alpha }}_x},\hspace{1em}{\gamma }_t=\frac{1}{m_t\Delta t}{\left(\left(\frac{\underset{{\overline{\alpha }}_t}{p_t}}{2}\right){\overline{\alpha }}_t!\right)}^{1/{\overline{\alpha }}_t}$$ (4.9)

are sufficient to regularize ill-conditioning due to poor scaling. Here ${\overline{\alpha }}_x$ and ${\overline{\alpha }}_t$ are the maximum spatial and temporal derivatives appearing in the library and $\overline{\beta }={\text{max}}_j{\beta }_j$ is the highest monomial power of the functions (f_j)_j∈[J]. From (4.9) we get that

$${\Vert {\tilde{U}}^{\overline{\beta }}\Vert }_{2^{\prime }}=\Vert U{\Vert }_{2^{\prime }}$$

and

$${\text{max}}_s{\Vert {\Psi }^s\Vert }_{1^{\prime }}\le \underset{s}{\text{max}}{\Vert D^{{\alpha }^s}\tilde{\psi }\Vert }_{\infty }|{\tilde{\Omega }}_R|\le |{\tilde{\Omega }}_R|,$$

hence, using Young’s inequality for convolutions,

$${\Vert {\Psi }^s*{\tilde{U}}^{\overline{\beta }}\Vert }_{2^{\prime }}\le {\Vert {\Psi }^s\Vert }_{1^{\prime }}{\Vert {\tilde{U}}^{\overline{\beta }}\Vert }_{2^{\prime }}\le |{\tilde{\Omega }}_R|\Vert U{\Vert }_{2^{\prime }}.$$

This shows that with scales γ_u, γ_x, γ_t set according to (4.9), the columns of $\tilde{G}$ are close in norm to the original dataset U. Similar scales γ_x, γ_t, γ_u can be chosen for different model libraries and reference test functions, and a more refined analysis will lead to scales that achieve closer agreement in norm. In the examples below we rescale the data and coordinates according to (4.9), which results in a low condition number $\kappa (\tilde{G})$ (see Table 4). Throughout what follows, quantities defined over scaled coordinates will be denoted by tildes.

Table 4.

Additional specifications resulting from the choices in Table 3. The last column shows the start-to-finish walltime of Algorithm 4.2 with all computations in serial measured on a laptop with an 8-core Intel i7-2670QM CPU with 2.2 GHz and 8 GB of RAM.

PDE	$\tilde{G}$	$\kappa \left(\tilde{G}\right)$	(Px, Pt)	(γu, γx, γt)	Walltime (sec)
IB	784 × 43	1.4 × 106	(7, 7)	(4.5 × 10−4, 0.0029, 1.1)	0.12
KdV	1443 × 43	3.2 × 106	(8, 7)	(5.7 × 10−4, 8.3, 1250)	0.39
KS	1806 × 43	3.7 × 103	(10, 10)	(0.26, 0.74, 0.091)	0.24
NLS	1804 × 190	1.2 × 105	(11, 10)	(0.33, 3.1, 9.4)	2.5
PM	4608 × 65	2.4 × 104	(8, 10)	(1.6, 2.7, 3.2)	16
SG	13000 × 73	1.3 × 104	(8, 10)	(0.23, 8.1, 8.1)	29
RD	11638 × 181	4.5 × 103	(13, 12)	(0.86, 6.5, 1.4)	75
NS	3872 × 50	8.2 × 102	(9, 12)	(0.53, 0.72, 2.4)	12

4.4. Query Points and Subsampling.

Placement of {(x_k, t_k)}_k∈[K] determines which regions of the observed data will most influence the recovered model¹⁸. In WSINDy for ODEs ([28]), an adaptive algorithm was designed for placement of test functions near steep gradients along the trajectory. Improvements in this direction in the PDE setting are a topic of active research, however, for simplicity in this article we uniformly subsample {(x_k, t_k)}_k∈[K] from (X, t) using subsampling frequencies s = (s₁, … , s_{D + 1}) along each coordinate, specified by the user. That is, along each one-dimensional grid $X_d,\lfloor \frac{N_d-2m_d}{s_d}\rfloor$ points are selected with uniform spacing s_dΔx for d ∈ [D] and s_{D + 1}Δt for d = D + 1. This results in a (D + 1)-dimensional coarse grid with dimensions $\lfloor \frac{N_1-2m_1}{s_1}\rfloor \times \cdots \times \lfloor \frac{N_{D+1}-2m_{D+1}}{s_{D+1}}\rfloor ,$, which determines the number of query points

$$K=\prod _{d=1}^{D+1}\lfloor \frac{N_d-2m_d}{s_d}\rfloor .$$ (4.10)

4.5. Model Library.

The model library is determined by the nonlinear functions (f_j)_j∈[J] and the partial derivative indices α and is crucial to the well-posedness of the recovery problem. In the examples below we choose (f_j)_j∈[J] to be polynomials and trigonometric functions as these sets are dense in many relevant function spaces. When the true PDE does not contain cross derivatives (e.g. $\frac{{\partial }^2}{\partial x_1\partial x_2}$), we remove them from the derivative library α and note that including these terms does not have a significant impact on the results.

5. Examples

We now demonstrate the effectiveness of WSINDy by recovering the PDEs listed in Table 2 over a range of noise levels. These examples show that WSINDy provides orders of magnitude improvements over derivative-based methods [39], with reliable and accurate recovery of four out of the eight PDEs under noise levels as high as 100% (defined in (5.1) and (5.2)) and for all examples under 20% noise. In contrast to the weak recovery methods in [37, 13], WSINDy uses (i) the convolutional weak form (3.6) and FFT-based implementation (3.12), (ii) improved thresholding and automatic selection of the sparsity threshold $\widehat{\lambda }$ via (4.6) and (4.7), and (iii) rescaling using (4.9). The effects of these improvements are discussed in Sections 5.4 and 5.5.

Table 2.

PDEs used in numerical experiments, written in the form identified by WSINDy. Domain specification and boundary conditions are given in Appendix B.

Inviscid Burgers (IB)	${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)$
Korteweg-de Vries (KdV)	${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)-{\partial }_{xxx}u$
Kuramoto-Sivashinsky (KS)	${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)-{\partial }_{xx}u-{\partial }_{\mathit{\text{xxxx}}}u$
Nonlinear Schrödinger (NLS)	$\{\begin{array}{l}{\partial }_{t}u=\frac{1}{2}{\partial }_{xx}v+u^{2}v+v^3\hfill \\ {\partial }_{t}v=-\frac{1}{2}{\partial }_{xx}u-u{v}^2-u^3\hfill \end{array}$
Anisotropic Porous Medium (PM)	∂tu = (0.3) ∂xx (u2) − (0.8) ∂xy (u2) + ∂yy (u2)
Sine-Gordon (SG)	∂ttu = ∂xxu + ∂yyu − sin (u)
Reaction-Diffusion (RD)	$\{\begin{array}{l}{\partial }_{t}u=\frac{1}{10}{\partial }_{xx}u+\frac{1}{10}{\partial }_{yy}u-u{v}^2-u^3+v^3+u^{2}v+u\hfill \\ {\partial }_{t}v=\frac{1}{10}{\partial }_{xx}v+\frac{1}{10}{\partial }_{yy}v+v-u{v}^2-u^3-v^3-u^{2}v\hfill \end{array}$
2D Navier-Stokes (NS)	${\partial }_t\omega =-{\partial }_x(\omega u)-{\partial }_y(\omega v)+\frac{1}{100}{\partial }_{xx}\omega +\frac{1}{100}{\partial }_{yy}\omega$

To test robustness to noise, a noise ratio σ_NR is specified and a synthetic “observed” dataset

$$U=U^{\star }+ϵ$$

is obtained from a simulation U^★ of the true PDE¹⁹ by adding i.i.d. Gaussian noise with variance σ² to each data point, where

$$\sigma ≔{\sigma }_{NR}{\Vert U^{\star }\Vert }_{RMS}≔{\sigma }_{NR}{\left(\frac{1}{\left(N_1\cdots N_D{N}_{D+1}\right)}\sum _{k_1=1}^{N_1}\cdots \sum _{k_{D+1}=1}^{N_{D+1}}{\left(U_{k_1,\dots ,k_{D+1}}^{\star }\right)}^2\right)}^{1/2}.$$ (5.1)

We examine noise ratios σ_NR in the range [0, 1] and often refer to the noise level as σ_NR or equivalently that the data contains 100σ_NR% noise. We note that the resulting true noise ratio

$${\sigma }_{NR}^{\star }≔\frac{\Vert ϵ{\Vert }_{RMS}}{{\Vert U^{\star }\Vert }_{RMS}}$$ (5.2)

matches the specified σ_NR to at least four significant digits in all cases and so we only list σ_NR. When the state variable is vector-valued, as with the nonlinear Schrödinger, reaction-diffusion, and Navier-Stokes equations (see Table 2), a separate noise variance σ² is computed for each vector component so that the noise ratio σ_NR of each component satisfies (5.2).

5.1. Performance Measures.

To measure the ability of the algorithm to correctly identify the terms having nonzero coefficients, we use the true positivity ratio (introduced in [22]) defined by

$$\text{TPR}(\widehat{w})=\frac{\text{TP}}{\text{TP}+\text{FN}+\text{FP}}$$ (5.3)

where TP is the number of correctly identified nonzero coefficients, FN is the number of coefficients falsely identified as zero, and FP is the number of coefficients falsely identified as nonzero. Identification of the true model results in a TPR of 1, while identification of half of the correct nonzero terms and no falsely identified nonzero terms results in TPR of 0.5 (e.g. the 2D Euler equations ∂_tω = −∂_x(ωu) − ∂_y(ωv) result in a TPR of 0.5 if the underlying true model is the 2D Navier-Stokes vorticity equation). We will see that in several cases that the average TPR remains above 0.95 even as the noise level approaches 1. The loss function $\mathcal{L}(\lambda )$ (defined in (4.4)) and the resulting learned sparsity threshold $\widehat{\lambda }$ (defined in (4.7)) provide additional information on the algorithm’s ability to identify the correct model terms with respect to the noise level. In particular, sensitivity to the sparsity threshold suggests that automatic selection of $\widehat{\lambda }$ is essential to successful recovery in the relatively large noise regime.

To assess the accuracy of the recovered coefficients we use two metrics. We measure the maximum error in the true non-zero coefficients using

$$E_{\infty }(\widehat{w})≔\underset{\left\{j:w_j^{*}\ne 0\right\}}{\text{max}}\frac{|{\widehat{w}}_j-w_j^{\star }|}{|w_j^{\star }|},$$ (5.4)

where |·| denotes absolute value, and the ℓ² distance in parameter space using

$$E_2(\widehat{w})≔\frac{{\Vert \widehat{w}-w^{\star }\Vert }_{RMS}}{{\Vert w^{\star }\Vert }_{RMS}}.$$ (5.5)

E_∞ determines the number of significant digits in the recovered true coefficients while E₂ provides information about the magnitudes of coefficients that are falsely identified as nonzero. Often when a term is falsely identified and the resulting nonzero coefficient is small, a larger sparsity factor will result in idenfitication of the true model.

Finally, when $\text{TPR}(\widehat{w})=1$, we report the prediction accuracy between the true data U^★ and a numerical solution U^dd to the data-driven PDE using the same initial conditions. We compute the relative L₂ error $P_t(\widehat{w})$ at time t = 0.5T (i.e. at the half-way point in time) defined by

$$P_t(\widehat{w})≔\frac{{\Vert U_t^{dd}-U_t^{\star }\Vert }_{RMS}}{{\Vert U_t^{\star }\Vert }_{RMS}}$$ (5.6)

Where $U_t^{dd}$, $U_t^{\star }$ denote the numerical solutions over the spatial domain at time t. Since solutions to the data-driven dynamics and the true dynamics will eventually drift apart, we also measure

$$T_{\text{tol}}(\widehat{w})≔\frac{1}{T}\text{inf}\left\{t\in [0,T]:P_t(\widehat{w})>\text{tol}\right\},$$ (5.7)

or, the first time t (relative to the final time T) that the numerical solution $U_t^{dd}$ reaches a relative L₂ distance of tol from the truth. The minimum in (5.7) is computed over t ∈ t and we set tol = 0.1. We provide results for $P_{0.5T}(\widehat{w})$ and $T_{0.1}(\widehat{w})$ averaged over the weights $\widehat{w}$ satisfying $\text{TPR}(\widehat{w})=1$.

For each system in Table 2 and each noise level σ_NR ∈ {0.025q : q ∈ {0, … , 40}} we run WSINDy on 200 instantiations of noise²⁰ and average the results of error statistics (5.3)–(5.7). Computations were carried out on a University of Colorado Boulder Blanca Condo cluster²¹.

5.2. Implementation Details.

The hyperparameters used in WSINDy applied to each of the PDEs in Table 2 are given in Table 3. To select test function discrete support lengths we used a combination of the changepoint method²² described in Appendix A and manual tuning. Across all examples the real-space decay tolerance for test functions is fixed at τ = 10⁻¹⁰.

Table 3.

WSINDy hyperparameters used to identify each example PDE.

PDE	U	f j	α	(mx, mt)	(sx, st)
IB	256 × 256	(uj−1)j∈[7]	((ℓ, 0))0≤ℓ≤6	(60, 60)	(5, 5)
KdV	400 × 601	(uj−1)j∈[7]	((ℓ, 0))0≤ℓ≤6	(45, 80)	(8, 12)
KS	256 × 301	(uj−1)j∈[7]	((ℓ, 0))0≤ℓ≤6	(23, 22)	(5, 6)
NLS	2 × 256 × 251	(uivj)0≤i + j≤6	((ℓ, 0))0≤ℓ≤6	(19, 25)	(5, 5)
PM	200 × 200 × 128	(ui−1)i∈[5]	${\left(\left({\mathcal{l}}_1,{\mathcal{l}}_2,0\right)\right)}_{0\le {\mathcal{l}}_1,{\mathcal{l}}_2\le 4}$	(37, 20)	(8, 5)
SG	129 × 403 × 205	(uj−1)i∈[5], (sin(ju), cos(ju))j=1, 2	((ℓ, 0, 0), (0, ℓ, 0))0≤ℓ≤4	(40, 25)	(5, 8)
RD	2 × 256 × 256 × 201	(uivj)0≤i + j≤4	((ℓ, 0, 0), (0, ℓ, 0))0≤ℓ≤5	(13, 14)	(13, 12)
NS	3 × 324 × 149 × 201	$\{\begin{array}{ll}{\left({\omega }^i{u}^j{v}^k\right)}_{0\le i+j+k\le 2},\hfill & |{\alpha }^s|=0\hfill \\ {\left({\omega }^i{u}^j{v}^k\right)}_{0\le i+j+k\le 3,i>0},\hfill & |{\alpha }^s|>0\hfill \end{array}$	((ℓ, 0, 0), (0, ℓ, 0))0≤ℓ≤2	(31, 14)	(12, 8)

In computing a sparse solution $\widehat{w}=\text{MSTLS}(G,b;\mathcal{L},\mathbf{\lambda })$ (see equation (4.7)), the search space λ for the learned threshold $\widehat{\lambda }$ is fixed for all examples at:

$$\lambda =\left\{{10}^{-4+j\frac{4}{49}}:j\in \{0,\dots ,49\}\right\},$$

in other words λ contains 50 points with log₁₀(λ) equally spaced from −4 to 0. This implies a stopping criteria of 50SJ thresholding iterations²³.

We fix the subsampling frequencies (s_x, s_t) to $\left(\frac{N_1}{50},\frac{N_2}{50}\right)$ for PDEs in one spatial dimension and to $\left(\frac{N_1}{25},\frac{N_3}{25}\right)$ for two spatial dimensions, where the dimensions (N₁, N₂, N₃) depend on the dataset. Additional information about the convolutional weak discretization is included in Table 4, such as the dimensions and condition number of the rescaled Gram matrix $\tilde{G}$ (computed from a typical dataset with 20% noise), test function polynomial degrees (p_x, p_t), scale factors (γ_u, γ_x, γ_t), and start-to-finish walltime of Algorithm 4.2 with all computations performed serially on a laptop with an 8-core Intel i7-2670QM CPU with 2.2 GHz and 8 GB of RAM.

5.3. Comments on Chosen Examples.

The primary reason for choosing the examples in Table 2 is to demonstrate that WSINDy can successfully recover models over a wide range of physical phenomena such as spatiotemporal chaos, nonlinear waves, nonlinear diffusion, shock-forming solutions, complex limit cycles, and pattern formation in reaction diffusion equations.

Recovery of the inviscid Burgers and anisotropic porous medium equations demonstrates (i) that WSINDy can discover PDEs from solutions that can only be understood in a weak sense and (ii) that discovery in this case is just as accurate and robust to noise and scaling as with smooth data (i.e. no special modifications of the algorithm are required to discover models from non-smooth data, as conjectured in [13]). We use analytical weak solutions, with inviscid Burgers data forming a shock which propagates at constant speed (see Figure 3 for plots of the characteristic curves) and porous medium data having a jump in the gradient ∇u. In addition, we discover the porous medium equation using an anisotropic diffusivity tensor to demonstate that WSINDy can identify the cross-diffusion term ∂_xy(u²) to high accuracy from a large candidate model library.

The inviscid Burgers and Korteweg-de Vries equations demonstrate that WSINDy successfully recovers the correct models for nonlinear transport data with large amplitude. Both datasets have mean amplitudes on the order of 10³ (in addition KdV is given over a short time window of t ∈ [0, 10⁻³]), and hence are not identifiable from large polynomial libraries using naive approaches. The sparsification and rescaling measures in Sections 4.2 and 4.3 are essential to removing this barrier.

The Sine-Gordon equation²⁴ is used to show both that trigonometric library terms can easily be identified alongside polynomials and that hyperbolic problems do not seem to present further challenges. Discovery of the Sine-Gordon equation also appears to be particularly robust to noise, which suggests that the added complexity of having multiple spatial dimensions is not in general a barrier to identification.

For the nonlinear Schrödinger and reaction-diffusion systems, we test the ability of WSINDy to select the correct monomial nonlinearities from an excessively large model library. Using a library of 190 terms for nonlinear Schrödinger’s and 181 terms for reaction-diffusion (see the dimensions of $\tilde{G}$ in Table 4), we demonstrate successful identification of the correct nonzero terms. Moreover, for the reaction-diffusion system, misidentified terms directly reflect the existence of a limit cycle²⁵. Finally, the vortex-shedding limit cycle for the 2D Navier-Stokes equations is used primarily to compare to previous results in [39], and we find that at large-noise WSINDy conveniently selects the Euler equations.

5.4. Results: Model Identification.

Performance regarding the identification of correct nonzero terms in each model is reported in Figures 4 and 5, which include plots of the average TPR, the learned threshold $\widehat{\lambda }$, and the loss function $\mathcal{L}(\lambda )$ (defined in (5.3), (4.7), and (4.4), respectively). As we will discuss, significant decreases in average TPR are often accompanied by transitions in the identified $\widehat{\lambda }$.

Figure 4.

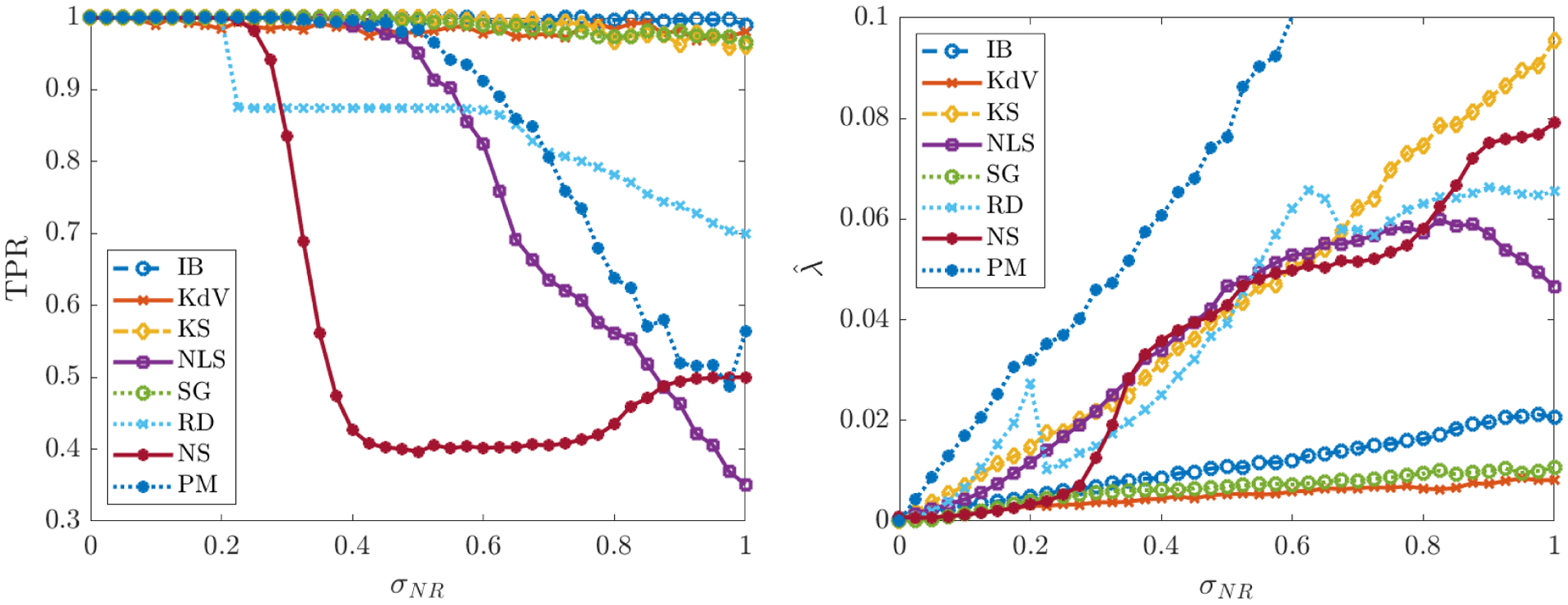
Left: average TPR (true positivity ratio, defined in (5.3)) for each of the PDEs in Table 2 computed from 200 instantiations of noise for each noise level σ_NR. Right: average learned threshold $\widehat{\lambda }$ (defined in (4.7)). For the porous medium equation (PM), $\widehat{\lambda }$ increases to 0:2 as σ_NR approaches 1 (we omit this from the plot in order to make visible the $\widehat{\lambda }$ trends for the other systems).

Figure 5.

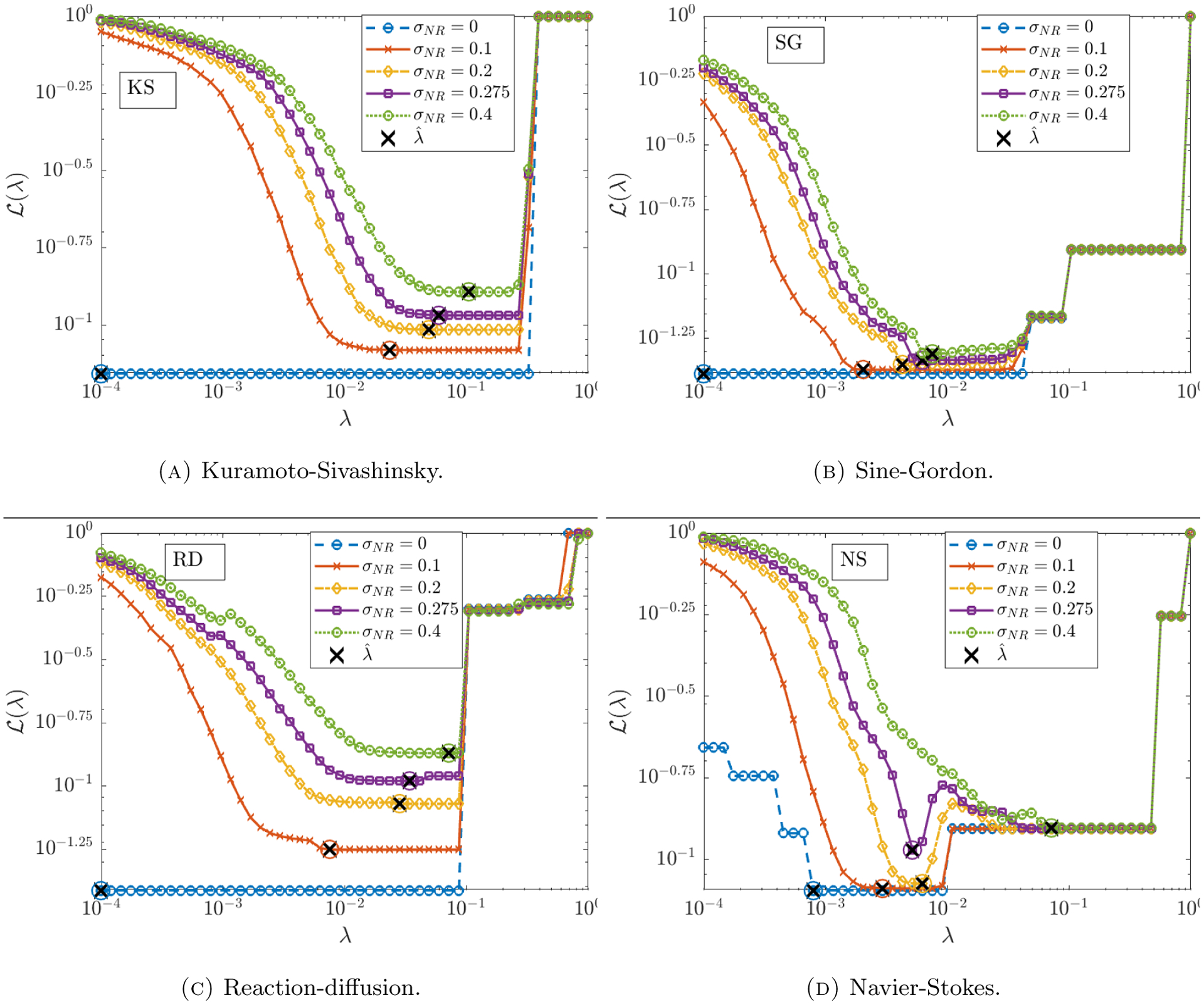
Plots of the average loss function $\mathcal{L}(\lambda )$ and resulting optimal threshold $\widehat{\lambda }$ for the Kuramoto Sivashinsky, Sine-Gordon, Reaction diffusion and Navier-Stokes equations.

Figure 4 (left) shows that for inviscid Burgers, Korteweg-de Vries, Kuramoto-Sivashinsky and Sine-Gordon, the average TPR stays above 0.95 even for noise levels as high as 100% (i.e. WSINDy reliably identifies these models in the presence of noise that has the same L²-norm as the underlying clean data). The average TPR for the nonlinear Schrödinger and porous medium equations stays above 0.95 until 50% noise, after which identification of the correct monomial nonlinearity is not as reliable. For NLS, this is a drastic improvement over previous studies [39], especially considering the large library of 190 terms used.

We observe in Figure 4 (right) that the learned threshold $\widehat{\lambda }$ increases with σ_NR, suggesting that automatic selection of $\widehat{\lambda }$ in the learning algorithm (4.7) is crucial to the algorithm’s robustness to noise. For example, the Kuramoto-Sivashinsky equation has a minimum nonzero coefficient of 0.5 (multiplying ∂_x(u²)), and we find that $\widehat{\lambda }$ approaches 0.1 as σ_NR approaches 1, which implies that at higher noise levels the range of $\widehat{\lambda }$ values that is necessary²⁶ for correct model identification is approximately (~ 0.1, ~ 0.5). Since it is highly unlikely that this range of admissible values would be known a priori, the chances of manually selecting a feasible $\widehat{\lambda }$ for Kuramoto-Sivashinsky are prohibitively low in the large noise regime (see Figure 5a for visualizations of the loss $\mathcal{L}$ applied to KS data). This effect is even greater for the porous medium equation. Automatic selection of $\widehat{\lambda }$ thus removes this sensitivity. In contrast, $\widehat{\lambda }$ is largely unaffected by increases in σ_NR for Burgers, Korteweg-de Vries and Sine-Gordon. In particular, Figure 5b shows little qualitative changes in the loss landscape for Sine-Gordon in the range 0.1 ≤ σ_NR ≤ 0.4.

Intriguingly, for reaction-diffusion, the average TPR falls below 0.95 at 22% noise, after which WSINDy falsely identifies linear terms in u and v. If the true model is given by the compact form ${\partial }_{t}u=\mathcal{A}(u)$ for u = (u, v)^T, then the misidentified model in all trials for noise levels in the range 0.25 ≤ σ_NR ≤ 0.55 is given by

$${\partial }_{t}u=\beta \mathcal{A}(u)+\alpha \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)u$$ (5.8)

for some α > 0 and β ≈ 1 dependent on σ_NR. This is explainable by the fact that the underlying solution settles into a limit cycle, which means that at every point in space the solution oscillates. Indeed, the falsely identified nonzero terms in (5.8) exactly convey that at each point in space the solution is oscillating at a uniform frequency (albeit with variable amplitude and phase determined by the initial conditions²⁷). Hence, in the presence of certain lower-dimensional structures (in this case a limit cycle), higher noise levels result in a mixture of the true model with a spatially-averaged reduced model. This shift between detection of the correct model and the oscillatory version (5.8) is also detectable in the learned threshold $\widehat{\lambda }$, which decreases at σ_NR = 0.22 (see RD data in Figure 4 (right)), and in the loss function $\mathcal{L}$ (Figure 5c). At σ_NR = 0.275 we see that $\mathcal{L}$ in Figure 5c is minimized for λ in the approximate range (~ 0.02, ~ 0.05) but also has a near-minimum for λ ∈ (~ 0.05, ~ 0.1). These two regions correspond to discovery of the oscillatory model (5.8) and the true model, respectively, but since the true model has a slightly higher loss at σ_NR = 0.275, model (5.8) is selected. For σ_NR ≥ 0.4 there is no longer (on average) a region of λ that results in discovery of the true model, and WINSDy returns (5.8) to compensate for noise.

For Navier-Stokes we see an averaging effect at higher noise, similar to the reaction-diffusion system. TPR drops below 0.95 for noise levels above 27% with the resulting misidentified model being simply Euler’s equations in vorticity form:

$${\partial }_t\omega =-{\partial }_x(\omega u)-{\partial }_y(\omega v).$$

This is due primarily to the small viscosity ν = 0.01 which prevents identification of the viscous forces at higher noise levels. Examining the loss function $\mathcal{L}$, Figure 5d shows that above σ_NR ≈ 0.275, minimizers of $\mathcal{L}$ are above 0.01, hence the viscous terms will be thresholded out. Another possible explanation is the low-accuracy simulation used for the clean dataset: in the noise-free setting, Table 5 shows that WSINDy recovers the model coefficients of Navier-Stokes to less than 3 significant digits in the absence of noise, which is the same level of accuracy exhibited on each of the other systems under 5% noise (see Figure 6). Nevertheless, with reliable recovery up to 27% noise, WSINDy makes notable improvements on previous results ([39]). Moreover, recovery of the Euler equations at high noise is desirable as this can be seen as the correct leader-order model.

Table 5.

Accuracy of WSINDy applied to noise-free data (σ_NR = 0).

	IB	KdV	KS	NLS	PM	SG	RD	NS
E ∞	4.3 × 10−5	3.1 × 10−7	8.1 × 10−7	9.4 × 10−8	2.2 × 10−6	4.3 × 10−5	3.9 × 10−10	1.1 × 10−3

Figure 6.

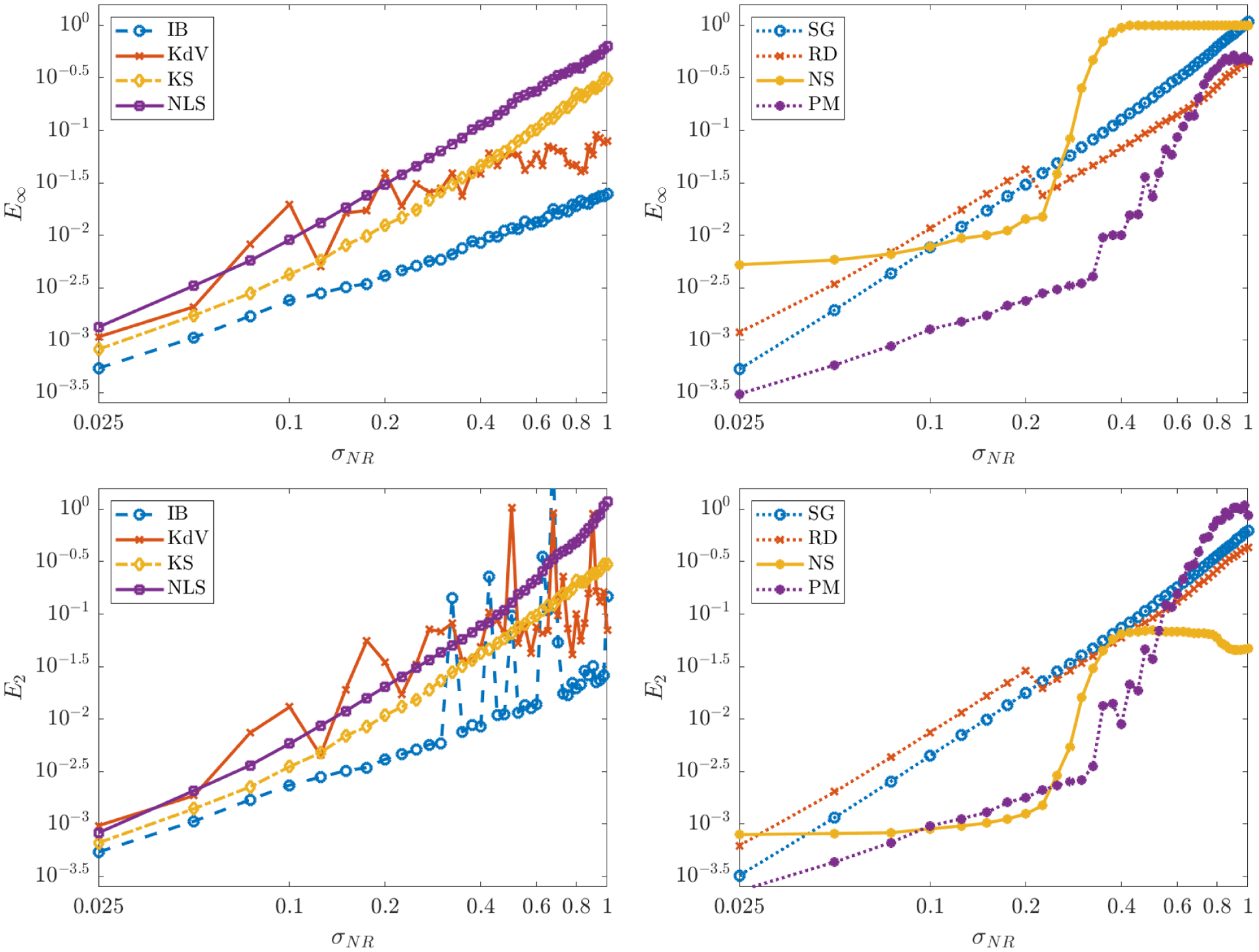
Coefficient errors E_∞ and E₂ (equations (5.4) and (5.5)) for each of the seven models Table 2. Models in one and two spatial dimensions are shown on the left and right, respectively.

5.5. Results: Coefficient Accuracy.

Accuracy in the recovered coefficients is measured by E_∞ and E₂ (defined in (5.4) and (5.5), respectively) and shown in Table 5 for σ_NR = 0 and in Figure 6 for σ_NR > 0. As in the ODE case, the coefficient error E_∞ for smooth, noise-free data is determined by the order of accuracy of the numerical simulation method²⁸, since the error resulting from the trapezoidal rule is of lower order for the values (p_x, p_t) used in Table 4 (see [28], Lemma 1). Table 5 also shows that the algorithm returns reasonable accuracy for non-smooth data, with E_∞ = 4.3 × 10⁻⁵ and E_∞ = 2.2 × 10⁻⁶ for the inviscid Burgers and porous medium equations, respectively. For reference, Table 6 shows that WSINDy improves over PDE-FIND by about two digits²⁹.

Table 6.

Accuracy comparison between WSINDy and PDE-FIND with σ_NR = 0.01 (results for PDE-FIND reproduced from [39]).

	KdV	KS	NLS	RD	NS
WSINDy	6.7 × 10−4	1.8 × 10−4	2.9 × 10−4	6.0 × 10−4	1.2 × 10−3
PDE-FIND	7.0 × 10−2	0.52	3.0 × 10−2	3.8 × 10−2	7.0 × 10−2

For σ_NR > 0, in Figure 6 it is apparent that E_∞ scales approximately as a power law $E_{\infty }~{\sigma }_{NR}^r$ for some r approximately in the range (~ 1, ~ 2) in all systems except Navier-Stokes. It was observed in [13] that E_∞ will approximately scale linearly with σ_NR for Kuramoto-Sivashinsky, however our results show that in general, for larger σ_NR, the rate will be superlinear and dependent on the reference test function and the nonlinearities present. A simple explanation for this in the case of normally-distributed noise is the following: linear terms Ψ^s * U will be normally-distributed with mean Ψ^s * U^★ and approximate variance $\Delta x^D\Delta t{\Vert D^{{\alpha }^s}\psi \Vert }_2^2{\sigma }^2$, hence are unbiased³⁰ and lead to perturbations that scale linearly with σ_NR. On the other hand, general monomial nonlinearities³¹ Ψ^s *U^j with j > 1 are biased and have approximate variance $\Delta x^D\Delta t{\Vert D^{{\alpha }^s}\psi \Vert }_2^2{p}_{2j}(\sigma )$ for p_2j a polynomial of degree 2j. Hence, nonlinear terms Ψ^s * f_j(U) lead to biased columns of the Gram matrix G with variance scaling with σ^2r for some r > 1 and proportional to ${\Vert D^{{\alpha }^s}\psi \Vert }_2$. Thus, for larger noise and higher-degree monomial nonlinearities, we expect superlinear growth of the error, as observed in particular with nonlinear Schrödinger’s, Sine-Gordon, and reaction-diffusion. Nevertheless, Figure 6 suggests that a conservative estimate on the coefficient error is $E_{\infty }\le \frac{{\sigma }_{NR}}{10}$, indicating 1 − log₁₀(σ_NR) significant digits (e.g. for σ_NR = 0.1 we have E_∞ ≤ 10⁻² for each system except KdV, indicating two significant digits), which is consistent with the ODE case [28].

For Burgers and Korteweg-De Vries, the average error E₂ at higher noise levels is affected by outliers containing a falsely-identified advection term ∂_xu. This is due to the large amplitude datasets used, which lead to the closest pure-advection model for each system being given by³²

$$(\text{Burgers}){\partial }_{t}u=-(498){\partial }_{x}u,\hspace{1em}(\text{KdV}){\partial }_{t}u=-(512){\partial }_{x}u.$$

Hence, a falsely identified ∂_xu term will have a large coefficient compared to the true model coefficients which have magnitudes 0.5 or 1. In all other cases, the values of E₂ and E_∞ are comparable, which implies that misidentified terms do not have large coefficients and might be removed with a larger threshold. Lastly, the sigmoidal shape of E_∞ and E₂ for Navier-Stokes is due again to the unidentified diffusive terms at larger noise. It is interesting to note that for σ_NR ≤ 0.27 the coefficient error for Navier-Stokes is relatively constant, in contrast to the other systems, and does not exhibit a power-law. However, at present, we do not have a concrete explanation for this behavior.

5.6. Results: Prediction Accuracy.

Lastly, Figure 7 shows the prediction accuracy on a subset of the systems in Table 2 as measured by $P_{0.5T}(\widehat{w})$ and $T_{0.1}(\widehat{w})$ (defined in (5.6) and (5.7), respectively). We report that data-driven solutions attain greater than 90% accuracy in the L₂ sense up to time 0.8T (80% of the trajectory) for noise levels as high as 40%. (This excludes the KS equation, which exhibits spatiotemporal chaos and cannot be expected to remain close to the noise-free data.) Data-driven solutions to the KS equation, while eventually divergent, also attain 90% accuracy up to time 0.5T for noise levels below 15%. Lastly, we note that for lower noise levels (up to 10%), the accuracy of data-driven solutions to the inviscid Burgers, Korteweg-de Vries and Sine-Gordon equations is on average above 96% along the entire trajectory (not shown in the figures).

Figure 7.

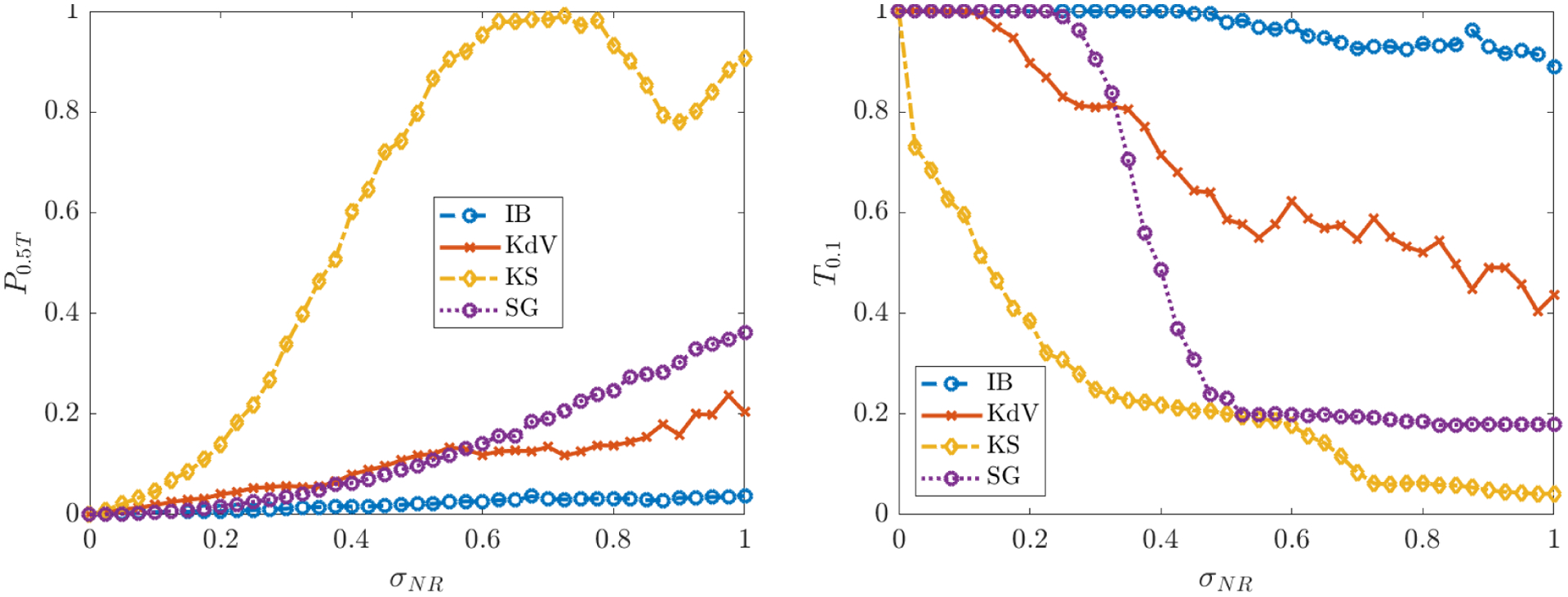
Prediction accuracy measured by $P_{0.5T}(\widehat{w})$ and $T_{0.1}(\widehat{w})$ (defined in (5.6) and (5.7), respectively).

6. Conclusion

We have extended the WSINDy algorithm to the setting of PDEs for the purpose of discovering models for spatiotemporal dynamics without relying on pointwise derivative approximations, black-box closure models (e.g. deep neural networks), dimensionality reduction, or other noise filtering. We have provided methods for learning many of the algorithm’s hyperparameters directly from the given dataset, and in the case of the threshold $\widehat{\lambda }$, demonstrated the necessity of avoiding manual hyperparameter tuning. The underlying convolutional weak form (3.4) allows for efficient implementation using the FFT. This naturally leads to a selection criterion for admissable test functions based on spectral decay, which is implemented in the examples above. In addition, we have shown that by utilizing scale invariance of the PDE together with a modified sparsification measure, models may be recovered from large candidate model libraries and from data that is poorly scaled. When unsuccessful, WSINDy appears to discover a nearby sparse model that captures the dominant spatiotemporal behavior (see the discussions surrounding misidentification of the reaction-diffusion and Navier-Stokes equations in Section 5.4).

We close with a summary of possible future directions. In Section 4.1 we discussed the significance of decay properties of test functions in real and in Fourier space, as well as general test function regularity. We do not make any claim that the class $\mathcal{S}$ defined by (4.2) is optimal, but it does appear to work very well, as demonstrated above (as well as in the ODE setting [28]) and also observed in [37, 13]. A valuable tool for future development of weak identification schemes would be the identification of optimal test functions. A preliminary step in this direction is our use of the changepoint method described in Appendix A.

In the ODE setting, adaptive placement of test functions provided increased robustness to noise. Convolution query points can similary be strategically placed near regions of the dynamics with high information content, which may be crucial for model selection in higher dimensions. Defining regions of high information content and adaptively placing query points accordingly would allow for identification from smaller datasets.

Ordinary least squares makes the assumption of i.i.d. residuals and should be replaced with generalized least squares to accurately reflect the true error structure. The current framework could be vastly improved by incorporating more precise statistical information about the linear system (G, b). The first step in this direction is the derivation of an approximate covariance matrix as in WSINDy for ODEs [28]. Previous results on generalized sensitivity analysis for PDEs may provide improvements in this direction [18, 46].

Accuracy in the recovered coefficients is still not entirely understood and is needed to derive recovery guarantees. It is claimed in [13] that at higher noise levels the scaling will approximately be linear in σ_NR, while we have demonstrated that this is not the case in general: the scaling depends on the nonlinearities present in the true model, the decay properties of the test functions, and accuracy of the underlying clean data. Analysis of coefficient error dependence (on noise, amplitudes, number of datapoints, etc.) could occur in tandem with development of a generalized least-squares framework.

The examples above show that WSINDy is very robust to noise for problems involving nonlinear waves (Burgers, Korteweg de-Vries, nonlinear Schrödinger, Sine-Gordon), spatiotemporal chaos (Kuramoto-Sivashinsky), and even nonlinear diffusion (porous medium), but is less robust for data with limit cycles (reaction-diffusion, Navier-Stokes). Further, identification of Burgers, Korteweg de-Vries, and Sine-Gordon appears robust to changes in the sparsity threshold $\widehat{\lambda }$ (see Figure 4 (right)). A structural identifiability criteria for measuring uncertainty in the recovery process based on identified structures (transport processes, mixing, spreading, limit cycles, etc.) would also be invaluable for general model selection.

Highlights.

• We present the WSINDy algorithm for data-driven discovery of partial differential equations in weak form. Pointwise derivative approximations are replaced by convolution against test functions for robust, high-accuracy model selection in the presence of large measurement noise.

• Reformulating the weak dynamics in terms of convolutions allows for fast FFT-based implementation and reveals that test function spectra plays a crucial role in guaranteeing robustness to noise.

• Scale invariance is used together with an improved thresholding algorithm with automatic threshold selection to enable PDE identification from poorly-scaled data and large candidate libraries.

• Successful discovery is demonstrated on the inviscid Burgers, Korteweg-de Vries, Kuramoto-Sivashinksy, nonlinear Schrödinger, anisotropic porous medium, Sine-Gordon, reaction-diffusion, and Navier-Stokes equations from highly corrupted datasets, and in the case of inviscid Burgers and porous medium, from non-classical (weak) solutions.

Appendix A. Learning Test Functions From Data

We present the following algorithm for automatic selection of test functions which utilizes the implicit smoothing of high-frequency noise afforded by the convolution. This approach is useful in practice but we leave rigorous justification of it to future work. We proceed in two steps: (1) estimation of critical wavenumbers $\left(k_1^{*},\dots ,k_{D+1}^{*}\right)$ separating noise- and signal-dominated modes in each coordinate and (2) enforcing decay in real and in Fourier space.

We will describe the process for detecting $k_x^{*}=k_1^{*}$ from data $U\in {ℝ}^{N_1\times N_2}$ given over the one-dimensional spatial grid $x\in {ℝ}^{N_1}$ at timepoints $t\in {ℝ}^{N_2}$. Figures 8–9 illustrate this approach using Kuramoto-Sivashinsky data with 50% noise. Below, ${\mathcal{F}}^x$ and ${\mathcal{F}}^t$ denote the discete Fourier transform (DFT) along the x and t coordinates, respectively, while $\mathcal{F}$ denotes the full two-dimensional DFT.

A.1. Detection of Critical Wavenumbers.

Assume the data has additive white noise U = U^★ + ϵ with $ϵ~\mathcal{N}\left(0,{\sigma }^2\right)$ and that $\mathcal{F}\left(U^{\star }\right)$ decays. The power spectrum of the noise $|{\mathcal{F}}^x(ϵ)|$ is then i.i.d, hence as discussed in Section 4.1, there will be a critical wavenumber $k_x^{*}$ in the power spectrum of the data ${\mathcal{F}}^x(U)$ after which the modes become noise-dominated. To detect $k_x^{*}$, we collapse ${\mathcal{F}}^x(U)$ into a one-dimensional array by averaging in time and then take the cumulative sum in x:

$$H_k^x≔\sum _{j=-N_1/2}^k\overline{|{\mathcal{F}}_j^x(U)|}$$ (A.1)

where $\overline{|{\mathcal{F}}_j^x(U)|}$ is the time-average of the jth mode of the discrete Fourier transform along the x-coordinate. Since $|{\mathcal{F}}^x(ϵ)|$ is i.i.d., H^x will be approximately linear over the noise-dominated modes, which is an optimal setting for locating $k_x^{*}$ as a changepoint, or in other words the corner point of the best piecewise-linear approximation³³ to H^x using two pieces (see Figure 8). An algorithm for this is given in [20] and implemented in MATLAB using the function findchangepts.

A.2. Enforcing Decay.

Having detected the changepoints $k_x^{*}$ and $k_t^{*}$, we compute hyperparameters for the coordinate test functions ϕ_x and ϕ_t using user-specified hyperparameters τ and $\widehat{\tau }$. As in Section 4.1, τ specifies the rate of decay of ϕ_x and ϕ_t in real space through equation (4.3). The hyperparameter $\widehat{\tau }$ is introduced to specify the rate of decay of ϕ_x and ϕ_t in Fourier space. Specifically, for a chosen $\widehat{\tau }$ we enforce that the changepoints $k_x^{*}$ and $k_t^{*}$ fall approximately $\widehat{\tau }$ standard deviations into the tail of the spectra ${\widehat{\varphi }}_x$ and ${\widehat{\varphi }}_t$. This is done by utilizing that ϕ_x and ϕ_t are functions of the form

$${\varphi }_{a,p}(s)≔C{\left(1-{\left(\frac{s}{a}\right)}^2\right)}_{+}^p,$$

(i.e. centered, symmetric functions in the class $\mathcal{S}$ defined in (4.2)) which are well-approximated by Gaussians for large enough p and appropriate scaling C. Indeed, letting C be such that ‖ϕ_a,p‖₁ = 1 and setting $\sigma ≔a/\sqrt{2p+3}$ we have that ϕ_a,p matches the first three moments of the Gaussian

$${\rho }_{\sigma }(s)≔\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-s^2/2{\sigma }^2},$$

which provides a bound on the error in the Fourier transforms and ${\widehat{\varphi }}_{a,p}$ and ${\widehat{\rho }}_{\sigma }$ for small frequencies ξ in terms of their 4th moments³⁴:

$$|{\widehat{\varphi }}_{a,p}(\xi )-{\widehat{\rho }}_{\sigma }(\xi )|\le |\xi {|}^4\left(\frac{a^4}{2}\left[\frac{p+3/2}{\left(4p^2+12p+9\right)\left(4p^2+16p+15\right)}\right]+o(1)\right)=\mathcal{O}\left(|\xi {|}^4{a}^4{p}^{-3}\right).$$

This implies that for small ξ and a and large p, it suffices to use ${\widehat{\rho }}_{\sigma }(\xi )={\rho }_{1/\sigma }(\xi )$ to estimate ${\widehat{\varphi }}_{a,p}$. Hence, we enforce decay of ${\widehat{\varphi }}_x$ (and similarly for ${\widehat{\varphi }}_t$) by choosing m_x and p_x such that

$$\frac{2\pi }{N_1\Delta x}{k}_x^{*}=\frac{\widehat{\tau }}{\sigma }=\widehat{\tau }\frac{\sqrt{2p_x+3}}{m_x\Delta x}\Rightarrow 2\pi k_x^{*}{m}_x=\widehat{\tau }{N}_1\sqrt{2p_x+3}.$$ (A.2)

so that $k_x^{*}$ is $\widehat{\tau }$ standard deviations into the tail of ${\widehat{\rho }}_{\sigma }(\xi )$, where $\sigma =m_x\Delta x/\sqrt{2p_x+3}$. To solve (4.3) and (A.2) simultaneously, we compute m_x as a root of

$$F(m)≔F\left(m;k_x,N_1,\widehat{\tau },\tau \right)≔\text{log}\left(\frac{2m-1}{m^2}\right)\left(4{\pi }^2{k}_x^{*2}{m}^2-3N_1^2{\widehat{\tau }}^2\right)-2N_1^2{\widehat{\tau }}^2\text{log}(\tau ).$$

F(m) has a unique root m_x ≥ 2 in the nonempty interval

$$\left[\frac{\sqrt{3}}{\pi }\left(\frac{N_1/2}{k_x^{*}}\right)\widehat{\tau },\hspace{1em}\frac{\sqrt{3}}{\pi }\left(\frac{N_1/2}{k_x^{*}}\right)\widehat{\tau }\sqrt{1-(8/\sqrt{3})\text{log}(\tau )}\right]$$

on which F monotonically decreases and changes sign, provided N₁ > 4, τ ∈ (0, 1) and $\frac{\sqrt{3}}{\pi }\frac{\widehat{\tau }}{k_x^{*}}\in \left[4/N_1,1\right]$, constraints which are easily satisfied. After finding m_x we can solve for p_x using either (4.3) or (A.2).

Figure 9 illustrates the implicit filtering of this process using the Burgers-type nonlinearity ∂_x(U²) and the same KS dataset as in Figure 9 with 50% noise. The top panel compares a one-dimensional slice in x taken at fixed time t = 99 of the clean data (U^★)² and noisy data (U)². The middle panel shows the Fourier transforms of (U^★)² and (U)² along the given slice, showing that modes after $k_x^{*}$ become noise-dominated. Finally, the bottom panel shows that after convolution with $\widehat{{\partial }_x\psi }$, where m_x and k_x are chosen with τ = 10⁻¹⁰ and $\widehat{\tau }=2$, the clean and noisy spectra agree well, indicating successful filtering of noise-dominated modes (note that (U)² is highly-corrupted, nonlinearly-transformed, and biased from the noise-free term (U^★)², making this agreement in spectrum nontrivial).

Appendix B. Simulation Methods

We now review the numerical methods used to simulate noise-free datasets for each of the PDEs in Table 2 (note that dimensions of the datasets are given in Table 3). Resolutions in space and time were chosen to limit computational overhead while exemplifying the dominant features of the solution. With the exception of the Navier-Stokes equations, which was simulated using the immersed boundary projection method in C + + [44], all computations were performed in MATLAB 2019b. An interesting extension for future work would be to examine the dependence of WSINDy on the resolution, similar to the work in [30].

B.1. Inviscid Burgers.

$${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)$$ (B.1)

We take for exact data the shock-forming solution

$$u(x,t)=\{\begin{array}{ll}A,\hfill & t\ge \text{max}\left\{\frac{1}{A}x+\frac{1}{\alpha },\frac{2}{A}x+\frac{1}{\alpha }\right\}\hfill \\ -\frac{\alpha x}{1-\alpha t},\hfill & A\left(t-\frac{1}{\alpha }\right)<x\le 0\hfill \\ 0,\hfill & \text{ otherwise }\hfill \end{array}.$$ (B.2)

which becomes discontinuous at t = α⁻¹ with a shock travelling along $x=\frac{A}{2}\left(t-\frac{1}{\alpha }\right)$ (see Figure 3). We choose α = 0.5 and an extreme value of A = 1000 to demonstrate that WSINDy still has excellent performance for large amplitude data. The noise-free data consists of (B.2) evaluated at the points (x_i, t_j) = (−4000 + iΔx, jΔt) with Δx = 31.25 and Δt = 0.0157 for 1 ≤ i, j ≤ 256.

Figure 8.

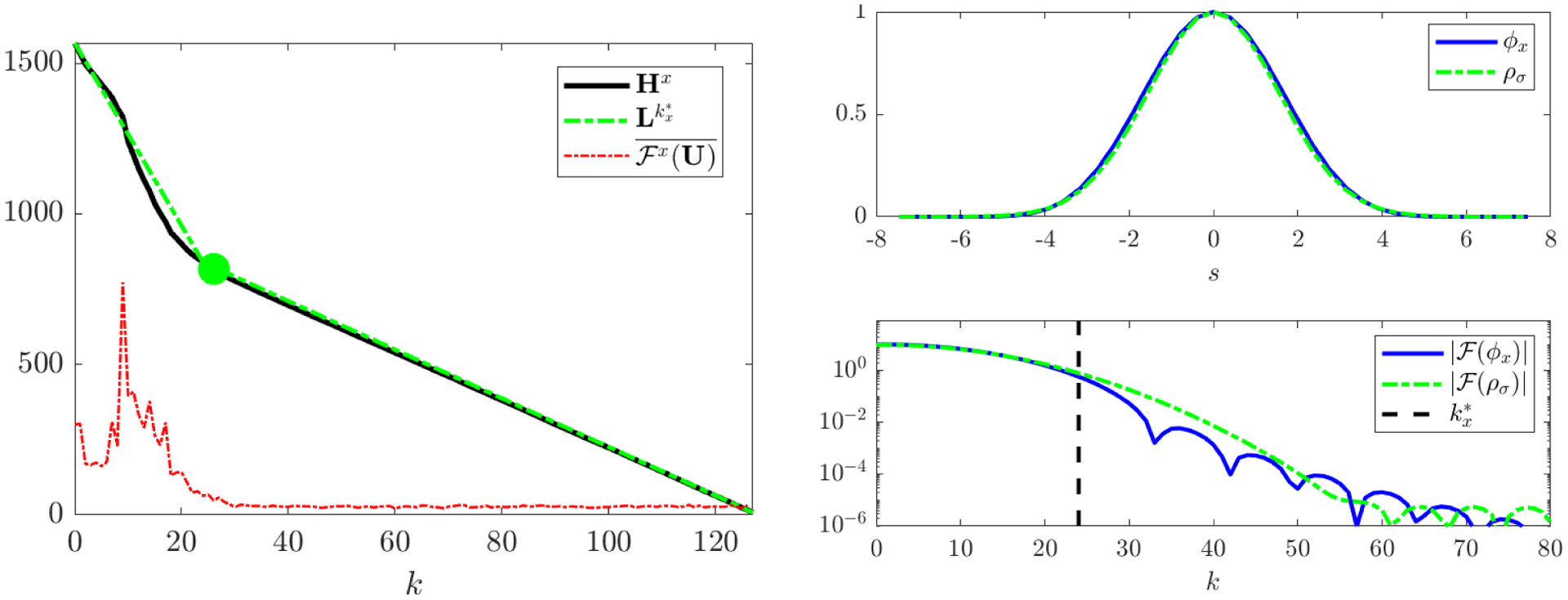
Visualization of the changepoint algorithm for KS data with 50% noise. Left: H^x (defined in (A.1)) and best two-piece approximation $L^{k_x^{*}}$ along with resulting changepoint $k_x^{*}=24$. The noise-dominated region of H^x (k > 24) is approximately linear as expected from the i.i.d. noise. (The time-averaged power spectrum $\overline{|{\mathcal{F}}^x(U)|}$ is overlaid and magnified for scale). Right: resulting test function ϕ_x and power spectrum $|\mathcal{F}\left({\varphi }_x\right)|$ along with reference Gaussian ρ_σ with $\sigma =m_x\Delta x/\sqrt{2p_x+3}$. The power spectra $|\mathcal{F}\left({\varphi }_x\right)|$ and $|\mathcal{F}\left({\rho }_{\sigma }\right)|$ are in agreement over the signal-dominated modes (k ≤ 24). (Note that the power spectrum is symmetric about zero.)

B.2. Korteweg-de Vries.

$${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)-{\partial }_{xxx}u$$ (B.3)

A solution is obtained for (x, t) ∈ [−π, π] × [0, 0.006] with periodic boundary conditions using ETDRK4 timestepping and Fourier-spectral differentiation [17] with N₁ = 400 points in space and N₂ = 2400 points in time. We subsample 25% of the timepoints for system identification and keep all of the spatial points for a final resolution of Δx = 0.0157, Δt = 10⁻⁵. For initial conditions we use the two-soliton solution

$$u(x,0)=3A^2\text{sech}{(0.5(A(x+2)))}^2+3B^2\text{sech}{(0.5(B(x+1)))}^2,\hspace{1em}A=25,B=16.$$

B.3. Kuramoto-Sivashinsky.

$${\partial }_{t}u=-\frac{1}{2}{\partial }_x\left(u^2\right)-{\partial }_{xx}u-{\partial }_{\mathit{\text{xxxx}}}u.$$ (B.4)

A solution is obtained for (x, t) ∈ [0, 32π] × [0, 150] with periodic boundary conditions using ETDRK4 timestepping and Fourier-spectral differentiation [17] with N₁ = 256 points in space and N₂ = 1500 points in time. For system identification we subsample 20% of the time points for a final resolution of Δx = 0.393 and Δt = 0.5. For initial conditions we use

$$u(x,0)=\text{cos}(x/16)(1+\text{sin}(x/16)).$$

Figure 9.

Illustration of the test function learning algorithm using computation of ∂_xψ*(U²) along a slice in x at fixed time t = 99 for the same dataset used in Figure 8. From top to bottom: (i) clean U^★ and noisy U variables, (ii) power spectra of the clean vs. noisy data along with the learned corner point $k_x^{*}$, (iii) power spectra of the element-wise products $\mathcal{F}\left({\partial }_x\psi \right)\odot \mathcal{F}\left({\left(U^{\star }\right)}^2\right)$ and $\mathcal{F}\left({\partial }_x\psi \right)\odot \mathcal{F}\left({(U)}^2\right)$ (recall that these computations are embedded in the FFT-based convolution (3.12)).

B.4. Nonlinear Schrödinger.

$$w_t=-\frac{i}{2}{\partial }_{xx}w+|w{|}^{2}w$$ (B.5)

Figure 10.

Noise-free data used for the anisotropic porous medium equation (B.7) at the initial time t = 0.5 (left) and final time t = 2.5 (right).

For the nonlinear Schrödinger equation (NLS) we reuse the same dataset from [39], containing N₁ = 512 points in space and N₂ = 502 timepoints, although we subsample 50% of the spatial points and 50% of the time points for a final resolution of Δx = 0.039, Δt = 0.0125. For system identification, we break the data into real and imaginary parts (w = u + iv) and recover the system

$$\{\begin{array}{l}{\partial }_{t}u=\frac{1}{2}{\partial }_{xx}v+u^{2}v+v^3\hfill \\ {\partial }_{t}v=-\frac{1}{2}{\partial }_{xx}u-u{v}^2-u^3.\hfill \end{array}$$ (B.6)

B.5. Anisotropic Porous Medium.

$${\partial }_{t}u=(0.3){\partial }_{xx}\left(u^2\right)-(0.8){\partial }_{xy}\left(u^2\right)+{\partial }_{yy}\left(u^2\right).$$ (B.7)

The equation can be rewritten

$${\partial }_{t}u=\nabla \cdot \left(D\nabla \left(u^2\right)\right)$$

for diffusivity tensor

$$D=\left(\begin{array}{cc}0.3& -0.4\\ -0.4& 1\end{array}\right).$$

For noise-free data we use the analytical weak solution

$$u(x,t)=\frac{1}{\sqrt{t}}\text{max}\left(C-\frac{x^T{D}^{-1}x}{16\sqrt{t}},0\right)$$

where x = (x, y)^T and $C={(8\pi \sqrt{\text{det}(D)})}^{-1/2}$ is chosen to enforce that ${\int }_{{ℝ}^2}u(x,t)dx=1$ for all time. The solution has a finite jump in the gradient ∇u. For reference, this is the anisotropic version of the classical Barenblatt-Pattle solution to the (isotropic) porous medium equation [3, 32]. For the computation grid we use 200 points equally spaced from −5 to 5 in both x and y and 128 timepoints equally spaced from 0.5 to 2.5. The resolution is then Δx = 0.05 and Δt = 0.0157.

B.6. Sine-Gordon.

$${\partial }_{tt}u={\partial }_{xx}u+{\partial }_{yy}u-\text{sin}(u)$$ (B.8)

A numerical solution is obtained using a pseudospectral method on the spatial domain [−π, π] × [−1, 1] with 64 equally-spaced points in x and 64 Legendre nodes in y. Periodic boundary conditions are enforced in x and homogeneous Dirichlet boundaries in y. Geometrically, waves can be thought of as propagating on a right cylindrical sheet with clamped ends. Leapfrog time-stepping is used to generate the solution until T = 5 with Δt = 6e−5. We then subsample 0.25% of the timepoints and interpolate onto a uniform grid in space with N₁ = 403 points in x and N₂ = 129 points in y. The final resolution is Δx = 0.0156, Δt = 0.025. We arbitrarily use Gaussian data for the initial wave disturbance:

$$u(x,y,0)=2\pi \text{exp}\left(-8{(x-0.5)}^2-8y^2\right).$$

It is worth noting that when STLS is used instead of MSTLS (see Section 4.2) for sparsity enforcement, WSINDy returns a combination of sin(u) and terms from Taylor expansion of sin(u),

$$\alpha \left(u-\frac{1}{6}{u}^3+\cdots \right)+(1-\alpha )\text{sin}(u).$$ (B.9)

MSTLS removes this problem. Furthermore, the test function selection method in Appendix A is essential for allowing robust recovery of the Sine-Gordon equation as σ → 1 (see Figure 4).

B.7. Reaction-Diffusion.

$$\{\begin{array}{l}{\partial }_{t}u=\frac{1}{10}{\partial }_{xx}u+\frac{1}{10}{\partial }_{yy}u-u{v}^2-u^3+v^3+u^{2}v+u\hfill \\ {\partial }_{t}v=\frac{1}{10}{\partial }_{xx}v+\frac{1}{10}{\partial }_{yy}v+v-u{v}^2-u^3-v^3-u^{2}v\hfill \end{array}$$ (B.10)

The system (B.10) is simulated over a doubly-periodic domain (x, y) ∈ [−10, 10]×[−10, 10] with t ∈ [0, 10] using Fourier-spectral differentiation in space and method-of-lines time integration via MATLAB’s ode45 with default tolerance. The computational domain has dimensions N₁ = N₂ = 256 and N₃ = 201, for a final resolution of Δx = 0.078, Δt = 0.0498. For initial conditions we use the spiral data

$$\{\begin{array}{l}u(x,y,0)=\text{tanh}\left(\sqrt{x^2+y^2}\right)\text{cos}\left(\theta (x+iy)-\pi \sqrt{x^2+y^2}\right)\hfill \\ v(x,y,0)=\text{tanh}\left(\sqrt{x^2+y^2}\right)\text{sin}\left(\theta (x+iy)-\pi \sqrt{x^2+y^2}\right),\hfill \end{array}$$

where θ(z) is the principle angle of $z\in ℂ$. Note that this is an unstable spiral which breaks apart over time but still settles into a limit cycle.

Using the traditional (stable) spiral wave data [39] (differing only from the dataset used here in that the term $\pi \sqrt{x^2+y^2}$ in the initial conditions above is replaced by $\sqrt{x^2+y^2}$) we noticed an interesting behavior in that for high noise the resulting model is purely oscillatory. In other words, the stable spiral limit cycle happens to be well-approximated by the pure-oscillatory model

$${\partial }_{t}u=\alpha \left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)u$$ (B.11)

with α ≈ 0.91496. A comparison between this purely oscillatory reduced model and the full model simulated from the same initial conditions is shown in Figure 11. For σ_NR ≤ 0.1 WSINDy applied to the stable spiral dataset returns the full model, while for σ_NR > 0.1 the oscillatory reduced model is more frequently detected. This suggests that although the stable spiral wave is a hallmark of the λ-ω reaction-diffusion system, from the perspective of data-driven model selection it is not an ideal candidate for identification of the full model.

Figure 11.

Comparison between the full reaction-diffusion model (B.10) (left) and the pure-oscillatory reduced model (B.11) (right) at the final time T = 10 with both models simulated from the same initial conditions leading to a spiral wave (only the v component is shown, results for u are similar). The reduced model provides a good approximation away from the boundaries.

B.8. Navier-Stokes.

$${\partial }_t\omega =-{\partial }_x(\omega u)-{\partial }_y(\omega u)+\frac{1}{100}{\partial }_{xx}\omega +\frac{1}{100}{\partial }_{yy}\omega$$ (B.12)

A solution is obtained on a spatial grid (x, y) ⊂ [−1, 8] × [−2, 2] with a “cylinder” of diameter 1 located at (0, 0). The immersed boundary projection method [44] with 3rd-order Runge-Kutta timestepping is used to simulate the flow at spatial and temporal resolutions Δx = Δt = 0.02 for 2000 timesteps following the onset of the vortex shedding limit cycle. The dataset (U, V, W) contains the velocity components as well as the vorticity for points away from the cylinder and boundaries in the rectangle (x, y) ∈ [1, 7.5] × [−1.5, 1.5]. We subsample 10% of the data in time for a final resolution of Δx = 0.02 and Δt = 0.2.