Genome Reconstruction Attacks Against Genomic Data-Sharing Beacons

Abstract

Sharing genome data in a privacy-preserving way stands as a major bottleneck in front of the scientific progress promised by the big data era in genomics. A community-driven protocol named genomic data-sharing beacon protocol has been widely adopted for sharing genomic data. The system aims to provide a secure, easy to implement, and standardized interface for data sharing by only allowing yes/no queries on the presence of specific alleles in the dataset. However, beacon protocol was recently shown to be vulnerable against membership inference attacks. In this paper, we show that privacy threats against genomic data sharing beacons are not limited to membership inference. We identify and analyze a novel vulnerability of genomic data-sharing beacons: genome reconstruction. We show that it is possible to successfully reconstruct a substantial part of the genome of a victim when the attacker knows the victim has been added to the beacon in a recent update. In particular, we show how an attacker can use the inherent correlations in the genome and clustering techniques to run such an attack in an efficient and accurate way. We also show that even if multiple individuals are added to the beacon during the same update, it is possible to identify the victim’s genome with high confidence using traits that are easily accessible by the attacker (e.g., eye color or hair type). Moreover, we show how a reconstructed genome using a beacon that is not associated with a sensitive phenotype can be used for membership inference attacks to beacons with sensitive phenotypes (e.g., HIV+). The outcome of this work will guide beacon operators on when and how to update the content of the beacon and help them (along with the beacon participants) make informed decisions.

1. Introduction

With plummeting sequencing costs, we look forward reaching a capacity of sequencing one billion individuals over the next 15–20 years, resulting in availability of very large genomic datasets [20, 49, 64]. Although such large datasets are promising a revolution in medicine, it has been shown in numerous studies that it is not straightforward to ensure anonymity of the participants in such datasets [19, 36, 42, 63, 71].

Human genome is the utmost personal identifier and sharing genomic data for research while preserving the privacy of the individuals have been challenging many different fields (e.g., medicine, bioinformatics, computer science, law, and ethics) for long, due to possibly dire ethical, monetary, and legal consequences. To address this challenge and create frameworks and standards to enable the responsible, voluntary, and secure sharing of genomic data, the Global Alliance for Genomics and Health (GA4GH) was formed by the community [1]. The current genomic data sharing standard of the GA4GH is called the genomic data-sharing beacons. Beacons are the gateways that let users (researchers) and data owners exchange information without -in theory-disclosing any personal information. A user who wants to apply for access to a dataset can learn whether individuals with specific alleles (nucleotides) of interest are present in the beacon through an online interface. That is, a user can submit a query, asking whether a genome exists in the beacon with a certain nucleotide at a certain position, and the beacon answers as “yes” or “no”. If the dataset does not contain the desired genome, genomic data is not shared and distributed unnecessarily. In addition, researchers do not have to go through the paperwork to obtain a dataset which will not be helpful for their research. The GA4GH provides a shared beacon interface [2] that as of December 2020 provides access to 81 beacons and acts as a hub where researchers and data owners meet.

Beacons are typically associated with a particular sensitive phenotype (e.g., the SFARI beacon that host individuals with autism). Therefore, presence of an individual in a particular beacon is considered as privacy-sensitive information and the main aim of the beacons is to protect this information. An attacker, using the responses of a beacon and genomic data of a victim, may try to infer the membership of the victim in a particular beacon by running a membership inference attack. Beacon framework sets a barrier against membership inference attacks by allowing only presence/absence queries for variants and not tying any response to any specific individual. In that sense, beacons are considered to have stronger privacy measures compared to other statistical genomic databases. Despite these barriers, several works have proven that beacons are not bulletproof and they are vulnerable to membership inference attacks [59, 65, 73].

However, threats against genomic data-sharing beacons are not limited to membership inference attacks. In this paper, for the first time, we identify and analyze the vulnerability of genomic data-sharing beacons for the “genome reconstruction” attack. We consider a scenario, in which the attacker knows the membership of a victim to a beacon that may not be associated with a sensitive phenotype. Therefore, we consider a targeted attack, in which either (i) the attacker knows that the victim donated their genome to take part in a study or (ii) infer the membership of the victim from beacon’s metadata (as done in [65]). Then, we show how the attacker can accurately infer the genome of the victim by using the beacon responses. Such an attack may result in serious consequences if the attacker uses the reconstructed genome to infer sensitive information (e.g., disease diagnosis) about the victim or to infer the victim’s membership to another statistical genomic database of interest (e.g., another beacon that is associated with a sensitive phenotype). In particular, we show how the attacker can use the inherent correlations in the genome to run such an attack in an efficient and accurate way compared to a baseline approach. We also show how clustering techniques can be used to further improve the accuracy of such an attack.

Previous works in the literature assume beacons are static and do not change over time. However, beacons are dynamic datasets (donors join and leave) and this results in an increased risk for the genome reconstruction attack. An attacker can monitor the number of newly added donors to the beacon and the number of donors leaving the beacon from the meta-information of the beacon. With this information, newly joined donors (or donor leaving the beacon) become more vulnerable for genome reconstruction attacks. Thus, for the first time, we consider the beacons as dynamic databases and formulate the genome reconstruction attack accordingly. Privacy vulnerabilities due to dynamic changes in a system has been recently explored in the context of dynamic model changes in machine learning models [61]. It has been shown that different model outputs can constitute a new attack surface for an adversary to infer information of the dataset used to perform a model update [61]. Here, rather than model updates, we focus on the changes in the query responses to a dynamic database.

In a genome reconstruction attack, the attacker reconstructs all or a subset of the genomes in the beacon. Among the reconstructed genomes, it is not trivial to infer which one belongs to the victim. Therefore, we also show how the attacker can identify the victim’s genome among the set of reconstructed genomes using moderate auxiliary information about the victim (i.e., a set of visible physical characteristics of the victim, which is public information). Finally, to show one of the consequences of the identified genome reconstruction attack, we show how the attacker can utilize the outcome of this attack to initiate a membership inference attack against the same victim in another beacon, which can be associated with a sensitive phenotype. To do this, we combine the identified genome reconstruction attack with the membership inference attacks against beacons from the literature.

We implement and evaluate the identified vulnerability using real genome data obtained from OpenSNP [32] and HapMap [21] datasets. We particularly evaluate the success of the attacker to reconstruct a victim’s point mutations that include at least one rare nucleotide (i.e., minor allele) since minor alleles (i) reveal sensitive attributes of individuals (e.g., predispositions to privacy-sensitive diseases); and (ii) provide rich information to the attacker for membership inference attacks [59, 73]. We show that for a beacon with 50 individuals, precision and recall of the reconstruction reach up to 0.9 (each) when 3 individuals are added to the beacon and the victim is one of the newcomers. Even when 10 new participants are added to the beacon (causing a 20% increase in beacon size), we show that the attacker has a precision of 0.7 and a recall of 0.8. Furthermore, our results show that when more than one individual is added to the beacon, the attacker can accurately pinpoint the victim’s reconstructed genome by using moderate (and publicly available) auxiliary information about the victim. For this, we show how the attacker can match the victim’s phenotypical characteristics to the reconstructed genomes using machine learning algorithms. We also show via experiments that the outcome of the genome reconstruction attack can be accurately used for the membership inference attack on another beacon and it helps an attacker infer the membership of a victim only with a few queries.

Overall, we identify an important vulnerability and show how it can be exploited. We notably show how dependencies between point mutations can be used in a clustering algorithm to have high accuracy in a genome reconstruction attack. Furthermore, our methodology consists of a complete pipeline, showing how an attacker use the information it infers in the genome reconstruction attack in a subsequent membership inference attack. Therefore, this study clearly shows that privacy risks for genomic data-sharing beacons are much severe than perceived. This is particularly important since the number of beacon participants, and hence the privacy risk of individuals increase rapidly.

2. Related Work

Genomic privacy has recently been explored by many studies [11, 27, 56]. In the following subsections, we will summarize existing work on privacy in statistical genomic databases, inference attacks, and privacy of genomic data-sharing beacons.

2.1. Privacy in Statistical Genomic Databases and Inference Attacks on Genomic Privacy

Several works have shown that anonymization does not effectively protect the privacy of genomic data [30, 33, 35, 45, 50, 53, 66]. It has been shown that the identity of a participant of a genomic study can be revealed by using a second sample (e.g., part of the DNA information from the individual) and the results of the clinical study [19, 37, 41, 75, 77]. Differential privacy (DP) [26] concept has been frequently used to mitigate membership inference attacks when releasing summary statistics from genomic databases [28, 44, 68, 76]. Compared to statistical databases, genomic data-sharing beacons have stronger privacy measures since they only allow presence/absence (or yes/no) queries for variants.

Humbert et al. proposed an inference attack on kin genomic privacy using the family ties between individuals, pairwise correlations between the SNPs, and publicly available statistics about DNA [38]. Then, Deznabi et al. demonstrated that stronger inference techniques can be generated by combining high-order correlations and family ties [25]. Furthermore, several studies have examined phenotype prediction from genomic data, as a means of tracing identity [10, 18, 39, 46, 51, 52, 54, 58, 74, 78]. To mitigate such attribute inference attacks, cryptographic solutions has been proposed for privacy-preserving processing and sharing of genomic data (e.g., to outsource the computation to a public cloud or to conduct collaborative association studies). Existing cryptographic solutions mainly focus on (i) private pattern-matching and the comparison of genomic sequences [15, 24, 43, 55, 69] and (ii) privacy-preserving personalized medicine [12, 13]. In this work, we identify and analyze a different type of attribute inference attack particularly against genomic data-sharing beacons.

2.2. Privacy in Genomic Data Sharing Beacons

Researchers showed that presence (membership) of an individual in a genome sharing beacon can be inferred by repeatedly querying the beacon. Here, the attacker is assumed to be an active (or authorized) user of the beacon, in practice, it can ask as many queries as it wishes to the beacon (there is no limitations and cost for this in the current beacon protocol), and it can decide which queries to ask to the beacon. Furthermore, the attacker is assumed to have access to the set of SNPs of the victim. Shringarpure and Bustamante introduced a likelihood-ratio test (LRT) that can predict whether an individual is in the beacon by querying the beacon for multiple SNPs of a victim [65]. Note that inferring the membership of an individual in a beacon that is associated with a sensitive phenotype is equivalent to uncovering the sensitive phenotype about the victim. Then, Raisaro et al. showed that if the attacker first queries the SNPs with low minor allele frequency (MAF) values, it needs fewer queries for a successful attack [59]. In Section 6.5, we use this attack when we show how the proposed genome reconstruction attack can be combined with the membership inference attack. We provide further background information about this attack in Appendix A. Later, von Thenen et al. showed that even if the attacker does not have victim’s low-MAF SNPs, it is still possible to infer membership by exploiting the correlations in the genome [73]. Furthermore, they showed that beacon responses can also be inferred using such correlations (via a query inference, or QI-attack). In an orthogonal work, Hagestedt et al. have hypothesized that while current beacons systems are limited to genomic data, in the near future, the community is going to need a similar system for other biomedical data types. They proposed a beacon system for sharing DNA methylation data (an epigenetic mechanism to regulate transcriptional activity) and then showed that it is possible to successfully launch a membership inference attack against this system. They proposed a DP-based solution in their proposed MBeacon [34] system. The approach retains utility by adjusting the noise level for high risk methylation regions that might leak phenotypic information (i.e., regions which are related to disease).

Contribution of this paper.

In this paper, we identify and analyze a genome reconstruction attack against genomic data-sharing beacons by particularly exploiting the information leaked due to beacon updates and the correlations between the point mutations. So far, all works in the literature have focused on membership inference attacks against genomic data-sharing beacons. To the best of our knowledge, this is the first work that identifies, thoroughly analyzes, and shows the consequences of the genome reconstruction attack against the beacons. Furthermore, as opposed to existing work (that only consider a snapshot of the beacon), we show the privacy risk in dynamic beacons, in which new donors may join or existing donors may leave.

3. Genomics Background

Approximately 99.9% of the all individuals’ DNA are identical and the remaining 0.1% is responsible for our differences. Single nucleotide polymorphism (SNP) is the most common source of variation in the human genome. SNP is a point mutation (e.g., substitution of a single nucleotide in the genome - A,T,C, or G) and there are around 50 million known SNPs in the human genome [3]. The alternative nucleotides for each locus (SNP position) are called alleles and each allele of a SNP can be either the major or the minor allele for that SNP. The major allele is the most frequently observed nucleotide for a SNP position and the minor allele is the rare nucleotide (i.e., the second most common). The frequency (or probability) of observing the minor allele at a SNP position is called the minor allele frequency (MAF) of that SNP. Human genome has two copies for each locus (one per chromosome) and a SNP can be represented in terms of the number of its minor alleles (i.e., 0 for homozygous major, 1 for heterozygous, or 2 for homozygous minor).

Particular SNPs in human population are inherently correlated and this correlation model may change for different populations. Linkage disequilibrium (LD) is the non-random association of alleles at two or more loci. If two SNPs are in LD, they are correlated and cooccur more frequently than expected. Some SNPs are pathogenic and cause genetic diseases [6] and hence, they may carry sensitive information regarding individuals’ health conditions. As discussed in Section 2, most existing works in genomic privacy literature focus on the protection of the SNPs to prevent the risk of genetic discrimination.

4. System Model

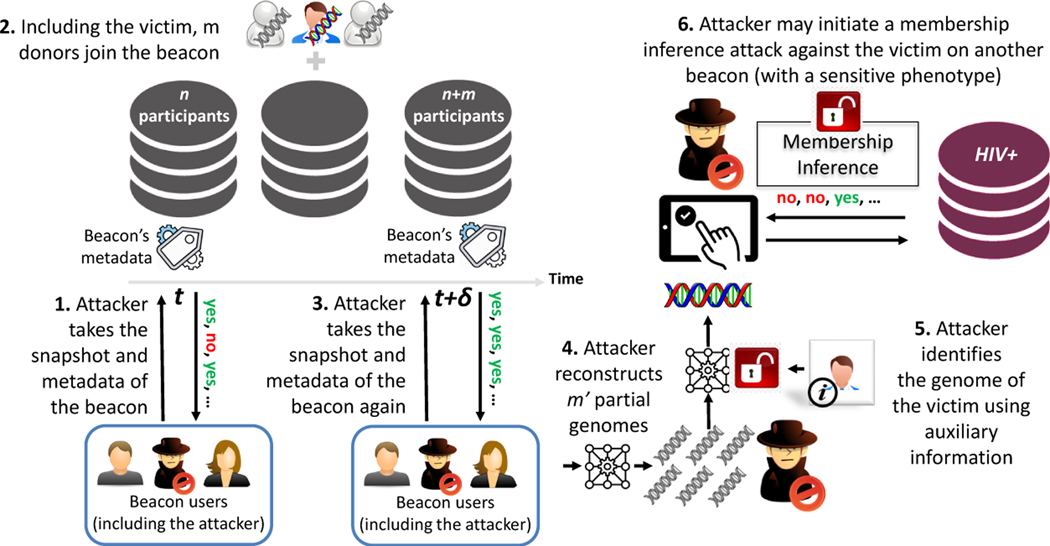
As shown in Figure 1, we consider a system between the beacon participants (e.g., donors), the beacon, and the beacon users (which may include the attacker). The donor shares their genome with the beacon. It is possible that the donor may share their genome with multiple beacons that may or may not be associated with sensitive traits. Genome donor is not active during the protocol after they share their data with the beacon. Also, beacon never publicly shares its dataset, but some beacons may share metadata about (i) their content (e.g., size) or (ii) their donors (e.g., their gender, age, or ethnicity). In general, we consider the beacon as a dynamic dataset, in which new donors may join and existing donors may leave over time. Beacon users issue queries to the beacon. As discussed, the beacon user can only ask the presence of a genome with a particular allele (nucleotide) at a particular position of a given chromosome and the beacon only responds as “yes” or “no”. In this work, we assume beacon honestly reports the result of each query to the user (e.g., without introducing intentional noise to the query results) and we do not consider a query limit for the users, as it is usually trivial to overcome such limits (e.g., by registering several times with different accounts).

Fig. 1.

Proposed system model.

5. Threat Model

Depending on the attacker’s objective, two attacks that can be launched against genomic data-sharing beacons are: (i) membership inference attack and (ii) genome reconstruction attack. In both attacks (including this work), the attacker is assumed to be a registered beacon user who can send unlimited number of queries to the beacon. In this work, for the first time, we identify and study the genome reconstruction attack. We assume that the attacker knows the membership of an individual to a beacon. Thus, we consider a targeted attack, in which the attacker knows that the victim donated their genome (to take part in a study). Given the current rise in personal genomics (people uploading their genomes to public sites), this is feasible. Also, beacons with no sensitive-phenotype report metadata about their donors. For instance, Shringapure and Bus-tamante [65] verified a specific person being in PGP and Kaviar [31] beacons via metadata, and hence the attacker can also identify the membership of the victim using such metadata. Using the membership information, the goal of the attacker is to reconstruct the victim’s genome by issuing queries to the corresponding beacon.

Genome inference attack can be considered both for static and dynamic beacons. In static beacons, knowing that the victim is a member of the beacon, only the “no” responses would provide certain information about the victim’s genome to the attacker. “Yes” responses may be due to any other participant of the beacon and as the size of the beacon increases, “yes” responses do not provide much information to the attacker. However, in dynamic beacons, when the beacon is updated, using the change in the responses of the beacon, the attacker can learn more about the genomes of new participants. Thus, in this paper, we analyze this vulnerability for dynamic beacons and we assume that the victim is added between times t and t+δ along with other (m−1) newly added donors to the beacon. As discussed before, the attacker can monitor the number of newly added donors to the beacon and the number of donors leaving the beacon from the metadata of the beacon.

We assume that, along with the fact that the victim is among the newly joined participants to the beacon, the attacker also knows (i) the number of other newly joined individuals that are added to the beacon along with the victim; (ii) a snapshot of the beacon before the victim is added (at time t). That is, responses to all queries before the victim joins to the beacon. The beacon protocol does not bar someone from taking a complete snapshot. Thus, querying a beacon to take a complete snapshot only requires a high-bandwidth internet connection. Economic cost of such an internet service is around 79$ per month [70] and there is no other economic cost, as the system is publicly available at [2]. Even though the number of SNPs in a complete snapshot is large, typically, only low-MAF SNPs are useful for the attacker (as they are typically the sensitive ones); (iii) auxiliary information about the victim to identify victim’s genome among the reconstructed ones. For this we assume the attacker has moderate information, such as a set of victim’s visible characteristics (phenotype); and (iv) publicly available information about genomics, such as minor allele frequencies (MAF values) of SNPs and correlation between the SNPs in the population of interest. Finally, we assume that the attacker does not collude with the beacon.

In genome reconstruction attack, due to the nature of beacon responses, the attacker can infer if a victim has at least one minor allele at every SNP position. This is because the response of the beacon only tells if there is an individual in the beacon with at least one minor allele at a given SNP position. Thus, for each SNP j of victim $v\left(S_j^v\right)$, the goal of the attacker is to infer $Pr(S_j^v=0)$ and $Pr(S_j^v\ne 0)$ (i.e., $Pr(S_j^v=1)$ or $Pr(S_j^v=2)$). For simplicity, we define the event ${\widehat{S}}_j^v=1_{S_j^v=1\vee S_j^v=2}$. Thus, ${\widehat{S}}_j^v=0$ if $S_j^v=0$, and ${\widehat{S}}_j^v=1$, otherwise. Note that inferring this information for a victim results in a serious privacy concern. As we will discuss and show later, using this information, an attacker can associate the genotype of the victim to related phenotypes (e.g., diseases) and initiate a membership inference attack for the victim by targeting another beacon that is associated with a sensitive phenotype (e.g., cancer or HIV+).

Our methodology consists of a complete pipeline, showing how an attacker uses the information it infers in the genome reconstruction attack in a subsequent membership inference attack. Therefore, we evaluate the success of the attacker using different metrics in different parts of the pipeline as follows. For genome reconstruction (in Section 6.3), we use precision and recall to quantify this inference power of the attacker. As we will show in Section 7, the success of genome reconstruction mainly depends on the size of the beacon, the number of newly added donors to the beacon between times t and t + δ, and the fraction of attacker’s snapshot at time t. In real life, sizes of beacons show a large variation. The size of a beacon can be as small as 100, such as NBDC Human Database [4] or as large as 100K, such as The Genome Aggregation Database (gnomAD) [5]. As discussed, these numbers can be monitored from the metadata of such beacons. Thus, as we will we show, for small-size beacons, even if the size of the beacon is significantly increased (compared to its original size), the attacker’s success may be high. For large-size beacons, on the other hand, the number of newly added donors should be a small fraction of the original size for a successful attack. As a result of the genome reconstruction, the attacker potentially reconstructs multiple genomes and among these, one belongs to the victim. For this part, we show how the attacker can utilize machine learning techniques to identify the victim’s genome among the reconstructed ones (in Section 6.4) and we use the classification accuracy of the attacker as its success metric. Finally, to quantify the success of the membership inference (Section 6.5), we use a power analysis as the success metric. To evaluate the success of the attacker in the membership inference attack, we first let the attacker run the genome reconstruction attack and then use the proposed machine learning technique to identify the victim’s genome among the reconstructed ones. Thus, the success metric for the membership inference considers the attacker’s success in the entire pipeline.

6. Genome Reconstruction Attack on Genomic Data-Sharing Beacons

As discussed, we define the genome reconstruction attack as inferring genomic data of a genome donor (i.e., victim) given their membership information to the beacon. To show the effect of genome reconstruction attack more clearly, we consider dynamic beacons and we assume the victim is among the newly joined donors to the beacon. For clarity of the discussion, we present the identified attack only considering newly joined donors. Considering the donors that leave the beacon is symmetrical and trivial. We discuss this case in Section 8.2.

We consider a scenario, in which the attacker has no information about the victim’s genome, but it knows that the victim is added to the beacon between times t and t + δ. Let n and (n + m) represent the number of individuals in the beacon at times t and t + δ, respectively. As discussed, for most real-life beacons, the attacker knows m (by monitoring the changes in beacon using the metadata of the beacon). In all attack scenarios, we assume that the attacker reconstructs m’ genomes (m’ can be different than m and the selection of m’ effects the precision and recall of the attacker). Our goal is to evaluate the performance for different m’ values to show the attack is robust even if the attacker does not know how many people are added. When metadata of the beacon, and hence m is not available, the attacker can determine a potential upper bound (k) for the number of newly added donors (m) by examining the number of flipped responses (from “no” to “yes”). Then, for each i from 1 to k, it can reconstruct genomes using $R_{N\to Y}$ assuming m = i, and hence instead of m, the attacker ends up having $\frac{k(k+1)}{2}$ potential genomes to identify the victim’s best matching reconstructed genome.

Using its auxiliary information (as discussed in Section 5), the attacker can probabilistically infer the genome of the victim by utilizing the changes in beacon’s responses (at times t and t + δ) as follows: (i) if the previous response (at time t) was “no” and the current response (at time t + δ) is “yes”, the probability that the victim having a minor allele at the corresponding query position increases depending on how many new individuals are added to the beacon in this time interval; (ii) if the previous response was “yes” and the current response is also “yes”, attacker cannot infer much about the victim’s genome, especially if the total size of the beacon is large; and (iii) if both the previous and the current responses are “no”, the attacker understands that the victim does not have a minor allele at the corresponding query position.

Here, the most important (or the most sensitive) information for the attacker can be considered as the “no” responses at time t that turn to “yes” at time t+δ. Because, such responses let the attacker infer the positions that the victim has at least one minor allele with a high probability (depending on how many new individuals are added to the beacon in this time interval). Since minor alleles of individuals are typically the indicators for privacy-sensitive information about them, in this work, we focus on the success of the attacker based on its success in inferring the minor alleles of a victim using the beacon responses that turn to “yes”. Exhaustively generating all potential solutions of this problem would result in a total of 2^β∗m′ genomes, where β is the total number of responses that turn to “yes” at time t + δ (which can be on the order of tens of thousands), and hence it is intractable. In the following, we first describe a baseline method that provides a tractable solution to this problem. Next, we present a greedy approach to run such an attack more accurately, and then we will detail a more sophisticated, clustering-based approach for the genome reconstruction attack.

6.1. Baseline Approach for Genome Reconstruction

Here, we describe a baseline approach, in which the attacker, using the responses of the beacon, reconstructs the genomes (of the newly joined donors) by assigning them to m′ bins according to MAF values of the SNPs. Genome reconstruction attack using the baseline algorithm for a particular victim v at time t + δ can be described as follows. The input of the attacker is (i) responses of the beacon to all possible queries at time t (i.e., complete snapshot of the beacon at time t); (ii) the fact that m new donors are added to the beacon between times t and t + δ; (iii) the fact that the victim is among the newly added donors; and (iv) publicly available MAF values of the SNPs.

First, the attacker identifies the set of SNPs for which the response of the beacon was “no” at time t and it becomes “yes” at time t + δ. Thus, the attacker constructs a set $R_{N\to Y}$, consisting of these SNPs. Then, the attacker creates m’ empty bins representing SNP sets of newcomer donors. For each SNP j in set $R_{N\to Y}$, the attacker retrieves its MAF value, MAF_j. Next, the attacker assigns the value of SNP j for each individual i (in each bin) consistent with the SNP’s MAF value as follows: (i) ${\widehat{S}}_j^i=0$ with probability (1 − MAF_j)² and (ii) ${\widehat{S}}_j^v=1$ with probability $MA{F}_j^2+2MA{F}_j\left(1-MA{F}_j\right)$. Since the beacon’s response for SNPs in $R_{N\to Y}$ has flipped from “no” to “yes”, for all SNPs in $R_{N\to Y}$, there should be at least one bin (among m’ bins) with at least one mutation (i.e., homozygous minor or heterozygous SNP). Thus, once the values of the SNPs in $R_{N\to Y}$ for all m’ bins are determined, the attacker checks if there is any SNP in set $R_{N\to Y}$ that is not assigned to any bin. If there is such a SNP, the attacker randomly picks a bin and assigns the value of the corresponding SNP as ${\widehat{S}}_j^i=1$ for the corresponding bin. The details of this baseline approach are also shown in Algorithm 2 (in Appendix B).

6.2. Greedy Algorithm for Genome Reconstruction

The above-mentioned baseline algorithm assumes every SNP is independent and the correlations among them are disregarded. However, SNPs are inherently correlated and considering such correlations in the genome reconstruction attack may result in significantly more accurate results. In the greedy algorithm discussed here, the attacker forms the bins considering the correlations between the SNPs in set $R_{N\to Y}$. Using an iterative approach, the attacker assigns each SNP (minor allele) to an individual such that the probability of assignment is proportional to the average correlation of the new SNP with the already assigned SNPs of the individual (i.e., bin i). If no assignment is made this way, a random individual is selected to make sure there is at least one person with the corresponding new SNP.

Genome reconstruction attack using the greedy algorithm for a particular victim v at time t + δ can be described as follows. The input of the attacker includes everything in the baseline approach and also a correlation model between the SNPs that is consistent with the population structure of the beacon (that can be computed using publicly available genomic datasets). Different correlation models have been explored for genomic data before. In [62], authors showed how the correlations in the genome can be modelled using a Markov chain model. We create our correlation model by considering the pairwise correlations between all the SNPs in the beacon (which results in richer information for the attacker). The attacker calculates the likelihood of the victim v having at least one minor allele at a SNP position j as $P_k\left({\widehat{S}}_j^v\right)=P\left({\widehat{S}}_j^v\mid {\widehat{S}}_k^v\right)$ where k may be any other position in the genome. We use Sokal-Michener distance to compute correlations between SNPs as follows:

$$A=2\left(n_{{\widehat{S}}_j^v=1,{\widehat{S}}_k^v=0}+n_{{\widehat{S}}_j^v=0,{\widehat{S}}_k^v=1}\right)$$

$$B=n_{{\widehat{S}}_j^v=1,{\widehat{S}}_k^v=1}+n_{{\widehat{S}}_j^v=0,{\widehat{S}}_k^v=0}$$

$$D_{Sokal-Michener}\left({\widehat{S}}_j^v,{\widehat{S}}_k^v\right)=\frac{A}{A+B}$$

In the greedy approach, first, the attacker constructs set $R_{N\to Y}$. Then, it creates m′ empty bins (m′ does not have to be equal to m) representing the number of rare SNPs in $R_{N\to Y}$. We assume that the SNPs with an MAF value below a threshold τ are categorized as rare SNPs. Observing rare SNPs do not have correlations among each other, assigning the rare SNPs in $R_{N\to Y}$ to different bins as seeds is assumed to result in an accurate initial separation of individuals. Next, for each remaining SNP j in $R_{N\to Y}$, the attacker computes the average correlation between that and all the previously assigned SNPs in bin i using the aforementioned correlation model. This is done for each bin i. Let ${\widehat{S}}_j^i$ be a binary random variable for SNP j and bin i. The attacker assigns ${\widehat{S}}_j^c=1$ for bin c which has the highest average correlation value and ${\widehat{S}}_j^i=0,\forall i\in \left[1,m^{\prime }\right]$ and i ≠ c. Eventually, the attacker constructs m′ potential genomes (in m′ bins) belonging to m newcomer donors.

6.3. Clustering-Based Algorithm for Genome Reconstruction

Greedy algorithm (in Section 6.2) reconstructs genomes by following a particular order (determined based on the MAFs of the SNPs). Different orders may provide different solutions. Thus, to consider all query responses together in a collective way, we propose clustering-based approaches for the genome reconstruction attack that cluster the identified minor alleles for the newly joined donors to the beacon. The proposed clustering techniques essentially use the correlations between the SNPs (that are computed using the aforementioned correlation model) to distribute SNPs into different bins. We use two types of clustering techniques: (i) hard clustering to create non-overlapping bins and (ii) soft or fuzzy clusterin to assign a SNP into multiple bins.

For (i), we employ spectral clustering, in which a standard clustering method (such as k-means clustering) is applied on certain eigenvectors of the Laplacian matrix of a graph [57]. In this graph, the SNPs correspond to vertices and correlations between the SNPs correspond to weights of edges. Spectral clustering is our method of choice as it has been shown to provide favorable results in many high dimensional feature spaces like ours [60]. And, for (ii) we employ the fuzzy c-means clustering (FCM) algorithm [14], which is a common choice for these types of tasks. The algorithm is similar to k-means clustering, but it also allows probabilistic assignments of samples to multiple clusters. Different from k-means clustering, FCM assigns a membership value $u_{ij}=P\left({\widehat{S}}_j^i=1\right)$ for each element j and for each cluster i. This membership values are used as weights in the objective function. After convergence, these membership values are used as the probability of assignments of elements to each cluster. The description of both clustering methods are similar except for the clustering steps. Thus, in the following, we describe both methods together.

The input of both clustering-based algorithms is the same as the input of the greedy algorithm. First, the attacker identifies the set of SNP positions for which the response of the beacon was “no” at time t and it becomes “yes” at time t + δ and constructs set $R_{N\to Y}$. Then, the attacker builds a graph of SNPs using the correlation model, in which the vertices are the SNPs in $R_{N\to Y}$ and undirected edges are weighted by the correlation values between these SNPs. This graph represents a pairwise similarity model for the SNPs and is used for a quantitative assessment of the correlation of each SNP pair in $R_{N\to Y}$.

Next, the attacker applies either the spectral or fuzzy clustering algorithms on the constructed graph. The outcome of spectral clustering is a set of disjoint clusters. Fuzzy clustering results in groups of SNPs that maximizes the similarity in a group while allowing a SNP to be shared by multiple individuals. Thus, in fuzzy clustering, each SNP i is assigned to clusters for which the algorithm returns a relatively high probability of association. After clustering, the attacker obtains m’ different clusters which corresponds to m’ reconstructed genomes. The details are shown in Algorithm 1.

6.4. Identifying the Victim Using Genotype-Phenotype Associations

In previous sections, for genome reconstruction, we assumed that the attacker can correctly identify the victim’s genome among several reconstructed bins. Assuming the attacker has some moderate auxiliary information about the victim, here, we study and show how accurately the attacker can identify the victim’s genome among other candidates. For this, we assume the attacker uses information about some phenotypic characteristics of the victim and it relies upon the fact that SNPs are intrinsically linked to phenotypic traits (such as eye color, hair color, etc.) This provides a complete methodology for the genome reconstruction attack against beacons in real-life. As we will discuss later, the success of the attacker to correctly identify the victim’s genome among the reconstructed ones increases if the attacker has access to more auxiliary information about the victim.

Assume victim v is among the m new additions to the beacon (it is trivial to extend the methodology if there are more than one victim). The attacker is assumed to have access to two distinct sets: (i) a set $\mathcal{S}=\left\{{\overrightarrow{S}}_1,{\overrightarrow{S}}_2,\dots ,{\overrightarrow{S}}_{m^{\prime }}\right\}$ of m′ reconstructed genotypes as a result of the genome reconstruction attack, where ${\overrightarrow{S}}_i=\left({\widehat{S}}_1^i,\dots ,{\widehat{S}}_k^i\right)$ is a vector containing the SNP values of genotype i (or bin i); and (ii) a set ${\mathcal{P}}_v=\left(p_1^v,\dots ,p_t^v\right)$ containing the values of t phenotypic traits of victim v. Such phenotype information can be obtained from publicly available resources or using the physical traits of the victim. For instance, the attacker can obtain such information from victim’s social media accounts. The goal of the attacker is to correctly match the victim’s phenotype to the correct reconstructed genome (that is the most similar to the victim’s) among all candidate reconstructed genome sequences. In the test phase, the attacker has m newly added donors and m’ reconstructed genomes. Attacker’s task is to match each donor with the best matching reconstructed genome. Thus, for each newly added donor, the attacker calculates the likelihood scores of matching with all m’ reconstructed genomes.

Algorithm 1:

Clustering-Based Algorithm for Genome Reconstruction Attack

In [40], Humbert et al. focused on the deanoymization risk and modelled genotype-phenotype association as an assignment problem. They showed this risk by using the Hungarian algorithm [47]. Different from [40], here, we rely on machine learning for maximizing the matching likelihood and genotype-phenotype associations. We observe that such a formulation provides more accurate results. Also, rather than using SNP values (0, 1 or 2), due to the nature of the proposed attack, we represent the state of each SNP j of individual i as ${\widehat{S}}_j^i$ which can be either 0 or 1, as discussed before.

For phenotype inference, we train a separate model for each of the considered phenotypes, where SNPs with flipped responses (from “no” to “yes”) are used as features. Since phenotype datasets are highly imbalanced, we apply Synthetic Minority Oversampling Technique (SMOTE) [16] for each of these datasets to resolve this problem. In SMOTE, a minority class instance is selected along with its nearest neighbors at random. Then, a new sample is generated as a combination of the original instance and a random neighbor. Next, we train a random forest model for each phenotype. We use repeated stratified 5-fold cross validation to tune the hyperparameters. After training the phenotype models, we form the ensemble classifier using the ones that have better validation F1-macro score than random guess. We discard the other models.

Ensemble classifier calculates the matching likelihood of given genome and set of phenotypic traits. Softmax output of each phenotype model corresponding to a given phenotypic trait of the victim (i.e., probability that a reconstructed genome having blue eye) are summed to calculate the matching likelihood. For single victim, this calculation is done for each reconstructed genome and the victim is matched with the reconstructed genome with the highest matching likelihood score. Note that this matching does not need to be one-to-one; a single reconstructed genome might match with different set of phenotypic traits. We discuss the performance of identification of victim’s reconstructed genome under different settings in Section 7.4.

6.5. Using Genome Reconstruction in Membership Inference Attack

To show one consequence of the proposed genome reconstruction attack, we also model and analyze how the proposed attack can be utilized for membership inference attack (introduced in Appendix A). We consider a scenario in which the attacker knows the membership of an individual to a beacon with which no sensitive associated phenotype (e.g., phenotype neutral). The attacker first utilizes the responses of this beacon to infer specific parts of a victim’s genome (i.e., SNPs). Then, it uses these inferred SNPs to infer the membership of the victim to a beacon with a sensitive phenotype. This attack is important and realistic, because knowing the membership of an individual to a phenotype neutral beacon (e.g., Kaviar Beacon) may not seem to pose a privacy issue. However, using the proposed genome reconstruction attack and the membership information of the victim to the beacon with non-sensitive phenotype, the attacker can first infer the SNPs of the victim and then, infer the membership of the victim to another beacon which is associated a sensitive phenotype (e.g., SFARI beacon which is associated with autism phenotype).

To show this, first, we run the proposed genome reconstruction attack that is explained in Section 6.3 and infer the SNPs of the victim with at least one minor allele on a beacon B₁. Using these inferred SNPs, we then run the membership inference attack to infer the membership of the victim in another beacon B₂. For membership inference attack, we use the optimal attack in [59] (described in Appendix A), which is shown to be an effective attack for membership inference (for our scenario, optimal attack in [59] and the QI-attack in [73] perform similarly, so we choose to use the optimal attack due to its simplicity). However, in contrast to the original optimal attack, in the null and alternate hypothesis equations in (1) and (2), there is an additional error due to the inference error of the genome reconstruction attack. This is because the attacker queries the alleles of the victim that it infers as a result of the genome reconstruction attack and there is a degree of uncertainty. Thus, we first experimentally compute the error rate of the genome reconstruction attack for a particular scenario (e.g., for particular m and n values). We then include this additional error on the γ parameter in (2), which represents the probability that the attacker’s copy of the victim’s genome does not match the beacon’s copy for a SNP. Furthermore, as opposed to original optimal attack, here the attacker may not have access to the SNPs of the victim with the lowest MAF values; instead the attacker only knows the SNPs that are inferred as a result of the genome reconstruction attack.

We evaluate the success of this attack in terms of the power of the attacker in Section 7.5. Similar to Raisaro et al. and von Thenen et al., we plot the power curve of the membership inference attack at 5% false positive rate. We empirically build the null hypothesis (H₀ in Appendix A). For every query, we determine the distribution of Λ under the null hypothesis using 20 individuals that are not in B₂. In this work, in order to model the uncertainty of correctly matching the victim (using phenotype inference as in Section 6.4), we first experimentally compute the error rate of the overall process. For instance, if the accuracy of correctly matching the phenotype of the victim to their reconstructed genome is p%, then p% of the 20 individuals are selected from correctly identified reconstructions and remaining individuals are selected from other new people added to the beacon along with the victim (incorrect identifications).

When Λ is less than a threshold t_α, the null hypothesis is rejected and we find t_α from the null hypothesis with α = 0.05 (corresponding to 5% false positive rate). Then, we computed the power as proportion of the individuals in the alternate hypothesis (including 20 different individuals in B₂) having a Λ value that is less than t_α. As before, p% of the 20 individuals are selected from correctly identified reconstructions and remaining people are selected from other new people added to the beacon along with the victim.

7. Evaluation

To evaluate the identified vulnerabilities, we evaluated our methods using real-life genomic datasets. Here, we describe the datasets and present the evaluation results.

7.1. Datasets

We used two different genome datasets for evaluation: (i) genome dataset of CEU population from the HapMap dataset [29] and (ii) OpenSNP genome dataset [7]. Using the HapMap dataset, we created the beacons and victims from CEU population which contains 164 donors and around 4 million SNPs for each donor. We created the correlation model (i.e., SNP-SNP relation network or similarity model) for this beacon using individuals from the same HapMap dataset that are not in the constructed beacon and set of victims. Using the OpenSNP dataset, we created the beacons and victims from a random population which contains 2980 donors and around 2 million SNPs for each donor. We created the correlation model using the rest of the OpenSNP dataset.

For the OpenSNP dataset, we also collected the reported phenotypes of individuals. Since sample sizes are small, we used the reported phenotypes in a binary form. From OpenSNP, we used the following commonly reported phenotypes: (i) eye color, 967 samples, (ii) hair type, 371 samples, (iii) hair color, 468 samples, (iv) tan ability, 287 samples, (v) asthma, 226 samples, (vi) lactose intolerance, 347 samples, (vii) earwax, 244 samples, (viii) tongue rolling, 434 samples, (ix) intolerance to soy, 136 samples, (x) freckling, 277 samples, (xi) ring finger being longer than index finger, 268 samples, (xii) widow peak, 176 samples, (xiii) ADHD, 154 samples, (xiv) acrophobia, 155 samples, (xv) finger hair, 155 samples, (xvi) myopia, 152 samples, (xvii) irritable bowel syndrome, 142 samples, (xviii) index finger being longer than big thumb, 131 samples, (xix) photoptarmis, 133 samples, (xx) migraine, 129 samples, and (xxi) Rh protein, 311 samples. We used 1320 genomes which are associated with at least one of the listed phenotypes while training the models. Newly added donors are chosen from the individuals who have reported at least 10 out of 21 considered phenotypes. We repeated each experiment for 10 times with different sets of newly added donors. For each experiment, remaining samples (except for the beacon participants and newly added donors) are used to train and validate phenotype models.

7.2. Evaluation Metrics

We evaluated the precision and recall for the reconstruction of a victim’s SNPs based on the changes in beacon responses. For precision and recall, we defined the success as correctly inferring the SNPs of the victim with at least one minor allele. Thus, for the calculation of precision and recall, we defined (i) true positive as correctly inferring a SNP j of victim v with ${\widehat{S}}_j^v=1$ (with at least one minor allele); (ii) false positive as incorrectly assigning ${\widehat{S}}_j^v=1$ for v who is homozygous major at that locus; (iii) true negative as correctly inferring a SNP j of victim v with ${\widehat{S}}_j^v=0$ (with no minor allele, homozygous major); and (iv) false negative as incorrectly assigning ${\widehat{S}}_j^v=0$ for v who has at least one minor allele at that locus (i.e., heterozygous or homozygous minor).

Furthermore, we quantified the success of identifying the victim’s genome among the reconstructed genomes in terms of the accuracy of the developed genotype-phenotype inference mechanism. We evaluated the accuracy of the ensemble classifier (to identify victim’s genome from phenotype) using the reconstructed genomes of newly added donors. Given ensemble classifier f, set of indices $\overrightarrow{J}=\left(j_1,\dots ,j_v\right)$ that represent the indices of best matching clusters for each newly added donors, vector containing SNP values of the i^th cluster ${\overrightarrow{S}}_i=\left({\widehat{S}}_1^i,\dots ,{\widehat{S}}_k^i\right)$ and set of phenotypic traits of victim $v,{\mathcal{P}}_v=\left(p_1^v,\dots ,p_t^v\right)$, we computed the accuracy as $\left(\sum _{v=1}^m{\mathbf{1}}_{\left(\underset{1\le i\le m^{\prime }}{\text{argmax}}f\left({\overrightarrow{S}}_i,{\mathcal{P}}_v\right)\right)=j_v}\right)/m$. Finally, we used power analysis for the membership inference to show how the outcome of the genome reconstruction attack can be used for membership inference attack. Power for the i^th query is calculated from given set of l case people as $P^i=\left({\sum }_{{\text{Λ}}_j^i\in {\text{Λ}}_{case}^i}{\mathbf{1}}_{{\text{Λ}}_j^i<t_{\alpha }^i}\right)/l$ which is defined as the fraction of the cases who have ${\text{Λ}}_j^i$ value that is less than $t_{\alpha }^i$ as described in Section 6.5. Then, the vector ${\overrightarrow{P}}^n=\left(P^1,\dots ,P^n\right)$ is plotted to see the power change with respect to a total of n queries. Higher power value represents a more successful attack.

7.3. Evaluation of Genome Reconstruction

First, using both OpenSNP and HapMap beacons and only focusing on genome reconstruction, we evaluated and compared the baseline method (in Section 6.1) and the proposed clustering-based approach (in Section 6.3) when the size of the beacon (n) is 50 and m = m’. Here, we assume that the attacker can identify the victim’s reconstructed genome among the other candidates. Later, we will also show that attacker can indeed identify this genome with high accuracy using public (i.e., not sensitive) phenotype information about the victim.

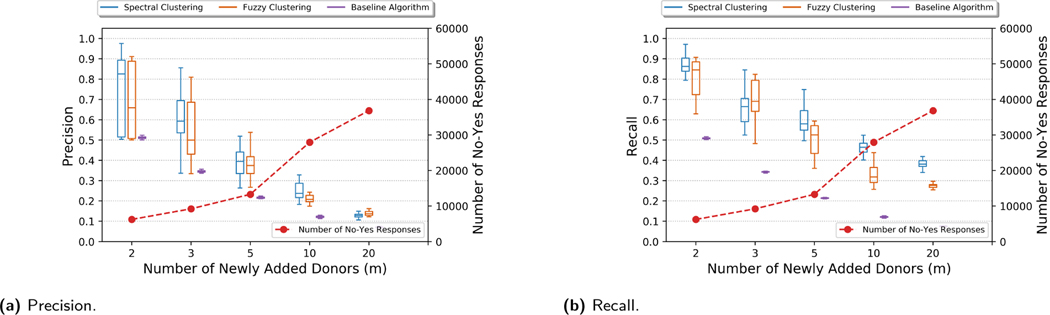
Figures 2 and 9 (in Appendix C) show the precision and recall of the reconstruction for various number of newly added donors (m) for OpenSNP and HapMap beacons, respectively. Overall, we observed that the success of the attack to be higher for OpenSNP beacon. The reason of this is the limited data we had to build the correlation model for HapMap dataset (we used 945 donors to build the correlation model in OpenSNP beacon, while we could only use 110 donors to build it for the HapMap beacon). For both datasets, we used individuals that are not in the beacon to construct the correlation models. When we compared the correlation models that are constructed using the individuals that (i) are not in the beacon and (ii) are in the beacon, we observed that correlation model constructed for the OpenSNP beacon is significantly more accurate (i.e., it is very close to the correlation model of the individuals that are in the OpenSNP beacon) mainly due to the number of individuals we used to create the model. Therefore, in the following, we mostly discuss the results we obtained from the OpenSNP beacon.

Fig. 2.

Precision and recall for the genome reconstruction of a newly added donor to OpenSNP beacon with varying number of newly added donors.

Fig. 9.

Precision and recall for the genome reconstruction of a newly added donor to HapMap beacon with varying number of newly added donors.

The results show that on average, the identified attack using spectral clustering can reconstruct the victim’s genome with a precision close to 0.9 when the size of the beacon is increased by adding 3 people (i.e., a 6% increase in beacon size). We also obtained more than 0.7 precision and 0.8 recall even when the size of the beacon is increased by adding 10 people (i.e., a 20% increase in beacon size). This indicates a substantial privacy risk, especially if the reconstructed SNPs are tied to sensitive phenotypes. Also, the baseline algorithm (in Section 6.1) performs substantially worse than the proposed clustering-based approach. The results also show that spectral clustering-based genome reconstruction is slightly better than the fuzzy clustering-based approach. We observed that allowing a SNP (that includes at least one minor allele) to be in multiple bins results in high false positives. Therefore, in the remaining of this section, we use spectral clustering-based genome reconstruction for the evaluations.

To show the benefit of utilizing a beacon (and beacon update) in its genome reconstruction attack, we also computed the reconstruction accuracy of an attacker when it only uses publicly available information (e.g., population statistics and victim’s phenotype). As discussed, each victim we consider has a subset of 21 phenotypes listed in Section 7.1. Using the associations of victim’s phenotypes with the corresponding SNPs (extracted from SNPedia [8]), we assigned some SNP values of the victim. We observed that, on the average, such a reconstruction achieves a precision of 18% and a recall of 47% on total of 232 SNPs. Therefore, we conclude that having access to a beacon and knowing the membership of a victim to a beacon significantly increases the success of the genome reconstruction attack.

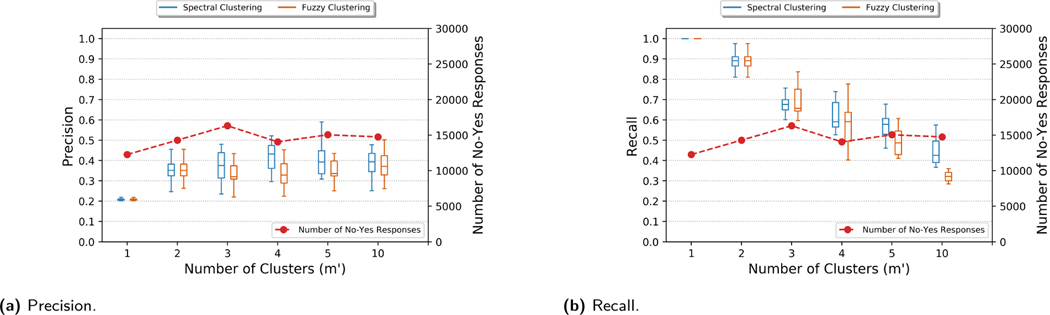
To show the effect of varying number of bins (m’) in the genome reconstruction attack, in Figures 3 and 10 (in Appendix C), we show the attacker’s success when the number of newly added donors m = 5 and beacon size n = 50 for OpenSNP and HapMap beacons, respectively. We observed that for both beacons, precision increases and recall decreases with increasing m’. Also, as expected, precision and recall becomes balanced when m’ = m.

Fig. 3.

Precision and recall for the genome reconstruction of a newly added donor to OpenSNP beacon with varying number of bins/clusters (m’) in the genome reconstruction attack. Number of newly added donors (m) is 5.

Fig. 10.

Precision and recall for the genome reconstruction of a newly added donor to HapMap beacon with varying number of bins/clusters (m’) in the genome reconstruction attack. Number of newly added donors (m) is 5.

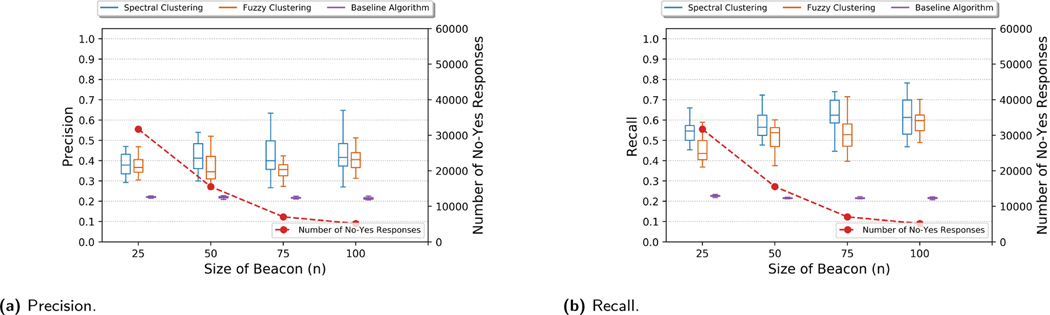
Next, in Figures 4 and 11 (in Appendix C), we show the effect of the beacon size (n) at time t when 5 new donors are added between times t and t + δ for OpenSNP and HapMap beacons, respectively. Here, we assume that the number of bins (m’) is equal to the number of newly added donors (m). We observed that as the size of the beacon increases, both the precision and recall of the reconstruction attack almost remains the same (for a fixed number of newly added donors).

Fig. 4.

Precision and recall for the genome reconstruction of a newly added donor to OpenSNP beacon with varying number of beacon size (n). Number of newly added donors m is 5 and m’ = m for all plots.

Fig. 11.

Precision and recall for the genome reconstruction of a newly added donor to HapMap beacon with varying number of beacon size (n). Number of newly added donors m is 5 and m’ = m for all plots.

Even if the success of the genome reconstruction remains high, the number of flipped responses (from “no” to “yes”) may decrease when beacon size is increased (as shown in Figure 4). In other words, the number of vulnerable SNPs (the ones that can be inferred using the change in the beacon responses) of a victim decreases and this might result in lower performance in phenotype inference and membership inference parts of the attack. However, with high probability, as the beacon size increase, low-MAF SNPs of the victim (which typically provide the most valuable information for the membership inference attack) still remain vulnerable, since with high probability, such SNPs are not observed in other donors in the beacon. For example, in the previous experiment (in Figure 4), when the size of the beacon is increased from 50 to 400, total number of vulnerable SNPs of a victim reduces by 94%, however, number of vulnerable SNPs of a victim with MAF value smaller than 0.01 only reduces by 52%.

Keeping the ratio of newly added donors fixed (to 5%), we also observed the change in the success of the attack with increasing beacon size when m’ = m in Figure 5 (we did this evaluation only for the OpenSNP beacon since HapMap beacon did not have more than 100 donors). We observed that, when the beacon size increases beyond 100, although the recall of the attacker still remains high, its precision starts decreasing. This shows that the success of the identified attack mainly relies on the number of clusters the attackers needs to generate (in the proposed clustering-based algorithm). For small or mid-size beacons (e.g., NBDC Human Database [4] with slightly more than 100 individuals), even if the beacon update significantly increases beacon’s size, the identified attack is still effective. On the other hand, for large size beacons (e.g., gno-mAD [5], with more than 100K individuals), the update size should be small to have a vulnerability.

Fig. 5.

Precision and recall for the genome reconstruction of a newly added donor to OpenSNP beacon with varying number of beacon size (n). Number of newly added donors m is always 5% of the beacon size and m’ = m for all plots.

Finally, we explored the scenario, in which the attacker only has a partial snapshot of the beacon (instead of a full snapshot). In Figure 6, we show the success of the reconstruction attack when m = 5 donors are added (at time t + δ) into the OpenSNP beacon with size 50 when the attacker has varying snapshots of the beacon at time t and when m = m’. We observed that the success (precision and recall) of reconstruction do not change with varying snapshots. However, the number of inferred SNPs (as a result of the genome reconstruction attack) decreases linearly with the decreasing snapshot that is known by the attacker at time t.

Fig. 6.

Precision and recall for the genome reconstruction of a newly added donor to OpenSNP beacon when the attacker knows varying fractions of beacon’s snapshot. Number of newly added donors m is 5, beacon size n is 50 and m’ = m for all plots.

7.4. Identifying the Victim’s Genome Using Phenotype Inference

Here, we evaluate the success of the attacker in identifying the reconstructed genome of the victim among all reconstructed genomes using the algorithm in Section 6.4. Since HapMap dataset does not include phenotype information about the genome donors, we only use the OpenSNP beacon for this evaluation.

We employed and compared several machine learning models for genotype-phenotype associations, including: Logistic Regression [23], SVM [22], Multi-layer Perceptron [72], Random Forest [67], and XGBoost [17]. Among these, we obtained the highest classifier accuracy with the Random Forest, and hence all reported results are based on this model.

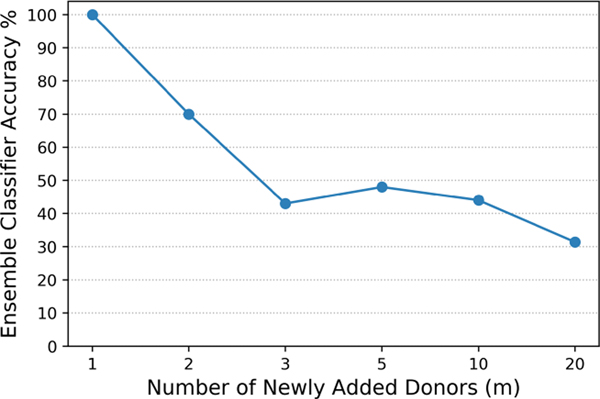
In Figure 7, we show the ensemble classifier accuracy for varying number of newly added donors to the beacon (here, we assumed m’ = m and we observed similar patterns when m’ ≠ m as well). We used the original genomes of individuals in the training dataset when building the model. For test, we used reconstructed genomes of the victims (that may have noise due to reconstruction error). Beacon size is 50 in these experiments (i.e., n = 50).

Fig. 7.

Classification accuracy of genotype inference from phenotype for varying number of newly added donors (m) to the beacon.

We observed that the proposed algorithm provides 70% accuracy when the size of the beacon is increased by adding 2 individuals in the update, and the accuracy slightly decreases with increasing number of newly added donors. These results show that the attacker can identify the reconstructed genome of the victim among all m’ reconstructed genomes with high accuracy. As discussed before, in this experiment, we assumed the attacker has moderate auxiliary knowledge about the victim (i.e., phenotypic-traits, which can be easily learnt from social network profiles of the victim). However, since genotype-phenotype associations are not strong yet, there is an accuracy bottleneck in the overall process due to this step. A stronger attacker (that has access to richer auxiliary information about the victim) may utilize victim’s known mutations or genomes of family members. Then, the phenotype inference part is not required and accuracy loss would not happen.

7.5. Using Genome Reconstruction in Membership Inference

In Section 7.3, we evaluated the success of the reconstruction and in Section 7.4, we showed that the attacker is able to identify the victim among many added donors with high accuracy. Here, we show a severe consequence of the proposed genome reconstruction attack, in which the outcome of the previous steps can be utilized in a membership inference attack. By doing so, we also explicitly explore the impacts of (i) incorrect inference of some SNPs during reconstruction and (ii) imperfect choice of the reconstructed genotype due to the use of genotype-phenotype associations in terms of the success of this membership inference attack.

We randomly constructed two non-overlapping beacons from the OpenSNP dataset: (i) B₁ includes 50, and (ii) B₂ includes 60 individuals. We assume that B₂ is associated with a privacy-sensitive phenotype and the goal of the attacker is to infer the membership of the victim to B₂. We also assume that m new individuals are added to B₁ at time t + δ and the victim is among these newly joined donors. The attacker only knows that the victim is among these m individuals that are added to B₁ at time t + δ along with a snapshot of B₁ at time t.

First, we applied the spectral clustering-based genome reconstruction (that provides the best performance in Section 7.3) to reconstruct the genomes of newly joined m donors to B₁. Then, we identified the reconstructed genome of the victim using phenotype information about the victim (as in Section 6.4). Finally, using the reconstructed genome of the victim, we conducted the membership inference attack on B₂ using the optimal attack (as described in Appendix A).

We used the identification accuracy in Section 6.4 to construct and infer victims’ genomes for alternate and null hypotheses. For instance, when m = 2 we have 70% identification accuracy. In this scenario, 14 genomes are chosen from correctly reconstructed genomes, while the remaining 6 genomes are chosen from incorrectly reconstructed genomes for corresponding victims.

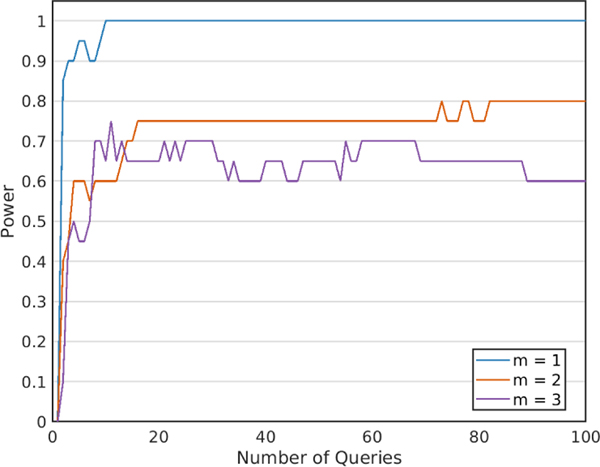
In Figure 8, we show the power plots of this attack with varying number of newly added donors (m) to beacon B₁. As expected, with decreasing values of m, the power increases faster since the accuracy of genome reconstruction increases (and hence the error rate of the membership inference attack decreases). For instance, when the victim is the only newly added donor to beacon B₁ (m = 1), the attacker can reconstruct their genome and then infer the victim’s membership to beacon B₂ with a very high confidence (100% power) in just slightly more than 15 queries. We also observed that when m is increased, the power decreases, yet still reaches to 0.8 with approximately 80 queries when 2 individuals are added. These results show that the attacker may confidently conduct membership inference attacks as a result of genome reconstruction even though it has many sources of uncertainties in its input for membership inference.

Fig. 8.

Power of membership inference attack on beacon B₂ with varying number of newly added donors (m) to beacon B₁.

8. Discussion

This work pinpoints a new information leak and identifies beacon updates as a new risk, which leads to genome reconstruction attacks. We show that an attacker can efficiently and accurately link this new vulnerability to a membership inference attack. Furthermore, recently, we observed that some beacons even report the number of occurrences for a “yes” response (e.g., Sinai Health System Beacon in [2]). Using such information in the identified attack would further improve the accuracy of the proposed clustering-based algorithm (in Section 6.3). We will explore this in future work.

8.1. Extension of the Proposed Attack

For the proposed genome reconstruction algorithm in Section 6.3, we only focused on the “no” responses of the beacon at time t that turn to “yes” at time t + δ (i.e., no-yes responses) since such responses reveal the SNPs of the victim with minor alleles and minor alleles are typically the indicators for privacy-sensitive information about individuals. As a result, we also only considered the correlations between such SNPs of a victim. As briefly discussed before, no-no responses also provide deterministic information to the attacker (about the victim certainly not having a minor allele in such SNP positions). Furthermore, using the information from no-no responses, the attacker can utilize the correlations between such SNPs (with no minor alleles) and others. In this work, we did not consider the no-no responses in the attack since (i) typically there are excessive number of no-no responses in a beacon and this creates a computational burden to compute all the pairwise correlations between such SNPs and (ii) SNPs with no minor alleles (learned from no-no responses) typically are not highly correlated with the SNPs with minor alleles, which are instrumental to the attacker for the membership inference attack. We will further consider the impact of such no-no responses in future work.

8.2. Donors Leaving the Beacon

In Sections 6 and 7, we presented and evaluated the identified vulnerability by only considering the newly joined donors to the beacons. It is also possible that existing donors may leave the beacon. However, such a scenario can be easily addressed by using the identified attack mechanism. Considering the donors that leave the beacon brings up two different scenarios: (i) victim is among the newly joined donors (while there are also donors leaving the beacon between times t and t+δ) and (ii) victim is among the donors that leave the beacon (while there may be other donors leaving or joining the beacon between times t and t + δ).

Scenario in (i) is no different than what we discussed in Section 6. The number of “no” responses at time t that turn to “yes” at time t + δ does not change due to the donors leaving the beacon. On the other hand, some “yes” responses at time t may turn to “no” at time t+δ due to the donors leaving the beacon. However, such responses do not provide information about the minor alleles of the victim, and hence we do not consider such responses in this work. In scenario (ii), “yes” responses at time t that turn to “no” at time t + δ will provide information about the minor alleles of the victim (and other donors that leave the beacon during that time interval). Using such responses, one will need to run the algorithms proposed in Section 6 to reconstruct the genome of the victim.

8.3. Risk Quantification for the Genome Reconstruction Attack

The identified vulnerability and the proposed attack algorithm can be used as a privacy risk quantification tool by the beacon operator. For this, we foresee a simulation-based technique to quantify the risk and show it to the beacon operator. This will be a customized technique for each donor in the beacon and the following discussion is for one particular donor. Assume that a total of m new donors are gathered by the beacon between times t and t+δ. To quantify the genome reconstruction risk, one may run the attack we introduced in Section 6, pretending the donor is added to the beacon along with the other (m−1) newcomer donors and compute the fraction of the SNPs that can be reconstructed. Then, using public sources (such as HapMap), one can gather a small number (e.g., s) of genomes belonging to individuals from the same population as the donor. Then, the same attack can be run for the selected s people (i.e., adding each random individual along with the other (m − 1) newcomer donors), their reconstruction rates can be set as the baseline, and eventually, a privacy risk percentile can be provided for the donor. Moreover, for all correctly inferred SNPs, one can perform a pathogenic scan on ClinVar [48] to inform the donor about what traits they might be linked should their genome is put onto the beacon. Using this information and based on the privacy risk of the donor, either the donor or the beacon operator will decide whether or not to add the donor to the beacon at time t + δ. This process can be repeated for all the newcomer donors.

We foresee that using such a quantification algorithm, a potential beacon participant can provide informed consent about how (and what portion of) their data can be used by the beacons (e.g., when the beacon can start using their data in its responses or when the beacon should stop using their data). Similarly, such a tool can guide a beacon operator on the number of participants to include in a batch to update the beacon.

8.4. Mitigation Techniques

To mitigate membership inference attacks against beacons, several countermeasures have been proposed [9, 59, 65]. However, most of such techniques directly reduce the utility of the beacon without carefully analyzing a balance between privacy (of beacon participants) and utility (of beacon responses). Thus, we believe that existing countermeasures proposed for membership inference are not directly applicable to mitigate genome reconstruction attack. To mitigate genome reconstruction, here we suggest three simple methods: (i) updating the beacon content considering the beacon size and the size of the update. For instance, as we showed in Section 7.3, for small and mid-size beacons, even largesized updates create a vulnerability, while for large-size beacons, only small-sized updates pose a threat; (ii) adding (or removing) donors after quantifying their risks against genome reconstruction (as discussed in Section 8.3); and (iii) adjusting diversity of the beacon to have beacons with mixed ethnicity genome donors. For beacons with mixed ethnicity donors, it is hard to construct the correlation model (unless the beacon discloses the ethnicities of the donors as metadata), and hence it is hard to conduct the proposed correlation-based genome reconstruction attacks. It is worth noting that the OpenSNP beacon in our evaluations was a diverse one, however we also created the correlation model from the same diverse population (i.e., in our settings, the attacker had access to a very similar population to the target population). We will further work on more sophisticated countermeasures in future work.

9. Conclusion

Thus far, the only privacy vulnerability that has been identified for beacons was membership inference. We have identified and, via extensive analysis, showed the impact of another serious privacy concern for beacons: genome reconstruction. We showed the practicality of the identified privacy concern in real-life by showing the whole attack strategy including genotype-phenotype inference. Furthermore, we showed how genome reconstruction attack can be used together with the membership inference to identify privacy-sensitive phenotypes of individuals.

Appendices

A. Membership Inference Attack Against Genomic Data-Sharing Beacons

In [59], Raisaro et al. introduced the “optimal attack” using the same attacker assumptions discussed in Section 2.2. In optimal attack, the attacker constructs a set of candidate SNPs S to be queried and submits queries starting from the lowest MAF SNP_i. Let the null hypothesis (H₀) refer to the case in which the queried genome is not in the beacon and alternative hypothesis (H₁) be the case in which the queried genome is a member of the beacon. In [59], the log-likelihood (L) under the null and alternate hypothesis are shown as follows:

$$L_{H_0}(R)=\sum _{i=1}^n{x}_i\log \left(1-D_N^i\right)+\left(1-x_i\right)\log \left(D_N^i\right)$$ (1)

$$L_{H_1}(R)=\sum _{i=1}^n{x}_i\log \left(1-\delta D_{N-1}^i\right)+\left(1-x_i\right)\log \left(\delta D_{N-1}^i\right),$$ (2)

where R is the response set, x_i is the answer of the beacon to the query at position i (1 for “yes”, 0 for “no”), and γ represents a small probability where the attacker’s copy of the victim’s genome does not match the beacon’s copy for a locus (e.g., due to difference in variant calling pipeline). n is the number of posed queries. $D_N^i$ is the probability that none of the N individuals in the beacon has the queried allele at position i and $D_{N-1}^i$ represents the probability of no individual except for the queried person having the queried allele at position i. The computations of $D_{N-1}^i$ and $D_N^i$ depend on the queried position i and they change at each query as follows: $D_{N-1}^i={\left(1-f_i\right)}^{2N-2}$ and $D_N^i={\left(1-f_i\right)}^{2N}$, where f_i represents the MAF of the SNP at position i. The likelihood-ratio test (LRT) statistic, Λ, is then determined as

$$\text{Λ}=\sum _{i=1}^n\log \left(\frac{D_N^i}{\delta D_{N-1}^i}\right)+\log \left(\frac{\delta D_{N-1}^i\left(1-D_N^i\right)}{D_N^i\left(1-\delta D_{N-1}^i\right)}\right)x_i.$$

B. Baseline Approach for Genome Reconstruction

The details of this baseline approach for genome reconstruction (described in Section 6.1) are shown in Algorithm 2.

C. Evaluation of Genome Reconstruction on the HapMap Beacon

In Figure 9 we show the success (precision, recall, and accuracy) of the reconstruction for various number of newly added donors (m) in HapMap beacon. In Figure 10, we show the effect of varying number of bins (m’) in the genome reconstruction attack when the number of newly added donors (m) is 5 for HapMap beacon. Next, in Figure 11, we show the effect of the beacon size (n) at time t when 5 new donors are added between times t and t + δ for HapMap beacon.

Algorithm 2:

Baseline Algorithm for Genome Reconstruction Attack