Deep Disentangled Hashing with Momentum Triplets for Neuroimage Search

Abstract

Neuroimaging has been widely used in computer-aided clinical diagnosis and treatment, and the rapid increase of neuroimage repositories introduces great challenges for efficient neuroimage search. Existing image search methods often use triplet loss to capture high-order relationships between samples. However, we find that the traditional triplet loss is difficult to pull positive and negative sample pairs to make their Hamming distance discrepancies larger than a small fixed value. This may reduce the discriminative ability of learned hash code and degrade the performance of image search. To address this issue, in this work, we propose a deep disentangled momentum hashing (DDMH) framework for neuroimage search. Specifically, we first investigate the original triplet loss and find that this loss function can be determined by the inner product of hash code pairs. Accordingly, we disentangle hash code norms and hash code directions and analyze the role of each part. By decoupling the loss function from the hash code norm, we propose a unique disentangled triplet loss, which can effectively push positive and negative sample pairs by desired Hamming distance discrepancies for hash codes with different lengths. We further develop a momentum triplet strategy to address the problem of insufficient triplet samples caused by small batch-size for 3D neuroimages. With the proposed disentangled triplet loss and the momentum triplet strategy, we design an end-to-end trainable deep hashing framework for neuroimage search. Comprehensive empirical evidence on three neuroimage datasets shows that DDMH has better performance in neuroimage search compared to several state-of-the-art methods.

1. Introduction

Neuroimage analysis plays a vital role in modern clinical analysis [1], image-guided surgery [2], and automated disease diagnosis [3]. Nowadays, tremendous amounts of neuroimaging data have been captured and recorded in digital formats. However, interpreting neuroimaging data usually requires extensive practical experience and professional knowledge, and may be affected by inter-observer variance [4,5]. To facilitate clinical decision-making, it is important to provide physicians with previous similar cases and corresponding treatment records to form case-based reasoning and evidence-based medicine [6]. In practice, such neuroimage search systems are required to be both scalable and accurate. Due to a sensible balance between search quality and computational cost, hashing-based search methods [7,8], which encode neuroimages as binary embeddings in Hamming space, have recently attracted increasing attention in the field.

According to whether supervisory signals are involved in the learning phase, existing hashing methods can be roughly divided into two groups: 1) unsupervised hashing [9-11] and 2) supervised hashing [12-18]. Unsupervised methods usually learn hash functions from original feature space to Hamming space by exploiting topological information and data distributions. In contrast, supervised hashing incorporates semantic labels to improve the quality of hash function learning. In this paper, we focus on supervised hashing, as it can take advantage of the supervisory signals and usually outperforms unsupervised methods.

Existing supervised hashing methods usually rely on ranking-based loss functions [15-17,19-21] to preserve similarity between samples, such as contrastive loss and triplet loss. Recent studies [22,23] have shown that the triplet loss encourages samples from the same category to reside on a manifold and generally outperforms the contrastive loss. Even though many triplet-based hashing methods have been proposed [17,19], we find a crucial misspecification problem in the traditional triplet loss, that is, traditional triplet loss is difficult to pull positive and negative pairs to make their Hamming distance discrepancies larger than a small fixed value. This may reduce the discriminative ability of the learned hash code, thereby degrading the performance of triplet loss-based methods.

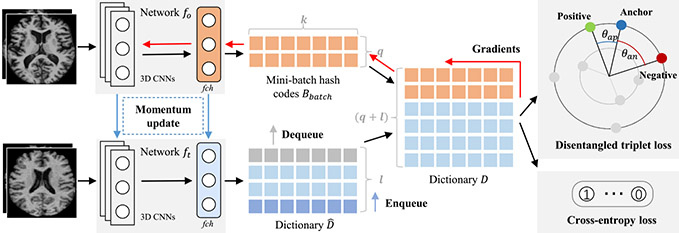
To this end, we propose a supervised hash model, called deep disentangled momentum hashing (DDMH), for neuroimage search. As illustrated in Fig. 1, the proposed DDMH consists of three key components: (1) a disentangled triplet loss, which decouples the traditional triplet loss with hash code norms and can effectively pull positive and negative pairs by a desired Hamming distance discrepancies for hash codes with different lengths; (2) a cross-entropy loss, which is used to optimize the hash codes with a jointly learned linear classifier; (3) a momentum triplet strategy to enable efficient triplet-based learning even with a small batch-size. These three components are seamlessly incorporated into an end-to-end trainable deep hashing framework for neuroimage search. Extensive experiments on three neuroimage datasets demonstrate that the proposed DDMH outperforms several state-of-the-art methods in neuroimage search.

Fig. 1.

Proposed deep disentangled momentum hashing (DDMH) framework for neuroimage search, including three key components: (1) a disentangled triplet loss, which improves the traditional triplet loss by decoupling it from the hash code length; (2) a cross-entropy loss, which is used to optimize the hash codes by jointly learning a linear classifier; (3) a momentum triplet strategy, which builds a large and consistent dictionary on-the-fly and enables efficient triplet-based learning even with a small batch-size.

2. Method

2.1. Problem Formulation

Boldface uppercase letters (e.g., A) denote matrices, and A^T represents the transpose of a matrix A. Also, sign(·) represents the element-wise signum function, defined as

$$sign(x)=\{\begin{array}{c}1,\text{if}x\ge 0,\hfill \\ -1,\text{if}x<0.\hfill \end{array}\phantom{\}}$$ (1)

Neuroimage hashing aims to learn hash functions that can map neuroimages into hash codes in Hamming space. Here, hash codes represent binary vectors, and the Hamming space contains a set of binary vectors. Assume that we have N neuroimages in a given dataset $\mathit{X}=\{{\mathit{x}}_i{\}}_{i=1}^N$, with each image x_i associated with a label vector l_i. We denote $\mathit{B}=\{{\mathit{b}}_i{\}}_{i=1}^N$ as the hash codes for X, where b_i ∈ {−1, +1}^k represents the binary hash code for the sample x_i, k is the hash code length, and b_ix indicates the x-th element of b_i.

2.2. Deep Disentangled Hash Code Learning

For effective neuroimage search, we aim to learn discriminative binary codes to well preserve the original semantic information, that is, semantically similar neuroimages are expected to have similar hash codes and vice versa. To achieve this goal, we employ a triplet-based ranking loss, which is defined as

$${\mathcal{L}}_o({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)=\log (1+e^{d_h({\mathit{b}}_a,{\mathit{b}}_p)-d_h({\mathit{b}}_a,{\mathit{b}}_n)})=\log (1+e^{-\alpha }),$$ (2)

where b_a is the learned hash code for an anchor neuroimage x_a, b_p is the binary code for a positive neuroimage x_p that shares the same semantic label with x_a, and b_n is the binary code for a negative neuroimage x_n that has a different label from x_a. Also, (b_a, b_p, b_n) is a randomly selected triplet sample. (b_a, b_p) represents a positive pair and (b_a, b_n) denotes a negative pair. d_h(·, ·) is the Hamming distance function for a pair of neuroimages. α = d_h(b_a, b_n)–d_h(b_a, b_p) represents the discrepancy between the corresponding Hamming distances. If there is no ambiguity, we will use ${\mathcal{L}}_o$ to represent ${\mathcal{L}}_o({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)$ in the following.

Since the Hamming distance function d_h(b_i, b_j) = ∣b_ix ≠ b_jx, 1 ≤ x ≤ k∣ requires discrete operations and is non-differentiable, directly optimizing Eq. (2) with back propagation is not feasible. As indicated in [12], there exists a nice relationship between the inner product and the Hamming distance as

$$d_h({\mathit{b}}_i,{\mathit{b}}_j)=\frac{k-\langle {\mathit{b}}_i,{\mathit{b}}_j\rangle }{2}.$$ (3)

Thus, we can obtain the following

$$\alpha =\frac{k-\langle {\mathit{b}}_a,{\mathit{b}}_n\rangle }{2}-\frac{k-\langle {\mathit{b}}_a,{\mathit{b}}_p\rangle }{2}=\frac{\langle {\mathit{b}}_a,{\mathit{b}}_p\rangle -\langle {\mathit{b}}_a,{\mathit{b}}_n\rangle }{2}.$$ (4)

Substituting Eq. (4) into Eq. (2), the loss function ${\mathcal{L}}_o$ can be readily optimized.

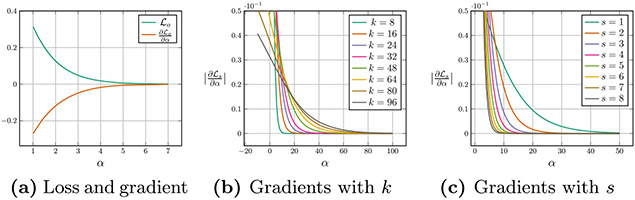
Although the loss in Eq. (2) can help preserve the original semantic information, we observe a key misspecification problem when directly applying Eq. (2) to hash code learning. As illustrated in Fig. 2 (a), when the Hamming distance discrepancy α is large than 6, the loss function value of ${\mathcal{L}}_o$ and its gradients (w.r.t. α) are close to 0. This implies that, no matter how large the hash code length k is, it is difficult to pull the Hamming distance between positive and negative pairs to be greater than 6 by optimizing the objective function ${\mathcal{L}}_o$. For effective hash code learning, we generally expect that longer hash codes can be more discriminative and the Hamming distance discrepancy α can be increased with the increase of the hash code length. Unfortunately, the triplet loss function in Eq. (2) is misspecified for this goal.

Fig. 2.

The loss and gradients of conventional triplet loss ${\mathcal{L}}_o$ w.r.t. α is close to 0 when α is larger than 6, which is ill-specified for hash code learning. By replacing α with sβ, the gradients of our disentangled triplet loss ${\mathcal{L}}_s$ are more meaningful for different k. We set s = 3 in (b) and k = 16 in (c).

To tackle the above misspecification problem, we investigate the relationship between the loss function ${\mathcal{L}}_o$ and the hash code length k carefully. From Eq. (2) and Eq. (4), we can see that the loss function ${\mathcal{L}}_o$ can be determined by the inner product of hash code pairs. Considering that both the norm and the direction of a vector can affect the inner product value, we disentangle these two items as

$$\alpha =\frac{k}{2}(\cos {\theta }_{ap}-\cos {\theta }_{an})=o\beta ,$$ (5)

where θ_ap is the angle between b_a and b_p, θ_an is the angle between b_a and b_n, $o=\frac{k}{2}$, and β = cos θ_ap – cos θ_an. It should be noted that this work performs the disentanglement to deal with the misspecification problem in Eq. (2), which is different from previous studies [24,25] in face verification. Actually, for a given fixed hash code length k, the cosine similarity discrepancy β is proportional to the Hamming distance discrepancy α, while for different hash code length k, α up-weights β with o. By combining Eq. (5) and Eq. (2), one can observe that when the hash code length k is relatively large, the weight o may greatly hinder the optimization. To eliminate this influence, we replace the weight o with a new scale factor s and design a unique disentangled triplet loss as follows

$${\mathcal{L}}_s({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)=\log (1+e^{s(\cos {\theta }_{an}-\cos {\theta }_{ap})})=\log (1+e^{-\frac{2s}{k}\alpha }).$$ (6)

The gradients of ${\mathcal{L}}_s({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)$ w.r.t. the Hamming distance discrepancy α with different k and s are illustrated in Fig. 2 (b) and (c), respectively. From these figures we can see that the saturation region can be tuned by selecting different s. That is, by using a proper s, we can decouple the hash code length from the loss function and enable desired Hamming distance discrepancies for hash codes with different lengths, which helps generate discriminative hash codes.

2.3. Overall Objective Function

Following previous studies [26,27], we assume that optimal hash codes can be jointly learned with a classification task, and use a linear classifier f(·) to model the relationship between learned binary codes and semantic labels, defined as

$$f({\mathit{b}}_i)=\sigma ({\mathit{W}}^{\mathsf{T}}{\mathit{b}}_i),$$ (7)

where σ is the sigmoid function and W is the parameter. A cross-entropy loss is then adopted as

$${\mathcal{L}}_c({\mathit{b}}_i)=-{\mathit{l}}_i^{\mathsf{T}}\text{ln}f({\mathit{b}}_i).$$ (8)

By combining Eq. (8) and Eq. (6), we can obtain the overall loss function as

$$\mathcal{L}={\sum }_{({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)\in \mathcal{T}}{\mathcal{L}}_s({\mathit{b}}_a,{\mathit{b}}_p,{\mathit{b}}_n)+\lambda \sum _{i=1}^N{\mathcal{L}}_c({\mathit{b}}_i),$$ (9)

where $\mathcal{T}$ is the set for all triplets, and λ is a hyper-parameter to balance the contributions of the disentangled triplet loss and the cross-entropy loss in Eq. (9).

2.4. Optimization with Momentum Triplets

A critical challenge for optimizing our triplet-based 3D deep model is the insufficient number of triplets. Actually, to construct a sufficient amount of triplets, triplet-based deep models often require a relatively large batch size to include more samples in a mini-batch. However, the memory requirement and computation time will increase as the batch size increases, which is particularly significant for 3D convolution neural networks (CNNs). Therefore, it is desirable to design a feasible solution to optimize our model in Eq. (9) using 3D neuroimages.

Motivated by [28], we introduce a momentum strategy to supervised hashing and propose momentum triplets to address the above insufficient triplet problem. As shown in Fig. 1, we design two 3D CNNs, i.e., f_o and f_t, which share the same architecture. Denote q as the mini-batch size. For each mini-batch entity X_batch = {x₁, x₂, ⋯ , x_q}, we calculate their corresponding hash codes B_batch = {b₁, b₂, ⋯ , b_q} by forward propagating them from f_o. We also maintain a l-length dynamic dictionary $\widehat{D}=\{{\widehat{\mathit{b}}}_1,{\widehat{\mathit{b}}}_2,\cdots ,{\widehat{\mathit{b}}}_l\}$, with each element obtained from the network f_t. In each iteration, the dictionary keys of $\widehat{D}$ are updated as a queue, with the current mini-batch enqueued and the oldest mini-batch dequeued. To facilitate the construction of more triplets, for X_batch = {x₁, x₂, ⋯ , x_q}, we concatenate its corresponding codes B_batch with the dynamic dictionary $\widehat{D}$, yielding a new dictionary $D=\{{\mathit{b}}_1,{\mathit{b}}_2,\cdots ,{\mathit{b}}_q,{\widehat{\mathit{b}}}_1,{\widehat{\mathit{b}}}_2,\cdots ,{\widehat{\mathit{b}}}_l\}$ with the length of q + l. The network f_o are then updated with the loss obtained with all triplets from the dictionary D by standard back-propagation. And the network f_t is updated with a momentum strategy via

$${\theta }_t=m{\theta }_t+(1-m){\theta }_o,$$ (10)

where θ_o and θ_t are parameters of f_o and f_t, respectively, and m ∈ (0, 1] is a momentum coefficient. The momentum update strategy for f_t is used to reduce the discrepancy between f_o and f_t and improve the hash code consistency.

2.5. Implementation

The 3D networks for f_o and f_t share the same architecture, which has 12 layers. The first 10 layers are 3D convolutional (Conv) layers (kernel size: 3 × 3 × 3; stride: 1; zero padding). The last 2 layers are fully-connected (FC) layers with 256 and k hidden units, respectively. Batch normalization and ReLU activation are applied to all Conv layers. A 3D max-pooling with stride 2 is also applied to every two Conv layers. For the last FC layer, we use Tanh(·) to squeeze activation within [−1, +1] to reduce quantization error and also denote it as fully-connected hash (fch) layer. We train the network from scratch with Adam [29] by setting the batch size as 2 and the dictionary size l as 10. The learning rate is set to 10⁻³, λ in Eq. (9) is set to 1, the scale factor s is set to 3, and m is set to 0.999. Assuming the computation cost for one similarity calculation is d, the computation cost to rank all points will be O(dN) and can be further reduced to O(1) with predefined hash look-up tables.

3. Experiments

3.1. Experimental Setup

Materials.

We evaluate the proposed DDMH method on three popular benchmark datasets: (1) Alzheimer’s Disease Neuroimaging Initiative (ADNI1) [30], (2) ANDI2, and (3) Australian Imaging, Biomarkers and Lifestyle dataset (AIBL) [31]. ADNI1 contains 821 subjects with 1.5T T1-weighted structural MRI scans. ADNI2 contains 636 subjects with 3T T1-weighted MRI scans. Besides, AIBL contains 614 subjects with 3T T1-weighted MRI data. Each subject from these three datasets was annotated by a category-level label, i.e., Alzheimer’s disease (AD), normal control (NC), or mild cognitive impairment (MCI). For each dataset, we randomly select 10% samples as a query set and others as a retrieval set. All MRIs were pre-processed via skull-stripping, intensity correction, and spatial normalization to Automated Anatomical Labeling (AAL) template.

Evaluation Setting.

Our DDMH is compared with five state-of-the-art shallow hashing methods, i.e., SH [32], SpH [33], ITQ [34], DSH [35], and KSH [12], as well as two recent deep hashing methods, i.e., DPSH [36] and SSDH [37]. Volumes of gray matter tissue inside 90 regions-of-interest (defined in AAL) are used as features for shallow hashing methods, while two deep models and our DDMH employ MRI scans as input. mean of average precision (MAP), topN-precision, and recall@K are used as evaluation metrics.

3.2. Results and Discussion

We first report MAP values of all methods with different lengths of hash code (i.e., k) to provide a global evaluation. Then we report the topN-precision and recall@K curves with k = 16 for comprehensive contrastive study.

MAP.

The MAP results achieved by all methods on the three datasets are reported in Table 1. The results suggest that, compared with shallow hashing methods, deep learning approaches usually yield better performance. This could be attributed to the fact that deep networks enable joint learning of image representations and hash codes directly from the original image. Besides, our DDMH usually outperforms other competing methods by large margins.

Table 1.

The MAP results of eight different methods on three datasets.

Method	ADNI1				ADNI2				AIBL
	8	16	24	32	8	16	24	32	8	16	24	32
SH	0.403	0.389	0.386	0.384	0.422	0.377	0.375	0.372	0.613	0.611	0.605	0.604
SpH	0.398	0.398	0.400	0.391	0.375	0.384	0.385	0.375	0.599	0.587	0.584	0.578
ITQ	0.391	0.396	0.396	0.393	0.398	0.389	0.384	0.390	0.596	0.582	0.579	0.577
DSH	0.390	0.402	0.398	0.396	0.408	0.387	0.393	0.394	0.596	0.577	0.575	0.576
KSH	0.372	0.384	0.386	0.391	0.385	0.369	0.376	0.374	0.600	0.591	0.588	0.583
DPSH	0.438	0.460	0.447	0.467	0.403	0.413	0.415	0.391	0.702	0.701	0.700	0.684
SSDH	0.421	0.427	0.435	0.422	0.397	0.408	0.406	0.411	0.712	0.710	0.715	0.698
Ours	0.478	0.480	0.498	0.511	0.602	0.612	0.618	0.632	0.758	0.763	0.761	0.764

TopN-Precision.

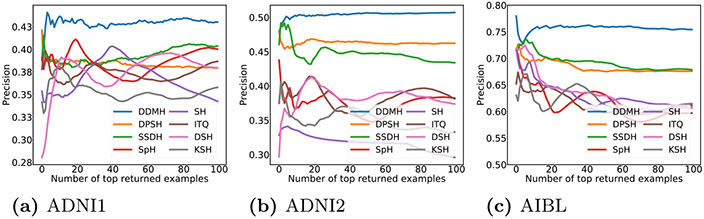
The topN-precision curves are shown in Fig. 3. This figure suggests that DDMH generally achieves higher precision, which is consistent with the MAP evaluation. It is worth noting that, in the task of neuroimage retrieval, users usually focus on top returned instances. Therefore, it is essential to provide users with top returned instances that are highly relevant to the query. From the results, one can see that DDMH outperforms other methods by a large margin when the number of returned instances is small. This verifies that DDMH can effectively return relevant examples and is suitable for neuroimage search.

Fig. 3.

The topN-precision results of different methods on three datasets.

Recall@K.

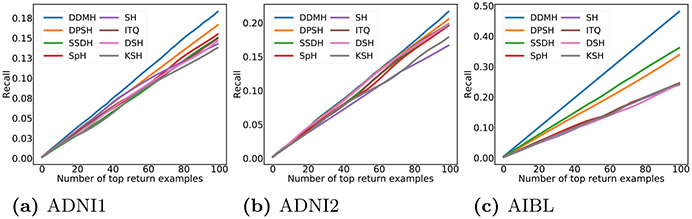
The recall@K curves of all methods are reported in Fig. 4. From Fig. 4, one can observe that our DDMH always yields higher recall values for different numbers of returned examples on three datasets, which further proves that DDMH can effectively learn hash codes with high quality.

Fig. 4.

The recall@k results of different methods on three datasets.

Ablation Study.

We investigate two variants of our DDMH, including (1) DDMH-C without using the cross-entropy loss, i.e., λ = 0 in Eq. (9); and (2) DDMH-D with the traditional triplet loss i.e., $s=\frac{k}{2}$ in Eq. (6). MAP results of DDMH and its two variants on ADNI1 are reported in Table 2. From the results, we can see that DDMH is consistently superior to its two variants, implying that both the classification loss and the disentangled triplet loss contribute to the performance improvement. In particular, DDMH achieves higher MAP values using longer hash codes, but DDMH-D benefits little from longer hash codes. These results show that compared with the traditional triplet loss (used in DDMH-D), the proposed disentangled loss (used in DDMH) can effectively promote the learning of longer hash codes. On the other hand, from Tables 1 and 2, one can observe that DDMH-D generally outperforms existing state-of-the-art hashing methods on ADNI1. This implies that, with the proposed momentum triplet strategy, DDMH-D enables efficient hashing learning even with the traditional triplet loss function.

Table 2.

The MAP values of DDMH and its two variants on ADNI1.

Method	k = 8	k = 16	k = 24	k = 32
DDMH-C	0.441	0.453	0.456	0.457
DDMH-D	0.462	0.460	0.459	0.466
DDMH	0.478	0.480	0.498	0.511

4. Conclusion

This paper presents a deep disentangled momentum hashing (DDMH) method for neuroimage search. Specifically, by disentangling the hash code norm and directions, we propose a unique disentangled triplet loss, which can pull positive and negative pairs to have a desired Hamming distance discrepancy with different hash code lengths. We also design a momentum triplet strategy to provide a sufficient number of triplets for model training, even with a small batch-size. Using a 3D CNN as hash functions, DDMH can generate discriminative hash codes by jointly optimizing the disentangled triplet loss and a cross-entropy loss. Extensive experiments on three neuroimage datasets show that our DDMH achieves better performance than several state-of-the-art methods.