Time to fixation in changing environments

Abstract

Although many experimental and theoretical studies on natural selection have been carried out in a constant environment, as natural environments typically vary in time, it is important to ask if and how the results of these investigations are affected by a changing environment. Here, we study the properties of the conditional fixation time defined as the time to fixation of a new mutant that is destined to fix in a finite, randomly mating diploid population with intermediate dominance that is evolving in a periodically changing environment. It is known that in a static environment, the conditional mean fixation time of a co-dominant beneficial mutant is equal to that of a deleterious mutant with the same magnitude of selection coefficient. We find that this symmetry is not preserved, even when the environment is changing slowly. More generally, we find that the conditional mean fixation time of an initially beneficial mutant in a slowly changing environment depends weakly on the dominance coefficient and remains close to the corresponding result in the static environment. However, for an initially deleterious mutant under moderate and slowly varying selection, the fixation time differs substantially from that in a constant environment when the mutant is recessive. As fixation times are intimately related to the levels and patterns of genetic diversity, our results suggest that for beneficial sweeps, these quantities are only mildly affected by temporal variation in environment. In contrast, environmental change is likely to impact the patterns due to recessive deleterious sweeps strongly.

Introduction

In a finite, recombining population where a selected locus is linked to neutral loci, if a new advantageous mutation fixes faster than the time it takes for neutral loci to get dissociated via recombination, the neutral genetic diversity in the neighborhood of the selected locus is reduced (beneficial sweep) (Maynard Smith and Haigh 1974; Stephan 2016); a similar pattern arises when a mildly deleterious mutation reaches fixation due to genetic drift (deleterious sweep). Thus, the time of fixation is intimately related to the level and patterns of neutral diversity (Tajima 1990). It is important to note that the fixation time under discussion here is obtained from a stochastic process that is conditioned on fixation. At the end of a selective sweep, one is observing only those trajectories of the new allele in which fixation has occurred, and not those in which the allele is lost due to drift and/or selection (Ewens 1973; Zhao et al. 2013).

Theoretical models of sweeps and their genomic applications assume the selective environment to be constant in time; however, environmental variation is ubiquitous in nature, and may potentially affect the fixation time. For example, suppose a mutant arises while selection is positive and increasing. In this case, the mean fixation time, conditional on fixation, is expected to be smaller than when the selection pressure remains the same as that when the mutant arose, and can result in a larger reduction in neutral diversity. One may then ask: how much does the fixation time in a changing environment (especially, if it varies slowly) differ from that in a static environment?

Furthermore, in static environments, the conditional mean fixation time has the important property of being the same for a mutant with selection coefficient s and dominance coefficient h and a mutant with respective parameters, – s and $1-h$ (Maruyama 1974; Maruyama and Kimura 1974), as a result of which it may be difficult to distinguish between diversity patterns due to positive and negative selection (Johri et al. 2020). In a changing environment, on general grounds, this symmetry can be expected to be absent, and one may delineate the parameter space where the lack of this symmetry has a strong effect on variability patterns.

As a first step toward an understanding of selective sweeps in changing environments, here we study the properties of the conditional fixation time of a mutant in a finite, diploid population when the selection coefficient is time-dependent. To the best of our knowledge, except for a preliminary study (Uecker and Hermisson 2011), the fixation time in a changing environment has not been investigated in detail. We consider evolution in an environment that changes periodically due to, for example, seasonal cycles (Williams et al. 2017), and study how the fixation time is affected by the rate of environmental change, the time of appearance of the mutant, the strength of selection and the dominance coefficient. Throughout the article, we assume random mating and autosomal inheritance.

Our results are obtained analytically using a diffusion theory for time-inhomogeneous processes when selection of either sign is weak or moderate and a semi-deterministic theory for strongly selected beneficial mutants, and are supplemented and checked by numerical simulations. Our main finding is that in slowly changing environments, the conditional mean fixation time of an initially beneficial mutant with intermediate dominance is well-approximated by that in a static environment, and the same holds true for an initially deleterious dominant mutant under moderate selection. However, if an initially deleterious mutant is recessive, its conditional mean fixation time is considerably longer or shorter in a slowly changing environment than in a static environment. In other words, the symmetry property for the conditional mean fixation time mentioned above (Maruyama 1974; Maruyama and Kimura 1974) does not hold between recessive deleterious and dominant beneficial mutants. Since by virtue of Haldane’s sieve, which operates in both static (Haldane 1927) and slowly varying environments (Devi and Jain 2020), most deleterious mutations are recessive and beneficial ones are dominant, the results obtained here are relevant to an understanding of selective sweeps in changing environments (see Discussion for details).

Model

We consider the model in Devi and Jain (2020) that deals with a randomly mating population of size N. We assume that a single biallelic locus is under selection and the three genotypes, aa, Aa and AA have the fitness $1+s(t),\hspace{0.17em}1+hs(t)$ and 1, respectively. Here, $0<h<1$ is the dominance parameter and $s(t)=\overline{s}+\sigma \hspace{0.17em}\text{sin}(\omega t+\theta ),t\ge 0$ is the time-dependent selection coefficient that varies periodically with cycling frequency ω. Without loss of generality, we assume that the oscillation amplitude $\sigma >0$ but the time-averaged selection coefficient $\overline{s}$ is arbitrary, and the initial phase $0\le \theta <2\pi$.

For large population size and small selection coefficient, instead of genotypic frequencies, we can work with the allelic frequencies (Nagylaki 1992). We start with a single mutant allele in the population and ignore any further mutations. The evolution of the population under selection and random genetic drift is modeled by a continuous time birth-death process [Chapter 4, Karlin and Taylor (1975)] in which the number i of alleles a increase or decrease by one at rate $r_b(t)$ or $r_d(t)$, respectively. These rates are given by

$$r_b(t)=\frac{2Ni{w}_a(t)}{i{w}_a(t)+(2N-i)w_A(t)}\times \frac{2N-i}{2N}$$ (1)

$$r_d(t)=\frac{2N(2N-i)w_A(t)}{i{w}_a(t)+(2N-i)w_A(t)}\times \frac{i}{2N}$$ (2)

where $w_a(t)=(1+s(t))i+(1+hs(t))(2N-i)$ and $w_A(t)=(2N-i)+(1+hs(t))i$ are, respectively, the marginal fitness of allele a and A. The allele numbers at time t are updated at time $t+\delta t$ where the interval δt is chosen from the probability distribution $p(\delta t)=r(t+\delta t)e^{-{\int }_t^{t+\delta t}d{t}^{\prime }r\left(t^{\prime }\right)}$ with $r(t)=r_b(t)+r_d(t)$ being the total rate at which either birth or death events occur.

For computational efficiency, numerical simulations of the above model were carried out assuming that the birth and death rates remain constant at r(t) during the interval δt. Then it follows that δt obeys an exponential distribution with rate r(t); however, we have checked that our results do not change if we relax this assumption. In our simulations, ${10}^6-{10}^8$ independent trajectories of the mutant allele were generated, but the data for the fixation time were averaged over only those trajectories that lead to the fixation of the mutant. The conditional mean fixation time was thus obtained by averaging over about 10³ and 10⁴ fixation events for deleterious and beneficial mutants, respectively. The standard error on the conditional mean fixation time was also calculated for some representative parameters and found to be at most 2% of the mean value.

Conditional fixation time in changing environments

In a constant environment, the expected fixation time of a new mutant that is destined to fix decreases with the magnitude of its selection coefficient s, since a strongly deleterious mutant fixes soon to avoid extinction, whereas a strongly beneficial mutant that has a low chance of extinction grows fast (Kimura and Ohta 1969; Teshima and Przeworski 2006; Charlesworth 2020). In a population of size N, this result holds only for a strongly selected mutant ($N\left|s\right|\gg 1$) but for weak selection ($N\left|s\right|\ll 1$), the conditional mean fixation time can vary nonmonotonically with s (Mafessoni and Lachmann 2015). Interestingly, for any selection strength, diffusion theory predicts that the conditional mean fixation time of a single mutant has a remarkable property: it is the same for a beneficial mutant with selective coefficient s and dominance coefficient h and a deleterious mutant with respective parameters – s and $1-h$ (Maruyama 1974; Maruyama and Kimura 1974). For a codominant mutant (h = 1/2), this symmetry is even stronger in that it holds for any initial mutant number $0<i<2N$ (Ewens 2004, p. 170).

In order to test whether the Maruyama-Kimura symmetry mentioned above also holds in a periodically changing environment, we need to compare the fixation time of mutants whose selection coefficients are of opposite sign at all times. Figure 1A shows the conditional mean fixation time ${\overline{T}}_c$ of mutants with dominance parameter h and $1-h$ and selection coefficient s(t) and $-s(t)$, respectively, when they are under moderate selection and on-average neutral (for nonzero average selection coefficient, see Supplementary Figure S1). It is clear from these figures that the Maruyama–Kimura symmetry does not hold when selection is time-dependent.

Figure 1.

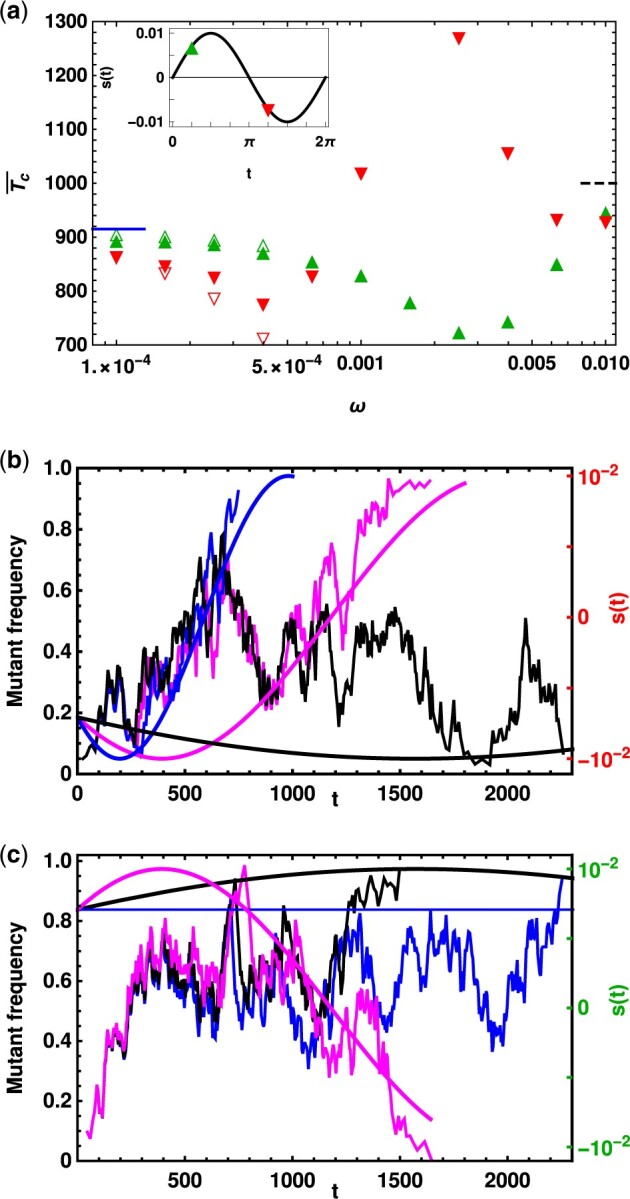
Top panel: Conditional mean fixation time ${\overline{T}}_c$ of a dominant mutant $(h=0.7,▲)$ and a recessive mutant ($h=0.3,▼$) with selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}(\omega t+\pi /4)$ and $-s(t)$, respectively [see inset for s(0)] to show that the symmetry between the conditional mean fixation time for dominant beneficial and recessive deleterious mutant in static environments is not preserved in changing environments. The data are obtained by numerical simulations (closed symbols) and numerically integrating the diffusion theory Equations (4) and (5) (open symbols) for small cycling frequencies in a population of size N. The conditional mean fixation time in the static environment with selection $|s(0)|$ (solid line) and in the neutral environment, given by 2 N, (dashed line) are obtained from diffusion theory and shown for comparison. Middle and Bottom panel: Mutant allele trajectories for (b) the initially deleterious mutant (h = 0.3) and cycling frequencies, $\omega =5\times {10}^{-4}(\text{black}),2\times {10}^{-3}(\text{magenta})$, and $4\times {10}^{-3}(\text{blue})$, and (c) the initially beneficial mutant (h = 0.7) for $\omega =0(\text{blue}),5\times {10}^{-4}(\text{black})$, and $2\times {10}^{-3}(\text{magenta})$. The allele trajectories in each panel are almost same at short times as they were started with the same random seed in the computer simulation. The smooth curves show the selection coefficient for the corresponding cycling frequency. In all the panels, $\sigma =0.01$ and N = 500 so that $\alpha =N|s(0)|\approx 3.5$.

To understand the qualitative behavior of the conditional mean fixation time ${\overline{T}}_c$ in Figure 1A, we first consider the fixation time of the initially deleterious mutant in a slowly deteriorating environment. If this mutant segregates in the population for too long, it is at a risk of extinction even if it manages to reach a high allele frequency (see mutant allele trajectory for cycling frequency $\omega =5\times {10}^{-4}$ in Figure 1B). For this reason, in Figure 1A, below $\omega \approx \pi /(4\times 900)=8\times {10}^{-4}$, the fixation time is smaller than the corresponding result in the static environment. The fixation time of the initially beneficial mutant in a slowly improving environment is also smaller than that in the constant environment, but for a different reason: here, as exemplified by the allele trajectories for ω = 0 (static environment) and $5\times {10}^{-4}$ in Figure 1C, the mutant in the latter case, by virtue of its larger selection coefficient, grows faster than the one in the static environment; therefore, for frequencies below $\omega \approx \pi /(2\times 900)=2\times {10}^{-3}$, the fixation time decreases.

However, if the environment changes fast enough ($\omega >8\times {10}^{-4}$ in Figure 1A) so that an initially deleterious mutant experiences a relatively better environment ($|ds/dt|>0$) on reaching a high frequency, fixation can occur at a later time than in a static environment (see allele trajectory for $\omega =2\times {10}^{-3}$ in Figure 1B). For a further increase in cycling frequency ($\omega >2\times {10}^{-3}$ in Figure 1A), the mutant can experience strong positive selection at late times (refer to allele trajectory for $\omega =4\times {10}^{-3}$ in Figure 1B), which, as explained above, results in a faster growth and a decrease in the fixation time. For the initially beneficial mutant, as the cycling frequency increases ($\omega >8\times {10}^{-4}$), the mutant allele experiences decreasing selection and must fix soon to avoid extinction (see allele trajectory for $\omega =2\times {10}^{-3}$ in Figure 1C). As the cycling frequency is further increased ($\omega >2\times {10}^{-3}$), the mutant population sees negative but improving selection at late time, and hence runs a lower risk of extinction, which results in an increase of the conditional mean fixation time. At even higher frequencies, as selection changes sign and direction several times during the fixation process, the fixation time for both mutants approaches the value in the time-averaged environment.

We also note that in Figure 1A, an extremum in the fixation time occurs at the resonance frequency, ${\omega }_r=2\times {10}^{-3}$ which is defined as the cycling frequency at which the environment changes at a rate proportional to a frequency scale in the population when the oscillation amplitude σ = 0. In Figure 1A, the resonance frequency ω_r is proportional to the reciprocal of the fixation time 2 N in the neutral environment (Kimura and Ohta 1969). Whether this extremum in the fixation time is a maximum or a minimum is determined by the initial phase θ [for a discussion of the resonance frequency for fixation probability in changing environments, refer to Devi and Jain (2020)].

Diffusion theory in slowly changing environments

To explore and better understand the qualitative observations discussed above, we now develop a diffusion theory for time-dependent selection coefficients. As explained in Appendix A, the probability distribution ${\Phi }_{\mathrm{b}}(x,t|p,t_0)$ that the mutant frequency is x at time t, given that it was p at time $t_0<t$ obeys the following backward Kolmogorov equation (Risken 1996):

$$-\frac{\partial {\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial t_0}=s(t_0)g(p)\frac{\partial {\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial p}+\frac{pq}{2N}\frac{{\partial }^2{\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial p^2}$$ (3)

where $s(t_0)=\overline{s}+\sigma \hspace{0.17em}\text{sin}(\omega t_0+\theta )$ and $g(p)=pq(p+h(1-2p))$. Using (3), it can be shown that the unconditional mean fixation time $\overline{T}(p,t_0)$ and the eventual fixation probability $u(p,t_0)$, respectively, obey (A.4) and (A.5). But, unfortunately, these equations do not appear to be solvable for the full range of parameters. For slow and fast-changing environments, simple expressions for the eventual fixation probability have been obtained in Devi and Jain (2020) using a perturbation theory. Below, using the same method, we find the mean fixation time in slowly changing environments.

In environments that change at a rate $\omega \ll N^{-1},s(0)$ with arbitrary $Ns(0)$, the unconditional mean fixation time $\overline{T}\approx {\overline{T}}_0+N\omega {\overline{T}}_1$ and the eventual fixation probability, $u\approx u_0+N\omega u_1$, where the subscripts 0 and 1 denote quantities in a static and slowly changing environment, respectively. As described in Appendix B, u₁ and ${\upsilon }_1={\overline{T}}_1/(2N)$ obey the following ordinary differential equations,

$$\frac{pq}{2}{u}_1^{\prime \prime }+\alpha g\left(p\right)u_1^{\prime }=-\frac{\partial u_0}{\partial \theta }$$ (4)

$$\frac{pq}{2}{\upsilon }_1^{\prime \prime }+\alpha g\left(p\right){\upsilon }_1^{\prime }=-N{u}_1-\frac{\partial {\upsilon }_0}{\partial \theta }$$ (5)

and the quantities u₀ and ${\upsilon }_0={\overline{T}}_0/(2N)$ in the static environment obey (Kimura and Ohta 1969)

$$\frac{pq}{2}{u}_0^{\prime \prime }+\alpha g\left(p\right)u_0^{\prime }=0$$ (6)

$$\frac{pq}{2}{\upsilon }_0^{\prime \prime }+\alpha g\left(p\right){\upsilon }_0^{\prime }=-N{u}_0$$ (7)

In the above equations, prime denotes the derivative with respect to p and $\alpha =Ns(0)$ is the scaled selection strength. Equations (4)–(7) are subject to boundary conditions $u_0(1,t_0)=1$ and $u_i(0,t_0)={\upsilon }_i(0,t_0)={\upsilon }_i(1,t_0)=0,i=0,1$. The conditional mean fixation time ${\overline{T}}_c$ scaled by the mean fixation time 2 N in the neutral environment is then given by

$$\frac{{\overline{T}}_c}{2N}=\frac{\overline{T}}{2Nu}\approx \frac{{\upsilon }_0}{u_0}+N\omega \left(\frac{{\upsilon }_1}{u_0}-{\upsilon }_{0,c}\frac{u_1}{u_0}\right)$$ (8)

where ${\upsilon }_{0,c}={\upsilon }_0/u_0$ (see Appendix B for details).

Although a formal solution of (4)–(7) can be written down, it appears difficult to obtain a simple analytical expression for the fixation time by using these results in (8). However, (4)–(7) can be easily integrated numerically, and as attested by Figure 1A, these numerical results are in good agreement with those obtained from the simulations at small cycling frequencies.

Weak selection

In a static environment, the conditional mean fixation time of a beneficial mutant under weak selection ($N\left|s\right|\ll 1$) and with dominance coefficient h > 1∕2 increases with the selection pressure and can be larger than the fixation time of a neutral mutant. This may be understood by noting that although the mutant population is subject to strong random fluctuations, the fixation probability of a beneficial mutant increases with the level of dominance (Kimura 1957) and therefore a beneficial dominant mutant can counter the risk of extinction at late times. By the Maruyama-Kimura symmetry, an analogous result is obtained for a deleterious mutant with dominance coefficient h < 1∕2 (Mafessoni and Lachmann 2015).

To see this result quantitatively, for small $\alpha =Ns$, we expand the fixation probability u₀ and the fixation time ${\upsilon }_0$ in a power series about α = 0 up to order ${\alpha }^2$, and substitute them in (6) and (7). Collecting terms with the same power of α on both sides of these equations, we get a set of second order ordinary differential equations which can be solved straightforwardly, and we finally obtain

$${\upsilon }_{0,c}\approx 1+\frac{\alpha H}{9}-\frac{{\alpha }^2}{72}$$ (9)

where $H=h-(1/2)$ is the deviation from codominance. The above result shows that the conditional mean fixation time (relative to the neutral fixation time) is a nonmonotonic function of α with a maximum at ${\alpha }^{*}=4H$ and the value at the maximum, ${\upsilon }_{0,c}({\alpha }^{*})=1+(2H^2/9)$. As $H^2<1/4$, the conditional mean fixation time of the selected mutant can exceed that of the neutral mutant at most by $\sim 5\%$, as observed numerically in Mafessoni and Lachmann (2015).

In a slowly changing environment, unlike in the last section where $\alpha >1$, the fixation time of an initially beneficial (deleterious) mutant in an improving (deteriorating) environment increases (decreases) with selection strength when $\alpha \ll 1$; this is due to a slight increase (decrease) in the fixation probability from the neutral value (see Figure 2). But with increasing selection strength, the fixation time in either case eventually decreases. Proceeding in a similar fashion as for the static environment, we expand $u_1(p)$ and ${\upsilon }_1(p)$ in a power series in α to quadratic orders, and plug them in (4) and (5). We then find the change in the fixation time due to slowly changing environment to be

$$\begin{array}{c}{\upsilon }_{1,c}\approx \frac{\alpha }{54}\left[\left(70-6{\pi }^2\right)H+9\left({\pi }^2-9\right)\right]\cot \theta \\ +\frac{{\alpha }^2}{108}\left(3{\pi }^2-38\right)\cot \theta \end{array}$$ (10)

for $\theta \ne 0,\pi$. Using this result, the maximum in the total conditional mean fixation time is found to occur at

$${\alpha }^{*}\approx 4H+\frac{2}{3}N\omega \cot \theta \left[(6{\pi }^2-82)H+9{\pi }^2-81\right]$$ (11)

Figure 2.

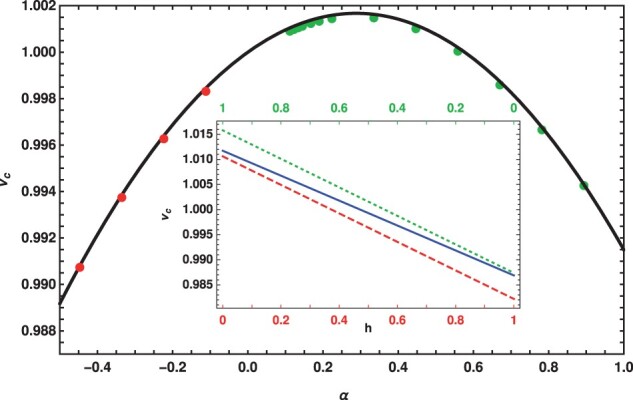
Scaled conditional mean fixation time, ${\upsilon }_c={\overline{T}}_c/2N$ for a co-dominant mutant under weak selection in slowly changing, on-average neutral environment in which the selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}(\omega t+\theta )$. The parameter $\alpha =N|s(0)|$ was varied with selection amplitude σ, keeping the population size N and the initial phase $\theta =\pi /4$ (for positive α) and $5\pi /4$ (for negative α) fixed. The inset shows the variation of the conditional mean fixation time with dominance in static environment (solid) and slowly varying environment for initial phase $\theta =\pi /4$ (dotted) and $5\pi /4$ (dashed), and $\sigma =0.000158$. In both plots, $N=2\times {10}^3$ and $N\omega =0.08$, and the lines show the analytical expressions (9) and (10) and the points show the numerical solution of (4)–(7).

Equations (9) and (10) and also Figure 2 show that the conditional mean fixation time continues to be a nonmonotonic function of the selection coefficient in changing environments. But, for a codominant mutant, while ${\upsilon }_{0,c}$ is symmetric about α = 0 in a constant environment [see (9)], due to the lack of the Maruyama-Kimura symmetry in the changing environment, the maximum in the fixation time occurs at a nonzero ${\alpha }^{*}$, as predicted by (11). For small α, from (10), we have ${\upsilon }_{1,c}\approx 0.2h\alpha \cot \theta$ which shows that the changing environment has the strongest effect when the mutant of either sign is dominant; however, the magnitude of these effects is quite small, see inset of Figure 2.

Moderate selection

We now consider the parameter regime where selection is moderately strong and the deleterious mutant has a significant chance of fixation ($1\ll |\alpha |\lesssim 20$). As in the last subsection, one would like to obtain simple analytical expressions for the time ${\overline{T}}_c$ but, unfortunately, it is generally not possible to develop consistent approximations when the parameters are of moderate size. Below, we therefore discuss the results obtained by numerically integrating (4)–(7).

To understand the results shown in Figure 3, we first consider the fixation time of the initially deleterious mutant in a deteriorating environment and the initially beneficial mutant in an improving environment (both denoted by open symbols) for a given dominance coefficient. On account of larger scaled selection strength, the former has a lower fixation probability than a deleterious mutant in the constant environment, and therefore should fix sooner to avoid extinction; the initially beneficial mutant, on the other hand, grows faster in an improving environment than in the corresponding static environment. In either case, the fixation time is smaller than that in the static environment. For similar reasons, the fixation time of the initially beneficial (deleterious) mutant in a deteriorating (improving) environment is larger than that in the static environment.

Figure 3.

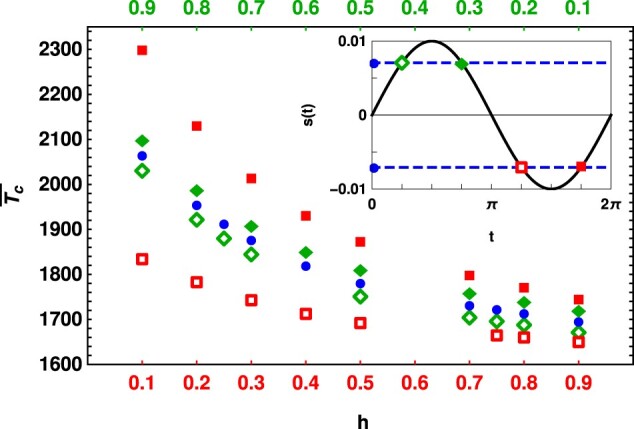
Conditional mean fixation time ${\overline{T}}_c$ for moderate selection in static ($•$) and slowly changing environment with selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}(\omega t+\theta )$ (diamonds) and $-s(t)$ (squares) for different dominance coefficients and the initial phase $\theta =\pi /4$ (open symbols) and $3\pi /4$ (closed symbols) in a population of size N. The other parameters are $N=2\times {10}^3,N\omega =0.05$ and $\sigma =0.01$. The inset depicts the arrival time of the mutant in all the cases. The data are obtained within the framework of diffusion theory by numerically solving (4)–(7).

Crucially, however, as Figure 3 shows, the magnitude of the deviation between the fixation time in the changing and the constant environment is larger for the initially deleterious mutant than for the initially beneficial mutant. The reason underlying this behavior is the strong asymmetry between the fixation probabilities of beneficial and deleterious mutants. In a static environment, for moderate-to-strong selection, a small change in the selection coefficient affects the chance of fixation of a beneficial mutant only by a small amount, but the fixation probability of a deleterious mutant changes by an exponential factor (Kimura 1957). This strong asymmetry holds even in slowly changing environments [refer to Figure 2 for moderate selection and Equation (11) for strong selection of Devi and Jain (2020)]. As a result, the fixation time of an initially deleterious mutant is more strongly affected by a changing environment.

Although a strongly deleterious mutation has a negligible chance of fixation, it is possible to obtain some analytical understanding of its fixation time. In Appendix S1, we find that $v_{1,c}$ which captures the effect of changing environment on the fixation time decays slowly, as $|\alpha {|}^{-1}$ for a deleterious mutant, while as shown in the following section for a mutant under strong positive selection, ${\upsilon }_{1,c}\sim {\alpha }^{-2}$ [see (20)]. These results again emphasize that the changing environment has a much stronger impact on deleterious mutations (see also Supplementary Figure S2).

To understand the dominance-dependence of the fixation time, we first recall that in the static environment, the fixation probability increases (decreases) with the dominance level for mutants under positive (negative) selection. This result known as Haldane’s sieve (Haldane 1927) operates in slowly changing environments also (Devi and Jain 2020), and explains the increasing (decreasing) fixation time of the initially beneficial (deleterious) mutant with increasing h. For the initially deleterious mutant, since the recessive mutant (as compared to the dominant mutant) spends more time in the varying environment, its trajectories are more influenced by the changing selection coefficient, and the fixation time differs considerably from that in the static environment.

Semi-deterministic theory for on-average beneficial mutants in a large population

In the preceding discussion, we assumed the mutant to be under weak-to-moderate selection, as strongly deleterious mutations are unlikely to fix (Kimura 1957). Here, we study the conditional mean fixation time of a mutant that is under strong positive selection ($|\alpha |\gg {10}^2$) at all times. Since the frequency of a mutant will rise faster (slower) if its selection coefficient remains larger (smaller) than s(0) until it fixes, the fixation time shown in Figure 4A initially decreases, then increases and finally approaches the fixation time in the time-averaged environment, exhibiting oscillations with decreasing amplitude. For nonzero $\overline{s}$, the resonance frequency ω_r is inversely proportional to the fixation time when the selection coefficient is $\left|\overline{s}\right|$ [which, for strong positive selection, is given by (19) on replacing s(0) by $\overline{s}$], and we verify that the data in Figure 4A is consistent with this assertion.

Figure 4.

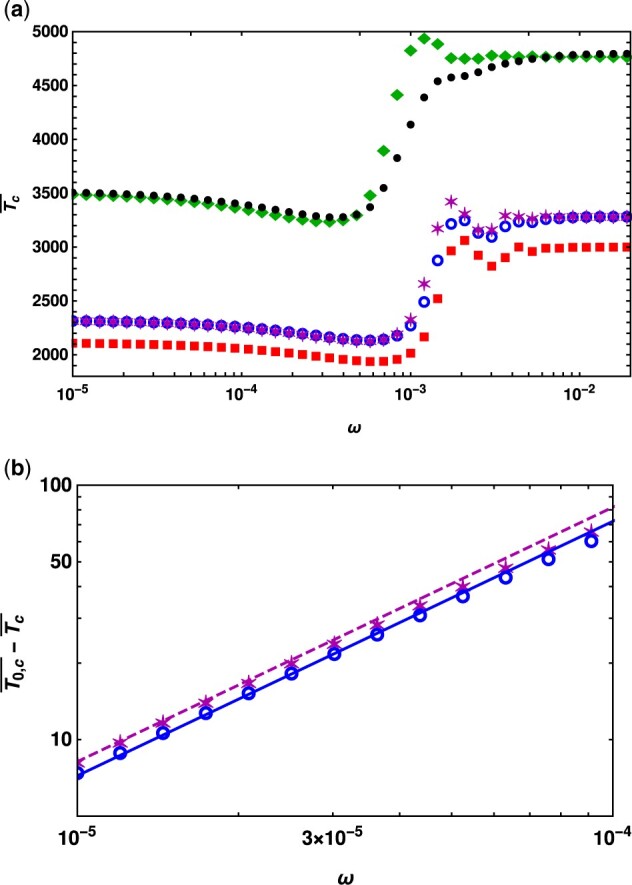
Top panel: Conditional mean fixation time ${\overline{T}}_c$ for a mutant under strong positive selection at all times with selection coefficient $s(t)=\overline{s}+\sigma \hspace{0.17em}\text{sin}(\omega t+\theta )$ when the mutant is beneficial at all times to show that, except for strongly recessive or dominant mutations, it depends weakly on the dominance coefficient h. The points are obtained by numerically calculating (18) for dominance coefficient $h=0.1(♦),0.3(\ast ),0.5(■),0.7(○),0.9(•)$ in a population of size N. The other parameters are $N={10}^5,\overline{s}=0.01,\sigma =0.007,\theta =\pi /4$. The bottom panel shows the comparison between (18) (points) and (20) (line) for the deviation in the conditional mean fixation time in a slowly changing environment where $\omega \ll s(0)\approx 0.014$.

Below we study the dependence of ${\overline{T}}_c$ on the dominance coefficient and the rate of environmental change within a semi-deterministic theory (Cohn and Jagers 1994). This approach has been recently used to find the distribution of the conditional fixation time in a constant environment (Martin and Lambert 2015); here, we are interested in generalizing these results to time-dependent environments.

Starting at a low initial frequency, if it escapes stochastic loss, the mutant population evolves stochastically until a time t₁ when it reaches a finite frequency (phase A). For such allele trajectories, it is a good approximation to treat the further evolution of the mutant population deterministically (phase B). However, at a time $t_2(>t_1)$, when the mutant frequency is close to one, as the wildtypes are in low number, they are subject to stochastic fluctuations and go extinct at a time T_c (phase C). The stochastic phases A and C can be described by a Feller process, as discussed below.

Time-inhomogeneous Feller process

In a time-dependent environment, the allele frequency distribution ${\Phi }_{\mathrm{f}}(p,t|p_0,0)$ which describes the probability that the mutant frequency is p given that its initial frequency was p₀ obeys the following forward Kolmogorov equation (Risken 1996),

$$\frac{\partial {\Phi }_{\mathrm{f}}(p,t|p_0,0)}{\partial t}=-s\left(t\right)\frac{\partial }{\partial p}\left[g\right(p\left){\Phi }_{\mathrm{f}}\right(p,t|p_0,0)]+\frac{{\partial }^2}{\partial p^2}[\frac{pq{\Phi }_{\mathrm{f}}(p,t|p_0,0)}{2N}]$$ (12)

where, as before, $g(p)=pq(p+h(1-2p))$ and $s(t)=\overline{s}+\sigma \hspace{0.17em}\text{sin}(\omega t+\theta ),t\ge 0$. At short times where the mutant frequency is low ($p\to 0$), the frequency distribution ${\Phi }_{\mathrm{f}}\to \mathcal{F}$, and (12) reduces to

$$\frac{\partial \mathcal{F}(p,t|p_0,0)}{\partial t}=-hs\left(t\right)\frac{\partial }{\partial p}\left[p\mathcal{F}\right(p,t|p_0,0)]+\frac{1}{2N}\frac{{\partial }^2}{\partial p^2}[p\mathcal{F}(p,t|p_0,0\left)\right]$$ (13)

where $\mathcal{F}(p,t|p_0,0)$ is the probability distribution of a Feller process (Feller 1951a, 1951b). This process describes the mutant frequency dynamics when the lineages can be assumed to grow independently, and is a continuous analog of classical branching process that is defined in discrete time and deals with the number of individuals. The Feller diffusion equation above can be easily generalized to include mutations and time-dependent population size (Cattiaux et al. 2009; Masoliver and Perelló 2012; Gan and Waxman 2015; Masoliver 2016). In the later discussion, we will use the Feller process to describe the wildtype dynamics also at large times where the wildtype frequency is low. As detailed in Appendix C, the exact solution of (13) is given by (C.4).

Fixation probability

Since the probability that the mutant dies out by time t is equal to $1-{\int }_0^{\infty }dp\mathcal{F}(p,t)$, its eventual fixation probability, $u={\text{Lim}}_{t\to \infty }{\int }_0^{\infty }dp\mathcal{F}(p,t)$ (see also Appendix C); using (C.4), we then obtain

$$u(p_0,0)=1-\text{exp}\hspace{0.17em}[-\frac{2N{p}_0}{{\int }_0^{\infty }dt{e}^{-h{\int }_0^{t}d{t}^{\prime }s\left(t^{\prime }\right)}}]$$ (14)

The above equation shows that u is nonzero provided the integral $J={\int }_0^{\infty }dt{e}^{-h{\int }_0^{t}d{t}^{\prime }s\left(t^{\prime }\right)}$ is finite. We verify that for constant selection and single initial mutant, (14) gives $u=1-e^{-hs}\approx hs,h>0$ for a beneficial mutant (Haldane 1927).

Before proceeding further, we compare the result (14) with that obtained using a birth-death process in earlier studies (Kendall 1948; Uecker and Hermisson 2011; Devi and Jain 2020). While $u^{(\text{Feller})}=1-e^{-1/J}$, the probability $u^{(\text{birth}-\text{death})}={(1+J)}^{-1}$ [refer to (4) of Devi and Jain (2020)] for a single mutant. For small selection coefficients, as the fixation probability is expected to be small, J must be large. Then, it follows that to leading order in $1/J$, both processes yield the fixation probability to be $1/J$.

Mean fixation time in slowly changing environments

As described in Appendix D, the distribution of the conditional fixation time for a mutant with initial phase θ is given by

$$P(T_c;\theta )=\frac{h{\Upsilon }_{\mathrm{A}}}{h-1}\frac{d{\Upsilon }_{\mathrm{C}}}{d{T}_c}{\int }_0^{\infty }dq{q}^{-\frac{h}{1-h}}{e}^{-{\Upsilon }_{\mathrm{C}}q}{e}^{-{\Upsilon }_{\mathrm{A}}{q}^{-\frac{h}{1-h}}}$$ (15)

where

$${\Upsilon }_{\mathrm{C}}=\frac{2N}{{\int }_0^{T_c}dt{e}^{(1-h){\int }_0^{t}d{t}^{\prime }s\left(t^{\prime }\right)}}$$ (16)

$${\Upsilon }_{\mathrm{A}}=2N{e}^{\frac{1-2h}{1-h}\ln \left(\frac{h}{1-h}\right)}u(\theta )$$ (17)

and the eventual fixation probability u is given by (14) for a single mutant. Supplementary Figure S3 shows a comparison between the expression (15) and the results obtained using numerical simulations when the cycling frequency is below, above, and close to the resonance frequency ω_r, and we find a good agreement in all the three cases. For constant selection, we find that the generating function for the conditional fixation time obtained using (15) reduces to (A.11) of Martin and Lambert (2015).

Figure 4A shows that, except for strongly recessive or dominant mutants, the conditional mean fixation time ${\overline{T}}_c={\int }_0^{\infty }d{T}_c{T}_{c}P(T_c)$ depends weakly on dominance for arbitrary rates of environmental change. Figure 4A also suggests that for small and large cycling frequencies, the conditional mean fixation time ${\overline{T}}_c(h,s)\approx {\overline{T}}_c(1-h,s)$. To understand this result, using (15), we rewrite the time ${\overline{T}}_c$ as

$${\overline{T}}_c=\frac{h{\Upsilon }_{\mathrm{A}}}{h-1}{\int }_0^{\infty }dq{e}^{-{\Upsilon }_{\mathrm{A}}{q}^{-\frac{h}{1-h}}}{q}^{-\frac{h}{1-h}}{\int }_0^{\infty }d{\Upsilon }_{\mathrm{C}}{T}_c({\Upsilon }_{\mathrm{C}})e^{-{\Upsilon }_{\mathrm{C}}q}$$ (18)

and analyze it for slowly changing environments using a perturbation theory. As explained in Appendix E, for $\omega \ll s(0)$, we get ${\overline{T}}_c\approx {\overline{T}}_{0,c}+(\omega /s(0)){\overline{T}}_{1,c}$ where,

$$\frac{{\overline{T}}_{0,c}}{2N}\approx \frac{\ln (2\alpha )}{2h(1-h)\alpha }+\frac{\gamma +(2-3h)\ln h+(3h-1)\ln (1-h)}{2h(1-h)\alpha }$$ (19)

$$\frac{{\overline{T}}_{1,c}}{2N}\approx -\frac{\sigma \hspace{0.17em}\text{cos}\hspace{0.17em}\theta {(\ln \alpha )}^2}{4h^2{(1-h)}^{2}s(0)\alpha }$$

$$\times \left[1+\frac{2(\ln 2-h+\gamma +(2-3h)\ln h+(3h-1)\ln (1-h))}{\ln \alpha }\right]$$ (20)

In the above equations, $\gamma \approx 0.577$ is the Euler constant and, as before, $\alpha =Ns(0)$. Note that while the fixation time ${\overline{T}}_c$ was expanded in powers of $N\omega$ in the last section, here the expansion parameter is $\omega /s(0)$.

The semi-deterministic theory described in this section is not a systematic, controlled approximation (unlike various perturbation theories) and it is not clear how good this approximation is; however, here we find that (19) matches exactly with (4.2) of Ewing et al. (2011) (on replacing N in the above expression by 2 N), which is obtained using a diffusion theory, and shows that the conditional mean fixation time in a population with dominance coefficient h is approximately equal to that in a population with the corresponding parameter $1-h$. Note that this result holds for large $\alpha (\gtrsim {10}^3)$, while as shown in Figure 3 for moderate selection, the dominant mutant takes longer than the recessive one to fix [see also Teshima and Przeworski (2006)].

Equation (20) captures the effect of a slowly changing environment on the conditional mean fixation time and matches well with the data obtained by numerically integrating (18) as shown in Figure 4B. The leading term on the right-hand side (RHS) of (20) is symmetric about h = 1/2, pointing to the approximate symmetry, ${\overline{T}}_c(h,s)\approx {\overline{T}}_c(1-h,s)$ discussed above. While the subleading correction does not have $h\leftrightarrow 1-h$ symmetry, its effect is small compared to the leading term for intermediate dominance. Supplementary Figure S4 further suggests that the distribution of the fixation time has $h\leftrightarrow 1-h$ approximate symmetry for small cycling frequencies but not for frequencies close to the resonance frequency, in accordance with the behavior of the mean fixation time shown in Figure 4A.

Equation (20) also shows that the mean fixation time decreases (increases) if the beneficial allele arises when the selection gradient (in time) is positive (negative), as intuitively expected; furthermore, both ${\overline{T}}_{0,c}$ and ${\overline{T}}_{1,c}$ decay with increasing selection. Finally, we mention that at the beginning of this section, we had assumed that $\sigma <\overline{s}$. But in a slowly changing environment, the semi-deterministic approximation may be expected to work for $\sigma >\overline{s}$ and $0<\theta <\pi$; this is indeed confirmed in Supplementary Figure S4.

Discussion

In this study, we have investigated how a selective environment that is varying periodically and predictably in time affects the fixation time of a mutant in a finite, diploid population.

Effect of the environmental parameters

We find that if the environment changes fast, the fixation time in the temporally varying environment differs considerably from that in the static environment, as can be seen in Figures 1A and 4A at intermediate cycling frequencies. But for a meaningful comparison with the body of work on the fixation time in constant environments (Charlesworth 2020), most of our analysis has focused on the effect of slowly changing environments.

It should be noted that for time-dependent selection coefficients, the stochastic process is time-inhomogeneous and therefore the fixation time depends on the time at which the mutant arose and whether the environment is improving or deteriorating (Uecker and Hermisson 2011; Devi and Jain 2020). If an initially deleterious mutant on the way to fixation experiences a more favorable environment, its chance of extinction reduces and such a mutant can be expected to have a larger time of fixation than in an environment that remained unfavorable. On the other hand, if an initially deleterious (or beneficial) mutant faces an even more unfavorable environment, due to the higher risk of extinction at late times, the mutant is likely to fix sooner. The dynamics of an initially beneficial mutant that remains beneficial until fixation are, however, less affected by random genetic drift—if selection increases, due to the higher growth rate, the mutant fixes sooner than in an environment that had remained constant.

Selection regimes

In static environments, the qualitative behavior of the conditional mean fixation time of a mutant depends on the sign and strength of the scaled selection coefficient, $\alpha =Ns$. For a beneficial mutant, if selection is weak ($0<\alpha \ll 1$), the fixation time increases with the dominance coefficient h and selection strength α, and can even exceed the fixation time of a neutral mutant (Mafessoni and Lachmann 2015). But for moderately strong selection ($1\ll \alpha \ll 100$), the conditional mean fixation time decreases with α and increases with h (Teshima and Przeworski 2006; Charlesworth 2020). For stronger selection, it decreases with α and is approximately identical for two mutants with the same selection coefficient but dominance coefficients h and $1-h$ (van Herwaarden and van der Wal 2002; Ewing et al. 2011). The patterns for deleterious mutations follow on realizing that the conditional fixation time for a beneficial mutant with dominance coefficient h and a deleterious mutant with the same magnitude of selection but dominance level $1-h$ are equal (Maruyama 1974; Maruyama and Kimura 1974).

Here, we find that all the qualitative patterns described above continue to hold when the environment changes slowly, but there are quantitative differences. While a slowly changing environment has only a mild effect on the conditional mean fixation if the mutant is beneficial, its impact is much stronger for deleterious mutants. This asymmetry can be traced back to the fact that the fixation probability of a deleterious mutant is much more sensitive to a change in selection than the fixation probability of a beneficial mutant. Furthermore, for initially deleterious mutants, as the fixation probability of the recessives is higher than the dominants, the former can segregate in the population for a longer time and are therefore exposed to the changing environment for a longer duration, resulting in a fixation time which is substantially different from that in a constant environment.

Implications

In a constant environment, due to the Maruyama-Kimura symmetry for the conditional mean fixation time (Maruyama 1974; Maruyama and Kimura 1974), similar diversity patterns for beneficial and deleterious sweeps may be generated (Johri et al. 2020). But in a changing environment, due to the lack of the Maruyama-Kimura symmetry, a beneficial mutant in a slowly improving (deteriorating) environment can generate a diversity pattern different from that due to the fixation of a deleterious mutant under the same selection pressure but in a slowly deteriorating (improving) environment.

To ascertain this effect, we have conducted a preliminary study of the effect of hard sweep on linked neutral variation in a two-locus model of a finite, diploid population in which the first locus is modeled as in the Model section but the second biallelic locus is neutral. Recombination is assumed to occur with a probability $c\ll 1$ but recurrent mutations are not allowed. As a result of genetic hitchhiking, the heterozygosity $H_{\text{fix}}$ at the neutral locus following the fixation event (relative to the heterozygosity H₀ before the new mutant appeared) is expected to decrease (Maynard Smith and Haigh 1974). Figure 5 shows the relative heterozygosity as a function of the cycling frequency for the parameters in Figure 1A, and we find that its qualitative behavior is the same as that of the conditional mean fixation time (Tajima 1990). The inset of Figure 5 emphasizes that the slowly changing selective environment only mildly influences the heterozygosity of an initially beneficial dominant mutant but has a strong effect on the heterozygosity of an initially deleterious recessive mutant. A more detailed study of the effect of environmental variation on various measures of genetic diversity will be taken up in a future work.

Figure 5.

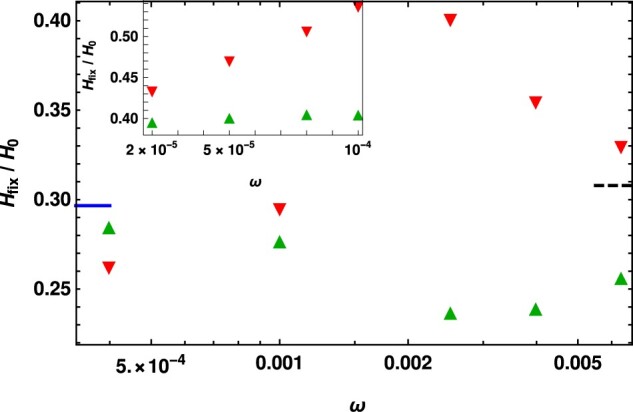
Reduction in the mean heterozygosity at the linked neutral locus due to the fixation of dominant $(h=0.7,▲)$ and recessive mutant ($h=0.3,▼$) with selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}\hspace{0.17em}\left(\omega t+\pi /4\right)$ and $-s(t)$, respectively, to show that the heterozygosity following the fixation of deleterious and beneficial mutant is significantly different in the changing environment, unlike in the static environment where they are identical. The reduction in the mean heterozygosity in the static environment with selection (solid line) and in the neutral environment (dashed line) are also shown for comparison. All the data are obtained by numerical simulations. The inset shows the heterozygosity reduction due to the fixation of dominant mutant $(h=0.9,▲)$ and recessive mutant ($h=0.1,▼$) in the slowly changing environment with selection coefficient $s(t)=\sigma \hspace{0.17em}\text{sin}\hspace{0.17em}\left(\omega t+3\pi /4\right)$ and -s(t), respectively. The other parameters for both figures are $\sigma =0.01,\hspace{0.17em}c=s(0)/10,\hspace{0.17em}{Q}_0=0,\hspace{0.17em}{R}_0=0.2002$ and $p_0=1/2N$, where c is the recombination probability, Q₀ and R₀ are, respectively, initial relative frequencies of a neutral allele in a chromosome with a and A allele on the first locus, and the population size N = 500 (main) and 1000 (inset).

As already mentioned, although the qualitative patterns for the fixation time in a static environment are robust with respect to a slow change in the environment, there are quantitative differences. As a consequence, the effect of varying environment may be interpreted as an effective selection coefficient or dominance parameter. For example, in Figure 3, the fixation time in slowly changing environment, and for dominance coefficient h = 1/2 and selection strength $\alpha =-14.14$ (initial phase $\theta =5\pi /4$) is about 1691. But if one assumes a constant environment, the same fixation time is obtained for $\alpha =-15.27$ which implies an 8% increase in the selection coefficient.

We therefore suggest to include the effect of changing environment in theoretical models of selective sweeps as this can potentially allow one to distinguish between the sign of selection, detect deleterious sweeps and correctly estimate the model parameters. Generalizing the above results to include the effect of inbreeding and sex-linked inheritance (Glémin 2012; Hartfield and Bataillon 2020) could also help to assess the importance of changing environment in evolutionary dynamics.

Data availability

The authors state that all data necessary for confirming the conclusions presented in the article are represented fully within the article. Supplemental material including the simulation program and a Mathematica notebook are available at GENETICS online.

Appendix A: Diffusion theory for time-inhomogeneous process

For a large finite population with small selection coefficient, the average fixation time can, in principle, be studied using the backward Fokker-Planck equation with time-dependent selection coefficient. The probability distribution ${\Phi }_{\mathrm{b}}(x,t|p,t_0)$ obeys the following partial differential equation:

$$-\frac{\partial {\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial t_0}=s(t_0)g(p)\frac{\partial {\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial p}+\frac{pq}{2N}\frac{{\partial }^2{\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial p^2}$$ (A1)

where $s(t_0)=\overline{s}+\sigma \hspace{0.17em}\text{sin}(\omega t_0+\theta )$ and $g(p)=pq(p+h(1-2p))$. In the above equation, the first term on the RHS is obtained on using that the deterministic rate of change of the mutant allele frequency is given by $dp/dt=s(t)g(p)$, and the second term is due to the sampling noise in a finite population. In (A1), the probability distribution is assumed to be a function of the initial time t₀ and the final time t. But one can also consider the variables t₀ and the time interval $t-t_0$ which leads to (S5) in Uecker and Hermisson (2011). However, as the formulation (A1) is much easier to handle, we work with it in the rest of the article.

The (unconditional) mean fixation time for a mutant arising at time t₀ can be written as

$$\overline{T}(p,t_0)={\int }_{t_0}^{\infty }dt(t-t_0){\Phi }_{\mathrm{b}}(x\to 1,t|p,t_0)$$ (A2)

Using Leibniz integral rule,

$${\int }_{t_0}^{\infty }dt(t-t_0)\frac{\partial {\Phi }_{\mathrm{b}}(x,t|p,t_0)}{\partial t_0}=\frac{\partial }{\partial t_0}{\int }_{t_0}^{\infty }dt(t-t_0){\Phi }_{\mathrm{b}}(x,t|p,t_0)+{\int }_{t_0}^{\infty }dt{\Phi }_{\mathrm{b}}(x,t|p,t_0),$$ (A3)

and (A.1), we then obtain

$$-\frac{\partial \overline{T}(p,t_0)}{\partial t_0}-u(p,t_0)=s(t_0)g(p)\frac{\partial \overline{T}(p,t_0)}{\partial p}+\frac{pq}{2N}\frac{{\partial }^2\overline{T}(p,t_0)}{\partial p^2}$$ (A4)

where the eventual fixation probability $u(p,t_0)={\int }_{t_0}^{\infty }dt{\Phi }_b(x\to 1,t|p,t_0)$ obeys (Uecker and Hermisson 2011; Devi and Jain 2020)

$$-\frac{\partial u(p,t_0)}{\partial t_0}=s(t_0)g(p)\frac{\partial u(p,t_0)}{\partial p}+\frac{pq}{2N}\frac{{\partial }^{2}u(p,t_0)}{\partial p^2}$$ (A5)

We verify that (A4) and (A5) reduce to the corresponding equations for the time-homogenous process where the fixation probability and the fixation time are independent of the initial time (Ewens 2004). The partial differential Equations (A4) and (A5) along with the boundary conditions

$$u(0,t_0)=0,u(1,t_0)=1 , \overline{T}(0,t_0)=\overline{T}(1,t_0)=0$$ (A6)

can, in principle, be used to find the mean fixation time for either sign of selection. However, these equations do not appear to be solvable, even for the dominance parameter h = 1/2, as the eigenfunction expansion method commonly employed for solving partial differential equations with time-dependent coefficients requires the eigenfunctions of the problem with constant selection that are, unfortunately, not known in a closed form (Jain and Devi 2020).

Appendix B: Mean fixation time in slowly changing environments

In slowly changing environments where $\omega \ll N^{-1},s(0)$ and $Ns(0)$ is arbitrary, the eventual fixation probability and the mean fixation time can be expanded in a power series in the small, dimensionless parameter $N\omega$, that is, $u={\sum }_{i=0}^{\infty }{(N\omega )}^i{u}_i,\overline{T}={\sum }_{i=0}^{\infty }{(N\omega )}^i{\overline{T}}_i$. But for small enough $N\omega$, it is a good approximation to terminate this series at i = 1.

To find the equation satisfied by u_i, it is useful to rewrite (A5) for the fixation probability as

$$-N\omega \frac{\partial u(p,t_0)}{\partial \Theta }=Ns(\Theta )g\left(p\right)\frac{\partial u(p,t_0)}{\partial p}+\frac{pq}{2}\frac{{\partial }^{2}u(p,t_0)}{\partial p^2}$$ (B1)

where $\Theta =\omega t_0+\theta$. Substituting the power series expansion for u on both sides of the above equation, collecting terms with the same power of $N\omega$ and taking $\Theta \to \theta$ (that is, $\omega \to 0$), we obtain (4) and (6) in the main text for u₁ and u₀, respectively. The fixation probability in a static environment obeys the boundary conditions, $u_0(0,t_0)=0,u_0(1,t_0)=1$. Therefore, due to (A6), $u_1(0,t_0)=u_1(1,t_0)=0$. In a similar fashion, the Equations (5) and (7) for the mean fixation time and the corresponding boundary conditions can be derived.

The conditional mean fixation time in slowly changing environment can be written as

$${\overline{T}}_c=\frac{\overline{T}}{u}\approx \frac{{\overline{T}}_0}{u_0}\left(\frac{1+N\omega \frac{{\overline{T}}_1}{{\overline{T}}_0}}{1+N\omega \frac{u_1}{u_0}}\right)$$ (B2)

from which (8) follows on using $(1+{ϵ}_1)/(1+{ϵ}_2)\approx 1+{ϵ}_1-{ϵ}_2$ for small ${ϵ}_1,{ϵ}_2$.

Appendix C: Feller process with time-dependent coefficients

Taking the Laplace transform on both sides of (13), we find that $\tilde{\mathcal{F}}(\kappa ,\tau )={\int }_0^{\infty }dp{e}^{-\kappa p}\mathcal{F}(p,\tau )$ obeys a first order differential equation,

$$\frac{\partial \tilde{\mathcal{F}}}{\partial \tau }=(\kappa -{\kappa }^2\ell (\tau ))\frac{\partial \tilde{\mathcal{F}}}{\partial \kappa }$$ (C1)

where $\tau \left(t\right)=h{\int }_0^{t}d{t}^{\prime }s\left(t^{\prime }\right)$ and $\ell (\tau )={(2Nhs(t))}^{-1}$. The above differential equation can be solved using the method of characteristics for the initial condition $\mathcal{F}(p,0)=\delta (p-p_0)$, and we obtain (Feller 1951b; Masoliver 2016)

$$\tilde{\mathcal{F}}(\kappa ,\tau )=\text{exp}\hspace{0.17em}[-\frac{p_0\kappa e^{\tau }}{1+\kappa e^{\tau }{\int }_0^{\tau }d\tau \prime e^{-{\tau }^{\prime }}\ell \left({\tau }^{\prime }\right)}]$$ (C2)

$$\begin{array}{c}=e^{-\frac{p_0}{{\int }_0^{\tau }d{\tau }^{\prime }{e}^{-{\tau }^{\prime }}\ell \left({\tau }^{\prime }\right)}}\\ \times \sum _{n=0}^{\infty }\frac{1}{n!}{\left(\frac{p_0}{{\int }_0^{\tau }d{\tau }^{\prime }{e}^{-{\tau }^{\prime }}\ell \left({\tau }^{\prime }\right)}\right)}^n\frac{1}{{(1+\kappa {\int }_0^{\tau }d{\tau }^{\prime }{e}^{\tau -{\tau }^{\prime }}\ell ({\tau }^{\prime }\left)\right)}^n}\end{array}$$ (C3)

Taking the inverse Laplace transform of the summand in the last expression and then carrying out the sum over n, we get

$$\mathcal{F}(p,t)=\frac{1}{⟨p⟩}\sqrt{\frac{⟨p⟩}{p}}\frac{2N{p}_0{e}^{-}\frac{2N{p}_0(1+\frac{p}{⟨p⟩})}{{\int }_0^{\tau }d{\tau }^{\prime }{e}^{-\tau \prime }{\left(hs\right(t^{\prime }\left)\right)}^{-1}}}{{\int }_0^{\tau }d{\tau }^{\prime }{e}^{-{\tau }^{\prime }}{\left(hs\right(t^{\prime }\left)\right)}^{-1}}{I}_1\left(\frac{4N{p}_0\sqrt{\frac{p}{⟨p⟩}}}{{\int }_0^{\tau }d{\tau }^{\prime }{e}^{-{\tau }^{\prime }}{\left(hs\right(t^{\prime }\left)\right)}^{-1}}\right)$$ (C4)

where $I_n(z)$ is modified Bessel function of the first kind. In (C4), $\langle p(t)\rangle ={\int }_0^{\infty }dp\mathcal{F}(p,t)p=p_0{e}^{\tau }$ is the expected mutant allele frequency at time t, as can also be checked using (13); however, when conditioned on fixation, this frequency grows as $p_0{e}^{\tau }/u$ which is faster than $\langle p\rangle$ (Uecker and Hermisson, 2011). We also note that the eventual fixation probability (14) can also be written as $u={\text{Lim}}_{\kappa ,\tau \to \infty }\tilde{\mathcal{F}}(\kappa ,\tau )$.

Appendix D: Distribution of the fixation time of on-average beneficial mutant

In the stochastic phase A, although the expected mutant frequency grows exponentially with time, (C4) and (14) show that at large times [where $\tau \to \infty$, since s(t) > 0 at all times], the random variable $y=p/\langle p\rangle$, conditioned on fixation, has a stationary distribution,

$${\mathcal{F}}_c(y,t)=\frac{\mathcal{F}(y\langle p\rangle ,t)\langle p\rangle }{1-\mathcal{F}(0,t)}\stackrel{\tau \to \infty }{\to }u{e}^{-uy}$$ (D1)

[see also Uecker and Hermisson (2011)]. Furthermore, in the vicinity of time t₁, the mutant frequency in the stochastic phase A is given by $p=(p_{0}y)e^{\tau (t)},t\lesssim t_1$ and in the deterministic phase B, the average mutant frequency grows as $p(t)\approx p(t_1)e^{\tau (t)-\tau (t_1)},t\gtrsim t_1$. Thus the initial mutant frequency in the deterministic phase is given by $p(t_1)=p_{0}y{e}^{\tau (t_1)}$, and from (D1), it follows that the random variable $p(t_1)e^{-\tau (t_1)}$ is exponentially distributed with mean ${(2Nu)}^{-1}$.

In the deterministic phase B that begins at time t₁ and ends at time t₂, the average mutant frequency obeys $dp/dt=s(t)g(p)$; integrating this equation over time from t₁ to t₂, we get $\tau (t_2)-\tau (t_1)=h[\mathcal{D}(p(t_2))-\mathcal{D}(p(t_1))]$, where

$$\mathcal{D}(p)=\frac{\ln p}{h}-\frac{\ln q}{1-h}+\frac{2h-1}{h(1-h)}\ln (h+(1-2h)p).$$ (D2)

But as the frequency $p(t_1)\to 0,q(t_2)\to 0$, the initial frequency $q(t_2)$ in phase C is related to $p(t_1)$ as

$$\frac{h}{h-1}\ln [q(t_2)e^{\frac{1-h}{h}\tau (t_2)}]\approx \ln [p(t_1)e^{-\tau (t_1)}]-\frac{1-2h}{1-h}\ln \left(\frac{h}{1-h}\right)$$ (D3)

In the stochastic phase C, the wildtype population evolves stochastically from time t₂ until it goes extinct at time T_c. The wildtype frequency can be described by a Feller process that obeys (12) for the distribution $\widehat{\mathcal{F}}(q,t)$ when $p\to q,s(t)\to -s(t),h\to 1-h$. For constant selection, it has been claimed that looking backward in time (that is, $t\to T_c-t$), the wildtype frequency obeys the same dynamics as the mutant frequency with $h\to 1-h$ but s unchanged (Martin and Lambert 2015); however, this prescription results in a forward Kolmogorov equation with negative population size which is clearly absurd. Therefore, we will work always looking forward in time.

Proceeding in a manner similar to that for stochastic phase A, the distribution $\widehat{\mathcal{F}}(q,t)$ for the wildtype frequency subject to the initial condition $q(t_2)$ can be found for $t>t_2$. Then the probability that the wildtype goes extinct by time T_c is given by [refer to (14) for a comparison]

$$1-{\int }_0^{\infty }dq\widehat{\mathcal{F}}(q,T_c)=\text{exp}\hspace{0.17em}[-\frac{2Nq\left(t_2\right)}{{\int }_{t_2}^{T_c}dt{e}^{(1-h){\int }_{t_2}^{t}d{t}^{\prime }s\left(t^{\prime }\right)}}]$$ (D4)

$$\stackrel{T_c\gg t_2}{\approx }\hspace{0.17em}\text{exp}\hspace{0.17em}[-\frac{2Nq\left(t_2\right)e^{\frac{1-h}{h}\tau \left(t_2\right)}}{{\int }_0^{T_c}dt{e}^{(1-h){\int }_0^{t}d{t}^{\prime }s\left(t^{\prime }\right)}}]$$ (D5)

On taking the derivative of the above cumulative distribution with respect to T_c and averaging over the distribution of $q(t_2)$ which can be found using (D1) and (D3), we finally arrive at (15) in the main text.

Appendix E: Mean fixation time of on-average beneficial mutant

To find the conditional mean fixation time given by (18), we need to express T_c as a function of ${\Upsilon }_{\mathrm{C}}$ using (16) which is given by

$$\frac{2N}{{\Upsilon }_{\mathrm{C}}}={\int }_0^{T}d{t}^{\prime }{e}^{(1-h)\overline{s}{t}^{\prime }}{e}^{-\frac{(1-h)\sigma }{\omega }\left(\text{cos}\right(\omega t^{\prime }+\theta )-\text{cos}(\theta \left)\right)}$$ (E1)

For small ω, we first expand the exponent of the integrand on the RHS to linear order in cycling frequency to obtain

$$\frac{2N}{{\Upsilon }_{\mathrm{C}}}\approx {\int }_0^{T}d{t}^{\prime }{e}^{s_0{t}^{\prime }}{e}^{s_1\omega \hspace{0.17em}\text{cos}\hspace{0.17em}\theta \frac{{t^{\prime }}^2}{2}}\approx {\int }_0^{T}d{t}^{\prime }{e}^{s_0{t}^{\prime }}(1+s_1\omega \hspace{0.17em}\text{cos}\hspace{0.17em}\theta \frac{{t^{\prime }}^2}{2})$$ (E2)

where $s_0=(1-h)s(0)$ and $s_1=(1-h)\sigma$. On carrying out the integrals and taking the logarithm on both sides, to order ω, we get

$$\ln \left(\frac{2N{s}_0}{{\Upsilon }_{\mathrm{C}}}\right)=s_{0}T+\frac{s_1\omega \hspace{0.17em}\text{cos}\hspace{0.17em}\theta }{s_0^2}\left(1-s_{0}T+\frac{s_0^2}{2}{T}^2\right)$$ (E3)

which can be inverted to finally give

$$s_{0}T=A+\frac{\omega s_1\hspace{0.17em}\text{cos}\hspace{0.17em}\theta }{s_0^2}\left(A-1-\frac{A^2}{2}\right)$$ (E4)

where $A=\ln \left(\frac{2N{s}_0}{{\Upsilon }_{\mathrm{C}}}\right)$. Using this expression in the inner integral of (18) and carrying out the integrals, to leading and subleading orders in α, we obtain (19) and (20) in the main text.