Abstract
Fitness effects of deleterious mutations can differ between females and males due to: (i) sex differences in the strength of purifying selection; and (ii) sex differences in ploidy. Although sex differences in fitness effects have important broader implications (e.g., for the evolution of sex and lifespan), few studies have quantified their scope. Those that have belong to one of two distinct empirical traditions: (i) quantitative genetics, which focusses on multi-locus genetic variances in each sex, but is largely agnostic about their genetic basis; and (ii) molecular population genetics, which focusses on comparing autosomal and X-linked polymorphism, but is poorly suited for inferring contemporary sex differences. Here, we combine both traditions to present a comprehensive analysis of female and male adult reproductive fitness among 202 outbred, laboratory-adapted, hemiclonal genomes of Drosophila melanogaster. While we find no clear evidence for sex differences in the strength of purifying selection, sex differences in ploidy generate multiple signals of enhanced purifying selection for X-linked loci. These signals are present in quantitative genetic metrics—i.e., a disproportionate contribution of the X to male (but not female) fitness variation—and population genetic metrics—i.e., steeper regressions of an allele’s average fitness effect on its frequency, and proportionally less nonsynonymous polymorphism on the X than autosomes. Fitting our data to models for both sets of metrics, we infer that deleterious alleles are partially recessive. Given the often-large gap between quantitative and population genetic estimates of evolutionary parameters, our study showcases the benefits of combining genomic and fitness data when estimating such parameters.
Keywords: sex differences, fitness, GWAS, X chromosome, autosomes, purifying selection, deleterious polymorphism, dominance, population genetics, quantitative genetics
Introduction
Most new mutations affecting fitness are deleterious (Eyre-Walker and Keightley 2007) and segregating deleterious alleles make up a large fraction of standing genetic variation for fitness (Charlesworth 2015). The evolutionary dynamics of deleterious alleles and their contributions to standing fitness variation depend on their “average effects” on fitness (sensu Fisher; see Theoretical background), which can differ between males and females. Such sex differences in the fitness effects of mutations have important implications for the evolutionary persistence of maladaptation (e.g., genetic load; Whitlock and Agrawal 2009), the severity of inbreeding depression (Eanes et al. 1985; Mallet and Chippindale 2011), the genetic basis of fitness variation (Connallon 2010), and the evolution of sex (Agrawal 2001; Siller 2001; Roze and Otto 2012) and lifespan (Maklakov and Lummaa 2013).
Sex differences can influence the fitness effects of deleterious variation in two ways. First, the strength of purifying selection can differ between sexes (Bateman 1948; Trivers 1972; Whitlock and Agrawal 2009; Janicke et al. 2016; Singh and Punzalan 2018), owing to the divergent strategies females and males employ in achieving reproductive success (Darwin 1871; Andersson 1994; Arnqvist and Rowe 2005), or to sex differences in the fraction of the genome with sex-limited expression (and thus experiencing sex-limited selection; Connallon and Clark 2011; Allen et al. 2013, 2017). Second, the sexes show asymmetries in ploidy for sex-linked genes, with diploid X chromosomes in females and hemizygous (haploid) X chromosomes in males. Haploid expression is expected to enhance the expression of X-linked deleterious alleles in males (Reinhold and Engqvist 2013) and thereby strengthen purifying selection against them (Avery 1984), whether or not the sexes systematically differ in the strength of purifying selection. Quantifying and distinguishing these two sources of sexually dimorphic fitness effects is essential to our understanding of the genetic basis and evolutionary dynamics of deleterious variants.
Two distinct empirical traditions have investigated how sex differences mediate the fitness effects of deleterious variation. First, researchers have used classical quantitative genetic designs to estimate standing genetic variation for fitness (or fitness components) (Chippindale et al. 2001; Gibson et al. 2002; Long et al. 2009; Collet et al. 2016; Sultanova et al. 2018) or the effects of new mutations on fitness in each sex (i.e., from mutation-accumulation experiments; Mallet and Chippindale 2011; Mallet et al. 2011; Sharp and Agrawal 2013, 2018; Grieshop et al. 2016; Allen et al. 2017; Prokop et al. 2017). The second empirical tradition—molecular population genetics—has addressed questions about sex differences through comparisons of genetic diversity between autosomal and X-linked genes (Vicoso and Charlesworth 2006; Ellegren 2009; Li et al. 2010; Leffler et al. 2012; Veeramah et al. 2014), which indirectly reflect sexually dimorphic fitness effects. For example, a disproportionate reduction in nonsynonymous X-linked polymorphism indicates stronger purifying selection on the X relative to autosomes, presumably as a consequence of male hemizygosity (see Theoretical background).
The two traditions differ in what they can, and cannot, tell us about sex differences in deleterious fitness effects. The quantitative genetic tradition is well suited for inferring broad-scale patterns of genetic variance and allows a straightforward assessment of multi-locus sex differences in fitness effects. However, quantitative genetic analyses cannot isolate the contributions of individual loci to fitness variance. Consequently, using the relationship between an allele’s average fitness effect and its frequency (e.g., Park et al. 2011; Josephs et al. 2015; Zeng et al. 2018), or comparing nonsynonymous and synonymous polymorphism (Li et al. 2010; Veeramah et al. 2014) to assess the strength of purifying selection, is out of reach with these data. Furthermore, quantitative genetic breeding designs rarely allow (or consider) partitioning fitness variances into X-linked and autosomal components (Simmons and Crow 1977; Eanes et al. 1985; Gibson et al. 2002; Brengdahl et al. 2018), despite the differential contributions of sex-linked and autosomal loci to female and male variances (James 1973; Connallon 2010; Reinhold and Engqvist 2013). The population genetic tradition, on the other hand, provides variant-level resolution and is well-suited for detecting differences in the effectiveness of purifying selection between autosomal and X-linked sites (Vicoso and Charlesworth 2006). However, autosomal and X-linked polymorphism data do not reflect contemporary (and sex-specific) fitness effects but instead represent long-term averages over many thousands of generations, and across the two sexes. Sex-differential fitness effects can therefore only be indirectly inferred by autosomal and X-linked contrasts.
In this study, we combined: (i) replicated measurements of male and female outbred lifetime reproductive fitness from ∼200 genotypes extracted from LHM, a laboratory-adapted population of Drosophila melanogaster (Ruzicka et al. 2019; see “Materials and Methods” for further details); and (ii) whole-genome sequences from these same lines (Gilks et al. 2016). These data enabled us to perform a genome-wide association study (GWAS) of female and male fitness, and thereby study fitness variation at the level of individual loci. Our general approach was to estimate various metrics associated with deleterious variation—multi-locus additive genetic variation () for fitness, regressions of estimated fitness effects of alleles on their frequencies, and levels of nonsynonymous vs synonymous polymorphism—among sexes and chromosome “compartments” (i.e., X and autosomes). By comparing these empirical estimates to theoretical models for each metric (see Theoretical background), we were able to comprehensively quantify sexually dimorphic fitness effects and dominance coefficients of deleterious variants. Given that estimates of evolutionary parameters (e.g., selection and dominance coefficients) often differ markedly between quantitative and population genetic approaches (Manna et al. 2011; Charlesworth 2015), our study showcases the benefits of combining measurements of fitness (in the quantitative genetic tradition) and genomic data (in the population genetic tradition) when estimating such parameters.
Theoretical background
We rely on three empirical metrics to make inferences about sex differences in the fitness effects of deleterious genetic variation: (A) multi-locus for fitness estimated from single nucleotide polymorphisms (SNPs); (B) regressions of estimated fitness effects of variants on their frequencies; and (C) allele frequency spectra for putatively deleterious (i.e., nonsynonymous) alleles relative to neutral (i.e., synonymous) alleles. Below, we use population genetic theory to briefly outline how these metrics can differ between the sexes or between the X and autosomes.
Our theoretical predictions focus on bi-allelic polymorphism maintained at an equilibrium between recurrent mutation, purifying selection and drift (i.e., mutation-selection-drift balance; which should apply to most loci) in a randomly mating population. Genotypic fitness values for an arbitrary polymorphic locus i, with wild-type allele Ai (at frequency pi) and deleterious allele ai (at frequency qi), are summarized in Table 1.
Table 1.
Fitness for each of three possible genotypes at the ith locusa
| Genotype (autosomal, X-linked) |
|||
|---|---|---|---|
| AiAi, Ai | Aiai, – | aiai, ai | |
| Female fitness (autosomal or X-linked) | 1 | 1—sf, ihi | 1—sf, i |
| Male fitness (autosomal) | 1 | 1—sm, ihi | 1—sm, i |
| Male fitness (X-linked) | 1 | – | 1—sm, i |
Selection and dominance coefficients are subject to the constraints: 0 < sf, i, sm, i, hi < 1.
Additive genetic variance for fitness (VA)
The contribution of the ith autosomal or X-linked locus to female VA for fitness is:
| (1) |
where is the “average effect” of the deleterious allele on female fitness. The same expression applies to male VA, with in place of . The contribution of an X-linked locus to male VA is:
| (2) |
with representing the “average effect” of the hemizygous X-linked deleterious allele in males (both results follow from standard theory, e.g.: James 1973; Reinhold and Engqvist 2013). With no epistasis or LD, multilocus fitness variance for a given sex is the sum of variances contributed by individual loci (see Charlesworth 2015).
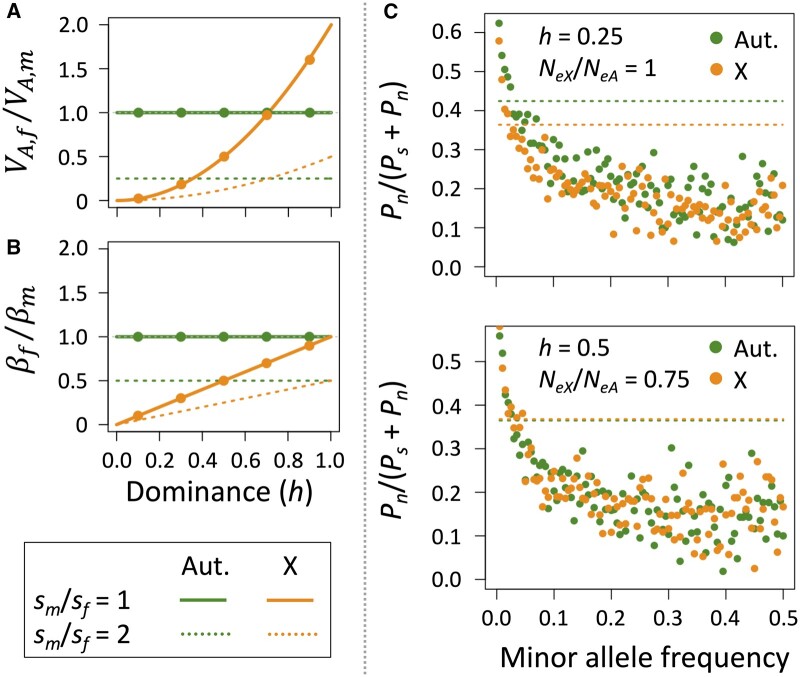
Each autosomal locus contributes more to variance of the sex that is subject to stronger purifying selection [Figure 1A, where for autosomal loci]. Consequently, sex asymmetries in multi-locus fitness variance at autosomal loci can emerge from sex differences in the strength of purifying selection and/or differences in the number of loci with male- vs female-limited expression (e.g., Sharp and Agrawal 2013). X-linked loci at mutation-selection balance contribute more to male than to female fitness variance for recessive or partially dominant mutations (Figure 1A, where for X-linked loci). X-linked loci also contribute disproportionately to fitness variance of males relative to autosomes (i.e., owing to heightened expression of X-linked alleles through hemizygosity; Figure 1A), whereas autosomal loci contribute disproportionately to variance of females (i.e., owing to the lower deleterious allele frequencies on the X that results from hemizygous selection in males; Figure 1A). These approximations (lines in Figure 1A) are robust to effects of genetic drift (filled circles in Figure 1A).
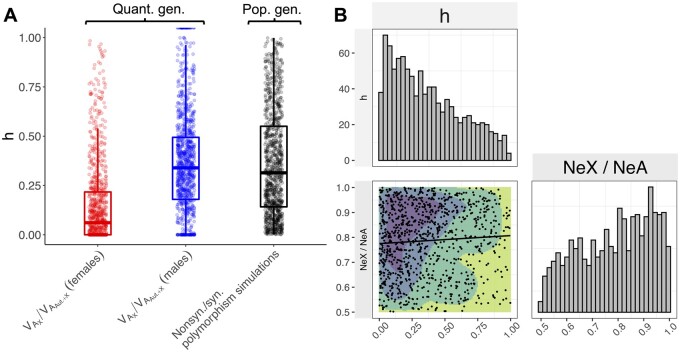
Figure 1.
Theoretical predictions outlining the effects of sex and chromosomal compartment (i.e., autosomes vs X) on three metrics of deleterious variation. (A) Contributions of autosomal and X-linked loci to sex-specific VA for fitness, illustrating that stronger purifying selection in a given sex increases autosomal VA for that sex, and that male VA is systematically elevated (and female VA systematically depleted) on the X chromosome, especially for partially recessive alleles. (B) Contributions of autosomal and X-linked loci to sex-specific regressions of average fitness effect on deleterious allele frequency (), illustrating that stronger purifying selection in a given sex increases for that sex, and male is systematically elevated (and female systematically depleted) on the X chromosome. (C) The proportion of protein-coding variants that are nonsynonymous is a function of the dominance coefficient (h) and the ratio of X-linked to autosome effective population size (NeX/NeA), with a deficit of nonsynonymous variants on the X when NeX/NeA > ¾ and or h < ½ (see also Supplementary Figure S2). Simulations assume =400, =10−3, = , a gamma distributed DFE with shape parameter k = 0.5. Datasets were simulated for a random sample of 200 haploid X chromosomes and 200 autosomes, with 107 synonymous and 2.5 × 107 nonsynonymous coding sites per chromosome, with population allele frequencies simulated using stationary distributions described in the main text. Broken lines show the results for Pn/(Ps + Pn) for all segregating sites pooled across MAF. In panels (A,B), filled circles represent stochastic simulations from the stationary distributions (assuming NeX/NeA = 3/4 and otherwise following the simulation approach of panel A), while curves are based on deterministic mutation-selection balance approximations in the main text.
Association between allele frequency and fitness effect
Assuming effectively strong selection [i.e., NeAhi(sf,i + sm,i), NeXhi(sf, i + sm, i) ≫ 1, so that allele frequencies are close to deterministic mutation-selection balance], and holding u (the per-locus mutation rate), h and sm/sf constant across loci, the slope of the regression of the “average effect” on the deleterious allele frequency will be:
| (3) |
for autosomal loci in females, and
| (4) |
for X-linked loci in females. Expressions for males are and . Regressions for autosomal loci are steeper for the sex that is subject to stronger purifying selection; regressions for X-linked loci tend to be steeper for males than females owing to hemizygosity of the former (lines in Figure 1B). Regressions are steeper for X-linked than autosomal loci when h < 1, owing to enhanced purifying selection on the X (Figure 1B). These predictions are robust to the effects of genetic drift (Figure 1B; filled circles).
Allele frequency distributions of deleterious alleles
Given the selection parameters from Table 1, the stationary allele frequency distribution for deleterious autosomal alleles is given by:
| (5) |
where , , NeA is the effective population size for autosomal loci (accounting for diploidy, such that NeA=2Ne) and C is a normalizing constant that ensures that the density function integrates to one. Equation (5) can be used for the stationary distribution of X-linked loci by replacing and with and , where NeX is the effective population size of X-linked loci. Where selection is much stronger than genetic drift [i.e., NeAhi(sf, i + sm, i), NeXhi(sf, i + sm, i) ≫ 1], the expected frequencies of an autosomal and X-linked deleterious allele correspond to the deterministic mutation-selection balance equilibria: and at autosomal and X-linked loci, respectively (e.g., Connallon 2010).
Among sites substantially affected by genetic drift, levels of diversity depend on the strength of purifying selection relative to drift (i.e., the “efficacy of selection”), which is captured by the terms and . Purifying selection is equally effective between the X and autosomes () with co-dominance and when , whereas combinations of and partial recessivity of deleterious alleles (h < ½) enhance purifying selection on the X (see Supplementary Figure S2). These predictions are manifest in simulated nonsynonymous vs synonymous polymorphism data (Figure 1C).
Materials and methods
Existing genomic and fitness data from LHM hemiclones
Our study used genomic and fitness data from Gilks et al. (2016) and Ruzicka et al. (2019), respectively. Both studies employed the hemiclonal design, in which the unit of observation is a haploid chromosome set (a complement of chromosomes X, 2, and 3, representing ∼99% of the D. melanogaster genome; the Y chromosome, fourth “dot” chromosome and mtDNA are allowed to vary among members of a given line). For phenotypic measurements, hemiclonal genomes are expressed alongside random sets of homologous chromosomes sampled from the base population to generate replicate “focal” females and males that express the same hemiclonal chromosome set in variable outbred genotypes (Abbott and Morrow 2011).
In Gilks et al. (2016), hemiclonal genomes were sampled from the LHM stock population using the crossing scheme depicted in Supplementary Figure S1. Briefly, each hemiclone line is initially derived from a single wild-type male, which is propagated by repeated crosses to “clone-generator” females. Hemiclone males can always be identified in crosses because clone-generator females carry fused autosomes and X chromosomes that are phenotypically marked; furthermore, the X-2-3 complement males carry is preserved intact owing to the absence of recombination in males. Focal individuals of a given line are obtained by crossing hemiclone males to a random set of wild-type females (generating focal hemiclone females), or to a random set of females carrying a fused X chromosome (generating focal hemiclone males).
In Ruzicka et al. (2019), sex-specific adult reproductive fitness was measured among 223 hemiclonal D. melanogaster genotypes from the LHM population [see Rice et al. (2005) for more details on the LHM population]. Briefly, female and male fitness assays were performed so as to closely mimic the strictly controlled rearing regime of the LHM population, which had been laboratory-adapted for ∼20 years (∼500 generations) at the time assays were undertaken. Female fitness was measured as competitive fecundity (number of eggs laid) and male fitness as competitive fertilization success (proportion of progeny sired), in competition with a stock homozygous for the recessive eye-color mutation brown (bw) (the bw stock is a good competitor and has been used in similar D. melanogaster studies; e.g.Mallet and Chippindale 2011; Mallet et al. 2011; Sharp and Agrawal 2013). For each hemiclone line and sex, reproductive fitness was measured in a blocked design, among 25 replicate focal individuals across all blocks. In each sex, fitness measurements were normalized, scaled, and centered within blocks, and averaged across blocks prior to subsequent analysis.
Gilks et al. (2016) generated whole-genome sequences for each hemiclonal line, while Ruzicka et al. (2019) called SNPs. Briefly, for each genotype, DNA was extracted from a female heterozygous for the hemiclonal genome and a complement derived from the sequenced reference stock. SNPs were called using the BWA-Picard-GATK pipeline and mapped to the D. melanogaster genome assembly (release 6). Indels, nondiallelic sites, sites with depth <10 and genotype quality <30, individuals with high missing rates (>15%) and an individual outlier from a PCA analysis were removed. Among the remaining hemiclonal genomes (n = 202), sites with missing rates <5% and MAF >0.05 were retained, yielding a final set of 765,764 stringently quality-filtered SNPs.
Genome-wide association studies
We performed a GWAS separately in each sex using a linear mixed model, such that:
where is a vector of sex-specific fitness values, the “average effect” of an allele on fitness (sensu Fisher; see Visscher and Goddard 2019), a vector of genotypic values (i.e., either 0 or 1 in the hemiclonal design), the heritable component of random phenotypic variation, the nonheritable component of random phenotypic variation, with:
where is the additive genetic variance, the kinship matrix derived from genome-wide SNPs, the residual variance and an individual identity matrix. This GWAS approach has been shown to appropriately control false positives and increase power to detect true associations in samples with moderate degrees of population structure and close relatedness (Astle and Balding 2009; Price et al. 2010), such as LHM (Ruzicka et al. 2019).
Female and male GWAS were implemented in LDAK (Speed et al. 2012), which corrects for linkage between neighboring SNPs when estimating kinships to avoid pseudo-replication among clusters of linked sites, and further allows SNPs to be weighted by their MAF when estimating kinships by specifying a scaling parameter (), as . We used a value of −0.25, which has been shown to provide a good fit to a range of quantitative trait data (Speed et al. 2017), though results from analyses using alternative values are also presented in the Supplementary Material (note that Speed et al. 2017 referred to this parameter as ; we use to distinguish it from the average effect parameter ). We applied a Wald test to generate P-values for each SNP, and corrected for multiple testing using Benjamini-Hochberg false discovery rates (Benjamini and Hochberg 1995), thereby converting P-values into FDR q-values. For each GWAS, we also estimated the genomic inflation factor (; calculated as median observed over median expected ) to quantify the extent of P-value inflation, where a value close to 1 indicates that relatedness and population structure have been well controlled.
We also performed gene-based association tests. Gene coordinates were obtained from the UCSC genome browser and extended by 5 kb up- and downstream to include potential regulatory regions. LDAK’s gene-based test estimates variance components for each gene by fitting a linear mixed model, such that:
with variables defined as previously and K corresponding to kinship matrix derived from SNPs in each gene. To correct for genome-wide relatedness and population structure, the top 20 principal components derived from genome-wide kinships were also included as covariates. Variance components were estimated using restricted maximum likelihood (REML), with SNP heritability calculated as , a likelihood ratio test performed to generate a gene-based P-value, and FDR correction applied as above.
Chromosomal distribution, biological functions, and polygenicity of fitness-associated loci
We designated a set of “candidate” loci associated with sex-specific fitness as loci with FDR q-values < 0.3. We further estimated the number of independently associated candidate SNPs through LD clumping in PLINK (Purcell et al. 2007). LD clumping takes the candidate SNP with the lowest association q-values as a “lead” SNP, clusters neighboring SNPs (i.e., those within a specified distance and LD threshold of the lead SNP), repeats this procedure for the SNP with the next-lowest q-values, and so on, eventually forming clusters of candidate SNPs that are approximately independent of one another. We specified a distance threshold of 10 kb and an LD (r2) threshold of 0.4, reflecting typical LD decay in LHM (Ruzicka et al. 2019).
We assessed the functional effects of candidate SNP clusters using annotations based on the Variant Effect Predictor, and used tests to compare the observed number of candidate SNP clusters in a given functional category to the expected number among 35,726 LD-pruned SNPs (generated through LD clumping as above but choosing a random SNP as lead SNP). We also investigated the functional properties of candidate genes by performing a Gene Ontology analysis in PANTHER (Protein Analysis Through Evolutionary Relationships) v.13.1 (Mi et al. 2017), using the statistical overrepresentation test.
We tested whether the genetic basis of sex-specific fitness was polygenic. High trait polygenicity implies a diffuse scattering of causal loci with small (and difficult to identify with statistical confidence) effects across the genome, generating a positive relationship between the length of a genomic segment and its SNP heritability, since longer regions are expected to contain more causal SNPs (Yang et al. 2010). Because D. melanogaster harbors only five major chromosome arms of approximately equal length, we quantified polygenicity at the level of random genome partitions. Specifically, we divided each chromosome arm into 500 partitions (i.e., 2,500 partitions across the five major arms) by randomly drawing 499 SNPs to represent “breakpoints” along a given arm. SNP heritability for a partition was then estimated using LDAK’s gene-based association analysis but with partitions as the unit of interest. We then quantified the relationship between the number of SNPs in a given partition and that partition’s SNP heritability using a Spearman’s rank correlation, with 95% confidence intervals obtained by randomly sampling 2,500 new partitions (1,000 times, without replacement) and re-estimating the correlation coefficient on each set of random partitions. To complement partition-based analyses, we also performed analyses at the level of genes.
Metrics associated with deleterious variation
estimates
To obtain SNP-based estimates of for each sex and chromosome compartment, we used LDAK to fit a linear mixed model, as:
with variables as previously defined, K corresponding to kinship matrix derived from SNPs in each chromosome compartment, and using REML to estimate variance components. We adjusted estimates and their standard errors upwards by a factor of two (in both sexes for autosomes; in females for the X) to account for the twofold reduction in induced by the hemiclonal design (Abbott and Morrow 2011).
To statistically compare between the sexes we used female and male estimates and their standard errors as inputs for Welch t-tests. To statistically compare among chromosome compartments relative to expectations based on proportional genome content, we used a permutation-based approach, in which SNPs were shifted to a random starting point along a “circular genome,” thus breaking the relationship between each SNP and its associated compartment while preserving the relative size of each compartment, the ordering of SNPs along the genome and their LD structure (Cabrera et al. 2012). For each of 1,000 permutations, we estimated for each “permuted X chromosome” and “permuted autosome,” thereby generating a null distribution of for each compartment. An empirical P-value was then obtained by comparing 1,000 permuted estimates of the fraction of total that is X-linked to the observed fraction of total that is X-linked.
Regressions of average allelic effect on allele frequency
GWAS provide estimates of the average effect of each allele on sex-specific fitness, as defined in the Theoretical background (i.e.: and , above, can be estimated as the regression of hemi-clone line fitness for a given sex on the allele count per line, which is zero or one). Purifying selection generates a negative regression slope (i.e., negative ) between and minor allele frequency, with a steeper slope expected in the sex where selection is stronger, or the chromosomal compartment where selection is more effective (see Theoretical background; Figure 1B). While sampling error alone can generate a negative (e.g., because estimates have higher sampling variances among rare SNPs), this artefact should affect each sex equally given that sample sizes are identical between sexes. Furthermore, we take this effect into consideration by using a permutation-based approach to obtain P-values (see below).
To compare estimates between sexes, we used the aforementioned set of 35,726 LD-independent SNPs. Then, for each chromosome compartment in turn, we modeled an allele’s absolute average effect on fitness ( as a function of MAF, sex, and the sex-by-MAF interaction, fitting a generalized linear model (GLM) with Gamma (log link) error structure. This modeling choice was justified by the positive and right-skewed distribution of and visual inspection of residuals from the fitted model. We then obtained P-values for each model term by running a GWAS on 1,000 permutations of male and female phenotypic values, and fitting the aforementioned GLM on permuted data, thereby obtaining a regression coefficient for each model term on each permutation run. The empirical P-value for the sex-by-MAF interaction term was obtained by comparing the observed coefficient to the null distribution of coefficients estimated in permuted data.
To compare between chromosome compartments, we repeated the procedure implemented for between-sex comparisons, with the following modifications: (i) the independent variables were MAF, chromosomal compartment, and the MAF-by-compartment interaction; (ii) a null distribution of model coefficients was generated through 1,000 circular permutations of genotypic values (as described in “ estimates”).
Comparisons of nonsynonymous and synonymous polymorphism
Purifying selection reduces the frequencies of deleterious nonsynonymous alleles relative to synonymous alleles, leading to fewer segregating nonsynonymous polymorphisms, as a fraction of all coding polymorphisms, in the chromosomal compartment under more effective purifying selection (see Theoretical background; Figure 1C). To compare nonsynonymous and synonymous polymorphism on the autosomes and X, we excluded all noncoding polymorphisms from our data and LD-pruned the remaining loci (as described previously), yielding a set of 15,232 LD-independent coding loci. We then modeled the binary status of these loci (nonsynonymous or synonymous) as a function of chromosome compartment and MAF, using a logistic regression (binomial GLM) to generate regression coefficients and P-values.
Quantitative inferences of evolutionary parameters
Autosomal and X-linked patterns of and polymorphism allow us to make indirect inferences into the genetic properties (e.g., dominance) and demographic parameters (i.e., NeX, NeA) of autosomal and X-linked genetic variants. However, such inferences are qualitative rather than quantitative.
To make quantitative inferences, we took two approaches. First, we used estimates of the fraction of that is X-linked in each sex to estimate the average dominance coefficient of deleterious variants. Specifically, under a model of genetic variation maintained at mutation-selection balance, where dominance (h) is constant across loci, the ratio of the strength of purifying selection in each sex (sm/sf) is constant across loci, and the per-locus mutation-rate and sex-specific selection coefficients have the same distribution across X-linked and autosomal loci, we can approximate h using female data as:
where is the fraction of the genome that is X-linked and FX is the fraction of total female that is X-linked. We can approximate h using male data as:
where MX is the fraction of total male that is X-linked. We assumed that =0.2, sm/sf=1, and we sampled autosomal and X-linked from a normal distribution with means and standard deviations as estimated in our data, thereby constructing confidence intervals for FX and MX—and, ultimately, h—that take into account sampling error. We chose sm/sf=1 because of limited evidence for sex differences in purifying selection in this population, though we present h estimates for sm/sf=2 and sm/sf=0.5 in the Supplementary Materials, along with full derivations for the above expression for h (Supplementary Text 1).
Second, we performed random draws of allele frequencies at nonsynonymous and synonymous sites using X-linked and autosomal stationary distributions (see Theoretical background). We then used Approximate Bayesian Computation (ABC) to obtain posterior distributions of dominance (h), NeX/NeA and other parameters (see below) that were consistent with our empirical polymorphism data. For each simulation run, we implemented the following algorithm:
107 autosomal “synonymous” loci and 2.5 × 107 autosomal “nonsynonymous” loci were generated, reflecting the approximate 1:2.5 ratio of synonymous: nonsynonymous mutational opportunities in D. melanogaster (Huber et al. 2017; Kim et al. 2017). A smaller set of X-linked loci (0.177 × 107 synonymous; 0.4425 × 107 nonsynonymous) was also generated, reflecting the 1:0.177 ratio of autosomal: X-linked synonymous polymorphisms in our data.
Allele frequencies at autosomal and X-linked nonsynonymous sites were generated by randomly drawing from the stationary distribution for each locus, given its mutation rate ), dominance coefficient (h), effective population size (NeA for autosomal loci, NeX for X-linked loci) and sex-specific selection coefficients (sm and sf) (sm and sf were allowed to vary among loci; the remaining parameters were fixed across loci for each simulation run; see below for details of the prior distributions for each parameter). Because there is no built-in random number generator for a stationary distribution for nonneutral sites, sampling allele frequencies from stationary distributions was achieved using the rejection-sampling algorithm from Smith and Connallon (2017), based on the stationary distribution in Equation (5) and subsequent text, which assumes symmetric forward and backward mutation rates, per locus.
Allele frequencies at synonymous autosomal and X-linked sites were generated by sampling from a beta distribution with parameters = 2NeA and = 2NeA (for autosomal sites) and = 2NeX, = 2NeX (for X-linked sites), as appropriate for neutral sites at mutation-drift equilibrium, where is the mutation rate per site and effects of ploidy are subsumed into NeA and NeX (i.e., NeA=2Ne).
Sample allele frequencies were obtained by binomial sampling from population allele frequencies obtained in Steps 2 and 3, with sample sizes matching the number of sequences in this dataset (n = 202), and further excluding sites with MAF < 0.05 to match the filtering of our data.
From the simulated site frequency spectra, we fitted a binomial GLM of segregating site status (nonsynonymous or synonymous) as a function of compartment, MAF and their interaction, obtaining regression coefficients for each.
Finally, the regression coefficients obtained in Step 5 were compared to the equivalent coefficients in the observed data. We accepted simulation parameter sets if all three simulated coefficients lay within a distance ±ε of the observed summary statistic, with ε defined as the 95% confidence interval of the regression coefficient in the observed data.
Priors for input parameters were as follows: NeA = uniform [102,104] (because NeA = 2 Ne in our models, our priors for NeA are consistent with the history of the population, which has been maintained at an adult census population size of 2 N = 3584 autosomal chromosomes; Rice et al. 2005); NeX = NeA uniform [0.5,1] (i.e., NeX may be roughly equal to or half of NeA, as predicted by theory and as observed in natural populations of D. melanogaster; see Pool and Nielsen 2007; Langley et al. 2012; Mackay et al. 2012); h = uniform [0,1] (estimates of h in D. melanogaster are typically partially recessive but associated with large uncertainties; see Simmons and Crow 1977; Mallet et al. 2011); = 10−8 (based on Haag-Liautard et al. 2007). For a given simulation, we allowed selection coefficients to vary among loci. Specifically, we drew sm and sf from a symmetric bivariate Gamma, with shape parameter k drawn from a uniform [0.25,0.4] [consistent with allele frequency-based estimates of the distribution of fitness effects (DFEs) in Drosophila; see Loewe et al. 2006; Keightley and Eyre-Walker 2007; Haddrill et al. 2010; Huber et al. 2017], mean parameter drawn from a uniform [10−5,3.5 × 10−3] (the approximate range of values estimated in Loewe et al. 2006; Haddrill et al. 2010; Kousathanas and Keightley 2013; Huber et al. 2017) and r (the correlation coefficient between sm and sf) drawn from a uniform [0,1] (estimates of r for new mutations are typically positive but vary widely in Drosophila; see Mallet et al. 2011; Sharp and Agrawal 2013; Allen et al. 2017).
Statistical software
All statistical analyses were performed in RStudio (RStudio Team 2015).
Results
A polygenic basis of female and male fitness
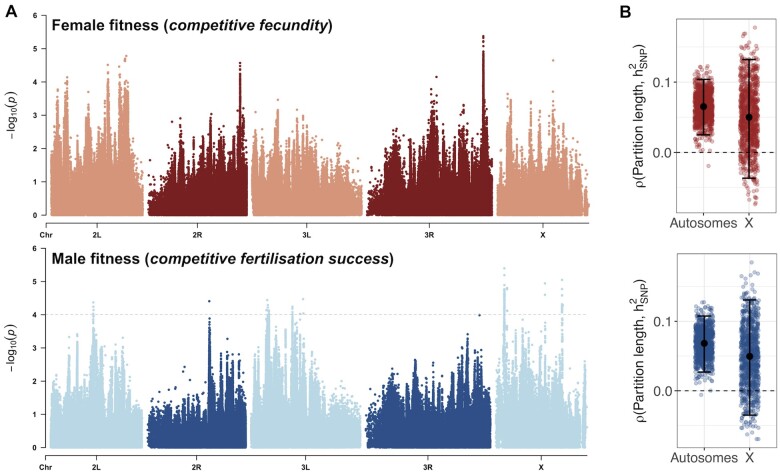
Figure 2A presents P-values from a GWAS of female and male fitness, respectively. The genomic inflation factors were close to 1 in both sexes (female = 1.073; male = 1.005), indicating that the mixed model appropriately controlled for relatedness and population structure in this sample (Supplementary Figure S3). For female fitness, the most significant individual SNP association P-value was 4.221 × 10−6 (the Bonferroni-corrected significance threshold was 6.529 × 10−8) and there were no SNPs with FDR q-values < 0.3 (the minimum q-value value was 0.364). In a gene-wise analysis, we found 70 genes with q-values < 0.3, representing candidate genes for the genetic basis of female fitness. For male fitness, the most significant individual SNP association P-value was 4.006 × 10−6 and there were 248 SNPs (31 LD-independent clusters) and 22 genes with q-values < 0.3, representing candidates SNPs and genes, respectively, for the genetic basis of male fitness. A full list of genes associated with female and male fitness can be found in Supplementary Table S1.
Figure 2.
A polygenic basis of sex-specific fitness. (A) –log10(p) values from a Wald association test of each SNP variant against female fitness (top) and male fitness (bottom), presented as Manhattan plots along the five major chromosome arms of the D. melanogaster genome. Grey dashed line denotes a 30% FDR threshold (q-values = 0.3) in males (no SNP reached the 30% FDR threshold in females, hence the absence of an equivalent line in females). (B) Spearman’s rank correlation coefficients between the length of a random chromosome partition and its SNP heritability, for females (red) and males (blue), on autosomes and X. Bars represent means and 95 confidence intervals across 1,000 partition sets.
After LD-pruning, candidate SNPs for male fitness were significantly enriched on the X chromosome ( = 28.809, observed = 15, expected = 4.745, odds ratio = 5.917, P < 0.001), as were candidate genes for male fitness ( = 54.520, observed = 16, expected = 3.238, odds ratio = 15.554, P < 0.001). This pattern of X-enrichment was not observed for female candidate genes (N = 70; =0.063, observed = 9, expected = 10.239, odds ratio = 0.861, P = 0.802). Functional annotations of candidate SNPs and genes (predicted variant effects and GO terms) showed no significant over- or under-represented of terms after FDR correction, although the low number of candidates only provides modest power to these tests. Anecdotally, the leading SNPs from each male candidate cluster were found in functional regions (3’UTR, N = 3; intronic, N = 17; nonsynonymous, N = 4) and none were intergenic.
The low number of individually significant candidate loci in both sexes, together with appreciable estimates of SNP-based additive genetic variance (see below), suggest that fitness is highly polygenic. If so, we expect to observe a positive relationship between the length of a chromosome region (e.g., a gene, or random chromosome partition) and its SNP heritability (Yang et al. 2010), whereas a mono- or oligo-genic architecture predicts no such relationship. In line with polygenicity, we found a significant positive correlation between the length of random autosomal chromosome partitions and SNP heritability in both sexes (N = 2,000 partitions; females—median (±95CI) = 0.066 [0.025–0.104], empirical P = 0.001; males—median (±95CI) = 0.068 [0.027–0.108], empirical P = 0.001), with a positive but nonsignificant correlation on the X (N = 500 partitions; females—median (±95CI) = 0.048 [−0.037 to 0.132], empirical P = 0.126; males—median (±95CI) = 0.051 [−0.035 to 0.131], empirical P = 0.135; Figure 2B). The relationship between gene length and SNP heritability provided similar results (Autosomes: females—= 0.101, P < 0.001; males—= 0.062, P < 0.001; X chromosome: females—= 0.068, P = 0.001, males – = 0.005, P = 0.807; Supplementary Figure S4). Overall, these analyses show that fitness is polygenic in both sexes.
Mixed evidence for sex differences in the strength of purifying selection
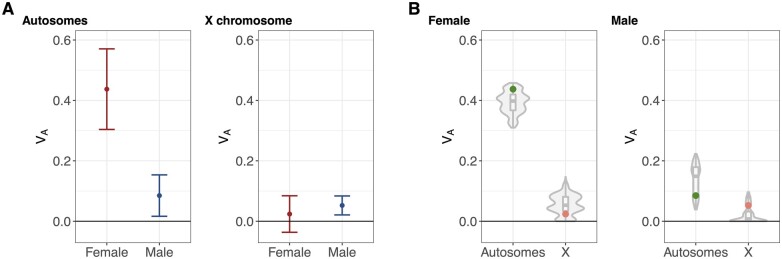
Multi-locus estimates of are informative about the relative strength of purifying selection in each sex, with the sex under stronger purifying selection expected to exhibit larger autosomal for fitness (because fitness effects are larger in that sex but allele frequencies are approximately equal between sexes; see Theoretical background; Figure 1A). We found that autosomal female = 0.437 ± 0.133 and autosomal male =0.085 ± 0.069 (Figure 3A;Supplementary Figure S5), corresponding to a statistically significant elevation in female on autosomes (Welch’s t = 2.349, P = 0.019), and suggesting that segregating variants tend to have larger fitness effects (and are therefore subject to stronger selection) in females.
Figure 3.
The effects of sex and sex-linkage on estimates of for fitness. (A) (±SE) for fitness in females (red) and males (blue), on autosomes and the X chromosome, respectively. (B) for fitness in observed data on autosomes (green dots) and the X chromosome (orange dots), along with 1,000 permuted estimates (gray boxplots and violin plots), in females and males, respectively.
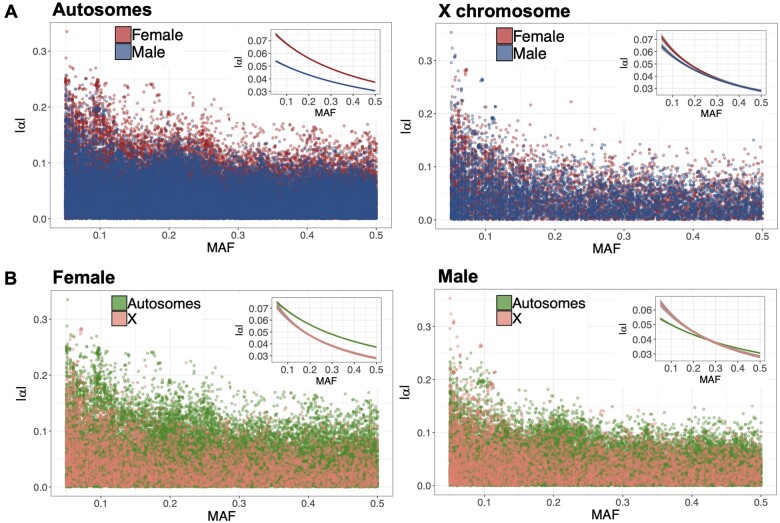
Purifying selection also reduces the frequencies of alleles with large effects on fitness relative to alleles with small fitness effects, leading to a negative correlation between the fitness effects of deleterious mutations and their population frequencies (e.g., Park et al. 2011; Zeng et al. 2018). The slope () of a linear regression of an allele’s average fitness effect () on its frequency is expected to be steeper in the sex under stronger purifying selection (see Theoretical background; Figure 1B). We found that estimates of did not differ significantly between the sexes (Gamma GLM, sex-by-MAF interaction; Autosomes—empirical P = 0.205; X chromosome—empirical P = 0.207; Figure 4A;Supplementary Figure S6), suggesting that—based on this metric—the sexes do not differ in the average strength of purifying selection.
Figure 4.
The effects of sex and sex-linkage on the regression of an allele’s average fitness effect on its frequency (). (A) Scatter plot of an allele’s absolute average effect on fitness () and its MAF for females and males, on autosomes (left) and the X chromosome (right), respectively. The insets present fitted lines from a Gamma GLM of as a function of MAF. (B) Scatter plot of and MAF for autosomes and X-linked loci, in females (left) and males (right), respectively. Inset as above.
Multiple signals of enhanced purifying selection on the X chromosome
and metrics also provide information about the expression of deleterious variation and the strength of purifying selection among chromosome compartments (i.e., X and autosomes). The heightened expression of recessive or partially dominant X-linked alleles in hemizygous males is expected to elevate X-linked in males relative to females and generate stronger net purifying selection against X-linked deleterious alleles (see Theoretical Background; Figure 1A). We found that SNP-based estimates of X-linked were roughly twofold greater in males than females, with female = 0.024 ± 0.060 and male = 0.052 ± 0.031 (Figure 3A), though the difference was not statistically significant (Welch’s t = –0.418, P = 0.676). The same theory also predicts that autosomal polymorphisms contribute disproportionately to total in females, while X-linked polymorphisms contribute disproportionately to total in males (Figure 1A). We therefore performed a quantitative test by comparing X-linked and autosomal estimates to 1000 permuted estimates (random shifts of SNPs along a circularized genome; see Materials and Methods), which reflect the number of segregating sites in each compartment (∼15% of sites are X-linked). Though the deviations were not statistically significant (Females—empirical P = 0.175; males—empirical P = 0.174), point estimates showed that the X accounted for 5.170% of total female and 38.128% of total male (Figure 3B;Supplementary Figure S5), which is consistent with partially recessive fitness effects of deleterious variants (see also Figure 6A).
Figure 6.
Quantitative and population genetic inferences of dominance and NeX/NeA. (A) Boxplots of h estimates, based on quantitative genetic data (i.e., the fraction of total VA that is X-linked in females, left; the fraction of total VA that is X-linked in males, middle) and population genetic data (simulated data fitted to logistic regression coefficients of nonsynonymous/synonymous status on MAF and chromosome compartment; right). For visualization purposes, estimates of h greater than one and smaller than zero are not presented. (B) Diagonal shows posterior distributions of dominance and NeX/NeA (N = 1,000 accepted simulations). Off-diagonal presents a scatter plot of both parameters, with contours and linear regression line for visual emphasis.
We also compared estimates of between chromosomal compartments. Consistent with higher efficacy of selection on the X (see Theoretical background; Figure 1B), we detected a significantly steeper on the X chromosome than autosomes in females (Gamma GLM, compartment-by-MAF interaction, empirical P = 0.048; Figure 4B;Supplementary Figure S6). Estimates of were also steeper on the X than autosomes in males, though the interaction term was not statistically significant (Gamma GLM, compartment-by-MAF interaction, empirical P = 0.140; Figure 4B;Supplementary Figure S6). Overall, statistical contrasts of fitness variation between chromosome compartments do not reveal pronounced differences, but in each case, the direction of the effect is consistent with more effective purifying selection on the X (Figures 3B and 4B).
We can gain further information on the relative efficacy of purifying selection among chromosome compartments by comparing levels of synonymous and nonsynonymous polymorphism. Here, more effective X-linked purifying selection is predicted to reduce nonsynonymous relative to synonymous polymorphism on the X (see Theoretical Background; Figure 1C). We found that a lower proportion of common alleles were nonsynonymous rather than synonymous (Binomial GLM with probability of nonsynonymous as response; MAF effect: odds ratio ± SE = 0.471 ± 0.061, P < 0.001; Figure 5), consistent with pervasive purifying selection against amino-acid changing mutations. Furthermore, we detected proportionally fewer nonsynonymous polymorphisms on the X chromosome than autosomes (X-chromosome effect: odds ratio ± SE = 0.801 ± 0.041, P < 0.001; Figure 5), providing strong statistical support for more effective purifying selection against deleterious nonsynonymous variants on the X.
Figure 5.
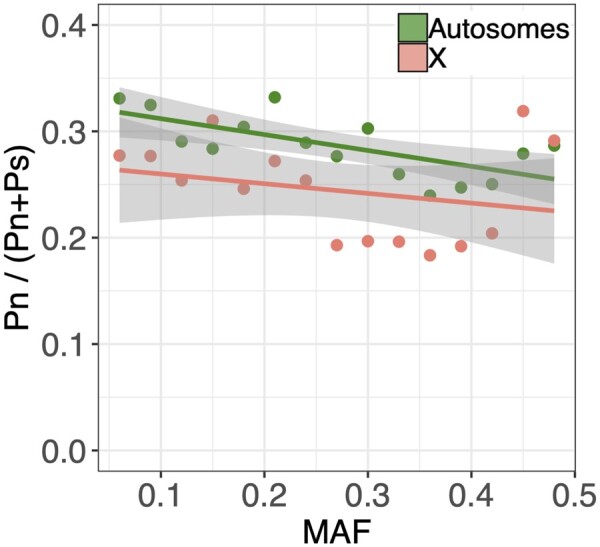
The effect of sex-linkage on synonymous and nonsynonymous polymorphism. Proportion of nonsynonymous sites among autosomal and X-linked LD-pruned protein-coding loci, for each of 15 MAF bins (MAF bin width = 0.03; points are at MAF bin mid-point), with linear regression lines (±95% CIs) presented for visual emphasis. Regression coefficients from this analysis were used to make inferences about dominance and NeX/NeA (i.e., Figure 6B).
Quantitative inferences of dominance and NeX/NeA
The patterns observed in quantitative and population genetic metrics together suggest that purifying selection operates more efficiently at X-linked than autosomal loci, which implies that deleterious mutations tend to be partially recessive (h < ½) (see Theoretical background and Supplementary Figure S2). To make quantitative inferences about dominance, we first fit mutation-selection balance models for to our estimates of autosomal and X-linked in each sex, thereby estimating h (while accounting for error in estimating genetic variances; see Materials and Methods). Second, we used ABC to infer distributions of h and NeX/NeA that are consistent with population genetic data (i.e., common coding polymorphisms in the set of 202 experimental lines; see Materials and Methods).
We estimated h (median ± 95% CI) to be 0.070 (−1.010 to 2.542) using estimates of the proportion of X-linked in females, and h (median ± 95% CI) to be 0.364 (0-Inf.) using estimates of the proportion of X-linked in males. The point estimates suggest that partially recessive effects of deleterious variants fit our data well (Figure 6A;Supplementary Figure S7), though confidence intervals are large because of estimation error. Using the ABC approach, we also found dominance estimates which were skewed toward partially recessive effects (h[±95% credible interval] = 0.314 [0.012–0.915]) and NeX/NeA estimates skewed toward values greater than three-quarters (NeX/NeA = 0.805[0.529–0.990]). Posterior distributions for both parameters differed markedly from their uniform prior distributions (Figure 6B), and posterior estimates for both parameters were positively correlated (Spearman’s = 0.067, P = 0.033), implying that relatively small NeX/NeA ratios and recessive fitness effects—or relatively large NeX/NeA ratios and dominant fitness effects—of nonsynonymous mutations provide a good fit to our data (Figure 6B). In line with the observed excess of nonsynonymous polymorphisms among low-frequency sites (Figure 5), and consistent with LHM’s small Ne, we estimated that new nonsynonymous mutations are on average subject to weak purifying selection in this population (Autosomes: median Ne = 2.238 [0.347–7.719]; X chromosome: Ne = 1.697 [0.290–6.161]). The posterior distributions for all model parameters are presented in Supplementary Figure S8 and Supplementary Table S2.
Discussion
Our analyses of genome-wide variation in D. melanogaster combine two traditions (Charlesworth 2015): quantitative genetic analyses of phenotypic variation, in particular fitness variation, and molecular population genomic analyses of selection. Studies combining fitness measurements and genomic data are rare (Chenoweth et al. 2015; Chen et al. 2019; Dugand et al. 2019; Ruzicka et al. 2019) and allowed us to circumvent several limitations of previous research. First, our study focused on measurements of outbred reproductive fitness in a laboratory-adapted population (Ruzicka et al. 2019). These measurements should represent near-ideal proxies for fitness and are much more relevant to theories about deleterious variation than measurements of quantitative trait variation for components of fitness (e.g., juvenile survival), or traits potentially covarying with fitness. Second, we estimated fitness among replicate individuals in a much larger array of genotypes than is typical for quantitative genetic studies of fitness, thereby increasing precision of our estimates. Third, whole-genome sequencing enabled us to quantify aspects of the genetic basis of fitness variation. We could therefore test and confirm that fitness is highly polygenic, and partition fitness variation between chromosomal contexts. Fourth, we estimated fitness variation in both sexes, allowing us to examine sexual dimorphism in deleterious fitness effects. Finally, our quantitative genetic estimates are SNP-based and therefore directly linked to sequence variability, which renders the connections between quantitative and population genetic variability far more explicit than possible for most studies.
Stronger X-linked purifying selection, but no clear evidence for sex differences in the strength of selection
Hemizygosity causes incompletely dominant X-linked alleles to exhibit heightened expression in males relative to females (Figure 1A). For example, several morphological and life-history traits in D. melanogaster (Cowley et al. 1986; Cowley and Atchley 1988; Griffin et al. 2016) and humans (Sidorenko et al. 2019) exhibit larger X-linked genetic variances in males, and phenotypic variances for body size are typically higher in the heterogametic sex (Reinhold and Engqvist 2013), consistent with the predicted effects of hemizygosity on genetic variances. We found that estimates of based on X-linked SNPs were roughly double in males compared to females, and X-linked SNPs contributed more to male than expected based on the proportion of the D. melanogaster genome that is X-linked, though not significantly so. Furthermore, we found that candidate loci for male fitness (SNPs and genes) were over-represented on the X, whereas this was not the case for candidate loci for female fitness. The outsized contribution of the X chromosome to male implies that selection is more effective on the X (Avery 1984; see Theoretical background). In line with this, we found a deficit of segregating nonsynonymous polymorphisms on the X relative to autosomes (Figure 5), as found previously in humans (Li et al. 2010; Veeramah et al. 2014). Furthermore, X-linked estimates in females were less than the fraction of X-linked polymorphism, consistent with more effective purifying selection on the X.
By contrast, our analyses did not suggest that selection is systematically stronger in one sex than the other. While SNP-based estimates of revealed larger autosomal in females than males, consistent with elevated female heritability in previous studies of this population (Chippindale et al. 2001; Gibson et al. 2002; Long et al. 2009; Innocenti and Morrow 2010; Collet et al. 2016) and potentially suggesting stronger selection in females, regressions of average effects on allele frequencies revealed no sex differences. There are additional reasons to doubt the hypothesis that females are, in general, under stronger selection. First, we focus on common polymorphisms (MAF > 0.05) and therefore fail to capture the rare deleterious variants with large effects on male fitness that are more easily picked up by other experimental designs (e.g., mutation-accumulation experiments), potentially reducing our estimate of male relative to females. Second, some research shows little evidence of male- or female-biased fitness effects of new deleterious mutations (Grieshop et al. 2016; Prokop et al. 2017), while other studies show male-biased effects (Mallet and Chippindale 2011; Mallet et al. 2011; Sharp and Agrawal 2013). Finally, it is likely that our fitness assays do not capture the totality of fitness variation in each sex, despite all attempts to mimic the laboratory rearing environment (Ruzicka et al. 2019). For example, our assays, like others (e.g., Sharp and Agrawal 2013), employ a bw competitor whose ability to compete for matings (in male fitness assays) may differ from its ability to compete for food resources (in female fitness assays), thus contributing to elevated autosomal fitness variances in females.
Combining sequence and fitness data to study the genetic basis of fitness variation: new insights, limitations, and future directions
Unlike previous studies (but see Chen et al. 2019; Dugand et al. 2019), including of the LHM population, our study can shed light on the specific genetic loci affecting fitness variation in each sex. GWAS revealed that no common large-effect loci affect fitness in either sex, despite appreciable multi-locus variances in both sexes. We also detected a positive genome-wide correlation between the length of chromosome regions (i.e., random partitions, or genes) and the fitness variance a region explains. Both patterns are indicative of polygenicity (Yang et al. 2010). Combining genomic and fitness data also allowed us to quantify regressions of allelic effect on allele frequency—an indicator of the strength of purifying selection that has not yet been applied to between-sex comparisons. The metric corroborated inferences from and nonsynonymous/synonymous comparisons: specifically, the X chromosome exhibited steeper than autosomes (in females, with a similar but nonsignificant pattern in males), while did not differ between sexes—both patterns are consistent with stronger purifying selection on the X chromosome but no sex differences in the strength of purifying selection, as we have argued above.
Because quantitative and population genetic data often provide conflicting estimates of evolutionary parameters (Charlesworth 2015), we were interested in fitting both types of metric to models, and thereby quantifying the drivers of more effective purifying selection on the X chromosome. Whether using simulations of nonsynonymous/synonymous polymorphism or fitting mutation-selection balance models to the proportion of that is X-linked in each sex, we inferred that deleterious mutations are partially recessive, though with 95% confidence/credible intervals overlapping 0.5. These results corroborate previous estimates of dominance for new mildly deleterious mutations in D. melanogaster (∼0.1–0.3, Simmons and Crow 1977; Eanes et al. 1985; Mallet and Chippindale 2011) and budding yeast (Agrawal and Whitlock 2011), which were obtained using entirely different methods (mutation-accumulation experiments and gene knock-outs, respectively).
It is important to note that our models rely on some simplifying assumptions. For example, we follow previous research in assuming that fitness variation arises predominantly from unconditionally deleterious variation under strong purifying selection (reviewed in Charlesworth 2015). While aspects of our data support this inference—e.g., nonsynonymous sites are enriched among rare variants, as expected under purifying selection—this is unlikely to be completely accurate. For example, fitness variation is highly polygenic, implying many loci of small effect (Turelli and Barton 2004), and suggesting relatively weak purifying selection at single loci. Nevertheless, our models for ratios of and (i.e., Figure 1) appear to be robust to the effects of genetic drift, and our ABC simulations explicitly incorporate genetic drift. Another potential issue is that previous studies of LHM (Ruzicka et al. 2019) and other D. melanogaster populations (Bergland et al. 2014; Charlesworth 2015; Sharp and Agrawal 2018) indicate that some fraction of fitness variance consists of loci under antagonistic selection between environments, sexes or traits. Antagonistic loci can exhibit proportionally different amounts of X-linked and autosomal than unconditionally deleterious loci (e.g., some types of balanced sexually antagonistic variation predict more on the X; Patten and Haig 2009; Fry 2010; Mullon et al. 2012; Ruzicka and Connallon 2020), and may therefore cause deviations from the models outlined here.
Our ABC simulations also rely on some simplifying assumptions. For example, we assumed a stationary population at demographic equilibrium, yet LHM underwent a bottleneck of 400 individuals when it was brought into the laboratory (Rice et al. 2005) and allele frequencies take on the order of 2–4 Ne generations (i.e., ∼2800–5600 generations for LHM and much more than the ∼500 generations of laboratory maintenance) to recover to mutation-selection-drift equilibrium (Nei et al. 1975). Though we focus on interdigitated nonsynonymous and synonymous sites to minimize the effects of nonequilibrium demography, such effects cannot be ruled out completely (Supplementary Figure S9). We also made some simplifying assumptions about the DFE, including that it is best described by a gamma distribution (Eyre-Walker and Keightley 2007), that synonymous sites are neutral, and that it is identical between X and autosomes. Such assumptions, though common, may not hold entirely. For example, alternative distributions (e.g., lognormal or various mixture distributions; Loewe and Charlesworth 2006; Kousathanas and Keightley 2013; Kim et al. 2017) may fit the DFE better than a gamma, while some fraction of synonymous sites may be under weak purifying selection due to codon usage bias (Singh et al. 2008). Given that codon bias tends to be more pronounced on the X than autosomes (Singh et al. 2005), nonneutrality among a subset of synonymous sites will tend to downwardly bias our estimates of the nonsynonymous DFE (more so for the X), potentially requiring increased recessivity of deleterious nonsynonymous mutations to explain the deficit of nonsynonymous X-linked variants in our data. Finally, the D. melanogaster X chromosome harbors nonrandom sets of genes (Meisel et al. 2012), which may imply different DFEs for autosomal and X-linked sites (Perry et al. 2014; Fraïsse et al. 2019), though this eventuality remains, to our knowledge, untested.
Given current difficulties in estimating evolutionary parameters (Charlesworth 2015), such as average selection and dominance coefficients, how can future studies use genomic and fitness data to better estimate such parameters? First, it is clear that more precise estimates of deleterious mutational effects are needed. Our metrics of deleterious variation are associated with large uncertainties despite the relatively large sample of genomes in our study. One promising dataset is the UK Biobank, which contains genotype and fitness data for ∼500,000 human males and females and can potentially be used to partition variances between sexes and chromosome compartments, compare between sexes, and compare autosomal X-linked polymorphism, though such an analysis remains to be undertaken (but see Sidorenko et al. 2019). Analyzing a larger dataset such as the UK Biobank also permits rarer variants to be captured. Rare variants are likely to be enriched for deleterious effects and should thus be especially informative for parameter estimation. Second, current inferences about whether selection is stronger in one sex than the other come from a surprisingly narrow range of species—primarily Drosophila (Chippindale et al. 2001; Gibson et al. 2002; Morrow et al. 2008; Mallet and Chippindale 2011; Mallet et al. 2011; Sharp and Agrawal 2013, 2018; Collet et al. 2016; Grieshop et al. 2016; Allen et al. 2017; Prokop et al. 2017; Sultanova et al. 2018). While selection gradients from a broader range of species suggest that selection is often male-biased (Janicke et al. 2016; Singh and Punzalan 2018), these studies suffer from two important limitations: (i) inferences are based on phenotypic rather than genetic variances, which can bias inferences about the relative strength of purifying selection between sexes when environmental variances also differ between sexes (see Wyman and Rowe 2014); (ii) such analyses do not account for the differential contributions of sex chromosomes to phenotypic variances in each sex, which can be sexually dimorphic even when the strength of purifying selection does not differ between sexes (see Theoretical background). Analyses in non-Drosophila systems where both limitations can be addressed are crucial to properly assess the relative strength of purifying selection between the sexes. Finally, there is scope for developing methods which further integrate both sets of metrics to estimate parameters (e.g., estimating h by jointly using data on nonsynonymous/synonymous polymorphism, and in a single analysis). This is not as easy as it first appears: for example, while one can reasonably neglect balanced polymorphisms when modeling polymorphism data, a few balanced polymorphisms can contribute substantially to multi-locus genetic variances. Nevertheless, developing such methods would likely help reduce uncertainty in parameter estimates.
Data availability
Fitness and genomic data are available at https://doi.org/10.5281/zenodo.571168 and https://zenodo.org/record/159472, respectively. All code for reproducing analyses in the manuscript is available at the following github respository: filipluca/GWAS_sex_specific_fitness_and_the_X_chromosome.
Supplementary material is available at GENETICS online.
Supplementary Material
Acknowledgments
The authors thank Kevin Fowler, Göran Arnqvist, Mark Thomas, Isobel Booksmythe, Ted Morrow, the editors, and two anonymous reviewers for helpful comments on earlier versions of this manuscript, as well as the Monash Bioinformatics Platform for facilities and assistance in performing simulations. F.R. and M.R. conceived the project; F.R. conducted analyses, wrote and edited the manuscript, with input from M.R. and T.C.; T.C. developed mathematical models.
Funding
F.R. was funded by the London NERC Doctoral Training Partnership (Natural Environment Research Council grant NE/L002485/1NERC) and an Australian Research Council Discovery Project grant (FT170100328) to T.C. M.R. was funded by a BBSRC responsive mode grant (BB/R003882/1).
Conflicts of interest
The authors declare that there is no conflict of interest.
Literature cited
- Abbott JK, Morrow EH.. 2011. Obtaining snapshots of genetic variation using hemiclonal analysis. Trends Ecol Evol. 26:359–368. doi:10.1016/j.tree.2011.03.011. [DOI] [PubMed] [Google Scholar]
- Agrawal AF. 2001. Sexual selection and the maintenance of sexual reproduction. Nature. 411:692–695. doi:10.1038/35079590 [DOI] [PubMed] [Google Scholar]
- Agrawal AF, Whitlock MC.. 2011. Inferences about the distribution of dominance drawn from yeast gene knockout data. Genetics. 187:553–566. doi:10.1534/genetics.110.124560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen SL, Bonduriansky R, Chenoweth SF.. 2013. The genomic distribution of sex-biased genes in Drosophila serrata: X chromosome demasculinization, feminization, and hyperexpression in both sexes. Genome Biol Evol. 5:1986–1994. doi:10.1093/gbe/evt145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen SL, McGuigan K, Connallon T, Blows MW, Chenoweth SF.. 2017. Sexual selection on spontaneous mutations strengthens the between-sex genetic correlation for fitness. Evolution. 71:2398–2409. doi:10.1111/evo.13310. [DOI] [PubMed] [Google Scholar]
- Andersson MB. 1994. Sexual Selection. Princeton University Press, Princeton, NJ. [Google Scholar]
- Arnqvist G, Rowe L.. 2005. Sexual Conflict. Princeton University Press, Princeton, NJ. [Google Scholar]
- Astle W, Balding DJ.. 2009. Population structure and cryptic relatedness in genetic association studies. Stat Sci. 24:451–471. doi:10.1214/09-STS307 [Google Scholar]
- Avery PJ. 1984. The population genetics of haplo-diploids and X-linked genes. Genet Res. 44:321–341. doi:10.1017/S0016672300026550 [Google Scholar]
- Bateman 1948. Intra-sexual selection in Drosophila. Heredity (Edinb). 2:349–368. doi:10.1038/hdy.1948.21. [DOI] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y.. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J R Stat Soc. 57:289–300. doi:10.2307/2346101 [Google Scholar]
- Bergland AO, Behrman EL, O'Brien KR, Schmidt PS, Petrov DA.. 2014. Genomic evidence of rapid and stable adaptive oscillations over seasonal time scales in Drosophila. PLoS Genet. 10:e1004775.doi:10.1371/journal.pgen.1004775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brengdahl M, Kimber CM, Maguire-Baxter J, Friberg U.. 2018. Sex differences in life span: females homozygous for the X chromosome do not suffer the shorter life span predicted by the unguarded X hypothesis. Evolution. 72:568–577. doi:10.1111/evo.13434. [DOI] [PubMed] [Google Scholar]
- Cabrera CP, Navarro P, Huffman JE, Wright AF, Hayward C, et al. 2012. Uncovering networks from genome-wide association studies via circular genomic permutation. G3 (Bethesda). 2:1067–1075. doi:10.1534/g3.112.002618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth B. 2015. Causes of natural variation in fitness: evidence from studies of Drosophila populations. Proc Natl Acad Sci USA. 112:1662–1629. doi:10.1073/pnas.1423275112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N, Juric I, Cosgrove EJ, Bowman R, Fitzpatrick JW, et al. 2019. Allele frequency dynamics in a pedigreed natural population. Proc Natl Acad Sci USA. 116:2158–2164. doi:10.1073/pnas.1813852116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chenoweth SF, Appleton NC, Allen SL, Rundle HD.. 2015. Genomic evidence that sexual selection impedes adaptation to a novel environment. Curr Biol. 25:1860–1866. doi:10.1016/j.cub.2015.05.034. [DOI] [PubMed] [Google Scholar]
- Chippindale AK, Gibson JR, Rice WR.. 2001. Negative genetic correlation for adult fitness between sexes reveals ontogenetic conflict in Drosophila. Proc Natl Acad Sci USA. 98:1671–1675. doi:10.1073/pnas.98.4.1671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collet JM, Fuentes S, Hesketh J, Hill MS, Innocenti P, et al. 2016. Rapid evolution of the intersexual genetic correlation for fitness in Drosophila melanogaster. Evolution. 70:781–795. doi:10.1111/evo.12892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connallon T. 2010. Genic capture, sex linkage, and the heritability of fitness. Am Nat. 175:564–576. doi:10.1086/651590. [DOI] [PubMed] [Google Scholar]
- Connallon T, Clark AG.. 2011. Association between sex-biased gene expression and mutations with sex-specific phenotypic consequences in Drosophila. Genome Biol Evol. 3:151–155. doi:10.1093/gbe/evr004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley DE, Atchley WR, Rutledge JJ.. 1986. Quantitative genetics of Drosophila melanogaster. I. Sexual dimorphism in genetic parameters for wing traits. Genetics. 114:549–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowley DE, Atchley WR.. 1988. Quantitative genetics of Drosophila melanogaster. II. Heritabilities and genetic correlations between sexes for head and thorax traits. Genetics. 119:421–433. doi:10.1016/S0378-4290(98)00157-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darwin C. 1871. The Descent of Man. London: John Murray. [Google Scholar]
- Dugand RJ, Tomkins JL, Kennington WJ.. 2019. Molecular evidence supports a genic capture resolution of the lek paradox. Nat Commun. 10:1359.doi:10.1038/s41467-019-09371-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eanes WF, Hey J, Houle D.. 1985. Homozygous and hemizygous viability variation on the X chromosome of Drosophila melanogaster. Genetics. 111:831–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren H. 2009. The different levels of genetic diversity in sex chromosomes and autosomes. Trends Genet. 25:278–284. doi:10.1016/j.tig.2009.04.005. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker A, Keightley PD.. 2007. The distribution of fitness effects of new mutations. Nat Rev Genet. 8:610–618. doi:10.1038/nrg2146. [DOI] [PubMed] [Google Scholar]
- Fraïsse C, Sala GP, Vicoso B.. 2019. Pleiotropy modulates the efficacy of selection in Drosophila melanogaster. Mol Biol Evol. 36:500–515. doi:10.1093/molbev/msy246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fry JD. 2010. The genomic location of sexually antagonistic variation: some cautionary comments. Evolution. 64:1510–1516. doi:10.1111/j.1558-5646.2009.00898.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibson JR, Chippindale AK, Rice WR.. 2002. The X chromosome is a hot spot for sexually antagonistic fitness variation. Proc Biol Sci. 269:499–505. doi:10.1098/rspb.2001.1863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilks WP, Pennell TM, Flis I, Webster MT, Morrow EH.. 2016. Whole genome resequencing of a laboratory-adapted Drosophila melanogaster population sample. F1000Res. 5:e2644.doi:10.12688/f1000research.9912.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grieshop K, Stångberg J, Martinossi-Allibert I, Arnqvist G, Berger D.. 2016. Strong sexual selection in males against a mutation load that reduces offspring production in seed beetles. J Evol Biol. 29:1201–1210. doi:10.1111/jeb.12862. [DOI] [PubMed] [Google Scholar]
- Griffin RM, Schielzeth H, Friberg U.. 2016. Autosomal and X-linked additive genetic variation for lifespan and aging: comparisons within and between the sexes in Drosophila melanogaster. G3 (Bethesda). 6:3903–3911. doi:10.1534/g3.116.028308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag-Liautard C, Dorris M, Maside X, Macaskill S, Halligan DL, et al. 2007. Direct estimation of per nucleotide and genomic deleterious mutation rates in Drosophila. Nature. 445:82–85. doi:10.1038/nature05388. [DOI] [PubMed] [Google Scholar]
- Haddrill PR, Loewe L, Charlesworth B.. 2010. Estimating the parameters of selection on nonsynonymous mutations in Drosophila pseudoobscura and D. miranda. Genetics. 185:1381–1396. doi:10.1534/genetics.110.117614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber CD, Kim BY, Marsden CD, Lohmueller KE.. 2017. Determining the factors driving selective effects of new nonsynonymous mutations. Proc Natl Acad Sci USA. 114:4465–4470. doi:10.1073/pnas.1619508114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Innocenti P, Morrow EH.. 2010. The sexually antagonistic genes of Drosophila melanogaster. PLoS Biol. 8:e1000335.doi:10.1371/journal.pbio.1000335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James JW. 1973. Covariances between relatives due to sex-linked genes. Biometrics. 29:584–588. doi:10.2307/2529178 [PubMed] [Google Scholar]
- Janicke T, Häderer IK, Lajeunesse MJ, Anthes N.. 2016. Darwinian sex roles confirmed across the animal kingdom. Sci Adv. 2:e1500983.doi:10.1126/sciadv.1500983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Josephs EB, Lee YW, Stinchcombe JR, Wright SI.. 2015. Association mapping reveals the role of purifying selection in the maintenance of genomic variation in gene expression. Proc Natl Acad Sci USA. 112:15390–15395. doi:10.1073/pnas.1503027112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley PD, Eyre-Walker A.. 2007. Joint inference of the distribution of fitness effects of deleterious mutations and population demography based on nucleotide polymorphism frequencies. Genetics. 177:2251–2261. doi:10.1534/genetics.107.080663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim BY, Huber CD, Lohmueller KE.. 2017. Inference of the distribution of selection coefficients for new nonsynonymous mutations using large samples. Genetics. 206:345–361. doi:10.1534/genetics.116.197145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kousathanas A, Keightley PD.. 2013. A comparison of models to infer the distribution of fitness effects of new mutations. Genetics. 193:1197–1208. doi:10.1534/genetics.112.148023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langley CH, Stevens K, Cardeno C, Lee YCG, Schrider DR, et al. 2012. Genomic variation in natural populations of Drosophila melanogaster. Genetics. 192:533–598. doi:10.1534/genetics.112.142018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leffler EM, Bullaughey K, Matute DR, Meyer WK, Ségurel L, et al. 2012. Revisiting an old riddle: What determines genetic diversity levels within species? PLoS Biol. 10:e1001388. doi:10.1371/journal.pbio.1001388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Vinckenbosch N, Tian G, Huerta-Sanchez E, Jiang T, et al. 2010. Resequencing of 200 human exomes identifies an excess of low-frequency non-synonymous coding variants. Nat Genet. 42:969–972. doi:10.1038/ng.680. [DOI] [PubMed] [Google Scholar]
- Loewe L, Charlesworth B.. 2006. Inferring the distribution of mutational effects on fitness in Drosophila. Biol Lett. 2:426–430. doi:10.1098/rsbl.2006.0481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewe L, Charlesworth B, Bartolomé C, Nöel V.. 2006. Estimating selection on nonsynonymous mutations. Genetics. 172:1079–1092. doi:10.1534/genetics.105.047217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long TAF, Miller PM, Stewart AD, Rice WR.. 2009. Estimating the heritability of female lifetime fecundity in a locally adapted Drosophila melanogaster population. J Evol Biol. 22:637–643. doi:10.1111/j.1420-9101.2008.01676.x. [DOI] [PubMed] [Google Scholar]
- Mackay TFC, Richards S, Stone EA, Barbadilla A, Ayroles JF, et al. 2012. The Drosophila melanogaster genetic reference panel. Nature. 482:173–178. doi:10.1038/nature10811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maklakov AA, Lummaa V.. 2013. Evolution of sex differences in lifespan and aging: causes and constraints. Bioessays. 35:717–724. doi:10.1002/bies.201300021. [DOI] [PubMed] [Google Scholar]
- Mallet MA, Bouchard JM, Kimber CM, Chippindale AK.. 2011. Experimental mutation-accumulation on the X chromosome of Drosophila melanogaster reveals stronger selection on males than females. BMC Evol Biol. 11:156.doi:10.1186/1471-2148-11-156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallet MA, Chippindale AK.. 2011. Inbreeding reveals stronger net selection on Drosophila melanogaster males: Implications for mutation load and the fitness of sexual females. Heredity (Edinb). 106:994–1002. doi:10.1038/hdy.2010.148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manna F, Martin G, Lenormand T.. 2011. Fitness landscapes: an alternative theory for the dominance of mutation. Genetics. 189:923–937. doi:10.1534/genetics.111.132944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meisel RP, Malone JH, Clark AG.. 2012. Disentangling the relationship between sex-biased gene expression and X-linkage. Genome Res. 22:1255–1265. doi:10.1101/gr.132100.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mi H, Huang X, Muruganujan A, Tang H, Mills C, et al. 2017. PANTHER version 11: expanded annotation data from Gene Ontology and Reactome pathways, and data analysis tool enhancements. Nucleic Acids Res. 45:D183–D189. doi:10.1093/nar/gkw1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrow EH, Stewart AD, Rice WR.. 2008. Assessing the extent of genome-wide intralocus sexual conflict via experimentally enforced gender-limited selection. J Evol Biol. 21:1046–1054. doi:10.1111/j.1420-9101.2008.01542.x. [DOI] [PubMed] [Google Scholar]
- Mullon C, Pomiankowski A, Reuter M.. 2012. The effects of selection and genetic drift on the genomic distribution of sexually antagonistic alleles. Evolution. 66:3743–3753. doi:10.1111/j.1558-5646.2012.01728.x. [DOI] [PubMed] [Google Scholar]
- Nei M, Maruyama T, Chakraborty R.. 1975. The bottleneck effect and genetic variability in populations. Evolution. 29:1.doi:10.2307/2407137 [DOI] [PubMed] [Google Scholar]
- Park JH, Gail MH, Weinberg CR, Carroll RJ, Chung CC, et al. 2011. Distribution of allele frequencies and effect sizes and their interrelationships for common genetic susceptibility variants. Proc Natl Acad Sci USA. 108:18026–18031. doi:10.1073/pnas.1114759108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patten MM, Haig D.. 2009. Maintenance or loss of genetic variation under sexual and parental antagonism at a sex-linked locus. Evolution. 63:2888–2895. doi:10.1111/j.1558-5646.2009.00764.x. [DOI] [PubMed] [Google Scholar]
- Perry JC, Harrison PW, Mank JE.. 2014. The ontogeny and evolution of sex-biased gene expression in Drosophila melanogaster. Mol Biol Evol. 31:1206–1219. doi:10.1093/molbev/msu072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool JE, Nielsen R.. 2007. Population size changes reshape genomic patterns of diversity. Evolution. 61:3001–3006. doi:10.1111/j.1558-5646.2007.00238.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price AL, Zaitlen NA, Reich D, Patterson N.. 2010. New approaches to population stratification in genome-wide association studies. Nat Rev Genet. 11:459–463. doi:10.1038/nrg2813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prokop ZM, Prus MA, Gaczorek TS, Sychta K, Palka JK, et al. 2017. Do males pay for sex? Sex-specific selection coefficients suggest not. Evolution. 71:650–661. doi:10.1111/evo.13151. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, et al. 2007. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 81:559–575. doi:10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reinhold K, Engqvist L.. 2013. The variability is in the sex chromosomes. Evolution. 67:3662–3668. doi:10.1111/evo.12224. [DOI] [PubMed] [Google Scholar]
- Rice WR, Linder JE, Friberg U, Lew TA, Morrow EH, et al. 2005. Inter-locus antagonistic coevolution as an engine of speciation: assessment with hemiclonal analysis. Proc Natl Acad Sci USA. 102(Suppl. 1):6527–6534. doi:10.1073/pnas.0501889102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roze D, Otto SP.. 2012. Differential selection between the sexes and selection for sex. Evolution. 66:558–574. doi:10.1111/j.1558-5646.2011.01459.x. [DOI] [PubMed] [Google Scholar]
- RStudio Team. 2015. RStudio: Integrated Development for R. Boston, MA: RStudio. RStudio, Inc. [Google Scholar]
- Ruzicka F, Connallon T.. 2020. Is the X chromosome a hot spot for sexually antagonistic polymorphisms? Biases in current empirical tests of classical theory. Proc Biol Sci. 287:20201869.doi:10.1098/rspb.2020.1869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruzicka F, Hill MS, Pennell TM, Flis I, Ingleby FC, et al. 2019. Genome-wide sexually antagonistic variants reveal long-standing constraints on sexual dimorphism in fruit flies. PLoS Biol. 17:e3000244. doi:10.1371/journal.pbio.3000244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp NP, Agrawal AF.. 2013. Male-biased fitness effects of spontaneous mutations in Drosophila melanogaster. Evolution. 67:1189–1195. doi:10.1111/j.1558-5646.2012.01834.x. [DOI] [PubMed] [Google Scholar]
- Sharp NP, Agrawal AF.. 2018. An experimental test of the mutation-selection balance model for the maintenance of genetic variance in fitness components. Proc R Soc B Biol Sci. 285:20181864.doi:10.1098/rspb.2018.1864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sidorenko J, Kassam I, Kemper KE, Zeng J, Lloyd-Jones LR, et al. 2019. The effect of X-linked dosage compensation on complex trait variation. Nat Commun. 10:3009.doi:10.1038/s41467-019-10598-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siller S. 2001. Sexual selection and the maintenance of sex. Nature. 411:689–692. doi:10.1038/35079578. [DOI] [PubMed] [Google Scholar]
- Simmons MJ, Crow JF.. 1977. Mutations affecting fitness in Drosophila populations. Annu Rev Genet. 11:49–78. doi:10.1146/annurev.ge.11.120177.000405. [DOI] [PubMed] [Google Scholar]
- Singh ND, Davis JC, Petrov DA.. 2005. X-linked genes evolve higher codon bias in Drosophila and Caenorhabditis. Genetics. 171:145–155. doi:10.1534/genetics.105.043497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A, Punzalan D.. 2018. The strength of sex-specific selection in the wild. Evolution. 72:2818–2824. doi:10.1111/evo.13625 [DOI] [PubMed] [Google Scholar]
- Singh ND, Larracuente AM, Clark AG.. 2008. Contrasting the efficacy of selection on the X and autosomes in Drosophila. Mol Biol Evol. 25:454–467. doi:10.1093/molbev/msm275. [DOI] [PubMed] [Google Scholar]
- Smith SRT, Connallon T.. 2017. The contribution of the mitochondrial genome to sex-specific fitness variance. Evolution. 71:1417–1424. doi:10.1111/evo.13238. [DOI] [PubMed] [Google Scholar]
- Speed D, Cai N, Johnson MR, Nejentsev S, Balding DJ, UCLEB Consortium. 2017. Reevaluation of SNP heritability in complex human traits. Nat Genet. 49:986–992. doi:10.1038/ng.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed D, Hemani G, Johnson MR, Balding DJ.. 2012. Improved heritability estimation from genome-wide SNPs. Am J Hum Genet. 91:1011–1021. doi:10.1016/j.ajhg.2012.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sultanova Z, Andic M, Carazo P.. 2018. The “unguarded-X” and the genetic architecture of lifespan: Inbreeding results in a potentially maladaptive sex-specific reduction of female lifespan in Drosophila melanogaster. Evolution. 72:540–552. doi:10.1111/evo.13426. [DOI] [PubMed] [Google Scholar]
- Trivers RL. 1972. Parental Investment and Sexual Selection. Chicago: Aldine Press. [Google Scholar]
- Turelli M, Barton NH.. 2004. Polygenic variation maintained by balancing selection: pleiotropy, sex-dependent allelic effects and GxE interactions. Genetics. 166:1053–1079. doi:10.1534/genetics.166.2.1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeramah KR, Gutenkunst RN, Woerner AE, Watkins JC, Hammer MF.. 2014. Evidence for increased levels of positive and negative selection on the X chromosome versus autosomes in humans. Mol Biol Evol. 31:2267–2282. doi:10.1093/molbev/msu166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vicoso B, Charlesworth B.. 2006. Evolution on the X chromosome: unusual patterns and processes. Nat Rev Genet. 7:645–653. doi:10.1038/nrg1914. [DOI] [PubMed] [Google Scholar]
- Visscher PM, Goddard ME.. 2019. From R.A. Fisher’s 1918 Paper to GWAS a century later. Genetics. 211:1125–1130. doi:10.1534/genetics.118.301594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock MC, Agrawal AF.. 2009. Purging the genome with sexual selection: reducing mutation load through selection on males. Evolution. 63:569–582. doi:10.1111/j.1558-5646.2008.00558.x. [DOI] [PubMed] [Google Scholar]
- Wyman MJ, Rowe L.. 2014. Male bias in distributions of additive genetic, residual, and phenotypic variances of shared traits. Am Nat. 184:326–337. doi:10.1086/677310. [DOI] [PubMed] [Google Scholar]
- Yang J, Benyamin B, McEvoy BP, Gordon S, Henders AK, et al. 2010. Common SNPs explain a large proportion of heritability for human height. Nat Genet. 42:565–569. doi:10.1038/ng.608.Common. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng J, De Vlaming R, Wu Y, Robinson MR, Lloyd-Jones LR, et al. 2018. Signatures of negative selection in the genetic architecture of human complex traits. Nat Genet. 50:746–753. doi:10.1038/s41588-018-0101-4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Fitness and genomic data are available at https://doi.org/10.5281/zenodo.571168 and https://zenodo.org/record/159472, respectively. All code for reproducing analyses in the manuscript is available at the following github respository: filipluca/GWAS_sex_specific_fitness_and_the_X_chromosome.
Supplementary material is available at GENETICS online.