A Stable Population Code for Attention in Prefrontal Cortex Leads a Dynamic Attention Code in Visual Cortex

Abstract

Attention often requires maintaining a stable mental state over time while simultaneously improving perceptual sensitivity. These requirements place conflicting demands on neural populations, as sensitivity implies a robust response to perturbation by incoming stimuli, which is antithetical to stability. Functional specialization of cortical areas provides one potential mechanism to resolve this conflict. We reasoned that attention signals in executive control areas might be highly stable over time, reflecting maintenance of the cognitive state, thereby freeing up sensory areas to be more sensitive to sensory input (i.e., unstable), which would be reflected by more dynamic attention signals in those areas. To test these predictions, we simultaneously recorded neural populations in prefrontal cortex (PFC) and visual cortical area V4 in rhesus macaque monkeys performing an endogenous spatial selective attention task. Using a decoding approach, we found that the neural code for attention states in PFC was substantially more stable over time compared with the attention code in V4 on a moment-by-moment basis, in line with our guiding thesis. Moreover, attention signals in PFC predicted the future attention state of V4 better than vice versa, consistent with a top-down role for PFC in attention. These results suggest a functional specialization of attention mechanisms across cortical areas with a division of labor. PFC signals the cognitive state and maintains this state stably over time, whereas V4 responds to sensory input in a manner dynamically modulated by that cognitive state.

SIGNIFICANCE STATEMENT Attention requires maintaining a stable mental state while simultaneously improving perceptual sensitivity. We hypothesized that these two demands (stability and sensitivity) are distributed between prefrontal and visual cortical areas, respectively. Specifically, we predicted attention signals in visual cortex would be less stable than in prefrontal cortex, and furthermore prefrontal cortical signals would predict attention signals in visual cortex in line with the hypothesized role of prefrontal cortex in top-down executive control. Our results are consistent with suggestions deriving from previous work using separate recordings in the two brain areas in different animals performing different tasks and represent the first direct evidence in support of this hypothesis with simultaneous multiarea recordings within individual animals.

Introduction

Nervous systems provide the following critical functions: (1) the ability to respond to input and (2) the ability to store information in the absence of input. These two functions conflict with each other because information storage requires a stable representation that is robust to outside perturbation, whereas sensitivity to perturbation is the essence of responsiveness. The functional specialization of cortical areas reflects one means to resolve this apparent conflict. Areas that are synaptically distant from the sensory periphery (such as frontal executive control areas) might function through highly stable activity patterns in line with the need to maintain cognitive states across long time scales, whereas activity patterns in sensory areas closer to the periphery might be more volatile, reflecting sensitivity of these patterns to sudden environmental changes (Murray et al., 2014; Runyan et al., 2017).

Indeed, there is substantial evidence for the dynamic nature of sensory responses within sensory cortical areas. For example, although the earliest spikes in response to a visual input generally carry the most information about the stimulus (Osborne et al., 2004), feature selectivity in visual cortex continues to develop over time. Such dynamic sensory coding has been observed in several contexts, including orientation selectivity (Ringach et al., 1997; Müller et al., 2003; Shapley et al., 2003) and contour integration (Chen et al., 2014) in area V1, texture selectivity (Kim et al., 2019) and object occlusion (Fyall et al., 2017) in area V4, and pattern motion sensitivity in area MT (Pack and Born, 2001; Smith et al., 2005).

In contrast, stable representations have been hypothesized to be essential for executive functions involving maintenance of information on long time scales (several seconds and longer). One brain area implicated in such executive functions is the lateral prefrontal cortex (PFC), and indeed evidence for stable neural representations in PFC has been reported for long time-scale behaviors including categorical reasoning (Freedman et al., 2003; Cromer et al., 2011; McKee et al., 2014), flexible rule-based decision-making (Bunge et al., 2003; Siegel et al., 2015), and working memory (Constantinidis et al., 2018; Wasmuht et al., 2018; Parthasarathy et al., 2019). It is important to emphasize that such stable representations can exist at the population level despite considerable temporal instability at the level of individual neurons (Druckmann and Chklovskii, 2012). The case of working memory provides an excellent illustration of this point. Work using population-level analyses has found that although the activity of PFC neurons can be highly dynamic during memory maintenance periods, a stable representation can persist in a subspace of the population activity that encodes the mnemonic information (Murray et al., 2017; Parthasarathy et al., 2019).

One cognitive function that exemplifies the tension between stability and sensitivity is selective attention, which is the ability to marshal limited processing resources preferentially for goal-relevant information while suppressing the processing of less relevant or distracting information. For example, consider searching for a friend wearing a red shirt in a crowd. This requires maintaining a stable representation that red is the relevant visual feature while also endeavoring to improve visual sensitivity to that feature. Correlates of attention have been found in the neural activity of multiple sensory areas (for review, see Hromádka and Zador, 2007; Maunsell, 2015; Gomez-Ramirez et al., 2016), as well as parietal (Desimone and Duncan, 1995) and frontal association cortex, including PFC (Paneri and Gregoriou, 2017). Previous work has suggested that PFC and V4 directly interact in the service of attention (Squire et al., 2013); but the functional specialization of those areas has not been tested with respect to the relative stability of population activity. Moreover, although previous researchers have speculated that diversity of intrinsic time scales across cortical areas reflects a computational division of labor (Murray et al., 2014), this type of interplay of stable and unstable processes has not been directly demonstrated moment to moment with simultaneous recordings in multiple brain areas. Previous studies have focused on trial-averaged activity rather than moment-to-moment signals from populations of neurons.

We asked if the conflicting demands of selective attention to maintain stable task-set representations and to enhance sensitivity to input might be distributed across nodes of this network, and if so, what is the nature of that areal specialization? Thus, for the present study, we sought to compare the temporal stability of, and interaction among, attention signals in two key nodes of the attention network: V4 and PFC. We predicted that PFC population activity would more stably represent the attention state compared with population activity in V4. This prediction is in line with the relative stability of task-set representations previously found in PFC compared with the relative dynamism of sensory processes in V4 but has not yet been explicitly tested with simultaneous measurement of population activity in the two brain areas. Thus, we provide the first direct evidence for this division of labor for temporal stability across frontal and visual cortical areas on a moment-by-moment basis on individual trials.

To test our prediction that PFC signals attention states stably whereas V4 attention states are more dynamic, we simultaneously recorded neural populations in V4 and dorsolateral PFC of monkeys while they performed a visuospatial selective attention task and then used a decoding approach to assay the degree to which the population codes for attention in each brain area were stable. We found neural codes for attention states remained highly stable in a subspace of prefrontal population activity, whereas corresponding codes in V4 were relatively dynamic. We also found that the estimated attention state in PFC predicted the future attention state in V4 on a centisecond time scale, in line with a top-down role of PFC in endogenous attention processes. These results suggest attention relies on areal specialization for subfunctions of selective attention processes; stable task-set representations are maintained over time in frontal cortex, freeing up visual cortex to remain sensitive to external events.

Materials and Methods

Ethical oversight

Experimental procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and were performed in accordance with the U.S. National Research Council Guide for the Care and Use of Laboratory Animals.

Subjects

We used two adult male rhesus macaques (Macaca mulatta) for this study. Two animals is the minimum number needed to demonstrate reproducibility and is customary for research with this model species. Surgeries were performed in aseptic conditions under isoflurane anesthesia. Opiate analgesics were used to minimize pain and discomfort perioperatively. A titanium head post was attached to the skull with titanium screws to immobilize the head during experiments. After each subject was trained to perform the spatial attention task, we implanted one 100 electrode Utah array (Blackrock Microsystems) in each of the brain areas V4 and PFC (area 8Ar; Fig. 1A). We implanted the electrode arrays in the right hemisphere for Monkey P and in the left hemisphere for Monkey W. A separate analysis of a portion of these data was previously reported, along with a complete description of the experimental methods (Snyder et al., 2018). The pattern of results was highly similar across the two animals, so we combined across animals for the results reported in the main text.

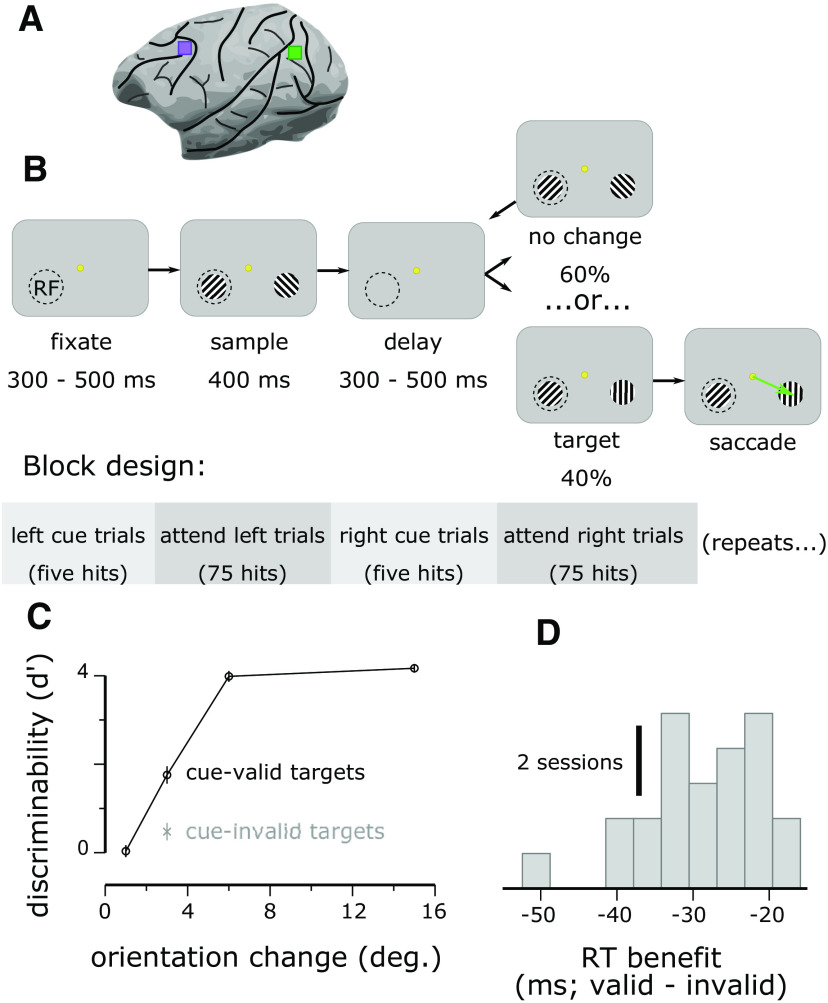
Figure 1.

Dual V4 and PFC recordings during a spatial attention task. A, Approximate location of Utah array implantations in V4 (green) and PFC (purple). B, Animals fixated a central dot while stimuli were repeatedly flashed bilaterally. Reinforcement was given if the animal made a saccade to a stimulus that changed orientation from the previous presentation (the target). In a blocked fashion, the target was more likely to occur in one hemifield (the valid location). Cue trials, in which only one stimulus appeared at the high-probability location, signaled the start of each block. C, Animals were more accurate at detecting Δ3° targets at the valid location than at the invalid location, confirming that they selectively attended to the valid location (Monkey P: cue-valid, $d\prime =1.76\pm 0.20,$ mean ± SEM; cue-invalid, $d\prime =0.47\pm 0.20,t_{23}=4.64,p=1.13·{10}^{-4}$; Monkey W: cue-valid $d\prime =0.46\pm 0.18$, cue-invalid $d\prime =-0.75\pm 0.18,t_{22}=5.22,p=3.12·{10}^{-5}$). Results for Monkey P are shown; results for Monkey W were similar (compare Snyder et al., 2018). D, Animals were also faster at detecting targets at the valid location than at the invalid location (Monkey P: RT benefit for cue-valid compared with cue-invalid targets, ΔRT = – 29.2 ± 1.6 ms, $t_{23}=-17.90,p=5.32·{10}^{-15};$ Monkey W: ΔRT = – 42.3 ± 4.8 ms, $t_{22}=-8.79,p=1.19·{10}^{-8}$). Results for Monkey P are shown; results for Monkey W were similar.

Visual change-detection task

Subjects maintained central fixation as sequences of drifting Gabor stimuli were presented in one or both of the visual hemifields and were rewarded with water or juice for detecting a change in orientation of one of the stimuli in the sequence (the target) and making a saccade to that stimulus (Fig. 1B). The probable target location was block randomized so that 90% of the targets would occur in one hemifield until the subject made 80 correct detections in that block (including cue trials, described below), at which point the probable target location was changed to the opposite hemifield.

The fixation point was a 0.6° yellow dot at the center of a flat-screen cathode ray tube monitor positioned 36 cm from the eyes of the subjects. The background of the display was 50% gray. We measured monitor luminance γ functions by photometer and linearized the relationship between input voltage and output luminance using look-up tables. We tracked the gaze of the subjects using an infrared eye-tracking system (EyeLink 1000, SR Research). Gaze was monitored online by the experimental control software to ensure fixation within ≈1° of the central fixation point throughout each trial. We excluded from analysis data segments during which the gaze of a subject left the fixation window.

After fixating for a randomly chosen duration of 300–500 ms (uniformly distributed), a visual stimulus was presented for 400 ms or until the gaze gaze of the subjects left the fixation window, whichever came first. For the initial trials within a block, a Gabor stimulus was presented only in the hemifield that was chosen to have a high probability of target occurrence for the block. These cue trials were to alert the subjects to a change in the probable target location and were excluded from the analysis. The initial cue location was counterbalanced across recording sessions. Once a subject correctly detected five orientation changes during the cue trials, bilateral Gabor stimuli were presented for the remainder of the block.

Each trial consisted of a sequence of 400 ms stimulus presentations separated by 300–500 ms interstimulus intervals (uniformly distributed). We varied the interstimulus intervals so that stimulus onset times would be relatively less predictable, encouraging the animal to deploy attention consistently over time (as opposed to transiently disengaging attention during the interstimulus interval). Stimulus sequences continued until the subject made an eye movement (data during saccades were excluded from analysis), or a target was presented, but the subject did not respond to it within 400 ms (i.e., a miss). For the first presentation in a sequence, the orientation of the stimulus at the cued location was randomly chosen to be 45 or 135°, and the orientation of the stimulus in the opposite hemifield, if present, was orthogonal to this. Subsequent stimulus presentations in the sequence each had a fixed probability (uniform hazard function) of containing a target (30% for Monkey P, 40% for Monkey W), that is, a change in orientation of one of the Gabor stimuli compared with the preceding stimulus presentations in the trial. Within a block, 90% of targets (randomly chosen) occurred in one hemifield (valid targets), and 10% of targets occurred in the opposite hemifield (invalid targets). For valid targets, the orientation change was randomly chosen to be 1, 3, 6, or 15° in either the clockwise or anticlockwise direction (number of valid targets of each orientation at each location: Monkey P: 11.49 ± 3.14, mean ± SD, across sessions, Monkey W: 14.56 ± 4.75). For invalid targets, the orientation change was always the near threshold value of 3°, clockwise or anticlockwise (because invalid targets occurred infrequently, we restricted the number of orientation change magnitudes for this condition to derive a reasonable estimate of the target detection rate). We analyzed trials including either valid or invalid targets but excluded from analysis all neural data from the time of target onset through the end of the trial.

Monkey P completed 24 sessions of the experiment, and Monkey W completed 25 sessions. One session for each subject was subsequently excluded from analysis because of recording equipment failure.

Microelectrode array recordings

Signals from the arrays were bandpass filtered (0.3–7500 Hz), digitized at 30 kHz, and amplified by a Grapevine system (Ripple). Signals crossing a threshold (periodically adjusted using a multiple of the root-mean-squared noise) were stored for off-line analysis. We first performed a semisupervised sorting procedure followed by manual refinement using custom MATLAB software (https://github.com/smithlabvision/spikesort), taking into account waveform shapes and interspike interval distributions. These initial sorting steps yielded 93.2 ± 8.9 (mean ± SD) candidate units per session in V4 and 119.6 ± 17.5 units per session in PFC for Monkey P and 61.9 ± 27.4 candidate units per session in V4 and 113.8 ± 21.9 units per session in PFC for Monkey W. We likely recorded a mixture of single units and multiunit activity, although for simplicity we refer to all units as “neurons.” The arrays were chronically implanted and likely recorded some, but not all, neurons over more than one recording session, but we calculated our results within each recording session and treated each session as an independent sample for the analysis. We note with respect to statistical inference that if we had, in fact, repeatedly sampled the same pool of neurons across sessions, then our p values would have a different meaning than if we had sampled a completely new set each time. In the former case, the interpretation would be that a particular sample of neurons shows the effects we found and that that effect was not because of chance (e.g., on the first session), whereas in the latter case the interpretation would be that neurons in general show the effect we found. Both are valid inferences, and both are interesting findings. In fact, our view is that attention mechanisms can be conceived as latent factors that affect neural populations and that we observed the same latent factors each session with our population-level analysis whether or not the neurons were the same or completely different between sessions.

To avoid potential confounds because of our blocked design, we excluded neurons that were not recorded stably throughout a session. These were identified by dividing all the recorded data for a session into 10 equally sized blocks, measuring the average firing rate of each neuron within each block and then calculating the coefficient of variation (CV) of the average firing rate of each neuron over the blocks. Neurons with a CV >1 were deemed to be unstable and were excluded (9.3 ± 8.7 neurons excluded for Monkey P per session, 14.3 ± 16.5 neurons excluded for Monkey W per session). We also excluded neurons with an average firing rate <0.1 spikes per second measured over the entire session (2.3 ± 2.2 additional neurons excluded for Monkey P per session, 6.0 ± 5.7 neurons excluded for Monkey W per session).

We used a factor analysis (FA) method to reduce the dimensionality of the population activity (see below, Dimensionality reduction of population activity). Neural activity recorded on different electrodes can, in rare cases, show highly correlated activity because of electrical cross-talk among electrodes on the array (Yu et al., 2009). Such correlated activity can confound methods such as FA or Gaussian process factor analysis (GPFA), which seek to identify shared variance among neurons. To be conservative, we measured the Pearson correlation between spike trains (1 ms time bins) for all pairs of neurons and randomly excluded one neuron from each pair with a correlation coefficient greater than r = 0.1. This criterion was quite liberal (12.9 ± 9.3 neurons excluded per session), and the results were not affected by substantial variation of this correlation threshold.

One of our goals was to test how much variability in one neural population was explained by the population activity of the other brain area (see below, Granger causal influence). Such an analysis may be biased if we used a greater number of neurons in one brain area to predict the activity of a fewer number of neurons in another brain area. To place the two areas on the same footing, for each session, we randomly selected neurons from the population with greater cardinality to equate the population size used for all analyses between the two brain areas (final population size in each area for the analysis was 79.1 ± 12.5, mean ± SD neurons for Monkey P per session; 50.9 ± 22.0 neurons for Monkey W per session).

From the continuous recording, we extracted data segments from 300 ms before stimulus onset to 300 ms following stimulus offset (1 s total segment duration; Monkey P: 2253.1 ± 591.3 data segments per session; Monkey W: 2894.2 ± 946.8 data segments per session) and counted spikes for each neural unit in 1 ms bins. For the calculation of peristimulus spike time histograms (PSTHs; Fig. 2), we smoothed spike trains with a causal half-Gaussian function with σ = 20 ms before averaging across data segments.

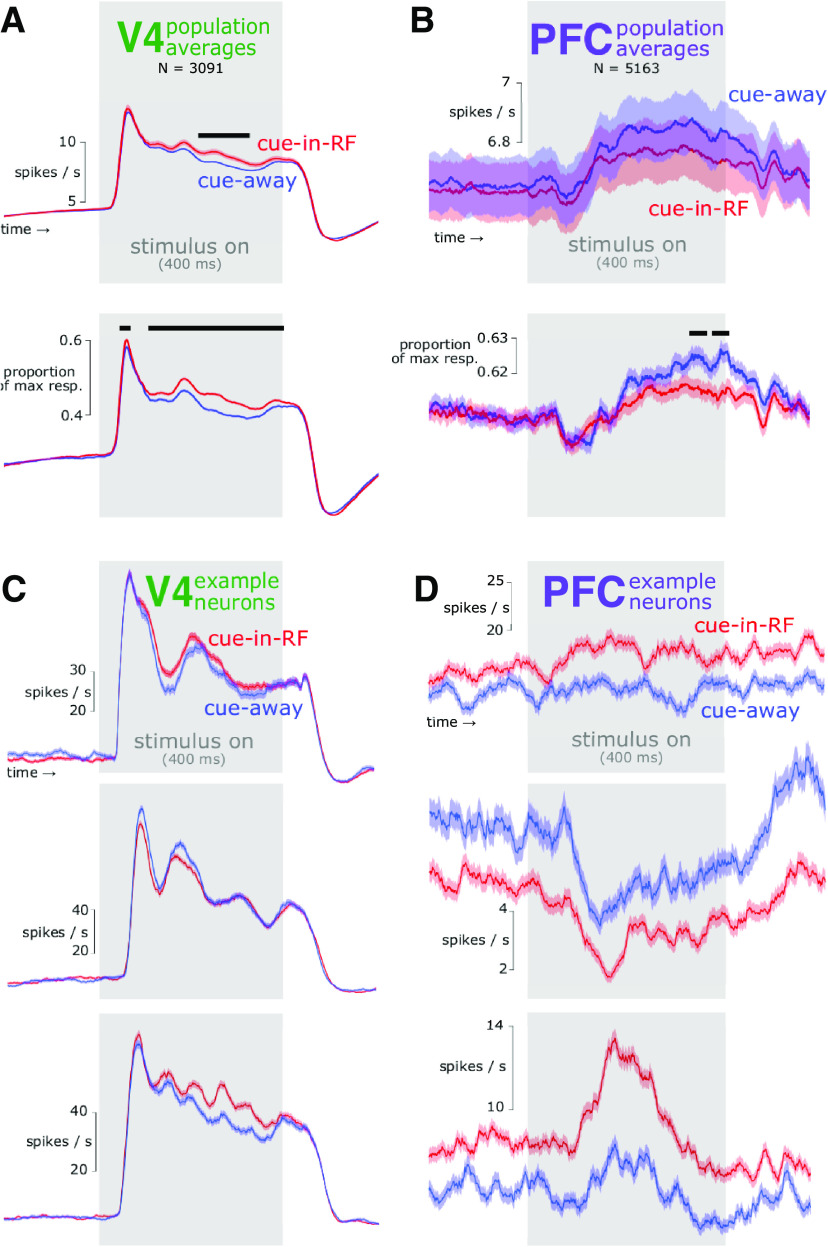
Figure 2.

Firing rate time courses in V4 and PFC under different attention conditions. A, Population average for V4. Top, Raw firing rate. Bottom, Normalized firing rate. Neurons in V4 generally responded more vigorously in response to an attended stimulus than an unattended stimulus, particularly during the late, sustained portion of the response. Baseline modulations were not observed on average. Black bars over data indicate time points with significant differences between cue-in-RF and cue-away conditions (independent samples t test, p < 0.05). B, Population average for PFC. On average, neurons in PFC responded slightly more vigorously near the end of the stimulus interval when attention was directed ipsilaterally compared with when it was directed contralaterally (bottom). C, PSTHs for example individual neurons in V4 illustrating diversity of attention modulations. Unlike the population average (A), some individual neurons showed baseline modulations (top), and/or more vigorous responses to unattended stimuli (middle). Other neurons more closely resembled the population average (bottom). The time course of attention modulation varied across neurons in the population, and changed magnitude or sign over time for individual neurons. These observations suggest a dynamic code for attention in V4. D, PSTHs for example individual neurons in PFC. In PFC, the effect of contralaterally directed attention on firing rates was much more consistent across time than in V4, suggesting a more stable code for attention. Responses to nontarget stimuli to which animals correctly withheld responding are shown. Shading represents ±1 SEM.

Receptive field mapping

Before beginning the visual change-detection experiment, we mapped the receptive fields (RFs) of the spiking neurons recorded on the V4 arrays by presenting small (≈1°) sinusoidal gratings (four orientations) at a grid of positions. We subsequently used Gabor stimuli scaled and positioned to roughly cover the aggregate RF area determined by the responses to the small gratings at the grid of positions. For Monkey P this was 7.02° full-width at half-maximum (FWHM) centered 7.02° below and 7.02° to the left of fixation, and for Monkey W this was 4.70° FWHM centered 2.35° below and 4.70° to the right of fixation. We next measured tuning curves by presenting gratings at the RF area with four orientations and a variety of spatial and temporal frequencies. For each subject we used full-contrast Gabor stimuli with a temporal and spatial frequency that evoked a robust response from the population overall (i.e., our stimulus was not optimized for any single neuron). For Monkey P this was 0.85 cycles/° and 8 cycles/s. For Monkey W this was 0.85 cycle/° and 7 cycles/s. For the task, we presented a Gabor stimulus at the estimated RF location, at the mirror-symmetric location in the opposite hemifield, or at both locations simultaneously. We did not measure RFs for the PFC neurons; stimulus properties were chosen solely on the basis of V4 responses. In a preliminary step, we electrically microstimulated each of our PFC electrodes at a range of current amplitudes and found that we were unable to evoke eye movements even at current amplitudes several times greater than those that typically evoke eye movements from electrodes implanted in the frontal eye field (FEF; Goldberg and Bruce, 1986), suggesting that our electrodes did not impinge on FEF but were rather exclusively in PFC.

Dimensionality reduction of population activity

To focus the decoding analyses (see below, Decoding attention state) on activity that is shared among neurons, we first applied GPFA to the spike counts recorded in each brain area separately (Yu et al., 2009; Fig. 3). We then orthonormalized the dimensions using the procedure described in Yu et al. (2009). This yielded a single-trial time series of latent factors, which summarize the shared activity among neurons over time. For this analysis, we restricted the dataset to presentations of standard stimuli to which the subject correctly withheld a response. We applied GPFA separately to each of the two stimulus configuration conditions (i.e., when the stimulus in the RF was oriented at 45° and when it was oriented at 135°). For each neuron we square-root transformed the spike counts (as a variance-stabilizing step), then subtracted the average PSTH for the included data segments from each individual trial. That is, our analysis focused on residual trial-to-trial variation in firing rates beyond the average stimulus-evoked response. We then binned the residual spike counts for each neuron in each data segment within 50 nonoverlapping 20 ms time bins. We aimed to specify a common model dimensionality across all brain areas and sessions so that values across brain areas and sessions would be directly comparable. We tested several potential dimensionalities for our GPFA models and found that 10 dimensions captured most of the explainable shared variance in all but one of our datasets, so we used this dimensionality consistently. We also tested different criteria to select the number of dimensions, such as using the minimum number of dimensions needed to retain 90% of the total shared variance of each population, and found the pattern of results to be highly consistent. Thus, our results and conclusions are not dependent on the precise criterion to choose the number of dimensions. Our goal in performing this initial dimensionality reduction step was to reduce the tendency to overfit the logistic regression model to noisy individual neurons and instead to emphasize shared variability. After separately applying GPFA for each stimulus configuration condition separately, we recombined the results for subsequent analyses. The patterns of results and the conclusions were not affected if we restricted our entire analysis to only one stimulus configuration or the other; therefore, we used all the data from both conditions.

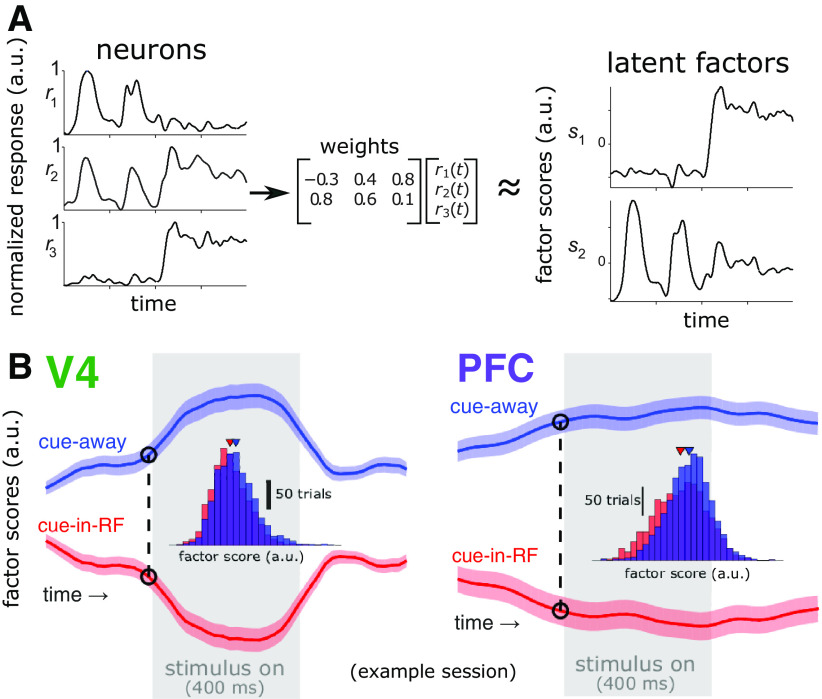
Figure 3.

Extracting latent factors from the V4 and PFC population activity. A, Schematic of dimensionality reduction with GPFA. A low-dimensional subspace of the neural population activity space was identified, which captured shared variability of activity among neurons within each brain area (left), resulting in a lower dimensional set of latent factor scores (right). B, Average factor scores for one factor for each brain area from a representative session. At each time point (e.g., the dashed line at −10 ms relative to stimulus onset; insets show distributions across trials of factor scores at the indicated time), we trained a logistic regression decoder to classify trials as cue-in-RF or cue-away using the factor scores. One factor is shown for illustrative purposes; in actuality 10 factors were used for decoding. The gray rectangle indicates the time when the stimulus was present (400 ms duration). Shading represents ±1 SEM.

In GPFA, the amount of temporal smoothing (i.e., τ, the time scale of the Gaussian processes) was determined in an unsupervised manner from the neural activity (through maximum likelihood estimation using expectation maximization with cross-validation), and not prespecified. Thus, differences across brain areas in how quickly latent variables change over time reflect inherent differences in the activity across areas. To confirm this, we repeated the main analyses using FA, which does not include temporal smoothing. We found similar qualitative results as with GPFA, although the results tended to be noisier without temporal smoothing, which motivated us to use GPFA instead of FA in the first place. Thus, our results and conclusions are robust to the use of temporal smoothing.

Decoding attention state

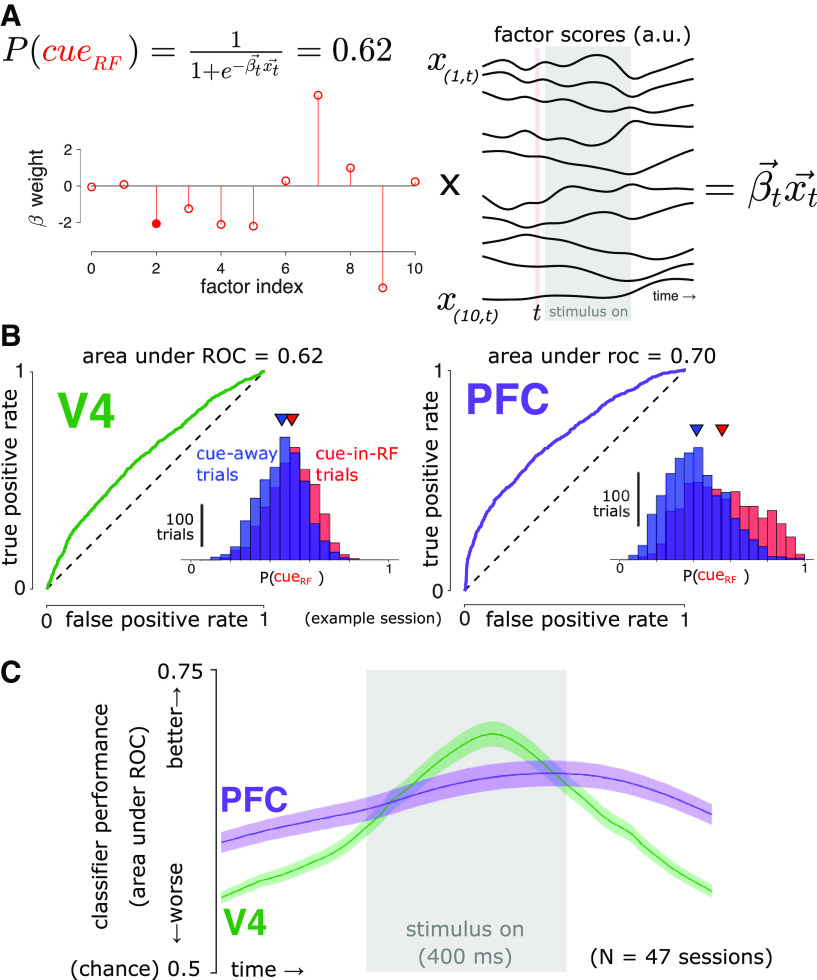
We used binomial logistic regression models to estimate the probability of which stimulus location was cued (i.e., attended) using the GPFA latent variables obtained from the population activity from each brain area (Fig. 5). Specifically, we used the MATLAB function mnrfit to find the ${\overrightarrow{\beta }}_t$ that optimizes the following equation:

$$P(cu{e}_{RF}|{\overrightarrow{x}}_t)=\frac{1}{1+e^{-{\overrightarrow{\beta }}_t{\overrightarrow{x}}_t}},$$

where ${\overrightarrow{x}}_t$ is the vector of 10-dimensional GPFA scores at time t. For each brain area, we fit a separate model at each time point during the stimulus-aligned data segments. We used 10-fold cross-validation to quantify the classification performance of the cue condition (Fig. 4C), as well as all subsequent analyses involving the decoded attention state. Where indicated in the text, we used the single decoder from the time point with the best performance and applied that decoder to the data from all time points, which enables a more straightforward comparison between time points. The pattern of results and conclusions was unchanged if we used a separate decoder trained at each time point for such analyses. To measure cross-temporal generalization of our decoders (Fig. 5C,D), we measured the Pearson product-moment correlation coefficient across trials between P(cue_RF) values obtained using a decoder trained on data from one time point (training time), on data from another time point (test time), and P(cue_RF) values obtained using decoders trained and tested at the same time point (in a cross-validated manner).

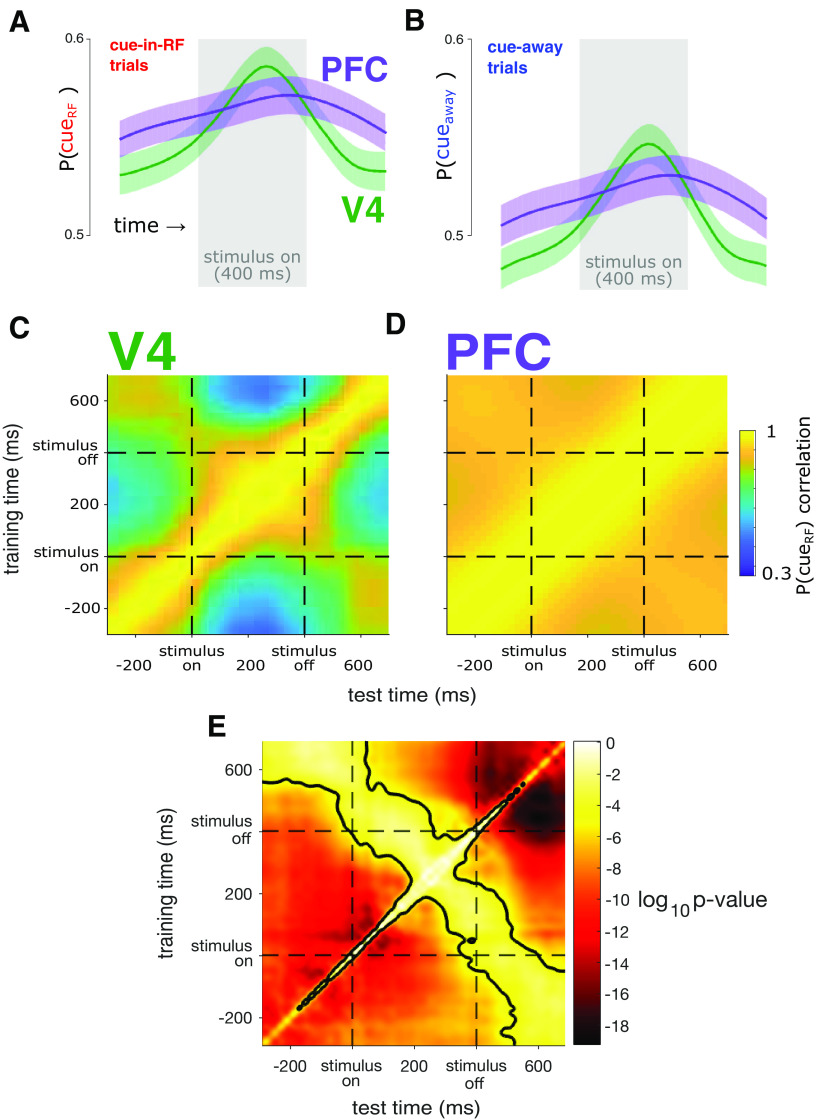
Figure 5.

The population code for cue condition is more dynamic in V4 than in PFC. A, Average probability that the RF was cued [P(cue_RF)], estimated from cue-in-RF trials. The average prediction was more dynamic over time in V4 (green) than in PFC (purple). The gray rectangle indicates the time the stimulus was present. Shading represents ±1 SEM, N = 47 sessions across two subjects. B, Same conventions as in A but for the average probability that the cue was away from the RF [P(cue_away)] using population activity on the cue-away trials. C, Decoding stability. In V4, decoded P(cue_RF) values were highly correlated only when using decoders trained at nearby time points, which indicates a dynamic code for attention. D, In PFC, decoded P(cue_RF) values were highly correlated when using decoders trained across a much wider range of time points, indicating a stable code. E, Statistical comparison of C and D. For each observed P(cue_RF) correlation value, we tested whether the correlation was significantly different between the two brain areas (dependent-samples t test, N = 47 sessions, α = 0.05, Bonferroni corrected for the number of time point pairs). P(cue_RF) values are significantly more correlated across a wider range of time points in PFC than in V4. The black contour indicates the significant p value threshold of p = 0.05.

Figure 4.

Decoding attention state. A, At each time point (t), we found the optimal coefficients (${\overrightarrow{\beta }}_t$) for the logistic regression equation shown, where ${\overrightarrow{x}}_t$ is a vector of GPFA scores. We then estimated the attention state, P(cue_RF), in a cross-validated manner. The filled marker indicates the example PFC factor illustrated in Figure 3B. B, Using the same representative session and time point indicated in Figure 3B, we estimated the probability that each trial came from the cue-in-RF condition, P(cue_RF). Inset, Distributions of P(cue_RF) values for that time point. Triangles indicate the distribution means. By varying the classification threshold, we constructed receiver operating characteristic curves to assess how separated the cue-in-RF and cue-away distributions were. Both brain areas carried predictive information about the cue condition. C, Decoder performance (cross-validated area under the receiver operating characteristic curve). Logistic regression models trained on population activity from each brain area performed significantly better than chance (0.5) at predicting which location was cued during the task at all time points (t test, p < 0.05, Bonferroni corrected). This indicates that population activity in both brain areas encoded information about the attention state at all times. Shading represents ±1 SEM, N = 47 sessions across two subjects.

Attention state prediction stability

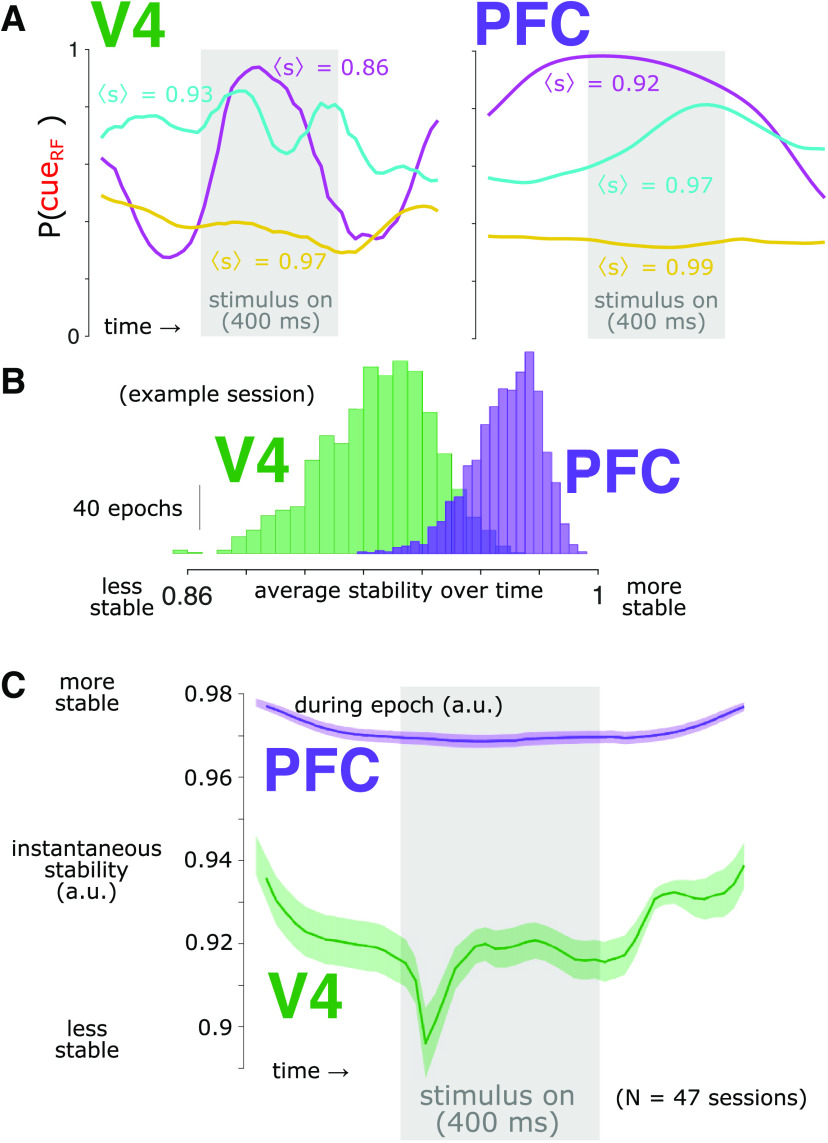
We sought to quantify how much the estimated attention state in each brain area fluctuated from moment to moment. Because the output of the logistic regression decoder was in units of probability (i.e., that the RF was attended), these values were bounded between zero and one. This boundedness would have created a compression of the moment-to-moment variation near those extreme values. To mitigate this ceiling/floor effect, we transformed the probabilities into z-scores using a normal inverse cumulative distribution function. We then computed the attention prediction stability, s_t, as one minus the absolute change in the z-transformed probability estimate from one time point to the next (Fig. 6) as follows:

$$s_t=1-|z(P\left(cu{e}_{RF}|{\overrightarrow{x}}_t\right))-z(P\left(cu{e}_{RF}|{\overrightarrow{x}}_{t-1}\right))|$$

Figure 6.

Decoded attention state is more stable for PFC than for V4. A, Single-trial attention prediction examples from a representative session. Within a single trial, the P(cue_RF) varied. To quantify this variation, we calculated the stability (s); a value of s = 1 indicates perfect stability, and a value of s = 0 indicates the expected stability if time points were independent (see above, Materials and Methods). The trials shown are the trial with the greatest average stability over time [$〈s〉$, gold], the trial nearest the median [$〈s〉$, cyan] and the trial with the $〈s〉$ nearest zero (magenta) for each brain area. B, Distributions of average stability during each peristimulus epoch (−300 ms to 700 ms relative to stimulus onset) for V4 (green) and PFC (purple). Same session as in A. C, The prediction stability was greater in PFC (purple) than in V4 (green) at all time points (t test, p < 0.05, Bonferroni corrected). This included prestimulus time points, indicating that differences in P(cue_RF) stability were not trivially because of, for example, different dynamics of stimulus responsiveness, (Note also that although stability dropped transiently in V4 around stimulus onset, in general, stability in V4 was at similar levels during spontaneous and stimulus-evoked activity, indicating stability was not trivially related to overall activity levels.) The gray rectangle indicates the time the stimulus was present. Shading represents ±1 SEM, N = 47 sessions.

Thus, the maximum value for prediction stability is one, which indicates no change in the attention prediction value over time. To compare the measured stability values to what might be expected if there was no temporal structure in the data, we randomly shuffled the time points of our data within each session, measured the stability of the shuffled data, and then averaged within each session. We repeated this shuffling procedure several times and found that because each session contained hundreds of thousands of time points, the same average stability resulted for each iteration to a precision of <0.0001, so we simply used that value. We then rescaled our observed stability measurements so that a value of 0 equaled the least average stability that was found in our shuffled dataset. Therefore, a value of 1 indicates perfect stability, and a value of 0 indicates the least expected stability if there was no temporal structure. Note that stability can be negative. To ease comparison of P(cue_RF) across time, for this analysis of instantaneous stability and the analysis of Granger causal influence (GCI) we used the decoder for each brain area from the time point with the best decoding performance for each session and applied it to the data across all the time points. The qualitative pattern of results and conclusions were the same if we used a separate decoder trained at each time point but would be more difficult to interpret as it would be ambiguous as to whether instability was accounted for by a change in decoder, a change in activity patterns, or both.

Granger causal influence

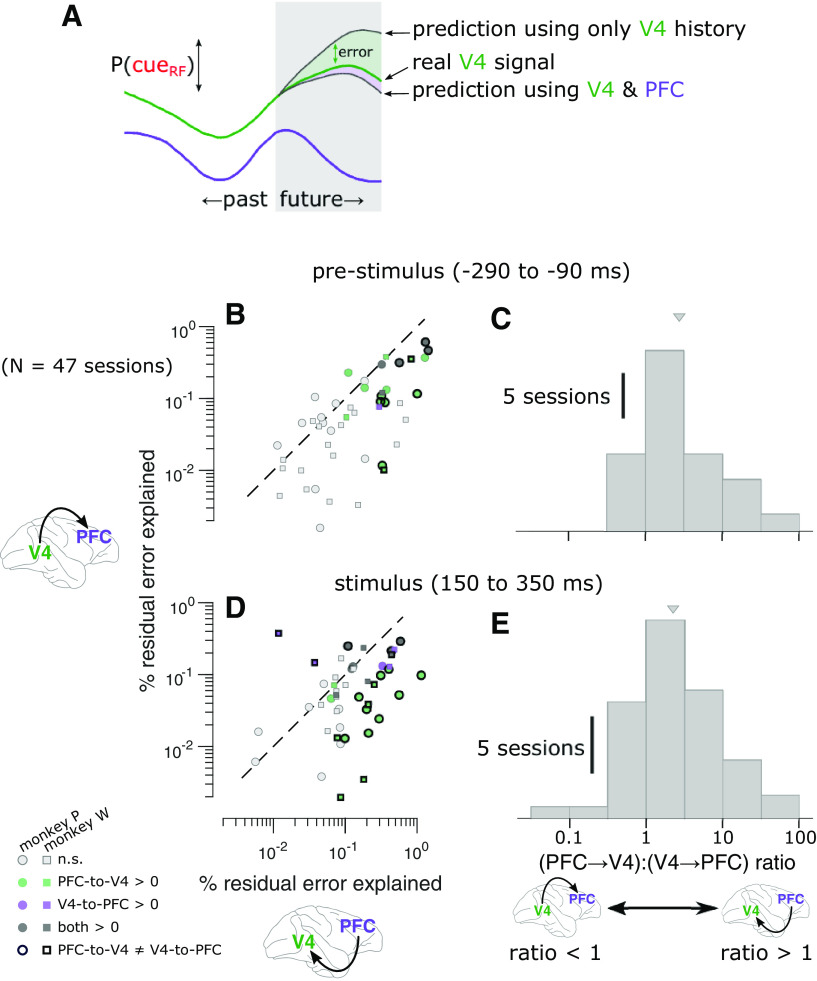
To estimate how much future information about the attention state in one brain area was predicted from the past history of the other brain area, we performed a GCI analysis using the Multivariate Granger Causality (MVGC) toolbox for MATLAB (Barnett and Seth, 2014; Fig. 7). Although this analysis is traditionally known as Granger causality, we caution that mechanistic causality may not be validly inferred as the procedure is strictly observational and the potential role of unobserved variables cannot be ruled out. Traditionally, GCI analysis involves estimating parameters for both a full and a reduced (nested) autoregressive model. The reduced model aims to predict the future state of one signal (the target, y; in our case the P(cue_RF) estimated from activity in one brain area) using the past history of that signal as follows:

$$y_t={\beta }_1{y}_{t-1}+{\beta }_2{y}_{t-2}\cdots {\beta }_n{y}_{t-n}+\eta ,$$

where n is a specified model order and η is residual error. In our model for V4, for example, the reduced model aimed to predict the value of P(cue_RF) in V4, and it did so by using the preceding values of P(cue_RF) from V4 in each trial (up to the model order and excluding any points in time that would span across trials).

Figure 7.

Between-area prediction of attention states is better in the PFC-to-V4 direction than in the V4-to-PFC direction. A, Schematic of GCI analysis. To test for GCI in the PFC-to-V4 direction, we measured the reduction in error predicting the future P(cue_RF) in V4 from the past history of both brain areas compared with when predicting from the past history of V4 alone. We also measured the reduction in error when predicting the future P(cue_RF) in PFC from the past history of both brain areas compared with when predicting from the past history of PFC alone. B, GCI in each direction during the prestimulus period. The value along each axis is the reduction in error in predicting P(cue_RF) with both brain areas, compared with one brain area alone. Each marker represents a session (green, PFC-to-V4 significantly greater than zero for individual session, p < 0.05, permutation test, Bonferroni corrected; purple, V4-to-PFC significant; dark gray, both significant; light gray, neither significant). Points lie below the unity slope line on average, indicating that adding PFC to V4 when predicting the upcoming P(cue_RF) in V4 is more helpful than adding V4 to PFC when predicting the upcoming P(cue_RF) in PFC. That is, the P(cue_RF) in PFC explained more residual error about the future P(cue_RF) in V4 than vice versa. Symbols with a thick black border indicate sessions with a significant difference between V4-to-PFC GCI and PFC-to-V4 GCI (p < 0.05, permutation test, Bonferroni corrected). C, Asymmetry in GCI during the prestimulus period. Values >1 indicate greater GCI in the PFC-to-V4 direction than in the V4-to-PFC direction (median, 2.39×, t₍₄₆₎ = 5.80, p = 5.79 · 10^{– 7}). D, GCI in each direction during the stimulus response. The P(cue_RF) in PFC explained more residual error about the future P(cue_RF) in V4 than vice versa (points below the diagonal). E, Asymmetry in GCI during the stimulus response. Values >1 indicate greater GCI in the PFC-to-V4 direction than in the V4-to-PFC direction (median, 2.31×, two tailed t₍₄₆₎ = 4.27, p = 9.68 · 10^{– 5}). Triangles indicate distribution means.

The full model aims to predict the future state of the target signal using the past history of the target signal and also an additional signal (the source, x; in our case the P(cue_RF) given the activity of the other brain area) as follows:

$$y_t={\beta }_1{y}_{t-1}+{\beta }_2{y}_{t-2}\cdots {\beta }_n{y}_{t-n}+{\alpha }_1{x}_{t-1}+{\alpha }_2{x}_{t-2}\cdots {\alpha }_n{x}_{t-n}+\eta .$$

In this full model for V4, the current value of P(cue_RF) in V4 was predicted by the preceding values of P(cue_RF) from both V4 and PFC in each trial (up to the model order and, again, excluding any points that span across trials). Note that the model order n is the same for both the reduced and full models.

If the full model predicts the target signal better than the reduced model, then this implies that the source signal carries additional information about the future state of the target. We quantified the GCI as the percentage of residual error from the reduced model, which was accounted for by the full model.

Because GCI analysis assumes stationarity, we restricted our GCI analysis to the following time windows relative to each stimulus onset where this assumption was most reasonable: (1) a 200 ms time window before stimulus onset (−290 to −90 ms) and (2) a 200 ms time window during the sustained stimulus response (i.e., after the initial onset transient; 150–350 ms). Our two signals of interest for this analysis were the time series of P(cue_RF) for each of the two brain areas. We first estimated an appropriate autoregressive model order (i.e., the number of 20 ms time bins of history used to predict the target) for each session by estimating optimal parameters for each model order from 1 to 6 (by ordinary least-squares regression) and then calculating the Bayes information criterion (BIC) for each model. The model order with the best BIC was taken as the best model order (almost always order 4, sometimes 3 or 5, rarely 2). Our general pattern of results was robust to deviations in this estimated optimal model order value. For example, if we performed our analysis setting the model order of all sessions to be 3, 4, 5, or 6, the qualitative pattern of results was highly similar to that of our main result. In cases where our estimated autoregressive model parameters resulted in an unstable process (i.e., a spectral radius ≥1, which is not realistic for brain activity), we rescaled the parameters to stabilize the process (using the var_specrad function of the MVGC toolbox).

Experimental design and statistical analyses

For details on subjects, including justification of number used, see above, Subjects. For details on the task design, including independent variables and the numbers of trials per condition, see above, Visual change-detection task. For details on the number of neurons recorded, including exclusion criteria, see above, Microelectrode array recordings.

To test differences between cue conditions for behavioral accuracy (Fig. 1C) and reaction time (Fig. 1D), we used two-tailed dependent samples Student's t tests (24 sessions for Monkey P and 23 sessions for Monkey W) with α = 0.05.

To test for differences between the characteristic time scales of the latent factors estimated by GPFA for the two brain areas of interest, we used a two-tailed independent samples Student's t test (two brain areas, each with 470 observations of latent factors, 47 sessions with 10 factors each) with α = 0.05.

To test the performance of our logistic regression decoders, we used the receiver operating characteristic (ROC; Fig. 4C). For each session, we estimated P(cue_RF) at every time point for every trial (with cross-validation; see above, Decoding attention state) for both brain areas. Then, we calculated the area under the curve (AUC) of ROC values at each time point, yielding a time series of AUC values for each session. We then tested the results of the 47 sessions against the null hypothesis chance value of AUC = 0.5 with a two-tailed, one sample Student's t test at each time point with α = 0.05, corrected for multiple comparisons with Bonferroni's method.

To test for differences in cross-temporal generalization of our decoders between brain areas (Fig. 5E), we applied Fisher's r to z transformation to correlation values then tested against a null hypothesis of no difference between brain areas with a two-tailed dependent samples Student's t test (N = 47 sessions, α = 0.05, Bonferroni corrected for the number of time point pairs).

To test the difference in prediction stability between brain areas (Fig. 6C), we used a two-tailed dependent samples Student's t test (47 sessions) with α = 0.05, corrected for multiple comparisons with Bonferroni's method.

For testing GCI values (Fig. 7), we used a nonparametric permutation test. For each session, we pseudorandomly permuted the trial order for PFC data, holding the trial order for the V4 data constant and taking care to ensure that no permuted trial ever ended up in its original sequence position by chance. Because in this permutation the within-trial order of the time points remained the same, it did not affect the prediction from the reduced model. Instead, it simply destroyed the ability of the added brain area to increase the prediction in the full model. This permutation procedure reflects the null hypothesis that there is no directed information flow between brain areas (i.e., the two brain areas are independent, in which case permuting the trial order should make no difference). We then recalculated GCI for the trial-order-permuted dataset (see above, Granger causal influence for all steps, including model selection and parameter estimation). This procedure was iterated 10,000 times for each session to yield a distribution of GCI values reflecting the null hypothesis. We also generated a null hypothesis distribution for GCI asymmetry by taking the ratio of the PFC-to-V4 null hypothesis distribution to the V4-to-PFC null hypothesis distribution. Observed GCI values were considered significant if they were more extreme than 5% of the permutation test distribution, Bonferroni corrected for the number of sessions tested. For testing the distribution of GCI asymmetry across sessions against a null hypothesis of zero asymmetry, we used a two-tailed one-sample t test with α = 0.05.

Results

We recorded neural population activity from PFC and V4 simultaneously in the same hemisphere of two adult male monkeys (Macaca mulatta; Fig. 1A) while they performed a spatial selective attention task (Fig. 1B). The animals were more accurate (Fig. 1C) and faster (Fig. 1D) at discriminating orientation changes at a high-target-probability location (cue-valid targets) than at a low-target-probability location (cue-invalid), confirming that they selectively attended to the high-target-probability location during the task.

Single-neuron attention signals

The firing rate of individual neurons differed depending on whether the RF location had a high target probability (i.e., was likely attended). As we previously reported (Snyder et al., 2018), most V4 neurons fired more vigorously in response to an attended stimulus than an unattended stimulus (Figure 2A). We did not observe a difference in the average spontaneous firing rate in V4 between attention conditions. In PFC, the average firing rate was slightly more vigorous toward the end of the stimulus interval when attention was directed ipsilaterally compared with when it was directed contralaterally (Fig. 2B). As in V4, average spontaneous firing rates in PFC did not differ between attention conditions.

The patterns of attention modulations observed for individual neurons diverged greatly from the population averages, however. For example, in V4 some neurons that had greater stimulus-related firing rates with attention were in contrast suppressed by attention in the absence of a stimulus (Fig. 2C, top). Other V4 neurons fired comparatively less in response to an attended stimulus than an unattended stimulus (Fig. 2C, middle). Specifically, we found that for 19% of neurons in our sample that had a significant attention effect both before and during the stimulus, the direction of that effect changed between the two time periods of interest (Snyder et al., 2018). This pattern of results suggests that the population code for attention in V4 is dynamic and depends on the stimulus context. For PFC, although the average firing rate was similar between attention conditions, individual neurons showed strong and stable attention effects in different directions (Fig. 2D). Some PFC neurons showed fairly constant firing rates over time (i.e., not stimulus dependent) that differed between attention conditions (Fig. 2D, top). Firing of other PFC neurons was suppressed (Fig. 2D, middle) or facilitated (Fig. 2D, bottom) by stimuli but nonetheless showed consistent differences between attention conditions over time. For example, the proportion of PFC neurons with significant attention effects both before and during the stimulus that changed the direction of their effect between the two time periods was significantly smaller than that for V4 (PFC, 59/1027, 5.4%; V4, 96/404, 19.2%; ${\chi }^2=73.59,p=9.61·{10}^{-18}$).

Population-level attention coding

Population-level analyses can reveal dynamics or stability of neural codes hidden at the single-neuron level (Murray et al., 2017; Snyder et al., 2018), so we tested for this possibility. We first reduced the dimensionality of the activity from each population using GPFA (Yu et al., 2009; Fig. 3A). This allowed us to focus subsequent decoding analyses on variance that was shared among neurons within each population, as well as to avoid overfitting when decoding (the qualitative pattern of results was similar if performed on the full population data, although with worse performance because of overfitting). It is important to note that we performed dimensionality reduction after subtracting the trial-averaged response of each neuron from each trial. That is, we were not interested in dynamics simply because of the average stimulus response but rather sought to emphasize nonstimulus-related activity. In our case, the fitted Gaussian processes for the latent factors that best explained the V4 population activity typically had faster characteristic time scales than the latent factors that best explained the PFC population activity (Fig. 3B), indicating that V4 activity changed more quickly than did PFC activity [V4 time scale: τ = 94.63 ± 46.14 ms, mean ± SD; PFC time scale: τ = 201.82 ± 125.80 ms; independent samples t test: t₍₉₃₈₎ = – 17.24, p = 1.18 · 10^{– 58}, N = 940, 470 factors (i.e., 10 factors for each session) × 2 brain areas]. This suggests that V4 and PFC have different intrinsic time scales, in line with our guiding thesis as well as previous findings (Murray et al., 2014; Runyan et al., 2017).

Although the latent factors for V4 varied more quickly than those for PFC, this does not necessarily mean that the population code for attention in V4 is less stable than in PFC, as previous research has shown encoded information can remain stable despite highly dynamic population activity (Murray et al., 2017; Parthasarathy et al., 2019). Thus, we next applied a decoding approach to the latent factors to assay and compare the time courses of encoded attention information in the two brain areas. We used logistic regression to decode whether the RF (or the opposite hemifield) had been cued from the neural population activity in each brain area (Fig. 4). Because the question of code stability is only interesting if the code carries predictive value, we confirmed our decoders performed significantly better than chance in both brain areas at all time points during a trial (Fig. 4C; t test, p < 0.05 at all time points, Bonferroni corrected). Importantly, we were able to decode attention states even during prestimulus periods during which population average firing rates were quiescent and similar between attention conditions (Fig. 2A). Having established that both V4 and PFC encoded the attention state throughout the experiments, we next asked if we could establish the comparative dynamics of those codes.

Dynamics of population attention codes

In subsequent analyses, rather than decoding a binary value (i.e., cue-in-RF or cue-away), we focused on a more sensitive metric—the probability that the RF had been cued (P(cue_RF)) as an estimate of the attention state. This value was obtained from the logistic regression described above and varies between 0 and 1, where 0 corresponds to cue-away and 1 corresponds to cue-in-RF. Because we were especially interested in the temporal stability of attention signals, we next examined the average time course of P(cue_RF) in each brain area for trials from each attention condition. On trials for which the RF had been cued, the average P(cue_RF) was greater than the equivocal level of 0.5 (Fig. 5A). On average, the P(cue_RF) using V4 activity started near low values and then increased to a peak during the later half of the stimulus presentation before falling again to low levels. In contrast, the average P(cue_RF) in PFC was more consistent over time through the trial. On trials for which the RF was not cued, a similar time course was seen when estimating the probability that the cue had been away from the RF (P(cue_away)), but with weaker overall prediction strengths (Fig. 5B). This qualitative pattern of results suggests that the average readouts of the attention code are more dynamic in V4 than in PFC.

In the analysis described above, we trained an independent decoder at each time point during the peristimulus interval. This enabled us to assess how consistent the decoder weights were over time for each brain area. In other words, we asked, regardless of any change in P(cue_RF), does the pattern of population activity that best encodes the attention state change over time? One way to test this would be to measure correlations between pairs of β weight vectors measured at different time points. Strong correlations persisting over time would be consistent with a stable code, whereas correlations that weakened more rapidly over time would suggest a more dynamic code. We found that β weight vectors in PFC were indeed more strongly correlated over a longer time range than β weight vectors in V4 (data not shown). However, it could be the case that small changes in β weights lead to large changes in decoding performance or that large changes in β weights lead to small changes in decoding performance. That is, it is difficult to interpret the importance of β weight changes by directly comparing these values. Rather, we reasoned it would be more informative to test the ability of decoders to generalize over time. Thus, we measured the correlation across trials among P(cue_RF) values obtained using the data from one time point and the β weights from another time point and P(cue_RF) values obtained using data and β weights from the same time point (in a cross-validated manner; Fig. 5C,D). For V4, the decoded P(cue_RF) values were highly correlated only between nearby time points, which indicates that the attention code in V4 changed over time (Fig. 5C). In contrast, the decoded P(cue_RF) values for PFC were correlated over a significantly greater time range than in V4 (Fig. 5D,E), indicative of a more stable attention code.

Our previous analyses considered the trial-averaged readout of the attention code over time and found that it was more stable in PFC than in V4. However, it may have yet been the case that the P(cue_RF) in PFC was highly dynamic on individual trials but appeared stable when averaged across trials. To test for this possibility, we examined the stability of P(cue_RF) on individual trials for each brain area. At each time point, we calculated the prediction stability as the negative absolute change in P(cue_RF) from the preceding time point (Fig. 6A). We scaled the resultant stability values so that a value of 1 indicated perfect stability (i.e., no change in P(cue_RF) over time), and a value of 0 indicated the expected value if time points were independent. For both animals, the prediction stability was substantially greater in PFC than in V4 (Fig. 6B,C; t test, p < 0.05 at all time points, Bonferroni corrected). This included prestimulus time points, indicating that differences in P(cue_RF) stability were not trivially because of different dynamics of stimulus responsiveness. We note also that although stability dropped transiently in V4 around stimulus onset, in general, stability in V4 was at similar levels during spontaneous and stimulus-evoked activity, indicating stability was not trivially related to overall activity levels. We also found that when comparing the average stability between the two brain areas on the same trial, PFC was consistently more stable than V4 (121,283 total trials, $\Delta 〈s〉=0.041\pm 0.036$, mean ± SD, t_(121282) = 395.46, p ≈ 0, paired t test). These results show that even on single trials, the decoded attention state in PFC was more stable than in V4.

Directionality of attention codes

Our guiding thesis for this study was that a stable attention code in PFC may serve as a consistent beacon of the attention state that may guide the dynamic behavior of sensory populations such as V4. Thus, we asked if there was evidence for a greater directed flow of the encoded attention state information from PFC to V4. To test this, we calculated the GCI between the estimated attention states in PFC and V4 (Fig. 7A). Intuitively, GCI estimates how much the future of one signal can be (linearly) predicted from the past history of another signal, beyond what was predictable from the first signal alone (Barnett and Seth, 2014), and can be quantified as the degree of improvement in that prediction (i.e., as percent residual error explained). Note that GCI does not directly imply mechanistic causality because the role of unobserved variables cannot be ruled out, but it does suggest that the potential for a causal relationship exists. In our case, we wanted to ask how well we could predict the P(cue_RF) of V4 neurons based on the history of those neurons alone compared with the history of both V4 and PFC neurons combined. By also making the analogous comparison in the complementary direction (PFC alone or PFC with V4), we could assess whether changes in PFC were more predictive of what happened next with the attention state in V4, or whether changes in V4 were more predictive of what happened next with the attention state in PFC.

We performed our analysis of GCI between PFC and V4 during two time windows we have focused on before: one before stimulus onset (−290 to −90 ms) and one during the sustained response to the stimulus (150 to 350 ms). In each 200 ms time window of interest, the goal was to test how well we could predict the P(cue_RF) in each 20 ms time bin based on past history within that larger time window. We chose these time windows for two reasons. First, GCI analysis assumes that the signals are stationary, an assumption that would be violated during the transition from the unstimulated to the stimulated state but was more reasonable during these two time windows before and after that transition. Second, they represent two distinct contexts of attention function—the anticipatory period when an attentional state of readiness is prepared and the period of stimulus processing when the benefits of that readiness are conferred. We found evidence for GCI in the PFC-to-V4 direction and/or the V4-to-PFC direction in many sessions (Fig. 7B,D), indicating that incorporating moment-to-moment knowledge of one brain area aided in prediction of upcoming activity in the other. The absolute quantity of residual variance accounted for by GCI was small (<1%), but this is attributable in large part to the difficulty in explaining the variance in the brief time periods of our analysis (20 ms bins). Most importantly, our measurements of GCI were substantially greater (by a factor of >2) in the PFC-to-V4 direction than in the V4-to-PFC direction, both during the prestimulus anticipatory period (Fig. 7B,C), as well as during the sustained stimulus response (Fig. 7D,E). These results are consistent with a framework in which the attention state in PFC influences the future attention state in V4 more than vice versa, in line with the hypothesized role of PFC in the executive control of endogenous selective attention.

Discussion

We found that the population code for attention in PFC was substantially stabler than the population code for attention in V4. Although evidence has been mounting for this type of areal specialization for temporal stability (Murray et al., 2014), previous studies have typically compared neural recordings from different brain areas measured in separate animals performing separate tasks, often in separate laboratories, limiting direct comparison. Furthermore, previous work has often analyzed trial-averaged activity from populations of neurons that were sometimes not simultaneously recorded. Without direct observation, the hypothesized division of labor of stable and unstable computational processes across cortical areas based on the intrinsic time scales of dynamics had been speculative. Our simultaneous recordings show that even moment to moment within an animal, neural codes for attention in PFC are more stable than those in V4.

We also found that the attention code in PFC carried more information from moment to moment about the future attention state of the V4 populations than vice versa. This type of causal role for attention has previously been suggested for FEF (Bressler et al., 2008; Squire et al., 2013), for which strong electrical stimulation causes eye movements to a particular location (movement field), whereas weaker electrical stimulation leads to attention-like gain modulations in extrastriate neurons sensitive to the movement field (Moore and Fallah, 2001), a pattern of results lending support to the so-called premotor theory of covert attention. The current results suggest an extension of this causal role to more rostral populations, which, in our hands, did not lead to eye movements under strong electrical stimulation (see above, Materials and Methods). We caution, however, that our observational GCI analyses should be taken merely as a suggestion that the potential for a causal relationship exists, and we cannot rule out alternatives such as both PFC and V4 receiving influence from a third, unobserved brain area. Together, however, our results provide the first evidence that PFC provides a stable attention code that leads a dynamic attention code in V4 at a time scale of tens of milliseconds, consistent with the hypothesized role of PFC as a source of top-down endogenous attention control signals in primate cerebral cortex.

For a system to be stable entails dynamics that are robust to outside perturbation. Such stability would be adaptive for maintaining cognitive states in mind while actively exploring a dynamic environment. From this perspective, the finding of a stable representation of a long-term attention state (as in PFC) is intuitive. A more challenging question concerns the corollary, that is, Why is the code for attention states in V4 dynamic? A prominent view of the neural correlates of attention is an enhancement of the activity of neurons tuned for relevant information that comes at the expense of suppressed activity for neurons processing less-relevant information through a normalized gain mechanism (Reynolds and Heeger, 2009). That is, each neuron shows a gain in responses that is roughly proportional to the alignment of the tuning curve of that neuron to the attended information. Under the simplest version of this framework, attention would be viewed as a stable modulation of activity levels; that is, the gain modulation in V4 would remain constant while attention is held constant. The current results are incompatible with this view because even during brief periods of spontaneous activity on single trials, we found attention signals to be dynamic on time scales much briefer than those that have been found to characterize attention shifts (on the order of 200–300 ms; Posner, 1980; VanRullen et al., 2007). Instead, our findings suggest a key role for dynamic coding of attention in sensory cortex; that is, if response gain is a key mechanism of attention, it is not applied equally to all sensory neurons at all times.

One potential explanation of dynamic attention codes in V4 is simply that they are a side effect of the function of sensory cortex to respond to sensory input. This is not to say that dynamic responses to sensory events trivially manifest dynamic attention signals. Indeed, in our experiment we took two steps to rule out a potentially trivial relationship between sensory response dynamics and attention signals in V4. First, we performed our analyses on residual firing rates after the average stimulus response had been subtracted, removing the greatest contribution of sensory response dynamics from the data. Second, we calculated P(cue_RF) stability moment to moment to hold stimulus context relatively constant (Fig. 6C). The strongest example of this is that we found P(cue_RF) stability differed among brain areas during spontaneous activity when there was no stimulus response, ruling out a difference in stimulus processing dynamics as a trivial explanation for the difference in attention signal dynamics. Instead, our results are consistent with a more interesting relationship in which the properties of sensory networks that enable them to be responsive predispose them to dynamic attention signaling independent of sensory input. For example, if a stable activity pattern were imposed on sensory populations, even weakly, this stabilizing influence would maladaptively reduce the sensitivity of those populations to sensory input. Indeed, evidence indicates that stable dynamics because of synchronizing input are associated with suppressed sensory processing, in particular in the form of 8–10 Hz oscillations measured as field potentials or electroencephalogram (Kelly et al., 2006; Bollimunta et al., 2011; Snyder et al., 2015). Although this provides a simple explanation for the presence of dynamic attention codes in V4, we can further consider whether such dynamic codes provide additional function.

One context where such a dynamic coding scheme might make sense is to distinguish between the stimulated and unstimulated state. Neural populations in visual cortex face different computational demands in the presence versus the absence of a stimulus. A pattern of neural activity that functions to enhance representation during visual processing may be inappropriate if instead there was no stimulus to process. In support of this notion, we and others reported that the pattern of modulations across the V4 population differed fundamentally between spontaneous and visual-evoked activity (Sani et al., 2017; Snyder et al., 2018). These observations are also consistent with human neuroimaging work, where attentional modulations of visual cortical areas are greatest during sensory processing, whereas attention modulations in frontal and parietal association cortices are in contrast greatest during nonsensory periods (Kastner et al., 1999; Hopfinger et al., 2000; Corbetta and Shulman, 2002). Human neuroimaging work further aligns with our Granger causality findings suggesting a top-down role of frontal anticipatory signals influencing sensory areas (Bressler et al., 2008). The stimulus-context-dependent population codes that we observed may provide a means to multiplex multiple signals within a neural population, enabling separable representations of sensory and cognitive information, such as expectation (Rungratsameetaweemana et al., 2018; Rungratsameetaweemana and Serences, 2019) or motor intention (Kaufman et al., 2014; Elsayed et al., 2016).

Even within the context of processing visual stimuli, there is a growing appreciation that attention is an inherently dynamic process. Evidence suggests that attention is automatically reoriented several times per second to sample multiple sources of sensory information (James, 1890; Posner, 1980; VanRullen et al., 2007; Fiebelkorn et al., 2011; Landau and Fries, 2012). These automatic attention cycles are associated with interactions occurring around the 3–5 Hz theta frequency range across a network including lateral prefrontal and parietal areas (Fiebelkorn et al., 2018), anterior cingulate cortex (Voloh et al., 2015), multiple visual cortical areas (Spyropoulos et al., 2018), and pulvinar nucleus of the thalamus (Fiebelkorn et al., 2019). The frequency of these reorientation cycles is similar to that of the periodic planning and execution of saccadic eye movements in primates, which researchers have also linked to attention-like perceptual effects (Hafed and Clark, 2002; Hafed et al., 2011; Hafed, 2013; Lowet et al., 2018). Although the time scale of these effects are too slow to fully explain our results, it underscores that attention and perception rely fundamentally on dynamic processes. Such periodic movements and covert shifts in perception may have evolved to help us explore our environment, even in the face of particularly salient or engrossing stimuli. This ethological tendency to regularly shift attention is sensible in natural contexts, which are highly dynamic. In contrast, our task was relatively static in that it required subjects to attend for long periods to a consistent location while target probabilities and reward expectations were held constant. Thus, one important remaining question for further study concerns how the division of labor of stable and dynamic attention codes between prefrontal and sensory cortex that we found operates in more naturalistic contexts.

Even within a period of relatively constant attention, the underlying mechanisms may be dynamic on fast time scales reflecting differential modulation of specific stages of sensory processing (Sripati and Johnson, 2006; Sani et al., 2017; Snyder et al., 2018). For example, Sani et al. (2017) found that different types of attention gain manifested in V4 activity across time during sensory responses; an early contrast gain followed by a stimulus-tuned multiplicative gain peaking ∼150 ms after stimulus onset, and then another later round of contrast gain. Those authors interpreted the gradual emergence of stimulus-dependent multiplicative effects that they observed as consistent with a mechanism in which relatively weak top-down input becomes amplified locally through a time-consuming dynamic process. Our current results are also consistent with this notion.

This faster time scale for dynamic attention in V4 is reminiscent of the emergence of feature-selectivity in visual cortex. For example, Ringach et al. (1997) used a reverse correlation approach to measure the temporal development of orientation selectivity in primary visual cortex of monkeys. They found that although neurons in input layers showed relatively static orientation tuning preferences, the orientation preferences of neurons in output layers continued to change over time, in many cases preferring one orientation at short delays but the orthogonal orientation at longer delays, or in some cases developing multimodal orientation preferences. The authors compared the predictions of feedforward and feedback models to conclude that the dynamics of orientation preferences in output layers were likely because of feedback influences, and they surmised the slower complex tuning preferences might encode subtler features of images. One implication of this pair of observations—dynamic attention and dynamic feature-selectivity—is that one potential mechanism for feature-based attention would be to preferentially allocate resources to the time period in the sequence of processing steps when selectivity for that feature emerges. One testable prediction of this hypothesis is that attention directed selectively toward the subtler features of images to which Ringach et al. (1997) alluded should manifest later during the sensory response when tuning for those features emerges, which may account for why attention modulation of sensory responses typically develops well after the initial stimulus-onset transient response (Mehta et al., 2000).

The current results are consistent with a framework in which maintaining stable task-set representations relies on brain areas with intrinsically stabler dynamics (Murray et al., 2014; Runyan et al., 2017); as we showed here for PFC populations. This particular brain area has been linked to many processes unfolding on slow time scales, including categorical reasoning (Freedman et al., 2003; Cromer et al., 2011; McKee et al., 2014), flexible rule-based decision-making (Bunge et al., 2003; Siegel et al., 2015), working memory (Constantinidis et al., 2018; Wasmuht et al., 2018; Parthasarathy et al., 2019), and attention (Ikkai and Curtis, 2011; Paneri and Gregoriou, 2017). It is important to note that the stability in this case resides not at the level of individual neuron firing rates, which in fact vary substantially over time, but rather at a population-level readout. This type of population-level stability has previously been reported for PFC populations in the context of working memory. For example, individual PFC neurons encode mnemonic information predominantly transiently during maintenance periods, with peak latencies distributed to tile the entire interval (e.g., Hussar and Pasternak, 2012, 2013; Spaak et al., 2017). In a compelling example, Tremblay et al. (2015) recorded populations of PFC neurons in monkeys performing a spatial attention task and found that patterns of ensemble activity encoding attention states generalized across time periods within a trial and even across multiple days over a month of recording sessions. This type of population-level stability despite single-cell variability may enable individual PFC neurons to temporally multiplex several concurrent processes while maintaining stable signals at the population level (Mante et al., 2013). Indeed, the activity of prefrontal and sensory populations have been linked to a number of cognitive processes other than selective attention relevant for our task, such as monitoring choice history (Mochol et al., 2021), arousal (Cowley et al., 2020), and reward expectation (Roesch and Olson, 2003), which are likely contributing to the mixtures of population activity that we observed. Although it is often difficult to disentangle these cognitive processes in the context of a given task (Maunsell, 2004), some studies have suggested distinct neural and behavioral signatures for attention compared with sensory expectation (Summerfield and de Lange, 2014; Rungratsameetaweemana et al., 2018; Rungratsameetaweemana and Serences, 2019), reward valuation (Baruni et al., 2015), arousal (Luo and Maunsell, 2019; Cowley et al., 2020), and other related processes. The current experiment cannot tease apart the precise contributions of these various cognitive processes because we did not vary the expected value of rewards separately from the attention cue (Thus, reward and expectation were confounded with attention.), and the animals almost always chose the cued target when making actions (Thus choice history and cue were also confounded.). A future study that separately manipulates rewards within the context of a given attention condition could further dissect the nuances of frontosensory interactions during cognition.

Perhaps our most novel finding is that population attention codes in V4 vary rapidly, and the moment-to-moment interactions between PFC and V4 have apparent control over the attention state. One lingering question remains whether the details of these population-level dynamics are specifically germane for behavior. For example, one reasonable but unintuitive prediction would be that stable attention signals in prefrontal cortex would be beneficial for behavior, whereas stable attention signals in sensory cortical areas such as V4 may actually be detrimental to behavior, as they may undermine responsiveness to external events. Another reasonable prediction is that shifts of attention (e.g., to detect invalidly cued targets) might be accompanied by rapid dynamics of attention signals in both V4 and PFC. The current study was not designed to address these predictions because targets were infrequent, and reactive saccades to targets prohibited disentanglement of sensory and motor signals; a future study with delayed responses and a greater proportion of targets could test these predictions and other issues related to target processing. Together, our results suggest that different cortical areas implicated in attention control are specialized to function in different regimes of stability to resolve the competing demands of attention; stable representations of task variables are maintained on long time scales in prefrontal cortical populations, freeing up sensory cortical populations to maintain the sensitivity to outside perturbation essential for efficient perception.