Skip to main content
PMC home page
Elsevier - PMC COVID-19 Collection logoLink to Elsevier - PMC COVID-19 Collection
. 2021 May 24;789:148004. doi: 10.1016/j.scitotenv.2021.148004

Effect of daily temperature fluctuations on virus lifetime

Te Faye Yap 1, Colter J Decker 1, Daniel J Preston 1,⁎
PMCID: PMC8570935  PMID: 34323833

Abstract

Epidemiological studies based on statistical methods indicate inverse correlations between virus lifetime and both (i) daily mean temperature and (ii) diurnal temperature range (DTR). While thermodynamic models have been used to predict the effect of constant-temperature surroundings on virus inactivation rate, the relationship between virus lifetime and DTR has not been explained using first principles. Here, we model the inactivation of viruses based on temperature-dependent chemical kinetics with a time-varying temperature profile to account for the daily mean temperature and DTR simultaneously. The exponential Arrhenius relationship governing the rate of virus inactivation causes fluctuations above the daily mean temperature during daytime to increase the instantaneous rate of inactivation by a much greater magnitude than the corresponding decrease in inactivation rate during nighttime. This asymmetric behavior results in shorter predicted virus lifetimes when considering DTR and consequently reveals a potential physical mechanism for the inverse correlation observed between the number of cases and DTR reported in statistical epidemiological studies. In light of the ongoing COVID-19 pandemic, a case study on the effect of daily mean temperature and DTR on the lifetime of SARS-CoV-2 was performed for the five most populous cities in the United States. In Los Angeles, where mean monthly temperature fluctuations are low (DTR ≈ 7 °C), accounting for DTR decreases predicted SARS-CoV-2 lifetimes by only 10%; conversely, accounting for DTR for a similar mean temperature but larger mean monthly temperature fluctuations in Phoenix (DTR ≈ 15 °C) decreases predicted lifetimes by 50%. The modeling framework presented here provides insight into the independent effects of mean temperature and DTR on virus lifetime, and a significant impact on transmission rate is expected, especially for viruses that pose a high risk of fomite-mediated transmission.

Keywords: Diurnal temperature range, Thermal inactivation, Coronavirus, WAVE model, SARS-CoV-2, COVID-19

Graphical abstract

Unlabelled Image

Open in a new tab

1. Introduction

Epidemiologists incorporate environmental effects when modeling the spread of diseases by applying statistical methods to determine whether environmental variables correlate with transmission rates (Malki et al., 2020; Rahman et al., 2020; Sajadi et al., 2020). Environmental temperature is often considered; however, most models only account for the daily mean temperature (Sethwala et al., 2020; Merow and Urban, 2020; Pirouz et al., 2020; Sajadi et al., 2020), despite studies reporting that the diurnal temperature range (DTR) also plays a significant role in forecasting the transmission of diseases (Islam et al., 2020; Liu et al., 2020; Luo et al., 2013; Ma et al., 2020). One recent study on the mosquito's (Aedes aegypti) ability to transmit dengue virus showed that an increase in DTR reduces transmission rates at mean temperatures above 18 °C (Lambrechts et al., 2011). This work studied the importance of considering both (i) daily mean temperatures and (ii) temperature fluctuations; the pathogen was transmitted by an active vector, where the virus lifetime may be less significant than in the case of a passive vector (e.g., fomite-mediated transmission), but DTR nevertheless played a role. Meanwhile, thermodynamic models built on first principles have been used to predict the lifetime of viruses based on constant-temperature surroundings (Yap et al., 2020), but a framework describing the relationship between virus inactivation rate and DTR has not been established.

The ongoing COVID-19 pandemic represents a critical area where such a fundamental physical model could find use. Recent literature describes epidemiological studies based on statistical analyses that document an inverse correlation between DTR and relative risk (RR), where RR represents the ratio of the probability of infection under a given condition to the probability of infection in a control group. For example, studies by Islam et al. and Liu et al. present statistical analyses accounting for DTR, and they both report a correlation coefficient between RR and DTR of less than one for COVID-19 (Islam et al., 2020; Liu et al., 2020), indicating lower infection rates at higher values of DTR. A study conducted during the onset of the pandemic in China seemingly showed the opposite relationship, reporting a positive correlation of DTR with number of deaths due to COVID-19; however, higher DTR is also known to increase the overall risk of mortality (Kim et al., 2016), and as such, mortality can be a poor indicator for the rate of transmission in this context. More recent studies in India, Indonesia, and Russia report negative correlations between DTR and COVID-19 infection rates or number of cases (Pramanik et al., 2020; Pratim, 2020; Supari et al., 2020), which is likely attributable, at least in part, to shorter virus lifetimes outside of a host at high DTR because fomites have served as a mode of transmission for other viruses (Abdelrahman et al., 2020; Boone and Gerba, 2007; Xiao et al., 2017). Although fomite-mediated transmission is not likely the primary mode of transmission for SARS-CoV-2, it still poses a risk (Bouchnita and Jebrane, 2020; Gao et al., 2021; Kampf et al., 2020; van Doremalen et al., 2020; Xiao et al., 2017; Zhao et al., 2020). These studies consider the aggregated statistical effects of environmental conditions to correlate DTR to number of cases, but they do not provide a fundamental understanding of the virus inactivation behavior.

Prior work introduced an analytical model that uses the rate law for a first-order reaction and the Arrhenius equation to predict the lifetime of coronaviruses as a function of constant temperature (Yap et al., 2020). This model treats viruses as macromolecules that are inactivated by thermal denaturation of the proteins comprising each virion to predict the time required to achieve an n-log inactivation, which is defined as the ratio of final viable concentration of a pathogen to its initial concentration in terms of 10 raised to the nth power ([C] / [C 0] = 10−n). For consistency throughout this work, we define the “lifetime” of a virus as the time required to achieve a 3-log reduction in concentration of that virus (i.e., n = 3) based on guidance from the US Food and Drug Administration (FDA); specifically, the FDA recommends a 3-log (99.9%) reduction in virus concentration for decontamination of non-enveloped viruses (CDC, 2008; FDA, 2020a, FDA, 2020b; Oral et al., 2020), which are typically more resistant to thermal inactivation than enveloped viruses (Firquet et al., 2015; Yeo et al., 2020), allowing a conservative prediction of lifetime for both types of viruses.

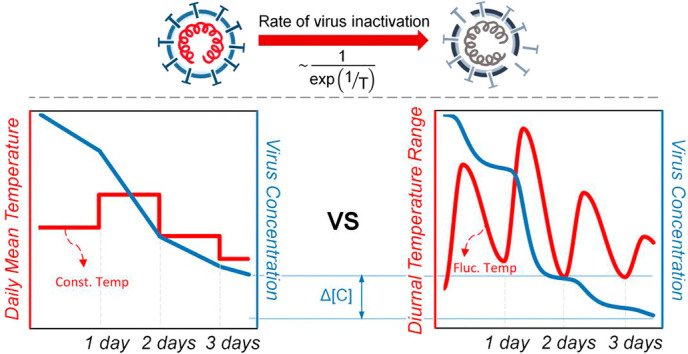
The lifetime of a virus has an exponential dependence on temperature, fundamentally underpinning our hypothesis that accounting for environmental temperature fluctuations will decrease virus lifetimes compared to relying only on daily mean temperature data. To further explore this hypothesis, we introduced a numerical model to incorporate environmental temperature fluctuations, enabling predictions of the lifetime of viruses and showing the disparities between the computed virus lifetime when using (i) daily mean temperature only (i.e., a constant daily temperature profile) and (ii) accounting for both daily mean temperature and DTR (i.e., a time-varying temperature profile). Fig. 1 shows a graphical illustration of the difference between models of virus lifetime based on these two profiles. The inactivation rate constant, k, varies exponentially with temperature (Fig. 1(a)), and this exponential dependence results in temperature fluctuations above the mean influencing the instantaneous rate of inactivation to a greater extent than fluctuations below the mean. Fig. 1(b) shows the difference in inactivation rate between the two temperature profiles. The plot on the right shows a greater increase in magnitude of the instantaneous value of k as a result of temperature fluctuations above the daily mean temperature (i.e., daytime) compared to the corresponding decrease in inactivation rate for temperatures below the mean (i.e., nighttime), resulting in a shorter overall virus lifetime. The illustration shows how incorporation of DTR generates shorter predicted virus lifetimes compared to daily mean temperature alone. We also show that the virus lifetime will always decrease when considering fluctuations in temperature in the Supplementary material to provide a quantitative fundamental understanding of the phenomenon. We compare the change in concentration at the mean temperature only to the change in concentration when considering temperature fluctuations while accounting for both symmetric and asymmetric time-varying temperature profiles. This physical behavior could explain the inverse correlation between DTR and RR observed in statistical epidemiological studies (Islam et al., 2020; Lambrechts et al., 2011; Lin et al., 2020; Liu et al., 2020; Pramanik et al., 2020; Pratim, 2020; Supari et al., 2020). We go on to present a case study on SARS-CoV-2 in the five most populous cities in the United States to illustrate the difference in virus lifetime when accounting for DTR. In this work, we model the inactivation rate of viruses based on temperature-dependent chemical kinetics with a time-varying environmental temperature profile to account for the daily mean temperature and DTR simultaneously. This physical model of the effect of DTR on virus lifetime will elucidate the role of environmental temperature in the spread of viruses. We also show that this physical model can be applied to a range of coronaviruses, as well as influenza, which exhibits similar temperature-dependent inactivation behavior and seasonality (McDevitt et al., 2010). This work may provide an explanation as to why regions with similar daily mean temperatures can have starkly different virus transmission rates. Our model may also explain—at least in part—the surge of COVID-19 that has been observed in winter, as temperatures dropped and the virus lifetime increased by orders of magnitude.

Fig. 1.

Fig. 1

Open in a new tab

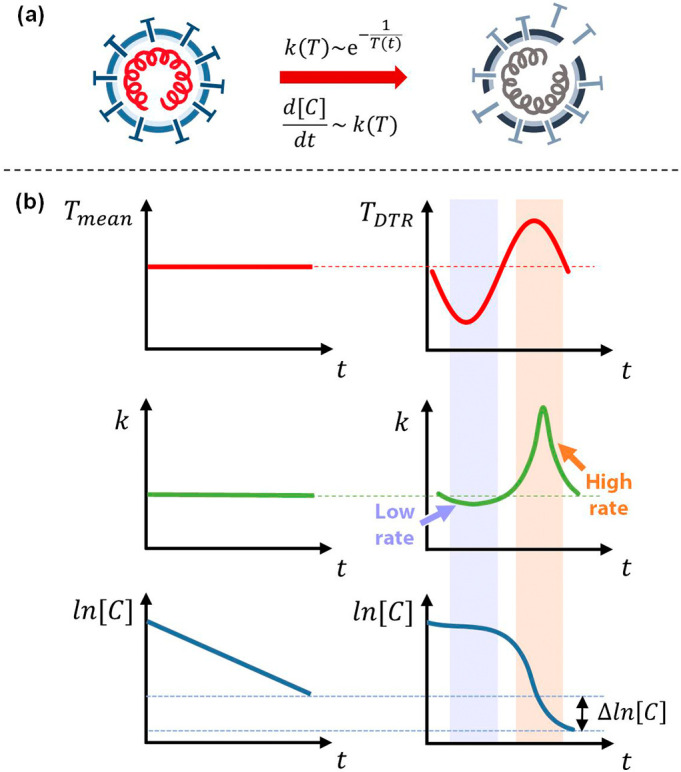
The rate of inactivation of a virus depends on temperature following the rate law and Arrhenius equation (a). The effect of a time-varying temperature profile about the mean temperature influences the rate constant, k, for inactivation of a virus and, consequently, the concentration of a virus over time (b). The exponential dependence of the rate constant on temperature results in a higher net rate of inactivation of a virus when incorporating environmental temperature fluctuations about the mean temperature.

2. Material and methods

2.1. Theoretical framework

The rate law for a first-order reaction (Eq. (1)) can be used to determine the inactivation of viruses (Yap et al., 2020).

dCdt=−kT·C (1)

The rate constant, k, is governed by the Arrhenius equation, and can be determined for a given temperature. Previous models have considered only a constant temperature profile: temperature, T, did not vary with time, t. In this work, we calculate a time-varying rate constant as a function of a time-varying temperature profile using the Arrhenius equation (Eq. (2)):

kT=A·e−EaR·Tt (2)

where R is the gas constant, E a is the activation energy associated with inactivation of the virus (i.e., the energy barrier that must be overcome for protein denaturation), and A is the frequency factor. The E a and ln(A) values for SARS-CoV-2, SARS-CoV-1, and MERS-CoV were determined in prior work (Yap et al., 2020) and are reported in Table 1 . The model can also be used to determine the lifetime of other viruses, including influenza viruses (responsible for the seasonal flu); we calculated values of E a and ln(A) for Influenza A based on existing literature (McDevitt et al., 2010) to highlight the versatility of the model (primary data included in the Supplementary material). These four enveloped viruses affect the respiratory system (Abdelrahman et al., 2020), and the corresponding results could be relevant to understanding the current pandemic (Abdelrahman et al., 2020; Zhu et al., 2020).

Table 1.

Activation energy and frequency factor values used to determine virus lifetime. Values for coronaviruses were determined in prior work (Yap et al., 2020). Primary datasets used to obtain activation energy and frequency factor for Influenza A are provided in the Supplementary material.

Activation energy, Ea [kJ/mol] Frequency factor, ln(A) [1/min]
SARS-CoV-2 135.7 48.6
SARS-CoV-1 142.6 51.9
MERS-CoV 135.4 49.5
Influenza A 41.0 12.2
Open in a new tab

Environmental temperatures vary continuously with time, and this time-varying temperature profile can be used to determine the rate constant as a function of time. The daily temperature maximum, T max, and minimum, T min, are available for most regions with weather stations, while daily hourly temperature data are not often reported; therefore, we chose the WAVE diurnal temperature model introduced by de Wit, based on maximum and minimum temperature values, to represent the continuous daily temperature profile for a given location (Baker et al., 1988; Cesaraccio et al., 2001; Reicosky et al., 1989). Two half-cosine functions were used to estimate this diurnal temperature profile. For the first half-cosine function, the period, p 1, was calculated as the time between sunrise, when the minimum temperature occurs, and 1400 h solar noon, when the maximum temperature occurs. The second half-cosine function continues from 1400 h solar noon throughout the remainder of the 24-hour day for the second period, p 2, and joins with the first half-cosine function of the following day, d + 1, at sunrise, where d represents the day for which the temperature used in the model is obtained. The sunrise times in each city were obtained to determine the periods for the WAVE model. The temperature profile is defined by a piecewise function, given by Eq. (3):

Tt=−Tmax,d−Tmin,d2cosπp1t+Tmax,d+Tmin,d2,sunrised≤t<1400hrd−Tmax,d−Tmin,d+12cosπp2t−πp2p1+Tmax,d+Tmin,d+12,1400hrd≤t<sunrised+1 (3)

The expression for the daily temperature profile (Eq. (3)) is substituted into Eq. (2), which is then combined with Eq. (1). Separation of variables is applied to yield the final expression used to determine the virus concentration after a given period of time:

∫C0CfinaldCC=∫t0tfinal−A·e−EaR·Ttdt (4)

Due to the cumbersome temperature profile function, analytical integration of the right-hand side of Eq. (4) was not possible; we solved it numerically using Euler's method (details included in the Supplementary material).

2.2. Data collection

The daily sunrise times and maximum and minimum temperature data for the five cities with the highest populations in the United States were obtained from the National Oceanic and Atmospheric Administration (NOAA) solar calculator and climate data online search. A sinusoidal temperature profile that takes into account each city's maximum and minimum temperature was created for the period of January through December of 2020. The temperature profile, T(t), was then used to solve for the reduction in concentration of virus as a function of time. The lifetime of the virus starting from sunrise on each calendar day was determined by calculating the concentration of viable virions as a function of the continuous temperature distribution over time, and then determining the time required to achieve a 3-log reduction in concentration. The maximum cutoff point of the predicted lifetime was taken to be 30 days for two reasons: (i) to correspond approximately to one month, after which the uncertainty in predictions becomes large due to other potential inactivation mechanisms (Yap et al., 2020); and (ii) to include the virus lifetime for the colder winter months through the end of November 2020 (the predicted virus lifetimes in some cities span more than one month, thus requiring temperature data from the subsequent month; at the time of preparing the results in this manuscript, only data through December 2020 were available). The n values were determined by taking the logarithm of the ratio of concentration at a given time, [C]final, to the initial concentration, [C]0.

2.3. Model development: activation energy and frequency factor

The relevant physical parameters governing thermal inactivation of viruses were quantified from primary data reported in the literature. The log of concentration reported in primary experimental data on temperature-based inactivation of viruses, ln([C]), was plotted as a function of time, t. According to the rate law for a first-order reaction (Eq. (1)), we determined the rate constant, k, for inactivation of a virus at a given temperature, T, by applying a linear regression and calculating the slope, k = –∆ln([C])/∆t, as detailed in prior work (Yap et al., 2020). Each pair of k and T determined for a given virus was plotted; according to the Arrhenius equation (Eq. (2)), these data points yield a linear relationship between ln(k) and 1/T. From the linear fit, the activation energy, E a, and natural log of frequency factor, ln(A), can be obtained from the slopes and intercepts, respectively, of the fitted curves for each virus. These values were used in our analysis to determine the lifetimes of viruses in different regions as a function of daily mean temperature and daily temperature fluctuations using the numerical model presented in this work. The activation energy and frequency factor used here for SARS-CoV-2, SARS-CoV-1, and MERS-CoV were already determined in prior work (Yap et al., 2020), whereas the procedure used to determine the thermodynamic parameters used in this work for Influenza A is detailed in the Supplementary material.

3. Results

The degree of inactivation of a virus, defined by the n-log reduction, is used to describe the order of magnitude decrease in virus concentration. The degree of inactivation is plotted against time to show the amount of time needed to achieve an n-log reduction, where Fig. 2 shows the lifetime (i.e., time until 3-log reduction) of three different coronaviruses and Influenza A computed using the time-varying temperature profile versus the daily mean temperature profile.

Fig. 2.

Fig. 2

Open in a new tab

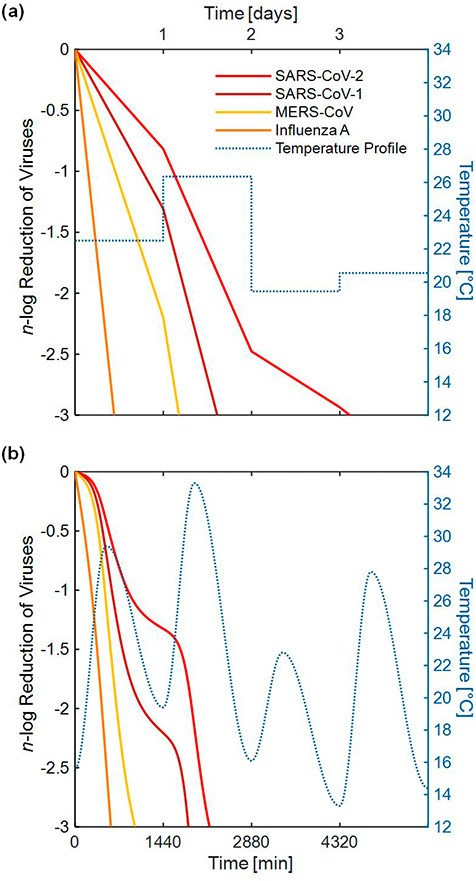
Comparison of the degree of inactivation of three coronaviruses and Influenza A between (a) a simple daily mean temperature profile and (b) a time-varying temperature profile (temperature data shown for Houston starting on May 7, 2020). SARS-CoV-2 would require approximately 3 days to reach decontamination to a 3-log reduction in concentration according to the simple daily mean temperature model, whereas the more realistic time-varying environmental temperature profile showed that decontamination would require less than 1.5 days. The percentage difference in predicted lifetime across all four viruses when accounting for the DTR was approximately 50%.

For illustration, temperature data for Houston starting on May 7, 2020, was used to determine the lifetime using the time-varying temperature profile versus the daily mean temperature profile. Fig. 2 shows the disparity in predicted lifetime when using the two different temperature profiles. In this case, when computing the lifetime of SARS-CoV-2 using daily mean temperatures (Fig. 2(a)), it took approximately 3 days to achieve a 3-log reduction, whereas the more realistic time-varying environmental temperature profile (Fig. 2(b)) showed that decontamination would require less than 1.5 days. The reduction in predicted virus lifetime across all four viruses when accounting for DTR was approximately 50%, highlighting the importance of DTR when modeling virus lifetime. All four of the viruses described in Table 1 are modeled in Fig. 2; however, due to the ongoing pandemic, only SARS-CoV-2 is emphasized throughout the remainder of this work.

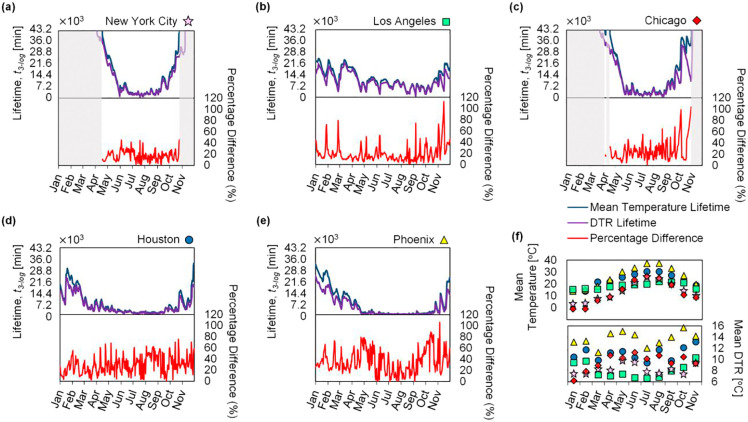
For the top five most populous cities in the United States (New York City, Los Angeles, Chicago, Houston, and Phoenix), the lifetime of SARS-CoV-2 was calculated using the mean temperature profile and the time-varying temperature profile, with results plotted as blue and purple lines, respectively, in Fig. 3 (a–e). The percentage difference in lifetime predictions for these two temperature profiles was also determined and plotted in red. The daily mean temperature and DTR values were averaged by month for each city and plotted in Fig. 3(f) to show the monthly variation in temperature and provide a comparison between the cities. During the winter months with low daily mean temperatures, the virus lifetime can be greater than one month; as the temperature increases during the summer, the lifetime of the virus becomes several orders of magnitude shorter. Cities like Los Angeles, which have relatively low variations in mean temperature throughout the year, exhibit correspondingly small variations in SARS-CoV-2 lifetime, whereas cities like New York City and Chicago show large variations in virus lifetime due to large variations in mean temperature throughout the year. We also observed that the percentage difference in lifetime predictions between the time-varying temperature profile and daily mean temperature profile is relatively low for Los Angeles when compared to Phoenix, in this case due to the higher typical DTR experienced by Phoenix (≈ 2× the DTR of Los Angeles).

Fig. 3.

Fig. 3

Open in a new tab

Lifetime of SARS-CoV-2 and percentage difference between predictions using the simple daily mean temperature profile (blue line) versus the time-varying temperature profile (purple line) for the five most populous cities in the U.S. as reported by the U.S. Census Bureau: (a) New York City, (b) Los Angeles, (c) Chicago, (d) Houston, and (e) Phoenix. The plots show the predicted lifetime of SARS-CoV-2 for the months of January 2020 through November 2020. The mean temperature and DTR pertaining to each city averaged by month are plotted in (f) to illustrate climate trends in each city. The symbols correspond to (a)-(e). The lifetime axis is scaled to reflect 30 days (7.2 × 103 min = 5 days); predicted values for lifetimes greater than one month are not reported, and the corresponding periods of time are shaded in gray. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We studied the generalized effect of DTR on the lifetime of SARS-CoV-2 (for applicability to any city) by implementing a parametric sweep across both daily mean temperature and DTR (Fig. 4 ), showing the predicted lifetime of the virus in Fig. 4(b) and the percentage difference between the lifetimes calculated using the two different temperature profiles (simple daily mean versus time-varying) in Fig. 4(c). The time-varying temperature profile used to calculate the virus lifetime in Fig. 4 maintains a fixed sunrise time at 0600 h; a comparison of virus lifetime computed between varied and fixed sunrise time showed an average percentage difference of 0.68% across all five cities discussed above (Fig. S8 in the Supplementary material). The lifetime at each point on the heat map was computed by holding the daily mean temperature and DTR constant in the WAVE temperature profile. The computed lifetime becomes dependent on the starting time of the temperature profile at high mean temperature and high DTR due to shorter virus lifetimes (i.e., less than one day); modeling the virus lifetime starting from solar noon (at the maximum temperature) versus sunrise (at the minimum temperature) can yield an order of magnitude higher initial rate constant due to the exponential dependence on temperature. To overcome this issue and accommodate generalized results, the values presented in the heat maps are provided on an averaged basis, determined by taking the geometric mean of lifetimes starting every hour for a full diurnal temperature cycle; i.e., the values shown in the plots represent an average of 24 predicted lifetimes, each offset by one hour in starting time throughout a diurnal cycle. The percentage difference is then calculated by comparing the averaged lifetimes determined using the time-varying temperature profile with those from the simple daily mean temperature profile.

Fig. 4.

Fig. 4

Open in a new tab

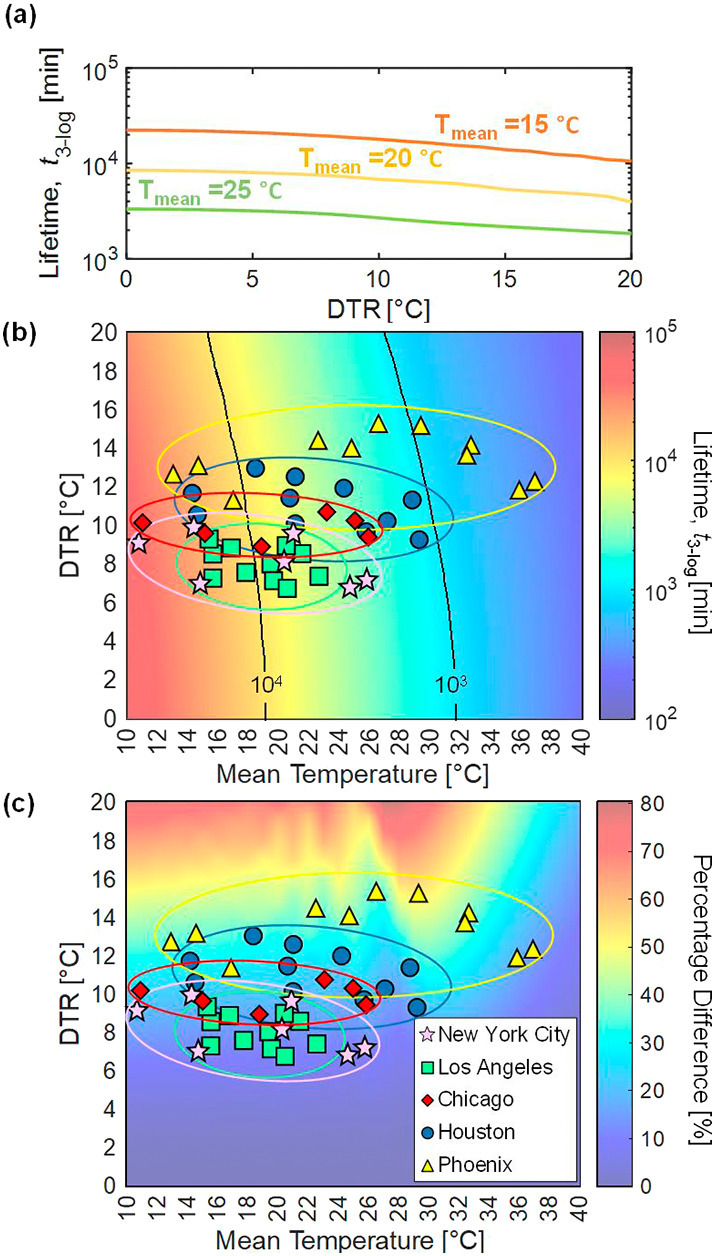
The lifetime of SARS-CoV-2 varies with both the mean environmental temperature and the DTR. The lifetime of the virus is plotted against DTR for mean temperatures of 15, 20, and 25 °C to show that an increased DTR results in a shorter lifetime (a). A parametric sweep shows the lifetime of SARS-CoV-2 versus mean temperature and DTR (b), where increasing mean temperature and DTR both result in shorter virus lifetime. The percentage difference between predicted lifetime of SARS-CoV-2 calculated with the simple mean temperature profile versus lifetime calculated with the time-varying temperature profile accounting for DTR (c) shows that disparities between the two models are larger for higher values of DTR, with up to 50% deviation in lifetime due to DTR in some climates considering monthly averaged temperatures. The mean monthly DTR and mean temperatures for each city are overlaid to highlight trends of virus lifetime in cities with disparate climates. City-specific data points for months corresponding to mean temperatures less than 10 °C are not included.

4. Discussion

As shown in Fig. 4(a), for a given daily mean temperature, the virus lifetime is shorter for regions with higher DTR. Cities like Los Angeles with relatively small temperature variations throughout the year see correspondingly small effects on virus lifetime, whereas cities like Phoenix, with both high DTR and large variations in mean temperature, exhibit a wider range of virus lifetimes spanning across the contour lines on the lifetime heat map throughout a year (Fig. 4(b)). Cities like New York City and Chicago experience extreme cold temperatures in winter, resulting in virus lifetimes greater than one month, but as the environmental temperatures become warmer, virus lifetime drastically decreases. Fig. 4(c) shows the percentage difference between predictions based on daily temperature fluctuations and those only considering daily mean temperatures. At DTR = 0, this plot shows predictions based only on the mean temperature; in this case, the percentage difference between the two models is effectively 0%. This heat map also shows where daily temperature fluctuations become important. For example, Phoenix typically has a high average monthly mean temperature and a large DTR, resulting in a high percentage difference (35–50%) between the two models. On the other hand, Los Angeles, with lower monthly mean temperatures and DTR, exhibits a relatively small percentage difference (10–20%). We also note that daily temperature variations could yield percentage differences as high as 120% (Fig. 3(b–d)), further highlighting the influence DTR has on the prediction of virus lifetime across regions and illustrating that, as the DTR increases, the difference in predicted virus lifetime becomes more pronounced. For a given mean temperature, as the magnitude of DTR increases, the percentage difference between the two models becomes monotonically larger, signifying the importance of accounting for fluctuating environmental temperatures. This knowledge of how DTR influences virus lifetime becomes crucial when comparing policy decisions for cities or regions with similar daily mean temperatures but different DTR because they may experience disparate virus lifetimes.

The model presented in this work elucidates the independent effects of the magnitude of DTR and mean temperature on virus lifetime. This information could be of use when predicting the spread of the COVID-19 pandemic by providing a physical understanding of the effects of DTR, allowing epidemiologists to treat the environmental temperature variables independently. We note that reports in the literature using statistical analyses to study the correlation between various meteorological variables have considered DTR and have found a negative correlation between the magnitude of DTR and number of cases of COVID-19. In one instance, Islam et al. studied the COVID-19 cases in seven climatic regions of Bangladesh from March to May 2020 and reported mean relative risk (RR) values of 0.95–0.97 as a function of increased DTR (with RR < 1 indicating that the risk of transmission is decreased) (Islam et al., 2020). Another study by Liu et al. reported a pooled RR of 0.9 for each 1 °C increase in the DTR for 30 cities in China from January 2020 to March 2020 and suggested that the viruses thrive in regions with low DTR or constant temperature (Liu et al., 2020). Recent studies on the number of COVID-19 cases in Indonesia, India, and Russia (the sub-arctic region) also reported negative correlations with DTR, all showing a similar trend despite representing vastly different regions of the world (Pramanik et al., 2020; Pratim, 2020; Supari et al., 2020). Prior work studying the dengue virus—an endemic virus in more than 100 countries—found that mosquitoes, the primary vector for transmission of the disease, are less susceptible to infection at high DTR, resulting in a lower rate of transmission of the disease (Ehelepola and Ariyaratne, 2016; Lambrechts et al., 2011); further investigation of the specifics of this vector of transmission in the context of DTR may be possible using our modeling framework. We also included Influenza A in Fig. 2 because Influenza A exhibits temperature-dependent inactivation (see Fig. S6 in Supplementary material). Several studies indicate a positive correlation between Influenza A transmission and DTR, but these studies also mention that large temperature fluctuations tend to lower the immune system and consequently increase the risk of infections (Park et al., 2020; Zhang et al., 2019), suggesting that a more detailed statistical analysis would be needed to determine the isolated effect of DTR on transmission of Influenza A.

In the context of these findings, we emphasize that the purpose of the model presented here is to provide a fundamental understanding of the impact of realistic environmental temperature fluctuations on virus lifetime as compared to only considering mean daily temperatures. The model does not consider relative humidity, fomite material (i.e. the surface contaminated with a virus), or solar irradiation on exposed outdoor surfaces, all of which are known to affect virus lifetime (Carleton et al., 2021; Ficetola and Rubolini, 2021; McDevitt et al., 2010; van Doremalen et al., 2020; Zhang et al., 2020; Zhao et al., 2020). Relative humidity and fomite material can be treated as catalytic effects (Morris et al., 2020; Roduner, 2014) (among other mechanisms (Lin and Marr, 2020)), and adjustments to the activation energy could allow for additional predictive capabilities. Varying non-pharmaceutical intervention methods and social structures also play a role in the transmission of diseases and must be carefully accounted for when modeling the site-specific spread of the current pandemic (Bouchnita and Jebrane, 2020; Ficetola and Rubolini, 2021; Lin et al., 2020; Thu et al., 2020; Zhao et al., 2020). For simplicity and ease of comparison between the environmental temperatures of different cities, the temperature profiles used in this work are assumed to follow a smooth sinusoidal profile as described by the WAVE model; in reality, the actual temperature profiles are not smooth, and deviations from a sinusoidal profile may occur. Fortunately, specific regional environmental temperatures can easily be incorporated into Eq. (4) in future work as T(t). Finally, we note that there are different methods to express time-varying temperature profiles; the WAVE profile was utilized in this study due to its simple, yet accurate, depiction of the diurnal temperature cycle, where prior work has shown that the WAVE model had an R2 value of 0.95 compared to actual observed hourly temperature data and exhibited an absolute error of less than 3 °C (Baker et al., 1988; Cesaraccio et al., 2001; Reicosky et al., 1989). The lifetimes presented in Fig. 3 have been limited to a maximum of one month due to inherent uncertainties in predictions at colder temperatures and longer times. In Fig. 4, the lower limit of the daily mean temperature was chosen as 10 °C because the lifetime at lower temperatures is greater than one month.

5. Conclusions

This study presents an analytical framework to understand the effects of temperature fluctuations on virus lifetime. We show that regions with similar mean temperatures can potentially exhibit a difference in virus lifetime of greater than 50% when accounting for DTR, and daily temperature variations in a city could result in differences as large as 120%. Our model allows for incorporation of realistic temperature profiles to predict the transmission of viruses and could therefore play a role in mitigating the spread of COVID-19. In addition, an array of mean environmental temperature and DTR values were used to determine the virus lifetime and highlight, for a given mean temperature, the magnitude of DTR at which temperature fluctuations become significant in predicting virus lifetime. Finally, we show that the model can be adapted to predict lifetimes and seasonal trends for other viruses—including, potentially, novel viruses that have not yet been encountered—and used as a tool based on lab-scale experimental characterization or simulation, rather than statistical analysis of transmission after a virus has already become widespread. Ultimately, this work describes how time-varying environmental temperature profiles result in shorter virus lifetime with a framework to bridge the gap between statistical analyses and physical understanding.

CRediT authorship contribution statement

Te Faye Yap: Conceptualization, Methodology, Visualization, Data curation, Formal analysis, Investigation, Writing – original draft, Writing – review & editing. Colter J. Decker: Data curation, Investigation, Writing – review & editing. Daniel J. Preston: Conceptualization, Methodology, Investigation, Formal analysis, Supervision, Funding acquisition, Writing – original draft, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

We gratefully acknowledge funding support from the National Science Foundation under Grant No. CBET-2030023, with Dr. Ying Sun as program director.

Editor: Jay Gan

Footnotes

Appendix A

Supplementary data to this article can be found online at https://doi.org/10.1016/j.scitotenv.2021.148004.

Appendix A. Supplementary data

The following are the supplementary data related to this article.

Supplementary material

mmc1.pdf (655.8KB, pdf)
Dataset S1

Temperature data corresponding to the five most populous cities in the United States.

mmc2.xlsx (91.6KB, xlsx)
Dataset S2

Sunrise time data corresponding to the five most populous cities in the United States. Highlighted cells are adjusted for daylight saving time (note that Phoenix does not observe daylight saving time).

mmc3.xlsx (27KB, xlsx)

References

  1. Abdelrahman Z., Li M., Wang X. Comparative review of SARS-CoV-2, SARS-CoV, MERS-CoV, and influenza a respiratory viruses. Front. Immunol. 2020;11 doi: 10.3389/fimmu.2020.552909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Baker J.M., Reicosky D.C., Baker D.G. Estimating the time dependence of air temperature using daily maxima and minima: a comparison of three methods. J. Atmos. Ocean. Technol. 1988;5:736–742. doi: 10.1175/1520-0426(1988)005&#x0003c;0736:ettdoa&#x0003e;2.0.co;2. [DOI] [Google Scholar]
  3. Boone S.A., Gerba C.P. Significance of fomites in the spread of respiratory and enteric viral disease. Appl. Environ. Microbiol. 2007;73:1687–1696. doi: 10.1128/AEM.02051-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bouchnita A., Jebrane A. A hybrid multi-scale model of COVID-19 transmission dynamics to assess the potential of non-pharmaceutical interventions. Chaos, Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109941. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Carleton T., Cornetet J., Huybers P., Meng K.C., Proctor J. Global evidence for ultraviolet radiation decreasing COVID-19 growth rates. Proc. Natl. Acad. Sci. 2021 doi: 10.1073/pnas.2012370118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. CDC Disinfection of healthcare equipment. 2008. https://www.cdc.gov/infectioncontrol/guidelines/disinfection/healthcare-equipment.html URL.
  7. Cesaraccio C., Spano D., Duce P., Snyder R.L. An improved model for determining degree-day values from daily temperature data. Int. J. Biometeorol. 2001;45:161–169. doi: 10.1007/s004840100104. [DOI] [PubMed] [Google Scholar]
  8. Ehelepola N.D.B., Ariyaratne K. The correlation between dengue incidence and diurnal ranges of temperature of Colombo district, Sri Lanka 2005–2014. Glob. Health Action. 2016;9 doi: 10.3402/gha.v9.32267. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. FDA . 2020. Investigating Decontamination and Reuse of Respirators in Public Health Emergencies. [Google Scholar]
  10. FDA . FDA; 2020. Recommendations for Sponsors Requesting EUAs for Decontamination and Bioburden Reduction Systems for Face Masks and Respirators During the Coronavirus Disease 2019 (COVID-19) Public Health Emergency. [Google Scholar]
  11. Ficetola G.F., Rubolini D. Containment measures limit environmental effects on COVID-19 early outbreak dynamics. Sci. Total Environ. 2021;761 doi: 10.1016/j.scitotenv.2020.144432. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Firquet S., Beaujard S., Lobert P.E., Sané F., Caloone D., Izard D., Hober D. Survival of enveloped and non-enveloped viruses on inanimate surfaces. Microbes Environ. 2015;30:140–144. doi: 10.1264/jsme2.ME14145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gao C.X., Li Y., Wei J., Cotton S., Hamilton M., Wang L., Cowling B.J. Multi-route respiratory infection: when a transmission route may dominate. Sci. Total Environ. 2021;752 doi: 10.1016/j.scitotenv.2020.141856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Islam A.R.M.T., Hasanuzzaman M., Azad M.A.K., Salam R., Toshi F.Z., Khan M.S.I., Alam G.M.M., Ibrahim S.M. Effect of meteorological factors on COVID-19 cases in Bangladesh. Environ. Dev. Sustain. 2020 doi: 10.1007/s10668-020-01016-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kampf G., Todt D., Pfaender S., Steinmann E. Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents. J. Hosp. Infect. 2020;104:246–251. doi: 10.1016/j.jhin.2020.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Kim J., Shin J., Lim Y.H., Honda Y., Hashizume M., Guo Y.L., Kan H., Yi S., Kim H. Comprehensive approach to understand the association between diurnal temperature range and mortality in East Asia. Sci. Total Environ. 2016;539:313–321. doi: 10.1016/j.scitotenv.2015.08.134. [DOI] [PubMed] [Google Scholar]
  17. Lambrechts L., Paaijmans K.P., Fansiri T., Carrington L.B., Kramer L.D., Thomas M.B., Scott T.W. Impact of daily temperature fluctuations on dengue virus transmission by Aedes aegypti. Proc. Natl. Acad. Sci. U. S. A. 2011;108:7460–7465. doi: 10.1073/pnas.1101377108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lin K., Marr L.C. Humidity-dependent decay of viruses, but not bacteria, in aerosols and droplets follows disinfection kinetics. Environ. Sci. Technol. 2020;54:1024–1032. doi: 10.1021/acs.est.9b04959. [DOI] [PubMed] [Google Scholar]
  19. Lin C., Lau A.K.H., Fung J.C.H., Guo C., Chan J.W.M., Yeung D.W., Zhang Y., Bo Y., Hossain M.S., Zeng Y., Lao X.Q. A mechanism-based parameterisation scheme to investigate the association between transmission rate of COVID-19 and meteorological factors on plains in China. Sci. Total Environ. 2020;737 doi: 10.1016/j.scitotenv.2020.140348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Liu J., Zhou J., Yao J., Zhang X., Li L., Xu X., He X., Wang B., Fu S., Niu T., Yan J., Shi Y., Ren X., Niu J., Zhu W., Li S., Luo B., Zhang K. Impact of meteorological factors on the COVID-19 transmission: a multi-city study in China. Sci. Total Environ. 2020;726 doi: 10.1016/j.scitotenv.2020.138513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Luo Y., Zhang Y., Liu T., Rutherford S., Xu Y., Xu X., Wu W., Xiao J., Zeng W., Chu C., Ma W. Lagged effect of diurnal temperature range on mortality in a subtropical megacity of China. PLoS One. 2013;8 doi: 10.1371/journal.pone.0055280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ma Y., Zhao Y., Liu J., He X., Wang B., Fu S., Yan J., Niu J. Effects of temperature variation and humidity on the death ofCOVID-19 in Wuhan, China. Sci. Total Environ. 2020;724 doi: 10.1016/j.scitotenv.2020.138226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Malki Z., Atlam E.S., Hassanien A.E., Dagnew G., Elhosseini M.A., Gad I. Association between weather data and COVID-19 pandemic predicting mortality rate: machine learning approaches. Chaos, Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.110137. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. McDevitt J., Rudnick S., First M., Spengler J. Role of absolute humidity in the inactivation of influenza viruses on stainless steel surfaces at elevated temperatures. Appl. Environ. Microbiol. 2010;76:3943–3947. doi: 10.1128/AEM.02674-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Merow C., Urban M.C. Seasonality and uncertainty in global COVID-19 growth rates. Proc. Natl. Acad. Sci. 2020 doi: 10.1073/pnas.2008590117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Morris D.H., Yinda K.C.H., Gamble A., Rossine F.W., Huang Q., Bushmaker T., Fischer R.J., Matson M.J., Doremalen N. van, Vikesland P.J., Marr L.C., Munster V., Lloyd-Smith J.O. Mechanistic theory predicts the effects of temperature and humidity on inactivation of SARS-CoV-2 and other enveloped viruses. bioRxiv. 2020:1–24. doi: 10.7554/eLife.65902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Oral E., Wannomae K.K., Connolly R., Gardecki J., Leung H.M., Muratoglu O., Griffiths A., Honko A.N., Avena L.E., Mckay L.G.A., Flynn N., Storm N., Downs S.N., Jones R., Emmal B. Vapor H 2 O 2 sterilization as a decontamination method for the reuse of N95 respirators in the COVID-19 emergency. 2020;4:1–5. doi: 10.1101/2020.04.11.20062026. [DOI] [Google Scholar]
  28. Park J.E., Son W.S., Ryu Y., Choi S.B., Kwon O., Ahn I. Effects of temperature, humidity, and diurnal temperature range on influenza incidence in a temperate region. Influenza Other Respir. Viruses. 2020;14:11–18. doi: 10.1111/irv.12682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Pirouz Behzad, Golmohammadi A., Saeidpour Masouleh H., Violini G., Pirouz Behrouz. Relationship between average daily temperature and average cumulative daily rate of confirmed cases of COVID-19. medRxiv. 2020 doi: 10.1101/2020.04.10.20059337. [DOI] [Google Scholar]
  30. Pramanik M., Udmale P., Bisht P., Chowdhury K., Szabo S., Pal I. Climatic factors influence the spread of COVID-19 in Russia. Int. J. Environ. Health Res. 2020;1–16 doi: 10.1080/09603123.2020.1793921. [DOI] [PubMed] [Google Scholar]
  31. Pratim R.M. Impact of temperature on Covid 19 in India. medRxiv. 2020 doi: 10.1101/2020.08.30.20184754. [DOI] [Google Scholar]
  32. Rahman M.A., Hossain M.G., Singha A.C., Islam M.S., Islam M.A. A retrospective analysis of influence of environmental/air temperature and relative humidity on Sars-CoV-2 outbreak. J. Pure Appl. Microbiol. 2020;14:1705–1714. doi: 10.22207/jpam.14.3.09. [DOI] [Google Scholar]
  33. Reicosky D.C., Winkelman L.J., Baker J.M., Baker D.G. Accuracy of hourly air temperatures calculated from daily minima and maxima. Agric. For. Meteorol. 1989;46:193–209. doi: 10.1016/0168-1923(89)90064-6. [DOI] [Google Scholar]
  34. Roduner E. Understanding catalysis. Chem. Soc. Rev. 2014;43:8226–8239. doi: 10.1039/c4cs00210e. [DOI] [PubMed] [Google Scholar]
  35. Sajadi M.M., Habibzadeh P., Vintzileos A., Shokouhi S., Miralles-Wilhelm F., Amoroso A. Temperature, humidity, and latitude analysis to estimate potential spread and seasonality of coronavirus disease 2019 (COVID-19) JAMA Netw. Open. 2020;3 doi: 10.1001/jamanetworkopen.2020.11834. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sethwala Anver, Akbarally Mohamed, Better Nathan, Lefkovits Jeffrey, Leeanne Grigg H.A. The effect of ambient temperature on worldwide COVID-19 cases and deaths – an epidemiological study. medRxiv Prepr. 2020:1–22. doi: 10.1101/2020.05.15.20102798. [DOI] [Google Scholar]
  37. Supari S., Nuryanto D.E., Setiawan A.M., Sopaheluwakan A., Alfahmi F., Hanggoro W., Gustari I., Safril A., Yunita R. The association between Covid19 data and meteorological factors in Indonesia. Res. Sq. 2020:1–25. doi: 10.1007/s42398-021-00202-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Thu T.P.B., Ngoc P.N.H., Hai N.M., Tuan L.A. Effect of the social distancing measures on the spread of COVID-19 in 10 highly infected countries. Sci. Total Environ. 2020;742 doi: 10.1016/j.scitotenv.2020.140430. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Tamin A., Harcourt J.L., Thornburg N.J., Gerber S.I., Lloyd-Smith J.O., de Wit E., Munster V.J. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020 doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Xiao S., Li Y., Wong T. wai, Hui D.S.C. Role of fomites in SARS transmission during the largest hospital outbreak in Hong Kong. PLoS One. 2017;12:1–13. doi: 10.1371/journal.pone.0181558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Yap T.F., Liu Z., Shveda R.A., Preston D.J. A predictive model of the temperature-dependent inactivation of coronaviruses. Appl. Phys. Lett. 2020;117 doi: 10.1063/5.0020782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Yeo C., Kaushal S., Yeo D. Enteric involvement of coronaviruses: is faecal–oral transmission of SARS-CoV-2 possible? Lancet Gastroenterol. Hepatol. 2020;5:335–337. doi: 10.1016/S2468-1253(20)30048-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zhang Y., Ye C., Yu J., Zhu W., Wang Y., Li Z., Xu Z., Cheng J., Wang N., Hao L., Hu W. The complex associations of climate variability with seasonal influenza A and B virus transmission in subtropical Shanghai, China. Sci. Total Environ. 2019;701:1–9. doi: 10.1016/j.scitotenv.2019.134607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhang A.L., Wang Y., Molina M.J. Correction for Zhang et al., Identifying airborne transmission as the dominant route for the spread of COVID-19. Proc. Natl. Acad. Sci. 2020;117:25942–25943. doi: 10.1073/pnas.2018637117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zhao L., Qi Y., Luzzatto-Fegiz P., Cui Y., Zhu Y. COVID-19: effects of environmental conditions on the propagation of respiratory droplets. Nano Lett. 2020;20:7744–7750. doi: 10.1021/acs.nanolett.0c03331. [DOI] [PubMed] [Google Scholar]
  46. Zhu Z., Lian X., Su X., Wu W., Marraro G.A., Zeng Y. From SARS and MERS to COVID-19: a brief summary and comparison of severe acute respiratory infections caused by three highly pathogenic human coronaviruses. Respir. Res. 2020;21:1–14. doi: 10.1186/s12931-020-01479-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary material

mmc1.pdf (655.8KB, pdf)
Dataset S1

Temperature data corresponding to the five most populous cities in the United States.

mmc2.xlsx (91.6KB, xlsx)
Dataset S2

Sunrise time data corresponding to the five most populous cities in the United States. Highlighted cells are adjusted for daylight saving time (note that Phoenix does not observe daylight saving time).

mmc3.xlsx (27KB, xlsx)

Articles from The Science of the Total Environment are provided here courtesy of Elsevier

RESOURCES