Increased close proximity airborne transmission of the SARS-CoV-2 Delta variant

Abstract

The Delta variant of SARS-CoV-2 causes higher viral loads in infected hosts, increasing the risk of close proximity airborne transmission through breathing, speaking and coughing. We performed a Monte Carlo simulation using a social contact network and exponential dose-response model to quantify the close proximity reproduction number of both wild-type SARS-CoV-2 and the Delta variant. We estimate more than twice as many Delta variant cases will reproduce infection in their close proximity contacts (64%) versus the wild-type SARS-CoV-2 (29%). Occupational health guidelines must consider close proximity airborne transmission and recommend improved personal respiratory protection for high-risk workers.

Graphical abstract

1. Introduction

Cortellessa et al. (2021) developed an integrated thermo-fluid dynamic model to quantify the risk of SARS-CoV-2 transmission from an infected host to a susceptible person during face-to-face conversation. Contrary to the assumption that the high transmission risk in close proximity (<1.5 m) to an infected person results from ballistic deposition of large droplets (>100 μm) onto mucous membranes, the study indicates the risk contribution from inhalation of airborne particles (<100 μm) dominates even at an interpersonal distance within 0.6 m. This corroborates the earlier modeling results of Chen et al. (2020), who found the large droplet route to dominate only within 0.2 m while talking or 0.5 m while coughing. Indeed, airborne transmission is more likely to occur within conversational distances because inhalable particles will be more concentrated closer to the emitting source (Tang et al., 2021). Furthermore, we expect this close proximity risk to be greater for the more transmissible B.1.617.2 (Delta) variant. Prior lineages of SARS-CoV-2 were overdispersed, with a minority of cases responsible for a majority of secondary transmission, and with the median COVID-19 case failing to infect anyone else (Endo et al., 2020). These relationships may no longer hold true for the Delta variant. Our aim is to estimate the increased transmissivity of the Delta variant through the close proximity airborne route and re-evaluate the proportion of COVID-19 cases expected to reproduce infection.

2. Materials and methods

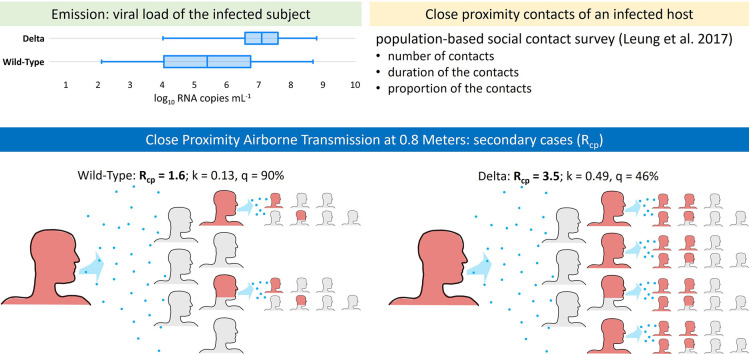
Sorokowska et al. (2017) reported a world-wide average of 0.81 ± 0.12 m for “personal distance,” defined as the physical separation maintained during interactions with friends. For simplicity, we assume the personal distance of ~0.8 m to be representative of the average interaction and apply it uniformly in our calculations. In reality, workplace and other less familiar settings are likely to have greater separation distances, whereas intimate contacts likely have closer distances. Cortellessa et al. (2021) estimated the volumetric dose of airborne particles pre-evaporation (V_{d-airborne-pre}) inhaled by a susceptible person engaged in face-to-face conversation with an infected speaker at a distance of ~0.8 m to be 1.31 × 10⁻⁶ mL per minute. We use the pre-evaporation volume because the dose of RNA copies inhaled relates to the original volume rather than the evaporated volume, as particles retain their RNA load while losing water during the instantaneous evaporation occurring upon expiration. This dose of RNA copies inhaled can be approximated as the product of V_{d-airborne-pre} (calculated as 1.31 × 10⁻⁶ multiplied by the duration of speaking in minutes) and the viral load (C_v) of the infected speaker.

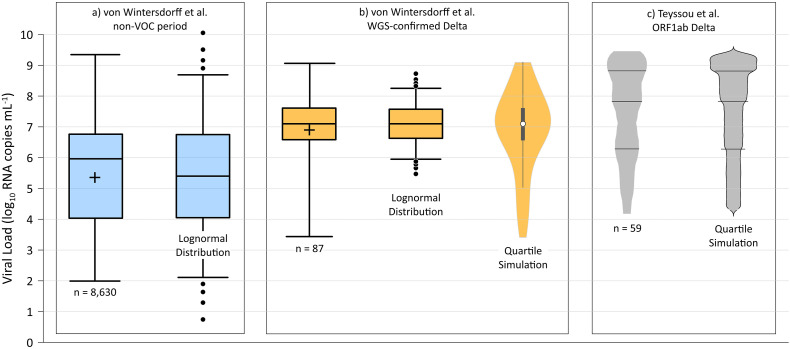
To model C_v, we used the preliminary data posted by von Wintersdorff et al. (2021) that indicates higher C_v values are associated with Delta variant infections. Fig. 1 presents the viral load data and distributions used in the modeling analysis. For wild-type SARS-CoV-2, we fit a lognormal C_v distribution to the approximate interquartile range (IQR) of all data from the non-variant of concern period (n = 8630, IQR ~ 4.1–6.7 log₁₀ RNA copies mL⁻¹), yielding a mean and standard deviation of 5.4 and 2.0 log₁₀ RNA copies mL⁻¹, respectively. For the Delta variant, the approximate IQR of sequence-confirmed Delta variant infection data only (n = 87) is 6.6–7.6 log₁₀ RNA copies mL⁻¹, consistent with a mean and standard deviation of 7.1 and 0.70 log₁₀ RNA copies mL⁻¹, respectively, of a lognormal distribution (von Wintersdorff et al., 2021). However, the Delta variant data set indicates a negative skew, with a much wider first quartile as compared to the fourth quartile as shown in Fig. 1. As a result, we modeled the Delta variant viral load using a simulation approach with random values selected from each quartile in the correct proportion. Specifically, 25% of the simulated viral load values are between 3.4 and 6.6 log₁₀ RNA copies mL⁻¹, 25% between 6.6 and 7.1 log₁₀ RNA copies mL⁻¹, 25% between 7.1 and 7.6 log₁₀ RNA copies mL⁻¹, and 25% between 7.6 and 9.1 log₁₀ RNA copies mL⁻¹.

Fig. 1.

Viral load data and distributional models for: a) the non-variant of concern (VOC) period (assumed herein to represent wild-type virus) from von Wintersdorff et al. (2021) (n = 8630 samples); b) whole genome sequencing (WGS)-confirmed Delta variant results from von Wintersdorff et al. (2021) (n = 87 samples); and c) Delta-variant ORF1ab target gene results from Teyssou et al. (2021) (n = 59 samples). Approximate mean values for the von Wintersdorff et al. (2021) data represented by crosses inside the IQR boxes. Lognormal distributions representing wild-type virus (a) and Delta variant (b) indicated by box-whisker plots with whiskers extending to the 5th and 95th percentile values, with dots placed at the 1-4th and 96-99th percentile values. Violin plot for WGS-confirmed Delta variant results (b) and bean plot for Delta ORF1ab target gene (c) produced using quartile-based sampling approach described in the text.

The preliminary Delta variant data from von Wintersdorff et al. (2021) are supported by the published data of Teyssou et al. (2021), with median viral loads of 7.8 and 7.7 log₁₀ RNA copies mL⁻¹ for Delta variant ORF1ab target gene and N target gene, respectively. The Teyssou et al. (2021) ORF1ab target gene data are also presented on Fig. 1. The data set of von Wintersdorff et al. (2021) is preferred for our evaluation as it is based on a greater number of samples, and the Teyssou et al. (2021) data are limited to initial diagnostic swabs only which are expected to be at or near the point of peak shedding. We did not aggregate data from the two reports because when comparing wild-type and Delta variant results it is better to use data from the same laboratory with the same methods. Regardless, to evaluate the sensitivity of our model to the viral load distribution, we also performed a Monte Carlo simulation using the Teyssou et al. (2021) ORF1ab target gene data by proportionally selecting random values within each quartile. Specifically, 25% of the simulation viral load values are between 4.3 and 6.3 log₁₀ RNA copies mL⁻¹, 25% between 6.3 and 7.8 log₁₀ RNA copies mL⁻¹, 25% between 7.8 and 8.8 log₁₀ RNA copies mL⁻¹, and 25% between 8.8 and 9.4 log₁₀ RNA copies mL⁻¹.

To estimate the number of close proximity contacts of an infected host, we use the population-based social contact survey in Hong Kong performed by Leung et al. (2017), which defined a close contact as either physical touching or a face-to-face conversation with three or more words within two meters. Data generated by the Leung et al. (2017) study were obtained from Leung et al. (2020) and indicate a mean number of approximately 7 close contacts per day for the study participants with an IQR of 2 to 9 daily contacts. Based on Klemmer and Snyder (1972), we assume the infected person is speaking two-thirds of the time to create the five contact duration bins for the model presented in Table 1 .

Table 1.

Close proximity contact durations for Monte Carlo simulation.

Contact duration	Model contact duration (speaking)	Proportion of contacts (Leung et al., 2020)
<5 min	2 min	21%
5–14 min	7 min	16%
15–59 min	25 min	17%
1–4 h	100 min	25%
>4 h	200 min	21%

To estimate the distribution of secondary cases resulting from this close contact network, we performed a Monte Carlo simulation with 100,000 realizations for both the wild-type and Delta lineage C_v values. For each realization, we randomly selected one of the contact networks from Leung et al. (2020) to establish the number of contacts within each duration bin (D), and randomly selected a C_v from the previously defined distributions fit to the viral load data.

To calculate the probability of infection (P_I) of the exposed contacts in each realization, we used a common exponential dose–response model as follows:

$$P_I=1-e^{-\frac{C_v{V}_{d-\mathit{airborne}-\mathit{pre}}}{{\mathrm{HID}}_{63}}}\left(\%\right)$$ (1)

where HID₆₃ represents the human infectious dose for 63% of susceptible subjects. For both the wild-type and Delta lineages, a HID₆₃ value of 700 RNA copies was adopted based on the thermodynamic equilibrium dose–response model of Gale (2020).

The final step is to calculate the number of secondary cases (C) arising from each realization by multiplying P_I by the number of susceptible contacts (S) within each duration bin (D) and then summing up the values for all bins, as follows:

$$C=\sum _D{P}_I{S}_D\left(\text{infections}\right)$$ (2)

The mean of the 100,000 C values represents a close proximity reproduction number (R_cp). To evaluate the effects of increased social distancing and/or universal masking, we also performed a sensitivity analysis on R_cp for both wild-type and Delta SARS-CoV-2 by reducing V_{d-airborne-pre} by up to 99%. To estimate the negative-binomial distribution overdispersion parameter, k, for our modeling results, we employed the following Eq. (3) for the probability generating function (g[s]) of the secondary case (offspring) distribution from Lloyd-Smith et al. (2005):

$$g\left(s\right)={\left(1+\frac{R_{\mathit{cp}}}{k}\left(1-s\right)\right)}^{-k}\left(\%\right)$$ (3)

Using the R_cp results from our simulations we solved for k for the special case of g(0), which is the probability an infected host fails to infect anyone else and is assumed to equal our simulation percentile value for C = 1. We also solved for the value of s where g(s) = s, which according to the negative-binomial branching process signifies the probability of stochastic outbreak extinction (q) (Lloyd-Smith et al., 2005).

3. Results

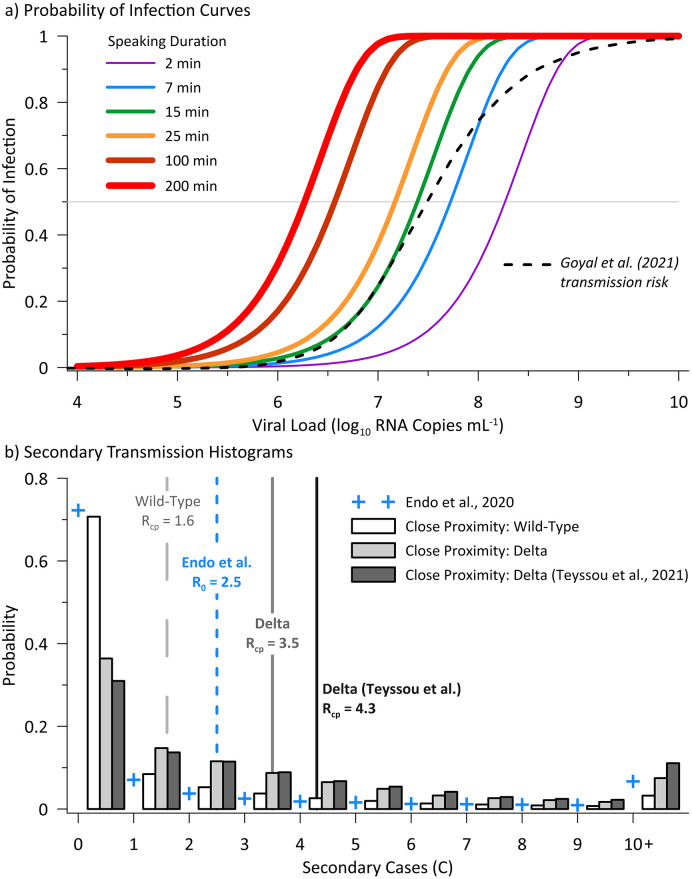
The viral load-dependent probability of infection curves and the secondary case distributions resulting from the Monte Carlo simulations for both wild-type and Delta SARS-CoV-2 are presented on Fig. 2 . Fig. 2a indicates that close proximity interactions less than 25 min in duration present a low risk (≤1%) to a susceptible person below a viral load of approximately log₁₀ 5.5 RNA copies mL⁻¹. Also presented on Fig. 2a is the transmission probability curve as modeled by Goyal et al. (2021), which is consistent with our model for 15 min of speaking up to a viral load of approximately log₁₀ 7.5 RNA copies mL⁻¹ at a ~50% probability of infection. The histograms on Fig. 2b indicate a much higher proportion of Delta variant cases will reproduce infection in their close proximity contacts (64–69%) versus the wild-type lineage (29%), with these percentages derived from the probability of exceeding C = 1. Estimated values of R_cp are 1.6 for wild-type SARS-CoV-2, 3.5 for Delta SARS-CoV-2 based on the viral load data of von Wintersdorff et al. (2021), and 4.3 for Delta SARS-CoV-2 based on the viral load data of Teyssou et al. (2021). The higher median viral load of the Teyssou et al. (2021) data set results in the higher R_cp value; however, the greater variability of the dataset with a much wider IQR results in the similar probability of exceeding one secondary case (64 versus 69%). As such, subsequent analysis is limited to modeling based on the von Wintersdorff et al. (2021) data set for more consistent comparison with the wild-type virus.

Fig. 2.

Probability of infection curves (a) for modeled speaking durations (15 min also presented for reference) as a function of viral load in the infected host, and secondary transmission histograms (b) for the Monte Carlo simulations for wild-type virus and the Delta variant. Wild-type simulation results are based on a lognormal model of viral load fit to von Wintersdorff et al. (2021) data, with Delta simulations using the quartile-based viral load model for both the von Wintersdorff et al. (2021) and Teyssou et al. (2021) data. Also presented on panel b is the negative-binomial offspring distribution of Endo et al. (2020) for R₀ of 2.5 and median overdispersion parameter (k) estimate of 0.1. The close proximity reproduction numbers (R_cp, mean of all realizations) are denoted by vertical lines on panel b.

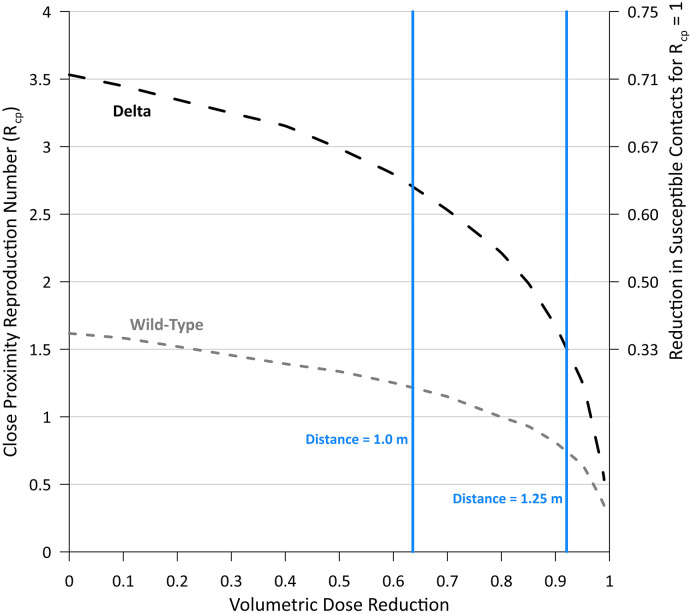
The results of the V_{d-airborne-pre} sensitivity analysis are presented on Fig. 3 , with vertical lines denoting the equivalent dose reductions achieved at increased separation distances of approximately 1.0 m and 1.25 m. For reference, increasing this distance from 0.8 m to 1.0 m and 1.25 m reduces V_{d-airborne-pre} by ~64% and ~92%, respectively, illustrating the substantial reduction in infection risk achieved by modest increases in social distancing (Cortellessa et al., 2021).

Fig. 3.

Effect of volumetric dose (V_{d-airborne-pre}) reduction on R_cp for Delta and wild-type SARS-CoV-2. The necessary reduction in the number of susceptible contacts (S) to achieve R_cp = 1 is also provided on the secondary Y axis, for reference, calculated as (R_cp – 1)/R_cp.

Fig. 3 demonstrates that reducing the inhaled dose an order of magnitude is sufficient to maintain R_cp below 1 for wild-type SARS-CoV-2, but not for the Delta variant, which also requires a corresponding reduction in the number of susceptible contacts by over one-third. Ensuring a social distance of at least 1.5 m reduces V_{d-airborne-pre} by over 97% (Cortellessa et al., 2021), and is sufficient to reduce R_cp below 1.0 for the Delta variant. This confirms the conclusion of Cortellessa et al. (2021) that a minimum safety distance of 1.5 m maintains an acceptable risk on a population level when neglecting room-scale airborne transmission.

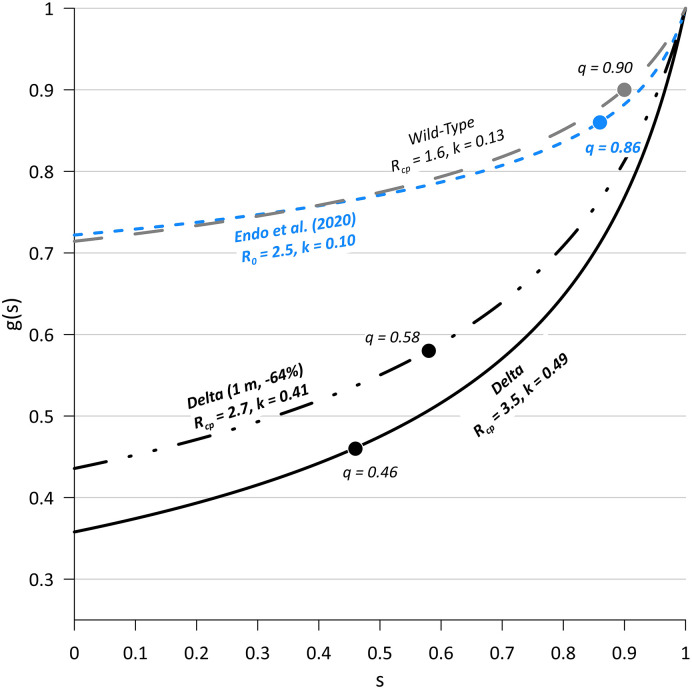
As shown on Fig. 4 , our simulation results suggest overdispersion parameters (k) of 0.13 and 0.49 for wild-type and Delta SARS-CoV-2 respectively, indicating transmission of the Delta variant is less reliant on superspreading events (SSEs). As a result, when considering close proximity airborne transmission alone, the predicted outbreak extinction probability (q) for Delta is only 46%, as compared to 90% for wild-type SARS-CoV-2.

Fig. 4.

Probability generating functions of offspring distributions with outbreak extinction probabilities, q, labeled at the point on each curve where g(s) = s.

Fig. 4 also presents the Delta variant g(s) curve for the case where V_{d-airborne-pre} is reduced ~64% either by increasing the separation distance to 1.0 m, or through masking that achieves an equivalent V_{d-airborne-pre} reduction. With respect to masking, we note that the respiratory jet is completely altered when an infected host wears a mask, and an entirely different thermo-fluid dynamic model would be required for more detailed analysis on the resulting reduction of inhaled dose. Regardless, a ~64% reduction in inhaled dose reduces R_cp to 2.7 and k to 0.41, which increases the extinction probability to 58%. The probability of C > 1 is lowered from 64% to 56%.

At the assumed separation distance of 0.8 m, the proportion of close proximity transmission expected from the most infectious 20% of cases, estimated from k in accordance with Lloyd-Smith et al. (2005), decreases from 91% for wild-type SARS-CoV-2 to 65% for the Delta variant. Described another way, the fraction of cases responsible for 80% of transmission increases from 13% for wild-type SARS-CoV-2 to 31% for the Delta variant (Nielsen et al., 2021).

4. Discussion

Our wild-type secondary case distribution is remarkably similar to that of Endo et al. (2020), except for the lower proportion of very high (10+) secondary cases, which increase the basic reproduction number (R₀) to 2.5 compared to our R_cp estimate of 1.6. The likely explanation is that our model omits room-scale airborne transmission, which results in extreme individual reproduction numbers for high emitters who expose more susceptibles to SARS-CoV-2 than would be expected from their close contact network (Goyal et al., 2021). Higher attack rates are predicted for the close proximity contacts of Delta cases, with our mean estimates being 50% for Delta versus 23% for wild-type, calculated as R_cp divided by the mean number of contacts of 7, similar to household attack rates reported by Dougherty et al. (2021). As such, additional emphasis should be placed on reducing household transmission.

Transmission of the Delta variant appears less overdispersed with lower outbreak extinction probability, indicating that lockdowns targeting SSEs will be less successful at eliminating community transmission (Ito et al., 2021). Our close proximity overdispersion parameter (k) of 0.13 for wild-type SARS-CoV-2 is consistent with past estimates of 0.16 and 0.17 for SARS-CoV-1, while our k value of 0.49 for Delta is within the range of 0.32–0.72 estimated for historic outbreaks of smallpox (Lloyd-Smith et al., 2005). Assuming our R₀/R_cp scaling ratio of ~1.6 for wild-type SARS-CoV-2 also applies to the Delta variant, our R₀ estimate for the Delta variant becomes 5.6, within the range of 5.0–9.5 reported by the United States Centers for Disease Control and Prevention (CDC) (2021). This estimate falls at the approximate 72nd percentile of the distribution of R₀ reported for smallpox (range of 1.5 to 10, with a mean of 4.5) (Costantino et al., 2018).

Limitations of our analysis include viral load data for the Delta variant that is only preliminary, with similar uncertainty surrounding the dose-response model for SARS-CoV-2. Further, we limit the model to one day of normal contacts by an infected person without any mitigation measures. However, the consistency of our secondary case distribution with that modeled by Endo et al. (2020) supports the conclusion that most transmission of SARS-CoV-2 occurs during a narrow 1–2 day window of peak infectivity (Goyal et al., 2021), and that our HID₆₃ is a reasonable approximation. While we did not include any large droplet deposition component in our simulations, modeling by Cortellessa et al. (2021) indicates it is negligible at separation distances beyond 0.6 m as in our analysis.

5. Conclusion

Mounting evidence suggests surgical masks inadequately protect health-care workers against SARS-CoV-2 (Ferris et al., 2021), consistent with our simulation analysis that shows close proximity airborne transmission may account for a majority of secondary transmission. This also supports the recent hypothesis that short-range (our close proximity) airborne transmission is the dominant mode for SARS-CoV-2 (Li, 2021). In response to the Delta variant, public health authorities should immediately revise guidelines to address the close proximity airborne pathway and recommend improved personal respiratory protection (e.g., N95 masks) for high-risk workers even in the absence of aerosol-generating procedures. Transmission of the Delta variant is more homogeneous, with a higher overdispersion parameter, indicating that lockdowns will not be as immediately successful as they were for wild-type SARS-CoV-2. Social distancing and masking remain effective mitigation strategies for the Delta variant where vaccination rates are low, as we estimate maintaining at least 1.5 m of separation during conversation drives R_cp below 1 even in a fully susceptible population. However, given the difficulty of maintaining at least 1.5 m of separation at all times, there is continuing need for masking in the absence of a high degree of population immunity. Our modeling also suggests room-scale airborne transmission contributes significantly to R₀ for wild-type SARS-CoV-2, meaning improved ventilation, air filtration, and/or air disinfection are needed to mitigate community spread of past, present, and future variants of concern.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

CRediT authorship contribution statement

Alex Mikszewski: Conceptualization, Calculations, Writing-Original draft preparation Luca Stabile: Data curation, Investigation, Calculation review, Writing- Reviewing and editing. Giorgio Buonanno: Conceptualization, Investigation, Writing- Reviewing and editing. Lidia Morawska: Supervision, Writing- Reviewing and Editing.

Declaration of competing interest

The authors have no conflicts or competing interests to disclose.

Editor: Pavlos Kassomenos