Abstract
The ability of individuals to leave a current breeding area and select a future one is important, because such decisions can have multiple consequences for individual fitness, but also for metapopulation dynamics, structure, and long‐term persistence through non‐random dispersal patterns. In the wild, many colonial and territorial animal species display informed dispersal strategies, where individuals use information, such as conspecific breeding success gathered during prospecting, to decide whether and where to disperse. Understanding informed dispersal strategies is essential for relating individual behavior to subsequent movements and then determining how emigration and settlement decisions affect individual fitness and demography. Although numerous theoretical studies have explored the eco‐evolutionary dynamics of dispersal, very few have integrated prospecting and public information use in both emigration and settlement phases. Here, we develop an individual‐based model that fills this gap and use it to explore the eco‐evolutionary dynamics of informed dispersal. In a first experiment, in which only prospecting evolves, we demonstrate that selection always favors informed dispersal based on a low number of prospected patches relative to random dispersal or fully informed dispersal, except when individuals fail to discriminate better patches from worse ones. In a second experiment, which allows the concomitant evolution of both emigration probability and prospecting, we show the same prospecting strategy evolving. However, a plastic emigration strategy evolves, where individuals that breed successfully are always philopatric, while failed breeders are more likely to emigrate, especially when conspecific breeding success is low. Embedding information use and prospecting behavior in eco‐evolutionary models will provide new fundamental understanding of informed dispersal and its consequences for spatial population dynamics.
Keywords: breeding failure, breeding habitat selection, conspecific breeding success, environmental changes, population dynamics, social information
Information use affects the evolution of emigration probability and the number of prospected patches. It has to be considered when addressing dispersal as a response of individuals and populations to environmental changes.

1. INTRODUCTION
Dispersal defines the movement of an individual from its natal or current breeding patch to a new one (Clobert et al., 2001). It represents a crucial process in ecology and evolution, since it has a major influence on population dynamics, structure and persistence (Bowler & Benton, 2005; Clobert et al., 2012), gene flow between populations (Ronce, 2007), and species’ range dynamics (Kokko & Lopéz‐Sepulcre, 2006; Travis et al., 2013). Dispersal can be decomposed into three main stages: emigration from the natal or current breeding patch, transience (movement between the two patches), and settlement in a new breeding patch (Clobert et al., 2009). Furthermore, each phase may incur different costs (Bonte et al., 2012; Travis et al., 2012) and involve numerous context‐dependent decisions made at the individual level which drive individual movements (Clobert et al., 2009).
In a variable but predictable environment, many organisms are able to gather and use information to decrease the uncertainty about the quality of their environment and make better decisions (Dall et al., 2005). When they do so in the context of dispersal, they adopt a strategy termed ‘informed dispersal’ (Clobert et al., 2009; Reed et al., 1999). The sources of information on the local environmental conditions are diverse and can be divided into three main types: (1) personal information obtained from the direct interaction of individuals with their environment (i.e., visual, hearing, and chemical cues) and their past experience (i.e., individual breeding success, familiarity with the environment; Dall et al., 2005), (2) social information obtained from the presence or density of conspecifics and defined as conspecific attraction (Stamps, 1988), and (3) social information obtained from the performance of con‐ or hetero‐specifics (i.e., breeding success, quantity and quality of the offspring) and defined as public information (Dall et al., 2005; Danchin et al., 2004; Seppänen et al., 2007). The acquisition and use of information can occur before emigration, when individuals choose whether to leave their current breeding patch, during transience, and/or just before choosing where to settle (Figure 1). Information acquisition often involves prospecting phases, which are visits of individuals to breeding areas or sites where they do not currently breed and where they can gather personal and social information on the local environmental quality to make emigration and/or settlement decisions (Reed et al., 1999). As a result, individuals do not disperse randomly in the landscape, and information acquisition and use are therefore essential to consider for better understanding dispersal processes (Bocedi et al., 2012; Delgado et al., 2011, 2014; Enfjäll & Leimar, 2009; Fronhofer et al., 2017; Ponchon, Garnier, et al., 2015; Schmidt et al., 2015; Vuilleumier & Perrin, 2006). Direct observations in the field, along with the recent development of miniaturized tracking devices, have revealed that dispersal in natural populations can be driven by complex emigration and settlement decision‐making processes (Clobert et al., 2009; Reed et al., 1999). Nevertheless, because they do not involve the same spatial and temporal scales, emigration and settlement phases have generally been studied separately, both in the field and in theoretical models (Clobert et al., 2009).
FIGURE 1.
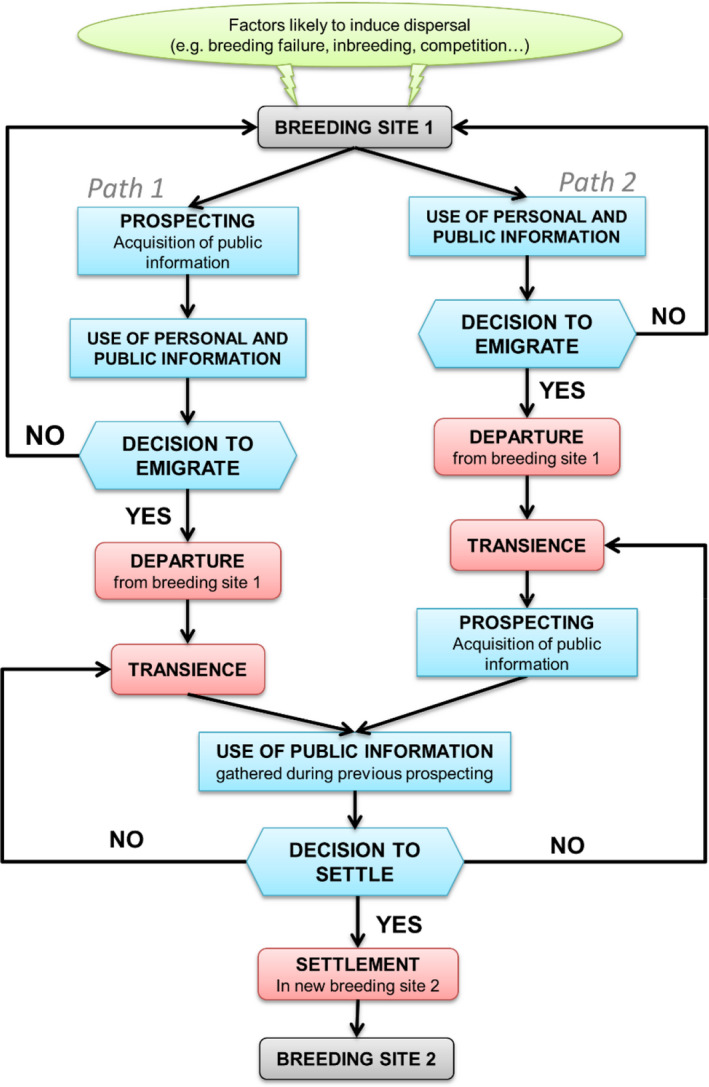
Flowchart of informed dispersal representing dispersal (red) and information acquisition and use in breeding habitat selection (blue). Breeding site 1 can be the natal or current breeding site. Depending on species life cycle, prospecting can occur before (Path 1 ‐ Best‐of‐n strategy) or after emigration decision (Path 2; sequential sampling)
Regarding the emigration phase, many empirical studies have demonstrated that individuals use both personal and public information to make informed emigration decisions, leading to higher emigration probabilities when individuals fail to breed among failed conspecifics (Boulinier et al., 2008; Danchin et al., 1998; Dugger et al., 2010; Pakanen et al., 2011; Rioux et al., 2011; Robert et al., 2014). Despite the growing empirical evidence of the use of these two types of information, theoretical models have been largely restricted to investigating the evolution of density‐dependent emigration probabilities, when individuals cue only on local conspecific density (Bocedi et al., 2012; Enfjäll & Leimar, 2009; Fronhofer et al., 2017). Those studies have shown that the evolved emigration rate decreased when individuals used patch densities as social information under conditions of high dispersal mortality cost and temporally uncorrelated (i.e., unpredictable) environmental fluctuation (Enfjäll & Leimar, 2009), whereas emigration rates increased when individuals used information in temporally auto‐correlated (i.e., predictable) environments (Bocedi et al., 2012). Bocedi et al. (2012) further showed that the acquisition of costly information on local conspecific density always evolved, especially in predictable environments. Nevertheless, selection rarely favored investment in the acquisition of high‐precision information.
Regarding the settlement phase, empirical studies have shown that many colonial and territorial species including birds (Reed et al., 1999), mammals (Mares et al., 2014; Mayer et al., 2017; Selonen & Hanski, 2010), reptiles (Cote & Clobert, 2007), amphibians (James et al., 2015; Pizzatto et al., 2016), and arthropods (De Meester & Bonte, 2010; Seeley & Buhrman, 2001; Stroeymeyt et al., 2017) gathered public information during prospecting in order to settle in more productive breeding areas. Importantly, the use of public information was often favored over conspecific density and personal information in both emigration and settlement decisions (Aparicio et al., 2007; Betts et al., 2008; Doligez et al., 2002; Forero et al., 1999; Pärt et al., 2011; Ponchon, Chambert, et al., 2015; Ponchon, Iliszko, et al., 2017), outlining its crucial role in informed dispersal.
A few theoretical studies have started implementing dispersal as a complex behavioral process, integrating the different phases of dispersal. For example, Travis et al. (2012) proposed an eco‐evolutionary framework for modeling dispersal, emphasizing the need to model explicitly the three dispersal phases and the associated costs. However, they only briefly mentioned information use and they did not explicitly implement it in their model example. To our knowledge, only one theoretical study explicitly considered the eco‐evolutionary dynamics of prospecting in the settlement phase (Delgado et al., 2014). It highlighted an important interplay between prospecting and dispersal strategies and showed that selection for informed dispersal in many cases resulted in lower population abundances and patch occupancies than under random dispersal. However, public information based on conspecific breeding performance was not incorporated, and the authors called for further studies integrating information use in emigration decisions as well. Additionally, two ecological models incorporated information use in both emigration and settlement decisions with a prospecting phase (Ponchon, Garnier, et al., 2015; Schmidt, 2017). They showed that in a changing environment, informed dispersal based on prospecting and public information use led to greater population size and persistence compared to random dispersal or philopatry. However, neither model incorporated the evolution of those informed dispersal strategies.
Overall, there has been a substantial discrepancy between the complex dispersal processes that have been described in natural populations and the ones implemented in evolutionary models. As a result, we currently lack a general understanding of the consequences of informed dispersal for individual fitness and population functioning. To fill this gap, we developed an eco‐evolutionary model that links emigration, prospecting, public information use, settlement, and demography in temporally auto‐correlated environments. We first determined how the number of prospected patches evolved depending on the use of personal and public information, the patch selection strategy, and the cost of prospecting. Then, we determined how emigration probabilities and prospecting evolved concurrently.
2. THE MODEL
We developed a stochastic individual‐based model that tracks ecological dynamics of populations and evolutionary changes in individual dispersal strategies. The life cycle of individuals is inspired by a long‐lived colonial species, but can be adapted to any species whose populations are spatially structured in a heterogeneous and temporally variable environment.
We constructed a female‐only model with three distinct life stages (juveniles, pre‐breeders, and adults), overlapping generations, and negative density dependence in fecundity. Importantly, we integrated the use of personal and public information in emigration decisions and an independent prospecting phase during which individuals gather public information to make settlement decisions. The dispersal genotype and social environment of individuals can both affect their behavior, of which population dynamics is an emergent outcome. Here, personal information corresponds to individual breeding success (success or failure of an individual at producing offspring), while public information corresponds to local conspecific reproductive success in a given breeding patch at the time of prospecting. All the defined parameters can be found in Table 1, and the source code and output files are freely available at https://github.com/auponchon/Informed‐dispersal‐IBM and are deposited on Zenodo (DOI: 10.5281/zenodo.5534084).
TABLE 1.
Common values used to parameterize the model in the two examples. Parameters specific to each model example are given in Section 3
| Parameters | Abbreviation | Value |
|---|---|---|
| Carrying capacity in a patch | K 0 | 100 |
| Maximum mean number of offspring produced by female | Offmax | 2 |
| Juvenile survival | S J | 0.6 |
| Pre‐breeder survival | S I | 0.7 |
| Adult survival | S A | 0.85 |
| Standard deviation for the environment | σ | 1 |
| Temporal autocorrelation coefficient | α | 0.8 |
| Mean age at recruitment | R | 5 |
| Mutation rate | μ | 0.01 |
| Mortality cost of prospecting per patch | M | 0.01 |
2.1. The environment
Previous theoretical models have demonstrated that informed dispersal can only evolve when the environment is variable but predictable in time, that is, temporally auto‐correlated (Boulinier & Danchin, 1997; Doligez et al., 2003). Therefore, we assume a spatially structured population existing within 25 discrete breeding habitat patches, each of which has an independent local and temporally auto‐correlated environmental quality Qx , y , t that varies annually. At time t = 0, each patch x,y is given a local environmental quality Qx , y ,0 based on a value wx , y ,0 drawn from a normal distribution N~(0,σ) so that:
| (1) |
At t + 1, the local environmental quality depends on and wx , y , t is resampled from a normal distribution N~(0,σ) and associated with an autocorrelation coefficient α so that:
| (2) |
The carrying capacity of each patch Kx , y , t , which is always ≥ 0, is directly affected by the local environment quality so that:
| (3) |
Note that changing σ changes the amplitude of the fluctuations of the environmental quality (Bocedi et al., 2014). Therefore, we ran preliminary simulations to check how σ and temporal autocorrelation α could affect the eco‐evolutionary dynamics of populations. As expected, when the temporal autocorrelation α was low, random dispersal was dominant and strongly affected the spatial distribution of individuals with weaker density‐dependent effects on fecundity (see Figure S1). Likewise, increasing σ increased the range of the environmental quality but this did not affect the patterns observed in the evolution of prospecting. Based on those simulations, we chose a high autocorrelation coefficient (α = .8) and a moderate standard deviation (σ = 1) to run the different experiments (Table 1).
2.2. Reproduction
The annual cycle of individuals in patch x,y starts with reproduction. Each female i produces a number of offspring sampled from a Poisson distribution with a mean μ Off given by:
| (4) |
where Offmax is the maximum mean number of offspring produced per female and Nx , y , t is the number of adults present in patch x,y in year t. If individuals successfully produce one or more offspring, they are successful breeders. Otherwise, they are failed breeders. The local conspecific breeding success LBS x , y , t is calculated as the ratio of the number of successful breeders to the number of adults Nx , y , t , as usually calculated in the field (e.g., Ponchon et al., 2014).
2.3. Life stages
The offspring produced are juveniles and have a probability S J of surviving to become pre‐breeders the following year (Table 1). The mean age at recruitment, that is, age at which pre‐breeders become adults and attempt to breed for the first time, is generated at birth from a Poisson distribution with a mean R. As long as pre‐breeders do not reach age of recruitment, they experience an annual survival probability S I (Table 1) and remain pre‐breeders. They neither breed nor disperse. When they recruit and become adult, they can disperse to select their first breeding patch. Adults have an annual survival probability S A (Table 1).
2.4. Emigration, prospecting, and settlement
Dispersal is modeled in three phases: emigration decision, prospecting, and settlement decision (Figure 1; Path 1). We considered three different emigration strategies: (i) the emigration decision is non‐informed (i.e., all individuals have the same emigration probability E); (ii) emigration probability depends on the individual's breeding status: if successful, E succ; if failed, E fail, which implies the use of personal information; (iii) emigration probability is a function of both personal and public information (i.e., local conspecific breeding success LBSx , y , t ) defined by the following:
| (5a) |
| (5b) |
Parameters defining each emigration strategy (i.e., E; E succ and E fail; or α fail, α succ, β fail, and β succ) can either be fixed for the population or evolving traits depending on the simulation scenario (see Section 4).
When pre‐breeders become adult, they can choose where to recruit and breed for the first time. As they have not reproduced yet, they have no past breeding performance. Nevertheless, they are assigned the same emigration probability as failed breeders, E fail, as they are assumed to use conspecific breeding success to make their emigration decision.
If individuals decide to emigrate, they prospect by randomly selecting a set of patches, corresponding to the number of prospected patches determined by an additional evolving trait, N p. The prospected patches are ranked according to their breeding success and assigned a probability of being chosen derived from their current breeding success. The probability pi to select the ith ranked prospected patch is determined according to three alternative patch selection processes reflecting the differential ability of individuals to discriminate patches with the highest breeding success: (i) an inaccurate process, where , so that individuals are somewhat likely to choose the best prospected patches, (ii) an accurate process, where so that individuals will tend strongly to settle in the best prospected patch but could still choose other patches with a small probability weighed by local breeding success, and (iii) a deterministic process, where p 1 = 1 and pi = 0 for all other prospected patches so that individuals always settle in the prospected patch with the highest breeding success (Figure S2). Individuals that do not prospect (N p = 0) choose a breeding patch at random. Likewise, as the initial selection of prospected patches is random, a prospecting strategy based on only one patch (N p = 1) is equivalent to random settlement. Once individuals have decided to emigrate, they cannot return to their immediately previous patch and must settle in another occupied patch.
2.5. Evolution of dispersal traits
Individuals are haploid and carry one locus for each evolving trait determining their emigration probability and their prospecting propensity, depending on the simulated scenario. E (random emigration probability), E succ and E fail (emigration probabilities based only on personal information), and α fail, α succ, β fail, β succ (parameters defining the relationship between emigration probability and local breeding success, Equation 5) are all coded by continuous alleles. N p, the trait defining the number of prospecting patches, is coded by discrete alleles. Offspring inherit alleles from their mother. In scenarios where more than one trait is evolving, loci are unlinked and each subject to a mutation probability μ = 0.01 per generation. When a mutation occurs for one of the continuous traits, the allelic value is altered by an increment drawn from a normal distribution N ~ (0, 0.1), while the allele coding for prospecting propensity is changed by ±1.
Simulations are initialized by assigning each individual a random allele for the number of prospected patches, N p, from 0 to 24. When one or more continuous traits determining emigration are evolving, each locus is initialized with a random value between 0 and 1, except α fail and α succ which are initialized with a random value between −1 and 0, assuming a negative relationship between emigration probability and local breeding success (Equation 5).
3. MODEL EXPERIMENTS
3.1. Evolution of prospecting only
First, we conduct one experiment comprising a set of simulations to determine how different non‐evolving emigration strategies and patch selection processes affect the evolution of prospecting and population spatial structure. Only one trait is evolving, that is N p. We consider the three different emigration strategies described above: constant emigration probability (E = 0.5), emigration depending only on personal information (E succ = 0.05 and E fail = 0.5), and emigration depending on both personal and public information (β succ = 0.05, α succ = 0.0, β fail = 0.5, α fail = −0.45). For each emigration strategy, we implement, in turn, each of the three different patch selection processes: inaccurate, accurate, and deterministic. Finally, for each scenario, we implement either no dispersal mortality cost or a mortality cost M cost proportional to the number of prospected patches, namely M cost = M * N p, where M = 0.01. We ran each scenario over 20,000 years and repeated it 10 times.
3.2. Evolution of both prospecting and emigration probability
In a second experiment, we test how the emigration probability and the number of prospected patches concomitantly evolve depending upon the patch selection process and prospecting cost. We conduct these experiments for each of the three emigration strategies that involve different levels of information use. Prospecting evolution and costs are based on the same rules as the previous model example.
Depending on the emigration strategy, one (E), two (E succ, E fail), or four (α fail, α succ, β fail, β succ) emigration parameters can evolve independently along with prospecting N p. We ran each scenario over 20,000 years and replicated it 10 times.
4. RESULTS AND DISCUSSION
4.1. Evolution of prospecting only
Independently from the cost of prospecting, emigration strategy influences individual distribution in the patches according to their local environmental quality (Figure 2). In general, while densities are similar in patches of intermediate quality among scenarios, they are lower in bad patches and higher in good patches. The more accurate the information used to select their new breeding patch is (patch selection process), the higher the number of individuals settling in good patches.
FIGURE 2.
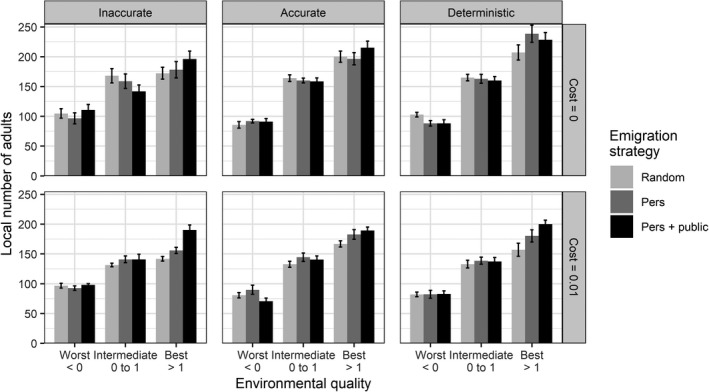
Local number of adults (±SE) depending on the local environmental quality, emigration strategy, patch selection process, and per‐patch prospecting mortality cost. Pers is the use of personal information (individual breeding performance). Pers + public is the use of both personal and public information (conspecific breeding success) in emigration decisions. Results are shown after 20,000 years over 10 replicates
When the patch selection process is inaccurate and prospecting is costless, strategies prospecting a high number of patches evolve (Figure 3). Contrastingly, with a deterministic or accurate selection process, selection favors individuals that prospect a limited number of patches (N p < 5). Indeed, if individuals prospected all the available patches and discriminated the best patches, they would all pile up in the same best patch. This would drastically affect their subsequent breeding success through negative density‐dependent effects on their fecundity, and there would be a dynamic imbalance in distribution of overcrowded good patches and underpopulated bad patches. When prospecting entails a mortality cost and individuals discriminate the best patches, prospecting is still favored over random dispersal, which is not the case when individuals apply an inaccurate patch selection process with personal and public information use (Figure 3). Emigration strategy has a weak effect on the evolution of prospecting, as the modal number of prospected patches increases by one when individuals use both personal and public information with an auccrate or deterministic patch selection process.
FIGURE 3.
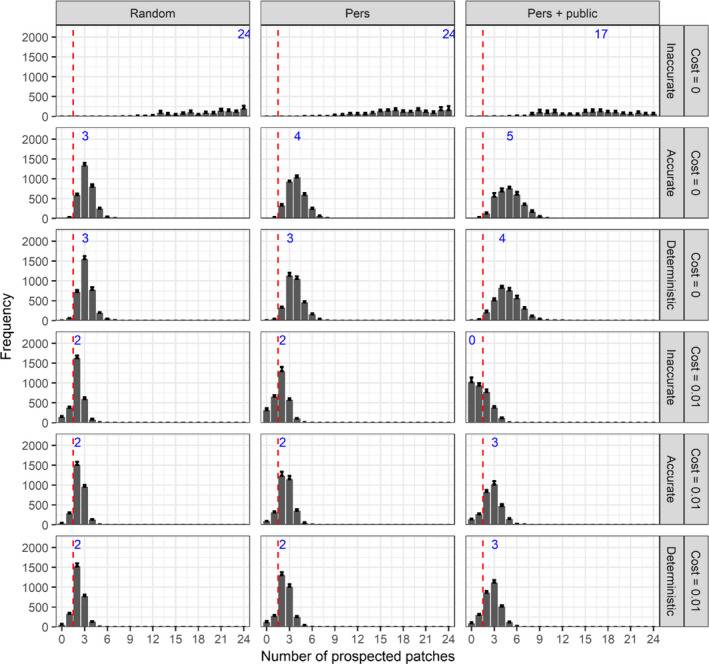
Mean (+SE) frequency of the number of prospected patches after 20,000 years over 10 replicates according to emigration strategy (columns), patch selection process, and prospecting cost per patch (rows) when only prospecting evolves. Bars left of the dashed red line correspond to random settlement (no prospecting). Blue numbers indicate the mode of the distributions
These results confirm that there is a trade‐off between the number of prospected patches and prospecting costs, as previously suggested by Bocedi et al. (2012). The prediction of a modest number of patches being prospected is also consistent with field observations in long‐lived colonial species. Although empirical data on prospecting movements are still scarce and potential associated costs are unknown (Ponchon et al., 2013), a few studies suggest that individuals do not prospect a large number of breeding areas. For instance, failed‐breeding black‐legged kittiwakes Rissa tridactyla prospected only a few cliffs among the tens available within a restricted area over a month of tracking (Ponchon, Iliszko, et al., 2017). The same trend was observed at larger spatial scales in black‐legged kittiwakes (Boulinier et al., 2016; Ponchon, Aulert, et al., 2017), northern gannets Morus bassanus (Votier et al., 2011), and black‐browed albatrosses Thalassarche melanophris (Campioni et al., 2017). Our results finally align with the theoretical study by Delgado et al. (2014) which shows that prospecting length (somehow equivalent to our number of prospected patches) decreases with increased mortality costs. Our model results, together with previous theory and empirical observations, suggest that prospecting is an effective means to avoid dispersing to a particularly poor patch but also allows individuals to find the best patches. This is due to the negative subsequent impacts of density dependence if too many individuals simultaneously choose to disperse to the best few patches.
4.2. Evolution of both emigration and prospecting strategies
Individual distribution among patches is mostly unchanged when both prospecting and emigration probability are evolving: low densities of adults in bad patches and high densities in the best patches (Figure S5). When emigration evolves along with costless prospecting (Figure 4), individuals still evolve to prospect a low number of patches when the patch selection process is accurate or deterministic. The emigration strategy is not influential, as all strategies lead to the same number of prospecting patches (N p = 3; Figure 3). Adding a prospecting cost slightly decreases the number of prospected patches for accurate and deterministic patch selection process, especially when individuals use information (Figure 4). With an inaccurate patch selection process and mortality cost, individuals mainly evolve to random dispersal when they use information (personal or both personal and public), but when emigration is random, prospecting based on a low number of patches is favored (Figure 4).
FIGURE 4.
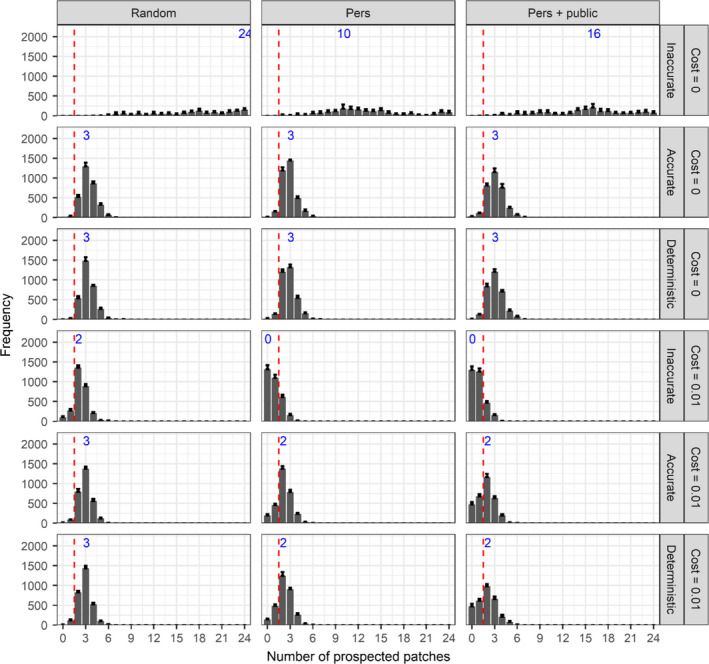
Mean (+SE) frequency of the number of prospected patches after 20,000 years over 10 replicates according to emigration strategy (columns), patch selection process, and prospecting cost per patch (rows) when both emigration and prospecting evolve. Bars left of the dashed red line correspond to random settlement (no prospecting). Blue numbers indicate the mode of the distributions
Emigration probabilities evolve very differently according to whether individuals use information in emigration decision. At the same time, accurate and deterministic patch selection strategies lead to very similar relationships between emigration probability and local breeding success (Figure 5). In the case of random emigration and no prospecting cost, emigration probability E evolves to 0.78 with an inaccurate patch selection strategy but decreases to 0.47–0.49 when individuals discriminate the best patches (Figure 5a). When individuals can evolve emigration probabilities conditional on breeding success, E fail evolves to 0.95 with an inaccurate patch selection strategy and 0.85 with an accurate or deterministic strategy, while E succ always evolves to 0 (Figure 5a), meaning that individuals do not emigrate after breeding successfully. When adding a cost to prospecting, E decreases to 0.26–0.28 with a random emigration, and the effect of the patch selection strategy is negligible. E fail remains around 0.95 with an inaccurate strategy but decreases to 0.59–0.63 with an accurate or deterministic strategy. Finally, when individuals can evolve emigration probabilities conditional on both personal and public information, E succ also always evolves to 0. On average the emigration probability of failed breeders evolves to be an inverse function of local conspecific breeding success except with an inaccurate strategy and in the absence of prospecting cost, where failed individuals tend to always disperse (Figure 5b).
FIGURE 5.
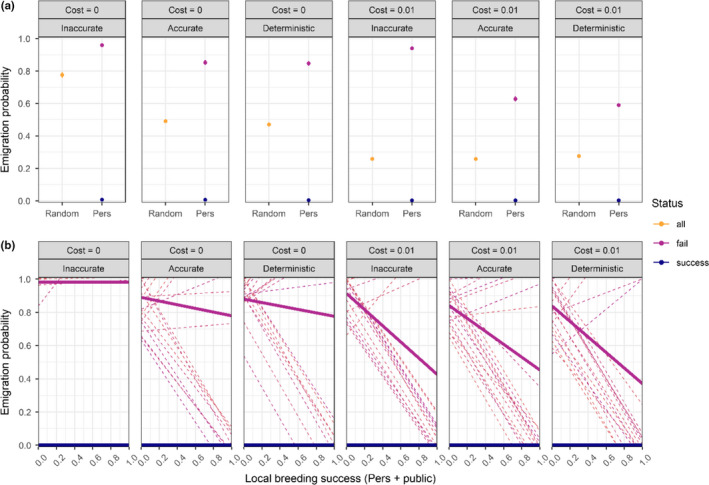
Emigration probability evolved under different patch selection processes and prospecting costs per patch after 20,000 years and over 10 replicates when both emigration probabilities and prospecting evolve. (a) Random emigration probability and emigration probability based on personal information of failed and successful breeders (error bars show ± SE) (b) Emigration probability based on personal and public information, where emigration probability is a function of the local breeding success. The bold lines represent the average reaction norm of failed breeders while thin dashed lines represent 20 random individual reaction norms. Emigration probability of successful breeders evolves to 0 independently of local breeding success
Our general results align with Enfjäll and Leimar (2009), who found that the use of conspecific densities as information led to decreased emigration rate because individuals were less prone to emigrate from high habitat quality and low conspecific densities. Here, we additionally show that the use of both personal and public information for emigration probabilities is crucial, since it completely suppresses emigration when individuals breed successfully and strongly increases it when individuals fail breeding, especially when conspecific breeding success is low and when prospecting is costly (Figure 5). Consequently, not accounting for both personal and public information use may lead to important biases when estimating emigration probabilities, either in theoretical models or empirically.
Overall, our results highlight that the patch selection process is crucial in prospecting evolution, as it drives the number of prospected patches, while personal and public information use is crucial in the evolution of emigration strategies as it completely suppresses emigration when individuals breed successfully.
5. PERSPECTIVES
By modeling a virtual long‐lived colonial species living in a heterogeneous but temporally auto‐correlated environment, we demonstrate that informed dispersal can change the eco‐evolutionary dynamics of spatially structured populations. The modeling approach proposed here can be adapted and extended in many ways to address more specific questions on the eco‐evolutionary dynamics of informed dispersal involving prospecting.
First, some spatial complexity may be added, such as explicitly modeling individual breeding sites within patches and explicitly accounting for distances between sites and patches. This may thereby integrate the notion of perceptual range (e.g., Delgado et al., 2014). Indeed, habitat quality may vary across a hierarchy of spatial scales, and the proportion and distribution of good breeding sites available in a patch are likely to affect the spatial scale of prospecting and dispersal movements and thereby the spatial dynamics of populations (Boulinier & Danchin, 1997; Ponchon, Chambert, et al., 2015; Ponchon, Iliszko, et al., 2017). At the same time, as prospecting and subsequent dispersal movements at larger spatial scales might be risky and time‐consuming for individuals (Stamps et al., 2005), there may be important trade‐offs between the adverse environmental factors to escape (predation, lack of food, bad breeding site, etc.) and the distance covered for prospecting and subsequent dispersal movements (Baguette & Van Dyck, 2007). Hence, prospecting could even occur within one breeding patch (e.g., Ponchon, Iliszko, et al., 2017). Despite its importance in understanding individual responses to environmental variability, the hierarchical spatial aspect of the environment is often overlooked in a dispersal context and needs to be better implemented in theoretical models (Gaillard et al., 2010). Settlement decisions could also be weighted according to the timing of their use (memory effect). For instance, if an individual gathers information one year and uses it only two or more years later without updating it, there will potentially be a mismatch between the value of the information and the actual local quality of the patch. It will potentially reduce individual reproductive success, and this may have some evolutionary consequences (Bocedi et al., 2012; McNamara et al., 2011).
Here, we have implemented prospecting as a decision‐making process based on a “best‐of‐n” strategy, where individuals select the best patch from the n patches they have prospected (Figure 1; Path 1). It would be interesting to compare this strategy with a sequential sampling process, where individuals continue searching for a patch if the encountered one does not reach their selectivity threshold (i.e., Stamps et al., 2005; Figure 1; Path 2). Previous studies conducted in mate search and choice theory have shown that sequential sampling was more beneficial for individuals to select better mates compared to the best‐of‐n strategy, especially when accounting for search costs (Ferreira et al., 2018; Real, 1990). This might be the same with informed dispersal, but this has not yet been tested (Arendt, 2015). By modifying the implementation of the prospecting process, our model may provide an opportunity to obtain further insights into how settlement decisions made through different prospecting strategies evolve and affect population dynamics and structure.
Third, this type of model may help address the evolutionary consequences of sex‐specific prospecting and dispersal strategies. Indeed, it is still difficult to empirically relate prospecting movements and dispersal decisions at large spatial scales, and it is still not clear whether males and females display the same prospecting patterns and favor the use of the same information sources (e.g., Doligez et al., 1999; Morinay et al., 2018; Ponchon, Iliszko, et al., 2017; Schuett et al., 2012; Ward, 2005). Our approach might help explore new hypotheses in this context by implementing evolving sex‐dependent prospecting and dispersal rules. Additionally, existing theory has highlighted the importance of inbreeding in driving the evolution of sex‐biased dispersal as a means of avoiding inbreeding depression (Guillaume & Perrin, 2009; Henry et al., 2016; Perrin & Mazalov, 2000). In this context, our proposed approach could be modified to implement information on population relatedness structure as information which could be used by individuals in emigration and settlement decisions.
Fourth, the model is stage‐structured and has overlapping generations. Hence, it will be possible to compare the evolution of informed dispersal for species with different life cycles. This aspect has recently been highlighted as critical in the evolution of dispersal (Massol & Débarre, 2015). Moreover, informed natal dispersal, during which prospecting helps individuals select the patch where they will breed for the first time, might be important. As the choice of the first breeding site is likely to affect the timing of recruitment, first breeding attempt, and thus age at first reproduction (Bosman et al., 2013; Fay et al., 2016; Hadley et al., 2006), the joint evolution of prospecting and emigration is expected to affect both population structure and individual life‐history traits, especially in long‐lived species.
Fifth, physiological, morphological, or behavioral traits may influence informed dispersal. For example, several empirical studies have recently demonstrated that dispersal is likely influenced by individual personality (Cote et al., 2010; Korsten et al., 2013), and this trait has begun to be incorporated in modeling inter‐individual variation in dispersal behaviors (Fogarty et al., 2011; Palmer et al., 2014). We may expect bold individuals to explore their environment more (Martins et al., 2012), travel further (Palmer et al., 2014), and be more prone to dispersal compared to shyer individuals (Dingemanse et al., 2003). Bold individuals may thereby be more likely to display prospecting strategies (Burkhalter et al., 2015 but see Schuett et al., 2012). The evolutionary consequences of personality on individual decisions, movements, and realized dispersal have already been addressed (Burkhalter et al., 2015; Cote et al., 2010; Duckworth, 2008; Duckworth & Badyaev, 2007), but public information use has never been explicitly included. Addressing them with our modeling approach may provide new hypotheses that could be later tested in the field.
Finally, ecological models will help to predict better the spatial distribution and population dynamics of species using informed dispersal (e.g., Ponchon, Garnier, et al., 2015). They will also help refine conservation strategies based on the use of decoys and playbacks to attract individuals to targeted restored or newly suitable breeding areas (e.g., Ahlering et al., 2010; James et al., 2015; VanderWerf et al., 2019).
6. CONCLUSION
The modeling approach proposed here offers new avenues both for theoretical and for applied purposes, as it can be developed for species displaying various life‐history traits and informed dispersal strategies. Building further theory and generating predictions from this new modeling approach can provide a powerful means to understand the potential range of individual and population responses to environmental change within a context of informed dispersal and may ultimately improve our capability for predicting species responses to environmental changes (Cote et al., 2017; Kokko & Lopéz‐Sepulcre, 2006; Ponchon, Garnier, et al., 2015; Urban et al., 2016).
CONFLICTS OF INTEREST
The authors declare no conflict of interest.
AUTHOR CONTRIBUTIONS
Aurore Ponchon: Conceptualization (lead); formal analysis (lead); funding acquisition (lead); investigation (lead); methodology (lead); project administration (lead); validation (lead); visualization (lead); writing—original draft (lead); writing—review and editing (lead). Alice Scarpa: formal analysis (supporting); investigation (supporting); methodology (supporting); validation (supporting); writing—review and editing (supporting). Greta Bocedi: methodology (supporting); validation (supporting); writing—review and editing (supporting). Steve C. F. Palmer: methodology (supporting); validation (supporting); writing—review and editing (supporting). Justin M. J. Travis: conceptualization (supporting); funding acquisition (supporting); methodology (supporting); supervision (supporting); validation (supporting); writing—review and editing (supporting).
OPEN RESEARCH BADGES
This article has been awarded Open Data, Open Materials Badges. All materials and data are publicly accessible via the Open Science Framework at https://github.com/auponchon/Informed‐dispersal‐IBM; https://doi.org/10.5281/zenodo.5534084.
Supporting information
Figures S1–S5
ACKNOWLEDGMENTS
AP was funded by a European Union's Horizon 2020 research and innovation program under the Marie Sklodowska‐Curie grant agreement no. 753420 (EcoEvoProspectS project). JMJT and AS were funded by the Biotechnology and Biological Sciences Research Council, project grant BB/S507349/1.
Ponchon, A. , Scarpa, A. , Bocedi, G. , Palmer, S. C. F. , & Travis, J. M. J. (2021). Prospecting and informed dispersal: Understanding and predicting their joint eco‐evolutionary dynamics. Ecology and Evolution, 11, 15289–15302. 10.1002/ece3.8215
DATA AVAILABILITY STATEMENT
The source code and output files are freely accessible on the GitHub repository https://github.com/auponchon/Informed‐dispersal‐IBM and are deposited on Zenodo (https://doi.org/10.5281/zenodo.5534084).
REFERENCES
- Ahlering, M. A. , Arlt, D. , Betts, M. G. , Fletcher, R. J. , Nocera, J. J. , & Ward, M. (2010). Research needs and recommendations for the use of conspecific‐attraction methods in the conservation of migratory songbirds. The Condor, 112, 252–264. 10.1525/cond.2010.090239 [DOI] [Google Scholar]
- Aparicio, J. M. , Bonal, R. , & Muñoz, A. (2007). Experimental test on public information use in the colonial Lesser Kestrel. Evolutionary Ecology, 21, 783–800. 10.1007/s10682-006-9151-7 [DOI] [Google Scholar]
- Arendt, J. D. (2015). Effects of dispersal plasticity on population divergence and speciation. Heredity, 115, 306–311. 10.1038/hdy.2015.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baguette, M. , & Van Dyck, H. (2007). Landscape connectivity and animal behavior: Functional grain as a key determinant for dispersal. Landscape Ecology, 22, 1117–1129. 10.1007/s10980-007-9108-4 [DOI] [Google Scholar]
- Betts, M. G. , Hadley, A. S. , Rodenhouse, N. , & Nocera, J. J. (2008). Social information trumps vegetation structure in breeding‐site selection by a migrant songbird. Proceedings of the Royal Society B: Biological Sciences, 275, 2257–2263. 10.1098/rspb.2008.0217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bocedi, G. , Heinonen, J. , & Travis, J. M. J. (2012). Uncertainty and the role of information acquisition in the evolution of context‐dependent emigration. The American Naturalist, 179, 606–620. 10.1086/665004 [DOI] [PubMed] [Google Scholar]
- Bocedi, G. , Palmer, S. C. F. , Pe'er, G. , Heikkinen, R. K. , Matsinos, Y. G. , Watts, K. , & Travis, J. M. J. (2014). RangeShifter: A platform for modelling spatial eco‐evolutionary dynamics and species’ responses to environmental changes. Methods in Ecology and Evolution, 5, 388–396. 10.1111/2041-210X.12162 [DOI] [Google Scholar]
- Bonte, D. , Van Dyck, H. , Bullock, J. M. , Coulon, A. , Delgado, M. , Gibbs, M. , Lehouck, V. , Matthysen, E. , Mustin, K. , Saastamoinen, M. , Schtickzelle, N. , Stevens, V. M. , Vandewoestijne, S. , Baguette, M. , Barton, K. , Benton, T. G. , Chaput‐Bardy, A. , Clobert, J. , Dytham, C. , … Travis, J. M. J. (2012). Costs of dispersal. Biological Reviews, 87, 290–312. 10.1111/j.1469-185X.2011.00201.x [DOI] [PubMed] [Google Scholar]
- Bosman, D. S. , Vercruijsse, H. J. P. , Stienen, E. W. M. , Vincx, M. , & Lens, L. (2013). Age of first breeding interacts with pre‐ and post‐recruitment experience in shaping breeding phenology in a long‐lived gull. PLoS One, 8, e82093. 10.1371/journal.pone.0082093 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boulinier, T. , & Danchin, E. (1997). The use of conspecific reproductive success for breeding patch selection in terrestrial species. Evolutionary Ecology, 11, 505–517. [Google Scholar]
- Boulinier, T. , Kada, S. , Ponchon, A. , Dupraz, M. , Dietrich, M. , Gamble, A. , Bourret, V. , Duriez, O. , Bazire, R. , Tornos, J. , Tveraa, T. , Chambert, T. , Garnier, R. , & McCoy, K. D. (2016). Migration, prospecting, dispersal? What host movement matters for infectious agent circulation? Integrative and Comparative Biology, 56, 330–342. 10.1093/icb/icw015 [DOI] [PubMed] [Google Scholar]
- Boulinier, T. , McCoy, K. D. , Yoccoz, N. G. , Gasparani, J. , & Tveraa, T. (2008). Public information affects breeding dispersal in a colonial bird: Kittiwakes cue on neighbours. Biology Letters, 4, 538–540. 10.1098/rsbl.2008.0291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowler, D. E. , & Benton, T. G. (2005). Causes and consequences of animal dispersal strategies: Relating individual behaviour to spatial dynamics. Biological Reviews, 80, 205–225. 10.1017/S1464793104006645 [DOI] [PubMed] [Google Scholar]
- Burkhalter, J. C. , Fefferman, N. H. , & Lockwood, J. L. (2015). The impact of personality on the success of prospecting behavior in changing landscapes. Current Zoology, 61, 557–568. 10.1093/czoolo/61.3.557 [DOI] [Google Scholar]
- Campioni, L. , Granadeiro, J. P. , & Catry, P. (2017). Albatrosses prospect before choosing a home: Intrinsic and extrinsic sources of variability in visit rates. Animal Behaviour, 128, 85–93. 10.1016/j.anbehav.2017.04.008 [DOI] [Google Scholar]
- Clobert, J. , Baguette, M. , Benton, T. G. , & Bullock, J. M. (2012). Dispersal ecology and evolution. Oxford University Press. [Google Scholar]
- Clobert, J. , Danchin, E. , Dhondt, A. A. , & Nichols, J. D. (2001). Dispersal (480 pp.) Oxford University Press. [Google Scholar]
- Clobert, J. , Le Galliard, J. F. , Cote, J. , Meylan, S. , & Massot, M. (2009). Informed dispersal, heterogeneity in animal dispersal syndromes and the dynamics of spatially structured populations. Ecology Letters, 12, 197–209. 10.1111/j.1461-0248.2008.01267.x [DOI] [PubMed] [Google Scholar]
- Cote, J. , Bestion, E. , Jacob, S. , Travis, J. , Legrand, D. , & Baguette, M. (2017). Evolution of dispersal strategies and dispersal syndromes in fragmented landscapes. Ecography, 40, 56–73. 10.1111/ecog.02538 [DOI] [Google Scholar]
- Cote, J. , & Clobert, J. (2007). Social information and emigration: Lessons from immigrants. Ecology Letters, 10, 411–417. 10.1111/j.1461-0248.2007.01032.x [DOI] [PubMed] [Google Scholar]
- Cote, J. , Clobert, J. , Brodin, T. , Fogarty, S. , & Sih, A. (2010). Personality‐dependent dispersal: Characterization, ontogeny and consequences for spatially structured populations. Philosophical Transactions of the Royal Society B: Biological Sciences, 365, 4065–4076. 10.1098/rstb.2010.0176 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dall, S. R. X. , Giraldeau, L. A. , Olsson, O. , McNamara, J. M. , & Stephens, D. W. (2005). Information and its use by animals in evolutionary ecology. Trends in Ecology & Evolution, 20, 187–193. 10.1016/j.tree.2005.01.010 [DOI] [PubMed] [Google Scholar]
- Danchin, E. , Boulinier, T. , & Massot, M. (1998). Conspecific reproductive success and breeding habitat selection: Implications for the study of coloniality. Ecology, 79, 2415–2428. [Google Scholar]
- Danchin, E. , Giraldeau, L. A. , Valone, T. S. , & Wagner, R. H. (2004). Public information: From nosy neighbors to cultural evolution. Science, 305, 487–491. 10.1126/science.1098254 [DOI] [PubMed] [Google Scholar]
- De Meester, N. , & Bonte, D. (2010). Information use and density‐dependent emigration in an agrobiont spider. Behavioral Ecology, 21, 992–998. 10.1093/beheco/arq088 [DOI] [Google Scholar]
- Delgado, M. M. , Bartoń, K. A. , Bonte, D. , & Travis, J. M. J. (2014). Prospecting and dispersal: Their eco‐evolutionary dynamics and implications for population patterns. Proceedings of the Royal Society B: Biological Sciences, 281(1778), 20132851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado, M. , Ratikainen, I. I. , & Kokko, H. (2011). Inertia: The discrepancy between individual and common good in dispersal and prospecting behaviour. Biological Reviews, 86, 717–732. 10.1111/j.1469-185X.2010.00167.x [DOI] [PubMed] [Google Scholar]
- Dingemanse, N. J. , Both, C. , van Noordwijk, A. J. , Rutten, A. L. , & Drent, P. J. (2003). Natal dispersal and personalities in great tits (Parus major). Proceedings of the Royal Society B: Biological Sciences, 270, 741–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doligez, B. , Cadet, C. , Danchin, E. , & Boulinier, T. (2003). When to use public information for breeding habitat selection? The role of environmental predictability and density‐dependence. Animal Behaviour, 66, 973–988. [Google Scholar]
- Doligez, B. , Danchin, E. , & Clobert, J. (2002). Public information and breeding habitat selection in a wild bird population. Science, 297, 1168–1170. 10.1126/science.1072838 [DOI] [PubMed] [Google Scholar]
- Doligez, B. , Danchin, E. , Clobert, J. , & Gustafsson, L. (1999). The use of conspecific reproductive success for breeding habitat selection in a non‐colonial, hole‐nesting species, the collared flycatcher. Journal of Animal Ecology, 68, 1193–1206. 10.1046/j.1365-2656.1999.00362.x [DOI] [Google Scholar]
- Duckworth, R. A. (2008). Adaptive dispersal strategies and the dynamics of a range expansion. The American Naturalist, 172, S4–S17. 10.1086/588289 [DOI] [PubMed] [Google Scholar]
- Duckworth, R. A. , & Badyaev, A. V. (2007). Coupling of dispersal and aggression facilitates the rapid range expansion of a passerine bird. Proceedings of the National Academy of Sciences of the United States of America, 104, 15017–15022. 10.1073/pnas.0706174104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dugger, K. M. , Ainley, D. G. , Lyver, P. B. , Barton, K. , & Ballard, G. (2010). Survival differences and the effect of environmental instability on breeding dispersal in an Adélie penguin meta‐population. Proceedings of the National Academy of Sciences of the United States of America, 107, 12375–12380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enfjäll, K. , & Leimar, O. (2009). The evolution of dispersal – The importance of information about population density and habitat characteristics. Oikos, 118, 291–299. 10.1111/j.1600-0706.2008.16863.x [DOI] [Google Scholar]
- Fay, R. , Barbraud, C. , Delord, K. , & Weimerskirch, H. (2016). Variation in the age of first reproduction: Different strategies or individual quality? Ecology, 97, 1842–1851. 10.1890/15-1485.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira, G. B. S. , Scheutz, M. , & Boyd, S. K. (2018). Mate choice strategies in a spatially‐explicit model environment. PLoS One, 13, e0202680. 10.1371/journal.pone.0202680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogarty, S. , Cote, J. , & Sih, A. (2011). Social personality polymorphism and the spread of invasive species: A model. The American Naturalist, 177, 273–287. 10.1086/658174 [DOI] [PubMed] [Google Scholar]
- Forero, M. G. , Donázar, J. A. , Blas, J. , & Hiraldo, F. (1999). Causes and consequences of territory change and breeding dispersal distance in the Black Kite. Ecology, 80, 1298–1310. [Google Scholar]
- Fronhofer, E. A. , Nitsche, N. , & Altermatt, F. (2017). Information use shapes the dynamics of range expansions into environmental gradients. Global Ecology and Biogeography, 26, 400–411. 10.1111/geb.12547 [DOI] [Google Scholar]
- Gaillard, J.‐M. , Hebblewhite, M. , Loison, A. , Fuller, M. , Powell, R. A. , Basille, M. , & Van Moorter, B. (2010). Habitat–performance relationships: Finding the right metric at a given spatial scale. Philosophical Transactions of the Royal Society B: Biological Sciences, 365, 2255–2265. 10.1098/rstb.2010.0085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillaume, F. , & Perrin, N. (2009). Inbreeding load, bet hedging, and the evolution of sex‐biased dispersal. The American Naturalist, 173, 536–541. 10.1086/597218 [DOI] [PubMed] [Google Scholar]
- Hadley, G. L. , Rotella, J. J. , Garrott, R. A. , & Nichols, J. D. (2006). Variation in probability of first reproduction of Weddell seals. Journal of Animal Ecology, 75, 1058–1070. 10.1111/j.1365-2656.2006.01118.x [DOI] [PubMed] [Google Scholar]
- Henry, R. C. , Coulon, A. , & Travis, J. M. J. (2016). The evolution of male‐biased dispersal under the joint selective forces of inbreeding load and demographic and environmental stochasticity. The American Naturalist, 188, 423–433. 10.1086/688170 [DOI] [PubMed] [Google Scholar]
- James, M. S. , Stockwell, M. P. , Clulow, J. , Clulow, S. , & Mahony, M. J. (2015). Investigating behaviour for conservation goals: Conspecific call playback can be used to alter amphibian distributions within ponds. Biological Conservation, 192, 287–293. 10.1016/j.biocon.2015.10.001 [DOI] [Google Scholar]
- Kokko, H. , & Lopéz‐Sepulcre, A. (2006). From individual dispersal to species ranges: Perspectives for a changing world. Science, 313, 789–791. 10.1126/science.1128566 [DOI] [PubMed] [Google Scholar]
- Korsten, P. , van Overveld, T. , Adriaensen, F. , & Matthysen, E. (2013). Genetic integration of local dispersal and exploratory behaviour in a wild bird. Nature Communications, 4, 2362. 10.1038/ncomms3362 [DOI] [PubMed] [Google Scholar]
- Mares, R. , Bateman, A. W. , English, S. , Clutton‐Brock, T. H. , & Young, A. J. (2014). Timing of predispersal prospecting is influenced by environmental, social and state‐dependent factors in meerkats. Animal Behaviour, 88, 185–193. 10.1016/j.anbehav.2013.11.025 [DOI] [Google Scholar]
- Martins, C. I. M. , Schaedelin, F. C. , Mann, M. , Blum, C. , Mandl, I. , Urban, D. , Grill, J. , Schößwender, J. , & Wagner, R. H. (2012). Exploring novelty: A component trait of behavioural syndromes in a colonial fish. Behaviour, 149, 215–231. 10.1163/156853912X634430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massol, F. , & Débarre, F. (2015). Evolution of dispersal in spatially and temporally variable environments: The importance of life cycles. Evolution, 69, 1925–1937. 10.1111/evo.12699 [DOI] [PubMed] [Google Scholar]
- Mayer, M. , Zedrosser, A. , & Rosell, F. (2017). Extra‐territorial movements differ between territory holders and subordinates in a large, monogamous rodent. Scientific Reports, 7, 15261. 10.1038/s41598-017-15540-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNamara, J. M. , Barta, Z. , Klaassen, M. , & Baue, S. (2011). Cues and the optimal timing of activities under environmental changes. Ecology Letters, 14, 1183–1190. 10.1111/j.1461-0248.2011.01686.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morinay, J. , Forsman, J. T. , Kivelä, S. M. , Gustafsson, L. , & Doligez, B. (2018). Heterospecific nest site copying behavior in a wild bird: Assessing the influence of genetics and past experience on a joint breeding phenotype. Frontiers in Ecology and Evolution, 5, 167. [Google Scholar]
- Palmer, S. C. F. , Coulon, A. , & Travis, J. M. J. (2014). Inter‐individual variability in dispersal behaviours impacts connectivity estimates. Oikos, 123, 923–932. 10.1111/oik.01248 [DOI] [Google Scholar]
- Pakanen, V.‐M. , Hildén, O. , Rönkä, A. , Belda, E. J. , Luukkonen, A. , Kvist, L. , & Koivula, K. (2011). Breeding dispersal strategies following reproductive failure explain low apparent survival of immigrant Temminck's stints. Oikos, 120, 615–622. 10.1111/j.1600-0706.2010.18953.x [DOI] [Google Scholar]
- Pärt, T. , Arlt, D. , Doligez, B. , Low, M. , & Qvarnström, A. (2011). Prospectors combine social and environmental information to improve habitat selection and breeding success in the subsequent year. Journal of Animal Ecology, 80, 1227–1235. 10.1111/j.1365-2656.2011.01854.x [DOI] [PubMed] [Google Scholar]
- Perrin, N. , & Mazalov, V. (2000). Local competition, inbreeding, and the evolution of sex‐biased dispersal. The American Naturalist, 155, 116–127. 10.1086/303296 [DOI] [PubMed] [Google Scholar]
- Pizzatto, L. , Stockwell, M. , Clulow, S. , Clulow, J. , & Mahony, M. (2016). Finding a place to live: Conspecific attraction affects habitat selection in juvenile green and golden bell frogs. Acta Ethologica, 19, 1–8. 10.1007/s10211-015-0218-8 [DOI] [Google Scholar]
- Ponchon, A. , Aulert, C. , Le Guillou, G. , Gallien, F. , Péron, C. , & Grémillet, D. (2017). Spatial overlaps of foraging and resting areas of black‐legged kittiwakes breeding in the English Channel with existing marine protected areas. Marine Biology, 164, 119. 10.1007/s00227-017-3151-8 [DOI] [Google Scholar]
- Ponchon, A. , Chambert, T. , Lobato, E. , Tveraa, T. , Grémillet, D. , & Boulinier, T. (2015). Breeding failure induces large scale prospecting movements in the black‐legged kittiwake. Journal of Experimental Marine Biology and Ecology, 473, 138–145. 10.1016/j.jembe.2015.08.013 [DOI] [Google Scholar]
- Ponchon, A. , Garnier, R. , Grémillet, D. , & Boulinier, T. (2015). Predicting population responses to environmental change: The importance of considering informed dispersal strategies in spatially structured population models. Diversity and Distributions, 21, 88–100. 10.1111/ddi.12273 [DOI] [Google Scholar]
- Ponchon, A. , Grémillet, D. , Christensen‐Dalsgaard, S. , Erikstad, K. E. , Barrett, R. , Reiertsen, T. K. , McCoy, K. D. , Tveraa, T. , & Boulinier, T. (2014). When things go wrong: Intra‐season dynamics of breeding failure in a seabird. Ecosphere, 5, Art. 4. 10.1890/ES13-00233.1 [DOI] [Google Scholar]
- Ponchon, A. , Grémillet, D. , Doligez, B. , Chambert, T. , Tveraa, T. , González‐Solís, J. , & Boulinier, T. (2013). Tracking prospecting movements involved in breeding habitat selection: Insights, pitfalls and perspectives. Methods in Ecology and Evolution, 4, 143–150. 10.1111/j.2041-210x.2012.00259.x [DOI] [Google Scholar]
- Ponchon, A. , Iliszko, L. , Grémillet, D. , Tveraa, T. , & Boulinier, T. (2017). Intense prospecting movements of failed breeders nesting in an unsuccessful breeding subcolony. Animal Behaviour, 124, 183–191. 10.1016/j.anbehav.2016.12.017 [DOI] [Google Scholar]
- Real, L. (1990). Search theory and mate choice. I. Models of single‐sex discrimination. The American Naturalist, 136, 376–405. 10.1086/285103 [DOI] [Google Scholar]
- Reed, J. M. , Boulinier, T. , Danchin, E. , & Oring, L. W. (1999). Informed dispersal: Prospecting by birds for breeding sites. Current Ornithology, 15, 189–259. [Google Scholar]
- Rioux, S. , Amirault‐Langlais, D. L. , & Shaffer, F. (2011). Piping plovers make decisions regarding dispersal based on personal and public information in a variable coastal ecosystem. Journal of Field Ornithology, 82, 32–43. 10.1111/j.1557-9263.2010.00305.x [DOI] [Google Scholar]
- Robert, A. , Paiva, V. H. , Bolton, M. , Jiguet, F. , & Bried, J. (2014). Nest fidelity is driven by multi‐scale information in a long‐lived seabird. Proceedings of the Royal Society B: Biological Sciences, 281, 20141692. 10.1098/rspb.2014.1692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronce, O. (2007). How does it feel to be like a rolling stone? Ten questions about dispersal evolution. Annual Review of Ecology, Evolution, and Systematics, 38, 231–253. 10.1146/annurev.ecolsys.38.091206.095611 [DOI] [Google Scholar]
- Schmidt, K. A. (2017). Information thresholds, habitat loss and population persistence in breeding birds. Oikos, 126, 651–659. 10.1111/oik.03703 [DOI] [Google Scholar]
- Schmidt, K. A. , Johansson, J. , Kristensen, N. , Massol, F. , & Jonzén, N. (2015). Consequences of information use in breeding habitat selection on the evolution of settlement time. Oikos, 124, 69–80. 10.1111/oik.01483 [DOI] [Google Scholar]
- Schuett, W. , Laaksonen, J. , & Laaksonen, T. (2012). Prospecting at conspecific nests and exploration in a novel environment are associated with reproductive success in the jackdaw. Behavioral Ecology and Sociobiology, 66, 1341–1350. 10.1007/s00265-012-1389-1 [DOI] [Google Scholar]
- Seeley, T. D. , & Buhrman, S. C. (2001). Nest‐site selection in honey bees: How well do swarms implement the “best‐of‐N” decision rule? Behavioral Ecology and Sociobiology, 49, 416–427. 10.1007/s002650000299 [DOI] [Google Scholar]
- Selonen, V. , & Hanski, I. K. (2010). Decision making in dispersing Siberian flying squirrels. Behavioral Ecology, 21, 219–225. 10.1093/beheco/arp179 [DOI] [Google Scholar]
- Seppänen, J. T. , Forsman, J. T. , Mönkkönen, M. , & Thomson, R. L. (2007). Social information use is a process across time, space, and ecology, reaching heterospecifics. Ecology, 88, 1622–1633. 10.1890/06-1757.1 [DOI] [PubMed] [Google Scholar]
- Stamps, J. A. (1988). Conspecific attraction and aggregation in territorial species. The American Naturalist, 131, 329–347. 10.1086/284793 [DOI] [Google Scholar]
- Stamps, J. A. , Krishnan, V. V. , & Reid, M. L. (2005). Search costs and habitat selection by dispersers. Ecology, 86, 510–518. 10.1890/04-0516 [DOI] [Google Scholar]
- Stroeymeyt, N. , Giurfa, M. , & Franks, N. R. (2017). Information certainty determines social and private information use in ants. Scientific Reports, 7, 43607. 10.1038/srep43607 [DOI] [Google Scholar]
- Travis, J. M. J. , Delgado, M. , Bocedi, G. , Baguette, M. , Bartoń, K. , Bonte, D. , Boulangeat, I. , Hodgson, J. A. , Kubisch, A. , Penteriani, V. , Saastamoinen, M. , Stevens, V. M. , & Bullock, J. M. (2013). Dispersal and species’ responses to climate change. Oikos, 122, 1532–1540. 10.1111/j.1600-0706.2013.00399.x [DOI] [Google Scholar]
- Travis, J. M. J. , Mustin, K. , Bartoń, K. A. , Benton, T. G. , Clobert, J. , Delgado, M. M. , Dytham, C. , Hovestadt, T. , Palmer, S. C. F. , Van Dyck, H. , & Bonte, D. (2012). Modelling dispersal: An eco‐evolutionary framework incorporating emigration, movement, settlement behaviour and the multiple costs involved. Methods in Ecology and Evolution, 3, 628–641. 10.1111/j.2041-210X.2012.00193.x [DOI] [Google Scholar]
- Urban, M. C. , Bocedi, G. , Hendry, A. P. , Mihoub, J.‐B. , Peer, G. , Singer, A. , Bridle, J. R. , Crozier, L. G. , De Meester, L. , Godsoe, W. , Gonzalez, A. , Hellmann, J. J. , Holt, R. D. , Huth, A. , Johst, K. , Krug, C. B. , Leadley, P. W. , Palmer, S. C. F. , Pantel, J. H. , … Travis, J. M. J. (2016). Improving the forecast for biodiversity under climate change. Science, 353. 10.1126/science.aad8466 [DOI] [PubMed] [Google Scholar]
- VanderWerf, E. A. , Young, L. C. , Kohley, C. R. , Dalton, M. E. , Fisher, R. , Fowlke, L. , Donohue, S. , & Dittmar, E. (2019). Establishing Laysan and black‐footed albatross breeding colonies using translocation and social attraction. Global Ecology and Conservation, 19, e00667. 10.1016/j.gecco.2019.e00667 [DOI] [Google Scholar]
- Votier, S. , Grecian, W. , Patrick, S. , & Newton, J. (2011). Inter‐colony movements, at‐sea behaviour and foraging in an immature seabird: Results from GPS‐PPT tracking, radio‐tracking and stable isotope analysis. Marine Biology, 158, 355–362. 10.1007/s00227-010-1563-9 [DOI] [Google Scholar]
- Vuilleumier, S. , & Perrin, N. (2006). Effects of cognitive abilities on metapopulation connectivity. Oikos, 113, 139–147. 10.1111/j.0030-1299.2006.14405.x [DOI] [Google Scholar]
- Ward, M. (2005). Habitat selection by dispersing yellow‐headed blackbirds: Evidence of prospecting and the use of public information. Oecologia, 145, 650–657. 10.1007/s00442-005-0179-0 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figures S1–S5
Data Availability Statement
The source code and output files are freely accessible on the GitHub repository https://github.com/auponchon/Informed‐dispersal‐IBM and are deposited on Zenodo (https://doi.org/10.5281/zenodo.5534084).


