Back to the basics: Rethinking partial correlation network methodology

Abstract

The Gaussian graphical model (GGM) is an increasingly popular technique used in psychology to characterize relationships among observed variables. These relationships are represented as elements in the precision matrix. Standardizing the precision matrix and reversing the sign yields corresponding partial correlations that imply pairwise dependencies in which the effects of all other variables have been controlled for. The graphical lasso (glasso) has emerged as the default estimation method, which uses ℓ₁-based regularization. The glasso was developed and optimized for high-dimensional settings where the number of variables (p) exceeds the number of observations (n), which is uncommon in psychological applications. Here we propose to go ‘back to the basics’, wherein the precision matrix is first estimated with non-regularized maximum likelihood and then Fisher Z transformed confidence intervals are used to determine non-zero relationships. We first show the exact correspondence between the confidence level and specificity, which is due to 1 minus specificity denoting the false positive rate (i.e., α). With simulations in low-dimensional settings (p ≪ n), we then demonstrate superior performance compared to the glasso for detecting the non-zero effects. Further, our results indicate that the glasso is inconsistent for the purpose of model selection and does not control the false discovery rate, whereas the proposed method converges on the true model and directly controls error rates. We end by discussing implications for estimating GGMs in psychology.

1. Introduction

An important goal for psychological science is to develop methods to characterize relationships between variables. The customary approach uses structural equation models (SEM) to connect latent factors on a structural level to a number of observed measurements (MacCallum & Austin, 2000). More recently, Gaussian graphical models (GGM) have been proposed as an alternative approach for describing the relation among variables, and they have become increasingly popular in psychology (Borsboom & Cramer, 2013; Epskamp & Fried, 2018; Van Borkulo et al., 2014). Rather than assessing a hypothesized model structure, as in an SEM, GGMs seek to capture conditional relationships (i.e., direct effects) between a set of observed variables. This is accomplished by identifying non-zero elements in the off-diagonal entries of the inverse covariance (i.e., precision) matrix (Dempster, 1972). When these elements are standardized and the sign reversed, they correspond to partial correlations that imply pairwise dependencies in which the linear effects of all other variables have been controlled for (Fan, Liao, & Liu, 2016; Whittaker, 1990). Since direct effects allow for rich inferences, this has resulted in a growing body of literature called ‘network mode;ling’ in both methodological (Epskamp & Fried, 2018; Epskamp, Kruis, & Marsman, 2017) and applied contexts (McNally et al., 2015; Rhemtulla et al., 2016).

The default approach for estimating network models in psychology uses ℓ₁-regularization (e.g., a form of penalized maximum likelihood; Epskamp & Fried, 2018), which can simultaneously improve predictive accuracy and perform variable selection by reducing some parameters to exactly zero (Dalalyan, Hebiri, & Lederer, 2017). In the context of regression, this is known as the least absolute shrinkage and selector operator (lasso) method (Dalalyan et al., 2017), whereas the extension to multivariate settings is called the graphical lasso (glasso; Friedman, Hastie, & Tibshirani, 2008). Importantly, the glasso method was primarily developed to overcome challenges in high-dimensional settings, in which the number of variables (p) often exceeds the number of observations (n; Fan et al., 2016). In these situations, the covariance matrix cannot be inverted due to singularity (Hartlap, Simon, & Schneider, 2007), which is overcome by the glasso method. Accordingly, most of the simulation work has focused on high-dimensional settings (n < p), where model selection consistency is not typically evaluated in more common asymptotic settings (n → ∞; Ha & Sun, 2014; Heinävaara, Leppä-aho, Corander, & Honkela, 2016; Peng, Wang, Zhou, & Zhu, 2009). Further, in behavioural science applications, the majority of network models are fitted in low-dimensional settings (p ≪ n; Costantini et al., 2015; Rhemtulla et al., 2016). Unfortunately, model selection consistency has not been demonstrated with simulation studies representative of typical psychological applications.

One aim of the current work is to fill this gap by investigating the properties of the most common glasso estimation techniques in situations where p is representative of the psychological literature and fixed, while n increases. This has a straightforward translation to applied settings: when a psychometric scale has been decided on (the number of variables p is fixed), an important goal is to obtain the smallest possible sample (n) to accurately estimate the network. A consistent method for model selection will ideally converge on the true model, with a probability approaching 100%, at some point as the sample size becomes larger (n → ∞; Casella, Girón, Martínez, & Moreno, 2009).

There is some indication in the literature that the performance of ℓ₁-regularization does not generalize to all settings, especially in the context of graphical models. For example, Heinävaara et al. (2016) demonstrated that ℓ₁-based methods have sub-optimal performance with highly correlated variables, and that the assumptions for consistency are rarely met in their particular field of study (genomics). According to Heinävaara et al. (2016, p. 106):

Our results strongly suggest that users of the numerous ℓ₁-penalised and other ℓ₁ based sparse precision matrix and GGM structure learning methods should be very careful about checking whether the conditions of consistency for precision matrix estimation are likely to be fulfilled in the application area of interest.

This finding paralleled Kuismin and Sillanpää (2016), who similarly noticed an inconsistency of the glasso method in that estimation errors did not diminish with increasing sample sizes. Further, Leppä-aho, Pensar, Roos, and Corander (2017) introduced an approximate Bayesian method, and their results showed that the glasso was not always consistent with respect to Hamming distance (HD; Norouzi, Fleet, Salakhutdinov, & Blei, 2012). These findings are consistent with the results of a less extensive simulation in Epskamp and Fried (2018) and Epskamp (2016) that incidentally also indicated errors did not diminish with larger sample sizes. Note that these finding can be attributed to ℓ₁-regularization making additional assumptions, compared to non-regularized methods (e.g., normality), for accurate estimation. These are outlined in Meinshausen and Bühlmann (2006), and require there to be few connections (i.e., the assumption of sparsity), in addition to minimal correlations between the important and unimportant variables. The latter is the so-called irrepresentable condition (Zhao & Yu, 2006), which was shown to rarely hold as the level of sparsity decreased. This is especially important for psychological applications, because estimated network structures are typically dense (Costantini et al., 2015).

Moreover, statistical inference is not straightforward from estimates obtained from ℓ₁-based methods (Hastie, Tibshirani, & Wainwright, 2015, Chapter 6). That is, the mere fact that a variable has been selected does not allow one to claim that the estimate is significantly different from zero, or that a non-selected variable has no effect. These claims would require formal hypothesis testing, whether Bayesian or frequentist (Lockhart, Taylor, Tibshirani, & Tibshirani, 2014; Mohammadi & Wit, 2015; Schäfer & Strimmer, 2005a), which does not equate to selecting variables based on predictive performance or minimizing a particular loss function. For example, selecting a model based on predictive performance can lead to inconsistent model selection (Leng, Lin, & Wahba, 2006). Further, ℓ₁-based methods use automated variable selection, in which valid inference needs to account for model selection bias (Efron, 2014; Lee, Sun, Sun, & Taylor, 2016; Taylor & Tibshirani, 2017), although under certain assumptions ‘naïve’ refitting of the selected variables can lead to valid inferences (Zhao, Shojaie, & Witten, 2017). The glasso method faces an additional limitation, because regularization biases the estimates towards zero, which then requires additional steps to obtain nominal frequentist properties (e.g., coverage rates), including debiasing techniques (Javanmard & Montanari, 2015) and non-traditional bootstrapping schemes (Chatterjee & Lahiri, 2011). Together, the central challenge for advancing network methodology in psychology is to investigate not only methods specifically for the most common applications (p ≪ n), but also those allowing for customary statistical inferences. Because the vast majority of psychological networks are estimated in low-dimensional settings (p ≪ n), this suggests that traditional methods, which do not employ regularization, can readily be used in the social-behavioural sciences.

In this paper, rather than building upon relatively recently introduced statistical procedures (e.g., ℓ₁-based methods), we propose a statistical technique that directly builds upon work from a century ago (Fisher, 1915, 1924; Yule, 1907), and thus has a closed-form solution. We first introduce GGMs. We then describe the current default statistical method in psychology, after which we outline our approach for estimating GGMs. With a ‘proof of concept’, we demonstrate an important advantage of the proposed method: nominal frequentist properties (e.g., coverage probabilities). We then use simulations to compare the methods with respect to correctly identifying non-zero relationships, in addition to accuracy measured with various loss functions. Because the proposed method is based on p-values, which raises the concern of multiple comparisons, an additional simulation examines the utility of framing network estimation in terms of the false discovery rate. We end with an application to real data, as well as discussing implications and future directions.

2. Gaussian graphical model

Undirected graphical models can refer to covariance selection models, random Markov fields, or network models (as in psychology). Here we adopt the term ‘Gaussian graphical model’, because it is the most general and provides an informative description of the method. For example, let X be a p-dimensional Gaussian random vector defined as

$$X=\left\{x_1,\dots ,x_p\right\}~\mathcal{N}(\mathbf{\mu },\Sigma ),$$ (1)

where, without loss of generality, we assume all variables have been standardized to have mean zero (i.e., 0 = {μ_1, …, μ_p}^⊤) and covariance Σ. A GGM is then a probability model that characterizes the conditional dependent structure of X with a graph. This is accomplished by identifying the non-zero elements within the inverse-covariance matrix Σ⁻¹ = Θ (i.e., the precision matrix). In the following notation, we denote the graph by $\mathcal{G}=(V,E)$, consisting of nodes V = {1, …, p} and the edge set (non-zero connections between nodes) E ⊂ V × V. The maximum number of edges possible in $\mathcal{G}$ is V(V − 1)/2, which corresponds to the number of unique off-diagonal elements of Σ. The edge set for $\mathcal{G}$ contains nodes (x_i, x_j) that share a conditional relationship x_i ⫫ x_j|X_V\i,j. In contrast, conditionally independent nodes x_i ⫫ x_j|X_V\i,j are not included in E.

The graph $\mathcal{G}$ obtained depends on accurate estimation of the precision matrix Θ. This is straightforward in low-dimensional settings (p ≪ n), because maximum likelihood provides an adequate estimate (Wang et al., 2016). However, in high-dimensional settings (p ≥ n), the maximum likelihood estimate (MLE) cannot be computed due to singularity: det(Σ) = 0. That is, since the determinant equals the product of the eigenvalues from the covariance matrix,

$$\begin{array}{cc}\text{det}\left(\Sigma \right)=\prod _{i=1}^p{\lambda }_i,& {\lambda }_i\in \left\{1,\dots ,p\right\},\end{array}$$ (2)

and the maximum number of non-zero eigen values is min (n,p) (Kuismin & Sillanpää, 2017), it can be shown that inversion is not possible (Hartlap et al., 2007). This is known as the ‘large p, small n’ problem and remains a central challenge in the field of statistics (Kuismin & Sillanpää, 2016). Although these kinds of data structures are common in fields such as genomics (Wang & Huang, 2014) and quantitative finance (Ledoit & Wolf, 2004a, 2004b), they are the exception in psychology. Nonetheless, in psychology, ℓ₁ penalized maximum likelihood has emerged as the default estimation method (Epskamp & Fried, 2018).

3. ℓ₁-regularization

In the familiar context of multiple regression, the lasso method uses the ℓ₁ norm to find coefficients that minimize

$$\sum _{i=1}^n{\left(y_i-\sum _{j=1}^p{X}_{ij}{\beta }_j\right)}^2+\lambda \sum _{j=1}^p\left|{\beta }_j\right|,$$ (3)

where λ is the tuning parameter on the sum of absolute values for the coefficients |β_j| (Tibshirani, 1996). Larger values of λ provide more regularization, whereas λ = 0 results in a non-penalized model. Under the assumption that $\mathbf{ϵ}~\mathcal{N}\left(0,{\sigma }^2\right)$, minimizing the ordinary least squares estimates is equivalent to maximizing the likelihood, or in this case the ℓ₁ penalized maximum likelihood. Importantly, optimizing equation 3 has the ability to reduce coefficients to exactly zero, which allows for variable selection. For this reason ℓ₁-based methods have become popular for both regression and estimating network models.

Extended to multivariate settings, the penalized likelihood for the precision matrix is defined as

$$l\left(\Theta \right)=\text{log}\text{det}\Theta -\text{tr}\left(S\Theta \right)-{\lambda }_{\text{p}}\sum _{i\ne j}\left(\left|{\Theta }_{i,j}\right|\right),$$ (4)

where S is the sample covariance matrix and λ_p a penalty function (Gao, Pu, Wu, & Xu, 2009). The glasso method applies a penalty on the sum of absolute covariance values λ_p(|Θ_i,j|) (Friedman et al., 2008). The performance of the glasso method is strongly influenced by the choice of λ, which can be made in at least four ways: (1) choose λ to minimize the extended Bayesian information criterion (EBIC; Foygel & Drton, 2010); (2) choose λ to minimize the rotation information criterion (RIC; Zhao, Liu, Roeder, Lafferty, & Wasserman, 2012); (3) choose λ to maximize the stability of the solution across subsamples of the data (stability approach to regularization selection; Liu, Roeder, & Wasserman, 2010); or (4) base the selection on k-fold cross-validation (Bien & Tibshirani, 2011).

While a method would ideally be selected with a particular goal in mind, or based on performance in simulations that are representative of the particular field, the default method in psychology is currently EBIC (Epskamp & Fried, 2018),

$$\text{EBIC}=-2l\left(\Theta \right)+E\text{log}\left(n\right)+4\gamma E\text{log}\left(p\right),$$ (5)

where l(Θ) is defined in equation 4, E is the size of the edge set (i.e., the number of non-zero elements of Θ), and γ ∈ [0, 1] is the EBIC hyperparameter that puts an extra penalty on the standard Bayesian information criterion (BIC, γ = 0). The selected network then minimizes EBIC with respect to λ. This is typically accomplished by assessing a large number of values of λ (e.g., 100) and selecting the one for which EBIC is smallest. There is no automatic selection procedure for the EBIC hyperparameter, but .5 was recommended in Foygel and Drton (2010) and Epskamp and Fried (2018).

4. Basic approach

Our proposed method differs from the glasso in several respects. We approach the problem in the simplest terms, in that we are simply estimating a (partial) correlation matrix following classic and well-known standard methods. We first compute the p × p covariance matrix with the MLE defined as

$$\begin{array}{cc}\Sigma =\left[\frac{1}{n}\sum _{i=1}^n\left(x_i-\overline{x}\right){\left(x_i-\overline{x}\right)}^{\top }\right],& \overline{x}=\frac{1}{n}\sum _{i=1}^n{x}_i,\end{array}$$ (6)

where the variables are centred to have mean zero. As is evident in equation 6, this method does not use any form of regularization. After the MLE is computed, it is straightforward to obtain the precision matrix Σ⁻¹ = Θ which contains the elements θ_ij and variances θ_ii:

$$\Theta =\left[\begin{array}{ccc}{\theta }_{ii}& & \\ ⋮& \ddots & \\ {\theta }_{ij}& \cdots & {\theta }_{jj}\end{array}\right].$$ (7)

The partial correlations can be obtained as

$${\rho }_{ij}=\frac{-{\theta }_{ij}}{\sqrt{{\theta }_{ii}{\theta }_{jj}}},$$ (8)

which denote the standardized conditional relationships. In contrast to ℓ₁-regularization, where exact zeros are obtained through optimization, this approach requires an explicit decision rule for setting ${\widehat{\rho }}_{ij}$ to zero. Here we first use the Fisher Z-transformation,

$$z_{ij}=\frac{1}{2}\text{log}\left(\frac{1+{\rho }_{ij}}{1-{\rho }_{ij}}\right),$$ (9)

which results in an approximate normal distribution defined as

$$z_{ij}~\mathcal{N}\left(\frac{1}{2}\text{log}\left(\frac{1+{\widehat{\rho }}_{ij}}{1-{\widehat{\rho }}_{ij}}\right),\frac{1}{n-3-s}\right).$$ (10)

Here s denotes the number of variables controlled for p − 1, and $\sqrt{1/\left(n-3-s\right)}$ the standard error. We then define α based on subjective grounds (e.g., the trade-off between false positives and negatives), and the corresponding critical value Z_α/2. In contrast to λ in the glasso, α is a calibrated measure with respect to false positives and coverage probabilities (i.e., 100(1 − α)%). The confidence interval (CI) for z_ij is defined as

$$\begin{gathered} Z_{\text{L}}=z_{ij}-Z_{\alpha /2}\sqrt{\frac{1}{n-3-s\text{'}}} \\ {Z}_{\text{U}}=z_{ij}+Z_{\alpha /2}\sqrt{\frac{1}{n-3-s\text{'}}} \end{gathered}$$ (11)

where Z_L and Z_U denote the lower and upper bounds. To obtain the interval for ${\widehat{\rho }}_{ij}$, a transformation is required:

$$\begin{array}{cc}{\widehat{\rho }}_{i{j}_{\text{L}}}=\frac{\text{exp}\left(2Z_{\text{L}}\right)-1}{\text{exp}\left(2Z_{\text{L}}\right)+1},& {\widehat{\rho }}_{i{j}_{\text{U}}}=\frac{\text{exp}\left(2Z_{\text{L}}\right)-1}{\text{exp}\left(2Z_{\text{U}}\right)+1}\end{array}.$$ (12)

From this method, we obtain an edge set E in which the CIs for ρ_ij exclude zero (i.e., classical null hypothesis significance testing). If the assumptions of this model are satisfied, the computed intervals will have the nominal coverage probabilities. In the context of GGMs, this suggests we can obtain approximately 100% coverage, or that the false positive rate will be close to zero. For example, the specificity (SPC), or true negative rate, is defined as

$$\text{SPC}=\frac{\text{ number of true negatives }}{\text{ number of true negatives }+\text{ number of false positives }},$$ (13)

which should correspond exactly to the coverage rate of ρ_ij = 0 for a given network. Accordingly, 1 − SPC corresponds to the false positive rate.

5. Proof of concept: coverage probabilities

In this section we investigate coverage probabilities of the proposed CI-based method. This was done for two reasons. First, the covariance matrix can be inverted in low-dimensional settings (p < n), but there can still be increased estimation errors when p approaches n (Ledoit & Wolf, 2004b). Second, alternative approaches, developed for high-dimensional settings in particular, construct an approximate null sampling distribution for the partial correlations, and then use p-values to determine the edge set E (Schäfer & Strimmer, 2005b). To our knowledge, coverage probabilities for partial correlations have not been examined in relatively large p settings.

We simulated data from null networks, in which all partial correlations were set to 0. The corresponding precision matrices Θ ~ W_G (df = 20, I_p) were then generated from a Wishart distribution with 20 degrees of freedom and scale I_p (Mohammadi & Wit, 2015). The number of variables p was fixed at 20 and the sample sizes varied: n ∈ {25, 50, 150, 250, 500, 1,000, 10,000}. The 95% and 99% coverage probabilities were averaged across 1,000 simulation trials. We also plotted results from a representative trial to illustrate coverage for a given network, with the 95% CI, which demonstrates the exact correspondence to specificity.

The results from one simulation trial are plotted in Figure 1. Part (a) shows the properties of the computed 95% intervals, in which false positives are denoted in black. Note that the estimated CIs have several desirable characteristics, including being bounded between −1 and 1. When the sample is larger than 25, they are symmetric and become narrower with increasing sample sizes. This stands in contrast to lasso estimation, in which only point estimates are provided by optimizing equation 4. Further, when bootstrap schemes are used, the sampling distribution can be distorted, which is a well-known result of ℓ₁-regularization (Hastie et al., 2015). This point is further discussed and demonstrated in the applied example (Figure 5 in Section 10).

Figure 1.

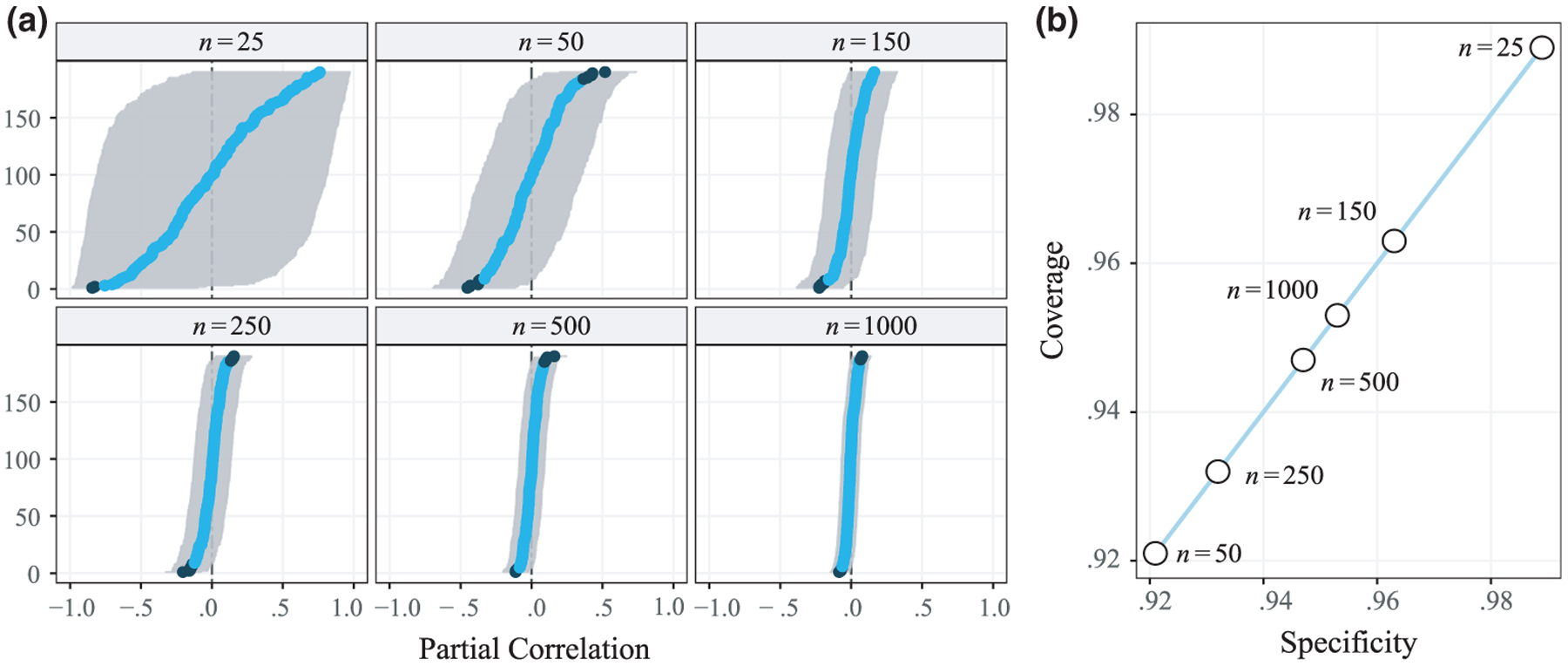
(a) Estimated partial correlations and confidence intervals. Black dots denote confidence intervals that exclude zero. (b) Specificity and coverage probabilities for the estimated networks in (a). This demonstrates that, for a given network, specificity and coverage are equivalent (i.e., 1 − α = SPC).

Figure 5.

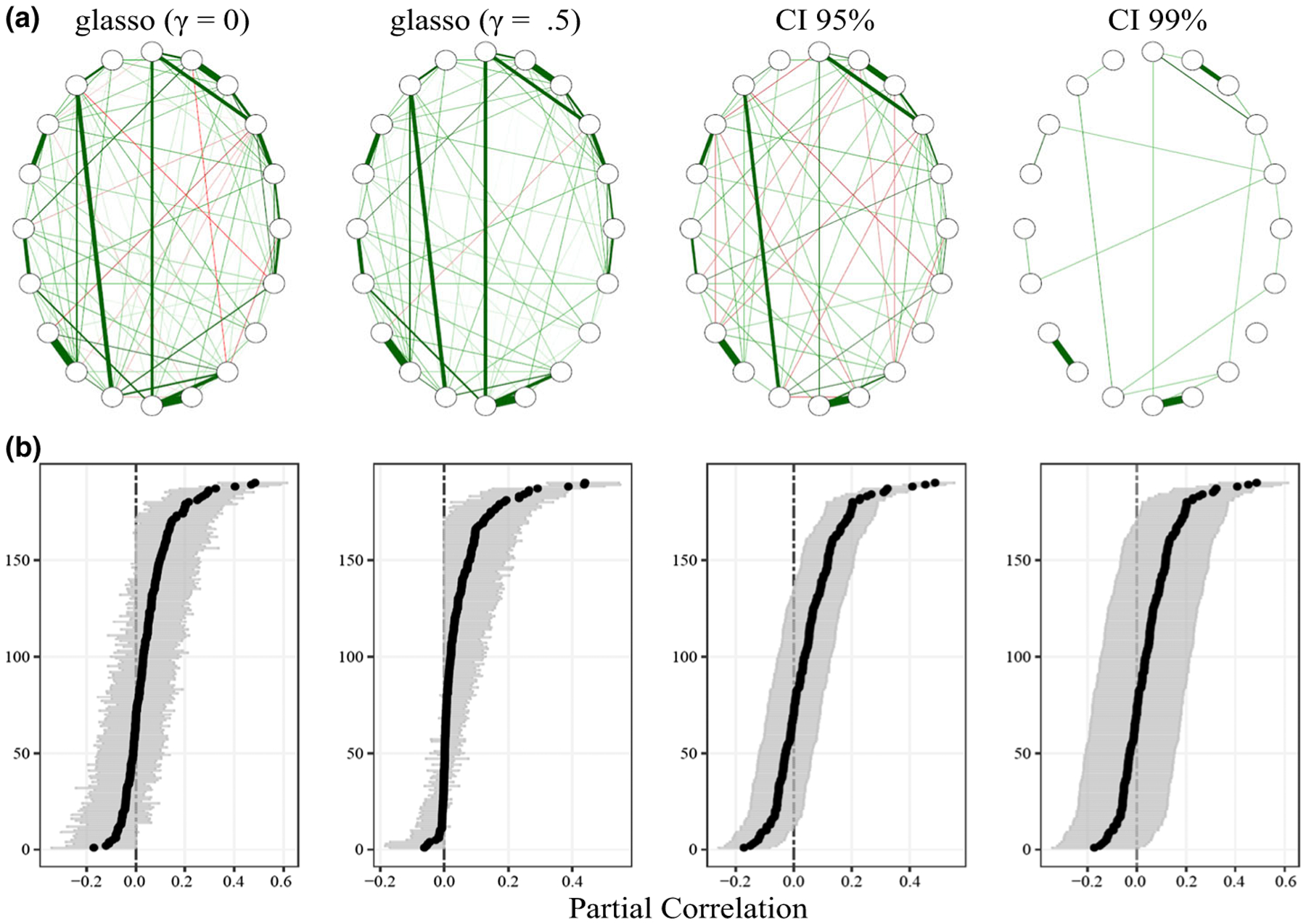
(a) Estimated networks for symptoms of post-traumatic stress disorder. γ denotes the parameter in extended Bayesian information criterion (equation 5). (b) A comparison between estimates, including CIs, for the estimated networks. The glasso CIs were constructed with a bootstrap procedure from the R package bootnet.

The corresponding coverage rates are provide in Figure 1b, where the expected level is 95%. Note that there is a direct one-to-one correspondence between specificity and coverage illustrated by the diagonal line. This was confirmed with the exact correspondence to specificity (equation 13), which is a measure of binary classification accuracy that is often used in the GGM literature. It should be noted that coverage was very close to nominal levels, for example, even for one simulation trial it ranged from 93.2% to 96.3% when the samples sizes were larger than 50. With sample sizes of 500 and 1,000, the coverage rate was 94.7% and 95.3%, respectively. Further, as seen in Table 1, long-run coverage probabilities were at the expected levels. This is especially important in applied settings, because it allows for a more principled and familiar rationale for determining the trade-off between false positives and negatives. The current alternative in psychology is to adjust the γ value in EBIC (equation 5), which paradoxically results in diminishing returns with increasing sample sizes (Epskamp & Fried, 2018), in addition to γ not having a straightforward meaning. In contrast, CIs are commonly used, have a straightforward frequentist interpretation, and allow for defining expected long-run error rates (α).

Table 1.

Average coverage probabilities for the partial correlation matrices

	Sample size (n)
	25	50	150	250	500	1,000
95% CI	.970 (0.06)	.953 (0.03)	.952 (0.02)	.951 (0.02)	.951 (0.02)	.950 (0.02)
99% CI	.995 (0.02)	.990 (0.01)	.990 (0.01)	.990 (0.01)	.990 (0.01)	.990 (0.01)

^aNote. The parentheses include the standard deviations.

6. Simulation description

In this section we present numerical experiments to assess the performance of the proposed CI method compared to the glasso. We specifically focus on model selection consistency in common situations where network models are fitted in psychology. We assumed fixed p = 20, and increased the sample size n ∈ {50, 150, 250, 500, 1,000, 10,000, 100,000}. The largest sample sizes were included to assess the consistency of each method. In applied settings this mimics choosing a psychometric scale (fixed p) and then assessing expected performance by increasing the sample size (n). Additionally, we included a range of sparsity levels, in which the proportion of connected edges varied (20%, 40%, 60%, 80%). The edge sets were randomly generated from a Bernoulli distribution, and the corresponding precision matrices Θ ~ W_G (df = 20, A_{p × p}) from a G-Wishart distribution with 20 degrees of freedom and scale A that had 20s along the diagonal and 0s as the off-diagonal elements. This choice of df ensured the partial correlations were within a reasonable range (ρ_ij ≈ ± .40), in addition to being approximately normally distributed with mean zero. This scale (A_{p × p}) differed from Mohammadi and Wit (2015), who used an identity matrix I_p, but was selected to provide the most favourable conditions for the glasso method, which we noted had worse performance (specifically for the risk of Θ) when the diagonal of the true precision contained too large or small values.

We used the R package qgraph to fit the glasso models (Epskamp, Cramer, Waldorp, Schmittmann, & Borsboom, 2012). Here we assumed γ values of 0 and .5. The latter is the default setting in qgraph. For the largest sample sizes, we observed warnings that the lowest λ values was chosen (Section 3). We followed the package recommendation, and allowed these settings to be changed during the simulation. For our proposed CI method, we used two confidence levels of 95% and 99%. These models were fitted with a custom function that is provided in Appendix B. The performance measures were averaged across 1,000 simulation trials. All computer code is publicly available on the Open Science Framework (https://osf.io/qgsz3/).

6.1. Edge set identification

We assessed three measures for identifying non-zero partial correlations. The first was specificity, which was previously defined in equation 13. The next measure is sensitivity (SN), or the true positive rate, and is defined as

$$\text{SN}=\frac{\text{ number of true positives }}{\text{ number of true positives }+\text{ number of false negatives }}.$$ (14)

We also wanted to include a measure that considers all aspects of binary classification (i.e., false positives [FP] and negatives [FN], as well as true positives [TP] and negatives [TP]). To our knowledge, the Matthews correlation coefficient (MCC) is the only measure that meets this criterion. MCC is defined as

$$\text{MCC}=\frac{\text{TP}\times \text{TN}-\text{FP}\times \text{FN}}{\sqrt{\left(\text{TP}+\text{FP}\right)\left(\text{TP}+\text{FN}\right)\left(\text{TN}+\text{FP}\right)\left(\text{TN}+\text{FN}\right)}},$$ (15)

and ranges between −1 and 1 (Powers, 2011). A correlation of 1 is perfect correspondence between the actual and estimated edges. Its value is equivalent to the phi coefficient that assesses the association (i.e., correlation) between two binary variables, but for the special case of binary classification accuracy.

The results are presented in Figure 2. We first discuss specificity (1 – SPC = false positive rate). All methods had similar performance when 20% of the nodes shared a connection. However, while not a large difference, specificity decreased slightly when the sample size (n) grew larger for both glasso models (γ = 0 and .5). This result was especially pronounced for denser networks. For example, with 60% connectivity, the specificity for glasso was 100% (n = 25) but was below 80% with a sample size of 500 and approached 50% with n = 10,000. In contrast, the proposed CI method (Section 4) performed uniformly across conditions. Indeed, these results confirm Figure 1 and Table 1 where confidence levels corresponded exactly to specificity.

Figure 2.

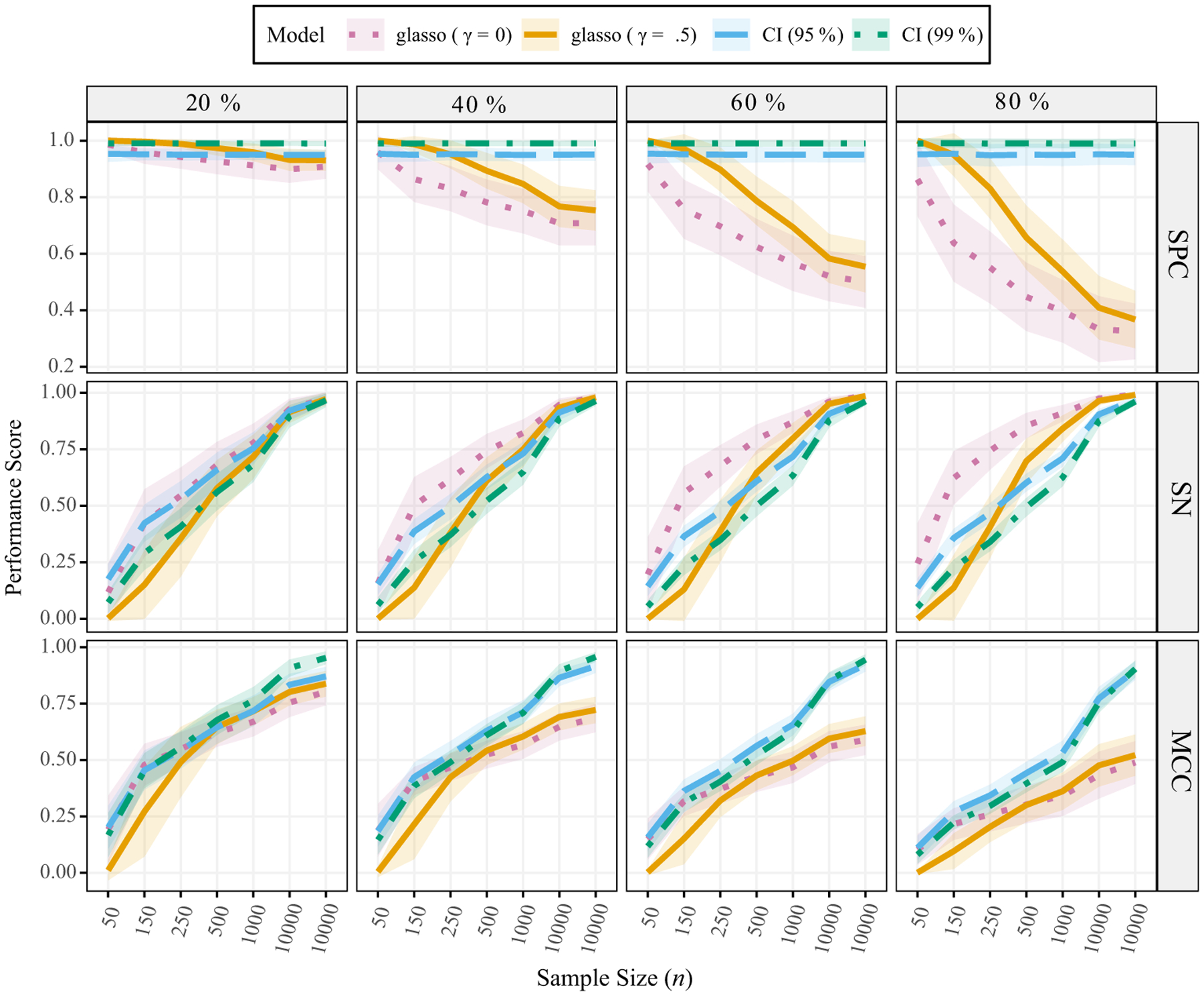
Edge set identification scores (1 minus specificity is the false positive rate). The probability of a connection varies from 20% to 80%. γ denotes the EBIC parameter (equation 5). EBIC = extended Bayesian information criterion; MCC = Matthews correlation coefficient; SN = sensitivity; SPC = specificity. The ribbons are ±1 SD.

Importantly, the high specificity of the proposed CI method did not result in substantially lower sensitivity than the glasso models. For glasso with γ = .5 in particular, sensitivity was comparable to the CI method, but the false positive rate was much higher and became increasingly so with larger sample sizes. These results parallel Heinävaara et al. (2016) and Kuismin and Sillanpää (2016), where it was noted that the glasso behaves inconsistently as n increases. That is, when sample sizes increase, a reasonable expectation is that the estimated model will become more reliable, but this is not always the case for the glasso method. Further, in the present simulation conditions the proposed CI method turned out to be a consistent estimator for the purpose of model selection. That is, specificity can be set to approximately 99% (i.e., the confidence level), and increasing n ultimately results in selecting the true model with a probability approaching 100%.

In terms of the MCC (equation 15), which provides a correlation for binary variables, all methods performed similarly for a network with 20% connectivity, which parallels the results for specificity and sensitivity. However, the CI-based methods often outperformed both glasso methods in the other conditions, although the MCC correlation increased with larger n in all cases. For example, the methods were similar for the smaller sample sizes, but the proposed CI methods resulted in larger correlations with increasing sample sizes. For the largest sample size (n = 10,000) and 60% connectivity, the CI methods had an almost perfect MCC score, whereas the glasso methods had a score of approximately .50.

6.2. Loss functions

To further assess the quality of the estimation methods, we compared the glasso and CI methods in terms of risk. Risk of the estimated precision matrices was assessed with two loss functions, each of which is commonly used in the GGM literature (Heinävaara et al., 2016; Kuismin & Sillanpää, 2017; Li, Craig, & Bhadra, 2019). The first is Kullback–Leibler divergence (KL), or entropy loss, defined as

$$\text{KL}\left(\Theta ,\widehat{\Theta }\right)=\text{tr}\left({\Theta }^{-1}\widehat{\Theta }\right)-\text{log}\left(\left|{\Theta }^{-1}\widehat{\Theta }\right|\right)-p,$$ (16)

where $\left(\left|{\Theta }^{-1}\widehat{\Theta }\right|\right)$ denotes the log determinant. This provides a measure of information loss between the estimated network $\widehat{\Theta }$ and true network Θ. As a measure of discrepancy between the true and estimated model we also computed the Hamming distance (HD; Heinävaara et al., 2016), which provides a measure of discrepancy between binary strings. Here, non-zero partial correlations were denoted by a 1, whereas the partial correlations that were set to zero were denoted by a 0. The HD addresses the discrepancy between the true and estimated model. For example,

(17)

results in an HD of 3. Note that the HD is also the squared Euclidean distance between a set of binary observations. For both measures, values closer to zero indicate less error from the actual precision or partial correlation matrix.

The results are presented in Figure 3. Before discussing these results in detail, it should be noted that there were some difficulties computing KL divergence. This occurred with the smallest samples size in particular, and was due to being assessed from the sparsified precision matrix. We revisit this issue in the discussion (Section 12). In terms of the HD, both glasso estimates (γ = 0 and .5) were inconsistent, in that risk appeared to plateau and did not reduce further with larger sample sizes. Importantly, glasso did have superior performance with the smallest sample sizes (p/n = 0.40) for KL divergence, while the CI models had consistent performance. For example, as n increased, the error consistently diminished to almost zero for the CI-based methods.

Figure 3.

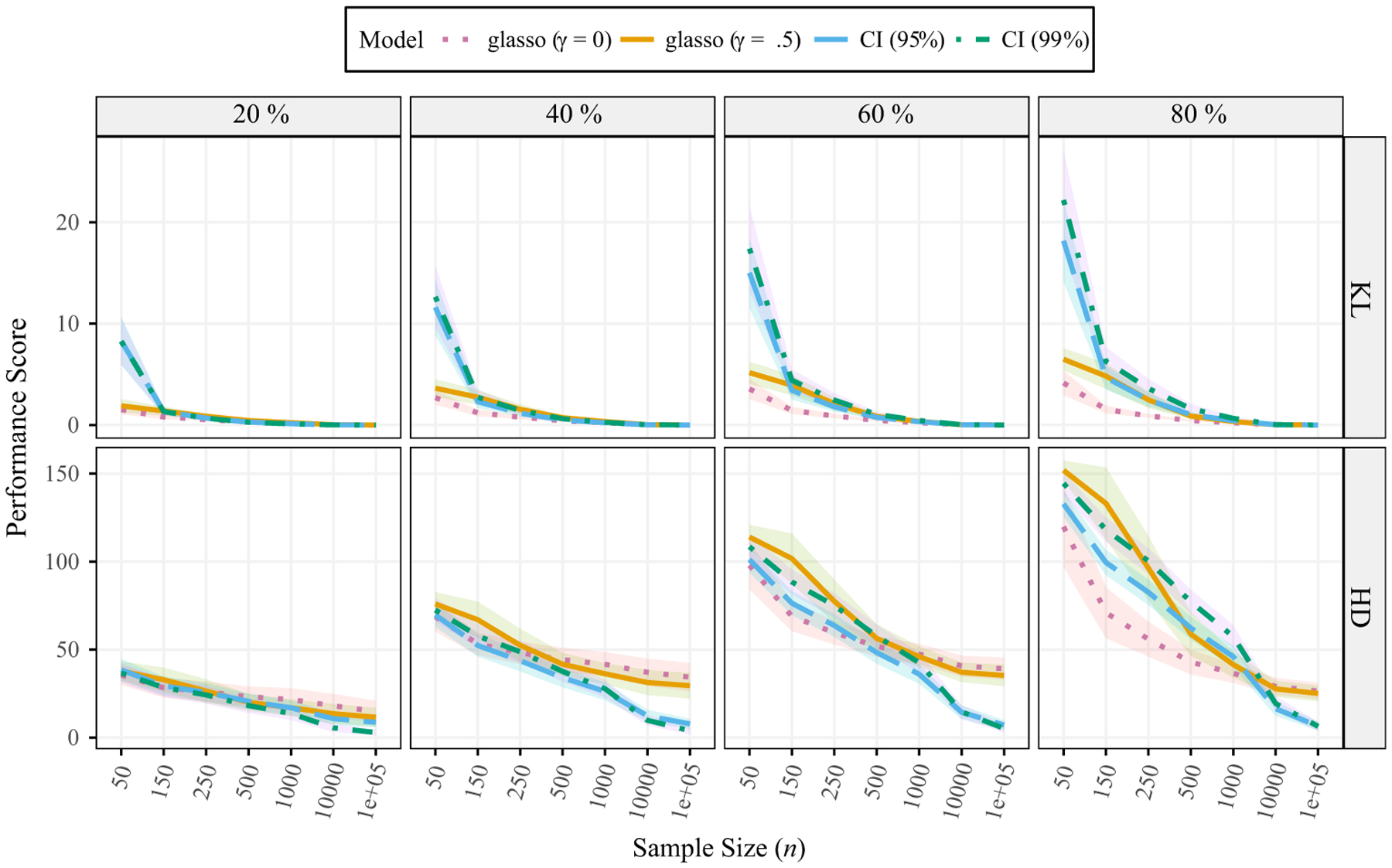
Risk of the estimated precision matrices. Lower scores are closer to the true network. The probability of a connection varies from 20% to 80%. γ denotes the EBIC parameter (equation 5). EBIC = extended Bayesian information criterion; HD = Hamming distance; KL = Kullback–Leibler divergence. The ribbons are ±1 SD.

6.3. False discovery rate

The previous simulations demonstrated that using CIs can achieve perfect calibration to the desired level of specificity. Further, as the networks approach typical settings in psychology (p/n → 0), the approach based on maximum likelihood provided an accurate estimate of the precision matrix. However, we did not explicitly address the multiple comparison issue. This is particularly important, because with α = .05 and p = 20, the familywise error rate is approximately 100% (i.e., 1 − .95¹⁹⁰ ≈ 1). We do not think there is a fully satisfactory approach for handling multiple comparisons, and, in particular, the Bonferroni correction may be too conservative. This is especially the case, considering psychological networks are not typically sparse. The number of false positives is a function of p, α, and sparsity. For example, with α = .05, p = 20 and 60% sparsity, the expected number of false positives is .05 × 190 × .60 ≈ 6 (on average). While this could be acceptable, depending on the application, it will be heavily influenced by the number of variables in the network (as noted by the editor). We thus conducted an additional simulation that explicitly addresses error control as a function of p. Because the CI, as shown in Figure 2, will be calibrated regardless of p, we focus on the false discovery rate that also takes into account the number of true positives:

$$\text{FDR}=\frac{\text{ number of false positives }}{\text{ number of false positives }+\text{ number of true positives }}.$$ (18)

We consider the same methods as Section 6, but with only one confidence level (α = .05). We then applied the false discovery rate adjustment with the R function p.adjust (Benjamini & Hochberg, 1995). Corrected p-values < .05 were considered significant. The samples sizes were n ∈ {150, 250, 500, 1,000, 10,000}, and we took four values for p ∈ {10, 20, 40, 80} and three levels of sparsity (20%, 40%, and 60%). The edge sets were again randomly generated from a Bernoulli distribution, and the corresponding precision matrices were sampled from a G-Wishart distribution, Θ ~ W_G (df = 20, A_{p × p}), with 20 degrees of freedom and scale A that had 20s along the diagonal and 0s as the off-diagonal elements. The scores were averaged over 1,000 simulation trials.

We first discuss the false discovery rates (Figure 4). Here it was revealed that the FDR-based correction did just what it was supposed to: for all simulation conditions, the FDR was controlled at the nominal level (α = .05). There was more variability with the smallest networks (p = 10) and sparse networks (20%), but the mean across trials was controlled. The results for the other methods revealed a complex relationship between the number of variables (p), the sample size (n). and degree of sparsity. This was especially the case for the uncorrected CI (α), in that the FDR decreased as the network became denser and as the sample size increased. The former is attributed to the fact that there are more non-zero edges, whereas the latter is a result of increased power. That is, as there are more effects to be detected, as well as more power to detect those effects, the FDR will necessarily decrease. Further, as these results show, it is possible to directly control the FDR irrespective of sparsity, the number variables, etc. On the hand, the glasso method had a much higher error rate for all conditions (compared to FDR). Indeed, the FDR was often >20%, which means that one in five edges included in the graph were actually false discoveries.

Figure 4.

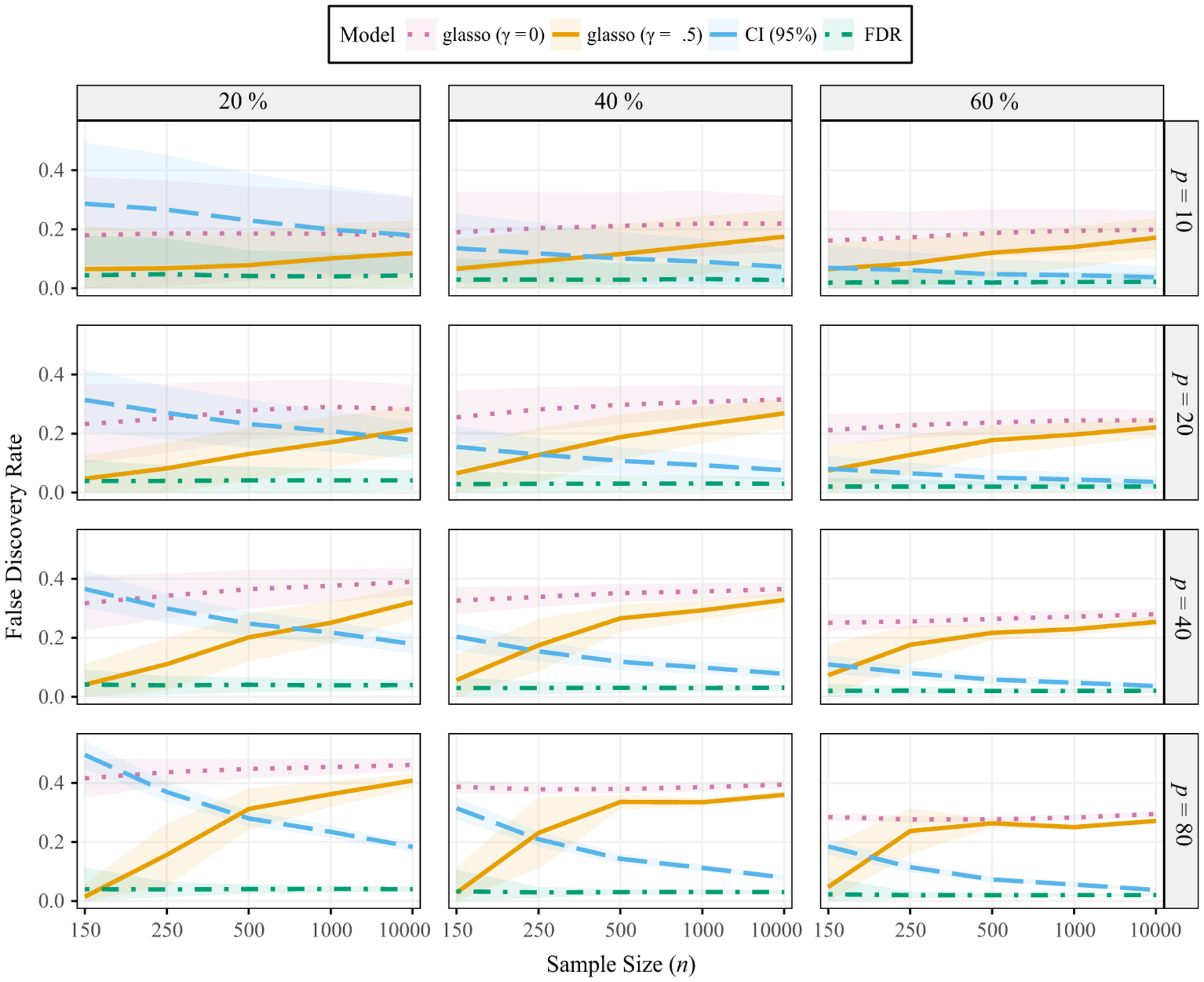
False discovery rates. The probability of a connection varies from 20% to 60%. γ denotes the extended Bayesian information criterion parameter (equation 5). p corresponds to the number of variables in the networks. The ribbons are ±1 SD.

The results for sensitivity are presented in the Appendix A (Figure A1), where it can be seen that the glasso (γ = 0) often had the highest power to detect non-zero edges. However, we emphasize this also came with the highest FDR and that, if a researcher wants to minimize Type II errors, the FDR-based α level can be adjusted accordingly. The non-regularized methods are advantageous, in this respect, because the error rate can be calibrated to the desired level. This was shown for both specificity and FDR.

7. Application

In this section, we estimate the network structure of post-traumatic stress disorder symptoms (McNally et al., 2015). Our interest is not in a substantive question, but in comparing the methods in two quantitative aspects: agreement (or disagreement) between methods, and in particular the degree of estimated sparsity; and to highlight post-selection estimates of the partial correlations, for example, bootstrapping the glasso models compared to the CI based approach. Since CIs are not readily available for the FDR-based approach, we provide this network in the Appendix A (Figure A2). The data consist of 20 variables (p) and 221 observations (n) measured on the Likert scale (0–4). For the glasso we used the default settings in the R package qgraph (Epskamp et al., 2012).

The results are presented in Figure 5. We first discuss the estimated network structures in Figure 5a. There are substantial differences between the methods, in that the glasso estimated dense networks where almost half of the possible edges were connected. In contrast, the CI methods had connectivity of 36% (CI 95%) and 11% (CI 99%), respectively. In addition to the simulations presented here (Figure 2), the glasso estimate (γ = .5) of these exact data was used to provide the data-generating matrix in Epskamp and Fried (2018). The limited simulation provided in Epskamp and Fried (2018) showed that the glasso was similarly inconsistent, which parallels the present simulation results, and that specificity was never higher than 75%. This suggests that the estimated network in this example has a false positive rate (1 minus specificity) close to 25%. In contrast, the proposed method not only had the highest specificity (and thus the lowest false positive rate), but similar sensitivity to the glasso methods in this simulation, which together suggests a more accurate estimate of the network.

We now focus on post-selection assessment of the partial correlations for the glasso method (Figure 5b). That is, after the glasso has selected a model, common practice in psychology is to use a bootstrapping procedure to approximate the sampling distributions. We thus implemented the default approach in the R package bootnet (Epskamp, Waldorp, Mõttus, & Borsboom, 2018). However, to be clear, the naïve use of bootstrapping does not necessarily allow for valid inferences such as null hypothesis testing with well-defined error rates (α). This is evident in Figure 5b, where it can be seen that the bootstrapped estimates (summarized with the mean and 95% intervals) are heavily skewed for the default glasso method (γ = .5). In the context of GGMs in particular (Janková & van de Geer, 2017), statistical inference is an emerging area of research in the field of statistics that often requires debiasing of the regularized estimates to compute CIs (Janková & van de Geer, 2015; Ren, Sun, Zhang, & Zhou, 2015) and p-values (Liu, 2013; Wang et al., 2016). There is a recent R package (SILGGM, which stands for ‘Statistical Inference of Large-scale Gaussian Graphical Model’) that provides many options for network model inference (Zhang, Ren, & Chen, 2018). However, it should be noted that the methods were optimized in high-dimensional settings (n < p), so performance confirmation would be needed in low-dimensional settings. In contrast, because typical psychological networks are fitted in low-dimensional settings, the proposed CI method already allows for calibrated CIs (and p-values; Figure 1).

Moreover, we see that the CI-based methods, described in the present paper, have symmetric intervals that readily allow for demonstrating nominal frequentist calibration (Figure 1 and Table 1). While there is still the issue of multiple comparisons, one could argue that 99% intervals mitigate these multiplicities, without further reducing sensitivity and because increasing the confidence levels results in trivial changes in the width of the intervals. Further, assuming the null is true for each partial correlation, coverage (or non-coverage of 0) and thus specificity can be inferred due to the large number of constructed intervals (Figure 1). This again stands in contrast to glasso with EBIC selection of the tuning parameter (equation 4), where the meaning of γ is unclear, in addition to the assumed γ (0 and .5) values estimating very similar networks.

8. Discussion

In this paper we have described the current default approach for estimating psychological networks, with a particular focus on the disconnect between the fields where the glasso was developed (n ≪ p) and the most common psychological applications (n ≫ p). We then described a method based on maximum likelihood and Fisher Z transformed partial correlations. With CIs as the decision rule for determining non-zero relationships, we then demonstrated superior performance compared to the glasso method in almost all instances (Figure 2). In particular, we showed the exact correspondence between the confidence level and specificity, which is due to 1 minus specificity denoting the false positive rate (e.g., α; Figure 1). As indicated by Figure 3, it is also clear that the glasso method does not reduce the risk of the estimated precision matrices, relative to the non-regularized method based on maximum likelihood. Indeed, the glasso methods actually showed increased estimation errors when the sample sizes became larger. Most importantly, we explicitly evaluated the model selection consistency of the glasso method. It was shown that glasso is not a consistent estimator for the purpose of model selection, in low-dimensional settings, whereas the proposed method converged on the true model with a probability that approached 100% (Figure 2).

Moreover, to address the multiple comparison issue, we looked at the false discovery rate as a function of the network size (p) and sparsity. These results made clear the relationship between the FDR and sparsity, which should be considered when addressing multiple comparisons in practice. That is, if psychological networks are indeed dense, then the FDR is lower for corrected and uncorrected p-values with α = .05 compared to the glasso. In other words, of the edges determined to be non-zero the vast majority are true effects when using non-regularized maximum likelihood estimation. This was not the case for the glasso, which is in direct contrast to the often stated primary motivation for using ℓ₁-regularization to estimate psychological networks. For example, according to Dodell-Feder, Saxena, Rutter, and Germine (2019, p. 3):

In order to deal with the large number of pairwise associations estimated in the network, we implemented a form of regularization known as least absolute shrinkage and selection operator (LASSO), which reduces many of the associations to zero, limiting the number of small/spurious edges, and in turn, producing a sparser and more interpretable network.

In fact, as revealed in our simulations and the application (Figure 5), each of these goals is apparently better achieved with significance testing. Note that we are not advocating a specific multiple comparison correction. Our results do make clear that it is important to consider not only the number of variables (p) but also the expected level of connectivity when applying a correction for multiple comparisons. Finally, we are not the first to consider this issue for network models. We refer to Steinley, Hoffman, Brusco, and Sher (2017), where alternative approaches are proposed for making inference in networks.

Although our focus here is statistical methodology, and not on the use or corresponding inferences in practice, these results can be used to inform the current discussion surrounding the replicability of psychological networks (Forbes, Wright, Markon, & Krueger, 2017). There are several less extensive simulations that have demonstrated that glasso is not consistent for the purpose of model selection in psychological settings. In fact, with data common to pschology, have not seen one instance in which glasso converged upon the true model. For example, in Epskamp and Fried (2018) and Epskamp (2016), it was shown that specificity either reduced slightly or remained constant at around 75–80% as n increased. That is, the false positive rate (1 minus specificity) of the glasso is regularly around 20–25%. Further, while Epskamp et al. (2017) cautioned that assuming sparsity will result in false negatives if the true network is dense, our results suggest that levels of sparsity not typically seen in psychological applications (<20% connectivity; Figure 2) are necessary for consistent model selection (although specificity declined slightly for the largest sample sizes). In the context of replication, high false positive rates (in excess of 20%) obscure the ability to consistently replicate network structures. Although the glasso method appears to estimate similar networks across data sets (Fried et al., 2018), for example, it is not entirely clear what is being replicated for a method whose performance is consistently inconsistent (Epskamp, 2016; Epskamp & Fried, 2018; Heinävaara et al., 2016; Kuismin & Sillanpää, 2016; Leppäaho et al., 2017).

These results may be surprising to some, because the glasso method has emerged as the default approach for network estimation in psychology. However, while the original glasso paper is highly cited (Friedman et al., 2008), it should be noted that the performance of the method for edge identification was not assessed. Similarly, in Foygel and Drton’s (2010) that introduced EBIC for tuning parameter (λ) selection, no comparison to other methods was made. However, there are numerous papers that have demonstrated performance superior to the glasso with EBIC (for a review of different methods, see Kuismin & Sillanpää, 2017). For example, Leppä-aho et al. (2017) introduced an approximate Bayesian method, using a marginal pseudo-likelihood approach, which showed that the glasso was not always consistent with respect to HD (Norouzi et al., 2012), whereas the lasso regression approach was consistent (Meinshausen & Bühlmann, 2006). This finding parallels that of Kuismin and Sillanpää (2016, p. 12), where the unusual behaviour of the glasso was explicitly noted:

We are surprised by the moderate performance of the graphical lasso in this simulation setting. Even when the sample size increases, the risk measures do not diminish, and that is quite unexpected. This is most certainly due [to] the EBIC used to choose the regularization parameter ρ [λ].

Again, these methods were developed for high-dimensional settings, and thus the focus was not on low-dimensional settings where classic methods perform well. In fact, most common statistical methods (e.g., maximum likelihood) are known to have optimal performance in situations common to psychology. In this light, it is clear that the results presented in the current paper are not too surprising if viewed from the position of going ‘back to the basics’. That is, in most psychological applications, partial correlation networks are most simply estimating correlation matrices in settings that do not pose challenges for statistical approaches developed over a century ago. Of course, while using a Fisher Z transformation does not have the appeal of novelty like the glasso, regularization, or EBIC, it is also clear that going ‘back to the basics’ provides consistent model selection in the most common situations where psychological networks are estimated.

9. Limitations

There are several limitations of this work. First, predictive accuracy is one possible advantage of ℓ₁-regularization, but we did not consider this here. However, it should be noted that ℓ₁-based methods do not always have improved predictive accuracy. For example, according to the original glasso paper Friedman et al. (2008, p. 9), ‘cross-validation curves indicate that the unregularized model is the best, [which is] not surprising given the large number of observations and relatively small number of parameters’. Nonetheless, alternative methods based on non-regularized regression models could be used to select variables with the Bayesian information criterion, which is known to be consistent for model selection (p ≪ n; Casella et al., 2009) and can be justified in terms of predictive accuracy (leave-n-outl Shao, 1997). Second, we only considered networks with a random structure. Future work would have to evaluate whether these findings generalize to various network structures, which seems reasonable since the proposed method is based on maximum likelihood (equation 6).

Although the bootstrap approach is recommended in Epskamp and Fried (2018), we were unable to locate any proofs in the statistics literature that this procedure generally allows for valid inferences. In fact, according to Bühlmann, Kalisch, and Meier (2014, pp. 7–8):

… [W]e typically use sparse estimators for high-dimensional data analysis, for example the Lasso … The (limiting) distribution of such a sparse estimator is non-Gaussian with point mass at zero, and this is the reason why standard bootstrap or subsampling techniques do not provide valid confidence regions or p-values. Thus, we have to use other approaches to quantify uncertainty.

Rather than attempting to overcome the biased estimates of ℓ₁-regularization, a non-regularized bootstrap could be applied directly on the maximum likelihood estimator (equation 6), from which differences as well as equivalence can be tested (Lakens, 2017). Of course, this would first require demonstrating that the constructed intervals and/or p-values are properly calibrated. Fourth, we only evaluated simulation conditions with p fixed at 20. While this is a reasonable choice based on the psychological literature, it should be noted that estimation errors of the MLE arise with larger p/n ratios. However, for the purpose of edge set identification, the CI-based methods outperformed the glasso (γ = .5, the default in qgraph) at the highest ratio evaluated (p/n = 0.40). Fifth, the proposed method had difficulties computing the KL divergence. In the context of determining non-zero partial correlations, in which sparsity is induced after equation 8, this is not problematic. This issue arose because KL divergence was assessed with covariances set to zero, which we viewed as a fairer comparison to the glasso method (which also has covariances set to zero) and allowed for assessing risk for each confidence level (using the non-sparsified precision matrix would have provided the same estimate for each decision rule). Importantly, in all instances the estimated precision matrices were positive definite.

To be clear, while not necessary a limitation of this work, it should be noted that we used the default settings in the package qgraph. This allowed for making our findings especially relevant for psychology, but does limit the generalizability of our results. For example, there are alternative default settings in other R packages (e.g., huge; Zhao et al., 2012), where the EBIC is not the default method for selecting λ. We did explore many of the settings for the glasso method. For example, in addition to different methods for selecting λ, the range of λs can change the results in meaningful ways. If the true model is known, it is possible to adapt a number of parameter settings to improve performance in the glasso. However, we view this as an additional benefit of the proposed method, because performance only depends on pre-specifying the confidence level which has a straightforward meaning in practice. Note that, while not having an interpretation in relation to error rates, λ can be understood as the thresholding value for the covariance matrix (Mazumder & Hastie, 2012).

We also emphasized model selection consistency, although it is well known that ℓ_1-regularization does not have oracle properties. That is, it is known to be inconsistent for model selection and the estimated coefficients are not asymptotically normal (Wang et al., 2016). The latter can be seen in Figure 5, where it was revealed that the glasso bootstrap distribution can be truncated at zero and skewed. However, these important points have largely gone unnoticed in the psychological network literature (McNeish, 2015). Note that there are now several methods, with the ℓ₁-penalty as a special case, that do have oracle properties (e.g., non-concave penalized likelihood; Fan & Li, 2001). We refer interested readers to Zhu and Cribben (2018), where these methods were extended from regression to precision matrix estimation with the glasso. This is an important future direction, in that these methods may offer advantages compared to the methods presented in this work.

10. Conclusion

Gaussian graphical models are useful tools in that they can provide important insights into psychological constructs. An important future direction is therefore to address the issues that we raised, in addition to further characterizing non-regularized methods, which together will provide a deeper understanding of this relatively novel approach for conceptualizing a correlation matrix. However, with regard to the current default approach in psychology, we believe the statistical foundations of partial correlation network methodology requires rethinking.

Appendix A : Supplementary plots

Figure A1.

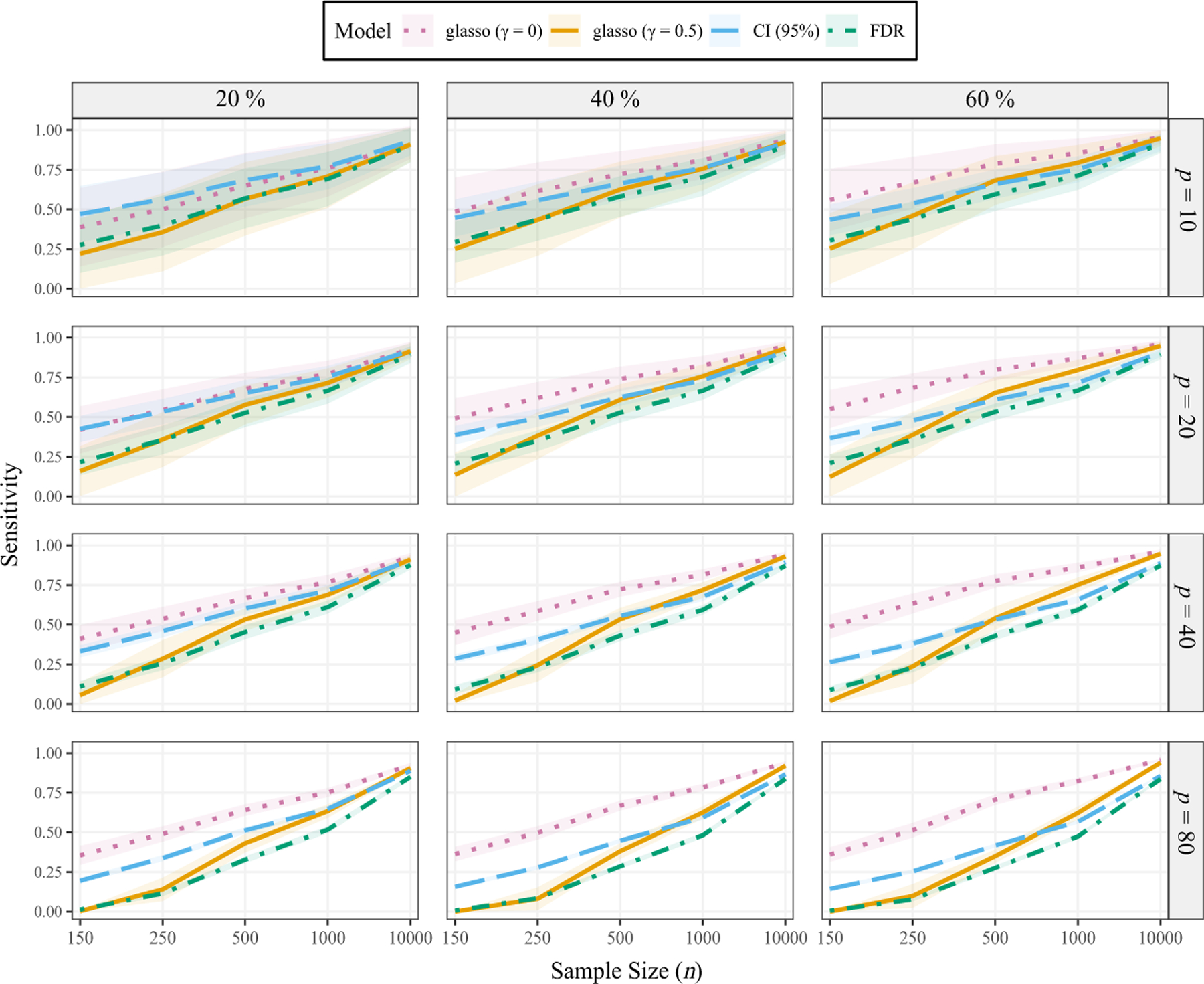
Sensitivity. γ denotes the parameter in extended Bayesian information criterion (equation 5). The probability of a connection varies from 20% to 60%. p corresponds to the number of variables in the network. The ribbons are ±1 SD.

Figure A2.

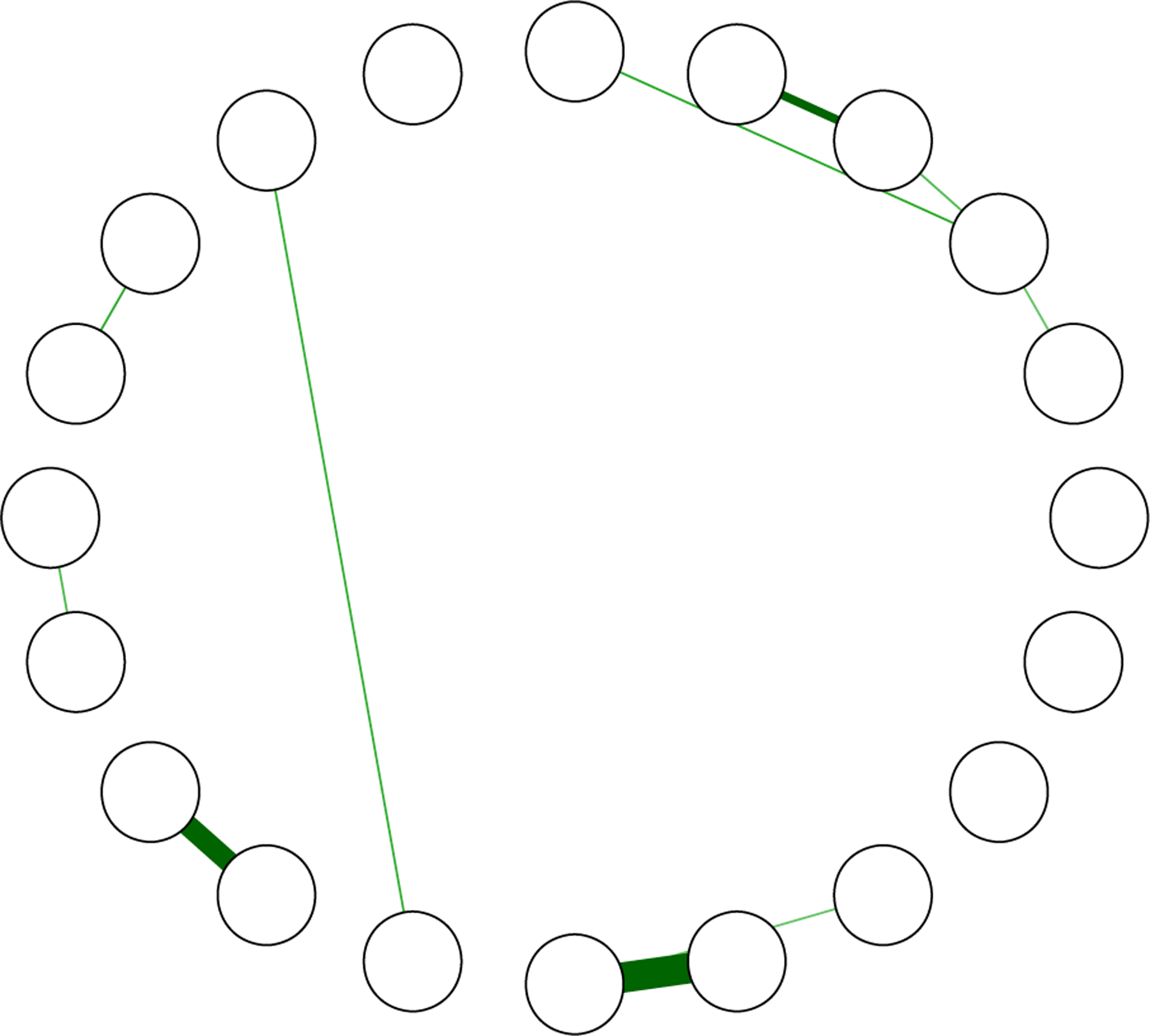
Network estimated with the false discovery rate (α = .05).

Appendix B : R code

R-code
mle_CI <- function(X, alpha) {
X <- as.matrix(X)
# X: data frame
if (!require(“qgraph”)) Install.packages(“qgraph”)
if (!require(“Matrix”)) install.packages (“Matrix”)
# number of observations (rows)
n <- nrow(X)
# number of variables (columns)
p <- ncol(X)
## compute maximum likelihood estimator
## for covariance matrix
mle_cov <- crossprod(scale(X, scale = F)) / n
## compute maximum likelihood estimator of precision matrix
## (inverse covariance matrix)
mle_inv <- solve(mle_cov)
## standardize and revese sign = partial correaltions
par_cors <- as.matrix(qgraph: :wi2net(mle_inv))
mle_parcors <- mle_ci_helper(alpha = alpha, par_cors = par_cors, n = n, s = p - 1)
mle_inv <- mle_parcors$sig_mat * mle_inv
list(mle_parcors = mle_parcors, mle_inv = mle_inv)
}
mle_ci_helper <- functian(alpha, par_cors, s, n) {
# n: sample size
# s: p - 1 (controlled for)
# alpha: confidence level
# par_cors: partial correlations
mat <- matrix(0,nrow = s + 1, ncol = s + 1)
CI_ls <- list()
par_cor <- par_cors [upper.tri(par_cors)]
cov <- list()
for(i in 1 :length(par_cor)) {
# critical value
z_crit <- qnorm(l - alpha/2)
# standard error
se <- sqrt(l/((n - s - 3)))
# z transformation
z <- log((l + par_cor[i])/(l - par_cor[i]))/2
# z lower bound
Z_L <- z - z_crit * se
# Z upper bound
Z_U <- z + z_crit * se
rho_L <- (exp(2*Z_L) − l)/(exp(2*Z_L) + 1)
rho_U <- (exp(2*Z_U) − l)/(exp(2*Z_U) +1)
Cl <- c(rho_L, rho_U)
CI_ls[[i]] <- Cl
cov[[i]] <- ifelse(CI[l] < 0 & CI[2] > 0, 0, 1)
}
ci_dat <- do. call(rbind. data. frame, Cl. _ls)
colnames(ci_dat) <- c(“low”, “up”) ci_dat$pcor <- unlist(par_cor)
diag(mat) <- 1
mat[upper.tr(mat)] <- unlist(cov)
mat <- as.matrix(Matrix: :forceSymmetric(mat))
list(sig_mat = mat, par_cors = par_cors, par_sig = mat * par_cors, cis = ci_dat, cov_prob = unlist(cov))
}
Assume X is a data matrix:
# 95 % Cl
est_mle_95 <- mle_CI(X, alpha = 1 – 0.95)
# sparsified partial correlation matrix
est_mle_95$mle_parcors$par_sig
# 99 % CI
est_mle_99 <- mle_CI(X, alpha = 1 – 0.99)
# sparsified partial correlation matrix
est_mle_99$mle_parcors$par_sig