A Mixed-Effects Location Scale Model for Dyadic Interactions

Abstract

We present a mixed-effects location scale model (MELSM) for examining the daily dynamics of affect in dyads. The MELSM includes person and time-varying variables to predict the location, or individual means, and the scale, or within-person variances. It also incorporates a submodel to account for between-person variances. The dyadic specification can accommodate individual and partner effects in both the location and the scale components, and allows random effects for all location and scale parameters. All covariances among the random effects, within and across the location and the scale are also estimated. These covariances offer new insights into the interplay of individual mean structures, intra-individual variability, and the influence of partner effects on such factors. To illustrate the model, we use data from 274 couples who provided daily ratings on their positive and negative emotions toward their relationship – up to 90 consecutive days. The model is fit using Hamiltonian Monte Carlo methods, and includes subsets of predictors in order to demonstrate the flexibility of this approach. We conclude with a discussion on the usefulness and the limitations of the MELSM for dyadic research.

Introduction

Modeling interactions between two individuals requires methods that are able to capture the dynamics of such interactions, as they unfold over time, and separate these interactions from dynamics that take place within each individual. A number of models have been developed to examine these dynamics (e.g., Kenny, 1996; Raudenbush, Brennan, & Barnett, 1995). We argue that, although some of these methods have very desirable features, an important shortcoming is the fact that all the unexplained variance goes into the residual component. In this paper, we propose a mixed-effects location scale model (MELSM). This model allows partitioning this unexplained variance, which consists of within-person variance over time, and explain it as a function of covariates. The MELSM is particularly well suited to examine the changes (or fluctuations) in a given process for each individual in a dyad, together with the interrelations between both individuals.

Intra-individual variability designs

A key methodological question in investigations of social interactions concerns the study design for yielding information about within- and between-person dynamics. One such design, suited to identify dynamics with a high temporal resolution, is based on intra-individual variability (IIV). In this design, individuals are measured across multiple variables and multiple occasions with short intervals, such as weekly, daily or hourly measurements, allowing researchers to study processes, as they unfold over time (e.g., Ferrer & Rast, 2017). Depending on particular features, these studies go by names such as Ecological Momentary Assessments (EMA; Shiffman, Stone, & Hufford, 2008) or experience sampling and daily diary studies (Bolger, Davis, & Rafaeli, 2003). These intensive measurements may be combined across multiple waves spanning years to obtain intensive measurement bursts allowing for the investigation of within- and between-person dynamics that span across different time scales (Nesselroade, 1991b; Sliwinski, 2008). Generally, short time intervals among measurement occasions in intra-individual variability designs are well suited to capture behavioral fluctuations or variation within persons and/or partners.

The focus on these designs is largely on day-to-day variability, which is typically referred to as within-person or intra-individual variability. The main assumption of IIV is that such variability does not merely reflect measurement error, but that it conveys systematic information that is potentially important and that would go otherwise unaccounted for (Cattell, Cattell, & Rhymer, 1947; Eizenman, Nesselroade, Featherman, & Rowe, 1997; Fiske & Rice, 1955; Horn, 1972; Hultsch, Hertzog, Small, McDonald-Miszczak, & Dixon, 1992; Nesselroade & Salthouse, 2004; Woodrow, 1932). IIV is commonly used to describe the amount of reversible, short-term behavioral fluctuations that are observed over time (Ram & Gerstorf, 2009). Fluctuations can also occur across situations and are often interpreted as carrying information about short-term adaptive processes, regulative mechanisms and the system’s vulnerability (Baltes, Reese, & Nesselroade, 1977; Nesselroade, 1991a; Röcke & Brose, 2013).

Most importantly, it is assumed that IIV reflects another quality of behavioral outcomes such as consistency or precision in responses, compared to individual levels, that are thought to provide information on average effects. Hence, with the availability of intensive data, the focus of the interaction among individuals can be widened to include dynamics of within-person variability in the sense that not only average effects may be influenced by the partner but also variability in one’s behavior may be related to, and interact with, a partner’s traits.

Models for dyadic interactions

There have been important advances in the development of methodology suited to model dynamics in social interactions, including dyads. Some of these models include, for example, the Actor-Partner Interdependence Model (Kenny, 1996) or the “Two-Intercept” multilevel model (Raudenbush et al., 1995), which incorporates individual and partner effects over time. While there are many ways to model data from intensive repeated designs, multilevel, or mixed-effects, modeling techniques are probably the most common choice, perhaps due to the fact that they take into account clustering in the data (repeated measures nested within individuals, nested within dyads) and partition the variance accordingly. Specifically, in research on dyads, multilevel models have been successfully used to distinguish among actor, partner, and interaction effects (Campbell & Kashy, 2002; Kenny, Kashy, & Cook, 2006), investigate the quality of marital roles in married couples (Raudenbush et al., 1995), characterize the interrelations of affect between romantic partners (Butner, Diamond, & Hicks, 2007), model daily intimacy and disclosure in married couples (Bolger & Laurenceau, 2013; Laurenceau, Troy, & Carver, 2005), and capture emotional contagion between couple members undergoing a stressful event (Thompson & Bolger, 1999).

Besides multilevel models, a number of other methods have been developed and implemented as well. One of such models is, for example, the dynamic factor analysis (DFA; Browne & Nesselroade, 2005; Molenaar, 1985), which combines factor analysis with time series and allows the identification of the factorial structure of the data as well as its time-related signature (Ferrer & Nesselroade, 2003; Ferrer & Zhang, 2009). Another method that has been applied to intensive measurement data is differential equation models (DEM) which are useful for modeling continuous data. In dyadic interactions, DEM have been used to develop theoretical models (Felmlee, 2006; Felmlee & Greenberg, 1999) but they have also proven useful for modeling empirical data on the emotional interaction between spouses and subsequent break-up (Gottman, 2002), daily intimacy and disclosure in married couples (Boker & Laurenceau, 2006), and the dynamics of emotional experiences between individuals in close relationships (Chow, Ferrer, & Nesselroade, 2007; Ferrer, Gonzales, & Steele, 2013; Ferrer & Steele, 2014; Ferrer, Steele, & Hsieh, 2012; Steele, Ferrer, & Nesselroade, 2014).

Another class of models that are well suited to capture the dynamics of change in the variance components are generalized autoregressive conditional heteroscedasticity (GARCH) models (Bollerslev, 1986). These models are popular in the econometric literature and are used to predict the mean and variance (volatility) in a time-series, conditional on past information. The typical GARCH model assumes that the current variance is the sum of an average variance, the lagged (e.g., t − 1, with t = 1, …T) variance, and the lagged error variance. The multivariate extension (MGARCH; Engle, 2002) includes a time-varying covariance matrix H_t that includes the covariances among the GARCH parameters for each time series. The covariance is allowed to change across time which makes the estimation of the H_t matrix challenging (Laurent, Rombouts, & Violante, 2012; Tse & Tsui, 2002). While MGARCH models have proven to be useful in economics settings with only few simultaneous time-series, their application in psychological research with multiple individual time-series remains limited. The research in psychology typically involves multiple individuals and, thus, each individual time series would have to enter the MGARCH covariance matrix. The dimension of H would expand to N × N × T, making it extremely difficult to estimate in the context of most psychological applications, even for small N (de Almeida, Hotta, & Ruiz, 2018).

In this paper, we focus on mixed-effects models because of their desirable features for extracting information about variability. Specifically, mixed-effects models partition the overall variance into between- and within-person variance. The within-person component represents the residual variance that remains unexplained at the individual level while controlling for all predictors at the person level. In research on IIV, this “unexplained” part is the very focus of interest, the target of exploration in further modeling steps (e.g., Hultsch, Strauss, Hunter, & MacDonald, 2008). To date, probably the most common index of IIV is the intra-individual standard deviation (iSD; see e.g., Ram & Gerstorf, 2009), which can be computed from the residuals of a mixed effects model or individual models, or from observed scores. As such, the investigation of IIV is often treated as a two-stage approach: In the first stage, IIV is extracted to compute some form of person-specific variability index, such as the iSD. In the second stage, the IIV index is then used in a model either as a predictor or as the outcome. While this approach has been widely adopted to extract within-person information, it is not without controversy. IIV indices can lead to estimates that are highly correlated with other within-person moments, such as the intra-individual mean, especially when Gaussian normality is violated (Mestdagh et al., n.d.; Rast, Hofer, & Sparks, 2012; Wang, Hamaker, & Bergeman, 2012). Moreover, IIV indices or estimates tend to be unreliable especially when the number of measurement occasions is small (Estabrook, Grimm, & Bowles, 2012; Wang & Grimm, 2012).

The model that we present here to examine IIV in dyads is the mixed-effects location scale model (MELSM; Hedeker, Mermelstein, & Demirtas, 2008), an extension of the standard multilevel model. This model is particularly well suited to examine changes (or fluctuations) in a given process for individuals in dyadic relationships. The model expands the focus from the “classic” actor-partner interrelation on location effects (individual means) to include dyadic interactions on the IIV, the scale effects. As outlined earlier, the investigation of IIV and dynamics in partner relationships is strongly tied to the design, which must entail some form of intensive repeated measurements.

A distinguishing feature of the MELSM with respect to multi-stage models, is that the MELSM does not rely on multiple steps but rather estimates intraindividual means (iM) and iSD’s simultaneously in one model. By estimating these two components simultaneously, we are able to account for possible correlations that arise among iM’s and iSD’s, which ensures that we can make valid inferences about our parameter estimates (Verbeke & Davidian, 2009). The MELSM jointly models location and scale random effects by keeping them in one covariance matrix – as with any covariance matrix, its individual values are conditional on the other values. Multi-stage approaches, on the other hand, do not jointly model the covariances among its location and scale parameters. This makes the covariances oblivious to the correlations among its parameters. As a result, they only provide unbiased estimates for the rare case when location and scale are indeed completely uncorrelated (for a simulation, see e.g., Leckie, French, Charlton, Browne, & Langford, 2014). Moreover, the MELSM includes explanatory components for the between- and within-person variance, which circumvents the need for multiple modeling steps to capture IIV (see also Leckie et al., 2014; Rast et al., 2012). That is, while standard mixed-effect models relegate all the unexplained variance into the residual term, the MELSM allows partitioning the within-person variance over time and modeling it as a function of time-varying as well as person-level covariates. This is a particularly important feature because such within-person variance can be examined in relation to variables external to the system. For example, a researcher interested in, say, emotion in romantic couples, will want to use variables related to emotion to predict the stability or volatility in emotions. But, in addition, there might be variables external to the modeled system (e.g., work, daily stressors, weather) that could potentially explain part of the emotional ups and downs that are not accounted for by the main components of the model (Ferrer & Rast, 2017).

The aim of this paper is to extend the MELSM to accommodate data from two individuals who are part of a dyadic system (e.g., romantic couple, teacher-student). The remainder of the manuscript is organized as follows. First, we formally describe the general MELSM for dyads (or other dyadic system). Second, we provide an example involving empirical data from daily fluctuations in emotion from romantic couples. Third, we discuss the findings in the context of dyadic interactions and list shortcomings and possible extensions of the MELSM model.

A mixed-effects location scale model (MELSM) for dyads

The mixed effects location scale model (MELSM) put forward by Hedeker et al. (2008), combines earlier work on variance heterogeneity (Aitkin, 1987) and models for random scale effects (Cleveland, Denby, & Liu, 2002). Here, we briefly recast the model and then we expand it to accommodate cases with dyadic interactions involving partner and individual predictors. The starting point is the standard linear mixed effects model with repeated measurement on occasions j (j = 1, 2, …, n_i occasions) that may be specified as

$${\mathbf{\text{y}}}_i={\mathbf{\text{X}}}_i\mathbf{\beta }+{\mathbf{Z}}_i{\mathbf{b}}_i+{ϵ}_i,$$ (1)

where y_i is the n_i × 1 response vector for observations in person i. X_i is the n_i × k design matrix for the fixed effects for observations in person i. β captures the fixed effects and its dimension is k × 1. The random effects are in the n_i × q matrix Z_i for observations in person i where b_i is the according q × 1 vector with the random effects coefficients. These effects characterize a person’s mean response or location. ϵ_i is a vector of errors specific to person i. The general assumption in standard mixed effects models is that random effects are b_i ~ N(0, Φ). Where Φ is a q × q covariance matrix for the random effects with the variances ${\sigma }_b^2$ and the covariances σ_bb′ (for q ≠ q′). The errors ϵ_i are also assumed to be normally distributed with a mean of 0 and covariance of ${\sigma }_{ϵ}^2{\Psi }_i$ where Ψ_i is a n_i × n_i matrix which can take different structures. In these models the between-person variance is captured by ${\sigma }_b^2$ and the within-person variance is represented in ${\sigma }_{ϵ}^2$.

Within-person variance

In this standard form, the error variance ${\sigma }_{ϵ}^2$ is a fixed entity. In order to allow it to differ at the individual level, we add the subscript i to the within-person variance term (cf. Hoffman, 2007; Myles, Price, Hunter, Day, & Duffy, 2003) but we also allow it to differ among j-time points to obtain ${\sigma }_{{ϵ}_{\mathit{\text{ij}}}}^2$. Changes in the within-person variance ${\sigma }_{{ϵ}_{\mathit{\text{ij}}}}^2$ are explained by time-varying covariates in the n_i × m matrix W_i for the fixed effects and V_i, with dimension n_i × p (and m ≥ p) for the random effects (Rast et al., 2012). Hence, with the inclusion of time-varying covariates the within-person variance not only varies across persons but also across time given the model:

$${\mathit{\phi }}_i=\text{exp}\left({\mathbf{\text{W}}}_i\mathbf{\eta }+{\mathbf{\text{V}}}_i{\mathbf{\text{t}}}_i\right).$$ (2)

φ_i then is the n_i × 1 vector that contains all error variances ${\sigma }_{{ϵ}_{\mathit{\text{ij}}}}^2$ for individuals i and for each measurement occasion j. η is comparable to the regression weights β in Equation (1). That is, for an intercept and slope term, η₀ defines the average within-person variance and η₁ weights the influence of the predictor on the variance. The individual departures from the fixed effects that are captured in the random effects t_i are normally distributed with t_i ~ N(0, Θ), where Θ is a covariance matrix dimension p × p that contains the random effects of the scale. Note that W_i and V_i may, or may not, be the same as X_i and Z_i. In fact, the model that we will discuss here contains different predictors for the location and the scale. Given that Equation (2) is for variances, we need to ascertain that the estimates are positive real values. This can be obtained, for example, via the exponential function (e.g., Hedeker et al., 2008; Rast et al., 2012). Note that by doing so, we assume that ${\sigma }_{{ϵ}_{\mathit{\text{ij}}}}^2$ is log-normally distributed.

Between-person variance

The MELSM also introduces a submodel for the between-person variance. It is important to note here that we now have random effects b_i from the location of the model (the means structure) and random effects t_i from the scale of the model (the within-person variance structure). All these random effects are assumed to come from a Gaussian Normal distribution with mean zero. Hence, we can stack both b_i and t_i vectors, resulting in u_i ~ N(0, Σ_i). This also means that Σ_i contains the variances and covariances of both, the location and scale. In order to define a variance model for Σ_i, we can decompose ${\Sigma }_i={\mathbf{\tau }}_i\Omega {\mathbf{\tau }}_{\mathit{\text{i}}}^{\prime }$, where τ_i is a diagonal matrix for person i in which the diagonal elements are the random-effect standard deviations and Ω is the correlation matrix that contains the correlations among all random effects. That is, Ω is of dimension (q + p) × (q + p) and contains the correlations among the random effects of the location, the correlations among the random effects of the scale, and the correlations among the random effects of the location and the scale. Given this definition, Ω remains constant across conditions. We can now define a model for the random effects, which, in SD metric, can be defined as

$${\mathbf{\tau }}_{\mathit{\text{i}}}=\text{exp}\left({\text{g}}_i\iota \right)$$ (3)

where, for example, ι₀ is an intercept and ι₁ is a slope parameter. g_i is the design matrix that contains between-person predictors. This means that the random-effects variance is not constant but may change due to person- or group-specific characteristics (e.g., Leckie et al., 2014).

Hence, having specified all elements, we can define the full MELSM as

$$\begin{gathered} {\mathit{\text{y}}}_{\mathit{\text{i}}}~N\left({\mathit{\mu }}_{\mathit{\text{i}}},{\phi }_i\right) \\ {\mathit{\mu }}_{\mathit{\text{i}}}={\mathbf{\text{X}}}_i\mathbf{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i \\ {\mathit{\varphi }}_{\mathit{\text{i}}}=\text{exp}\left({\mathbf{\text{W}}}_i\mathbf{\eta }+{\mathbf{\text{V}}}_i{\mathbf{\text{t}}}_i\right) \end{gathered}$$

with the random effects for both the location and the scale coming from the same multivariate distribution

$$\begin{gathered} \left[\begin{array}{c}{\mathbf{\text{b}}}_i\\ {\mathbf{\text{t}}}_i\end{array}\right]~N\left(0,{\Sigma }_i\right) \\ {\Sigma }_i={\mathbf{\tau }}_{\mathit{\text{i}}}\mathbf{\Omega }{\tau }_i^{\prime } \\ {\mathbf{\tau }}_i=\text{exp}\left({\text{g}}_i\iota \right). \end{gathered}$$

Dyadic effects

In order to account for the interrelationship of the dyad members, we introduce dummy variables to address each of the two partners of the couple (cf. Ferrer & Rast, 2017; Raudenbush et al., 1995). In particular, we introduce a dyad-specific level k at both the location and scale part. The mean structure from Equation (1) can be expanded to

$${\widehat{\mathit{y}}}_{ki}=\sum _{k=1}^m{d}_k\left({\mathbf{\text{X}}}_{ki}{\mathbf{\beta }}_k+{\mathbf{\text{Z}}}_{ki}{\mathbf{\text{b}}}_{ki}\right)$$ (4)

where, k = 1, …, m represents the number of units in the level (two in our case). Hence, in this specification for dyads, we define m = 2 dummy variables, one for each partner, where d_k = 1 if a given measure is y_k and d_k = 0 otherwise. Considering a given value in ${\widehat{y}}_{\mathit{\text{kij}}*}$, then d_k = 1 if k = k* and d_k = 0 if k ≠ k*. The elements in d_k are mutually exclusive and ensure that the model is estimated either for one or the other partner in the dyad. The same approach can be used for the scale part, so Equation (2) can be rewritten as

$${\mathit{\phi }}_{ki}=\sum _{k=1}^m{d}_k\left[\text{exp}\left({\mathbf{\text{W}}}_{ki}\mathbf{\eta }+{\mathbf{\text{V}}}_{ki}{\mathbf{\text{t}}}_{ki}\right)\right].$$ (5)

In order to model within-dyad dependencies, the design matrices X and W typically contain variables that are thought to influence the other partner’s outcome. For example, the same-day positive affect of partner A might influence partner’s B positive affect for that same day – and vice versa.

Again, the within-person variances are estimated for both partners and are mutually exclusive. This approach does not preclude one from obtaining covariances among random effects of both partners, as they are still drawn from a common multivariate distribution. This enables one to model the correlations among the individuals in the dyads, within and across the location and the scale part of the model. This constitutes a unique feature of the MELSM for dyads.

Estimation

Mixed-effects location scale models can be estimated via maximum-likelihood methods in standard software (Ferrer & Rast, 2017; Hedeker, Mermelstein, Berbaum, & Campbell, 2009; Leckie et al., 2014), using specific software such as MIXREGLS (Hedeker & Nordgren, 2013), or Bayesian estimation procedures (Kapur, Li, Blood, & Hedeker, 2015; Rast et al., 2012). To minimize estimation issues when relying on maximum-likelihood techniques, we take advantage of a Bayesian framework that performs better with covariance matrices (such as Σ) that are prone to high collinearity and multidimensionality (cf. Rast et al., 2012; Rast & MacDonald, 2014). No-U-turn sampling (NUTS), an extension of the Hamiltonian Monte Carlo (HMC) Sampler, is particularly well suited to handle these situations (Hoffman & Gelman, 2014). This method is implemented in Stan (Stan Development Team, 2016b) and it has the added advantage, compared to Gibbs-sampling that the priors do not need to be conjugate to the likelihood of parameters.

Illustrative example

Subjects and procedure

The data for this empirical example come from 274 heterosexual couples that were recruited as part of a study of dyadic interactions (Ferrer et al., 2012; Ferrer & Widaman, 2008). Participants included couples involved in a romantic relationship who completed a daily questionnaire about their affect for up to 90 consecutive days. They ranged in age from 17 to 74 years (M = 25.08, SD = 10.39) and reported having been in the relationship from 1 month to 54 years (M = 3.26 years, SD = 6.06).

Materials and design

To obtain daily measures of affect, we used the Relationship-Specific Affect scale (RSA; Ferrer et al., 2012), a set of 18 Likert-scale items (ranging from 1 to 5) that tapped into positive and negative emotions specific to one’s relationship. In this example, positive affect (PA) serves as the dependent variable and negative affect (NA) as a predictor for within-person variance. In addition, we use a measure of relationship satisfaction based on six items from the Perceived Relationship Quality Component Inventory (Fletcher, Simpson, & Thomas, 2000). These items were rated on a 7-point Likert scale ranging from 1 (not at all) to 7 (extremely) and were completed by the participants at the beginning of the study.

Statistical analyses

We tested a sequence of increasingly more complex models, starting from an empty linear mixed effects model to the final mixed effects location scale model with all predictors.¹ Here, we describe the final model that was used to obtain the parameter estimates reported in the results section. In order to make the structure of the model more visible, we rewrite Equations (4) and (5) following multilevel notation.

Location model

The location submodel of positive affect RSA (PA) for each person i at day j is given at level 1 as:

$${\widehat{y}}_{\mathit{\text{kij}}}=\sum _{k=1}^m{d}_k\left({\beta }_{k0i}+{\beta }_{k1i}{\text{PA}}_{\text{Lag}{1}_{\mathit{\text{ij}}}}+{\beta }_{k2i}{\text{PA}}_{{\text{Partner}}_{\mathit{\text{ij}}}}\right).$$ (6)

The predictors in level 1 of the location are each person’s own PA rating of the previous day (PA_Lag1) as well as the partner’s PA rating (PA_Partner) at the same day. Both level 1 predictors PA_Lag1 and PA_Partner are person-mean centered.

The person effects are defined at level 2 separately for both partners. For females

$$k=0=F\{\begin{array}{l}{\beta }_{F0i}={\gamma }_{F00}+{\gamma }_{F01}\text{Rel}{\text{.sat}}_{\mathit{\text{Fi}}}+{\gamma }_{F02}{\text{PA}}_{\text{Partner},\mathit{\text{Fi}}}^{*}+u_{F0i}\hfill \\ {\beta }_{F1i}={\gamma }_{F10}+{\gamma }_{F11}\text{Rel}{\text{.sat}}_{\mathit{\text{Fi}}}+{\gamma }_{F12}{\text{PA}}_{\text{Partner},\mathit{\text{Fi}}}^{*}+u_{F1i}\hfill \\ {\beta }_{F2i}={\gamma }_{F20}+{\gamma }_{F21}\text{Rel}{\text{.sat}}_{\mathit{\text{Fi}}}+{\gamma }_{F22}{\text{PA}}_{\text{Partner},\mathit{\text{Fi}}}^{*}+u_{F2i}\hfill \end{array}$$

and for males

$$k=1=M\{\begin{array}{l}{\beta }_{M0i}={\gamma }_{M00}+{\gamma }_{M01}\text{Rel}{\text{.sat}}_{\mathit{\text{Mi}}}+{\gamma }_{F02}{\text{PA}}_{\text{Partner},\mathit{\text{Mi}}}^{*}+u_{M0i}\hfill \\ {\beta }_{M1i}={\gamma }_{M10}+{\gamma }_{M11}\text{Rel}{\text{.sat}}_{\mathit{\text{Mi}}}+{\gamma }_{F12}{\text{PA}}_{\text{Partner},\mathit{\text{Mi}}}^{*}+u_{M1i}\hfill \\ {\beta }_{M2i}={\gamma }_{M20}+{\gamma }_{M21}\text{Rel}{\text{.sat}}_{\mathit{\text{Mi}}}+{\gamma }_{F22}{\text{PA}}_{\text{Partner},\mathit{\text{Mi}}}^{*}+u_{M2i}\hfill \end{array}$$

At level 2, we introduce the moderator Rel.sat_ki (individual relationship satisfaction), which was measured at the beginning of the study. This variable was centered at its grand-mean (M = 6.2). ${\text{PA}}_{\text{Partner},ki}^{*}$ is the person-mean that was obtained when centering the corresponding level 1 variable PA_Partner,ij and it captures between-person differences in individual levels of partner affect. The person-mean for the lagged effect is practically identical to the random intercept and is thus not included as a level 2 variable (Hamaker & Grasman, 2015). The F and M subscripts denote the model for females (F) and males (M).

Scale model

Equivalently, the scale part of the model follows Equation (5) with level 1:

$${\sigma }_{ϵ\mathit{\text{kij}}}^2=\sum _{k=1}^m{d}_k\left[\text{exp}\left({\eta }_{0ki}+{\eta }_{1ki}{\text{NA}}_{\text{Partner,}\mathit{\text{ij}}}\right)\right].$$ (7)

The predictor for the scale is the person-mean centered negative affect of the partner (NA_Partner) for the same day. Negative affect has been shown to influence affect, both positive and negative (e.g., Röcke, Li, & Smith, 2009) and here we test its effect on the scale parameter. It is worthwhile reconsidering what predictions from Equation (5) signify in terms of observed values. For days where the partner reports higher NA, ${\sigma }_{ϵ\mathit{\text{kij}}}^2$ will result in larger (or smaller, depending on the valence) values resulting in more (or less) variance around the location parameter for that same day. In other words, NA_Partner influences the daily changes in uncertainty or unreliability that surround the location estimate.

Level 2 is defined for the female as

$$k=0=F\{\begin{array}{l}{\eta }_{F0i}={\xi }_{F00}+{\xi }_{F01}\text{Rel}{\text{.sat}}_{\mathit{\text{Fi}}}+{\xi }_{F02}{\text{NA}}_{\text{Partner},\mathit{\text{Fi}}}^{*}+u_{F3i}\hfill \\ {\eta }_{F1i}={\xi }_{F10}+{\xi }_{F11}\text{Rel}{\text{.sat}}_{\mathit{\text{Fi}}}+{\xi }_{F12}{\text{NA}}_{\text{Partner},\mathit{\text{Fi}}}^{*}+u_{F4i}\hfill \end{array}$$

and for the male

$$k=1=M\{\begin{array}{l}{\eta }_{M0i}={\xi }_{M00}+{\xi }_{M01}\text{Rel}{\text{.sat}}_{\mathit{\text{Mi}}}+{\xi }_{M02}{\text{NA}}_{\text{Partner},\mathit{\text{Mi}}}^{*}+u_{M3i}\hfill \\ {\eta }_{M1i}={\xi }_{M10}+{\xi }_{M11}\text{Rel}{\text{.sat}}_{\mathit{\text{Mi}}}+{\xi }_{M12}{\text{NA}}_{\text{Partner},\mathit{\text{Mi}}}^{*}+u_{M4i}\hfill \end{array}$$

At level 2, we have again Rel.sat_ki, the grand mean centered relationship satisfaction that moderates the level 1 effects in the within-person variance, and ${\text{NA}}_{\text{Partner},ki}^{*}$, the person-mean of NA_Partner,ij.

Random effects variance model

All level 1 parameters (location intercept, PA_Lag1 slope, PA_Partner slope, scale intercept and NA_Partner slope) for both female and male, have associated random effects that allow individual departures from the individual (male or female) mean. As described earlier, this is true for both the location and scale components, and all random effects are assumed u_i ~ N(0, Σ_i). Σ_i contains the variances of the random effects of the location and the scale as well as all covariances. Hence, the off-diagonal elements of Σ_i contain information on how individual differences are related both within individuals and within dyads. That is, we obtain relations within and between females and males but also across the location and the scale components. As noted earlier, this is a unique feature of the MELSM as it not only models dependencies among partners via level 2 predictors but it also identifies the relatedness within dyads as correlated random effects throughout the location and the scale.

As described in Equation (3) we also include a between-person model to govern the random effects standard deviations across different conditions. We re-expressed Σ_i as ${\mathbf{\tau }}_i\mathbf{\Omega }{\mathbf{\tau }}_i^{\prime }$, where Ω is a (q + p) × (q + p) correlation matrix and τ_i are the SD’s. The final model contains three location random effects for each partner (Female: ${\sigma }_1^2$, ${\sigma }_2^2$, ${\sigma }_3^2$; Male: ${\sigma }_4^2$, ${\sigma }_5^2$, ${\sigma }_6^2$) resulting in q = 6 random effect variances and two scale random effects for each partner (Female: ${\sigma }_7^2$, ${\sigma }_8^2$; Male: ${\sigma }_9^2$, ${\sigma }_{10}^2$), resulting in p = 4 variances for the scale. Hence, the dimension of the final covariance matrix Σ_i is 10 × 10 with the diagonal $\text{diag}\left({\Sigma }_i\right)={\left[{\sigma }_1^2,\dots {\sigma }_6^2,{\sigma }_{7_i}^2,\dots {\sigma }_{{10}_i}^2\right]}^{\prime }$. Note that only the scale elements have a subscript i, indicating that they are allowed to vary between participants.

In order to capture changes in the scale random effects only, we introduce a submodel for the four elements ${\left[{\sigma }_{7_i},\dots {\sigma }_{{10}_i}\right]}^{\prime }$, where g₁ = log(years in the relationship) influences the random effect SD of the scale as

$$\begin{gathered} {\sigma }_{7_i}=\text{exp}\left({\iota }_{F30}+g_{1i}{\iota }_{F31}\right) \\ {\sigma }_{8_i}=\text{exp}\left({\iota }_{F40}+g_{1i}{\iota }_{F41}\right) \\ {\sigma }_{9_i}=\text{exp}\left({\iota }_{M30}+g_{1i}{\iota }_{F31}\right) \\ {\sigma }_{{10}_i}=\text{exp}\left({\iota }_{M40}+g_{1i}{\iota }_{M41}\right). \end{gathered}$$ (8)

The first two lines in Equation (8) refer to the random effects SDs of the females and the last two lines refer to the SD’s of males. The ι_kp0’s (e.g. ι_F30) are the intercepts that define the average random effect SD of the scale for partners who were, on average, one year in their relationship (note that years in relationship was on the log scale where log(1) = 0). The ι_kp1’s (e.g., ι_F31) capture the change in the average random effects variance given the relationship length, resulting in possibly different random effect variances for the scale component of the model. That is, individual differences in the scale random effects are not constant but are allowed to vary across individuals as a function of differences in relationship length.

A note on centering

Once we include time-varying predictors, we need to decide on how they should enter the model. There are mainly three options on how we can include these variables: uncentered, grand-mean centered, and person-mean centered (Wang & Maxwell, 2015). Uncentered predictors that are included at level 1 can be conceptualized as carrying two kinds of information. An average, between-person part for each individual, and a within-person fluctuation around that average. In the logic of multilevel models, we can separate these two sources of variation and place them in the corresponding levels: level 1 for the within-person fluctuation and level 2 for the between person effect. As such, uncentered variables confound within- and between-person effects and potentially bias the results (Curran, Lee, Howard, Lane, & MacCallum, 2012; Raudenbush & Bryk, 2002). This issue cannot be resolved by grand-mean centering level 1 variables, as the within-person effect remains confounded with the between-person differences, and hence, only within-person centering can resolve this issue. A viable approach is to extract the person-mean from time-varying predictors and introduce it as a level 2 predictor while the centered within-person time-varying effects enter the model as a level 1 predictor (for a discussion on different versions of centering and detrending, see Curran & Bauer, 2011).

In the case of autoregressive effects, the decision on whether or not to center is less clear. For example, Hamaker and Grasman (2015) noted that person-mean centering autoregressive effects can downward bias the within-person slope of the lagged parameter while no centering does not lead to bias in the level 1 parameter. However, once level 2 predictors are added, the person-mean centered autoregressive parameters fares better than the noncentered. For the current application, we chose to person-mean center all time-varying level 1 predictors, including the autoregressive predictors.

Software, estimation and prior specification

All models were fitted in Stan with the NUTS algorithm using the RStan package (Stan Development Team, 2016a), with four chains and a warm-up period of half the total chain length. To ensure good quality of the parameter estimates, we chose to keep the number of iterations at a level where the models converged with potential scale reduction factors $\widehat{R}$ smaller than 1.1 (cf. Gelman, 2006). As measures of relative model fit, we report the deviance and the Pareto smoothed importance sampling-Leave-one-out cross-validation (PSIS-LOO; Vehtari, Gelman, & Gabry, 2017) with the corresponding standard errors. PSIS-LOO is a fully Bayesian approach to assess predictive accuracy of the converged model and it is asymptotically equivalent to the widely applicable information criterion (WAIC; Watanabe, 2010) which is, in turn, asymptotically equivalent to the Akaike information criterion (Akaike, 1973). Further, we report 95% credible intervals (C.I.) to indicate the statistical relevance of the parameters. If a given point estimate (e.g., zero) is included in the C.I., the estimate may not be considered to be different from zero or a null-effect – and vice-versa, if the point estimate is not within the reach of the C.I. we conclude that the parameter is relevant. Models were compared on their respective differences in the values of PSIS-LOO and standard errors are reported as units of reference. We report a sequence of comparisons starting with a standard mixed effects model and ending with the final MELSM (cf. Table 1). PSIS-LOO or WAIC can be used to select among (nested or nonnested) models with respect to their predictive performance as long as few models are compared. As the number of compared models increases, the estimated predictive performance becomes increasingly biased (Gelman et al., 2013; Piironen & Vehtari, 2017). Approaches for variable selection are described elsewhere in the literature (e.g., O’Hara & Sillanpää, 2009).

Table 1.

Sequence of estimated models and fit statistics.

Model	Deviance	PSIS-LOO (S.E.)	Difference in PSIS-LOO (S.E)
Mixed Model	36205.3	−18102.7 (169.3)	–
MELSM 1	33544.8	−16772.4 (165.5)	1330.3 (116.3)
MELSM 2	30416.9	−15208.5 (157.8)	1563.9 (81.8)
MELSM 3	30436.3	−15218.1 (158.0)	−9.7 (3.2)

Note. The difference in the PSIS-LOO is always with respect to the previous model reported in the row above. The first reference model (Mixed Model) is a standard linear mixed effects model with all predictors in the location part and different error variances for females and males. MELSM 1 extends the mixed model with random intercepts in the scale part for females and males. MELSM 2 introduces the partners same-day NA rating in the scale. MELSM 3 is the final model with the additional between-person submodel.

Given the complexity of the models, we first started with a mixed effects model with all location predictors (Rel.sat and ${\text{PA}}_{\text{Partner}}^{*}$), then added random intercepts for females and males in the scale (u_F3i and u_M3i) to obtain MELSM 1. MELSM 2 was obtained by adding the remaining predictors in the scale (Rel.sat and ${\text{NA}}_{\text{Partner}}^{*}$). Finally, we added the submodel for the random effects variance of the scale [see Equation (8)] to obtain MELSM 3.

The likelihood for the MELSMs was specified as

$$\begin{gathered} {\mathit{\text{y}}}_{\mathit{\text{i}}}~N\left({\mathit{\mu }}_{\mathit{\text{i}}},{\mathit{\phi }}_i\right) \\ {\mathit{\mu }}_{\mathit{\text{i}}}={\mathbf{\text{X}}}_i\mathbf{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i \\ {\mathit{\phi }}_i=\text{exp}\left({\mathbf{\text{W}}}_i\mathbf{\eta }+{\mathbf{\text{V}}}_i{\mathbf{\text{t}}}_i\right). \end{gathered}$$

MELSM 1 and 2 were given the same weakly informative priors

$$\begin{gathered} \left[\begin{array}{c}{\mathbf{\text{b}}}_i\\ {\mathbf{\text{t}}}_i\end{array}\right]~N\left(\mathbf{0},{\Sigma }_i\right) \\ {\Sigma }_i={\mathbf{\tau }}_i\mathbf{\Omega }{\mathbf{\tau }}_i^{\prime } \\ {\mathbf{\tau }}_i~H{C}^{+}(0,2) \\ \mathbf{\Omega }~LKJcorr(\nu =1) \\ \mathbf{\beta }~N(0,100) \\ \mathbf{\eta }~N(0,100). \end{gathered}$$

Regardless of their sample mean and variance, the priors for the location and scale parameters in the MELSM were set to cover a parameter space that was considerably larger than the admissible parameter space in the observed data. For example, given the range of the PA scale, we know that the intercept can only lie between 1 and 5. Our prior was defined to have mean of zero and a SD of 100, as such, this approach regularizes the parameters only mildly and the data easily overwhelm the prior.

For the covariance matrix Σ, we followed standard recommendations (Barnard, McCulloch, & Meng, 2000) and modeled it in terms of its corresponding correlation matrix Ω (Σ = τΩτ′). Hence, instead of specifying a (scaled) inverse-Wishart as prior for the random effects (cf. Rast et al., 2012), we use the Lewandowski-Kurowicka-Joe (LKJ; Lewandowski, Kurowicka, & Joe, 2009) correlation prior with shape ν ≥ 1, Ω ~ LKJcorr(ν). ν governs the correlation among the parameters, and with ν = 1, the LKJ correlation distribution can be considered uninformative. This approach adds the benefit of reducing issues that arise from the Wishart distribution that biases posteriors either toward the variance or the covariances (Gelman, 2006). Note that there are several alternative approaches to parameterize the covariance matrix. For example, Kapur et al. (2015) successfully used the spherical parameterization (as discussed in Barnard et al., 2000) to assign weak priors to the elements of the correlation matrix in a simulation study on a multivariate MELSM. The SDs of the random effects were assumed to come from a heavy tailed half-Cauchy (HC⁺) distribution with location 0 and scale 2.

For the final MELSM 3, we re-specified the priors for the random effects.

$$\begin{gathered} \left[\begin{array}{c}{\mathbf{\text{b}}}_i\\ {\mathbf{\text{t}}}_i\end{array}\right]~N\left(\mathbf{0},\left[\text{exp}\left({\mathbf{\text{g}}}_i\mathit{\iota }\right)\right]\Omega {\left[\text{exp}\left(g_i\mathit{\iota }\right)\right]}^{\prime }\right) \\ {\mathit{\iota }}_{\mathbf{1},\dots \mathbf{6}}~N(-1.5,3) \\ {\mathit{\iota }}_{\mathbf{7},\dots \mathbf{10}}~N(-1.5,3) \\ \Omega ~\mathit{\text{LKJcorr}}(\nu =1.5) \\ \mathbf{\beta }~N\left({\mu }_{\text{MELSM}2},0.5\right) \\ \mathbf{\eta }~N\left({\mu }_{\text{MELSM}2},0.5\right) \end{gathered}$$

Notably, the HC⁺ prior was replaced by a log-normal distribution for the parameters in the random effects SD’s submodel (τ_i = exp(g_iι)). The priors for ι were defined separately for the location (ι₁, …ι₇) and the scale elements (ι₈, …ι₁₀). Although they are set to be the same here, one could define different priors for the location and the scale elements. Overall, the priors for the final model were more informative to increase regularization and reduce computation time. For example, the prior for ι which defines the random effects SD was set to −1.5 with a SD of 3 on the log-scale. The mode of this prior is at exp(−1.5) = 0.2 SDs and it puts 95% of the probability mass between exp(−1.5±2 × 3) = [0.0006, 90.02] SDs – which is still largely unspecific. The location and scale parameters were not expected to change substantially from MELSM 2 to MELSM 3. Hence, the priors were informed by the previous model; the prior means were close to the posterior means of MELSM 2 and the SDs of 0.5 were more narrow. This approach mainly reduced the computation time to 15 h in 3000 iterations while hardly influencing the posterior estimates, compared to an earlier model with less informed priors that took almost the double amount of time with 5000 iterations to converge.

Results

We investigated a sequence of models, starting with a standard linear mixed-effects model, as described in Equation (1), and ending with the final MELSM described in Equations (4), (5) and (8). This sequence allowed us to verify the plausibility of results and model fit. All PSIS-LOO and deviance values as well as their increment in model fit are reported in Table 1. A positive difference denotes an increment in model fit while a negative difference indicates a decrement in fit. Note that PSIS-LOO from MELSM 3 indicates a somewhat poorer fit compared to MELSM 2 but we decided to report this model to illustrate the use of the between-subject variance submodel defined in Equation (3).

The final model was fit using four chains and 3000 iterations, with 1500 warm-up iterations. The values in the priors were all chosen to be mildly informative and the range of the parameter space was inferred from previous models in the sequence. ν, the LKJ prior for the correlation matrix of random effects Ω, was set to ν = 1.5 to reflect our assumption that we would see correlations among the random effects. The final model converged after 15 h on a Linux operated system with an IntelCore i7 at 3.4 GHz, with four cores (8 threads) and 16 GiB RAM.

Fixed location

The results for the full location and scale parameters, for both females and males, are reported in Table 2. All fixed location parameters are interpretable as in any standard mixed-effects model. The overall pattern and effect sizes of the parameter estimates for both female and male were very similar. All main effects were relevant (more than 99.2% of the posterior probability mass was above a parameter value of zero) and contributed to changes in their reported PA. While the males reported, on average, higher PA (compared via the posterior density of the difference between males and females; Kruschke, 2013), all other effects were very similar in size across both genders. Given that all predictors were grand-mean and person-mean centered, the intercept represents the average PA rating across the study. The level 2 predictors, overall relationship satisfaction (Rel.sat.) and the average partner PA rating (${\text{PA}}_{\text{Partner}}^{*}$) were positively linked to the average PA of the respondent. That is, the average respondent’s PA was higher for those who reported higher than average satisfaction with their relationship and for those who’s partners also reported higher than average PA. The time-varying level 1 predictors, the lagged PA rating (PA_Lag1) and the daily changes in the partners PA (PA_Partner.pc) were also positively related to the daily PA reports. Hence, the mood from the previous day carried forward to the next day, and the daily partner’s changes in PA affected the respondents’ same day PA in the same direction. The interaction term between the average partner’s PA and the daily changes in the partner’s PA (${\text{PA}}_{\text{Partner.pc}}\times {\text{PA}}_{\text{Partner}}^{*}$) was positive, indicating that the effect of the daily partner’s changes in PA was amplified (reduced) for partners who reported on average higher (lower) PA. Figure 1 shows individual predictions for PA as a function of changes in partner’s PA ratings (while keeping the PA_Lag1 effect constant at the person average, panel a) and lagged PA response (while keeping the PA_Partner effect constant at the person average, panel b). Both panels show an obvious positive effect on PA.

Table 2.

Fixed effects from a mixed effects location scale model for positive affect.

	Female			Male
Parameters	Mean	2.5%	97.5%	Mean	2.5%	97.5%
Fixed location
Intercept (γk00)	3.45	3.39	3.51	3.55	3.50	3.61
Rel.sat. (γk01)	0.30	0.21	0.38	0.24	0.15	0.33
${\text{PA}}_{\text{Partner}}^{*}\left({\gamma }_{k02}\right)$	0.55	0.46	0.64	0.48	0.39	0.57
PALag1 (γk10)	0.24	0.21	0.26	0.26	0.23	0.28
PALag1 × Rel.sat. (γk11)	−0.03	−0.07	0.01	−0.01	−0.05	0.03
${\text{PA}}_{\text{Lag}1}\times {\text{PA}}_{\text{Partner}}^{*}\left({\gamma }_{k12}\right)$	−0.03	−0.07	0.02	−0.03	−0.08	0.01
PAPartner.pc (γk20)	0.36	0.32	0.39	0.30	0.26	0.33
PAPartner.pc × Rel.sat. (γk21)	0.04	−0.01	0.09	0.05	−0.00	0.10
${\text{PA}}_{\text{Partner.pc}}\times {\text{PA}}_{\text{Partner}}^{*}\left({\gamma }_{k22}\right)$	0.06	0.00	0.12	0.06	0.00	0.11
Fixed scale
Intercept (ξk00)	−0.83	−0.87	−0.78	−0.91	−0.95	−0.87
Rel.sat. (ξk01)	−0.08	−0.14	−0.02	−0.06	−0.12	−0.00
${\text{NA}}_{\text{Partner}}^{*}\left({\xi }_{k02}\right)$	0.18	0.07	0.29	0.28	0.16	0.39
NAPartner.pc (ξk10)	0.20	0.15	0.26	0.19	0.15	0.24
NAPartner.pc × Rel.sat. (ξk11)	0.10	0.04	0.16	0.08	0.02	0.14
${\text{NA}}_{\text{Partner.pc}}\times {\text{NA}}_{\text{Partner}}^{*}\left({\xi }_{k12}\right)$	−0.27	−0.39	−0.15	−0.16	−0.27	−0.05

Note. All estimates are posterior means. The 2.5 and 97.5% represent the boundary of the lower and upper credible intervals (CI). Bolded estimates represent means where the according CI’s exclude 0. Fixed Scale estimates are the SD’s of the random effects on the log scale. Rel.sat. is relationship satisfaction, $\text{PA}{\left(\text{NA}\right)}_{\text{Partner}}^{*}$ is the time-invariant partner’s person-mean PA (NA), PA(NA)_Partner.pc is the partner’s daily person-mean-centered PA (NA), and PA_Lag1 is the person-mean-centered previous day PA.

Figure 1.

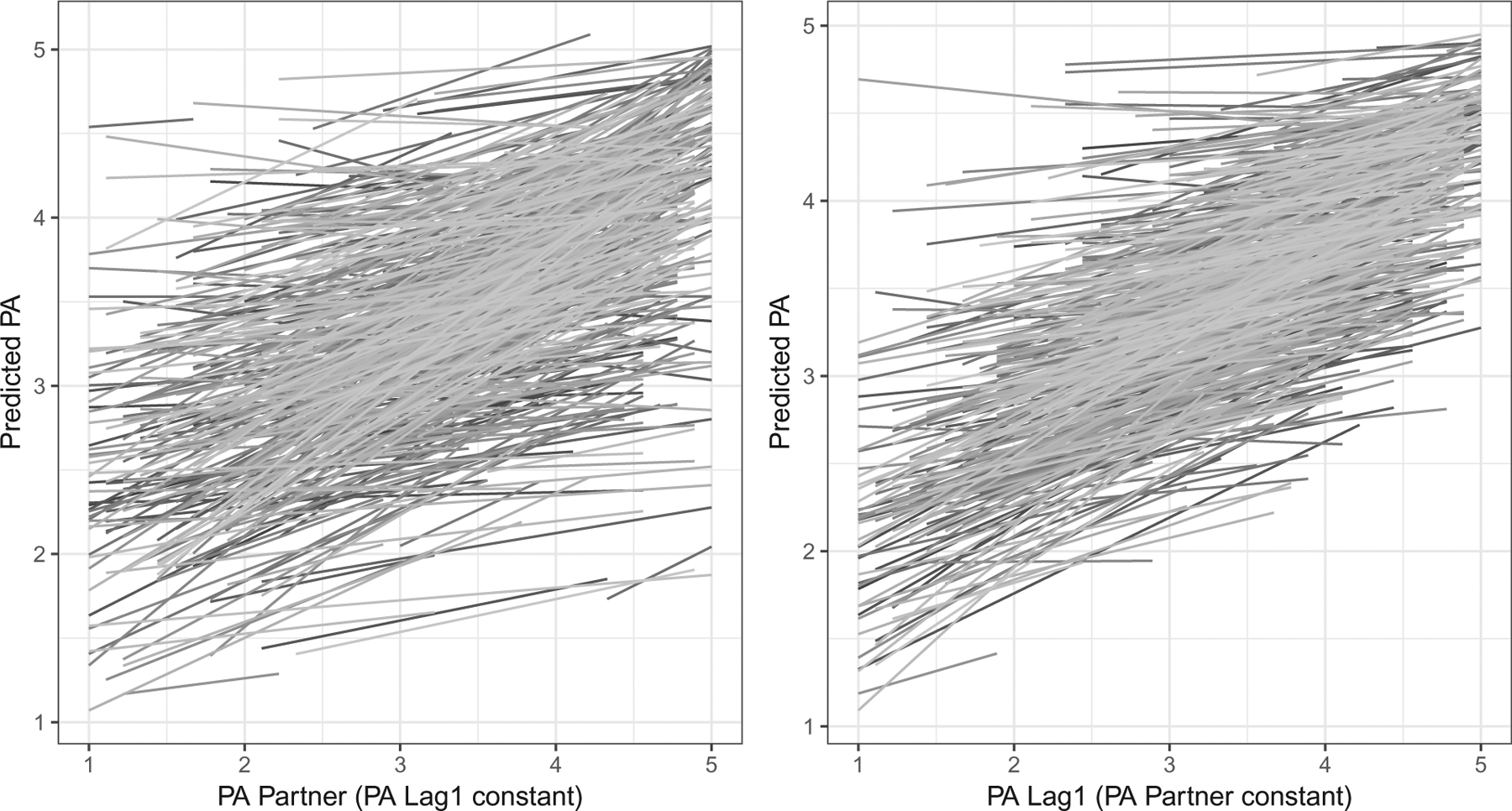
Predicted slopes of positive affect versus PA Lag 1 (PA partner) holding the PA partner (PA Lag 1) effects constant at the person-level. Each line represents the predicted line for an individual.

Fixed scale

The effects for the fixed scale are reported on the log-metric. In order to obtain the average within-person SDs, the parameters need be exponentiated (e.g., exp(−.83) = 0.44). All predictors (Rel.sat., ${\text{NA}}_{\text{Partner}}^{*}$, and NA_Partner.pc) contributed to changes in the average within-person SD. The time-invariant level 2 predictors had opposite effects on the average within-person variance. The association from relationship satisfaction was negative so, on average, higher satisfaction ratings were associated with smaller within-person SDs. That is, the PA ratings tended to be more stable over time for participants with higher relationship satisfaction, whereas the PA ratings from participants with lower relationship satisfaction, on average, tended to fluctuate more. These effects were similar in size for both genders, except for the intercept which was considerably smaller for the males (more than 99.7% of the posterior probability mass for the difference between males and females was below zero). In turn, average partner NA influenced the variance positively, indicating that the overall within-person variance was higher for those respondents whose partners, on average, reported higher NA.

At level 1, there was only one time-varying predictor (NA_Partner.pc). The partner’s daily changes in NA ratings had a positive effect on the within-person SDs. That is, on days when the partner reported higher than average NA, variability increased, whereas on days when NA was lower than average, variability decreased. This relation is depicted in Figure 2, where partner’s NA ratings are related to larger within-person SDs. The positive interaction between daily fluctuations in partner’s NA and relationship satisfaction (NA_Partner.pc × Rel.sat.) suggests that increased relationship satisfaction amplifies the effect of daily fluctuations in the partner’s NA on the within-person variance. That is, those who were more satisfied with their relationship also reacted more strongly to changes in their partner’s NA and vice versa. The interaction between the partners daily changes with their average NA rating (${\text{NA}}_{\text{Partner.pc}}\times {\text{NA}}_{\text{Partner}}^{*}$) was negative and thus larger average partner NA attenuated the effect of the daily changes in the partners NA on the respondents within-person variance.

Figure 2.

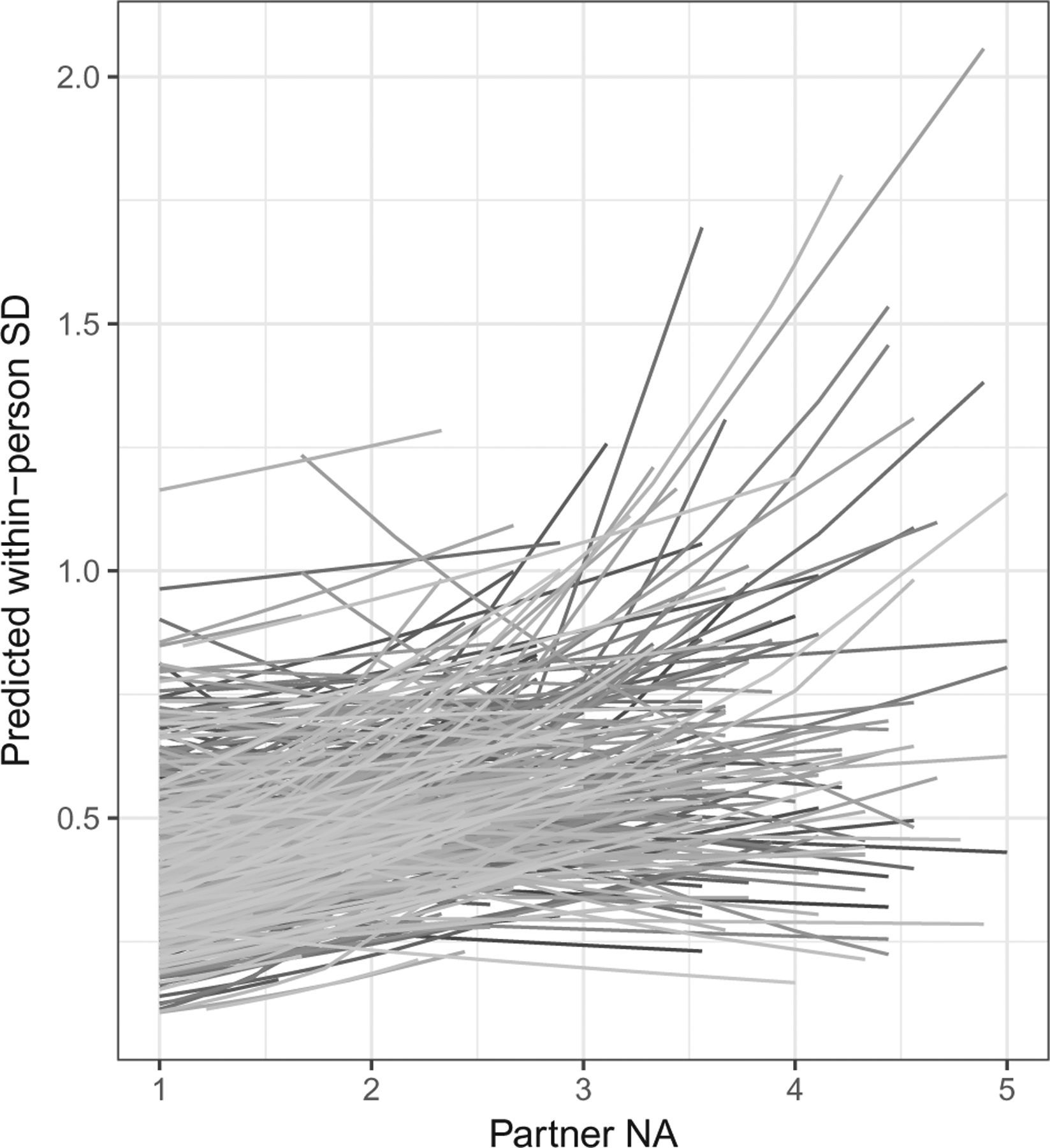
Predicted within-person SD’s for each individual with respect to different Partner NA ratings. Overall, increasing Partner NA ratings result in higher within-person variability. The individual lines indicate large heterogeneity among individuals in terms of reactivity to NA ratings of the partner.

Random effects

From Figures 1 and 2 it is apparent that there were considerable amounts of individual differences around the fixed effects in both the scale and the location components. These individual differences are captured by the random effects reported in the diagonal of Table 3. The first three diagonal elements (τ_LF1, τ_LF2, τ_LF3) are the random effects for the intercept, the PA_Lag1 and the PA_Partner.pc of the location component, for the females. The following three elements (τ_LM1, τ_LM2, τ_LM3) are the same parameters for the males. Note that all three parameters showed large variation across individuals, for both females and males.

Table 3.

Random effects and correlations within and across location and scale for positive affect.

Parameter	1	2	3	4	5	6	7	8	9	10
1. τLF1	0.22	[−0.24,0.01]	[−0.19,0.06]	[−0.61,0.43]	[−0.55,0.44]	[−0.52,0.39]	[−0.38,−0.17]	[0.23,0.54]	[−0.51,0.53]	[−0.57,0.43]
2. τLF2	−0.10	0.03	[−0.50,−0.25]	[−0.52,0.42]	[−0.52,0.47]	[−0.50,0.41]	[−0.06,0.21]	[−0.42,−0.06]	[−0.53,0.41]	[−0.56,0.43]
3. τLF3	−0.05	−0.36	0.07	[−0.57,0.48]	[−0.58,0.36]	[−0.56,0.42]	[−0.01,0.24]	[−0.13,0.25]	[−0.54,0.38]	[−0.53,0.45]
4. τLM1	−0.01	−0.00	0.01	0.23	[−0.32,−0.06]	[−0.28,−0.03]	[−0.60,0.39]	[−0.52,0.43]	[−0.40,−0.19]	[0.15,0.48]
5. τLM2	0.01	0.03	−0.04	−0.17	0.03	[−0.51,−0.25]	[−0.58,0.40]	[−0.53,0.43]	[−0.07,0.21]	[−0.41,−0.01]
6. τLM3	−0.02	0.00	0.02	−0.14	−0.36	0.05	[−0.63,0.47]	[−0.55,0.41]	[0.01,0.27]	[−0.13,0.25]
7. τSF1	−0.26	0.10	0.14	−0.03	−0.04	−0.02	0.11	[−0.57,−0.26]	[−0.50,0.39]	[−0.52,0.41]
8. τSF2	0.41	−0.21	0.09	0.01	−0.00	0.00	−0.40	0.07	[−0.59,0.45]	[−0.56,0.43]
9. τSM1	0.07	0.00	−0.01	−0.28	0.09	0.16	0.01	−0.00	0.11	[−0.56,−0.24]
10. τSM2	−0.02	−0.00	0.02	0.34	−0.19	0.09	−0.00	0.01	−0.38	0.04

Note. Brackets contain the 95% credible intervals (CI) for the corresponding correlations in the lower triangular. Bolded parameters exclude zero in the CI. In the diagonal we report the random effects variances for couples who’s partnership duration was on average 1 year. τ_LF1 is the intercept parameter where F is for females (and M for males) and L is location. τ_Lk2 corresponds to PA_LAG1 and τ_Lk3 to PA_Partner.pc. The scale effects are denoted by the S subscript. τ_Sk1 is the intercept and τ_Sk2 the NA_Partner.pc.

The top left quadrant (6 × 6 matrix) of Table 3 captures the correlations among the location parameters. The brackets contain the 95% credible intervals of the corresponding correlations in the lower triangular. The pattern of correlations among females and males was remarkably similar, except for the correlation between the intercept and the PA partner effects (τ_LF1 with τ_LF2) and the lagged effect (τ_LF1 with τ_LF3). For both females and males, the relevant correlations were negative. However, males had two additional correlations indicating that individuals who reported higher than average PA tended to have smaller carry-over effects from one day to the next (correlation r among τ_LM1 and τ_LM2 = −.18) and were less susceptible to their partner’s PA the same day (r among τ_LM1 and τ_LM3 = −.14). Both, females and males, showed a negative correlation among τ_Lk2 and τ_Lk3 (r = −.36) suggesting that larger lag effects are associated with smaller effects from partner’s PA the same day (and vice versa).

The lower right quadrant (4 × 4 matrix) includes the scale effects. Given that we introduced a variance model for the four diagonal random effect variances (see Equation (3)), these values represent the average random effects for participants who had been in their relationship for one year. The two correlations among τ_Sk1 and τ_Sk2 indicated that increasing the partner’s NA the same day correlated negatively with the variance of average PA ratings. In other words, those participants with larger than average PA variance estimates were less reactive to their partners’ NA ratings. And, alternatively, those with generally low PA variability reacted more strongly to their partners’ increase in NA with an increase in PA variability (for a similar result with stress reactivity, see Rast et al., 2012).

The lower left quadrant (4 × 6 matrix) captures the correlations of the random effects across the location and the scale components. The negative correlations indicate that higher average PA ratings were associated with smaller within-person variances, whereas larger PA_Lag1 effects were associated with smaller changes in the within-person variance due to increased partner NA. The positive correlation among the random intercept of the location and the partner NA (τ_Lk1 with τ_Sk2) indicates that those who reported higher overall PA values also showed larger effects from daily fluctuations in their partners’ NA.

Between-person variance prediction

In Equation (8), we specified a submodel for between-person differences in the scale component. This model predicts differences in the random effects of the scale due to relationship duration (RelDur). Note that this variable RelDur was transformed via the natural logarithm to account for very long partnership lengths. Hence, the intercept represents a relationship length of one year (since ln(1) = 0). Results from these analyses are reported in Table 4. The reported SD ι_k30 and ι_k40 parameters reproduced the corresponding variances in the diagonal of Table 3. Relationship duration only had a perceptible effect for the males in the sample. That is, on average, males who had been in their relationship for longer were more heterogeneous (i.e., showed larger random effects in their intercept). In other words, all participants showed individual differences in their PA variability and in the change in such variability as a response to their partner’s NA. However, relative to females, only males were more heterogeneous in their variability estimates as their relationship length increased, and vice versa.

Table 4.

Between-person estimates for scale effects.

	Female			Male
Parameters	Mean SD	2.5%	97.5%	Mean SD	2.5%	97.5%
Random scale
SD int. (ιk30)	0.33	0.30	0.37	0.33	0.30	0.37
RelDur (ιk31)	1.05	.96	1.14	1.10	1.01	1.19
NAPartner.pc (ιk40)	0.26	0.20	0.32	0.21	0.16	0.27
NApartner.pc × RelDur (ιk41)	0.95	0.77	1.15	1.05	0.87	1.28

Note. All estimates are posterior means. The 2.5% and 97.5% represent the boundary of the lower and upper credible intervals (CI). Bolded estimates represent means where the according CI’s on the log scale exclude 0.

Discussion

In this paper, we expanded the standard actor-partner and multilevel models onto a mixed-effects location scale model (MELSM) for dyadic interactions. This model was built to identify and account for IIV in each of the dyad members as well as their interrelations, as their interaction unfolds over time. Modeling and explaining dyadic interactions at both the mean and variance level requires repeated measurement data and flexible methods that are able to capture changes within and differences between individuals over time as well as the partner effects. The MELSM is one such model. This approach introduces predictors for both the mean structure, in the location component, and the variance structure, in the scale part, in a single modeling step. Moreover, partner interactions can be added at either the location or the scale submodel, or both, and they may include predictors that operate at the location and/or scale part. This approach also results in the estimation of random effects for both the location and the scale parts. This is done, for one, controlling for effects of mean and variance dependency (resulting in heteroscedasticity) but also obtaining correlations across these two parts and across both partners in the dyad (or more units in higher-order systems such as triads).

The information extracted from the covariance across the location and the scale is a unique feature of the MELSM. In our empirical illustration, we found that partners’ average and same day NA resulted in larger within-person variability. At the same time, not all participants conformed to this relation. The negative correlation between the intercept of the within-person SD and the within-person NA partner slope (females: r of τ_SF2 with τ_SF1 = −.41; males: r of τ_SF2 with τ_SF1 = −.38) indicated that those who were generally stable in their PA ratings (small PA SD) were reactive to their partners’ NA. However, those who were, on average, inconsistent in their PA ratings (large overall PA SD) did not react with an increase of within-person variability. This association was depicted in Figure 2, where some individuals showed a decrease in within-person variability. Again, these types of findings, with a fine-grained level of detail about IIV, are unique to the MELSM and would be hard to obtain with other standard models.

Another unique feature of the MELSM is the possibility of including between-person factors that could moderate the person-level variables at both the location and the scale components. In our example, we used time in the relationship as such factor. This variable affected the magnitude of individual differences in the within-person intercept variance. In our analyses, males who were at earlier stages in their relationship were more similar to each other than those who had been in their relationship for a longer time. This effect, however, was not evident for females.

Whenever variances are the focus of a model, one needs to take into account that their magnitude is also defined by the location of the average response. That is, in variables that are bounded (either at one or both ends), the variance will be a function of the person’s mean (Baird, Le, & Lucas, 2006; Eid & Diener, 1999; Kalmijn & Veenhoven, 2005) and, thus, covariances among the random location and scale intercepts merely reflect this constraint. This problem persists in the MELSM (but see Mestdagh et al., n.d., for a solution in multi-stage approaches). In the current application this correlation was medium (r ≈ −.30 among τ_Lk1 and τ_Sk1), and negative, as one would expect for PA. In general, participants reported PA that was closer to the ceiling than the floor. While the magnitude of the correlation was rather moderate, it could be substantial in other applications involving NA ratings (Rast et al., 2012) or reaction time data (Rast & MacDonald, 2014). This does not necessarily reflect a problem for the MELSM but it should be taken into account when interpreting the random effects correlations – some of these effects are dictated by the design and might not necessarily reflect the actual relation in a setting with unbounded variables.

One of the key strengths of the MELSM is its flexibility, as it allows researchers to include person- and time-varying predictors at both the location and scale components. However, it is important to keep in mind that the relation among the random effects of the location and scale are modeled as covariances, and they do not imply any sense of directionality or hierarchy. One alternative parameterization to counter this issue partially is to include the estimated individual mean as a predictor of the variance in the scale part of the model. Rast and Zimprich (2011) used this approach to predict within-person variability in a reaction time task to account for the heteroscedasticity arising from slower reaction times being related to larger variances (see also chapters 7.2.2 and 10.3 in Gałecki & Burzykowski, 2013, for a general description of variance functions in the context of linear mixed effect models). However, for researchers who are interested in modeling within-person variability, dynamics, and lead-lagged relations, one limitation is that IIV itself cannot serve as a predictor. To circumvent this issue, approaches such as multi-stage studies first extract IIV and then use it as a predictor in a subsequent regression-type analysis (cf. MacDonald, Hultsch, & Dixon, 2008).

Another point worth mentioning is that, in the current form, the MELSM does not differentiate between within-person variability due to actual fluctuations in the individuals’ behavior from fluctuations that arise from measurement error. Here, these two sources of variability are confounded. Although, if we are willing to assume that the measurement error variance is constant over time and situations, the intercept term will likely absorb a larger portion of the error variance than the slope term. With other designs, and other variables, however, one might include an additional term in the variance model that captures measurement error (for an application with EMA data. see Vansteelandt & Verbeke, 2016).

The models discussed here, especially the final model, comprise a large number of parameters. This raises questions regarding data requirements for obtaining accurate parameter estimates. Most studies examining data requirements for estimating IIV made use of two-stage approaches and are not directly transferable to the MELSM, as the latter models all variances jointly from a constrained covariance matrix. Hence, the MELSM should benefit from regularization in the sense that the random effects (co)-variances can only vary within a certain limit. In fact, the few simulations using a MELSM suggest that, in simple cases with only one random location and scale intercept, the MELSM parameters can be recovered with relatively few within-group or subject data points. For example, Leckie et al. (2014) recovered the variance parameters in a simulation with N = 250 and 10 repeated measurements. Similarly, Leckie (2014) was able to recover all parameters in another simulation study with 50 schools and 25 students per school. Given that our model was much more complex, we ran a small scale simulation with 200 replications using the parameters from the males in our final model. Due to convergence time, we limited ourselves to two random effects, an intercept and slope, for the location and the scale resulting in a 4 × 4 covariance matrix and no between-person predictors. The simulation was based on posteriors from the estimated population model (see Kruschke, 2015, Chapter 13) and suggested that large correlations (r ≈ .40) were recoverable with approximately 75 participants and 75 repeated measurements while medium sized correlations (r ≈ .20) required up to 180 participants and 100 repeated measurement. The parameters that defined the minimal requirements for N and number of repeated measurements were the covariances among the location and the scale random effects. This fits the findings in Table 3 where the smallest detectable correlation between location and scale was r = 0.16 with a credible interval of [0.01, 0.27]. It is very likely that the design and sample size requirements needed to obtain accurate estimates in demanding settings, such as the one presented here with 10 random effects, will increase. However, from the small simulation, it seems that the requirements for sample size grows faster than that for the repeated measurements. As such, our data example with N > 500 and up to 90 repeated measurements probably covered the requirements for our full model. These are speculations and future simulation work needs to formally address the data and design requirements in a broader context.

Likewise, the extent to which missing data affects the quality of the estimates or whether the location and scale parameters are similarly impacted is currently unknown. In our application we assumed a missing at random process (Rubin, 1976), but this assumption is not necessarily reasonable or tenable. In cases where data are missing not at random one could implement an imputation mechanism into the model that estimates all missing and nonmissing parameters simultaneously (Molenberghs, Fitzmaurice, Kenward, Tsiatis, & Verbeke, 2014).

The model presented in this paper serves as an illustration of a linear MELSM for dyads. This model can be modified easily in either the location or the scale functions to accommodate different structures (Goldstein, Leckie, Charlton, Tilling, & Browne, 2017). Some possible modifications include, for example, adding inherently nonlinear mean or variance structures, or altering the random-effects covariance matrix Σ to follow prespecified covariance structures. It is important to note, however, that each addition to the random effects increases the computational demand dramatically. Thus, our recommendation would be to start with a basic model and add terms at basic and manageable steps.

The purpose of this paper was to present the MELSM as a flexible model for longitudinal research on dyads. Our proposed MELSM is suited to model dyadic interactions in processes that show fluctuations, and where such ups and downs can have structure that is predictive of individual and dyadic behaviors. In principle, such a model could be applied to any dyadic interaction where the interdependence between the dyadic members is of key interest, given certain data conditions. Consider, for example, the interrelations between a therapist and a client, either over time, or in the course of a therapy session. Or, alternatively, the interaction between a mother and her infant child, during play time or through the development of the child. In either case, there will most likely be ups and downs in the individuals’ emotions, bonding, or adherence to therapy that can be modeled with the MELSM to detect aspects of the interactions that would otherwise go unnoticed (for additional examples, see Estrada, Sbarra, & Ferrer, n.d.). By focusing on the within-person variance, this approach opened up possibilities for modeling a component that is often disregarded as unexplained residuals. We hope that we illustrated such possibilities and the fact that such residuals may show systematic patterns that are important to understand psychological processes.

Appendix

Stan code for models 2 and 3. Model 2 was the best fitting model and served to provide priors for model 3. Parameter names are chosen to reflect the multilevel model specifications in the manuscript. The code and example data for the full sequence can be obtained from https://github.com/phrast/MELSM

model_2 <- ′
data {
int < lower =0> nobs; //num of observations
int < lower =1> J; //number of groups or subjects
int < lower =1, upper = J> group[nobs]; //vector with group ID
matrix[nobs,6] x; //design matrix w. time-varying wp predictors for location
matrix[nobs,4] w; //design matrix w. time-varying wp predictors for scale
matrix[J,3] z; //between person predictors at level 2 for location
matrix[J,3] m; //between person predictors at level 2 for scale
vector < lower =1, upper =5 > [nobs] y; //column vector with outcomes
}
parameters { //Parameters to be estimated
cholesky_factor_corr[10] L_Omega; //Cholesky decomposition of Omega
matrix[6,3] gamma; //Location fixed effects
matrix[4,3] xi; //Scale fixed effects
matrix[10,J] stdnorm; //Standard normal, multiply w. cholesky factor to
//obtain multivariate normal beta
vector < lower =0 > [10] tau; //Vector of random effect SDs
}
transformed parameters {
matrix[J,6] z_gamma;
matrix[J,4] m_xi;
matrix[J,10] mu;
matrix[J,10] beta;
//Level 2
z_gamma = z * transpose(gamma);
m_xi = m * transpose(xi);
mu = append_col(z_gamma, m_xi);
beta = mu+transpose(diag_pre_multiply(tau, L_Omega)*stdnorm);
}
model {
//Priors
tau~cauchy(0, 2);
to_vector(stdnorm) ~normal(0,1);
L_Omega~lkj_corr_cholesky(1);
to_vector(xi)  ~normal(0, 100);
to_vector(gamma) ~normal(0, 100);
//likelihood
y~normal(rows_dot_product(beta[group, 1:6], x),
exp(rows_dot_product(beta[group, 7:10], w)));}
generated quantities { //This section is not necessary, but contains useful
//transformations and generates data for posterior checks.
corr_matrix[10] Omega;//Obtain Omega from Cholesky factor to print in output
Omega = L_Omega*transpose(L_Omega);//Correlation matrix for output
}′
Model 3: Note that the priors were kept informative for the γ and ξ parameters in order alleviate model complexity. This model takes considerably more time to converge compared to the MELSM 2 as we also need to estimate parameters in the submodel for the scale random effects.
model_3<-’
data {
int < lower =0> nobs; //number of observations
int < lower =1> J; //number of groups or subjects
int < lower =1, upper = J> group[nobs]; //vector with group ID
matrix[nobs,6] x; //design matrix w. time-varying wp predictors for location
matrix[nobs,4] w; //design matrix w. time-varying wp predictors for scale
matrix[J,3] z; //between person predictors at level 2 for location
matrix[J,3] m; //between person predictors at level 2 for scale
matrix[J,1] g; //between person predictors for location ranefvar (intercept only)
matrix[J,2] a; //between person predictors for scale ranefvar (intercept and slope)
vector < lower =1, upper =5 > [nobs] y; //column vector with outcomes
}
parameters {
cholesky_factor_corr[10] L_Omega; //Cholesky decomposition of Omega
matrix[6,3] gamma; //Location Fixed effects
matrix[4,3] xi; //Scale fixed effects
matrix[6,1] iota_l; //iota, SD, for location random effects
matrix[4,2] iota_s; //iota, SD, for scale random effects
//(modeled with predictors in a)
matrix[10,J] stdnorm; //Standard normal, used to multiply w. cholesky
//factor to obtain multivariate normal beta
}
transformed parameters {
matrix[J, 6] z_gamma;
matrix[J, 4] m_xi;
matrix[J,10] mu;
matrix[J, 6] g_iota_l;
matrix[J, 4] a_iota_s;
matrix[J,10] tau;
matrix[J,10] beta;
z_gamma = z * transpose(gamma);
m_xi = m * transpose(xi);
mu = append_col(z_gamma, m_xi);
g_iota_l = exp(g*transpose(iota_l)); //submodel for location random effect SDs
//(intercept only)
a_iota_s = exp(a*transpose(iota_s)); //submodel for scale random effect SDs
//(intercept and slope)
tau = append_col(g_iota_l, a_iota_s);
for(j in 1:J){
beta[j,] = mu[j, ]+transpose(diag_pre_multiply(tau[j, ], L_Omega)*stdnorm[ ,j]);
}
}
model {
//priors
to_vector(stdnorm) ~n;ormal(0,1);
L_Omega~lkj_corr_cholesky(1.5);
to_vector(gamma) ~normal(0.1, 0.5);
gamma[1,1]~normal(3.45, 0.5);//intercepts obtain mean from MELSM 2
gamma[4,1]~normal(3.60, 0.5);
to_vector(xi)~normal(−0.5, 0.5);
to_vector(iota_l) ~normal(−1.5, 3);
to_vector(iota_s) ~normal(−1.5, 3);
//likelihood
y ~normal(rows_dot_product(beta[group, 1:6], x),
exp(rows_dot_product(beta[group, 7:10], w)));
}
generated quantities {//Obtain Omega from Cholesky factor.
corr_matrix[10] Omega;
Omega = L_Omega transpose(L_Omega);
}′