Abstract
Autism spectrum disorder (ASD) is a neuro-developmental disorder that affects the social abilities of patients. Studies have shown that a small number of abnormal functional connections (FCs) exist in the cerebral hemisphere of ASD patients. The identification of these abnormal FCs provides a biological ground for the diagnosis of ASD. In this paper, we propose a combined deep feature selection (DFS) and graph convolutional network method to classify ASD. Firstly, in the DFS process, a sparse one-to-one layer is added between the input and the first hidden layer of a multilayer perceptron, thus each functional connection (FC) feature can be weighted and a subset of FC features can be selected accordingly. Then based on the selected FCs and the phenotypic information of subjects, a graph convolutional network is constructed to classify ASD and typically developed controls. Finally, we test our proposed method on the ABIDE database and compare it with some other methods in the literature. Experimental results indicate that the DFS can effectively select critical FC features for classification according to the weights of input FC features. With DFS, the performance of GCN classifier can be improved dramatically. The proposed method achieves state-of-the-art performance with an accuracy of 79.5% and an area under the receiver operating characteristic curve (AUC) of 0.85 on the preprocessed ABIDE dataset; it is superior to the other methods. Further studies on the top-ranked thirty FCs obtained by DFS show that these FCs are widespread over the cerebral hemisphere, and the ASD group appears a significantly higher number of weak connections compared to the typically developed group.
Keywords: ASD, Deep feature selection, Classification
Introduction
Autism spectrum disorder (ASD) is a severe neurological condition that affects social behavior and communication abilities of patients (Association 2013). The understanding of the disease mechanisms is still incomplete due to the complexity and heterogeneity of ASD. Functional magnetic resonance imaging (fMRI) is a powerful technique that has provided a more in-depth insight into the pathophysiology of ASD (Kennedy and Courchesne 2008; Biswal et al. 1995). Large-scale collaborative initiatives, such as Autism Brain Imaging Data Exchange (ABIDE) (Di Martino et al. 2014), share terabytes of brain fMRI data aggregated from laboratories around the world facilitating the understanding of disease mechanisms. Thousands of subject samples provide comprehensive materials for understanding the disease yet increase the difficulty of analysis.
Many researchers have reported that some specific abnormal functional connections (FCs) exist in the brains of ASD patients. For example, Monk et al. (2009) found that ASD subjects had altered intrinsic connectivity within the default mode network, and connectivity between these regions was associated with specific ASD symptoms. Using independent component analysis, Assaf et al. (2010) found that ASD patients showed some decreased FCs in default mode sub-networks compared to typically developed (TD) controls. The magnitude of FC in these regions relates to the severity of social and communication deficits. Keown et al. (2013) investigated the local connectivity in ASD and reported local brain connectivity was atypically increased in autism in the posterior brain. Supekar et al. (2013) concluded that children with ASD had shown functional hyper-connectivity across multiple brain regions. Even fathers of children with autism show abnormal activity and connectivity in the brain network for the processing of emotional faces (Mehdizadehfar et al. 2020).
Furthermore, Jamal et al. (2014) extracted brain connectivity features of 24 children who were handling particular cognitive tasks and used a support vector machine (SVM) to classify autism. Based on whole-brain FCs, Abraham et al. (2017) used L2-regularized classifiers to classify a large cohort of individuals of ASD from TD controls, and achieved a classification accuracy of 66.8%. Yahata et al. (2016) developed a novel machine-learning algorithm which identified a small number of FCs for separating ASD versus TD controls on a self-collected dataset. They also studied the generalization of the identified FCs to other datasets. The above findings indicate that a small proportion of FCs is critical for the cause of ASD and it is necessary to develop methods to explore ASD-related FCs from the whole-brain.
With the availability of fast computing devices and big data sharing, deep learning has become a powerful technique for pattern recognition and classification tasks among massive data (Litjens et al. 2017). It shows remarkable performance in medical data analysis. Chen et al. (2019) proposed an intuitive form of electroencephalography data, and adopted convolutional neural network technique for discriminating children with attention-deficit/hyperactivity disorder from controls. Plis et al. (2014) used restricted Boltzmann machine to learn physiologically important representations and detect latent relations in neuroimaging data. Shi et al. (2017) proposed multimodal stacked deep polynomial networks to fuse and learn feature representations from multimodal neuroimaging data for the diagnosis of Alzheimer’s disease. As an efficient unsupervised method, autoencoder has also been used for feature learning and dimensionality reduction in disease classification tasks. Kim et al. (2016) adopted a deep neural network based on whole-brain resting-state FCs to classify schizophrenic patients. The weights of the network were initialized via stacked autoencoder in the pre-training process to improve the classification performance. In the work of Kong et al. (2019), multiple sparse autoencoders are stacked to classify ASD on a one-site dataset from the ABIDE database. Guo et al. (2017) applied a fisher score method to measure the discrimination of the features learned by autoencoders. A bunch of sparse autoencoders was trained to compose a feature pool based on input data, and then the learned features were selected for building a classifier to classify ASD. Hazlett et al. (2017) studied 106 infants at high familial risk of ASD and 42 low-risk infants; based on the brain magnetic resonance imaging of 6–12-month-old individuals, they used a deep-learning algorithm to predict the diagnosis of autism in individual high-risk children at 24 months. Heinsfeld et al. (2018) used two stacked denoising autoencoders to extract lower-dimensional data from the ABIDE database. Then they applied the encoder weights to a multilayer perceptron (MLP) to achieve an accuracy of 70%. The above studies reflect the effectiveness of deep learning methods in medical data classification tasks to a large extent.
Recently, there is an increasing interest in extending deep learning approaches for graph data. Graphs are widely used as a natural framework that captures interactions between individual elements represented as nodes in a graph. Bruna (2014) introduced convolutional neural networks on graphs. Since then, the use of graph-based models has gained a lot of attention in medical imaging applications. Kipf and Welling (2017) presented a scalable approach for semi-supervised learning on graph-structured data with graph convolutionary network (GCN). They demonstrated that their approach outperformed related methods by a significant margin. Furthermore, Parisot et al. (2018) proposed using a GCN method to classify ASD. They combined the imaging and non-imaging data in a single framework and achieved a significant improvement in classification accuracy with an accurate graph structure. However, ASD-related FC features were not explored in the above mentioned deep learning methods.
In fact, in biomedical applications many studies used or developed deep learning methods for feature selection or feature extraction. For example, for further understanding the mechanisms of complex systems, Li et al. (2016) have proposed a deep feature selection (DFS) model which can take advantage of neural network structures to handle nonlinearity and conveniently select a subset of features right at the input level. Nezhad et al. (2016) proposed a new feature selection method based on deep architecture. The method used stacked auto-encoders for feature abstraction at higher levels, and it was applied to a specific precision medicine problem. The above works show that DFS can not only reduce the dimensionality of data with many features but also improve the performance of classification tasks.
In this paper, we investigate deep learning methods for feature selection and classification of ASD. We propose a combined deep feature selection (DFS) and graph convolutional network (GCN) method to aid the diagnosis of ASD. Firstly, based on the whole-brain FCs of subjects, a neural-network-based DFS method has been developed for identifying critical FCs related to ASD. Then using the identified key FCs and demographical information of patients, a GCN is built to classify ASD and TD controls. The proposed method is tested on the ABIDE database, and it is compared with MLP and four classical machine learning (ML) methods. The main contributions of our work are as follows.
Key FCs related to ASD on the multi-site ABIDE database have been identified by the DFS network.
Experimental results show that classification accuracies have been improved remarkably through the DFS process.
Compared to the other methods in the literature, our proposed method has superior performance.
The rest of the paper is organized as follows. In "Materials and methods" section, first, the procedure of data preprocessing and the method for computing functional connections based on resting-state fMRI are introduced. Then we present our proposed combined DFS and GCN method. In "Results" section, we show some experimental results and compare our method with several reported methods in the literature. In "Discussion" section, we discuss the limitations of the method and the challenging nature of ASD classification. In "Conclusions" section, we draw the conclusion.
Materials and methods
Data and preprocessing
The present study was carried out using resting-state fMRI (rs-fMRI) data obtained from the ABIDE database (Di Martino et al. 2014). The ABIDE database aggregates data from 20 acquisition sites and openly shares neuroimaging (rs-fMRI) and phenotypic data of 1112 subjects. In order to easily replicate and extend our work as well as to make a fair comparison with the work of Parisot et al. (2018), we use the preprocessed version of the dataset provided by the Preprocessed Connectome Project (publicly available at http://preprocessed-connectomes-project.org/) (Craddock et al. 2013). Through quality visual inspection (mainly for largely incomplete brain coverage, high movement peaks, ghosting and other scanner artifacts), the rs-fMRI data were actually evaluated and selected by three experts. This yielded 871 subjects out of the initial 1112. Among them, 403 individuals are with ASD and 468 are TD individuals. The demographic information of the 871 subjects is summarized in Table 1.
Table 1.
Demographic information of the participants (mean ± standard deviation)
| Site | ASD | TD | ||||
|---|---|---|---|---|---|---|
| Age (year) | FIQ* | Sex (M/F) | Age (year) | FIQ* | Sex (M/F) | |
| CALTECH | 24.0 ± 7.6 | 99.5 ± 2.6 | 4/1 | 28.2 ± 12.2 | 111.0 ± 9.2 | 6/4 |
| CMU | 26.0 ± 5.4 | 109.5 ± 12.1 | 4/2 | 27.8 ± 4.4 | 116.4 ± 10.2 | 3/2 |
| KKI | 10.7 ± 1.3 | 97.7 ± 20.6 | 9/3 | 10.1 ± 1.2 | 112.3 ± 9.8 | 15/6 |
| LEUVEN_1 | 21.9 ± 4.1 | 109.4 ± 13.1 | 14/0 | 23.0 ± 2.8 | 115.4 ± 13.1 | 14/0 |
| LEUVEN_2 | 13.9 ± 1.5 | N/A | 9/3 | 14.4 ± 1.5 | N/A | 12/4 |
| MAX_MUN | 28.4 ± 13.2 | 108.5 ± 15.0 | 16/3 | 25.2 ± 8.4 | 111.7 ± 9.5 | 26/1 |
| NYU | 14.8 ± 7.1 | 107.4 ± 16.4 | 64/10 | 15.8 ± 6.2 | 113.4 ± 13.1 | 72/26 |
| OHSU | 11.4 ± 2.2 | 106.0 ± 22.0 | 12/0 | 10.2 ± 1.0 | 114.1 ± 11.1 | 13/0 |
| OLIN | 17.1 ± 3.3 | 110.2 ± 20.1 | 11/3 | 16.9 ± 3.6 | 116.4 ± 13.9 | 12/2 |
| PITT | 18.3 ± 7.0 | 111.1 ± 14.8 | 21/3 | 18.7 ± 6.7 | 109.5 ± 8.9 | 22/4 |
| SBL | 34.0 ± 6.6 | 106.5 ± 14.1 | 12/0 | 33.6 ± 6.8 | N/A | 14/0 |
| SDSU | 15.3 ± 1.8 | 123.1 ± 11.6 | 8/0 | 14.0 ± 1.9 | 107.3 ± 10.5 | 13/6 |
| STANFORD | 10.2 ± 1.6 | 115.1 ± 15.6 | 9/3 | 9.8 ± 1.7 | 112.9 ± 15.2 | 9/4 |
| TRINITY | 17.0 ± 3.2 | 108.2 ± 16.5 | 19/0 | 17.1 ± 3.8 | 110.9 ± 12.2 | 25/0 |
| UCLA_1 | 13.3 ± 2.6 | 103.2 ± 12.1 | 31/6 | 13.4 ± 2.1 | 105.3 ± 9.1 | 24/3 |
| UCLA_2 | 12.8 ± 2.0 | 93.5 ± 12.0 | 11/0 | 12.1 ± 1.2 | 113.2 ± 10.1 | 8/2 |
| UM_1 | 13.3 ± 2.5 | 107.3 ± 17.3 | 26/8 | 14.1 ± 3.2 | 107.2 ± 9.7 | 35/17 |
| UM_2 | 14.9 ± 1.6 | 114.1 ± 12.9 | 12/1 | 16.7 ± 4.0 | 111.1 ± 9.5 | 20/1 |
| USM | 23.6 ± 8.4 | 99.6 ± 17.0 | 43/0 | 20.9 ± 8.3 | 115.5 ± 15.4 | 24/0 |
| YALE | 13.1 ± 3.0 | 94.2 ± 22.8 | 14/8 | 13.6 ± 2.1 | 103.2 ± 15.9 | 11/8 |
| Total | 17.1 ± 8.0 | 105.8 ± 17.1 | 349/54 | 16.8 ± 7.2 | 111.1 ± 12.1 | 378/90 |
FIQ Full Scale Intelligence Quotient
The Configurable Pipeline for the Analysis of Connectomes (C-PAC) (Craddock et al. 2013) was used for the preprocessing. Preprocessing includes slice time correction, motion correction, global mean intensity normalization, nuisance signal regression to remove signal fluctuations induced by head motion, respiration, cardiac pulsation, and scanner drift (Lund et al. 2005; Fox et al. 2005), band-pass filtering (0.01–0.1 Hz), functional image registration and standard space registration. In particular, the component based noise correction method (CompCor) of Behzadi et al. (2007) was used for physiological noise correction. Physiological noise was modeled using 5 principal components with highest variance from a decomposition of white matter and CSF voxel time series. Head motion was modeled using 24 regressors derived from the parameters estimated during motion realignment (Friston et al. 1994) whereas scanner drift was modeled using a quadratic and linear term. As for image registration, a transform from original to template (MNI152) space was calculated for each dataset from a combination of functional-to-anatomical with FSL BBreg and anatomical-to-template transforms with the non-linear registration from Advanced Normalization Tools (ANTS).
Subsequently, to reduce the dimensionality of features, the mean time series for a set of regions extracted from the Harvard Oxford (HO) atlas (Desikan et al. 2006) were computed and normalised to zero mean and unit variance. The HO atlas distributed with the FSL (FMRIB Software Library) (Jenkinson et al. 2012) was split into cortical and subcortical probabilistic atlases (Desikan et al. 2006), which were bisected into left and right hemispheres. Regions of interest (ROIs) representing left/right white matter, left/right gray matter, left/right cerebrospinal fluid and brainstem were removed from the subcortical atlas, which leaded to 111 ROIs being obtained. Hence, the preprocessed data we downloaded from the ABIDE Preprocessed repository is actually 111 rs-fMRI ROI mean time series. Then we computed the functional connection between each pair of rs-fMRI ROI time-series by a correlation distance metric. Therefore, there are 6105 FCs in total for each subject. The selected subjects and the preprocessing process is exactly the same as the ones used in Parisot et al. (2018).
Combined deep feature selection and graph convolutional network method
We propose a combined deep feature selection and graph convolutional network method to classify ASD. Figure 1 shows the whole workflow of the proposed classification method. First, the functional connection feature vectors extracted in "Data and preprocessing" section are fed into a deep feature selection network with a spare one to one feature selection layer. Thus, after training, the weights of the features at the feature selection layer are ranked and the top ranked features can be selected. Then the ABIDE dataset is divided into training set and testing set. A GCN model which integrates the selected FC features and non-imaging features as inputs is trained on the training set. Finally, the GCN model is evaluated on the testing set.
Fig. 1.
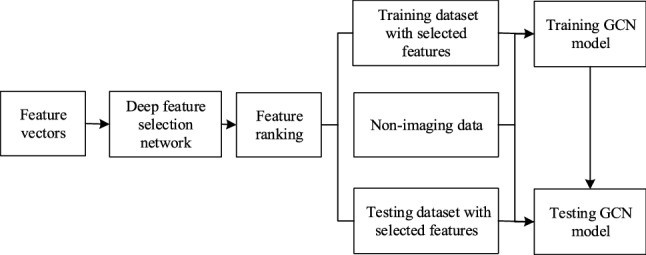
The workflow of the ASD classification
Deep feature selection network
In this section, we apply the DFS method of Li et al. (2016) for identifying a subset of relevant input FC features of ASD. The advantages of the DFS network are as follows. Firstly, given the hyper-parameter setting, it efficiently selects a subset of features in different sparseness for classification tasks. It overcomes the limitation of linear methods, which makes feature selection more straightforward. Secondly, the feature selection procedure is intuitive and easy, without involving complex feature fusion and decomposition. Finally, by using a deep nonlinear structure, it can automatically extract nonlinear features for the classification task, which is superior to low-level linear methods.
Compared with the popular framework MLP, the DFS network has a new layer for deep neural networks. It straightforwardly adds a sparse one-to-one linear layer between the input layer and the first hidden layer of an MLP. This layer is different from a fully connected layer. In the fully connected layer, every neuron has connections to every input, whereas neurons in the new layer have only one connection to one particular input feature, thus it can help to identify a subset of relevant input features (variables) in a dataset.
Consider a DFS network with L layers, its model parameter can be denoted by , where is the weight vector of one-to-one feature selection layer and () is the weight matrix connecting to the th layer. Suppose there is an input feature vector , its ith feature only connects to the ith node of the first hidden layer with an activation function ( and could be taken as ). The output of the feature selection layer becomes , where is element-wise multiplication. In order to select input features, has to be sparse. Figure 2 shows the structure of a DFS network with two hidden layers. An elastic-net-style sparse regularization term is used to penalize the loss for the feature selection layer:
| 1 |
where and are the hyper-parameter used to leverage the smoothness and sparseness of .
Fig. 2.
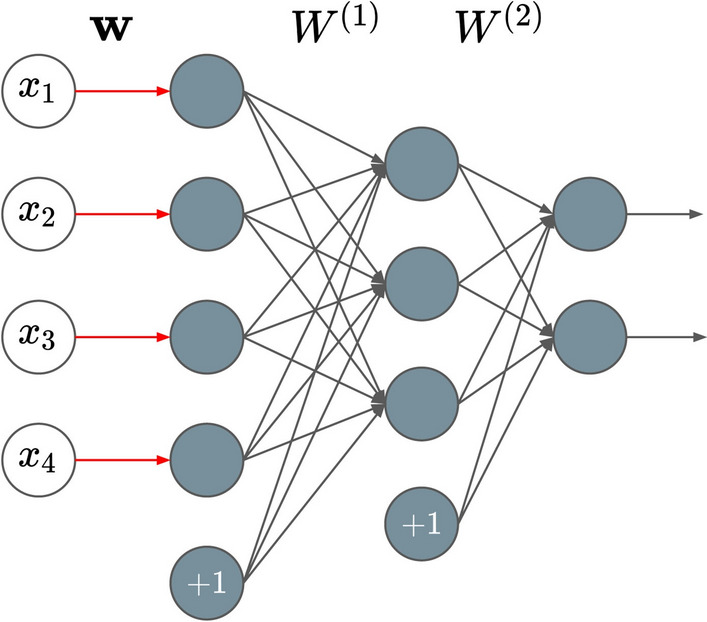
A DFS network example with a feature selection layer (where w is the weight vector) on the left and two hidden fully connected layers (where , are the two weight matrices) on the right, the input is a feature vector with 4 dimensions, the output is a vector with 2 dimensions
As the other hidden layers of DFS are fully connected layers with nonlinear activation function and the output layer is a softmax layer, the overall cost function of DFS is as below:
| 2 |
where is a mean softmax cross-entropy loss and the third term is an L2 regularization, which is used to reduce the model complexity and prevent overfitting during network training.
To train the DFS network, suitable values for parameters , , need to be specified. In our experiment, we use a grid search strategy to select these parameters. Then the overall cost function of DFS needs to be minimized to learn the model parameter . It should be noted that a random weight initialization is not expected for the feature selection layer, since it may give an advantage for one subset of features over another. Therefore, feature weights are initialized with the same positive value. Considering Adam optimizer (see Kingma and Ba 2015) can learn model parameter and it performs reasonably well in network parameter learning, we use Adam optimizer to learn the model parameter . Moreover, as the main objective of the training is tuning the sparse feature weights in the feature selection layer, the network needs to be moderately shallow.
Feature ranking
To identify the related FCs of ASD, the DFS network needs to be trained. Input features (FCs) with higher weights impact the final classification result to a large extent while input features with lower weights (e.g., zero) do not affect the classification results that much. During the training process, we adopt the cross-validation (CV) procedure. Due to different random splits on the dataset, each CV iteration has different training and validation datasets, thus the weights of the same feature from different training and validation sets may vary. To measure the overall contribution of a certain feature, we define cumulative absolute weight criteria for each feature k as follows:
| 3 |
where N is the number of CV folds, and is the weight corresponding to the kth feature in the ith CV fold. The greater magnitude of indicates a more significant contribution by the kth feature to the classification throughout the CV procedure, whereas close to zero indicates the kth feature does not contribute much for the classification. We rank features according to the value of and only features with nonzero value can be selected. To explore the impact of feature number to classification results, in our experiment, we use different top-ranked feature subsets to train classifiers.
Graph convolutional network
In this work, to predict the label from the identified FCs of ASD, we employed the GCN model of Kipf and Welling (2017) for the classification task. GCN formulates the subject classification task as a graph labeling problem, it requires a pre-defined weighted graph on which graph convolution operations are performed. In the GCN model, a node represents an individual feature data while the edge weights are used to capture the similarities between each pair of nodes. The edges can integrate the feature data and phenotypic data.
Suppose a weighted graph is represented by , where and W are the vertices, edges, and edge weight matrix of the graph, respectively. The normalized Laplacian matrix of the graph is defined as , where is an identity matrix with size and D is the diagonal node degree matrix, respectively. L is real symmetric positive semidefinite, it can be factored as , where is the matrix of eigenvectors ordered by eigenvalues, is the diagonal matrix of eigenvalues , i.e., .
GCN generalizes the operation of convolution from grid data to graph data via graph fourier transform. Suppose is a filter function matrix of the eigenvalues with parameter , the graph convolution of the input signal (every node has one element) is defined as
| 4 |
Due to the computational complexity of eigen-decomposition, uses a truncated expansion of Chebyshev polynomials up to Kth order, i.e where and is Chebyshev coefficient. The Chebyshev polynomials are defined recursively by with and , see Hammond et al. (2011). Let , then , the convolution of a graph signal can be simplified as
| 5 |
| 6 |
To allow multi-channels (dimensions) of inputs and outputs, GCN modifies (5) into a compositional layer. As a result, GCN uses the following layer-wise propagation rule:
| 7 |
where is the matrix of activations in the lth layer of C channels , and equals to the matrix of node feature data X (). is a layer-specific trainable weight matrix.
A neural network model based on graph convolutions can, therefore, be built by stacking multiple convolutional layers of the form of Eq. (7), see Fig. 3. For ASD classification, each node of GCN presents individual functional connectivity (ASD or TD) and the weight of an edge encodes the relationship between two individuals. Three phenotypic characteristics (including sex, imaging site and handedness), and one similarity measure defined in Parisot et al. (2018) are used to construct the weight matrix W of the graph. The similarity is measured by the distance correlation, it reflects the similarity between two individuals’ brain FCs. If two individuals have the same phenotypic characteristics, the edge between them on the graph has larger weight.
Fig. 3.
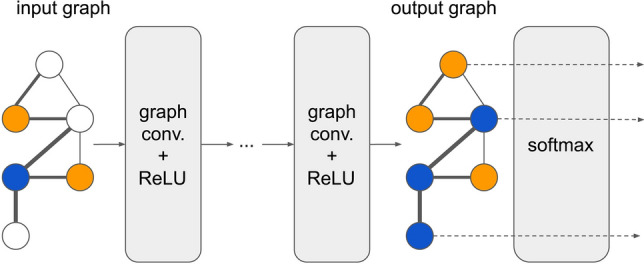
The structure of GCN model. Each node in the input graph represents a sample with a feature vector with N dimensions, and each edge in the input graph represents the similarity of the two samples. Each node in the output graph represents a sample with a vector with 2 dimensions
Specifically, suppose there are H non-imaging phenotypic features for each sample, and the weight matrix W of the graph is defined as follows:
| 8 |
where is the weight of the edge between node i and node j, and are the hth phenotypic data of node i and node j, respectively. is a measure function of distance using non-imaging phenotypic features. For non-imaging data, sex, imaging site and handedness, is Kronecker delta function. That is, if and only if the phenotypic data values of the two nodes are the same, the function return 1, otherwise return 0. is a measure function of similarity between nodes, it is defined as follows:
| 9 |
where dCor is the distance correlation, and are selected feature vectors of node i and node j, and t determines the width of the kernel.
For a detailed description of the GCN model, the reader is referred to Parisot et al. (2018).
Results
In this section, we show some experimental results. First, we explore the impact of FC feature numbers on the performance of ASD classifiers. Then we compare different feature selection and classification methods. At last, we report the top-ranked thirty FC features obtained by the DFS network.
Impact of feature numbers to classification results
To investigate the impact of feature numbers, we have selected different numbers of features according to the value of cumulative absolute weight obtained from the DFS network, then input them into GCN classifier to distinguish ASD from TD.
For comparison, we also implemented MLP method and several other classic ML algorithms. We use scikit-learn (Pedregosa et al. 2011) library implementation for classic ML algorithms. We tested different numbers of features with all possible ML algorithms (more than 8 different ones), but report only the four best performing ones. The reported algorithms are logistic regression, Gaussian process (GP), Adaboost, and SVM. The parameters in the four ML algorithms are tuned by grid search. For SVM, linear kernel is used, the regularization parameter is set to be 1.0; for logistic regression, norm penalization is used, regularization parameter is set to be 1.0, and tolerance for stopping criteria is ; for Adaboost, the base classifier is decision-tree, maximum number of estimators is 100, and the learning rate is set to be 1.0; for GP, the length scale radial-basis function kernel is 1.0, maximum number of iterations is set to be 100. We have evaluated each classifier using the 10-fold CV procedure. Since it is hard to determine the optimal number of selected FCs, we investigate the influence of the different number of top-ranked FCs on the classification performance.
For the MLP model, we searched the parameters, i.e, the number of hidden layers H and the number of hidden neurons N, using a grid search strategy. Hence H is set to be 3, N is set to be 16, dropout rate is 0.2 and L2 regularization parameter is set to be . For GCN, we used the well-explored parameter settings in Parisot et al. (2018). The edge weights of the graph encode the pairwise similarities obtained from phenotypic data, i.e., sex, imaging site, handedness, and similarity metric. Other parameters are: the number of hidden layers 1, dropout rate 0.3, L2 regularization parameter and the learning rate of Adam optimizer 0.005. We trained both the GCN and MLP models with a patience value of 30 epochs, which means if the loss does not get improved on the validation set for 30 epochs, the training process is stopped to avoid overfitting.
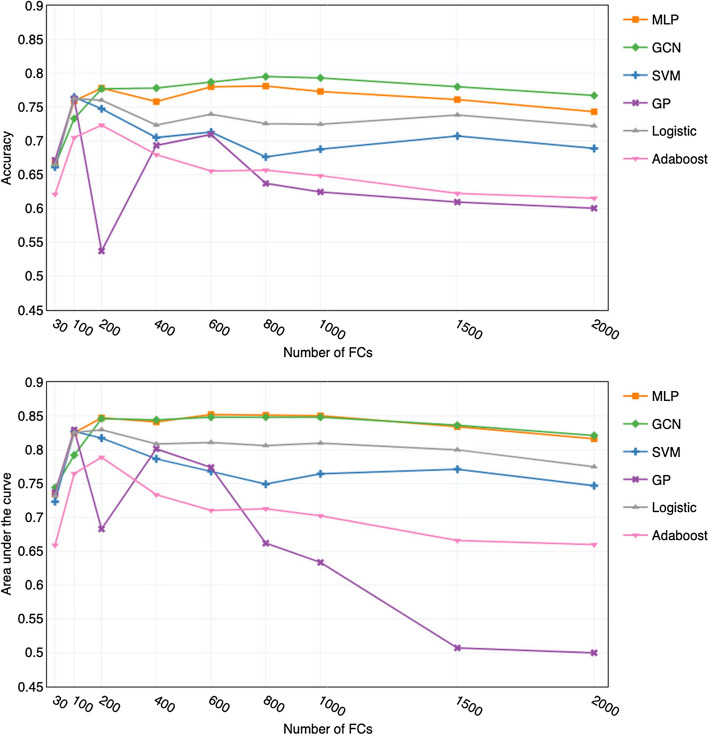
For GCN and MLP classifiers, we use 9 different top-ranked feature subsets and show the related mean accuracy and area under the curve (AUC) values in Fig. 4. From the accuracy and AUC curves, we can see that in general GCN obtains better mean accuracy values than MLP. The GCN classifier achieves the best accuracy of 79.5±3.3% (mean ± standard deviation) with the top 800 FCs. Its corresponding AUC is 0.848±0.027, indicating high discriminatory ability. While with the same 800 FCs, MLP achieves an accuracy of 78.1±4.6%, slightly worse than GCN, but it achieves the best AUC of 0.851±0.031. When using less than 200 features, the performance of MLP is better, with higher accuracy and smaller standard deviation than GCN. However, when using more than 200 features, the result is the opposite. Both the MLP and GCN have similar AUC scores, and the GCN classifier outperforms MLP in classification accuracy.
Fig. 4.
Performances of GCN, MLP and ML classifiers with different number of top-ranked FCs as input features
For the four classical ML algorithms, we show their performance with using the same nine top-ranked feature subsets as the ones used for the GCN and MLP classifiers in Fig. 4. From the figure we can see that when feature numbers are less than 200, SVM, MLP and GP behave similarly. We can see that the best performance of GP, SVM and Logistic regression is quite competitive to the two deep learning models (GCN and MLP). Nevertheless, we found it is highly unstable with the increase of selected features. When feature numbers exceed 200, as the number of features increases, the performances of the four classical ML classifiers decrease, and the Adaboost algorithm has inferior performance.
Throughout the experiment, we found that in general deep learning models are more compatible with large numbers of features than the ML models. The performance of classical ML algorithms are suitable for a small number of features, whereas deep learning models can extract higher-order features from a large number of features. The results further verify that the FC features obtained from the DFS network have contributed to the prediction.
Comparison with other feature selection methods
We study the impact of three different feature selection methods to the performance of classifiers on the ABIDE database. In addition to DFS, recursive feature elimination (RFE) (Guyon et al. 2002) and fisher score (Duda et al. 2001), two of the most widely used supervised feature selection methods, were adopted to extract informative subsets from all the FC features. Since RFE is an iterative process, we use the ridge classifier (regularization strength is 1.0) with a fixed number of features and eliminate the last 100 features in each iteration. Fisher score measures the discrimination of each feature to classification and ranks the features according to the measurement. We use the grid search strategy for an optimal number of FCs for fisher score. All the classifiers use the same parameters as well as are trained and evaluated in the same setting as described in "Impact of feature numbers to classification results" section as well. Again, for each classifier, 10 fold CV is used. We only report the best mean accuracy, AUC, sensitivity and specificity with standard deviation. It needs to be noted that the results in Table 2 obtained by different methods have different optimal numbers of FCs (see Table 3).
Table 2.
Different criteria of classifiers with different feature selection methods
| Criterion | Model | DFS | RFE | Fisher | Nonea |
|---|---|---|---|---|---|
| ACC | SVM | 76.9 ± 4.3% | 66.1 ± 6.7% | 65.6 ± 5.9% | 66.1 ± 6.8% |
| GP | 78.1 ± 2.3% | 63.7 ± 5.5% | 63.5 ± 5.0% | 55.5 ± 5.4% | |
| Logistic | 76.7 ± 2.2% | 68.9 ± 6.4% | 67.4 ± 5.3% | 67.7 ± 5.2% | |
| Adaboost | 71.7 ± 2.9% | 61.9 ± 3.1% | 63.4 ± 4.3% | 59.1 ± 3.7% | |
| GCN | 79.5 ± 3.3% | 71.1 ± 4.2% | 69.6 ± 3.8% | 69.8 ± 4.3% | |
| MLP | 78.1 ± 4.7% | 69.5 ± 5.6% | 68.3 ± 4.8% | 66.4 ± 5.3% | |
| AUC | SVM | 0.830 ± 0.048 | 0.700 ± 0.072 | 0.688 ± 0.084 | 0.673 ± 0.072 |
| GP | 0.852 ± 0.036 | 0.697 ± 0.063 | 0.674 ± 0.051 | 0.653 ± 0.065 | |
| Logistic | 0.842 ± 0.039 | 0.725 ± 0.072 | 0.716 ± 0.076 | 0.687 ± 0.076 | |
| Adaboost | 0.761 ± 0.045 | 0.641 ± 0.037 | 0.672 ± 0.039 | 0.654 ± 0.064 | |
| GCN | 0.848 ± 0.027 | 0.733 ± 0.035 | 0.718 ± 0.030 | 0.724 ± 0.078 | |
| MLP | 0.851 ± 0.031 | 0.728 ± 0.042 | 0.702 ± 0.029 | 0.667 ± 0.076 | |
| SEN | SVM | 74.0 ± 8.3% | 59.9 ± 12.6% | 57.4 ± 14.4% | 59.1 ± 12.8% |
| GP | 75.7 ± 7.7% | 57.3 ± 10.2% | 53.8 ± 7.2% | 53.2 ± 8.5% | |
| Logistic | 74.0 ± 7.1% | 62.1 ± 10.7% | 60.6 ± 11.5% | 60.1 ± 11.8% | |
| Adaboost | 67.0 ± 7.7% | 56.1 ± 10.1% | 56.3 ± 9.1% | 56.8 ± 8.7% | |
| GCN | 78.3 ± 3.5% | 68.8 ± 5.3% | 65.7 ± 4.5% | 66.8 ± 7.8% | |
| MLP | 77.2 ± 4.9% | 66.3 ± 5.8% | 64.3 ± 6.7% | 63.2 ± 8.2% | |
| SPE | SVM | 78.5 ± 6.3% | 70.6 ± 8.1% | 71.2 ± 11.1% | 70.5 ± 9.3% |
| GP | 79.0 ± 7.2% | 68.7 ± 7.7% | 73.2 ± 3.7% | 57.9 ± 9.2% | |
| Logistic | 79.2 ± 7.5% | 72.6 ± 8.2% | 72.7 ± 8.3% | 72.4 ± 8.8% | |
| Adaboost | 73.3 ± 6.8% | 63.0 ± 7.8% | 63.3 ± 6.1% | 66.9 ± 6.8% | |
| GCN | 81.2 ± 3.6% | 73.5 ± 4.9% | 69.9 ± 4.3% | 71.8 ± 4.8% | |
| MLP | 79.8 ± 4.8% | 71.5 ± 6.3% | 69.2 ± 6.4% | 68.2 ± 7.2% |
aNo feature selection adopted
Table 3.
The optimal numbers of FCs for different feature selection methods
| Model | DFS | RFE | Fisher | Nonea |
|---|---|---|---|---|
| SVM | 80 | 700 | 3000 | 6105 |
| GP | 160 | 40 | 250 | 6105 |
| Logistic | 160 | 800 | 6000 | 6105 |
| Adaboost | 80 | 300 | 900 | 6105 |
| GCN | 800 | 2000 | 2500 | 6105 |
| MLP | 600 | 2000 | 3000 | 6105 |
aNo feature selection adopted
The DFS method leads a significant accuracy improvement in classification compared to RFE, fisher score and without feature selection. It improves the classification accuracy of the classifiers by a minimum of 8% and a maximum of 15% compared to the RFE method. Compared to the other methods, the standard deviation of the accuracy obtained by DFS has also been reduced to some extent. Among the three feature selection methods, the fisher score with GCN and logistic regression classifiers do not improve the classification accuracy compared to without feature selection. In other words, it fails to find contributing features. From Table 2, we can also see that, for every classifier, its specificity value is always higher than its sensitivity value. This may be due to the slight imbalance between the ASD and TD samples in the dataset.
Characteristics of critical functional connections
We used Adam optimizer for training DFS network in order to learn the feature weights . The challenge in training comes from high-dimensional data. The existence of irrelevant and redundant features affects the optimization process. In the experiment, is set to 0.5, is set to and L2 regularization parameter is . The Adam optimizer had a learning rate of 0.005.
The DFS network was trained by 10-fold CV procedure. After each CV split training, feature weights can be obtained from the feature selection layer. A greater magnitude of weight represents a more considerable degree of contribution by that FC to the classifiers. We rank these FCs using the cumulative absolute weights metric described in "Feature ranking" section.
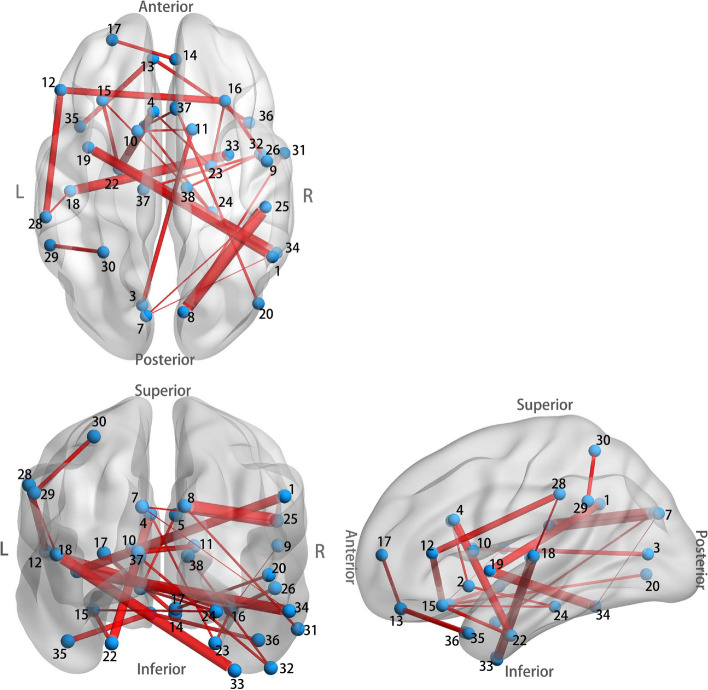
Figure 5 shows the ranked cumulative absolute weights. From the figure, we can see that about 3215 () weights are zero, their corresponding FCs are not picked for classification. We further study the top 30 FCs since they are the top 30 informative ones. We plot the spatial distribution of the top 30 FCs in Fig. 6 via BrainNet Viewer (Xia et al. 2013) and calculated the mean magnitude for each of them in the ASD/TD group and denoted it as /. A detailed list of the properties of the 30 FCs is provided in Table 4.
Fig. 5.
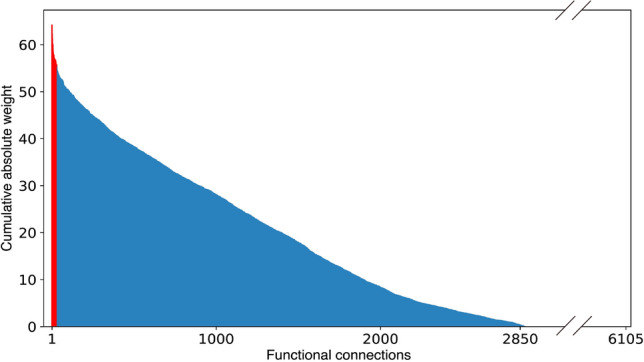
Contribution of each FC to the classification, the top ranked 30 FCs are colored in red
Fig. 6.
The spatial distribution of the identified top 30 FCs. Thicker connections indicate FCs have larger cumulative absolute weights, and vice versa
Table 4.
Properties of the top 30 FCs
| ID | Gyral region | Laterality | Mean magnitude of FCs | |
|---|---|---|---|---|
| 1 | (8) Cuneal Cortex | R | 0.17 | 0.22 |
| (25) Parietal Operculum Cortex | R | |||
| 2 | (33) Temporal Fusiform Cortex; anterior division | R | 0.14 | 0.17 |
| (18) Heschl’s Gyrus (includes H1 and H2) | L | |||
| 3 | (19) Insular Cortex | L | 0.17 | 0.23 |
| (34) Inferior Temporal Gyrus; temporooccipital part | R | |||
| 4 | (4) Cingulate Gyrus; anterior division | L | 0.18 | 0.23 |
| (22) Parahippocampal Gyrus; anterior division | L | |||
| 5 | (19) Insular Cortex | L | 0.25 | 0.30 |
| (1) Angular Gyrus | R | |||
| 6 | (12) Inferior Frontal Gyrus; pars triangularis | L | 0.16 | 0.20 |
| (16) Frontal Operculum Cortex | R | |||
| 7 | (12) Inferior Frontal Gyrus; pars triangularis | L | 0.25 | 0.29 |
| (28) Supramarginal Gyrus; anterior division | L | |||
| 8 | (35) Temporal Pole | L | 0.27 | 0.33 |
| (13) Frontal Medial Cortex | L | |||
| 9 | (11) Caudate | R | 0.07 | 0.10 |
| (3) Intracalcarine Cortex | L | |||
| 10 | (29) Superior Temporal Gyrus; posterior division | L | 0.21 | 0.26 |
| (30) Superior Parietal Lobule | L | |||
| 11 | (16) Frontal Orbital Cortex | R | 0.30 | 0.35 |
| (26) Planum Polare | R | |||
| 12 | (22) Parahippocampal Gyrus; anterior division | L | 0.19 | 0.17 |
| (15) Frontal Operculum Cortex | L | |||
| 13 | (36) Temporal Pole | R | 0.25 | 0.30 |
| (13) Frontal Medial Cortex | L | |||
| 14 | (17) Frontal Pole | L | 0.31 | 0.35 |
| (14) Frontal Medial Cortex | R | |||
| 15 | (20) Lateral Occipital Cortex; inferior division | R | 0.20 | 0.16 |
| (27) Subcallosal Cortex | R | |||
| 16 | (23) Parahippocampal Gyrus; anterior division | R | 0.04 | 0.07 |
| (16) Frontal Operculum Cortex | R | |||
| 17 | (37) Thalamus | L | 0.23 | 0.20 |
| (32) Inferior Temporal Gyrus; anterior division | R | |||
| 18 | (2) Accumbens | L | 0.22 | 0.25 |
| (24) Parahippocampal Gyrus; posterior division | R | |||
| 19 | (2) Accumbens | L | 0.27 | 0.32 |
| (5) Cingulate Gyrus; anterior division | R | |||
| 20 | (31) Middle Temporal Gyrus; anterior division | R | 0.24 | 0.31 |
| (8) Cuneal Cortex | R | |||
| 21 | (10) Caudate | L | 0.35 | 0.40 |
| (11) Caudate | R | |||
| 22 | (38) Thalamus | R | 0.23 | 0.19 |
| (32) Inferior Temporal Gyrus; anterior division | R | |||
| 23 | (28) Superior Temporal Gyrus; anterior division | L | 0.35 | 0.40 |
| (18) Heschl’s Gyrus (includes H1 and H2) | L | |||
| 24 | (4) Cingulate Gyrus; anterior division | L | 0.09 | 0.12 |
| (23) Parahippocampal Gyrus; anterior division | R | |||
| 25 | (24) Parahippocampal Gyrus; posterior division | R | 0.11 | 0.07 |
| (15) Frontal Operculum Cortex | L | |||
| 26 | (7) Cuneal Cortex | L | 0.20 | 0.25 |
| (25) Parietal Operculum Cortex | R | |||
| 27 | (34) Inferior Temporal Gyrus; temporooccipital part | R | 0.23 | 0.29 |
| (7) Cuneal Cortex | L | |||
| 28 | (16) Frontal Orbital Cortex | R | 0.15 | 0.19 |
| (9) Central Opercular Cortex | R | |||
| 29 | (2) Accumbens | L | 0.27 | 0.30 |
| (21) Paracingulate Gyrus | L | |||
| 30 | (6) Cingulate Gyrus; posterior division | L | 0.22 | 0.26 |
| (24) Cuneal Cortex | R | |||
As can be seen from Fig. 6 and Table 4, of the top 30 key FCs hemispheric distributions, 9 FCs are in the left hemisphere, 10 FCs are in the right hemisphere, and 11 FCs are in the inter hemisphere, with abnormal FCs being universally distributed throughout the brain, which also further illustrates the complexity of ASD pathogenic mechanisms. It can be seen that ASD exhibits under-connectivity () in 25 FCs and over-connectivity () in merely 5 FCs compared with TD. It may account for the prevalence of low resting state brain activity in patients with ASD. The results showed that ASD and control brains had obvious differences in FC characteristics, and the FC of brain could provide a biological basis for ASD diagnosis to some extent. Similar results can be found in Yahata et al. (2016).
We emphasize that these 30 FCs were automatically identified from the multi-site data for reliable classification of ASD and TD by the DFS network. These 30 FCs are much more trustworthy in revealing neural substrates of ASD than the FCs that were selected in many previous studies by traditional statistic analysis of ASD/TD differences within a limited dataset, this has been verified by our comparison results.
Discussion
In the present study, we adopted an efficient deep learning technique, DFS, for identifying key FCs of ASD. We tested the method on the dataset with 403 ASD samples and 468 TD controls from the ABIDE database. The samples are collected from multiple imaging sites and they have different demographic distributions. After training the DFS network, the weight of each feature is acquired, which reflects the contribution to the classification. We have ranked these features according to the magnitude of cumulative absolute weights and selected different numbers of top-ranked features as the input features of the tested classifiers (GCN, MLP, logistic regression, GP, Adaboost and SVM). Our experiments show that GCN classifier with 800 FCs (13% of the entire FCs) as input features achieves the best mean accuracy of 79.5% and an AUC of 0.85, improving the current stats-of-the-art classification performance (70.4% obtained in Parisot et al. (2018) by GCN method on the very same dataset with using the same FC features) by 9.1%. The MLP, SVM, and GP classifiers also perform well, all of them approximately achieve a mean accuracy of 77%. The results not only confirm that the FCs obtained are contributing to the ASD/TD prediction, but also illustrate the effectiveness of the combined DFS and GCN method.
Compared with other feature selection methods which are based on ML models, the DFS network straightforwardly identifies the critical features for classification, dramatically improves the accuracy of ASD prediction, and reduces the model variance. Nevertheless, the DFS has a limitation that it is only suitable for feature selection of big data. The difficulty of training on small datasets is also a common limitation in deep structure. Another limitation comes from using the GCN model for ASD prediction. The GCN can only be applied to data with graphs of a fixed structure. If new subjects need to be predicted, it is necessary to reconstruct the graph using the phenotypic information of all the subjects (including both the original samples and the new samples). Then the GCN network uses the trained model parameters and the whole population (including the new subjects) graph as input with the original subjects labeled and new subjects unlabeled. Then, the GCN performs a forward propagation to output prediction results (see Fig. 3), i.e., through L hidden layers and the output layer, finally the softmax activations are computed for the new subjects (unlabeled set), and thus the new subjects (unlabelled nodes) are assigned the labels maximizing the softmax output.
We have also investigated the FC pattern of ASD concerning feature contribution to classification obtained from the feature selection layer. The hemispheric distribution of the top 30 FCs shows that there is no significant difference between the right and left intra-hemispheric, but intra-hemispheric FCs are slightly higher than the anatomically expected number. This phenomenon may indicate the complexity of the disease-causing mechanisms of ASD, involving FCs throughout the cerebral hemisphere. An interesting finding is that, of the 30 FCs with high contributions, 25 FCs exhibit under-connectivity in the ASD samples, and only 5 FCs showed over-connectivity. It worth noting that these patterns are generally derived from a large amount of imaging data with different demographic characteristics, compared to many previous studies with limited data.
In addition to the heterogeneity of the ASD, the ABIDE database is particularly challenging due to the fact that images were acquired at different sites with different protocols. Classification across multiple sites has to accommodate additional sources of variance in subjects, scanning procedures, and equipment protocols in comparison to single-site databases (see Nielsen et al. 2013; Patriat et al. 2013; Birn et al. 2013). This brings challenges for drawing biomarkers from the brain activation to classify disease states. To the best of our knowledge, our work presents the first achievement of high classification accuracy (79.5%) and the analysis of crucial FCs related to ASD in large multi-sites ABIDE database (with 871 samples). Despite the variation generated from different protocols and demographics, the achievement of the classification accuracy shows promise for deep learning in the application of clinical datasets.
Conclusions
In this work, we have proposed a combined DFS and GCN method to classify ASD and typical developed controls. We established an efficient neural-network-based feature selection method for identifying key FCs related to ASD. The top 30 identified FCs were investigated. GCN, MLP, logistic regression, GP, Adaboost and SVM classifiers based on the different numbers of selected FCs are studied. The results have shown that our proposed method achieves the state-of-the-art prediction accuracy of 79.5% with high discriminating AUC of 0.85, it is superior to other tested methods. The high accuracy of the classifier also indicates the effectiveness of identified FCs for ASD classification. Our proposed method can not only be used for aiding the diagnosis of ASD, but it can also be applied to other mental disorder prediction. In the future, it is worth investigating the application of deep learning methods in the diagnosis of attention-deficit/hyperactivity disorder, schizophrenia and Alzheimer’s disease etc.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 12071025), and the Scientific and Technological Innovation Foundation of Shunde Graduate School of University of Science and Technology Beijing (Nos. BK19CE017 and BK20AE004).
Declaration
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Data availability
The datasets generated during and/or analysed during the current study are available in the Preprocessed Connectomes Project repository, http://preprocessed-connectomes-project.org/.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Lizhen Shao, Email: lshao@ustb.edu.cn.
Cong Fu, Email: haphac@163.com.
Yang You, Email: g20188708@xs.ustb.edu.cn.
Dongmei Fu, Email: fdm2003@163.com.
References
- Abraham A, Milham MP, Di Martino A, Craddock RC, Samaras D, Thirion B, Varoquaux G. Deriving reproducible biomarkers from multi-site resting-state data: an autism-based example. NeuroImage. 2017;147:736–745. doi: 10.1016/j.neuroimage.2016.10.045. [DOI] [PubMed] [Google Scholar]
- Assaf M, Jagannathan K, Calhoun VD, Miller L, Stevens MC, Sahl R, O’Boyle JG, Schultz RT, Pearlson GD. Abnormal functional connectivity of default mode sub-networks in autism spectrum disorder patients. Neuroimage. 2010;53(1):247–256. doi: 10.1016/j.neuroimage.2010.05.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Association AP, et al. Diagnostic and statistical manual of mental disorders?: DSM-5. Arlington: American Psychiatric Association; 2013. [Google Scholar]
- Behzadi Y, Restom K, Liau J, Liu TT. A component based noise correction method (compcor) for bold and perfusion based fMRI. NeuroImage. 2007;37(1):90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Molloy EK, Patriat R, Parker T, Meier TB, Kirk GR, Nair VA, Meyerand ME, Prabhakaran V. The effect of scan length on the reliability of resting-state fMRI connectivity estimates. NeuroImage. 2013;83:550–558. doi: 10.1016/j.neuroimage.2013.05.099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Zerrin Yetkin F, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34(4):537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bruna J, Zaremba W, Szlam A, LeCun Y (2014) Spectral networks and locally connected networks on graphs. In: International conference on learning representations (ICLR2014)
- Chen H, Song Y, Li X. Use of deep learning to detect personalized spatial-frequency abnormalities in EEGs of children with ADHD. J Neural Eng. 2019;16(6):066046. doi: 10.1088/1741-2552/ab3a0a. [DOI] [PubMed] [Google Scholar]
- Craddock C, Sikka S, Briann C, Ranjeet K, Michael M. Towards automated analysis of connectomes: the configurable pipeline for the analysis of connectomes (C-PAC) Front Neuroinform. 2013;7:189–210. [Google Scholar]
- Craddock C, Sikka S, Cheung B, Khanuja R, Ghosh SS, Yan C, Li Q, Lurie D, Vogelstein J, Burns R, Colcombe S, Mennes M, Kelly C, Di Martino A, Castellanos FX, Milham M. Towards automated analysis of connectomes: the configurable pipeline for the analysis of connectomes (C-PAC) Front Neuroinform. 2013 doi: 10.3389/conf.fninf.2013.09.00042. [DOI] [Google Scholar]
- Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage. 2006;31(3):968–980. doi: 10.1016/j.neuroimage.2006.01.021. [DOI] [PubMed] [Google Scholar]
- Di Martino A, Yan CG, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Mol Psychiatry. 2014;19(6):659. doi: 10.1038/mp.2013.78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern classification. 2. New York: Wiley; 2001. [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston HKJ, Holmes AP, Worsley KJ, Poline JP, Frackowiak RSJ. Statistical parametric maps in functional imaging: a general linear approach. Hum Brain Mapp. 1994;2(4):189–210. doi: 10.1002/hbm.460020402. [DOI] [Google Scholar]
- Guo X, Dominick KC, Minai AA, Li H, Erickson CA, Lu LJ. Diagnosing autism spectrum disorder from brain resting-state functional connectivity patterns using a deep neural network with a novel feature selection method. Front Neurosci. 2017;11:460. doi: 10.3389/fnins.2017.00460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Mach Learn. 2002;46(1–3):389–422. doi: 10.1023/A:1012487302797. [DOI] [Google Scholar]
- Hammond DK, Vandergheynst P, Gribonval R. Wavelets on graphs via spectral graph theory. Appl Comput Harmon Anal. 2011;30(2):129–150. doi: 10.1016/j.acha.2010.04.005. [DOI] [Google Scholar]
- Hazlett HC, Gu H, Munsell BC, Kim SH, Styner M, Wolff JJ, Elison JT, Swanson MR, Zhu H, Botteron KN, et al. Early brain development in infants at high risk for autism spectrum disorder. Nature. 2017;542(7641):348–351. doi: 10.1038/nature21369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinsfeld AS, Franco AR, Craddock RC, Buchweitz A, Meneguzzi F. Identification of autism spectrum disorder using deep learning and the ABIDE dataset. NeuroImage Clin. 2018;17:16–23. doi: 10.1016/j.nicl.2017.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamal W, Das S, Oprescu IA, Maharatna K, Apicella F, Sicca F. Classification of autism spectrum disorder using supervised learning of brain connectivity measures extracted from synchrostates. J Neural Eng. 2014;11(4):046019. doi: 10.1088/1741-2560/11/4/046019. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. Neuroimage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Kennedy DP, Courchesne E. The intrinsic functional organization of the brain is altered in autism. Neuroimage. 2008;39(4):1877–1885. doi: 10.1016/j.neuroimage.2007.10.052. [DOI] [PubMed] [Google Scholar]
- Keown CL, Shih P, Nair A, Peterson N, Mulvey ME, Müller RA. Local functional overconnectivity in posterior brain regions is associated with symptom severity in autism spectrum disorders. Cell Rep. 2013;5(3):567–72. doi: 10.1016/j.celrep.2013.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Calhoun VD, Shim E, Lee JH. Deep neural network with weight sparsity control and pre-training extracts hierarchical features and enhances classification performance: evidence from whole-brain resting-state functional connectivity patterns of schizophrenia. Neuroimage. 2016;124:127–146. doi: 10.1016/j.neuroimage.2015.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. In: International conference on learning representations (ICLR)
- Kipf TN, Welling M (2017) Semi-supervised classification with graph convolutional networks. In: 5th international conference on learning representations, ICLR 2017, Toulon, France, April 24–26, 2017, conference track proceedings, OpenReview.net
- Kong Y, Gao J, Xu Y, Pan Y, Wang J, Liu J. Classification of autism spectrum disorder by combining brain connectivity and deep neural network classifier. Neurocomputing. 2019;324:63–68. doi: 10.1016/j.neucom.2018.04.080. [DOI] [Google Scholar]
- Li Y, Chen CY, Wasserman WW. Deep feature selection: theory and application to identify enhancers and promoters. J Comput Biol. 2016;23(5):322–336. doi: 10.1089/cmb.2015.0189. [DOI] [PubMed] [Google Scholar]
- Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, Van Der Laak JA, Van Ginneken B, Sánchez CI. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- Lund T, Nrgaard M, Rostrup E, Rowe J, Paulson OB. Motion or activity: their role in intra- and inter-subject variation in fMRI. Neuroimage. 2005;26(3):960–964. doi: 10.1016/j.neuroimage.2005.02.021. [DOI] [PubMed] [Google Scholar]
- Mehdizadehfar V, Ghassemi F, Fallah A, Mohammad-Rezazadeh I, Pouretemad H. Brain connectivity analysis in fathers of children with autism. Cogn Neurodyn. 2020;14(6):781–793. doi: 10.1007/s11571-020-09625-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monk CS, Peltier SJ, Wiggins JL, Weng SJ, Carrasco M, Risi S, Lord C. Abnormalities of intrinsic functional connectivity in autism spectrum disorders. Neuroimage. 2009;47(2):764–772. doi: 10.1016/j.neuroimage.2009.04.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nezhad MZ, Dongxiao Zhu, Xiangrui Li, Kai Yang, Levy P (2016) Safs: a deep feature selection approach for precision medicineabraham2017deriving. In: 2016 IEEE international conference on bioinformatics and biomedicine (BIBM), pp 501–506. 10.1109/BIBM.2016.7822569
- Nielsen JA, Zielinski BA, Fletcher PT, Alexander AL, Lange N, Bigler ED, Lainhart JE, Anderson JS. Multisite functional connectivity MRI classification of autism: ABIDE results. Front Hum Neurosci. 2013;7:599. doi: 10.3389/fnhum.2013.00599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisot S, Ktena SI, Ferrante E, Lee M, Guerrero R, Glocker B, Rueckert D. Disease prediction using graph convolutional networks: application to autism spectrum disorder and alzheimer’s disease. Med Image Anal. 2018;48:117–130. doi: 10.1016/j.media.2018.06.001. [DOI] [PubMed] [Google Scholar]
- Patriat R, Molloy EK, Meier TB, Kirk GR, Nair VA, Meyerand ME, Prabhakaran V, Birn RM. The effect of resting condition on resting-state fMRI reliability and consistency: a comparison between resting with eyes open, closed, and fixated. NeuroImage. 2013;78:463–473. doi: 10.1016/j.neuroimage.2013.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. Scikit-learn: machine learning in python. J Mach Learn Res. 2011;12(Oct):2825–2830. [Google Scholar]
- Plis SM, Hjelm DR, Salakhutdinov R, Allen EA, Bockholt HJ, Long JD, Johnson HJ, Paulsen JS, Turner JA, Calhoun VD. Deep learning for neuroimaging: a validation study. Front Neurosci. 2014;8:229. doi: 10.3389/fnins.2014.00229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi J, Zheng X, Li Y, Zhang Q, Ying S. Multimodal neuroimaging feature learning with multimodal stacked deep polynomial networks for diagnosis of Alzheimer’s disease. IEEE J Biomed Health Inform. 2017;22(1):173–183. doi: 10.1109/JBHI.2017.2655720. [DOI] [PubMed] [Google Scholar]
- Supekar K, Uddin LQ, Khouzam A, Phillips J, Gaillard WD, Kenworthy LE, Yerys BE, Vaidya CJ, Menon V. Brain hyperconnectivity in children with autism and its links to social deficits. Cell Rep. 2013;5(3):738–747. doi: 10.1016/j.celrep.2013.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M, Wang J, He Y. Brainnet viewer: a network visualization tool for human brain connectomics. PLoS ONE. 2013;8(7):e68910. doi: 10.1371/journal.pone.0068910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yahata N, Morimoto J, Hashimoto R, Lisi G, Shibata K, Kawakubo Y, Kuwabara H, Kuroda M, Yamada T, Megumi F, Imamizu H, Náñez J, Sr, Takahashi H, Okamoto Y, Kasai K, Kato N, Sasaki Y, Watanabe T, Kawato M. A small number of abnormal brain connections predicts adult autism spectrum disorder. Nat Commun. 2016;7(1):11254. doi: 10.1038/ncomms11254. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated during and/or analysed during the current study are available in the Preprocessed Connectomes Project repository, http://preprocessed-connectomes-project.org/.