Influence of various temporal recoding on pavlovian eyeblink conditioning in the cerebellum

Abstract

We consider the Pavlovian eyeblink conditioning (EBC) via repeated presentation of paired conditioned stimulus (tone) and unconditioned stimulus (US; airpuff). In an effective cerebellar ring network, we change the connection probability $p_c$ from Golgi to granule (GR) cells, and make a dynamical classification of various firing patterns of the GR cells. Individual GR cells are thus found to show various well- and ill-matched firing patterns relative to the US timing signal. Then, these variously-recoded signals are fed into the Purkinje cells (PCs) through the parallel-fibers (PFs). Based on such unique dynamical classification of various firing patterns, we make intensive investigations on the influence of various temporal recoding (i.e., firing patterns) of the GR cells on the synaptic plasticity of the PF-PC synapses and the subsequent learning process for the EBC. We first note that the variously-recoded PF signals are effectively depressed by the (error-teaching) instructor climbing-fiber (CF) signals from the inferior olive neuron. In the case of well-matched PF signals, they are strongly depressed through strong long-term depression (LTD) by the instructor CF signals due to good association between the in-phase PF and the instructor CF signals. On the other hand, practically no LTD occurs for the ill-matched PF signals because most of them have no association with the instructor CF signals. This kind of “effective” depression at the PF-PC synapses coordinates firings of PCs effectively, which then makes effective inhibitory coordination on the cerebellar nucleus neuron [which elicits conditioned response (CR; eyeblink)]. When the learning trial passes a threshold, acquisition of CR begins. In this case, the timing degree ${\mathcal{T}}_d$ of CR becomes good due to presence of the ill-matched firing group which plays a role of protection barrier for the timing. With further increase in the number of trials, strength $\mathcal{S}$ of CR (corresponding to the amplitude of eyelid closure) increases due to strong LTD in the well-matched firing group, while its timing degree ${\mathcal{T}}_d$ decreases. In this way, the well- and the ill-matched firing groups play their own roles for the strength and the timing of CR, respectively. Thus, with increasing the number of learning trials, the (overall) learning efficiency degree ${\mathcal{L}}_e$ (taking into consideration both timing and strength of CR) for the CR is increased, and eventually it becomes saturated. Finally, we also discuss dependence of the variety degree for firing patterns of the GR cells and the saturated learning efficiency degree ${\mathcal{L}}_e$ of the CR on $p_c$ and their relations.

Introduction

The cerebellum plays a crucial role in precise temporal and spatial motor control for coordination of voluntary movements (e.g., locomotion, balance, and posture), leading to smooth and balanced body movement (Ito 1984, 2002a, 2012). In addition, it also participates in higher cognitive functions (e.g., attention, language, and speech) (Ito 2002a, 2012). The purpose of cerebellar motor learning is to carry out precise timing (associated with temporal information of movement) and gain (related to spatial information of movement) control for movements (Yamazaki and Nagao 2012). Experimental studies on timing and gain control for eye movements have been done in the two kinds of paradigms; (1) timing control for the Pavlovian eyeblink conditioning (EBC) (Gormezano et al. 1983; Ivry 1996; Mauk and Donegan 1997; Medina et al. 2000b; Christian and Thompson 2003; Ivry and Spencer 2004; Ohyama et al. 2003)and (2) gain control for the vestibulo-ocular reflex and the optokinetic response (Ito 1984, 1998).

Here, we are interested in the Pavlovian EBC [see Fig. 1a] which is a representative example for the classical conditioning (Wagner and Brandon 1989). An animal (e.g., rabbit, rat, or mouse) receives repeated presentations of paired conditioned stimulus (CS; tone) and (eyeblink-eliciting) unconditioned stimulus (US; airpuff). When the training trial passes a threshold, the animal acquires the ability to elicit eyelid conditioned response (CR; acquisition of learned eyeblink) via learning representation of the time passage between the onsets of CS and US (i.e., the animal becomes conditioned to close its eye in response to the tone CS with a time delay equal to the inter-stimulus interval (ISI) between the CS and the US onsets). The CRs exhibit two distinct features: (1) gradual acquisition of CR (i.e., CRs are acquired gradually over many training trials of repeated CS-US pairings) (Hilgard and Marquis 1935, 1936; Schneiderman et al. 1962; Skelton 1988; Ivarsson and Svesson 2000) and (2) adaptive timing of CR (i.e., CRs are well timed such that the time of peak eyelid closure matches well the ISI between the onsets of CS and US) (Boneau 1958; Mauk and Ruiz 1992; Domingo et al. 1997; Freeman et al. 2003; Koekkoek et al. 2003). Experimental works on EBC have been done in several animal species such as humans (Hilgard and Campbell 1936), monkeys (Hilgard and Marquis 1936), dogs (Hilgard and Marquis 1935), ferrets (Ivarsson and Svesson 2000), rabbits (Schneiderman et al. 1962), rats (Skelton 1988), and mice (Heiney et al. 2014). Particularly, since a series of groundbreaking experiments in rabbits (McCormick et al. 1982; McCormick and Thomson 1984), EBC in restrained rabbits has served as a good model for motor learning.

Fig. 1.

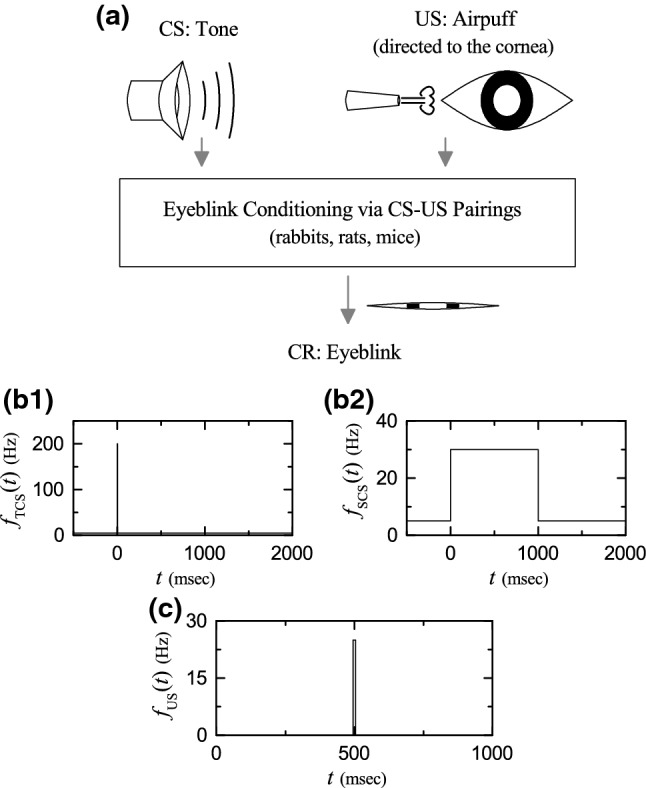
Pavlovian eyeblink conditioning (EBC). a Eyelid conditioned response (CR) (i.e., learned eyeblink) via repeated presentation of paired CS (conditioned stimulus) and US (unconditioned stimulus). Firing rates of b1 transient conditioned stimulus (TCS) for resetting and b2 sustained conditioned stimulus (SCS) (EBC signal). c Firing rate of transient unconditioned stimulus (US) for timing (eliciting unconditioned response)

Marr (1969) and, later, Albus (1971) formulated their seminal theory for cerebellar motor learning on the basis of its structure. Particularly, they paid attention to the recurrent network between the granule (GR) and the Golgi (GO) cells as a device of representation of spatial information (i.e., spatial coding). The input spatial patterns, conveyed via the mossy fibers (MFs), become more sparse and dissimilar to each other (i.e., pattern separation occurs) through recoding procedure in the granular layer composed of GR and GO cells. These recoded inputs are conveyed into the Purkinje cells (PCs) through the parallel fibers (PFs) (corresponding to the axons of GR cells). In addition to the PF recoded signals, the PCs also receive the error-teaching signals through the climbing-fiber (CF) from the inferior olive (IO) neuron. We assume that the PF-PC synapses are the only synapses where motor learning takes place. Thus, synaptic plasticity (i.e., potentiation or depression of synaptic strengths) may occur at the PF-PC synapses. It is assumed by Marr (1969)that a Hebbian type of long-term potentiation (LTP) occurs at the PF-PC synapses when both the PF and the CF signals are conjunctively excited (Hebb 1949; Brindley 1964). In opposition to Marr’s learning via LTP, it is assumed by Albus (1971)that an anti-Hebbian type of long-term depression (LTD) takes place in the case of conjunctive excitations of both the PF and the CF signals. In the case of Albus’ learning via LTD, PCs learn when to stop their inhibition (i.e. when to disinhibit) rather than when to fire, because their firing activities become reduced. Several later experimental works have provided the support for the Albus’ learning via LTD (Ito et al. 1982; Ito and Kano 1982; Sakurai 1987). Thus, LTD became established as a kind of synaptic plasticity for motor learning in the cerebellum (Ito 1989, 2000, 2001, 2002b).

A number of computational works for the EBC have been done. Several artificial models have been proposed for the time-passage representation (i.e., time coding) in the cerebellum (Desmond and Moore 1988; Moore et al. 1989; Gluck et al. 1990; Chapeau-Blondeau and Chauvet 1991; Bullock et al. 1994; Fiala et al. 1996). However, these artificial models lacked biological plausibility. A realistic cerebellar model, based on many biological properties, has been built by focusing on the recurrent loop between the GR and the GO cells in the granular layer as a time-coding device (Buonomano and Mauk 1994). Then, the realistic model generated a temporal code based on the population of active GR cells, and also, it was extended to reproduce the experimental results of the Pavlovian EBC (Medina et al. 2000a; Medina and Mauk 2000). However, the computational mechanism to generate such a temporal code was unclear mainly due to complexity of the realistic model. To understand the computational mechanism for the time coding, a rate-coding model was developed in a simple recurrent inhibitory network, and its dynamics was analyzed in both the numerical and analytical way (Yamazaki and Tanaka 2005). This rate-coding model generated a non-recurrent sequence of active neurons, corresponding to representation of a time-passage. Due to randomness in the recurrent connections, individual neurons exhibited random repetition of transitions between the active (bursting) and the inactive (silent) states which were persistent long-lasting ones. However, this rate-coding model is free of actual time scales. A spiking neural network model (with actual time scales) was built to examine representation of time passage in the cerebellum (Yamazaki and Tanaka 2007), and a large-scale computational simulation was also performed to reproduce some features of the EBC in the experiments.

In this work, as an effective spiking neural network for study of the Pavlovian EBC, we employ a cerebellar ring network, the basic framework of which was first developed in our previous work for optokinetic response (OKR) (Kim and Lim 2021). Our cerebellar ring network is essentially the same as the square-lattice network in the previous works used for both EBC (Yamazaki and Tanaka 2007)and OKR (Yamazaki and Nagao 2012). The authors in (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012) explained that the structural parameters of their square-lattice network model were selected on the basis of the anatomical observations for the cat (Palkovits et al. 1971a, b, 1972). The parameters for the single neuron models and the synaptic currents were also adopted from the known physiological data. Hence, the square-lattice network may be considered as a biological neural network, based on the anatomical and the physiological data. For the effective study of EBC, we use the one-dimensional ring network. In comparison with the two-dimensional square-lattice network, our ring network with simple architecture has advantage for computational and analytical efficiency, and its visual representation may be easily made. We note that most of the parameters for the architecture, the single LIF neuron models, and the synaptic currents in our ring network are the same as those in the biological square-lattice network (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012). Furthermore, we also employ a refined rule for the synaptic plasticity, based on the experimental results (Safo and Regehr 2008). Thus, our (one-dimensional) ring network becomes more effective for the study of EBC than the (two-dimensional) square-lattice network.

In such an effective ring network, we vary the connection probability $p_c$ from GO to GR cells and make a dynamical classification of various firing patterns of GR cells. GR cells in the whole population are divided into GR clusters. Then, the GR clusters show various well- and ill-matched firing patterns with respect to the US (i.e., airpuff unconditioned stimulus) timing signal (which is strongly localized in the middle of each trial). Each firing pattern is characterized in terms of its “matching” index, representing the similarity (or resemblance) degree between the firing pattern and the US timing signal. To the best of our knowledge, this kind of dynamical classification of firing patterns of the GR cells is unique in the study of EBC. Dynamical origin of these various firing patterns of the GR cells is also investigated. It is thus found that, various total synaptic inputs (including both the excitatory inputs via MFs and the inhibitory inputs from the pre-synaptic GO cells) into the GR clusters lead to generation of various firing patterns (i.e. outputs) in the GR clusters.

Based on our unique dynamical classification of various firing patterns in the GR clusters, we employ a refined rule for synaptic plasticity (developed from the experimental result in (Safo and Regehr 2008)), and investigate intensively the influence of various temporal recoding (i.e., firing patterns) of the GR cells on synaptic plasticity at PF-PC synapses and subsequent learning process. PCs (corresponding to the cerebellar output) receive both the variously-recoded PF signals from the GR cells and the error-teaching CF signals from the IO neuron. The CF signals are also well-matched with the US timing signal (supplied to the IO neuron). In this case, CF and PF signals may be considered as “instructors” and “students,” respectively. Then, the well-matched PF student signals are strongly depressed via strong LTD by the instructor CF signals due to good association between the well-matched PF and CF signals. On the other hand, practically no LTD occurs for the ill-matched PF student signals because most of them have no associations with the (well-matched) instructor CF signals. In this way, the student PF signals are effectively depressed by the instructor CF signals.

During learning trials with repeated presentation of CS-US pairs, the “effective” depression at PF-PC synapses coordinates activations of PCs effectively, which then makes effective inhibitory coordination on the cerebellar nucleus (CN) neuron [which elicits CR (i.e., learned eyeblink)]. When the learning trial passes a threshold, acquisition of CR begins. In this case, the timing degree ${\mathcal{T}}_d$ of CR becomes good because of presence of the ill-matched firing group which plays a role of protection barrier for the timing. As the number of trials is further increased, strength $\mathcal{S}$ of CR [denoting the amplitude of eyelid closure (measured by the electromyography (EMG))] increases due to strong LTD in the well-matched firing group, while its timing degree ${\mathcal{T}}_d$ decreases. In this way, the well- and the ill-matched firing groups play their own roles for the strength and the timing of CR, respectively. Thus, the (overall) learning efficiency degree ${\mathcal{L}}_e$ (considering both timing and strength of CR) for the CR increases with the training trial, and eventually it gets saturated.

In the above way, our dynamical classification of various firing patterns of GR cells leads to clear understanding of effective synaptic plasticity at the PF-PC synapses [depending on the type (well- or ill-matched) of the PF signals] and the following learning procedure [including the effective inhibitory coordination of PCs on the CN neuron (evoking the CR)]. Consequently, understanding on the rate of acquisition and the timing and strength of CR is expected to be much enhanced via our approach for the study of EBC.

This paper is organized as follows. In Sect. 2, an effective cerebellar ring network for the Pavlovian EBC is introduced. The governing equations for the population dynamics in the ring network are also given, together with a refined rule for the synaptic plasticity at the PF-PC synapses. Then, in the main Sect. 3, we first consider a case of $p_c=0.029$ where the firing patterns of the GR cells are the most various and the Pavlovian EBC learning is also the most efficient, and make a detailed investigation of the influence of various temporal recoding of GR cells on learning for the Pavlovian EBC. Then, by varying $p_c$, we also investigate the effect of various temporal recoding of the GR cells on the EBC, and discuss dependence of the variety degree for firing patterns of the GR cells and the timing degree ${\mathcal{T}}_d,$ the strength $\mathcal{S},$ and the learning efficiency degree ${\mathcal{L}}_e$ of the CR on $p_c$. Finally, summary and discussion are given in Sect. 4. In Appendix C, list of abbreviations is given to help readers keep track of them.

Cerebellar ring network for the pavlovian eyeblink conditioning

In this section, we describe our cerebellar ring network for the Pavlovian EBC. The basic framework of such a ring network was first developed in our previous work for OKR (Kim and Lim 2021). Our cerebellar ring network is essentially the same as the biological square-lattice network (used for both EBC (Yamazaki and Tanaka 2007) and OKR (Yamazaki and Nagao 2012)), based on the anatomical and the physiological data (Palkovits et al. 1971a, b, 1972); most of the system parameters for the structure, the single LIF neuron models, and the synaptic currents in our ring network are the same as those in the biological square-lattice network. We note advantages of the ring network with simple architecture for computational and analytical efficiency and easy visual representation, in comparison with the square-lattice network. Furthermore, we use a rule for the synaptic plasticity, based on the experimental results (Safo and Regehr 2008). This rule is a refined one for the LTD in comparison to the square-lattice network. Thus, our (one-dimensional) ring network becomes more effective for the study of EBC than the (two-dimensional) square-lattice network. For the sake of completeness, we also include a detailed explanation on the cerebellar ring network within this paper.

Conditioned stimulus and unconditioned stimulus

Figure 1a shows the Pavlovian EBC. During the training trials, repeated presentations of paired tone CS and delayed airpuff US are made to an animal (e.g., rabbit, rat, or mouse). As the training trial passes a threshold, the animal acquires the ability to elicit eyelid CR (i.e., acquisition of learned eyeblink) through learning representation of the time passage between the CS and the US onsets. Accordingly, the animal gets conditioned to closes its eye in response to the tone CS with a time delay equal to the ISI between the onsets of CS and US.

In this subsection, we give explanations on the two external input signals. We first consider the CS for the EBC signal. When the CS is a tone, the pontine nucleus in the pons receives the auditory information, and then it sends the “context” signal for the EBC via MFs to both the GR cells and the CN neuron. There are a transient CS for resetting and a sustained CS (representing the tone) (Yamazaki and Tanaka 2007). Each step ($0<t<2000$ msec) for EBC learning consists of the trial stage ($0<t<1000$ msec) and the break stage ($1000<t<2000$ msec); t denotes the time. In the trial stage, the transient CS is modeled in terms of strong and brief Poisson spike trains of 200 Hz for $0<t<5$ msec and the subsequent background Poisson spike trains of 5 Hz for $5<t<1000$ msec. On the other hand, the sustained CS is modeled in terms of Poisson spike trains of 30 Hz for $0<t<1000$ msec. In the following break stage, the CS is modeled in terms of the background Poisson spike trains of 5 Hz for $1000<t<2000$ msec. The firing rates $f_{\mathrm{TCS}}(t)$ and $f_{\mathrm{SCS}}(t)$ of the transient CS and the sustained CS are shown in Figs. 1b1 and b2, respectively. These figures also show the preparatory step for $-500<t<0$ msec where the CS is modeled in terms of the background Poisson spike trains of 5 Hz; this preparatory step precedes just the 1st step for the EBC learning.

Next, we consider the US for the desired timing signal. When an airpuff US is delivered to the cornea of an eye, sensory information is carried to the sensory trigeminal nucleus (which extends through the whole of midbrain, pons, and medulla and into the high cervical spinal cord). Then, the trigeminal nucleus also sends the desired timing signal to the IO. In the trial stage ($0<t<1000$ msec), the US (eliciting unconditioned response) is modeled in terms of the strong and brief Poisson spike trains of 25 Hz for a short interval in the middle of the trial stage, $t^{\ast }-\Delta t<t<t^{\ast }+\Delta t$ ($t^{\ast }=500$ msec and $\Delta t=$ 5 msec) (Yamazaki and Tanaka 2007). The firing rate $f_{\mathrm{US}}(t)$ of the US is shown in Fig. 1c.

Framework of the cerebellar ring network for the pavlovian EBC

A cerebellar ring network was first introduced in our previous work for OKR (Kim and Lim 2021). We note that our cerebellar ring network is essentially the same as the biological square-lattice network whose parameters were selected on the basis of the anatomical and the physiological data (Palkovits et al. 1971a, b, 1972; Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012). The parameters for the architecture, the the single LIF neuron models, and the synaptic currents in the ring network are shown in Tables 1, 2, 3, and 4 in Appendix A, most of which are the same as those (see Tables 1, 2 and 3 in (Yamazaki and Nagao 2012)) in the biological square-lattice network. As in the famous small-world ring network (Watts and Strogatz 1998; Strogatz 2001), a one-dimensional simple ring architecture was developed, which is in contrast to the two-dimensional square-lattice structure. As a result of such simple architecture, this kind of ring network has advantage for computational and analytical efficiency, and its visual representation may also be easily made, in comparison to the square-lattice network.

Table 1.

Parameter values for LIF neuron models with AHP currents for the granule (GR) cell and the Golgi (GO) cell in the granular layer, the Purkinje cell (PC) and the basket cell (BC) in the Purkinje-molecular layer, and the cerebellar nucleus (CN) and the inferior olive (IO) neurons

X-population		Granular layer		Purkinje-molecular layer		CN neuron	IO neuron
		GR cell	GO cell	PC	BC
$C_X$		3.1	28.0	107.0	107.0	122.3	10.0
$I_L^{(X)}$	$g_L^{(X)}$	0.43	2.3	2.32	2.32	1.63	0.67
	$V_L^{(X)}$	$-$ 58.0	$-$ 55.0	$-$ 68.0	$-$ 68.0	$-$ 56.0	$-$ 60.0
$I_{\mathit{AHP}}^{(X)}$	${\overline{g}}_{\mathit{AHP}}^{(X)}$	1.0	20.0	100.0	100.0	50.0	1.0
	${\tau }_{\mathit{AHP}}^{(X)}$	5.0	5.0	5.0	2.5	2.5	10.0
	$V_{\mathit{AHP}}^{(X)}$	$-$ 82.0	$-$ 72.7	$-$ 70.0	$-$ 70.0	$-$ 70.0	$-$ 75.0
	$v_{\mathit{th}}^{(X)}$	$-$ 35.0	$-$ 52.0	$-$ 55.0	$-$ 55.0	$-$ 38.8	$-$ 50.0
$I_{\mathit{ext}}^{(X)}$		0.0	0.0	250.0	0.0	0.0	0.0

Table 2.

Parameter values for synaptic currents $I_R^{(T,S)}(t)$ into the granule (GR) and the Golgi (GO) cells in the granular layer. The GR cells receive excitatory inputs via mossy fibers (MFs) and inhibitory inputs from GO cells. The GO cells receive excitatory inputs via parallel fibers (PFs) from GR cells

Target cells (T)	GR			GO
Source cells (S)	MF	MF	GO	PF	PF
Receptor (R)	AMPA	NMDA	GABA	AMPA	NMDA
${\overline{g}}_R^{(T)}$	0.18	0.025	0.028	45.5	30.0
$J_{\mathit{ij}}^{(T,S)}$	4.0	4.0	10.0	0.00004	0.00004
$V_R^{(S)}$	0.0	0.0	$-$ 82.0	0.0	0.0
${\tau }_R^{(T)}$	1.2	52.0	7.0, 59.0	1.5	31.0, 170.0
$A_1$, $A_2$			0.43, 0.57		0.33, 0.67

Table 3.

Parameter values for synaptic currents $I_R^{(T,S)}(t)$ into the Purkinje cells (PCs) and the basket cells (BCs) in the Purkinje-molecular layer. The PCs receive two types of excitatory inputs via parallel fibers (PFs) from granular (GR) cells and through climbing fibers (CFs) from the inferior olive (IO) and one type of inhibitory inputs from the BCs. The BCs receive excitatory inputs via PFs from GR cells

Target cells (T)	PC			BC
Source cells (S)	PF	CF	BC	PF
Receptor (R)	AMPA	AMPA	GABA	AMPA
${\overline{g}}_R^{(T)}$	0.7	0.7	1.0	0.7
$J_{\mathit{ij}}^{(T,S)}$	0.006	1.0	5.3	0.006
$V_R^{(S)}$	0.0	0.0	$-$ 75.0	0.0
${\tau }_R^{(T)}$	8.3	8.3	10.0	8.3

Table 4.

Parameter values for the synaptic currents $I_R^{(T,S)}(t)$ into the cerebellar nucleus (CN) and the inferior olive (IO) neurons. The CN neuron receives excitatory inputs via MFs and inhibitory inputs from PCs. The IO neuron receives excitatory input via the US signal and inhibitory input from the CN neuron

Target cells (T)	CN			IO
Source Cells (S)	MF	MF	PC	US	CN
Receptor (R)	AMPA	NMDA	GABA	AMPA	GABA
${\overline{g}}_R^{(T)}$	50.0	25.8	30.0	1.0	0.18
$J_{\mathit{ij}}^{(T,S)}$	0.002	0.002	0.008	1.0	5.0
$V_R^{(S)}$	0.0	0.0	-88.0	0.0	$-$ 75.0
${\tau }_R^{(T)}$	9.9	30.6	42.3	10.0	10.0

Here, we employ such an efficient cerebellar ring network for the Pavlovian EBC. Figure 2a shows the box diagram for the cerebellar network. The granular layer, corresponding to the input layer of the cerebellar cortex, is composed of the excitatory GR cells and the inhibitory GO cells. On the other hand, the Purkinje-molecular layer, corresponding to the output layer of the cerebellar cortex, consist of the inhibitory PCs and the inhibitory BCs (basket cells). (The BCs were not considered in the original square-lattice network model for the EBC (Yamazaki and Tanaka 2007), while they were included in the later improved square-lattice network model for the OKR (Yamazaki and Nagao 2012).) The MF context signals for the EBC are fed from the pontine nucleus in the pons to the GR cells; each GR cell receives two transient and two sustained CS signals via four MFs (i.e., two pairs of transient and sustained CS signals are fed into each GR cell). Various temporal recoding is made in the granular layer via inhibitory coordination of GO cells on GR cells. Then, these various-recoded outputs are fed via PFs to the PCs and the BCs in the Purkinje-molecular layer.

Fig. 2.

Cerebellar ring network for the EBC. a Box diagram for the cerebellar network. Lines with triangles and circles represent excitatory and inhibitory synapses, respectively. GR (granule cell), GO (Golgi cell), and PF (parallel fiber) in the granular layer, PC (Purkinje cell) and BC (basket cell) in the Purkinje-molecular layer, and other parts for CN (cerebellar nuclei), IO(inferior olive), MF (mossy fiber), and CF (climbing fiber). b Schematic diagram for granular-layer ring network with concentric inner GR and outer GO rings. Numbers represent granular layer zones (bounded by dotted lines) for $N_C=32$. In each Ith zone ($I=1,\cdots ,N_C$), there exists the Ith GR cluster on the inner GR ring. Each GR cluster consists of GR cells (solid circles), and it is bounded by 4 glomeruli (stars). On the outer GO ring in the Ith zone, there exists the Ith GO cell (diamonds). c Schematic diagram for Purkinje-molecular-layer ring network with concentric inner PC and outer BC rings. Numbers represent the Purkinje-molecular-layer zones (bounded by dotted lines) for $N_{\mathrm{PC}}=16$. In each Jth zone, there exist the Jth PC (solid circle) on the inner PC ring and the Jth BC (solid triangle) on the outer BC ring

The PCs receive another excitatory error-teaching CF signals from the IO, along with the inhibitory inputs from the BCs. Then, depending on the type of PF signals (i.e., well- or ill-matched PF signals), various PF (student) signals are effectively depressed by the error-teaching (instructor) CF signals. Such “effective” depression at the PF-PC synapses coordinates firings of PCs effectively, which then exert effective inhibitory coordination on the CN neuron. The CN neuron also receives two excitatory signals; one transient and one sustained CS signals via MFs. In the earlier trials, the CN neuron can not fire, due to strong inhibition from the PCs. As the learning trial passes a threshold, the CN neuron starts firing, and then it exerts excitatory projections onto the eyeblink pre-motoneurons in the midbrain which then supply motor commands to eyeblink motoneurons. Thus, acquisition of CR begins (i.e., acquisition of learned eyeblink starts). This CN neuron also provides inhibitory inputs to the IO neuron which also receives the excitatory signals for the desired timing from the trigeminal nucleus. Then, the IO neuron supplies excitatory error-teaching CF signals to the PCs.

Figure 2b shows a schematic diagram for the granular-layer ring network with concentric inner GR and outer GO rings. Numbers represent granular-layer zones (bounded by dotted lines); the numbers 1, 2, $\cdots$, and $N_C$ represent the 1st, the 2nd, $\cdots$, and the $N_C$th granular-layer zones, respectively. Thus, the total number of granular-layer zones is $N_C$; Fig. 2b shows an example for $N_C=32$. In each Ith zone ($I=1,\cdots ,N_C$), there exists the Ith GR cluster on the inner GR ring. Each GR cluster consists of $N_{\mathrm{GR}}$ excitatory GR cells (solid circles). Then, location of each GR cell may be denoted by the two indices (I, i) which represent the ith GR cell in the Ith GR cluster, where $i=1,\cdots ,N_{\mathrm{GR}}$. Here, we consider the case of $N_C=2^{10}$ and $N_{\mathrm{GR}}=50$, and thus the total number of GR cells is 51,200. (For computational efficiency, $N_{\mathrm{GR}}$ is decreased from 100 in the square-lattice network (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012) to 50. Then, to keep the firing activity in the overall network, the connection probability from the GR to the GO cells is increased from 0.05 (Yamazaki and Nagao 2012)to 0.1, and the synaptic weights from the GR cells to the PCs and the BCs are increased from 0.003 to 0.006.) In this granular-layer ring network, the Ith zone covers the angular range of $(I-1){\theta }_{\mathrm{GR}}^{\ast }<\theta <I{\theta }_{\mathrm{GR}}^{\ast }$ (${\theta }_{\mathrm{GR}}^{\ast }=0.{35}^{\circ }$). On the outer GO ring in each Ith zone, there exists the Ith inhibitory GO cell (diamond), and thus the total number of GO cells is $N_C$.

We note that each GR cluster is bounded by 4 glomeruli (corresponding to the axon terminals of the MFs) (stars) at both boundaries of the GR cluster; at each boundary, a pair of glomeruli (upper and lower ones) exist. (We note that the number of glomeruli (=4), associated with each GR cluster, is the same as that in the square-lattice network where each GR cluster is bounded by 4 glomeruli located at 4 vertices of the square lattice for the GR cluster.) GR cells within each GR cluster share the same inhibitory and excitatory synaptic inputs through their dendrites which contact the four glomeruli at both ends of the GR cluster. Each glomerulus receives inhibitory inputs from nearby 81 (clockwise side: 41 and counter-clockwise side: 40) GO cells with a random connection probability $p_c(=0.029)$. Hence, on average, about 2 GO cell axons innervate each glomerulus. Thus, each GR cell receives about 9 inhibitory inputs through 4 dendrites which synaptically contact the glomeruli at both boundaries. In this way, each GR cell in the GR cluster shares the same inhibitory synaptic inputs from nearby GO cells through the intermediate glomeruli at both ends.

In addition, each GR cell shares the same four excitatory inputs via the four glomeruli at both boundaries, because a glomerulus receives an excitatory MF input. We note that transient CS signals are supplied via the two upper glomeruli, while sustained CS signals are fed through the two lower glomeruli. Here, we take into consideration stochastic variability of synaptic transmission from a glomerulus to GR cells, and supply independent Poisson spike trains with the same firing rate to each GR cell for the excitatory MF signals. In this GR-GO feedback system, each GO cell receives excitatory synaptic inputs through PFs from GR cells in the nearby 49 (central side: 1, clockwise side: 24 and counter-clockwise side: 24) GR clusters with a random connection probability 0.1. Hence, 245 PFs (i.e. GR cell axons) innervate a GO cell.

Figure 2c shows a schematic diagram for the Purkinje-molecular-layer ring network with concentric inner PC and outer BC rings. Numbers represent the Purkinje-molecular-layer zones (bounded by dotted lines). In each Jth zone ($J=1,\cdots ,N_{\mathrm{PC}}$), there exist the Jth PC (solid circles) on the inner PC ring and the Jth BC (solid triangles) on the outer BC ring. Here, we consider the case of $N_{\mathrm{PC}}=16,$ and thus the total numbers of PC and BC are 16, respectively. In this case, each Jth ($J=1,\cdots ,N_{\mathrm{PC}}$) zone covers the angular range of $(J-1){\theta }_{\mathrm{PC}}^{\ast }<\theta <J{\theta }_{\mathrm{PC}}^{\ast },$ where ${\theta }_{\mathrm{PC}}^{\ast }\simeq 22.5^{\circ }$ (corresponding to about 64 zones in the granular-layer ring network). We note that variously-recoded PFs innervate PCs and BCs. Each PC (BC) in the Jth Purkinje-molecular-layer zone receives excitatory synaptic inputs via PFs from all the GR cells in the 288 GR clusters (clockwise side: 144 and counter-clockwise side: 144 when starting from the angle $\theta =(J-1){\theta }_{\mathrm{PC}}^{\ast }$ in the granular-layer ring network). Thus, each PC (BC) is synaptically connected via PFs to the 14,400 GR cells (which corresponds to about 28 $\%$ of the total GR cells). In addition to the PF signals, each PC also receives inhibitory inputs from nearby 3 BCs (central side: 1, clockwise side: 1 and counter-clockwise side: 1) and excitatory error-teaching CF signal from the IO.

Here, for simplicity, we consider just one CN neuron and one IO neuron. Both excitatory inputs (corresponding to one transient and one sustained CS signals) via 2 MFs and inhibitory inputs from all the 16 PCs are fed into the CN neuron. Then, the CN neuron provides excitatory input to the eyeblink pre-motoneurons in the midbrain and also supplies inhibitory input to the IO neuron. One additional excitatory desired timing signal from the trigeminal nucleus is also fed into the IO neuron. Then, through integration of both excitatory and inhibitory inputs, the IO neuron provides excitatory error-teaching CF signals to the PCs.

Elements of the cerebellar ring network

As elements of the cerebellar ring network, we choose leaky integrate-and-fire (LIF) neuron models (Gerstner and Kistler 2002). Here, the LIF neuron models incorporate additional afterhyperpolarization (AHP) currents that determine refractory periods. This LIF neuron model is one of the simplest spiking neuron models. Because of its simplicity, it may be easily analyzed and simulated. Hence, it has been very popularly employed as a neuron model.

Dynamics of states of individual neurons in the X population are governed by the following equations:

$$\begin{array}{c}\hfill C_X\frac{d{v}_i^{(X)}}{\mathit{dt}}=-I_{L,i}^{(X)}-I_{AHP,i}^{(X)}+I_{\mathit{ext}}^{(X)}-I_{syn,i}^{(X)},i=1,\cdots ,N_X,\end{array}$$ 1

where $N_X$ is the total number of neurons in the X population, $X=$ GR and GO in the granular layer, $X=$ PC and BC in the Purkinje-molecular layer, and in the other parts $X=$ CN and IO. The state of the ith neuron in the X population at a time t (msec) is characterized by its membrane potential $v_i^{(X)}$ (mV), and $C_X$ (pF) denotes the membrane capacitance of the cells in the X population. The time-evolution of $v_i^{(X)}(t)$ is governed by 4 types of currents (pA) into the ith neuron in the X population; the leakage current $I_{L,i}^{(X)}$, the AHP current $I_{AHP,i}^{(X)}$, the external constant current $I_{\mathit{ext}}^{(X)}$ (independent of i), and the synaptic current $I_{syn,i}^{(X)}$.

We consider a single LIF neuron model [without the AHP current and the synaptic current in Eq. (1)] which describes a simple parallel resistor-capacitor circuit. Here, the leakage term is due to the resistor and the integration of the external current is due to the capacitor which is in parallel to the resistor. Thus, in Eq. (1), the 1st type of leakage current $I_{L,i}^{(X)}$ for the ith neuron in the X population is given by:

$$\begin{array}{c}\hfill I_{L,i}^{(X)}=g_L^{(X)}(v_i^{(X)}-V_L^{(X)}),\end{array}$$ 2

where $g_L^{(X)}$ and $V_L^{(X)}$ are conductance (nS) and reversal potential for the leakage current, respectively.

The ith neuron fires a spike when its membrane potential $v_i^{(X)}$ reaches a threshold $v_{\mathit{th}}^{(X)}$ at a time $t_{f,i}^{(X)}$. Then,the 2nd type of AHP current $I_{AHP,i}^{(X)}$ follows after firing (i.e., $t\ge t_{f,i}^{(X)}$):

$$\begin{array}{c}\hfill I_{AHP,i}^{(X)}=g_{\mathit{AHP}}^{(X)}(t)(v_i^{(X)}-V_{\mathit{AHP}}^{(X)})\mathrm{for}t\ge t_{f,i}^{(X)},\end{array}$$ 3

where $V_{\mathit{AHP}}^{(X)}$ is the reversal potential for the AHP current. The conductance $g_{\mathit{AHP}}^{(X)}(t)$ is given by an exponential-decay function:

$$\begin{array}{c}\hfill g_{\mathit{AHP}}^{(X)}(t)={\overline{g}}_{\mathit{AHP}}^{(X)}{e}^{-(t-t_{f,i}^{(X)})/{\tau }_{\mathit{AHP}}^{(X)}},\end{array}$$ 4

where ${\overline{g}}_{\mathit{AHP}}^{(X)}$ and ${\tau }_{\mathit{AHP}}^{(X)}$ are the maximum conductance and the decay time constant for the AHP current. As ${\tau }_{\mathit{AHP}}^{(X)}$ increases, the refractory period becomes longer.

The 3rd type of external constant current $I_{\mathit{ext}}^{(X)}$ for spontaneous firing is provided to only PCs because of their high spontaneous firing rate (Thach 1968; Häusser and Clark 1997). In Appendix A, Table 1 shows the parameter values for the capacitance $C_X$, the leakage current $I_L^{(X)}$, the AHP current $I_{\mathit{AHP}}^{(X)}$, and the external constant current $I_{\mathit{ext}}^{(X)}$. These values were adopted from physiological data (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012).

Three kinds of synaptic currents

Here, we are concerned about the 4th type of synaptic current $I_{syn,i}^{(X)}$ into the ith neuron in the X population in Eq. (1). It is composed of the following 3 kinds of synaptic currents:

$$\begin{array}{c}\hfill I_{syn,i}^{(X)}=I_{\mathrm{AMPA},i}^{(X,Y)}+I_{\mathrm{NMDA},i}^{(X,Y)}+I_{\mathrm{GABA},i}^{(X,Z)}.\end{array}$$ 5

Here, $I_{\mathrm{AMPA},i}^{(X,Y)}$ and $I_{\mathrm{NMDA},i}^{(X,Y)}$ are the excitatory AMPA ($\alpha$-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) receptor-mediated and NMDA (N-methyl-D-aspartate) receptor-mediated currents from the pre-synaptic source Y population to the post-synaptic ith neuron in the target X population. In contrast, $I_{\mathrm{GABA},i}^{(X,Z)}$ is the inhibitory $\mathrm{G}AB{A}_A$ ($\gamma$-aminobutyric acid type A) receptor-mediated current from the pre-synaptic source Z population to the post-synaptic ith neuron in the target X population.

As in the case of the AHP current, the R (= AMPA, NMDA, or GABA) receptor-mediated synaptic current $I_{R,i}^{(T,S)}$ from the pre-synaptic source S population to the ith post-synaptic neuron in the target T population is given by:

$$\begin{array}{c}\hfill I_{R,i}^{(T,S)}=g_{R,i}^{(T,S)}(t)(v_i^{(T)}-V_R^{(S)}),\end{array}$$ 6

where $g_{(R,i)}^{(T,S)}(t)$ and $V_R^{(S)}$ are synaptic conductance and synaptic reversal potential (determined by the type of the pre-synaptic source S population), respectively. We obtain the synaptic conductance $g_{R,i}^{(T,S)}(t)$ from:

$$\begin{array}{c}\hfill g_{R,i}^{(T,S)}(t)={\overline{g}}_R^{(T)}\sum _{j=1}^{N_S}{J}_{\mathit{ij}}^{(T,S)}{w}_{\mathit{ij}}^{(T,S)}{s}_j^{(T,S)}(t),\end{array}$$ 7

where ${\overline{g}}_R^{(T)}$ and $J_{\mathit{ij}}^{(T,S)}$ are the maximum conductance and the synaptic weight of the synapse from the jth pre-synaptic neuron in the source S population to the ith post-synaptic neuron in the target T population, respectively. The inter-population synaptic connection from the source S population (with $N_s$ neurons) to the target T population is given in terms of the connection weight matrix $W^{(T,S)}$ $\left(=,\left\{w_{\mathit{ij}}^{(T,S)}\right\}\right)$ where $w_{\mathit{ij}}^{(T,S)}=1$ if the jth neuron in the source S population is pre-synaptic to the ith neuron in the target T population; otherwise $w_{\mathit{ij}}^{(T,S)}=0$.

The post-synaptic ion channels are opened because of the binding of neurotransmitters (emitted from the source S population) to receptors in the target T population. The fraction of open ion channels at time t is represented by $s^{(T,S)}$. The time course of $s_j^{(T,S)}(t)$ of the jth neuron in the source S population is given by a sum of exponential-decay functions $E_R^{(T,S)}\left(t,-,t_f^{(j)}\right)$:

$$\begin{array}{c}\hfill s_j^{(T,S)}(t)=\sum _{f=1}^{F_j^{(S)}}{E}_R^{(T,S)}\left(t,-,t_f^{(j)}\right),\end{array}$$ 8

where $t_f^{(j)}$ and $F_j^{(S)}$ are the fth spike time and the total number of spikes of the jth neuron in the source S population, respectively. The exponential-decay function $E_R^{(T,S)}(t)$ (which corresponds to contribution of a pre-synaptic spike occurring at $t=0$ in the absence of synaptic delay) is given by:

$$\begin{array}{cc}\hfill E_R^{(T,S)}(t)=& e^{-t/{\tau }_R^{(T)}}\Theta (t)\mathrm{or}\hfill \end{array}$$ 9

$$\begin{array}{cc}\hfill =& (A_1{e}^{-t/{\tau }_{R,1}^{(T)}}+A_2{e}^{-t/{\tau }_{R,2}^{(T)}})\Theta (t),\hfill \end{array}$$ 10

where $\Theta (t)$ is the Heaviside step function: $\Theta (t)=1$ for $t\ge 0$ and 0 for $t<0$. Depending on the source and the target populations, $E_R^{(T,S)}(t)$ may be a type-1 single exponential-decay function of Eq. (9) or a type-2 dual exponential-decay function of Eq. (10). In the type-1 case, there exists one synaptic decay time constant ${\tau }_R^{(T)}$ (determined by the receptor on the post-synaptic target T population), while in the type-2 case, two synaptic decay time constants, ${\tau }_{R,1}^{(T)}$ and ${\tau }_{R,2}^{(T)}$ appear. In most cases, the type-1 single exponential-decay function of Eq. (9) appears, except for the two synaptic currents $I_{\mathrm{GABA}}^{(\mathrm{GR},\mathrm{GO})}$ and $I_{\mathrm{NMDA}}^{(\mathrm{GO},\mathrm{GR})}$.

In Appendix A, Tables 2, 3, and 4 show the parameter values for the maximum conductance ${\overline{g}}_R^{(T)}$, the synaptic weight $J_{\mathit{ij}}^{(T,S)}$, the synaptic reversal potential $V_R^{(S)}$, the synaptic decay time constant ${\tau }_R^{(T)}$, and the amplitudes $A_1$ and $A_2$ for the type-2 exponential-decay function in the granular layer, the Purkinje-molecular layer, and the other parts for the CN and IO, respectively. These values were adopted from physiological data (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012).

We also employ a rule for synaptic plasticity, based on the experimental result in (Safo and Regehr 2008). This rule is a refined one for the LTD in comparison with the rule used in (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012), the details of which will be explained in the Appendix B. Numerical integration of the governing Eq. (1) for the time-evolution of states of individual neurons, together with the update rule for synaptic plasticity of Eq. (34), is made by using the 2nd-order Runge-Kutta method with the time step 1 msec. In each realization, we choose random initial points $v_i^{(X)}(0)$ for the ith neuron in the X population with uniform probability in the range of $v_i^{(X)}(0)\in (V_L^{(X)}-5.0,V_L^{(X)}+5.0)$; the values of $V_L^{(X)}$ are given in Table 1.

Influence of various temporal recoding in gr clusters on learning for the pavlovian eyeblink conditioning

In this section, we investigate the influence of various temporal recoding of GR cells on learning for the EBC by changing the connection probability $p_c$ from the GO to the GR cells. First, we consider a case of $p_c=0.029$ where the firing patterns of the GR cells are the most various and the Pavlovian EBC learning is also the most efficient, which will be clearly shown in Figs. 14b and c3, respectively. In this case, we make a detailed dynamical classification of various firing patterns of the GR cells, and then make an intensive investigation on the influence of various firing patterns on the synaptic plasticity at the PF-PC synapses and the subsequent learning process in the PC-CN-IO system. Next, by changing $p_c$ we also investigate the effect of various temporal recoding of the GR cells on the EBC, and discuss dependence of the variety degree for firing patterns of the GR cells and the timing degree, the strength, and the (overall) learning efficiency degree of CR (i.e., learned eyeblink) on $p_c$.

Fig. 14.

Strong correlation between the variety degree $\mathcal{V}$ of the firing patterns and the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$. a Fractions of well-matched (solid circles) and ill-matched (open circles) firing groups versus the connection probability $p_c$. b Plot of variety degree $\mathcal{V}$ of the firing patterns in the GR clusters versus $p_c$. Plots of saturated c1 timing degree ${\mathcal{T}}_d^{\ast }$, c2strengths ${\mathcal{S}}^{\ast }$, and c3 learning efficiency degree ${\mathcal{L}}_e^{\ast }$ of the CR versus $p_c$. d Plot of ${\mathcal{L}}_e^{\ast }$ versus $\mathcal{V}$

Collective firing activity in the whole population of GR cells

Temporal recoding process is performed in the granular layer (corresponding to the input layer of the cerebellar cortex), composed of GR and GO cells (see Fig. 2). GR cells (principal output cells in the granular layer) receive excitatory context signals for the EBC via the MFs [see Figs. 1b1 and 1b2] and make various recoding of context signals through receiving effective inhibitory coordination of GO cells. Thus, variously recoded signals are fed into the PCs (principal output cells in the cerebellar cortex) via PFs.

We first consider the firing activity in the whole population of GR cells for $p_c=0.029$. Collective firing activity may be well visualized in the raster plot of spikes which is a collection of spike trains of individual neurons. As a collective quantity showing whole-population firing behaviors, we use an instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ which may be got from the raster plots of spikes (Brunel and Hakim 1999; Brunel 2000; Brunel and Wang 2003; Geisler et al. 2005; Brunel and Hansel 2006; Brunel and Hakim 2008; Wang 2010; Kim and Lim 2014). To get a smooth instantaneous whole-population spike rate, we employ the kernel density estimation (kernel smoother) (Shimazaki and Shinomoto 2010). Each spike in the raster plot is convoluted (or blurred) with a kernel function $K_h(t)$, and then a smooth estimate of instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ is got by averaging the convoluted kernel function over all spikes of GR cells in the whole population:

$$\begin{array}{c}\hfill R_{\mathrm{GR}}(t)=\frac{1}{N}\sum _{i=1}^N\sum _{s=1}^{n_i}{K}_h\left(t,-,t_s^{(i)}\right),\end{array}$$ 11

where $t_s^{(i)}$ is the sth spiking time of the ith GR cell, $n_i$ is the total number of spikes for the ith GR cell, and N is the total number of GR cells (i.e., $N=N_c·N_{\mathrm{GR}}=51,200$). As a kernel function $K_h(t)$, we use a Gaussian kernel function of band width h:

$$\begin{array}{c}\hfill K_h(t)=\frac{1}{\sqrt{2\pi }h}{e}^{-t^2/2h^2},-\infty <t<\infty .\end{array}$$ 12

Throughout the paper, the band width h of $K_h(t)$ is 10 msec.

Figure 3a shows a raster plot of spikes of ${10}^3$ randomly chosen GR cells. At the beginning of trial stage ($0<t<7$ msec), all GR cells fire spikes due to the effect of strong transient CS signal of 200 Hz. In the remaining part of the trial stage ($7<t<1000$ msec), GR cells make random repetition of transitions between active and inactive states because of sustained CS signal of 30 Hz, and thus they seem to exhibit various spiking trains. Time passage from the CS onsets may be represented by the various firing patterns of GR cells, which will be explained in details in Figs. 4 and 5. In the break stage ($1000<t<2000$ msec), GR cells fire very sparse spikes. For simplicity, only the raster plot in the range of $1000<t<1100$ msec is shown; the raster plot in a part of the preparatory stage (essentially the same as the break stage) ($-100<t<0$ msec), just before the 1st trial stage, is also shown. Figure 3b shows the instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ in the whole population of GR cells. $R_{\mathrm{GR}}(t)$ is basically in proportion to the transient and sustained CS inputs via MFs [see Figs. 1b1–1b2]. Thus, $R_{\mathrm{GR}}(t)$ is sharply peaked in the beginning of the trial stage due to the strong transient CS, and then it becomes nearly flat in the remaining part of the trial stage where the sustained CS is present. However, due to the inhibitory effect of GO cells, the overall firing rates are uniformly lowered as follows. The time-averaged whole-population spike rates $\overline{R_{\mathit{GR}}(t)}$ in the time intervals of $0<t<5$ msec, $5<t<1000$ msec, and $1000<t<2000$ msec are 155.4 Hz, 32.5 Hz, and 3.4 Hz, respectively.

Fig. 3.

Firing activity of GR cells in the case of $p_c$ (connection probability from GO to GR cells) = 0.029. a Raster plots of spikes of ${10}^3$ randomly chosen GR cells and b instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ in the whole population of GR cells for the 1st step in the learning process for the EBC. Plots of the activation degrees c1 A(t) in the whole population of GR cells and c2 $A^{(G)}(t)$ in the G firing group [$G(=w):$ well-matched (solid curve) and $G(=i):$ ill- matched (dotted curve)]. Plots of d1 instantaneous individual firing rate $f_{\mathrm{GR}}^{(i)}(t)$ for the active GR cells and d2 instantaneous population spike rate $f_{\mathrm{GR}}^{(p)}(t)$ in the whole population of GR cells

Fig. 4.

Various firing patterns in the GR clusters in the case of $p_c=0.029$. Raster plots of spikes and instantaneous cluster spike rates $R_{\mathit{GR}}^{(I)}(t)$ for various firing patterns. Six well-matched firing patterns in the Ith GR clusters; $I=$ a1 245, a2 174, a3 505, a4 722, a5 154, and a6 458. Four ill-matched firing patterns in the Ith GR cluster; $I=$ b1 288, b2 654, b3 411, and b4 1001. ${\mathcal{M}}^{(I)}$ represents the matching index of the firing pattern in the Ith GR cluster. Distribution of the reproducibility degree ${\mathcal{R}}^{(I)}$ in the c1 whole population and the c2 well- and c3 ill-matched firing groups. Bin size for the histograms in c1–c3 is 0.01

Fig. 5.

Characterization of various firing patterns in the GR clusters in the case of $p_c=0.029$. a Distribution of matching indices $\{{\mathcal{M}}^{(I)}\}$ in the whole population. b Fraction of well-matched and ill-matched firing groups. Distribution of matching indices $\{{\mathcal{M}}^{(I)}\}$ for the (c1) well- and (c2) the ill-matched firing groups. Bin size for the histograms in (a) and in (c1)–(c3) is 0.1. d Plots of reproducibility degree ${\mathcal{R}}^{(I)}$ versus ${\mathcal{M}}^{(I)}$ in the well-matched (${\mathcal{M}}^{(I)}>0$) and the ill-matched (${\mathcal{M}}^{(I)}<0)$ firing groups

We next consider the activation degree of GR cells. To examine it, we divide the whole learning step into bins. In the beginning of the trial stage ($0<t<10$ msec), we divide the time interval into small bins (bin size: 1 msec) to properly take into consideration the effect of strong transient CS; the effect of transient CS seems to persist until the 7th bin. Then, in the remaining trial stage ($10<t<1000$ msec), to use wide bins (bin size: 10 msec) seems to be sufficient for considering the effect of sustained CS. Thus, we obtain the activation degree $A_i$ for the active GR cells in the ith bin:

$$\begin{array}{c}\hfill A_i=\frac{N_{a,i}}{N}.\end{array}$$ 13

here, $N_{a,i}$ and $N(=51,200)$ are the number of active GR cells in the ith bin and the total number of GR cells, respectively. Figure 3c1 shows a plot of the activation degree A(t) in the whole population of GR cells. In the initial 7 bins ($0<t<7$ msec), $A=1$ due to the effect of strong transient CS. In the presence of sustained CS for $7<t<1000$ msec, the activation degree A decreases monotonically from 0.189 to 0.131. In this case, the time-averaged activation degree $\overline{A(t)}$ is 0.161. On the other hand, in the break stage ($1000<t<2000$ msec), the time-averaged activation degree $\overline{A(t)}$ is 0.011 and small variations occur, which may be regarded as nearly “silent” stage, in comparison with the trial stage.

The whole population of GR cells may be decomposed into two types of well-matched and ill-matched firing groups; details will be given in Figs. 4 and 5. Firing patterns in the well-matched (ill-matched) firing group are well (ill) matched with the airpuff US timing signal. In this case, the activation degree $A_i^{(G)}$ of active GR cells in the ith bin in the G firing group is given by:

$$\begin{array}{c}\hfill A_i^{(G)}=\frac{N_{a,i}^{(G)}}{N^{(G)}}.\end{array}$$ 14

here, $N_{a,i}^{(G)}$ and $N^{(G)}$ are the number of active GR cells in the ith bin and the total number of GR cells in the G firing group, respectively ($G=w$ and i for the well-matched and the ill-matched firing groups, respectively). The number of clusters, belonging to the well- and the ill-matched firing groups are 841 and 183, respectively, and hence $N^{(w)}=42,050$ and $N^{(i)}=9,150$ because $N_{\mathit{GR}}=50$ (number of GR cells in each cluster).

Figure 3c2 shows plots of activation degree $A^{(G)}(t)$ in the well-matched (solid line) and the ill-matched (dotted curve) firing groups. In the beginning of the trial stage [i.e., in the initial 7 bins ($0<t<7$ msec)], $A^{(G)}=1$, independently of the firing groups, due to the effect of strong transient CS. On the other hand, in the remaining trial stage ($7<t<1000$ msec) where the sustained CS is present, $A^{(G)}(t)$ varies, strongly depending on the type of firing groups. In the case of well-matched firing group, $A^{(w)}(t)$ decreases monotonically from 0.2 to 0.133, which is a little higher than A(t) in the whole population. In contrast, in the case of ill-matched firing group, $A^{(i)}(t)$ forms a well-shaped curve with a central “zero-bottom” with the time-averaged activation degree $\overline{A^{(i)}(t)}=5.32·{10}^{-4}$ for $330<t<580$ msec. Due to appearance of the central zero-bottom, contribution of the ill-matched firing group to A(t) in the whole population may be negligible in the range of $330<t<580$ msec. In the break stage ($1000<t<2000$ msec), the time-averaged activation degree $\overline{A^{(G)}(t)}=0.011$ ($G=w$ or i) with small variations, independently of the firing groups, which is the same as $\overline{A(t)}$ in the whole population.

In each ith bin, the contribution $C_i^{(G)}$ of each firing group to the activation degree $A_i$ in the whole population is given by the product of the fraction $F^{(G)}$ and the activation degree $A_i^{(G)}$ of the firing group:

$$\begin{array}{c}\hfill C_i^{(G)}=F^{(G)}·A_i^{(G)}=\frac{N_{a,i}^{(G)}}{N},\end{array}$$ 15

where $F^{(G)}=N^{(G)}/N$; $F^{(w)}=0.821$ ($82.1\%$) and $F^{(i)}=0.179$ ($17.9\%$) [see Fig. 5b]. Hence, we can easily get the contribution $C_i^{(G)}$ of each firing group by just multiplying $A_i^{(G)}$ in Fig. 3c2 with the fraction $F^{(G)}$. The sum of $C_i^{(G)}(t)$ over the well- and the ill-matched firing groups is just the activation degree $A_i(t)$ in the whole population (i.e., $A_i=C_i^{(w)}+C_i^{(i)}$). In this case, contribution $C_i^{(i)}$ of the ill-matched firing group becomes small due to both low activation degree $A_i^{(i)}$ and small fraction $F^{(i)}$. Particularly, because of existence of the central zero-bottom, contribution $C_i^{(i)}$ is negligibly small in the middle ($330<t<580$ msec) of the trial stage.

In the whole population, the activation degree A(t) showing decreasing tendency is in contrast to the instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ which is flat in the trial stage. To understand this discrepancy, we consider the bin-averaged instantaneous individual firing rate $f_{\mathrm{GR}}^{(i)}$ of active GR cells:

$$\begin{array}{c}\hfill f_{\mathrm{GR}}^{(i)}=\frac{N_{s,i}}{N_{a,i}\Delta t}.\end{array}$$ 16

here, $N_{s,i}$ is the number of spikes of GR cells in the ith bin, $N_{a,i}$ is the number of active GR cells in the ith bin, and $\Delta t$ is the bin size. Figure 3d1 shows a plot of $f_{\mathrm{GR}}^{(i)}(t)$ for the active GR cells. In the initial 7 bins ($0<t<7$ msec) of the trial stage where $A(t)=1$, $f_{\mathrm{GR}}^{(i)}(t)$ decreases very slowly from 155.6 to 155.3 Hz with the time t (i.e., the values of $f_{\mathrm{GR}}^{(i)}(t)$ are nearly the same). In the remaining part ($7<t<1000$ msec) of the trial stage, $f_{\mathrm{GR}}^{(i)}(t)$ increases monotonically from 173 to 258 Hz. In this case, the bin-averaged instantaneous population spike rate $f_{\mathrm{GR}}^{(p)}$ is given by the product of the activation degree $A_i$ of Eq. (13) and the instantaneous individual firing rate $f_{\mathrm{GR}}^{(i)}$ of Eq. (16):

$$\begin{array}{c}\hfill f_{\mathrm{GR}}^{(p)}=A_i{f}_{\mathrm{GR}}^{(i)}=\frac{N_{s,i}}{N\Delta t}.\end{array}$$ 17

Figure 3d2 shows a plot of the instantaneous population spike rate $f_{\mathrm{GR}}^{(p)}(t)$. It is flat except for the sharp peak in the beginning of the trial stage, as in the case of $R_{\mathrm{GR}}(t)$. We note that both $f_{\mathrm{GR}}^{(p)}(t)$ and $R_{\mathrm{GR}}(t)$ correspond to bin-based estimate and kernel-based smooth estimate for the instantaneous whole-population spike rate of the GR cells, respectively (Kim and Lim 2014). Although the activation degree A(t) of GR cells decreases with t, their population spike rate keeps the flatness (i.e., $f_{\mathrm{GR}}^{(p)}(t)$ becomes flat), because of the increase in the individual firing rate $f_{\mathrm{GR}}^{(i)}(t)$. As a result, the bin-averaged instantaneous population spike rate $f_{\mathrm{GR}}^{(p)}(t)$ in Fig. 3d2 becomes essentially equal to the instantaneous whole-population spike rate $R_{\mathrm{GR}}(t)$ in Fig. 3b.

Dynamical classification and dynamical origin of various firing patterns in the GR clusters

There exist $N_C(=2^{10})$ GR clusters in the whole population. $N_{\mathrm{GR}}(=50)$ GR cells in each GR cluster share the same inhibitory and excitatory inputs via their dendrites which synaptically contact the four glomeruli (i.e., terminals of MFs) at both ends of the GR cluster [see Fig. 2b]. Nearby inhibitory GO cell axons innervate the four glomeruli. Due to the shared inputs, GR cells in each GR cluster exhibit similar firing behaviors.

As in the case of $R_{\mathrm{GR}}(t)$ in Eq. (11), the firing activity of the Ith GR cluster is described in terms of its instantaneous cluster spike rate $R_{\mathrm{GR}}^{(I)}(t)$ ($I=1,\cdots ,N_C$):

$$\begin{array}{c}\hfill R_{\mathrm{GR}}^{(I)}(t)=\frac{1}{N_{\mathrm{GR}}}\sum _{i=1}^{N_{\mathrm{GR}}}\sum _{s=1}^{n_i^{(I)}}{K}_h\left(t,-,t_s^{(I,i)}\right),\end{array}$$ 18

where $t_s^{(I,i)}$ is the sth firing time of the ith GR cell in the Ith GR cluster and $n_i^{(I)}$ is the total number of spikes for the ith GR cell in the Ith GR cluster.

We introduce the matching index ${\mathcal{M}}^{(I)}$ of each GR cluster between the firing behavior $\left[R_{\mathrm{GR}}^{(I)},(t)\right]$ of each Ith GR cluster and the airpuff US signal $f_{\mathrm{US}}(t)$ for the desired timing [see Fig.1c]. The matching index ${\mathcal{M}}^{(I)}$ is given by the cross-correlation at the zero-time lag [i.e., $Cor{r}_{\mathrm{GR}}^{(I)}(0)$] between $R_{\mathrm{GR}}^{(I)}(t)$ and $f_{\mathrm{US}}(t)$:

$$\begin{array}{c}\hfill Cor{r}_{\mathrm{GR}}^{(I)}(\tau )=\frac{\overline{\Delta f_{\mathrm{US}}(t+\tau )\Delta R_{\mathrm{GR}}^{(I)}(t)}}{\sqrt{\overline{\Delta f_{\mathrm{US}}^2(t)}}\sqrt{\overline{{\Delta R_{\mathrm{GR}}^{(I)}}^2(t)}}},\end{array}$$ 19

where $\Delta f_{\mathrm{US}}(t)=f_{\mathrm{US}}(t)-\overline{f_{\mathrm{US}}(t)}$, $\Delta R_{\mathrm{GR}}^{(I)}(t)=R_{\mathrm{GR}}^{(I)}(t)-\overline{R_{\mathrm{GR}}^{(I)}(t)}$, and the overline denotes the time average. We note that ${\mathcal{M}}^{(I)}$ represents well the phase difference between the firing patterns $\left[R_{\mathrm{GR}}^{(I)},(t)\right]$ of GR clusters and the US signal [$f_{\mathrm{US}}(t)$].

Figure 4 shows various firing patterns of GR clusters. This type of variety results from inhibitory coordination of GO cells on the firing activity of GR cells in the GR-GO feedback loop in the granular layer. Time passage from the CS onsets may be well represented by the various firing patterns of GR clusters because MF inputs become less similar (i.e., more orthogonal) to each other through recoding in the granular layer.

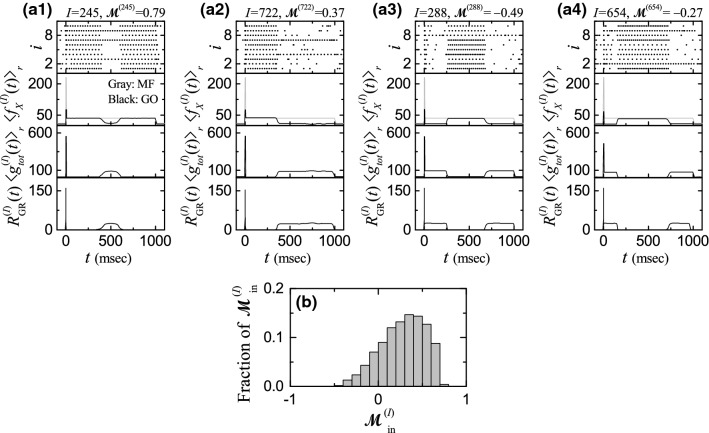
Six examples for the well-matched firing patterns in the Ith ($I=$ 245, 174, 505, 722, 154, and 458) GR clusters are given in Figs. 4a1–a6, respectively. Raster plot of spikes of $N_{\mathrm{GR}}(=50)$ GR cells and the corresponding instantaneous cluster spike rate $R_{\mathrm{GR}}^{(I)}(t)$ are shown, along with the value of the matching index ${\mathcal{M}}^{(I)}$ in each case of the Ith GR cluster. In all these cases, the instantaneous cluster spike rates $R_{\mathrm{GR}}^{(I)}(t)$ are well-matched with the US signal $f_{\mathrm{US}}(t)$, and hence these well-matched GR clusters have positive matching indices (i.e., ${\mathcal{M}}^{(I)}>0$).

In the 1st case of $I=245$ with the highest ${\mathcal{M}}^{(I)}$ $(=0.79)$, $R_{\mathrm{GR}}^{(245)}(t)$ is strongly localized around the middle of the trial stage (i.e. a central band of spikes is formed around $t=500$ msec), and hence it is the most well-matched with the US signal $f_{\mathrm{US}}(t)$. In the 2nd case of $I=174$ with ${\mathcal{M}}^{(I)}=0.73,$ $R_{\mathrm{GR}}^{(174)}(t)$ is also localized around $t=500$ msec, but its central firing band spreads a little more to the left side, in comparison with the case of $I=245$. Hence, its matching index relative to $f_{\mathrm{US}}(t)$ is a little decreased.

We note that LTD at the PF-PC synapses occurs within an effective range of $\Delta t_l^{\ast }(\simeq -117.5)<\Delta t<\Delta t_r^{\ast }(\simeq 277.5)$ (see Fig. 3 in Ref. (Kim and Lim 2021)). Here, $\Delta t$ [= $t_{\mathrm{CF}}$ (CF activation time) - $t_{\mathrm{PF}}$ (PF activation time)] is the relative time difference between the firing times of the error-teaching instructor CF and the variously-recoded student PF. The CF activation occurs approximately at $t_{\mathrm{CF}}=500$ msec due to the strong brief US (strongly localized at $t=500$ msec). Then, LTD may occur when the PF activation time $t_{\mathrm{PF}}$ lies in an effective LTD range of 222.5 msec $<t_{\mathrm{PF}}<$ 617.5 msec. In the above two cases of GR clusters ($I=$ 245 and 174) with higher ${\mathcal{M}}^{(I)}$, their PF signals (corresponding to axons of the GR cells) are strongly depressed by the instructor CF signal because most parts of their firing bands are well localized in the effective LTD range.

We next consider the 3rd and the 4th cases of the Ith GR cluster ($I=$ 505 and 722) with intermediate ${\mathcal{M}}^{(I)}$. In the cases of $I=505$ (722), the firing band in the raster plot extends to the left (right) until $t\simeq 0(1000)$ msec. Thus, big left- and right-extended firing bands appear for $I=505$ and 722, respectively. Some part of this big firing band lies inside the effective LTD range where LTD occurs in conjunction with the CF firing. On the other hand, its remaining part lies outside the effective LTD range, and hence LTP occurs for the PF firings alone without association with the CF signal.

We also consider the case of lower ${\mathcal{M}}^{(I)}$ for $I=154$ and 458 (i.e., the 5th and the 6th cases). In both cases, they have tendency to fill the raster plots with more spikes via appearance of two or more firing bands. Thus, some central part of these bands lies inside the effective LTD range where LTD occurs. In contrast, LTP occurs in the other left and right parts of the firing bands because they lie outside the effective LTD range; in comparison with the case of intermediate ${\mathcal{M}}^{(I)}$, LTP region is extended. In this way, as ${\mathcal{M}}^{(I)}$ is decreased toward the zero, the raster plot tends to be filled with more spikes (constituting firing bands), and hence the region where LTP occurs is extended.

In addition to the well-matched firing patterns, ill-matched firing patterns with negative matching indices (i.e., ${\mathcal{M}}^{(I)}<0$) also appear. Four examples for the ill-matched firing patterns in the Ith ($I=$ 288, 654, 411, and 1001) GR clusters are given in Figs. 4b1–b4, respectively. We first consider the case of $I=288$ with the lowest ${\mathcal{M}}^{(I)}(=-0.49)$ (i.e., its magnitude $|{\mathcal{M}}^{(I)}|$: largest). This lowest case corresponds to the “opposite” case of the highest one for $I=245$ with ${\mathcal{M}}^{(I)}=0.79$ in the following sense. A central gap with negligibly small number of spikes (i.e., practically no spikes) appears around $t=500$ msec, in contrast to the highest case where a central firing band exists. Hence, in this lowest case, occurrence of LTD in the central gap may be practically negligible. On the other hand, mainly LTP occurs in the left and right firing bands, most of which lie outside the effective LTD range. The right firing band lies completely outside the effective LTD range, and hence no LTD occurs. The width of the central gap is larger than the width of the effective LTD range. However, since the gap is shifted a little to the right, a small part near the right boundary ($t\simeq 261$ msec) of the left firing band overlaps with a small region near the left boundary ($t\simeq 222.5$ msec) of the effective LTD region. In this small overlapped region of $239<\Delta t<277.5$ msec, the values of the synaptic modification $\Delta J_{\mathrm{LTD}}$ (i.e., the average synaptic modification $⟨\Delta J_{\mathrm{LTD}}⟩\simeq 0.031$) are very small, and hence very weak LTD may occur.

As the magnitude $|{\mathcal{M}}^{(I)}|$ is decreased, the central gaps becomes widened, and the widths of the left and the right firing bands also get decreased, as shown in the cases of $I=654$, 411, and 1001. In these cases, the two left and right firing bands lie completely outside the effective LTD range, and hence only LTP occurs for the PF signals alone without conjunction with the CF signal. In this way, as $|{\mathcal{M}}^{(I)}|$ approaches the zero from the negative side, spikes become more and more sparse, which is in contrast to the well-matched case where more and more spikes fill the raster plot as ${\mathcal{M}}^{(I)}$ goes to the zero from the positive side.

The above firing patterns are shown in the 1st learning step [consisting of the 1st trial stage ($0<t<1000$ msec) and the 1st break stage ($1000<t<2000$ msec)]. For simplicity, they are shown in the range of $1000<t<1100$ msec in the break stage, and a part of the preliminary stage ($-100<t<0$ msec), preceding the 1st learning step, is also shown. We examine the reproducibility of the firing patterns across the learning steps. To this end, we consider the cross-correlation between the instantaneous cluster spike rates $R_{\mathrm{GR}}^{(I,l)}(t)$ in the Ith GR cluster for the kth ($l=k$) and the $(k+1)$th ($l=k+1$) learning steps;

$$\begin{array}{c}\hfill Cor{r}_{\mathrm{GR}}^{(I,k)}(\tau )=\frac{\overline{\Delta R_{\mathrm{GR}}^{(I,k)}(t+\tau )\Delta R_{\mathrm{GR}}^{(I,k+1)}(t)}}{\sqrt{\overline{{\Delta R_{\mathrm{GR}}^{(I,k)}}^2(t)}}\sqrt{\overline{{\Delta R_{\mathrm{GR}}^{(I,k+1)}}^2(t)}}},\end{array}$$ 20

where $\Delta R_{\mathrm{GR}}^{(I,l)}(t)=R_{\mathrm{GR}}^{(I,l)}(t)-\overline{R_{\mathrm{GR}}^{(I,l)}(t)}$ ($l=k$ and $k+1$) and the overline represents the time average. Then, the reproducibility degree ${\mathcal{R}}^{(I)}$ of the Ith GR cluster is given by the average value of the cross-correlations at the zero-time lag between the instantaneous cluster spike rates $R_{\mathrm{GR}}^{(I,l)}(t)$ for the successive learning steps:

$$\begin{array}{c}\hfill {\mathcal{R}}^{(I)}=\frac{1}{N_{\mathrm{step}}-1}\sum _{k=1}^{N_{\mathrm{step}}-1}Cor{r}_{\mathrm{GR}}^{(I,k)}(0),\end{array}$$ 21

where $N_{\mathrm{step}}$ is the total number of learning steps. Here, we consider the case of $N_{\mathrm{step}}=100$.

Figure 4c1 shows the distribution of the reproducibility degrees ${\mathcal{R}}^{(I)}$ for the whole GR clusters. Double peaks appear; large broad peak and small sharp peaks at ${\mathcal{R}}^{(I)}=0.925$ and 0.815, respectively. The range of ${\mathcal{R}}^{(I)}$ is (0.812, 0.997). Hence, the firing patterns are highly reproducible across the learning steps. Figure 4c2 and c3 also show the distributions of ${\mathcal{R}}^{(I)}$ of the GR clusters in the well- and the ill-matched firing groups, respectively. In the case of well-matched firing group, the distribution of ${\mathcal{R}}^{(I)}$ has a broad peak and its range is (0.842, 0.997). On the other hand, in the ill-matched case, the distribution decreases from its maximum at ${\mathcal{R}}^{(I)}=0.815$, and its range is (0.812, 0.879). We note that the average values of $\{{\mathcal{R}}^{(I)}\}$ in the well- and the ill-matched firing group are 0.927 and 0.828, respectively. Hence, on average, the firing patterns of the GR clusters in the well-matched firing group may be more reproducible than those in the ill-matched firing group, because the average individual firing rate in the well-matched firing group is higher than that in the ill-matched firing group.

Results on characterization of the various well- and ill-matched firing patterns are given in Fig. 5. Figure 5a shows the plot of the fraction of matching indices ${\mathcal{M}}^{(I)}$ in the whole GR clusters. ${\mathcal{M}}^{(I)}$ increases slowly from the negative value to the peak at 0.35, and then it decreases rapidly. For this distribution of $\{{\mathcal{M}}^{(I)}\}$, the range is (-0.49, 0.79), the mean is 0.3331, and the standard deviation is 0.6135. Then, we obtain the variety degree $\mathcal{V}$ for the firing patterns [$R_{\mathrm{GR}}^{(I)}(t)$] of all the GR clusters:

$$\begin{array}{c}\hfill \mathcal{V}=\mathrm{Relative}\mathrm{Standard}\mathrm{Deviation}\mathrm{for}\mathrm{the}\mathrm{Distribution}\mathrm{of}\{{\mathcal{M}}^{(I)}\},\end{array}$$ 22

where the relative standard deviation is just the standard deviation divided by the mean. In the case of $p_c=0.029$, $\mathcal{V}\simeq 1.842$, which is just a quantitative measure for the various recoding made through feedback cooperation between the GR and the GO cells in the granular layer. It will be seen that the value of $\mathcal{V}(\simeq 1.842)$ for $p_c=0.029$ is just the maximum in Fig. 14b for the plot of $\mathcal{V}$ versus $p_c$. Hence, firing patterns of the GR clusters for $p_c=0.029$ is the most various.

We decompose the whole GR clusters into the well-matched ($\{{\mathcal{M}}^{(I)}\}>0$) and the ill-matched ($\{{\mathcal{M}}^{(I)}\}<0$) firing groups. Figure 5b shows the fraction of firing groups. The well-matched firing group is a major one with fraction 82.1$\%$, while the ill-matched firing group is a minor one with fraction 17.9$\%$. In this case, the firing-group ratio ${\mathcal{R}}_{\mathrm{sp}}$, given by the ratio of the fraction of the well-matched firing group to that of the ill-matched firing group is 4.59. For this firing-group ratio, firing patterns of the GR clusters are the most various.

Figures 5c1–c2 also show the plots of matching indices ${\mathcal{M}}^{(I)}$ of the GR clusters in the well- and the ill-matched firing groups, respectively. In the case of well-matched firing group, the distribution of ${\mathcal{M}}^{(I)}$ with a peak at 0.35 has only positive values in the range of (0.0, 0.79), and its mean and standard deviations are 0.428 and 0.372, respectively. On the other hand, in the case of the ill-matched firing group, the distribution of ${\mathcal{M}}^{(I)}$ with a maximum at -0.05 has only negative values in the range of $(-0.49,0.0)$, and its mean and standard deviations are $-$ 0.104 and 0.129, respectively. In this case, ${\mathcal{M}}^{(I)}$ increases slowly to the maximum. As will be seen in the next subsection, these well- and the ill-matched firing groups play their own roles in the synaptic plasticity at PF-PC synapses and the subsequent learning process for the EBC, respectively.

We also examine the correlation between the matching index ${\mathcal{M}}^{(I)}$ and the reproducibility degree ${\mathcal{R}}^{(I)}$. Figure 5d show the plots of ${\mathcal{M}}^{(I)}$ versus ${\mathcal{R}}^{(I)}$ in the well- and the ill-matched firing groups. In both cases, there appear strong negative correlations between ${\mathcal{M}}^{(I)}$ and ${\mathcal{R}}^{(I)}$; for the well-matched (ill-matched) firing group, the Pearson’s correlation coefficient is $r=-0.9999(-0.9978)$. When left-right reflections are made on Figs. 5c1–c2, shapes of the reflected ones are similar to the shapes of Figs. 4c2–c3, respectively, which implies the negative correlation between ${\mathcal{M}}^{(I)}$ and ${\mathcal{R}}^{(I)}$ in each firing group. As shown in Figs. 4a1–a6, as ${\mathcal{M}}^{(I)}$ decreases to the zero from the positive side, the raster plot tends to be filled with more spikes due to increased individual firing rates, which leads to increase in ${\mathcal{R}}^{(I)}$. On the other hand, as ${\mathcal{M}}^{(I)}$ increases to the zero from the negative side, the raster plot of spikes tends to be more sparse because of decreased individual firing rates [see Figs. 4b1–b4], which results in decrease in ${\mathcal{R}}^{(I)}$. Consequently, there appears a gap at the limit ${\mathcal{M}}^{(I)}=0$.

Finally, we study the dynamical origin of various firing patterns in the Ith GR clusters. As examples, we consider two well-matched firing patterns for $I=245$ and 722 [see the firing patterns in Figs. 4a1 and a4] and two ill-matched firing patterns for $I=288$ and 654 [see the firing patterns Figs. 4b1 and b2]. In Fig. 6a1–a4 correspond to the cases of $I=$245, 722, 288, and 654, respectively.

Fig. 6.

Dynamical origin of various firing patterns in the GR clusters in the case of $p_c=0.029$. Well-matched firing patterns for I= (a1) 245 and (a2) 722 and ill-matched firing patterns for I= (a3) 288 and (a4) 654. In a1–a4, top panel: raster plots of spikes in the sub-population of pre-synaptic GO cells innervating the Ith GR cluster, 2nd panel: plots of $f_X^{(I)}(t):$ bin-averaged instantaneous spike rates of the MF signals ($X=\mathrm{MF}$) into the Ith GR cluster (gray line) and bin-averaged instantaneous spike rates of the sub-population of pre-synaptic GO cells ($X=\mathrm{GO}$) innervating the Ith GR cluster (black line); ${⟨\cdots ⟩}_r$ represents the realization average (number of realizations is 100), 3rd panel: time course of ${⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r:$ conductance of total synaptic inputs (including both the excitatory and inhibitory inputs) into the Ith GR cluster, and bottom panel: plots of $R_{\mathrm{GR}}^{(I)}(t):$ instantaneous cluster spike rate in the Ith GR cluster. (b) Distribution of matching indices $\{{\mathcal{M}}_{\mathrm{in}}^{(I)}\}$ for the conductances of total synaptic inputs into the GR clusters

Various recodings for the MF signals are made in the GR layer, consisting of excitatory GR and inhibitory GO cells (i.e., in the GR-GO cell feedback loop). Thus, firing activities of GR cells are determined by two types of synaptic input currents (i.e., excitatory synaptic inputs via MF signals and inhibitory synaptic inputs from randomly connected GO cells). Then, investigations on the dynamical origin of various firing patterns of the GR clusters are made via analysis of total synaptic inputs into the GR clusters. As in Eq. (6), synaptic current is given by the product of synaptic conductance g and potential difference. In this case, synaptic conductance determines the time-course of synaptic current. Hence, it is sufficient to consider the time-course of synaptic conductance. The synaptic conductance g is given by the product of synaptic strength per synapse, the number of synapses $M_{\mathrm{syn}}$, and the fraction s of open (post-synaptic) ion channels [see Eq. (7)]. Here, the synaptic strength per synapse is given by the product of maximum synaptic conductance $\overline{g}$ and synaptic weight J, and the time-course of s(t) is given by a summation for exponential-decay functions over pre-synaptic spikes, as shown in Eqs. (7) and (8).

Here, we make an approximation of the fraction s(t) of open ion channels (i.e., contributions of summed effects of pre-synaptic spikes) by the bin-averaged spike rate $f_X^{(I)}(t)$ of pre-synaptic neurons ($X=$ MF and GO); $f_{\mathrm{MF}}^{(I)}(t)$ is the bin-averaged spike rate of the MF signals into the Ith GR cluster and $f_{\mathrm{GO}}^{(I)}(t)$ is the bin-averaged spike rate of the pre-synaptic GO cells innervating the Ith GR cluster. In the case of MF signal, we get:

$$\begin{array}{c}\hfill f_{\mathrm{MF}}^{(I)}(t)=f_{\mathrm{TCS}}^{(I)}(t)+f_{\mathrm{SCS}}^{(I)}(t),\end{array}$$ 23

where $f_{\mathrm{TCS}}^{(I)}(t)$ and $f_{\mathrm{SCS}}^{(I)}(t)$ are the bin-averaged spike rates of the transient and the sustained CS signals, respectively.

Then, the conductance $g_X^{(I)}(t)$ of synaptic input from X (=MF or GO) into the Ith GR cluster ($I=1,\cdots ,N_C$) is given by:

$$\begin{array}{c}\hfill g_X^{(I)}(t)\simeq {\mathrm{M}}_f^{(R)}·f_X^{(I)}(t).\end{array}$$ 24

here, the multiplication factor ${\mathrm{M}}_f^{(R)}$ [= maximum synaptic conductance ${\overline{g}}_R$ $\times$ synaptic weight $J^{(\mathrm{GR},X)}$ $\times$ number of synapses $M_{\mathrm{syn}}^{(\mathrm{GR},X)}$] varies depending on X and the receptor R on the post-synaptic GR cells. In the case of excitatory synaptic currents into the Ith GR cluster with AMPA receptors via TCS or SCS MF signal, ${\mathrm{M}}_f^{(\mathrm{AMPA})}=2.88;$ ${\overline{g}}_{\mathrm{AMPA}}=0.18,$ $J^{(\mathrm{GR},\mathrm{MF})}=8.0,$ and $M_{\mathrm{syn}}^{(\mathrm{GR},X)}=2$ (X=TCS, SCS). On the other hand, in the case of the Ith GR cluster with NMDA receptors, ${\overline{g}}_{\mathrm{NMDA}}=0.025,$ and hence ${\mathrm{M}}_f^{(\mathrm{N}MDA)}=0.4,$ which is much less than ${\mathrm{M}}_f^{(\mathrm{A}MPA)}$. For the inhibitory synaptic current from pre-synaptic GO cells to the Ith GR cluster with GABA receptors, ${\mathrm{M}}_f^{(\mathrm{G}ABA)}=2.63$; ${\overline{g}}_{\mathrm{GABA}}=0.028,$ $J^{(\mathrm{GR},\mathrm{GO})}=10,$ and $M_{\mathrm{syn}}^{(\mathrm{GR},\mathrm{GO})}=9.4.$ Then, the conductance $g_{\mathit{tot}}^{(I)}$ of total synaptic inputs (including both the excitatory and the inhibitory inputs) into the Ith GR cluster is given by:

$$\begin{array}{cc}\hfill g_{\mathit{tot}}^{(I)}(t)=& g_{\mathrm{MF}}^{(I)}-g_{\mathrm{GO}}^{(I)}=g_{\mathrm{AMPA}}^{(I)}+g_{\mathrm{NMDA}}^{(I)}-g_{\mathrm{GO}}^{(I)}\hfill \\ \hfill =& 3.28f_{\mathrm{MF}}^{(I)}(t)-2.63f_{\mathrm{GO}}^{(I)}(t).\hfill \end{array}$$ 25

In Figs. 6a1–a4, the top panels show the raster plots of spikes in the sub-populations of pre-synaptic GO cells innervating the Ith GR clusters. From these raster plots, bin-averaged (sub-population) spike rates $f_{\mathrm{GO}}^{(I)}(t)$ may be obtained. The bin-averaged spike rate of pre-synaptic GO cells in the ith bin is given by $\frac{n_i^{(s)}}{N_{\mathit{pre}}\Delta t}$, where $n_i^{(s)}$ is the number of spikes in the ith bin, $\Delta t$ is the bin size, and $N_{\mathit{pre}}$ (=10) is the number of pre-synaptic GO cells. As in Fig. 3, in the beginning of the trial stage ($0<t<10$ msec), we employ the small bin-size of $\Delta t=1$ msec to properly take into consideration the effect of strong transient CS, and in the remaining trial stage ($10<t<1000$ msec), we use the wide bin-size of $\Delta t=10$ msec for considering the effect of sustained CS. Through an average over 100 realizations, we obtain the realization-averaged (bin-averaged) spike rate of pre-synaptic GO cells ${〈f_{\mathrm{GO}}^{(I)},(t)〉}_r$ because $N_{\mathit{pre}}(=10)$ is small; ${⟨\cdots ⟩}_r$ represent a realization-average. The 2nd panels show ${〈f_{\mathrm{GO}}^{(I)},(t)〉}_r$ (black line) and ${〈f_{\mathrm{MF}}^{(I)},(t)〉}_r$ (gray line). We note that $〈f_{\mathrm{GO}}^{(I)},(t)〉$ varies depending on I, while $〈f_{\mathrm{MF}}^{(I)},(t)〉$ is independent of I. Then, we obtain the realization-averaged conductance ${〈g_{\mathit{tot}}^{(I)},(t)〉}_r$ of total synaptic inputs in Eq. (25), which is shown in the 3rd panels.

We note that the shapes of ${〈g_{\mathit{tot}}^{(I)},(t)〉}_r$ (corresponding to the total input into the Ith GR cluster) in the 3rd panels are nearly the same as those of $R_{\mathrm{GR}}^{(I)}(t)$ (corresponding to the output of the Ith GR cluster) in the bottom panels. It is thus expected that well-matched (ill-matched) inputs into the GR clusters may lead to generation of well-matched (ill-matched) outputs (i.e., responses) in the GR clusters. To confirm this point clearly, as in case of the firing patterns $\left[R_{\mathrm{GR}}^{(I)},(t)\right]$ in the GR clusters, we introduce the matching index for the total synaptic input of the Ith GR cluster between ${〈g_{\mathit{tot}}^{(I)},(t)〉}_r$ (conductance of total synaptic input into the Ith GR cluster) and the (airpuff) US signal $f_{\mathrm{US}}(t)$ for the desired timing. Similar to the matching index ${\mathcal{M}}^{(I)}$ for the firing patterns (i.e. outputs) in the Ith GR cluster [see Eq. (19)], the matching index ${\mathcal{M}}_{\mathrm{in}}^{(I)}$ for the total synaptic input is given by the cross-correlation at the zero-time lag (i.e., $Cor{r}_{\mathrm{in}}^{(I)}(0)$) between ${〈g_{\mathit{tot}}^{(I)},(t)〉}_r$ and $f_{\mathrm{US}}(t)$:

$$\begin{array}{c}\hfill Cor{r}_{\mathrm{in}}^{(I)}(\tau )=\frac{\overline{\Delta f_{\mathrm{US}}(t+\tau )\Delta {⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r}}{\sqrt{\overline{\Delta f_{\mathrm{US}}^2(t)}}\sqrt{\overline{{\Delta {⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r}^2}}},\end{array}$$ 26

where $\Delta f_{\mathrm{US}}(t)=f_{\mathrm{US}}(t)-\overline{f_{\mathrm{US}}(t)}$, $\Delta {⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r={⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r-\overline{{⟨g_{\mathit{tot}}^{(I)}(t)⟩}_r}$, and the overline represents the time average. Thus, we have two types of matching indices, ${\mathcal{M}}^{(I)}$ [output matching index: given by $Cor{r}_{\mathrm{GR}}^{(I)}(0)$] and ${\mathcal{M}}_{\mathrm{in}}^{(I)}$ [input matching index: given by $Cor{r}_{\mathrm{in}}^{(I)}(0)$] for the output and the input in the Ith GR cluster, respectively.

Figure 6b shows the plot of fraction of input matching indices $\left\{{\mathcal{M}}_{\mathrm{in}}^{(I)}\right\}$ in the whole GR clusters. We note that the distribution of input matching indices in Fig. 6b is nearly the same as that of output matching indices in Fig. 5a. ${\mathcal{M}}_{\mathrm{in}}^{(I)}$ increases slowly from the negative value to the peak at 0.35, and then it decreases rapidly. In this distribution of $\left\{{\mathcal{M}}_{\mathrm{in}}^{(I)}\right\}$, the range is ($-$ 0.49, 0.79), the mean is 0.3332, and the standard deviation is 0.6137. Then, we get the variety degree ${\mathcal{V}}_{\mathrm{in}}$ for the total synaptic inputs $\left\{{〈g_{\mathit{tot}}^{(I)},(t)〉}_r\right\}$ of all the GR clusters:

$$\begin{array}{c}\hfill {\mathcal{V}}_{\mathrm{in}}=\mathrm{Relative}\mathrm{Standard}\mathrm{Deviation}\mathrm{for}\mathrm{the}\mathrm{Distribution}\mathrm{of}\{{\mathcal{M}}_{\mathrm{in}}^{(I)}\}.\end{array}$$ 27

hence, ${\mathcal{V}}_{\mathrm{in}}\simeq 1.842$ for the synaptic inputs, which is nearly the same as $\mathcal{V}(\simeq 1.842)$ for the firing patterns of GR cells. Consequently, various synaptic inputs into the GR clusters results in generation of various outputs (i.e., firing patterns) of the GR cells.

Influence of various temporal recoding on synaptic plasticity at PF-PC synapses

Based on dynamical classification of firing patterns of GR clusters, we study the influence of various temporal recoding in the GR clusters on synaptic plasticity at PF-PC synapses. As shown in the preceding subsection, MF context input signals for the EBC are variously recoded in the granular layer (corresponding to the input layer of the cerebellar cortex). The variously-recoded well- and ill-matched PF (student) signals (coming from the GR cells) are fed into the PCs (i.e., principal cells of the cerebellar cortex) and the BCs in the Purkinje-molecular layer. The PCs also receive well-matched error-teaching (instructor) CF signals from the IO, together with the inhibitory inputs from the BCs. Then, the synaptic weights at the PF-PC synapses vary depending on the matching degree between the PF and the CF signals.

We first consider the change in normalized synaptic weights $\tilde{J}$ of active PF-PC synapses during the learning trials in the case of $p_c=0.029$;

$$\begin{array}{c}\hfill {\tilde{J}}_{\mathit{ij}}(t)=\frac{J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)}{J_0^{(\mathrm{PC},\mathrm{PF})}}.\end{array}$$ 28

here, the initial synaptic strength ($J_0^{(\mathrm{PC},\mathrm{PF})}=0.006$) is the same for all PF-PC synapses. Figures 7a1–a9 show trial-evolution of distribution of $\tilde{J}$ of active PF-PC synapses. As the learning trial is increased, normalized synaptic weights $\tilde{J}$ change due to synaptic plasticity at PF-PC synapses. We note that the distribution of $\tilde{J}$ in each trial is composed of two markedly separated structures (i.e., a combination of separate top horizontal line with a central gap and lower band). Here, the top horizontal line with a central gap has no essential change with the trials, while the lower bands come down with the trials and their vertical widths increase. This kind of distribution of $\tilde{J}$ becomes saturated at about the 250th trial.

Fig. 7.

Change in synaptic weights of active PF-PC synapses during learning trials in the case of $p_c=0.029$. a1–a9 Trial-evolution of distribution of normalized synaptic weights $\tilde{J}(t)$ of active PF signals. b1–b9 Trial-evolution of bin-averaged (normalized) synaptic weights $⟨\tilde{J}(t)⟩$ of active PF signals. Bin size: $\Delta t=50$ msec. Plots of (c) trial-averaged mean $\overline{⟨\tilde{J}(t)⟩}$ and d modulation ${\mathcal{M}}_J$ for the bin-averaged (normalized) synaptic weights $⟨\tilde{J}(t)⟩$ versus trial

The top horizontal line with a central gap arises from the ill-matched firing group (with negative matching indices). In the case of ill-matched PF signals, practically no LTD occurs because most of them have no associations with the error-teaching CF signals which are strongly localized in the middle of trial (i.e., near $t=500$ msec). As shown in Fig. 3c2, the activation degree $A^{(i)}(t)$ (denoted by the dotted line) of GR cells in the ill-matched firing group has a central “zero-bottom” where $A^{(i)}(t)\simeq 0$ (i.e., negligibly small number of spikes in the middle part of trial). In the initial and the final parts of the trial (outside the middle part), practically no LTD takes place due to no practical conjunctions with the strongly-localized CF signals. Thus, the normalized synaptic weights $\tilde{J}$ of the active GR cells in the ill-matched firing group forms the top horizontal line with a central gap which is nearly invariant with the trial.

On the other hand, lower bands arise from the well-matched firing group (with positive matching indices). In the case of well-matched PF signals, they are strongly depressed by the error-teaching CF signals (i.e., strong LTD occurs) in each trial due to good association between the well-matched PF and CF signals. As a result, a lower band is formed, it comes down with the trial, and eventually becomes saturated.

To more clearly examine the above trial evolutions, we obtain the bin-averaged (normalized) synaptic weight in each ith bin (bin size: $\Delta t=$ 50 msec):

$$\begin{array}{c}\hfill {〈\tilde{J},(t)〉}_i=\frac{1}{N_{s,i}}\sum _{f=1}^{N_{s,i}}{\tilde{J}}_{i,f}(t),\end{array}$$ 29

where ${\tilde{J}}_{i,f}$ is the normalized synaptic weight of the fth active PF signal in the ith bin, and $N_{s,i}$ is the total number of active PF signals in the ith bin. Figures 7b1–b9 show trial-evolution of bin-averaged (normalized) synaptic weights $〈\tilde{J},(t)〉$ of active PF signals. In each trial, $〈\tilde{J},(t)〉$ forms a step-well-shaped curve. As the trial is increased, the step-well curve comes down, its width and depth increase, and saturation seems to occur at about the 250th cycle.

We also obtain the trial-averaged mean $\overline{〈\tilde{J},(t)〉}$ via time average of $⟨\tilde{J}(t)⟩$ over a trial:

$$\begin{array}{c}\hfill \overline{〈\tilde{J}〉}=\frac{1}{N_b}\sum _{i=1}^{N_b}{〈\tilde{J},(t)〉}_i.\end{array}$$ 30

here, $N_b$ is the number of bins for trial averaging, and the overbar represents the time average. Figures 7c and d show plots of the trial-averaged mean $\overline{〈\tilde{J},(t)〉}$ and the modulation [=(maximum - minimum)/2] ${\mathcal{M}}_J$ for $〈\tilde{J},(t)〉$ versus trial. The trial-averaged mean $\overline{〈\tilde{J},(t)〉}$ decreases monotonically from 1.0 due to LTD at PF-PC synapses, and it becomes saturated at 0.367 at about the 250th trial.

However, strength of the LTD varies depending on the parts of the trial. In the middle part without practical contribution of ill-matched firing group, strong LTD occurs, due to contribution of only well-matched active PF signals. On the other hand, at the initial and the final parts, somewhat less LTD takes place, because both the ill-matched firing group (with practically no LTD) and the well-matched firing group make contributions together. Consequently, with increasing the number of trials, the middle-stage part comes down more rapidly than the initial and final parts. Hence, the modulation ${\mathcal{M}}_J$ increases monotonically from 0, and it gets saturated at 0.0867 at about the 250th trial.

Influence of PF-PC synaptic plasticity on subsequent learning process in the PC-CN-IO system

As a result of various recoding in the GR clusters, well- and ill-matched firing groups appear. In the case of well-matched PF signals, they are strongly depressed by the error-teaching (instructor) CF signals due to good association between the PF and CF signals. On the other hand, in the case of ill-matched PF signals, practically no LTD occurs because most of them have no conjunctions with the error-teaching CF signals. In this subsection, we investigate the influence of this kind of effective PF-PC synaptic plasticity on the subsequent learning process in the PC-CN-IO system.

Figure 8 shows change in firing activity of PCs during learning trial in the case of $p_c=0.029$. Trial-evolutions of raster plots of spikes of 16 PCs and the corresponding instantaneous population spike rates $R_{\mathrm{PC}}(t)$ are shown in Figs. 8a1–a9 and Figs. b1–b9, respectively. Realization-averaged smooth instantaneous population spike rates ${⟨R_{\mathrm{PC}}(t)⟩}_r$ are also shown in Figs. 8c1–c9. Here, ${⟨\cdots ⟩}_r$ denotes realization average and the number of realizations is 100. ${⟨R_{\mathrm{PC}}(t)⟩}_r$ seems to be saturated at about the 250th cycle.

Fig. 8.

Change in firing activity of PCs during learning trial in the case of $p_c=0.029$. a1–a9 Raster plots of spikes of PCs and b1–b9 instantaneous population spike rates $R_{\mathrm{PC}}(t)$. c1–c9 Realization-averaged instantaneous population spike rates ${⟨R_{\mathrm{PC}}(t)⟩}_r$; number of realizations is 100. Plots of d1 trial-averaged mean $\overline{{⟨R_{\mathrm{PC}}(t)⟩}_r}$ and d2 modulations ${\mathcal{M}}_{\mathrm{PC}}$ for ${⟨R_{\mathrm{PC}}(t)⟩}_r$ versus trial

As shown in Figs. 7b1–b9, bin-averaged normalized synaptic weights $〈\tilde{J},(t)〉$ form a step-well-shaped curve. In the middle part of each trial, strong LTD occurs due to contribution of only well-matched firing group. On the other hand, at the initial and the final parts, somewhat less LTD takes place because both the ill-matched firing group (with practically no LTD) and the well-matched firing group make contributions together. As a result of this kind of effective depression at the (excitatory) PF-PC synapses, with increasing the number of learning trials, raster plots of spikes of all the 16 PCs become more and more sparse in the middle part of each trial (i.e, near $t=500$ msec), which may be clearly seen in the instantaneous population spike rate ${⟨R_{\mathrm{PC}}(t)⟩}_r$. ${⟨R_{\mathrm{PC}}(t)⟩}_r$ becomes lower in the middle part than at the initial and the final parts. Thus, ${⟨R_{\mathrm{PC}}(t)⟩}_r$ also forms a step-well-shaped curve with a minimum in the middle part.

As the number of trials is increased, such step-well-shaped curve for ${⟨R_{\mathrm{PC}}(t)⟩}_r$ comes down and the (top) width and the depth of the well increase. Eventually, at the 141st trial, a “zero-bottom” is formed in the step-well in the middle part of the trial (i.e., ${⟨R_{\mathrm{PC}}(t)⟩}_r\simeq 0$ for $468<t<532$  msec). Appearance of the zero-bottom in the step-well is the prerequisite condition for acquisition of CR. At the zero-bottom of the step-well, PCs stop inhibition completely. This process may be seen well in Figs. 8c1–c5. Thus, from the 141st threshold trial, the CN neuron may fire spikes which evoke CR, which will be seen in Fig. 9. With increasing the number of trials from the 141st trial, both the (top) width of the step-well and the zero-bottom width are increased, although the depth of the well remains unchanged [see Figs. 8c6–c9]. As a result, the strength $\mathcal{S}$ of CR increases, while its timing degree ${\mathcal{T}}_d$ is decreased; the details will be given in Fig. 9. The (overall) learning efficiency degree ${\mathcal{L}}_e$, taking into consideration both ${\mathcal{T}}_d$ and $\mathcal{S}$, increases with the trial, and becomes saturated at about the 250th trial.

Fig. 9.

Change in firing activity of the CN neuron during learning trial in the case of $p_c=0.029$. a1–a6 Raster plots of spikes of the CN neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and b1–b6 bin-averaged instantaneous individual firing rate $f_{\mathrm{CN}}(t)$; the bin size is $\Delta t=$ 50 msec. Plots of (c1) timing degree ${\mathcal{T}}_d$ and c2 strength $\mathcal{S}$ of CR versus trial. d Plot of (overall) learning efficiency degree ${\mathcal{L}}_e$ for the CR versus trial

Figures 8d1 and d2 show plots of trial-averaged mean $\overline{{⟨R_{\mathrm{PC}}(t)⟩}_r}$ (i.e., time average of ${⟨R_{\mathrm{PC}}(t)⟩}_r$ over the trial) and modulation ${\mathcal{M}}_{\mathrm{PC}}$ of ${⟨R_{\mathrm{PC}}(t)⟩}_r$ versus trial, respectively. Due to effective LTD at the PF-PC synapses, the trial-averaged mean $\overline{{⟨R_{\mathrm{PC}}(t)⟩}_r}$ decreases monotonically from 92.47 Hz, and it gets saturated at 19.91 Hz at about the 250th cycle. On the other hand, the modulation ${\mathcal{M}}_{\mathrm{PC}}$ increases monotonically from 0.352 Hz, and it becomes saturated at 16.11 Hz at about the 141st cycle. After the 141st threshold trial, ${\mathcal{M}}_{\mathrm{PC}}$ remains unchanged due to no change in the depth of the step-well, unlike the case of $\overline{{⟨R_{\mathrm{PC}}(t)⟩}_r}$. These PCs (principal cells of the cerebellar cortex) exert effective inhibitory coordination on the CN neuron which evokes the CR (i.e., learned eyeblink).

Figure 9 shows change in firing activity of the CN neuron which produces the final output of the cerebellum during learning trial in the case of $p_c=0.029$. Trial-evolutions of raster plots of spikes of the CN neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and the bin-averaged instantaneous individual firing rates $f_{\mathrm{CN}}(t)$ (i.e., the number of spikes of the CN neuron in a bin with the bin width $\Delta t=50$ msec) are shown in Figs. 9a1–a6 and Figs. 9b1–b6, respectively. At the 140th trial, the CN neuron does not fire due to strong inhibition from the PCs, and thus it is silent (i.e., it lies in the silent period) during the whole trial stage ($0<t<1000$ msec). However, as a result of appearance of the zero-bottom in the step-well for ${⟨R_{\mathrm{PC}}(t)⟩}_r$ at the 141st threshold trial, the CN neuron begins to fire spikes in the middle part of the trial. In this case, as the time is increased from $t=0,$ the CN neuron first lies in the silent period, then a transition to the firing state occurs in the middle part, and finally another transition to the silent state also takes place. With increasing the number of trials, raster plots of spikes of the CN neuron become more and more dense in the middle part of each trial, in contrast to the case of PCs.

This process may be clearly seen in the instantaneous individual firing rates $f_{\mathrm{CN}}(t)$. Due to the effective inhibitory coordinations of PCs on the CN neuron, $f_{\mathrm{CN}}(t)$ begins to increase from 0 in the middle part of the trial, it reaches a peak, and then it decreases to 0 relatively slowly. The peak of $f_{\mathrm{CN}}(t)$ appears a little earlier than the US presentation ($t=500$ msec) which may denote the anticipatory CR (Medina et al. 2000b; Yamazaki and Tanaka 2007). Thus, $f_{\mathrm{CN}}(t)$ forms a bell-shaped curve. As the number of trials is increased, the bottom-base width and the peak height of the bell are increased, and $f_{\mathrm{CN}}(t)$ seems to be saturated at about the 250th trial.

Figures 9c1 and c2 show plots of the timing degree ${\mathcal{T}}_d$ and the strength $\mathcal{S}$ of the CR versus trial, respectively. The timing degree ${\mathcal{T}}_d,$ representing the matching degree between the firing activity of the CN neuron [$f_{\mathrm{CN}}(t)$] and the US timing signal $f_{\mathrm{US}}(t)$, is given by the cross-correlation $Cor{r}_{\mathrm{T}}(0)$ at the zero lag between $f_{\mathrm{CN}}(t)$ and $f_{\mathrm{US}}(t)$:

$$\begin{array}{c}\hfill Cor{r}_{\mathrm{T}}(\tau )=\frac{\overline{\Delta f_{\mathrm{US}}(t+\tau )\Delta f_{\mathrm{CN}}(t)}}{\sqrt{\overline{\Delta f_{\mathrm{US}}^2(t)}}\sqrt{\overline{\Delta f_{\mathrm{CN}}^2(t)}}},\end{array}$$ 31

where $\Delta f_{\mathrm{US}}(t)=f_{\mathrm{US}}(t)-\overline{f_{\mathrm{US}}(t)}$, $\Delta f_{\mathrm{CN}}(t)=f_{\mathrm{CN}}(t)-\overline{f_{\mathrm{CN}}(t)}$, and the overline denotes the time average. Practically, ${\mathcal{T}}_d$ reflects the width of the bottom base of the bell curve. With increasing the number of trials, the width of the bottom base increases, due to increase in the (top) width of the step-well curve for the PCs. As a result, ${\mathcal{T}}_d$ decreases monotonically from 0.912 at the 141st trial, and it becomes saturated at 0.346 at about the 250th trial. On the other hand, as the number of trials is increased, the peak height of the bell increases. Thus, the strength $\mathcal{S}$ of CR (representing the amplitude of eyelid closure), given by the modulation [(maximum - minimum)/2] of $f_{\mathrm{CN}}(t),$ increases monotonically from 1.803 at the 141st trial, and it gets saturated at 32.38 at about the 250th trial.

Then, the (overall) learning efficiency degree ${\mathcal{L}}_e$ for the CR, taking into consideration both the timing degree ${\mathcal{T}}_d$ and the strength $\mathcal{S}$ of CR, is given by their product:

$$\begin{array}{c}\hfill {\mathcal{L}}_e={\mathcal{T}}_d·\mathcal{S}.\end{array}$$ 32

Figure 9d shows a plot of ${\mathcal{L}}_e$ versus trial. ${\mathcal{L}}_e$ increases monotonically from 1.645 at the 141st trial, and it becomes saturated at about the 250th cycle. Thus, we get the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ $(\simeq 11.19)$. As will be seen in the next subsection, ${\mathcal{L}}_e^{\ast }$ is the largest one among the available ones. Hence, in the case of $p_c=0.029$ where firing patterns of GR clusters with the variety degree $\mathcal{V}(\simeq 1.842)$ are the most various, motor learning for the EBC with the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ is the most effective.

Learning progress can be clearly seen in the IO system. During the learning trial, the IO neuron receives both the excitatory (airpuff) US signal for the desired timing and the inhibitory signal from the CN neuron (representing a realized eye-movement). Then, the learning progress degree ${\mathcal{L}}_p$ is given by the ratio of the time-averaged inhibitory input from the CN neuron to the magnitude of the time-averaged excitatory input of the desired US timing signal:

$$\begin{array}{c}\hfill {\mathcal{L}}_p=\frac{\overline{I_{\mathrm{GABA}}^{(\mathrm{IO},\mathrm{CN})}}}{\left|\overline{I_{\mathrm{AMPA}}^{(\mathrm{IO},\mathrm{US})}}\right|}.\end{array}$$ 33

here, $\overline{I_{\mathrm{GABA}}^{(\mathrm{IO},\mathrm{CN})}}$ is the trial-averaged inhibitory GABA receptor-mediated current from the CN neuron to the IO neuron, and $\overline{I_{\mathrm{AMPA}}^{(\mathrm{IO},\mathrm{US})}}$ is the trial-averaged excitatory AMPA receptor-mediated current into the IO neuron via the desired US timing signal; no (excitatory) NMDA receptors exist on the IO neuron. [Note that the 4th term in Eq. (1) is given by $-I_{syn,i}^{(X)}(t)$, because $I_{\mathrm{GABA}}^{(\mathrm{IO},\mathrm{CN})}>0$ and $I_{\mathrm{AMPA}}^{(\mathrm{IO},\mathrm{US})}<0.$]

Figure 10a1 shows plots of ${〈\overline{I_{\mathrm{GABA}}^{(\mathrm{IO},\mathrm{CN})}}〉}_r$ (open circles) and ${〈|,\overline{I_{\mathrm{AMPA}}^{(\mathrm{IO},\mathrm{US})}},|〉}_r$ (crosses) versus trial in the case of $p_c=0.029$; ${⟨\cdots ⟩}_r$ represents an average over 100 realizations. At the 141st threshold trial, acquisition of CR starts (i.e., the CN neuron begins to fire spikes). Hence, before the threshold the trial-averaged inhibitory input from the CN neuron is zero, it begins to increase from the threshold and converges to the constant trial-averaged excitatory input through the US signal for the desired timing. Thus, with increasing the number of trials, ${\mathcal{L}}_p$ is zero before the threshold, it begins to increase from the threshold, and becomes saturated at ${\mathcal{L}}_p=1$, as shown well in Fig. 10a2. In this saturated case, the trial-averaged excitatory and inhibitory inputs to the IO are balanced.

Fig. 10.

Change in firing activity of the IO neuron during learning trial in the case of $p_c=0.029$. Plots of (a1) realization-average for the time-averaged inhibitory synaptic current from the CN neuron (${⟨\overline{I_{\mathrm{GABA}}^{(\mathrm{IO},\mathrm{CN})}}⟩}_r$) (open circles) and realization-average for the time-averaged excitatory synaptic current via the (airpuff) US signal (${⟨\overline{|I_{\mathrm{AMPA}}^{(\mathrm{IO},\mathrm{US})}|}⟩}_r$) versus trial; number of realizations ${⟨\cdots ⟩}_r$ is 100. a2 Plot of learning progress degree ${\mathcal{L}}_p$ versus trial. b1–b5 Raster plots of spikes of the IO neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and c1–c5 bin-averaged instantaneous individual firing rate $f_{\mathrm{IO}}(t)$; the bin size is $\Delta t=$ 40 msec. d Plot of trial-averaged individual firing rate $\overline{f_{\mathrm{IO}}(t)}$ versus trial

We also investigate the firing activity of IO neuron during learning process. Figures 10b1–b6 and Figures 10c1–c6 show trial-evolutions of raster plots of spikes of the IO neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and the bin-averaged instantaneous individual firing rates $f_{\mathrm{IO}}$ (i.e., the number of spikes of the IO neuron in a bin with the bin width $\Delta t=40$ msec), respectively. Before the 141st threshold trial, relatively dense spikes appear in the middle part of the trial in the raster plot of spikes, due to the effect of excitatory US timing signal. However, with increasing the number of trials from the threshold, spikes in the middle part become sparse, because of increased inhibitory input from the CN neuron. In this case, the bin-averaged instantaneous individual firing rate $f_{\mathrm{IO}}(t)$ of the IO neuron forms a bell-shaped curve due to the US timing signal into the IO neuron. With increasing the number of trials from the 141st threshold, the amplitude of $f_{\mathrm{IO}}(t)$ begins to decrease due to the increased inhibitory input from the CN neuron, and it becomes saturated at about the 250th trial. Thus, the trial-averaged individual firing rate $\overline{f_{\mathrm{IO}}(t)}$ is constant (=1.5 Hz) before the threshold without the inhibitory input from the CN neuron. However, with increasing the number of trials from the threshold, it is decreased from 1.326 Hz due to increase in the inhibitory input from the CN neuron, and gets saturated at 0.0902 Hz at about the 250th trial, as shown in Fig. 10d.

The firing output of the IO neuron is fed into the PCs via the CFs. Hence, with increasing the trial from the threshold, the error-teaching (instructor) CF signals become weaker and saturated at about the 250th cycle. While the saturated CF signals are fed into the PCs, saturation for the trial-averaged bin-averaged synaptic weights $\overline{〈\tilde{J},(t)〉}$ appears [see Fig. 7c]. Then, the subsequent learning process in the PC-CN system also gets saturated, and we obtain the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ $(\simeq 11.19)$, which is shown in Fig. 9d.

Variation of the connection probability $p_c$ and strong correlation between variety degree $\mathcal{V}$ for the firing patterns and learning efficiency degree ${\mathcal{L}}_e$ of CR

In the above subsections, we consider the case of $p_c=0.029$ (i.e., $2.9\%$) where the firing patterns of the GR cells are the most various and the Pavlovian EBC learning is also the most efficient [which will be clearly shown in Figs. 14b and c3, respectively]. From now on, we change the connection probability $p_c$ from GO to GR cells, and study dependence of the variety degree $\mathcal{V}$ for the firing patterns in the GR clusters and the learning efficiency degree ${\mathcal{L}}_e$ of the CR on $p_c$.

We first consider both the highly-connected case of $p_c=0.3$ (i.e., $30\%$) and the lowly-connected case of $p_c=0.003$ (i.e., $0.3\%$). Figures 11a1 and a2 show the raster plots of spikes of ${10}^3$ randomly chosen GR cells for $p_c=0.3$ and 0.003, respectively. The population-averaged firing activities in the whole population of GR cells may be well seen in the instantaneous whole-population spike rates $R_{\mathrm{GR}}(t)$ in Figs. 11b1 and b2 for $p_c=0.3$ and 0.003, respectively.

Fig. 11.

Highly-connected ($p_c=0.3$) and lowly-connected ($p_c=0.003$) cases. Raster plots of spikes of ${10}^3$ randomly chosen GR cells for a1 $p_c=0.3$ and a2 $p_c=0.003$. Instantaneous whole-population spike rates $R_{\mathrm{GR}}(t)$ in the whole population of GR cells for b1$p_c=0.3$ and (b2) $p_c=0.003$. Band width for $R_{\mathrm{GR}}(t)$: $h=10$ msec. Distributions of matching indices $\{{\mathcal{M}}^{(I)}\}$ of the firing patterns in the GR clusters in the whole population for c1 $p_c=0.3$ and c2 $p_c=0.003$. Bin size for the histograms in (c1) and (c2) is 0.1. Fractions of well-matched and ill-matched firing groups for d1 $p_c=0.3$ and d2 $p_c=0.003$

As shown in Fig. 2b, each GR cluster is bounded by four glomeruli (corresponding to the terminals of the MFs) at both ends. Each glomerulus receives inhibitory inputs from nearby 81 GO cells with the connection probability $p_c$. In the highly-connected case of $p_c=0.3$, on average, about 24 GO cell axons innervate each glomerulus. Then, each GR cell in a GR cluster receives about 97 inhibitory inputs via four dendrites which contact the four glomeruli at both ends. In this highly-connected case, inhibitory inputs from the pre-synaptic GO cells are increased, in comparison with the case of $p_c=0.029.$ As a result, spike density in the raster plot of spikes is decreased (i.e., spikes become sparse) due to decreased individual firing rates, and hence the flat top part of $R_{\mathrm{GR}}(t)$ becomes lowered, in comparison to the case of $p_c=0.029$ in Fig. 3b.

In the highly-connected case of $p_c=0.3,$ differences between total inhibitory synaptic inputs from pre-synaptic GO cells to each GR cells are decreased due to increase in the number of pre-synaptic GO cells. In addition, the excitatory inputs into each GR cells via MFs are Poisson spike trains with the same firing rates, and hence they are essentially the same. Hence, differences between the total synaptic inputs (including both the inhibitory and the excitatory inputs) into each GR cells become reduced. These less different inputs into GR cells produce less different outputs (i.e. firing activities) of GR cells, which become more similar to the population-averaged firing activity $R_{\mathrm{GR}}(t)$ with a flat top in Fig. 11b1. Thus, GR cells tend to exhibit relatively regular firings during the whole trial stage ($0<t<1000$ msec), in comparison with the case of $p_c=0.029$. Consequently, the raster plot of sparse spikes for $p_c=0.3$ becomes relatively uniform [compare Fig. 11a1 with Fig. 3a].

On the other hand, in the lowly-connected case of $p_c=0.003$, the inhibitory inputs from GO cells into GR cells are so much reduced, and the excitatory MF signals into the GR cells become dominant inputs. Hence, spike density in the raster plot of spikes is increased (i.e., spikes become dense), because of increased individual firing rate, and the flat top part of $R_{\mathrm{GR}}(t)$ becomes raised, in comparison to the case of $p_c=0.029$ in Fig. 3b. Furthermore, differences between the total synaptic inputs into each GR cells become reduced, because the dominant excitatory MF signals, generated by the Poisson spike trains with the same firing rates, are essentially the same, and thus firing activities of GR cells become more similar to $R_{\mathrm{GR}}(t)$ with a flat top in Fig. 11b2. Hence, as in the highly-connected case, GR cells tend to show relatively regular firings during the whole trial stage. As a result, the raster plot of dense spikes for $p_c=0.003$ also becomes relatively uniform, as shown in Fig. 11a2, in comparison with the case of $p_c=0.029$ in Fig. 3a.

Figures 11c1 and c2 show the distributions of matching indices $\left\{{\mathcal{M}}^{(I)}\right\}$ for $p_c=0.3$ and 0.003, respectively. The ranges in the distributions of $\left\{{\mathcal{M}}^{(I)}\right\}$ for $p_c=0.3$ and 0.003 are ($-$ 0.21, 0.44) and ($-$ 0.18, 0.48), respectively. In both cases, their ranges are narrowed from both the positive and the negative sides, in comparison with the range ($-$ 0.49, 0.79) in the case of $p_c=0.029$. As explained above, in both the highly- and the lowly-connected cases of $p_c=0.3$ and 0.003, GR cells tend to exhibit relatively regular firings in the whole trial stage, due to decrease in the differences in the total synaptic inputs from GO cells into each GR cells, which is in contrast to the case of $p_c=0.029$ where random repetitions of transitions between bursting and silent states (both of which are persistent long-lasting ones) occur. Then, in both the highly- and the lowly-connected cases, highly well-matched firing patterns with higher ${\mathcal{M}}^{(I)}$ and highly ill-matched firing patterns with higher magnitude $\left|{\mathcal{M}}^{(I)}\right|$ disappear, which leads to reduction in the ranges of the distributions of $\left\{{\mathcal{M}}^{(I)}\right\}$ arise.

Due to the narrowed distribution of $\left\{{\mathcal{M}}^{(I)}\right\}$, both the mean ($\simeq 0.239$) and the standard deviation ($\simeq 0.360$) in the highly-connected case of $p_c=0.3$ are decreased, in comparison to the case of $p_c=0.029$ where the mean and the standard deviation are 0.333 and 0.614, respectively. Then, the variety degree $\mathcal{V}$ for the firing patterns $\left[R_{\mathrm{GR}}^{(I)},(t)\right]$ in the GR clusters, denoting a quantitative measure for various recoding in the granular layer, is given by the relative standard deviation for the distribution of $\{{\mathcal{M}}^{(I)}\}$ [see Eq. (22)]. For $p_c=0.3$, its variety degree is $\mathcal{V}\simeq 1.506$ which is smaller than $\mathcal{V}(\simeq 1.842)$ in the case of $p_c=0.029$. Similar to the highly-connected case, for $p_c=0.003$ both the mean ($\simeq 0.272$) and the standard deviation ($\simeq 0.315$) for the distribution of $\left\{{\mathcal{M}}^{(I)}\right\}$ are also decreased. In this lowly-connected case, the variety degree $\mathcal{V}$ for the firing patterns $\left[R_{\mathrm{GR}}^{(I)},(t)\right]$ in the GR clusters is $\mathcal{V}\simeq 1.157$ which is much smaller than $\mathcal{V}(\simeq 1.842)$ in the case of $p_c=0.029$. We also note that the variety degree $\mathcal{V}$ for $p_c=0.003$ is smaller than that for $p_c=0.3$; $\mathcal{V}=1.842(p_c=0.029)>\mathcal{V}=1.506(p_c=0.3)>\mathcal{V}=1.157(p_c=0.003).$

Figures 11d1 and d2 show fractions of well-matched $\left(\left\{{\mathcal{M}}^{(I)},>,0\right\}\right)$ and ill-matched $\left(\left\{{\mathcal{M}}^{(I)},<,0\right\}\right)$ firing groups for $p_c=0.3$ and 0.003, respectively. In the highly-connected case of $p_c=0.3,$ the well-matched firing group is a major one with fraction 88.2$\%$, while the ill-matched firing group is a minor one with fraction 11.8$\%$. In comparison with the case of $p_c=0.029$ where the fraction of well-matched firing group is 82.1$\%$, the fraction of well-matched firing group for $p_c=0.3$ is increased. In this highly-connected case, the firing-group ratio, given by the ratio of the fraction of the well-matched firing group to that of the ill-matched firing group, is ${\mathcal{R}}_{\mathrm{sp}}\simeq 7.48$ which is larger than that (${\mathcal{R}}_{\mathit{sp}}\simeq 4.59$) in the case of $p_c=0.029$. In the lowly-connected case of $p_c=0.003,$ the fraction of well-matched firing group is more increased to 93.9$\%$. Hence, the firing-group ratio is ${\mathcal{R}}_{\mathrm{sp}}\simeq 13.8$ which is much larger than that in the case of $p_c=0.029$.

Due to decrease in differences between the total synaptic inputs into each GR cells, firing activities of GR cells for $p_c=0.3$ and 0.003 become more similar to the population-averaged firing activity $R_{\mathrm{GR}}(t)$, in comparison with the case of $p_c=0.029$. We note that $R_{\mathrm{GR}}(t)$ is well-matched with the US signal $f_{\mathrm{US}}(t)$ [i.e, $R_{\mathrm{GR}}(t)$ has a positive conjunction index with respect to $f_{\mathrm{US}}(t)$], which results in increase in the fraction of well-matched firing group for $p_c=0.3$ and 0.003. In contrast to the case of $p_c=0.3,$ in the lowly-connected case of $p_c=0.003,$ inhibitory inputs into each GR cells are so much reduced, and hence the dominant inputs are just the excitatory MF signals which are well-matched with the US signal $f_{\mathrm{US}}(t)$. Thus, the fraction of well-matched firing group for $p_c=0.003$ becomes larger than that for $p_c=0.3$.

These changes in the variety degree $\mathcal{V}$ of the firing patterns in the GR clusters have direct effect on the synaptic plasticity at the PF-PC synapses and the subsequent learning process in the PC-CN system. As shown in the case of $p_c=0.029$, the ill- and the well-matched firing groups play their own roles for the CR. The ill-matched firing group plays a role of protection barrier for the timing of CR, while the strength of CR is determined by strong LTD in the well-matched firing group. Due to break-up of highly well-matched and highly ill-matched firing patterns, the distributions of $\left\{{\mathcal{M}}^{(I)}\right\}$ for the highly- and the lowly-connected cases of $p_c=0.3$ and 0.003 are narrowed. Hence, both the timing degree ${\mathcal{T}}_d$ and the strength $\mathcal{S}$ of CR are decreased for both $p_c=0.3$ and 0.003, which are well shown in Figs. 12 and 13.

Fig. 12.

Change in firing activity of the CN neuron in the highly-connected ($p_c=0.3$) and the lowly-connected ($p_c=0.003$) cases. Case of $p_c=0.3$: a1–a6 raster plots of spikes of the CN neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and b1–b6 bin-averaged instantaneous individual firing rate $f_{\mathrm{CN}}(t)$; the bin size is $\Delta t=50$ msec. Case of $p_c=0.003$: c1–c6 raster plots of spikes of the CN neuron and (d1)-(d6) bin-averaged instantaneous individual firing rate $f_{\mathrm{CN}}(t)$

Fig. 13.

Timing degree, strength, and learning efficiency degree of the CR in the highly-connected ($p_c=0.3$) and the lowly-connected ($p_c=0.003$) cases. a Plots of timing degree ${\mathcal{T}}_d$ of the CR versus trial. b Plots of strengths $\mathcal{S}$ of the CR versus trial. c Plots of learning efficiency degree ${\mathcal{L}}_e$ for the CR versus trial. Solid circles, open circles, and crosses represent data in the cases of $p_c=$ 0.3, 0.003, and 0.029, respectively

Figure 12 shows change in the firing activity of the CN neuron which generates the final output of the cerebellum during learning trial in the highly- and the lowly-connected cases of $p_c=0.3$ and 0.003. For $p_c=0.3,$ trial-evolutions of the raster plots of spikes of the CN neuron (i.e., collection of spike trains for all the realizations; number of realizations is 100) and the bin-averaged instantaneous individual firing rates $f_{\mathrm{CN}}(t)$ (i.e., the number of spikes of the CN neuron in a bin with the bin width $\Delta t=50$ msec) are shown in Figs. 12a1–a6 and Figs. 12b1–b6, respectively. In this highly-connected case, at the 142nd threshold trial, the CN neuron begins to fire in the middle part of the trial. Thus, acquisition of CR occurs a little later, in comparison with the case of $p_c=0.029$ with the 141st threshold. In this case, $f_{\mathrm{CN}}(t)$ forms a bell-shaped curve. With increasing the number of trials from the threshold, raster plots of spikes of the CN neuron become more and more dense in the middle part of each trial, and bottom-base width and peak height of the bell curve for $f_{\mathrm{CN}}(t)$ increase. At about the 250th trial, $f_{\mathrm{CN}}(t)$ seems to become saturated. Thus, the number of the threshold trial for acquisition of CR and the number of trial for the saturation of $f_{\mathrm{CN}}(t)$ are nearly the same in both cases of $p_c=0.3$ and 0.029, although $p_c=0.3$ is about 10 times as large as $p_c=0.029$. However, the main concern in the Pavlovian EBC lies in the learning efficiency degree at the saturated state. ${\mathcal{T}}_d$ [timing degree representing the bottom-base width of $f_{\mathrm{CN}}(t)$], $\mathcal{S}$ [strength of CR representing the peak height of $f_{\mathrm{CN}}(t)$], and the learning efficiency degree ${\mathcal{L}}_e$ (given by product of ${\mathcal{T}}_d$ and $\mathcal{S}$) are significantly decreased for $p_c=0.3$ from those values for $p_c=0.029$, which is well explained in the next paragraph.

For $p_c=0.3,$ the bottom-base width of the bell curve is wider and its peak height is shorter, in comparison with the case of $p_c=0.029$ (see Fig. 9). Due to break-up of highly ill-matched firing patterns (which play the role of protection barrier for timing of CR), bottom-base width (associated with the reciprocal of timing degree of CR) of the bell increases. Also, peak height of the bell (related to the strength of CR) decreases because of break-up of highly well-matched firing patterns (which induce strong LTD and determine the strength of CR). Consequently, as the variety degree $\mathcal{V}$ of the firing patterns in the GR clusters is deceased from 1.842 ($p_c=0.029$) to 1.507 ($p_c=0.3$), the bottom-base width of the bell curve is increased, and the peak height is decreased.

For $p_c=0.003,$ trial-evolutions of the raster plots of spikes of the CN neuron and the bin-averaged instantaneous individual firing rates $f_{\mathrm{CN}}(t)$ are shown in Figs. 12c1–c6 and Figs. 12d1–d6, respectively. In this lowly-connected case, acquisition of CR occurs at the 143rd trial which is a little later in comparison with the 142nd threshold for $p_c=0.3$. Similar to the highly-connected case, with increasing the number of trials from the threshold, raster plots of spikes of the CN neuron become more and more dense in the middle part of each trial, and the bottom-base width and the peak height of the bell curve for $f_{\mathrm{CN}}(t)$ increase. Eventually, saturation occurs at about the 250th trial. In comparison to the highly-connected case, the bottom-base width of the bell curve is wider and its peak height is shorter, because of more break-up of highly ill-matched firing patterns and highly well-matched firing patterns (which results in more decrease in the variety degree of firing patterns). As a result, with decreasing the variety degree $\mathcal{V}$ from 1.507 ($p_c=0.3$) to 1.157 ($p_c=0.003$), the bottom-base width of the bell curve increases, and the peak height decreases (i.e., less variety in the firing patterns results in decrease in the timing degree and the strength of CR).

Figures 13a and b show plots of the timing degree ${\mathcal{T}}_d$ and the strength $\mathcal{S}$ of CR versus trial for $p_c=0.3$ (solid circles), 0.003 (open circles), and 0.029 (crosses), respectively. The timing degree ${\mathcal{T}}_d,$ denoting the matching degree between the firing activity of the CN neuron [$f_{\mathrm{CN}}(t)$] and the US signal $f_{\mathrm{US}}(t)$ for a timing, is given by the cross-correlation $Cor{r}_{\mathrm{T}}(0)$ at the zero lag between $f_{\mathrm{CN}}(t)$ and $f_{\mathrm{US}}(t)$ in Eq. (31). This timing degree ${\mathcal{T}}_d$ reflects the width of the bottom base of the bell curve. With increasing the number of trials, the width of the bottom base increases, as shown in Fig. 12, and hence ${\mathcal{T}}_d$ decreases monotonically, and it becomes saturated at about the 250th trial. We note that, as the variety degree $\mathcal{V}$ of the firing patterns is decreased ($\mathcal{V}=$ 1.507, 1.157, and 1.842 for $p_c=0.3,$ 0.003, and 0.029, respectively), ${\mathcal{T}}_d^{\ast }$ (saturated value of ${\mathcal{T}}_d$) decreases; ${\mathcal{T}}_d^{\ast }=0.346(p_c=0.029)>{\mathcal{T}}_d^{\ast }=0.266(p_c=0.3)>{\mathcal{T}}_d^{\ast }=0.187(p_c=0.003)$.

On the other hand, as the number of trials is increased, the peak height of the bell increases. Hence, the strength $\mathcal{S}$ of CR, given by the modulation of $f_{\mathrm{CN}}(t),$ increases monotonically, and it becomes saturated at about the 250th trial. In this case, ${\mathcal{S}}^{\ast }$ (saturated value of $\mathcal{S}$) also is decreased with decrease in the variety degree $\mathcal{V}$; ${\mathcal{S}}^{\ast }=32.382(p_c=0.029)>{\mathcal{S}}^{\ast }=27.099(p_c=0.3)>{\mathcal{S}}^{\ast }=21.656(p_c=0.003)$.

We then consider the learning efficiency degree ${\mathcal{L}}_e$ for the CR, given by product of the timing degree ${\mathcal{T}}_d$ and the strength $\mathcal{S}$ in Eq. (32). Figure 13c shows a plot of ${\mathcal{L}}_e$ versus trial. ${\mathcal{L}}_e$ increases monotonically from the threshold trial, and it becomes saturated at about the 250th cycle. Thus, we obtain the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$, the values of which are 7.216, 4.054, and 11.19 for $p_c=$ 0.3, 0.003, and 0.029, respectively. Among the three cases, ${\mathcal{L}}_e^{\ast }(=11.19)$ in the case of $p_c=0.029$ is the largest one, and ${\mathcal{L}}_e^{\ast }$ is decreased with decrease in the variety degree $\mathcal{V}$; ${\mathcal{L}}_e^{\ast }=11.19(p_c=0.029)>{\mathcal{L}}_e^{\ast }=7.216(p_c=0.3)>{\mathcal{L}}_e^{\ast }=4.054(p_c=0.003)$.

Finally, based on the above two examples for the highly- and the lowly-connected cases, we investigate dependence of the variety degree $\mathcal{V}$ for the firing patterns of the GR clusters and the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ on $p_c$ by varying it from the value of $p_c=0.029$. Figure 14a shows plots of fractions of the well- and the ill-matched firing groups versus $p_c$. The fraction of the well-matched firing group (solid circles) forms a well-shaped curve with a minimum in the case of $p_c=0.029$, while the fraction of the ill-matched firing group (open circles) forms a bell-shaped curve with a maximum in the case of $p_c=0.029$. In the case of $p_c=0.029$, the firing-group ratio (i.e., ratio of fraction of the well-matched firing group to fraction of the ill-matched firing group) is ${\mathcal{R}}_{\mathrm{sp}}=4.59$. As $p_c$ is changed (i.e., increased or decreased) from $p_c=0.029$, the fraction of the well-matched firing group increases, and then the firing-group ratio ${\mathcal{R}}_{\mathrm{sp}}$ increases from ${\mathcal{R}}_{\mathit{sp}}=4.59$ in the case of $p_c=0.029$.

Figure 14b show a plot of the variety degree $\mathcal{V}$ for the firing patterns in the GR clusters. The variety degrees $\mathcal{V}$ forms a bell-shaped curve with a maximum $\mathcal{V}(\simeq 1.842)$ in the case of $p_c=0.029$. With changing $p_c$ from $p_c=0.029,$ $\mathcal{V}$ decreases from $\mathcal{V}\simeq 1.842$. Hence, in the case of $p_c=0.029$, temporal recoding of GR cells is the most various. Figures 14c1–c3 show plots of the saturated timing degree ${\mathcal{T}}_d^{\ast }$, the saturated strength ${\mathcal{S}}^{\ast }$, and the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ of CR, respectively. All of them form bell-shaped curves with maxima ${\mathcal{T}}_d^{\ast }(\simeq 0.346)$, ${\mathcal{S}}^{\ast }(\simeq 32.38)$, and ${\mathcal{L}}_e^{\ast }(\simeq 11.19)$ in the case of $p_c=0.029$. As $p_c$ is changed from $p_c=0.029$, ${\mathcal{T}}_d^{\ast }$, ${\mathcal{S}}^{\ast }$, and ${\mathcal{L}}_e^{\ast }$ are decreased. Hence, the case of $p_c=0.029$ may be regarded as an “optimal” one with both the maximum variety degree $\mathcal{V}(\simeq 1.842)$ for the firing patterns of the GR cells and the maximum saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }(\simeq 11.19)$. That is, for $p_c=0.029,$ the firing patterns of the GR cells are the most various, which also results in the most efficient learning for the EBC. Hereafter, we call the case of $p_c=0.029$ as an optimal one. Figure 14d shows a plot of ${\mathcal{L}}_e^{\ast }$ versus $\mathcal{V}$. As shown clearly in Fig. 14d, both ${\mathcal{L}}_e^{\ast }$ and $\mathcal{V}$ have a strong correlation with the Pearson’s correlation coefficient $r\simeq 0.9982$. Consequently, the more various in temporal recoding of the GR cells (i.e., the larger the variety degree $\mathcal{V}$ of the firing patterns of the GR cells), the more effective in learning for the Pavlovian EBC (i.e., the greater the learning efficiency degree ${\mathcal{L}}_e$ for the EBC), which is our main result.

Summary and discussion

We are concerned about the Pavlovian EBC. Various works on the EBC have been done experimentally in many mammalian species such as humans, monkeys, dogs, ferrets, rabbits, rats, and mice (Hilgard and Campbell 1936; Hilgard and Marquis 1935, 1936; Schneiderman et al. 1962; Skelton 1988; McCormick et al. 1982; McCormick and Thomson 1984; Ivarsson and Svesson 2000; Heiney et al. 2014). Also, computational works reproduced some features (e.g., representation of time passage) of the EBC in artificial models (Desmond and Moore 1988; Moore et al. 1989; Gluck et al. 1990; Chapeau-Blondeau and Chauvet 1991; Bullock et al. 1994; Fiala et al. 1996), a realistic biological model (Buonomano and Mauk 1994; Medina et al. 2000a; Medina and Mauk 2000), a rate-coding model (Yamazaki and Tanaka 2005), and a spiking neural network model (Yamazaki and Tanaka 2007). However, more clarification is necessary for influences of various temporal recoding in GR clusters on the Pavlovian EBC.

To the best of our knowledge, for the first time, we made complete quantitative classification of various firing patterns in the GR clusters in terms of the newly-introduced matching index $\left\{{\mathcal{M}}^{(I)}\right\}$ and variety degree $\mathcal{V}$ in the case of Pavlovian EBC. Each firing pattern is characterized in terms of its matching index ${\mathcal{M}}^{(I)}$ between the firing pattern and the US signal for the desired timing. Then, the whole firing patterns are clearly decomposed into the well-matched $\left({\mathcal{M}}^{(I)},>,0\right)$ and the ill-matched $\left({\mathcal{M}}^{(I)},<,0\right)$ firing groups. Furthermore, the degree of various recoding of the GR cells may be quantified in terms of the variety degree $\mathcal{V}$, given by the relative standard deviation in the distribution of $\left\{{\mathcal{M}}^{(I)}\right\}$. Thus, $\mathcal{V}$ provides a quantitative measure for various temporal recoding of GR cells. It has also been shown that various total synaptic inputs (including both the excitatory inputs via MFs and the inhibitory inputs from the pre-synaptic GO cells) into the GR clusters result in generation of various firing patterns (i.e. outputs) in the GR clusters.

Based on the above dynamical classification of various firing patterns in the GR clusters, we made clear investigations on the influence of various recoding of GR cells on the Pavlovian EBC (i.e., their effect on the synaptic plasticity at the PF-PC synapses and the subsequent learning process in the PC-CN-IO system). To the best of our knowledge, this kind of approach, based on the well- and the ill-matched firing groups, is unique in studying the Pavlovian EBC. The well-matched firing patterns are strongly depressed (i.e., strong LTD) by the instructor CF signals due to good association between the well-matched PF and the CF signals, and they make dominant contributions in the middle part of each trial. In contrast, for the ill-matched firing patterns with central gaps in the middle part, practically no LTD occurs because most of the ill-matched firing patterns have no matching with the instructor CF signals. Thus, in the middle part of each trial, strong LTD occurs via dominant contributions of well-matched firing group, and hence a minimum of the bin-averaged synaptic weight $〈\tilde{J}〉$ appears. On the other hand, at the initial and the final parts of each trial, less LTD takes place because both the ill-matched firing group with practically no LTD and the well-matched firing group with strong LTD make contributions together, and hence maxima of $〈\tilde{J}〉$ occur. As a result, a big modulation in $〈\tilde{J}〉$ arises via constructive interplay of the well- (strong LTD) and ill-matched (practically no LTD) firing groups.

Due to this type of effective synaptic plasticity at the PF-PC synapses, the (realization-averaged) population spike rate $⟨R_{\mathrm{PC}}(t)⟩$ of PCs forms a step-well-shaped curve with a minimum in the middle part of each trial. When passing a threshold trial, a “zero-bottom” (where $⟨R_{\mathrm{PC}}(t)⟩\simeq 0$) appears in the central well. At this threshold trial, the CN neuron begins to fire in the middle part of trial. Hence, appearance of the zero-bottom in the step-well for $⟨R_{\mathrm{PC}}(t)⟩$ is a prerequisite condition for acquisition of CR. In the subsequent trials, the individual firing rate $f_{\mathrm{CN}}(t)$ of the CN neuron forms a bell-shaped curve with a maximum in the middle part (which is up-down reversed with respect to $⟨R_{\mathrm{PC}}(t)⟩$). Outside the bottom of the bell in the middle part, the CN neuron cannot fire, due to inhibition of ill-matched firing group (with practically no LTD). Hence, the ill-matched firing group plays a role of protection barrier for timing, and the timing degree of CR is reciprocally associated with the bottom width of the bell. In this case, the peak of the bell in the middle part is formed due to strong LTD in the well-matched firing group, and its height is directly related to the strength of CR (corresponding to the amplitude of eyelid closure). In this way, both the well- and the ill-matched firing groups play their own roles for the timing and the strength of CR, respectively.

By changing $p_c,$ we investigated dependence of the variety degree $\mathcal{V}$ of the firing patterns and the saturated learning efficiency degree ${\mathcal{L}}_e^{\ast }$ for the CR (given by the product of the timing degree and the strength of CR) on $p_c.$ Both $\mathcal{V}$ and ${\mathcal{L}}_e^{\ast }$ have been found to form bell-shaped curves with peaks ($\mathcal{V}\simeq 1.842$ and ${{\mathcal{L}}_e}^{\ast }(\simeq 11.19)$) at the same optimal value of $p_c=0.029$. In Refs. (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012)where the parameter values were taken, based on anatomical and physiological data, the connection probability from the GO to the GR cells is $p_c=0.025,$ which is very close to that in the optimal case. Thus, we hypothesize that the granular layer in the cerebellar cortex has evolved toward the goal of the most various recoding. Moreover, Both $\mathcal{V}$ and ${\mathcal{L}}_e^{\ast }$ have also been found to have a strong correlation with the Pearson’s correlation coefficient $r\simeq 0.9982$. Hence, the more various in the firing patterns of GR cells, the more efficient in learning for the Pavlovian EBC, which is the main result in our work.

To examine our main result, we also suggest a real experiment for the EBC. To control $p_c$ in a given species of animals (e.g., a species of rabbit, rat, or mouse) in an experiment seems to be practically difficult, in contrast to the case of computational neuroscience where $p_c$ may be easily varied. Instead, we may consider an experiment consisting of several species of animals (e.g., 3 species of rabbit, rat, and mouse). In each species, a large number of randomly chosen GR cells ($i=1,\cdots ,M$) are considered. Then, through many CS-US trials, one may get the peristimulus time histogram (PSTH) for each ith GR cell [i.e., (bin-averaged) instantaneous individual firing rate $f_{\mathrm{GR}}^{(i)}(t)$ of the ith GR cell]. GR cells are expected to exhibit various PSTHs. Then, in the case of each ith GR cell, one can get its matching index ${\mathcal{M}}_i$ between its PSTH $f_{\mathrm{GR}}^{(i)}(t)$ and the CF signal for the desired timing [i.e., the PSTH of the IO neuron $f_{\mathrm{IO}}(t)$]. In this case, the matching index ${\mathcal{M}}_i$ is given by the cross-correlation at the zero-time lag between $f_{\mathrm{GR}}^{(i)}(t)$ and $f_{\mathrm{IO}}(t)$. Thus, one may get the variety degree $\mathcal{V}$ of PSTHs of GR cells, given by the relative standard deviation in the distribution of $\{{\mathcal{M}}_i\}$, for the species.

In addition to the PSTHs of GR cells, under the many CS-US trials, one can also obtain a bell-shaped PSTH of a CN neuron [(bin-averaged) instantaneous individual firing rate $f_{\mathrm{CN}}(t)$ of the CN neuron]. The reciprocal of bottom-base width and the peak height of the bell curve correspond to timing degree ${\mathcal{T}}_d$ and strength $\mathcal{S}$ for the EBC, respectively. In this case, the (overall) learning efficiency degree ${\mathcal{L}}_e$ for the EBC is given by the product of ${\mathcal{T}}_d$ and $\mathcal{S}$. In this way, a set of $(\mathcal{V},{\mathcal{L}}_e)$ may be experimentally obtained for each species, and depending on the species, the set of $(\mathcal{V},{\mathcal{L}}_e)$ may change. Then, for example in the case of 3 species of rabbit, rat, and mouse, with the three different data sets for $(\mathcal{V},{\mathcal{L}}_e)$, one can examine our main result (i.e., whether more variety in PSTHs of GR cells leads to more efficient learning for the EBC).

Finally, we make discussion on limitations of our present work and future works. In the present work where the ISI between the onsets of CS and US was set at 500 msec, we investigated the effect of various temporal recoding of GR cells on the Pavlovian EBC. The acquisition rate and the timing degree and strength of CR have been known to depend on the ISI (Mauk and Ruiz 1992; Yamazaki and Tanaka 2007). Hence, in a future work, it would be interesting to study dependence of EBC on the ISI. Based on the results of our work, it would also be interesting to study extinction of CR, as a future work. After acquisition of CR, we turn off the airpuff US. Then, the CR is expected to become gradually extinct via LTP at the PF-PC synapses (Mauk and Donegan 1997). In this work, we considered only the PF-PC synaptic plasticity. In the cerebellum, synaptic plasticity takes place at various synapses (Hansel et al. 2001; Gao et al. 2012)(e.g., MF-CN and PC-CN synapses (Zheng and Raman 2010), PF-BC and BC-PC synapses (Lennon et al. 2015), and MF-GR cells synapses (D’Angelo and De Zeeuw 2008)). Hence, it would be interesting to make a future study on the influence of various synaptic plasticity at various synapses on the cerebellar learning for the Pavlovian EBC; particularly, we are interested in the effect of the synaptic plasticity at the MF-CN synapse on the EBC (Mauk and Donegan 1997). In addition to change in $p_c$ (i.e., connection probability from GO to GR cells), one can vary synaptic inputs into the GR cells by changing NMDA receptor-mediated maximum conductances ${\overline{g}}_{\mathrm{NMDA}}^{(\mathrm{GR})}$ and ${\overline{g}}_{\mathrm{NMDA}}^{(\mathrm{GO})}$ (Yamazaki and Tanaka 2007). Hence, as a future work, it would also be interesting to study the influence of NMDA receptor-mediated synaptic inputs on various recoding of GR cells and learning for the EBC by varying ${\overline{g}}_{\mathrm{NMDA}}^{(\mathrm{GR})}$ and ${\overline{g}}_{\mathrm{NMDA}}^{(\mathrm{GO})}$.

Parameter values for the LIF neuron models and the synaptic currents

In Appendix A, we list four tables which show parameter values for the LIF neuron models in Subsect. 2.3 and the synaptic currents in Subsect. 2.4. These values are adopted from physiological data (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012).

For the LIF neuron models, the parameter values for the capacitance $C_X$, the leakage current $I_L^{(X)}$, the AHP current $I_{\mathit{AHP}}^{(X)}$, and the external constant current $I_{\mathit{ext}}^{(X)}$ are shown in Table 1.

For the synaptic currents, the parameter values for the maximum conductance ${\overline{g}}_R^{(T)}$, the synaptic weight $J_{\mathit{ij}}^{(T,S)}$, the synaptic reversal potential $V_R^{(S)}$, the synaptic decay time constant ${\tau }_R^{(T)}$, and the amplitudes $A_1$ and $A_2$ for the type-2 exponential-decay function in the granular layer, the Purkinje-molecular layer, and the other parts for the CN and IO neurons are shown in Tables 2, 3, and 4, respectively.

Refined rule for synaptic plasticity

In Appendix B, we introduce a refined rule for synaptic plasticity. The coupling strength of the synapse from the pre-synaptic neuron j in the source S population to the post-synaptic neuron i in the target T population is $J_{\mathit{ij}}^{(T,S)}$. Initial synaptic strengths for $J_{\mathit{ij}}^{(T,S)}$ are given in Tables 2, 3, and 4. In this work, we assume that learning occurs only at the PF-PC synapses. Hence, only the synaptic strengths $J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}$ of PF-PC synapses may be modifiable (i.e., they are depressed or potentiated), while synaptic strengths of all the other synapses are static. [Here, the index j for the PFs corresponds to the two indices (M, m) for GR cells representing the mth ($1\le m\le 50$) cell in the Mth ($1\le M\le 2^{10}$) GR cluster.] Synaptic plasticity at PF-PC synapses have been so much studied in many experimental (Ito et al. 1982; Ito and Kano 1982; Sakurai 1987; Ito 1989; De Schutter 1995; Chen and Thompson 1995; Wang et al. 2000; Lev-Ram et al. 2003; Coesmans et al. 2004; Steuber et al. 2007; Safo and Regehr 2008; Molnár 2014; Yang and Lisberger 2014; Gallimore et al. 2018) and computational (Albus 1971; Gerstner and van Hemmen 1992; Buonomano and Mauk 1994; Kenyon et al. 1998; Medina et al. 2000a; Yamazaki and Tanaka 2007; Roberts 2007; Achard and De Schutter 2008; Yamazaki and Nagao 2012; Bouvier et al. 2018) works.

As the time t is increased, synaptic strength $J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)$ for each PF-PC synapse is updated with the following multiplicative rule (depending on states) (Safo and Regehr 2008; Kim and Lim 2021):

$$\begin{array}{c}\hfill J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)\to J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)+\Delta J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t),\end{array}$$ 34

where

$$\begin{array}{cc}\hfill \Delta J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)=& \Delta {\mathrm{LTD}}_{\mathit{ij}}^{(1)}(t)+\Delta {\mathrm{LTD}}_{\mathit{ij}}^{(2)}(t)+\Delta {\mathrm{LTP}}_{\mathit{ij}}(t),\hfill \end{array}$$ 35

$$\begin{array}{cc}\hfill \Delta {\mathrm{LTD}}_{\mathit{ij}}^{(1)}(t)=& -{\delta }_{\mathit{LTD}}·J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)·C{F}_i(t)\hfill \\ \hfill & ·\sum _{\Delta t=0}^{\Delta t_r^{\ast }}\Delta J_{\mathit{LTD}}(\Delta t),\hfill \end{array}$$ 36

$$\begin{array}{cc}\hfill \Delta {\mathrm{LTD}}_{\mathit{ij}}^{(2)}(t)=& -{\delta }_{\mathit{LTD}}·J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)·[1-C{F}_i(t)]·P{F}_{\mathit{ij}}(t)\hfill \\ \hfill & ·D_i(t)\times \sum _{\Delta t=0}^{\Delta t_l^{\ast }}\Delta J_{\mathit{LTD}}(\Delta t),\hfill \end{array}$$ 37

$$\begin{array}{cc}\hfill \Delta {\mathrm{LTP}}_{\mathit{ij}}(t)=& {\delta }_{\mathit{LTP}}·[J_0^{(\mathrm{PC},\mathrm{PF})}-J_{\mathit{ij}}^{(\mathrm{PC},\mathrm{PF})}(t)]·[1-C{F}_i(t)]\hfill \\ \hfill & ·P{F}_{\mathit{ij}}(t)\times [1-D_i(t)].\hfill \end{array}$$ 38

Here, $J_0^{(\mathrm{PC},\mathrm{PF})}$ is the initial value (=0.006) for the synaptic strength of PF-PC synapses. Synaptic modification (LTD or LTP) occurs, depending on the relative time difference $\Delta t$ [= $t_{\mathrm{CF}}$ (CF activation time) - $t_{\mathrm{PF}}$ (PF activation time)] between the spiking times of the error-teaching instructor CF and the variously-recoded student PF. In Eqs. (36)-(38), $C{F}_i(t)$ denotes a spike train of the CF signal coming into the ith PC. When $C{F}_i(t)$ activates at a time t, $C{F}_i(t)=1$; otherwise, $C{F}_i(t)=0$. This instructor CF activation gives rise to LTD at PF-PC synapses in conjunction with earlier ($\Delta t>0)$ student PF activations in the range of $t_{\mathrm{CF}}-\Delta t_r^{\ast }<t_{\mathrm{PF}}<t_{\mathrm{CF}}$ ($\Delta t_r^{\ast }\simeq 277.5$ msec), which corresponds to the major LTD in Eq. (36).

We next consider the case of $C{F}_i(t)=0$, which corresponds to Eqs. (37) and (38). Here, $P{F}_{\mathit{ij}}(t)$ denotes a spike train of the PF signal from the jth pre-synaptic GR cell to the ith post-synaptic PC. When $P{F}_{\mathit{ij}}(t)$ activates at time t, $P{F}_{\mathit{ij}}(t)=1$; otherwise, $P{F}_{\mathit{ij}}(t)=0$. In the case of $P{F}_{\mathit{ij}}(t)=1$, PF firing may cause LTD or LTP, depending on the presence of earlier CF firings in an effective range. If CF firings exist in the range of $t_{\mathrm{PF}}+\Delta t_l^{\ast }<t_{\mathrm{CF}}<t_{\mathrm{PF}}$ ($\Delta t_l^{\ast }\simeq -117.5$ msec), $D_i(t)=1$; otherwise $D_i(t)=0$. When both $P{F}_{\mathit{ij}}(t)=1$ and $D_i(t)=1$, the PF activation causes another LTD at PF-PC synapses in conjunction with earlier ($\Delta t<0$) CF activations [see Eq. (37)]. The probability for occurrence of earlier CF firings within the effective range is very low because mean firing rates of the CF signals (corresponding to output firings of individual IO neurons) are $\sim$ 1.5 Hz (Mathy et al. 2009; Llinás 2014). Hence, this 2nd type of LTD is a minor one. In contrast, in the case of $D_i(t)=0$ (i.e., absence of earlier associated CF firings), LTP occurs because of the PF firing alone [see Eq. (38)]. The update rate ${\delta }_{\mathit{LTD}}$ for LTD in Eqs. (36) and (37) is 0.005, while the update rate ${\delta }_{\mathit{LTP}}$ for LTP in Eqs. (38) is 0.0005 (=${\delta }_{\mathit{LTD}}/10$) (Yamazaki and Nagao 2012).

In the case of LTD in Eqs. (36) and (37), the synaptic modification $\Delta J_{\mathit{LTD}}(\Delta t)$ changes depending on the relative time difference $\Delta t$ $(=t_{\mathrm{CF}}-t_{\mathrm{PF}}$). We use the following time window for the synaptic modification $\Delta J_{\mathit{LTD}}(\Delta t)$ (Safo and Regehr 2008; Kim and Lim 2021):

$$\begin{array}{c}\hfill \Delta J_{\mathit{LTD}}(\Delta t)=A+B·e^{-{(\Delta t-t_0)}^2/{\sigma }^2},\end{array}$$ 39

where $A=-0.12$, $B=0.4$, $t_0=80$, and $\sigma =180$. The time window for $\Delta J_{\mathit{LTD}}(\Delta t)$ is well shown in Fig. 3 in Ref. (Kim and Lim 2021), where LTD occurs in an effective range of $\Delta t_l^{\ast }<\Delta t<\Delta t_r^{\ast }$. We note that a peak appears at $t_0=80$ msec, and hence peak LTD takes place when PF firing precedes CF firing by 80 msec. A CF firing gives rise to LTD in association with earlier PF firings in the black region ($0<\Delta t<\Delta t_r^{\ast }$), and it also causes to another LTD in conjunction with later PF firings in the gray region ($\Delta t_l^{\ast }<\Delta t<0$). The effect of CF firing on earlier PF firings is much larger than that on later PF firings. However, outside the effective range (i.e., $\Delta t>\Delta t_r^{\ast }$ or $<\Delta t_l^{\ast }$), PF firings alone results in occurrence of LTP, because of absence of effectively associated CF firings.

Our refined rule for synaptic plasticity has the following advantages for the $\Delta \mathrm{LTD}$ in comparison with that in (Yamazaki and Tanaka 2007; Yamazaki and Nagao 2012). Our rule is based on the experimental result in (Safo and Regehr 2008). In the presence of a CF firing, a major LTD ($\Delta {\mathrm{LTD}}^{(1)}$) occurs in conjunction with earlier PF firings in the range of $t_{\mathrm{CF}}-\Delta t_r^{\ast }<t_{\mathrm{PF}}<t_{\mathrm{CF}}$ ($\Delta t_r^{\ast }\simeq 277.5$ msec), while a minor LTD ($\Delta {\mathrm{LTD}}^{(2)}$) takes place in conjunction with later PF firings in the range of $t_{\mathrm{CF}}<t_{\mathrm{PF}}<t_{\mathrm{CF}}-\Delta t_l^{\ast }$ ($\Delta t_l^{\ast }\simeq -117.5$ msec). The magnitude of LTD varies depending on $\Delta t$ (= $t_{\mathrm{CF}}$ - $t_{\mathrm{PF}}$); a peak LTD occurs when $\Delta t=80$ msec. In contrast, the rule in (Yamazaki and Nagao 2012; Yamazaki and Tanaka 2007)considers only the major LTD in association with earlier PF firings in the range of $t_{\mathrm{CF}}-50<t_{\mathrm{PF}}<t_{\mathrm{CF}}$, the magnitude of major LTD is equal, independently of $\Delta t$, and minor LTD in conjunction with later PF firings is not considered. Outside the effective range of LTD, PF firings alone lead to LTP in both rules. However, we also note that some features of Pavlovian EBC were successfully reproduced by using the simple synaptic rule with only the major LTD in (Yamazaki and Tanaka 2007).

List of abbreviations

In Appendix C, we present a list of abbreviations which is shown in Table 5.

Table 5.

List of abbreviations

Abbreviation	Description
AHP	Afterhyperpolarization
AMPA	$\alpha$-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid
BC	Basket cell
CF	Climbing-fiber
CN	Cerebellar nucleus
CR	Conditioned response
CS	Conditioned stimulus
EBC	Eyeblink conditioning
EMG	Electromyography
GABA${}_{\mathrm{A}}$	$\gamma$-aminobutyric acid type A
GO	Golgi
GR	Granule
IO	Inferior olive
ISI	Inter-stimulus interval
LIF	Leaky integrate-and-fire
LTD	Long-term depression
LTP	Long-term potentiation
MF	Mossy fiber
NMDA	N-methyl-D-aspartate
OKR	Optokinetic response
PC	Purkinje cell
PF	Parallel-fiber
PSTH	Peristimulus time histogram
SCS	Sustained conditioned stimulus
TCS	Transient conditioned stimulus
US	Unconditioned stimulus