Brain response to color stimuli: an EEG study with nonlinear approach

Abstract

Color perception is a major guiding factor in the evolutionary process of human civilization, but most of the neurological background of the same are yet unknown. This work attempts to address this area with an EEG based neuro-cognitive study on response of brain to different color stimuli. With respect to a Grey baseline seven colors of the VIBGYOR were shown to 16 participants with normal color vision and corresponding EEG signals from different lobes (Frontal, Occipital & Parietal) were recorded. In an attempt to quantify the brain response while watching these colors, the corresponding EEG signals were analysed using two of the latest state of the art non-linear techniques (MFDFA and MFDXA) of dealing complex time series. MFDFA revealed that for all the participants the spectral width, and hence the complexity of the EEG signals, reaches a maximum while viewing color Blue, followed by colors Red and Green in all the brain lobes. MFDXA, on the other hand, suggests a lower degree of inter and intra lobe correlation while watching the VIBGYOR colors compared to baseline Grey, hinting towards a post processing of visual information. We hope that along with the novelty of methodologies, the unique outcomes of this study may leave a long term impact in the domain of color perception research.

Introduction

From the advent of human civilization, color and perception of color has been intimately involved with it. For survival or evolutionary purposes such as choosing safe foods, finding safe routes to navigate or perception of time during the day, for aesthetic purposes such as variations in artistic expressions of different era, for changing range of emotional experiences to various stimuli, even in the modern world for corporate branding—color reshapes the richness of complex visual information (Hanson 2012). And that is precisely what both helps and hinders research on the effect of color on humans: the sheer volume of research done on visual than any other sensory modality is due to the fact that our interaction with the world has historically depended more on the vision and processing visual information (Hutmacher 2019; Pike et al. 2012). And the hindrance stems from the fact that the experience of color is very subjective and to some extent, context dependent (Lotto and Purves 2002; Elliot and Maier 2012). Nevertheless, the study of color perception and its effects in human brain is fascinating as well as important because it entertains both practical and theoretical concerns.

The existing literature on this component of visual perception highlights two main aspects: psychological and physiological.

Color and psychological functioning

The theory that colors can cause psychological arousal dates back to Nineteenth century when Goethe (Goethe 1810) first mentioned the connection between colors and emotional responses. Since then, with the advancement of science and gradual understanding of the underlying mechanism of light and vision, the focus shifted towards the change in behavioral or psychological manifestation with changing color wavelengths (Nakshian 1964). But after half a century of research on this domain, no concrete conclusion could be drawn as of yet. For example, a study (Hill and Barton 2005) suggests that the color red can be associated with dominance and aggression in both human and non-humans. Another one associates similar responses in human with black (Frank and Gilovich 1988). A number of empirical works on association of color with different psychological attributes indicated that colors with longer wavelengths (like red) have enhanced the arousal level of the component in consideration (see (Elliot 2015) for a more detailed review): From showing attentional advantage in studies regarding color and selective attention (Buechner et al. 2014) to being a performance enhancing factor in sports (Hill and Barton 2005; Greenlees et al. 2013; Caldwell and Burger 2011). Again, despite showing a restricting effect in intellectual performance (Elliot et al. 2007; Shi et al. 2015), Red has been found to enhance attraction when worn by the opposite sex (Elliot and Niesta 2008; Stephen and McKeegan 2010). On the other hand, shorter wavelength colors such as Blue increase alertness (Lockley et al. 2006; Vandewalle et al. 2007) and perception of quality and trustworthiness, found in marketing evaluation studies (Lee and Rao 2010; Labrecque and Milne 2012). In some studies (Mehta and Zhu 2009; Elliot et al. 2009), conducted on the effect of color on cognitive task performances, shows that Red activates avoidance motivation and enhances performance in detail oriented analytic tasks. Whereas, color Blue (activates approach motivation) is ideal for creative task performances. Contrary to this, experiments done in (Olsen (2010); Bakker et al. 2013) or (Castell et al. 2018) could not replicate such results. It seems that most of the studies use mainly two or three colors (Red, Blue, Green in few) as the experimental setup. Although, very few studies associated Green to calmness (Suk and Irtel 2010; Hanada 2018) and orange/yellow to excitement (Ridgway and Myers 2014; AL-Ayash et al. 2016) but a number of other studies didn’t agree (Briki and Hue 2016; Wilms and Oberfeld 2018; Costa et al. 2018). The general trend in the literatures available shows that the association between Red and excitement is the most reported scenario. The association of calmness/relaxation has been divided majorly between colors Blue and Green. In addition to that, some studies like (Labrecque and Milne 2012; AL-Ayash et al. 2016) and (Wilms and Oberfeld 2018) reported correlation between high saturation and excitement as well.

Color and physiological responses

Physiological responses to color stimulus is another direction that has been investigated in color perception research. Studies done in this area are mostly motivated by the hypothesis that long-wavelength colors (red/yellow) are more arousing than short-wavelength colors (blue/green) (Valdez and Mehrabian 1994). Although the fundamental question that remains unanswered in this field is whether the response is direct (i.e., stimulus evokes the response directly without cognitive intermediation) or indirect (cognition acts as an intermediary) (Kaiser 1984). Some of the studies used different means like GSR (Galvanic Skin Response), EEG, Heart rate and Respiration, Oxiometry, Blood pressure etc. to measure physiological signals against color stimulus. Among these experimental techniques, EEG or electroencephalograms remain the most used one. Various forms of EEG driven cortical activations have been used so far. In 1958, probably the earliest work describing EEG effects of color (Gerard 1958), lower prominence of alpha waves under red was reported, indicating higher cortical arousal. Since then, analyzing the changes in alpha waves under different experimental conditions has been the usual form of investigation (Elliot 2019). Though few of those studies supported the driving hypothesis of red color associating with arousal (Ali 1972; Shen et al. 1999), majority either disagreed or remained inconclusive (Erwin et al. 1961; Caldwell and Jones 1985; Mikellides 1990; Yoto et al. 2007). Apart from red, the color that has been experimented with the most is blue, because of its shorter wavelength. Higher arousal and brain activity during cognitive tasks is found in the presence of blue light as well (Klimesch 1999; Cabeza and Nyberg 2000; Baek and Min 2015). As for the other colors, Orange and yellow had been reported to cause enhanced physiological arousal in some of the studies mentioned (AL-Ayash et al. 2016; Erwin et al. 1961). Also, shorter wavelength color like violet has induced more pronounced arousal than higher wavelength color like green in atleast one study (Nourse and Welch 1971).

To sum up, research on the physiological response is relatively less and relatively sparse than that on psychological effects of it. And in both cases, finding any conclusive pattern is rather difficult (although in psychological studies the agreement between different results seem a bit more consistent). Also, most of the existing work has focused on the applied part of the problem, as in they have sought to establish relationships between a specific color and a psychological attribute or a behavioral pattern, for practical purposes. Hardly had they cared to explain the underlying reasons behind it (Elliot et al. 2007). Detailed studies on the physiological manifestations (especially that on the brain) will undoubtedly help address the issue. It is more than evident that the number of studies in the field of color induced EEG is inadequate. In view of this, in the present study, we have made an attempt to assess in depth the effect of color stimulus on EEG pattern in humans quantitatively using chaos based novel non-linear methodology.

EEG, fractality and multifractality

The brain constantly carries out information transfer and processing via the neural system, making it extremely complex. It works through the interactions between large assemblies of neurons in the central nervous system (CNS) and the peripheral neural system. Neurons transfer and process the information via the action potentials and neural firing (also known as spikes). When this kind of electrical activity transfers to the surface of the cortex and to the surface of the scalp, we can record it as the EEG. The properties of the EEG signal are very complex and display qualities such as (Paluš 1996; Thakor and Tong 2004):

1. Noisy and stochastic with high degree of randomness

2. Time-varying and non-stationary (for any signal more than ~ 3.5 s duration)

3. High nonlinearity

Quantifying such a system using linear methods like FFT or power spectral density leads to coarse approximation and overlooking of underlying intricacies. As numerous studies suggest (Pritchard and Duke 1992,1995; França et al. 2018), the highly nonlinear and chaotic dynamics of human brain need to be addressed via tools which are useful for quantifying such a system, namely, Fractals.

Fractals are said to be the visual identity of Chaos. Chaotic systems appear seemingly random and patternless on the surface. But when investigated using ‘mathematical microscopes’ i.e., fractals, shows a hidden order among them. Fractal is a rough or fragmented geometrical object that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole. They possess some unique properties such as fractional dimension (called fractal dimensions or FD) and scale invariance, indicating that their nature remains same at many different scales. Also, in other words, this is called self-similarity: consisting of parts that are similar to the whole (Mandelbrot 1983). These distinctive properties of fractals make them ideal to analyse complex systems with greater precision. Fractals are found throughout nature—in coastlines, seashells, rivers, clouds, snowflakes, musical compositions and even in biological systems—heart rhythms, lungs, blood vessels etc. Fractal geometry has been applied to human brain dynamics for various measures, healthy and non-healthy (Pereda et al. 1998; Eke et al. 2002; Linkenkaer-Hansen et al. 2001; Gong et al. 2003; Esteller et al. 1999). In recent past, the fractal based analysis method that had been instrumental in addressing the fractal scaling properties and long-range correlations in EEG related studies is Detrended Fluctuation Analysis or DFA. With the help of a scaling exponent, DFA quantifies correlation properties of a signal, indicative of its self-similar nature. Using this method, existence of scale invariance and the investigation on the long range correlations present in EEG signals was studied successfully, during various cognitive (visual and auditory) tasks (Bhattacharya 2009; Karkare et al. 2009; Banerjee et al. 2016).

Now, one major shortcoming of DFA is that it only uses single scaling ratio to examine the whole system under observation. Usually, in nature, complex systems feature different scaling patterns in different parts of the system, that is to say, the measure of self-similarity can be of multiple nature. Hence, more often than not, fractal technique with single scaling ratio (also known as ‘Monofractals’) is not adequate. To study such systems more accurately, one needs to use a more robust technique having multiple scaling ratios. These are ‘Multifractals’ (Stanley et al. 1999). Analogous to a string made of beads, Multifractals are made up of parts which have their own distinct FDs and hence, it is often expressed in a multifractal spectrum with a unique Spectral Width. To analyse complex natural systems, multifractal DFA or MFDFA has been developed by Kantelhardt et al. (Kantelhardt et al. 2002). Interestingly, it has been found that along with various natural phenomenon (explained later), human physiological signatures are also multifractal: from heartbeat dynamics (Ivanov et al. 1999) to actigraphy (França et al. 2019). Also, considerable amount of literature exists that indicate the human brain dynamics exhibits multifractal nature (Suckling et al. 2008; Ihlen and Vereijken 2010; Zorick and Mandelkern 2013). In the past few years, we have also found evidence that support the idea of multifractality in human brain and have used the spectral width parameter in the quantification of wide range of cognitive properties to a good success (Maity et al. 2015a, 2015b; Roy et al. 2016; Ghosh et al. 2018; Sanyal et al. 2019).

Another important part of this work is the cross-correlation analysis of the EEG data. In signal processing, cross-correlation is used broadly to provide the quantitative measure of similarity between two time series. This method has been applied in EEG signals as well. But unlike the assumptions in cross-correlation studies until the recent past, the time series in consideration here are non-stationary. To counter the problem, Podobnik and Stanley (Podobnik and Stanley 2008) proposed Detrended Cross-Correlation Analysis (DCCA) to investigate power-law cross-correlations between two non-stationary time series. Zhou (Zhou 2008) took a step further and developed the method of Multifractal Detrended Cross-Correlation Analysis or MFDXA, which is a technique that originates from MFDFA and investigates the multifractal features of two cross-correlated signals. It uses a cross correlation coefficient (γ_x) which gives the degree of correlation between two categories of signals. For uncorrelated data, γ_x has a value 1; the lower the value of γ_x the more correlated is the data. Negative value of γ_x signifies very high degree of correlation between the signals, i.e., a large increment in one would more likely to follow a large increment of the other. In recent times, there are multiple cross-correlation studies on EEG signals using DCCA or MFDXA which have argued the existence of power law cross-correlation (Jun and Da-Qing 2012) and have been instrumental in revealing underlying dynamics in the brain (Ghosh et al. 2018, 2014; Chen et al. 2018).

Overview of the work

The principal aim of this work is to study, with state-of-the-art robust chaos-based non-linear methodologies, the different levels of neuronal complexities that arise in the brain when it receives various colors as a visual stimulus. We took the EEG data of 16 participants while they were exposed to seven colors of VIBGYOR (Violet, Indigo, Blue, Green, Yellow, Orange, Red) in that order; each separated from the next by a neutral color (grey), to set a baseline for comparison. Unlike previous works which have studied mostly two or three colours and their comparisons, our experiment consisted of the whole spectrum of natural colours. For the analysis of the collected EEG data, we have applied two fractal based non-linear techniques MFDFA and MFDXA. These high precision tools have been proven to work on non-stationary EEG data very accurately to reveal the underlying self-similar patterns and complexity measures by quantifying them via different parameters. MFDFA assesses the degree of complexity present in the signal using multifractal width as a parameter. Higher the width, higher the long range cross-correlations present in the series, implying higher complexity. MFDXA, on the other hand, measures the degree of how much correlation is present between various inter and intra lobe electrodes in the EEG signals using a cross correlation co-efficient (γ_x). Five Frontal electrodes (F3, F4, F7, F8, Fz), two Parietal (P3, P4) and two Occipital (O1, O2) electrodes were analysed since these areas are mostly reported to be associated with cognition and perceptions of visual stimulus (Ganis et al. 2004; Siok et al. 2009; Spillmann et al. 2012). The degrees of complexity corresponding to each color and their respective changes from the baseline are studied. This work, along with fulfilling its primary goal of reporting the changes in brain activity during color perception, also hopes to establish a novel investigatory paradigm in EEG based visual perception studies that will include advanced physical tools to magnify underlying mechanisms beyond the realm of conventional methods.

Materials and methods

Participant summary

16 participants, age ranging from 20 to 59 (7 females; mean age = 27.51, Standard Deviation =  ± 5.92), voluntarily took part in the experiment. None of the participants reported any history of neurological or psychiatric diseases (e.g.: epilepsy, anxiety etc.) or colour blindness, confirmed by Ishihara test (https://www.color-blindness.com/ishihara-38-plates-cvd-test) and they all had normal/corrected to normal vision. Informed consent about the testing procedure was obtained from each participant according to the ethical guidelines of the Ethical Committee of Jadavpur University. The participants were uninformed about the experimental hypotheses. The experiment was conducted at the Sir C.V. Raman Centre for Physics and Music, Jadavpur University, Kolkata.

Experimental details

Participants were seated in a comfortable chair with back and elbow rests in a dark room with normal temperature of 25°C. The visual stimulus was displayed in a 21 inch LCD monitor (screen resolution 1920 × 1080, 24-bit color depth, 75 Hz refresh rate), kept 1.2 m above ground. The distance between the monitor and the participant’s eyes was 91 cm. The luminosity of each color and the grey in between was kept constant to factor out brightness issues. The participants were asked to focus on a point marked ‘ + ’ at the centre of the screen (subtended at 2° visual angle).

The colorimetric values of the colors used as stimuli are shown in Table 1. Here, X, Y, and Z display the CIE XYZ tristimulus values according to the 2° CIE 1931 standard observer (Cie 1932) and columns L*, C* and h* display the lightness, chroma and hue values according to the CIE LCh 1976 system (Commission Internationale de l'Éclairage. Vol. CIES 014–4/E:2007 (ISO 11664–4:2008)(2007).

Table 1.

Colorimetric values of color stimuli used

Color	Hex triplet	sRGB [r,g,b]	X	Y	Z	L*	C*	h*
Violet	#7F00FF	(127, 0, 255)	26.79	11.73	95.44	40.79	127.09	311.63
Indigo	#3F00FF	(63, 0, 255)	20.09	08.28	95.13	34.55	131.23	307.55
Blue	#0000FF	(0, 0, 255)	18.04	7.22	95.03	32.30	133.81	306.29
Green	#00FF00	(0, 255, 0)	35.76	71.52	11.92	87.74	119.78	136.02
Yellow	#FFFF00	(255, 255, 0)	77.00	92.78	13.85	97.14	96.91	102.85
Orange	#FF7F00	(255, 127, 0)	48.84	36.45	4.46	66.86	85.66	59.62
Red	#FF0000	(255, 0, 0)	41.25	21.27	1.93	53.24	104.55	39.99
Grey	#808080	(128, 128, 128)	20.52	21.59	23.50	53.59	0.00	270.00

The EEG experiments were conducted in the afternoon in a normal temperature room with the participants sitting in a comfortable chair in a normal diet condition. EEG data was acquired with an EEG recording cap with 19 electrodes (Ag/AgCl sintered ring electrodes) placed in the international 10/20 system. Figure 1: depicts the positions of the electrodes (Sanyal et al. 2019). Impedances were kept below 5 k Ohms. The EEG recording system (Recorders and Medicare Systems) was operated at 256 samples/sec recording on customized software of RMS. Same reference electrodes, ear electrodes A1 and A2, are used for all the channels. The ear electrodes were linked, and the average of A1 and A2 was used as reference. The forehead electrode, FPz has been used as the ground.

Fig. 1.

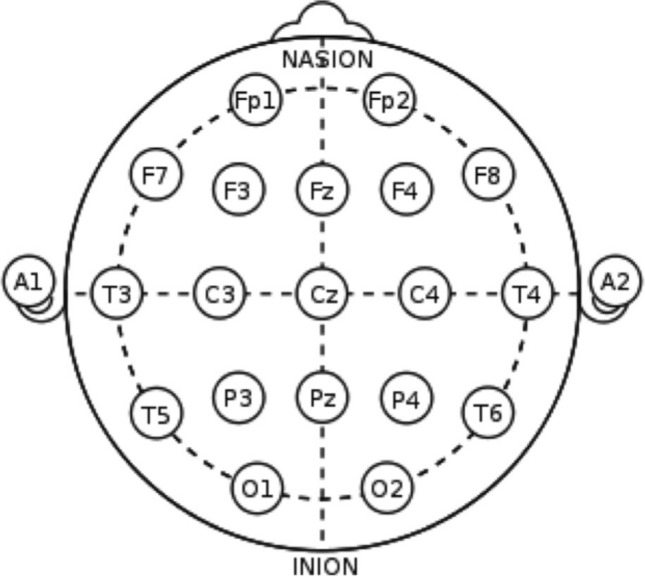
The position of electrodes according to the 10–20 international system. Ear electrodes A1 and A2 are used as references

Experimental protocol

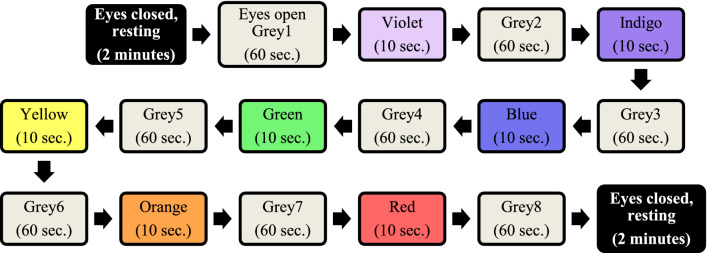
The visual stimulus consisted of seven VIBGYOR colors in that order (Violet, Indigo, Blue, Green, Yellow, Orange, Red), each separated from the next by a uniform grey background. The VIBGYOR colors featured for 10 s durations each and the neutral grey persisted for 60 s, intended to neutralise the effect of one color on the others. Before and after the whole experiment protocol, participants were asked to keep their eyes closed for a period of 2 min. Order of the protocol has been illustrated in Fig. 2:

Fig. 2.

Flow chart of experimental protocol

EEG was recorded during the whole protocol, all 13 min. 10 s. The obtained EEG data, after cleaning out the noise portions, have been analysed using two non-linear techniques- MFDFA and MFDXA. The detailed methodologies are discussed in the following section.

Methodologies

Pre-processing of EEG signals

Raw EEG signals were filtered using a low and high pass filter with cut-off frequencies of 0.5 to 70 Hz. The electrical interference noise (50 Hz) was eliminated using notch filter. High frequency muscle artifacts were removed in the pre-processing stage by selecting the inbuilt EMG filter, which is a second order low pass filter with cut off frequency 35 Hz (35 Hz double-pole). Before proceeding to the analysis stage, the EEG data need to be further cleaned of the low frequency artifacts such as minuscule muscular movements and eye blinks. For this, a method called Empirical Mode Decomposition (EMD) was applied. EMD decomposes the signal into various artifact free components preserving its non-linear and non-stationary features. This processing technique has been detailed in Maity et al. (2015) (see Appendix). The noise-free EEG data, hereafter, will be the main component of further analysis. Signals corresponding to nine electrodes from different lobes of the brain [five Frontal (F3, F4, F7, F8, Fz), two Parietal (P3, P4) and two Occipital (O1, O2)] are obtained and analysed.

Decomposing EEG waveform: frequency bands vs. broadband EEG signal

The traditional approach in EEG analysis consists of decomposing the original signal into different frequency bands alpha, beta, theta and the likes. The necessity and methodological approach that went into such divisions were constrained by mechanical and computational limitations of 1930s and 40 s (see (Bladin 2006) for the historical development). Since Fourier Transform, a technique to decompose the signal into its composite frequencies, was available and used successfully in fields of engineering and communications, the practice found its application in EEG analysis as well. This tradition has continued in modern day EEG researches, despite the concern forwarded by one of its inventors in the early days itself (Walter 1938). Should the EEG signal be a superposition of only the combining waves such analysis would be sensible. But in reality, the signal contains high level of complexity beyond simple associative and distributive intuitions. In fact, the power spectrum scaling of EEG shows 1/f like relations (Pritchard 1992), which is indicative of a complex chaotic system. Various ‘bumps’ in this frequency structure is used to segregate the delta, theta, alpha, beta and gamma parts of the wave, from lower to higher frequency respectively. Now, as some recent researches suggest (Newson and Thiagarajan 2019), the definition of such bands varies in different studies. Considerable inconsistency in marking the start and the end of the bands are prevalent, making the results harder to compare. Moreover, the nature of the 1/f noise displays change with factors such as age (Voytek et al. 2015). So, the bands and related frequencies have a huge degree of variability to begin with—which again, resorts to approximation and makes them unreliable neural markers (although a lot of literature and clinical methodologies continue to use the traditional divisions).

Returning to the complexity argument, the oscillatory archetype tends to miss one of the most important factors which needs addressing—the amount of information loss. While breaking the whole signal down into several ‘wave’ parts, one tends to gross out the complex non-stationary nature of the series neglecting important complexity features. Such information deficit, in turn, could end up portraying an incomplete illustration of the system in question. As put eloquently by Thiagarajan (2018), spectral decomposition of a complex EEG signal is analogous to describing an artwork by reducing it to its basic color components and discussing how much red, green or blue it has, while throwing away the data on the pixel’s relative positioning. Though this might churn out occasional accuracy (like higher green and blue is more likely to be a landscape), but to identify the scene more appropriately, one should approach the complex structure as a whole instead of in parts.

Considering these arguments, the entire artifact-free EEG signal was used for complexity analysis in this study.

Multifractal detrended fluctuation analysis (MFDFA)

Originated from Chaos theory, fractal techniques are essential to underline the complex details hidden in an otherwise random or chaotic process. In many natural processes which are chaotic in nature, fractals help to scale the nature of chaos to an accessible level. From the structure of viruses to the distribution of earthquakes, fractal patterns are inherent in nature. These techniques determine the scaling exponent of the signal or structure in question to indicate the presence or absence of fractal properties (self-similarity). The essence of the technique hides into finding the Fractal Dimension (FD) which proves to be a powerful tool to detect self-similarity. Multifractals, a step further, are sets of intertwined fractals. The real-life fractal patterns that we see hardly scale according to a single scaling exponent, rather there should be multiple scaling laws to capture their growth or variation over time. These spatial and temporal scale variations indicate a multifractal structure of a particular signal. For these more practical cases, Kantelhardt et al. (Kantelhardt et al. 2002) formulated the MFDFA algorithm. Since its inception, it has been applied in diverse fields starting from turbulence analysis (Telesca and Lovallo 2011), traffic movements (Shang et al. 2008), blood flow oscillations (Liao and Jan 2011) to stock exchange (Yuan et al. 2009), and prognosis of diseases (Dutta et al. 2013). Also, in a recent work, which involves human participation, using the multifractal nature of acoustic signal we have shown a correlation between preferred emotional states, signal complexity and RGB values of self-reported colors (Roy et al. 2020).

The analysis of the EEG signals is done using MATLAB in this paper, as described in Ihlen (2012) and for each step an equivalent mathematical representation is given which is taken from the prescription of Kantelhardt et al. (Kantelhardt et al. 2002).

The complete procedure is divided into the following steps:

• Step 1: Converting the noise like structure of the signal into a random walk like signal. It can be represented as:

  $$\text{Y}\left(i\right)=\sum _{k=1}^i\left(x_k-\overline{x}\right)$$ 1

  where $\overline{x}$ is the mean value of the signal.

• Step 2: The whole length of the signal is divided into Ns number of segments consisting of certain no. of samples. For s as sample size and N the total length of the signal the segments are

  $$Ns=\text{int}\left(\frac{N}{s}\right)$$ 2
• Step 3: The local RMS variation for any sample size s is the function F(s,v). This function can be written as follows (detrending of the time series is done by subtracting polynomial fits from profile Y):

  $$F^2(s,v)=\frac{1}{s}\sum _{i=1}^s{\{Y[(v-1)s+i]-y_v(i)\}}^2$$ 3

  Here, y_ν(i) is the form of the fitting polynomial in segment ν (where ν = 1,..., N_s) (Kantelhardt et al. 2002). The polynomial fitted is of order m = 1 (linear detrending).

• Step 4: The q-order overall RMS variation for various scale sizes can be obtained by the use of following equation

  $$F_q(s)={\left\{\frac{1}{\mathit{Ns}}\sum _{v=1}^{\mathit{Ns}}{[F^2(s,v)]}^{\frac{q}{2}}\right\}}^{\left(\frac{1}{q}\right)}$$ 4
• Step 5: The scaling behaviour of the fluctuation function is obtained by drawing the log–log plot of F_q(s) vs. s for each value of q.

  $$F_q\left(s\right)\sim s^{h\left(q\right)}$$ 5

The h(q) is called the generalized Hurst exponent. The Hurst exponent is measure of self-similarity and correlation properties of time series produced by fractal. The presence or absence of long range correlation can be determined using Hurst exponent. A monofractal time series is characterized by unique h(q) for all values of q.

The generalized Hurst exponent h(q) of MFDFA is related to the classical scaling exponent τ(q) by the relation:

$$\tau (q)=qh(q)-1$$ 6

A monofractal series with long range correlation is characterized by linearly dependent q order exponent τ(q) with a single Hurst exponent H. Multifractal signal on the other hand, possess multiple Hurst exponent and in this case, τ(q) depends non-linearly on q (Ashkenazy et al. 2003).

The singularity spectrum f(α) is related to h(q) by

$$\alpha =h(q)+q{h}^{\prime }(q)$$ 7

$$f\left(\alpha \right)=q[\alpha -h\left(q\right)]+1$$ 8

where α denoting the singularity strength and f(α), the dimension of subset series that is characterized by α. The width of the multifractal spectrum essentially denotes the range of exponents. The spectra can be characterized quantitatively by fitting a quadratic function with the help of least square method (Figliola et al. 2007) in the neighbourhood of maximum ${\alpha }_0$,

$$f(\alpha )=A{(\alpha -{\alpha }_0)}^2+B(\alpha -{\alpha }_0)+C$$ 9

Here C is an additive constant C = f(α₀) = 1 and B is a measure of asymmetry of the spectrum. So obviously it is zero for a perfectly symmetric spectrum. We can obtain the width of the spectrum very easily by extrapolating the fitted quadratic curve to zero.

Width W is defined as,

$$W={\alpha }_1-{\alpha }_2$$

With.

$$f({\alpha }_1)=f({\alpha }_2)=0$$ 10

The width of the spectrum gives a measure of the multifractality of the spectrum. Greater is the value of the width W, greater will be the multifractality of the spectrum. For a monofractal time series, the width will be zero as h(q) is independent of q.

The origin of multifractality in an EEG time series can be verified by randomly shuffling the phases in the original data and producing a randomised shuffled series. Most of the long-range correlations that existed in the original data are removed by this random shuffling and what remains is a completely uncorrelated sequence. Hence, if the multifractality of the original data was due to long range correlation, the shuffled data will show non-fractal scaling. To corroborate the findings by comparison, besides phase randomised shuffling a set of surrogate series produced from the original using iAAFT (Iterative Amplitude Adjusted Fourier Transform) (Schreiber and Schmitz 1996) method is also used.

Multifractal detrended cross-correlation analysis (MFDXA)

MFDXA method was first used by Zhou (Zhou 2008). It is an offshoot of the generalized MFDFA method and is used to study the degree of correlation between two non-stationary time series having multifractal features. Here, we compute the profiles of the underlying data series X(i) and Y(i) as

$$\text{X}(\text{i})\equiv [\sum _{(k=1)}^{i}x(k)-{\text{X}}_{\text{avg}}]\text{for}\text{i}=1...\text{N}$$

$$\text{Y}(\text{i})\equiv [\sum _{(k=1)}^{i}x(k)-{\text{X}}_{\text{avg}}]\text{for}\text{i}=1...\text{N}$$ 11

The next steps proceed in the same way as the MFDFA method, with the only difference being we have to take 2N_s bins here. The qth order detrended covariance F_q(s) is obtained after averaging over 2N_s bins.

$$\text{Fq}(\text{s})={\{1/2\text{Ns}{\mathrm{\Sigma }}_{(v=1)}^{2Ns}{[F(s,v)]}^{\text{q}/2}\}}^{1/\text{q}}$$ 12

where q is an index which can take all possible values except zero because in that case the factor 1/q blows up. The procedure can be repeated by varying the value of s. F_q(s) increases with increase in value of s. If the series is long range power correlated, then F_q(s) will show power law behavior

$$F_q(s)\sim s^{\lambda (q)}$$ 13

If such a scaling exists ln F_q will depend linearly on ln s, with λ(q) as the slope. Scaling exponent λ(q) represents the degree of the cross-correlation between the two time series. In general the exponent λ(q) depends on q. We cannot obtain the value of λ(0) directly because F_q blows up at q = 0. F_q cannot be obtained by the normal averaging procedure; instead a logarithmic averaging procedure is applied

$$F_0(s)=\{1/4N_s{\mathrm{\Sigma }}_{(v=1)}^{2Ns}[F(s,v)]\}\sim s^{\lambda (0)}$$ 14

For q = 2 the method reduces to standard DCCA. If scaling exponent λ(q) is independent of q, the cross-correlations between two time series are monofractal. If scaling exponent λ(q) is dependent on q, the cross-correlations between two time series are multifractal. Furthermore, for positive q, λ(q) describes the scaling behavior of the segments with large fluctuations and for negative q, λ(q) describes the scaling behavior of the segments with small fluctuations. Scaling exponent λ(q) represents the degree of the cross-correlation between the two time series X(i) and Y(i). The value λ(q) = 0.5 denotes the absence of cross-correlation. λ(q) > 0.5 indicates persistent long-range cross-correlations where a large value in one variable is likely to be followed by a large value in another variable, while the value λ(q) < 0.5 indicates anti-persistent cross-correlations where a large value in one variable is likely to be followed by a small value in another variable, and vice versa (Movahed and Hermanis 2008).

Zhou found that for two time series constructed by binomial measure from p-model, there exists the following relationship:

$$\lambda \left(q=2\right)\approx \left[h_x\left(q=2\right)+h_y\left(q=2\right)\right]/2$$ 15

Podobnik and Stanley (Podobnik and Stanley 2008) have studied this relation when q = 2 for monofractal Autoregressive Fractional Moving Average (ARFIMA) signals and EEG time series.

In case of two time series generated by using two uncoupled ARFIMA processes, each of both is autocorrelated, but there is no power-law cross correlation with a specific exponent (Movahed and Hermanis 2008). According to auto-correlation function given by:

$$C\left(\tau \right)=〈\left[X\left(i+\tau \right)-〈X〉\right]\left[X(i)-〈X〉\right]〉\sim {\tau }^{-\gamma }$$ 16

The cross-correlation function can be written as

$$C_x\left(\tau \right)=〈⌈X\left(i+\tau \right)-〈X〉⌉\left[Y\left(i\right)-〈Y〉\right]〉\sim {\tau }_x^{-\gamma }$$ 17

where γ and γ_x are the auto-correlation and cross-correlation exponents, respectively. Due to the non-stationarities and trends superimposed on the collected data, direct calculation of these exponents are usually not recommended; rather the reliable method to calculate auto-correlation exponent is the DFA method, namely (Movahed and Hermanis 2008),

$$\gamma =2-2h\left(q=2\right)$$ 18

Podobnik et al. (Podobnik et al. 2011), have demonstrated the relation between cross-correlation exponent, γ_x and scaling exponent λ(q). Using Eq. (15) & (18),

$${\gamma }_x=2-2\lambda \left(q=2\right)$$ 19

For uncorrelated data, γ_x has a value 1 and the lower the value of γ and γ_x more correlated is the data. In general, λ(q) depends on q, indicating the presence of multifractality. Using cross-correlation co-efficient γ_x, we want to point out how two non-linear signals are cross-correlated in various time scales.

Methodological approaches

Using the methodologies discussed above, this paper attempts to explore the neural responses of the participants from two different comparative approaches. To study the brain response change corresponding to each individual color of the VIBGYOR, a comparative analysis of the multifractal spectral width as well as multifractal cross correlation coefficient was done for different pairs of experimental conditions, where each pair consists of a color from VIBGYOR and the adjacent gray just appearing before that particular color (for example, Violet—Grey1 or Green—Grey4). Similarly, to identify the changes among the response from different electrodes corresponding to a particular color, a comparative study of spectral widths and cross-correlation was done for different electrode pairs. Among all the electrode pair combinations some were from the homologous brain regions which in turn reflected the hemispheric differences in the neuronal responses for a particular experimental condition, while the other electrode combinations indicated the nature of connectivity or correlations between different lobes of human brain during viewing a color.

Result and discussions

For the analysis of the EEG data, we studied 9 electrodes, namely: F3, F4, F7, F8, Fz (Frontal), O1, O2 (Occipital) and P3, P4 (Parietal). Although the areas in the brain that are traditionally related to visual perception are Frontal and Occipital lobes, but researches in the recent past have indicated that Parietal lobe too plays key role in visual information processing (Avillac et al. 2005).

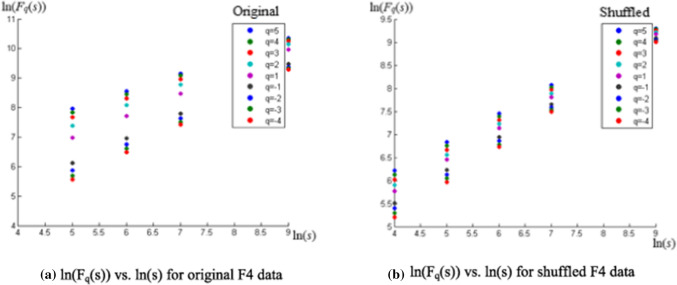
With the noise cleaned EEG signal using EMD process, as described in Maity et al. (2015), first we performed the MFDFA methodology mentioned in the previous section. To emphasize on the unique properties pertaining to such a nonstationary nonlinear time series, features of the original time series is compared with a shuffled series constructed by reorganising the phases in the original data in a randomised fashion, in every step of the process (also in case of MFDXA). The qth order fluctuation function F_q(s) (from Eq. (5)) for 10 values of q in between −5 and + 5 was obtained in the first step. The time series values of the EEG waves have been randomly shuffled to destroy all the long range correlations present in the data, and what remained is a completely uncorrelated sequence. The regression plot of ln(F_q(s)) vs. ln(s) averaged for different values of q (q =  −5 to q =  +5), i.e., the q-order RMS fluctuations, for a sample electrode F4 is given in Fig. 3 a, b (in the graph, q =  −4 to q =  +5 is shown):

Fig. 3.

a, b Plot of ln(F_q(s)) vs. ln(s) showing different h(q) corresponding to each q; the scaling range being 16 to 1024. For the original series (a), the scaling function F_q and regression slope h(q) is dependent on q, unlike the shuffled series (b) which has a fixed slope H, indicating monofractality

The scaling range is 16 to 1024 (scales used are: 16, 32, 64, 128, 256, 512 and 1024). Again from Eq. (5), we see that Hurst exponent h(q) is obtained from the slope of the best fit line in the ln(Fq(s)) vs. ln(s) plot. It can be seen from Fig. 3a that for the original data, the slopes change (the points gradually converge) with changing q’s. But they remain same with different values of q, for the shuffled data (Fig. 3b). Thus, they have a fixed slope h(q) = H (~2, generally), which is the conventional Hurst exponent for monofractal time series.

The next step is to calculate the statistical fit of the different values of h(q) corresponding to different values of q for the nine electrodes in all the experimental conditions. Now, for positive values of q, h(q) describes the scaling behaviour of the segments with large fluctuations. Usually, the large fluctuations are characterized by a smaller scaling exponent h(q) for multifractal series. On the contrary, for negative values of q, the segments v with small variance F²(s,v) will dominate the average F_q(s). Hence, for negative values of q, h(q) describes the scaling behaviour of the segments with small fluctuations, which are usually characterized by larger scaling exponents. For all the EEG data in our experiment, considerable variation of h(q) with the change of q from −5 to + 5 were observed, indicating the presence of strong multifractality in the EEG waves. The randomly shuffled series, bereft of the long-range correlations present in the original, exhibits a non-multifractal scaling, h_shuf(q) ∼ 0.5, in most cases. This value remains almost constant with the change of q values. This confirms the monofractal nature of the shuffled series. On the other hand, for the original data, h(q) changes with changing q (higher values for negative q, lower values for positive). This variance of h(q) indicates that long range correlations, and by extension multifractality, are present in the original EEG data in different scales.

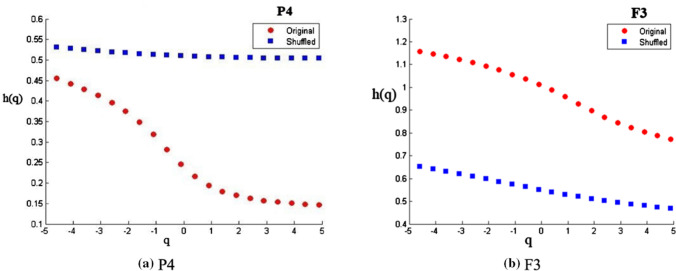
Figure 4a, b contains two representative figures of h(q) vs q plots from two randomly chosen electrodes F3 and P4. It is evident from the figures that for original series (in red), h(q) decreases with increasing q, showing multifractal scaling in both the electrodes. The shuffled series (in blue), very similar to a monofractal signal, has almost constant values of h(q) for different q’s.

Fig. 4.

The variations of h(q) vs. q for (a) P4 and (b) F3 electrodes. For the original series (red dots) h(q) changes with q (higher for −ve q, lower for + ve). The shuffled series (blue dots) has almost a constant h(q) ~ 0.5. Variance of h(q) shows the presence of long-range correlations in the original series

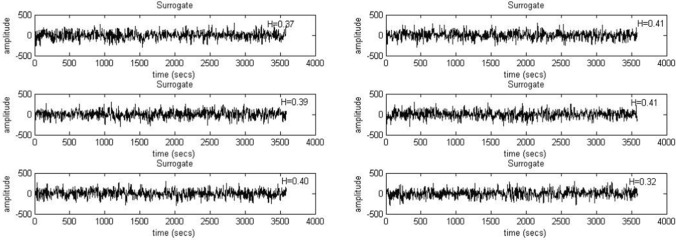
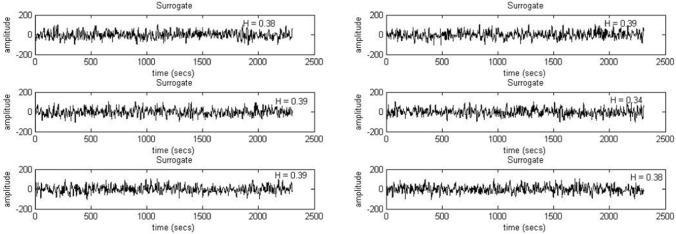
The EEG time series corresponding to each experimental condition was shuffled and the hurst values were calculated and compared with the same for the original series. The results suggest that in the original time series, the presence of multifractality can be observed. Next, to reassure the same findings, we calculated 6 phase randomized surrogates for each EEG time series segments (corresponding to each electrode during each experimental condition) following the iAAFT method (Schreiber and Schmitz 1996) and calculated the hurst values for all the surrogate series to compare them with the original series. The results clearly demonstrate that hurst values of the surrogate series were much lower than that of the original ones (≤ 0.5). This indicates that the multifractality present in the original signal gets destroyed when the surrogates are generated through phase randomization. Two such sample plots are given in Fig. 5 (F3, Blue) and Fig. 6 (O2, Yellow) for two random participants.

Fig. 5.

Six surrogates generated for F3 electrode under Blue color exposure for a random participant using iAAFT. The H stands for respective Hurst values which are far lower than 0.5, pointing at loss of multifractal properties when the data is shuffled randomly

Fig. 6.

Six surrogates generated for O2 electrode under Yellow color exposure for a random participant using iAAFT. H stands for respective Hurst values which are far lower than 0.5, pointing at the loss of multifractal properties when the data is shuffled randomly

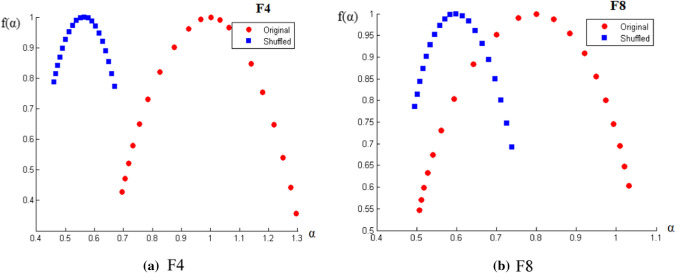
Now, after confirming the presence, next step is the quantitative analysis of multifractality. The amount of multifractality can be determined for each of the experimental window for every signal from the width of the multifractal spectrum (w) from the f(α) vs. α curve as per Eq. (9). Two representative figures of such curves for two electrodes along with their shuffled series are shown in Fig. 7. As seen from the equation, the nature of the curve is parabolic. Also, the shuffled width is found to be smaller than the width of the original signal; which tells us that the long range correlations are present in the signal which gives rise to the multifractality. Ideally, for a sufficiently long series, the shuffled data exhibit monofractal properties (no mulifractal scaling) and f(α) would be of constant value, independent of α. Thus, as discussed previously, Hurst exponent remains independent of q and in the f(α) vs. α curve, the shuffled width has a constant f(α) peaked around α₀ ~ 0.5.

Fig. 7.

a, b The variation of f(α) vs. α for two randomly chosen electrodes (a) F4 and (b) F8, along with shuffled data. This parabolic curve represents the multifractal spectrum where α is q-order singularity exponent and f(α) are its dimensions. Δα (= α_max – α_min) is the spectral width, which, for original series (red) is higher than its shuffled form (blue)—indicates multifractal nature

The values of the spectral width of EEG data corresponding to each electrode for all the experimental conditions were computed. Spectral width values and their standard deviations are averaged for 16 participants. The data are presented both electrode-wise and color-wise in Tables 2 and 3, for better interpretation purposes.

Table 2.

Multifractal Spectral width for different colors (Electrode-wise); averaged over n = 16

	Multifractal width (w) corresponding to the colors with SD
Electrode	Grey1	Violet	Grey2	Indigo	Grey3	Blue	Grey4
F3	0.364 ± 0.038	0.516 ± 0.048	0.393 ± 0.046	0.501 ± 0.050	0.351 ± 0.049	0.648 ± 0.049	0.371 ± 0.017
F4	0.350 ± 0.032	0.508 ± 0.038	0.347 ± 0.044	0.492 ± 0.036	0.371 ± 0.048	0.654 ± 0.044	0.380 ± 0.026
F7	0.360 ± 0.046	0.511 ± 0.048	0.397 ± 0.041	0.494 ± 0.015	0.359 ± 0.026	0.651 ± 0.038	0.391 ± 0.028
F8	0.360 ± 0.048	0.505 ± 0.029	0.363 ± 0.050	0.501 ± 0.051	0.340 ± 0.047	0.669 ± 0.050	0.391 ± 0.037
Fz	0.378 ± 0.010	0.511 ± 0.018	0.403 ± 0.040	0.493 ± 0.024	0.375 ± 0.016	0.622 ± 0.025	0.376 ± 0.038
O1	0.387 ± 0.15	0.518 ± 0.038	0.389 ± 0.013	0.497 ± 0.006	0.381 ± 0.026	0.645 ± 0.012	0.398 ± 0.009
O2	0.385 ± 0.010	0.508 ± 0.016	0.389 ± 0.033	0.502 ± 0.006	0.384 ± 0.015	0.682 ± 0.024	0.397 ± 0.029
P3	0.374 ± 0.035	0.506 ± 0.017	0.382 ± 0.022	0.501 ± 0.018	0.360 ± 0.038	0.636 ± 0.033	0.387 ± 0.027
P4	0.404 ± 0.029	0.512 ± 0.037	0.408 ± 0.038	0.498 ± 0.020	0.403 ± 0.046	0.664 ± 0.020	0.406 ± 0.031

	Multifractal width (w) corresponding to the colors with SD
Electrode	Green	Grey5	Yellow	Grey6	Orange	Grey7	Red	Grey8
F3	0.559 ± 0.038	0.381 ± 0.043	0.492 ± 0.033	0.373 ± 0.037	0.542 ± 0.048	0.403 ± 0.049	0.585 ± 0.022	0.389 ± 0.028
F4	0.547 ± 0.049	0.376 ± 0.038	0.507 ± 0.014	0.402 ± 0.036	0.542 ± 0.026	0.434 ± 0.041	0.587 ± 0.026	0.406 ± 0.039
F7	0.550 ± 0.039	0.383 ± 0.057	0.504 ± 0.028	0.392 ± 0.046	0.534 ± 0.039	0.390 ± 0.018	0.580 ± 0.026	0.411 ± 0.031
F8	0.563 ± 0.031	0.381 ± 0.030	0.508 ± 0.026	0.397 ± 0.046	0.526 ± 0.019	0.412 ± 0.021	0.606 ± 0.025	0.384 ± 0.018
Fz	0.539 ± 0.015	0.385 ± 0.022	0.499 ± 0.011	0.397 ± 0.006	0.521 ± 0.033	0.415 ± 0.009	0.592 ± 0.020	0.422 ± 0.012
O1	0.547 ± 0.034	0.404 ± 0.036	0.509 ± 0.014	0.412 ± 0.004	0.544 ± 0.014	0.416 ± 0.010	0.585 ± 0.027	0.428 ± 0.007
O2	0.558 ± 0.014	0.428 ± 0.039	0.526 ± 0.034	0.408 ± 0.020	0.547 ± 0.030	0.416 ± 0.012	0.589 ± 0.026	0.433 ± 0.019
P3	0.547 ± 0.013	0.394 ± 0.021	0.499 ± 0.049	0.399 ± 0.015	0.554 ± 0.038	0.408 ± 0.030	0.583 ± 0.024	0.412 ± 0.010
P4	0.565 ± 0.021	0.415 ± 0.044	0.511 ± 0.040	0.413 ± 0.048	0.548 ± 0.028	0.434 ± 0.019	0.598 ± 0.025	0.441 ± 0.051

Table 3.

Multifractal Spectral width for different electrodes (Color-wise); averaged over n = 16

	Multifractal width (w) corresponding to the electrodes with SD
Colors	F3	F4	F7	F8	Fz	O1	O2	P3	P4
Violet	0.516 ± 0.048	0.508 ± 0.038	0.511 ± 0.048	0.505 ± 0.029	0.511 ± 0.018	0.518 ± 0.038	0.508 ± 0.016	0.506 ± 0.017	0.512 ± 0.037
Indigo	0.501 ± 0.050	0.492 ± 0.036	0.494 ± 0.015	0.501 ± 0.051	0.493 ± 0.024	0.497 ± 0.006	0.502 ± 0.006	0.501 ± 0.018	0.498 ± 0.020
Blue	0.648 ± 0.049	0.654 ± 0.044	0.651 ± 0.038	0.669 ± 0.050	0.622 ± 0.025	0.645 ± 0.012	0.682 ± 0.024	0.636 ± 0.033	0.664 ± 0.020
Green	0.559 ± 0.038	0.547 ± 0.049	0.550 ± 0.039	0.563 ± 0.031	0.539 ± 0.015	0.547 ± 0.034	0.558 ± 0.014	0.547 ± 0.013	0.565 ± 0.021
Yellow	0.492 ± 0.033	0.507 ± 0.014	0.504 ± 0.028	0.508 ± 0.026	0.499 ± 0.011	0.509 ± 0.014	0.526 ± 0.034	0.499 ± 0.049	0.511 ± 0.040
Orange	0.542 ± 0.048	0.542 ± 0.026	0.534 ± 0.039	0.526 ± 0.019	0.521 ± 0.033	0.544 ± 0.014	0.547 ± 0.030	0.554 ± 0.038	0.548 ± 0.028
Red	0.585 ± 0.022	0.587 ± 0.026	0.580 ± 0.026	0.606 ± 0.025	0.592 ± 0.020	0.585 ± 0.027	0.589 ± 0.026	0.583 ± 0.024	0.598 ± 0.025

The graphical representation of the Tables 2 and 3 is given in Figs. 8 and 9, respectively.

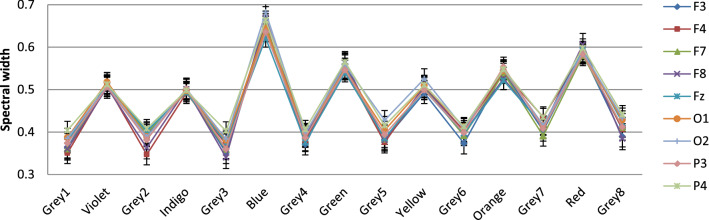
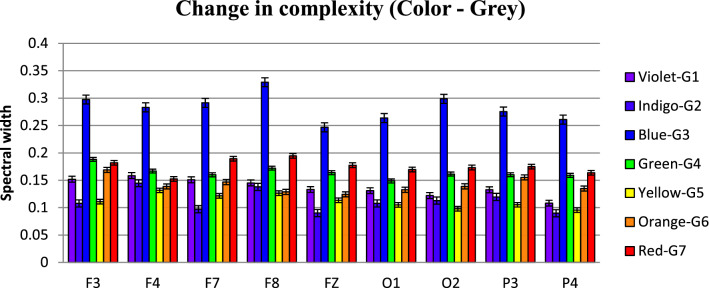
Fig. 8.

Variation in Multifractal spectral width due to different colors in nine chosen electrodes: the complexity pattern stays similar across electrodes. Three primary colors Blue, Green and Red exhibit highest multifractal widths, baseline Gray stays almost the same. Shorter wavelengths have higher width than longer ones

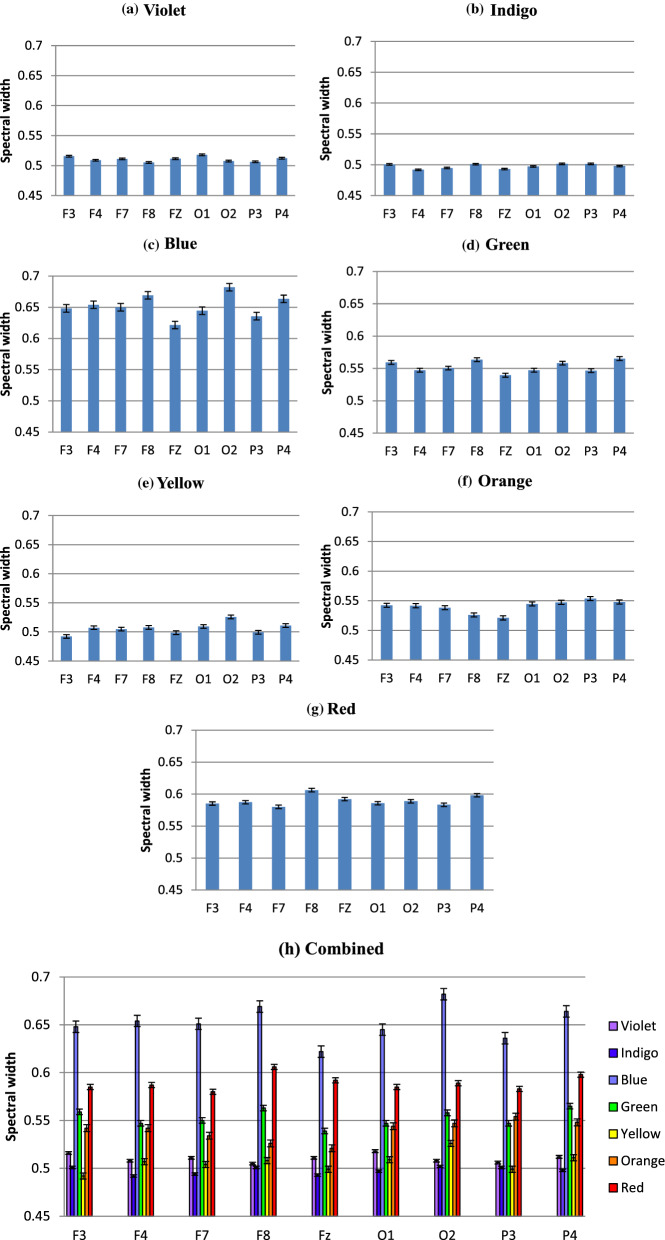
Fig. 9.

a–h Variation in average Multifractal Spectral width in different electrodes, color-wise: Blue-Green end of the spectrum (c–d) has higher width than Orange-Red end (f–g), Indigo (b) and Yellow (e) being the lowest. Even electrodes O2, F8 and P4 register highest width (h), suggestive of right brain arousal preference

Figure 8 describes the electrode-wise changes due to various color stimuli. It is clearly evident from the figure that the change of multifractality is present in all the electrodes under consideration. The usual participation of Frontal and Occipital lobes in visual perception is confirmed, with the addition that Parietal lobes, too exhibit appreciable changes in arousal level. All electrodes, interestingly, exhibit similar pattern, too—multifractal width increases with the exposure to VIBGYOR colors and decrease with Grey baseline. This behavior is consistent throughout the electrodes, during the whole experimental procedure. Another major trend which is similar across all 16 participants is the nature of variation in spectral width in presence of some specific colors. The value of spectral width is maximum in case of Blue, followed by Red and then Green. This trend has also been exhibited by all of the electrodes in general, which is a unique and important observation. In fact, the shorter wavelength part of the spectrum has higher width than the longer wavelength end, indicating that changes in signal complexity are more pronounced in former than the latter (to demonstrate this, the difference between the width during colors and the width during baseline Grey is necessary, which has been done later). This observation is novel since previous studies involved with colors are done to correlate them with some specific psychological attributes using task based experimental setup and no study, specially not one with non-linear techniques, has compared the colors solely on their influence on brain activity. From this perspective, the fact that color Blue induces the highest long range correlations followed by Red and then Green might help explain some of the results obtained in prior researches. That being said, it is noteworthy that, three of the primary colors exhibit clearer complexity changes than the other colors in the spectrum. This supports the reasoning behind the usage of Red, Blue and Green in most of the studies in this field.

Lastly, it can be seen that the complexity for baseline Grey over the experiment has changed as well, although not that prominent. This could be because of the existence of the color exactly prior to it, since the long range correlations present during that may not have perished completely, i.e., a residual effect might be present. Future experiments, focusing on this very aspect, are needed for detailed explanations.

Figure 9, representing the information in Table 3, shows multifractal width variations in different electrodes, color-wise. The observations made from the previous figure are more evident here. Complexity changes in shorter wavelengths like Blue or Green is higher than Red (and Orange). Width is lowest in case of Indigo and Yellow, whereas Violet and Orange is comparatively close. Another noteworthy observation is, in most cases (considering absolute values of multifractal width) F8, O2 and P4 has the highest complexity among the Frontal, Occipital and Parietal electrodes, respectively. So, the even electrodes show higher complexity than odd electrodes, which is an indicator that in our experimental setup, the long range correlations found during color perceptions are higher in the right hemisphere in the brain.

To compare this result with the pattern for change in complexity (i.e., the complexity value of the grey baseline subtracted from the absolute complexity value corresponding to the immediately next color), a graph similar to Fig. 9h has been computed. It is given in Fig. 10.

Fig. 10.

Increase in Multifractal width from baseline Grey in nine elctrodes: the relative change of multifractal width is highest in F8 and O2, showing right hemispere bias in color perception. Also, change in width is highest in Frontal > Occipital > Parietal

Similar to the absolute values, the changes in multifractal width are also highest in case of F8 and O2 (Violet being the only exception). Additionally, significant increase in F3 is noticed. For Parietal lobe, it is P3 which shows higher change in complexity instead of P4. Now, lateralization of color perception is a hotly debated issue in neuroscience literatures. Evidences have credited the bias to left (Franklin et al. 2008) as well as to right hemisphere (Njemanze et al. 1992). Some have found a balanced opinion that both hemispheres contribute in same extent (Witzel and Gegenfurtner 2011). According to the lateralized category effect of colors, in the color naming tasks, left hemisphere advantage is dominant since the language lateralization also favors the left. On the other hand, the right hemisphere bias is seen during color working memory and discriminating properties like hue or saturation (Davidoff 1976). In this light, aforementioned finding of our study, of course not related to color naming but color perception, the presence of increased complexity in mostly the right hemisphere electrodes could be very significant.

There is one more takeaway from Figs. 9 and 10 worth mentioning. When the absolute values of complexity are considered, the Occipital lobe is seen to have the highest values followed by Frontal and then Parietal. But in the case of relative changes to baseline Grey, the complexity measures changes to Frontal > Occipital > Parietal. This indicates that during Grey viewing, Occipital and Parietal lobes display higher complexities than the Frontal lobe. Knowing the fact that Occipital lobes are primarily responsible for visual perception, this result doesn’t come as a surprise. But the interesting part is—Parietal lobe also takes part in the visual process actively. Previous studies have reported such involvements (Battelli et al. 2009), though in a different context. This study, through measuring brain complexity via electrical activities, renders support to these claims.

Lastly, from both plots of Figs. 9 and 10, it is seen that signal corresponding to the frontal midline electrode Fz has recorded lower complexity compared to other frontal electrodes. Frontal midline power has usually been associated with emotional processing and positive emotional state (Suetsugi et al. 2000; Aftanas and Golocheikine 2001; McFarland et al. 2016). Lower complexity, and therefore, lower activation of Fz might be an indication that in this case, the color perception didn’t involve any emotional arousal among the participants.

For the next part of the analysis using MFDXA, the combinations with the electrodes that were studied are: Left and Right hemisphere in Frontal (F3–F4, F7–F8, F3–F8, F4–F7) Occipital (O1–O2) and Parietal (P3–P4) lobes, Intra left (F3–F7) and right (F4–F8) hemisphere, Left Frontal and Occipital lobes (F3–O1, F3–O2, F7–O1, F7–O2), Right Frontal and Occipital lobes (F4–O1, F4–O2, F8–O1, F8–O2), Left Frontal and Parietal lobes (F3–P3, F3–P4, F7–P3, F7–P4), Right Frontal and Parietal lobes (F4–P3, F4–P4, F8–P3, F8–P4) and finally, Occipital and Parietal lobes (O1–P3, O1–P4, O2–P3, O2–P4). The total 28 combinations of electrodes were studied for all the experimental conditions. First, the noise cleaned EEG data were divided into N_s bins where N_s = int (N/s), N is the length of the series. The q-th order detrended covariance F_q(s) was obtained for values of q from −5 to + 5 in steps of 1. Power law scaling of F_q(s) with s is observed for all values of q. As shown in Eq. (13), the slope of this scaling λ(q) is the desired scaling exponent, which depends on q. A representative figure of the variation of λ(q) with changing q is given in Fig. 11 for F4-O2 electrodes during Violet color stimulus.

Fig. 11.

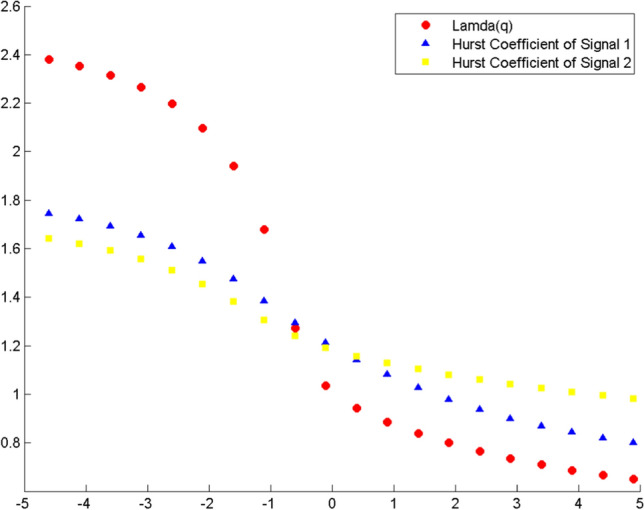
Variation of scaling exponent λ(q) with q for F4–O2 electrode combination for Violet color exposure. The combination (red) is plotted against h(q) versus q of the individual signals F4 (blue) and O2 (yellow). The series has monofractal properties if the scaling exponent stays ~ 0.5 at q = 2. Here, λ(q) > 0.5, showing multifractality

For comparison, the variation of H(q) with q individually for the same two electrodes F4 and O2 using MFDFA is shown in the same figure. The scaling exponent should have a constant value for a monofractal series, otherwise it implies multifractality. The plot indicates multifractal behavior of the cross-correlated time series, as for q = 2 the cross-correlation scaling exponent λ(q) is greater than 0.5 which is a confirmation of persistent long-range cross-correlation between the two electrodes. In a similar manner, λ(q) was evaluated for all the electrode combinations under consideration. The q-dependence of the classical multifractal scaling exponent τ(q) is shown in Fig. 12 for the electrodes F4 and O2. From the figure, it can be seen that the dependence of τ(q) on q is non-linear, which is another evidence of multifractality of the series.

Fig. 12.

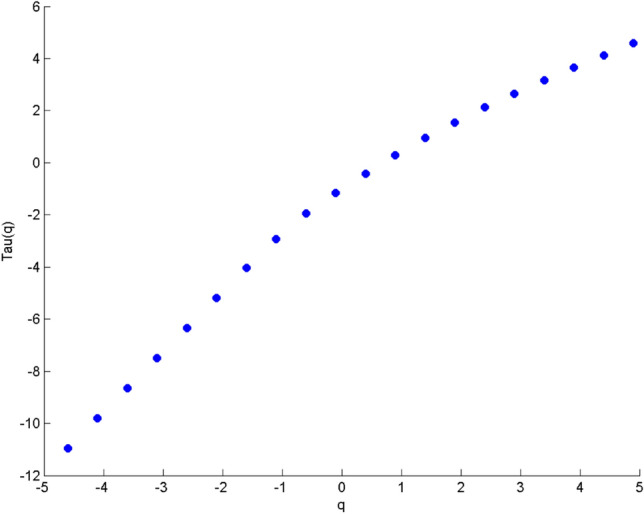
Variation of classical multifractal scaling exponent τ(q) (Kantelhardt et al. 2002) with q for F4-O2 electrode combination. In this case, τ(q) is a non-linear function of q, which suggests the presence of multifractality

Now, the multifractal width of the cross correlated signals of F4 and O2 is given in Fig. 13. The presence of spectral width in cross correlation data confirms the presence of multifractality in the correlated signal yet again.

Fig. 13.

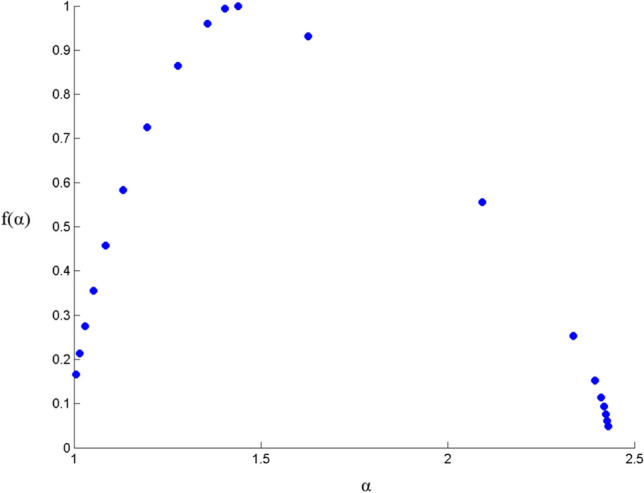
Multifractal spectral width for cross-correlated electrodes F4 and O2. The relation of α (q-order singularity exponent) and f(α) (dimension of the series) represents the multifractal spectrum. Δα (= α_max – α_min) is the spectral width. The parabolic nature and the peak at α > 0.5 indicate presence of multifractal properties (Ihlen 2012)

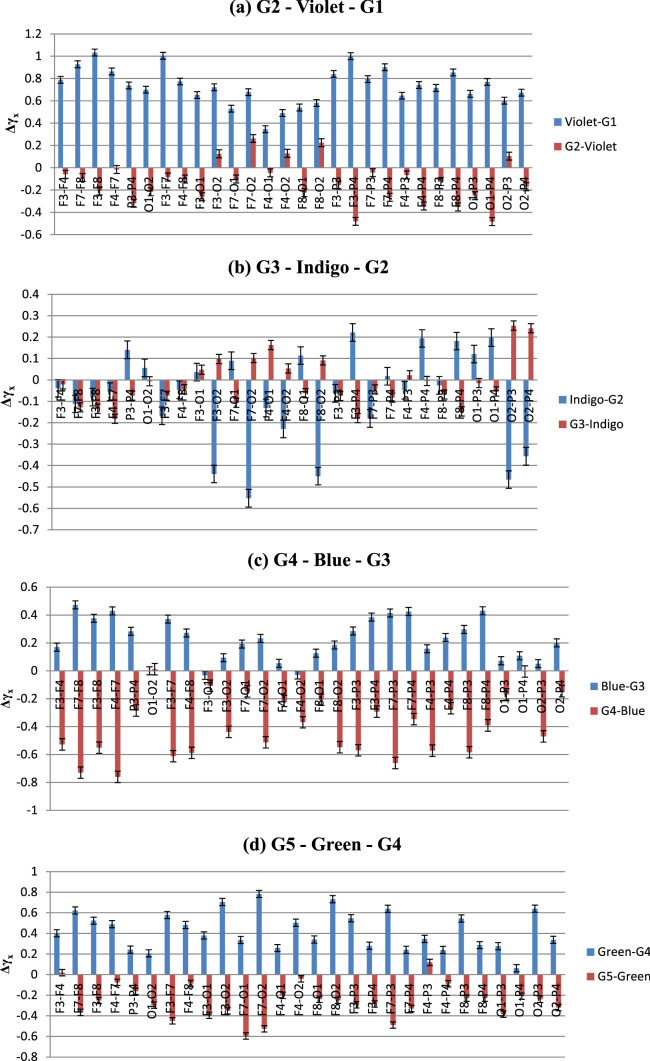
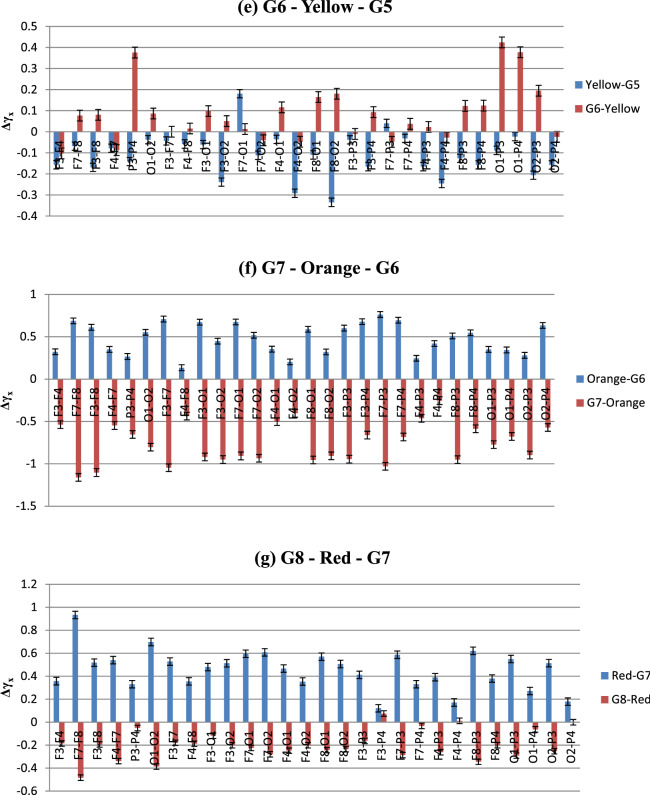
The fact that correlated signals from two electrodes in experimental conditions showing multifractality is an important observation for colour perception studies using nonlinear EEG analysis. The same analysis was done for the rest of the electrode combinations as well to find out the cross-correlation coefficient (γ_x) for all 16 participants. After that, similarly as MFDFA analysis, the averaged change in γ_x due to the color stimulus and the baseline Grey has been computed by calculating their differences. This gives us the change in cross-correlation co-efficient (Δγ_x) which is an effective tool for spotting the increase/decrease in cross-correlation pattern with the subsequent changes in experimental conditions (Sanyal et al. 2019). The data and the plots depicting the variations of Δγ_x during different stages of the experiment are shown in Table 4 and Fig. 14. Increase and decrease in the values of Δγ_x corresponds to reduced and enhanced degree of cross-correlations, respectively.

Table 4.

Changes in cross-correlation coefficient γ_x in electrode combinations in both (color—Grey) and (Grey—color) conditions; for n = 16. The bold ones (F3-F4, F7-F8, F3-F8, F4-F7, P3-P4, O1-O2, F3-F7, F4-F8) belong to the combinations representing homologous brain areas (Frontal, parietal and Occipital)

	Average difference in γx in experimental conditions (color—Grey) and (Grey—color)
Electrode combinations	Violet—G1	G2—Violet	Indigo—G2	G3—Indigo	Blue—G3	G4—Blue	Green—G4	G5—Green	Yellow—G5	G6—Yellow	Orange—G6	G7—Orange	Red—G7	G8—Red
F3–F4	0.788	−0.058	−0.039	−0.021	0.170	−0.528	0.401	0.019	−0.156	−0.103	0.323	−0.537	0.357	−0.185
F7–F8	0.928	−0.089	−0.112	−0.128	0.473	−0.730	0.622	−0.366	−0.068	0.077	0.687	−1.160	0.933	−0.483
F3–F8	1.032	−0.208	−0.080	−0.135	0.377	−0.551	0.524	−0.251	−0.169	0.081	0.611	−1.103	0.518	−0.194
F4–F7	0.863	−0.015	−0.055	−0.182	0.430	−0.760	0.490	−0.075	−0.078	−0.087	0.351	−0.548	0.539	−0.339
P3–P4	0.737	−0.318	0.140	−0.073	0.283	−0.284	0.243	−0.161	−0.141	0.376	0.267	−0.653	0.330	−0.051
O1–O2	0.700	−0.216	0.056	−0.006	0.000	0.011	0.207	−0.297	−0.037	0.087	0.553	−0.802	0.698	−0.386
F3–F7	1.003	−0.084	−0.168	−0.075	0.372	−0.612	0.578	−0.448	−0.043	0.000	0.709	−1.046	0.528	−0.179
F4–F8	0.773	−0.101	−0.046	−0.044	0.272	−0.588	0.482	−0.086	−0.058	0.016	0.134	−0.437	0.355	−0.187
F3–O1	0.653	−0.261	0.036	0.048	−0.032	−0.106	0.380	−0.395	−0.061	0.098	0.672	−0.920	0.479	−0.117
F3–O2	0.720	0.125	−0.440	0.098	0.094	−0.437	0.705	−0.351	−0.239	0.051	0.448	−0.950	0.513	−0.201
F7–O1	0.529	−0.101	0.090	−0.107	0.192	−0.147	0.337	−0.595	0.181	0.013	0.674	−0.907	0.595	−0.224
F7–O2	0.678	0.262	−0.553	0.102	0.232	−0.513	0.783	−0.525	−0.112	−0.040	0.517	−0.933	0.608	−0.279
F4–O1	0.345	−0.046	−0.131	0.163	0.054	−0.215	0.258	−0.201	−0.036	0.116	0.354	−0.502	0.467	−0.248
F4–O2	0.489	0.129	−0.229	0.053	−0.030	−0.368	0.504	−0.041	−0.292	−0.047	0.203	−0.404	0.354	−0.201
F8–O1	0.540	−0.223	0.114	−0.062	0.127	−0.208	0.341	−0.239	−0.110	0.165	0.589	−0.955	0.571	−0.244
F8–O2	0.581	0.224	−0.450	0.091	0.185	−0.547	0.732	−0.249	−0.335	0.181	0.320	−0.906	0.506	−0.235
F3–P3	0.840	−0.155	−0.063	−0.075	0.286	−0.570	0.546	−0.292	−0.038	−0.010	0.602	−0.945	0.412	−0.163
F3–P4	1.006	−0.481	0.221	−0.179	0.385	−0.293	0.281	−0.284	−0.165	0.094	0.678	−0.661	0.121	0.075
F7–P3	0.794	−0.043	−0.180	−0.045	0.414	−0.660	0.639	−0.490	0.040	−0.048	0.763	−1.029	0.586	−0.287
F7–P4	0.901	−0.265	0.017	−0.083	0.426	−0.346	0.241	−0.328	−0.031	0.038	0.695	−0.684	0.331	−0.032
F4–P3	0.646	−0.065	−0.049	0.021	0.159	−0.572	0.347	0.119	−0.165	0.023	0.245	−0.463	0.391	−0.261
F4–P4	0.741	−0.343	0.194	−0.005	0.238	−0.268	0.239	−0.088	−0.245	−0.028	0.420	−0.254	0.171	0.012
F8–P3	0.715	−0.123	−0.025	−0.068	0.298	−0.584	0.545	−0.228	−0.126	0.122	0.509	−0.950	0.621	−0.344
F8–P4	0.854	−0.351	0.181	−0.147	0.431	−0.391	0.286	−0.228	−0.157	0.124	0.547	−0.586	0.380	−0.201
O1–P3	0.662	−0.250	0.121	−0.015	0.072	−0.169	0.276	−0.384	−0.088	0.424	0.350	−0.773	0.549	−0.291
O1–P4	0.768	−0.483	0.198	−0.054	0.108	−0.005	0.063	−0.209	−0.023	0.377	0.344	−0.677	0.272	−0.063
O2–P3	0.601	0.104	−0.466	0.254	0.051	−0.471	0.640	−0.240	−0.206	0.195	0.280	−0.896	0.514	−0.253
O2–P4	0.673	0.170	−0.357	0.241	0.200	−0.147	0.338	−0.319	−0.157	−0.024	0.633	−0.571	0.179	−0.003

Fig. 14.

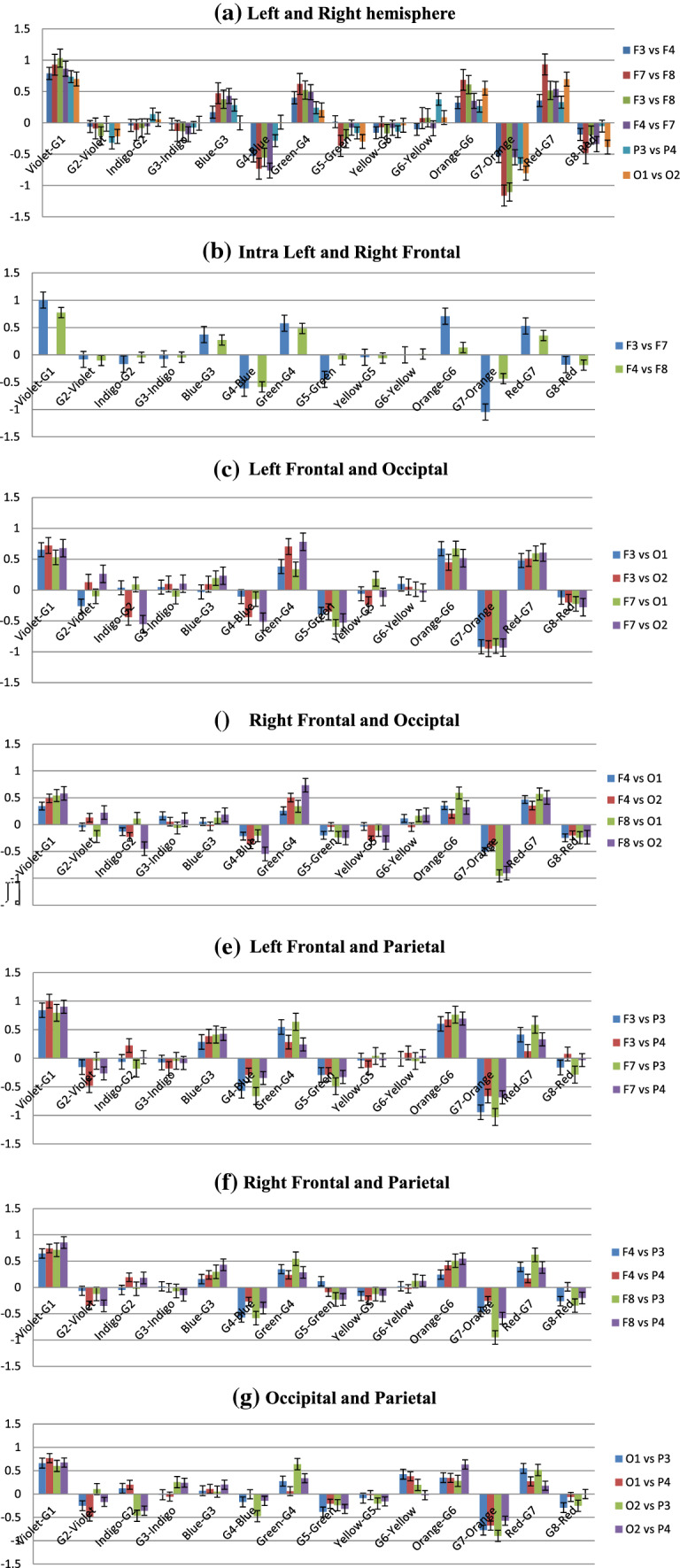
a–g Changes in cross-correlation coefficient (Δγ_x) in electrode combinations in both (color—Grey) and (Grey—color) conditions. Negative values indicate higher cross-correlation. Pattern of change is consistent across different brain areas, remarkably higher correlation after stimulus color removal than during exposure

The graphical representation of Table 4 is shown below in Fig. 14 (Standard deviations are included as error bars).

From Fig. 14, it is seen that although the degree of cross-correlation has varied throughout the experiment, the nature of the change is somewhat similar in electrode combinations. One of the most remarkable features seen in this data is the existence of high cross-correlation in the electrodes during the baseline Grey period, in various occasions. This is fascinating considering the fact that it happened in almost all the inter/intra lobe combinations, which indicates that the responses across different lobes of the brain have stayed correlated irrespective of their spatial distribution. Moreover, in most cases, colour exposure has increased the Δγ_x, meaning that introduction of color stimulus has reduced the cross-correlation. This observation is unique and hitherto unseen from the point of view of color perception. The highest Δγ_x, and least correlations, is observed during the introduction of Violet from Grey1. On the other hand, shift to Grey7 from color Orange displayed lowest Δγ_x and most enhanced degree of cross-correlations. Interestingly, exposure to colors that exhibited highest complexity in MFDFA—Blue, Red and Green—resulted in reduced cross-correlation whereas the Greys before or after them expressed enhanced effects of the same. To study the correlations in more spatial manner, we rearranged the plots highlighting each experimental condition. They are given in Fig. 15.5

Fig. 15.

a–g Color-wise distribution of Δγ_x in specific (color—Grey) and (Grey—color) conditions. Negative values indicate higher correlation. Except for Indigo (b) and Yellow (e), correlation decreases on color exposure and increases on removal; magnitude of Δγ_x is highest during Orange (f)

Figure 15a–g shows the changes in cross-correlation co-efficient in specific experimental conditions in all the electrode combinations (Standard deviations are included as error bars). In case of Violet and related Greys, Δγ_x increases in all the electrodes when stimulus is changed from Grey1 to violet, implying lower cross-correlation. During Violet to G2, correlation increases mainly in Occipital and Parietal electrodes, slightly in F3 and F8 combinations. In the next colour, this pattern is reversed. When exposed to Indigo, high correlations are seen in O2 electrode combinations and in left Frontal electrodes F3 and F7. Change to G3 results in reduced correlation in most of the electrodes, except the Frontal ones. For Blue, the pattern follows Violet once again. While G3 to Blue, correlations decrease throughout with higher Δγ_x and Blue to G4 sees significant increase in cross-correlation throughout the brain. Green, too, shows the similar trend—correlation vanishes during its presence and increases hugely after going to next Grey, i.e., G5. Yellow, like Indigo, breaks the norm with high correlations in general (except in F7–O1) which gets destroyed with its removal. The next color shows striking consistency in all the participants. Orange follows the Blue and Green pattern, but with higher amplitude than any other colors. The cross-correlation is as high during the stimulus removal as the decrease while the color is on. This trend continues for the last color stimulus, Red, albeit in lower volumes.

To sum up, the figures indicate that except for Indigo and Yellow (interestingly the colors with lowest complexities), rest of the colors show similar patterns in the change of degree of cross-correlation (Δγ_x)—during the color viewing, Δγ_x increases which results in reduced correlations. Once the stimulus is removed, the correlations spike up. We argue that this ebb and flow of cross-correlations are linked with the processing of visual information—which might be manifested well after the removal of the stimulus. Exposure to the color stimulus affects the bio signals emanating from the areas directly involved in its perception, thus providing the increase in signal complexity, demonstrable via MFDFA. In the post-stimulus period the sensory information collected during the color-viewing window gets processed and integrated via various inter/intra lobe exchanges until the information is sufficiently segregated. These connections and exchanges manifest themselves via the cross-correlation parameter. Such perceptual retention of information has been studied in neuroscience for a long time (some have called it ‘perceptual hysteresis’, analogous to magnetic hysteresis). There have been reports of hysteresis or retention of stimulus perception in visual (Kleinschmidt et al. 2002) and auditory stimulus (Banerjee et al. 2016). Although the purpose or the experimental design in this work is not intended to find out hysteresis of color perception, but the findings could advocate for possible investigations towards it. These findings on the neuronal activity are evidently novel in this field of study and provide a strong argument for the future of robust non-linear methodologies in EEG based color perception research.

Statistical analysis

To test the statistical significance of our results 2-way ANOVA was performed on the multifractal spectral width values considering the colors and the channels as factors and the detailed result of the same has been presented in Table 5.

Table 5.

Detailed result of 2-way ANOVA on multifractal spectral width

Overall ANOVA	df	Sum of squares (SS)	Mean square	F-value	p-value (significance level < .05)
Color	6	2.63599	0.43933	23.30954	9.15E–26
Electrode	8	0.02985	0.00373	0.19795	0.99116
Interaction	48	0.06001	0.00125	0.06634	1
Model	62	2.72585	0.04397	2.33266	8.30E–08
Error	945	17.81107	0.01885	–	–
Corrected total	1007	20.53692	–	–	–

At the 0.05 level (i.e., 95% confidence level), the population means of colors are significantly different.

At the 0.05 level, the population means of Electrodes are not significantly different.

At the 0.05 level, the interaction between color and Electrode is not significant.

Tukey test was done only for the variables with significance. Table 6 includes the post-hoc analysis.

Table 6.

Post hoc analysis (Tukey test) for colors

Means comparisons
Tukey test colors	Mean diff	SEM	q Value	Prob	Alpha	Sig	LCL	UCL
Indigo—Violet	-0.01307	0.01618	1.1421	9.84E-01	0.05	0	−0.06087	0.03474
Blue—Violet	0.14135	0.01618	12.35531	3.53E-09	0.05	1	0.09355	0.18916
Blue—Indigo	0.15442	0.01618	13.49741	2.65E-09	0.05	1	0.10661	0.20222
Green—Violet	0.04233	0.01618	3.69984	1.22E-01	0.05	0	−0.00548	0.09013
Green—Indigo	0.05539	0.01618	4.84195	0.01145	0.05	1	0.00759	0.1032
Green—Blue	−0.09902	0.01618	8.65546	4.12E-08	0.05	1	−0.14683	−0.05122
Yellow—Violet	−0.00461	0.01618	0.40339	0.99996	0.05	0	−0.05242	0.04319
Yellow—Indigo	0.00845	0.01618	0.73871	0.99854	0.05	0	−0.03935	0.05626
Yellow—Blue	−0.14597	0.01618	12.75869	3.21E-09	0.05	1	−0.19377	−0.09816
Yellow—Green	−0.04694	0.01618	4.10323	0.05812	0.05	0	−0.09475	8.63E-04
Orange—Violet	0.02963	0.01618	2.5903	0.52686	0.05	0	−0.01817	0.07744
Orange—Indigo	0.0427	0.01618	3.7324	0.11554	0.05	0	−0.00511	0.09051
Orange—Blue	−0.11172	0.01618	9.76501	1.04E-08	0.05	1	−0.15952	−0.06391
Orange—Green	−0.01269	0.01618	1.10954	0.98644	0.05	0	−0.0605	0.03511
Orange—Yellow	0.03425	0.01618	2.99369	0.34343	0.05	0	−0.01356	0.08206
Red—Violet	0.07896	0.01618	6.90194	2.56E-05	0.05	1	0.03116	0.12677
Red—Indigo	0.09203	0.01618	8.04404	3.62E-07	0.05	1	0.04422	0.13983
Red—Blue	−0.06239	0.01618	5.45337	0.00235	0.05	1	−0.1102	−0.01458
Red—Green	0.03663	0.01618	3.2021	0.26267	0.05	0	−0.01117	0.08444
Red—Yellow	0.08358	0.01618	7.30533	6.07E-06	0.05	1	0.03577	0.13138
Red—Orange	0.04933	0.01618	4.31164	0.038	0.05	1	0.00152	0.09713

Tukey test results, calculated over the population means of the multifractal spectral widths of the color wise EEG responses of the 16 participants also confirm that population mean of spectral width in response to color Blue is significantly different from all other colors. The response to Red and Green also show significant differences from others. But rest of the colors (Indigo, Violet, Yellow and Orange) does not yield such significant changes in the EEG complexities in different lobes of the brain. For the other factors, like electrode channels or interaction between electrode and color, this significance may not appear to be so significant at our predetermined 95% confidence level, but enhancement of sample size, in future, is expected to give further support.

Conclusion and general discussion

The question of how colors affect human beings is a long, much-debated one and has remained so despite years of work. The present literatures concentrate more on the applicative potential of colors in psychological perspective. They report divided opinions on the effects since color perception is often likely to be contextual and overlaps with cultural and linguistic dependency. Moreover, comprehensive studies on the physiological responses are sparse and due to the analysis technique, limited by severe approximations. With this backdrop, our work had set out in an exhaustive investigation of neuronal activities in brain during color perception via its physiological manifestation in EEG. The uniqueness our work offered was twofold—methodological and analysis related. Most of the studies use two or three colors together for comparison and to study their roles in specific psychological attributes. Usage of the whole color spectrum is unconventional otherwise. We have used it in our work to explore the effects of the whole wavelength range of visible light altogether instead of comparing some of them. This, we believe, could demonstrate how brain responds to color in a more extensive manner. And for the analysis part, no other studies have used such rigorous non-linear tools like MFDFA and MFDXA in the domain of color perception. Over the course of the paper, we have seen that this novel approach provides interesting new data in regard to the color perception process which has not been reported ever before. Findings of the MFDFA analysis may be summarized in the following:

1. The presence of fractality in the color induced bio-signals indicates towards their complex non-linear nature. Tackling such systems with linear analysis methods like FFT or power spectral density is not sufficient in understanding the intricacies of color perception. They approximate various parameters and can lead to misleading results. Rigorous statistical tools such as MFDFA are necessary, considering they can identify parameters directly related to the complexities and quantify them, in due course.

2. MFDFA analysis of the color induced EEG shows the presence of multifractality in all the brain areas under consideration i.e., electrodes in Frontal, Occipital and Parietal lobes. Multifractality is quantified by multifractal spectral width, which is a measure of degree of complexity or randomness. The fact that complexity is observed in these brain areas simultaneously suggests that they participate actively during color perception. Occipital and Frontal lobes, being the visual and cognitive centers of the sensory perception, are expected to be involved in the process. But MFDFA analysis additionally point towards Parietal lobe activation during color perception as well.

3. The increase in complexity during color viewing and decrease during baseline Grey—such change in the complexity pattern is similar throughout the electrodes for the whole experimental duration. This indicates that the process of color perception includes the ability of separating a color from the set baseline by means of the change in respective degrees of long range correlations; which makes the multifractal spectral width an efficient marker in bio-signal analysis for color perception studies in future.

4. A novel and interesting finding that must be mentioned is the nature of spectral width with respect to color stimulus. The values of the multifractal width are found highest for color Blue, followed by Red and then Green. Yellow recorded the lowest width, followed by Indigo. Multifractal spectral width measures the long range correlations present in the signal. So, it can be said without doubt that such correlations are higher in Blue than Red, indicating higher arousal. Overall, Blue-Green part (shorter wavelengths) of the spectrum showed higher arousal than Red/Orange part (higher wavelength). This result is remarkable in terms of offering support to previous ideas. Though studies have previously reported the arousal during Blue (Lockley et al. 2006; Vandewalle et al. 2007; Yoto et al. 2007), but any consensus is yet to be reported, much less the how’s and why’s of the perceptual detail. Our study, backed by robust non-linear tools, could embolden the validity of these claims.

5. An offshoot of the previous observation is the fact that the highest complexity is recorded for the three primary colors. This could be due to the fact that the photoreceptors which are directly responsible for color vision consist of the three types—red, green and blue—and perceives these colors more actively than others. The manifestation of this activation is displayed via spectral width. When the arousal due to colors other than these three is reported, it is mostly in light of some cognitive task based study. Hence, cognition plays a role in those scenarios which might favor other colors. This work, designed specifically to address the electrical activity due to color vision, doesn’t factor in such involvements. We reckon this is why the primary colors show high activation in EEG data.

6. For the color-wise breakdown of the absolute values of multifractal width, the electrodes that recorded the highest complexity were F8, O2 and P4, all of which belong to the right hemisphere. This suggests that the long range correlations in the right part of the brain is more prominent while color viewing than the left. Data for the relative increase of width, i.e., increase from the immediately prior baseline color repeats this trend for the Occipital lobe. But P3 and F3 electrodes in Parietal and Frontal lobe show higher relative increase. This result is an indicator of hemispherical asymmetry in color perception in atleast Occipital and Parietal lobes. Frontal lobes, too, could be considered for such lateralization (right brain bias) as the amplitude of increase in F8 is significantly higher than F3.

7. Lastly, substantial activation of Parietal electrodes is seen not only during color stimulus, but even for baseline Grey too. The visual process is related directly to Occipital area. Our results hint at Parietal participation in the process as well. Since part of the Parietal lobe is involved in the integration of sensory information, the complexity change seems justified. Although targeted future investigations could help reveal specific details of this involvement.

From the next part of the experiment, Multifractal detrended cross-correlation analysis (MFDXA) provides few more important conclusions regarding the cross-correlation pattern in different parts of the brain during color perception. Those are given below:

1. The cross-correlated series between all the electrode combinations shows the presence of multifractality implying long range correlations between not only in the signals themselves, but in the cross-correlated data as well. Hence, MFDXA analysis definitely has the potential to offer necessary parameters for quantifying cross-correlation process between different areas of the human brain.

2. Considering lobe-wise cross-correlation pattern, it is seen that the electrodes in general share very similar trends barring few exceptions. That is to say, during each experimental condition, the change in γ_x for most of the inter/intra lobe combinations was by and large similar. This advocates for the cross-correlation pattern to be very consistent throughout, irrespective of their spatial distribution. It is a definitive illustration of the inter/ intra lobe dependency of color vision.

3. The most significant observation in this segment of the experiment is the overall trend of reduced cross-correlation among electrodes with the introduction of color stimulus and its increase when the color is removed. Most of the colors—Blue, Green, Red, Orange and Violet—resulted in cross-correlation reduction when applied (Violet being the highest). On the other hand, enhanced cross-correlations were observed when they were changed to the next baseline Grey (Orange to G7 showing the highest magnitude). We argue that this pattern emerges due to the processing of visual data well after the stimulus retrieval. The cross-correlation coefficient γ_x is the manifestation of the enhanced connection between various parts of the brain during this phase. The two colors that fall outside this norm are Indigo and Yellow, interestingly both had low complexity compared to others. This fuels the argument further; since in these two cases, the arousal levels were far lower which points at having to process less sensory information content. Hence, the need for the correlation during and after being exposed to Indigo and Yellow appears to be far limited (apart from Right Frontal-Occipital combinations like F4–O2 and F8–O2, the magnitude of cross-correlation is quite small, too).

4. Destruction of cross-correlation was highest in case of G1 to Violet and lowest during Orange to G7. In both of the cases, Inter-frontal or Fronto-Parietal combinations have registered optimum changes.

From these vital and newfound results emerging from both the MFDFA and MFDXA analysis, it can be said with certainty that the principal aim of this study has been met successfully. We have studied the changes in several brain activities in detail and were able to challenge or consolidate the existing ideas from the stout platform set by the aforementioned methods. Also, the correlation study of the brainwaves indicates that the correlation between various lobes is significantly higher during specific color stimulus exposure and more importantly, even after the stimulus retrieval. The obtained data may be of immense importance when it comes to studying the neuro-cognitive basis of color perception. Previous researches on color perception have presented an array of psychological and physiological aspects of it, as discussed before. The points below encapsulate how this study could contribute to the growing literature:

Firstly, we would like to refer to the necessary methodological treatment. Studies in this field of research have shown some methodological shortcomings that has been eloquently summarised in Elliot (2019). Based on those weaknesses, some of the points are recommended to increase reliability and reproducibility of the work. They include confirming participant naiveté and confidentiality, checking color vision deficiency among them, adequate sample size of the trial, reporting color specification and controls during experiment, monitoring ambient illumination etc. In this work, we tried to comply with these to the best of our efforts. The participants were ensured of their anonymity and kept uniformed about anything but the procedure required for them to follow. They were asked to take an online variation  (https://www.color-blindness.com/ishihara-38-plates-cvd-test/) of the Ishihara test (Ishihara 1987) to ensure they don’t have color-blindness or color vision deficiency. Consulting other EEG studies on sensory perceptions (Ghosh et al. 2018), adequate sample size was also ensured. Specifications of the experimental instruments and the color notations are given as per the recommendations. One important point which needs to be emphasised here is that the investigation was focused to study the complexity patterns of cortical electrical activity and to analyse it quantitatively. Hence the color control was not set to compare the effect of one/two specific colors or their colorimetric properties like hue or chroma. Although we found the change in complexity of color-induced EEG patterns, more effect-specific experimental design are necessary to comment on which properties of the colors cause said changes in a more definitive manner. Going back to the experimental process, another suggestion of keeping the ambient illumination to a minimum was also met as the participants were kept in a dark room during the procedure. This way, we have followed the recommendations to have the quality of the overall methodological arrangement be of higher standards.

Secondly, as mentioned in the above point, analysis of color-induced bio-signals was the idea of the work. Hence, the whole gamut of visual spectrum was displayed instead of few colors (as is done in majority studies). The complexity changes due to various wavelengths could be examined this way and with the emerging pattern, further explorations can be pinpointed.

Thirdly, the most important novelty that this study offers is the usage of non-linear tools for analyzing the EEG signals. Previous literatures were limited in this area since they haven’t factored in the chaotic aspect of the biological manifestations. Complexity and long range correlations are inherent properties of such series. Hence, without considering these properties, complete scrutiny of them couldn’t be carried out. Establishing this fact is an important point that this study hopes to achieve; something which might be the next step in future investigations of color perception.

Fourth and finally, the parameters this study has resulted (multifractal width w, cross-correlation coefficient γ_x) are unprecedented in this field of research and of high significance. These parameters emerge from the non-linear dynamics of brain signals under color stimuli and quantifying them is a step towards understanding the signatures of such dynamics more elaborately and with more rigour. Another byproduct of this analysis is obtaining such quantifiable parameters which are reproducible under different experimental circumstances. Hence, even with altered aims, the dynamics in the brain can be well understood.

Having said the abovementioned contributions, our study eventually is a stepping stone to a larger horizon of color perception and cognition research that can be traversed by extending the work further. This study was conducted with 16 participants, which may limit us from global interpretation of the findings presented for now. To attain the same, we plan to further extend this study with a larger pool of participants. In future, for pinpointing the most relevant parameters/leads that contribute to the major findings of this work, machine learning techniques can be used during analysis. This will, in turn, improve the overall interpretability of the parameters. This paper aimed to explore the changes in the broadband EEG signal with exposure to different colors of the VIBGYOR. For further validation study, the results of this work can be compared to the results of frequency dependent analysis of the same EEG data corresponding to specific experimental conditions (to investigate if any particular EEG frequency band gets more pronounced while viewing any particular color). Also, further classifications of the participants based on their age, sex, color preference can be made before interpreting the findings of this study to reach a more generalized conclusion in the global scenario. One more interesting extension of our report could be in the direction of non-random order presentation of the visual stimulus and its subsequent influences on the results found. To best of our knowledge, reported studies on order effects in visual or color perception tasks are very scarce. Yet it wouldn’t be entirely accurate, theoretically at the least, to dismiss the possibility of its presence in this case. For example: interference effect of one experimental color on the perception of the next, given the short exposure time (although the visual perception of color takes only ~150–200 ms, reported in Amano et al. (Amano et al. 2006)). It, therefore, remains another avenue which could be delved into in future.

Before concluding the paper, it is worth calling out that human color perception is a domain vast enough to induce interest from a plethora of disciplines like physics, neuroscience, cognitive science, psychology, psychophysics, marketing industry and even visual arts and linguistics. Needless to say that to advance our knowledge on how we perceive and process colors the requirement of rigorous scientific tools is absolutely crucial. This work takes such a step to tackle the electrophysiological aspect of the problem. The novel approach described attempts to study the color perception by analyzing its physiological signatures meticulously using state-of-the-art non-linear tools. We demonstrate that quantifying parameters like degree of complexity and degree of cross-correlation can categorically reveal exclusive information about neuronal dynamics and nature of their interdependency. Our work, therefore, argues heavily in favor of using such advanced tools in color perception studies and hopes to initiate a modern paradigm of research in this field.

Appendix

Empirical Mode Decomposition (EMD)

EMD is a decomposition method for non-stationary and nonlinear signals (Huang et.al. 1998). The EMD technique decomposes a signal into a number of intrinsic mode functions (IMFs) that represent fast to slow oscillations. An IMF is a function that satisfies two conditions:

(1) the number of extrema and the number of zero crossings must either be equal or differ by at most one; and (2) at any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero. To obtain an IMF from the original signal x, a sifting process is performed (Huang et.al. 1998) as follows:

First, all extrema of the original signal x need to be identified. All local maximum points are connected by a cubic spline line to form the upper envelope e_u. All local minima points are connected likewise to form the lower envelope e_l. The mean of e_u and e_l, a₁, is calculated as:

$$a_1=\frac{\left(e_u+e_l\right)}{2}$$ 20

The difference between the original signal and the mean is defined as the first component h₁:

$$h_1=x-a_1$$ 21

In the next sifting process, h₁ is treated as the signal, and the mean a₁₁ of its local maxima and local minima is found. Thus, we have:

$$h_{11}=h_1-a_{11}$$ 22

Subsequently, we can repeat this sifting procedure k times until h_1k is an IMF, with:

$$h_{1k}=h_{1(k-1)}-a_{1k}$$ 23

Therefore, the first IMF component derived from the original signal is designated as:

$$c_1=h_{1k}$$ 24

The sifting process has been stopped when an IMF has been established by limiting the size of the standard deviation (SD), calculated from the two consecutive sifting sequences as below:

$$SD=\sum _{t=0}^T\frac{{[h_{1(k-1)}(t)-h_{1k}(t)]}^2}{h_{1(k-1)}^2(t)}$$ 25

A typical value for SD can be set between 0.2 and 0.3 (Huang et.al., 1998). In our case the value was set to 0.25. To extract the 2nd IMF component, we remove c1 from the original signal x:

$$r_1=x-c_1$$ 26

The residual r₁ is treated as a new signal, and the same sifting process is applied to obtain the 2^nd IMF component c₂ and the residual:

$$r_2=r_1-c_2$$ 27

This procedure is repeated on the subsequent residuals r_j’s, until the final residual r_J no longer contains any oscillation information,

$$r_j=r_{j-1}-c_j$$ 28

By summing up Eqs. (7)–(9), we can obtain:

$$x=\sum _{j=0}^J{c}_j+r_j$$ 29

Thus, original signal x is decomposed into J empirical modes c_j’s and a residue r_J.

Since, the artifacts lie in the low frequency regions (< 3.5 Hz) (Bizopoulos et al. 2013; Jung & Saikiran 2016), the IMFs that appear in this band are rejected. Thus, the filtered signal is the sum of the remaining IMFs and more specifically, only the first few IMFs including the residue were kept (Bizopoulos et al. 2013). We have obtained noise free EEG data for all the electrodes using the EMD technique and used this data for further analysis and classification of EEG features.

Fig. 16a–k shows a representative figure of the F3 electrode in 10 s duration which was subjected to EMD technique to obtain noise-free EEG data. The sifting process was continued until the final residue is a constant, a monotonic function, i.e., a function with only one maxima or minima from which no more IMF’s can be derived. We have set the value of SD to be 0.25 after which the sifting process has been stopped.

Fig. 16.

Empirical Mode decomposition of a 10 s EEG signal of F3 electrode

The EMD process was followed for all the experimental conditions for all the subjects. The noise-free signal thus obtained after the removal of muscular and blink artifacts has been used for the subsequent MFDFA and MFDXA analysis (Fig. 17).

Fig. 17.

Raw EEG signal and artifact free EEG signal of 10 s

See Figs. 16 and 17

Data availability

All the datasets generated during and/or analyzed regarding the analysis will be made available from the corresponding author on reasonable request.

Compliance with ethical standards

Conflict of interest

The authors declare no conflict of interest related to the research work.