Conducting correlation analysis: important limitations and pitfalls

Abstract

The correlation coefficient is a statistical measure often used in studies to show an association between variables or to look at the agreement between two methods. In this paper, we will discuss not only the basics of the correlation coefficient, such as its assumptions and how it is interpreted, but also important limitations when using the correlation coefficient, such as its assumption of a linear association and its sensitivity to the range of observations. We will also discuss why the coefficient is invalid when used to assess agreement of two methods aiming to measure a certain value, and discuss better alternatives, such as the intraclass coefficient and Bland–Altman’s limits of agreement. The concepts discussed in this paper are supported with examples from literature in the field of nephrology.

BACKGROUND

‘Correlation is not causation’: a saying not rarely uttered when a person infers causality from two variables occurring together, without them truly affecting each other. Yet, though causation may not always be understood correctly, correlation too is a concept in which mistakes are easily made. Nonetheless, the correlation coefficient has often been reported within the medical literature. It estimates the association between two variables (e.g. blood pressure and kidney function), or is used for the estimation of agreement between two methods of measurement that aim to measure the same variable (e.g. the Modification of Diet in Renal Disease (MDRD) formula and the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) formula for estimating the glomerular filtration rate (eGFR)]. Despite the wide use of the correlation coefficient, limitations and pitfalls for both situations exist, of which one should be aware when drawing conclusions from correlation coefficients. In this paper, we aim to describe the correlation coefficient and its limitations, together with methods that can be applied to avoid these limitations.

The basics: the correlation coefficient

Fundamentals

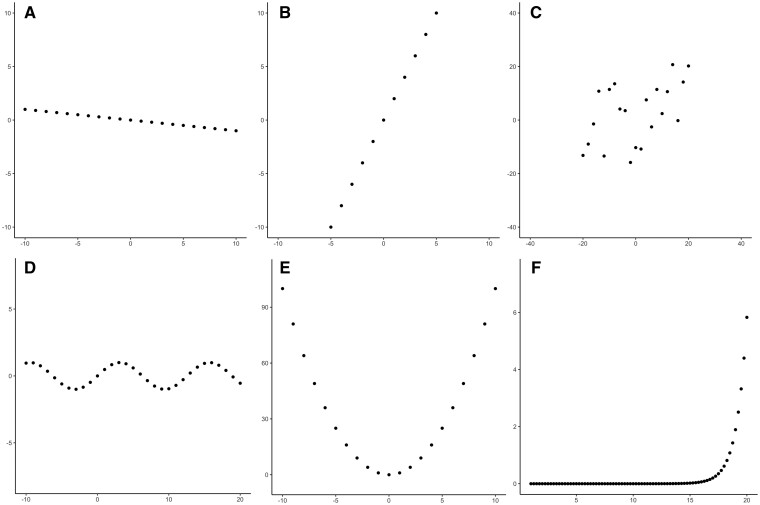
The correlation coefficient was described over a hundred years ago by Karl Pearson [1], taking inspiration from a similar idea of correlation from Sir Francis Galton, who developed linear regression and was the not-so-well-known half-cousin of Charles Darwin [2]. In short, the correlation coefficient, denoted with the Greek character rho (ρ) for the true (theoretical) population and r for a sample of the true population, aims to estimate the strength of the linear association between two variables. If we have variables X and Y that are plotted against each other in a scatter plot, the correlation coefficient indicates how well a straight line fits these data. The coefficient ranges from −1 to 1 and is dimensionless (i.e., it has no unit). Two correlations with r = −1 and r = 1 are shown in Figure 1A and B, respectively. The values of −1 and 1 indicate that all observations can be described perfectly using a straight line, which in turn means that if X is known, Y can be determined deterministically and vice versa. Here, the minus sign indicates an inverse association: if X increases, Y decreases. Nonetheless, real-world data are often not perfectly summarized using a straight line. In a scatterplot as shown in Figure 1C, the correlation coefficient represents how well a linear association fits the data.

FIGURE 1:

Different shapes of data and their correlation coefficients. (A) Linear association with r = −1. (B) A linear association with r = 1. (C) A scatterplot through which a straight line could plausibly be drawn, with r = 0.50. (D) A sinusoidal association with r = 0. (E) A quadratic association with r = 0. (F) An exponential association with r = 0.50.

It is also possible to test the hypothesis of whether X and Y are correlated, which yields a P-value indicating the chance of finding the correlation coefficient’s observed value or any value indicating a higher degree of correlation, given that the two variables are not actually correlated. Though the correlation coefficient will not vary depending on sample size, the P-value yielded with the t-test will.

The value of the correlation coefficient is also not influenced by the units of measurement, but it is influenced by measurement error. If more error (also known as noise) is present in the variables X and Y, variability in X will be partially due to the error in X, and thus not solely explainable by Y. Moreover, the correlation coefficient is also sensitive to the range of observations, which we will discuss later in this paper.

An assumption of the Pearson correlation coefficient is that the joint distribution of the variables is normal. However, it has been shown that the correlation coefficient is quite robust with regard to this assumption, meaning that Pearson’s correlation coefficient may still be validly estimated in skewed distributions [3]. If desired, a non-parametric method is also available to estimate correlation; namely, the Spearman’s rank correlation coefficient. Instead of the actual values of observations, the Spearman’s correlation coefficient uses the rank of the observations when ordering observations from small to large, hence the ‘rank’ in its name [4]. This usage of the rank makes it robust against outliers [4].

Explained variance and interpretation

One may also translate the correlation coefficient into a measure of the explained variance (also known as R²), by taking its square. The result can be interpreted as the proportion of statistical variability (i.e. variance) in one variable that can be explained by the other variable. In other words, to what degree can variable X be explained by Y and vice versa. For instance, as mentioned above, a correlation of −1 or +1 would both allow us to determine X from Y and vice versa without error, which is also shown in the coefficient of determination, which would be (−1)² or 1² = 1, indicating that 100% of variability in one variable can be explained by the other variable.

In some cases, the interpretation of the strength of correlation coefficient is based on rules of thumb, as is often the case with P-values (P-value <0.05 is statistically significant, P-value >0.05 is not statistically significant). However, such rules of thumb should not be used for correlations. Instead, the interpretation should always depend on context and purposes [5]. For instance, when studying the association of renin–angiotensin–system inhibitors (RASi) with blood pressure, patients with increased blood pressure may receive the perfect dosage of RASi until their blood pressure is exactly normal. Those with an already exactly normal blood pressure will not receive RASi. However, as the perfect dosage of RASi makes the blood pressure of the RASi users exactly normal, and thus equal to the blood pressure of the RASi non-users, no variation is left between users and non-users. Because of this, the correlation will be 0.

The linearity of correlation

An important limitation of the correlation coefficient is that it assumes a linear association. This also means that any linear transformation and any scale transformation of either variable X or Y, or both, will not affect the correlation coefficient. However, variables X and Y may also have a non-linear association, which could still yield a low correlation coefficient, as seen in Figure 1D and E, even though variables X and Y are clearly related. Nonetheless, the correlation coefficient will not always return 0 in case of a non-linear association, as portrayed in Figure 1F with an exponential correlation with r = 0.5. In short, a correlation coefficient is not a measure of the best-fitted line through the observations, but only the degree to which the observations lie on one straight line.

In general, before calculating a correlation coefficient, it is advised to inspect a scatterplot of the observations in order to assess whether the data could possibly be described with a linear association and whether calculating a correlation coefficient makes sense. For instance, the scatterplot in Figure 1C could plausibly fit a straight line, and a correlation coefficient would therefore be suitable to describe the association in the data.

The range of observations for correlation

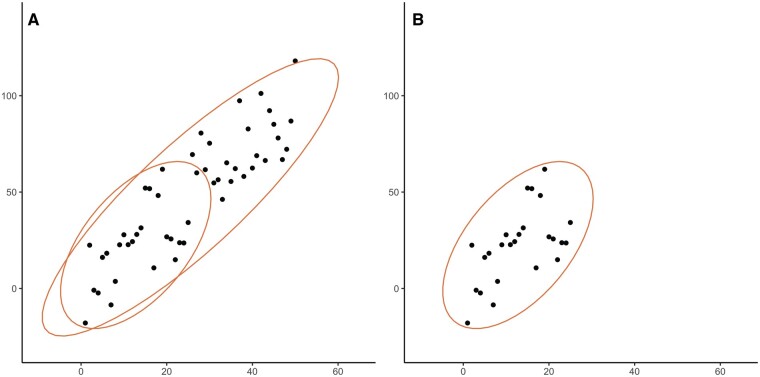
An important pitfall of the correlation coefficient is that it is influenced by the range of observations. In Figure 2A, we illustrate hypothetical data with 50 observations, with r = 0.87. Included in the figure is an ellipse that shows the variance of the full observed data, and an ellipse that shows the variance of only the 25 lowest observations. If we subsequently analyse these 25 observations independently as shown in Figure 2B, we will see that the ellipse has shortened. If we determine the correlation coefficient for Figure 2B, we will also find a substantially lower correlation: r = 0.57.

FIGURE 2:

The effect of the range of observations on the correlation coefficient, as shown with ellipses. (A) Set of 50 observations from hypothetical dataset X with r = 0.87, with an illustrative ellipse showing length and width of the whole dataset, and an ellipse showing only the first 25 observations. (B) Set of only the 25 lowest observations from hypothetical dataset X with r = 0.57, with an illustrative ellipse showing length and width.

The importance of the range of observations can further be illustrated using an example from a paper by Pierrat et al. [6] in which the correlation between the eGFR calculated using inulin clearance and eGFR calculated using the Cockcroft–Gault formula was studied both in adults and children. Children had a higher correlation coefficient than adults (r = 0.81 versus r = 0.67), after which the authors mentioned: ‘The coefficients of correlation were even better […] in children than in adults.’ However, the range of observations in children was larger than the range of observations in adults, which in itself could explain the higher correlation coefficient observed in children. One can thus not simply conclude that the Cockcroft–Gault formula for eGFR correlates better with inulin in children than in adults. Because the range of the correlation influences the correlation coefficient, it is important to realize that correlation coefficients cannot be readily compared between groups or studies. Another consequence of this is that researchers could inflate the correlation coefficient by including additional low and high eGFR values.

The non-causality of correlation

Another important pitfall of the correlation coefficient is that it cannot be interpreted as causal. It is of course possible that there is a causal effect of one variable on the other, but there may also be other possible explanations that the correlation coefficient does not take into account. Take for example the phenomenon of confounding. We can study the association of prescribing angiotensin-converting enzyme (ACE)-inhibitors with a decline in kidney function. These two variables would be highly correlated, which may be due to the underlying factor albuminuria. A patient with albuminuria is more likely to receive ACE-inhibitors, but is also more likely to have a decline in kidney function. So ACE-inhibitors and a decline in kidney function are correlated not because of ACE-inhibitors causing a decline in kidney function, but because they have a shared underlying cause (also known as common cause) [7]. More reasons why associations may be biased exist, which are explained elsewhere [8, 9].

It is however possible to adjust for such confounding effects, for example by using multivariable regression. Whereas a univariable (or ‘crude’) linear regression analysis is no different than calculating the correlation coefficient, a multivariable regression analysis allows one to adjust for possible confounder variables. Other factors need to be taken into account to estimate causal effects, but these are beyond the scope of this paper.

Agreement between methods

We have discussed the correlation coefficient and its limitations when studying the association between two variables. However, the correlation coefficient is also often incorrectly used to study the agreement between two methods that aim to estimate the same variable. Again, also here, the correlation coefficient is an invalid measure.

The correlation coefficient aims to represent to what degree a straight line fits the data. This is not the same as agreement between methods (i.e. whether X = Y). If methods completely agree, all observations would fall on the line of equality (i.e. the line on which the observations would be situated if X and Y had equal values). Yet the correlation coefficient looks at the best-fitted straight line through the data, which is not per se the line of equality. As a result, any method that would consistently measure a twice as large value as the other method would still correlate perfectly with the other method. This is shown in Figure 3, where the dashed line shows the line of equality, and the other lines portray different linear associations, all with perfect correlation, but no agreement between X and Y. These linear associations may portray a systematic difference, better known as bias, in one of the methods.

FIGURE 3:

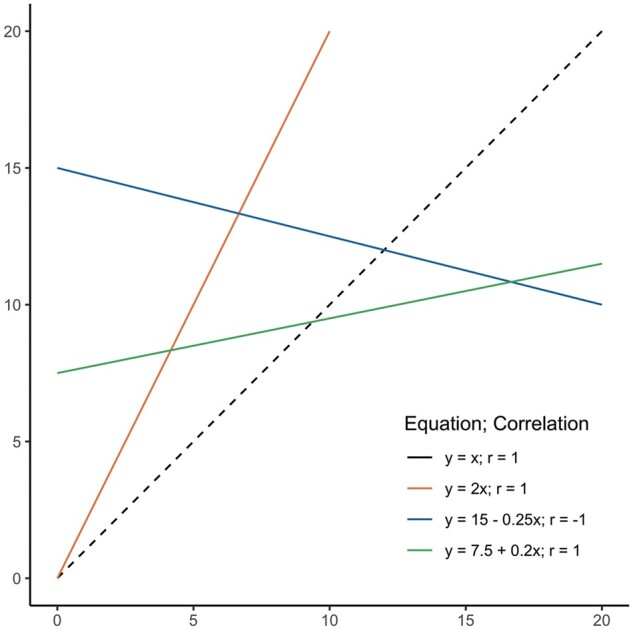
A set of linear associations, with the dashed line (- - -) showing the line of equality where X = Y. The equations and correlations for the other lines are shown as well, which shows that only a linear association is needed for r = 1, and not specifically agreement.

This limitation applies to all comparisons of methods, where it is studied whether methods can be used interchangeably, and it also applies to situations where two individuals measure a value and where the results are then compared (inter-observer variation or agreement; here the individuals can be seen as the ‘methods’), and to situations where it is studied whether one method measures consistently at two different time points (also known as repeatability). Fortunately, other methods exist to compare methods [10, 11], of which one was proposed by Bland and Altman themselves [12].

Intraclass coefficient

One valid method to assess interchangeability is the intraclass coefficient (ICC), which is a generalization of Cohen’s κ, a measure for the assessment of intra- and interobserver agreement. The ICC shows the proportion of the variability in the new method that is due to the normal variability between individuals. The measure takes into account both the correlation and the systematic difference (i.e. bias), which makes it a measure of both the consistency and agreement of two methods. Nonetheless, like the correlation coefficient, it is influenced by the range of observations. However, an important advantage of the ICC is that it allows comparison between multiple variables or observers. Similar to the ICC is the concordance correlation coefficient (CCC), though it has been stated that the CCC yields values similar to the ICC [13]. Nonetheless, the CCC may also be found in the literature [14].

The 95% limits of agreement and the Bland–Altman plot

When they published their critique on the use of the correlation coefficient for the measurement of agreement, Bland and Altman also published an alternative method to measure agreement, which they called the limits of agreement (also referred to as a Bland–Altman plot) [12]. To illustrate the method of the limits of agreement, an artificial dataset was created using the MASS package (version 7.3-53) for R version 4.0.4 (R Corps, Vienna, Austria). Two sets of observations (two observations per person) were derived from a normal distribution with a mean (µ) of 120 and a randomly chosen standard deviation (σ) between 5 and 15. The mean of 120 was chosen with the aim to have the values resemble measurements of high eGFR, where the first set of observed eGFRs was hypothetically acquired using the MDRD formula, and the second set of observed eGFRs was hypothetically acquired using the CKD-EPI formula. The observations can be found in Table 1.

Table 1.

Artificial data portraying hypothetically observed MDRD measurements and CKD-EPI measurements

Participant ID	eGFR with MDRD, mL/min/ 1.73 m2	eGFR with CKD-EPI, mL/min/1.73 m2	Difference (CKD-EPI – MDRD)
1	119.1	118.4	−0.7
2	123.7	121.6	−2.1
3	123.5	117.6	−5.9
4	121.1	118.1	−3.0
5	115.7	119.4	3.7
6	117.4	120.5	3.1
7	119.2	120.8	1.6
8	120.0	119.4	−0.6
9	126.7	118.0	−8.7
10	122.1	123.1	1.0
11	117.8	120.9	3.1
12	116.8	118.8	2.0
13	119.2	121.7	2.5
14	119.2	117.8	−1.4
15	118.9	118.8	−0.1
16	120.7	115.8	−4.9
17	117.5	124.1	6.6
18	121.2	122.1	0.9
19	116.6	125.4	8.8
20	119.4	120.0	0.6
			Mean: 0.32 SD: 4.09

The 95% limits of agreement can be easily calculated using the mean of the differences ($\overline{d}$) and the standard deviation (SD) of the differences. The upper limit (UL) of the limits of agreement would then be UL = $\overline{d}+1.96\mathrm{*}\mathrm{SD}$ and the lower limit (LL) would be LL = $\overline{d}-1.96\mathrm{*}\mathrm{SD}$. If we apply this to the data from Table 1, we would find $\overline{d}$ = 0.32 and SD = 4.09. Subsequently, UL = 0.32 + 1.96 * 4.09 = 8.34 and LL = 0.32 − 1.96 * 4.09 = −7.70. Our limits of agreement are thus −7.70 to 8.34. We can now decide whether these limits of agreement are too broad. Imagine we decide that if we want to replace the MDRD formula with the CKD-EPI formula, we say that the difference may not be larger than 7 mL/min/1.73 m². Thus, on the basis of these (hypothetical) data, the MDRD and CKD-EPI formulas cannot be used interchangeably in our case. It should also be noted that, as the limits of agreement are statistical parameters, they are also subject to uncertainty. The uncertainty can be determined by calculating 95% confidence intervals for the limits of agreement, on which Bland and Altman elaborate in their paper [12].

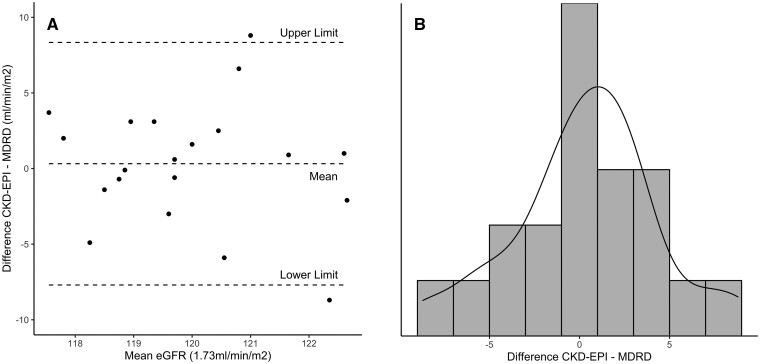
The limits of agreement are also subject to two assumptions: (i) the mean and SD of the differences should be constant over the range of observations and (ii) the differences are approximately normally distributed. To check these assumptions, two plots were proposed: the Bland–Altman plot, which is the differences plotted against the means of their measurements, and a histogram of the differences. If in the Bland–Altman plot the means and SDs of the differences appear to be equal along the x-axis, the first assumption is met. The histogram of the differences should follow the pattern of a normal distribution. We checked these assumptions by creating a Bland–Altman plot in Figure 4A and a histogram of the differences in Figure 4B. As often done, we also added the limits of agreement to the Bland–Altman plot, between which approximately 95% of datapoints are expected to be. In Figure 4A, we see that the mean of the differences appears to be equal along the x-axis; i.e., these datapoints could plausibly fit the horizontal line of the total mean across the whole x-axis. Nonetheless, the SD does not appear to be distributed equally: the means of the differences at the lower values of the x-axis are closer to the total mean (thus a lower SD) than the means of the differences at the middle values of the x-axis (thus a higher SD). Therefore, the first assumption is not met. Nonetheless, the second assumption is met, because our differences follow a normal distribution, as shown in Figure 4B. Our failure to meet the first assumption can be due to a number of reasons, for which Bland and Altman also proposed solutions [15]. For example, data may be skewed. However, in that case, log-transforming variables may be a solution [16].

FIGURE 4:

Plots to check assumptions for the limits of agreement. (A) The Bland–Altman plot for the assumption that the mean and SD of the differences are constant over the range of observations. In our case, we see that the mean of the differences appears to be equal along the x-axis; i.e., these datapoints could plausibly fit the horizontal line of the total mean across the whole x-axis. Nonetheless, the SD does not appear to be distributed equally: the means of the differences at the lower values of the x-axis are closer to the total mean (thus a lower SD) than the means of the differences at the middle values of the x-axis (thus a higher SD). Therefore, the first assumption is not met. The limits of agreement and the mean are added as dashed (- - -) lines. (B) A histogram of the distribution of differences to ascertain the assumption of whether the differences are normally distributed. In our case, the observations follow a normal distribution and thus, the assumption is met.

It is often mistakenly thought that the Bland–Altman plot alone is the analysis to determine the agreement between methods, but the authors themselves spoke strongly against this [15]. We suggest that authors should both report the limits of agreement and show the Bland–Altman plot, to allow readers to assess for themselves whether they think the agreement is met.

CONCLUSION

The correlation coefficient is easy to calculate and provides a measure of the strength of linear association in the data. However, it also has important limitations and pitfalls, both when studying the association between two variables and when studying agreement between methods. These limitations and pitfalls should be taken into account when using and interpreting it. If necessary, researchers should look into alternatives to the correlation coefficient, such as regression analysis for causal research, and the ICC and the limits of agreement combined with a Bland–Altman plot when comparing methods.

CONFLICT OF INTEREST STATEMENT

None declared.