The Organ Sparing Potential of Different Biological Optimization Strategies in Proton Therapy

Abstract

Purpose

Variable relative biological effectiveness (RBE) models allow for differences in linear energy transfer (LET), physical dose, and tissue type to be accounted for when quantifying and optimizing the biological damage of protons. These models are complex and fraught with uncertainties, and therefore, simpler RBE optimization strategies have also been suggested. Our aim was to compare several biological optimization strategies for proton therapy by evaluating their performance in different clinical cases.

Methods and Materials

Two different optimization strategies were compared: full variable RBE optimization and differential RBE optimization, which involve applying fixed RBE for the planning target volume (PTV) and variable RBE in organs at risk (OARs). The optimization strategies were coupled to 2 variable RBE models and 1 LET-weighted dose model, with performance demonstrated on 3 different clinical cases: brain, head and neck, and prostate tumors.

Results

In cases with low ${\left(\alpha /\beta \right)}_x$ in the tumor, the full RBE optimization strategies had a large effect, with up to 10% reduction in RBE-weighted dose to the PTV and OARs compared with the reference plan, whereas smaller variations (<5%) were obtained with differential optimization. For tumors with high ${\left(\alpha /\beta \right)}_x,$ the differential RBE optimization strategy showed a greater reduction in RBE-weighted dose to the OARs compared with the reference plan and the full RBE optimization strategy.

Conclusions

Differences between the optimization strategies varied across the studied cases, influenced by both biological and physical parameters. Whereas full RBE optimization showed greater OAR sparing, awareness of underdosage to the target must be carefully considered.

Introduction

Currently, a constant relative biological effectiveness (RBE) of 1.1 (RBE_1.1) is applied in clinical proton therapy (PT), as recommended by the International Commission on Radiation Units and Measurements.^1,2 However, based on the broad range of in vitro data showing variability in the RBE, as well as recent in vivo data³ and clinical results,4, 5, 6, 7, 8 there is a growing concern that the constant RBE approach may lead to suboptimal treatment. This has given rise to both phenomenologic and mechanistic RBE models, which can be applied to estimate the variation in RBE in PT treatment plans.9, 10, 11, 12, 13, 14, 15 Most models show the same general dependencies, such as increasing RBE with decreasing dose, increasing linear energy transfer (LET), and decreasing α/β of the reference radiation (photon-based${\left(\alpha /\beta \right)}_x$).¹⁶ Owing to these observations, there is a growing consensus that incorporation of LET- or RBE-based parameters in the optimization of PT treatment plans is a natural step to improve the precision and quality of the treatment.^17,18 In a recent comprehensive report,¹⁹ the PT community emphasized the risk of unexpected toxicities from ignoring RBE variation, underlining the importance to address RBE uncertainties and to provide clinical solutions for LET- or RBE-based optimization in PT.⁶

Full biological optimization, where variable RBE is used for both the planning target volume (PTV) and the organ at risk (OAR), is a strategy to reduce the suspected elevated RBE-weighted doses in both the target and healthy tissue. However, a significant uncertainty in RBE models lies in the cell-line dependency derived from in vitro data with considerable deviations in response.²⁰ This uncertainty is circumvented by instead using LET-weighted dose (LWD) models. McMahon et al²¹ found that an LET-dependent dose is almost as effective as variable RBE models when it comes to reducing biological variability. The main reservations of full biological optimization have been a risk of underdosage to the target, a possible consequence if the RBE is overestimated. As a solution, a combination of multiple RBE models in the optimization was recently suggested in which the traditional RBE of 1.1 was applied to the target, whereas a variable RBE was allowed for OARs (differential biological optimization).²² However, although different approaches to RBE-weighted dose optimization have been proposed,23, 24, 25, 26, 27 a coherent comparison between different techniques has not yet been done. Hence, our aim was to compare full and differential biological optimization strategies using different RBE models, to quantify how the physical and RBE-weighted dose is affected in different clinical scenarios. For this purpose, we developed a flexible framework for biological optimization based on the FLUKA Monte Carlo (MC) code28, 29, 30 and a prototype optimization algorithm.^31,32 Two recent proton RBE models and an LWD model were implemented into the biological optimization software and applied for 3 different clinical cases.

Materials and Methods

We used MC-based treatment plan optimization, enabling scoring of dose, LET, and secondary particles and biological parameters, thus allowing optimization with respect to the RBE-weighted dose. The FLUKA-based treatment plan reoptimization method consists of 3 steps: a FLUKA MC simulation of a treatment plan from a commercial treatment planning system using the FLUKA development version, reoptimization of the pencil beam weightings with respect to the variable RBE-based strategies using the dose estimates for each pencil beam from the initial simulation, and a second FLUKA MC simulation of the new plan for verification. The scored values (the proton radiosensitivity parameters along with the physical dose ($\alpha D$ and $\sqrt{\beta }D$), along with spatial information about the planning target volume and OARs and their respective ${\left(\alpha /\beta \right)}_x$, are used as input to the optimization algorithm. To achieve a homogeneous RBE-weighted dose to the PTV while minimizing the dose to the OARs according to the selected objectives, the optimizer adjusts the weightings of the pencil beams without adding or removing pencil beams from the original plan to achieve a homogeneous RBE-weighted dose to the PTV while minimizing the dose to the OARs according to the selected objectives.

Optimization strategies

We implemented full and differential RBE optimization strategies by applying RBE-weighted dose objectives. During the RBE optimization, the RBE-models by Rørvik et al (ROR)¹⁵ and McNamara et al (MCN)¹³ were incorporated. These models include LET, dose, and (α/β)_x as input parameters. The MCN model assumes a linear relationship between LET and RBE and can therefore make use of the dose-weighted LET (LET_d) as an input parameter, whereas the ROR model is based on a nonlinear LET-RBE relationship and requires the full LET spectrum to estimate the RBE. We also applied the LWD approach, which combines only the physical dose and LET_d.^23,27 This approach does not account for tissue dependence and uses a normalization factor to maintain the mean RBE of 1.1 to the clinical target volume, as described by Fjaera et al³³ (details are provided in Appendix E1 in the Supplement). Identical target prescription for the RBE-weighted dose was applied for all the different strategies; that is, all optimization strategies aimed to give the same prescribed dose accounting for their respective RBE variations, primarily enabling comparison of the optimization strategies and the resulting physical parameters of absorbed dose and LET resulting from the different optimization processes. In addition, all patient cases were also optimized using a global RBE of 1.1 for reference. The RBE_1.1 optimized plans were also recalculated using the different RBE models for comparison in terms of variable-RBE weighted doses.

The following optimization strategies were thereby explored:

• 1.Full RBE optimization (FO): Optimizing the dose to both the PTV and the OARs with respect to each of the models—MCN (FO_MCN), ROR (FO_ROR), and LWD (FO_LWD)—using organ-specific tissue parameters in RBE modeling for the MCN and ROR models.
• 2.Differential RBE optimization (DO): Optimizing the dose to the PTV using RBE_1.1 to avoid potential underdosage while applying the MCN (DO_MCN), ROR (DO_ROR), and LWD (DO_LWD) models when optimizing the RBE-weighted dose to the OARs.

In the results, the RBE-weighted doses are denoted $D_Y^X,$ X is the model used for plan optimization, and Y is the model applied to calculate the reported dose (eg, $D_{MCN}^{RB{E}_{1.1}}$ is the RBE-weighted dose from a plan optimized with RBE_1.1 and recalculated with the MCN model).

The generated dose distributions were compared in terms of dose-volume histograms and dose metrics for the PTVs and OARs. The RBE-weighted dose difference between the strategies and the reference RBE_1.1 were also quantified, where the RBE_1.1-optimized dose was recalculated to the respective RBE models of the different strategies to provide a comparison of the variable RBE-weighted dose. The evaluated values for the PTV were mean dose, volumes receiving 95% and 107% dose (V_95% and V_107%), and for OARs, the mean dose and dose to 95% and 2% of the volume (D_95% and D_2%).

Treatment plans

Intensity modulated proton therapy (IMPT) treatment plans were generated in the Eclipse treatment planning system (Varian Medical Systems, Palo Alto, California) applying an RBE of 1.1. For verification of the biological optimization software, simple treatment plans were created for a water phantom. An RBE-weighted dose of 2 Gy (RBE) was prescribed to a spread-out Bragg peak 4 cm wide.

The 3 patient cases included a brain tumor (pituitary adenoma), a prostate cancer case, and a head and neck cancer case (rhabdomyosarcoma). Multifield optimization was used for all 3 cases. The ${\left(\alpha /\beta \right)}_x$ for the different regions of interest were found in the literature^13,34, 35, 36, 37, 38 and are given in Appendix E2 together with treatment specifications. In many cases, depending on the ${\left(\alpha /\beta \right)}_x$value, the MCN and ROR models’ RBE estimates will differ significantly from the LWD estimates (no ${\left(\alpha /\beta \right)}_x$ dependency). Owing to the large differences between models in RBE and RBE-weighted dose in the OARs, the use of the identical OAR dose constraint across different models likely would not give optimal OAR sparing for all strategies. To achieve the best possible OAR sparing with the different strategies, the planning and optimization process was done in 2 steps. First, a pure PTV-based optimization (no constraints on the OAR dose) was performed with respect to RBE-weighted dose. Then, the OAR dose constraint levels were set below the maximum values from the previous step to penalize the OAR dose equally for all strategies (values are provided in Table EB.1). The highest priority during optimization was the mean dose to the PTV. We defined a homogeneity criterion specifying that 100% of the PTV should be receiving 95% and 107% of the dose after step 2.

The optimizer

The framework for biological optimization was based on a prototype optimizer for particle therapy developed by Mairani et al.^31,32 The optimizer uses the information about pencil beams, physical dose, biological variables from the linear-quadratic model ($\alpha D$ and $\sqrt{\beta }D$), and voxel information to achieve an optimized treatment plan with respect to either physical or RBE-weighted dose.

The optimization algorithm is described in Appendix E2 and the calculation of RBE-weighted dose in Appendix E3. In short, for the MCN and ROR models, the dose is calculated as a combination of the linear quadratic model and the definition of RBE, which makes the RBE dependent on $\alpha$ and $\beta$ for both reference radiation and the physical dose. For the LWD, the RBE is defined as a linear function of the LET, normalized to provide a mean RBE of 1.1 to the clinical target volume. For differential RBE optimization, the variable RBE-weighted dose in the PTV-term is replaced with a constant RBE_1.1-weighted dose, whereas a variable RBE-weighted dose is used in the OAR term. This allowed us to apply different biological and physical objectives to different segmented volumes during the same optimization. For regions where the PTV and OARs overlapped, the cost for each volume was calculated independently using their respective ${\left(\alpha /\beta \right)}_x$ values, with no additional priority of the PTV.

Results

All optimization strategies resulted in a homogeneous RBE-weighted dose within the spread-out Bragg peak for the water phantom (Appendix E4), verifying the implementation of the optimization software. RBE values were consistent with previous results from the respective RBE models, and as expected, a lower ${\left(\alpha /\beta \right)}_x$ reduced the physical dose to the PTV (Fig E4.1).

Prostate cancer case

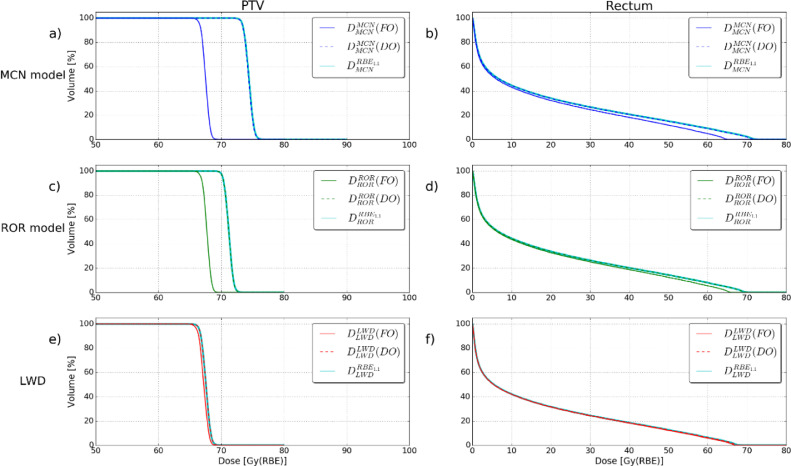
Full optimization with ${\left(\alpha /\beta \right)}_x$-dependent models gave alterations of the dose to the PTV and lower RBE-weighted doses to the rectum and bladder compared with the differential strategies and the RBE_1.1 reference plan. The FO_MCN model provided a mean PTV RBE-weighted dose reduction of 10% compared with the reference plan, whereas the FO_ROR model gave a mean dose reduction of 5% (Fig 1A and 1C). For the OARs, the FO_MCN model reduced the maximum dose (D_2%) by 10% for the rectum. The corresponding value for the FO_ROR model was 5% (Fig 1B and 1D).

Figure 1.

The RBE-weighted dose difference between the reference RBE_1.1 plan and the variable RBE models in the different strategies. The blue, red and green areas represent the PTV for the respective cases. In the brain tumor case, the OARs are brain stem (yellow), left optic nerve (turquoise), and chiasm (yellow). For the prostate case, the OARs are bladder (blue) and rectum (pink). For the head and neck case, the OARs are the right pterygoid (orange) and left parotid gland (light green). Abbreviations: OAR = organ at risk; PTV = planning target volume; RBE = relative biological effectiveness.

The high RBE in the target volume, owed to a low ${\left(\alpha /\beta \right)}_x$, provided large differences between the reference plan and the variable RBE plans from the FO strategies with the MCN and ROR models. This is shown in Figure 2B for both the mean and maximum RBE_1.1-weighted dose to the PTV and OARs, respectively; the full RBE strategies provided significantly lower doses compared with the other strategies. Both LWD-based strategies and the differential MCN and ROR strategies provided only negligible differences compared with the RBE_1.1 reference plan.

Figure 2.

Overview of RBE_1.1-weighted dose (top row) and LET_d (bottom row) resulting from the different optimization strategies. The colors indicate the respective RBE and LWD models and the cyan line represents the reference plan (RBE_1.1 optimization). The square markers represent the full strategy and the circle markers represent the differential strategies. Abbreviations: LET = linear energy transfer; LWD = LET-weighted dose; RBE = relative biological effectiveness.

Brain tumor case

The results from the optimization strategies for the brain-tumor case showed less variation compared with the results for the prostate case. However, the differential MCN and ROR optimization as well as the FO_LWD strategy achieved some OAR sparing in terms of both the RBE_1.1 dose (Fig 2A) and the RBE-weighted dose (Fig 3B and 3D). The DO_MCN strategy reduced the RBE-weighted maximum dose by 3% to 5% for the OARs compared with the RBE_1.1 plan, and the DO_ROR strategy showed a reduction of 2% to 3%, whereas for the DO_LWD strategy, the dose difference was negligible (Fig 3F). The reduction in the maximum OAR dose compared with the reference plan for FO_MCN and FO_ROR was small (<1%), whereas for FO_LWD, the reduction varied from 2% to 3% (Fig 3B, D, and F).

Figure 3.

Dose-volume histograms for all strategies in the prostate case. The solid line represents the RBE-weighted dose for the full RBE optimization strategies and the dashed line represents the RBE-weighted dose for the differential RBE optimization strategies. The teal color represents the respective model recalculated from the RBE_1.1 reference plan. The dose on the axis is the RBE-weighted dose for the given model. Abbreviation: RBE = relative biological effectiveness.

The largest reductions in dose were observed at the distal part of the beams where the chiasm and left optic nerve are located (first column in Fig 4). For the tissue-dependent models, the DO strategy gave the largest reduction in OAR dose (Fig 3B and 3D), whereas FO gave the largest reduction when applying the LWD model (Fig 3F). We observed only minor changes in the median LET_d between the different strategies (Fig 2D), which indicates that the difference between the strategies are mainly based on the physical dose and the ${\left(\alpha /\beta \right)}_x.$

Figure 4.

Dose-volume histograms for all strategies in the brain tumor case. The solid line represents the RBE-weighted dose for the full RBE optimization strategies (FO) and the dashed line represents the RBE-weighted dose for the differential RBE optimization strategies (DO). The teal color represents the respective model recalculated from the RBE_1.1 reference plan. The dose on the axis is the RBE-weighted dose for the given model. Abbreviation: RBE = relative biological effectiveness.

Patient with head and neck cancer

In the case of head and neck cancer, the full RBE optimization strategies provided a larger reduction in OAR dose compared with the differential strategies, whereas the MCN strategies provided the greatest OAR dose reduction and the LWD strategies provided the lowest compared with the RBE_1.1 reference plan (Fig 2C). Full optimization with ${\left(\alpha /\beta \right)}_x$-dependent models provided a lower RBE-weighted dose overall compared with the RBE-weighted dose recalculated from the reference plan (Fig 4P and 4Q). Here, the greatest change relative to the reference plan was seen for the FO_MCN model, in which the maximum dose to the right pterygoid was reduced by 10% (Fig 5B). The FO_ROR model provided similar results, with a reduction in maximum dose of 7% (Fig 5D). For FO_LWD, the corresponding dose was reduced by 2% (Fig 5F). The observed variations between strategies were likely owed to the low ${\left(\alpha /\beta \right)}_x$ values for the target volume and the OARs, leading to a high RBE in both the target organ and OARs for the ${\left(\alpha /\beta \right)}_x$-dependent models. Not allowing a variable RBE in the target from the differential RBE strategies, the DO_MCN strategy provided a 4% reduction in the maximum dose to the right pterygoid, whereas the DO_LWD strategy provided a reduction of 1%. The DO_ROR model provided a similar but slightly smaller reduction in the OAR dose compared with DO_MCN. There was no significant change in the median LET_d between the strategies in this case (Fig 2F). The trends from the differential optimizations are similar to those observed in the brain tumor case, suggesting lower case variability for the differential strategies.

Figure 5.

Dose-volume histograms for all strategies in the head and neck cancer case. The solid line represents the RBE-weighted dose for the full RBE optimization strategies and the dashed line represents the RBE-weighted dose for the differential RBE optimization strategies. The teal color represents the respective model recalculated from the RBE_1.1 reference plan. The dose on the axis is the RBE-weighted dose for the given model. Abbreviation: RBE = relative biological effectiveness.

The head and neck case provided plans outside the homogeneity criterion, but a comparison between the original treatment plan and the RBE-optimized plans from our optimizer (Fig E7.3 in Appendix E7) showed only small differences between the original treatment plan and the optimized plans in terms of dose coverage to the PTV.

Discussion

Motivated by the concern for unanticipated toxicity from LET and RBE effects when using RBE_1.1 in treatment planning^7,19,39 and the need to assess the impact of different biological optimization strategies, variable RBE models, and an LWD model were implemented and applied for dose calculation in 2 optimization strategies. Overall, the full RBE optimization was found to give the greatest reduction in the RBE-weighted dose to both the PTV and the OARs compared with the reference plan. However, in the brain tumor case, where the high target ${\left(\alpha /\beta \right)}_x$resulted in low RBE values, differential RBE optimization gave the greatest reduction in the RBE-weighted dose to the OARs. We also observed that LWD strategies reduced the RBE-weighted dose to the OARs, but generally to a lesser degree than the MCN and ROR models.

The FO_MCN and FO_ROR strategies showed similar RBE-weighted dose distributions for all cases, although the MCN-based optimization provided a greater RBE-weighted dose reduction compared with the reference plan (RBE_1.1). This implies that introducing the MCN model clinically will be a greater step away from an RBE of 1.1 compared with applying the ROR model. For the brain tumor case, with high ${\left(\alpha /\beta \right)}_x$ to the PTV and low ${\left(\alpha /\beta \right)}_x$ elsewhere, the optimizer was not able to significantly reduce the RBE-weighted dose to the OARs through full RBE optimization (Fig 3B and 3D). Therefore, the full LWD optimization strategy gave the largest differences in RBE-weighted dose compared with the reference plan in this case, because it was not affected by the large difference in ${\left(\alpha /\beta \right)}_x$ between the OARs and the PTV. This suggests that for high ${\left(\alpha /\beta \right)}_x$ tumors, full RBE optimization may overestimate the need for physical dose deposition in the PTV. Also, to our knowledge, observation of underdosage in proton therapy from using an RBE of 1.1 has not been an issue raised, with the exception of medulloblastoma cases with high ${\left(\alpha /\beta \right)}_x$.⁴⁰

For the case of full RBE optimization of the prostate, the mean physical dose reduction to the reference plan for the PTV was 10% and for the MCN and ROR models, 5%, showing both a larger difference to the reference plan and a difference between the RBE models as compared with the brain tumor case. This is a reflection of the low PTV ${(\alpha /\beta )}_x$ value for the prostate, giving opportunities for OAR dose reduction at the cost of reduced physical dose delivered to the target. The relatively homogeneous LET distribution, owed to the opposing fields, resulted in a small effect for both the full and differential LWD-optimization strategies, with marginal differences compared with the reference plan. This was also the case for all the differential RBE optimization results, indicating that this strategy is indeed more effective in reducing dose to OARs when having notable high LET values. Overall, these results suggest that applying a differential strategy or an LWD-based strategy for a prostate case, or similar cases with opposing fields, would have little potential to reduce OAR doses. On the other hand, for such cases with a low target${\left(\alpha /\beta \right)}_x$ value, full MCN and ROR could be a good option if OAR sparing is of high priority. This should only be done after a careful consideration of potential underdosage of the tumor because this strategy will significantly reduce the physical dose (up to 10% in this case) in the high-LET regions in the target.

In the head and neck case, the 3 fields, combined with an identical ${(\alpha /\beta )}_x$ value for both the PTV and the OARs, resulted in a clear reduction in maximum dose for all the full RBE strategies, because the higher degree of freedom allowed reduction of the RBE-weighted dose at the distal beam ends. Because the largest differences in this case were found in the distal part of the beams, as in the brain tumor case (Fig 4, columns 1 and 3), it is clear that the effect of a certain optimization strategy in general will depend on the field configuration. Further investigation of this could be relevant (eg, for proton arc therapy).

The ${(\alpha /\beta )}_x$ parameter has uncertainties and is thereby a current intrinsic limitation of the variable RBE models. They are, however, commonly accepted in clinics, and we therefore found it relevant to use them in this study. Other limitations of the study include the parameter D_2%, which was applied to assess the maximum dose levels to the OARs. In this study, we used the parameter for case comparisons, although an alternative approach would be to compare dose levels directly associated with reported toxicity. The cases in this study were selected to show and compare the optimization strategies relative to each other, and therefore, 3 common cases for proton therapy were chosen. Another factor that could be included would be to keep the same OAR constraint for all models and then see how the different strategies would differ from the results in this study. Because the dose constraint to the OARs varied between the cases, a common physical dose constraint could be applied to compare the strategies’ abilities.

The largest differences between the optimization strategies were observed at the distal part of the beams. This could relate to clinical LET effects; possible evidence of this was found by Eulitz et al, Peeler et al, Underwood et al, Bahn et al, and Engeseth et al,4, 5, 6, 7^,39 who observed treatment-related change, mostly at the distal end of the PTV, in magnetic resonance imaging and computed tomography follow-up in patients who received proton therapy. The treatment plans from these studies were optimized using an RBE of 1.1, which might indicate that there is some overdosage at the distal end of the beam, and this may have negative consequences both inside and outside the target. Although more clinical evidence is warranted, the emerging clinical observations support the introduction of OAR dose reduction through full RBE or LWD optimization by reducing the dose within OARs. A combination between this study's strategies and robust optimization could provide a good continuation from this work. With robust optimizaton, for example, biological range uncertainties would be taken into account. Robust optimization of set-up errors could also reveal potential LET and RBE hotspots in the patient. The disadvantage is that with MC-based treatment-planning tools, robust optimization would be time consuming.

The results in this study could be generalized for cases with similar properties in terms of field positioning. The prostate case, especially, could be generalized becuase it is a very standard case in terms of field positioning. For the other cases, the field configuration created high LET values in the distal end, which will likely be similar for many brain tumor and head and neck cases.

Conclusion

This study shows that RBE- and LET-based optimization has great potential for OAR dose reduction, but the risk of target underdosage must be carefully considered. The varying effects of the optimization strategies depending on case-specific parameters illustrate that applicability of a certain model and optimization strategy requires solid understanding of the models, input variables, and potential dosimetric pitfalls. For tumors with high ${(\alpha /\beta )}_x$, better OAR sparing may in some cases be achieved with differential RBE optimization or LWD optimization strategies compared with full RBE optimization. However, applying a differential strategy or an LWD-based strategy for a prostate case, or similar cases with opposing fields and low target ${(\alpha /\beta )}_x$, would have little potential for lowering OAR doses.