Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Oct 26;125(43):23968–23975. doi: 10.1021/acs.jpcc.1c07464

Effect of Ligands and Solvents on the Stability of Electron Charged CdSe Colloidal Quantum Dots

Indy du Fossé †, Snigdha Lal †, Aydin Najl Hossaini †, Ivan Infante ‡, Arjan J Houtepen †,*
PMCID: PMC8573769  PMID: 34765075

Abstract

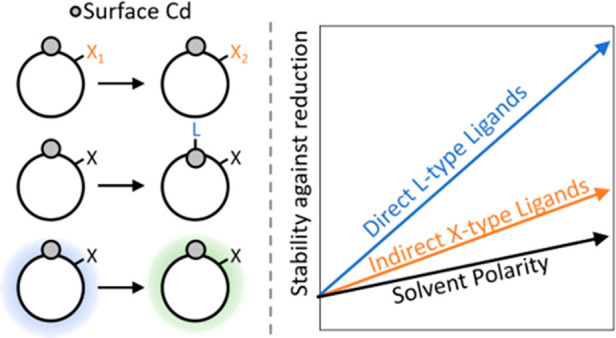
graphic file with name jp1c07464_0007.jpg

Many colloidal quantum dot (QD)-based devices involve charging of the QD, either via intentional electronic doping or via electrical charge injection or photoexcitation. Previous research has shown that this charging can give rise to undesirable electrochemical surface reactions, leading to the formation of localized in-gap states. However, little is known about the factors that influence the stability of charged QDs against surface oxidation or reduction. Here, we use density functional theory to investigate the effect of various ligands and solvents on the reduction of surface Cd in negatively charged CdSe QDs. We find that X-type ligands can lead to significant shifts in the energy of the band edges but that the in-gap state related to reduced surface Cd is shifted in the same direction. As a result, shifting the band edges to higher energies does not necessarily lead to less stable electron charging. However, subtle changes in the local electrostatic environment lead to a clear correlation between the position of the in-gap state in the bandgap and the energy gained upon surface reduction. Binding ligands directly to the Cd sites most prone to reduction was found to greatly enhance the stability of the electron charged QDs. We find that ligands bind much more weakly after reduction of the Cd site, leading to a loss in binding energy that makes charge localization no longer energetically favorable. Lastly, we show that increasing the polarity of the solvent also increases the stability of QDs charged with electrons. These results highlight the complexity of surface reduction reactions in QDs and provide valuable strategies for improving the stability of charged QDs.

Introduction

Because of their high surface-to-volume ratio, colloidal quantum dots (QDs) have properties that are significantly influenced by the nature of the surface.1,2 As atoms at the surface typically have a lower coordination than in the bulk, the QD surface often gives rise to localized energy levels in the bandgap.2−4 These in-gap states can trap generated charge carriers, leading to reduced radiative recombination5 or hindered charge transport,6,7 which limits the efficiency of QD devices.8 Much of the study geared toward improving the performance of these devices has been focused on reducing the density of surface traps via ligand capping5,9−11 or core/shell synthesis.12,13

Many QD devices involve charging of the QD, be it via intentional electronic doping,14,15 or via electrical charge injection16−18 or photoexcitation and subsequent charge separation.19−22 However, this charging can lead to the unwanted formation of new surface defects.23 In bulk systems, the degradation of semiconductor materials through reduction of the metal cations or oxidation of the anions has long been known.24,25 In contrast, our understanding of surface electrochemical reactions in charged QDs remains limited. In a previous computational study, we used density functional theory (DFT) calculations to show that electron charging of II–VI semiconductor QDs can lead to the formation of in-gap states due to the reduction of metal atoms. Upon addition of multiple electrons to a CdTe model QD, charge localization on Cd atoms in the (111) facets was found to create metal-based in-gap states.26 We later showed that surface reduction can also occur upon photoexcitation of charge neutral QDs with suboptimal ligand coverage.27

However, these initial studies only start to scratch the surface of the problem. For instance, the energetics of surface reduction are expected to be significantly affected by the ligands present on the surface and the solvent surrounding the QD. In addition to the passivating effect discussed above, ligands can have an electrostatic effect that leads to an energetic shift of the band edges.28−32 The dielectric constant of the surrounding solvent has been reported to influence the charge distribution over the QD.33 Moreover, solvent molecules can essentially be seen as weakly binding ligands and may hence bind directly to the QD surface, an effect that is expected to be more pronounced for solvents with a lone electron pair, like acetonitrile or propylene carbonate.

The aim of the current work is to look closer at the influence of ligand passivation and solvent interaction on the stability of electron charged CdSe QDs. We use DFT calculations to model the effect of different X- and L-type ligands as well as solvents on the localization of charge on surface Cd sites. We show that X-type ligands can lead to significant shifts of the band edge energies but that the in-gap state related to reduced Cd largely shifts in the same direction. As a result, X-type ligands only weakly affect the energetics of surface reduction. In contrast, L-type ligands, binding directly to the Cd sites that are most prone to reduction, can greatly stabilize the QD and thus prevent surface reduction. Finally, polar solvents stabilize the delocalized charges in the CB more than in localized surface states, resulting in a further stabilization of the charged QD. These results can be used to design QDs and QD environments with strongly increased stability against surface reduction.

Methods

Calculations on systems with different X-type ligands or explicit ligand binding were performed at the DFT level by using a PBE exchange-correlation functional34 and double-ζ basis set, as implemented in the CP2K quantum chemistry software package.35 GTH pseudopotentials incorporate the effective core potentials to account for scalar relativistic effects. Geometry optimizations were performed at 0 K in the gas phase. We use the following criteria of convergence for the optimizations: max_force: 4.50 × 10–4; rms_force: 3.0 × 10–4; max_step: 3.0 × 10–3; rms_step: 1.5 × 10–3. Unrestricted spin calculations were used for systems with an odd total number of electrons (i.e., ⟨n⟩ = 1,3, ...). Solvation effects were studied with the COSMO model36 as implemented in the ADF package37 by using a TZP basis set and PBE exchange-correlation functional in combination with a large frozen core. Scalar relativistic effects were included through the zeroth-order regular approximation (ZORA).38−40 Predefined solvents are used within the COSMO model with the default parameters.

Results and Discussion

Model System

This study uses a zincblende Cd68Se55Cl26 QD model that has been used as a basis for previous DFT studies.26,27,41 In accordance with experiments, it contains an excess of cations,42,43 compensated by the presence of 26 X-type chloride ligands, so that the complete system is charged balanced as defined by Voznyy et al.44 Details regarding the substitution of different X-type ligands or addition of L-type ligands are given throughout the text where relevant for the discussion. The QDs were charged with extra electrons by adding neutral potassium atoms. Because of the very negative reduction potential, each potassium will inject one electron into the QD and then remain as a K+ counterion.26 Throughout this work, the number of excess electrons in the QD will be indicated by ⟨n⟩. Further details of the model system have been reported previously.41

Energetics of Reduction

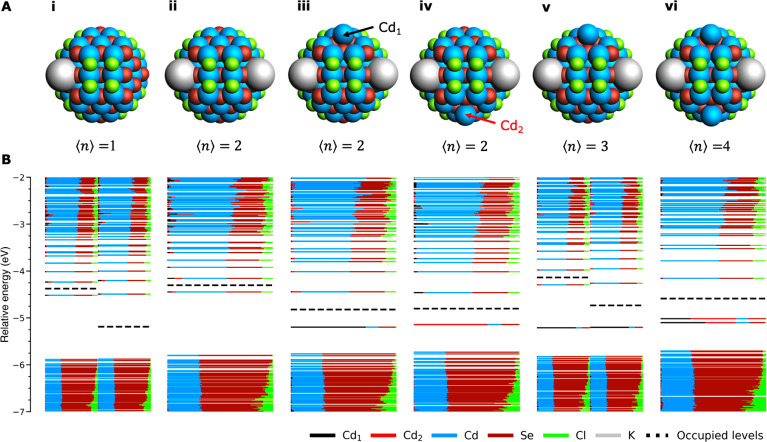
To introduce the problem of surface reduction,26Figure 1 shows the charging of the CdSe model system with an increasing amount of electrons. Figure 1B-i shows the density of states (DOS) at ⟨n⟩ = 1. Here, each horizontal line indicates a molecular orbital (MO). The length of each colored segment indicates the contribution of a specific element or atom. The levels above the dashed line are empty, whereas they are filled below the line. For all calculations with an odd total number of electrons (i.e., ⟨n⟩ = 1, 3, ....), spin-unrestricted calculations have been carried out. This allows the spin-up (α) and spin-down (β) orbitals to relax independently from each other, resulting in two distinct densities of states that are shown on the left and right side of Figure 1B-i, respectively. It can be seen that at ⟨n⟩ = 1 the electron remains delocalized in the conduction band (CB) and that no charge localization takes place. At ⟨n⟩ = 3 (see Figure 1A-v, we will discuss the effects at ⟨n⟩ = 2 soon), a Cd atom (indicated in black as Cd1) is ejected from the (111) facet at the top of the QD. At the same time, an in-gap state appears in the bandgap, which is localized for ∼75% on Cd1 (see Figure 1B-v). This indicates that the excess electrons have localized on Cd1, thus reducing it from Cd∼2+ to Cd∼0. At ⟨n⟩ = 4 (Figure 1-vi), a second Cd atom (indicated in red as Cd2) is ejected from an (111) facet at the bottom of the QD, and a second in-gap state appears.

Figure 1.

Figure 1

Open in a new tab

Reduction of a CdSe QD as a result of increasing electron charging. (A) Structure of the QD when 1–4 electrons are injected. The addition of one K+ counterion per injected electron ensures the total system remains uncharged. For n = 3 and n = 4 the additional K+ ions are not visible as they are located on the backside of the QD. (B) DOS for each of the structures. Each horizontal line corresponds to an MO. The length of each colored line segment indicates the relative contribution of an element or specific atom to that MO. For systems with an odd total number of electrons, unrestricted calculations were used. This results in two distinct densities of states for spin-up and spin-down orbitals, which are shown on the left and right side of the graph, respectively. MOs below the dashed line are filled, and MOs above the line do not contain electrons.

From these results, it becomes clear that a limited number of electrons can remain delocalized in the CB (⟨n⟩ ≤ 1 for our model system) but that injection of too many charges (n ≥ 3) will result in charge localization and concomitant surface reduction and trap formation. For our model system, the transition between these two effects occurs at ⟨n⟩ = 2. We previously reported that two electrons still remain delocalized in the CB edge,26 as also shown in Figure 1-ii. Here, we report that the system, after overcoming an energy barrier of ∼0.07 eV (∼2.9 kBT at room temperature, see Figure S1), can lower its energy further by ∼0.09 eV (∼3.4 kBT) by reduction and ejection of Cd1 (see Figure 1-iii). Reduction of Cd2, as show in Figure 1-iv, lowers the energy ∼0.03 eV (1.1 kBT). Throughout this paper, we will refer to the structure with two electrons delocalized in the CB as the QD in its “nonreduced” configuration. The structure with either of the Cd atoms ejected and the concomitant trap will be termed the “reduced” conformation of the QD. The energy change of the system upon its moving from the nonreduced to the reduced configuration will be defined as ΔER = Ered – Enonred, where Ered and Enonred are the energies of the optimized QD in the reduced and nonreduced configuration, respectively.

We note that due to its complex potential energy surface, a QD can further lower its energy upon reduction through ensuing surface reconstructions. Ligand diffusion and subsequent formation of a Cd–Cd dimer or the diffusion of an ejected Cd over the (111) facet can both lower the energy of the QD in Figure 1 even further. Indeed, it is also expected that upon further charging of a QD, reduced Cd atoms will diffuse together and form metallic Cd clusters. However, the ejection of Cd from the (111) facet shown in Figure 1 constitutes the first step in surface reduction. Hence, throughout this paper we will use this surface configuration as a measure of the energetics of surface reduction.

Figure 2 shows the main processes and related energy changes that occur upon surface reduction: (i) ΔEtrap: trapping of the two CB electrons into an in-gap state; (ii) ΔEbind: ejection of a Cd atom from the (111) facet; and (iii) ΔEsolv: readjustment of the surrounding solvent. As the two CB electrons lower their energy by moving from the CB to a lower-lying in-gap state, we define ΔEtrap = 2(Etrap-state – ECB), where Etrap-state and ECB are the energies of the in-gap level and CB, respectively. We posit that the ejection of the Cd atom from the surface has two main contributions: the energy penalty related to expulsion of the Cd from its lattice and the change in binding strength between the Cd atom and the surrounding ligands. As the ejection of the Cd atom is accompanied by subtle rearrangements of the surrounding CdSe lattice, an exact value for the first contribution is difficult to give. Throughout this work, we will therefore focus on the change in ligand binding. ΔEsolv refers to any dielectric effect or reorganization of the solvent that may occur when reduction leads to a different charge distribution over the QD.

Figure 2.

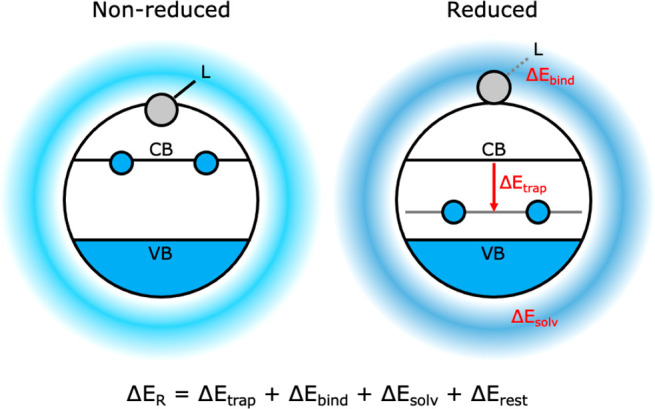
Figure 2

Open in a new tab

Summary of the main processes and related energy changes that occur upon charge localization to surface Cd in an electron charged CdSe QD. (i) ΔEtrap: during charge localization, the two CB electrons can lower their energy by falling into the Cd-localized in-gap state. (ii) ΔEbind: concomitant ejection of the reduced Cd atom from the (111) facet will cost energy by disrupting the surrounding CdSe lattice and weakening the binding to ligands (here indicated as “L”). (iii) ΔEsolv: lastly, localization to surface Cd will change the charge distribution, leading to readjustments of the solvent interaction.

We note that these energy terms are not entirely independent of each other and that more processes will influence ΔER. However, we will use the energy contributions specified above as handles, with which we can explain the complex effects seen in the DFT calculations in a chemically intuitive manner. Therefore, any other effects not specifically studied here, like subtle reorganizations of the ligand shell or slight changes in the valence band (VB) DOS, will be grouped into the term ΔErest. Hence, the final equation which we will use to interpret the results becomes ΔER = Ered – Enonred = ΔEtrap + ΔEbind + ΔEsolv + ΔErest.

X-Type Ligand Induced Energy Shifts

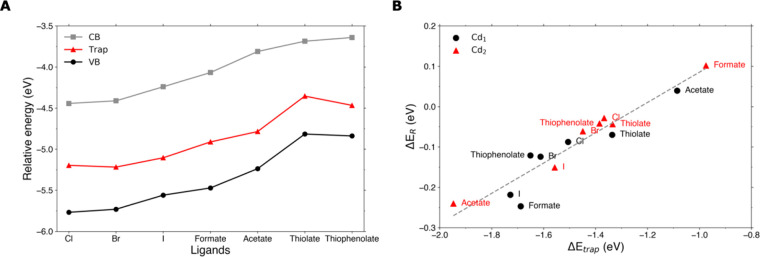
To assess the effect of changing the X-type ligands on the stability of electron charged CdSe QDs, we successively change the 26 chloride ligands of the model system at ⟨n⟩ = 2 for bromide, iodide, formate, acetate, methanethiolate (which we will refer to as “thiolate” throughout the paper), and thiophenolate. In agreement with previous experimental and theoretical studies,29,30 the ligand-dependent surface dipoles lead to energy shifts of the CB and VB edges, as shown in Figure 3A. We observe a downward shift of the energy levels of halogen X-type ligands compared to thiolate ligands, which is similar in trend and magnitude to the shifts reported by Brown et al. for these ligands on PbS QDs.29 At first glance, one may expect that the QDs with higher-lying CB edges (i.e., the QDs with thiolate ligands) are more prone to surface reduction than QDs with lower CB energies (i.e., the QDs with halide passivation). After all, the higher the CB energy, the higher the electrochemical potential of electrons in the CB edge and the easier it should become to reduce surface Cd. However, as shown in Figure S2, there is no clear correlation between CB energy and the energy gain upon reduction (ΔER). The reason for this, as also shown in Figure 3A, is that the energy of the in-gap state due to localization on surface Cd is shifted in the same direction as the band edges. We attribute this effect to the ligand-induced surface dipoles. Although localized, the electrons in the in-gap state will still feel the electrostatic effect of the ligands, and their energy will hence be pushed in the same direction as the band edges.

Figure 3.

Figure 3

Open in a new tab

Effect of X-type ligands on the stability of electron charged CdSe QDs. (A) Energies of CB edge, in-gap level, and VB edge of Cd68Se55X26 QDs in the reduced configuration at ⟨n⟩ = 2, with X = Cl, Br, I, etc., as indicated on the x-axis. (B) Correlation between ΔER and ΔEtrap with reduction of Cd1 (black circles) or Cd2 (red triangles). The gray dashed line is a linear fit to the data points.

Yet, whereas the CB edge is completely delocalized over the entire QD and will hence be affected by an average of all ligands, the in-gap state is localized and will hence be mainly influenced by nearby ligands. This results in the energy of the in-gap state not exactly following the CB energy and hence in small differences in ΔEtrap (as defined in the previous section). Figure 3B shows there is a linear correlation between ΔEtrap and ΔER. The larger ΔEtrap and hence the more the CB electrons can lower their energy by relaxing into the in-gap state, the more favorable reduction becomes (i.e., ΔER becomes more negative). Figure 3B also shows that due to the local effects that influence ΔEtrap, there can be a significant energy difference between reducing and ejecting Cd1 (black circles) and Cd2 (red triangles). For acetate and formate, the effect of local electrostatics is even large enough to make reduction unfavorable (i.e., ΔER ≥ 0) for Cd2, whereas ΔER < 0 for reduction of Cd1. Nevertheless, both the data sets of Cd1 and Cd2 reduction follow the linear correlation between ΔEtrap and ΔER Lastly, it should be noted that the slope of the trend in Figure 3B is not 1, as one would expect from the definition of ΔER given in the introduction, but 0.38. This indicates that as ΔEtrap changes as a function of ligand or ejected Cd atom, other effects take place (which we have grouped under ΔErest in the previous section) in parallel, which changes the slope of the correlation between ΔER and ΔEtrap. These effects could be related to the reorganization of the CdSe lattice near the reduced Cd, as the atoms closest to the ejected Cd are likely to experience a similar electrostatic effect of the ligands.

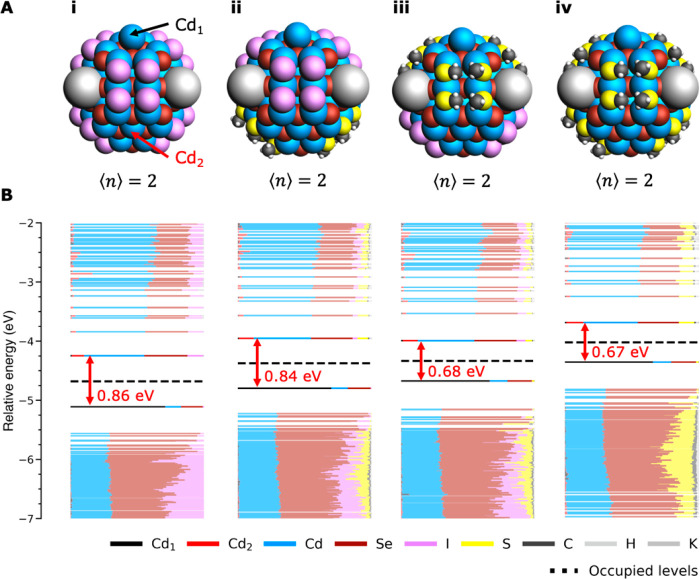
To further investigate the local effects of the ligand shell on ΔEtrap, we compare the DOS of fully iodide and thiolate passivated QDs with mixed iodide/thiolate systems in Figure 4. Figure 4-i shows the structure of a fully iodide passivated QD in the reduced configuration at ⟨n⟩ = 2. Analogous to Figure 1-iii, an in-gap state is present that is largely localized on Cd1. Figure 4-iv shows the same behavior for a fully thiolate-capped QD, with the difference that the CB edges lies higher and the energy difference between the CB and the in-gap state is smaller than in Figure 4-i. Figures 4-ii/iii both show a QD with a mixed ligand passivation consisting of iodide:thiolate = 50:50. In Figure 4-ii the ligands closest to Cd1 are iodides. In Figure 4-iii the thiolate ligands lie closest to Cd1. A comparison of the two mixed-ligand systems shows that the CB edge has the same energy in both cases, indicating that the shift of the band edges depends on the average electrostatic effect of all the ligands. In contrast, the energy difference between the CB edge and the in-gap state is different in Figures 4B-ii and 4B-iii. In Figure 4B-ii, where Cd1 is surrounded by iodide ligands, the in-gap state lies 0.84 eV below the CB edge, which is very similar to the value of 0.86 eV for the fully iodide passivated QD. In Figure 4B-iii, in which Cd1 is surrounded by thiolates, the trap lies 0.68 eV below the CB, which closely resembles the 0.67 eV for the fully thiolate passivated system. This shows that the shift of the in-gap state is mainly influenced by the ligands that are close to the site where the wave function localizes. These trends can be generalized to other mixed-passivated systems, as shown for Cl/I in Figure S3.

Figure 4.

Figure 4

Open in a new tab

In-gap formation in QDs with mixed passivation. (A) Structure of QDs with (i) complete iodide passivation, (ii) iodide:thiolate = 50:50 passivation with the iodide ligands closest to Cd1 (indicated in black), (iii) iodide:thiolate = 50:50 passivation with the thiolate ligands closest to Cd1, and (iv) complete thiolate passivation. (B) DOS of each system. The energy difference between the CB edge and the in-gap state is indicated in red.

To summarize, X-type ligand exchange causes the band edges and the in-gap state to move largely in parallel. Only subtle changes in the local environment of the trap state influence ΔEtrap and by extension ΔER. Although X-type ligands can hence only play a minor role in making electron charged QDs more stable against intrinsic reduction (i.e., reduction of surface Cd), they are expected to have a large effect on the importance of reduction reactions with external impurities. Contrary to the in-gap states, the reduction potentials of external impurities (e.g., O2 or H2O)23,45,46 are not expected to shift along with the band edge energies. Hence, X-type ligands that lead to a lower CB edge (higher VB edge) may still lead to the more stable electron charging (hole charging) of the QDs.

Direct Ligand Binding

Next, we investigate the effect of ligands directly binding to Cd1 or Cd2 on the energetics of surface reduction. For that we bind a range of L-type ligands (aniline, methylamine, and acetonitrile) as well as hexane and toluene directly to Cd1 and Cd2. As argued in the Introduction, compounds commonly considered as solvent can also be seen as weakly binding ligands. Although hexane and toluene do not have a lone pair and hence are not L-type ligands, they can still interact, albeit weakly, with the QD surface through dispersion forces. As summarized in Figure S4, we assess the effect of direct ligand binding to the QD by adding one ligand to both Cd1 and Cd2. By removing one of the ligands, we can compute the binding energy to the Cd atom by using that Ebind = EQD–2L – EQD–1L – EL, where EQD–2L stands for the energy of the QD with one ligand to both Cd1 and Cd2, EQD–1L for the QD with one ligand attached to either Cd1 or Cd2, and EL for the energy of a loose ligand. We passivate both Cd sites at the same time to prevent the situation where passivation of one Cd site will simply lead to the CB electrons localizing on the other Cd atom.

As summarized in Table S1, the binding energy of the ligands to the nonreduced QD ranges from ∼0.1 eV (hexane) to ∼0.7 eV (methylamine), with no significant differences between the binding to Cd1 and Cd2. As defined by Green,47 L-type ligands (a Lewis base) bind to Cd (a Lewis acid) by donation of an electron pair.42 If a Cd atom is reduced from Cd∼2+ to Cd∼0, this interaction becomes much less favorable. Indeed, upon reduction of the surface Cd sites, the binding energy decreases with an average of ∼90% for the three L-type ligands tested here. In contrast, the binding energy of hexane and toluene, which could only bind to Cd with weak dispersion forces from the start, is on average reduced by ∼65% (see Table S1).

Clearly, the reduction in binding strength with the ligands forms an energy penalty the system has to pay to localize charge on surface Cd. To quantify this effect, we define ΔEbind = Ebind,red – Ebind,nonred, where Ebind,red and Ebind,nonred are the binding energy of the ligands to the QD in its reduced and nonreduced configuration, respectively. Figure 5 shows that there is a linear correlation between ΔEbind and ΔER. Although hexane and toluene bind only weakly to the QD and hence increase ΔER by a relatively small amount, it is already enough to ensure that ΔER ≥ 0 and hence make charge localization unfavorable. The L-type amine ligands bind stronger and hence increase ΔER even further. The linear fit to the data indicated by the dashed gray line in Figure 5 has a slope of 0.91, indicating that the direct binding of ligands has a larger effect on ΔER than changing the X-type ligands (as shown in Figure 3B). However, as the slope is not 1, other effects must take place in parallel. For instance, as shown in Figure S5, we found that ΔEtrap becomes less negative with increasing ΔEbind. We conclude that the addition of L-type ligands to the surface is a powerful tool to enhance the stability of electron charged QDs and that even weakly binding solvent molecules can help stabilize the system.

Figure 5.

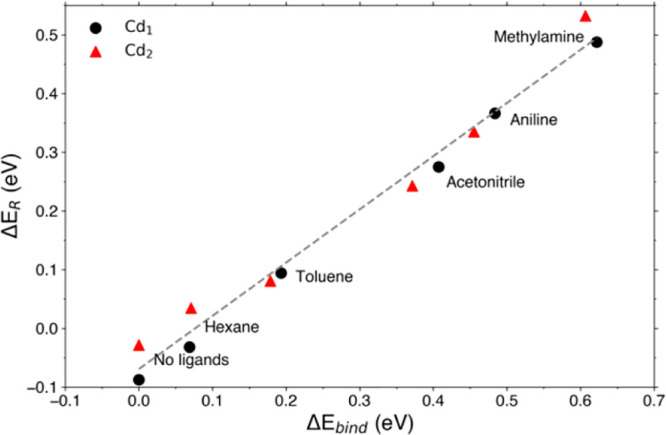
Figure 5

Open in a new tab

Correlation between ΔER and ΔEbind for electron charged CdSe QDs with different ligands binding directly to Cd1 and Cd2, as determined with the reduction of Cd1 (black circles) and Cd2 (red triangles). The gray dashed line is a linear fit to the data points.

Although no direct experimental evidence is available for the relation between surface reduction and L type ligand passivation, there are various observation in the literature that support this conclusion. First, it is well-known that addition of L-type ligands can enhance the PLQY of II–VI QDs48 and that L-type ligands in the form of amines or phosphines are required for near-unity PLQY, even in core–shell QDs.49,50 There is, however, no clear atomistic picture of the trap level that is passivated by L-type ligands, since these should bind to undercoordinated surface Cd ions, which should theoretically not expose states in the bandgap.51 One explanation is that the photoexcitation of CdSe QDs results in surface reduction unless L-type ligands are employed to stabilize the surface Cd ions.27

Perhaps more direct evidence could come from electrochemical studies of CdSe QD films. It is well-known that treatment of films of CdSe QDs with molecules like 1,7-heptanediamine increase the stability and reversibility in electrochemical measurements. Yu et al.52 showed in a comparison of various surface treatments that cyclic voltammograms of CdSe QD films treated with 1-butylamine, and especially 1,7-heptanediamine, exhibit more reversible electron charging and discharging than films treated in other ways. This could reflect the higher stability of amine passivated CdSe QDs against surface reduction, although it is difficult to draw hard conclusions, since such treatments will also change other properties of the QD films, including an increase in the electron mobility which will also affect the shape of the cyclic voltammograms. In addition, the addition of ligands like 1,7-heptanediamine will result in the stripping of Z type ligands, in addition to adding L-type ligands, changing the surface composition in multiple ways.42,53

Solvation Effects

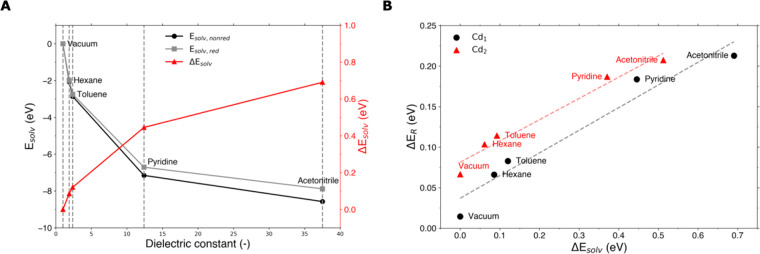
In the previous section, we discussed the direct bonding interaction between solvent molecules and the QD. However, solvents also screen the charge distribution of the QD. In this section, we model this dielectric effect by adding an implicit solvent as implemented in the COSMO model in ADF.36 Inclusion of the solvent lowers the energy of the system by the solvation energy Esolv (i.e., with Esolv < 0). Following the definition used in the COSMO model,36Esolv includes the stabilizing contribution of the electrostatic interaction between the QD and the solvent, as well as the energy penalty of creating a solute cavity in the continuum, but excludes changes in the energy of the solute (i.e., the QD itself). To quantify the change in Esolv upon charge localization and assess its effect on ΔER, we define ΔEsolv = Esolv,red – Esolv,nonred, where Esolv,red and Esolv,nonred are the solvation energy of the QD in its reduced and nonreduced conformation, respectively. As can be seen in Figure 6A, in all solvents the QD is stabilized more in its nonreduced form (Esolv,nonred) than in its reduced configuration (Esolv,red). Moreover, ΔEsolv becomes more positive with increasing dielectric constant of the solvent. We infer that the solvation effect of delocalized CB electrons is larger than of electrons localized on surface Cd. This can be understood by considering that the CB wave function extends over more of the QD surface than the localized trap level, causing a larger solvation effect in the former case.

Figure 6.

Figure 6

Open in a new tab

Effects of inclusion of implicit solvents on electron charged CdSe QDs. (A) Relation between the dielectric constant of the solvent and Esolv,nonred, Esolv,red, and ΔEsolv. (B) Relation between ΔER and ΔEsolv when changing the solvent for a chloride passivated QD at ⟨n⟩ = 2, when reducing Cd1 (black circles) and Cd2 (red triangles). The gray and light red dashed lines are linear fits to the data points.

Figure 6B shows the correlation between ΔEsolv and ΔER for a chloride passivated QD in increasingly polar solvents. It can be seen that for more positive values of ΔEsolv reduction becomes less favorable (i.e., ΔER increases), a trend which also holds for various X-type ligands (see Figure S6B). However, as was the case for the effect of X-type ligands discussed previously, the slope of the linear fit is not 1, as one would expect. Moreover, although the reduction of Cd1 and Cd2 depends on ΔEsolv in the same way (with slopes of 0.28 and 0.26, respectively), the trends do show an offset that was not present in Figures 3B and 5. This shows that while the change in ΔEsolv clearly affects ΔER, there are additional energy terms that partially compensate for the effect. For instance, we found for the chloride passivated QD that ΔEtrap is not constant when changing the solvent but changes with ΔEsolv (see Figure S6A). This partially explains the small slope in Figure 6A, although there must be additional effects that are currently not completely understood. The overall trend, however, clearly shows that the stability of electron-charged QDs increases with the dielectric constant of the solvent.

The calculations presented here were performed on CdSe QDs only. In a previous paper,26 we showed results for charging of various II–VI QDs (CdSe, CdSe, CdTe, ZnS, ZnSe, and ZnTe) using a single type of surface coverage and without any solvent interaction. We showed that charging of Zn chalcogenide QDs is stable up to at least four electrons, while for none of the Cd-chalcogenide QDs this is the case. This is attributed to the higher intrinsic stability of Zn2+ against reduction (E° in water is −0.76 V vs NHE) than of Cd2+ against reduction (E° = −0.40 V vs NHE). We expect that the trends reported here for X- and L-type ligands and solvent polarity also hold for other II–VI QDs, on top of the differences in intrinsic stability against surface reduction.

Conclusions

In conclusion, DFT calculations have been used to study the effects of ligand passivation and solvent interaction on the stability of electron charged CdSe QDs. We show that X-type ligands can lead to significant shifts of the band edges. However, as the in-gap state related to metallic Cd moves largely in parallel with the band edges, X-type ligands only have a minor effect on the energetics of surface reduction. Binding L-type ligands directly to the most labile Cd sites was found to greatly enhance the stability of the electron charged QDs. The loss in binding energy upon reduction of the surface creates an energy penalty that is larger than the energy gain related to charge localization, meaning that reduction of the Cd atom is no longer favorable. Lastly, we show that electron charged QDs can be further stabilized by increasing the polarity of the solvent. These results show that the nature of the ligand shell and the surrounding solvent significantly affect the energetics of surface reduction reactions, providing valuable strategies for improving the stability of charged QDs.

Acknowledgments

A.J.H. acknowledges the European Research Council Horizon 2020 ERC Grant Agreement No. 678004 (Doping on Demand) for financial support. I.I. acknowledges support from The Netherlands Organization of Scientific Research (NWO) through the Innovational Research Incentive (Vidi) Scheme (Grant No. 723.013.002). This work was sponsored by NWO Exact and Natural Sciences for the use of supercomputer facilities and was performed on the Dutch national e-infrastructure with the support of the SURF Cooperative.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.1c07464.

  • Potential energy surfaces of QDs at ⟨n⟩ = 1–3; correlation between ΔER and the CB edge for different X-type ligands; structures and DOS for QDs with mixed Cl/I passivation; schematic summary of how Ebind was calculated; overview of Ebind,nonred and Ebind,red for the investigated ligands; correlation between ΔEtrap and ΔEbind for ligands bound directly to the QD; and overview of the effect of solvent on ΔEtrap and on systems with different X-type ligand passivations (PDF)

Author Contributions

I.d.F. and S.L. contributed equally to this work.

The authors declare no competing financial interest.

Special Issue

Published as part of The Journal of Physical Chemistry virtual special issue “Marie-Paule Pileni Festschrift”.

Supplementary Material

jp1c07464_si_001.pdf (437.9KB, pdf)

References

  1. Hartley C. L.; Kessler M. L.; Dempsey J. L. Molecular-Level Insight into Semiconductor Nanocrystal Surfaces. J. Am. Chem. Soc. 2021, 143 (3), 1251–1266. 10.1021/jacs.0c10658. [DOI] [PubMed] [Google Scholar]
  2. de Mello Donegá C. Synthesis and Properties of Colloidal Heteronanocrystals. Chem. Soc. Rev. 2011, 40 (3), 1512–1546. 10.1039/C0CS00055H. [DOI] [PubMed] [Google Scholar]
  3. Giansante C.; Infante I. Surface Traps in Colloidal Quantum Dots: A Combined Experimental and Theoretical Perspective. J. Phys. Chem. Lett. 2017, 8 (20), 5209–5215. 10.1021/acs.jpclett.7b02193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Boles M. A.; Ling D.; Hyeon T.; Talapin D. V. The Surface Science of Nanocrystals. Nat. Mater. 2016, 15 (2), 141–153. 10.1038/nmat4526. [DOI] [PubMed] [Google Scholar]
  5. Kirkwood N.; Monchen J. O. V.; Crisp R. W.; Grimaldi G.; Bergstein H. A. C.; du Fossé I.; van der Stam W.; Infante I.; Houtepen A. J. Finding and Fixing Traps in II-VI and III-V Colloidal Quantum Dots: The Importance of Z-Type Ligand Passivation. J. Am. Chem. Soc. 2018, 140 (46), 15712–15723. 10.1021/jacs.8b07783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Katsiev K.; Ip A. H.; Fischer A.; Tanabe I.; Zhang X.; Kirmani A. R.; Voznyy O.; Rollny L. R.; Chou K. W.; Thon S. M.; et al. The Complete In-Gap Electronic Structure of Colloidal Quantum Dot Solids and Its Correlation with Electronic Transport and Photovoltaic Performance. Adv. Mater. 2014, 26 (6), 937–942. 10.1002/adma.201304166. [DOI] [PubMed] [Google Scholar]
  7. Ip A. H.; Thon S. M.; Hoogland S.; Voznyy O.; Zhitomirsky D.; Debnath R.; Levina L.; Rollny L. R.; Carey G. H.; Fischer A.; et al. Hybrid Passivated Colloidal Quantum Dot Solids. Nat. Nanotechnol. 2012, 7 (9), 577–582. 10.1038/nnano.2012.127. [DOI] [PubMed] [Google Scholar]
  8. Kagan C. R.; Lifshitz E.; Sargent E. H.; Talapin D. V.. Building Devices from Colloidal Quantum Dots. Science (Washington, DC, U. S.) 2016, 10.1126/science.aac5523. [DOI] [PubMed] [Google Scholar]
  9. Knowles K. E.; Tice D. B.; McArthur E. A.; Solomon G. C.; Weiss E. A. Chemical Control of the Photoluminescence of CdSe Quantum Dot-Organic Complexes with a Series of Para-Substituted Aniline Ligands. J. Am. Chem. Soc. 2010, 132 (3), 1041–1050. 10.1021/ja907253s. [DOI] [PubMed] [Google Scholar]
  10. Tang J.; Kemp K. W.; Hoogland S.; Jeong K. S.; Liu H.; Levina L.; Furukawa M.; Wang X.; Debnath R.; Cha D.; et al. Colloidal-Quantum-Dot Photovoltaics Using Atomic-Ligand Passivation. Nat. Mater. 2011, 10 (10), 765–771. 10.1038/nmat3118. [DOI] [PubMed] [Google Scholar]
  11. Calvin J. J.; Swabeck J. K.; Sedlak A. B.; Kim Y.; Jang E.; Alivisatos A. P. Thermodynamic Investigation of Increased Luminescence in Indium Phosphide Quantum Dots by Treatment with Metal Halide Salts. J. Am. Chem. Soc. 2020, 142 (44), 18897–18906. 10.1021/jacs.0c08954. [DOI] [PubMed] [Google Scholar]
  12. Van Der Stam W.; Grimaldi G.; Geuchies J. J.; Gudjonsdottir S.; Van Uffelen P. T.; Van Overeem M.; Brynjarsson B.; Kirkwood N.; Houtepen A. J. Electrochemical Modulation of the Photophysics of Surface-Localized Trap States in Core/Shell/(Shell) Quantum Dot Films. Chem. Mater. 2019, 31 (20), 8484–8493. 10.1021/acs.chemmater.9b02908. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Reiss P.; Protière M.; Li L. Core/Shell Semiconductor Nanocrystals. Small 2009, 5 (2), 154–168. 10.1002/smll.200800841. [DOI] [PubMed] [Google Scholar]
  14. Shim M.; Wang C.; Norris D. J.; Guyot-Sionnest P. Doping and Charging in Colloidal Semiconductor Nanocrystals. MRS Bull. 2001, 26 (12), 1005–1008. 10.1557/mrs2001.257. [DOI] [Google Scholar]
  15. Mocatta D.; Cohen G.; Schattner J.; Millo O.; Rabani E.; Banin U. Heavily Doped Semiconductor Nanocrystal Quantum Dots. Science (Washington, DC, U. S.) 2011, 332 (6025), 77–81. 10.1126/science.1196321. [DOI] [PubMed] [Google Scholar]
  16. Pietryga J. M.; Park Y.-S.; Lim J.; Fidler A. F.; Bae W. K.; Brovelli S.; Klimov V. I. Spectroscopic and Device Aspects of Nanocrystal Quantum Dots. Chem. Rev. 2016, 116 (18), 10513–10622. 10.1021/acs.chemrev.6b00169. [DOI] [PubMed] [Google Scholar]
  17. Lim J.; Park Y. S.; Wu K.; Yun H. J.; Klimov V. I. Droop-Free Colloidal Quantum Dot Light-Emitting Diodes. Nano Lett. 2018, 18 (10), 6645–6653. 10.1021/acs.nanolett.8b03457. [DOI] [PubMed] [Google Scholar]
  18. Chang J. H.; Park P.; Jung H.; Jeong B. G.; Hahm D.; Nagamine G.; Ko J.; Cho J.; Padilha L. A.; Lee D. C.; et al. Unraveling the Origin of Operational Instability of Quantum Dot Based Light-Emitting Diodes. ACS Nano 2018, 12 (10), 10231–10239. 10.1021/acsnano.8b03386. [DOI] [PubMed] [Google Scholar]
  19. Ganesan A. A.; Houtepen A. J.; Crisp R. W. Quantum Dot Solar Cells: Small Beginnings Have Large Impacts. Appl. Sci. 2018, 8 (10), 1867. 10.3390/app8101867. [DOI] [Google Scholar]
  20. Kershaw S. V.; Jing L.; Huang X.; Gao M.; Rogach A. L. Materials Aspects of Semiconductor Nanocrystals for Optoelectronic Applications. Mater. Horiz. 2017, 4 (2), 155–205. 10.1039/C6MH00469E. [DOI] [Google Scholar]
  21. Carey G. H.; Abdelhady A. L.; Ning Z.; Thon S. M.; Bakr O. M.; Sargent E. H. Colloidal Quantum Dot Solar Cells. Chem. Rev. 2015, 115 (23), 12732–12763. 10.1021/acs.chemrev.5b00063. [DOI] [PubMed] [Google Scholar]
  22. Liu M.; Yazdani N.; Yarema M.; Jansen M.; Wood V.; Sargent E. H. Colloidal Quantum Dot Electronics. Nat. Electron. 2021, 4, 548–558. 10.1038/s41928-021-00632-7. [DOI] [Google Scholar]
  23. Schimpf A. M.; Gunthardt C. E.; Rinehart J. D.; Mayer J. M.; Gamelin D. R. Controlling Carrier Densities in Photochemically Reduced Colloidal ZnO Nanocrystals: Size Dependence and Role of the Hole Quencher. J. Am. Chem. Soc. 2013, 135 (44), 16569–16577. 10.1021/ja408030u. [DOI] [PubMed] [Google Scholar]
  24. Gerischer H. On the Stability of Semiconductor Electrodes Against Photodecomposition. J. Electroanal. Chem. Interfacial Electrochem. 1977, 82 (1–2), 133–143. 10.1016/S0022-0728(77)80253-2. [DOI] [Google Scholar]
  25. Nadjo L. The Characterization and Behaviour of N-and p-CdTe Electrodes in Acetonitrile Solutions. J. Electroanal. Chem. Interfacial Electrochem. 1980, 108 (1), 29–47. 10.1016/S0022-0728(80)80090-8. [DOI] [Google Scholar]
  26. Du Fossé I.; Ten Brinck S.; Infante I.; Houtepen A. J. Role of Surface Reduction in the Formation of Traps in N-Doped II-VI Semiconductor Nanocrystals: How to Charge without Reducing the Surface. Chem. Mater. 2019, 31 (12), 4575–4583. 10.1021/acs.chemmater.9b01395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. du Fossé I.; Boehme S. C.; Infante I.; Houtepen A. J. Dynamic Formation of Metal-Based Traps in Photoexcited Colloidal Quantum Dots and Their Relevance for Photoluminescence. Chem. Mater. 2021, 33 (9), 3349–3358. 10.1021/acs.chemmater.1c00561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Grimaldi G.; Van Den Brom M. J.; Du Fossé I.; Crisp R. W.; Kirkwood N.; Gudjonsdottir S.; Geuchies J. J.; Kinge S.; Siebbeles L. D. A.; Houtepen A. J. Engineering the Band Alignment in QD Heterojunction Films via Ligand Exchange. J. Phys. Chem. C 2019, 123 (49), 29599–29608. 10.1021/acs.jpcc.9b09470. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Brown P. R.; Kim D.; Lunt R. R.; Zhao N.; Bawendi M. G.; Grossman J. C.; Bulović V. Energy Level Modification in Lead Sulfide Quantum Dot Thin Films through Ligand Exchange. ACS Nano 2014, 8 (6), 5863–5872. 10.1021/nn500897c. [DOI] [PubMed] [Google Scholar]
  30. Kroupa D. M.; Vörös M.; Brawand N. P.; McNichols B. W.; Miller E. M.; Gu J.; Nozik A. J.; Sellinger A.; Galli G.; Beard M. C. Tuning Colloidal Quantum Dot Band Edge Positions through Solution-Phase Surface Chemistry Modification. Nat. Commun. 2017, 8 (1), 15257. 10.1038/ncomms15257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Yang S.; Prendergast D.; Neaton J. B. Tuning Semiconductor Band Edge Energies for Solar Photocatalysis via Surface Ligand Passivation. Nano Lett. 2012, 12 (1), 383–388. 10.1021/nl203669k. [DOI] [PubMed] [Google Scholar]
  32. Shalom M.; Rühle S.; Hod I.; Yahav S.; Zaban A. Energy Level Alignment in CdS Quantum Dot Sensitized Solar Cells Using Molecular Dipoles. J. Am. Chem. Soc. 2009, 131 (29), 9876–9877. 10.1021/ja902770k. [DOI] [PubMed] [Google Scholar]
  33. Liu H.; Brozek C. K.; Sun S.; Lingerfelt D. B.; Gamelin D. R.; Li X. A Hybrid Quantum-Classical Model of Electrostatics in Multiply Charged Quantum Dots. J. Phys. Chem. C 2017, 121 (46), 26086–26095. 10.1021/acs.jpcc.7b08224. [DOI] [Google Scholar]
  34. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77 (18), 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  35. Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4 (1), 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  36. Pye C. C.; Ziegler T. An Implementation of the Conductor-like Screening Model of Solvation within the Amsterdam Density Functional Package. Theor. Chem. Acc. 1999, 101 (6), 396–408. 10.1007/s002140050457. [DOI] [Google Scholar]
  37. te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22 (9), 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
  38. van Lenthe E.; Ehlers A.; Baerends E.-J. Geometry Optimizations in the Zero Order Regular Approximation for Relativistic Effects. J. Chem. Phys. 1999, 110 (18), 8943–8953. 10.1063/1.478813. [DOI] [Google Scholar]
  39. Lenthe E. v.; Baerends E. J.; Snijders J. G. Relativistic Regular Two-component Hamiltonians. J. Chem. Phys. 1993, 99 (6), 4597–4610. 10.1063/1.466059. [DOI] [Google Scholar]
  40. van Lenthe E.; Baerends E. J.; Snijders J. G. Relativistic Total Energy Using Regular Approximations. J. Chem. Phys. 1994, 101 (11), 9783–9792. 10.1063/1.467943. [DOI] [Google Scholar]
  41. Houtepen A. J.; Hens Z.; Owen J. S.; Infante I. On the Origin of Surface Traps in Colloidal II-VI Semiconductor Nanocrystals. Chem. Mater. 2017, 29 (2), 752–761. 10.1021/acs.chemmater.6b04648. [DOI] [Google Scholar]
  42. Anderson N. C.; Hendricks M. P.; Choi J. J.; Owen J. S. Ligand Exchange and the Stoichiometry of Metal Chalcogenide Nanocrystals: Spectroscopic Observation of Facile Metal-Carboxylate Displacement and Binding. J. Am. Chem. Soc. 2013, 135 (49), 18536–18548. 10.1021/ja4086758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Greaney M. J.; Couderc E.; Zhao J.; Nail B. A.; Mecklenburg M.; Thornbury W.; Osterloh F. E.; Bradforth S. E.; Brutchey R. L. Controlling the Trap State Landscape of Colloidal CdSe Nanocrystals with Cadmium Halide Ligands. Chem. Mater. 2015, 27 (3), 744–756. 10.1021/cm503529j. [DOI] [Google Scholar]
  44. Voznyy O.; Zhitomirsky D.; Stadler P.; Ning Z.; Hoogland S.; Sargent E. H. A Charge-Orbital Balance Picture of Doping in Colloidal Quantum Dot Solids. ACS Nano 2012, 6 (9), 8448–8455. 10.1021/nn303364d. [DOI] [PubMed] [Google Scholar]
  45. Gudjonsdottir S.; Koopman C.; Houtepen A. J. Enhancing the Stability of the Electron Density in Electrochemically Doped ZnO Quantum Dots. J. Chem. Phys. 2019, 151 (14), 144708. 10.1063/1.5124534. [DOI] [PubMed] [Google Scholar]
  46. Rinehart J. D.; Schimpf A. M.; Weaver A. L.; Cohn A. W.; Gamelin D. R. Photochemical Electronic Doping of Colloidal CdSe Nanocrystals. J. Am. Chem. Soc. 2013, 135 (50), 18782–18785. 10.1021/ja410825c. [DOI] [PubMed] [Google Scholar]
  47. Green M. L. H. A New Approach to the Formal Classification of Covalent Compounds of the Elements. J. Organomet. Chem. 1995, 500 (1–2), 127–148. 10.1016/0022-328X(95)00508-N. [DOI] [Google Scholar]
  48. Kirkwood N.; Monchen J. O. V.; Crisp R. W.; Grimaldi G.; Bergstein H. A. C.; Du Fossé I.; Van Der Stam W.; Infante I.; Houtepen A. J. Finding and Fixing Traps in II-VI and III-V Colloidal Quantum Dots: The Importance of Z-Type Ligand Passivation. J. Am. Chem. Soc. 2018, 140 (46), 15712–15723. 10.1021/jacs.8b07783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Pu C.; Peng X. To Battle Surface Traps on CdSe/CdS Core/Shell Nanocrystals: Shell Isolation versus Surface Treatment. J. Am. Chem. Soc. 2016, 138 (26), 8134–8142. 10.1021/jacs.6b02909. [DOI] [PubMed] [Google Scholar]
  50. Zhou J.; Zhu M.; Meng R.; Qin H.; Peng X. Ideal CdSe/CdS Core/Shell Nanocrystals Enabled by Entropic Ligands and Their Core Size-, Shell Thickness-, and Ligand-Dependent Photoluminescence Properties. J. Am. Chem. Soc. 2017, 139 (46), 16556–16567. 10.1021/jacs.7b07434. [DOI] [PubMed] [Google Scholar]
  51. Houtepen A. J.; Hens Z.; Owen J. S.; Infante I. On the Origin of Surface Traps in Colloidal II-VI Semiconductor Nanocrystals. Chem. Mater. 2017, 29 (2), 752–761. 10.1021/acs.chemmater.6b04648. [DOI] [Google Scholar]
  52. Yu D.; Wehrenberg B. L.; Jha P.; Ma J.; Guyot-Sionnest P. Electronic Transport of N-Type CdSe Quantum Dot Films: Effect of Film Treatment. J. Appl. Phys. 2006, 99 (10), 104315. 10.1063/1.2192288. [DOI] [Google Scholar]
  53. Sandeep C. S. S.; Azpiroz J. M.; Evers W. H.; Boehme S. C.; Moreels I.; Kinge S.; Siebbeles L. D. A.; Infante I.; Houtepen A. J. Epitaxially Connected PbSe Quantum-Dot Films: Controlled Neck Formation and Optoelectronic Properties. ACS Nano 2014, 8 (11), 11499–11511. 10.1021/nn504679k. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp1c07464_si_001.pdf (437.9KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES