PScL-HDeep: image-based prediction of protein subcellular location in human tissue using ensemble learning of handcrafted and deep learned features with two-layer feature selection

Abstract

Protein subcellular localization plays a crucial role in characterizing the function of proteins and understanding various cellular processes. Therefore, accurate identification of protein subcellular location is an important yet challenging task. Numerous computational methods have been proposed to predict the subcellular location of proteins. However, most existing methods have limited capability in terms of the overall accuracy, time consumption and generalization power. To address these problems, in this study, we developed a novel computational approach based on human protein atlas (HPA) data, referred to as PScL-HDeep, for accurate and efficient image-based prediction of protein subcellular location in human tissues. We extracted different handcrafted and deep learned (by employing pretrained deep learning model) features from different viewpoints of the image. The step-wise discriminant analysis (SDA) algorithm was applied to generate the optimal feature set from each original raw feature set. To further obtain a more informative feature subset, support vector machine–based recursive feature elimination with correlation bias reduction (SVM-RFE + CBR) feature selection algorithm was applied to the integrated feature set. Finally, the classification models, namely support vector machine with radial basis function (SVM-RBF) and support vector machine with linear kernel (SVM-LNR), were learned on the final selected feature set. To evaluate the performance of the proposed method, a new gold standard benchmark training dataset was constructed from the HPA databank. PScL-HDeep achieved the maximum performance on 10-fold cross validation test on this dataset and showed a better efficacy over existing predictors. Furthermore, we also illustrated the generalization ability of the proposed method by conducting a stringent independent validation test.

Introduction

The biological reproductive system is composed of unique systems of organs involved in reproduction or more simply creating a new life. At the cellular level, the biological reproductive system has many cells containing thousands of proteins, where each cell is the smallest unit of life while proteins are the very basic biological molecules in a cell [1]. Therefore, understanding and exploring the natural function of these proteins at the cellular level is a fundamental task in the research of proteomics. It is broadly recognized that the particular function of protein is closely related to its corresponding cellular compartments [2]. To assure its normal functionalities, protein needs to interact with its corresponding interacting molecules at the right location at the right time. Aberrant localization of protein can cause loss of biological functionalities, which may lead to serious diseases like cancer [3, 4]. Thus, characterizing protein subcellular location can provide important clues for understanding the mechanism of biological molecular interaction, identification of drug discovery and genome annotation [5].

Traditional wet-lab experiments are expensive and time consuming and cannot catch up with the increasing amount of newly discovered proteins. As a useful complementation to time-consuming and costly experimental methods, computational models are becoming the main focus in biomedical research. The performance of these computational models is increasing, and some models even outperformed human experts [6, 7]. For example, since 2013, the HPA data source began to use the TMAx-automated recognition software application to facilitate the annotation. Besides, some databases such as OMERO [8] and BisQue [9] have been developed that concurrently store and annotate protein images. However, they are not just bioimage databases but also encompass analysis software as well.

Currently, there are many automated computational systems that have been deployed for accurate prediction of protein subcellular location. All these models can be categorized as either sequence-based [10–15] or image-based [2, 16–18], according to the representation of the protein data. Both categories (sequence-based and image-based) work on the idea of a two-step framework: selecting the most proper features that represent the protein data and applying a trained machine learning classifier for label decision [19].

Sequence-based methods can be applied to proteins that are represented in 1-D amino acid sequence via a modern sequencing technology. However, the fact is that most of the current machine learning approaches can handle vector-based samples and not the sequence directly, making it a necessary but challenging step to represent a protein sequence with discrete model or vector while still preserving the sequence information [20]. A variety of sequence encoding techniques, such as position-specific scoring matrix [21] and pseudo–amino acid composition [22], have been deployed to avoid complete sequence information loss. Ever since, such sequence encoding methods have been widely used in the field of bioinformatics and computational biology [23–29].

With recent advances in automated microscopic imaging technologies, increasing amounts of bioimaging data are being rapidly generated and accumulated. On the other hand, detection of protein translocation is difficult for sequence-based approaches, which motivated researchers to devote efforts to the development of two-dimensional (2D) image-based pattern recognition methods. Accordingly, a number of bioimage-based approaches have been recently developed for the prediction of protein subcellular location. For example, Xu et al. developed a multilabel predictor using global and local descriptors extracted from protein images and applied support vector machine (SVM) classifier using the one-vs-all strategy [30]. Yang et al. employed Haralick texture features, local binary patterns (LBP), local ternary patterns (LTP) and local quinary patterns (LQP) with the SVM classifier [1]. In another work, Shao et al. used the kernel combination strategy to combine global DNA, Haralick features and local binary pattern and developed a codeword matrix to predict protein subcellular localization through the error-correcting output coding (ECOC) and SVM [19]. More recently, the SAE-RF method was proposed by Liu et al. [31]. They predicted protein subcellular localization using stacked autoencoder and random forest through the fusion of histogram characteristic, Gabor filters, gray level co-occurrence matrix (GLCM), perception features, Haralick texture features, local binary patterns and DNA features. They selected the optimal feature set using the minimum Redundancy Maximum Relevance (mRMR) feature selection method [32]. Supplementary Table S1, available online at http://bib.oxfordjournals.org/, in the SI Text S1 summarizes the existing methods. Considerable achievement has been made so far in the area of protein subcellular localization prediction. However, the performance of the existing models is not satisfactory and there remains a gap for further improvement.

Deep learning has recently emerged as a powerful and effective machine learning algorithm and achieved an outstanding performance across many research areas including computer vision and natural langue processing [33–38]. Although it has been applied successfully to address various bioinformatics problems, few studies have used convolutional neural networks as a feature extractor up to now [33, 39–41]. Moreover, fusion of multiple types of features in an appropriate way has proven to be effective for improving the prediction of protein subcellular localization [1, 30, 31, 42]. Some studies used either stepwise discernment analysis (SDA) [43] or mRMR [32] to select the optimal feature subsets. However, the effectiveness of the selected features needs to be examined by training and testing the classification model. Most of the bioimage-based protein subcellular localization prediction methods do not use the idea of training and testing a classifier to select optimal feature set. In this study, we develop a new computational framework to address the above-mentioned shortfalls of the existing methods. Our study is as structured as follows.

We constructed two datasets from the Human Protein Atlas (HPA) (http://www.proteinatlas.org) data bank, namely the benchmark training dataset and independent test dataset. Deep features were learned from the original protein images, while the handcrafted features were extracted from both DNA and protein channel after linear color separation. In order to identify the most optimal feature set, we proposed an effective two-layer feature selection strategy where, in the first layer, the SDA technology was applied to the individual feature set, and in the second layer, SVM-RFE + CBR was applied to the fused feature set. Then, the SVM prediction models based on both the radial basis function (SVM-RBF) and linear kernel (SVM-LNR) were constructed using the optimal feature set. Ten-fold cross validation and independent tests were performed to systematically examine the performance of the prediction model, i.e. PScL-HDeep. The source code and datasets are publicly available at http://csbio.njust.edu.cn/bioinf/psclhdeep or https://github.com/csbio-njust-edu/PScL-HDeep.

Datasets and Methods

Datasets

Selection of appropriate datasets in statistical machine learning is a significant step as it deals with the problem of learning discriminative rules from the data. The Human Protein Atlas (http://www.proteinatlas.org) database [44] contains immunohistochemistry (IHC) microscopy bioimages and is a bountiful source of human proteome data. Therefore, in this study, we constructed the benchmark bioimage datasets from the HPA database (version 19) according to the confidence in two aspects: the reliability score (enhanced, supported and approved only) and the validation score (e.g. IH and western blot (WB) validation scores). For more details about the reliability and validation scores, please refer to the HPA website.

In the current work, the benchmark training dataset consists of 2876 immunohistochemistry images based on the high validation score, enhanced and supported reliability score. All the images belong to 23 proteins from 46 normal human tissues. Each of the 2876 collected bioimages appeared in one of the seven major subcellular locations: cytoplasm (Cytopl.), endoplasmic reticulum (ER), Golgi apparatus (Gol.), mitochondrion (Mito.), lysosome (Lyso.), nucleus (Nucl.) and vesicles (Vesi.). A statistical summary of the benchmark training dataset is provided in Table 1.

Table 1.

Statistical summary of the protein subcellular localization dataset

Class label	Subcellular localization	Size
1	Cytoplasm	490
2	Endoplasmic reticulum	356
3	Golgi apparatus	366
4	Lysosome	242
5	Mitochondrion	391
6	Nucleus	515
7	Vesicles	516
Total		2876

Similarly, we constructed the independent test dataset in the same way as previously described in [31]. The dataset contained 107 IHC images of five proteins selected from the HPA database. Each of the 107 IHC images belonged to one of the five protein subcellular locations including Cytopl., ER, Gol., Lyso. and Nucl.

Image object separation

In this study, we used the HPA datasets as our benchmark datasets. Each original image in the HPA database stored in the RGB model is the fusion of two mixed staining protein and DNA. The protein background is labeled with brown color, while the DNA section is labeled with purple color. Since the main focus of this study is to analyze the protein, it is necessary to segment the protein from the DNA by some color separation procedures. We employed the linear spectral separation (lin) scheme because the two colors purple and brown are easily separable.

The linear spectral separation can be expressed mathematically as follows:

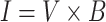(1)

where 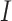is the original image sample from the HPA dataset; 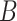is the color base matrix that is obtained via calculation, while 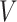is the obtained vector after color separation that contains two columns—one for protein and the other for DNA. The intensity range for each channel in the vector 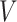is normalized between 0 and 255 gray levels.

Besides, each HPA image is also composed of many cells and separating these cells in a region of interest is recognized as a very challenging task. Fortunately, the use of the multicell protein image gave promising classification accuracy [1, 18]. Inspired by the previous studies, we also use the multicell protein images in this study.

Feature extraction

Feature extraction is considered as one of the most vital steps for constructing accurate classification models. The classification accuracy relies on the choice of the features used for model training. Subcellular location features (SLFs) are the global feature vectors that describe the whole image. These features are shown to be useful in the field of bioinformatics. However, they ignore the local image features. Therefore, the global and local feature descriptors can be used together to represent image as a whole. In this study, we also used the combination of these two strategies along with the deep learned features to form a super vector for the classification task:

DNA distribution features

The significant dissimilarity between eukaryote and prokaryote cells is the membrane-enclosed organelle nucleus. As human belongs to the former, each bioimage will have DNA staining. The DNA spatial distribution has been evidenced in previous studies to be valuable for improving the classification accuracy [18]. Thus, here we also extracted the following four types of DNA-protein overlapping features:

• (i) Ratio of the overall sum of pixel values in protein segment to DNA segment

• (ii) Ratio of those number of pixels in the protein segment that co-localize with the DNA segment to the number of pixels in the protein segment

• (iii) Ratio of the overall sum of pixel values in the protein segment that co-localize with the DNA region to the sum of pixels in the protein segment

• (iv) Average distance between the protein segments that overlap with the DNA region and the nearest nuclear pixel

Haralick texture features

After linear color separation, we extracted the Haralick texture features. These features were obtained through gray level co-occurrence matrix (GLCM). The GLCM was obtained via 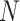number of gray levels in the image constructed on a fixed angle 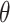and the measurement of the pixel distance 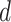. In 2-dimensional square pixel image, the Haralick texture features can be extracted from the four directions of GLCM (i.e. horizontal and vertical directions, left and right diagonal directions). The total 13 texture features calculated from the GLCM in this study included angular second moment, the contrast, correlation, the sum of square, the inverse difference moment, the sum average, the sum variance, the sum entropy, entropy, the differential variance, the difference entropy, the information measurement of correlation 1 and the information measurement of correlation 2. A total of 26 Haralick features were gained from the original protein channel (including 13 features from the averaged horizontal and vertical directions, and other 13 from the averaged left and right diagonal directions). Next, 810 (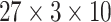) features were extracted after decomposing the protein segmented image into 10 levels by discrete wavelet transform (DWT) using Daubechies 1 filter. ‘27’ indicate the 26-dimensional Haralick features and 1-dimensional energy feature obtained on each of the three detailed coefficients sets at each decomposition level. Finally, after integrating the previous 26 Haralick features, we obtained 836-dimensional Haralick texture features per image, referred to as Har.

Local binary pattern (LBP)

The local features in the patches of protein image are difficult to be reflected by global descriptors. Local descriptors, therefore, can be used as a complement to the global features. LBP [45, 46] is one such local descriptor that is simple yet efficient (simple computation, insensitive to light intensity). Besides, the LBP operator can be easily used in combination with other image descriptors.

LBP calculates the gray values of the center pixel with the gray values of the neighboring pixels and a given threshold. The mathematical description of LBP is:

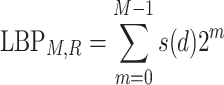(2)

where 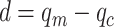in the function is the difference between the gray levels of the center pixel and the neighborhood pixel 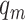. 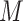is the neighboring pixels and 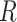is the radius of the circular region in the neighborhood. The function 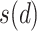is expressed as:

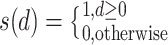(3)

where 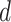is set to 1 if the intensity value of the neighboring pixel is larger than or equal to the threshold, and 0 otherwise.

The LBP features are described by a histogram of binary patterns calculated over the neighborhood. In this work, 256 histograms of regions were calculated and accordingly 256-dimensional LBP features were obtained based on 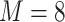and .

Completed local binary pattern

Completed Local Binary Pattern (CLBP) proposed in [47] calculates three components to represent the local region: the center pixel, the different sign and the difference magnitude. The operator CLBP_Center or CLBP_C is defined for the center pixel that encodes the center pixel and converts to the binary code by global thresholding. Mathematically, CLBP_C can be defined as:

(4)

where 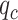is the value of the center pixel and threshold 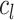is the averaged gray level of the entire input image. 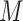is the number of the involved neighbors and 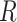is the neighborhood radius.

The CLBP-Sign (CLBP_S) operator is defined for the different sign and is the same as the LBP. The difference magnitude component of CLBP is defined by the operator CLBP-Magnitude, abbreviated as CLBP_M. CLBP_M is expressed as:

(5)

where 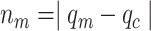. The threshold 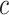is set to the mean value of 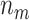from the entire image. 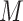, , 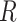, 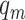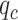and 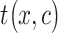are defined in equations (2) and (4).

The two operators CLBP_S and CLBP_M are produced from the Local Difference Sign-Magnitude Transform (LDSMT), which is calculated based on the referenced pixel and all the pixels that belong to the specified neighborhood.

All the three CLBP operators are in binary-encoded format and thus they can be combined together to form a CLBP histogram. We concatenated all the three operators and obtained the final 906 CLBP features based on the two configurations 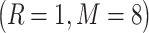and .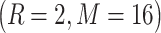

Rotation invariant co-occurrence of adjacent LBP

The LBP descriptor does not keep the spatial relationships among binary patterns. Co-occurrence Among LBP (CoALBP) [48] solves this problem by using four autocorrelation matrices. Rotation Invariant Co-occurrence of Adjacent LBP (RICLBP) [49] is the modified version of CoALBP, which ensures the rotation invariance by attaching a label of rotation invariant to each CLBP pair.

RICLBP uses two parameters: the scale of LBP radius and the displacement among different LBP pairs. In our experiment, three different parameter sets (1, 2), (2, 4) and (4, 8) were used to extract three different feature vectors from the target protein image. Each feature vector contained features with the dimension of 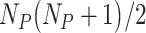. 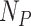is the number of possible LBPs, 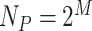, where 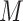is the neighboring pixels in LBP. In our study, 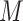is set to 4 (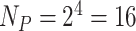), and therefore, a 136-dimensional feature vector would be obtained for each parameter set. Finally, we integrated all three extracted feature vectors into our final proposed feature vector of 408 (136 × 3) dimension.

Adaptive hybrid pattern

Here, the Adaptive Hybrid Pattern (AHP) [50] is used specifically to overcome the LBP drawbacks: sensitivity to noise in quasiuniform regions and sensitivity to small variation in the target input image caused by quantization thresholds that use exact values. AHP presents Hybrid Texture Model (HTM) and Adaptive Quantization Algorithm (AQA) to overcome the aforementioned problems. HTM is composed of local microfeatures and global spatial structure. AQA is designed to be adaptive to the contents of local patches.

We extracted features from protein images using two quantization levels 2 and 5 with two configurations 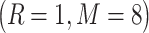and 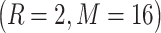for the local patches’ radius R and number of neighboring point M in each local patch. An 84-dimensional feature and a 336-dimensional feature were generated based on the quantitation level 2 and 5, respectively. Finally, by serially integrating these two feature sets, we obtained a 420-dimensional feature vector that represents the protein image. Further details on AHP parameters can be found in [32].

Histogram of oriented gradients

Histogram of oriented gradient (HOG) proposed in [51] divides the image into small windows/cells and for each window the HOG direction is compiled over the pixels of window. The histogram for each window is then evaluated and finally a descriptor is obtained by concatenating these histograms.

HOG is computed in dense grid at a single-scaled cell level without dominant orientation that makes it unique than the Scale Invariant Feature Transform (SIFT) [52] descriptors. In our experiment, we used the window size of 5 × 6 and extracted a final feature vector with the dimension of 270 for the target protein image.

Locally encoded transform feature histogram

Locally encoded transform feature histogram (LETRIST) proposed by Song et al. [53] is a simple, low-dimensional yet efficient descriptor to represent an image. The LETRIST descriptors (referred to as LET in this study) encode the mutual information within a target image across features and scale space.

First, transform features set that describes the local texture structures and the correlation among them were constructed and then quantized into texture codes. Next, the cross scale joint coding was applied to these texture codes to construct three histograms. Finally, these histograms were concatenated to generate the final 413-dimensional feature vector. The experimental setup used here was the same as [35].

Deep learned features

Deep learning proposed by Hinton et al. [54] in 2006 has revolutionized the area of machine learning and artificial intelligence. Since then, numerous deep learning algorithms have been applied. The key feature of deep learning algorithms lies in their layered structure organized in hierarchy. Each layer captures specific information. For example, the layers near the input capture the low-level features, while the farthest layers, for example, the layer close to classification layer, capture the classification level information. As the layers get deeper, the complexity of layers arises.

There are currently different deep learning architectures available such as convolutional neural networks (CNN) [55–59], recurrent neural network (RNN) [60–62] and deep belief networks (DBN) [54, 63, 64]. In our work, we considered the pretrained CNN, because an advantage of using a pretrained network is that CNN does not need to be trained (a stage that is computationally very costly to accomplish). Several bioimage-based studies [65–67] have successfully applied VGG-19 as the feature extractor on various datasets [66]. The reason is that VGG-19 is particularly useful due to its feature representation in terms of the detection or localization of specific contents in an input image. Further, it can also mount convolutional filters with a smaller receptive field (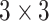) on top to increase the depth level. Therefore, in our study, we also utilized the pretrained VGG-19 [37] for transfer learning. We extracted the feature maps of deeper layers that were used as the feature vector in our settings.

The flowchart of extracting deep learned features from the VGG-19 is illustrated in Figure 1. As can be seen, there are five blocks of convolutional layers followed by three fully connected layers. The first two blocks have two convolutional layers, while the last three blocks have four convolutional layers. Each block of the convolutional layer is followed by a max-pooling layer. The first two fully connected layers have 4096 channels, while the last fully connected layer has 1000 channels. The detailed architecture and parameters of pretrained VGG-19 are provided in Supplementary Table S2, available online at http://bib.oxfordjournals.org/, under Text S2 in SI.

Figure 1 .

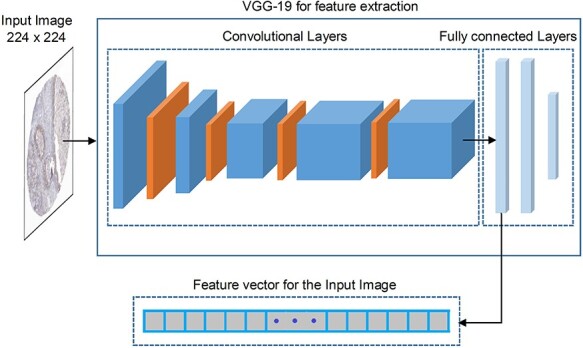
Deep learned feature extraction strategy using the VGG-19 deep learning architecture.

In order to utilize CNN efficiently, some prior steps need to be considered, including (1) all images need to be preprocessed because CNN requires all images in equal size. As the VGG-19 needs all the images to have the size of 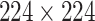, before inputting the image to pretrained VGG-19, we resized the images to ; (2) In order to reduce the outlier effect, the images need to be subtracted from the given image with CNN as suggested in [68]. Accordingly, we also subtracted each image from the given image with CNN.

Finally, after feeding the input image into pretrained VGG-19, we extracted the feature maps from the first fully connected layer with the dimension of 4096 to serve as the feature vector for the input image, as shown in Figure 1. Since the deeper inner layers provide high-dimensional feature maps, to avoid the curse of dimensionality and reduce the computational time required by classifier training, the feature vector needs to be optimized and reduced in size. Therefore, we applied the SDA to both reduce the dimension of the feature vector and to preserve the unique characteristics of the features. We named such deep learned features as Deep.

Features selection

Training a classifier with such a large dimension of feature space is not effective; there may exist redundant, irrelevant and noisy information that can potentially cause either overfitting or underfitting of the trained classifier. In this context, an optimal subset of relevant features is essential to represent the intrinsic variance among different classes. Therefore, feature selection has become a common prerequisite in the design of the prediction algorithm.

In order to reduce time complexity and enhance the predictive power of our computational model for protein subcellular localization prediction, we applied a two-layer feature selection strategy comprising of SDA followed by SVM-RFE + CBR. The details are provided below.

Stepwise discriminant analysis

SDA [43] is an efficient approach for dimension reduction. An optimal subset of features is selected via iteratively identifying which features maximize the criterion (Wilks’ Λ) in the feature space that tightly separates the classes from each other.

The Wilks’ Λ statistics is a probability distribution mathematically defined as:

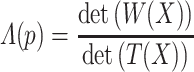(6)

where 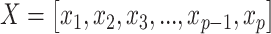denotes a vector of 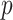features that currently describes the target protein image. 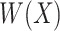is the within-class covariance matrix that is defined as

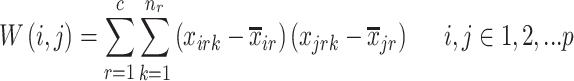(7)

and is the between-class covariance matrix that is expressed mathematically as:

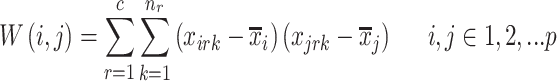(8)

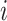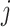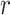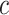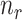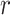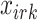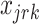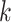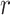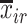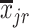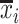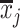where is the feature at the i-th position and is the feature at the j-th position, represents one class in the total classes, is the total number of samples in class . and are the i-th and j-th feature values for the sample of class . and are the means of the i-th and j-th features over the r-th class. and are the means of the i-th and j-th features over all the classes.

The lower values obtained in Λ show the features with better discriminative power among classes. To further increase the discriminative ability by accommodating the stepwise process, an additional feature 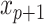is added to 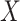that describes the partial Wilks’ (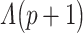) statistic:

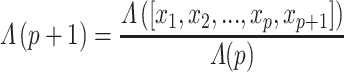(9)

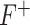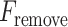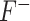To quantify the discriminative power of the new feature, F-statistic is employed to assign a statistical significance level to the feature. The larger value of F-statistic means the particular feature has a better discriminative power ( or criterion) and vice versa ( or criterion). The 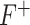criterion is defined as:

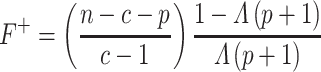(10)

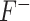is defined as:

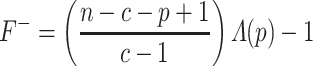(11)

where 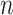is the total number of features in all classes, 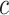is the total number of classes and 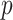is the features currently analyzed.

In our model, we applied the SDA feature selection technique to each feature set individually, i.e. Har, LBP, CLBP, RICLBP, AHP, HOG, LET and Deep features. was calculated for each feature. The feature that had the lowest 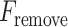value and significance level (P-value) greater than a preassigned threshold was removed from the feature set. Note that this process was skipped when removing the first feature.

After a feature was remove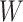d, and 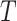in equation (6) were updated and then 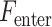was calculated for the feature that was not currently included in the set. The feature with the largest 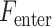value, which had the significance level less than a preassigned threshold, was added to the set. The process stopped when there were no features to be entered or removed. We set the threshold value to 0.15.

SVM-RFE + CBR

The performance of the classifier mainly depends on the input feature set. In order to select the most optimal set for our prediction algorithm, we applied an embedded feature selection technique namely support vector machine-based recursive feature elimination method with correlation bias reduction (SVM-RFE + CBR) [69] to the integrated features set obtained by serially concatenating the individual subset of features obtained in the ‘Stepwise discriminant analysis’ section. Many existing studies [70–72] have used SVM-RFE [73] for multiclass classification problems; however, when the feature set has highly correlated features, the SVM-RFE ranking criteria for these features will be biased. SVM-RFE + CBR uses the correlation bias reduction strategy to reduce this correlation bias in SVM-RFE. It accommodates both linear and nonlinear versions.

To extend the SVM-RFE + CBR algorithm from two-class to multiclass problem, we adopted the one-versus-one (OVO) strategy under which the features’ weights for each binary subclass problem were calculated and then added together, in order to determine the ranking criteria. We used nonlinear SVM-RFE + CBR with the Gaussian radial basis function (RBF). After gaining the ranked features as an output of SVM-RFE + CBR, we then empirically selected the best subset of features based on the SVM-RFE + CBR ranked features (see the section ‘SVM-RFE + CBR can further improve the performance’). For more details about SVM-RFE + CBR, please refer to the work in [69].

Prediction algorithm

Support vector machine (SVM), developed by Cortes and Vapnik [74], has been successfully applied to numerous classification and regression problems [75, 76]. Initially, SVM was used for the two class classification problems and later extended to multiclass problems, i.e. one-versus-all (OVA) and OVO. Since then, it has been widely used for solving multiclass problems in bioinformatics including protein subcellular location prediction [1, 30].

Here in this study, we also implemented SVM by utilizing the LIBSVM toolbox to construct the classifier. The LIBSVM [77] version 3.24 (libsvm-3.24) was downloaded from http://www.csie.ntu.edu.tw/∼cjlin/libsvm/. We used RBF as the kernel function, whose two parameters regularization C = 2⁷ and kernel width γ = 2⁻⁶ were optimized using 10-fold cross validation and grid search optimization. We adopted the OVO approach for our multiclass classification.

Architecture of the proposed PScL-HDeep

Figure 2 shows a schematic overview of the proposed multiclass prediction algorithm PScL-HDeep. For a given IHC input image from the benchmark datasets, PScL-HDeep first decomposes the images into DNA channel and protein channel using the linear spectral separation program (segmentation phase) and then extracts DNA, Har, LBP, LET, RICLBP, HOG, CLBP, AHP and Deep feature sets by calling the corresponding feature extraction program (feature extraction phase). In the establishment of the optimal feature subset, PScL-HDeep applies a two-layer feature selection technique to the extracted features (2L feature selection phase). In the first layer, the SDA is called to select the reduced nonredundant optimal subset of features from all of the extracted single feature sets except DNA features. A hybrid features set is obtained after serially combining all the features. SVM-RFE + CBR is used in the next layer to re-rank the features. Consequently, the top ranked features are selected as the final super feature set (optimal features) that represents each protein image. In the training phase, the obtained super feature set is directly input to SVM to train the model. In the testing phase, after generating the final super feature set for the corresponding IHC input image, the trained model can be used to classify it as one of the seven subcellular locations (classification phase).

Figure 2 .

Schematic workflow of the developed PScL-HDeep.

Performance evaluation

Different performance evaluation strategies are used to assess the performance of the proposed PScL-HDeep method. Among these, the k-fold cross validation and the independent tests are the commonly used methods in the existing literature. Therefore, we employed k-fold cross validation to evaluate the effectiveness of the method. Besides, we also conducted experiments on the independent test dataset to further assess the generalization ability of PScL-HDeep.

As our problem is multiclass classification, to investigate the effectiveness of PScL-HDeep, we calculated the meanAUC, stdAUC and accuracy as the performance measures. meanAUC is the mean value of the area under the ROC curves (AUC). A larger meanAUC value indicates that the classification model has a more robust performance. For example, when the meanAUC score is 1, the classification model is perfect with 100% correct predictions. stdAUC is the standard deviation of AUC, while accuracy is the percentage of the number of labels correctly predicted relative to the total number of labels being predicted. The meanAUC and stdAUC were calculated based on the AUC values of seven protein subcellular locations.

In addition, it is worth mentioning that we only conducted experiments on the training dataset during the selection of the optimal features and the parameter optimization for SVM.

Results and Discussion

Performance evaluation of individual features and different classifiers

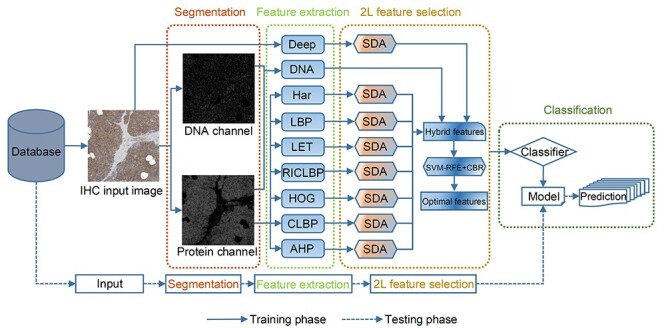
The success of a prediction algorithm relies on the choice of an appropriate feature set. In this regard, we applied DNA, Har, LBP, RICLBP, LET, AHP, CLBP and HOG feature descriptors along with the Deep features to effectively capture the global and local features from IHC images. We trained the models on each handcrafted feature set to testify the above discussed features. In this section, we trained random forest (RF) [78], linear SVM (SVM-LNR) and radial basis function SVM (SVM-RBF). When the number of trees = 300 and maximum number of features in individual tree = 80, the RF classifier achieved the best results. The optimal regularization parameter C = 2⁷ for the SVM-LNR was obtained in the same way as the SVM-RBF classifier. We performed 10-fold cross validation on the benchmark training dataset to evaluate and examine the prediction performance of the three classifiers. The classification success rates of these feature sets on RF, SVM-LNR and SVM-RBF are illustrated in Figure 3 in terms of accuracy. From the experimental results, we can see that the CLBP features achieved the highest accuracy of 78.63% under the SVM-LNR classifier, while the LBP and RICLBP features under the SVM-RBF classifier were ranked the second and third with an accuracy of 78.55 and 78.44%, respectively. By examining the Har, AHP and LET features, we found that they showed better performance on the three classifiers while DNA and HOG achieved almost similar success rates.

Figure 3 .

Performance comparison of eight types of pure individual features on three different classifiers.

Similarly, the classification performance of the SVM-RBF, SVM-LNR and RF classifiers was also examined. As a result, we found that the success rates of SVM-RBF and SVM-LNR classifiers on the LBP, RICLBP, LET, HOG and AHP were higher than that of the RF classifier. Although SVM-LNR achieved better classification results on CLBP and AHP, however, the better classification results of SVM-RBF on the DNA, Har, LBP, RICLBP, LET and HOG descriptors showed the superiority of the SVM-RBF classifier over SVM-LNR. The performance of SVM-LNR was better than that of the RF classifier. Therefore, we used the SVM-RBF and SVM-LNR in the following sections.

Improving the predictive performance by selecting the optimal features via SDA

The original high-dimensional feature space potentially has redundant and noisy information, which can degrade the performance of a prediction model. To improve the performance of the model by avoiding noisy and redundant information, feature selection is performed to identify highly informative and nonredundant features from the original feature set. The feature subset obtained via the feature selection step can also significantly reduce the time complexity. That is why feature selection is often practiced as a strategic step for data preprocessing across many areas of pattern recognition, machine learning and data mining.

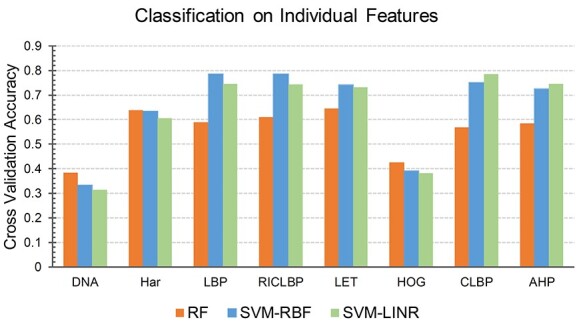
For this purpose, we applied SDA to each individual feature set except DNA. Each optimal set was then fed into the SVM-RBF and SVM-LNR classifiers to testify the significance of feature selection. Empirically, we found that the accuracy of SVM-RBF was increased by 10.95% on Har, 2.6% on LBP, 4.49% on RICLBP, 7.79% on LET, 6.92% on CLBP, 0.73% on AHP and 1.11% on HOG, respectively, with 10-fold cross validation. Similarly, the accuracy of SVM-LNR on Har, LBP, RICLBP, LET, CLBP, AHP and HOG was increased by 11.75, 1.74, 6.54, 3.41, 0.25, 0.18 and 1.04%, respectively. The accuracy (Acc%), meanAUC and stdAUC of each individual feature set are reported in Table 2. For a fair judgement, we also plotted bar graphs for the accuracy index of the pure feature sets (i.e. ‘Before SDA’) and the feature sets with the SDA feature selection (i.e. ‘After SDA’) in Figure 4.

Table 2.

Performance results of models trained using individual features after the SDA feature selection

Feature set	SVM-LNR			SVM-RBF
	Acc (%)	meanAUC	stdAUC	Acc (%)	meanAUC	stdAUC
Har	72.29	0.9435	0.0179	74.27	0.9549	0.0154
LBP	76.32	0.9598	0.0162	81.15	0.9699	0.0093
RICLBP	80.81	0.9699	0.0119	82.93	0.9736	0.0108
LET	76.53	0.956	0.0116	81.82	0.9660	0.0097
HOG	39.11	0.7519	0.0536	40.33	0.7576	0.057
CLBP	80.88	0.9692	0.0093	82.02	0.9704	0.0099
AHP	74.76	0.9487	0.0181	73.3	0.9457	0.02

Figure 4 .

Performance comparison of individual features before and after the SDA feature selection.

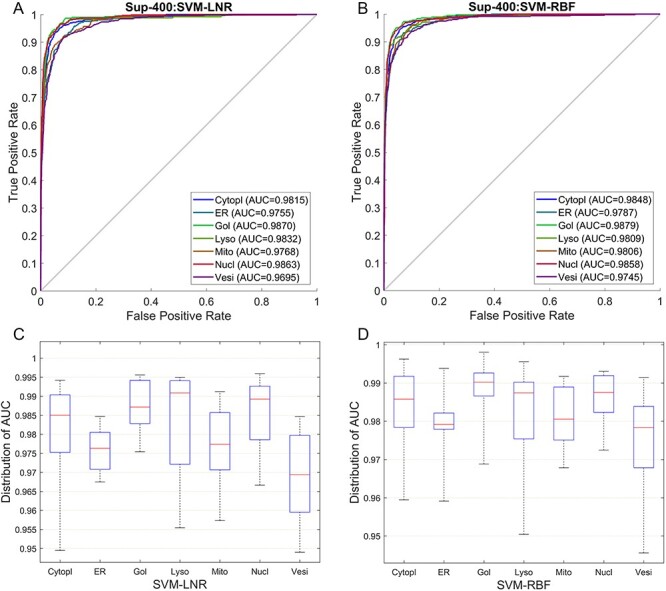
Both the SVM-RBF and SVM-LNR classifiers showed the highest increase in the accuracy on the Har optimal feature set compared to the Har pure feature set and the other feature sets. Therefore, extensive comparison was further performed between the Har pure feature set and the Har optimal feature set using 10-fold cross validation. The performance was evaluated in terms of receiver operating characteristic curve (ROC curve) and the distribution of area under curve (AUC). Figure 5A and B provides the comparison of the ROC curves, while Figure 5C and D shows the comparison of the AUC distribution without and with the SDA feature selection, respectively, on the SVM-RBF classifier. For example, the meanAUC of the model was increased by 4.78%, while the error rate of stdAUC was decreased by 1.05% after selecting the optimal feature set via the SDA feature selection. In Figure 5C and D, the central line in the box indicates the median, while the lower and the upper edges of each box indicate the lower and upper quartiles, respectively. The whiskers are the extreme limits for the points that are not considered as outliers. Supplementary Figure S1, available online at http://bib.oxfordjournals.org/, in the SI Text S4 compares the confusion matrix graph of both feature sets under the SVM-RBF model. Similarly, we also performed experiments under the SVM-LNR classifier. The corresponding results are reported in Supplementary Figures S2 and S3, available online at http://bib.oxfordjournals.org/, in the SI Text S4. In addition, it is worth mentioning that the ROC curves used in this study that plot the true positive rate against the false positive rate are multiclass ROC curves based on the OVA strategy.

Figure 5 .

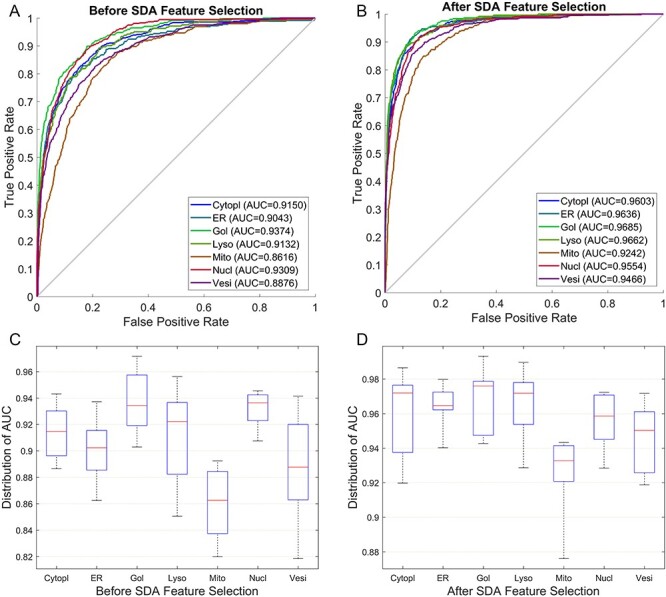
Performance comparison between the Har pure feature set and the Har optimal feature set under the SVM-RBF model: (A) ROC curves of the Har pure feature set; (B) ROC curves after applying the SDA feature selection method; (C) Distribution of AUC values of the Har pure feature set and (D) Distribution of AUC values after applying the SDA feature selection technique.

Integrating handcrafted and deep learned features improved the performance

In the preceding sections of results and discussion, we evaluated the predictive performance of the traditional single-view features. This section focuses on performance evaluation of multiview features.

In comparison with single-view features, we found that the classification performance of DNA and HOG features was poor compared to the other traditional features. Therefore, we made two combinations of the feature space from traditional features:

• tradFus1 = Har + LBP + CLBP + RICLBP + LET + AHP

• tradFus2 = DNA + Har + LBP + CLBP + RICLBP + LET + HOG + AHP

Here ‘+’ sign means the simple serial combination. We then tested each multiview feature set on the SVM-RBF and SVM-LNR classifiers. The results of tradFus1 and tradFus2 are reported in Table 3. The accuracy, meanAUC and stdAUC were used to measure the performance. By feeding tradFus1 and tradFus2 to both SVM-RBF and SVM-LNR classifiers, the accuracy and meanAUC of the tradFus2 on the SVM-RBF increased by 0.87 and 0.24%, respectively, compared to tradFus1. The stdAUC of tradFus2 was 0.68%, which was decreased by 0.1% compared to that of tradFus1, which was 0.78%.

Table 3.

Performance comparison of tradFus1, tradFus2, tradFus1 + Deep and tradFus2 + Deep on 10-fold cross validation using the benchmark training dataset

Classifier	Feature set	Acc (%)	meanAUC	stdAUC
SVM-LNR	tradFus1	79.73	0.9693	0.0092
	tradFus2	80.18	0.9702	0.0092
	tradFus1 + Deep	83.20	0.9711	0.0071
	tradFus2 + Deep	84.21	0.9796	0.0064
SVM-RBF	tradFus1	81.43	0.9739	0.0078
	tradFus2	82.30	0.9763	0.0068
	tradFus1 + Deep	83.93	0.9802	0.0059
	tradFus2 + Deep	84.91	0.9813	0.0051

Similarly, we also noticed that the SVM-LNR classifier achieved a better performance on the tradFus2 compared to tradFus1. The accuracy and meanAUC were increased by 0.45 and 0.09%, respectively. The stdAUC index for tradFus2 and tradFus1 was 0.92%, which was similar.

By comparing SVM-RBF and SVM-LNR classifiers, the accuracy and meanAUC of the SVM-RBF classifier on the tradFus1 features set were increased by 1.7 and 0.46%, while the stdAUC was 0.14% lower in comparison with the SVM-LNR classifier. Besides, SVM-RBF also showed a better performance on the tradFus2 feature set. Under the SVM-RBF, the accuracy and meanAUC were 82.3 and 97.63%, respectively, which were increased by 2.12 and 0.61% than the SVM-LNR classifier. The stdAUC error index was also lowered by 0.24% than the stdAUC index of SVM-LNR.

Based on the above experimental analysis, it can be concluded that although the individual performance of DNA and HOG is not convincing, it has improved the predictive performance of the classifier when being combined with other features due to their unique distributions.

We then considered deep learned features and combined them with the tradFus1 and tradFus2 to generate:

• tradFus1 + Deep

• tradFus2 + Deep

The performance of both feature sets is also reported in Table 3. As can be seen, tradFus2 + Deep achieved a better predictive performance than tradFus1, tradFus2 and tradFus1 + Deep. On SVM-RBF, the accuracy of tradFus2 + Deep was increased by 3.48, 2.61 and 0.98% in comparison with tradFus1, tradFus2 and tradFus1 + Deep, respectively. Likewise, meanAUC was increased by 0.83, 0.5 and 0.11% compared with that of tradFus1, tradFus2 and tradFus1 + Deep, respectively. Besides, stdAUC was also 0.27, 0.17 and 0.08% lower than tradFus1, tradFus2 and tradFus1 + Deep, respectively.

On the SVM-LNR classifier, the accuracy of tradFus2 + Deep was increased by 4.48, 4.03 and 1.01% compared with tradFus1, tradFus2 and tradFus1 + Deep, respectively. Similarly, the meanAUC of tradFus2 + Deep was 97.96%, which was improved by 1.03, 0.94 and 0.05% than tradFus1, tradFus2 and tradFus1 + Deep, respectively. Likewise, stdAUC was 0.64%, which was 0.28, 0.28 and 0.07%, respectively, lower than tradFus1, tradFus2 and tradFus1 + Deep.

Based on the performance comparison of four different feature combinations in Table 3, it can be established that tradFus2 + Deep, which is the fusion of DNA, Har, LBP, CLBP, RICLBP, LET, HOG, AHP and Deep feature sets, is superior to tradFus1, tradFus2 and tradFus1 + Deep.

SVM-RFE + CBR can further improve the performance

In order to further improve the performance of our classification algorithm and reduce the computational time, we applied the SVM-RFE + CBR algorithm as the second-layer feature selection to the combined feature space, which was obtained in the previous section through experimental analysis, i.e. tradFus2 + Deep. The output of SVM-RFE + CBR is the ranked feature set as discussed in ‘SVM-RFE + CBR’ section. Since SVM-RFE + CBR cannot automatically guarantee the optimal number of the selected features, we first removed the last 25% features in the ranked feature set and then empirically extracted the optimal number of the features from the remaining ranked feature set. We started by feeding the first 50 features to the SVM-RBF classifier and then gradually increased with the step size of 50. We assessed the performance of each feature set by macroaverage F1 or F1-Score_M, and Matthews correlation coefficient (MCC) (see Text S3 in SI for details about F1-Score_M and MCC) using the training set on 10-fold cross validation. The variation curves of F1-Score_M and MCC are shown in Figure 6. The obtained F1-Score_M and MCC results for different number of features are provided in SI Supplementary Table S3, available online at http://bib.oxfordjournals.org/, under Text S5. In addition, Text S5 in SI also shows the effectiveness of our proposed two-layer feature selection strategy in comparison to the single-layer feature selection strategy. (The result for the single-layer feature selection strategy is provided in Supplementary Table S4, available online at http://bib.oxfordjournals.org/, under Text S5 in SI).

Figure 6 .

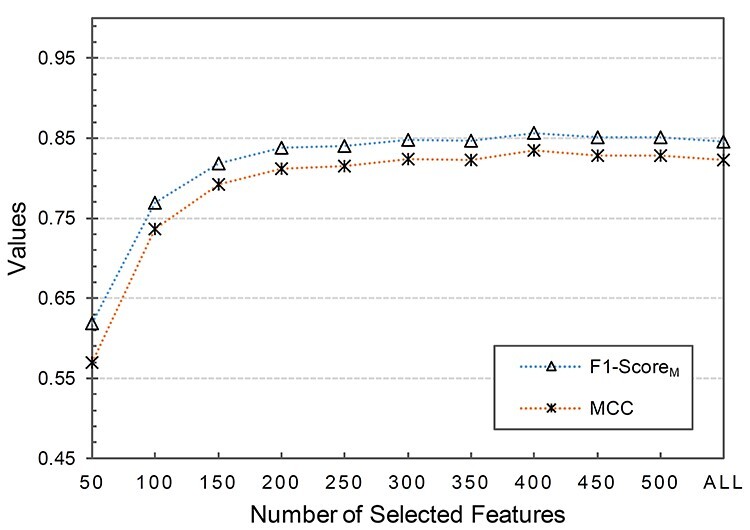
Variation curves of F1-Score_M and MCC values against different number of selected features based on the ranked features.

It can be observed from Figure 6 that when the selected features (SF) set consisted of the first 400 ranked features, the corresponding F1-Score_M and MCC on the 10-fold cross validation achieved the best result. When 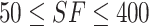, both F1-Score_M and MCC were increased with a little fluctuation; however, both were slowly decreased when 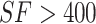. Thus, our final feature subset included the 400 top-ranked features, referred to as Sup-400.

To further examine the effectiveness of SVM-RFE + CBR, Table 4 shows the performance result of two feature sets, with SVM-RFE + CBR (Sup-400) and without SVM-RFE + CBR (tradFus2 + Deep) feature selection. The experiments were conducted under the SVM-RBF classifier on the benchmark training dataset using 10-fold cross validation. From Table 4, it is clear that the results obtained with Sup-400 consistently outperformed those obtained with tradFus2 + Deep. The results in Table 4 show that the performance of the model could indeed be improved in terms of the performance by applying the SVM-RFE + CBR feature selection.

Table 4.

Performance comparison of SVM-RBF with and without SVM-RFE + CBR on 10-fold cross validation using the benchmark training dataset

Feature set	Acc (%)	meanAUC	stdAUC
tradFus2 + Deep	84.91	0.9813	0.0051
Sup-400	85.95	0.9818	0.0046

We then fed the Sup-400 to the SVM-LNR classifier and conducted experiments using the benchmark training dataset on 10-fold cross validation. The accuracy, meanAUC and stdAUC of SVM-LNR were 84.66%, 0.98 and 0.0063, respectively, which are clearly better than those of tradFus2 + Deep (see Supplementary Table S5, available online at http://bib.oxfordjournals.org/, under Text S6 in SI).

To better reflect the performance of the models, Figure 7A and B shows the predictive performance of the SVM-LNR and SVM-RBF models on the Sup-400 feature set in terms of ROC curve, while the distribution of AUC is given in Figure 7C and D. We further measured the performance of the models using macroaverage precision, macroaverage recall, macroaverage F1 and MCC (see the details about performance metrics in SI Text S3) and the results are given in Supplementary Table S6, available online at http://bib.oxfordjournals.org/, under Text S6 in SI. The results of the confusion matrices of both models are also given in Supplementary Figure S4, available online at http://bib.oxfordjournals.org/, and can be found in SI under Text S6.

Figure 7 .

ROC curves and AUC distribution of the Sup-400 feature set: (A) shows the ROC curves under the SVM-LNR classifier; (B) shows the ROC curves under the SVM-RBF classifier; (C) shows the AUC distribution under the SVM-LNR classifier and (D) shows the AUC distribution under the SVM-RBF classifier.

By carefully examining the prediction results of our proposed method, we found that vesicles and mitochondrion were relatively harder to predict before applying the SVM-RFE + CBR. About 5.1–13.0% of the protein images with mitochondrion pattern were predicted as vesicles, while 4.6–9.7% of vesicles were predicted as nucleus by the SVM-RBF classifier. Similarly, under the SVM-LNR classifier, 5.1–15.0% of protein images with mitochondrion pattern were predicted as vesicles and 9.4–11.0% of protein images with vesicles pattern were predicted as mitochondria. Considering the biological structure (hierarchy) of these cellular compartments (i.e. mitochondrion wrongly predicted as vesicles and vesicles that were wrongly predicted as nucleus and mitochondrion), they have no similar part of the cell (nucleus and mitochondrion are located in the intracellular part of the cell, while vesicles is located in the secreted pathway [19]) that could have made the prediction harder. The difficult prediction was because of two reasons: 1) both the mitochondrion and vesicles are vesicular and 2) the mitochondrial-derived vesicles (MDVs), in which mitochondria bud vesicles [79]. However, after employing the SVM-RFE + CBR feature selection technique in our method, the prediction accuracy of mitochondrion and vesicles was improved as shown in Figure 7.

Performance comparison of PScL-HDeep against existing predictors

To show the efficacy of our proposed PScL-HDeep method, we further compared it with several published models of HPA bioimage-based protein subcellular localization predictors. As in the current research, we dealt with the single-label data, thus, we only compared the proposed method to existing single-label methods. These included the method proposed by Yang et al. [1], SC-PSorter [19] and SAE-RF [31]. Table 5 provides the performance results of the existing methods derived from Liu et al.’s research [31] and the proposed method. Table 5 reveals that our developed method PScL-HDeep substantially outperformed all the existing predictors in terms of three performance metrics on the benchmark training dataset. In particular, our method achieved an accuracy of 85.95% using SVM-RBF on the benchmark training dataset over 10-fold cross validation, while the latest method SAE-RF, which is the runner-up, achieved an accuracy of 81.76%. Our method has achieved 4.19% increase in accuracy than this latest method (SAE-RF). Besides, the meanAUC of our method was increased by 1.03%, while stdAUC was decreased by 1.39% in comparison with SAE-RF.

Table 5.

Performance comparison of the proposed PScL-HDeep with other existing methods on 10-fold cross validation using the benchmark training dataset

Method	Acc (%)	meanAUC	stdAUC
Yang et al.	77.62	0.9661	0.0229
SC-PSorter	80.45	0.9702	0.0193
SAE-RF	81.76	0.9715	0.0185
PScL-HDeep	85.95	0.9818	0.0046

Compared with the other existing methods by Yang et al. and SC-PSorter, the accuracy of PScL-HDeep was 8.33 and 5.5% higher, while meanAUC was improved by 1.57 and 1.16%, respectively. The stdAUC of the proposed method was also decreased by 1.83 and 1.47%, respectively. These results again highlight the efficiency of PScL-HDeep compared with other predictors.

Performance comparison with existing predictors on the independent test dataset

To validate PScL-HDeep against the existing predictors, we further performed experiments on the independent test dataset and compared their performance. Here, we only considered the accuracy index for performance evaluation because it is not worthy to calculate the seven classes’ meanAUC and stdAUC for the independent test dataset, which only contained five classes. The result is shown in Figure 8. Note that part of the performance results in Figure 8 was excerpted from Liu et al.’s SAE-RF work [31].

Figure 8 .

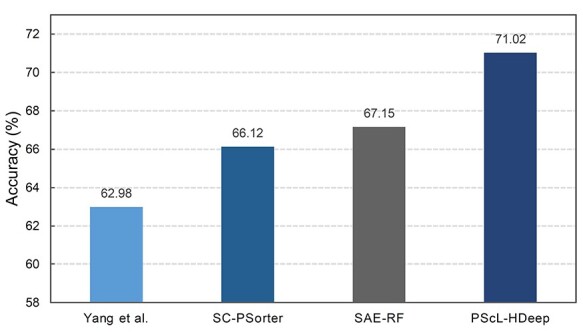
Performance comparison of the proposed PScL-HDeep with other existing methods on the independent test dataset.

Figure 8 shows that the prediction performance of PScL-HDeep was better than the existing models on the independent test. In particular, the accuracy of PScL-HDeep was 71.02%, which was increased by 8.04, 4.9 and 3.87% in comparison with Yang et al., SC-PSorter and SAE-RF, respectively. Together, the independent validation test results suggest that our proposed PScL-HDeep method has a better generalization capability than the existing methods.

Conclusion

In this work, we have developed a novel computational approach, referred to as PScL-HDeep, for multiclass prediction of protein subcellular location from bioimage data. Specifically, we leveraged a variety of handcrafted features, including DNA, Har, LBP, CLBP, AHP, LET, RICLBP and HOG, as well as deep learned features as the initial features. We then extracted the optimal feature set from each original raw feature set using the SDA feature selection technique. After combining all the optimal feature spaces obtained through SDA, we fed the integrated features to the SVM-RFE + CBR and obtained a more powerful feature subset termed Sup-400. We then fed the Sup-400 feature set to SVM-RBF and SVM-LNR classifiers and evaluated the classification performance on both 10-fold cross validation and independent test. The experimental results revealed that our proposed method has significantly outperformed several existing protein subcellular localization prediction methods. Several important attributes contribute to the performance improvement of PScL-HDeep, including the careful selection of appropriate training set, embedding of Deep features, more discriminative feature selection and vigilant design of the prediction model.

Several strategies have proven to be effective through the integration of different feature sets such as kernel combination [19], weighted feature combination [80] etc. Although PScL-HDeep achieved a much promising result, in future works, we plan to further improve PScL-HDeep by applying the combination strategies other than the serial combination. As demonstrated in several other studies [81–85], to better make PScL-HDeep easily accessible to the public, development of a user-friendly webserver is also included in the future direction of our study as well. Moreover, another limitation of this study is that it only takes into consideration single-label multiclass problem. In future work, we will consider multilabel classification problems.

Key Points

• A novel computational approach is developed, which uses the SVM algorithm with the ensemble of unique characteristics from traditional global and local handcrafted features along with deep learned features to accurately predict protein subcellular location.

• Two-layered feature selection strategy is proposed to design an ensemble of the optimal feature set, where in the first layer, the unique features are extracted from each individual feature set, and in the second layer, the training and testing model-based strategy is applied to the ensemble of the optimized features from the first layer.

• Based on the designed pipeline, a novel protein subcellular localization predictor, PScL-HDeep, is implemented. Benchmarking experiments on the newly created training and independent datasets demonstrate the efficacy of PScL-HDeep compared to state-of-the art subcellular location predictors.

• The main advantages of PScL-HDeep include the careful selection of appropriate training set, embedding of deep features, more discriminative feature selection and vigilant design of the prediction model.

Matee Ullah received his BS degree in computer science from Abdul Wali Khan University Mardan, Pakistan, in 2014, and his master’s degree in computer science and technology from Nanjing University of Science and Technology, China, in 2018. He is currently pursuing his PhD degree in the School of Computer Science and Engineering, Nanjing University of Science and Technology and is a member of the Pattern Recognition and Bioinformatics Group. His research interests include image processing, machine learning, deep learning and bioinformatics.

Ke Han received her MS degree in computer science from Nanjing University of Science and Technology in 2019. She is currently a PhD candidate in the School of Computer Science and Engineering, Nanjing University of Science and Technology and a member of Pattern Recognition and Bioinformatics Group. Her research interests include pattern recognition, machine learning and bioinformatics.

Fazal Hadi received his MS degree in computer science from Pakistan Institute of Engineering and Applied Sciences, Islamabad, Pakistan, in 2017. He is currently a PhD candidate in the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interests include pattern recognition, bioinformatics, computer vision and hyperspectral image analysis.

Jian Xu received his PhD degree from Nanjing University of Science and Technology, on the subject of data mining in 2007. In 2013 and 2016, he acted as an academic visitor at the School of Computer Science, Florida International University. He is currently a full professor in the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interests include event mining, log mining and their applications to complex system management, and machine learning. He is a member of both China Computer Federation (CCF) and IEEE.

Jiangning Song is an associate professor and group leader in the Monash Biomedicine Discovery Institute and Department of Biochemistry and Molecular Biology, Monash University, Melbourne, Australia. He is also affiliated with the Monash Centre for Data Science, Faculty of Information Technology, Monash University. His research interests include bioinformatics, computational biomedicine, machine learning, data mining and pattern recognition.

Dong-Jun Yu received the PhD degree from Nanjing University of Science and Technology in 2003. He is currently a full professor in the School of Computer Science and Engineering, Nanjing University of Science and Technology. His research interests include pattern recognition, machine learning and bioinformatics. He is a senior member of the China Computer Federation (CCF) and a senior member of the China Association of Artificial Intelligence (CAAI).

Conflict of Interest

The authors declare that they have no competing interests.

Availability

All the data and source codes used in this study are freely available at http://csbio.njust.edu.cn/bioinf/psclhdeep or https://github.com/csbio-njust-edu/PScL-HDeep.

Funding

National Natural Science Foundation of China (62072243, 61772273 and 61872186); the Natural Science Foundation of Jiangsu (BK20201304); the Foundation of National Defense Key Laboratory of Science and Technology (JZX7Y202001SY000901); the National Health and Medical Research Council of Australia (NHMRC) (1144652, 1127948); the Australian Research Council (ARC) (LP110200333, DP120104460); the National Institute of Allergy and Infectious Diseases of the National Institutes of Health (R01 AI111965) and a Major Inter-Disciplinary Research (IDR) project awarded by Monash University.