Abstract
Circadian rhythmicity in transcriptomic profiles has been shown in many physiological processes, and the disruption of circadian patterns has been found to associate with several diseases. In this paper, we developed a series of likelihood-based methods to detect (i) circadian rhythmicity (denoted as LR_rhythmicity) and (ii) differential circadian patterns comparing two experimental conditions (denoted as LR_diff). In terms of circadian rhythmicity detection, we demonstrated that our proposed LR_rhythmicity could better control the type I error rate compared to existing methods under a wide variety of simulation settings. In terms of differential circadian patterns, we developed methods in detecting differential amplitude, differential phase, differential basal level and differential fit, which also successfully controlled the type I error rate. In addition, we demonstrated that the proposed LR_diff could achieve higher statistical power in detecting differential fit, compared to existing methods. The superior performance of LR_rhythmicity and LR_diff was demonstrated in four real data applications, including a brain aging data (gene expression microarray data of human postmortem brain), a time-restricted feeding data (RNA sequencing data of human skeletal muscles) and a scRNAseq data (single cell RNA sequencing data of mouse suprachiasmatic nucleus). An R package for our methods is publicly available on GitHub https://github.com/diffCircadian/diffCircadian.
Keywords: circadian rhythmicity, differential circadian analysis, gene expression, likelihood-based test, R package, comparison study
Introduction
Circadian rhythms are an endogenous 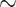 24 hours cycle of behavior and physiology including sleep–wake cycles, body temperature and melatonin [1, 3, 7, 19]. Underlying circadian rhythms is the clock mechanism that is found in virtually all cells of body. This mechanism is defined by a transcriptional-translational feedback loop involving a set of core clock genes [11, 18], including CLOCK, BMAL1, period family (PER1, PER2, PER3) and cryptochrome family (CRY1, CRY2). Beyond the core clock mechanism, genome-wide transcriptomic studies have uncovered circadian genes expression patterns in many tissues, including postmortem brain [4, 33], skeletal muscle [12], liver [15] and blood [26]. Zhang et al. [46] and Ruben et al. [31] conducted genome-wide circadian analyses using transcriptomic data of 12 unique mouse organs and 13 unique human organs, respectively, and showed that the profiles of circadian gene expression were tissue specific. It is now recognized from studies in humans and rodents that disruption in clock and circadian gene expression are linked to diseases including type II diabetes [35], sleep [26], major depression disease [22], aging [4], schizophrenia [33] and Alzheimer’s disease [23].
24 hours cycle of behavior and physiology including sleep–wake cycles, body temperature and melatonin [1, 3, 7, 19]. Underlying circadian rhythms is the clock mechanism that is found in virtually all cells of body. This mechanism is defined by a transcriptional-translational feedback loop involving a set of core clock genes [11, 18], including CLOCK, BMAL1, period family (PER1, PER2, PER3) and cryptochrome family (CRY1, CRY2). Beyond the core clock mechanism, genome-wide transcriptomic studies have uncovered circadian genes expression patterns in many tissues, including postmortem brain [4, 33], skeletal muscle [12], liver [15] and blood [26]. Zhang et al. [46] and Ruben et al. [31] conducted genome-wide circadian analyses using transcriptomic data of 12 unique mouse organs and 13 unique human organs, respectively, and showed that the profiles of circadian gene expression were tissue specific. It is now recognized from studies in humans and rodents that disruption in clock and circadian gene expression are linked to diseases including type II diabetes [35], sleep [26], major depression disease [22], aging [4], schizophrenia [33] and Alzheimer’s disease [23].
In the literature, several algorithms have been developed to detect circadian rhythmicity, including 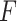 -test via cosinor-based rhythmometry [5], Lomb-Scargle periodograms [10], COSOPT [36], ARSER [44], RAIN [38], JTK CYCLE [16] and MetaCycle [43]. These algorithms were widely applied in transcriptomic studies, and the comparisons of these algorithm have been evaluated in several review studies [14, 21, 25]. Though promising, concerns have been raised [21] that the
-test via cosinor-based rhythmometry [5], Lomb-Scargle periodograms [10], COSOPT [36], ARSER [44], RAIN [38], JTK CYCLE [16] and MetaCycle [43]. These algorithms were widely applied in transcriptomic studies, and the comparisons of these algorithm have been evaluated in several review studies [14, 21, 25]. Though promising, concerns have been raised [21] that the 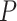 -values generated by many of these existing methods may not be correct (i.e. do not follow a uniform distribution [i.e.
-values generated by many of these existing methods may not be correct (i.e. do not follow a uniform distribution [i.e. 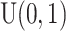 ] under the null), implying a potential inflated or deflated type I error rate.
] under the null), implying a potential inflated or deflated type I error rate.
Another increasingly important research question is to identify differential circadian patterns associated with different experimental conditions [13, 17, 26]. Figure 1 shows four types of differential circadian patterns identified in our brain aging data application (see Section 4.1 for details), among which 31 subjects were from the young group (age 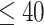 years), and 37 subjects were from the old group (age
years), and 37 subjects were from the old group (age 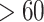 years). Gene CIART in Figure 1A shows the differential amplitude, where the amplitude in the young group is larger than the old group; Gene PER2 in Figure 1B shows the differential phase, where the phases in young and old groups are different; Gene TRIB2 in Figure 1C shows the differential basal level, where the basal level in the young group is higher than the old group; Gene MYO5A in Figure 1D shows the differential fit, where there exists a good circadian rhythmicity fit in the young group, but not in the old group. The definition of amplitude, phase, and basal level is illustrated in Figure 2. The traditional approach to compare circadian rhythmicity between two experimental conditions is to adopt a hard threshold (e.g.
years). Gene CIART in Figure 1A shows the differential amplitude, where the amplitude in the young group is larger than the old group; Gene PER2 in Figure 1B shows the differential phase, where the phases in young and old groups are different; Gene TRIB2 in Figure 1C shows the differential basal level, where the basal level in the young group is higher than the old group; Gene MYO5A in Figure 1D shows the differential fit, where there exists a good circadian rhythmicity fit in the young group, but not in the old group. The definition of amplitude, phase, and basal level is illustrated in Figure 2. The traditional approach to compare circadian rhythmicity between two experimental conditions is to adopt a hard threshold (e.g. 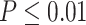 ) as the significance cutoff, and then declare deferential circadian rhythmicity if a gene is significant in only one condition [26, 30]. Though straightforward, this approach may fail under the following two scenarios. Scenario (i): gene PER2 in Figure 1B is showing significant circadian rhythmicity in both the young group (
) as the significance cutoff, and then declare deferential circadian rhythmicity if a gene is significant in only one condition [26, 30]. Though straightforward, this approach may fail under the following two scenarios. Scenario (i): gene PER2 in Figure 1B is showing significant circadian rhythmicity in both the young group (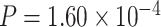 ) and the old group (
) and the old group (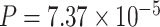 ), and thus did not satisfy the definition of differential circadian pattern. However, Figure 1B shows a clear phase difference comparing young and old groups, and the underlying differential phase
), and thus did not satisfy the definition of differential circadian pattern. However, Figure 1B shows a clear phase difference comparing young and old groups, and the underlying differential phase 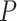 -value using our proposed method was
-value using our proposed method was 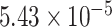 . Scenario (ii): gene EEF2K had a circadian
. Scenario (ii): gene EEF2K had a circadian 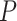 -value 0.0096 in the young group, and a
-value 0.0096 in the young group, and a 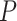 -value 0.0305 in the old group. Though this gene satisfied this definition of differential circadian pattern using
-value 0.0305 in the old group. Though this gene satisfied this definition of differential circadian pattern using 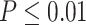 as the significance criteria, the rhythmicity
as the significance criteria, the rhythmicity 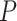 -values under both conditions were close to 0.01. In fact, the resulting differential fit
-values under both conditions were close to 0.01. In fact, the resulting differential fit 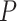 -value using our proposed method was 0.709, indicating EEF2K was not showing differential circadian pattern comparing the young group and the old group.
-value using our proposed method was 0.709, indicating EEF2K was not showing differential circadian pattern comparing the young group and the old group.
Figure 1.
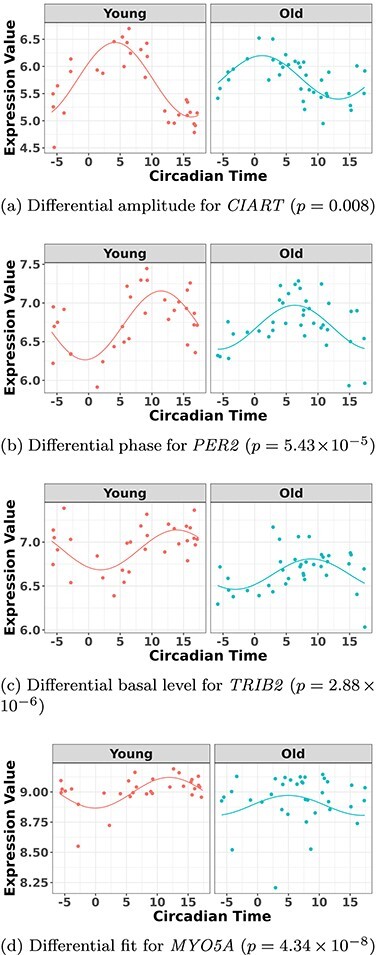
The most significant genes showing four types of differential circadian patterns from the brain aging data.
Figure 2.
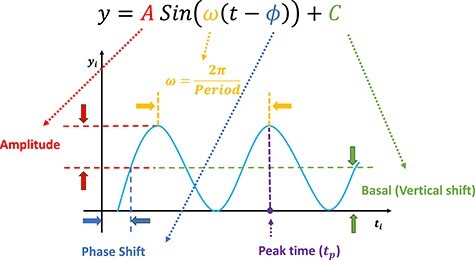
Illustration of a sinusoidal wave fitting and its related terminologies.
In the literature, some methods have been developed to identify genes showing differential circadian patterns. Chen et al. [4] developed a permutation test to quantify the statistical significance of these four types of differential circadian patterns. However, the non-parametric permutation test could suffer from low  -value precision and heavy computational burdens. DODR [39] and LimoRhyde [34] were developed to examine the hypothesis that the circadian rhythmicity across two conditions are identical, but they failed to further categorize different subclasses of differential circadian patterns illustrated in Figure 1. More recently, circaCompare [29] was developed to detect differential amplitude, differential phase and differential basal level using non-linear least square methods, but it could not characterize differential fit. To our knowledge, there is still a lack of unified parametric method that could identify all four differential circadian patterns simultaneously. In addition, the performance of these existing methods has not been systematically evaluated.
-value precision and heavy computational burdens. DODR [39] and LimoRhyde [34] were developed to examine the hypothesis that the circadian rhythmicity across two conditions are identical, but they failed to further categorize different subclasses of differential circadian patterns illustrated in Figure 1. More recently, circaCompare [29] was developed to detect differential amplitude, differential phase and differential basal level using non-linear least square methods, but it could not characterize differential fit. To our knowledge, there is still a lack of unified parametric method that could identify all four differential circadian patterns simultaneously. In addition, the performance of these existing methods has not been systematically evaluated.
In the statistics field, likelihood-based methods enjoyed tremendous popularity for its simplicity when testing single parameter and its flexibility to extend to test multiple parameters or complex models. In addition, the testing procedures based on the likelihood-based methods are generally considered as asymptotically the most efficient. However, this concept has not been fully developed in the field of circadian analysis. To close these research gaps, and to fully incorporate the merit of likelihood-based approaches, we propose a series of likelihood-based methods to detect circadian rhythmicity (within one condition) as well as differential circadian patterns (comparing two conditions). The contribution and novelty of this paper includes the following: (i) systematically evaluated the accuracy of  -values in detecting circadian rhythmicity of our likelihood-based methods and other existing methods; (ii) the first to propose likelihood-based methods to identify all four types of differential circadian patterns; (iii) systemically evaluated our likelihood-based methods in detecting differential circadian patterns, and compared with existing methods in terms of the correctness of
-values in detecting circadian rhythmicity of our likelihood-based methods and other existing methods; (ii) the first to propose likelihood-based methods to identify all four types of differential circadian patterns; (iii) systemically evaluated our likelihood-based methods in detecting differential circadian patterns, and compared with existing methods in terms of the correctness of 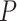 -value and statistical power; (iv) implemented our proposed methods in R software package, which has been made publicly available on GitHub.
-value and statistical power; (iv) implemented our proposed methods in R software package, which has been made publicly available on GitHub.
Method
We developed likelihood-based methods for (i) circadian rhythmicity detection within one experimental condition and (ii) differential circadian pattern analysis comparing two experimental conditions. The statistical inference of these methods were based on the Wald statistics and the likelihood ratio statistics. Since the accurate inference of the likelihood-based methods required large sample size, we also employed finite sample corrections to improve the performance under small sample sizes.
Notations for a sinusoidal wave fitting
Our methods assume that the relationship between the gene expression level and the circadian time fits a sinusoidal wave curve. As illustrated in Figure 2, denote 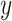 as the expression value for a gene;
as the expression value for a gene; 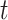 as the circadian time;
as the circadian time; 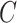 as the basal level (vertical shift of the sinusoidal wave baseline from 0);
as the basal level (vertical shift of the sinusoidal wave baseline from 0); 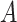 as the amplitude.
as the amplitude. 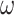 is the frequency of the sinusoidal wave, where
is the frequency of the sinusoidal wave, where 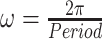 . Without loss of generality, we set
. Without loss of generality, we set 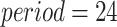 hours to mimic the diurnal period.
hours to mimic the diurnal period. 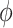 is the phase of the sinusoidal wave curve. Whenever there is no ambiguity, we will omit the unit ‘hours’ in period, phase, and other related quantities. Due to the periodicity of a sinusoidal wave, (
is the phase of the sinusoidal wave curve. Whenever there is no ambiguity, we will omit the unit ‘hours’ in period, phase, and other related quantities. Due to the periodicity of a sinusoidal wave, (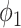 ,
, 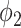 ) are not identifiable when
) are not identifiable when 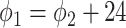 . Therefore, we will restrict
. Therefore, we will restrict 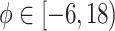 .
. 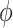 may be difficult to read from a sinusoidal wave (Figure 2), and a closely related quantify is the peak time
may be difficult to read from a sinusoidal wave (Figure 2), and a closely related quantify is the peak time 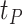 . The connection between
. The connection between 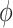 and
and 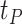 is that
is that 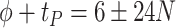 , where
, where  is an arbitrary natural number.
is an arbitrary natural number.
Circadian rhythmicity detection
In this section, we develop likelihood-based methods to test the existence of a circadian rhythmicity within one experimental condition. Denote 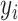 is the expression value of one gene for subject
is the expression value of one gene for subject 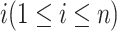 , where
, where 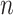 is the total number of subjects.
is the total number of subjects. 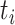 is the circadian time for subject
is the circadian time for subject 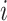 . We assume
. We assume
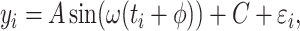 |
(1) |
where 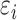 is the error term for subject
is the error term for subject 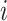 ; we assume
; we assume 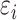 ’s are identically and independently distributed (i.e.
’s are identically and independently distributed (i.e. 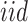 ) and
) and 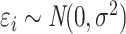 , where
, where 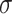 is the noise level. To benchmark the goodness of sinusoidal wave fitting, we define the coefficient of determination
is the noise level. To benchmark the goodness of sinusoidal wave fitting, we define the coefficient of determination 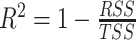 , where
, where 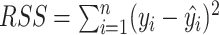 ,
, 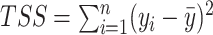 ,
, 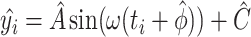 ,
, 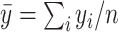 , with
, with 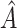 ,
, 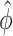 and
and 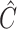 being the fitted value for
being the fitted value for 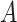 ,
, 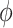 and
and  in Equation 1 under least square loss, respectively.
in Equation 1 under least square loss, respectively.  ranges from 0 to 1, with 1 indicating perfect sinusoidal wave fitting, and 0 indicating no fitting at all. Based on these assumptions, we derive procedures for testing circadian rhythmicity. For the ease of discussion, we re-write Equation 1 as
ranges from 0 to 1, with 1 indicating perfect sinusoidal wave fitting, and 0 indicating no fitting at all. Based on these assumptions, we derive procedures for testing circadian rhythmicity. For the ease of discussion, we re-write Equation 1 as
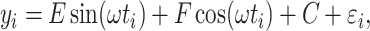 |
(2) |
where 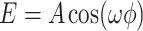 , and
, and 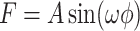 . The hypothesis setting for testing the existence circadian rhythmicity is
. The hypothesis setting for testing the existence circadian rhythmicity is 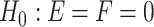 v.s.
v.s.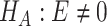 or
or 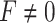 . We will derive the Wald statistics and the likelihood ratio statistics to perform hypothesis testing. Since both Wald statistics and likelihood ratio statistics are designed based on large sample theories, we will also employ finite sample statistics for these methods.
. We will derive the Wald statistics and the likelihood ratio statistics to perform hypothesis testing. Since both Wald statistics and likelihood ratio statistics are designed based on large sample theories, we will also employ finite sample statistics for these methods.
Likelihood ratio test
Based on Equation 2, the likelihood function of all 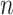 samples is
samples is
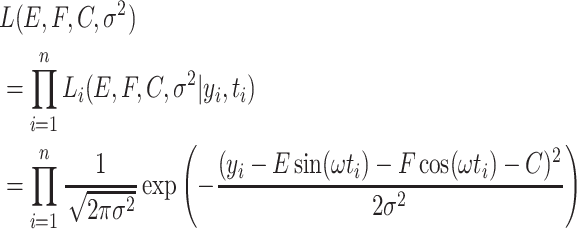 |
The log-likelihood function is
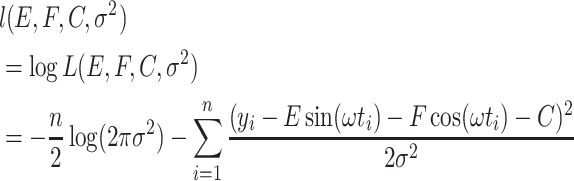 |
Under 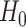 ,
, 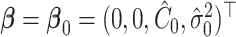 , and
, and 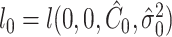 , where
, where 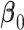 is the least square estimate of Equation 2 under
is the least square estimate of Equation 2 under 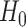 . Under
. Under 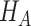 ,
, 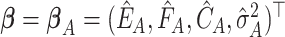 and
and 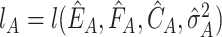 , where
, where 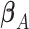 is the least square estimate of Equation 2. The likelihood ratio test statistic is:
is the least square estimate of Equation 2. The likelihood ratio test statistic is: 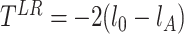 . Since the degree of freedom is 2, under
. Since the degree of freedom is 2, under 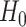 ,
, 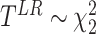 .
.
Wald test
The Wald test statistic can be derived as 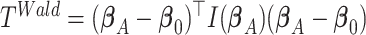 , where
, where 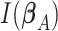 is Fisher information matrix evaluated at
is Fisher information matrix evaluated at 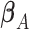 . Under
. Under 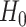 ,
, 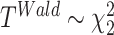 .
.
Finite sample Wald/LR tests
The Wald test and the likelihood ratio test may have inflated type I error when sample size is small since they rely on large sample asymptotic theory. Parker [28] introduced finite sample Wald and likelihood ratio test statistics, which could better control the type I error rate to the nominal level even with small sample sizes. The finite sample Wald statistics (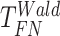 ) and the finite sample likelihood ratio statistics (
) and the finite sample likelihood ratio statistics (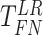 ) can be derived as the following:
) can be derived as the following:
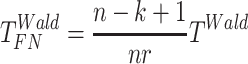 |
(3) |
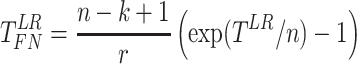 |
(4) |
where 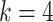 is total number of parameters and
is total number of parameters and 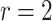 is number of parameters of interest. Under the null hypothesis,
is number of parameters of interest. Under the null hypothesis, 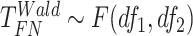 , and
, and 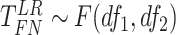 , where
, where 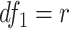 and
and 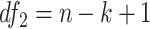 .
.
 -test
-test
The 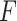 -test method to detect the circadian rhythmicity has been previously established [5].
-test method to detect the circadian rhythmicity has been previously established [5]. 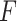 -test constructs its test statistic by decomposing total variability into model sum of square, and residual sum of square, which is closely related to our proposed finite sample likelihood method. Thus, we also describe the
-test constructs its test statistic by decomposing total variability into model sum of square, and residual sum of square, which is closely related to our proposed finite sample likelihood method. Thus, we also describe the 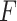 -test method in our manuscript and will draw connection between
-test method in our manuscript and will draw connection between 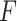 -test and our likelihood method.
-test and our likelihood method.
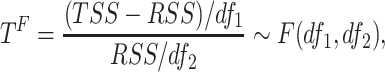 |
where residual sum of squares 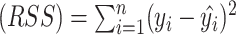 , total sum of squares
, total sum of squares 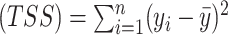 ,
, 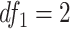 and
and 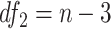 . Under the null hypothesis,
. Under the null hypothesis, 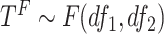 .
.
Other competing methods
We will compare our proposed likelihood-based method to other existing methods, including 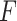 -test [5], ARSER [44], Lomb–Scargle periodograms [10], JTK CYCLE [16], RAIN [38], MetaCycle [43] and the permutation test [4]. ARSER, RAIN, JTK CYCLE and MetaCycle have some special requirement for the input circadian time—the input circadian time has to be integer value, and the intervals between two adjacent circadian time points must be the same. Thus, we will accommodate such design in our simulation settings when needed.
-test [5], ARSER [44], Lomb–Scargle periodograms [10], JTK CYCLE [16], RAIN [38], MetaCycle [43] and the permutation test [4]. ARSER, RAIN, JTK CYCLE and MetaCycle have some special requirement for the input circadian time—the input circadian time has to be integer value, and the intervals between two adjacent circadian time points must be the same. Thus, we will accommodate such design in our simulation settings when needed.
Differential circadian analysis
In this section, we develop likelihood-based testing procedures to identify genes showing differential circadian patterns, including (i) differential amplitude, (ii) differential phase, (iii) differential basal level and (iv) differential fit, as shown in Figure 1.
Denote 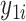 as the gene expression value of subject
as the gene expression value of subject 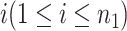 in experimental condition 1, where
in experimental condition 1, where 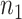 is the total number of subjects;
is the total number of subjects; 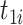 is the circadian time for subject
is the circadian time for subject 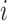 ;
; 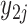 is the gene expression value of subject
is the gene expression value of subject 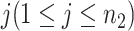 in experimental condition 2, where
in experimental condition 2, where 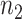 is the total number of subjects;
is the total number of subjects; 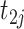 is the circadian time for subject
is the circadian time for subject 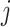 . Note that
. Note that 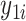 and
and 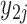 are from the same gene, but under different experimental conditions. We assume the following models:
are from the same gene, but under different experimental conditions. We assume the following models:
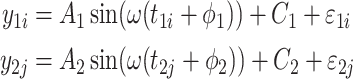 |
(5) |
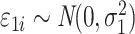 is the error term for subject
is the error term for subject 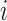 (
(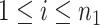 ) for experimental condition 1 and
) for experimental condition 1 and 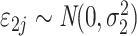 is the error term for subject
is the error term for subject 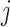 (
(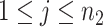 ) for experimental condition 2. These error terms are assumed to be
) for experimental condition 2. These error terms are assumed to be 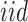 .
. 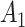 ,
, 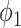 ,
, 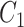 and
and 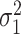 are the amplitude, phase, basal level and noise level for the experimental condition 1, and
are the amplitude, phase, basal level and noise level for the experimental condition 1, and 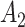 ,
, 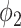 ,
, 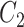 and
and 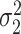 are for experimental condition 2.
are for experimental condition 2.
Hypothesis testing framework for differential circadian analysis
Below we state the null hypothesis and the alternative hypothesis for testing these four categories of differential circadian patterns, based on Equation 5.
Differential amplitude:
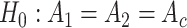 v.s.
v.s.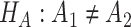 .
.Differential phase:
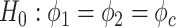 v.s.
v.s.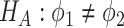 .
.Differential basal level:
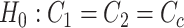 v.s.
v.s.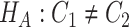 .
.Differential fit:
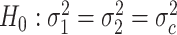 v.s.
v.s.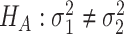 .
.
We have several remarks on our procedure. (i) As suggested by Chen et al. [4], the circadian rhythmicity can be characterized by the goodness of fit statistics 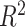 . Since it is not easy to derive statistical inference on
. Since it is not easy to derive statistical inference on 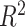 , we will use a closely related quantity,
, we will use a closely related quantity, 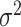 , to quantify the goodness of fit. (ii) The prerequisite for differential amplitude, differential phase, and differential basal level is that there should exist circadian rhythmicity in both conditions under comparisons. Therefore, we suggested users to set
, to quantify the goodness of fit. (ii) The prerequisite for differential amplitude, differential phase, and differential basal level is that there should exist circadian rhythmicity in both conditions under comparisons. Therefore, we suggested users to set 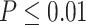 or
or 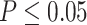 from our previous likelihood-based circadian rhythmicity test to ensure the existence of the circadian rhythmicity in both conditions. (iii) The prerequisite for differential fit is that there should exist a circadian rhythmicity in either experimental conditions. We suggested users to set
from our previous likelihood-based circadian rhythmicity test to ensure the existence of the circadian rhythmicity in both conditions. (iii) The prerequisite for differential fit is that there should exist a circadian rhythmicity in either experimental conditions. We suggested users to set 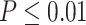 or
or 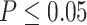 from our previous likelihood-based circadian rhythmicity test to ensure such prerequisite.
from our previous likelihood-based circadian rhythmicity test to ensure such prerequisite.
Likelihood ratio test
Based on Equation 5, the log-likelihood function for  samples in both experimental conditions is as follows:
samples in both experimental conditions is as follows:
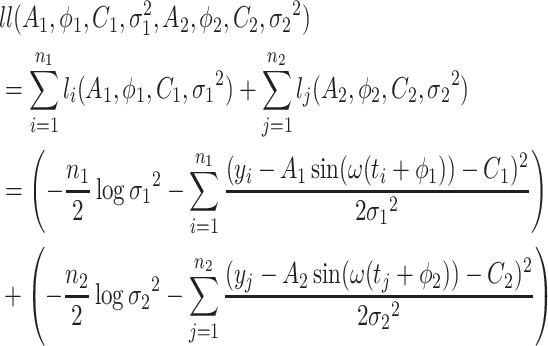 |
(6) |
The test statistic is the following: 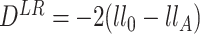 , where
, where 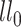 is the log likelihood under
is the log likelihood under 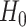 ; and
; and 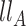 is the log likelihood under
is the log likelihood under 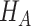 . Here the null can be one of the following: (i)
. Here the null can be one of the following: (i) 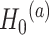 :
: 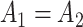 for differential amplitude; (ii)
for differential amplitude; (ii) 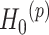 :
:  for differential phase; (iii)
for differential phase; (iii) 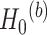 :
: 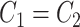 for differential basal level; (iv)
for differential basal level; (iv) 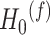 :
: 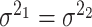 for differential fit. For all these null hypotheses, the degree of freedom is 1, and
for differential fit. For all these null hypotheses, the degree of freedom is 1, and 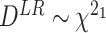 under
under 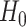 . For example when testing different amplitude, under
. For example when testing different amplitude, under 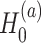 ,
, 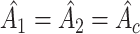 ,
, 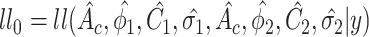 ; and under
; and under 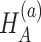 ,
,  ,
, 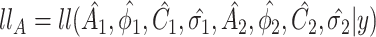 .
.
Wald test
Denote 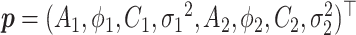 .
. 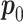 is
is 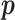 under
under 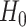 , where
, where 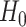 is one of the null hypotheses in Section 2.3.1;
is one of the null hypotheses in Section 2.3.1; 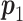 is
is 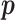 under
under 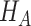 , where there is no restriction on
, where there is no restriction on 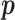 . Then the Wald test statistic is
. Then the Wald test statistic is 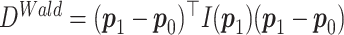 . Under
. Under 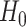 ,
, 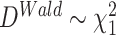 , where
, where 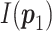 is Fisher information matrix evaluated at
is Fisher information matrix evaluated at 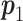 .
.
Finite sample Wald/LR tests
Again, in order to control type I error for small sample sizes, we derive finite sample version of the Wald statistics and likelihood ratio statistics 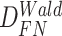 and
and 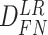 by Equations 3 and 4. Under
by Equations 3 and 4. Under 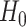 ,
, 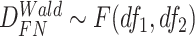 , and
, and 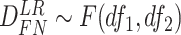 , where
, where 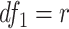 and
and 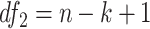 .
.
Competing methods for differential circadian analysis
We will compare the performance of our method with other existing methods, including the permutation test [4], DODR [39], LimoRhyde [34] and circaCompare [29]. We acknowledge that HANOVA, robustDODR and LimoRhyde are designed to detect differential rhythmicity (i.e. whether the circadian rhythmicity across two conditions are identical) and cannot distinguish the four subcategories in Figure 1. Thus we will apply these two methods in detecting differential fit, which is closely related to differential rhythmicity conceptually; circaCompare can examine differential amplitude, differential phase and differential basal level, while the permutation test as well as our proposed method can examine all four types if differential circadian patterns illustrated in Figure 1.
Computational consideration
Parameter estimations for Equation 1 were performed by the nonlinear least square algorithm in R package minpack.lm [9]. In addition, for differential circadian analysis, we used optimization method in R package nloptr [45] for parameter estimation in Equation 6.
Simulation
In terms of circadian rhythmicity detection, we demonstrated that our proposed method correctly controlled the type I error rate to the nominal level, while some of the other methods failed to control the type I error rate. In terms of differential circadian pattern detection, our method still controlled the type I error rate to the nominal level. For differential fit, which is one type of the differential circadian pattern shown in Figure 1b, we demonstrated our method achieved higher statistical power compared to the existing methods.
Simulation for circadian rhythmicity analysis
Simulation settings
Denote 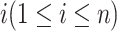 as the sample index, where
as the sample index, where 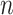 was the total number of samples. The circadian time
was the total number of samples. The circadian time 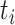 for sample
for sample 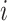 was generated from uniform distribution
was generated from uniform distribution 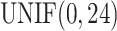 . We simulated the gene expression value for sample
. We simulated the gene expression value for sample 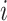 using Equation 1.
using Equation 1.
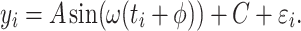 |
Our basic parameter setting for simulation is listed as below. For each gene, the sample size 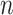 was set to be 12; the circadian time were sampled every 2 hours (i.e.
was set to be 12; the circadian time were sampled every 2 hours (i.e. 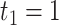 ,
, 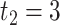 ,
, 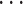 ,
, 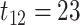 ), such integer circadian time and evenly spaced interval time are required by some other existing methods. Whenever the statistical methods have no such requirement, we sampled circadian time directly from
), such integer circadian time and evenly spaced interval time are required by some other existing methods. Whenever the statistical methods have no such requirement, we sampled circadian time directly from 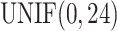 . Amplitude
. Amplitude 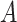 was fixed at 1; phase
was fixed at 1; phase 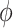 was generated from
was generated from 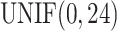 . Basal level C was generated from
. Basal level C was generated from 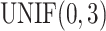 . Error term
. Error term 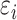 was generated from normal distribution
was generated from normal distribution 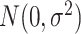 where
where 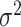 was set to be 1. We simulated
was set to be 1. We simulated 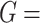 10 000 genes for each simulation, and each simulation was repeated
10 000 genes for each simulation, and each simulation was repeated 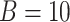 times to increase numbers of replications and to obtain an standard deviation estimate. To examine whether our method is robust against higher signal-noise ratios, correlated gene structures and violations of normality distributions, we further simulates the following variations:
times to increase numbers of replications and to obtain an standard deviation estimate. To examine whether our method is robust against higher signal-noise ratios, correlated gene structures and violations of normality distributions, we further simulates the following variations:
Impact of sample sizes. We varied
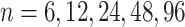 while fixing other parameters in the basic parameter setting fixed. Note that when
while fixing other parameters in the basic parameter setting fixed. Note that when 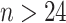 , we would allow repetitive circadian time for different samples. For example, when
, we would allow repetitive circadian time for different samples. For example, when 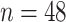 , the circadian time sequence would be
, the circadian time sequence would be 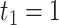 ,
, 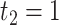 ,
, 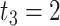 ,
, 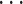 ,
, 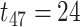 and
and 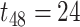 .
.Impact of signal noise ratio. The signal noise ratio is defined as
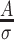 . Thus we varied
. Thus we varied 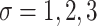 to mimic varying levels of signal noise ratio, while fixing other parameters in the basic parameter setting.
to mimic varying levels of signal noise ratio, while fixing other parameters in the basic parameter setting.- Impact of correlated genes. In transcriptomic data applications, individual genes can be correlated. Thus, we simulated the following correlated structure. For every m = 50 genes, we simulated
where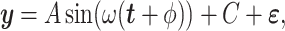
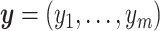 ,
, 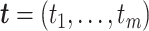 and
and 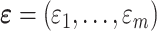 . In this case,
. In this case, 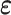 were generated from a multivariate normal distribution
were generated from a multivariate normal distribution 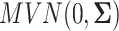 . And
. And 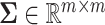 was the covariance matrix generated from the inverse Wishart distribution
was the covariance matrix generated from the inverse Wishart distribution 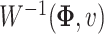 . In order to mimic correlated gene structure, we first designed
. In order to mimic correlated gene structure, we first designed 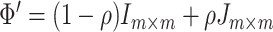 and then standardized
and then standardized 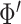 to correlation matrix
to correlation matrix 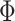 , where
, where 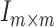 was the identify matrix, and
was the identify matrix, and 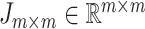 a matrix with all elements 1. We fixed
a matrix with all elements 1. We fixed 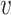 to be 60, and vary
to be 60, and vary 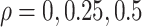 .
. Violation of the Gaussian assumption. Instead of assuming the error term was generated from a standard normal distribution (i.e.
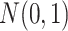 ), we generated
), we generated 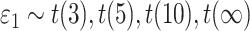 , where
, where 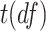 is the t-distribution with degree of freedom
is the t-distribution with degree of freedom 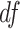 . This family of t-distributions represents long-tailed error distribution, with smaller
. This family of t-distributions represents long-tailed error distribution, with smaller 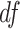 indicating longer tailed error distribution, and thus larger violation of the normality assumption. When
indicating longer tailed error distribution, and thus larger violation of the normality assumption. When 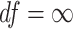 ,
, 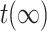 is the same as
is the same as 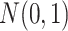 .
.
The best performer of the likelihood based methods in detecting circadian rhythmicity
Before comparing with other existing methods, we first evaluated the type I error rate (nominal 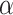 level 5%) of our proposed four likelihood-based methods in detecting circadian rhythmicity, including Wald test (regular), Wald test (finite sample), likelihood ratio test (regular) and likelihood ratio test (finite sample). Since the limiting distribution of both Wald statistics (finite sample) and likelihood ratio statistics (finite sample) follows an
level 5%) of our proposed four likelihood-based methods in detecting circadian rhythmicity, including Wald test (regular), Wald test (finite sample), likelihood ratio test (regular) and likelihood ratio test (finite sample). Since the limiting distribution of both Wald statistics (finite sample) and likelihood ratio statistics (finite sample) follows an 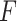 -distribution, we also include the
-distribution, we also include the 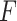 -test method [5] as benchmark.
-test method [5] as benchmark.
Figure S2 showed type I error rates (nominal 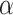 level 5%) of our proposed four methods and the
level 5%) of our proposed four methods and the 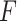 -test method. Regardless of the varying sample sizes, the Wald test (finite sample), the likelihood ratio test (finite sample) and the
-test method. Regardless of the varying sample sizes, the Wald test (finite sample), the likelihood ratio test (finite sample) and the 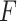 -test controlled the type I error rate close to the 5% nominal level, while the Wald test (regular) and the likelihood ratio test (regular) obtained inflated type I error rate. The Wald test (regular) and the likelihood ratio test (regular) had better performance when sample size became larger, which was not unexpected because these asymptotic tests rely on large sample sizes. Remarkably, we observed that the Wald test (finite sample) and the likelihood ratio test (finite sample) achieved almost the same test statistics as the
-test controlled the type I error rate close to the 5% nominal level, while the Wald test (regular) and the likelihood ratio test (regular) obtained inflated type I error rate. The Wald test (regular) and the likelihood ratio test (regular) had better performance when sample size became larger, which was not unexpected because these asymptotic tests rely on large sample sizes. Remarkably, we observed that the Wald test (finite sample) and the likelihood ratio test (finite sample) achieved almost the same test statistics as the 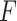 -test, indicating the finite sample approximation procedure [28] successfully convert our likelihood-based statistics to
-test, indicating the finite sample approximation procedure [28] successfully convert our likelihood-based statistics to 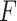 -statistics.
-statistics.
Similar results was also observed by varying signal noise ratio (Figure S3) and varying the strength of gene correlations (Figure S4). The Wald test (finite sample), the likelihood ratio test (finite sample) and the 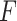 -test could better control the type I error rate to the 5% nominal level compared to the Wald test (regular) and the likelihood ratio test (regular).
-test could better control the type I error rate to the 5% nominal level compared to the Wald test (regular) and the likelihood ratio test (regular).
As shown in Figure S5, when we varied the level of normality violation by varying 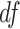 of the t-distribution, we observed that all test procedures became slightly more conservative.
of the t-distribution, we observed that all test procedures became slightly more conservative.
In particular, for the likelihood ratio test (finite sample), when these was a slight (df=10) or moderate (df=5) violation of the normality assumption, this method still controlled the type I error rate well (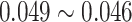 ). When there was severe (df=3) violation of the normality assumption, the type I error rate was still 0.043, which was not far away from the nominal 5% level. These results indicate our method is robust against normality assumptions. In practice, if the residuals (i.e.
). When there was severe (df=3) violation of the normality assumption, the type I error rate was still 0.043, which was not far away from the nominal 5% level. These results indicate our method is robust against normality assumptions. In practice, if the residuals (i.e. 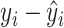 ) violated the Gaussian distribution, we would recommend data transformations (e.g. Box–Cox transformation [2]) to improve normality. In supplementary material Section 1, we included a concrete simulated example to demonstrate how to use the Box–Cox transformation to rescue the normality assumption under the setting of detecting circadian rhythmicity.
) violated the Gaussian distribution, we would recommend data transformations (e.g. Box–Cox transformation [2]) to improve normality. In supplementary material Section 1, we included a concrete simulated example to demonstrate how to use the Box–Cox transformation to rescue the normality assumption under the setting of detecting circadian rhythmicity.
To summarize, the Wald test (finite sample) and the likelihood ratio test (finite sample) are the best performer of our proposed likelihood-based methods in detecting circadian rhythmicity, which could control the type I error rate to the nominal level under the Gaussian assumption. And these two methods are equivalent to the 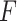 -test method in terms of the test statistics. Therefore, we will pick up the likelihood ratio test (finite sample) as the representative of our proposed methods in detecting circadian rhythmicity, and we denoted LR_rhythmicity as the short name for this method in all later evaluations.
-test method in terms of the test statistics. Therefore, we will pick up the likelihood ratio test (finite sample) as the representative of our proposed methods in detecting circadian rhythmicity, and we denoted LR_rhythmicity as the short name for this method in all later evaluations.
Type I error rate comparison with other methods
We compared the likelihood-based method (LR_rhythmicity) with other existing methods in detecting circadian rhythmicity, including Lomb-Scargle, JTK, ARSER, Rain, MetaCycle and the permutation test. We excluded the 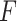 -test in our evaluation, since it is essentially the same as LR_rhythmicity. Figure 3 showed type I error rates by varying sample sizes. In general, LR_rhythmicity and the permutation test controlled the type I error rate to the 5% nominal level, while the other methods had inflated or deflated type I error rate. Similar results were also observed by varying signal noise ratio (Figure S6) and varying the strength of gene correlations (Figure S7). As shown in Figure S8, we observed that violation of normality assumption will lead to a slightly smaller than expected type I error rate for LR_rhythmicity.
-test in our evaluation, since it is essentially the same as LR_rhythmicity. Figure 3 showed type I error rates by varying sample sizes. In general, LR_rhythmicity and the permutation test controlled the type I error rate to the 5% nominal level, while the other methods had inflated or deflated type I error rate. Similar results were also observed by varying signal noise ratio (Figure S6) and varying the strength of gene correlations (Figure S7). As shown in Figure S8, we observed that violation of normality assumption will lead to a slightly smaller than expected type I error rate for LR_rhythmicity.
Figure 3.
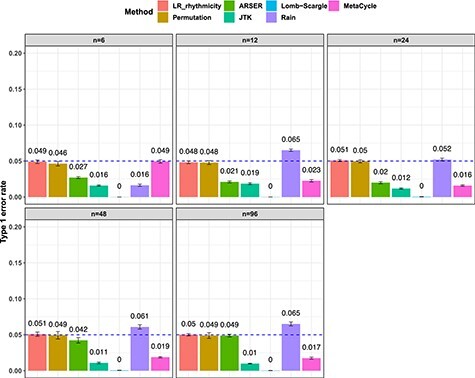
Type I error rate at nominal 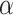 level 5% for 7 different methods in detecting circadian rhythmicity. The sample sizes were varied at n=6, 12, 24, 48 and 96. The blue dashed line is the 5% nominal level. A higher than 5% blue dashed line bar indicates an inflated type I error rate; a lower than 5% blue dashed line bar indicates a smaller than expected type I error rate; and a bar at the blue dashed line indicates an accurate type I error rate (i.e.
level 5% for 7 different methods in detecting circadian rhythmicity. The sample sizes were varied at n=6, 12, 24, 48 and 96. The blue dashed line is the 5% nominal level. A higher than 5% blue dashed line bar indicates an inflated type I error rate; a lower than 5% blue dashed line bar indicates a smaller than expected type I error rate; and a bar at the blue dashed line indicates an accurate type I error rate (i.e. 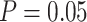 ). The standard deviation of the mean type I error rate was also marked on the bar plot.
). The standard deviation of the mean type I error rate was also marked on the bar plot.
To summarize, under the Gaussian assumption (i.e. the residuals follow normal distribution), only the LR_rhythmicity and the permutation test can achieve nominal type I error rate control (i.e. 5%). And when there is a violation of the Gaussian assumption, LR_rhythmicity is robust and we only observed a slight deviation of the type I error rate.
These type I error rates ranged from 0.038 to 0.048, which were close to the nominal 5% level. indicating our method is robust against normality assumptions.
Power analysis
For the power analysis, we only examined the method that could successfully control the type I error rate to the 5% nominal level. Otherwise, the power is directly not comparable because it cannot be distinguished whether a higher/lower power is a result of the test procedure itself, or because of inflated/deflated type I error rate control. Only the LR_rhythmicity and the permutation test survived these criteria. Figure S9 shows the power with respect to varying sample sizes. Both these methods are similarly powerful at 5% nominal level of type I error rate. When the sample size is larger, both tests became more powerful. However, we want to point out that the precision of the permutation test depends heavily on the number of permutations. For example, it may need at least 1,000,000 permutations in order to achieve a 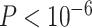 , which could be a computational burden. The LR_rhythmicity has no such restriction and could obtain an arbitrarily small
, which could be a computational burden. The LR_rhythmicity has no such restriction and could obtain an arbitrarily small 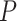 -values without extra computational concerns.
-values without extra computational concerns.
Sensitivity analysis
To examine how the perturbations of the model parameters affected our results, we further performed sensitivity analysis. Based on the basic simulation settings in previous sections, we varied 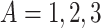 ;
; 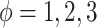 ;
; 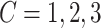 ; and
; and 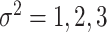 . As shown in Table S1, the type I error control remained the same regardless of the perturbation in
. As shown in Table S1, the type I error control remained the same regardless of the perturbation in 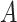 ,
, 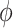 ,
, 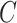 and
and 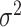 . In terms of the power, we observed that
. In terms of the power, we observed that 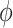 and
and 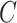 had no impact.
had no impact. 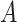 and
and 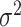 had an impact on the power, which was not unexpected because
had an impact on the power, which was not unexpected because 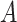 and
and 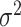 are directly related to the goodness of fit of a circadian curve.
are directly related to the goodness of fit of a circadian curve.
Differential circadian analysis
In this section, we used simulation to evaluate the performance of the likelihood-based method in detecting differential circadian patterns, including differential amplitude, differential phase, differential basal level and differential fit. We first compared among our proposed likelihood-based methods including Wald test (regular), Wald test (finite sample), likelihood ratio test (regular) and likelihood ratio test (finite sample). We found that likelihood ratio test (finite sample) was the best performer of our proposed methods. We then compared this best performer with other existing methods for differential circadian pattern analysis, including Circacompare, limorhyde, HANOVA, robustDODR and the permutation test under variety of simulation settings.
Simulation settings
The simulation setting is based on Equation 5. The basic parameter setting for simulation is listed as below. We set number of genes 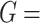 10 000 and the sample size
10 000 and the sample size 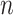 was set to be 10. For each gene
was set to be 10. For each gene 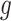 (
(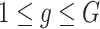 ), amplitudes
), amplitudes 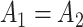 were set to be 3; phases
were set to be 3; phases  were generated from
were generated from 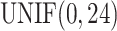 . Basal levels
. Basal levels 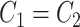 were generated from
were generated from 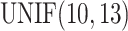 . Error terms
. Error terms 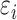 ,
, 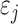 were generated from normal distribution
were generated from normal distribution 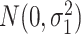 and
and 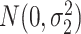 , respectively.
, respectively.  were set to be 1. This simulation was repeated 10 times to increase numbers of replications and to obtain standard deviation estimate. To examine the impact of sample size, correlation between genes and distribution violations, we further simulated the following variations.
were set to be 1. This simulation was repeated 10 times to increase numbers of replications and to obtain standard deviation estimate. To examine the impact of sample size, correlation between genes and distribution violations, we further simulated the following variations.
Impact of sample sizes. We varied
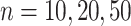 while fixing other parameters in the basic parameter setting.
while fixing other parameters in the basic parameter setting.Impact of correlated genes. For every m = 50 genes, we simulated the correlated gene structure as described in Section 3.1.1. We varied the strength of correlation
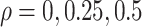 while fixing other parameters in the basic parameter setting.
while fixing other parameters in the basic parameter setting.Violation of the Gaussian assumption. As described in Section 3.1.1, we varied the error distribution
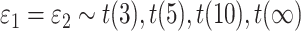 to mimic different levels of violation of normality assumptions.
to mimic different levels of violation of normality assumptions.
The best performer of the likelihood-based methods in detecting differential circadian patterns
We evaluated the type I error rate (nominal 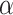 level 5%) of our proposed likelihood-based methods, including Wald test (regular), Wald test (finite sample), likelihood ratio test (regular) and likelihood ratio test (finite sample), under all pre-mentioned simulation settings. Figures S10 and S11 show that the likelihood ratio test (finite sample) had the best performance in terms of type I error rate control with varying sample size or strength of correlation among genes. Thus, we denoted this method as LR_diff and will further compared LR_diff with other existing methods. In Figure S12, when there was a violation of the Gaussian assumption, we observed that LR_diff still controlled the type I error rate for differential amplitude, differential phase and differential basal levels but resulted in inflated type I error rate of differential fit. This is not unexpected since likelihood-based methods utilized the Gaussian assumption to derive the test statistics. Under this situation, we would recommend users to take transformation (i.e. Box–Cox transformation) to improve normality (see Section 5 for more discussions).
level 5%) of our proposed likelihood-based methods, including Wald test (regular), Wald test (finite sample), likelihood ratio test (regular) and likelihood ratio test (finite sample), under all pre-mentioned simulation settings. Figures S10 and S11 show that the likelihood ratio test (finite sample) had the best performance in terms of type I error rate control with varying sample size or strength of correlation among genes. Thus, we denoted this method as LR_diff and will further compared LR_diff with other existing methods. In Figure S12, when there was a violation of the Gaussian assumption, we observed that LR_diff still controlled the type I error rate for differential amplitude, differential phase and differential basal levels but resulted in inflated type I error rate of differential fit. This is not unexpected since likelihood-based methods utilized the Gaussian assumption to derive the test statistics. Under this situation, we would recommend users to take transformation (i.e. Box–Cox transformation) to improve normality (see Section 5 for more discussions).
Type I error rate comparison with other methods
We evaluated the type I error rate (nominal 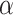 level 5%) of the following methods: LR_diff, Circacompare, limorhyde, HANOVA, robustDODR and permutation test under different simulation settings (See Section 3.2.1 for details). Here, LR_diff and the permutation test are applicable for testing all four types of differential circadian analysis in Figure 1; HANOVA, robustDODR and LimoRhyde are designed to detect differential rhythmicity (i.e. whether the circadian rhythmicity across two conditions are identical) and cannot distinguish the four subcategories. Thus, we will apply these three methods in detecting differential fit, which is closely related to differential rhythmicity conceptually, and Circacompare is applicable for testing differential amplitude, differential phase and differential basal levels (Also see Table 1 for their applicability).
level 5%) of the following methods: LR_diff, Circacompare, limorhyde, HANOVA, robustDODR and permutation test under different simulation settings (See Section 3.2.1 for details). Here, LR_diff and the permutation test are applicable for testing all four types of differential circadian analysis in Figure 1; HANOVA, robustDODR and LimoRhyde are designed to detect differential rhythmicity (i.e. whether the circadian rhythmicity across two conditions are identical) and cannot distinguish the four subcategories. Thus, we will apply these three methods in detecting differential fit, which is closely related to differential rhythmicity conceptually, and Circacompare is applicable for testing differential amplitude, differential phase and differential basal levels (Also see Table 1 for their applicability).
Table 1.
Comparison of LR_diff with other existing methods in detecting differential circadian patterns. 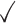 indicates a method is applicable or could control the type I error to the nominal level; * indicates the most powerful method among all applicable methods. − indicates the method could roughly control the type I error to the nominal level, but with a non-negligible deviation
indicates a method is applicable or could control the type I error to the nominal level; * indicates the most powerful method among all applicable methods. − indicates the method could roughly control the type I error to the nominal level, but with a non-negligible deviation
| Differential amp/phase/basal | Differential fit | |||
|---|---|---|---|---|
| Applicable | Type I error | Applicable | Type I error | |
| LR_diff |
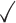
|
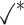
|
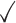
|
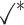
|
| Permutation |
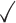
|
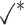
|
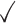
|
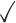
|
| Circacompare |
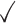
|
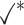
|
||
| limorhyde |
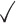
|
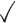
|
||
| HANOVA |
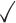
|
- | ||
| robustDODR |
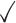
|
- | ||
Impact of sample sizes. Based on the basic parameter setting, we varied
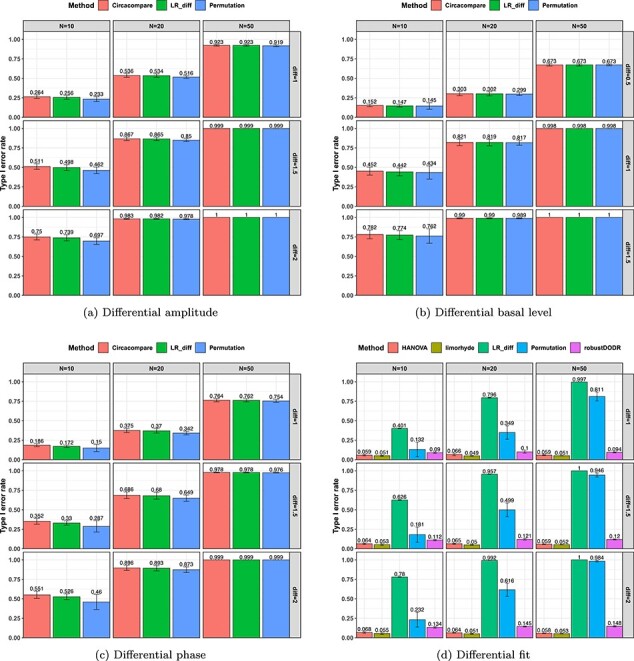
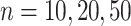 . Figure 4 shows the type I error rate control for the 6 methods. Among which three methods were applicable for detecting differential amplitude, differential basal level and differential phase, including LR_diff, Circacompare and the permutation test. All these three methods could control the type I error rate to the 5% nominal level, though Circacompare is slightly better than LR_diff and the permutation test. In addition, five methods were applicable for detecting differential fit, including LR_diff, limorhyde, HANOVA, robustDODR and the permutation test. We observed that LR_diff, limorhyde and the permutation test could control the type I error rate to the 5% nominal level, while HANOVA and robustDODR may have slightly inflated type I error rate. We observed their performance did not rely heavily on the sample size, which is expected since these methods did not necessarily rely on large sample size.
. Figure 4 shows the type I error rate control for the 6 methods. Among which three methods were applicable for detecting differential amplitude, differential basal level and differential phase, including LR_diff, Circacompare and the permutation test. All these three methods could control the type I error rate to the 5% nominal level, though Circacompare is slightly better than LR_diff and the permutation test. In addition, five methods were applicable for detecting differential fit, including LR_diff, limorhyde, HANOVA, robustDODR and the permutation test. We observed that LR_diff, limorhyde and the permutation test could control the type I error rate to the 5% nominal level, while HANOVA and robustDODR may have slightly inflated type I error rate. We observed their performance did not rely heavily on the sample size, which is expected since these methods did not necessarily rely on large sample size.Impact of correlated genes. Figure S13 shows the type I error rate control by varying the strength of correlations between genes. Similar to the previous simulation setting, we did not observe the correlated gene structure had a big impact on their performance.
Violation of the Gaussian assumption. Instead of assuming the error term was generated from a standard normal distribution (i.e.
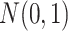 ), we generated
), we generated 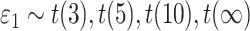 , where
, where 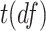 was the t-distribution with degree of freedom
was the t-distribution with degree of freedom 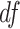 . Smaller
. Smaller 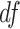 represents longer tailed error distribution, and thus larger violation of the normality assumption. Figure S14 shows the type I error rate control for the six methods. In terms of differential amplitude, differential basal level and differential phase, LR_diff, Circacompare and the permutation test successfully controlled the type I error rate to the 5% nominal. In terms of differential fit, we observed that the LR_diff would obtain inflated type I error rate, while the performance of limorhyde, HANOVA, robustDODR and the permutation test were similar regardless of violation of the Gaussian assumption. This is not unexpected because our likelihood-based method relied on the Gaussian assumption to derive its test statistics. Under this situation, we would recommend uses to take transformation (i.e. Box–Cox transformation) to improve normality (see Section 5 for more discussions).
represents longer tailed error distribution, and thus larger violation of the normality assumption. Figure S14 shows the type I error rate control for the six methods. In terms of differential amplitude, differential basal level and differential phase, LR_diff, Circacompare and the permutation test successfully controlled the type I error rate to the 5% nominal. In terms of differential fit, we observed that the LR_diff would obtain inflated type I error rate, while the performance of limorhyde, HANOVA, robustDODR and the permutation test were similar regardless of violation of the Gaussian assumption. This is not unexpected because our likelihood-based method relied on the Gaussian assumption to derive its test statistics. Under this situation, we would recommend uses to take transformation (i.e. Box–Cox transformation) to improve normality (see Section 5 for more discussions).
Figure 4.
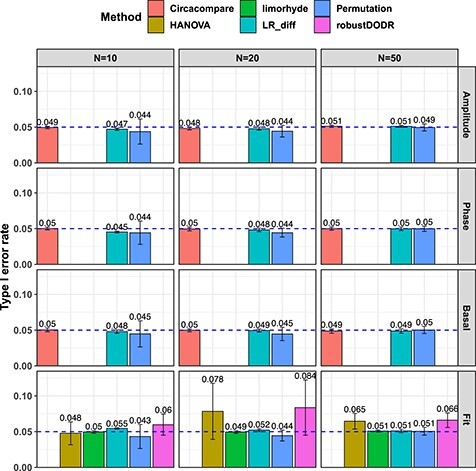
Type I error rate at nominal 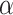 level 5% for six different methods in detecting differential circadian patterns. The differential circadian patterns include differential amplitude (Amplitude), differential phase (Phase), differential basal level (Basal) and differential fit (Fit). The sample sizes were varied at N=10, 20 and 50. The blue dashed line is the 5% nominal level. A higher than 5% blue dashed line bar indicates an inflated type I error rate; a lower than 5% blue dashed line bar indicates a smaller than expected type I error rate; and a bar at the blue dashed line indicates an accurate type I error rate (i.e.
level 5% for six different methods in detecting differential circadian patterns. The differential circadian patterns include differential amplitude (Amplitude), differential phase (Phase), differential basal level (Basal) and differential fit (Fit). The sample sizes were varied at N=10, 20 and 50. The blue dashed line is the 5% nominal level. A higher than 5% blue dashed line bar indicates an inflated type I error rate; a lower than 5% blue dashed line bar indicates a smaller than expected type I error rate; and a bar at the blue dashed line indicates an accurate type I error rate (i.e. 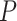 -value = 0.05). The standard deviation of the mean type I error rate was also marked on the bar plot.
-value = 0.05). The standard deviation of the mean type I error rate was also marked on the bar plot.
To summarize, in terms of differential amplitude, differential basal level and differential phase, LR_diff, Circacompare and the permutation test could control the type I error rate to the 5% nominal level. In terms of differential fit and under normality assumption, LR_diff, limorhyde and the permutation test could control the type I error rate to the 5% nominal level, while HANOVA and robustDODR may have slightly inflated type I error rate.
Power analysis
In principle, all methods could control the type I error rate to the 5% nominal level, we included all these methods in the power evaluation (Figure 5). In terms of differential amplitude, differential basal level and differential phase, with increasing sample size or larger effect size, all three methods, including LR_diff, Circacompare and the permutation test, became more powerful. Fixing the sample size and effect size, we observed that LR_diff and Circacompare are a little bit more powerful than the permutation test. In terms of differential fit, remarkably, our proposed LR_diff is much more powerful than the permutation test, limorhyde, HANOVA and robustDODR. In addition, with increasing sample size or larger effect size, LR_diff and the permutation test are becoming more powerful, while the other methods remained similar power or had a little bit elevated power. Table 1 summarizes applicability, performance of type I error rate control and power for all these methods.
Figure 5.
Power evaluation for six different methods in detecting differential circadian patterns. The differential circadian patterns include differential amplitude, differential phase, differential basal level and differential fit. The sample sizes were varied at N=10, 20 and 50. The standard deviation of the mean type I error rate was also marked on the bar plot.
We observed that our proposed LR_diff had very similar type I error rate and statistical power compared to Circacompare. In fact, both LR_diff and Circacompare were designed to address the same question (i.e. differential amplitude, phase and basal level) by deploying cosinor-based rhythmometry. The difference is that LR_diff utilized a likelihood ratio test, whereas Circacompare employed a non-linear least square approach. In addition, LR_diff is capable of testing different fit, while Circacompare cannot be used to perform this test.
Real data applications
We evaluated our likelihood-based methods (LR_rhythmicity and LR_diff) in four real data applications, including a gene expression microarray data of human postmortem brain (comparing chronological age [i.e. young versus old]), a gene expression RNA sequencing data of human skeletal muscles (comparing time-restricted feeding [i.e. restricted versus unrestricted]), a gene expression RNA sequencing data of mouse skeletal muscles (comparing exercise status [i.e. exercise group versus sedentary group]) and a single cell RNA sequencing data of mouse suprachiasmatic nucleus (no comparison groups). Throughout this section, we used 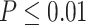 as the cutoff to declare statistical significance unless otherwise specified. Since our likelihood-based method includes both circadian rhythmicity
as the cutoff to declare statistical significance unless otherwise specified. Since our likelihood-based method includes both circadian rhythmicity 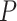 -values and differential circadian pattern
-values and differential circadian pattern 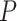 -values, we denote
-values, we denote 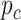 as a
as a 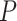 -value for circadian rhythmicity detection (i.e. from LR_rhythmicity), and
-value for circadian rhythmicity detection (i.e. from LR_rhythmicity), and 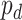 as a
as a 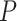 -value for differential circadian pattern analysis i.e. from LR_diff).
-value for differential circadian pattern analysis i.e. from LR_diff). 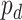 can also be expanded as
can also be expanded as 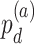 (differential amplitude);
(differential amplitude); 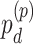 (differential phase);
(differential phase); 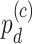 (differential basal level);
(differential basal level); 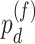 (differential fit). We did not systematically compare our methods with existing methods in the real data application, because there is no underlying truth in the real data, and thus it is difficult to benchmark their performance.
(differential fit). We did not systematically compare our methods with existing methods in the real data application, because there is no underlying truth in the real data, and thus it is difficult to benchmark their performance.
Human brain aging data
We first examined our methods in a transcriptomic profile in a human postmortem brain data (Brodmann’s area 11 in the prefrontal cortex). Detailed description of this study has been previously described by Chen et al. [4]. The final samples included 146 individuals whose time of death (TOD) could be precisely determined. The mean age at death was 50.7 years; 78% of the individuals were male, and the mean postmortem interval was 17.3 hours. The TODs were further adjusted as the Zeitgeber time (ZT), which adjusted factors including time zone, latitude, longitude and altitude. The ZT was used as the circadian time, which was comparable across all individuals. A total of 33 297 gene probes were available in this microarray data, which was publicly available in GEO (GSE71620). After filtering 50% gene probes with lower mean expression level, 16 648 gene probes remained in the analysis.
Circadian rhythmicity detection
Under 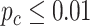 , we detected 528 significant circadian genes using LR_rhythmicity. Figure 6 shows the six core circadian genes, including PER1, PER2, PER3, ARNTL, NR1D1 and DBP, which are known to have persistent circadian rhythmicity. All these six circadian genes rendered significant
, we detected 528 significant circadian genes using LR_rhythmicity. Figure 6 shows the six core circadian genes, including PER1, PER2, PER3, ARNTL, NR1D1 and DBP, which are known to have persistent circadian rhythmicity. All these six circadian genes rendered significant 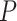 -values (
-values (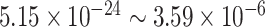 ), showing the good detection power of our method in identifying circadian patterns. The number of significant circadian genes using other methods is shown in Table S2. We further performed pathway enrichment analysis. Using pathway analysis
), showing the good detection power of our method in identifying circadian patterns. The number of significant circadian genes using other methods is shown in Table S2. We further performed pathway enrichment analysis. Using pathway analysis 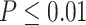 as cutoff, LR_rhythmicity detected four pathways. The most significant pathway was the circadian rhythm signaling pathway (
as cutoff, LR_rhythmicity detected four pathways. The most significant pathway was the circadian rhythm signaling pathway (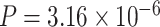 ). The second most significant pathway was the senescence pathway (
). The second most significant pathway was the senescence pathway (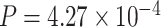 ), which was also known to be associated with circadian oscillation [20].
), which was also known to be associated with circadian oscillation [20].
Figure 6.
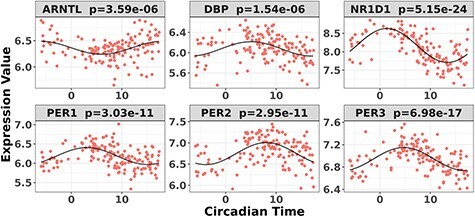
Circadian rhythmicity for six core circadian genes in the brain aging data, including PER1, PER2, PER3, ARNTL, NR1D1 and DBP, using LR_rhythmicity.
Differential circadian analysis
In order to examine whether the chronological age was associated with disruption of circadian patterns, we further performed differential circadian analysis comparing the young group and the old group using our likelihood-based method. We first divided the 146 individuals into two groups: young group (age 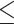 40, n=31) and old group (age > 60, n=37). Under
40, n=31) and old group (age > 60, n=37). Under 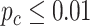 , we identified 205 genes showing circadian rhythmicity in young group and 164 genes in old group, with a total of 363 unique genes, and 6 common genes.
, we identified 205 genes showing circadian rhythmicity in young group and 164 genes in old group, with a total of 363 unique genes, and 6 common genes.
In terms of differential fit, we started with 363 candidate genes that showed circadian rhythmicity (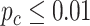 ) in either young or old. Comparing the old group to the young group (baseline group), LR_diff identified six genes showing differential fit (
) in either young or old. Comparing the old group to the young group (baseline group), LR_diff identified six genes showing differential fit (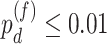 ). As shown in Figure 1d, MYO5A is the gene showing most differential fit (
). As shown in Figure 1d, MYO5A is the gene showing most differential fit (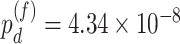 ), where there was circadian rhythmicity in the young group, but not in the old group. In terms of differential amplitude, differential phase and differential basal level, we started with six candidate genes that showed circadian rhythmicity (
), where there was circadian rhythmicity in the young group, but not in the old group. In terms of differential amplitude, differential phase and differential basal level, we started with six candidate genes that showed circadian rhythmicity (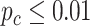 ) in both young and old groups. Comparing the old group to the young group (baseline group), our likelihood-based method identified one gene showing differential amplitude (
) in both young and old groups. Comparing the old group to the young group (baseline group), our likelihood-based method identified one gene showing differential amplitude (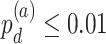 ), four genes showing differential phase (
), four genes showing differential phase (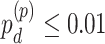 ) and two genes showing differential basal level (
) and two genes showing differential basal level (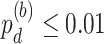 ). Figure 1A– 1C showed the most significant genes in terms of differential amplitude (CIART,
). Figure 1A– 1C showed the most significant genes in terms of differential amplitude (CIART, 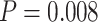 ), differential phase (PER2,
), differential phase (PER2, 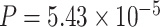 ) and basal level (TRIB2,
) and basal level (TRIB2, 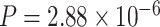 ) comparing young and old groups, respectively.
) comparing young and old groups, respectively.
Due to the small sample size and relatively weak transcriptomic alterations in brain tissues, the number of candidate genes for differential circadian analysis was small. Thus, we further relaxed the criteria to be 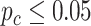 , and we identified 897 rhythmic genes in the young group and 846 rhythmic genes in the old group. In terms of differential fit, among 1688 genes that showed circadian rhythmicity (
, and we identified 897 rhythmic genes in the young group and 846 rhythmic genes in the old group. In terms of differential fit, among 1688 genes that showed circadian rhythmicity (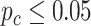 ) in either young or old group, LR_diff identified 345 genes showing gain or loss of rhythmicity. In terms of differential amplitude, differential phase and differential basal level, we started with 55 candidate genes that showed circadian rhythmicity (
) in either young or old group, LR_diff identified 345 genes showing gain or loss of rhythmicity. In terms of differential amplitude, differential phase and differential basal level, we started with 55 candidate genes that showed circadian rhythmicity (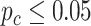 ) in both young and old groups. Comparing the old group to the young group (baseline group), LR_diff identified 2 genes showing differential amplitude, 23 genes showing differential phase and 19 genes showing differential basal level.
) in both young and old groups. Comparing the old group to the young group (baseline group), LR_diff identified 2 genes showing differential amplitude, 23 genes showing differential phase and 19 genes showing differential basal level.
Human time-restricted feeding data
We evaluated the performance of our likelihood-based methods in transcriptomic profiles of mouse skeletal muscle tissue. Eleven overweight or obese men were included in this dataset; the age range was 30–45 years; the body mass index range was 27–35 kg/m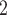 . These participants were randomized into time-restricted feeding (TRF) group and the un-restricted feeding (URF) group by adopting a cross over design, where each participant was assigned to both TRF and URF groups in different time periods. The skeletal muscle samples of each participant under each experimental group were repeatedly measured every 4 hours over 24 hours. There were some missing measurement, but each participant had 4
. These participants were randomized into time-restricted feeding (TRF) group and the un-restricted feeding (URF) group by adopting a cross over design, where each participant was assigned to both TRF and URF groups in different time periods. The skeletal muscle samples of each participant under each experimental group were repeatedly measured every 4 hours over 24 hours. There were some missing measurement, but each participant had 4  6 measurement, resulting in a total of 63 samples in restricted group and 62 samples in unrestricted group. Detailed description of this study has been previously published [24]. This RNA-seq dataset is publicly available in GEO (GSE129843). After filtering the genes with mean cpm less than 1, 13 167 gene probes remained for further analysis. We further performed log2 transformation (i.e.
6 measurement, resulting in a total of 63 samples in restricted group and 62 samples in unrestricted group. Detailed description of this study has been previously published [24]. This RNA-seq dataset is publicly available in GEO (GSE129843). After filtering the genes with mean cpm less than 1, 13 167 gene probes remained for further analysis. We further performed log2 transformation (i.e. 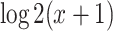 , where
, where 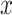 is the cpm of a gene in a sample) to improve the normality of the data.
is the cpm of a gene in a sample) to improve the normality of the data.
Circadian pattern detection
We first applied the LR_rhythmicity method to this time-restricted feeding dataset. Under 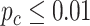 , we identified 1407 and 935 genes showing significant circadian rhythmicity for the restricted group and the unrestricted group, respectively. Figure S15 and S16 shows the six core circadian genes in the TRF group and the URF group, including PER1, PER2, PER3, ARNTL, NR1D1 and DBP, which are known to have persistent circadian rhythmicity. For these six circadian genes for the restricted group and the unrestricted group, our method (LR_rhythmicity) yielded highly significant
, we identified 1407 and 935 genes showing significant circadian rhythmicity for the restricted group and the unrestricted group, respectively. Figure S15 and S16 shows the six core circadian genes in the TRF group and the URF group, including PER1, PER2, PER3, ARNTL, NR1D1 and DBP, which are known to have persistent circadian rhythmicity. For these six circadian genes for the restricted group and the unrestricted group, our method (LR_rhythmicity) yielded highly significant 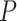 -values (
-values (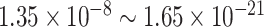 ), showing the strong detection power of circadian rhythmicity. The number of significant circadian genes using other methods is shown in Table S2. We further performed pathway enrichment analysis. Using
), showing the strong detection power of circadian rhythmicity. The number of significant circadian genes using other methods is shown in Table S2. We further performed pathway enrichment analysis. Using 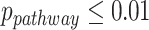 as cutoff, our likelihood methods detected 61 and 105 significant pathways for the TRF group and URF group, respectively. The top pathways enriched in both groups included circadian rhythm signaling pathway, prolactin signaling pathway and IGF-1 signaling pathway; both these pathways are related with circadian rhythmicity [6, 27].
as cutoff, our likelihood methods detected 61 and 105 significant pathways for the TRF group and URF group, respectively. The top pathways enriched in both groups included circadian rhythm signaling pathway, prolactin signaling pathway and IGF-1 signaling pathway; both these pathways are related with circadian rhythmicity [6, 27].
Differential circadian analysis
We further performed differential circadian analysis comparing TRF and URF groups using LR_diff. In terms of differential fit, we started with candidate genes that showed circadian rhythmicity (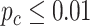 ) in either restricted or unrestricted (n=1864). Comparing the TRF group to the URF group (baseline group), LR_diff identified 57 genes showing differential fit (
) in either restricted or unrestricted (n=1864). Comparing the TRF group to the URF group (baseline group), LR_diff identified 57 genes showing differential fit (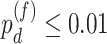 ). The most significant gene,
). The most significant gene, 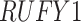 , is shown in Figure S17D, where there was a rhythmicity in the TRF group but not in the URF group.
, is shown in Figure S17D, where there was a rhythmicity in the TRF group but not in the URF group.
In terms of differential amplitude, differential phase and differential basal level, we started with candidate genes that showed circadian rhythmicity (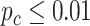 ) in both TRF and URF (n=478). Comparing TRF to URF, 11 genes showing differential amplitude (
) in both TRF and URF (n=478). Comparing TRF to URF, 11 genes showing differential amplitude (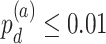 ), 25 genes showing differential phase
), 25 genes showing differential phase 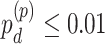 and 8 genes showing differential basal level
and 8 genes showing differential basal level 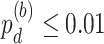 . Figure S17A–C showed the most significant genes for differential amplitude, phase and basal level comparing TRF and URF groups, respectively.
. Figure S17A–C showed the most significant genes for differential amplitude, phase and basal level comparing TRF and URF groups, respectively.
Mouse exercise data
We further evaluated the performance of our proposed methods in an RNA-seq gene expression profile generated from mouse skeletal muscle. A total of 69 mice samples were collected, which can be divided to the sedentary group and exercise group (acute treadmill exercise). Skeletal muscles were harvested after 0, 4, 8, 12, 16 and 20 hours after sedentary or exercise treatment. Detailed description of this study has been previously published [32]. This RNA-seq dataset is publicly available in GEO (GSE126962). With 11 461 gene probes after filtering, we performed log2 transformation [i.e. 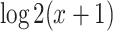 , where
, where 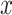 is the cpm of a gene in a sample] to improve the normality of the data.
is the cpm of a gene in a sample] to improve the normality of the data.
Circadian pattern detection
We first applied the LR_rhythmicity method to this mouse exercise dataset. Under 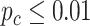 , we identified 621 and 752 genes showing significant circadian rhythmicity for the sedentary group and the exercise group, respectively. Figures S18 and S19 show the six core circadian genes in the sedentary group and the exercise group, including Per1, Per2, Per3, Arntl, Nr1d1 and Ddp, which are known to have persistent circadian rhythmicity. For these six circadian genes for the sedentary group and the exercise group, our method (LR_rhythmicity) obtained highly significant
, we identified 621 and 752 genes showing significant circadian rhythmicity for the sedentary group and the exercise group, respectively. Figures S18 and S19 show the six core circadian genes in the sedentary group and the exercise group, including Per1, Per2, Per3, Arntl, Nr1d1 and Ddp, which are known to have persistent circadian rhythmicity. For these six circadian genes for the sedentary group and the exercise group, our method (LR_rhythmicity) obtained highly significant  -values (
-values (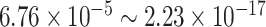 ), demonstrating the strong detection power of circadian rhythmicity. The number of significant circadian genes using other methods is shown in Table S2. Using
), demonstrating the strong detection power of circadian rhythmicity. The number of significant circadian genes using other methods is shown in Table S2. Using 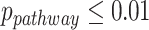 as cutoff, our likelihood methods detected 25 and 63 significant pathways for the sedentary group and exercise group, respectively. We further performed pathway enrichment analysis and found that the circadian rhythm signaling pathway is the top pathway for both the sedentary group and the exercise group. In addition, the NRF2-mediated oxidative stress response pathway was very significant in the exercise group (
as cutoff, our likelihood methods detected 25 and 63 significant pathways for the sedentary group and exercise group, respectively. We further performed pathway enrichment analysis and found that the circadian rhythm signaling pathway is the top pathway for both the sedentary group and the exercise group. In addition, the NRF2-mediated oxidative stress response pathway was very significant in the exercise group (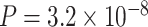 ), but much less significant in the sedentary group (
), but much less significant in the sedentary group (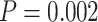 ). This is consistent with the literature that Nrf2 pathway plays important roles in mediating oxidative stress after acute exercise [8].
). This is consistent with the literature that Nrf2 pathway plays important roles in mediating oxidative stress after acute exercise [8].
Differential circadian analysis
We further performed differential circadian analysis comparing sedentary and exercise groups using LR_diff. In terms of differential fit, we started with candidate genes that showed circadian rhythmicity (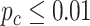 ) in either sedentary or exercise (n=1060). Comparing the exercise group to the sedentary group (baseline group), LR_diff identified 32 genes showing differential fit (
) in either sedentary or exercise (n=1060). Comparing the exercise group to the sedentary group (baseline group), LR_diff identified 32 genes showing differential fit (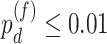 ). The most significant gene,
). The most significant gene,  , is shown in Figure S20D, where there was a rhythmicity in the exercise group but not in the sedentary group. In terms of differential amplitude, differential phase and differential basal level, we started with candidate genes that showed circadian rhythmicity (
, is shown in Figure S20D, where there was a rhythmicity in the exercise group but not in the sedentary group. In terms of differential amplitude, differential phase and differential basal level, we started with candidate genes that showed circadian rhythmicity (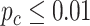 ) in both sedentary and exercise groups (n=313). Comparing the exercise group to the sedentary group, four genes showing differential amplitude (
) in both sedentary and exercise groups (n=313). Comparing the exercise group to the sedentary group, four genes showing differential amplitude (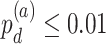 ), 10 genes showing differential phase
), 10 genes showing differential phase 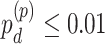 and 33 genes showing differential basal level
and 33 genes showing differential basal level 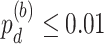 . Figure S20A–C showed the most significant genes for differential amplitude, phase and basal level comparing sedentary and exercise groups, respectively.
. Figure S20A–C showed the most significant genes for differential amplitude, phase and basal level comparing sedentary and exercise groups, respectively.
Mouse single-cell RNA Sequencing (scRNAseq) data
In mammals, the suprachiasmatic nucleaus (SCN) is considered as the master pacemaker to overarch prepheriphal circadian clocks. To examine circadian pattern at single cell level in SCN, we applied the LR_rhythmicity algorithm in a mouse SCN scRNAseq data. The scRNAseq data are publicly available under GSE117295, and detailed descriptions about these data were described elsewhere [42]. To be brief, mice were housed in a 12 hour light:dark cycle for 2 weeks, followed by 2 days constant darkness. During the constant darkness period, these mice were separately sacrificed at 12 circadian time points (CT14, CT18,... CT58). A total of 62 071 cells from all 12 mouse samples were pooled together for data analysis. After applying the following filtering procedures: (i) cells with less than 200 genes were removed; (ii) dead cells with less than 5% mitochondrial genes detection ratio were removed, 59 803 cells remained and were used for clustering analysis. The data were further normalized using the LogNormalize method with a scale factor 10,000. Top 2000 highly variable genes were identified using the vst method of the Seurat package [37], followed by principal component analysis. Cell clustering analysis was performed by using a graph-based local moving algorithm [41]. To visualize the clusters in a 2-dimensional plot, we performed dimension reduction via t-distributed stochastic neighbor embedding [40]. Eighteen clusters were identified, which were further merged into seven unique cell types (Figure S21) after comparing brain cell signature genes [42]. Number of cells for each cell type is shown in Figure S22A. For each of these seven cell types, we performed the LR_rhythmicity analysis to detect genes with circadian rhythmicity, respectively.
Circadian pattern detection
As shown in Figure S22B, under 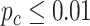 , neurons had the most number of circadian genes (n=4658), followed by oligodendrocytes (n=2219), ependymocytes (n=1431), astrocytes (n=1156), endothelials (n=1044), NG2_cells (n=760) and microglia (n=458). A total of 28 genes showed circadian rhythmicity pattern across all these seven cell types. Figure S23 shows the core circadian genes (Arntl, Dbp, Nr1d1, Per1, Per2 and Per3) by cell types. We found Dbp (
, neurons had the most number of circadian genes (n=4658), followed by oligodendrocytes (n=2219), ependymocytes (n=1431), astrocytes (n=1156), endothelials (n=1044), NG2_cells (n=760) and microglia (n=458). A total of 28 genes showed circadian rhythmicity pattern across all these seven cell types. Figure S23 shows the core circadian genes (Arntl, Dbp, Nr1d1, Per1, Per2 and Per3) by cell types. We found Dbp ( -values ranged from
-values ranged from 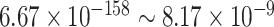 ) and Per3 (
) and Per3 (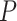 -values ranged from
-values ranged from 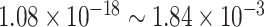 ) showed circadian rhythmicity in all seven cell types. Interestingly, Arntl showed circadian rhythmicity pattern in ependymocytes, endothelials, neurons and NG2_cells (
) showed circadian rhythmicity in all seven cell types. Interestingly, Arntl showed circadian rhythmicity pattern in ependymocytes, endothelials, neurons and NG2_cells (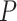 -values ranged from
-values ranged from 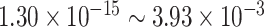 ), but not in astrocytes, microglia or oligodendrocytes (
), but not in astrocytes, microglia or oligodendrocytes (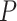 -values ranged from
-values ranged from  ), indicating a potential cell type specific circadian rhythmicity pattern for Arntl in mouse SCN.
), indicating a potential cell type specific circadian rhythmicity pattern for Arntl in mouse SCN.
Discussion
In summary, we developed a series of likelihood-based methods for detecting (i) circadian rhythmicity and (ii) differential circadian patterns. In terms of circadian rhythmicity detection, our method (LR_rhythmicity) could better control the type I error rate to its nominal level (i.e. produce an accurate  -values) than the other competing methods. In terms of differential circadian patterns, our likelihood-based method is the first parametric method to characterize four subcategories of differential circadian patterns, including differential amplitude, differential phase, differential basal level and differential fit. Simulation shows that our method (LR_diff) successfully controlled the type I error rate to the 5% nominal level for all four types of differential circadian patterns under the Gaussian assumption. In addition, LR_diff was more powerful than the competing methods in terms of differential fit. We also applied our methods in transcriptomic data applications including a human brain aging gene expression microarray data, a human time restricted feeding data, a mouse exercise RNA sequencing data, and a mouse SCN single cell RNA sequencing data. Superior performance has been observed in these applications.
-values) than the other competing methods. In terms of differential circadian patterns, our likelihood-based method is the first parametric method to characterize four subcategories of differential circadian patterns, including differential amplitude, differential phase, differential basal level and differential fit. Simulation shows that our method (LR_diff) successfully controlled the type I error rate to the 5% nominal level for all four types of differential circadian patterns under the Gaussian assumption. In addition, LR_diff was more powerful than the competing methods in terms of differential fit. We also applied our methods in transcriptomic data applications including a human brain aging gene expression microarray data, a human time restricted feeding data, a mouse exercise RNA sequencing data, and a mouse SCN single cell RNA sequencing data. Superior performance has been observed in these applications.
Our methods have the following strengths. (i) The type I error rates of both LR_rhythmicity and LR_diff were well controlled, indicating the  -values from these methods are accurate. While in the literature, it remained a concern about the type I error rate control for existing methods in terms of detecting circadian rhythmicity. (ii) Some methods require integer input circadian time, and even intervals between adjacent circadian time, while our methods have no such restrictions. Circadian time from modern epidemiology studies usually unevenly distributed between 0 hours and 24 hours. Thus, our method can be more applicable in biomedical applications. (iii) For examining differential fit, our method is statistically more powerful compared to other existing methods. (iv) LR_rhythmicity is robust against the violation of the Gaussian assumptions. As shown in our simulation, the severe violation of the Gaussian assumptions will only result in slightly smaller than expected type I error rate. We feel that being slightly conservative is not a bad thing because this won’t contribute false positive results.
-values from these methods are accurate. While in the literature, it remained a concern about the type I error rate control for existing methods in terms of detecting circadian rhythmicity. (ii) Some methods require integer input circadian time, and even intervals between adjacent circadian time, while our methods have no such restrictions. Circadian time from modern epidemiology studies usually unevenly distributed between 0 hours and 24 hours. Thus, our method can be more applicable in biomedical applications. (iii) For examining differential fit, our method is statistically more powerful compared to other existing methods. (iv) LR_rhythmicity is robust against the violation of the Gaussian assumptions. As shown in our simulation, the severe violation of the Gaussian assumptions will only result in slightly smaller than expected type I error rate. We feel that being slightly conservative is not a bad thing because this won’t contribute false positive results.
Our methods could potentially suffer from the following limitation. Our proposed methods are based on likelihood, which assume the residuals (i.e. 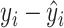 ) are normally distributed. The violation of the Gaussian assumptions may result in an inflated/deflated type I error rate for some of our methods. In this case, we would recommend users to check the normality assumptions of the residuals. If the residuals violated the Gaussian assumption, we would recommend data transformations (e.g. Box–Cox transformation) before applying our method. We have included a concrete example to show how to use the Box–Cox transformation to rescue the normality assumption in Supplementary Material Section 1.
) are normally distributed. The violation of the Gaussian assumptions may result in an inflated/deflated type I error rate for some of our methods. In this case, we would recommend users to check the normality assumptions of the residuals. If the residuals violated the Gaussian assumption, we would recommend data transformations (e.g. Box–Cox transformation) before applying our method. We have included a concrete example to show how to use the Box–Cox transformation to rescue the normality assumption in Supplementary Material Section 1.
We plan to do the following future works. (i) In epidemiology studies, many other biological factors (e.g. age, gender, etc.) could have a confounding impact on the circadian rhythmicity. Adjusting for covariates may potentially improve parameter estimations and biological interpretations. Our likelihood-based framework is capable of being extended to adjust for covariates. (ii) To the best of our knowledge, no circadian rhythmicity detection method could handle repeated measurement from the same individuals. For example, the time restricted feeding data example employed a cross-over design, and the 11 participants with each participant repeatedly measured four to six times. By extending our methods to model this within subject correlation, we would expect higher power to detect circadian rhythmicity and differential circadian patterns. An R package for our method is publicly available on GitHub https://github.com/diffCircadian/diffCircadian.
Key Points
Systematically evaluated the accuracy of
 -values in detecting circadian rhythmicity of our likelihood-based methods and other existing methods.
-values in detecting circadian rhythmicity of our likelihood-based methods and other existing methods.The first to propose likelihood-based methods to identify four subcategories of differential circadian patterns.
Systemically evaluated our likelihood-based methods in detecting differential circadian patterns, and compared with existing methods in terms of the correctness of
 -value and statistical power.
-value and statistical power.Implemented our proposed methods in R software package, which has been made publicly available on GitHub.
Supplementary Material
Acknowledgments
We thank the anonymous reviewers for their valuable suggestions.
Funding
H.D., L.M., K.E., Z.H. are supported by the National Institutes of Health grants R01HL153042 and R01AR079220; C.M. and G.T. are supported by the National Institutes of Health grant R01MH111601.
Haocheng Ding is a PhD candidate in the Department of Biostatistics at the University of Florida. His research interest includes developing statistical methodology for circadian analysis and differential circadian analysis.
Lingsong Meng is a PhD candidate in the Department of Biostatistics at the University of Florida. His research interest includes genomic applications in identifying circadian rhythmicity and differential circadian patterns.
Dr Andrew C. Liu is an Associate Professor in the Department of Physiology and Functional Genomics at the University of Florida College of Medicine. The major focus of his lab is to study the molecular, cellular and physiological mechanisms of circadian clocks in mammals.
Dr Michelle L. Gumz is an Associate Professor in the Division of Nephrology, Hypertension and Renal Transplantation in the Department of Medicine at the University of Florida. She is interested in the clinical implications of circadian rhythms in human health, particularly kidney function.
Dr Andrew J. Bryant is an Assistant Professor in the Division of Pulmonary, Critical Care and Sleep Medicine in the Department of Medicine at the University of Florida. He is interested in the role of circadian influence on leukocyte activation and involvement in pulmonary hypertension secondary to fibrosis or emphysema.
Dr Colleen A. McClung is a Professor of Psychiatry and Clinical and Translational Science at the University of Pittsburgh. She is interested in studying the association between circadian clock and various psychiatric disorders, including bipolar disorder, major depression and drug addiction.
Dr George C. Tseng is a Professor in the Department of Biostatistics at the University of Pittsburgh. His research group focuses on developing rigorous, timely and impactful methodologies in the area of genomics and bioinformatics, to help understand disease mechanisms and improve disease diagnosis and treatment.
Dr Karyn A. Esser is a Professor in the Department of Physiology and Functional Genomics at the University of Florida College of Medicine. Her lab focuses research on the role of circadian rhythms and the molecular clock mechanism in skeletal muscle homeostasis and health.
Dr Zhiguang Huo is an Assistant Professor in the Department of Biostatistics at the University of Florida. His research interest includes developing statistical and machine learning methodology for the broad field of genomics and bioinformatics.
Contributor Information
Haocheng Ding, Department of Biostatistics at the University of Florida, Gainesville, FL, 32608, USA.
Lingsong Meng, Department of Biostatistics at the University of Florida, Gainesville, FL, 32608, USA.
Andrew C Liu, Department of Physiology and Functional Genomics at the University of Florida College of Medicine, Gainesville, FL, 32608, USA.
Michelle L Gumz, Department of Medicine at the University of Florida, Gainesville, FL, 32608, USA.
Andrew J Bryant, Department of Medicine at the University of Florida, Gainesville, FL, 32608, USA.
Colleen A Mcclung, Psychiatry and Clinical and Translational Science at the University of Pittsburgh, Gainesville, FL, 32608, USA.
George C Tseng, Department of Biostatistics at the University of Pittsburgh, Gainesville, FL, 32608, USA.
Karyn A Esser, Department of Physiology and Functional Genomics at the University of Florida College of Medicine, Gainesville, FL, 32608, USA.
Zhiguang Huo, Department of Biostatistics at the University of Florida, Gainesville, FL, 32608, USA.
References
- 1. Badia P, Myers B, Boecker M, et al. Bright light effects on body temperature, alertness, EEG and behavior. Physiol Behav 1991; 50(3): 583–8. [DOI] [PubMed] [Google Scholar]
- 2. Box GEP, Cox DR. An analysis of transformations. J R Stat Soc B Methodol 1964; 26(2): 211–43. [Google Scholar]
- 3. Cagnacci A, Elliott JA, Yen SS. Melatonin: a major regulator of the circadian rhythm of core temperature in humans. J Clin Endocrinol Metabol 1992; 75(2): 447–52. [DOI] [PubMed] [Google Scholar]
- 4. Chen C-Y, Logan RW, Ma T, et al. Effects of aging on circadian patterns of gene expression in the human prefrontal cortex. Proc Natl Acad Sci 2016; 113(1): 206–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Cornelissen G. Cosinor-based rhythmometry. Theor Biol Med Model 2014; 11(1): 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Crosby P, Hamnett R, Putker M, et al. Insulin/igf-1 drives period synthesis to entrain circadian rhythms with feeding time. Cell 2019; 177(4): 896–909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Dijk D-J, Duffy JF, Czeisler CA. Circadian and sleep/wake dependent aspects of subjective alertness and cognitive performance. J Sleep Res 1992; 1(2): 112–7. [DOI] [PubMed] [Google Scholar]
- 8. Done AJ, Traustadóttir T. Nrf2 mediates redox adaptations to exercise. Redox Biol 2016; 10:191–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Elzhov TV, Mullen KM, Spiess A-N, et al. minpack.lm: R Interface to the Levenberg–Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds, 2016. R package version 1:2–1. [Google Scholar]
- 10. Glynn EF, Chen J, Mushegian AR. Detecting periodic patterns in unevenly spaced gene expression time series using Lomb–Scargle periodograms. Bioinformatics 2006; 22(3): 310–6. [DOI] [PubMed] [Google Scholar]
- 11. Hastings MH, Brancaccio M, Maywood ES. Circadian pacemaking in cells and circuits of the suprachiasmatic nucleus. J Neuroendocrinol 2014; 26(1): 2–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hodge BA, Wen Y, Riley LA, et al. The endogenous molecular clock orchestrates the temporal separation of substrate metabolism in skeletal muscle. Skelet Muscle 2015; 5(1): 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hsu PY, Harmer SL. Circadian phase has profound effects on differential expression analysis. PLoS One 2012; 7(11): e49853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Hughes ME, Abruzzi KC, Allada R, et al. Guidelines for genome-scale analysis of biological rhythms. J Biol Rhythms 2017; 32(5): 380–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hughes ME, DiTacchio L, Hayes KR, et al. Harmonics of circadian gene transcription in mammals. PLoS Genet 2009; 5(4): e1000442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hughes ME, Hogenesch JB, Kornacker K. Jtk_cycle: an efficient nonparametric algorithm for detecting rhythmic components in genome-scale data sets. J Biol Rhythms 2010; 25(5): 372–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Hughey JJ, Butte AJ. Differential phasing between circadian clocks in the brain and peripheral organs in humans. J Biol Rhythms 2016; 31(6): 588–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Hurley JM, Loros JJ, Dunlap JC. Circadian oscillators: around the transcription–translation feedback loop and on to output. Trends Biochem Sci 2016; 41(10): 834–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Jung CM, Khalsa SBS, Scheer FAJL, et al. Acute effects of bright light exposure on cortisol levels. J Biol Rhythms 2010; 25(3): 208–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kunieda T, Minamino T, Katsuno T, et al. Cellular senescence impairs circadian expression of clock genes in vitro and in vivo. Circ Res 2006; 98(4): 532–9. [DOI] [PubMed] [Google Scholar]
- 21. Laloum D, Robinson-Rechavi M. Methods detecting rhythmic gene expression are biologically relevant only for strong signal. PLoS Comput Biol 2020; 16(3): e1007666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Li JZ, Bunney BG, Meng F, et al. Circadian patterns of gene expression in the human brain and disruption in major depressive disorder. Proc Natl Acad Sci 2013; 110(24): 9950–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Lim ASP, Klein H-U, Yu L, et al. Diurnal and seasonal molecular rhythms in human neocortex and their relation to Alzheimer’s disease. Nat Commun 2017; 8(1): 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Lundell LS, Parr EB, Devlin BL, et al. Time-restricted feeding alters lipid and amino acid metabolite rhythmicity without perturbing clock gene expression. Nat Commun 2020; 11(1): 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Mei W, Jiang Z, Chen Y, et al. Genome-wide circadian rhythm detection methods: systematic evaluations and practical guidelines. Briefings in Bioinformatics. 2021; 22(3): bbaa135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Möller-Levet CS, Archer SN, Bucca G, et al. Effects of insufficient sleep on circadian rhythmicity and expression amplitude of the human blood transcriptome. Proc Natl Acad Sci 2013; 110(12): E1132–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Morris CJ, Aeschbach D, Scheer FAJL. Circadian system, sleep and endocrinology. Mol Cell Endocrinol 2012; 349(1): 91–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Parker T. Finite-sample distributions of the Wald, likelihood ratio, and Lagrange multiplier test statistics in the classical linear model. Commun Stat Theory Methods 2017; 46(11): 5195–202. [Google Scholar]
- 29. Parsons R, Parsons R, Garner N, et al. Circacompare: a method to estimate and statistically support differences in mesor, amplitude and phase, between circadian rhythms. Bioinformatics 2020; 36(4): 1208–12. [DOI] [PubMed] [Google Scholar]
- 30. Pelikan A, Herzel H, Kramer A, et al. Studies overestimate the extent of circadian rhythm reprogramming in response to dietary and genetic changes. bioRxiv, 2020. [Google Scholar]
- 31. Ruben MD, Wu G, Smith DF, et al. A database of tissue-specific rhythmically expressed human genes has potential applications in circadian medicine. Sci Transl Med 2018; 10(458). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Sato S, Basse AL, Schönke M, et al. Time of exercise specifies the impact on muscle metabolic pathways and systemic energy homeostasis. Cell Metab 2019; 30(1): 92–110. [DOI] [PubMed] [Google Scholar]
- 33. Seney ML, Cahill K, Enwright JF, et al. Diurnal rhythms in gene expression in the prefrontal cortex in schizophrenia. Nat Commun 2019; 10(1): 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Singer JM, Hughey JJ. Limorhyde: a flexible approach for differential analysis of rhythmic transcriptome data. J Biol Rhythms 2019; 34(1): 5–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Stenvers DJ, Jongejan A, Atiqi S, et al. Diurnal rhythms in the white adipose tissue transcriptome are disturbed in obese individuals with type 2 diabetes compared with lean control individuals. Diabetologia 2019; 62(4): 704–16. [DOI] [PubMed] [Google Scholar]
- 36. Straume M. DNA microarray time series analysis: automated statistical assessment of circadian rhythms in gene expression patterning. Methods in Enzymology 2004; 383: 149–66. [DOI] [PubMed] [Google Scholar]
- 37. Stuart T, Butler A, Hoffman P, et al. Comprehensive integration of single-cell data. Cell. 2019; 177(7): 1888–902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Thaben PF, Westermark PO. Detecting rhythms in time series with rain. J Biol Rhythms 2014; 29(6): 391–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Thaben PF, Westermark PO. Differential rhythmicity: detecting altered rhythmicity in biological data. Bioinformatics 2016; 32(18): 2800–8. [DOI] [PubMed] [Google Scholar]
- 40. van der Maaten L, Hinton G. Visualizing data using t-sne. J Mach Learn Res 2008; 9(86): 2579–605. [Google Scholar]
- 41. Waltman L, van Eck NJ. A smart local moving algorithm for large-scale modularity-based community detection.The European physical journal B. 2013; 86(1): 1–4. [Google Scholar]
- 42. Ma D, Zhao M, Xie L, et al. Spatiotemporal single-cell analysis of gene expression in the mouse suprachiasmatic nucleus. Nature neuroscience. 2020; 23(3): 456–67. [DOI] [PubMed] [Google Scholar]
- 43. Wu G, Anafi RC, Hughes ME, et al. Metacycle: an integrated r package to evaluate periodicity in large scale data. Bioinformatics 2016; 32(21): 3351–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Yang R, Zhen S. Analyzing circadian expression data by harmonic regression based on autoregressive spectral estimation. Bioinformatics 2010; 26(12): i168–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ypma J. Introduction to nloptr: an r interface to nlopt. R Package 2014; 2. [Google Scholar]
- 46. Zhang R, Lahens NF, Ballance HI, et al. A circadian gene expression atlas in mammals: implications for biology and medicine. Proc Natl Acad Sci 2014; 111(45): 16219–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


