Genome-wide hierarchical mixed model association analysis

Abstract

In genome-wide mixed model association analysis, we stratified the genomic mixed model into two hierarchies to estimate genomic breeding values (GBVs) using the genomic best linear unbiased prediction and statistically infer the association of GBVs with each SNP using the generalized least square. The hierarchical mixed model (Hi-LMM) can correct confounders effectively with polygenic effects as residuals for association tests, preventing potential false-negative errors produced with genome-wide rapid association using mixed model and regression or an efficient mixed-model association expedited (EMMAX). Meanwhile, the Hi-LMM performs the same statistical power as the exact mixed model association and the same computing efficiency as EMMAX. When the GBVs have been estimated precisely, the Hi-LMM can detect more quantitative trait nucleotides (QTNs) than existing methods. Especially under the Hi-LMM framework, joint association analysis can be made straightforward to improve the statistical power of detecting QTNs.

Introduction

In a genome-wide association study (GWAS), it is important to dissect the confounding biases caused by population structures and cryptic relatedness. Linear mixed models (LMMs) [1, 2] can separate true signals from a vast number of false signals caused by confounders, improving statistical power to detect quantitative trait nucleotides (QTNs). When applying an LMM to GWAS [3], the variance components or the polygenic effects in the LMM need to be estimated using a genome relationship matrix (GRM) [4], excluding the single nucleotide polymorphisms (SNPs) that are going to be tested, before the association tests are conducted. In spite of using all markers to estimate variance components or polygenic effects, without repeatedly calculating the GRMs for each SNP, LMMs are much more computationally intensive at nonlinearly solving different variance components among high-throughput SNPs.

In initial genome-wide mixed model association studies, variance components were generally estimated using the maximum likelihood or restricted maximum likelihood (REML) methods [5], which have been implemented in various numerical optimization algorithms [3]. To reduce computationally expensive matrix operations at each iteration, EMMA [6], GEMMA [7] and FaST-LMM [8] use a single eigendecomposition of a GRM to rotate data. BOLT-LMM [9] introduces the Monte Carlo REML method [10, 11] to estimate variance components that only require the solutions of LMM equations. The H-E regression [12, 13], another variance component method, can estimate polygenic and residual variances by linearly regressing the product of the phenotypes on the off-diagonal elements of the GRM in the most straightforward way [14]. Other than that, CMLM [15] and fastGWA [16] are more appropriate for accelerating the estimations of variance components in the stratified population or the population with sparse GRMs. As approximations of the mixed model association analysis, two popular simplified algorithms, such as EMMAX [17] or P3D [15] and GRAMMAR [18], attempt to replace different variance components and polygenic effects among candidate markers with the same variance components and genomic breeding values (GBVs), respectively, that were estimated under the null LMM, which greatly saves computing costs. In particular, GRAMMAR-Gamma [19] and BOLT-LMM [9] improve the statistical power used to detect QTNs by calibrating GRAMMAR.

If QTNs exist, over-estimation of polygenic variances and effects by genomic variances and GBVs may cause GRAMMAR and EMMAX to produce potential false-negative errors. In this study, we divide a genomic mixed model into two hierarchies: the LMM for the phenotypes of GBVs and the linear regression model of GBVs on the tested SNPs. Based on the resulting hierarchical mixed model, we first estimate GBVs using the genomic best linear unbiased prediction (GBLUP) method [4, 20] and then statistically infer the genetic effects of each SNP using the generalized least square (GLS) method, regarding the GBVs with GRMs as ‘phenotypes’. Especially in the linear regression model, the genetic effects for the tested SNPs were excluded from the polygenic effects or variance as the residuals to prevent the over-estimation of polygenic effects or variances by EMMAX and GRAMMAR. Computer simulations and real data analysis demonstrate the utility of the genome-wide hierarchical mixed model association analysis.

Method

Genomic mixed model

In general, LMMs for GWAS can be described as

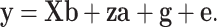(1)

where y is the justified phenotype of quantitative traits; b is the fixed effects such as ethnicity, sex and age; X is the corresponding design matrix to fixed effects b; a is the genetic effects of the tested SNP on the phenotype; z is the indicator variables of the SNP genotypes, which are generally coded as 0, 1 or 2 for the three genotypes AA, AB and BB, respectively; g is the polygenic effects, excluding the tested SNP and assumed to 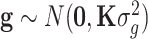, with 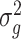being the polygenic variance and K being the GRM among individuals; e is the residual error and , with 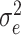being the residual variance and I being the identity matrix.

Statistical inference

According to genomic selection, we define GBVs as

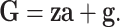(2)

Then, model (1) is divided into two hierarchies

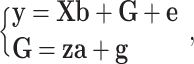(3)

Where, g is regarded as the residual for GBVs when testing an SNP.

In the first hierarchy of the mixed model, many methods can estimate the GBVs for genomic selection. Given genomic heritability, GBLUP is the most commonly used and the most efficient method for estimating GBVs [4, 20]. If only one SNP is tested at a time, then the model at the second hierarchy is a simple linear regression model, but with a residual variance–covariance structure due to GRM K among individuals. Therefore, the genetic effect of the tested SNP can be statistically inferred using the GLS method [21].

The genome-wide hierarchical mixed model association analysis, which can be abbreviated as Hi-LMM, is summarized in the following steps:

Firstly, we calculated the GRMs with all SNPs

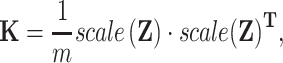(4)

where Z is the indicator variable matrix of all SNPs.

Secondly, we estimated the GBVs with GBLUP

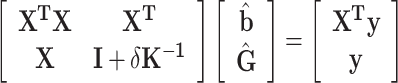(5)

with 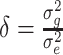being the ratio of the residual variance to the polygenic variance. Prior to solving equations (5), 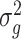and 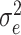need to be efficiently estimated with the spectrally transformed REML [17].

Thirdly, we estimated SNP effect with GLS

We decomposed 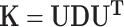, where D is diagonal matrix of eigenvalues and U eigenvector matrix, to spectrally transform , z and g to 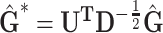, and 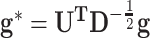, respectively. The model at the second hierarchy becomes

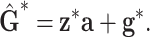(6)

Since 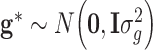, least square estimate for SNP effect is obtained

(7)

At the same times, .

Lastly, we statistically infer SNP effect by the Wald statistic

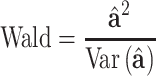(8)

which follows a Chi-square distribution with one degree of freedom under the null model.

Joint association analysis

Through one test at a time, many SNPs were chosen as QTN candidates at the significance level lower than the stringent Bonferroni corrected criterion [22], but for computing efficiency of variable selection, the number of QTN candidates should be limited to less than the population size. After obtaining the GBVs' estimates with the GBLUP, we jointly analyzed multiple QTN candidates to improve the statistical power to detect QTNs. Thus, we applied a backward regression approach to optimize the multiple linear model

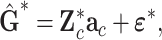(9)

where 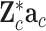are the regression terms of QTN candidates, as transformed in model (6). Given the Bonferroni corrected significance level for variable selection, the genetic effects were selected stepwise, and the corresponding QTNs were identified according to the test statistics (8) used in multiple regression analyses.

Based on the method mentioned above, the user-friendly Hi-LMM software with separate and joint association options was developed, which is freely available at https://github.com/RunKingProgram/Hi-LMM.

Simulations

We used the genomic datasets of humans [23] and maize [24] to simulate the adaptability of Hi-LMM to population structures. Of the two datasets, the maize population had a more complex structure than the human one. We extracted 300 000 SNPs for 3000 people and 2640 maize through higher quality control. The QTNs were distributed randomly over these SNPs. Their additive effects were drawn from a gamma distribution with shape = 1.66 and scale = 0.4 so that few QTNs have large effects and most have minor effects. Phenotypes were obtained by summing up the genotypic effects of all the simulated QTNs and their residual errors. When sampling residual errors from normal distributions with zero expectations, residual variance is regulated by the given genomic heritability of traits.

We simulated phenotypes controlled by 40, 200 and 1000 QTNs with varying levels of low (0.2), moderate (0.5) and high (0.8) heritabilities and drawn 10, 20, 30, 40, 50 and 60 K SNPs to calculate GRMs. Base on the simulated phenotypes, we investigated (i) the statistical property of Hi-LMM under different combinations of genomic heritability and the number of QTNs simulated; (ii) sensitivities to estimate genomic heritability or GBVs at the moderate heritability and (iii) the effects of the sampled markers on statistical powers at the moderate heritability. In all simulations, we compared Hi-LMM, a test at once, to FaST-LMM, EMMAX, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM. In the first simulation alone, the Hi-LMM with joint association analysis was made to improve statistical power.

Under good genomic control (very close to 1.0), the ROC profiles can be plotted with the statistical power to detect QTNs relative to a given series of Type I errors. Statistical power is defined as the percentage of identified QTNs with the maximum test statistic among their 20 closest neighbors over the total number of simulated QTNs. We repeated these simulations 50 times and recorded the average results. Note that there are different positions and effects for the QTNs in each repeated simulation.

Real data

We illustrate the performance of Hi-LMM by using the datasets of three species: (i) the Arabidopsis thaliana dataset included 216 130 SNPs and 107 phenotypes observed in 199 samples [25]; (ii) the mouse dataset had 1940 samples with 12 226 SNPs and 123 phenotypes [26]; (iii) the maize dataset included 2279 inbred lines with the 681 258 SNPs genotyped and the flowering time measured as days to silk [24].

Results

Statistical property of the Hi-LMM

We compared the Hi-LMM with FaST-LMM, EMMAX, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM in statistical property. Main features of the six competing mixed model association methods were summarized in Table 1. The association results were obtained with the five competing methods and the Hi-LMM, a test at once, which are displayed selectively in Figure 1 for Q-Q profiles and Figure 2 for ROC profiles (Supplementary Figure S1, see Supplementary Data available online at http://bib.oxfordjournals.org/, and Supplementary Figure S2 in detail, see Supplementary Data available online at http://bib.oxfordjournals.org/). At the same time, genomic control values were recorded in Supplementary Tables S1 and S2, see Supplementary Data available online at http://bib.oxfordjournals.org/. Under genomic controls very close to 1.0, Hi-LMM performed almost the same statistical power to detect QTNs as FaST-LMM and EMMAX, regardless of how many QTNs and heritabilities were simulated. However, with the null model that had no QTNs, both FaST-LMM and EMMAX yielded slightly higher negative false rates than Hi-LMM, and the false-negative rates increased with the complexity of population structures, especially for EMMAX. GRAMMAR had the lowest genomic controls and statistical power among the five competing methods, and it more strongly deflated test statistics in a more complex population structure. Although GRAMMAR-Gamma and BOLT-LMM genome-widely corrected the test statistics of GRAMMAR by their defined calibration factors [9, 19], GRAMMAR-Gamma slightly deflated the test statistics for complex population structure, which generated a genomic control of below 1.0, and BOLT-LMM strongly increased the false-positive rate due to overcorrecting test statistics.

Table 1.

Main features of the six competing mixed model association methods

Method	Estimates polygenic effects (time)	Association test method	Joint association analysis	Avoids proximal contamination	Potential statistical error
FaST-LMM	m	GLS	Not	Yes	No
EMMAX	1	GLS	Not	Not	FN
GRAMMAR	1	LS	Not	Not	FN
GRAMMAR-Gamma	1	LS	Not	Not	No
BOLT-LMM	m	LS	Yes	Yes	FP
Hi-LMM	1	GLS	Yes	Yes	No

m is number of markers, FN false negative, FP false positive and LS least square.

Figure 1.

Comparison of Hi-LMM with the five competing methods in the Q-Q profiles. The simulated phenotypes are controlled by 200 QTNs with the low, moderate and high heritabilities in human and maize. The Q-Q profiles for all simulated phenotypes are reported in Supplementary Figure S1, see Supplementary Data available online at http://bib.oxfordjournals.org/.

Figure 2.

Comparison of Hi-LMM with the five competing methods in the ROC profiles. The ROC profiles are plotted using the statistical powers to detect QTNs relative to the given series of Type I errors. Here, the simulated phenotypes are controlled by 200 QTNs with the low, moderate and high heritabilities in human and maize. The ROC profiles for all simulated phenotypes are reported in Supplementary Figure S2, see Supplementary Data available online at http://bib.oxfordjournals.org/.

Furthermore, Hi-LMM jointly analyzed multiple QTN candidates chosen from one association test at a time, given a significance level of 0.05. We depicted the statistical powers obtained with joint analyses and those with a test at once together for convenience to compare. Using backward regression analysis, Hi-LMM increased statistical power. In comparison, BOLT-LMM also significantly increased statistical power, but it did not control false-positive errors in detecting QTNs, especially for complex population structure.

Sensitivities to estimate genomic heritability or GBVs

In the competing methods, EMMAX estimates genomic heritability to replace polygenic heritabilities, whereas GRAMMAR, GRAMMAR-Gamma and BOLT-LMM estimate GBVs to replace polygenic effects. Similarly, Hi-LMM also estimates genomic heritability and GBVs to associate with markers. Therefore, what are the sensitivities of Hi-LMM, EMMAX, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM to estimate genomic heritability or GBVs?

Regarding the genomic heritability or GBVs simulated as polygenic estimates, we analyzed the simulated phenotypes with the five methods and the Hi-LMM, a test at once. As shown in Figure 3 and Supplementary Figure S3, see Supplementary Data available online at http://bib.oxfordjournals.org/, Hi-LMM, one test at a time could achieve more highest statistical power under the more ideal genomic controls than joint association analysis if genomic heritability or breeding values were completely accurately estimated. In contrast, EMMAX had somewhat decreased in both statistical power and genomic control. Additionally, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM did not find any QTNs from the residuals of GBLUP.

Figure 3.

Sensitivity of statistical powers to estimate heritabilities or GBVs for Hi-LMM. Statistical powers are dynamically evaluated with the ROC profiles. Both GRAMMAR-Gamma and BOLT-LMM do not detect any QTN with the simulated GBVs. The simulated phenotypes are controlled by 200 QTNs with the low, moderate and high heritabilities in human and maize.

Instead of GBLUP, we adopted a Lasso technique implemented in R/glmnet [27] to estimate GBVs rapidly. Through association tests of the Hi-LMM, were also drawn corresponding ROC and Q-Q profiles in Figure 3 and Supplementary Figure S3, see Supplementary Data available online at http://bib.oxfordjournals.org/, respectively. As could be seen, Hi-LMM achieved higher statistical power with the Lasso technique than GBLUP, and the tendency to improve the statistical power is consistent with that of the simulated GBVs. With selecting ridge estimation [28] in R/glmnet, we demonstrated that Hi-LMM also gained a statistical power as high as that GBLUP did. In conclusion, Hi-LMM could improve statistical powers by precisely estimating genomic heritability or breeding values, compared with EMMAX, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM.

Calculation of the GRM with the sampling markers

With GBLUP, estimation of genomic heritability and GBVs mainly depends on the density of markers used to calculate the GRMs in the structured population [4, 29]. To improve computing efficiency, FaST-LMM, GRAMMAR-Gamma and BOLT-LMM sampled or screened a small proportion of the whole genomic SNPs to estimate the GBVs or genomic heritability as precisely as possible. Based on this, we also try to simplify the computation of Hi-LMM by sampling markers.

Figure 4 shows that the changes in genomic controls Hi-LMMs and four competing methods made by a test at once with numbers of sampling markers. Similar to FaST-LMM, EMMAX and GRAMMAR-Gamma, Hi-LMM gradually controlled false-positive errors. The number of sampling markers increased and yielded high statistical power using all genomic markers. GRAMMAR seemed to calibrate false negative rates by under-estimating GBVs with fewer markers. In contrast, BOLT-LMM produced serious positive false errors caused by inflating test statistics, regardless of how many the markers were drawn. To retain the ideal genomic control and statistical power to detect QTNs (see Supplementary Figures S4 and S5, see Supplementary Data available online at http://bib.oxfordjournals.org/), Hi-LMM needed to draw no fewer than 40 000 markers to estimate GRMs in the simulation.

Figure 4.

Changes in genomic controls with the number of sampling SNPs for Hi-LMM and the five competing methods. Genomic control is calculated by averaging genome-wide test statistics. The simulated phenotypes are controlled by 40, 200 and 1000 QTNs with the moderate heritability in human and maize.

Real data analyses

Using previously published datasets on A. thaliana，mice and maize, we illustrated both genomic control and QTN mapping with Hi-LMM and compared our findings to those obtained using FaST-LMM GRAMMAR, GRAMMAR-Gamma and BOLT-LMM. Using a visual test for normality, we selected 32 phenotypes with less than 120 records for GWAS in A. thaliana and 109 phenotypes in mice. We did not record the computing times for these two datasets because either population size or the number of markers is enough to significantly differentiate these competing methods.

We depicted the Q-Q and Manhattan profiles for the traits of detectable QTNs in Supplementary Figure S6, see Supplementary Data available online at http://bib.oxfordjournals.org/, for A. thaliana, Supplementary Figure S7, see Supplementary Data available online at http://bib.oxfordjournals.org/, for mice and Supplementary Figure S8, see Supplementary Data available online at http://bib.oxfordjournals.org/, for maize for all competing methods, GRAMMAR, GRAMMAR-Gamma and BOLT-LMM achieved almost the same statistical properties as they did in the simulations. GRAMMAR detected several QTNs with strong false-negative errors. In contrast, with higher false-positive errors, BOLT-LMM found more QTNs than the other competing methods, but fewer QTNs than Hi-LMM did with joint analysis. Even though a test at once, Hi-LMM could identify more QTNs than GRAMMAR-Gamma. Using Hi-LMM with joint analyses, we found QTNs from 21 of 32 phenotypes in A. thaliana and 104 of 109 phenotypes in mice. With FaST-LMM, however, QTNs were not found for 1/21 and 51/104 of the traits in A. thaliana and mice, respectively. Under the ideal genomic control condition, Hi-LMM identified 19 and 94 more QTNs with joint analysis than exact FaST-LMM in A. thaliana and mice, respectively. Moreover, for phenotypes in mice, Hi-LMM could cover 94% of the QTNs obtained using FaST-LMM. In comparison, ~72% for the traits analyzed in A. thaliana, wherein FaST-LMM arose unstable genomic controls.

Finally, we applied the Hi-LMM to map the QTNs for flowering time and simultaneously executed the method using 50 000 SNPs randomly drawn from high-throughput markers. By a test at once, Hi-LMM detected 6 QTNs distributed on chromosomes 1, 2, 3, 8 and 10 and covered 3 of 4 QTNs on chromosomes 3, 8 and 10 detected using exact FaST-LMM. Furthermore, Hi-LMM found the same QTNs using sampling markers beside the two QTNs located on chromosomes 5 and 2 detected using entire genomic markers. Joint analysis can separate all signals that correspond to the QTN candidates generated from a test at once, which improves the statistical power to detect QTNs and the comparability by sampling markers. Upon inputting the genotypes and phenotypes to obtain QTN mapping outputs, Hi-LMM ran for 3.200 and 1.900 min in R software, respectively, for entire and sampling markers, respectively. In contrast, GRAMMAR and GRAMMAR-Gamma took 2.073 and 3.637 min, respectively. Additionally, FaST-LMM ran for 32.147 min in Single-Runking [30] and BOLT-LMM for 166.448 min in BOLT [9]. All data analyses were performed in a CentOS Linux server with 2.60 GHz Intel(R) Xeon(R) 40 CPUs E5–2660 v3, and 512 GB memory.

Discussion

With the GBVs that included the genotypic effects of all the candidate markers, we stratified the genomic mixed model into the mixed model of random GBVs and the generalized linear regression model of the correlated GBVs to the tested markers. In contrast to GRAMMAR and EMMAX, which overestimated polygenic effects and variances with GBVs and genomic heritability, respectively, the Hi-LMM best and unbiasedly estimated polygenic effects by regressing the GBVs on candidate markers in association tests. As a result, it can avoid potential false-negative errors and achieve statistical power as high as the exact mixed model association analysis. Theoretically, it has the same computational complexity as EMMAX because EMMAX also uses GLS for association tests.

To improve statistical power to detect QTNs for economic traits in plant and animal, peoples always replaced the phenotypic values with the estimated in advanced breeding values (EBVs) by pedigree or genomic markers. If the association of EBVs with candidate markers was statistically inferred using a simple linear regression model rather than a generalized regression model, it would produce higher false-positive rates than that for phenotypes, especially in breeding populations with complex structures (simulations not shown). Exact and simplified mixed model association analyses for EBVs not only repeatedly estimate the heritability and breeding values but also enhance computational complexity. Once the EBVs of traits have been provided before a GWAS, we recommend using the GLS method efficiently.

Under the assumption of minor polygenes, GBLUP is inappropriate to accurately estimate GBVs for quantitative traits controlled by less major genes. Meanwhile, it requires to estimate genomic heritability in advance, which increases computational complexity. For genomic selection, many methods, such as a series of Bayesian methods [31], can estimate GBVs by specifying various priors for markers effects without estimate genomic heritability. Our simulations demonstrate that the statistical power to detect QTNs can be significantly improved as long as the GBVs have been accurately estimated. Therefore, highly efficient genomic selection methods play a critical role in achieving the performance of the Hi-LMM.

With an increasing number of high-throughput SNP markers genotyped by deep resequencing, we can implement the GLS method at the second hierarchy of the Hi-LMM in a straightforward manner to finely map QTNs because the GBVs that obtained from previous GWAS in the same population are enough to ensure statistical power of the Hi-LMM. Once the GBVs for multiple correlated quantitative traits have been more accurately pre-estimated, the Hi-LMM can be easily extended to map pleiotropic QTNs within the framework of multivariate regression efficiently. For GWAS on dynamic quantitative traits, genomic random regression models can be divided into three hierarchies: random regression model with individuals' dynamic trajectories, the multivariate animal model for the parameters in dynamic trajectories, and generalized multivariate regression model for the GBVs of the parameters in dynamic trajectories, which would greatly improve computing efficiency. If the GBVs can be estimated once with a generalized LMM, then the Hi-LMM is highly suited for binary disease traits because of the resulting normal distributions of the GBVs.

Key Points

• Genomic mixed model is partitioned into two hierarchies, first, to estimate GBVs, and then associate GBVs with genetic markers.

• The Hi-LMM can effectively correct confounders with polygenic effects in association tests, preventing false-negative errors.

• The Hi-LMM performs the same statistical power as the exact mixed model association with the same computing complexity as EMMAX.

• Joint association analysis greatly improves statistical power to detect QTNs, using generalized least square of multiple QTN candidates.

Zhiyu Hao is a research assistant at the Research Centre for Aquatic biotechnology, Chinese Academy of Fishery Sciences. His research focuses on genome-wide association study.

Jin Gao is currently a PhD student at the Wuxi Fisheries College, Nanjing Agricultural University.

Yuxin Song is currently a PhD student at the Wuxi Fisheries College, Nanjing Agricultural University.

Runqing Yang is a Professor at the Research Centre for Aquatic biotechnology, Chinese Academy of Fishery Sciences. He is interested in developing statistical methodology of genome-wide association study.

Di Liu is a Professor at the Institute of Animal Husbandry, Heilongjiang Academy of Agricultural Sciences. Her research interests are animal breeding and genetics.

Data availability

The datasets can be available at http://archive.gramene.org/db/diversity/diversity_view for Arabidopsis thaliana, http://gscan.well.ox.ac.uk for mouse, https://www.panzea.org/%21#genotypes/cctl for maize, and http://www.wtccc.org.uk/ with authorization for human genomic data.

Funding

Special Scientific Research Funds for Central Non-profit Institutes, Chinese Academy of Fishery Sciences (2020C001); National Natural Science Foundations of China (32072726).