Detecting methylation quantitative trait loci using a methylation random field method

Abstract

DNA methylation may be regulated by genetic variants within a genomic region, referred to as methylation quantitative trait loci (mQTLs). The changes of methylation levels can further lead to alterations of gene expression, and influence the risk of various complex human diseases. Detecting mQTLs may provide insights into the underlying mechanism of how genotypic variations may influence the disease risk. In this article, we propose a methylation random field (MRF) method to detect mQTLs by testing the association between the methylation level of a CpG site and a set of genetic variants within a genomic region. The proposed MRF has two major advantages over existing approaches. First, it uses a beta distribution to characterize the bimodal and interval properties of the methylation trait at a CpG site. Second, it considers multiple common and rare genetic variants within a genomic region to identify mQTLs. Through simulations, we demonstrated that the MRF had improved power over other existing methods in detecting rare variants of relatively large effect, especially when the sample size is small. We further applied our method to a study of congenital heart defects with 83 cardiac tissue samples and identified two mQTL regions, MRPS10 and PSORS1C1, which were colocalized with expression QTL in cardiac tissue. In conclusion, the proposed MRF is a useful tool to identify novel mQTLs, especially for studies with limited sample sizes.

Introduction

The patterns of DNA methylation can be influenced by genetic variants within a region, referred to as methylation quantitative trait loci (mQTLs) [1, 2]. Many studies have suggested that a substantial proportion of CpG sites are associated with mQTLs, especially cis-acting mQTLs [3]. Further, mQTLs are enriched in promotor and enhancer regions and may colocalize with causal genetic variants for various complex diseases, such as neurological disorders [4, 5], metabolic syndrome [6, 7] and cardiovascular disease [3, 8]. These findings have provided a plausible basis to postulate an underlying biological pathway from genetic variations to epigenetic alterations and subsequent transcriptional changes for disease development. Detecting such mQTLs helps identify candidate loci contributing to disease susceptibility, and provides insights into the pathogenesis of disease development.

To date, the most commonly used statistical methods for mQTL detection are regression-based models [9–12], such as multiple regression or linear mixed models. However, the normality assumption of DNA methylation is often violated, which can lead to insufficient power or biased results. DNA methylation at a CpG site is usually measured by a beta value, a ratio between methylated signals (e.g. probe intensities or sequence reads) and the sum of methylated and unmethylated signals. Naturally, the methylation level ranges between 0% (unmethylated) and 100% (fully methylated), and its distribution tends to be bimodal, with two peaks representing hypomethylation and hypermethylation. In addition, the homoscedasticity assumption is often violated. For methylation trait, the variance of error near the boundaries of the interval [0,1] is usually much smaller than that in the middle. To address these issues, some have adopted a logit transformation of beta values [13, 14] or M values [15, 16]. Although this avoids the interval limit, the deviation from a normal distribution and heterogeneity of variance remains. The non-normal distribution may be less concerning for studies with a large sample size. However, DNA methylation is usually tissue specific, and it is quite common for a methylation study to have a relatively small sample size given the difficulty to collect certain tissues (e.g. heart, brain). A few studies have suggested that modeling methylation data with a beta distribution may be able to capture the bimodal shape and account for the heteroscedasticity [17–19].

Another limitation of existing studies for detecting mQTLs is their focus on individual loci, by testing the association between all possible SNP-CpG pairs one at a time. However, a cluster of closely linked variants may be responsible for the quantitative variation of a trait, and may be detected as one QTL [20]. Though many single nucleotide polymorphisms (SNPs) have been successfully identified as potential mQTLs [9–12], there are also a few limitations. First, a genomic region may have a large number of SNPs that are in strong linkage disequilibrium. Testing them individually imposes a heavy burden on statistical power due to multiple testing and computation. Second, multiple genetic variants may jointly contribute to complex traits with each variant conferring a small to moderate effect [21, 22]. The joint action of variants, including their interactions, may be overlooked if they are tested in isolation. Third, a large number of variants in the genome have very low minor allele frequencies (MAFs), and these rare variants may also influence complex human traits [23, 24]. The single-locus testing usually lacks the power to detect these rare variants, especially when the sample size is small.

We and others have recently proposed a generalized genetic random filed (GGRF) method for testing the association between multiple genetic variants and a single complex trait [25, 26]. In particular, the GGRF can be applied to population-based studies with unrelated subjects, testing the association between a set of SNPs and a trait that follows either a normal or binomial distribution. In this article, we extend the GGRF method to a methylation random field (MRF) for traits that follow a beta distribution, in order to detect multi-locus mQTLs that regulate the methylation level of a CpG site. We compared the performance of the MRF with other existing methods, and further illustrated the method with an application to 83 cardiac tissue samples for a study of congenital heart defects (CHDs).

Materials and methods

MRF framework

Random field is a stochastic process defined in a multidimensional space indexed by a location vector [27]. It has been widely used in spatial statistics. Under the current MRF framework, the methylation trait of a CpG site can be viewed as a random field on a genetic space where the multi-locus genotypes serve as location coordinates. If there is a genetic-epigenetic association, genotype similarity will lead to closer spatial location, suggesting epigenetic similarity. The random field modeling enables MRF to be a dimension-reduction method that allows potential interactions and linkage disequilibrium between multiple genetic variants [25] to test the joint association of multi-locus genotypes with a methylation trait.

Assume we have a study of n subjects sequenced for q genetic variants in a genomic region and measured for p covariates. We denote 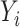as the methylation level of a CpG site for the i-th subject , 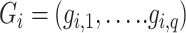as the genotype vector for q variants, and 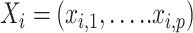as the covariates. A conditional auto-regressive model is used for the DNA methylation levels:

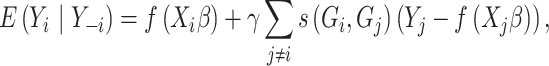(1)

where represents the methylation levels for all subjects but 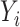. To model DNA methylation with a beta distribution, a beta regression with logit link is used so that 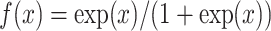is the nongenetic mean of methylation level based on covariates. 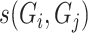denotes the genetic similarity between subject i and j, and is measured by a genetic relation (GR) [28]: , where is the average MAF within the study population, is a weighting scheme to give flexible considerations to each SNP and is a coefficient to measure the association between the methylation level and q genetic variants. Intuitively, Eq.(1) assumes that if there is a genetic-epigenetic association, subjects with similar genetic profiles will share similar epigenetic profiles, and the epigenetic similarity between subjects is proportional to their genetic similarity after adjusting for effects from covariates. The genetic-epigenetic association can thus be tested against the null hypothesis.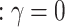

Generalized estimating equation (GEE)-based statistics were adopted for hypothesis testing. Eq.(1) can be written in matrix representation:

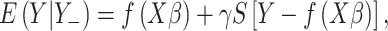(2)

where 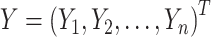, , , 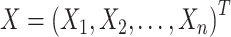and S is a symmetric matrix denoting the genetic similarity. The methylation trait is assumed to follow a beta distribution with mean 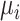and a precision parameter , which can be estimated by fitting a beta regression between and under the null hypothesis. A logit link was used in the beta regression so that 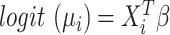. We showed previously that a quadratic test statistic, 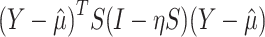, follows an asymptotic Chi-square distribution of 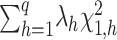, where 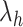are the eigenvalues of the matrix , , and is a diagonal matrix with . The precision parameter, 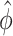, was estimated via beta regression [29]. The R codes for the proposed method are available at https://github.com/chenlyu2656/MRF.

Simulation studies

To evaluate the performance of the MRF, we compared it to a number of existing methods—including the burden test, the sequence kernel association test (SKAT) and the single-locus test—using a series of simulation studies. To mimic real genetic data, we used exome-sequencing data of 697 unrelated individuals from the 1000 Genomes Project [30]. The genotype data included a total of 508 variants from chromosome 22 with MAFs ranging from 0.07 to 49.93%. Around 74% of the variants were less common or rare, with MAFs less than 0.05. To capture the bimodal and interval properties, the methylation trait was simulated based on a beta distribution 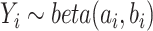. Two shape parameters and were associated with a mean parameter 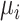and a precision parameter such that and . The precision parameter was a nuisance parameter and was set to 30 as suggested by previous studies [31], and the mean parameter 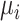varied across simulation scenarios (described below). To evaluate type I error, the mean parameter was simulated independently from genetic variants. To evaluate statistical power, the mean parameter was determined by both genetic and nongenetic components, representing scenarios with varying patterns of effect sizes for causal variants (mQTL SNPs), directions of effect for mQTL SNPs, frequencies of variants being tested, sample sizes, proportions of variants that are mQTLs and modeling of trait distribution in the analysis. The detailed explanations are illustrated in Table 1.

While testing the genetic-epigenetic association, existing studies have a number of commonly used analysis strategies, including (1) a linear regression for beta values; (2) a beta regression for beta values; and (3) a linear regression for M-values (i.e. logit transformed beta values). These strategies implicitly assumed different distributions of a methylation trait. In the simulation, we evaluated the performance of each method (MRF, burden or the single-locus test) using three analysis strategies, including (1) an identity link for methylation trait assuming a normal distribution; (2) a logit link for methylation trait assuming a beta distribution; and (3) an identity link for logit transformed methylation trait assuming a normal distribution after transformation. In the following text, we denoted three strategies as ‘normal’, ‘beta’ and ‘logit’, respectively. Because beta regression is not implemented in SKAT, only ‘normal’ and ‘logit’ were applied. For fair comparisons, linear kernel was used for SKAT and the genetic variants were weighted by their MAFs via the beta distribution density function, Beta(MAF, 1, 25), to upweight rare variants. For the single-locus test, Benjamin–Hochberg false discovery rate was applied to account for the multiple testing within a region.

Type I errors

Based on real data from the cardiac tissue samples, the distribution of DNA methylation was bimodal, with two peaks around 0.1 and 0.9, representing hypo-methylation or hyper-methylation, respectively (Figure 1). Thus, to examine type I errors, we simulated the methylation trait independently from the genetic data, assuming an expected mean . The methylation trait thus followed a beta distribution . Type I errors were evaluated under various sample sizes (n = 50, 100, 300 and 697) and a total of 100, 000 replicates were simulated.

Figure 1.

Density plot of DNA methylation across 83 samples in application study.

Table 1.

Simulation scenario explanations

Simulation scenarios	Descriptions
Effect size
WSS	Effect sizes were inversely correlated with the MAFs of mQTL SNPs: .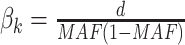
Constant	Effect sizes were the same for all mQTL SNPs: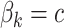
Effect direction
One-directional	The mQTL SNPs were simulated to upregulate the methylation traits
Bidirectional	The mQTL SNPs were simulated to either upregulate or downregulate the methylation traits
Genetic frequency to test
Mixed	The simulated methylation traits were tested for association with a mixture of both common and rare variants
Rare	The simulated methylation traits were tested for association with rare variant only
Sample size
n = 50	50 subjects were randomly sampled
n = 100	100 subjects were randomly sampled
n = 300	300 subjects were randomly sampled
n = 697	All 697 subjects were sampled
Proportion of mQTL SNPs
10%	10% of genetic variants within the region were simulated as causal mQTL SNPs
20%	20% of genetic variants within the region were simulated as causal mQTL SNPs
Strategy to model methylation traits
Normal	Using a linear regression with identity link for methylation traits assuming normal distribution
Beta	Using a beta regression with logit link for methylation traits assuming beta distribution
Logit	Using a linear regression with identity link for logit-transformed traits assuming normal distribution after logit-transformation

Statistical power

To evaluate the statistical power of the four methods, we conducted three sets of simulation that varied by effect sizes for causal variants (mQTL SNPs), directions of effect for mQTL SNPs and frequencies of variants being tested. In all simulation scenarios, we also varied the proportion of mQTL SNPs (10% or 20%) and sample size of the study (n = 50, 100, 300 and 697). A total of 1000 replicates were performed for power calculation.

Simulation I: varying effect sizes for mQTL SNPs.

In this simulation scenario, we evaluated the performance of MRF, burden test and SKAT. The single-locus test was not considered because of its inflated type I errors. For simplicity, we illustrated the scenario assuming that 10% of 508 SNPs were mQTLs. A total of 51 SNPs were randomly selected as mQTLs regulating the methylation trait. The mean parameter 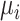for the i-th subject was simulated based on the following model:

where 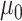corresponds to the expected methylation level when none of the variants are causal, and 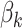is the effect size for the k-th mQTL SNP within the region. In the current study, we set 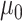to 0.1 as described in type I error section. We considered two patterns of effect sizes in our simulation: (1) effect sizes were the same for all mQTL SNPs: 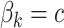; and (2) effect sizes were inversely correlated with the MAFs of mQTL SNPs. The weighted sum statistics (WSS) was used, and 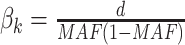. Here, 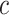and were fixed constants, and selected to ensure that the statistical power was within a reasonable range.

Simulation II: bidirectional effect for mQTL SNPs

In this simulation setting, we evaluated the performance of MRF, burden test and SKAT when mQTL SNPs had bidirectional effect on methylation trait (i.e. either upregulate or downregulate). In simulation I, all causal SNPs were expected to upregulate methylation trait. For bidirectional scenario, we used the same effect sizes as described in simulation I, but randomly selected half of the mQTL SNPs to downregulate methylation trait (i.e. a negative sign was assigned to their effect ).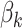

Simulation III: common variants only

In contrast to a mixture of common and rare variants in simulation I & II, in this simulation, we evaluated the performance of all methods when the genetic variants being tested were all relatively common variants with MAF ≥ 5%. We assumed the effects of mQTL SNPs were a constant and may be either one-directional or bidirectional.

Application to cardiac tissue samples

We further applied MRF, burden test and SKAT for cis-acting mQTLs detection within 83 cardiac tissues samples from a study of CHDs. Each subject was genotyped for ~5 million SNPs using Illumina HumanOmni5 Beadchip and profiled for ~450 K or ~ 850 K CpG sites using Illumina HumanMethylation450 Beadchip or Illumina MethylationEPIC Beadchip, respectively. SNPs were removed if they had a low call rate (< 95%), or deviated from Hardy–Weinberg Equilibrium among controls (P-value <10e-04). About half of the SNPs were relatively rare, with MAFs less than 5% and as low as 0.6%. CpG sites were removed if they had more than 5% missing values, had an SNP in the probe, or did not overlap between two methylation platforms. More details of the dataset and quality control process can be found elsewhere [32].

To detect cis-acting mQTLs, we applied MRF, burden test and SKAT to evaluate the genetic-epigenetic association within the same genomic region. The single-locus test was not considered because of the inflated type I errors with rare variants. We used the UCSC Genome Browser (assembly GRCh37/hg19) to define a candidate region as a gene unit with 7.5 KB upstream and downstream sequences. Within each candidate region, the methylation level of each CpG site was tested for association with all SNPs within the region, adjusting for sex, case control status, top five principal components (PCs) of genetic data and top five PCs of epigenetics data. Similar to simulation studies, we applied three analysis strategies (‘normal’, ‘beta’, ‘logit’) for MRF and burden test, and two strategies (‘normal’ and ‘logit’) for SKAT. Within 21,450 candidate genes, a total of 275,357 CpG-gene pairs were tested for association. Bonferroni correction was used for multiple testing adjustment.

Bayesian colocalization analysis

Previous studies have suggested that mQTLs may colocalize with causal variants of complex diseases [33] or gene expression QTLs (eQTLs) [13]. We further conducted a Bayesian colocalization analysis to leverage results from existing CHD GWASs or eQTLs [34]. For example, the colocalization analysis of mQTL and eQTL data estimates five posterior probabilities (PP0–PP4) for five respective hypotheses regarding a candidate region: H0: no association with either methylation trait or expression trait; H1: association with methylation trait, but not with expression trait; H2: association with expression trait, but not with methylation trait; H3: association with both methylation trait and expression trait through two independent SNPs; and H4: association with methylation trait and expression trait through one shared SNP. To prioritize findings with independent source of evidence, we were most interested in identifying regions with high values of PP4.

We conducted colocalization analysis between mQTL results and other data sources, including findings from two phases of CHD GWASs from the National Birth Defects Prevention Studies (NBDPS) and eQTL findings within heart tissues from the Genotype-Tissue Expression (GTEx) database [35]. NBDPS is the largest population-based case–control study of birth defects in the United States. Both phases of CHD GWASs had a case-parental trio design, and consisted of 440 and 225 trios, respectively. The eQTL findings were identified from five types of heart tissues, including artery aorta (AA), artery coronary (AC), artery tibial (AT), heart atrial appendage (HA) and heart left ventricle (HLV). For colocalization analysis, we only considered overlapping SNPs between mQTLs and each of the other data sources (i.e. GWASs and eQTLs). R package ‘coloc’ was used for analysis [34].

Results

Simulation studies

Type I errors

The results of type I errors are summarized in Figure 2. In Figure 2A, the type I errors for MRF and burden test were well controlled at an α level of 5%. However, the type I errors of SKAT appeared to be overly conservative when the sample size was small (n = 50 and 100). In addition, the single-locus test was able to successfully control type I errors when common variants (MAF > 0.05) were tested and sample size was relatively large (n = 300 or 697), but had inflated type I errors when rare variants were tested. When the sample size was relatively small (n = 50 or 100), linear regression with methylation level (i.e. ‘normal’) or logit transformed methylation level (i.e. ‘logit’) was able to control type I error for common variants, while beta regression (i.e. ‘beta’) had slightly inflated type I error. Similar pattern was seen at α level of 0.1% (Figure 2B). The results of the single-locus test were not shown due to the significant inflations (between 0.013 and 0.083).

Figure 2.

Type I error rates of MRF, burden tests, SKAT and the single-locus test in simulation study at α level of (A) 5%; or (B) 0.1%. The results of the single-locus test were not shown in Figure 2B due to the significant inflations (P-values ranged from 0.013 to 0.083).

Statistical power

Simulation I: varying effect sizes for mQTL SNPs

Simulation I corresponded to disease scenarios of mQTL SNPs affecting methylation trait in one direction with either WSS (Figure 3A) or constant effect size (Figure 3B). The methylation trait was tested for association with a mixture of common and rare variants. In Figure 3A, burden test outperformed all the other methods when all mQTL SNPs impacted the methylation trait in one direction, and rare variants contributed to relatively large effect. However, if the effect size was constant, SKAT performed better compared to MRF and burden test (Figure 3B). The pattern of statistical power for each method was similar when 10% or 20% of mQTL SNPs were causal.

Figure 3.

Power results from simulation I: mQTL SNPs affected the methylation trait in one direction with either (A) WSS effect size, or (B) constant effect size. The methylation trait was tested for association with a mixture of common and rare variants.

In terms of three analysis strategies (i.e. ‘normal’, ‘beta’ or ‘logit’), the performance varied across methods and causal mechanisms. When rare variants contributed to relatively large effect (Figure 3A), for MRF, the ‘beta’ strategy achieved the higher power, especially when sample size was small; for burden test, all strategies had similar performance; and for SKAT, the ‘normal’ appeared to work slightly better with small sample size (n = 50 or 100), while ‘logit’ was more advantageous with larger sample size (n ≥ 300). Nevertheless, when the effect size was constant (Figure 3B), for MRF and burden test, the ‘beta’ strategy achieved higher power for small sample size (n = 50 or 100), while ‘logit’ strategy performed slightly better for larger sample size (n ≥ 300); and for SKAT, ‘logit’ strategy had relatively higher power for all sample sizes.

Simulation II: bidirectional effect for mQTL SNPs

Simulation II corresponded to disease scenarios of mQTL SNPs of bidirectional effect with either WSS (Figure 4A) or constant effect size (Figure 4B). The methylation trait was also tested for association with a mixture of common and rare variants. When half of the mQTL SNPs influenced the methylation trait in opposite directions, burden test lost power significantly (Figure 4A & B). MRF attained highest power when rare variants had larger effect sizes (Figure 4A), while SKAT consistently yielded the highest power when all mQTL SNPs had same effect sizes (Figure 4B).

Figure 4.

Power results from simulation II: mQTL SNPs affected the methylation trait in bi-directions with either (A) WSS effect size, or (B) constant effect size. The methylation trait was tested for association with a mixture of common and rare variants.

The differences between three analysis strategies under bidirectional scenario were less evident than those under one direction scenario. When the effect size was in favor of rare variants (Figure 4A), MRF achieved highest power by using ‘beta’ strategy, and SKAT showed very similar performance by using either ‘normal’ or ‘logit’ strategy. In contrast, when the effect size was a constant (Figure 4B), for both MRF and SKAT, ‘normal’ or ‘beta’ strategy performed slightly better than ‘logit’ strategy when sample size was small (n = 50 or 100), while ‘logit’ strategy was better for larger sample (n ≥ 300).

Simulation III: common variants only

Simulation III corresponded to scenarios of mQTL SNPs with constant effect size influencing methylation trait in either one direction (Figure 5A) or two directions (Figure 5B). The trait was tested for association with common variants only. In general, the single-locus test had the highest power when sample size was small (e.g. n = 50 or 100), and the proportion of causal variants was relatively low (e.g. 10%). However, when the sample size and/or causal proportion increased, region-based tests, such as MRF and SKAT, outperformed the single-locus test. Although the single-locus test assuming beta distribution may achieve highest power than other methods when the sample size was relatively small (n = 50 and 100), inflated type I error made the results less reliable. Among region-based tests, MRF and SKAT showed similar power across all scenarios, both of which were significantly higher than that of burden test, especially when the effect was bidirectional.

Figure 5.

Power results from simulation III: the methylation trait was tested for association with common variants only. The mQTL SNPs affected the methylation trait with constant effect size, affecting the methylation trait in either (A) one direction, or (B) bi-direction.

Simulation summary

From our simulation results, MRF outperformed other methods if mQTL SNPs were mostly rare variants with relatively large and bidirectional effect. It was also a viable option to detect CpG-gene association for common variants, especially when sample size is relatively large and the proportion of causal variants in the gene is relatively high.

The single-locus test is able to detect mQTL SNPs that are common in the population. However, the single-locus test is not appropriate for detecting rare mQTL SNPs because of the inflated type I errors. If the candidate region includes a mixture of common and rare variants, region-based tests appear to be better options. Among region-based tests, burden test showed highest power when mQTL SNPs affected the methylation trait in one direction and rare variants contributed to relatively large effect. However, burden test lost power significantly under the bidirectional scenario. On the other hand, SKAT had more advantages when common variants and rare variants have similar bidirectional effect.

Among the three commonly used analysis strategies related to the distributions of methylation traits, ‘beta’ strategy usually achieves greater power for small sample size (n = 50 or 100), while ‘logit’ strategy often performs better with relatively large sample (n ≥ 300).

Application to cardiac tissue samples

We further illustrated the proposed MRF with an application to 83 cardiac tissue samples for cis-mQTLs detection. A total of 275,357 CpG-gene pairs were tested by evaluating the association between each CpG site and a set of SNPs within the same genomic region. We considered all three analysis strategies (i.e. ‘normal’, ‘beta’ or ‘logit’). Based on our simulation results and the aim of our study (i.e. n = 83, a mixture of common and rare variants), we have prioritized our finding by using MRF with the ‘beta’ strategy.

A total of 97 significant CpG-gene associations were identified after multiple testing adjustment. The full results are shown in Supplemental Table 1, including 90 distinct genes as potential mQTL regions. Among these 90 regions, a total of 74 and 44 harbored nominally significant SNPs in one or both phases of the CHD GWASs, respectively. In Table 2, we summarized the top 10 mQTL findings among those 44 regions. These regions consisted of 75 to 929 SNPs, including both common and rare variants, that might jointly affect the methylation level of a CpG site. Three of these regions were located on chromosome 6. One CpG-gene pair, cg09655876 and AGPAT4, also achieved statistical significance by applying SKAT with the ‘normal’ strategy.

Table 2.

Top 10 significant CpG – gene associations identified by MRF with beta strategy and nominal significant loci in CHD GWAS^*

CpG site	Chr	Region	Gene	# SNPs in Region	# of sig. SNPs in CHD GWAS1	# of sig SNPs in CHD GWAS2	Method	Beta	Normal	Logit
cg20048260	chr13	110,793,804–110,967,004	COL4A1	448	3	15	MRF	9.28*10−11	1.00*10−7	1.00*10−7
							SKAT	-	0.032	0.045
							Burden	0.502	0.400	0.447
cg26160889	chr17	27,710,442–27,886,421	TAOK1	115	17	15	MRF	1.86*10−10	1.03*10−6	6.77*10−6
							SKAT	-	0.367	0.332
							Burden	0.280	0.403	0.278
cg01108872	chr6	166,815,351–167,283,539	RPS6KA2/MIR1913	929	46	9	MRF	3.24*10−10	3.39*10−9	7.73*10−9
							SKAT	-	6.45*10−4	1.30*10−3
							Burden	0.966	0.998	0.978
cg04248373	chr10	97,064,029–97,328,677	SORBS1	452	9	3	MRF	4.67*10−10	9.05*10−9	1.62*10−7
							SKAT	-	0.444	0.433
							Burden	0.985	0.829	0.941
cg14498674	chr1	41,485,370–41,715,315	SCMH1	170	8	2	MRF	5.69*10−10	3.76*10−9	3.72*10−7
							SKAT	-	0.221	0.345
							Burden	0.905	0.868	0.786
cg08610326	chr8	141,522,749–141,653,145	AGO2	201	5	6	MRF	6.12*10−10	5.13*10−8	4.84*10−6
							SKAT	-	0.378	0.328
							Burden	0.664	0.575	0.974
cg26834192	chr6	161,543,556–161,702,607	AGPAT4	294	36	40	MRF	7.19*10−10	5.56*10−10	3.83*10−9
							SKAT	-	2.27*10−7	5.18*10−7
							Burden	0.353	0.335	0.384
cg09655876	chr6	161,543,556–161,702,607	AGPAT4	294	36	40	MRF	8.93*10−10	2.46*10−10	2.96*10−10
							SKAT	-	1.45*10−7	2.32*10−7
							Burden	0.550	0.395	0.375
cg11456854	chr2	43,450,474–43,830,685	THADA	405	2	9	MRF	9.58*10−10	3.92*10−9	9.23*10−7
							SKAT	-	0.039	0.028
							Burden	0.290	0.330	0.281
cg15037420	chr19	48,463,802–48,502,927	BSPH1	75	2	1	MRF	1.07*10−9	4.68*10−9	4.72*10−8
							SKAT	-	0.340	0.477
							Burden	0.016	0.040	0.018

^*logit transform represents M values here since M values are proportional to the logit transformation of beta values

Bayesian colocalization

We further conducted colocalization analysis to leverage results from CHD GWASs and expression QTLs, evaluating whether the mQTL findings share the same causal loci with previous studies. The full colocalization results for 97 mQTL associations were summarized in Supplemental Table 2. None of these regions achieved the commonly used threshold of 0.8 for PP4, which may largely due to the limited samples size of the CHD GWAS and unavailable summary statistics of eQTLs. Among the 97 mQTL regions, two genes (i.e. MRPS10 and PSORS1C1) located on chromosome 6 achieved relatively high PP4 values (PP4 > 0.6) for potential colocalization in artery tibial (Table 3). In addition, gene PSORS1C1 was overlapped with nominal significant loci of both phases of the CHD GWASs. For the rest of 95 mQTL regions, none of them showed high PP4 values for colocalization with CHD GWAS or eQTLs. Such results are not surprising since both GWAS and existing eQTLs adopt the single-locus testing strategy and are limited to identify common variants with large effects, while our MRF is a region-based analysis that is better at detecting rare variants of relatively large effect and common variants with moderate or even small effects.

Table 3.

mQTL regions colocalized with expression QTLs in heart tissues with threshold of PP4 > 0.6

Chr	Regions	Gene	Source for colocalization	PP0	PP1	PP2	PP3	PP4	MRF.beta P-value	# of nominal significant SNPs in CHD GWAS1	# of nominal significant SNPs in CHD GWAS2
chr6	42,167,038–42,193,133	 MRPS10	mQTL - Artery Tibial	1.101*10−2	0.279	1.398*10−3	0	0.708	1.288*10−7	0	0
chr6	31,075,107–31,115,369	 PSORS1C1	mQTL - Artery Tibial	6.296*10−4	0.288	1.481*10−4	3.387*10−2	0.677	1.658*10−9	10	1

We also evaluated the genomic regions which were not detected by MRF and tested for their colocalization with CHD GWASs and expression QTLs in cardiac tissues. The significant results are summarized in Supplemental Table 3. Seven distinct genomic regions were found to colocalize with eQTLs in heart tissues with a threshold of PP4 > 0.8. Two regions (i.e. TNKS2-AS1 and BORCS7/AS3MT) located on chromosome 10 harbored significant single-CpG single-locus associations and were found to colocalize with eQTLs in our previous study [32].

Comparison with burden tests and SKAT

We identified a total of 374, 1698 and 1850 significant CpG-gene associations by applying burden test with ‘beta’ strategy, SKAT with ‘normal’ strategy and SKAT with ‘logit’ strategy, respectively. The results varied largely across methods (Supplemental Figure 1). We hypothesize that the heterogeneity is largely due to the underlying causal mechanism. Based on the simulation results, the regions identified by burden test are more likely to harbor rare variants with homogeneous effects, but those identified by SKAT are more likely to have common variants influencing the variation of methylation levels. And the associations detected by MRF are more likely to be novel signals that rare variants contribute to with relatively large and heterogeneous effect.

Discussion

We present an MRF method for mQTLs detection by testing the association between a CpG site and a set of SNPs, both common and rare, within a genomic region. The main feature of the MRF is using a beta distribution to address the bimodal and interval properties of DNA methylation. The benefit is most evident when the sample size is small to moderate. Such a scenario is common in tissue-specific methylation studies given that some sample resources, such as cardiac tissues or brain tissues, are difficult to obtain. The proposed MRF also inherits the advantage of GGRF method such that it accounts for the linkage disequilibrium and potential interactions between multiple genetic variants. Moreover, the weighting scheme implemented in genetic similarity allows us to study the rare variants of relatively large effect.

Based on our simulation results, we expect that MRF will be more advantageous than other methods when rare variants exert relatively large and heterogeneous effect. We have also conducted additional simulations to compare with alternative methods, including SKAT-O (combining SKAT and burden test) and Cauchy’s method (combining correlated testing P-values from single-locus test) [36]. The results have suggested similar conclusions (Supplemental Figure 2 & 3). The application of MRF identified 97 mQTL regions that were associated with a nearby CpG site. Several genes have been reported in relation to CHDs. For example, copy number variants RPS6KA2 have been reported in relation to CHDs [37, 38], suggesting a novel insight of interplay among DNA methylation, copy number variants and SNPs. As another example, a case–control study in China suggested the association between genetic variants in COL4A1 and coronary artery disease [39]. In addition, two genes (MRPS10 and PSORS1C1) located on chromosome 6 were potentially colocalized with eQTLs in artery tibial, and gene PSORS1C1 was overlapped with nominal significant loci of both CHD GWASs. Previous literature suggested gene PSORS1C1 was enriched in the inflammatory pathway and was differentially expressed between pre- and post-surgery groups among children with congenital heart disease [40]. On the other hand, gene MRPS10 encodes a subunit of mitochondrial ribosomes and was found expressed differently among normal dogs and heart failure dogs [41]. Further investigation is needed to assess these potential mQTLs-CHD associations. For the rest of 95 regions, none of them showed strong evidence (i.e. PP4 > 0.8) for colocalization with previous CHD GWAS or expression QTL in cardiac tissues. In general, the colocalization analysis was underpowered. Although many studies agree that cis-mQTLs have relatively large effect sizes and can be detected with sample size less than 100 [42, 43], the statistical power is still limited, especially for rare variants. On the other hand, we believe the mQTL regions identified by the proposed MRF are more likely to be novel signals representing rare variants of relatively large and heterogenous effect. Such rare variants usually cannot be detected by GWAS and expression QTL studies using the single-locus testing strategy.

The proposed method should be viewed with a few limitations. First, MRF achieved highest power of the different approaches for methylation studies with small to moderate sample size. We think this is largely due to the use of beta distribution that better models the methylation data. However, when the sample size is large enough, linear regression with logit transformation showed more robust power in the simulation. In addition, MRF is developed for population-based studies where the subjects are unrelated to one another. If there exists any family structure within the study population, a family-based genetic random field method [44] would be more appropriate. Moreover, the current MRF is a single-trait multi-locus test. Considering the potential correlation between neighboring CpG sites, it would be reasonable to model the methylation levels of multiple CpG sites simultaneously. Therefore, one of our future directions will focus on extending the MRF into a multi-trait multi-locus analysis.

Key Points

• The single-locus test is only viable for detecting mQTLs that are relatively common in the study population.

• We proposed a methylation random field (MRF) method for detecting mQTLs considering both common and rare variants.

• The MRF is robust to heterogeneous genetic effects and has higher power than the other methods investigated here for detecting rare variants of relatively large effect.

• The MRF can model methylation trait with a beta distribution, and is particularly suitable for tissue-specific methylation studies with small to moderate sample size.

Chen Lyu is a PhD candidate in the Department of Epidemiology and Biostatistics at Indiana University Bloomington. Her research is focused on statistical genetics and genetic epidemiology.

Manyan Huang is a PhD candidate in the Department of Epidemiology and Biostatistics at Indiana University Bloomington. Her research is focused on statistical genetics and genetic epidemiology.

Nianjun Liu is a Professor in the Department of Epidemiology and Biostatistics at Indiana University Bloomington. His research is focused on statistical genomics, bioinformatics, and precision medicine.

Zhongxue Chen is an Associate Professor in the Department of Epidemiology and Biostatistics at Indiana University Bloomington. His research is focused on statistical methodologies and their applications to public health datasets.

Philip J. Lupo is an Associate Professor in the Department of Pediatrics at Baylor College of Medicine. His research is focused on the molecular epidemiology of pediatric diseases and conditions.

Benjamin Tycko is a Member of the Center for Discovery and Innovation. His research is focused on the genetic and epigenetics in human development and disease.

John S. Witte is a Professor in the Department of Epidemiology and Biostatistics at University of California, San Francisco. His research is focused on the understanding of genetic and environmental contributions to disease risk and progression.

Charlotte A. Hobbs is a Professor and Vice President for Research and Clinical Management at Rady Children's Institute for Genomic Medicine. Her research interest is focused on unraveling the complex etiology of major structural birth defects.

Ming Li is an Associate Professor in the Department of Epidemiology and Biostatistics at Indiana University Bloomington. His research interest is focused on the development of biostatistical methods and their applications to complex human diseases, such as birth defects.

Data Availability

The genetic and epigenetic data supporting the current study will be deposited to the database of Genotypes and Phenotypes (dbGaP) following the data sharing guideline of NHLBI and NICHD, and are available from the corresponding author on reasonable request.

Author Contribution

CL and ML conceived and designed the analysis.

CAH, PJL, BT collected the data.

CL, NL, JSW, ML contributed data or analysis tools.

CL, MH, ML performed the analysis.

CL, MH, NL, PJL, JSW, CAH, ML wrote the paper.