Won’t you be my neighbor? A review of microtubule growth

Abstract

Microtubules are dynamic cytoskeletal filaments comprised of αβ-tubulin heterodimers. Historically, the dynamics of single tubulin interactions at the growing microtubule tip have been inferred from steady-state growth kinetics. However, recent advances in recombinant tubulin and high-resolution optical and cryo-electron microscopies have opened new windows into understanding the impacts of specific intermolecular interactions during growth. The microtubule lattice is held together by lateral and longitudinal tubulin-tubulin interactions, and these interactions are in turn regulated by the hydrolysis state of the tubulin. Furthermore, tubulin can exist in either an extended or a compacted state in the lattice. Growing evidence suggests that binding of microtubule associated proteins (MAPs) or motors can induce changes in tubulin conformation, and that this information can be communicated through the microtubule lattice. Progress in understanding of how dynamic tubulin-tubulin interactions control dynamic instability has benefitted from visualizing structures of growing microtubule plus-ends and through stochastic biochemical models constrained by experimental data. Here, we review recent progress in understanding the molecular basis of microtubule growth, and discuss how MAPs and regulatory proteins alter tubulin-tubulin interactions to exert their effects on microtubule growth and stability.

Introduction

Microtubules are long cytoskeletal filaments found throughout all cell types and are essential for mitosis, cell motility, and intracellular transport. They are composed of αβ-tubulin heterodimers that assemble with neighboring tubulin through the formation of lateral (side-to-side) and longitudinal (top-to-bottom) interactions, creating a hollow cylinder typically composed of 13 protofilaments ^1–3 (Fig. 1). Microtubules are created through either the spontaneous assembly of the αβ-tubulin into a microtubule seed, a process known as nucleation, or through growth from a stabilized template^4–6. Once formed, microtubules present two kinetically distinct ends known as the plus-end and the minus-end⁷. Since the 1980s, measuring the steady-state growth rate as a function of the free tubulin concentration has been an invaluable tool for estimating the tubulin binding kinetics that occur at the microtubule end ^7,8. In recent years, innovations in microscopy that have increased signal-to-noise ratios, together with novel tracking algorithms that allow for sub-pixel localization, have greatly improved the precision with which the tips of growing microtubule ends can be localized^9–11. These advances provide a much more detailed view of growth dynamics, but they are still insufficient to discern the addition and loss of individual ~8 nm tubulin at a growing end.

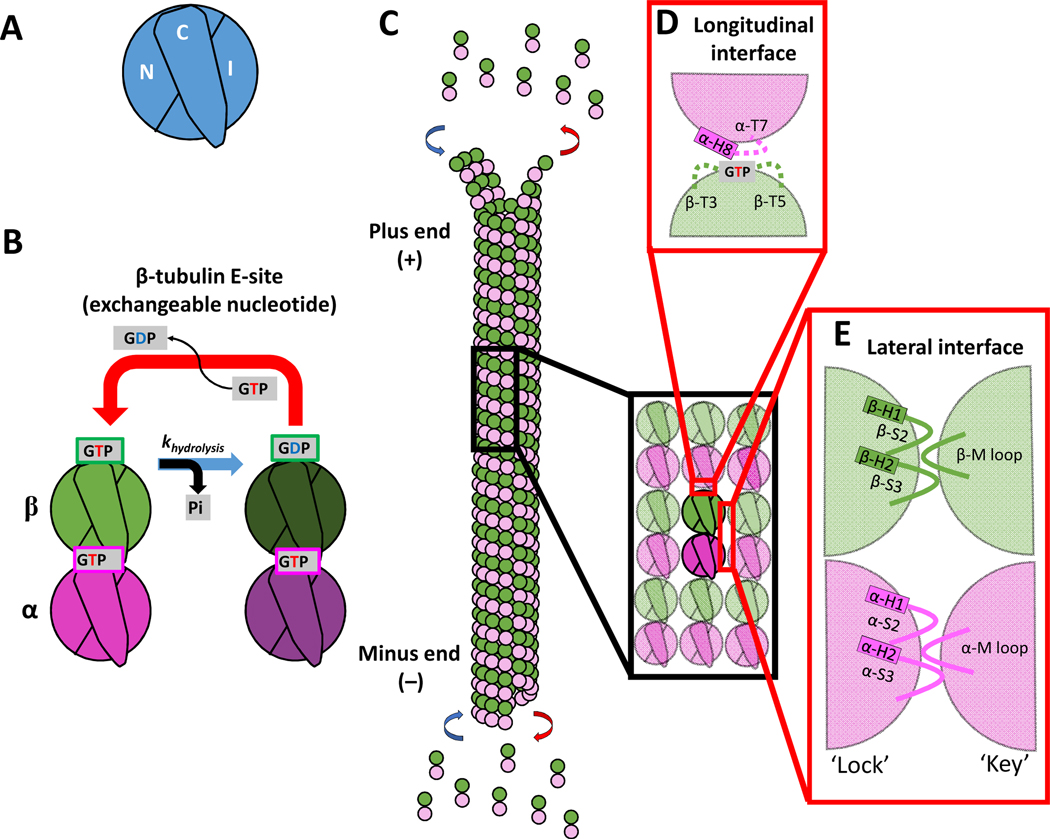
Figure 1. Domains of tubulin and the interdimer contacts involved in microtubule growth.

(A) Three domains that make up a tubulin monomer: the N-terminal domain containing the nucleotide pocket (N), the intermediate domain made from the globular region of the protein (I), and the C-terminal tail (C) facing the outside of the microtubule.

(B) The exchangeable GTP binding site (E-site), where GTP hydrolysis and nucleotide exchange occurs, is located in the N-domain of β-tubulin. Tubulin can be in either the GTP or GDP state.

(C) Schematic of a microtubule growing by tubulin addition at the plus- and minus-ends.

(D) Longitudinal (top-to-bottom) dimer-dimer contacts involve interactions between the N-domain of β-tubulin of one dimer and the I-domain of α-tubulin of a second dimer. This longitudinal interaction between dimers forms a nucleotide pocket around the exposed GTP on the β-tubulin.

(E) Lateral (side-to-side) dimer-dimer contacts form a lock-and key pocket between the I-domain of one tubulin dimer and the N-domain of the adjacent dimer.

One of the unique characteristics of microtubules is their ability to undergo dynamic instability, a switching from growth to shrinkage (catastrophe), and from shrinkage back to growth (rescue)¹². The addition of GTP-bound tubulin to the growing end has been proposed to act as a protective cap against catastrophe, with the onset of a catastrophe resulting from GTPase-activity of the αβ-tubulin in the lattice¹³. This ‘GTP cap’ model was proposed^12,14–16 and later confirmed through the use of GMPCPP, a non-hydrolyzable GTP analog, in which microtubules continuously grow without undergoing catastrophe⁸. By visualizing fluorescent End-Binding Protein 1 (EB1), which binds the GTP-like confirmation of tubulin^17–19, the cap size were determined to increase proportionally with the free tubulin concentration^13,20,21. This observation, along with the finding that the cap deteriorates immediately preceding catastrophe, support the idea that at a growing plus-end a kinetic race exists between the addition of GTP-tubulin from solution and GTP hydrolysis in the microtubule lattice^13,20,21.

This review focuses on microtubule growth and the tubulin-tubulin interactions that dictate the likelihood of incorporation of incoming tubulin at a growing end. Apparent on-rates and off-rates of single tubulin were initially estimated by measuring the average growth rates over increasing tubulin concentrations (Fig. 2B)⁷. Utilizing this growth rate data, biochemical models were developed and constrained to interpret the specific tubulin-tubulin interactions occurring at the microtubule tip^22–27. Although these models of microtubule growth have provided invaluable insights into potential tubulin-tubulin interactions, parameters in these models can vary orders of magnitude from one another. Fortunately, recent advances in structural and single-molecule approaches have allowed this parameter space to be narrowed considerably. Our goal in this review is to consolidate the large amount of data that has been generated in recent years through the use of recombinant tubulin, single particle analysis, and improved Cryo-Electron Microscopy (Cryo-EM) resolution to move closer to a consensus model that describes the dynamic interactions that underlie microtubule growth.

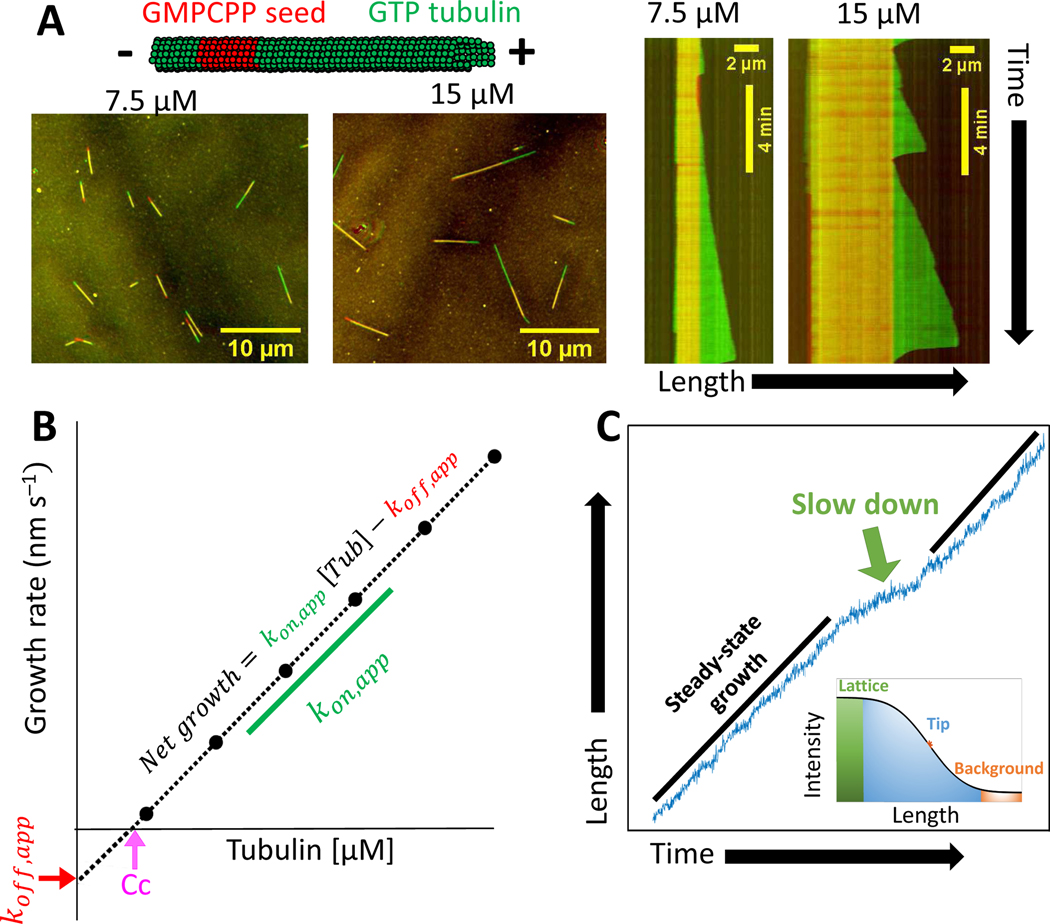
Figure 2. Experimental measurements of tubulin kinetics.

(A) Schematic of microtubule growth in vitro from stabilized GMPCPP seeds. Images show growth from GMPCPP seeds after 10 minute incubation in 7.5 μM and 15 μM free tubulin. Kymographs show the associated growth dynamics, which include periods of steady growth and catastrophes. (Unpublished data.)

(B) Schematic plot of the mean microtubule growth rate as a function of the free tubulin concentration. The critical concentration for growth (C_c) is estimated from the x-intercept, the apparent tubulin on-rate constant (k_on,app,) is estimated from the slope, and the apparent tubulin off-rate constant (k_off,app,) is estimated from the negative of the y-intercept.

(C) Localization of microtubule end positions at a high spatial resolution is resolved by fitting the spatial decay of intensity using a survival function (inset) reveals fluctuations in growth and slowdown events. (Unpublished data.)

Longitudinal and lateral neighbor interactions

αβ-tubulin heterodimers are formed through dimerization of two structurally similar monomers of α- and β-tubulin. Each of these monomers is composed of three domains: the N-domain containing the nucleotide binding pocket; the I-domain made from the primarily globular portion of the tubulin; and the C-domain that contains an unstructured, negatively charged C-terminal tail that extends out from the lattice and interacts electrostatically with microtubule associated proteins (MAPs) and microtubule motors. (Fig. 1A)^28–31. Formation of a heterodimer creates an asymmetry in which an exchangeable GTP lies at the top exposed longitudinal interface of the β-tubulin and the I-domain lies at the bottom exposed longitudinal interface of the α-tubulin (Fig. 1B)^32,33. Thus, microtubules that polymerize from tubulin heterodimers are polarized filaments that present an exposed N-domain of the β-tubulin on the faster growing plus-end and an exposed I-domain of the α-tubulin on the slower growing minus-end (Fig. 1C)³⁴.

In the microtubule lattice, αβ-tubulin heterodimers interact both longitudinally (head-to-tail) and laterally (side-to-side). Advances in cryo-electron microscopy (Cryo-EM) have enabled visualization of the specific loops and helices involved in these interactions^28,29. Longitudinal interactions at the plus-end are mediated by the βT3 and βT5 loops that surround the exposed GTP in the β-subunit, and the αT7-H8 loops in the incoming α-subunit (Fig. 1D). Formation of a longitudinal interface between heterodimers brings the catalytically active α-tubulin Glu 254 of the incoming heterodimer close to the β-tubulin GTP of the second heterodimer, enabling GTP hydrolysis (Fig. 1B)^{28,29,35–37}. Thus, an incoming tubulin must land to trigger hydrolysis of the GTP exposed at the plus-end. The second nearest neighbor interaction that αβ-tubulin makes is the lateral binding interface. The most stable lateral interactions involve β-β and α-α contacts, as a B-lattice configuration^1,38. Lateral contacts have been described as a lock-and-key interaction in which the flexible M-loop, comprised of α/β S7-H9 in the I-domain, docks into a corresponding lock, formed from α/β H1-S2 and α/β S7-H9 in the N-domain, of an adjacent tubulin (Fig. 1E)^{28,29,39–41}. Although the microtubule lattice is predominantly in the B-lattice configuration, a shallow pitch in the lattice results in a mismatch or seam of A-lattice, in which structurally similar α- and β-tubulin laterally interact^1,38. The A-lattice seam is thought to be thermodynamically weaker based on molecular modeling and the observation that A-lattice rich microtubules catastrophe more frequently and shrink faster than B-lattice rich microtubules⁴². The strength of the longitudinal and lateral interactions dictate growth kinetics at the growing microtubule tip, and differences in these interactions upon GTP hydrolysis underlies dynamic instability.

A simple kinetic model of microtubule growth

The microtubule growth rate has been shown to vary linearly with the free tubulin concentration in vitro⁷, providing insights into tubulin binding kinetics at the growing tip (Fig. 2). The growth rate reflects a balance of tubulin association and dissociation; thus in a plot of the growth rate versus the free tubulin concentration (Fig. 2B), the apparent tubulin on-rate constant is given by the slope, and the apparent tubulin off-rate is given by the negative y-intercept. Regulation of microtubule growth by regulatory proteins or other perturbations can be described by modulation of these apparent rate constants; however, these apparent rates do not describe with molecular detail the specific tubulin-tubulin interactions occurring at the microtubule tip. Determining the true intermolecular on- and off-rates at the tip requires quantitative models that are constrained by the experimental data, and there is a rich literature of models that have evolved in parallel with experimental advances^{22–25,43–45}. The simplest model to describe microtubule growth utilizes three parameters: the bimolecular on-rate constant, the longitudinal bond strength, and the lateral bond strength. The model developed by van Buren et al.²² was the first to be trained against comprehensive measurements of microtubule dynamics, and it has been applied widely to interpret quantitative experiments ^{22,24–26,45,46}. Despite its apparent simplicity, this model captures much of the complexity of microtubule growth and is an excellent tool for framing many of the current questions in the field.

In this simple kinetic model (Fig. 3), the kinetics of tubulin-tubulin interactions are dictated by their binding free energy, where the binding affinity (K_a) increases exponentially with the total free energy of interaction, $K_a=\frac{k_{on}}{k_{off}}=e^{-\frac{\Delta G_{tot}}{k_{B}T}}$. This relationship makes it especially important to understand the energetic contributions of each of the lateral and longitudinal interactions occurring at the growing microtubule tip. Because lateral interactions are thought to be weaker than longitudinal, single lateral bonds are generally not considered. Thus, the simplest interaction, and the one with the highest likelihood of reversibility is the “loner” interaction consisting of one longitudinal interface^22,40 (Fig. 3A). Adding one lateral neighbor creates a “corner” interaction that is exponentially stronger and thus has a much lower likelihood of detachment. The addition of a second lateral neighbor results in a “bucket” configuration, which has the highest interaction energy and lowest likelihood of detaching from the microtubule tip. Finally, if a second longitudinal neighbor is added to surround a tubulin on all four sides, that subunit is assumed to be tightly but reversibly incorporated into the lattice^45–48. Combining these simple kinetic rules together with a tubulin binding rate that is proportional to the free tubulin concentration, the growth of the 13 protofilaments in the lattice can be simulated to gain insights into microtubule growth. Because an incoming tubulin dimer interacts with loner, corner, and bucket binding with such different interaction energies, the shape of the taper at the plus-end, which determines the proportion of different binding events, strongly affects the growth dynamics.^22,24,45.

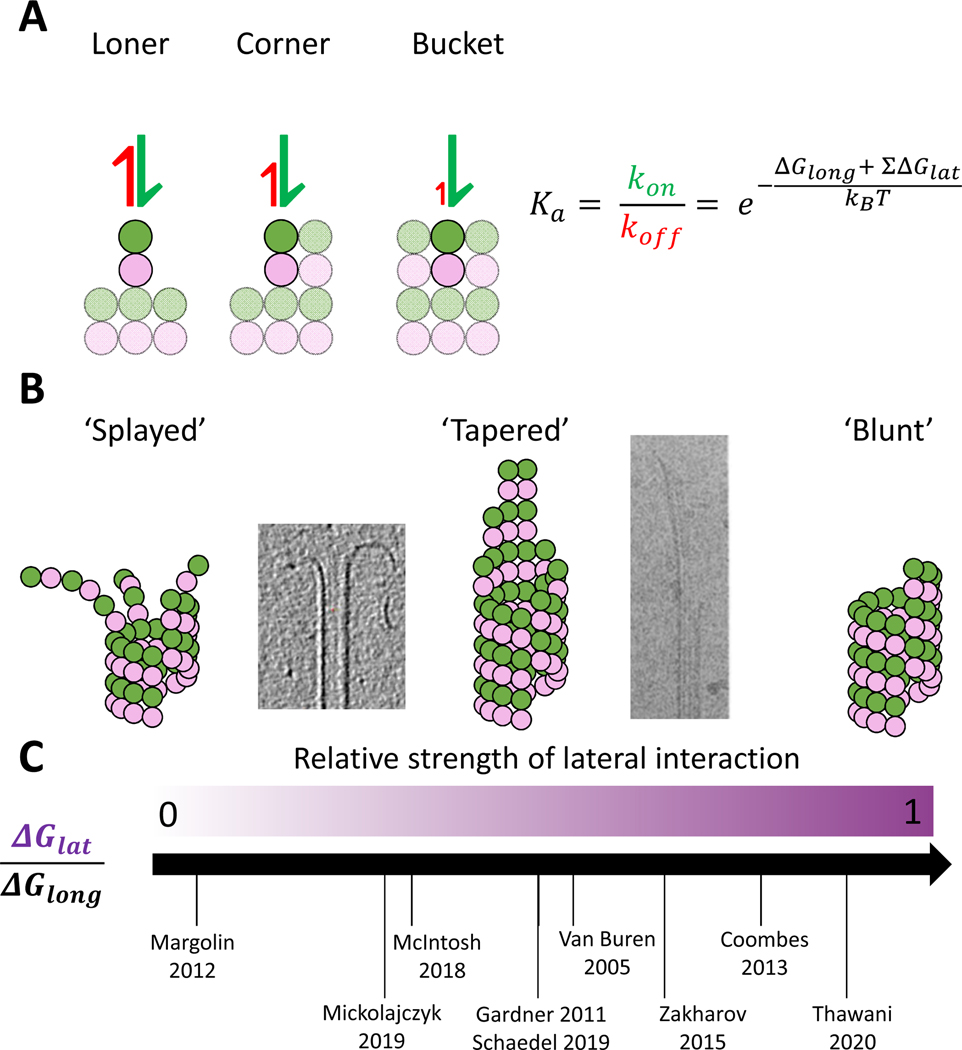
Figure 3. A simple model of microtubule growth.

(A) The affinity of loner, corner, and bucket sites at the growing plus-end are exponential functions of the free energy of the underlying lateral and longitudinal contacts (based on Van Buren et al. (2002))²².

(B) As the relative free energies of lateral to longitudinal bonds increases, the growth dynamics transition from “splayed” where protofilaments grow relatively independently, to “tapered” where incorporation predominantly occurs at corner sites, to “barber pole” where the weak longitudinal bond dictates that growth occurs only from corner sites. Accompanying cryoEM-images display a splayed end from McIntosh et al (2018) ⁷¹ and a tapered end from Chretien (1995) ⁵¹.

(C) Different microtubule growth models in the field incorporate very different values for the relative free energy of lateral and longitudinal bonds. Specific parameter values for the different models are presented in Table 1.

Although these fundamental kinetic principles are generally agreed upon, experimental steady-state growth rate data are not sufficient to constrain the model parameter values. The result, as shown in Table 1, is that a number of models exist in the literature that can reproduce the experimental growth data employing vastly different parameters. More importantly, the different models imply different mechanisms of growth and predict qualitatively different microtubule tip structures (Fig. 3B)⁴⁵. To develop intuition about how relative longitudinal and lateral binding free energies lead to different mechanisms of growth, we outline below a simple biochemical model where the corner affinity, defined by the free energy of one lateral plus one longitudinal bond, is held constant. It has been shown that the tubulin on-rate constant and the relative lateral and longitudinal free energies can be varied while still recapitulating the experimental growth curve shown in Fig. 2B^22,49,50. Varying the relative strengths of the lateral and longitudinal bonds results in three different “modes” of microtubule growth (Fig. 3B).

Table 1.

Model parameters of prominent biochemical and chemomechanical models of microtubule growth. Dwell times are calculated by using free energy to solve for the equilibrium constant, using the on-rate to calculate the off-rate, and inverting the off-rate.

Paper	kon (μM−1 s−1 pf−1)	ΔGlong (kBT)	ΔGlat (kBT)	Loner dwell time (ms)	Corner dwell time (ms)
Mickolajcyzk et al. 201945	0.8 - Yeast	−12	−3.6	203.4	7445.7
Schaedel et al. 201946	1	−18.8	−9.4	0.1a	984.6a
Margolin et al. 2012118	1.25	−9.4	−0.3	9.7	13.1
Thawani et al.60	1.3	−7.2	−6.5	1	685.3
vanBuren et al. 200222	2	−9.4	−3.2	6	148.3
	4	−6.8	−5.7	0.2	67.1
Piedra et al. 201526	4 - Yeast	−5.8	−6.6	0.1	60.7
Gardner et al. 2011 64	4	−9.5	−5	3.3	495.7
Coombes et al. 201352	5	−7.2	−5.7	0.3	80.1
Chaaban et al. 201841	6 – C. elegans	−7.1	−6.4	0.2	121.6
	6	−6.3	−5	0.1	13.5
Zakharov et al. 2015116	0.63	−15.5	−9.1
McIntosh et al. 201875	0.63	−16.6	−5.3
Gudimchuk et al. 2020117	0.63	−16.9	−13.5
Castle et al. 201363	12.7 - Loner	−6.7		0.1 a
	7.4 - Corner	−6.7	−3.6		4 a

Notes:

^aIncludes entropic penalty specified in the paper.

“Splayed” model.

If growth involves strong longitudinal bonds and weak lateral bonds, growth is dominated by ‘loner’ interactions, resulting in independently elongating protofilaments at the microtubule end. Continuous growth in this model depends on the rate of lateral bond formation between protofilaments that close the microtubule into a cylinder. In this scenario, the tubulin on-rate constant would need to be relatively slow because loners that make only one longitudinal interaction have relatively high probability of being incorporated into the growing protofilament.

“Tapered” model.

As the lateral affinity is dialed up, with a compensatory decrease in the longitudinal affinity, the microtubule is predicted to grow with a sheet-like taper at its tip. Tapered growth results from an increased importance of ‘corner’ interactions, since ‘loners’ tend to dissociate before being incorporated. Because of this rapid dissociation of loners, a compensatory increase in the tubulin on-rate constant is required to match steady-state growth rates. Though loner dissociation rates are higher, the increased on-rate increases the likelihood of the association of a neighboring tubulin trapping it in a ‘corner’ interaction.

“Blunt” model.

If the longitudinal affinity is further weakened to where it matches the lateral bond affinity, then the probability of ‘loners’ incorporating is negligible and microtubule growth will occur solely through ‘corner’ interactions. The result is that the microtubule grows in a spiral ‘barber pole’ fashion, with a blunt microtubule tip. The tubulin on-rate constant in this case would need to be sufficiently high that there is a high likelihood of two tubulin landing in adjacent protofilament before detaching from the microtubule end. Growth of a new ring of tubulin could also start at the seam, where there will always be a half-heterodimer offset.

The structure of the growing microtubule tip and the specific parameter values for the on-rate constant and the longitudinal and lateral affinities are hotly debated in the field (Fig 3C and Table 1). Below, we describe the experimental evidence and the kinetic and thermodynamic arguments for each of these models.

Microtubule end structures

Tapered microtubules

Microtubule tapers, which provide a range of possible binding configurations for incoming tubulin, are the most widely supported model for the tips of growing microtubules. Microtubule tapers were first visualized by electron microscopy as long, gradually curved, sheet-like structures projecting from the ends of growing microtubules ⁵¹. Further evidence for tapered plus-ends came from fluorescence imaging, with the challenge being the inherent blurring of ends by point-spread-function of the microscope. By performing model convolution on simulated images, the predicted spatial decay of fluorescence at the microtubule tip for different tip taper lengths can be predicted and used to infer tip structure^52,53. Using this approach, Coombes et al.⁵² presented evidence that the taper evolves during microtubule growth from a seed and reaches a steady-state length that varies with the free tubulin concentration. This approach has been extended to show that microtubule plus-tips are elongated in cells and when microtubules are grown in vitro in the presence of regulatory proteins^11,54,55. However, using similar approaches, Maurer et al. concluded that taper lengths for microtubules grown under standard conditions in vitro were below the detection limit of ~180 nm for this technique, which they established using model convolution²⁰. These conflicting results may arise from differences in tubulin labeling ratios, signal-to-noise ratios of the imaging systems, or averaging techniques used to fit the microtubule end. Label-free approaches such as interference reflection and interferometric scattering microscopy^56–58, where the scattering intensity is proportional to the mass of protein present, may provide greater precision into measuring taper lengths below the optical limit.

A third line of evidence in support of the tapered model of growth comes from the kinetics of templated nucleation, in which microtubules are grown from blunt GMPCPP-stabilized seeds. Wieczorek and colleagues⁵⁹ observed that near the critical concentration for growth (C_c at the x-intercept in 2B) there was no measurable growth from blunt-tipped GMPCPP seed microtubules. Although growth from seeds near C_c has been observed under some conditions⁶⁰, this result is also consistent with the relatively low number of seeds that have plus-end extensions at moderate tubulin concentrations^54,59. One explanation is that because loners rarely incorporate on a blunt end, there is a kinetic battle to establish sufficient corner sites to enable steady microtubule growth. This model was tested by exposing microtubule seeds to a high concentration of free tubulin that allowed for the formation of a tapered template, and then dropping the tubulin concentration close to the critical concentration where growth was previously not observed. Growth rates following this “priming” matched the predicted steady-state growth at the lower tubulin concentration (e.g., Fig. 2B), consistent with formation of a tapered tip being a prerequisite for steady-state growth. At this point, evidence for tapered microtubule plus-ends is sufficiently widespread that the possibility that growing microtubule ends are blunt is no longer considered in the field. However, the tapered model of microtubule growth leaves a wide parameter space for the on-rate constant and lateral and longitudinal bond strengths. Fortunately, these “tapered tip” models can be split into two camps: a fast kinetics model in which the longitudinal affinity is relatively low and the on-rate high to compensate²⁴, and a slow-kinetics model in which the longitudinal bond strength is relatively strong and growth is achieved by a moderate bimolecular on-rate for tubulin addition to a growing protofilament⁴⁵.

Tubulin addition can be described as either efficient, meaning that most tubulin that land are incorporated, or inefficient where only a small fraction contribute to growth due to rapid dissociation. Based on this reasoning, Gardner and colleagues²⁴ created an analytical model coupled with simulations to show that these two scenarios predict very different fluctuation behavior of the growing microtubule tip. Growing microtubule plus-tips were then tracked by high-precision fluorescence microscopy in both GMPCPP and GTP. The large amplitude length fluctuations observed were consistent with an inefficient model of growth, in which tubulin on- and off-rates are considerable faster than previously reported (Fig. 2B)^21,24. These observations were supported by optical trapping experiments in which microtubules were grown against a barrier and rapid fluctuations with amplitudes matching single tubulin or tubulin oligomers were detected ^61,62. In the simple kinetic model in Figure 3, the ‘fast-kinetics’ model would correspond to a weak longitudinal affinity with tubulin addition occurring almost exclusively through corner interactions in a ‘barber-pole’ fashion⁴⁵. However, the authors were able to measure relatively large tapers based on fluorescent images at the growing plus-end²⁴. This was reconciled by positing an on-rate penalty based on the structure of the binding site – loners land with a fast on-rate, binding into corners occurs somewhat more slowly, and the on-rate for bucket sites is an order of magnitude slower²⁴. Support for the penalty was provided using Brownian Dynamics simulations arguing that constraints from lateral neighbors suppress the on-rate⁶³. This on-rate penalty, which is physically reasonable but difficult to experimentally verify, creates a positive feedback loop in which lagging protofilaments grow even more slowly while longer protofilaments grow at normal rates, generating a large taper over time. One appealing feature of this “fast kinetics” model is that it provides a simple explanation for how diverse regulatory proteins can alter microtubule growth rates – if the on- and off-rates are fast and the difference between them is small, then small variations in these fast rate constants can produce large changes in the net growth rate⁶⁴.

One reason that numerous models for microtubule growth exist in the field is that there are a range of reasonable assumptions that can be made that result in quite different mechanisms of growth. Therefore, without the ability to measure single tubulin kinetics directly, it is difficult to limit the range of bond strengths and on-rates used to model microtubule growth. This situation was addressed recently by Mickolajczyk and coworkers⁴⁵ who used Interferometric Scattering (iSCAT) microscopy to measure the reversible binding of gold nanoparticle-labeled tubulin at growing microtubule plus-ends. This work employed recombinant yeast tubulin that was labeled at its C-terminus by a 20 nm gold particle, and microtubules grown from immobilized axonemes in the presence of GTPγS, a slowly hydrolysable GTP analog. The gold decreased the diffusion constant of the tubulin by ~3-fold, but control experiments showed that the labeling did not alter the ability of tubulin to be incorporated into the lattice. When gold-labeled tubulin was visualized at the growing plus-end in the presence of a ~1000-fold excess of unlabeled tubulin, three types of events were observed: incorporation into the lattice, reversible binding with a long dwell time (~1 s), and reversible binding with a short dwell time (~30 ms). These results were consistent with expectations if the incoming tubulin binds to a tapered microtubule tip, but it left open the question of whether fast and slow events corresponded to ‘loners’ and ‘corners’ or ‘corners’ and ‘buckets’, with the ‘loner’ events being too fast to measure in the latter (Fig. 3A). This uncertainty was resolved using mutants with altered lateral or longitudinal interfaces, and modeling the results using a computational model similar to that shown in Figure 3^45,65,66. The conclusion was that the fast events reflected loners, the slow events were corners, and the irreversible events were bucket sites. The data were best fit by a model in which the on-rate was constant for all binding sites at 10 μM⁻¹ s⁻¹ tip⁻¹, roughly six-fold slower than the fast kinetics model²⁴.

Thus, the “fast kinetics” and “slow kinetics” models are able to match experimental tubulin-dependent growth rates and predict a tapered plus-end by slightly different mechanisms. The fast kinetics model of Gardner generates a tapered tip using the added feature of a slow on-rate to bucket sites, whereas the iSCAT work achieves a tapered tip because the slower dissociation rate of loners enables more corner interactions to occur. As detailed in Table 1, fast kinetics models incorporate a very low loner affinity and slow kinetics models have a moderate loner affinity. Expanding the picture, a third class of models that model the plus-end as a splayed structure incorporate even higher loner affinities.

Are growing microtubule ends splayed?

Early electron microscopy revealed curved protofilaments, commonly referred to as Ram’s horns, present at the tips of depolymerizing microtubules⁶⁷. This finding along with our understanding of the role of hydrolysis in microtubule catastrophe led to the textbook model in which GTP-bound tubulin was in a straight confirmation, while GDP-bound tubulin was in a curved confirmation⁶⁸. This model was invalidated, however, by the finding that isolated tubulin is curved in both a GTP- and GDP-bound states ^69,70. Adding to this picture, recent work using Cryo Electron Tomography (Cryo-ET) captured curved protofilaments at the growing plus-ends of microtubules, and described growing plus-ends as “flared” or “splayed” ⁷¹. The splayed protofilaments were measured to be ~2–4 tubulin in length and had curvatures of 12–20°, nearly matching the curvature measured from the depolymerizing Ram’s horns⁷¹. The presence of these plus-end protofilament curls argues for a model in which longitudinal interactions are the dominant stabilizing feature during growth (Fig. 3B). This model has led to a fair degree of controversy in the field, as it challenges the textbook model of a tapered microtubule end. The methodological difference in this study lay in the analysis of the tilt series. In this study, images of the microtubule end were segmented and aligned with the center of the microtubule positioned along the y-axis. Slices of the microtubule were then generated by rotary sectioning through the center of the microtubule. The standard approach uses axial sectioning, in which the slices are generated parallel to the microtubule axis, thus passing through the center in only one slice^72–74. The advantage of the rotary sectioning is that it maximizes the signal-to-noise ratio of the rendered microtubule tip, a necessary aid in a technique that has a low signal-to-noise ratio. The disadvantage is that, because the microtubule tip is a notoriously difficult structure to image using standard electron microscopy techniques due to its heterogeneity, all the structures measured in this study required tracing by hand, making it a cumbersome process and one that requires a highly trained eye^75–77.

Supporting these experimental data, a detailed computational model that incorporates splayed protofilaments into the microtubule assembly process was shown to reproduce experimentally observed growth rates⁴³. This chemomechanical model proposes that protofilament stiffness allows for fast fluctuations that increase the likelihood of forming a weak lateral interactions that seal the splayed protofilament into the lattice. Notably, recapitulating experimental growth dynamics required using a fairly low tubulin on-rate which, together with the relatively high longitudinal affinity, means that a large fraction of the tubulin that bind to the end of protofilaments are incorporated into the growing lattice (an efficient mechanism). These strong longitudinal interactions resemble another “efficient” model of polymer growth, that of bacterial tubulin, FtsZ ⁷⁸. In the case of FtsZ, there is a transition from a weak-binding conformation found in solution, to a strong-binding conformation that is favored when subunits are incorporated into a growing filament. These conflicting views of the structure of growing microtubule tips will likely persist for a time due to the challenge of imaging these heterogeneous, dynamic structures with high resolution. However, in parallel with continuing advances in Cryo-EM imaging, additional lines of evidence are being pursued to reconcile the “splayed” and “tapered” models. Resolving this structural question will help to more quantitatively define the relative magnitudes of the longitudinal and lateral bonds that stabilize the microtubule lattice.

The curved-to-straight transition

Up to this point, we have primarily focused on the longitudinal and lateral interactions that stabilize GTP tubulin in the lattice, and have neglected details of the mechanical straightening that is required for curved tubulins in solution to become incorporated into the straight microtubule lattice. At the tip of a growing microtubule, there is a competition between the elastic bending of the dimer that favors the curved conformation, and lateral bond formation that locks tubulin in a straight conformation. Models that predict a tapered tip (e.g. Fig. 3), generally account for the elastic energy involved in straightening as a penalty against lateral binding energy that stabilizes tubulin in the lattice ²³. Models incorporating splayed ends generally treat the protofilament bending flexibility, the thermal fluctuations that drive protofilament bending, and the activation energy for forming a lateral bonds in greater detail, which allows for much richer behavior in the simulations but which also introduces more free parameters^25,43. The straightening process in these Brownian Dynamics models is a form of a thermal ratchet, where the protofilaments sample many different curvatures due to thermal fluctuations, and become captured in the straight conformation when a lateral bond is formed with a neighboring protofilament. The relative kinetics tubulin straightening, lateral bond formation, and tubulin dissociation from the end of a protofilament likely play an important role in determining the growth rate and concentration dependence of growth and catastrophe.

Where does GTP hydrolysis exert its influence?

Early models of tubulin association were based on the nucleotide state of the incoming tubulin, where GTP-bound tubulin had a higher affinity to the lattice than GDP-bound tubulin⁷⁹. This can be termed a “cis-acting” model, in which the nucleotide state of an incoming tubulin is what determines its affinity for the microtubule tip ^68,80 (Fig. 4A). However, once structures of soluble GTP- and GDP-bound tubulin were resolved to have no inherent curvature differences⁷⁰, this model lost some of its momentum because for the nucleotide state of an incoming tubulin to determine its binding affinity in the absence of curvature differences, it would require a long-distance allosteric communication from the nucleotide pocket of the β-tubulin to the distal longitudinal interfaces of the α-tubulin that is interfacing with the lattice. In contrast, a “trans-acting” model (Fig. 4A) proposes that the nucleotide state of the terminal exposed β-tubulin at the microtubule plus-end dictates the affinity of an incoming tubulin from solution^26,44,70. Thus, structural rearrangements upon GTP hydrolysis would only need to occur around the nucleotide binding pocket, which lies at the longitudinal interface between tubulin subunits. Furthermore, structural studies provide a plausible mechanism for how the nucleotide in the terminal β-subunit may regulate binding of the incoming tubulin. It was shown that the βT5 loop, which resides at the α/β interface, changes its conformation based the identity of the bound nucleotide^69,81. When GTP is bound, the loop flips “out”, exposing Asp177 and increasing the longitudinal interface interacting with the incoming α-tubulin. Meanwhile, when GDP is bound, the βT5 loop is able to flip “in”, resulting in a decrease in the longitudinal bond strength and faster dissociation of the terminal tubulin ^69,82.

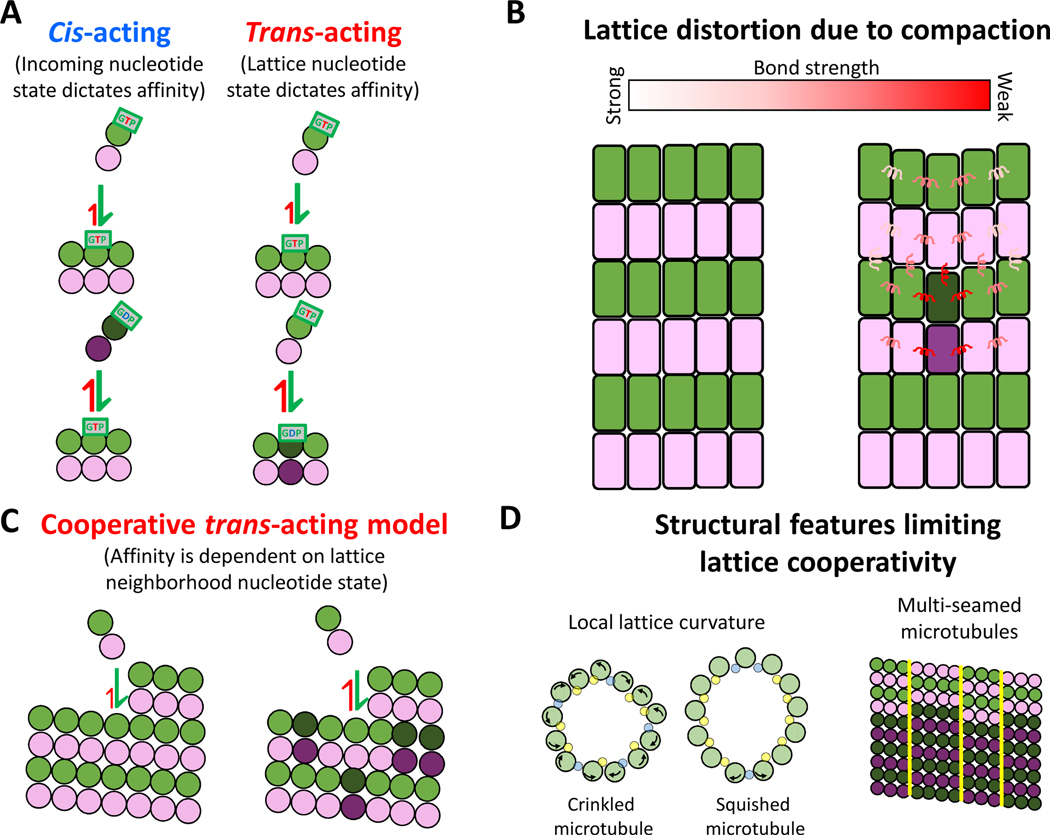
Figure 4. Trans-acting model of growth and lattice cooperativity.

(A) Cis-acting model proposes that the nucleotide state of the incoming tubulin dictates binding affinity. Trans-acting model proposes that the nucleotide state of the terminal lattice-bound tubulin dictates binding affinity.

(B) Effect of a single tubulin’s compaction not only has the potential to change the bond strength of nearest neighbors but can be spread through accommodation within the lattice.

(C) Cooperative trans-acting model proposes that the nucleotide states of neighboring tubulin in the lattice dictate the binding affinity of the incoming tubulin⁴⁴.

(D) Structural features that may limit the propagation of cooperative binding effects through the lattice. Local curvature changes in ‘crinkled’ or ‘squished’ microtubule lattices (left) and multiple seams (right) may limit the size of the neighborhood over which cooperative effects may act. Images of deformed microtubules based on Debs et al. (2020)⁹⁴

The “trans-acting” model²⁶ involves a kinetic race at the growing microtubule plus-end that may clarify some unexplained aspects of microtubule growth in the literature. This race results from: a) the GTP hydrolysis state of the penultimate tubulin in the lattice determining the affinity of the newly added tubulin at the end, and b) the requirement of a newly added subunit to trigger GTP hydrolysis in lattice-bound tubulin. If hydrolysis occurs rapidly upon addition of a new tubulin, this newcomer may dissociate, which then exposes a lattice-bound GDP tubulin at the plus-end. Any tubulin subsequently added to this protofilament would then be at a disadvantage of incorporating due to the lower binding affinity. This phenomenon may explain the unexplained increased growth rates of GMPCPP compared to GTP tubulin^8,83. When first observed, this two-fold difference in the apparent on-rate was thought to be insignificant and perhaps due to the modified nucleotide. However, a recent study created a hydrolysis resistant tubulin by mutating α-tubulin E254, the residue found at the inter-tubulin longitudinal interface believed to be responsible for forming a catalytically active nucleotide pocket⁸⁴. Along with the expected resistance to catastrophe, this mutant also grew two-fold faster than wild-type tubulin under similar conditions. The fact that two different perturbations that prevent the creation of exposed GDP tubulin at the plus-end both show faster growth rates lends support to the trans-acting model. Additionally, during steady microtubule growth in GTP, transient pauses and slowing have been observed^13,20,85 (Fig. 2C), which also may be explained by exposed GDP tubulin at the plus-end slowing incorporation of incoming tubulin^21,23,86,87.

Another tool that may prove useful in understanding the trans-acting model is the microtubule minus-end. At the minus-end, the terminal tubulin has its exchangeable nucleotide buried in the lattice and the incoming tubulin arrives with its exchangeable nucleotide exposed. Thus, GTP hydrolysis in the lattice may have different effects on incoming tubulin. Relevant to this, Strothman et al⁸⁸ recently showed that, compared to the plus-end, minus-ends have a 3–4 fold slower apparent on-rate and a compensatory 3-fold slower off-rate, but have similar growth lifetimes preceding catastrophe. This suggests that the relationship between GTP cap size and catastrophe frequency is different at the two ends. The minus-end is sorely understudied compared to the plus-end, but any unified model of microtubule dynamics should be able to describe why the structural differences between the plus- and minus-end lead to their different polymerization dynamics.

Lattice compaction and structural plasticity

First mentioned 25 years ago⁸⁹, tubulin in the lattice of microtubules polymerized in GMPCPP is roughly 2 Å longer than tubulin in a GDP lattice. The structural disparity between these two tubulin conformations suggest that microtubules may switch their lattice states in a concerted way. This phenomenon was revisited more recently using Cryo-EM, where it was found that both subunits of tubulin undergo compaction that is correlated with the nucleotide state of the lattice²⁹, and that compaction results in a smaller lateral contact interface and a greater longitudinal contact interface between neighboring tubulin²⁸. This structural transition offers a potential mechanism for the formation of Ram’s horns during depolymerization – protofilaments in a compacted lattice peel away more easily from their lateral neighbors due to weakened lateral contacts but stay intact due to strengthened longitudinal contacts²⁸. Complicating matters somewhat, recent work has suggested that there is not a tight correlation between the nucleotide state and the compaction state of tubulin. First, microtubule associated proteins, such as kinesin and EB3 have shown to alter the compaction state of the tubulin^90–92. Secondly, it was shown that the GDP analog, GMPCP was able to expand the lattice despite lacking a terminal phosphate; instead, it was suggested that the methylene group may be driving the lattice expansion in GMPCPP microtubules rather than the terminal phosphate⁸². Thus, it is clear that the microtubule lattice can exist in either compacted or expanded states, but the mechanisms affecting the expansion/compaction state of the lattice are an active current area of investigation.

The bistability of lattice expansion also opens a number of questions related to structural communication through the lattice⁹³. For instance, compaction of a single tubulin subunit within the lattice is expected to cause compensatory strain within the lattice to accommodate the defect. This strain may spread some distance through the lattice, and one way to relive this strain is for the surrounding lattice to switch its compaction state. This opens up the possibility that a protein binding to one tubulin dimer may alter the structure of tubulin in an entire neighborhood of the lattice. This lattice cooperativity was shown in a recent study that used kinesin to expand the lattice and found that only ~20% occupancy was sufficient for full lattice expansion ⁹¹. These cooperative interactions have been incorporated into detailed chemomechanical models in which tubulin-tubulin contacts are modeled as spring-like interactions that allow for energy dissipation across neighboring tubulin in the lattice ^25,43 (Fig. 4B). Coupled lattice interactions have also been incorporated into simpler biochemical models in which hydrolysis impacts the affinity of neighboring tubulin within a ring one tubulin deep ⁴⁴ (Fig. 4C). Even this fairly minor addition significantly improved the prediction of catastrophe events. Although to date these models have been primarily applied to understanding catastrophe, implementing their principles to study microtubule growth may make new testable predictions regarding growth fluctuations and microtubule tip structure.

If structural transitions can propagate some distance through the lattice, what limits the distance these structural changes can communicate? One limit may be the microtubule seam, where the standard B lattice involving β-β and α-α lateral interactions is interrupted by an A-lattice seam containing β-α and α-β interfaces³⁸. A recent cryo-EM study that used enhanced refinement algorithms to study lattice structure found that although the lattices studied mostly contained only one seam, multi-seamed microtubules are common (Fig. 4D, right) ⁹⁴. The addition of multiple seams creates smaller neighborhoods of contiguous B-lattice that may limit the extent of cooperative communication. Both protofilament number and the helix-start number have been shown to vary along individual microtubules⁹⁵, which could serve as limits for communication along the microtubule axis. These different lattice configurations lead to different protofilament skew angles and potentially different degrees of lattice strain in different regions of the lattice⁹⁶. A recent study also showed that microtubules displayed regions of local distortion, resulting in lattice structures that were either “squished” or “crinkled” (Fig. 4D, left) ⁹⁴. The distortions stemmed from changes in inter-protofilament curvature accommodated by a different hinge configuration of the M-loop, the driver of lateral interactions. These lattice deformations alter lateral contacts and provide a potential mechanism for lattice defects. Thus, the microtubule lattice is far from a static and regular structure. This structural plasticity has the benefit of allowing for different conformational states of tubulin, but it also puts potential constraints on the extent of cooperative communication through the lattice.

Cellular mechanisms for regulating microtubule growth

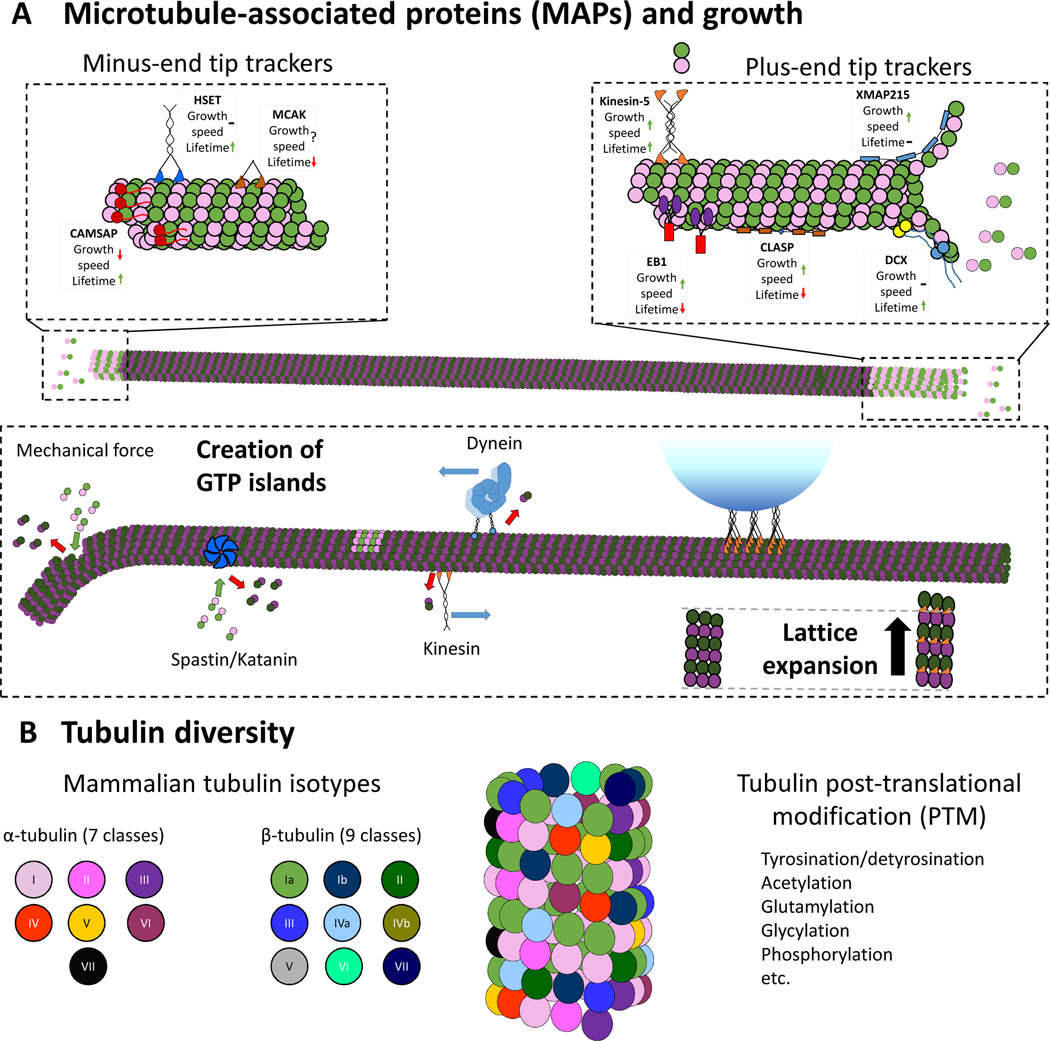
Most studies designed to understand the biochemical principles that underlie microtubule growth are carried out in controlled in vitro environments using purified tubulin. In contrast, the intracellular environment contains numerous regulatory proteins that alter microtubule structure and dynamics. One class of these is tip-trackers (Fig. 5A, top), which interact with microtubule plus- or minus-ends and alter polymerization rates and/or catastrophe frequencies⁹⁷. A more detailed understanding of mechanisms underlying microtubule growth should provide a framework for understanding how these regulatory protein achieve their functions. Conversely, studying how these regulators exert their actions can provide new insights into fundamental aspects of microtubule growth and depolymerization. End-binding proteins can exert effect through lattice compaction⁷⁴, capping of microtubule ends^72,98,99, promoting the curved-to-straight transition of tubulin at the tip^11,54,100, and by shuttling tubulin along the lattice to increase the local tubulin concentration at the growing tip¹⁰¹.

Figure 5. Cellular mechanisms for regulating microtubule growth.

(A) Microtubule associated proteins (MAPs) that alter microtubule dynamics. Tip-tracking proteins (top) can be specific to either the plus- or minus-end, and can alter either microtubule growth rates, growth lifetimes, or both (denoted by arrows). Motors and microtubule severing enzymes (bottom) can enhance lattice turnover and enable formation of GTP islands. Motor binding can also drive expansion of the lattice.

(B) Mammalian microtubules are formed from a number of different α- and β-tubulin isotypes, creating a mosaic microtubule lattice. Each isotype has its own unique impact on the structure, kinetics, and stability of the microtubules. Each tubulin isotype can be post-translationally modified, which can influence microtubule structure and dynamics.

In addition to exerting their influence at microtubule ends, regulatory proteins can also affect microtubule structure and dynamics through interactions with the microtubule lattice. Tubulin subunits can be removed from the lattice by physical perturbations, such as bending^46–48, or by chemomechanical forces exerted by microtubule severing proteins such as spastin and katanin^102–105. It was also recently shown that kinesin and dynein motors can exert sufficient force perpendicular to the microtubule wall to extract tubulin from the lattice¹⁰⁶. While extracting tubulin from the lattice can lead to microtubule breakage or depolymerization, it also allows for the incorporation of new GTP-tubulin into the lattice to create “GTP-islands” that can serve as sites where rescues occur during microtubule depolymerization^107–109. The mechanical forces and thermodynamics of how these proteins extract tubulin from the lattice are still being worked out, but this work has opened a new appreciation that microtubules as dynamic structures that are continually turning over and being remodeled not only at their ends but throughout the lattice.

Most cells contain multiple isotypes of both α- and β-tubulin that dimerize to generate a range of heterodimers ¹¹⁰ (Fig. 5), and isotype expression levels vary with cell type, resulting in cell-specific microtubule dynamics ¹¹¹. Accordingly, the brain-derived bovine or porcine tubulin used in most in vitro studies of microtubule dynamics contain a heterogeneous mixture of tubulin isotypes with diverse post-translational modifications. With recent breakthroughs in producing recombinant tubulin, it has become possible to uncover the functional impact of tubulin isotype on microtubule dynamics ^39,45,84,112. Along with functional assessments, single-isotype microtubules are being used to understand the structural differences that may be guiding these functional differences. Additionally, isotype-specific post-translational modifications such as detyrosination, glutamylation, and acetylation may alter the structural interactions between tubulin as well as their dynamic properties¹¹³. This diversity opens up a number of possible mechanisms by which microtubule dynamics can be altered over time, over space, and across cell types, a system referred to as the “tubulin code” ^114,115.

Conclusion

In recent years, the microtubule field has employed recombinant tubulin, advanced single-molecule techniques, and cutting-edge structural studies to rapidly expand our understanding of the kinetics of single tubulin interactions at growing microtubule tips. Despite this progress, the ultimate goal of connecting the mechanics and biochemistry of tubulin still lies in the future, and will require ongoing work on multiple fronts. As described here, there are very fundamental aspects of microtubule structure and growth that are hotly debated in the field. These include the magnitudes of the on- and off-rate constants for tubulin association at the growing plus end, the relative magnitudes of lateral and longitudinal bond free energies that stabilize tubulin in the lattice, and the mechanical work necessary to straighten tubulin in different nucleotide states. The precise shape of the growing microtubule tip, from blunt to tapered to splayed, is a manifestation of these different variables; thus, defining the plus- and minus-tip structures under various conditions is a high priority pursuit. Even more tantalizing is the emerging appreciation of the structural plasticity of the microtubule lattice, which brings up the possibility that protein binding can alter the structure and properties of the microtubule some distance away from the binding site. Thus, microtubules could serve as a mid- to long-distance communication pathway in cells. It is an exciting time in the microtubule field, and the advances on the biophysics and biochemistry of microtubule growth should lead to new paradigms with which to interpret cellular mechanisms of microtubule dynamics regulation and new perspectives to consider the impacts of tubulin diversity on microtubule function.