Abstract
Aims
Accurate determination of intra-atrial conduction velocity (CV) is essential to identify arrhythmogenic areas. The most optimal, commonly used, estimation methodology to measure conduction heterogeneity, including finite differences (FiD), polynomial surface fitting (PSF), and a novel technique using discrete velocity vectors (DVV), has not been determined. We aim (i) to identify the most suitable methodology to unravel local areas of conduction heterogeneities using high-density CV estimation techniques, (ii) to quantify intra-atrial differences in CV, and (iii) to localize areas of CV slowing associated with paroxysmal atrial fibrillation (PAF).
Methods and results
Intra-operative epicardial mapping (>5000 sites, interelectrode distances 2 mm) of the right and left atrium and Bachmann’s bundle (BB) was performed during sinus rhythm (SR) in 412 patients with or without PAF. The median atrial CV estimated using the DVV, PSF, and FiD techniques was 90.0 (62.4–116.8), 92.0 (70.6–123.2), and 89.4 (62.5–126.5) cm/s, respectively. The largest difference in CV estimates was found between PSF and DVV which was caused by smaller CV magnitudes detected only by the DVV technique. Using DVV, a lower CV at BB was found in PAF patients compared with those without atrial fibrillation (AF) [79.1 (72.2–91.2) vs. 88.3 (79.3–97.2) cm/s; P < 0.001].
Conclusions
Areas of local conduction heterogeneities were most accurately identified using the DVV technique, whereas PSF and FiD techniques smoothen wavefront propagation thereby masking local areas of conduction slowing. Comparing patients with and without AF, slower wavefront propagation during SR was found at BB in PAF patients, indicating structural remodelling.
Keywords: Atrial fibrillation, Sinus rhythm, High-resolution epicardial mapping, Cardiac electrophysiology, Effective conduction velocity
What’s new?
Polynomial surface fitting (PSF) and finite differences (FiD) are techniques to estimate intra-atrial conduction velocity (CV). The most optimal, commonly used, estimation methodology to measure local conduction heterogeneity has not been determined. We developed a novel technique using discrete velocity vectors (DVV). Areas of local conduction heterogeneities were most accurately identified using this DVV technique, whereas PSF and FiD techniques smoothen wavefront propagation thereby masking local areas of conduction slowing.
Various regional differences in CV and slowing of CV are present in all patients with different underlying heart diseases.
Comparing patients with and without atrial fibrillation (AF), slower wavefront propagation during sinus rhythm and an increased amount of slow CV areas were found at Bachmann’s bundle in paroxysmal AF patients, indicating areas of structural remodelled tissue.
Introduction
Speed and direction of atrial wavefront propagation through myocardium is described by the cardiac conduction velocity (CV). It provides important information about the underlying myocardium and is therefore widely used in electrophysiological studies to identify potential mechanisms for arrhythmogenesis. Areas with slower CV are considered as ‘diseased tissue’ and are associated with increased risk of wavefront re-entry which may initiate arrhythmias.1 Calculation of wavefront CV is frequently empirically determined based on relative distances and time differences of local tissue activation derived from activation maps, which requires that the direction of activation is known. However, the complexity of activity during arrhythmias such as atrial fibrillation (AF), low signal-to-noise ratio, and interference of far-field signals hampers accurate estimation of CV. Prior studies have introduced several techniques to estimate CV based on single- or multi-electrode catheters, such as finite differences (FiD) and polynomial surface fitting (PSF).2–5 However, spatial and temporal resolution is typically coarse and local conduction heterogeneities could be easily missed. Therefore, we developed a novel technique using discrete velocity vectors (DVV) to estimate CV and identify these areas of conduction heterogeneities. Intra-operative mapping during cardiac surgery provides the opportunity to collect high-density recordings of the epicardial surface of both atria. These recordings can be used to compute effective CV, and test and compare the different methodologies on large scale high-density mapping data. The goal of this study was therefore (i) to identify the most suitable methodology to unravel local areas of conduction heterogeneities using high-density CV estimation techniques, (ii) to quantify intra-atrial differences in CV, and (iii) to localize areas of CV slowing associated with paroxysmal atrial fibrillation (PAF).
Methods
Study population
The study population consisted of 412 successive adult patients undergoing elective open heart coronary artery bypass grafting, aortic or mitral valve surgery or a combination of valvular and bypass grafting surgery in the Erasmus Medical Centre Rotterdam. This study was approved by the institutional medical ethical committee (MEC2010-054/MEC2014-393).6,7 Written informed consent was obtained from all patients and patient characteristics (e.g. age, medical history, cardiovascular risk factors, and time in AF) were obtained from the patient’s medical record. The study population was classified into two groups: those without a history of AF (no AF group) and those with a history of PAF (PAF group).
Mapping procedure
Epicardial high-resolution mapping was performed prior to commencement of extra-corporal circulation, as previously described in detail.6,7 A temporal bipolar epicardial pacemaker wire attached to the RA free wall served as a reference electrode and the indifferent electrode consisted of a steel wire fixed to subcutaneous tissue of the thoracic cavity.
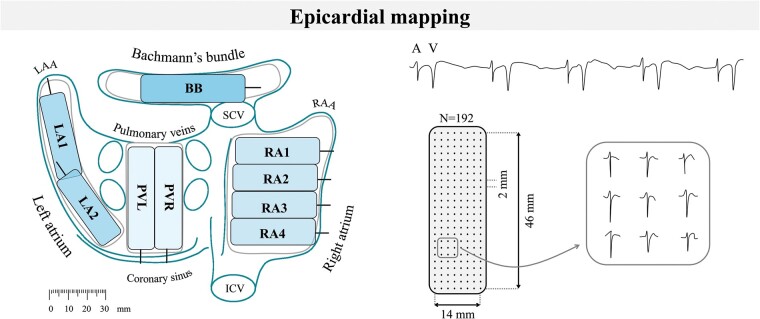
Epicardial mapping was performed with a 128-electrode array or 192-electrode array (electrode diameter, respectively, 0.65 or 0.45 mm, interelectrode distances 2.0 mm). Mapping was conducted by shifting the electrode array along predefined areas of the right atrium (RA), Bachmann’s bundle (BB), posterior wall between the pulmonary veins (PVA) and left atrial free wall (LA) between anatomical borders in a systematic order, covering the entire atrial epicardial surface as illustrated in the left panel of Figure 1. Omission of areas was avoided at the expense of possible small overlap between adjacent mapping sites. The RA was mapped from the cavotricuspid isthmus, shifting perpendicular to the caval veins towards the RA appendage; the PVA from the transverse sinus fold along the borders of the right and left pulmonary veins (PVR and PVL) down towards the atrioventricular groove and the left atrioventricular groove from the lower border of the left inferior pulmonary vein towards the LA appendage. Bachmann’s bundle was mapped from the tip of the LA appendage across the roof of the LA, behind the aorta towards the superior cavo-atrial junction.
Figure 1.
Projection of the 192-unipolar electrode array on a schematic posterior view of the atria (left) and epicardial, unipolar potentials recorded during 5 s of sinus rhythm containing atrial deflections (A) and far-field ventricular signals (V). Typical examples of nine unipolar potentials obtained from the RA are shown outside the mapping array (right). BB, Bachmann’s bundle; ICV, inferior caval vein; LA, left atrium; LAA, left atrial appendage; PV, pulmonary veins; RAA, right atrial appendage; RA, right atrium; SCV, superior caval vein.
Five seconds of sinus rhythm (SR) were recorded from every mapping site, including a surface ECG lead, a calibration signal of 2 mV and 1000 ms, a bipolar reference electrogram (EGM), and all unipolar epicardial EGMs. In patients who presented in AF, SR mapping was performed after electrical cardioversion. Data were stored on a hard disk after amplification (gain 1000), filtering (bandwidth 0.5–400 Hz), sampling (1 kHz), and analogue to digital conversion (16 bits).
Data analysis
Unipolar EGMs were semi-automatically analysed using custom-made software. Electrograms with injury potentials, recording sites with ≥25% excluded or missing EGMs and premature atrial complexes or aberrant beats were excluded from analysis.
The steepest negative slope of an atrial potential was marked as the local activation time (LAT), provided that the amplitude of the deflection was at least two times the signal-to-noise ratio of the EGM. In case of fractionated potentials, the activation time of the deflection with the steepest negative slope within a potential was taken as LAT. All annotations were manually checked with a consensus of two investigators. Conduction velocity was computed from LATs using three different methodologies including a FiD, PSF, and DVV technique. Slowing of conduction was defined as a local CV of <28 cm/s and conduction block as a difference in LAT between adjacent electrodes of ≥12 ms.8
Estimation of local conduction velocity
The CV vector of a point on a wavefront is given by
| (1) |
To estimate this vector, derivatives approximated at a given active grid-point are used to compute local CV estimates through time differences between neighbouring grid-points, as illustrated in Figure 2B.2,9 Using this FiD technique, CV vectors are computed at each point () in the grid. Gradients of activation were computed horizontally and vertically using the LATs of the neighbouring electrodes:
| (2) |
and
| (3) |
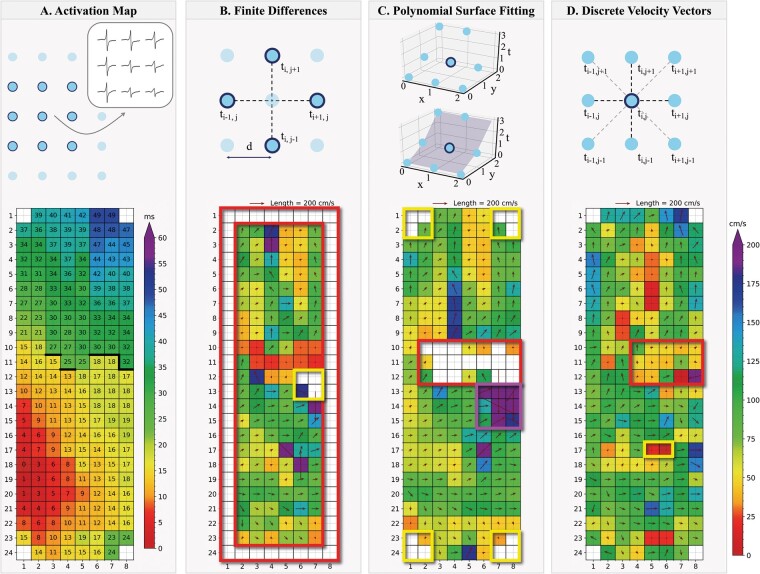
Figure 2.
Example of a colour-coded activation map (A) with corresponding CV maps estimated using the FiD (B), PSF (C), and DVV (D) techniques recorded at Bachmann’s bundle. Thick black lines in the activation map correspond with conduction block according to a time difference between adjacent electrodes of ≥12 ms. The coloured boxes indicate areas interest, e.g. border electrodes, areas of conduction block, simultaneous activated electrodes and conduction heterogeneities. (A) Selection of a 3 × 3 area containing LATs obtained from an activation map. (B) The FiD technique uses LATs on a grid with interelectrode distance . Gradients are computed along the dotted lines in the horizontal and vertical directions, using the LATs of the four highlighted electrodes to calculate the CV for the active point in the centre. (C) The PSF technique fits the surface (blue area) to a set of LATs adjacent to an active point (circled). The gradients of the fitted surface are used to calculate the CV for the active point. (D) The DVV technique uses LATs on a grid with interelectrode distance . Velocities are computed along the dotted lines in the horizontal, vertical and diagonal directions, using the LATs of the adjacent electrodes of an active point (circled). The CV of this active point is computed as the average of the velocity components in the horizontal and vertical directions. CV, conduction velocity; DVV, discrete velocity vectors; FiD, finite differences; LAT, local activation time; PSF, polynomial surface fitting.
The CV vector is then defined as
| (4) |
To reduce the impact of outliers and noise, local CV can also be estimated relying on fitting polynomial surfaces to space-time coordinates of activity, as demonstrated in Figure 2C.3 Both CV and direction of propagation are then computed from the gradient of the local polynomial surface. To estimate this vector, each active electrode and its neighbours were fitted using a standard least-squares algorithm to a smooth local quadratic polynomial surface covered by at least six electrodes
| (5) |
The fitted surface describes activation time as a function of continuous position , and to as coefficients of the fitted quadratic surface. If there are more than six electrodes available, the fit is minimized to smooth the data and reduce the impact of outliers. The gradient vector of the fitted surface defines the direction of propagation and can be found analytically,
| (6) |
The CV vector is then expressed as
| (7) |
where and . A measure for the reliability of the fit is the residual error estimated from the standard deviation over the N electrode site involved in the calculation of the polynomial surface:
| (8) |
where are the measured and the calculated LATs at N electrode sites. To avoid inclusion of inadequately represented CV vectors of areas containing spatial LAT heterogeneities, only surfaces with a residual error of <1.5 and quadratic coefficients (, and ) <1.5 were included in the analysis.10
A third method to estimate a CV vector uses neighbouring electrodes to the centre electrode at coordinates () to compute an average local propagation velocity by DVV, as illustrated in Figure 2D. There is a maximum of eight pairs of electrodes, the four diagonal pairs have components in both the horizontal and vertical directions, the horizontal pairs components in only the horizontal direction and the two vertical pairs in only the vertical direction. All the pairs with valid LATs are used to compute the mean velocity in both directions:
| (9) |
where
and
| (10) |
where
The number of valid electrode pairs in the horizontal and vertical direction is represented by and , respectively, which can be six at most. If adjacent electrodes have the same LAT, the velocity element of that electrode pair becomes zero. In order to increase the reliability of the CV estimate, only CVs with at least three CV vector estimates in both the horizontal and vertical direction are included. The average CV vector is then expressed as
| (11) |
From all CV vector estimates, the magnitude is calculated to compare all estimates independently of the propagation direction angle. The difference in CVs computed using two different methods is quantified by the normalized difference velocity index (NDVI) and is expressed as
| (12) |
The NDVI always ranges from −1 to +1, in which a negative value accounts for a larger CV of method 2, whereas a positive value accounts for a larger CV of method 1.
Statistical analysis
All data were tested for normality. Normally distributed data are expressed as mean ± standard deviation and analysed with a (paired) T-test or one-way ANOVA. Skewed data are expressed as median (25th–75th percentile) and analysed with a Kruskal–Wallis test, Mann–Whitney U test, or Wilcoxon signed-rank test. Categorical data are expressed as numbers and percentages, and analysed with a χ2 or Fisher’s exact test when appropriate. Correlation was determined by an ordinary least squares regression model. Distribution data were analysed with a two-sample Kolmogorov–Smirnov test. A P-value <0.05 was considered statistically significant. A Bonferroni correction was applied for comparison of the four atrial regions; a P-value of <0.0083 (0.05/6) was considered statistically significant.
Results
Study population
Clinical characteristics of the study population [N = 412, 305 male (74%), age 67 ± 10 years] are summarized in Supplementary material online, Table S1. Patients had ischaemic heart disease (IHD) (N = 238, 58%), valvular heart disease (VHD) (N = 97, 24%), or a combination of ischaemic and valvular heart disease (iVHD) (N = 77, 19%). (i)VHD (N = 174, 42%) was categorized by the predominant valvular lesion and consisted of aortic valve disease (AVD) (N = 107, 61%) or mitral valve disease (MVD) (N = 67, 39%). A minority of patients (N = 58, 14%) had a history of PAF.
Paroxysmal atrial fibrillation was most prevalent in patients with MVD (N = 22, 33%) compared with patients with AVD (N = 18, 17%) or only IHD (N = 18, 8%) (both P < 0.001). In addition, PAF was also more prevalent in patients with LA dilation (N = 24, 27% vs. N = 25, 14%, P = 0.011). Most patients had a normal left ventricular function (N = 314, 76%) and the majority used class II (N = 271, 66%) antiarrhythmic drugs.
Mapping data characteristics
A total of 4 019 926 potentials were analysed out of 5261 SR recordings of 5-s duration (±6 beats per recording). For all atrial regions, there was no difference between the median number of potentials per patient between the no AF and PAF group [RA: 4293 (3516–5554) vs. 4293 (3287–5412), P = 0.213; BB: 1110 (752–1316) vs. 954 (739–1217), P = 0.048; PVA: 2172 (1692–2719) vs. 2112 (1681–2602), P = 0.253; and LA: 1861 (1303–2531) vs. 1669 (1292–2279), P = 0.201].
Figure 2 shows a reference activation map during one SR beat (panel A) and the corresponding CV maps estimated using FiD, PSF, and DVV techniques (panels B–D). The CV estimates ranged from 78.4 (55.5–97.0) cm/s (FiD) to 80.7 (60.0–101.9) cm/s (PSF) and 88.2 (61.1–106.1) cm/s (DVV). Slowed CV was present in 10 mm2 (3.88%) (FiD), 0 mm2 (PSF), and 18 mm2 (4.79%) (DVV) of the estimated CV sites.
As demonstrated in Figure 2B, using the FiD technique, it was not possible to compute CVs of the electrodes located on the outer edge of the array (red box) or when LATs of all neighbouring electrodes contained the same LAT (yellow box). The FiD technique even estimated CVs up to maximal 400 cm/s, corresponding to twice the inter-electrode distance divided by the time resolution (1 kHz).
The PSF technique resulted in smoothened CV maps (Figure 2C), but therefore failed near areas of large local differences between LATs (caused by, e.g. conduction block) as the residual error and quadratic error was too large (red box). The PSF technique also failed to estimate CV vectors at electrodes adjacent to missing LATs near the outer edge of the electrode as <6 electrodes remained available at those areas (yellow boxes). In addition, this technique estimated very large CVs up to 600 cm/s or even larger at areas with multiple simultaneously activated electrodes (purple box).
In contrast, as demonstrated in Figure 2D, complete CV maps using all available LATs were constructed by applying the DVV technique. In addition, the DVV technique enables visualization of local conduction heterogeneities (yellow box), which were, in contrast, masked by the FiD and PSF techniques (panels B and C). In areas of conduction block and delay, the technique resulted in fasting of CV, while the PSF technique was not able to visualize CV (red boxes in panels C and D). The maximal CV estimated was 233 cm/s, whereas areas of simultaneously activated electrodes resulted in a CV of 0 cm/s.
Efficiency of conduction velocity estimation techniques
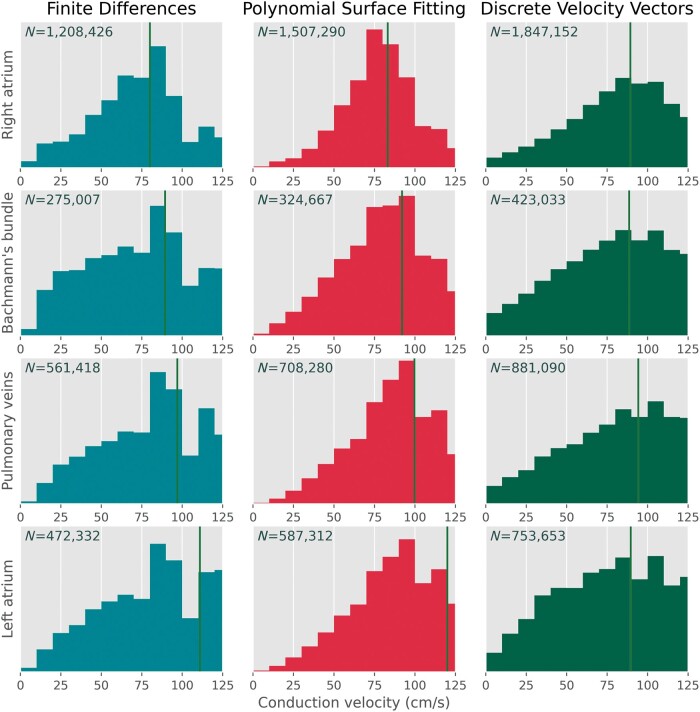
Comparisons of the CV magnitudes and propagation directions estimated by the three investigated methodologies are demonstrated in Table 1. The highest number of CVs were estimated using the DVV technique [N = 3 904 928 (97%)], followed by the PSF technique [N = 3 127 549 (78%), P < 0.001], whereas the FiD technique accounted for the least amount of CV estimates [N = 2 517 183 (63%), P < 0.001]. The distributions of CV estimates are demonstrated in Figure 3; ranges between 0 and 125 cm/s are depicted as especially areas of slow conduction are of particular interest in determining local conduction heterogeneities. Though the median CVs of the distributions for every region were relatively comparable between the three techniques, the PSF technique detected only a few very low CV estimates, while the FiD and specifically the DVV technique identified a larger number of low CV estimates.
Table 1.
Conduction velocity and propagation direction estimation
| Method | Location | N | CV (cm/s) | θ (°) |
|---|---|---|---|---|
| Finite differences | Total | 2 517 183 (63) | 89.4 (62.5–126.5) | 45.0 (−90.0 to 135.0) |
| RA | 1 208 426 (64) | 80.0 (57.1–100.0) | 108.4 (−18.4 to 146.3) | |
| BB | 275 007 (64) | 89.4 (55.5–126.5) | −53.1 (−90.0 to 0.0) | |
| PVA | 561 418 (61) | 97.0 (66.7–133.3) | −71.6 (−135.0 to 143.1) | |
| LA | 472 332 (60) | 110.9 (78.4–178.9) | 0.0 (−76.0 to 63.4) | |
| Polynomial surface fitting | Total | 3 127 549 (78) | 92.0 (70.6–123.2) | 18.4 (−105.4 to 126.9) |
| RA | 1 507 290 (80) | 83.2 (66.6–102.9) | 108.4 (−58.4 to 144.0) | |
| BB | 324 667 (76) | 92.0 (68.2–121.8) | −56.3 (−90.0 to −15.9) | |
| PVA | 708 280 (77) | 99.7 (77.3–130.2) | −102.5 (−145.0 to 123.7) | |
| LA | 587 312 (74) | 120.0 (85.7–187.4) | −21.8 (−82.4 to 51.1) | |
| Discrete velocity vectors | Total | 3 904 928 (97) | 90.0 (62.4–116.8) | 12.5 (−102.5 to 125.0) |
| RA | 1 847 152 (98) | 89.4 (64.9–111.8) | 91.7 (−85.9 to 143.1) | |
| BB | 423 033 (98) | 88.6 (58.3–117.3) | −56.1 (−90.7 to 0.0) | |
| PVA | 881 090 (96) | 94.3 (62.9–121.8) | −78.2 (−135.0 to 126.5) | |
| LA | 753 653 (96) | 89.6 (56.6–121.7) | −15.0 (−83.9 to 66.8) |
Values are presented as median (interquartile ranges) or as N (%).
BB, Bachmann’s bundle; CV, conduction velocity; LA, left atrium; PVA, pulmonary vein area; RA, right atrium; θ, propagation direction angle.
Figure 3.
Distribution histograms of all CV estimates computed using the FiD (turquoise/left, N = 2 517 549), PSF (red/middle, N = 3 127 549), and DVV (green/right, N = 3 904 928) techniques visualized between 0 and 125 cm/s. Each row represents CV estimate distribution recorded at the right atrium, Bachmann’s bundle, pulmonary vein area, and left atrium respectively. The green vertical line represents the median of the corresponding distribution. CV, conduction velocity; DVV, discrete velocity vectors; FiD, finite differences; PSF, polynomial surface fitting.
Comparison of the conduction velocity estimates
As demonstrated in Supplementary material online, Table S2, CV magnitudes of the FiD technique strongly correlated with estimates of the PSF technique (R2 = 0.864), while the largest difference in CV magnitudes and propagation direction angles was found between the PSF and DVV technique. These differences were mainly provoked by a larger amount of low CV magnitudes estimated by the DVV technique.
Focusing on the atrial regions, differences in the three techniques were most pronounced at the LA. Though the differences between the FiD and PSF were again relatively small, between the FiD and DVV, and PSF and DVV techniques the differences were more pronounced. In both comparisons, the majority of these CV magnitudes estimated by DVV was lower.
Examples of heterogeneous conduction using discrete velocity vectors
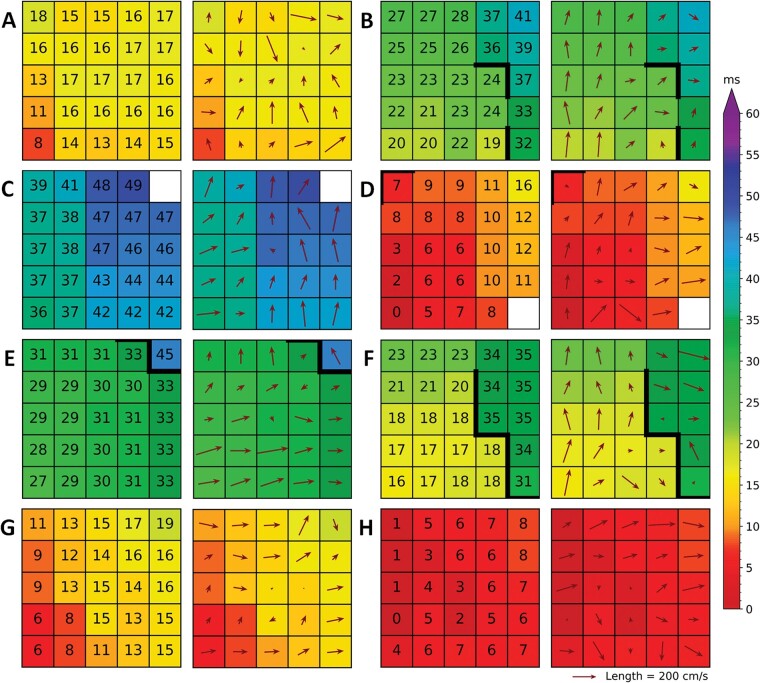
Figure 4 shows eight examples of local heterogeneous conduction at various locations of the atria. As demonstrated by the corresponding coloured activation maps, activation is locally disrupted. This is in turn visualized by a deviant CV arrow when compared with the surrounding electrodes. At some sites local heterogeneous conduction is accompanied by a line of conduction block (time difference between adjacent electrodes of ≥12 ms), near areas of conduction delay (time difference between adjacent electrodes of ≥7 ms), a colliding wavefront or small local changes in activation direction and velocity.
Figure 4.
Various examples (A–H) of local heterogeneities visualized by the discrete velocity vectors (DVV) technique (right with vectors) accompanied by the colour-coded local activation maps (left with local activation times). Thick black lines in the activation map correspond with conduction block according to a time difference between adjacent electrodes of ≥12 ms.
Regional differences in conduction velocity
Characteristics of CV estimates were subdivided according to the corresponding atrial recording regions (RA, BB, PVA, and LA) and are demonstrated in Table 2. All atrial regions differed significantly (P < 0.001 for each), except between the RA and LA using the DVV technique (P = 0.021). In general, higher CV estimates were found on the left side of the atria. Interestingly, CVs estimated at BB were higher compared with the RA, but lower compared with the left side.
Table 2.
Conduction velocities per patient subdivided in those with or without AF
| Total | Without AF | PAF | P-value | |
|---|---|---|---|---|
| Right atrium | ||||
| Number of potentials | 4293 (3485–5511) | 4293 (3516–5554) | 4293 (3287–5412) | 0.213 |
| FiD: CV (cm/s) | 78.4 (74.3–80.0) | 78.4 (74.3–80.0) | 78.4 (74.3–80.0) | 0.284 |
| Slow CV (%) | 5.5 (2.6–9.2) | 5.5 (2.6–9.1) | 5.3 (2.5–9.9) | 0.462 |
| PSF: CV (cm/s) | 82.4 (77.3–88.2) | 83.2 (77.3–88.2) | 80.4 (77.6–89.2) | 0.284 |
| Slow CV (%) | 1.6 (0.7–2.7) | 1.6 (0.7–2.6) | 1.8 (0.8–3.0) | 0.250 |
| DVV: CV (cm/s) | 89.1 (83.3–94.3) | 89.3 (83.3–94.3) | 88.0 (82.3–93.4) | 0.309 |
| Slow CV (%) | 4.9 (3.6–6.8) | 4.9 (3.6–6.7) | 5.2 (3.6–6.9) | 0.422 |
| Bachmann’s bundle | ||||
| Number of potentials | 1104 (748–1314) | 1110 (752–1316) | 954 (739–1217) | 0.048 |
| FiD: CV (cm/s) | 80.0 (74.3–97.0) | 89.4 (78.4–97.0) | 78.4 (65.1–89.4) | <0.001 |
| Slow CV (%) | 6.5 (2.4–14.2) | 5.8 (2.2–13.3) | 10.1 (5.5–18.2) | <0.001 |
| PSF: CV (cm/s) | 92.3 (84.4–99.7) | 94.3 (85.5–99.7) | 85.9 (79.2–94.9) | <0.001 |
| Slow CV (%) | 2.4 (0.8–4.6) | 2.1 (0.8–4.3) | 3.9 (2.3–7.8) | <0.001 |
| DVV: CV (cm/s) | 86.9 (77.3–96.4) | 88.3 (79.3–97.2) | 79.1 (72.2–91.2) | <0.001 |
| Slow CV (%) | 6.7 (4.1–11.5) | 6.6 (3.9–11.1) | 8.3 (5.8–13.6) | 0.004 |
| Pulmonary vein area | ||||
| Number of potentials | 2146 (1692–2717) | 2172 (1692–2719) | 2112 (1681–2602) | 0.254 |
| FiD: CV (cm/s) | 97.0 (89.4–100.0) | 97.0 (89.4–100.0) | 94.3 (80.0–97.0) | 0.012 |
| Slow CV (%) | 2.5 (0.5–6.4) | 2.4 (0.4–6.0) | 3.8 (0.8–8.5) | 0.077 |
| PSF: CV (cm/s) | 99.7 (92.3–110.9) | 99.7 (93.7–111.0) | 98.6 (89.4–104.0) | 0.009 |
| Slow CV (%) | 1.0 (0.3–2.1) | 0.9 (0.3–1.9) | 1.4 (0.5–3.3) | 0.014 |
| DVV: CV (cm/s) | 94.3 (83.4–101.0) | 94.3 (83.3–101.0) | 91.7 (85.8–100.5) | 0.371 |
| Slow CV (%) | 5.6 (3.5–9.4) | 5.6 (3.5–9.4) | 5.8 (3.5–9.6) | 0.486 |
| Left atrium | ||||
| Number of potentials | 1853 (1303–2515) | 1861 (1303–2531) | 1669 (1292–2279) | 0.201 |
| FiD: CV (cm/s) | 110.9 (100.0–133.3) | 110.9 (100.0–133.3) | 110.9 (97.0–126.5) | 0.003 |
| Slow CV (%) | 1.5 (0.2–4.6) | 1.5 (0.2–4.5) | 2.6 (0.6–6.6) | 0.060 |
| PSF: CV (cm/s) | 120.0 (107.3–134.2) | 121.8 (108.6–139.5) | 115.0 (105.2–123.0) | 0.002 |
| Slow CV (%) | 0.7 (0.2–1.8) | 0.7 (0.2–1.7) | 0.7 (0.2–2.0) | 0.280 |
| DVV: CV (cm/s) | 90.2 (82.2–97.0) | 90.4 (82.2–97.2) | 89.6 (83.1–95.0) | 0.450 |
| Slow CV (%) | 6.8 (5.1–9.7) | 6.8 (5.1–9.8) | 7.0 (5.0–9.2) | 0.354 |
Values are presented as median (inter-quartile ranges). The P-values indicate significance between the without AF and PAF group.
AF, atrial fibrillation; DVV, discrete velocity vectors; FiD, finite differences; PAF, paroxysmal atrial fibrillation; PSF, polynomial surface fitting.
All atrial regions differed significantly in the amount of slow CV areas (P < 0.006 for each). The most amount of slow CV areas were found at BB, followed by the RA. Using the DVV technique, a high amount of slow CV areas were found at the LA while the other techniques did not identified large areas of slow CV.
Impact of atrial fibrillation episodes
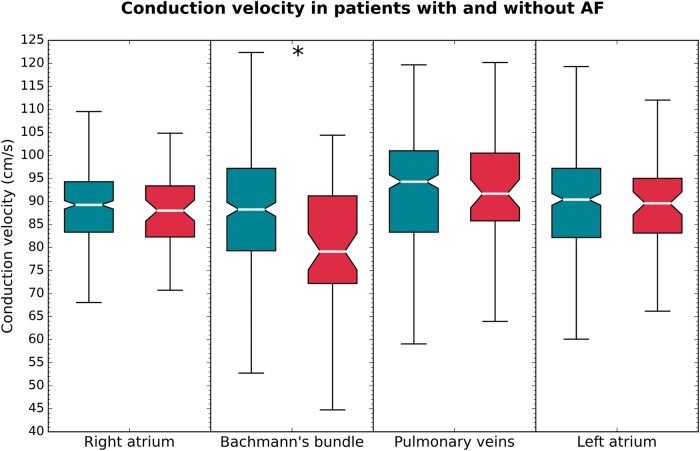
Regional median CV distributions using the DVV technique in patients with and without history of AF are illustrated in Figure 5. All CV techniques demonstrated that the median CV at BB was lower in PAF patients compared with those without AF (P < 0.001 for all comparisons). In addition, using the FiD and PSF techniques, a lower median CV was found at the PVA and LA in PAF patients as well [FiD, PVA: 94.3 (80.0–97.0) vs. 97.0 (89.4–100.0) cm/s; P = 0.012 and LA: 110.9 (97.0–126.5) vs. 110.9 (100.0–133.3) cm/s; P = 0.003. PSF, PVA: 98.6 (89.4–104.0) vs. 99.7 (93.7–111.0) cm/s; P = 0.009 and LA: 115.0 (105.2–123.0) vs. 121.8 (108.6–139.5) cm/s; P = 0.002], although the difference was less prominent compared with BB.
Figure 5.
Boxplots of the conduction velocities at various atrial regions in patients without (turquoise) and with (red) history of paroxysmal atrial fibrillation. Statistical significance is indicated by an asterisk.
Using all CV techniques, more slow CV areas were identified at BB in patients with history of PAF compared with those without AF [FiD: 10.1 (5.5–18.2) % and 5.8 (2.2–13.3) %; P < 0.001 an PSF: 3.9 (2.3–7.8) % vs. 2.1 (0.8–4.3) %; P < 0.001 and DVV: 8.3 (5.8–13.6) % vs. 6.6 (3.9–11.1) %; P = 0.004]. In addition, using the PSF technique, more slow CV areas were found at the PVA in patient with PAF [0.9 (0.3–1.9) % vs. 1.4 (0.5–3.3) %, P = 0.014].
Discussion
By estimating high-density CVs, this study demonstrated that local conduction heterogeneities could be most accurately identified by the DVV technique. All techniques revealed that the slowest conduction was observed at the RA and BB yet both the FiD and PSF techniques were unable to identify local conduction heterogeneities as these were masked by the smoothing properties of both techniques. All CV estimation techniques showed that there was a considerable variation in CV between all atrial regions. A lower CV was found at BB in patients with PAF compared with those without AF.
Conduction velocity estimate techniques
Calculation of CV is frequently based on a distance travelled by a wavefront in a unit of time, resulting in an accurate estimate if there is a one-dimensional propagation and the direction of propagation is known. However, in the case of local conduction heterogeneities, a more sophisticated method is required enabling estimation of local CV (‘effective’ CV estimate) indicative of the underlying local substrate.
During a standard electrophysiology study, multi-electrode catheters enable CV estimation by triangulation. However, this methodology is limited by the number and size of electrodes and it is assumed that the wavefront is locally planar.9 In a number of mapping studies, this method has been used to construct global CV maps which were sequentially acquired during stable rhythms. Data interpolation was then additionally used to generate high-density CV maps. However, this technique may be sensitive to errors as exact positions of the catheter electrodes with relatively larger electrode diameters and interelectrode distances are required in order to estimate CV and reconstruct global CV maps. Using regularly spaced high-density electrode arrays, simultaneous recordings on a high spatial resolution scale enable analysis of complex and heterogeneous patterns of activation. Hence, insufficient spatial and temporal resolution is therefore essential. A low temporal resolution can result in areas of simultaneous activation, though simultaneous activated electrodes on a larger area (e.g. the full 3 × 3 area) were a very rare event in our data. Furthermore, the handling of simultaneous activation by the three different techniques varies as well, though this is mostly in the methods’ nature. Inappropriate application may result in high conduction velocities which are physiologically impossible. These areas can, however, easily be recognized and removed from the data. Despite a widely use of the FiD and PSF techniques in literature, these methodologies have disadvantages as demonstrated in the present study and these techniques are mainly applied on optical mapping recordings.
Although the FiD technique is straightforward to implement, it is very sensitive to missing data and generally amplifies noise artefacts. These effects could be prevented by data interpolation or modification of the algorithm, but the accuracy of such interpolation can be questioned. In addition, as this technique uses only 4 LATs with twice the interelectrode distance, the FiD technique has a lower resolution compared with the other techniques. This lower resolution leads to less detailed velocity estimates which result in more smoothened velocity vectors, thereby masking areas of local conduction heterogeneity. The PSF technique, on the other hand, is robust to missing or noisy data, but needs at least six electrodes to estimate a local polynomial surface from which the CV can be determined, which is a problem at electrodes near the outer edge of a multi-electrode array. A solution might be to include a larger area of electrodes in the algorithm. However, this is disadvantageous as a larger atrial area is then fitted to a polynomial surface, thereby generalizing local conduction heterogeneities which, consequently, may disappear. Moreover, as this technique is based on surface fitting, in which a fit is minimized to smooth the data and reduce the impact of outliers, it also smoothens true local conduction heterogeneities. This approach masks these conduction heterogeneities which are of specific interest in defining areas of structural remodelled tissue. The DVV technique, however, is always able to perform a CV estimation using the surrounding electrodes, but its reliability drops when there are less electrodes available. Therefore, at least three electrodes in both the horizontal and vertical direction have to be available to perform an estimation. In addition, by using all surrounding electrodes, but without any smoothing properties, the DVV technique is able to identify local conduction heterogeneity, whereas these areas are missed by both other techniques.
Regional differences in conduction velocity
Atrial wavefront propagation occurs preferentially and faster along the longitudinal direction to the fibre orientation.11 It is therefore generally assumed that the longitudinal parallel orientation of prominent muscle bundles, e.g. the crista terminalis and BB, results in a higher CV, making it preferential routes of interatrial conduction. On the other hand, differently aligned overlapping fibres will result in more complex activation patterns. As all techniques tested use the same LATs, the major difference between the techniques is that the FiD and PSF techniques resulted in more smoothened velocity maps which may mask areas with varying fibre orientations. Hence, chaotic fibre arrangement causing conduction heterogeneity might be missed with the FiD and PSF methodologies.
In early animal studies, CV in the prominent muscle bundles was indeed increased.12–14 However, Teuwen et al.15 demonstrated that CV at BB is only ∼90 cm/s in patients without AF, comparable with a CV of 88 cm/s recorded at the RA free wall in a study of Hansson et al.16 As in the early animal studies CV was measured between only a few points, CV at BB could have easily been overestimated because wavefronts from the RA could have been fused with wavefronts entering the central part of BB from the septum. Our study showed that CV computed locally from high-density electrode arrays at the RA and BB is indeed comparable with the CV estimates at RA and BB of both studies.
In our study, CV estimates from the PVA were even higher compared with the RA and BB in all used techniques. Arora et al.17 found slowed epicardial conduction of 31.3 cm/s at the superior pulmonary veins, while an epicardial CV of 90.2 cm/s was recorded at the remainder of the PVA. These results are in accordance with our results computed using the DVV technique and the LA recordings. However, even larger CV estimates were computed using the FiD and PSF techniques at these areas. This could be the result of the smoothing properties of the aforementioned techniques, as the absolute differences and NDVI between these techniques were very small at the PVA.
However, at the LA these differences were much larger, probably caused by the limited time resolution (1 kHz), which results in simultaneously activated electrodes. A high CV at the LA and PVA could be caused by their tissue structure and wavefront geometry. As the excitation front in the RA is mostly convex (curving outward), CV is consequently slower compared with a planar or concave (curving inward) wavefronts resulting into current-to-load mismatches.18 In addition, the LA is composed of several overlapping layers of differently aligned myocardial fibres, resulting a smooth and uniform thick wall, although small regional variations in thickness have been found.19 In contrast, muscular bundles in the RA are larger, e.g. the terminal crest, and due to the presence of pectinate muscles, the RA wall is not of uniform thickness. As CV is also affected by muscle thickness and wall curvature, these smaller differences in the LA could result in higher CVs.20 In addition, as morphology of the LA and RA is completely different (smooth vs. trabeculated wall), regional differences between the LA and RA could be expected.
Influence of atrial fibrillation episodes
Changes in CV can be caused by various mechanisms, e.g. remodelling of gap junctions, mechanical stress, or non-uniform anisotropy. In our study, the most prominent differences in CV between patients with and without AF were found at BB. At this site, recent studies indeed found more conduction disorders and decreased unipolar single potential amplitudes due to loss of S-wave amplitudes during SR in patients with AF or developed post-operative AF.15,21,22 In addition, more fibro-fatty tissue and fibrotic patches were found at BB in patients with PAF, which may result in a decreased CV caused by impaired cell-to-cell connections.23 This could also explain the increased amount of slow CV areas at BB in patients with PAF.
Study limitations
Whether general anaesthesia and intraoperative drugs influence conduction is yet to be investigated; however, a standard anaesthetic protocol was used for all patients and SR was confirmed during all mapping procedures. Therefore, possible effects of anaesthesia would be equally dispersed among the patient population. In addition, high‐resolution mapping of the interatrial septum could not be performed with our closed beating heart approach.
Conclusion
Areas of local conduction heterogeneities were most accurately identified using the DVV technique, whereas PSF and FiD techniques smoothen wavefront propagation thereby masking local areas of conduction slowing. In addition, DVV is able to estimate substantially more CVs when compared with the other techniques. Using all techniques, various regional differences in CV were found in all patients. Comparing patients with and without AF, slower wavefront propagation during SR and an increased amount of slow CV areas were found at BB in PAF patients, indicating areas of structural remodelled tissue.
Supplementary material
Supplementary material is available at Europace online.
Supplementary Material
Acknowledgements
The authors would like to kindly thank our colleagues A. Yaksh, MD, PhD, C.P. Teuwen, MD, PhD, E.A.H. Lanters, MD, J.M.E. van der Does, MD, PhD, E.M.J.P. Mouws, MD, PhD, C.A. Houck, MD, PhD, R. Starreveld, PhD, C.S. Serban, DVM, R.K. Kharbanda, MD, L.N. van Staveren, MD, W.F.B. van der Does, MD for their help with acquiring the mapping data and we also would like to kindly thank the cardiothoracic surgeons J.A. Bekkers, MD, PhD, W.J. van Leeuwen, MD, F.B.S. Oei, MD, F.R.N. van Schaagen, MD, P.C. van de Woestijne, MD for their contribution to this work.
Funding
N.M.S.G. was supported by funding grants from CVON-AFFIP [914728], NWO-Vidi [91717339], Biosense Webster USA [ICD 783454], and Medical Delta. This research (IIS-331) was conducted with financial support from the Investigator-Initiated Study Program of Biosense Webster, Inc.
Conflict of interest: none declared.
Data availability
The data underlying this article will be shared on reasonable request to the corresponding author.
References
- 1. King JH, Huang CL, Fraser JA.. Determinants of myocardial conduction velocity: implications for arrhythmogenesis. Front Physiol 2013;4:154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Salama G, Kanai A, Efimov IR.. Subthreshold stimulation of Purkinje fibers interrupts ventricular tachycardia in intact hearts. Experimental study with voltage-sensitive dyes and imaging techniques. Circ Res 1994;74:604–19. [DOI] [PubMed] [Google Scholar]
- 3. Bayly PV, KenKnight BH, Rogers JM, Hillsley RE, Ideker RE, Smith WM.. Estimation of conduction velocity vector fields from epicardial mapping data. IEEE Trans Biomed Eng 1998;45:563–71. [DOI] [PubMed] [Google Scholar]
- 4. Weber FM, Schilling C, Seemann G, Luik A, Schmitt C, Lorenz C. et al. Wave-direction and conduction-velocity analysis from intracardiac electrograms—a single-shot technique. IEEE Trans Biomed Eng 2010;57:2394–401. [DOI] [PubMed] [Google Scholar]
- 5. Konings KT, Kirchhof CJ, Smeets JR, Wellens HJ, Penn OC, Allessie MA.. High-density mapping of electrically induced atrial fibrillation in humans. Circulation 1994;89:1665–80. [DOI] [PubMed] [Google Scholar]
- 6. Lanters EA, van Marion DM, Kik C, Steen H, Bogers AJ, Allessie MA. et al. HALT & REVERSE: hsf1 activators lower cardiomyocyt damage; towards a novel approach to REVERSE atrial fibrillation. J Transl Med 2015;13:347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. van der Does LJ, Yaksh A, Kik C, Knops P, Lanters EA, Teuwen CP. et al. QUest for the Arrhythmogenic Substrate of Atrial fibRillation in Patients Undergoing Cardiac Surgery (QUASAR Study): rationale and design. J Cardiovasc Transl Res 2016;9:194–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Allessie MA, de Groot NM, Houben RP, Schotten U, Boersma E, Smeets JL. et al. Electropathological substrate of long-standing persistent atrial fibrillation in patients with structural heart disease: longitudinal dissociation. Circ Arrhythm Electrophysiol 2010;3:606–15. [DOI] [PubMed] [Google Scholar]
- 9. Cantwell CD, Roney CH, Ng FS, Siggers JH, Sherwin SJ, Peters NS.. Techniques for automated local activation time annotation and conduction velocity estimation in cardiac mapping. Comput Biol Med 2015;65:229–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Houben RP, Allessie MA.. Processing of intracardiac electrograms in atrial fibrillation. Diagnosis of electropathological substrate of AF. IEEE Eng Med Biol Mag 2006;25:40–51. [DOI] [PubMed] [Google Scholar]
- 11. Spach MS, Miller WT III, Geselowitz DB, Barr RC, Kootsey JM, Johnson EA.. The discontinuous nature of propagation in normal canine cardiac muscle. Evidence for recurrent discontinuities of intracellular resistance that affect the membrane currents. Circ Res 1981;48:39–54. [DOI] [PubMed] [Google Scholar]
- 12. Dolber PC, Spach MS.. Structure of canine Bachmann's bundle related to propagation of excitation. Am J Physiol 1989;257:H1446–1457. [DOI] [PubMed] [Google Scholar]
- 13. Goodman D, van der Steen AB, van Dam RT.. Endocardial and epicardial activation pathways of the canine right atrium. Am J Physiol 1971;220:1–11. [DOI] [PubMed] [Google Scholar]
- 14. Wagner ML, Lazzara R, Weiss RM, Hoffman BF.. Specialized conducting fibers in the interatrial band. Circ Res 1966;18:502–18. [DOI] [PubMed] [Google Scholar]
- 15. Teuwen CP, Yaksh A, Lanters EA, Kik C, van der Does LJ, Knops P. et al. Relevance of conduction disorders in Bachmann's bundle during sinus rhythm in humans. Circ Arrhythm Electrophysiol 2016;9:e003972. [DOI] [PubMed] [Google Scholar]
- 16. Hansson A, Holm M, Blomstrom P, Johansson R, Luhrs C, Brandt J. et al. Right atrial free wall conduction velocity and degree of anisotropy in patients with stable sinus rhythm studied during open heart surgery. Eur Heart J 1998;19:293–300. [DOI] [PubMed] [Google Scholar]
- 17. Arora R, Verheule S, Scott L, Navarrete A, Katari V, Wilson E. et al. Arrhythmogenic substrate of the pulmonary veins assessed by high-resolution optical mapping. Circulation 2003;107:1816–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kleber AG, Rudy Y.. Basic mechanisms of cardiac impulse propagation and associated arrhythmias. Physiol Rev 2004;84:431–88. [DOI] [PubMed] [Google Scholar]
- 19. Ho SY, Anderson RH, Sanchez-Quintana D.. Atrial structure and fibres: morphologic bases of atrial conduction. Cardiovasc Res 2002;54:325–36. [DOI] [PubMed] [Google Scholar]
- 20. Rossi S, Gaeta S, Griffith BE, Henriquez CS.. Muscle thickness and curvature influence atrial conduction velocities. Front Physiol 2018;9:1344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Van Schie MS, , StarreveldR, , Roos-SeroteMC, , TaverneYJHJ, , Van SchaagenFRN, , Bogers AJJC. et al. Classification of sinus rhythm single potential morphology in patients with mitral valve disease. Europace 2020;22:1509–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Heida A, van der Does WFB, van Staveren LN, Taverne YJHJ, Roos-Serote MC, van Bogers AJJC et al.. Conduction heterogeneity: impact of underlying heart disease and atrial fibrillation. JACC 2020;6:1844–54. [DOI] [PubMed] [Google Scholar]
- 23. Becker AE. How structurally normal are human atria in patients with atrial fibrillation? Heart Rhythm 2004;1:627–31. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying this article will be shared on reasonable request to the corresponding author.