Spatial distribution characteristics of stomata at the areole level in Michelia cavaleriei var. platypetala (Magnoliaceae)

Abstract

Background and Aims

In hierarchically reticulate venation patterns, smaller orders of veins form areoles in which stomata are located. This study aimed to quantify the spatial relationship among stomata at the areole level.

Methods

For each of 12 leaves of M. cavaleriei var. platypetala, we assumed that stomatal characteristics were symmetrical on either side of the midrib, and divided the leaf surface on one side of the midrib into six layers equidistantly spaced along the apical–basal axis. We then further divided each layer into three positions equidistantly spaced from midrib to leaf margin, resulting in a total of 18 sampling locations. In addition, for 60 leaves, we sampled three positions from midrib to margin within only the widest layer of the leaf. Stomatal density and mean nearest neighbour distance (MNND) were calculated for each section. A replicated spatial point pattern approach quantified stomatal spatial relationships at different distances (0–300 μm).

Key Results

A tendency towards regular arrangement (inhibition as opposed to attraction or clustering) was observed between stomatal centres at distances <100 μm. Leaf layer (leaf length dimension) had no significant effect on local stomatal density, MNND or the spatial distribution characteristics of stomatal centres. In addition, we did not find greater inhibition at the centre of areoles, and in positions farther from the midrib.

Conclusions

Spatial inhibition might be caused by the one-cell-spacing rule, resulting in more regular arrangement of stomata, and it was found to exist at distances up to ~100 μm. This work implies that leaf hydraulic architecture, consisting of both vascular and mesophyll properties, is sufficient to prevent important spatial variability in water supply at the areole level.

INTRODUCTION

The photosynthetic capacity of vascular plants depends on the amount of photosynthetic biomass per unit area (Jurik, 1986; Niinemets, 1999; Poorter et al., 2009). Maximum leaf photosynthesis rate scales positively with the density of stomata and vein density (Xiong and Flexas, 2020). In addition, the rate of photosynthesis also depends on leaf size, which determines leaf temperature at a given radiation input and water loss rate (Wright et al., 2017). This interdependence presumably reflects the relationship between stomatal conductance and photosynthetic rate (McElwain et al., 2016; Baresch and Crifò, 2019; Xiong and Flexas, 2020). Vein density across the majority of dicot species is a function of the hierarchically reticulate venation patterns, which permit larger lamina areas and a very efficient hydraulic delivery system compared with other leaf venation patterns (Carvalho et al., 2018). Hierarchical reticulate venation patterns, in turn, lead to division of the leaf lamina into many small areoles in which stomata are located (Brodribb et al., 2010).

Prior studies have shown that stomatal density is negatively correlated with stomatal size, i.e. a lower stomatal density corresponds to a larger stomatal size (Franks and Beerling, 2009). On average, the number of stomata within an areole is observed to be positively related to the areole size for many plant groups (Fiorin et al., 2016). Although prior studies have shown a negative correlation between the lamina surface area occupied by vascular bundle sheaths and stomatal density (Baresch and Crifò, 2019), the spatial relationship between stomata has not been extensively examined, despite the importance of physiological characteristics that depend on the spatial relationships between stomata, including stomatal density (Royer and Wilf, 2006; Sack and Scoffoni, 2013).

In this study we use methods of replicated spatial point pattern analysis to quantify the spatial relationship between the loci of stomata and other morphometric features of a selected group of leaves drawn from the Magnoliaceae. These taxa were selected because the Magnoliaceae have an entire leaf lamina (which makes sampling of stomatal distribution patterns relatively simple), a typical hierarchical structure of reticulate leaf venation patterns (from first-order to fourth-order veins), and because variation in areole size is smaller than in other plant families. This feature permits a more robust spatial statistical analysis using fewer species. We used Ripley’s K function (Ripley, 1977) to examine the spatial distribution of stomata with respect to transects across the lamina surface. This function characterizes the second-order properties of any stationary isotropic point process. It is used widely in the analysis of spatial and spatio-temporal point patterns to detect inhibitory, random or aggregated relationships among events at different distances (Ripley, 1977). The majority of spatial point pattern analysis methods have focused on non-replicated point processes, which limits the generalizability of any findings (Loosmore and Ford, 2006). Comparatively few studies have employed replicated spatial point pattern analysis methods, which are helpful for analysing the spatial structures and patterns among events in microscopic sections (Diggle et al., 1991, 2000; Hahn, 2012).

In this study, we hypothesized that within a limited epidermal area (within an areole) there exists an inhibitory relationship between stomata at a small spatial scale because of competition among stomata for available space. Ripley’s K function was used to estimate the spatial scale of this effect. The inhibitory hypothesis was driven by the one-cell-spacing rule followed by the majority of plant species during epidermal development: stomata are separated by at least one epidermal cell (Salisbury, 1928; Bergmann and Sack, 2007). This has been functionally interpreted by Papanatsiou et al. (2016) in terms of epidermal cells acting as reservoirs of ions to supply adjacent stomata, as well as by Franks and Farquhar (2007), where epidermal cells between stomata are necessary as they give up volume to allow pores to open. The ratio of the distance between veins to the depth of the veins away from the leaf surface, the vascular architecture and transport capacity can largely affect leaf hydraulic optimization, stomatal conductance and water use efficiency (Zwieniecki and Boyce, 2014; Rockwell and Holbrook, 2017). Fiorin et al. (2016) found the presence of free-ending veinlets (FEVs) caused the minimum mean distance of stomata from the nearest leaf veins to be invariant with areole size for most of the studied 31 angiosperm species from different biomes. Considering that FEVs are common in hierarchical reticulate veins of dicots, we further hypothesized that FEVs might have resulted in a homogeneous environment for stomatal distribution within an areole because of the availability of water transport from surrounding veins around the areole and the veinlet. This might lead to a lack of spatial interaction between stomata outside of the small-scale inhibition that preserves the one-cell-spacing rule. These hypotheses were evaluated empirically by sampling stomatal distributions along different transects passing through different vein orders to determine whether different positions on the leaf lamina have statistically significant differences in stomatal densities and spatial arrangements. This study addressed three issues: (1) whether there is spatial inhibition (regularity), randomness or clustering (aggregation) between stomatal centres at the areole level; (2) whether there are significant differences in the spatial arrangements of stomata between different positions along transects (e.g. near the leaf margin versus near the midrib); and (3) whether replicated spatial point pattern data provide a more robust statistical picture of the spatial relationship of stomata than does a single spatial point pattern data set.

MATERIALS AND METHODS

Leaf collection and microscopic sections

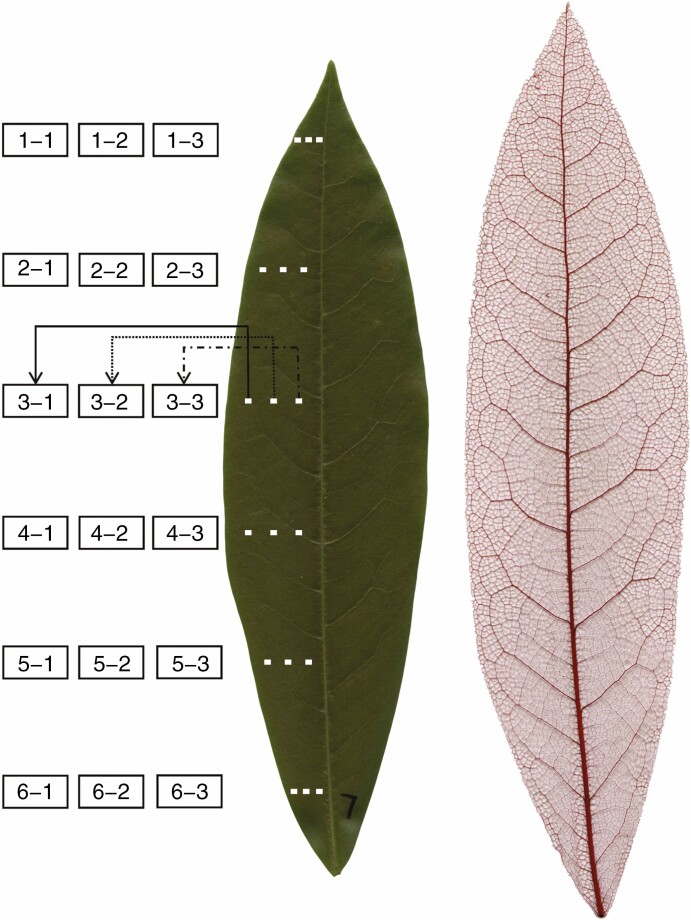
A total of 72 leaves were sampled from four mature trees of Michelia cavaleriei var. platypetala (Magnoliaceae), growing in Nanjing Forestry University campus, Nanjing, China (32°4′53.14″ N, 118°48′27.68″ E) in early September, 2020. The trees ranged in diameter at breast height from 9·5 to 12·5 cm and in height from 5·5 to 6 m. All leaves were sampled from the middle canopy of trees without distinguishing current-year leaves from older leaves (the leaf life-span of M. cavaleriei var. platypetala is 2–3 years). From the sampled leaves, 12 leaves were randomly selected, and 18 rectangular sections (1·2 mm × 0·9 mm) were collected from each of these leaves as illustrated in Fig. 1. The sections were positioned equidistantly from the leaf apex to the petiole (six layers). Because of the bilateral symmetry of the elliptical leaf shape of this tree species, we only needed to take sections of stomata from the left side of each leaf. From each layer, three sections were positioned equidistantly between the left leaf margin and the midrib (see Fig. 1 for details). Among the six layers, layer 3 was the closest to the leaf minor (width) axis, i.e. the maximum leaf dimension perpendicular to the leaf major (length) axis (straight line through the leaf apex and base). From the remaining 60 leaves, three sections (1.2 mm × 0.9 mm) were sampled from the left leaf margin to the midrib on the leaf width axis; their sampling positions are similar to those on layer 3 as shown in Fig. 1. The sections were taken between major veins to avoid leaf locations lacking stomata.

Fig. 1.

Positions of the sections sampled for analysis of stomatal distributions (left panel) and an image of a representative chemically cleared leaf showing the venation pattern (right panel) of the warm temperate evergreen tree M. cavaleriei var. platypetala. There are six layers from leaf apex to leaf petiole and three positions from the left leaf margin to the midrib on each layer (18 sections per leaf). In total, stomatal sections from 18 locations were sampled in 12 leaves (i.e. 12 replicates for different positions). In addition, in a separate collection of 60 leaves, leaf sections for analysis of stomatal distribution were taken from three positions along the leaf width axis similar to the three horizontal positions on the third layer in the left panel.

Extraction of the planar coordinates of stomatal centres

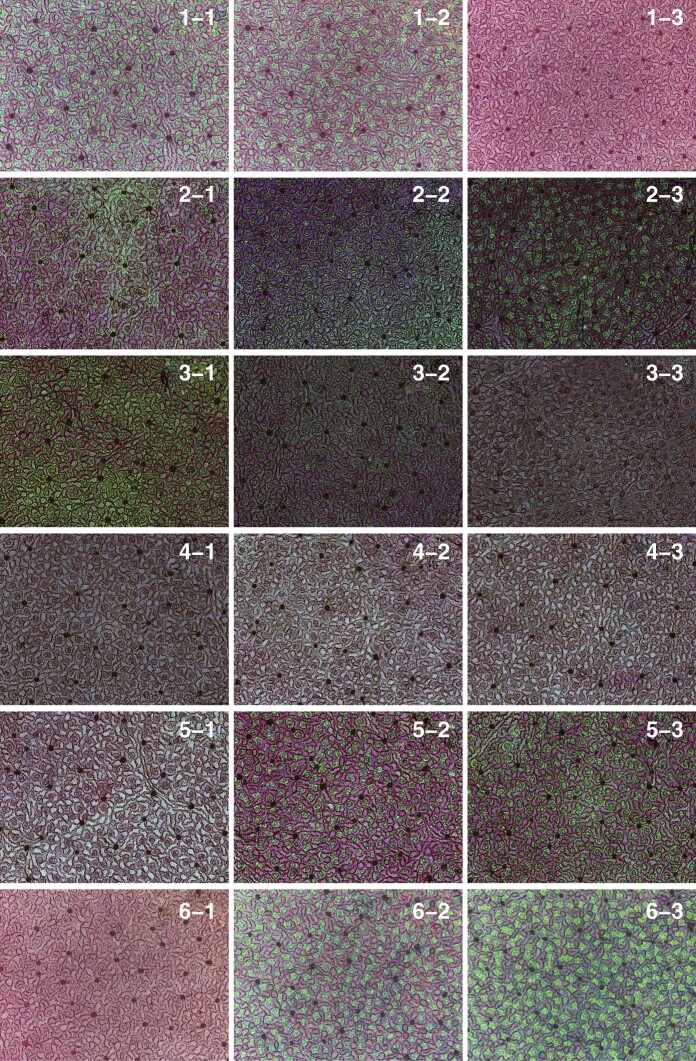
The segregation method (Jiao et al., 2021) was used to obtain stomatal images using a Leica DM 2500 light microscope (Leica Microsystems Shanghai, Shanghai, China). The sections were viewed at ×10 magnification (see Fig. 2 for representative stomatal images of 18 sections consisting of six layers and three positions per layer). ImageJ (https://imagej.nih.gov/ij/index.html) with the multipoint tool (https://imagejdocu.tudor.lu/macro/multiple_points) was used to extract the planar coordinates of stomatal centres within an observation window equal to [0, 1200 μm] × [0, 900 μm] (see Fig. 3 for the extracted points of stomatal centres in the 18 sections). All raw data of the planar coordinates of stomatal centres can be found in the online Supplementary Data (Tables S1 and S2).

Fig. 2.

Leaf sections showing stomata for the 18 positions for a representative leaf of M. cavaleriei var. platypetala (see Fig. 1 for the location of leaf sections). Each section has dimensions 1200 μm × 900 μm, which means that the length and width of each panel in this figure are 1200 μm and 900 μm, respectively.

Fig. 3.

Point patterns of extracted stomatal centres for a representative leaf of M. cavaleriei var. platypetala (the same leaf as in Fig. 2). For each panel, the range of the x-axis is 0–1200 μm and that of the y-axis is 0–900 μm.

Replicated spatial point pattern analysis

Point patterns can be characterised in terms of two concepts. The first is the concept of ‘intensity’, the average number of points per unit area. The second, more subtle, concept is that of ‘interaction’ between points, the details of which may vary in endlessly complicated ways. Figure 4 illustrates this with three simple examples, all of which have the same intensity. In the left-hand panel, there is no interaction at all; we refer to this as complete spatial randomness (CSR). In the central panel, points may not be located within a specified distance of each other, resulting in a more regular pattern of points. In the right-hand panel, points cluster together.

Fig. 4.

Simple examples of patterns exhibiting complete spatial randomness (CSR), repulsion and attraction respectively. All three patterns have identical intensity (or density), i.e. 100 points per unit area.

Ripley’s K function provides a tool with which to characterize interaction in spatial point process data, usually assuming stationarity (the properties of the underlying point process, including its intensity, are the same at all locations) and isotropy (no directional effects), although these assumptions can be relaxed to some extent (Ripley, 1977; Diggle, 2003; Baddeley et al., 2014, 2015). The K function can summarize the interaction properties of the underlying point process over a range of inter-event distances (Dixon, 2002). This is important, because in biological systems the interaction between points can be different at different scales, e.g. regular at a smaller scale but with a tendency for attraction at a larger scale. The K function is defined formally as

$${\displaystyle \begin{array}{l}{\displaystyle K\left(s\right)={\mathrm{\lambda }}^{-1}\mathbf{E}\left[{\mathbf{N}}_{\mathbf{0}}\left(\mathbf{s}\right)\right]\mathbf{,}}\end{array}}$$

where λ is the intensity, i.e. the mean number of events (here representing the stomatal centres) per unit area, N₀(s) is the number of additional events within distance s of an arbitrary event, and E denotes expectation, i.e. E[N₀(s)] is the mean number of additional events within distance s of an arbitrary event. For a realization of a homogeneous Poisson process (i.e. CSR), K(s) = πs². Processes whose realizations show a greater degree of aggregation than CSR typically have K functions K(s) > πs², whereas realizations of processes with K(s) < πs² show a degree of spatial regularity, typically as a result of inhibitory interactions between events (Diggle, 2014; Baddeley et al., 2015). Estimation of the K function replaces the theoretical expectation E[N₀(s)] by observed averages with a correction for edge effects (see Appendix).

In the present study, 12 of the 72 leaves were examined to determine the significance of the differences in the K functions between any layers (from the leaf apex to the leaf petiole) for each of three positions (from the margin to the midrib). We also tested the significance of the differences in the K functions among three positions (from the left leaf margin to the midrib) for each of six layers (from the apex to the leaf petiole) (Fig. 1). For the remaining 60 leaves, we tested the significance of the differences in the K functions among three positions on the leaf width axis. To highlight departures from CSR, we plotted the estimated K(s) − πs².

The packages spatstat (version 1.61-0) and splancs (version 2.01) based on R (version 3.6.1; R Core Team, 2019) were used to carry out the spatial point pattern analysis. For each section of stomata, we calculated the nearest neighbour distance of each stomatal centre from the others by using the package splancs, and further obtained the mean nearest neighbour distance for all stomatal centres within this section.

Statistical comparisons of leaf stomatal density and mean nearest neighbour distance

The stomatal densities of different positions in the leaves were compared using a linear mixed-effects model (Pinheiro and Bates, 2000) with layers or positions as a categorical fixed effect and leaves as a random effect. We also compared leaf stomatal densities and mean nearest neighbour distances between any two of the six layers for each of three positions, and between any two of three positions for each of six layers. The reduced major axis protocol was used to fit the linear relationship between stomatal density and the mean nearest distance of stomata on a log–log plot (Niklas et al., 2007).

The package nlme (version 3.1-140) based on R was used to fit the linear mixed model.

RESULTS

Comparisons of leaf stomatal densities among three positions from the left leaf margin to the midrib for each of the six layers demonstrated that the position closest to the midrib had a higher stomatal density than that closest to the leaf margin (P < 0·05, Fig. 5A). For position 1, leaf stomatal density of layer 6 (i.e. the layer closest to the leaf base) was significantly greater than those of the other five layers (P < 0·05, Fig. 5A). For position 2, leaf stomatal density of layer 5 was significantly greater than that for other five layers (P < 0·05, Fig. 5A). The stomatal density for position 3 did not vary significantly among the layers (Fig. 5A). Overall, the position (leaf width dimension) variable had a significant influence on leaf stomatal density, but the layer variable (leaf length dimension) had a weak or no significant influence on leaf stomatal density.

Fig. 5.

Box-and-whisker plots for leaf stomatal density (A) and the mean nearest distance between points in each section (B), and a plot demonstrating a linear relationship between them on a log–log scale (panel C). For each section, there were 12 replicates corresponding to the 12 leaves sampled. Uppercase letters A and B at the top of the whiskers indicate the significance of the difference between any two of six layers (from the leaf apex to leaf base) based on a linear mixed-effects model with the leaf number taken to be a random effect. Boxes with label A are not significantly different from each other; boxes with label B are not significantly different from each other; however, boxes with label A are significantly different from those with label B. Lowercase letters a, b and c show the significance of the difference between any two of three positions (from the leaf margin to the midrib) based on a linear mixed-effects model with leaf number as the random effect. The numbers at the top of the whiskers are the coefficients of variation (%) of stomatal densities in panel (A) and of mean nearest neighbour distances in (B). In panel (C), n is the sample size (i.e. the number of sections), r² is the coefficient of determination, and CI is the 95% confidence interval of the slope.

The mean nearest neighbour distance decreased with increasing distance from leaf margin (from position 1 to position 3, Fig. 5B), whereas the layer (leaf length dimension) had a weak or no significant influence on the mean nearest neighbour distance (Fig. 5B). Across all sections sampled, there was a strong negative linear association between log-transformed stomatal density and log-transformed mean nearest neighbour distance of stomata over the given 216 sections (r² = 0.856; P < 0·05; Fig. 5C).

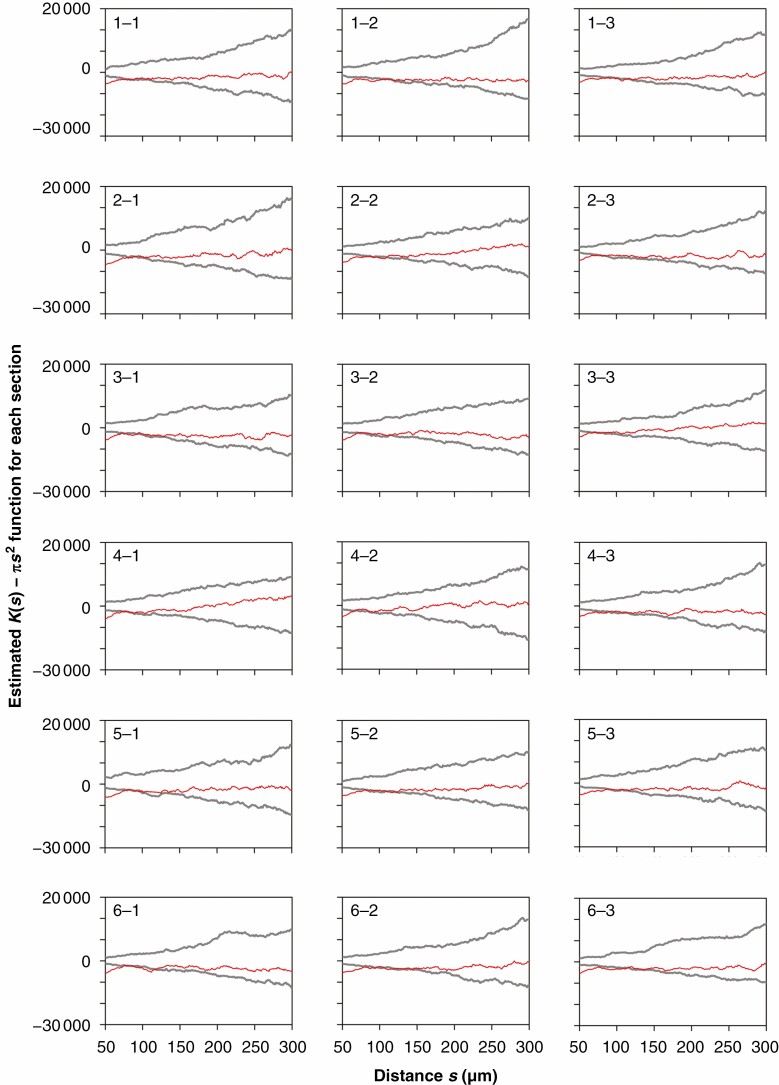
Analysis of the estimates of K(s) − πs² demonstrated that for the 18 sections taken from a single leaf (Fig. 6) and across 12 leaves (intra-group mean K(s) − πs² for 18 sections, Fig. 7), there was inhibition (as opposed to aggregation or clustering) between stomata at a small scale (<~100 μm); beyond this scale, there was no spatial interaction between stomata. The estimates of the mean K(s) − πs² averaged over the 12 leaves provided smoother and more robust curves than the individual estimates of K(s) − πs² (cf. Figs 6 and 7). Replicated spatial point pattern analysis was applied to test for a layer effect within each of the three positions. The resulting P-values were 0·080, 0·738 and 0·534 for positions 1, 2 and 3, respectively. Thus, the layer variable is not significant at the 0·05 level for any of the three positions. In other words, the spatial structure (as assessed by the K function) is the same, over layers, for all three positions. Likewise, a test for a position effect was conducted within each of the six layers. The P-values were 0·266, 0·093, 0·001, 0·145, 0·091 and 0·256 for layers 1, 2, ..., 6 respectively. Thus the position variable is significant at the 0·05 level only for layer 3. In other words, the same spatial structure (as assessed by the K function) is the same, over position, for all layers except for layer 3.

Fig. 6.

Estimates of K(s) − πs² versus s for patterns of stomatal centres from the 18 sections of a representative leaf of M. cavaleriei var. platypetala (the same leaf as in Fig. 2) based on a single (as opposed to replicated) spatial point pattern analysis. The estimated K(s) − πs² curves are shown as red lines. The upper and lower grey curves represent the upper and lower envelopes based on 399 simulations assuming complete spatial randomness.

Fig. 7.

Estimates of intra-group mean K(s) − πs² versus s for the 18 groups (12 replicates for each group) based on the repeated spatial point pattern analysis method proposed by Diggle et al. (2000). Red lines correspond to the estimates of intra-group K(s) − πs². The upper and lower grey curves represent the upper and lower envelopes based on 399 simulations assuming complete spatial randomness.

In summary, layer (leaf length dimension) has no significant effect (at the 0·05 significance level) on spatial structure (as assessed by the K function) for any of the three positions, and position (leaf width dimension) has a significant effect (at the 0·05 level) on the spatial structure only for layer 3. Note that layer 3 is the layer that is closest to the leaf width axis (maximum leaf width dimension).

Since the layer variable had no significant impact upon the K function, we calculated, for each of the 12 leaves, estimates of mean K(s) − πs² over the six layers (considered as replicates) at each of the three positions, i.e. three estimates of mean K(s) − πs² (Fig. 8). This demonstrated that the critical values of the scales for distinguishing an inhibitory relationship from a completely random pattern differed across three positions from the left leaf margin to the midrib (Fig. 8).

Fig. 8.

Estimates of intra-group mean K(s) − πs² for the three groups (with 72 replicates for each group, which came from the product of 12 leaves and six different layers per leaf). There are significant differences in the estimates of intra-specific mean K(s) − πs² between any two groups (P < 0·05 for each of the pairwise comparisons).

For the remaining 60 leaves, we sampled three positions from the left leaf margin to the midrib on the leaf width axis. The results also showed significant differences in the estimates of K(s) − πs² across the three positions (P < 0·05). However, the difference in the estimates of K(s) − πs² between positions 1 and 2 was not significant at the 0·05 level (P = 0·063). This result of a significant difference among the three positions from the sections on the leaf width axis (layer) for these 60 leaves was qualitatively the same as those for the third layer (close to the leaf width axis) for the original 12 leaves.

DISCUSSION

Spatial repulsion and independence

The configuration of stomata of M. cavaleriei var. platypetala did not appear to be in accordance with a constant-intensity Poisson point process. Significant departures from CSR appeared over distances from 50 to 300 μm. The configurations of all investigated sections showed evidence of the influence of distance on the spatial relationship between stomatal centres. Above a small scale (~100 μm), the curve of the estimated K(s) − πs² versus s lies between the simulated envelopes based on CSR. In contrast, the estimated curve wanders outside the envelopes at smaller scales (~100 μm). This suggests a competition for epidermal space between stomata at the areole level, a consideration that has been largely neglected by prior studies. Because of the limitations of space within an areole, stomatal size and the number of stomata exhibit a negative correlation (Franks and Beerling, 2009; Xiong and Flexas, 2020). This relationship is similar to the self-thinning law in ecology, which describes a negative relationship between population density and mean individual biomass for plants due to competition for space and resources. Although the vascular bundle sheath and bundle sheath extensions (BSEs, achlorophyllous cells that in some plants extend from the bundle sheaths to the epidermis and consequently separate a leaf into chambers [Sack and Scoffoni, 2013]) compete with stomata for epidermal space, at the areole level the spatial repulsion appears to result from the arrangement of stomata in a limited space. Franks and Farquhar (2007) studied the relationship between guard cell turgor, subsidiary cell turgor and stomatal aperture in four species of plants, and found that the guard cells and their adjacent subsidiary cells influenced each other during stomatal opening in two species. The subsidiary cells were observed to be almost squashed to accommodate the open stomata (Franks and Farquhar, 2007). In the present study, the mean nearest neighbour distance between stomata for a section fell in the range of 40–60 μm (Fig. 5C). This explains why stomata tended to have a spatial repulsion <100 μm, because the peripheral epidermal cells (polygonal objects) surrounding the guard cells also need to occupy epidermal space (Fig. 9). Our results suggest that the one-cell-spacing rule (Papanatsiou et al., 2016), which means that there is at least one epidermal cell between stomata, might have caused spatial inhibition between stomata at small scales. At a larger scale (>100 μm), there was no evidence of spatial interaction between stomata, suggesting that the limitation from the peripheral epidermal cells surrounding guard cells can be neglected at a larger scale. Stomata do not exhibit a sub-regional aggregation in M. cavaleriei var. platypetala and in many other Magnoliaceae species (Wang, 2021). This suggests that the areole can be regarded as a homogeneous environment and clustering at the areole level does not affect leaf function (Liu et al., 2021). Our results support the idea that the vascular topology and areole size are such that stomata do not show any clustering that might indicate insufficient water supply. The only exception is the position near the midrib, mid-way along the length, where density is higher, but this could be compensating for increased boundary layer thickness, which will be largest over the leaf regions farthest from an edge.

Fig. 9.

Representative image of a leaf section viewed at ×40 magnification.

Leaf stomatal density and spatial dependence of stomata at the areole level

There was only minor variation in stomatal density among the six layers from leaf apex to leaf petiole, whereas stomatal density increased from leaf margin towards the midrib (Fig. 5A). The lack of longitudinal variation in stomatal density indicates that the hierarchical reticulate venation in M. cavaleriei var. platypetala results in similar areole structures with approximately the same numbers of stomata per unit area for similar horizontal positions with respect to the midrib, regardless of the distance from the leaf petiole. On the other hand, the higher stomatal density closer to the leaf midrib might result from higher water supply nearer to the midrib (Buckley et al., 2017), reflecting greater dimensions of major veins branching from the midrib. Because of greater dimensions closer to the midrib, the leaf hydraulic conductance of larger veins around the midrib is higher than that around higher order veins (Scoffoni et al., 2011).

We observed that the spatial second-order characteristics for positions close to the leaf margin and close to the midrib did not differ significantly for most layers (P > 0·05; Fig. 1), except for positions close to and on the leaf width axis. This suggests that, for most areas on a leaf, the spatial structure characteristics and spatial relationships between stomatal centres are similar for different displacements from the midrib at the areole level, and the difference is only reflected in stomatal number per unit area. Because of the limitations of our experimental design, it is still unclear whether stomatal densities differ significantly between positions close to the secondary vein and far away from the midrib and the secondary vein. In future studies, it would be worth taking sections at a position that is between two approximately parallel secondary veins and far away from the midrib, in order to examine whether stomatal density at the areole level is related to the order of leaf veins to which stomata are closest.

Estimated K function based on replicated spatial point patterns

In prior studies, using non-replicated spatial point pattern analysis methods, the results tended to be not sufficiently robust. Figures 6–8 show how averaging over more replicates produces smoother estimated curves of K(s) − πs², whose precision can be estimated without making specific assumptions about the underlying point process. An analysis of this kind can suggest, but not verify, an underlying generative process. In future studies, it would be worth formulating and fitting specific, biologically informed spatial point process methods to investigate mechanistic hypotheses about the generation of stomatal distributions for different plant species.

CONCLUSIONS

In our study leaf stomatal densities did not differ along the longitudinal direction from the leaf apex to the leaf base in the leaves of M. cavaleriei var. platypetala, but at a given leaf width dimension stomatal density was smaller at the leaf margin than closer to the midrib. The spatial second-order characteristics of stomatal centres did not differ significantly between different positions from the leaf apex to the leaf base, and generally also not in the horizontal direction from the leaf margin to the midrib. The exception was the intermediate widest leaf position, where the spatial inhibition of stomatal centres tended to occur at a smaller scale from the leaf margin to the midrib. There was no interaction between stomata of this Michelia species when the scale was greater than the scale of stomata with associated epidermal cells (~100 μm). A spatial inhibition between stomata was found when the scale was <100 μm. This likely results from the competition between stomata and the surrounding epidermal cells for epidermal surface space. The mean nearest neighbour distance per section between stomata ranged from 40 to 60 μm. This suggests a trade-off between stomatal density and stomatal spatial arrangement at the areole level. In addition, at a large scale (>100 μm), spatial interaction was not confirmed between stomata. In particular, there was no evidence of clustering between stomata. This suggests that areoles can be regarded as homogeneous environments for stomata, and that there is no gradient effect of stomatal distribution within an areole. This means that in hierarchical reticulate venation networks, leaf veins surrounding areoles form homogeneous environments and the spatial pattern of stomata is mainly caused by small-scale epidermal competition. Whether the current conclusions can be potentially extended to other tree species deserves future investigation.

SUPPLEMENTARY DATA

Supplementary data are available online at https://academic.oup.com/aob and consist of the following files. Table S1: raw data consisting of planar coordinates of stomatal centres on 12 leaves. Table S2: raw data consisting of planar coordinates of stomatal centres on 60 leaves.

Appendix

Replicated spatial point pattern analysis method

The estimate of the K(s) function is:

$${\displaystyle \begin{array}{l}{\displaystyle {\displaystyle \widehat{K}}\left(s\right)=\frac{\left|A\right|}{n(n-1)}{\sum }_{i=1}^n{\sum }_{j=1,j\ne i}^n\frac{I\left(s_{ij}\right)}{{\omega }_{ij}},}\end{array}}$$

where $\left|A\right|$ represents the area of the study region A; n represents the number of events (i.e. stomatal centres); s_ij is the distance from point i to point j; ${\omega }_{ij}$ is an edge-correction weight, and $I\left(s_{ij}\right)$ is an indicator function depending on s:

$$\text{Undefined control sequence vspace}$$

The edge-correction weight, ω_ij, is equal to 1 when the circle with centre s_i and radius s_ij lies entirely within A. Otherwise, ω_ij is the proportion of the perimeter of the circle that lies within A. Assume that there are g groups (e.g. the positions of sections on a leaf) which we denote as i = 1, 2, 3, …, g. Assume also that there are r_i replicates for the ith group (e.g. the number of leaves that include the ith position). We use j to denote the jth replicate and n_ij to denote the number of events in the jth replicate section of the ith group. The total number of events in the ith group is then $n_i={\sum }_{j=1}^{r_i}{n}_{ij}$ and the total number of events in all groups is $n={\sum }_{i=1}^g{n}_i$. For a given distance s, the intra-group meanKfunction, ${\overline{K}}_i\left(s\right)$, and the inter-group meanKfunction, $\overline{K}\left(s\right)$, are defined as follows (Diggle et al., 1991, 2000):

$${\displaystyle \begin{array}{l}{\displaystyle {{\displaystyle \overline{K}}}_i\left(s\right)={\displaystyle \sum _{j=1}^{r_i}}\left[\frac{n_{ij}}{n_i}{{\displaystyle \widehat{K}}}_{ij}\left(s\right)\right],}\end{array}}$$

and

$${\displaystyle \begin{array}{l}{\displaystyle {\displaystyle \overline{K}}\left(s\right)={\displaystyle \sum _{i=1}^g}\left[\frac{n_i}{n}{{\displaystyle \overline{K}}}_i\left(s\right)\right].}\end{array}}$$

The D statistic to test whether there is a significant difference in the K functions between groups is (Diggle et al., 2000):

$${\displaystyle \begin{array}{l}{\displaystyle D={\displaystyle \sum _{i=1}^g}{\displaystyle \underset{0}{\overset{s_0}{\int }}}\left(\omega \left(s\right)n_i{[{{\displaystyle \overline{K}}}_i\left(s\right)-{\displaystyle \overline{K}}\left(s\right)]}^2\right)ds}\end{array}}$$

where $w\left(s\right)=s^{-2}$ is a distance-weighting function. Statistical significance is assessed by Monte Carlo simulations following Diggle et al. (2000) as briefly described here.

• Step 1: Calculate the value, D₁ say, of the D-statistic for the observations.

• Step 2: Calculate a set of approximately exchangeable residual K functions,

$${\displaystyle \begin{array}{l}{\displaystyle R_{ij}\left(s\right)=n_{ij}^{1/2}[{{\displaystyle \widehat{K}}}_{ij}\left(s\right)-{{\displaystyle \overline{K}}}_i\left(s\right)].}\end{array}}$$

• Step 3: Randomly permute the residual K functions, and calculate

$${\displaystyle \begin{array}{l}{\displaystyle {{\displaystyle \widehat{K}}}_{ij}^{\ast }\left(s\right)={\displaystyle \overline{K}}\left(s\right)+n_{ij}^{-1/2}{R}_{ij}^{\ast }\left(s\right)}\end{array}}$$

• where $R_{ij}^{\ast }\left(s\right)$ is the ijth randomly permutated residual K function.

• Step 4: Calculate the intra-group mean K function, the inter-group mean K function, and the value, D₂, of the D-statistic based on the permuted K functions.

• Step 5: Repeat steps 3 and 4 to get to get values D₃, D₄, …, D_m of the D-statistic.

• Step 6: Order the values D₁, D₂, …, D_m from the largest to the smallest. The P value of the test is k/m, were k is the rank of D₁. In the current study, we set m = 1000, which is sufficient for testing at conventional levels of significance (Marriott, 1979).