A secure system for genomics clinical decision support

Abstract

We developed a prototype genomic archiving and communications system to securely store genome data and provide clinical decision support (CDS). This system operates on a client-server model. The client encrypts the data, and the server stores data and performs the computations necessary for CDS. Computations are directly performed on encrypted data, and the client decrypts results. The server cannot decrypt inputs or outputs, which provides strong guarantees of security. We have validated our system with three genomics-based CDS applications. The results demonstrate that it is possible to resolve a long-standing dilemma in genomic data privacy and accessibility, by using a principled cryptographical framework and a mathematical representation of genome data and CDS questions.

1. Introduction

New discoveries are being made at a fast pace, linking genetic variants with disease risk and drug interactions. As next-generation genome sequencing becomes more reliable, economical, and widely available, the findings from research are being incorporated into clinical practice. Making responsible and meaningful use of human genomic data to support healthcare, including clinical decision support (CDS) applications, is an emerging challenge of great importance. CDS can provide answers to questions such as: ‘what is the patient’s CYP2C19 genotype and drug-metabolism phenotype’, and ‘does the patient have any pathogenic BRCA1 variants’.

Genome data are large, comprising billions of base-pairs on thousands of genes and intergenic regions. Next-generation sequencing can identify thousands to millions of variants, whose clinical significance can change over time as our knowledge evolves. Sequencing can produce gigabytes of data for a single individual. It is impractical to securely store and analyze such large data in contemporary electronic health record (EHR) systems, which clinicians use when delivering care to patients. The challenges for storage can be more acute for smaller healthcare facilities that may not have large, secure data repositories. This means that genomic data must be stored outside the EHR system and retrieved for CDS.

A Genome Archiving and Communications System (GACS) can make genomic data accessible for clinical applications [1] [2]. This is analogous to how radiological images are stored in a Picture Archiving and Communications System [3]. Further, a cloud-based GACS can provide a cost-effective solution due to economies of scale [4]. However, cloud storage of genome data increases privacy concerns. Theft and misuse of genome data can cause long-term harm to individuals and their families because the data are unique, heritable, and immutable. Given this highly-sensitive nature of genome data, appropriately strict levels of protection must be applied to their storage.

The competing demands of accessibility and privacy create a challenging problem that has been studied for years. Solutions have been proposed for securely outsourcing computation and data sharing [5]–[24]. Many of these solutions have vulnerabilities during computation, inefficiencies, or require special hardware. One promising solution that meets the requirements, is to use fully homomorphic encryption technology, which enables computation over encryption. Since data are never decrypted during storage, transfer, or computation, there is a strong guarantee of privacy [25], [26]. We have developed a prototype client-server system for encrypting and storing genomic data and providing secure CDS. In this model, a client encrypts the data using a public key and sends it to the server for storage. The same client or another client asks CDS questions. The server stores the encrypted data and performs the computations without decrypting the data or the CDS questions. The results are returned to the client, who has the private key (also called secret key or decryption key) to decrypt them. Only the custodian of the data, (the client that has the secret key), can decrypt results. We have evaluated our system with three use-cases representing a breadth of CDS scenarios: (1) screening for eligibility in a clinical trial based on the presence of certain haplotypes in the APOE gene, (2) inferring the drug metabolism phenotype for clopidogrel based on the CYP2C19 genotype, and (3) assessing risk for familial hypercholesterolemia (FH) based on the LDLR gene. Our system currently retrieves ‘key variants’, calculates genotypes, and computes phenotypes based on genotype-matching or scoring. Key variants are known variants that are of interest for a given scenario, e.g., because they are known to be associated with a disease or with altered drug metabolism.

2. Background

2.1. Ancillary Genomics Systems and Genomics-based CDS

A typical person’s DNA can have several million variants from a given reference DNA, and the significance of any of these variants to the person can change over time. Management of such a large and dynamic data set has prompted exploration of ancillary genomic systems (aka genomic data repository; GACS) that sit outside the EHR [2]. Experience and use of such ancillary systems is growing [27]–[29], prompting the Office of the National Coordinator’s Sync for Genes project to emphasize the need for pilots that test GACS integration with EHRs [30]. Furthermore, institutions are turning to cloud-based solutions for hosting genomic data repositories, raising additional concerns over genomic data privacy and security.

Our previous work on integrating genomic data into the EHR has followed a model in which a CDS engine monitors events occurring within the EHR [31]. When triggered by an event, the CDS engine obtains additional genomic data from the GACS. For example, the CDS is triggered by a new medication order in the EHR. Upon being triggered, the CDS engine queries the GACS for variants in the patient’s genome that interact with the ordered drug. The CDS engine returns appropriate recommendations to the ordering provider. It is with this context in mind, GACS communicating with CDS which communicates with EHR, that we have designed the secure GACS.

Pharmacogenomics CDS applications are of particular interest. Over half of all primary care patients are exposed to drugs with potential pharmacogenomic interactions [32]. Studies have found that 7% of FDA-approved medications and 18% of the 4 billion prescriptions written in the US per year are affected by actionable variants [33], that nearly all individuals (98%) have at least one known, actionable variant by current Clinical Pharmacogenetics Implementation Consortium (CPIC) guidelines [34]. An example is Clopidogrel, which was prescribed over 20 million times in 2015 [35]. For patients on clopidogrel who are found to have CYP2C19 genotypes that produce non-functional or reduced functional proteins, there is an increased risk for adverse cardiovascular events. In such cases, CPIC guidelines recommend alternative antiplatelet therapy [36].

Genome sequence data also can be used for early detection and diagnosis of a variety of disorders. The American College of Genetics and Genomics (ACMG) recommends reporting secondary findings in 56 genes [37]. The ACMG considers genetic variants that cause monogenic disorders where early diagnosis is clinically actionable. Studies have found as many as 7% of patients harbor pathogenic or likely pathogenic variants in these 56 ACMG genes [38]–[40]. Analysis of the ClinVar [41] archive data indicates the number of known pathogenic or likely pathogenic variants in these genes was 18,718 in 2018 [42]. A case in point is familial hypercholesterolemia (FH), which has an estimated prevalence of 1 in 250 to 1 in 500 persons [43], [44], and is most commonly due to mutations in the LDLR gene. Over 1,500 pathogenic or likely pathogenic LDLR variants are registered in ClinVar, and have an associated Clinical Actionability summary in ClinGen [45].

Specific genetic markers are used as criteria to determine eligibility in clinical trials. Easier access to genome sequence data while providing the appropriate protections for the privacy of subjects, compliant with regulations and ethical principles, can also facilitate and promote recruitment in clinical trials. For example, in a trial of CNP520 versus placebo in the treatment of early Alzheimer’s Disease [46], trial entry criteria include being a carrier of certain APOE haplotypes. This and the other CDS applications described in this section are well-served with privacy-protecting storage and computation.

2.2. Privacy-Protecting Solutions

Inappropriate disclosure of genomic data can put people’s privacy at risk, which might have a long-term impact on an individual’s education, employment, insurance [47], [48], and on their relatives (e.g., the Golden State killer case [49]). Genomic data yield unique biometrics. Early studies showed merely 75 single-nucleotide polymorphisms (SNP) are sufficient to uniquely re-identify an individual [50] and a few dozen database queries can determine the database membership of a victim [51]–[53]. There are some recent findings showing that genomic data can infer physical appearance and diseases that are linkable to anonymized phenotype records [5], [54]. It is therefore critical to protect genomic data hosted in clinical systems. Traditionally, clinical data are encrypted during storage (labeled “encryption at rest” [6]) as a mechanism to protect data loss, which is required by HIPAA security rules [7]. However, the value of genomics resides in data analysis (rather than depositing data in storage) and existing solutions have no way but to decrypt the data for analysis (e.g., on a 3rd party commercial cloud), which has raised many public concerns [55].

In the past few years, privacy and cryptographic techniques for secure computation have been extensively studied. Multi-party computation (MPC) is considered a promising solution for secure computation [8]–[10]. In this approach, multiple parties maintain local data and communicate intermediate results. MPC can be vulnerable when the computing parties collude, and is thus inappropriate for long-term storage and outsourcing computation [11]–[14]. Aziz et al. surveyed various secure computation techniques for genomic data [15]. Among the most relevant mechanisms, there are two camps of solutions: (1) hardware-based methods [16]–[18], and (2) homomorphic encryption (HE) based approaches [19], [20]. The former solutions rely on special hardware and engineering skills while the latter depend on advanced mathematics. The hardware-based methods provide a secure enclave within the CPU. The data is decrypted within this secure enclave for computation with the assumption that enclave contents are invisible to the rest of the CPU. An implementation of this approach is found in the Software Guard Extensions (SGX) technology built into Intel’s recent CPUs. Hardware-based methods are fast and easy to implement but vulnerable under new attacks [21]–[23]. On the other hand, HE is backed by principled algebraic number theory, which allows one to perform arithmetic operations over encrypted data without decryption. Security is guaranteed by cryptographic hardness assumptions, which even quantum computers cannot break [24].

Traditionally, HE has been considered too slow and too memory-intensive for practical applications. While this might have been true 5 to 8 years ago, the field has progressed rapidly (indeed, faster than Moore’s law) as benchmarked by the iDASH genome privacy competition series [56], [26]. HE is starting to demonstrate its feasibility in offering rigorous yet practical solutions to real-world clinical applications. Shimizu et al. proposed a HE-based string search to locate sequences of SNPs in large genome databases [57]. Kim et al. developed a secure matching algorithm for biomarkers and a secure training protocol for building a logistic regression model for genome-wide association studies [58], [59].

3. Method

3.1. System Overview

Our system models a client-server architecture. In this model, a sequence client, e.g., a laboratory, encodes, and encrypts patient data with a public key of the HE system. The encrypted data, also called ciphertext, are sent to the GACS server which stores the data. Subsequently, the CDS client, e.g., a hospital poses encrypted CDS questions and sends them to the GACS. The GACS performs computations over encryption and returns the result to the CDS client for decryption with a private key.

The data flow is illustrated in Figure 1. The input data consists of variant call format (VCF) files [60], which are text files. Since computation requires numerical representation, we encode the variants from a VCF file as a vector shown as ν. The variant vector is homomorphically encrypted (shown as $\widehat{v}$) and sent to the server for storage. Descriptions of encoding and encryption are given in Sections 3.2 and 3.3, respectively. Patient and sequence identifiers are meta-data, and are deterministically encrypted before being sent to the server for storage to conceal them from the server. Questions (called queries) are posed by a CDS client. In Figure 1, the CDS client encodes the question as a matrix or vector A, encrypts it to $\widehat{A}$, along with the deterministically encrypted patient identifiers and sends that to the server. The server computes a result $\widehat{h}$ and sends it to the client for decryption to h The result h is the same (within a noise margin defined by the precision parameter) as the unencrypted computation on the plain data, O(A,ν). The data, questions or results are not decrypted by the server.

Figure 1.

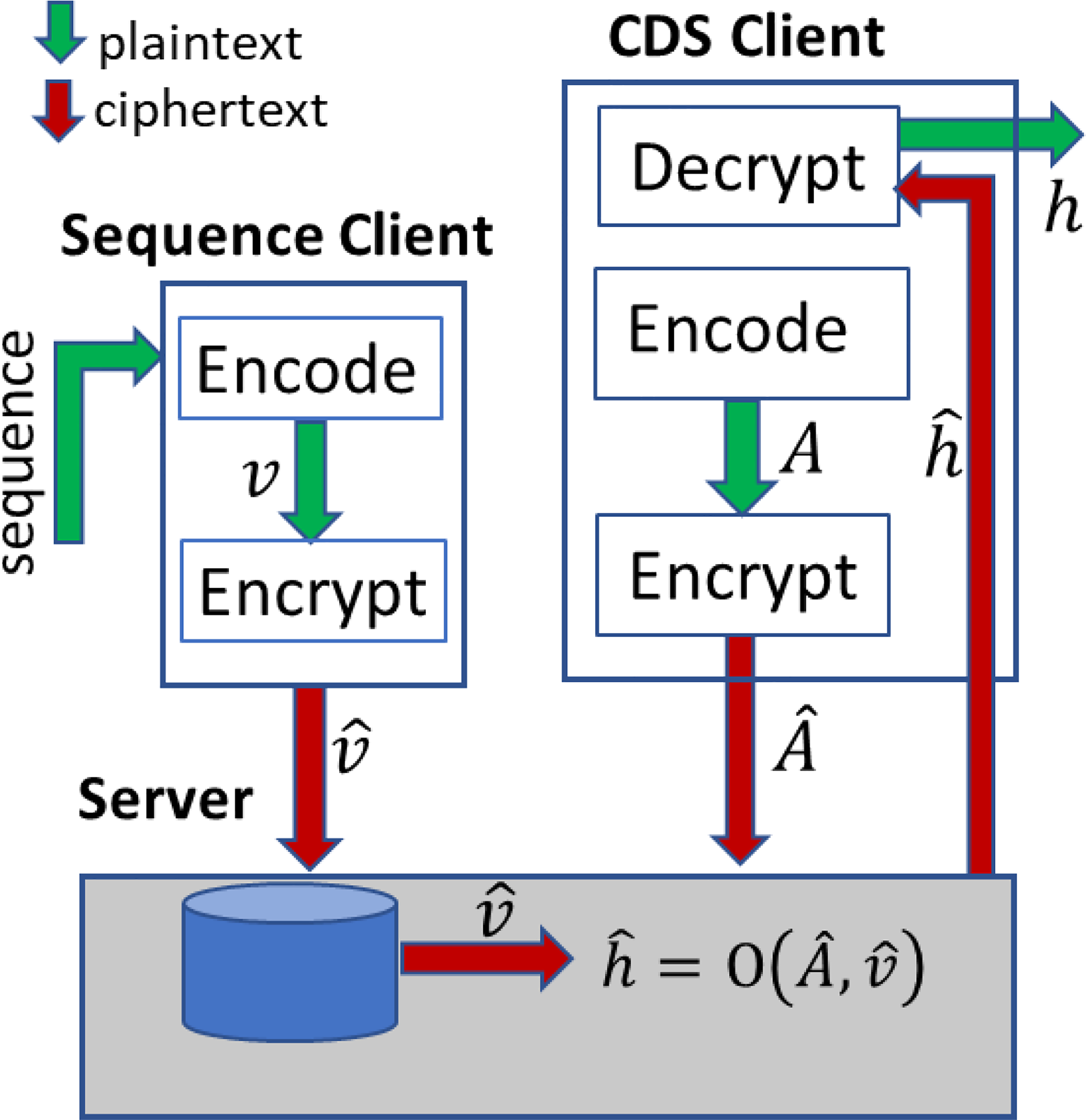
Illustration of system components and data flow.

We defined operations in the GACS that can be used by CDS systems to obtain variants or calculate genotypes (pairs of haplotypes). These operations include weighted summation of variants and evaluation of zygosity (heterozygous or homozygous). Haplotyping includes a special case of finding a particular haplotype, e.g., in the clinical trial application. For our pharmacogenomics application, we must compute a phenotype from the genotype. We compute this phenotype on the client. Although it is possible to chain queries (genotyping, followed by phenotyping), chaining requires increasing the multiplicative depth of the evaluation circuit, which in turn requires greater memory and time.

In this paper, we focus on CDS with key variants, but not with novel variants (i.e. those that have not been registered in databases such as ClinVar) or structural variants (variants that may have hundreds of bases differing from the reference genome, often with imprecise endpoints). Computation on novel and structural variants requires additional considerations for encoding the data and will be addressed in future work.

3.2. Vector-encoding of key variants

For computation over encryption, analysis questions must be expressed mathematically. We developed a novel framework to represent variant data and CDS questions numerically. In this framework, key variants are encoded as vectors, and the analysis questions are encoded as linear operations on these vectors. Each known key variant is represented by a fixed element in a vector. The variant and its element position in a vector are stored in a lookup table on the client. The presence of a variant is encoded by a “1” (one), and its absence is encoded by a “0” (zero). We create pairs of vectors because chromosomes exist in pairs. Each vector-pair represents a region of the genome. There are groups of variants that can be considered together because they are in a particular region, define particular haplotypes, or determine phenotypes. In our model, it is optimal to encode such a group of variants into the same vector-pair. The encoding is done by the client before encryption.

We use two types of encoding schemes that we call “phased” and “unphased”. Unphased encoding allows us to compute on variants. We use it when CDS does not need to calculate haplotypes (e.g., for LDLR variants). Phased encoding allows us to calculate haplotypes and genotypes in addition to computing on variants. Consider two key variants in the APOE gene as shown in the rightmost two columns of Table A1. Two variants can generate four haplotypes. If a patient has the heterozygous variant rs7412, the genotype is ε₂/ε₃. For this patient, a representative pair of vectors is [1, 0] and [0, 0]. Phased encoding is illustrated in Figure 2.

Table A1.

Haplotypes of the APOE gene. The phenotype column indicates haplotype-associated risk for development of Alzheimer’s Disease. Haplotypes are determined by the alleles at rs7412 and rs429358 as shown.

Haplotype	Phenotype	rs7412	rs429358
ε1 (0.2%)	Normal risk	T	C
ε2 (7%)	Decreased risk	T	T
ε3 (wild type, 79%)	Normal risk	C	T
ε4 (14%)	Increased risk	C	C

Figure 2.

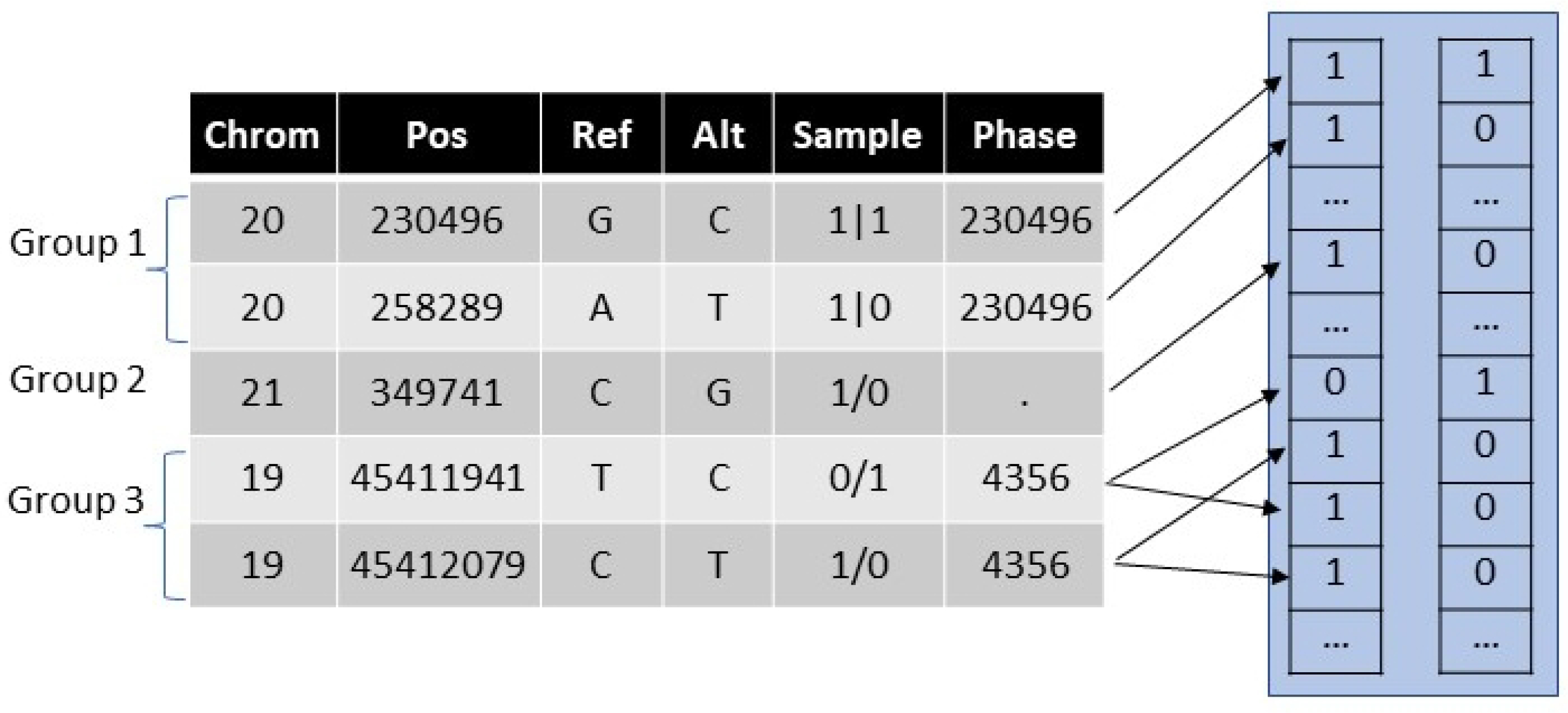
Illustration of phased encoding. The table on the left shows partially phased genome sequence data from a VCF file. In the Sample column, the pipe delimiters indicate phased variants and slashes indicate unphased variants. The unphased heterozygous data generates two combinations. A lookup table (not shown) is used to assign a variant to a vector and an element position in the vector.

When phase information is present in the VCF file, the pair of vectors is uniquely determined, although we do not know which is maternally or paternally derived. When phase information is absent or partial, and heterozygous variants are present, there are ambiguities regarding which homologous chromosome (e.g., maternally- vs. paternally-derived) has particular key variants. In other words, the haplotypes are uncertain. To accommodate ambiguity, we generate multiple combinations of variants that capture all the possible haplotypes. If the patient had two unphased heterozygous variants, the vector pairs could be [1,0]/[0,1], representing ε₂/ε₄, or [1,1]/[0,0] representing ε₁/ε₃. In general, with P distinct or unknown phases, the number of combination pairs is 2^{P − 1}. Ambiguous genotype calls are often resolved clinically according to population probability distributions, which we anticipate occurring in the CDS client.

For efficient computation and storage, the combinations of variants (in a group of variants) are concatenated vertically within the pair of vectors. This allows us to efficiently pack the vectors into the ciphertexts, whose lengths are fixed by the multiplicative depth of the encryption circuit, as described in Section 3.3.

In unphased encoding, we ignore partial phase information from the VCF file. When a heterozygous variant is present, we can encode the “1” into the relevant element in either vector of the pair. Here, we do not generate various combinations of unphased variants. Unphased encoding allows us to do variant-level operations, but it does not allow us to calculate genotypes, except for those genotypes defined by a single variant. For many CDS applications, unphased encoding is sufficient to answer the clinical question. An example is the application to determine the risk of FH, in which we need to detect the presence of certain variants in the LDLR gene. In this application, there are over 2000 variants and as many possible haplotypes. A possible combinatorial explosion of unphased variants is avoided by unphased encoding.

3.3. Homomorphic Encryption

We use the CKKS homomorphic encryption scheme developed by Cheon et al., to encrypt our data [61]. Compared to other HE schemes such as BGV [62] and BFV [63], CKKS is capable of controlling the magnitude of encrypted messages during homomorphic computation. It creates a trade-off between precision and efficiency, and offers a practical and effective solution for applications such as ours, which do not require high precision. Additionally, this HE scheme supports ciphertext packing techniques to encrypt multiple messages into a single ciphertext, so that we can compute a function on multiple data simultaneously. For instance, it provides element-wise addition, multiplication, and rotation (shift) of vector elements. As a result, it enables us to achieve good performance in terms of amortized ciphertext size and timing per plaintext slot.

We use the Microsoft SEAL library for homomorphic encryption functions. The library is written in C++. Our software implementation is in Python. We wrote binding functions using the Pybind11 software [64], to allow Python scripts to call the SEAL library C++ functions. The selection of encryption parameters is explained in Appendix A

3.4. Computations on the server

As mentioned in Section 3.1, the analysis questions are framed as linear operations on vector data. This is because HE data are closed under addition and multiplication only. Surrogate solutions are sometimes necessary to frame analysis questions as linear operations. These solutions must balance complexity, memory, and the need to coordinate the computation with the client. Our computations are of the forms $\widehat{h}=\widehat{A}\widehat{v},<\widehat{a},{\widehat{v}}_1+{\widehat{v}}_2>$ and $<\widehat{a},{\widehat{v}}_1\otimes {\widehat{v}}_2>$, where ⊗ represents element-wise multiplication. Logical operations (e.g., $<\widehat{a},{\widehat{v}}_{1}OR{\widehat{v}}_2>$) and logical template matching are also allowed.

We describe the linear operation $\widehat{h}=\widehat{A}\widehat{v}$ here, and describe logical template matching in Appendix B. The plaintext operator A is a matrix whose rows are the haplotype template vectors, i.e., each row defines a particular haplotype. Each row of A is encrypted as a ciphertext. $\widehat{h}=\widehat{A}\widehat{v}$ is calculated using dot-products. To calculate a dot-product we must do an element-wise multiplication followed by summation across the vector. Summation across the vector is performed by performing n left shifts and additions, as described in Appendix C, where n is the power of two greater than or equal to the length of the plaintext vector, $n=\lceil lo{g}_2|v|\rceil$. The plaintext equivalent vector ℎ is a real number vector, and the patient haplotype corresponds to the element with the largest result, i.e., it requires us to compare values, which is not computationally friendly over our encryption scheme. To overcome this, a surrogate operation can be used or the result $\widehat{h}$ can be returned to the client, which decrypts it to h and then computes argmax(ℎ). We have used the latter approach because of its efficiency.

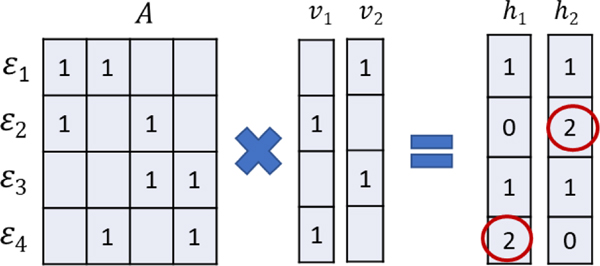
In Section 3.2 we explained encoding using the example of a two-element plaintext vector, ν. In practice, in our phased encoding method, we add elements to ν to include wildtypes, i.e., the absence of variants at key-variant positions. This is because different haplotypes have different numbers of variants, which means normalization by the number of variants is required. By including the wildtype elements, ν has a constant amplitude, providing implicit normalization. Figure 3 represents haplotyping of a pair of unambiguous vectors. The figure shows the plaintext equivalent: ℎ =Aν.

Figure 3.

Haplotypes for APOE found by argmax(Aν). The rows of A are the haplotypes and the columns are variants. The zero-valued elements are shown blank for clarity. For the pair of variant vectors shown, ν₁ = [0 1 0 1] and ν₂ = [1 0 1 0], the genotype is ε₄/ε₂.

As stated in Section 3.2, if the variant vector is ambiguous due to incomplete phasing, then we stack the variant combinations vertically before encryption. Since the dot-product uses shift and add operations, each combination is padded with zeros to the nearest power of two, to avoid contamination from the next combination. The CDS client replicates the matrix A horizontally to match the stacked ν and encrypts it.

4. Testing and Results

4.1. CDS applications

We tested our method against three CDS applications: 1) clinical trial eligibility based on APOE haplotypes; 2) screening for familial hypercholesterolemia based on LDLR pathogenic variants; and 3) interaction with clopidogrel based on CYP2C19 genotyping.

To test clinical trial eligibility, the query matrix encodes the question ‘does the patient have at least one ε4 haplotype?’. The variants and haplotypes associated with this question are explained in Section 3.2. This query is of the form $<{\widehat{A}}_4,\widehat{v}>$ for each vector in the pair, where A₄ is the row-vector corresponding to the ε₄ haplotype.

To assess for FH and to differentiate between moderate and severe phenotypes, we can ask two queries: 1. How many pathogenic or likely pathogenic alleles are present in the LDLR gene? 2. How many homozygous pathogenic or likely pathogenic variants are present in the LDLR gene? The first query is a weighted summation of the form $<\widehat{a},{\widehat{v}}_1+{\widehat{v}}_2>$. The second query is a weighted summation $<\widehat{a},{\widehat{v}}_1\otimes {\widehat{v}}_2>$. The vector a encodes pathogenic or likely pathogenic alleles, with a “1”. If the answer to question 1 is zero, there is no evidence of FH. If the answer to question 1 is exactly one (i.e. only one gene affected), we predict a moderate phenotype. If the answer to question 2 is >=1 (i.e. both genes affected), we predict a severe phenotype. (For example, given. a = [ 0...1 1 0...1 0], if the patient had one homozygous pathogenic variant and a non-pathogenic variant, the vectors are ν₁ = [0...1 0 ….0] and ν₂ = [0...1 0 ….1], the answers would be 2 and 1 respectively, and the inference would be a severe risk of FH.) The phenotype is indeterminate (either moderate or severe) with other answers. For LDLR, we obtained key variants from ClinVar. These were filtered to indels and single nucleotide variants (SNVs) with pathogenic or likely pathogenic clinical status, review status of at least one star, and known start and end coordinates.

The phenotype for clopidogrel metabolism depends on the haplotypes of CYP2C19. We compute $\widehat{h}=\widehat{A}\widehat{v}$ and return $\widehat{h}$ to the client for decryption and argmax(ℎ) to obtain haplotypes. The client applies a score to the haplotypes. The score maps to the phenotype: poor, intermediate, normal, rapid, ultra-rapid, or indeterminate metabolizer. We obtained variants, haplotype definitions, and genotype-phenotype mapping from PharmGKB [65]. An alternative solution that chains the genotype and phenotype queries is possible. In the chained method, the genotype is calculated by logical template matching and does not have to be decrypted by the client for the phenotype calculation. However, this solution is slower, requires greater circuit depth and consequently, requires more memory.

4.2. Study population

Genomic data in VCF files from 287 individuals from the publicly available 1000 Genomes database were obtained for testing [66]. This data is publicly accessible and its use in research does not require approval by an Institutional Review Board. Regions of the genomes containing key-variants in APOE (NC_000019.9:45408005–45413652), LDLR (NC_000019.9:11199037–11245506), and CYP2C19 (NC_000010.10:96521437–96613962) were extracted from the files using the tabix software tool [67]. To ensure consistent encoding, the key variants were normalized to canonical SPDI form using NCBI Variation Services [68].

4.3. Results

The operations for each application are given in Table 2. Measurements of time and memory consumption are given in Table 3. Timings were measured for key-generation, encryption, computation and decryption. The mean and standard deviation of these timings were computed over all the patients in our test set. The software was run on a virtual Linux machine on a PC with an Intel i7–6500 CPU and was allocated 6 GB memory. We verified that the genotypes and phenotype results calculated over encryption matched ground-truth results generated with plaintext calculations and manual labeling of haplotypes.

Table 2.

The operations used for each application. The match in the first row of this table is the element of h that equals one.

Application	Operations	Meaning
CYP2C19/Clopidogrel	${\widehat{h}}_1=\widehat{A}{\widehat{v}}_1$, ${\widehat{h}}_2=\widehat{A}{\widehat{v}}_2$	Haplotype match
LDLR/FH	$<\widehat{a},{\widehat{v}}_1+{\widehat{v}}_2>$, $<\widehat{a},{\widehat{v}}_1\otimes {\widehat{v}}_2>$	Sum pathogenic mutations, Sum pathogenic homozygous variants
APOE/clinical trial	$<{\widehat{A}}_4,{\widehat{v}}_1>$, $<A_4,{\widehat{v}}_2>$	Is the haplotype ε4?

Table 3.

Time and memory consumption for the use-cases. Time (mean/std dev) was measured in seconds.

Application	Size of operator	Key generation	Encryption of operator	Encryption of vectors	Computation	Decryption	Memory (MB)
CYP2C19/Clopidogrel	A = (31, 68)	0.65/0.07	0.58/0.03	0.04/0.01	3.94/0.53	0.02/0.01	67
LDLR/FH	a = (1,2039)	1.26/0.11	0.03/0.01	0.06/0.01	0.30/0.03	0.02/0.01	127
APOE/clinical trial	A_4 = (1,4)	0.65/0.03	0.02/0.01	0.04/0.01	0.10/0.02	0.02/0.01	56

The genome data and CDS query can be encrypted ahead of time in an offline, asynchronous manner. Table 3 does not show the timing for parsing the VCF file, which can be slow, or for encoding, which is sub-second. The query computation (shown by the “Query time” column) and the result decryption are real-time calculations, and the timings for these operations are more important for usability. Since the ciphertext vector length is fixed by the multiplication circuit-depth, the memory consumption or time do not increase with plaintext vector length, as long as the plaintext vector is smaller than the limit allowed by the ciphertext. The presence of multiple ambiguous haplotypes does not change the timing or memory consumption because they are packed into the same ciphertext.

The table shows that the query time is different for the different applications. The CYP2C19 application requires as many dot-products as there are haplotypes. The APOE application requires only one dot-product because there is only one haplotype. The LDLR application requires an element-wise multiplication, followed by a dot-product, and an addition operation followed by a dot-product. The key generation depends on the multiplicative depth. The encryption of the operator depends on the operator. Each row of the matrix A is separately encrypted for CYP2C19, and therefore the encryption takes approximately 31 times as long as the encryption of the other operators. Since the vector length is fixed in all these applications, the encryption and decryption time is fixed.

5. Discussion

A new framework for secure computation on genomic data has been developed. The framework includes a vector representation for genomic data and a matrix or vector representation of CDS questions that can be applied as linear operations to the vectors. The representation allows HE and thus enables computation on a remote server with guarantees of security and privacy. Our framework was validated with three CDS applications and 287 patients from the 1000-genomes dataset. Timing and memory measurements from our test-cases demonstrate the feasibility of using this approach. While homomorphic operations are slower than plaintext operations, we anticipate that query results (such as identified drug-gene interactions or positive genetic screening results), once computed, can be stored in EHRs where they can be accessed quickly for CDS.

A key component of the framework is the vector representation of the genome sequence, that allows queries on genome data to be expressed as mathematical operations. This representation is generalizable to a range of CDS applications as demonstrated by the three applications in our study that all used the same representation. As explained previously, each known variant is assigned a vector element. The scheme is extensible such that new variants of interest can be assigned to unoccupied elements of existing vectors or to new vectors. CDS queries are performed as mathematical operations, unlike other CDS systems that commonly use Boolean logical operations. To make it easier for CDS systems to query the secure GACS, we can encapsulate common patterns of queries into functions that automatically generate the query matrices.

HE provides guarantees of privacy for the genomic data stored in the cloud. Variant queries, and genotype and phenotype computation can be performed in the cloud without decrypting the stored genomic data. In fact, even the results of the computation are only revealed on the client which has the private key to decrypt the results. A cloud-based GACS removes barriers for healthcare organizations in delivering precision medicine. It allows precision medicine-based clinical care to stay current with the very rapid evolution in sequencing technologies, data formats, and research and best practice recommendations in clinical genomics. Furthermore, smaller healthcare organizations, including those in rural areas, can subscribe to a secure GACS service in the cloud, empowering them to deliver precision-medicine, without requiring large investments in this technology.

An alternative to using HE for cloud-based GACS is to use encryption-at-rest to store variant data in segments. The server would return the appropriate encrypted segments when requested by the client and all computation would be done on the client. However, this approach has several disadvantages: (1) there is potentially more data transfer since the GACS is sending sequence data rather than the results of the computation (e.g., genotype or phenotype), (2) an HE GACS can allow sharing of permissible phenotype data across a patient’s healthcare providers whereas an encryption-at-rest GACS requires exposure of sequence data which creates a greater risk to privacy, and (3) complex software must be maintained on all clients.

Nevertheless, there are many areas of our approach that require improvement. We have proposed grouping variants within genome regions for optimal ciphertext packing. However, optimal grouping requirements may change with new medical knowledge, and a mechanism is required to modify the clusters efficiently. A related area is to determine the optimal encryption parameters and optimal size of the ciphertext to improve computational performance and storage.

Currently, we only work with key variants because CDS computations are defined for key variants. This framework does not support novel variants because the vector positions cannot be defined for unknown variants. Therefore, the encoding framework must be extended to retain and provide information on the existence of novel variants, even if no CDS questions are defined for them. A similar problem exists for structural variants, which are variants that may have hundreds of bases differing from the reference genome. These variants are complex, often with imprecise start and end positions. As a result, they are poorly defined. As with novel variants, we have not yet included them in our encoding framework. Despite this current limitation, we have shown the ability to work with homomorphically encrypted simple variants (SNVs and Indels) that have been previously identified and that have precise start and end positions. Such capabilities enable a wide range of potential clinical applications, such as screening for genetic risk, pharmacogenomics CDS, clinical trials eligibility determination, and other applications that have historically relied on SNVs and Indel data generated by DNA chips.

Our testing must be expanded to cover many more CDS applications, to validate the variant clustering and the selection of parameters. This could lead to more efficient ciphertext packing methods. Similarly, testing must be expanded to more patients. Additionally, we need to develop efficient methods for population-level queries. Finally, to use HE in a real-world system requires further development, such as integration with an EHR, storing metadata, regions studied, and managing multiple sequences per patient.

6. Conclusion

We have successfully prototyped a secure GACS and tested it against pharmacogenomic and genetic screening CDS applications. We have demonstrated an encrypted solution for inferring genotypes from variants and detecting known pathogenic variants from encrypted patient genomic data. The ability to address these common scenarios suggests that HE shows promise for clinical application, at least for a subset of genetic use cases. We need to address practical issues in integrating with real-world systems. Further research is required to address the limitations of how HE solves genomic computation, such as improvements to our encoding scheme. Many additional scenarios, such as querying over novel variants or CDS based on structural variants, remain to be tested.

Highlights.

• A secure remote repository and computation for genomic data is proposed

• A numerical representation of genomic data has been defined

• Homomorphic encryption enables secure computations for decision support

Appendices

A. Encryption Parameters

In CKKS, a freshly encrypted ciphertext is represented as a pair of polynomials of degree with N coefficients modulo Q. When a circuit to be evaluated has multiplication depth=L, the ciphertext modulus Q is a product of L+ 1 pairwise small co-primes (i.e. $Q={\prod }_{i=0}^L{q}_i$) such that each prime q_iis chosen to have roughly the same size as the scaling factor of a message. In particular, the output ciphertext represents the desired result but is multiplied by the scaling factor, so the output ciphertext modulus q₀ should be larger than the scaling factor. The size of the largest modulus is $PQ=P\cdot {\prod }_{i=0}^L{q}_i$ where P is specially chosen to reduce the noise growth during homomorphic multiplications. This special modulus P has a similar size to the base modulus q₀. For more detail, we refer to Kim et al. [59]. In our protocol, we require L=2 for genotyping and L = 4 for phenotyping. We set the scaling factor (to convert real numbers to integers) as 2³¹( ≈ q_i for i > 0) and we select q₀ ≈ P ≈ 2⁴⁰. As a result, the value of PQ is 2²⁰⁴ for L=4 and 2¹⁴² for L = 2. We take the ciphertext dimension N= 2¹³ to ensure at least 128 bits of security according to the Homomorphic Encryption Standardization [69], which implies that the number of plaintext slots is 2¹².

B. Logical Template Matching

Consider logical template matching to calculate haplotypes. Every known haplotype is represented by a template vector. Logical template matching can be done with an element-wise XOR operation between a template vector and patient vector, followed by an OR operation across the result vector, and finally taking the ones’ complement. The result is “1” when the allele template vector and the patient vector are identical, and “0” otherwise. Given a set of distinct allele vectors, at most one will match the patient vector. As before, we illustrate with the APOE genotype shown in Table A1. Consider a patient vector with a plaintext representation ν = [1, 0]. Table B.1 illustrates intermediate and match results. Since HE does not support logical operations, we use their arithmetic equivalents:

$$XOR\left(a,b\right)=a+b–2ab,$$

$$OR\left(a,b\right)=a+b–ab.$$

The advantage of using logical template matching over multiplication is that queries can be chained. There is no need for the client to interpret the results of the template match. The disadvantage of template matching is that the circuit depth is greater, and it depends upon the length of the variant vector.

Table B.1.

Template matching for APOE genotype. The template is shown in the left column, the intermediate result of the XOR operation is shown in the middle column. The match result is in the right column.

Template (t)	x = XOR(v,t)	h = 1 − OR(x)
[0, 1]	[1, 1]	0
[1, 1]	[0, 1]	0
[0, 0]	[1, 0]	0
[1, 0]	[0, 0]	1

C. Summation along a vector.

Summation of the elements of a vector is performed using shift and addition functions in the SEAL library. For a vector with n elements, we require ⌈n ⌉ shifts and additions. Each shift is by 2^(s−1) elements, where s is the stage. Table C.1 shows the operations on a plaintext vector of four elements. The final answer is given in the first element of the result vector. We multiply by a plaintext vector whose first element is one “1”, and other elements are zero. This operation increases multiplicative depth by one.

Table C.1.

Summation of values in a vector. Successive shift and add operations can be used to sum the elements of a vector. A four-element vector needs two stages. The first element of the result vector contains the sum (in bold font).

Stage	Initial	x0	x1	x2	x3	0
1	shift-1	x1	x2	x3	0
	add	x0+x1	x1+x2	x2+x3	x3
2	shift-2	x2+x3	x3	0	0
	add	x0+x1+x2+x3	x1+x2+x3	x2+x3	x3