Experimental and Computational Analysis of Bending Fatigue Failure in Chopped Carbon Fiber Chip Reinforced Composites

Abstract

With a better balance among good mechanical performance, high freedom of design, and low material and manufacturing cost, chopped carbon fiber chip reinforced sheet molding compound (SMC) composites show great potential in different engineering applications. In this paper, bending fatigue behaviors of SMC composites considering the heterogeneous fiber orientation distributions have been thoroughly investigated utilizing both experimental and computational methods. First, four-point bending fatigue tests are performed with designed SMC composites, and the local modulus is adopted as a metric to represent the local fiber orientation of two opposing sides. Interestingly, SMC composites with and without large discrepancy in local modulus of opposing sides show different fatigue behaviors. Interrupted tests are conducted to explore the bending fatigue failure mechanism, and the damage processes of valid specimens are also closely examined. We find that the fatigue failure of SMC composites under four-point bending is governed by crack propagation instead of crack initiation. Because of this, the heterogeneous local fiber orientations of both sides of the specimen influence fatigue life. The microstructure of the lower side shows a direct influence while that of the upper side also exhibiting influence which becomes more prominent for high cycle fatigue cases. Furthermore, a hybrid micro-macro computational model is proposed to efficiently study the cyclic bending behavior of SMC composites. The region of interest is reconstructed with a modified random sequential absorption algorithm to conserve all the microstructural details including the heterogeneous fiber orientation, while the rest of the regions are modeled as homogenized macro-scale continua. Combined with a framework to capture the progressive fatigue damage under cyclic bending, the bending fatigue behaviors of SMC composites are accurately captured by the hybrid computational model comparing with our experimental analysis.

1. Introduction

Carbon fiber reinforced polymer (CFRP) composites, such as unidirectional fiber reinforced composites [1–9], woven textile composites [10–14], short fiber reinforced composites [15–20], and chopped fiber chip reinforced composites [21–24], show prominent advantages as lightweight alternatives to metals. In particular, chopped carbon fiber chip reinforced sheet molding compound (SMC) composites can reach a better balance among good mechanical performance, high freedom of design, and low material and manufacturing cost. SMC composites have become one of the most promising materials in structural components in the automotive, marine, and aerospace industries, e.g., vehicle hood, hatchback, and guide vane of gas turbine engines [25, 26]. Then, a comprehensive understanding of the material performance under these operating conditions is important to ensure their safe applications.

Over the last decade, a number of studies on the internal microstructure, mechanical behavior, and fatigue performance of SMC composites have been performed. The heterogeneity and anisotropy at the macro-scale level have been demonstrated to be correlated with the internal microstructures. Feraboli et al. [21, 27–29], Selezneva et al. [30–32], Wan et al. [33, 34], and Johanson et al. [35] have evaluated the material properties of SMC composites fabricated by different manufacturing processes. The variations of microstructure and local modulus in SMC composites have been observed with advanced testing techniques, including Digital Image Correlation (DIC) and ultrasound C-scan instruments. Using similar equipment, our previous work [36] has revealed the correlation among tensile failure, local modulus, and fiber orientation distribution for different types of SMC composites. Further, a constant fatigue life diagram of SMC composites is established based on the fiber orientation tensor [37]. Nony-Davadie et al. [38] have also investigated the mechanical and fatigue behavior of randomly and highly oriented SMC composites, and the anisotropy induced by the thermo-compression process is pronounced. Recently, Martulli et al. [39–42] have linked the tensile, compression, and fatigue properties of SMC composites with the morphology captured using X-ray micro-CT. Meanwhile, Alves et al. [43, 44] have improved the strength of SMC composites via a physically-based model for microstructural design [45]. The optimal microstructure has been fabricated and tested, which is closing the gap to quasi-isotropic continuous-fiber laminates.

In addition, numerical simulations with microstructure- or mesostructure-based models to predict the material properties of SMC composites have also been widely conducted. Representative volume element (RVE) models generated by different algorithms have been employed in the stiffness analysis as well as quasi-static/cyclic failure predictions for SMC composites. Feraboli et al. [29] have developed a random RVE model, in which statistical distributions of fractions and orientations of chips are generated with a randomization process. The elastic properties can be predicted when the classical laminated plate theory is applied. Selezneva et al. [32] have established a stochastic finite element technique, in which the variability is modeled with randomly oriented strands, and then the strength can be predicted based on Hashin’s failure criteria and fracture energies. Harper et al. [46] have reconstructed the 3D geometry of discontinuous fiber composites by using a force-directed algorithm, and a high fiber volume fraction (~50%) is achieved. Li et al. [47] have built up a Voronoi diagram-based algorithm to reconstruct substructure features of chips in SMC composites. It has a unique advantage as the modulus of SMC composites can be predicted based on the material processing information. Meanwhile, we have proposed the voxel-based and conforming-based RVE models for SMC composites, respectively [48, 49], and we have demonstrated that the uniaxial mechanical and fatigue behavior of SMC composites under different loadings can be well reproduced with the conforming-based algorithm [49–52]. Sommer et al. [53–55] and Kravchenko et al. [56, 57] take a step further and integrate the compression molding simulation, meso-structure reconstruction, and tensile property prediction.

SMC components in real-world applications are large-scale structural components, which are more often subjected to out-of-plane load [58, 59]. However, the research works on the bending behavior are limited for carbon fiber SMC composites. Palmer et al. [60] have compared the flexural strength of recycled carbon and glass fiber SMC composites. Ogi et al. [61] have analyzed the effect of temperature on the flexural strength of carbon fiber SMC composites. Lee et al. [62] have evaluated the effect of carbon fiber content on the tensile and flexural behavior of carbon fiber SMC composites. Ishikawa et al. [63] have pointed out that bending strength and modulus are correlated with the local fiber orientation distribution. Martulli et al. [42] have analyzed the bending behavior of automotive components fabricated with carbon fiber SMC composites, and the effect of manufacturing conditions on the mechanical performance has been evaluated with X-ray micro-CT. Despite these efforts, the cyclic bending behavior of carbon fiber SMC composites, especially the effect of local fiber orientation distribution, remains uncharted. However, it is extremely significant in the performance prediction and optimal design of these large-scale structural components.

This paper aims to explore the bending fatigue behavior of carbon fiber SMC composites by utilizing both experimental and numerical methods. First, four-point bending fatigue tests are performed with designed SMC specimens, and the local modulus is adopted as a metric to characterize the local fiber orientation distribution of two opposing sides. The effect of heterogeneous fiber orientation distribution of both sides of the specimen on the bending fatigue performance is systematically compared. Meanwhile, the interrupted tests are performed to explore the bending fatigue failure mechanism. Next, a hybrid micro-macro computational model is generated to simulate the cyclic bending behavior of SMC composites. The region of interest is reconstructed with modified random sequential absorption (RSA) algorithm, while other regions are modeled as homogenized macro-scale continua. We then use the hybrid computational model integrating a progressive damage fatigue law to predict the bending fatigue performance of SMC composites.

2. Materials and Four-Point Bending Fatigue Test Setup

The chopped carbon fiber chip reinforced SMC composites used in the four-point bending fatigue tests are composed of pseudo-planar randomly distributed carbon fiber chips and vinyl ester resin matrix, which are the same as those in our previous work [37, 50]. Since the notch-insensitivity under different loadings has been demonstrated for SMC composites [50, 64, 65], a circular hole is introduced in all specimens to reduce the possibility of invalid results, e.g., the fractures around the pins. Note that notch-insensitivity is referred to that the failure strength is proportional to the net section (the cross-section at the hole area) as shown in Fig. 1, while the effect of notch-induced stress concentration is minor [66, 67]. As the cross-section area at the hole is smaller, specimens would still fail at the hole area despite notch-insensitivity. The specimen preparation is illustrated in Fig. 2. The dimensions of the four-point bending fatigue specimen are 274 mm × 60 mm × 4.8 mm. Though the fiber orientation distribution tends to be isotropic random globally for SMC composites, chips at the local areas may have a dominant orientation. Thus, before the four-point fatigue bending fatigue tests, the material heterogeneity measurement for the gauge section is performed through quasi-static pre-tension, during which the strain evolutions of two opposing surfaces are captured with two aligned DIC systems (ARAMIS). It has been shown that the local internal fiber orientation distribution can be correlated to the local modulus calculated by surface strain measured with DIC systems for SMC composites [36, 37]. To keep consistent with our previous work on the aspect ratio [36, 37, 49, 50], the local area with a spacing of 2 mm along the longitudinal direction is selected to calculate the local modulus. Since the local moduli measured from two opposing surfaces are different [36] and the stress states at two opposing sides are also different under four-point bending loading, the nominal modulus E_nominal defined in Ref. [36] is introduced to describe the local fiber orientation distribution of either side (from the surface to the center),

$$E_{\mathrm{nominal}}=\frac{\sigma }{{\epsilon }_{\mathrm{local}}}$$ (1)

where σ is the nominal stress under quasi-static pre-tension, and ε_local is the local surface strain captured from either side. Here, the effect of the internal microstructure at the opposing side (from the center to the opposing surface) on the surface strain evolution is not considered. The circular hole, the diameter of which is 12.7 mm, is positioned at the local area with a relatively lower nominal modulus, and the side with the relatively lower nominal modulus is set as the lower side, i.e., the tension-dominated side.

Fig. 1.

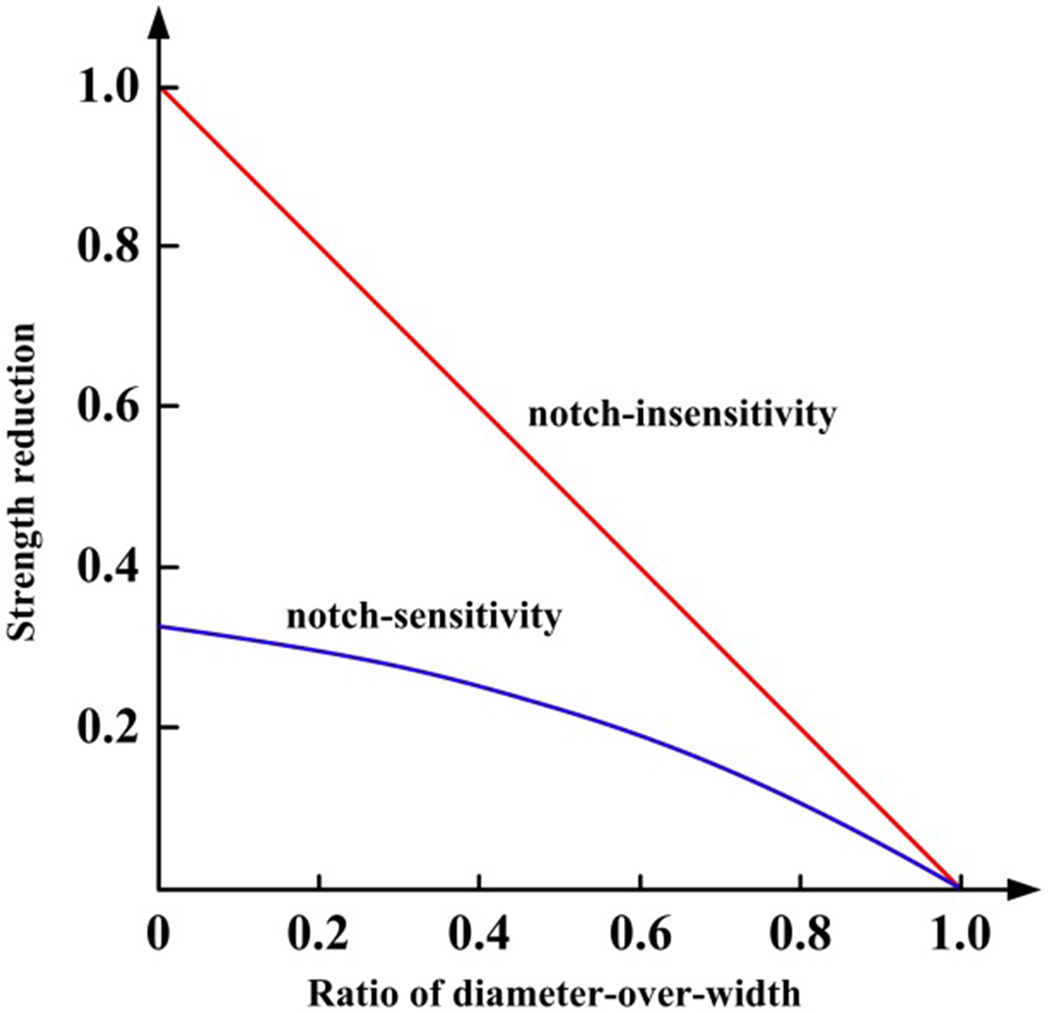
Schematic of notch-insensitivity vs. notch-sensitivity [66, 67]. The red straight line is referred to the strength reduction of notch-insensitive materials, which is only attributed to the reduced area at the net section. Blue curved line represents notch-sensitive materials, e.g., conventional metals.

Fig. 2.

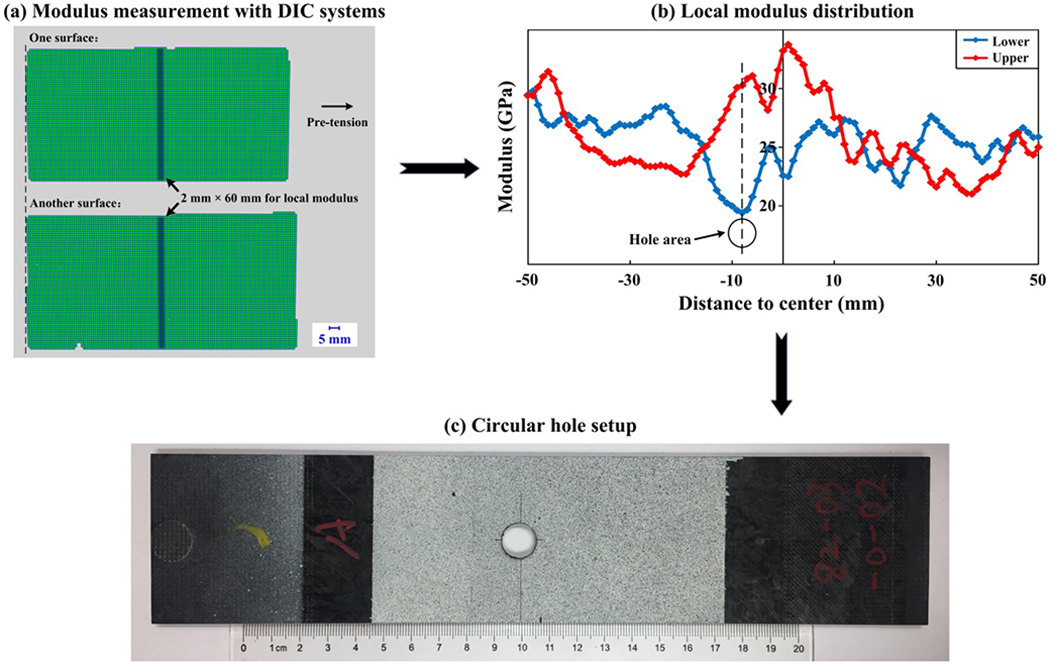
Specimen preparation and hole area determination for four-point bending fatigue tests for (a) modulus measurement with DIC systems, (b) local modulus distribution, and (c) circular hole setup. The strain evolutions of two opposing surfaces are measured under pre-tension (till ~100MPa).

An MTS servo-controlled hydraulic frame is used to perform four-point bending fatigue tests for SMC composites. The four-point bending fixture is shown in Fig 3. The loading and support spans are 100 mm and 200 mm, respectively. Double-sided tapes are used at the contact regions between specimen and fixture to suppress the sliding under cyclic bending. We conduct the load-controlled tests with a frequency of 2 Hz at an ambient temperature of 23 °C. The load ratio is 0.1. Afterwards, the interrupted tests are also designed to explore the failure processes of SMC composites under cyclic bending. The bending fatigue tests are suspended after a certain number of cycles, and the crack initiation and propagation around the circular hole will be analyzed.

Fig. 3.

Four-point bending fatigue test setup using an MTS servo-controlled hydraulic frame. The loading and support spans are 100 mm and 200 mm, respectively.

3. Fatigue Results and Failure Mechanisms

Eighteen valid bending fatigue results are obtained from the four-point bending fatigue tests of SMC composites. The amplitude of theoretical bending stress ${\sigma }_{\text{bend}}^{\text{amplitude}}$ is adopted to evaluate the loading level under cyclic bending. The theoretical bending stress ${\sigma }_{\text{bend}}$ is given as,

$${\sigma }_{\text{bend}}\text{ = }\frac{3FL}{(w-d)t^2}$$ (2)

where F is the applied total force; L is the span between the loading and support pins; w is the width of the specimen; d is the diameter of the circular hole; t is the thickness of the specimen. The S-N data of SMC composites under four-point bending are collected in Fig. 4, and the corresponding bending fatigue life model can be given as,

$${\sigma }_{\text{bend}}^{\text{amplitude}}\text{ = }{g}_1{N}^{g_2}$$ (3)

where g₁ = 119 MPa and g₂ = −3E-3 are calibrated through nonlinear curve fitting of the valid bending fatigue results. Among those valid data (details are also listed in Appendix A), the stress amplitude ranges from 101 MPa to 127 MPa, which is generally higher than that of the uniaxial fatigue results (68 MPa to 99 MPa) collected in Ref. [37]. This is reasonable as the stress employed in the uniaxial fatigue model of SMC composites is the nominal stress. Under the uniaxial fatigue loading, the stress within the critical layers should be higher than the mean value (the nominal stress). Therefore, if the uniaxial fatigue model of SMC composites was applied in the present work directly, the fatigue life under cyclic bending would be underestimated. As shown in Fig. 4, owing to the variation of fiber orientation distribution at the critical local area, a large scatter can be observed in the obtained bending fatigue data, and no obvious correlation can be found between the stress amplitude and bending fatigue life, which is similar as the fatigue results under uniaxial fatigue loadings [37, 50].

Fig. 4.

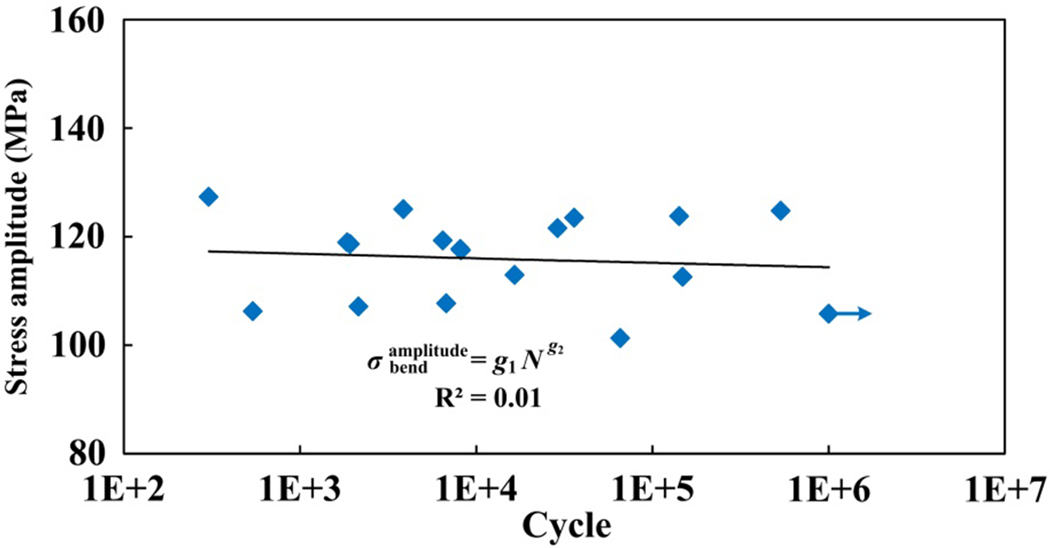
S-N data of SMC composites under bending fatigue loading.

During the setup of the four-point bending tests, the weaker side, which has the relatively lower nominal modulus, is placed at the lower side. It should be mentioned that the lower modulus is correlated to the situation that more chopped carbon fibers align along the transverse direction, and the fiber reinforcement is less pronounced. Then, the fatigue failure of SMC composites under cyclic bending will be tension-dominated in the present study, and the effect of fiber orientation distribution at the lower side is more prominent than that at the upper side. In general, the effect of fiber orientation distribution on quasi-static and fatigue strength can be considered in a consistent manner. Thus, the predicted quasi-static strength given by a linear equation of the local modulus has been adopted to characterize this effect on uniaxial fatigue loadings [37]. Following the normalized fatigue model of SMC composites with a stress ratio of 0.1 proposed in our previous work, the normalized bending fatigue model of SMC composites is given as,

$$\frac{{\sigma }_{\text{bend}}^{\text{amplitude}}}{d_1^T{E}_{\text{nominal}}^{\text{lower}}+d_2^T}\text{ = }{g}_3{N}^{g_4}$$ (4)

where $d_1^T$= 7.8E-3 and $d_2^T$= 58 MPa are provided in Ref. [37], which are used to characterize the effect of local fiber orientation distribution on fatigue behavior of SMC composites with a stress ratio of 0.1, and $E_{\text{nominal}}^{\text{lower}}$ is the nominal modulus at the lower side of the net section.

Different from conventional metals or CFRP composites, the material heterogeneity along the thickness direction is also distinct in SMC composites [35, 36]. It can be expected that if the bending fatigue failure of SMC composites is crack initiation dominated, then the bending fatigue life would be mainly determined by the internal microstructure of the lower side. However, if crack propagation dominates, the material property of the upper side would also have some influence on the bending life. Thus, in the present study, we also focus on the effect induced by material heterogeneity of two opposing sides and look into whether the upper side also shows influence in the fatigue behavior of SMC composites. In order to describe the discrepancy of the local fiber orientation distribution at upper and lower sides, the modulus deviation between upper and lower sides ξ is defined,

$$\xi =\frac{E_{\text{nominal}}^{\text{upper}}-E_{\text{nominal}}^{\text{lower}}}{E_{\text{nominal}}^{\text{lower}}}$$ (5)

where $E_{\text{nominal}}^{\text{upper}}$ is the nominal modulus at the upper side of the net section.

For convenience, the valid data are classified into two groups based on the measured ξ: group A (ξ < 0.5) and group B (ξ ≥ 0.5). The normalized S-N data of SMC composites under bending fatigue loading are drawn in Fig. 5. = 0.58 and = −2.2E-2 are fitted for group A data, while g₃ = 0.57 and g₄ = −1.2E-2 are calibrated for group B data. By considering this effect of local fiber orientation distribution, the correlation between the new failure parameter and bending fatigue life is significantly improved, and the correlation coefficient R² increases from 0.01 to 0.71 for both groups. Note that the alignment of carbon fiber chips along the longitudinal direction corresponds to the increment of the modulus. Therefore, the bending fatigue strength of SMC composites increases when the carbon fiber chips are more aligned to the longitudinal direction, similar to the uniaxial fatigue behaviors [37]. The generality of the normalization with local modulus to characterize the effect of fiber orientation distribution is verified under cyclic bending. By comparison, the bending fatigue life becomes longer for SMC composites with a higher nominal modulus at the upper side, which becomes more remarkable for high cycle fatigue cases.

Fig. 5.

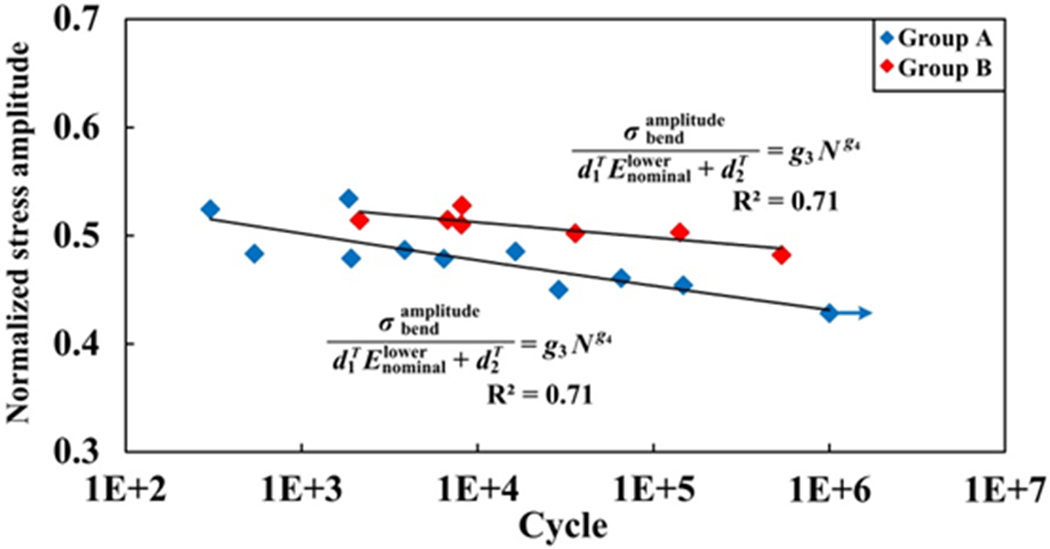
Normalized S-N data of SMC composites under bending fatigue loading considering the material heterogeneity of two opposing sides. The blue points are the experimental results in group A (ξ < 0.5). The red points are the experimental data in group B (ξ ≥ 0.5).

It is important to mention that component a₁₁ in fiber orientation tensor [68] has been introduced in the fatigue modeling of SMC composites, which characterizes the alignment of carbon fiber chips. The correlation between a₁₁ and modulus has also been studied in our previous work [37, 47, 48]. Then, the normalized bending fatigue models of SMC composites also can be transformed to fiber orientation-based forms. In real-world applications, the fiber orientation tensor of SMC components can be obtained by simulation software of manufacturing process, e.g., CoreTech Moldex3D and Autodesk Moldflow. Accordingly, the bending fatigue behavior of SMC components can be predicted based on the results from the present work.

The failure mechanism is further explored to better understand the bending fatigue behavior of SMC composites and the reason for enhanced fatigue life with a higher nominal modulus at the upper side. First, the interrupted tests are designed based on the proposed normalized bending fatigue model given in Eq. (4). The bending fatigue tests are suspended at the early stage of the fatigue failure procedure (approximately 10% of the predicted bending fatigue life). Small macro-scale cracks already exist at the lower side for all interrupted specimens, and one typical case is shown in Fig. 6. We can see that crack propagation plays a significant role in the bending fatigue failure of SMC composites as cracks appear at such early fatigue life. Moreover, we further examine the valid specimens after four-point bending fatigue tests. The final fractures at the lower side, upper side, and edge of a representative specimen are given in Fig. 7(a)-(c). In addition to the obvious cracks at the lower side, visible macro-cracks also can be found at the upper side. From the edge, delamination is distinct from the lower side to the layers which are close to the upper side. The fractures of SMC composites under bending fatigue loading indicate that the specimens can still bear the cyclic load while the bottom layers are experiencing breakage. Under this condition, the material property of the upper side also becomes important to the bending fatigue failure of SMC composites, which is consistent with the bending fatigue performance plotted in Fig. 5. It is important to point out that the failure modes of SMC composites under uniaxial fatigue loadings with different stress ratios are similar, which include chip splitting failure, matrix failure, and interface failure [37, 50]. Theoretically, the stress states at the lower and upper sides are close to that under uniaxial tension-tension and compression-compression fatigue loadings, respectively. As a result, the failure modes of SMC composites under bending fatigue loading should be very similar to those under uniaxial fatigue loadings.

Fig. 6.

Obvious cracks form at the lower side of a typical interrupted specimen (~10% of the predicted bending fatigue life). Observable macro-scale cracks are marked by red ellipses.

Fig. 7.

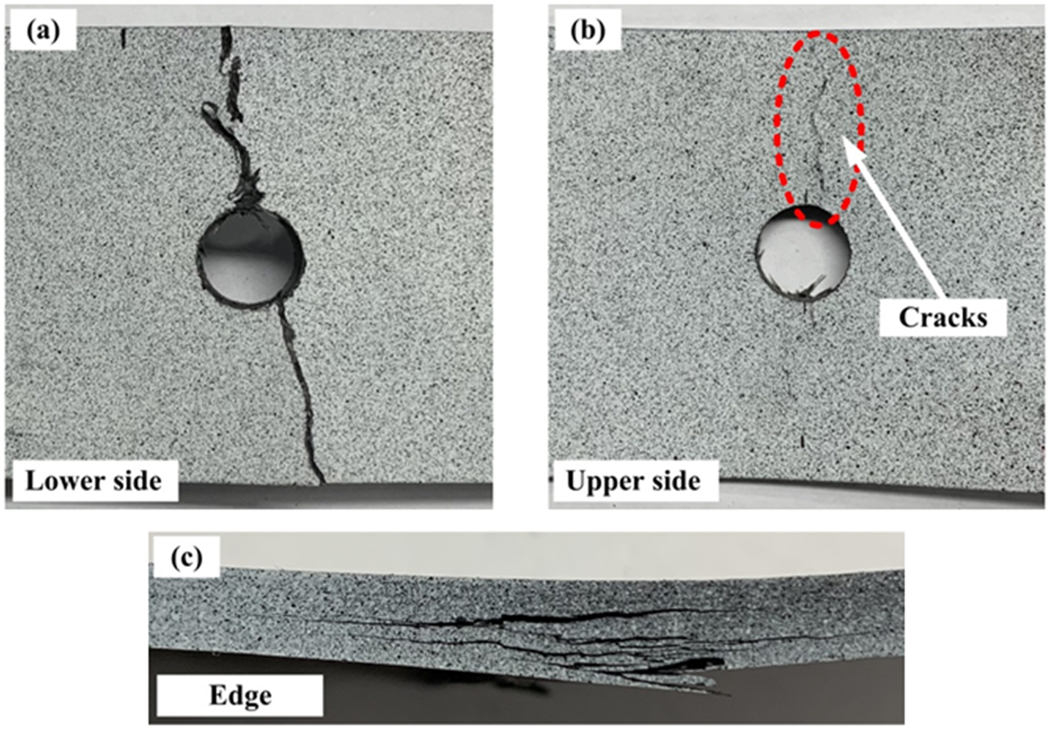
Fractures of a representative specimen after cyclic bending at (a) the lower side, (b) the upper side, and (c) the edge.

4. Fatigue Simulation for SMC Composites under Four-Point Bending

4.1. A hybrid micro-macro computational model for bending simulation

In order to accurately and efficiently simulate the bending fatigue behavior of SMC composites, a hybrid micro-macro computational model is established in this subsection. The modified RSA algorithm (Fig. 8) proposed in our previous work [49] is adopted to reconstruct the microstructure at the region of interest. The dimensions of the carbon fiber chip are 15~25 mm × 2~5 mm × 0.1 mm, and the chip volume fraction in SMC composites is approximately 80% [50]. Since the theoretical stress states at different layers vary through the thickness direction, the thickness of the computational model should be the same as that of the specimen, which is 4.8 mm. Then, the corresponding layer number at the region of interest generated by the modified RSA algorithm is 48, given the mean thickness of each layer is 0.1 mm. As introduced in the modified RSA algorithm, the second-order fiber orientation tensor a_ij is adopted to describe the fiber orientation distribution [68]:

$$\begin{gathered} a_{ij}=\oint p_i{p}_j\psi (\Phi )d\Phi (i,j=1,2) \\ {p}_1=\cos \Phi \\ {p}_2=\sin \Phi \end{gathered}$$ (6)

Fig. 8.

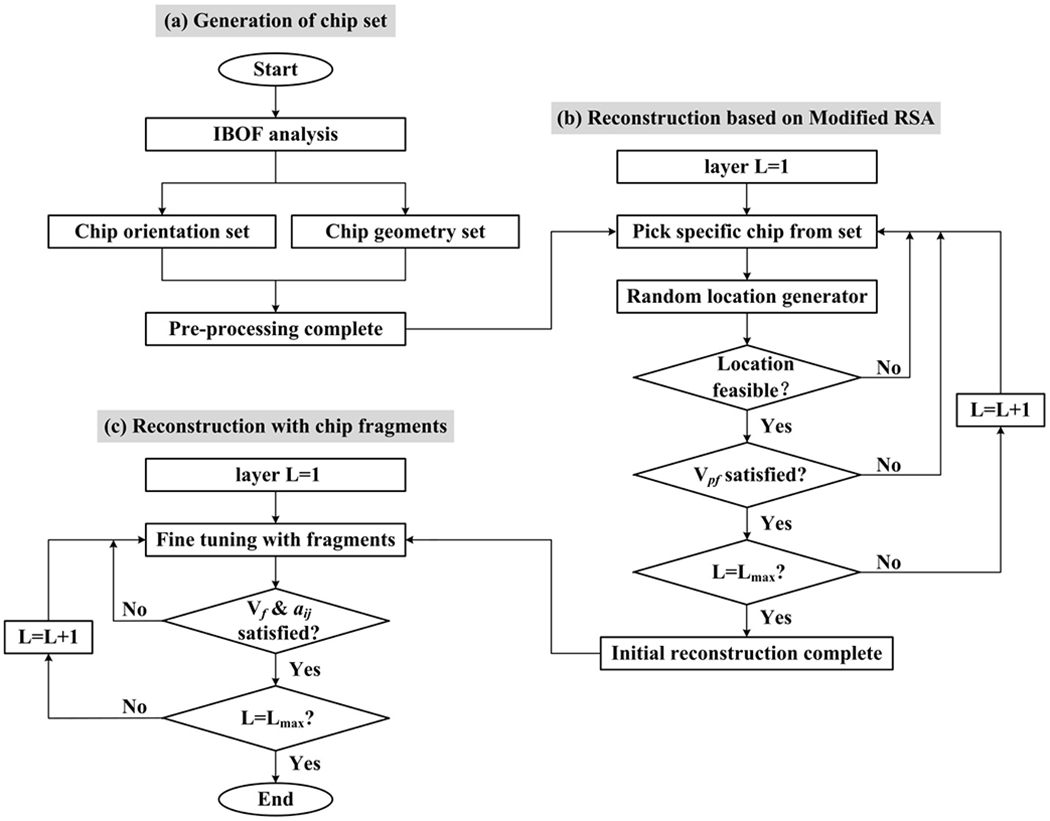
Flow chart of the modified RSA algorithm [49] for (a) generation of chip set, (b) reconstruction based on modified RSA algorithm, and (c) reconstruction with chip fragments.

where Φ is the fiber angle in the Cartesian coordinate system; $\psi \left(\Phi \right)$ is the probability distribution function. Note that the measured $E_{\text{nominal}}^{\text{lower}}$ for SMC composites used in the bending fatigue tests ranges from 19.3 GPa to 27.2 GPa. Correspondingly, the main component a₁₁ in the tensor is designed from 0.3 to 0.5 for layers from the bottom to the center, which gives rise to the range of local modulus from 18.1 GPa to 30.7 GPa (the relationship between modulus and a₁₁ has been given in Ref. [37]). To simulate the bending fatigue behavior of SMC composites without a large discrepancy between the lower and upper side, first, a₁₁ of layers from the center to the top is set as the same as that from the bottom to the center in each case. Second, to study the effect of the discrepancy between the lower and upper side on the bending fatigue performance of SMC composites, a₁₁ = 0.5 is used to build up layers from the center to the top at the region of interest, while a₁₁ = 0.3 is applied for layers from the bottom to the center (ξ = 0.7).

Other regions of SMC composites in the computational model are modeled as homogenized continua. One representative computational model for four-point bending fatigue simulation is shown in Fig. 9. The dimensions of the region of interest (the micro-scale model) are 25.4 mm × 25.4 mm × 4.8 mm. The different colored stripes involved in the micro-scale model represent the chopped carbon fiber chips, while the white areas refer to the vinyl ester matrix. Zero-thickness cohesive elements have also been introduced to describe the interfaces between chips and those between chip and matrix in the micro-scale model. In the hybrid micro-macro computational model, the gray beams connected to the micro-scale model are the homogenized regions of SMC composites. The length of the full SMC bending model should be longer than the support span, which is set as 175 mm. The radius of the steel pins is 5 mm, which is consistent with that in the bending fixture. The loading and support spans are 65 mm and 125 mm, respectively. It should be mentioned that the theoretical stress distribution between two loading pins is uniform. By adjusting the applied total force following Eq. (2), the shorter loading and support spans have limited influence on the numerical simulation. In addition, as the notch-insensitivity of SMC composites has been proved in Ref. [50, 64, 65], we use the specimens with a circular hole to improve the proportion of valid data. In contrast, it is not necessary to introduce the circular hole in the computational model as the failure at the loading region can be prohibited in numerical simulations. So, we just use the regular reconstruction model for the region of interest.

Fig. 9.

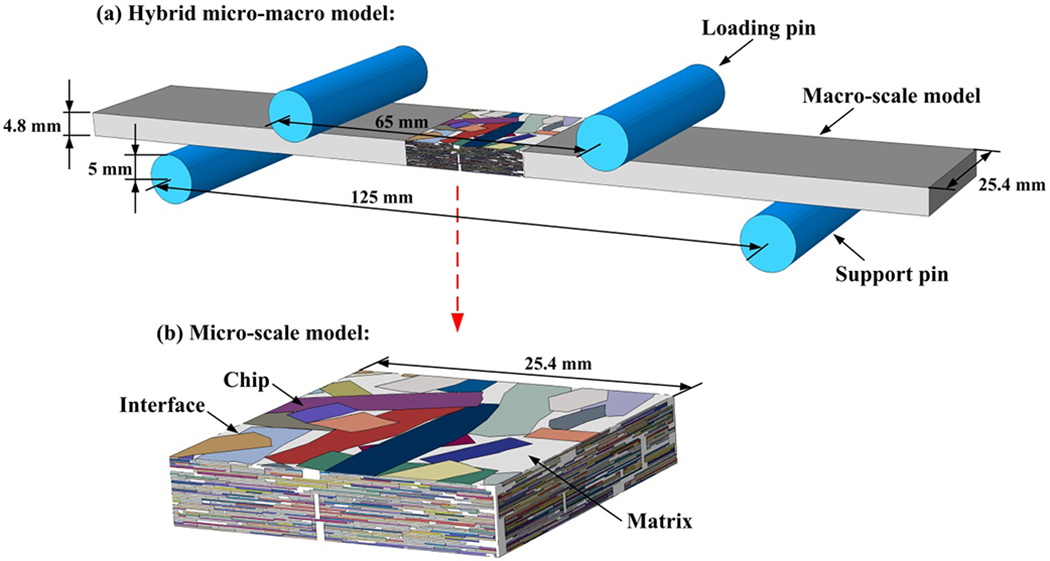
A hybrid micro-macro computational model for four-point bending fatigue simulation with magnified micro-scale model shown in (b). In the micro-scale model, different color strands represent different chips. The white regions are matrix. Zero-thickness cohesive elements have been introduced between chips and between chip and matrix.

In the finite element analysis, first-order tetrahedral element (C3D4), wedge element (C3D6), and reduced-order hexahedral element (C3D8R) are adopted for the carbon fiber chips, vinyl ester matrix, homogenized regions as well as the steel pins, while 6-node cohesive element (COH3D6) and 8-node cohesive element (COH3D8) are used to represent the interfaces. The chips are treated as transversely isotropic, and the resin matrix is assumed to be isotropic. The elastic properties of chip, vinyl ester resin, interface, homogenized region, and steel pin are listed in Table 1 [47, 50, 69, 70]. The material properties of the carbon fiber chip [47] have been calculated and validated by an RVE model of unidirectional composites [71]. Since the SMC composites used in the present study are globally isotropic, the elastic property of SMC composites with a₁₁ = 0.5 is used for the homogenized regions. During the bending simulation, the support pins are fixed. The loading pins are coupled to a reference node, and a concentrated force perpendicular to the SMC bending model is applied to the reference node.

Table 1.

Elastic properties of chip, resin, interface, homogenized region, and steel pin.

Chip		Matrix		Homogenized region
E11 (GPa)	125.9	E (GPa)	3.3	E (GPa)	30.7
E22 (GPa)	8.6	v	0.38	v	0.32
G12 (GPa)	4.8	Interface		Steel pins
v 12	0.32	K (GPa/mm)	30	E (GPa)	190
v 23	0.61			v	0.265

4.2. Progressive fatigue damage under cyclic bending

The framework of the progressive fatigue damage for SMC composites has been developed in our previous work [50], in which the fatigue failure of each element is independent and controlled by the corresponding continuum damage model. The flowchart for SMC composites under four-point bending fatigue loading is also similar to our previous efforts in modeling fatigue SMC composites under in-plane loadings, as given in Fig. 10. The explicit analysis in Abaqus is performed for the hybrid micro-macro computational model step-by-step. Nevertheless, only the stress states of elements in the region of interest are extracted to calculate the damage accumulation. The continuum damage models and the corresponding inputs of each phase at the region of interest, i.e., chip, resin, and interface, have been introduced in Ref. [50], while the synopsis of the damage models and the corresponding inputs is shown in Fig. 10. The continuum damage models of the chip, resin, and interface are proposed as a power law function of the local stress, following the works in Ref. [72–74]. The material parameters in the continuum damage models are calculated by the corresponding fatigue data. The progressive fatigue damage simulation is performed step-by-step. In each step, the stress distribution is re-simulated in Abaqus. The damage accumulation of each element is then calculated according to the designed cycle increment procedure. The failed elements would be deleted after that. It should be mentioned that a simplified cycle increment procedure is adopted at the stage ‘update cycle & delete elements’ (as shown in Fig. 10) to reduce the computational cost in the bending fatigue simulation. In general, the designed cycle increment procedure would have some influence on the predicted results. Thus, the value of interface strength is recalibrated based on SMC bending fatigue results.

Fig. 10.

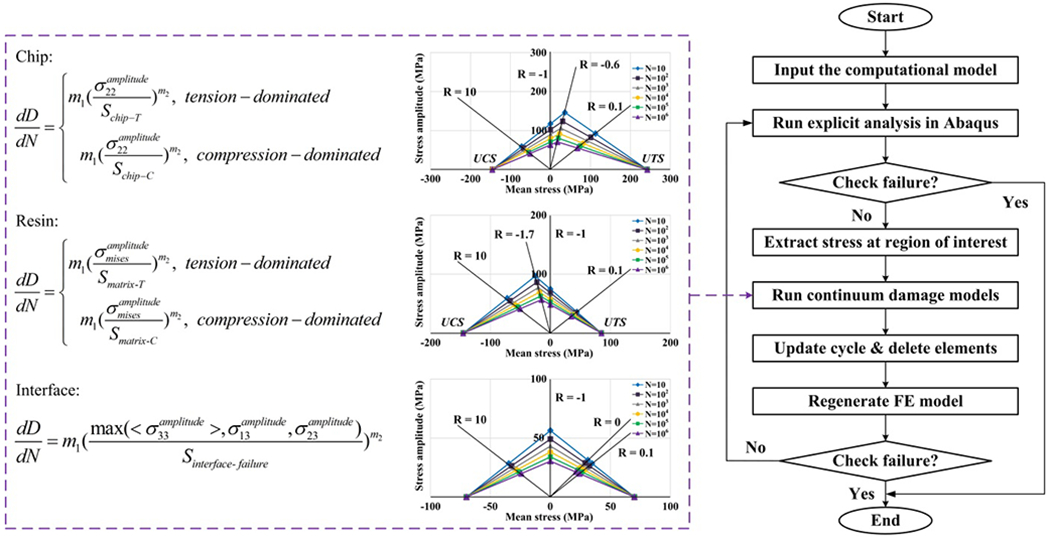
The flowchart of simulating progressive fatigue damage under cyclic bending [50].

4.3. Simulation results of SMC composites under bending fatigue loading

The generated hybrid micro-macro computational models are employed to evaluate the effect of fiber orientation distribution on the SMC bending fatigue performance in this section. The configuration for cyclic bending is the same for all cases. First, the loading level is set the same for cases with a₁₁ = 0.3, 0.4, and 0.5. Further, to validate the effect of the discrepancy between the lower and upper sides on high cycle fatigue of SMC composites, another loading level is set for cases with the same lower side but different upper sides. Details are summarized in Table 2. We note that the reliability of the reconstruction model for the region of interest has been tested in our previous works [49, 50].

Table 2.

The loading level in bending fatigue simulation.

Case	a11 (bottom to center)	a11 (center to top)	Maximum F (N)	${\sigma }_{\text{bend}}^{\text{amplitude}}$ (MPa)
#1	0.3	0.3	1600	113
#2	0.4	0.4	1600	113
#3	0.5	0.5	1600	113
#4	0.3	0.3	1350	95
#5	0.3	0.5	1350	95

The moduli of SMC composites with different a₁₁ have been given in Ref. [37]. Then, the normalized stress amplitude for the computational models can be calculated based on Eq. (4). The predicted bending fatigue results of the reconstructed computational models are plotted in Fig. 11 together with the experimental data for comparison. While the applied load in Case #1, #2, and #3 is the same, the predicted bending fatigue life increases with the increment of the a₁₁, which is consistent with the experimental data. Moreover, while the a₁₁ of the lower side keeps constant, the predicted bending fatigue life becomes longer for computational models with a higher a₁₁ at the upper side. This corroborates our experimental finding that the material property of the upper side is also influential to the bending fatigue failure of SMC composites. It can be found that the effect of the heterogeneous fiber orientation distribution on the bending fatigue behavior can be well reproduced by combining the hybrid micro-macro computational model and the framework of progressive fatigue damage for cyclic bending.

Fig. 11.

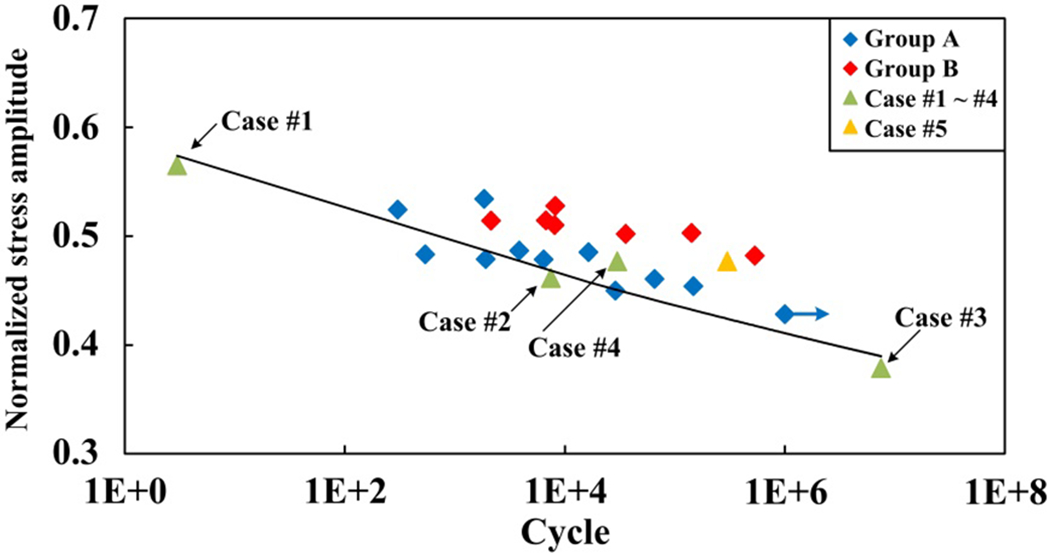
The predicted bending fatigue results with the reconstructed computational models. The blue points are the experimental results in group A (ξ < 0.5). The red points are the experimental data in group B (ξ ≥ 0.5). The green points are the simulation results for Case #1 ~ #4, of which the fiber orientation distribution is the same for two opposing sides (ξ = 0). The yellow point is the simulation data of Case #5 (ξ = 0.7).

The bending fatigue failure processes of a typical hybrid micro-macro computational model (Case #2 in Table 2) are shown in Fig. 12. At the early stage of the fatigue failure procedure, cracks are observed at the region of interest, and delamination can be found at the lower side. In addition, chip splitting failure, matrix failure, and interface failure can be well reproduced in bending fatigue prediction. The delamination is obvious from the edge of the region of interest when the computational model is broken. Therefore, the hybrid computational model constructed in this study can accurately predict the S-N diagrams of SMC composites under bending fatigue loading, and also capture the realistic bending fatigue failure behavior.

Fig. 12.

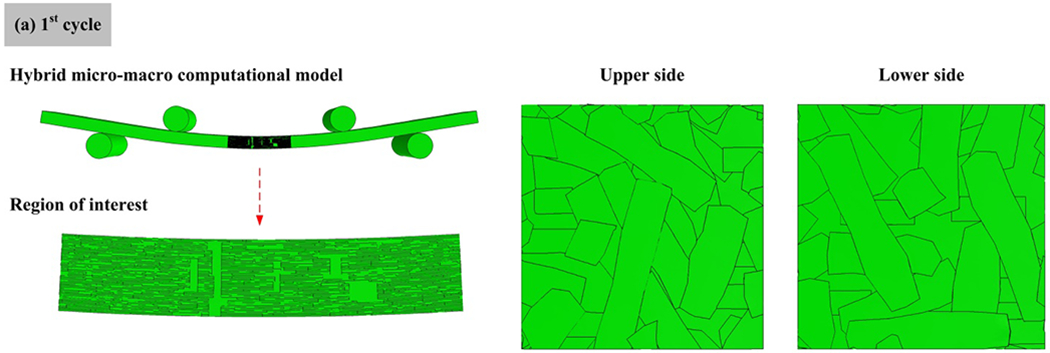
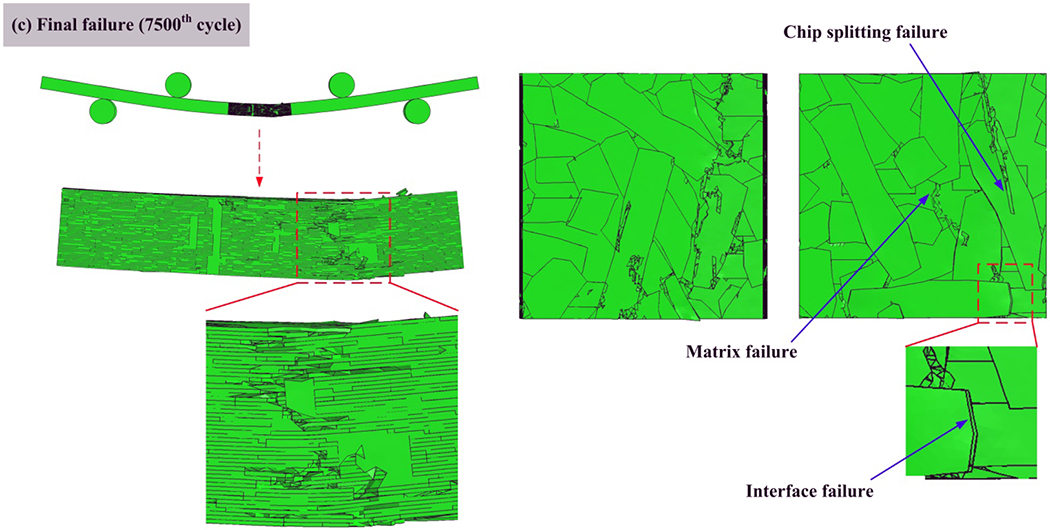
Bending fatigue failure processes of a typical computational model (Case #2), at (a) 1^st cycle, (b) 500^th cycle, and (c) final failure (7500^th cycle).

5. Closing remarks

5.1. Discussions

As illustrated in our previous investigation on the structure-property relationship of SMC composites [36, 37], the variations of local chip volume fraction, especially in the resin-rich regions, influence the measured local modulus and material performance. Since the chip volume fraction of SMC composites used in the present study reaches approximately 80% and the variation of local chip volume fraction is not remarkable, the fiber orientation plays the most dominant role in the bending fatigue of SMC composites. However, the effects of local chip volume fraction and local fiber orientation should be both considered when SMC composites with low chip volume fraction are adopted in real-world applications.

In the designed experiments, we choose the side with the relatively lower nominal modulus as the lower side, i.e., the tension-dominated side. We note that the stress states of the lower and upper sides are close to that under uniaxial tension-tension and compression-compression fatigue loading, respectively. For materials with low modulus, i.e., a₁₁ is small, the compression-compression fatigue strength of SMC composites is higher than the tension-tension fatigue strength [37]. Then, in engineering application, though low modulus would occur at both sides, the tension-dominate side would still fail earlier. Hence, the fatigue model proposed in the present study is suited for the majority of cases.

5.2. Conclusions

In this paper, we have investigated the bending fatigue behavior of SMC composites utilizing both experimental and numerical methods. We have carried out the four-point bending fatigue tests for SMC composites, and adopted the local modulus as a metric to represent the local fiber orientation of two opposing sides. We find that the local microstructures of both sides influence bending fatigue performance. While it is straightforward that higher local modulus at the lower side increases the fatigue life as bending fatigue failure of SMC composites is tension-dominated, it is more interesting to see that higher modulus at the upper side gives rise to longer fatigue life, which becomes more remarkable for high cycle fatigue cases. This observation promotes us to categorize the bending fatigue results for SMC composites by whether there is a large discrepancy between two opposing sides or not. With consideration of this heterogeneous local fiber orientation distribution at both sides, more accurate bending fatigue models can be developed. Meanwhile, we perform the interrupted tests to explore the bending fatigue failure mechanism, and also examine the damage processes of valid specimens after four-point bending fatigue tests. It is found that the bending fatigue failure of SMC composites is dominated by crack propagation instead of crack initiation, and this is the reason that the local structural features and mechanical properties of the upper side is also influential to the bending fatigue failure of SMC composites. Furthermore, a hybrid micro-macro computational model is proposed to simulate the cyclic bending behavior of SMC composites. The region of interest, having all the microstructural details, is reconstructed with a modified RSA algorithm in which the fiber orientation tensor is used to characterize the fiber orientation distribution, while other regions are modeled as homogenized continua. The developed computational model has been shown to accurately predict the S-N diagrams of SMC composites under bending fatigue loading and capture the realistic failure behavior of bending fatigue. The integrated computational and experimental efforts presented here provide important insights into the fatigue behaviors of SMC composites under cyclic bending and their dependence on the internal structures of the composites.

Appendix A. Details of the valid experimental results of SMC composites under cyclic four-point bending

Specimen	$E_{\text{nominal}}^{\text{lower}}$ (GPa)	$E_{\text{nominal}}^{\text{upper}}$ (GPa)	ξ	${\sigma }_{\text{bend}}^{\text{amplitude}}$ (MPa)	Cycle
B-1	27.2	38.4	0.41	121	28956
B-2	24.4	28.2	0.16	113	148269
B-3	24.2	27.2	0.12	106	1003000 (run out)
B-4	24.5	30.5	0.24	119	6457
B-5	20.8	30.5	0.47	101	65708
B-6	21.1	28.8	0.36	119	1854
B-7	23.7	32.4	0.37	127	303
B-8	25.5	29.7	0.16	125	3860
B-9	20.8	23.9	0.15	106	540
B-10	22.4	30.1	0.34	113	16491
B-11	24.3	33.6	0.38	119	1919
B-12	22.2	38.4	0.73	118	8115
B-13	25.7	42.4	0.65	125	535295
B-14	21.1	36.3	0.72	117	8186
B-15	24.1	37.1	0.54	123	35989
B-16	19.4	30.3	0.56	108	6758
B-17	24.1	36.2	0.50	124	141682
B-18	19.3	33.8	0.75	107	2143