Ocular Biomechanics Due to Ground Blast Reinforcement

Abstract

Background and Objective:

Bomb blast injuries exerts a shearing force on the air-tissue interfaces, causing devastating ocular injury from the blast wave. Improvised explosive devices (IEDs) are usually placed at different heights from the ground to induce more severe injury through ground blast reinforcement (GBR). However, there is still a lack of knowledge of the role of GBR and IED height from the ground on ocular biomechanics, and how they can affect the intraocular pressure (IOP) in the eye. This study aimed to estimate the IOP due to frontal IED explosion at different heights from the ground using a fluid-structure interaction model with and without GBR effects.

Methods:

A 2kg IED was placed within 5 m of the victim at 5 different heights from the ground, including 0, 0.42, 0.85, 1.27, and 1.70 m. Two different blast formulations were used to simulate the IED explosion: a) spherical airburst, with no amplification of the initial shock wave due to interaction with the ground-surface, and b) hemispherical surface-burst, where the initial blast wave is immediately reflected and reinforced by the ground (GBR).

Results:

Results revealed that the blast wave due to GBR reaches to the skull prior to the IED blast itself. The GBR also reached to the skull ~ 0.6 ms earlier when the IED was on the ground compared to the height of 1.70 m. The highest and lowest IOPs of ~ 17,000 and ~ 15,000 mmHg were observed at the IED heights of 1.70 and 0 m from the ground considering GBR. However, when the role of the GBR is ignored, IOP of ~ 9,000 mmHg was observed regardless of the IED height from the ground. The deformation in the apex of the cornea was higher when considering the GBR (~ 0.75 cm) versus no GBR (~ 0.65 cm). Considering GBR led to higher stresses and strains in the sclera.

Conclusions:

When the role of GBR was ignored, the results showed similar patterns and magnitudes of stresses and deformations in the skull and eye regardless of the height of the IED from the ground. The findings of this study suggest the critical role of GBR in ocular blast simulations.

1. Introduction

Although most trauma centers have experience with ocular trauma, blast wounds such as the ones encountered in terrorist attacks with the use of improvised explosive devices (IEDs) are infrequently encountered outside the battlefield. An IED, also known as a roadside bomb, is a homemade bomb constructed and deployed in ways other than in conventional military action and are very destructive, causing various degrees of ocular injury [1]. These bombs are usually hidden along the edges of main roads and are detonated when a vehicle passes by [2, 3]. Sometimes IEDs are deployed by suicide bomber vests and vehicular bombs [4]. IEDs remain a leading cause of injuries and deaths of armed forces personnel in Afghanistan and Iraq. More than 24,000 injuries to American service members in the military action have been reported [5], and ocular injuries are responsible for ~ 5-13% [6, 7], 29% [8], and 72% [9] of battlefield casualties, depending on the study. As global terrorism becomes a greater concern, it is important for ophthalmologists, particularly those working in urban trauma centers, to be aware of the mechanisms of injury and the spectrum of IED blast injury patterns [10]. However, estimating the ocular injuries due to the IED explosion is difficult experimentally due to complicated experimental setups, cost of the experiment, variations in the weight, angle, and distance of the IED from the victim, and other complexities. Finite element (FE) modeling is the preferred method to estimate the ocular injury computationally. FE allows us to perform analysis at various IED weights, heights, and angles.

Increased IOP due to blast injury in humans can result in globe rupture and damage to virtually every tissue in eye, including retinal commotio and detachment, hyphema, angle recession, cataract and, rarely, optic nerve avulsion [11-13]. Ocular blast injuries may be either primary, secondary, tertiary, or quaternary respectively, due to direct effect of blast wave, effect of fragments/debris from explosion, structural collapse and other mechanisms, such as thermal, chemical injuries to eye and ocular adnexa, cataract vitreous haemorrhage, and retinal detachment [14]. While some experimental studies [15-21] have been carried out to estimate the injury to the eye due to high explosive detonation, these studies are limited, as none considered the role of the ground blast reinforcement (GBR) on the severity of the injury to the victim, especially the eye.

We recently developed a fluid structure interaction model of the eye to estimate the stresses and deformations in the eye due to high explosive detonation [22], glass shard impact [23], and the combination of glass shards and blast wave blunt trauma [24]. Other FE models of the eye have been used to calculate ocular injury based on the resultant stresses and strains in the eye due to the blast overpressure [25-29]. However, most of the numerical studies [27-29] to date have focused on the damage to the anterior segment of the eye and so the posterior pole has not been extensively studied. In addition, the few studies that focused on posterior pole blast injury [25, 26] have all used a generic model and all used Conwep (a blast formulation) based on the empirical model in the TM-855 US army handbook [30], but this approach considers only the primary blast and ignores the interaction of the blast wave with the ground that induces blast reinforcement [31]. Many prior studies also ignored modeling the skull [29, 32-35] or considered it as a rigid/elastic body [36, 37] with a fixed boundary condition at the bottom. The numerical studies have been carried out thus far [25-29] only simulated the injury until the IED blast wave reaches to the victim’s face, and at most ~ 2 ms in duration or after the IED blast. However, the IED blast wave can merge with the GBR by the passage of the explosion and may result in higher stresses and strains in the ocular tissues. To the authors’ knowledge, no study has ever been conducted to simulate the IED blast at different heights.

This study was aimed to establish a 3D fluid structure interaction model of the eye, skull, air, soil, and IED, using a coupled load blast enhanced and multi-material arbitrary Eulerian-Lagrangian approach to estimate the stresses and strains in the human eye connective tissues. An eye-specific FE model of the human optic nerve head (ONH) was constructed, mated to a generic anterior segment. The eye was then incorporated into a 3D FE model of the human skull and the gap between the orbital bone and the globe was filled with extra ocular tissue. The skull FE model, which was unfixed at the bottom and allowed to dislocate, was then subjected to an IED explosion from the front in a way that the blast pressure from the IED hits the frontal bone of the skull. Two different blast formulations: a) no amplification no GBR (spherical airburst) and b) charge is located on or very near the ground surface (hemispherical surface burst), were used to simulate the IED explosion. In the latter case, the initial blast wave is immediately reflected and reinforced by the ground to produce a hemispherical reflected wave from the point of the burst.

2. Materials and Methods

2.1. Finite Element Model

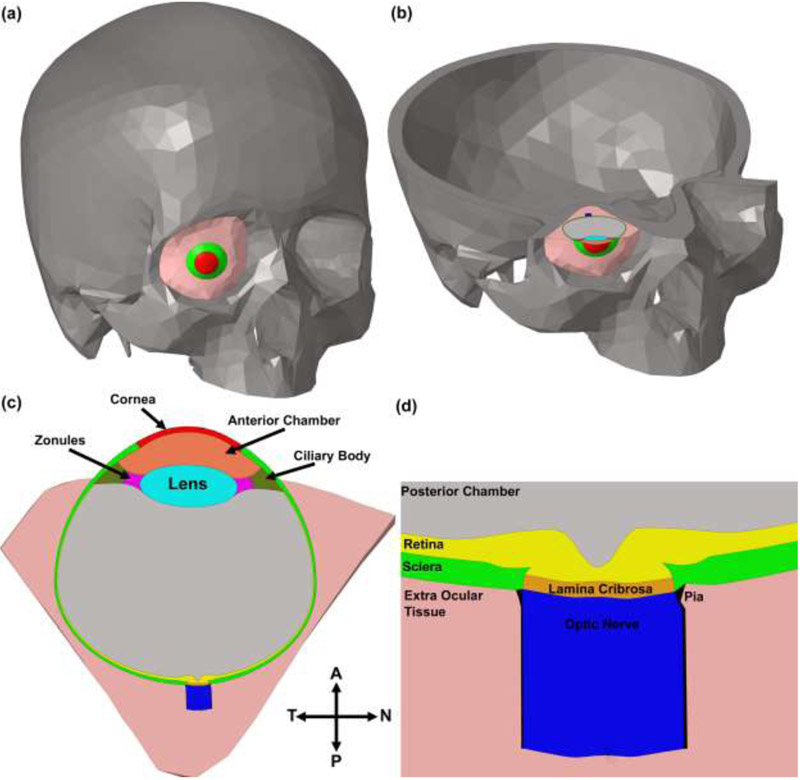
We developed a complete eye model based on data from three sources: high fidelity reconstructions of the ONH coupled with magnetic resonance imaging data for the anatomy of the posterior scleral shell, and a generic anterior segment model. To segment high fidelity reconstructions of the ONH, the meso-architecture of the human ONH model is first defined by 3D delineation of anatomic surfaces within a high-resolution, fluorescent 3D reconstruction of the posterior eye and ONH obtained from a human donor of European descent with normality confirmed by ophthalmic clinical record review [38]. In brief, custom delineation software (MultiView, courtesy of Dr. Claude F. Burgoyne) was used to section the 3D ONH reconstruction volume at forty, equally spaced, radial, sagittal planes centered on the ONH [39]. Within each radial image section, the anatomic surfaces were delineated using 2D Bezier curves to define the morphology of the neural canal, LC, peripapillary sclera, and pia [40-43]. 3D surfaces are fit to the families of Bezier curves defining each anatomic surface and the resulting eye-specific geometries of the ONH and peripapillary sclera are then fit into a larger generic posterior scleral shell with anatomic shape and thickness based on magnetic resonance imaging scans of normal human donor eyes [44]. The scleral thickness of the generic posterior scleral shell was scaled such that it best matched the peripapillary scleral thickness in the eye-specific 3D ONH reconstruction, with a 200-micrometer-wide buffer zone to smooth the transition between the eye-specific and generic posterior scleral thickness data. Finally, a parameterized, anatomic surface defining the prelaminar neural tissue, retina, and choroid is added [45]. These surfaces are then used to build the high fidelity, eye-specific, 3D FE surface mesh of the human posterior eye. The posterior pole geometry and the scleral shell were then mated to a generic anterior segment based on the Virginia Tech-Wake Forest University (VT-WFU) eye model [46]. The morphological characteristics of the human skull (healthy male adult) [47] were obtained from a 16 multislice computed tomography/magnetic resonance imaging system (Activion, Toshiba Medical Systems Corporation, Tokyo, Japan) based on our prior work [48, 49]. The bony structure of the skull in the computed tomography/magnetic resonance imaging data was segmented using Mimics (Materialise Inc., Belgium). An STL surface mesh was generated and the enclosed volume was meshed with 10-noded tetrahedral elements using a custom Matlab script (Mathworks, Natick, Massachusetts, US) [50], as the 10-noded tetrahedral elements have been shown to yield accuracy similar to 20-noded hexahedral elements at significantly a lower simulation cost [50]. The connectivity of the elements across tissue/geometric boundaries was maintained at their nodal interfaces using an automated mapping algorithm, which allowed us to avoid defining contacts between model components, thereby minimizing simulation time and eliminating any possible contact complications [50, 51]. A mass element with the weight of 80 kg was defined underneath of the skull to mimic the body weight of the victim. The acceleration of gravity was applied to the victim and the blast wave as 9.80 m/s². The final FE model of human donor #118 is presented in Fig. 1. The model is consisted of 409,503 and 548,032 elements and nodes, respectively. The material properties of the ocular connective tissues are listed in Table 1. The mechanical properties of the lamina cribrosa were determined as the shear modulus (μ) of the laminar beams multiplied by the laminar connective tissue volume fraction density to represent the average stiffness of the tissue considering the encapsulated neural tissues in the lamina cribrosa.

Fig. 1.

Screenshots showing (a) FE model of the skull, including the eye; (b) cross-section of the skull-eye model; (c) temporal-nasal cross section of the eye; (d) close-up view through the temporal-nasal section of the ONH of the eye model.

Table 1.

Mechanical properties and element types in the model of human donor 118. The bulk modulus was set to κ=100μ for all tissues (C_neo= μ/2).

Structures	Element type	Density Kg/m3	Material model	Material properties
Retina [81]	Lagrangian	1100	Hyperelastic	Cneo=0.005
Sclera [81]	Lagrangian	1243	Hyperelastic	Cneo=0.113
Lamina cribrosa [81]	Lagrangian	1243	Hyperelastic	Cneo=0.113×0.38 (CTVF)=0.042
Pia [81]	Lagrangian	1100	Hyperelastic	Cneo=0.113
Optic nerve [81]	Lagrangian	1100	Hyperelastic	Cneo=0.005
Cornea [82]	Lagrangian	1076	Hyperelastic	Cneo=0.276
Zonules [33]	Lagrangian	1000	Hyperelastic	Cneo=0.0595
Lens [33]	Lagrangian	1078	Hyperelastic	Cneo=0.1394
Ciliary body [33]	Lagrangian	1600	Hyperelastic	Cneo=0.1394
Extra ocular tissue [83]	Lagrangian	970	Hyperelastic	Cneo=0.0017
Aqueous [26]	Lagrangian	1000	Hyperelastic	Cneo=0. 0000035
Vitreous [84]	Lagrangian	1000	Viscoelastic	G0=0.01 kPa, G∞=0.0003 kPa, β=14.26 1/s, K=2 GPa
Skull [22]	Lagrangian	1009	Elastic	E=13.7 GPa, v=0.3
IED [27]	Eulerian	1570	Jones-Wilkins-Lee equation	Detonation velocity = 6930 m/s, Chapman-Jouget pressure‡ = 21 GPa, Internal energy density (E0) = 4.3 GPa
Air [27]	Eulerian	1.22	Ideal-gas gamma-law	Internal energy density (E0) = 0.258 MPa, γ = 1.4, Pressure cut off=1e7 GPa
Soil [85]	Eulerian	1986	Federal Highway Administration soil model	Pore Water Pressure = 5, Specific Gravity of Soil used to get porosity= 2.65, ρwater (Density of water in model units - used to determine air void strain (saturation)) = 1, Viscoplasticity parameter (strain-rate enhanced strength) =2, Viscoplasticity parameter (strain-rate enhanced strength) =1e-4, Maximum number of plasticity iterations = 10, K (Bulk Modulus) = 5.19 GPa, G (Shear modulus) = 343 MPa, Peak Shear Strength Angle (friction angle) (radians) = 0.611, Coefficient A for modified Drucker-Prager Surface = 4.4e-9, Cohesion ñ Shear Strength at zero confinement (overburden) = 6.2e-8, Eccentricity parameter for third invariant effects = 1, Strain hardening percent of phi max where non-linear effects start = 0.25, Strain Hardening Amount of non-linear effects = 0.01, Moisture Content of Soil (Determines amount of air voids) (0.0 - 1.00) = 0.252, Parameter for pore water effects on bulk modulus = 463, Skeleton bulk modulus- Pore water parameter ñ set to zero to eliminate effects = 5.199e-4, The minimum internal friction angle, radians (residual shear strength) = 0.001, Volumetric Strain at Initial damage threshold = 0.1, Void formation energy (like fracture energy) = 1, Level of damage that will cause element deletion (0.0 - 1.00) = 0, Maximum principle failure strain = 1

^‡The Chapman-Jouguet pressure is reached if the sonic velocity of the reaction gases reaches the detonation velocity.

The average IOP of 15 mmHg [52] was applied to the model as an initial condition and it was allowed to propagate in response to the induced blast load. A custom Matlab script was used to detect the load surface, equivalence the nodes at the components’ interfaces, define the materials’ sections, define the element sets, and write the final LS-Dyna input file [50], A 10-core Intel® Xeon® CPU W-2155@3.30 GHz computer with 256GB RAM was used to run the simulations in explicit-dynamic LS-DYNA (Ansys/LST, AL, US). The simulations were conducted in three steps, including IOP elevation from 0 to 15 mmHg for 0.10 ms to pre-blast physiologic value, constant IOP of 15 mmHg for 0.40 ms, and then IED explosion for 19.50 ms with time steps of 0.10 μs (200 time steps). The entire simulation took 20 hours to run on our workstation.

2.2. Validation of the Eye Finite Element Model

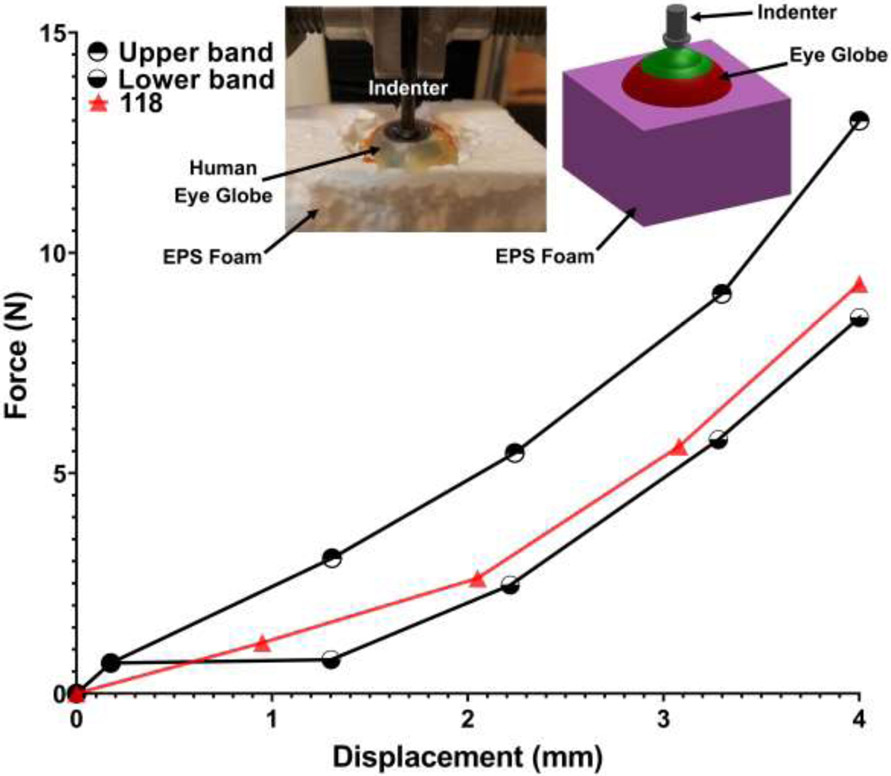
In a prior experimental study, we performed an indentation test on human cadaver eyes at the corneal apex [53]. In this experiment, the orbital fat was removed and then the globe was placed into expanded polystyrene (EPS) foam to hold the globe in place and constraint radial expansion of that motion during the experimental testing. An indenter was used to indent the globe in the anterior-to-posterior direction at the corneal apex. The force and displacement were recorded via a load cell and an extensometer, respectively (Fig. 2). To validate the eye models used in this study and compare their force-displacement response against the experimental data, the models used herein were incorporated into an identical experimental setup and simulated in LS-DYNA as presented in the inset of Fig. 2. The screw indenter was simulated moving downward and the force and displacement at the interaction site were estimated and plotted for the eye model of human donor #118. Results were compared against our previously published experimental data [53]. The main objective of this validation was to show the accuracy of the geometry and material properties of the ocular connective tissues, and not the dynamic behavior of the eye.

Fig. 2.

The force-displacement experimental data of the human eye indentation test [53]. The upper and lower bands data are related to the range of the data. The force-displacement responses of the eye model 118 were calculated and plotted for a loading rate of 50 mm/min.

2.3. Detonation Model

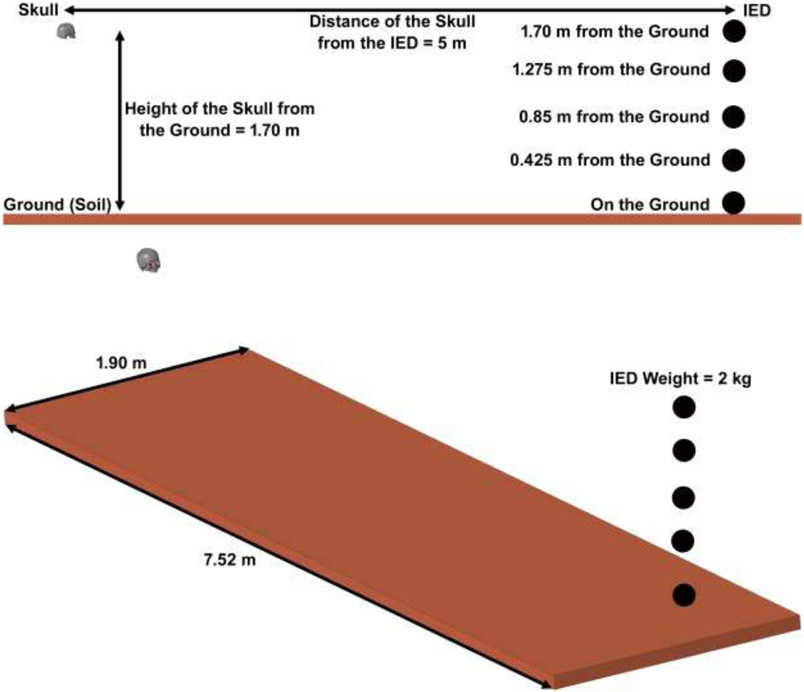
A typical IED consists of a container, a power source (usually a battery), an initiator (detonator), a switch (trigger), and a charge. A cell phone or other remote device that can be activated from a distance often serves as the trigger. As the term IED would imply, these devices are “improvised” from readily available materials [10]. In an explosive detonation, a solid is converted rapidly to a hot gas [54]. The expanding hot gases created by the explosive form a blast wave of compressed, high-pressure air moving at supersonic speeds [55]. The point of highest pressure is known as the peak overpressure. This point is followed by a “blast wind,” or “dynamic overpressure,” that can move in excess of 2000 km/h. After the blast wind is a drop in pressure resulting from the displaced air pushed outward by the blast wind and wave. When a blast front reaches a victim in spherical shape (no GBR) or hemispherical shape (GBR), it causes a very large, near instantaneous rise in ambient pressure, filling the space with high-pressure gases in 0.1 ms. Because explosive gases continue to expand from their point of origin, a longer negative underpressure (relative vacuum) follows the peak positive overpressure. Both the positive overpressure and the negative underpressure are capable of causing significant primary blast injury [56]. The air blast spherical function for the application of pressure loads due to the detonation of a conventional explosive (no GBR) was defined based on our recent publications [22, 24]. However, in this study, we aimed to compare the conventional spherical airburst function with the hemispherical surface burst one to show how the GBR can influence the magnitude and pattern of ocular injury. Detonation development was presumed to be upright to the frontal surface of the skull at the distance of 5 m from the victim and at five different heights from the ground as displayed in Fig. 3. In this case, the initial blast wave is immediately reflected and reinforced by the ground (the model accounts for yield, as the ground is covered with deformable soil) to produce a hemispherical reflected wave from the point of the burst. This reflected wave merges with the initial incident wave producing overpressures that are greater than those produced by the initial wave alone [31]. In confined spaces, the walls, floor, and ceiling also reflect the blast wave, and result in amplification of the blast energy by as much as four to eightfold [10]. However, in open spaces only the ground can reflect the blast wave and, therefore, IEDs are typically placed at different heights from the ground (for example at the height of the vehicle) so as to cause fatal injury [57]. Such open-space explosions can reinforce the blast energy through the ground reflection as well and cause a serious injury to the victim [31].

Fig. 3.

The fluid structure interaction of the skull, eye, IED, air, and soil. The IED was placed within 5 m of the victim at five different heights from the ground. After detonation, the blast wave and its reflection from the ground impact the frontal bone of the skull.

The air was considered as an ideal gas and its equation is expressed as following [58]:

$$p=(\gamma -1)\rho e$$ (1)

where P is the pressure, γ is the ratio of specific heats, which is supposed to be 1.4, ρ is the density and e is the specific internal energy. Its internal energy of the air was defined as 2.068×10⁵ J and the pressure was 101.325 kPa [27]. In the 3D model, the Lagrangian mesh of the eye and the orbit are comprised into an Eulerian mesh through which the blast wave expands. The general coupling algorithm was used to enable the interaction between the Eulerian and Lagrangian meshes. This is based on the creation of a coupling surface on the Lagrangian structure. Here, forces are calculated and transferred between two solver domains. At the same time, stress in the Eulerian elements generates force, causing deformation of Lagrangian elements [36].

The weight of the IED was set to 2 kg with a density of 1570 kg/m³. Several methods can be used to approximate the equivalent mass of IED for a given explosive. The most typical approach is to scale the mass by the ratio of the Chapman-Jouget detonation velocities given by:

$$M_{TNT}=M_e\frac{v_e^2}{v_{IED}^2}$$ (2)

where M_IED is the equivalent IED mass and V_IED is the Chapman-Jouget detonation velocity of IED. M_e and V_e are, respectively, the mass and Chapman-Jouget velocity of the explosive under consideration. IEDs are typically placed at various heights from the ground so as to cause fatal injury. Therefore, injuries from IEDs are strongly associated with head injuries and bilateral ocular involvement requiring extensive surgical repair and debridement [57]. The boundary of the airfield and the soil was demarcated as ‘flow out’ which allows the particles to flow out easily.

In the model, the detonation was initiated at the core and a “programmed burn” model was used with a “burn fraction” augmentation, material high explosive burn, and initial detonation. In this model, the ignition time of a particle in the explosive was identical with that of the distance point separated by the detonation velocity. Burn fraction, F, which multiplies the equation of state for high explosive, controls the release of chemical energy for simulating detonations. At any time, the pressure in a high explosive element is given by:

$$p=F{p}_{eos}(V,E)$$ (3)

where p_eos, is the pressure from the equation of state, V is the relative volume, and E is the internal energy density per unit initial volume. In the initialization phase, a lighting time, t₁ is computed for each element by dividing the distance from the detonation point to the center of the element by the detonation velocity D. The burn fraction F is taken as the maximum

$$F=max(F_1,F_2)$$ (4)

where

$$F_1\{\begin{array}{cc}\frac{2(t-t_1)D{A}_{e_{max}}}{3v_e}\hfill & ift>t_1\hfill \\ 0\hfill & ift\le t_1\hfill \end{array}\phantom{\}}$$ (5)

$$F_2=\beta =\frac{1-V}{1-V_{CJ}}$$ (6)

where V_CJ is the Chapman-Jouguet relative volume and t is current time. If F exceeds 1, it will reset to 1. This calculation of the burn fraction usually requires several time steps for F to reach unity, thereby spreading the burn front over several elements [58].

The federal highway administration soil material model (Eulerian element) was used to simulate the soil. The federal highway administration is an isotropic material with damage. The model incorporates a modified Mohr-Coulomb surface to determine the pressure-dependent peak shear strength, which was developed by Lewis for applications involving road base soils [59].

The interface of Euler and Lagrange elements at the detonation model were coupled using load blast enhanced-multi-material arbitrary Eulerian-Lagrangian method [60]. Multi-material arbitrary Eulerian-Lagrangian algorithms provide the framework to model sections of a simulation as either Lagrangian, arbitrary Eulerian-Lagrangian, or Eulerian. In addition, sections of a simulation can switch in time between mesh motions as the distortion of the problem dictates. Multi-material arbitrary Eulerian-Lagrangian method provides the accuracy of Lagrangian mesh motion and the robustness of Eulerian mesh motion within the same framework.

3. Results

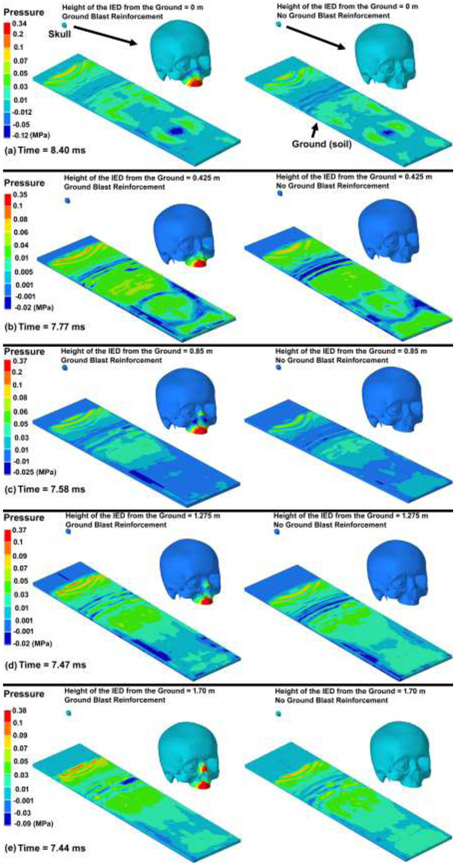
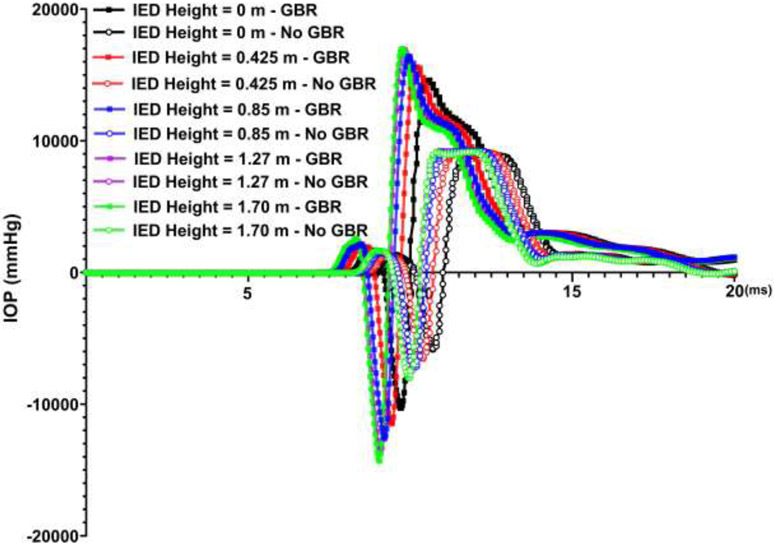
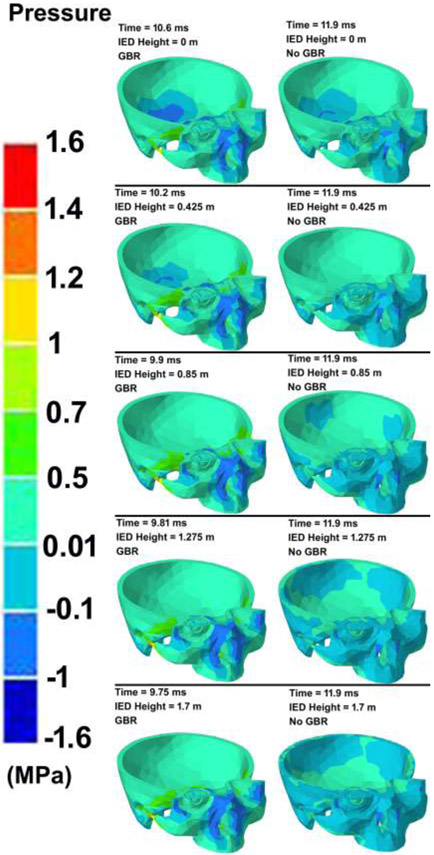
The contour maps of pressure in the skull models under various IED heights considering the GBR and no GBR are illustrated in Fig. 4. The blast reached the ground (soil) sooner when the IED was located near the ground compared to the IEDs at higher heights. At the same simulation time, the results showed that blasts considering the GBR leads to a faster expansion of the blast pressure and, as a result, the blast pressure reached the skull prior to blasts with no GBR. The variations in the IOP versus the simulation time under various IED heights from the ground and GBR are plotted in Fig. 5. The contour maps of pressure in the skull models under various IED heights and GBR are attached as separate videos throughout 20 ms of the blast simulation (Supplementary Materials).

Fig. 4.

The contour maps of pressure in the ground (soil) and skull-eye model from the initiation of the explosion through the end of the simulation. The skull-eye model is magnified for each model to better represent the pressure distribution in the tissues.

Fig. 5.

Variations in IOP versus time for various IED heights, as well as ground blast reinforcement.

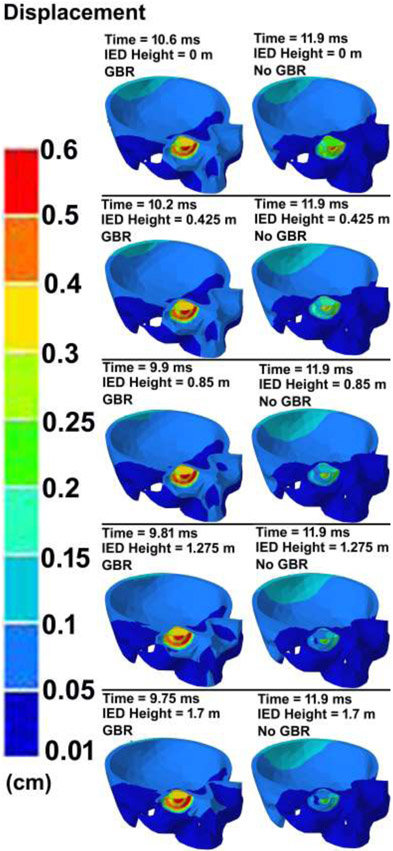
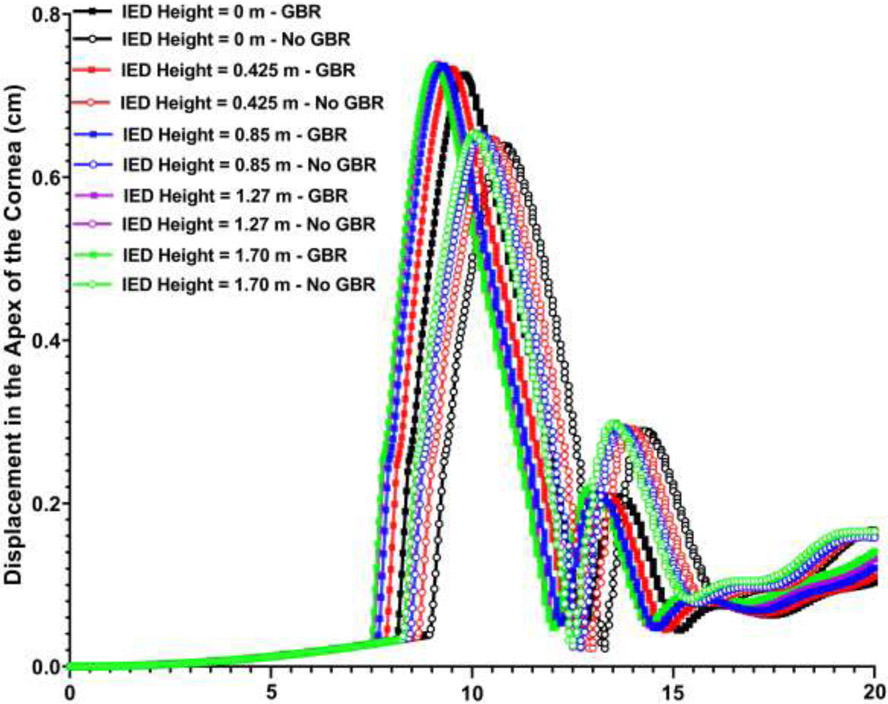
The contour maps of pressure and displacement in the skull at various IED heights from the ground and GBR at the time of the highest IOP values are shown in Figs. 6 & 7, respectively. To compare the deformation of the cornea throughout the course of 20 ms simulation, the variations of the corneal apex deformation versus the simulation time under various IED heights from the ground and considering the GBR/no GBR are plotted in Fig. 8.

Fig. 6.

The contour maps of pressure in the skull-eye model for various IED heights from the ground considering the ground blast reinforcement.

Fig. 7.

The contour maps of displacement in the skull-eye model for various IED heights from the ground, considering ground blast reinforcement.

Fig. 8.

Variations of corneal apex displacement versus the time for various IED heights from the ground, as well as ground blast reinforcement.

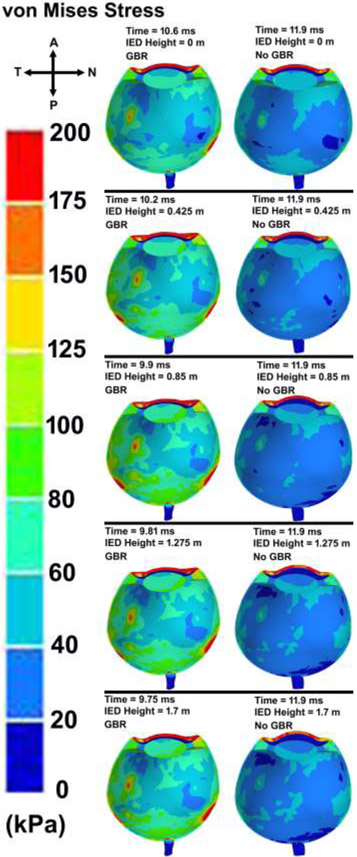
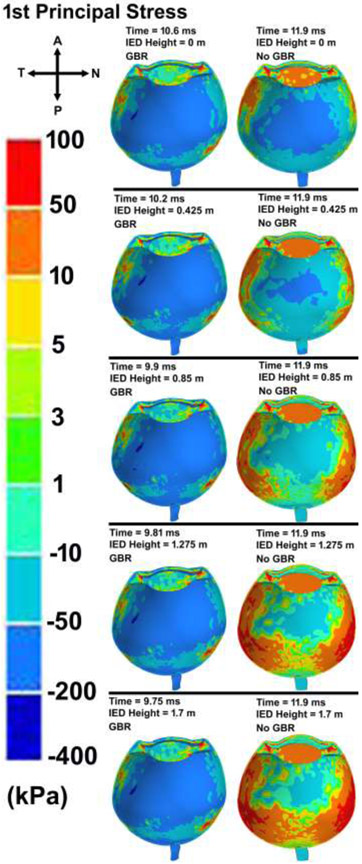
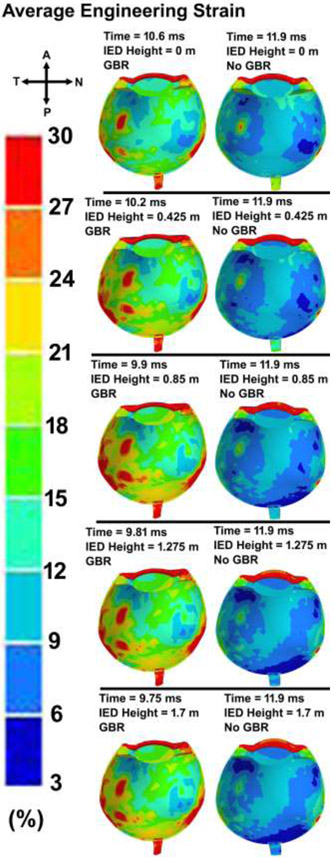
The contour maps of von Mises stress and first (maximum or tensile) principal stress in the eye with various IED heights and GBR at the time of the highest IOP values are shown in Figs. 9 and 10, respectively. The patterns of the stresses revealed that ignoring the GBR leads to a similar distribution of stresses in the eye regardless of the IED heights from the ground. However, when considering GBR, higher stresses and strains occurred in the scleral tissue. The contours of the average engineering strain as depicted in Fig. 11, exhibited the same trend in the stresses and deformations.

Fig. 9.

Contour maps of von Mises stress in the skull-eye model for various IED heights from the ground, considering ground blast reinforcement.

Fig. 10.

Contour maps of first (maximum) principal stress in the skull-eye model for various IED heights from the ground, considering the ground blast reinforcement.

Fig. 11.

Contour maps of average engineering strain in the skull-eye model for various IED heights from the ground, considering the ground blast reinforcement.

4. Discussion

Terrorist activities using IED are on the rise throughout the world [61], and ocular injuries from IEDs are among the injuries associated with severe ocular damage requiring extensive surgical repair or evisceration/enucleation [57, 62-64]. However, IED explosion and its impacts on the ocular connective tissues are complicated and cannot be easily analyzed experimentally, mostly due to their severity and variations in the injury profiles [19, 65, 66]. FE analysis allows us to have various forms of simulations and analyses in an eye at different blast angles, distances, and intensities at lower cost and in a shorter time. In this study, the IED was located at the distance of 5 m from the victim and at five different heights from the ground. The main objective of this work was to understand the role of the IED height from the ground and the GBR on the stresses and deformations in the human eye connective tissues using an experimentally verified eye-specific model (Figs. 1-2). The primary and tertiary injuries were simulated as for the primary the initial blast wave strikes the victim's skull (Fig. 3).

Our results showed the importance of the GBR in ocular biomechanics assessment (Fig. 4), as GBR reached to the skull prior to the IED blast pressure itself. The results also revealed that when the IED was placed on the ground, it took longer for the GBR to reach to the skull rather than when the IED was at the height of 1.70 m from the ground. This implies the important role of GBR [31], as it has been shown that the GBR can increase the blast energy by as much as four-to eightfold [10]. Experimental studies have also found a very rapid overpressure from ground blast reflection [67]. Our results showed that the blast wave reflected off the ground struck the victim prior to the direct bomb blast pressure. In addition, increasing the height of the IED from the ground led to a higher pressure in the skull and reduced the time that GBR took to reach to the skull. This is in agreement with the literature, as IEDs are typically placed at different heights from the ground (for example at the height of the vehicle) so as to cause fatal injury [57].

To date, the motion of the head during the blast has been neglected [68], however, our results revealed the rigid body translation of 0.1 and 0.06 cm with and without considering GBR, respectively. These small values could be related to the victim distance of 5 m from the IED, which decreases the intensity of the blast pressure on the victim’s body. The deformation in the skull itself, as well as the rigid body translation of the skull can alter the vectors of the pressure that apply to the victim throughout the simulation process. Therefore, ignoring head motion could introduce error into the numerical findings.

Most studies to date [22, 24, 26, 27, 29, 32, 36] have simulated the detonation using Conwep based on the empirical model in TM-855 US army handbook [30], as the load blast without considering interaction of the shockwave with the ground. However, it has been reported that the ground induces blast reinforcement and can significantly alter the pattern and magnitude of the injury to the body [31]. In this study, we formulated the reflection of the blast wave with the ground into the Conwep detonation model, which resulted a considerable amount of reinforcement for the released overpressure in the skull (Fig. 4). When the GBR overpressure merged with the bomb blast pressure itself, they led to a higher amount of overpressure in the skull, specifically around the orbital bone. The overpressure in the eye evoked an abrupt IOP elevation of ~ 17,000 and 15,000 mmHg under the IED height of 1.70 and 0 m from the ground (Figs. 5 & 6). Ignoring the GBR, however, led to an IOP increase of ~ 9,000 mmHg, regardless of the IED height from the ground. A delay of ~ 0.9 ms between the IOP elevation, both with and without GBR, implies the importance of the ground reinforcement in reaching to the victim prior to the bomb blast overpressure itself.

All studies to date have ignored the overpressure due to GBR and only reported the IOP within 0.75 to 1.6 ms after the blast. Within 1.6 ms after the blast, our results revealed an IOP elevation of 2730 and 1670 mmHg with and without considering GBR, respectively, which is within the reported ranges of 2625 mmHg [37], 3150 mmHg [69], 1739±307 mmHg [70], and 3000 mmHg [29] in prior studies. This is consistent with the experimental study on porcine eyes under blast loading by Alphonse [16]. The highest IOPs monitored ranged from 3000 to 5850 mmHg (95% confidence interval) at a peak incident pressure of 1575 mmHg. Compared to Alphonse’s experiment, we found a slightly lower IOP in our study, which might be due to the differences in geometry and material properties between the human and porcine eyes. For example, previous studies have shown that rupture pressure of the eye is significantly higher in porcine than in human eyes (1.64 MPa versus 0.91 MPa) [71]. Notghi et al., also found the IOP range of −3750 to +2250 mmHg (minus sign only represents the direction of the applied pressure) for the IED weight of 2.27 at the distance of 2.5 m from the victim in the front blast simulation [26].

In this study, the peak displacement of the ONH was found to be ~ 0.085 mm (Fig. 7) which is in good agreement with that of 0.09 mm [26]. Such elongation of the optic nerve may account for the axon tortuosity observed in the experimental traumatic optic neuropathy [72]. The highest deformations in the apex of the cornea were found to be ~ 0.75 and 0.65 cm for the GBR and no GBR cases regardless of the height of the IED from the ground (Fig. 8). The results also revealed that when the IED was at the height of 1.70 m from the ground it could deform the cornea prior (~ 0.63 ms) to when the IED was placed on the ground. The models with GBR experienced the highest corneal deformation, which implies the important role of GBR in ocular biomechanics. The globe rupture stress of 9.4 MPa (static test), 23 MPa (dynamic test) [73], as well as the pressure of 1.6 MPa have been reported in the literature [29]. Our results revealed the highest pressure and stress of 0.6 MPa and 1.3 MPa in the eye, respectively, which are lower than that of reported stresses for globe rupture (Fig. 6).

Peak corneoscleral stresses were observed at the limbus with a peak stress of 6.4 MPa for the blast located at 1.25 m [74]. Here, the distance between the victim and the IED was 5 m, which led to the peak pressure of ~ 1 MPa at the corneal apex, vitreous base, globe equator, and macula, respectively (Fig. 6). In the limbus, the stress was found to be ~ 1 MPa, which is lower than that of found by Liu et al., [74]. The results revealed a higher stresses at the temporal and nasal quadrants of the eye, more specifically at the scleral wall, regardless of the height of the IED from the ground (Figs. 9-10). This could be related to the anatomy of the sclera, which has the lowest thickness at the equator and is prone to rupture in that area [75]. The stresses were highest around the rectus muscle insertions into the sclera (Figs. 9-10), a frequent site of globe rupture in traumatic eye injury [76-79]. In addition, the temporal sclera is more exposed, as it is less protected by the nose and has a different embryologic origin, which could play a role in its differential structure and material properties. Eye ruptures in the region of the limbus are often circumferentially oriented, and ruptures at the equator are often oriented coronally. These patterns are related to the predominant collagen fibril orientations in those two regions: circumferential at the limbus and meridional at the equator [80]. The results showed the highest stresses and strains in the sclera when role of the GBR is taken into account (Fig. 9-11). Ignoring the GBR led to the same magnitude and distribution of the strain in the eyes regardless of the IED height from the ground. The strain was mostly located at the temporal and nasal sides of the eye which the sclera has the lowest thickness and buckle from there (Fig. 11).

4.1. Limitations

First, validation of the FE simulation results is challenging, in many cases because experimental results are either not available or unsuitable to provide direct measurement of the parameters estimated in the models. In this case, prior experimental studies on the role of the blast pressure in the eye have used a setup to generate an overpressure in front of the eye; all neglected the crucial role of the GBR. Although we could not validate our numerical findings against experimental blast data, the eye models were partially validated under quasi-static blunt loading. However, a portion of the numerical results from blast loading, such as IOP, were shown to be in good agreement with the available data in the literature. Second, our results are focused on the ocular tissues, which are represented by anatomically correct geometries, but somewhat simplified material properties in our models. Specifically, the LC of the ONH is a porous connective tissue that has locally variable microstructure, but it was simulated herein as a continuum material with isotropic neo-Hookean properties. Similarly, the sclera and pia were simulated in our recent publications as a heterogeneous anisotropic material with locally variable collagen fibril orientation, especially at the peripapillary sclera [45, 50]. However, in the current study the sclera and pia were simulated as an isotropic neo-Hookean material. In the future, we plan to incorporate the laminar microstructure and collagen fibers into the optic nerve head, sclera, and pia to increase simulation accuracy. Third, only a 2 kg IED was exploded at the front of the victim with the distances of 5 m while it has been shown that various distances and weight for the IED could result in different levels of injury to the eye [27]. Fourth, only one eye used for the simulations, however, the objective of the study was mostly relied on the IED itself so having different eye models with diverse geometries would not affect the findings of this study. Fifth, the scleral thickness away from the ONH was anatomic, but it was based on the average scleral thickness maps from magnetic resonance imaging scans. While the scleral thickness distribution is therefore anatomic and reasonable, thickness is likely somewhat eye-specific, and can alter the pattern and magnitude of the stresses and strains due to the blast. This could be considered for a future parametric study to ascertain the role of the sclera’s thickness on the resultant stresses and strains during blast injury. Regardless of the simplifications in the material model as well as the weight, distance, and height of the IED from the victim/ground, this study could provide a set of valuable information for the ophthalmologists and army medical experts. This study could show the importance of the IED height and ground blast reinforcement in blast injury assessment using a modified detonation formulation and multi-material arbitrary Eulerian-Lagrangian coupling algorithm.

In conclusion, an eye-specific FE model of the human ONH was incorporated into the human skull FE model and was subjected to the IED blast from the front. The IED was placed at five different heights from the ground and two different blast formulations, including with and without GBR, were used to simulate the biomechanics of the eye. The results revealed a significant association between acute IOP elevation following IED detonation and GBR indicating IED GBR is critical factor in these blast related ocular injuries and should be considered in modeling studies and in the design of protective interventions.

Highlights.

• The blast wave due to GBR reached the skull prior to the IED blast itself

• The highest and lowest IOPs were observed at IED heights of 1.70 and 0 m

• Similar IOPs were observed regardless of the IED height from the ground (no GBR)

• GBR led to higher stresses and strains in the sclera

• Results suggest the critical role of the GBR in head and ocular blast simulations