Cut points and contexts

Abstract

In research, policy, and practice, continuous variables are often categorized. Statisticians have generally advised against categorization for many reasons, such as loss of information and precision as well as distortion of estimated statistics. Here, a different kind of problem with categorization is considered: the idea that, for a given continuous variable, there is a unique set of cut points that is the objectively correct or best categorization. It is shown that this is unlikely to be the case because categorized variables typically exist in webs of statistical relationships with other variables. The choice of cut points for a categorized variable can influence the values of many statistics relating that variable to others. This essay explores the substantive trade‐offs that can arise between different possible cut points to categorize a continuous variable, making it difficult to say that any particular categorization is objectively best. Limitations of different approaches to selecting cut points are discussed. Contextual trade‐offs may often be an argument against categorization. At the very least, such trade‐offs mean that research inferences, or decisions about policy or practice, that involve categorized variables should be framed and acted upon with flexibility and humility.

Lay Summary

• In research, policy, and practice, continuous variables are often turned into categorical variables with cut points that define the boundaries between categories. This involves choices about how many categories to create and what cut‐point values to use.

• This commentary shows that different choices about which cut points to use can lead to different sets of trade‐offs across multiple statistical relationships between the categorized variable and other variables.

• These trade‐offs mean that no single categorization is objectively best or correct. This context is critical when one is deciding whether and how to categorize a continuous variable.

Short abstract

In practical settings, the choice of cut points for categorizing a continuous variable is likely to entail trade‐offs across multiple statistical relationships between the categorized variable and other variables. These trade‐offs mean that no single categorization is objectively best or correct.

Introduction

Why is diabetes defined as a fasting plasma glucose concentration of at least 126 mg/dL rather than a value higher or lower? ¹ Why are body mass index cut points of 18.5, 25.0, and 30.0 kg/m² commonly used to define weight categories of underweight, normal weight, overweight, and obese? ² These are questions about categorizing phenomena that are inherently continuous.

Statisticians have generally advised against categorization for many reasons, including loss of information, ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ statistical power, ⁹ , ¹⁰ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ and efficiency ⁷ , ¹³ , ¹⁹ ; unrealistic assumptions of constant within‐category risks ³ , ⁷ , ¹² and about the nature of dose‐response relationships ⁵ , ¹² , ²⁰ ; biased estimates ³ , ⁷ , ⁹ , ¹¹ , ¹² , ¹³ ; the incomplete control of confounding by adjustment for categorized confounders ⁷ , ⁹ , ¹³ , ²¹ ; exacerbation of problems due to measurement error in the original continuous variable ⁷ , ²² , ²³ , ²⁴ , ²⁵ ; unrealistic exaggeration of differences between individuals with values just above and just below a cut point ¹⁵ , ¹⁸ ; and a diminished ability to discern or estimate nonlinear relationships. ¹⁶ , ¹⁸ Opinions diverge on when it remains acceptable to categorize. Some believe that it is almost never appropriate, at least not until all data collection and analyses are complete and one is ready to interpret. ¹⁵ Others suggest that it may be fine in particular circumstances, such as discussions between clinicians and patients about patient health goals, specific fields requiring quick decisions like emergency medicine, ²⁶ or statistical situations like estimating values from a cumulative distribution function when the true and assumed models are highly different. ²⁷

Here, I want to talk about a different kind of problem with categorization: the idea that, for a given continuous variable, there is a unique set of cut points that is the objectively correct or best choice. This is not necessarily a matter of whether to categorize, but rather of comparing different possible categorizations to each other. The problem arises because most biological, medical, public health, and social science variables exist in webs of statistical relationships with other variables. As we will see, the selection of cut points to categorize 1 continuous variable can, by itself, simultaneously influence the values of many statistical relationships between that variable and others. When changing the cut points leads to changes in the values of multiple statistical relationships, trade‐offs are likely to emerge that make it difficult to say that any particular choice of cut points is objectively best. These trade‐offs can then have implications for policy, practice, and scientific inference.

Impact of Cut‐Point Selection on Analytic Results

Let us explore how the choice of cut points can influence the values of statistical relationships between the categorized variable and other variables. For simplicity, most of the examples use dichotomization so that only a single cut point is involved, but the upshot extends to ordinal variables with more than 2 categories and therefore multiple cut points. To illustrate the context of different variables, Figure 1 depicts a generic health process with hypothetical relationships between population exposures, the distribution of a health state, and outcomes. The left half of the figure—relationships between the exposures and health state—is the etiologic portion of the process, whereas the right half—relationships between the health state and outcomes—is the survivorship portion. Within each of the etiologic and survivorship settings, we may be interested in differing mixtures of causal and predictive analyses.

Figure 1.

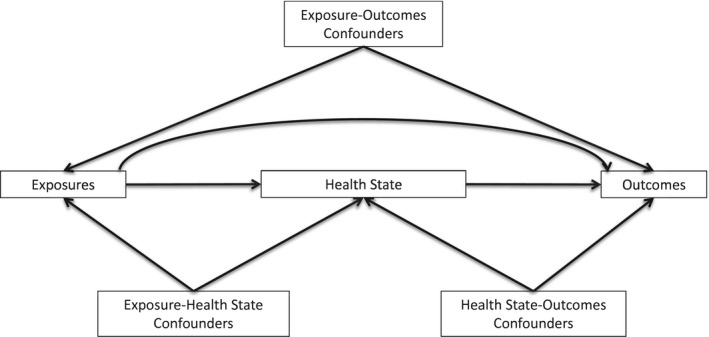
Simple process of health or disease.

Measures of Association

We begin purely in terms of association. Although the following example uses 2 common types of relative measures of association—odds ratios and hazard ratios—the implications extend to other types of relative measures (eg, risk ratios) as well as absolute measures (eg, risk differences).

In an analysis of patients with endometrial cancer, ²⁸ the exposure of immediate concern was body mass index (specifically obesity), the disease state was endometrial tumor expression of the estrogen receptor (ER) biomarker, and the outcome was mortality, of which 2 kinds were evaluated: 1) the time from endometrial cancer diagnosis to all‐cause mortality and 2) the time from diagnosis to endometrial cancer–specific mortality. ER, measured as the continuous percentage of tumor cells that expressed the marker, was dichotomized as high expression (ie, above the cut point) or low expression (ie, below the cut point). Varying the ER cut point changed which tumors were considered to have high expression.

For ER cut points ranging from 0% to 50% in increments of 10%, Table 1 presents estimates for 3 different associations: between obesity and dichotomous tumor ER status (odds ratios), between ER status and time to all‐cause mortality (hazard ratios), and between ER status and time to endometrial cancer–specific mortality (hazard ratios). ER status was the dependent variable in the association with obesity and an independent variable in the associations with mortality. Each estimate represented a result from a different model. From row to row within each type of association—for example, comparing all the obesity‐ER models to one another—the only change was the cut point to dichotomize ER. Everything else remained the same, including, as appropriate, the set of participants in the model, the coding of obesity and other variables, and the observed time from diagnosis to mortality.

TABLE 1.

Associations of Endometrial Tumor ER Expression With Obesity and Mortality Outcomes

ER Cut Point, %	Obesity/ER Association			ER/All‐Cause Mortality Association			ER/Cancer‐Specific Mortality Association
	OR	95% CI	CLR	HR	95% CI	CLR	HR	95% CI	CLR
0	2.83	1.26‐6.37	5.06	0.62	0.29‐1.30	4.48	0.32	0.13‐0.83	6.38
10	2.92	1.34‐6.33	4.72	0.61	0.30‐1.22	4.07	0.27	0.11‐0.65	5.91
20	2.40	1.22‐4.74	3.89	0.55	0.30‐1.03	3.43	0.29	0.12‐0.69	5.75
30	1.54	0.86‐2.75	3.20	0.55	0.31‐0.97	3.13	0.23	0.10‐0.51	5.10
40	1.35	0.78‐2.36	3.03	0.55	0.31‐0.96	3.10	0.21	0.09‐0.48	5.33
50	1.10	0.65‐1.87	2.88	0.59	0.34‐1.02	3.00	0.20	0.09‐0.47	5.22

Abbreviations: CI, confidence interval; CLR, confidence limit ratio (upper limit/lower limit); ER, estrogen receptor; HR, hazard ratio; OR, odds ratio.

ER expression was measured as the continuous percentage of positive tumor cells (0%‐100%) and then dichotomized at a given cut point (ER+ vs ER–). ER+ was defined as expression at or above the cut point except for a cut point of 0%, where ER+ was only expression above the cut point. The dichotomous ER status was the dependent variable in obesity‐ER models and an independent variable in ER‐mortality models. The obesity variable was a dichotomization of the body mass index (≥30 vs <30 kg/m²). This table was adapted with permission from Tables 2 and 4 in Busch et al. ²⁸

Inspecting Table 1, we find several consequences of choosing one cut point over other possibilities. First, for each of the 3 associations, the magnitude and precision of the estimate changed as the cut point changed. For a particular association, one cut point may yield the estimate of greatest magnitude (the point estimate furthest from the null value of 1.00) and another may yield the best precision (the smallest confidence limit ratio). For the obesity‐ER association, the greatest magnitude was at an ER cut point of 10% and the most precise estimate was at 50%.

Second, when comparing associations, the cut point with the greatest magnitude for one association may not have the greatest magnitude for other associations. In Table 1, the ER cut point yielding the greatest magnitude was 10% for the association with obesity; a tie between 20%, 30%, and 40% for the association with all‐cause mortality; and 50% for the association with endometrial cancer–specific mortality.

Third, while the choice of cut point can influence the numerical values of estimates of association, it can also affect our inferences. Suppose we interpreted the results strictly by statistical significance. Making 10% the cut point would lead to the conclusions that ER expression was associated with obesity and was not associated with all‐cause mortality. Had 30% been chosen, we would have reached the opposite conclusions.

Examining multiple cut points revealed a series of trade‐offs between them, even though we confined our attention to 1 exposure, 1 measure of the disease state, and 2 outcomes. The story becomes vastly more complicated when we remember that each node in Figure 1 could include any number of variables and that many processes require more complicated figures with more nodes. The cut points chosen for a variable could potentially affect the magnitude and precision of its association with every variable at every node.

When cut points are identified using a particular dataset to make the selection based on largest effect sizes or smallest P values, they may not replicate in other data sets. ³ , ²⁹ But even if the final choice of cut points replicates successfully, we would still have to contend with trade‐offs such as those shown before.

Other Statistics

Trade‐offs between cut‐point values extend to statistics other than measures of association. Sensitivity and specificity are well‐known examples. Table 2 presents a variety of prediction statistics that can vary with the choice of cut points. ³⁰ The C‐index, a measure of discrimination, is the censored‐outcomes analogue of the area under the receiver operating characteristic (ROC) curve. ³¹ The rest of the table consists of various measures from the risk reclassification framework for prediction models. ³¹ , ³² , ³³ The risk reclassification calibration statistic is a measure of model calibration (larger P values indicate better calibration), whereas the event and nonevent net reclassification indices (NRIs) and integrated discrimination improvement are measures of improvement in model discrimination (larger values indicate greater improvement).

TABLE 2.

Prediction of All‐Cause Mortality After the Addition of E‐Cadherin Measurements to Standard Diagnostic Tests of Cancer Cell Detachment From Colorectal Primary Tumors

	E‐Cadherin Variable Added to Standard Tests
	Continuous	Dichotomous E‐Cadherin Cut Point
		0.52	0.60	0.85
C‐index, % (95% CI)	66 (58 to 72)	51 (41 to 59)	54 (45 to 62)	56 (48 to 63)
Reclassification metric
No. (%) moved to higher risk category	47 (25)	11 (6)	27 (14)	41 (22)
No. (%) moved to lower risk category	55 (29)	93 (49)	83 (44)	70 (37)
Total No. (%) reclassified	102 (54)	104 (55)	110 (59)	111 (59)
Reclassification calibration statistic P value	.1	.1	.1	.2
Event net reclassification index, % (95% CI)	14 (–11 to 30)	–22 (–38 to –7)	–7 (–23 to 10)	3 (–15 to 21)
Nonevent net reclassification index, % (95% CI)	13 (3 to 35)	54 (44 to 63)	41 (29 to 52)	24 (12 to 37)
Integrated discrimination improvement, % (95% CI)	3.4 (1.9 to 5.6)	4.3 (2.2 to 6.8)	3.4 (1.8 to 5.3)	3.7 (1.7 to 5.9)

Abbreviation: CI, confidence interval.

E‐cadherin was measured on a continuous average intensity scale of 0 to 3 and then modeled as either continuous or dichotomized at a given cut point. Each C‐index value is for a Cox model of all‐cause mortality based on standard diagnostic tests of cancer cell detachment (lymph node evaluation and radiologic imaging) plus the respective E‐cadherin variable. Reclassification metrics compare a Cox model of standard diagnostic tests estimating all‐cause mortality to a Cox model of standard diagnostic tests plus the respective E‐cadherin variable. This table was modified with permission from Table 4 in Busch et al. ³⁰ , which was published under a CC BY 4.0 license.

As with measures of association, for each statistic, the magnitude can change depending on whether a variable is modeled as continuous or categorized, and if categorized, the magnitude also depends on cut‐point selection. Comparing the 3 dichotomization cut points in Table 2 to each other, once again we find trade‐offs. A cut point of 0.85 yields the best calibration. In terms of discrimination, 0.85 is best according to the C‐index and event NRI, whereas 0.52 is best according to the nonevent NRI and integrated discrimination improvement. Furthermore, the event NRI and the nonevent NRI are best considered together as a pair of values without being collapsed into a single summary measure. ³² The table illustrates different trade‐offs between the event/nonevent NRI “pairs.” Which pair should be considered best depends on substantive considerations of the cost of misclassifying a true event compared to misclassifying a true nonevent. Similarly to association measures, none of these findings would necessarily replicate in other data sets, but if they did, the trade‐offs would remain.

Weighing costs also applies to predictive calibration in the form of the relative costs of overprediction versus underprediction. Consider prostate cancer screening using the continuous biomarker prostate‐specific antigen. The consequences of underdiagnosing potentially lethal tumors (death) may be more serious than those of overdiagnosing indolent tumors (unnecessary surgeries sometimes leading to complications such as impotence or incontinence), but the costs of overdiagnosis are not negligible, and more patients are likely to be overdiagnosed than underdiagnosed. ³⁴ The trade‐off between overdiagnosis and underdiagnosis depends on the cut point defining a positive test. Creating this trade‐off by categorizing occurs regardless of whether categorization is done directly on the biomarker measurements or is delayed until after calculating the probability of cancer based on the biomarker and any other predictors. Miscalibration in either direction has costs, and there can be a further trade‐off between calibration and discrimination. ³⁵ , ³⁶ , ³⁷

Summarizing and extending these observations, Table 3 lists examples of statistical quantities that can be sensitive to the selection of cut‐point values. The list is not exhaustive.

TABLE 3.

Quantities Sensitive to Choices of Variable Category Cut‐Point Values

Number and proportion of units within the category

Measures of association (relative and absolute) a

Model fit statistics (eg, AIC and BIC)

P values

Hypothesis test statistics

Correlations a

Splines

Sensitivity a

Specificity a

Positive predictive value a

Negative predictive value a

C‐statistic (ie, area under ROC curve) a

C‐index

Predicted probability of an outcome

Event net reclassification index a

Nonevent net reclassification index a

Integrated discrimination improvement a

Reclassification calibration statistic a

Number and proportion of units reclassified across outcome risk categories

Abbreviations: AIC, Akaike information criterion; BIC, Bayesian information criterion; ROC, receiver operating characteristic.

The list in this table is not exhaustive.

^a Both the magnitude and the precision of the measure are sensitive to cut‐point selection.

Limitations of Cut‐Point Selection Approaches

The choice of cut points might affect the values of many different quantities, but are there not several ways to objectively identify the best possible choice? Many statistical tools are thought of this way, but none of them deserve that much deference. We will consider 7 approaches to cut‐point selection: quantiles, model fit statistics, magnitude of effect, statistical significance, mean squared error, ROC curves, and machine learning. An exhaustive, theoretically rigorous discussion will not be attempted here. Instead, practical problems will be illustrated that cast doubt on the notion that any of these tools invariably selects the best or correct cut points in real‐world applications.

Perhaps the most common way of setting category cut points is to use quantiles of the distribution, such as the median or quartiles. This approach has at least 2 problems. ³⁸ First, since quantile cut points derive from the distribution irrespective of how the categorized variable relates to any other variable, the cut points may not correspond to physically, biologically, or socially important thresholds within the distribution. Second, the observed distribution of the variable could vary from study to study, so that the values defining the quantile cut points in one study may not match their counterparts in another study. This last point means that studies ostensibly categorizing the variable in the same way—say, into quartiles—might not be genuinely comparable. Using a larger number of categories, such as creating a 4‐ or 5‐category variable rather than dichotomizing, may soften, but not eliminate, the drawbacks of categorization. ⁴ , ²¹ , ²⁵ , ²⁹

The use of magnitudes of association, statistical significance, model fit, or the mean squared error as cut‐point selection tools is premised on the idea of choosing cut points that, in a certain data set, provide an extreme (“optimal”) value of a particular statistic: largest magnitude of association or smallest P value, model fit statistic, or mean squared error. Such an approach can be biased in the sense that selection is based on a value in a particular direction; in addition, the chosen cut points may not replicate using the same procedures in other data sets. ³ , ⁷ , ⁹ , ¹¹ , ¹² , ¹³ , ²⁹ The mean squared error has another problem in that it is heavily influenced by outliers because squaring the terms weights large errors more than small errors. ³⁹ It is worth noting that statistical significance thresholds such as α = .05 are themselves cut points on a continuum.

The limitations of choosing cut points based on extreme statistical values are illustrated by a study of a candidate biomarker to identify patients with colorectal cancer at risk for distant spread of disease, the major cause of cancer‐related death. ⁴⁰ Prior literature had suggested that at least 25% of the patients should be flagged as high risk. ⁴¹ The biomarker analysis examined multiple cut points to dichotomize patients into high‐risk and low‐risk groups based on tumor expression of the biomarker. For the association between dichotomous marker status and time to mortality, the best model fit and the largest magnitude of association each corresponded to a cut point that would have flagged fewer than 10% of patients as high risk, much lower than the target proportion. In this case, picking a cut point based on model fit or magnitude of association would lead to a clinical disaster.

The ROC curve is used for research questions about prediction rather than causality. Researchers commonly generate an ROC curve and select the variable cut point corresponding to the most upper‐left point of the curve. ⁴² However, this choice tells us nothing about model calibration, ³⁵ absolute levels of risk, ⁴³ or the proportion of subjects at a given level of risk. ⁴³ It also assumes that false‐negative and false‐positive results are of equal consequence, which is unlikely in many applications.

One could also select cut points using various machine learning methods, but their results can still create substantive trade‐offs. Machine learning does not erase the biases, errors, or limitations of the data used to develop, test, or validate the model. In addition, categorization algorithms usually have methodologic trade‐offs embedded in them because they must account for 2 competing considerations: first, finding intervals of the continuous variable that are uniform in terms of some attribute of interest (information quality) and, second, maintaining enough sample size within each interval to ensure quality estimation (statistical quality). ⁴⁴ Some machine learning methods focus on information quality, others focus on statistical quality, and still others make different intermediate trade‐offs between information and statistical quality. ⁴⁴ Many categorization algorithms have been developed, such as entropy‐based, χ²‐based, Gini, and Fusinter criteria; Bayesian scores; description length; overall percent accuracy in classification; and effect strength for sensitivity. ⁴⁴ , ⁴⁵ , ⁴⁶ In practice, the best one would normally do is to run multiple learning algorithms on the best available data and hope to obtain similar results. However, to claim that machine learning has delivered an inarguably best or correct categorization of a variable requires clearing a high bar. One would need to arrive at the same categorization from each of an exhaustive set of algorithms run in multiple large, unbiased, error‐free real‐world data sets and repeat this for every relationship of the categorized variable to every other variable in its context.

This brings us to a problem with most approaches to cut‐point selection. They typically involve choosing a statistic, identifying the cut‐point values that optimize the statistic—often for the relationship of the categorized variable to just 1 other variable—and then treating that set of cut points as “objectively” best simply for that reason. Nothing guarantees that the categorization that optimizes any particular statistic will optimize every statistic relating the categorized variable to every other variable in its context, raising the question of why the chosen statistic is the one necessary and sufficient arbiter of the best categorization. Given that the choice of cut points may influence an entire web of statistical relationships between the categorized variable and other variables, a better approach would be to use statistics such as those discussed in this section as one of several contributions to evaluating cut points, but not definitive by themselves.

Why the Search for Objectively Best Cut Points May Often Be Pointless

What would make a particular categorization the objectively correct or best choice for a given continuous variable? It would have to optimize every statistical property of every substantively relevant statistical relationship to every other variable in every study of every process in which the variable is involved. Anything less would mean that another choice is better in some way, and then we are dealing with trade‐offs and judgment calls.

To illustrate, let us return to the study of endometrial tumor ER expression. The disease process involves more variables than those mentioned earlier. Besides body mass index, additional exposures include age, hormone therapy use, smoking, parity, oral contraceptive use, and genetic factors. Patient outcomes beyond mortality could be disease progression, response to therapy, recurrence, and a return to normal levels of circulating monitoring biomarkers. An objectively best cut point to dichotomize the tumor ER status would yield the greatest magnitude and best precision of the associations of ER with each exposure and outcome of interest. That same cut point would also yield the best model fit, minimize the loss function, and be suggested by the dose‐response curve for the relationship of the variable with each of the other variables in the process, and so far this might account only for causal analyses. If there are important prediction questions, the cut point would need to optimize every measure of discrimination, calibration, classification accuracy, and improvement in decision‐making for any prediction models of disease etiology and survivorship. These do not exhaust the statistical requirements that the cut point would need to satisfy to be considered objectively best, and it would also need to outperform every other possible cut‐point value on all statistical measures in every replication study.

This is easier to see with a variable such as ER that is being dichotomized and sits in the middle of a diagram like Figure 1, but the same requirements apply to variables at any diagram node or with multiple cut points. Body mass index, an exposure in the context of endometrial cancer, is commonly categorized into 4 bins with cut points at 18.5, 25.0, and 30.0 kg/m². ² The World Health Organization has suggested that relationships between body mass index and a range of health outcomes might vary across different populations. ⁴⁷ But even if the stated 4‐category scheme optimized every statistical relationship between body mass index and other variables for every population in the context of endometrial cancer, for 18.5, 25.0, and 30.0 kg/m² to be the objectively best set of cut points would require that they also optimize the relationship of body mass index to every other variable upstream and downstream from it in any context. Figure 2 suggests the implausibility that any single categorization of body mass index would optimize every statistical aspect of every causal or predictive relationship in the figure.

Figure 2.

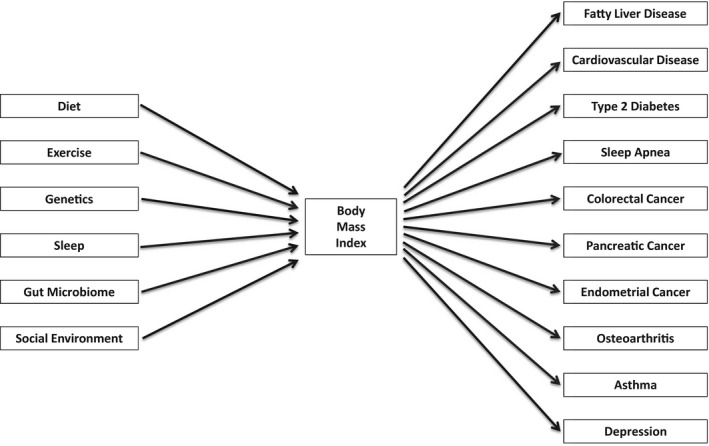
Partial context of body mass index: a sampling of upstream and downstream variables.

While perhaps possible in theory, in practice it is extremely unlikely that any particular categorization of a continuous variable can be proven to be objectively best, with no quantitative arguments in favor of any other possibility.

Conclusions

The cut points used to categorize continuous variables can influence our conclusions about causal and predictive relationships, and about whether and how to act for public health, medical, economic, or social purposes. The mathematical sharpness of cut points can obscure a real‐life fuzziness, as the choice of cut points for one variable at any part of a process can lead to a complicated cascade of statistical consequences that reverberate throughout that process and other processes involving the variable. Demonstrating the contextual trade‐offs entailed by a categorization would be a useful contribution whenever categorization is warranted. The fact that there are likely no objectively correct or best cut points to categorize any particular continuous variable may often amount to an argument against categorization. At the very least, it means that inferences, or decisions about policy or practice, that involve categorized variables should be framed and acted upon with flexibility and humility.

Funding Support

This work was supported by the National Cancer Institute (grant 5T32CA009001). The sponsor had no role in the conception, composition, submission, or any other aspect of the work.

Conflict of Interest Disclosures

The author made no disclosures.

Busch EL. Cut points and contexts. Cancer. 2021. 10.1002/cncr.33838