Abstract
Background:
In a Closed Claims study, most patients experiencing cervical spinal cord injury had stable cervical spines. This raises two questions. First, in the presence of an intact (stable) cervical spine, are there tracheal intubation conditions in which cervical intervertebral motions exceed physiologically normal maximum values? Second, with an intact spine, are there tracheal intubation conditions in which potentially injurious cervical cord strains can occur?
Methods:
We utilized a computational model of the cervical spine and cord to predict intervertebral motions (rotation, translation) and cord strains (stretch, compression). Routine (Macintosh) intubation force conditions were defined by a specific application location (mid-C3 vertebral body), magnitude (48.8 N), and direction (70 degrees). A total of 48 intubation conditions were modeled: all combinations of 4 force locations (cephalad and caudad of routine), 4 magnitudes (50–200% of routine), and 3 directions (50, 70, 90 degrees). Modeled maximum intervertebral motions were compared to motions reported in previous clinical studies of the range of voluntary cervical motion. Modeled peak cord strains were compared to potential strain injury thresholds.
Results:
Modeled maximum intervertebral motions occurred with maximum force magnitude (97.6 N) and did not differ from physiologically normal maximum motion values. Peak tensile cord strains (stretch) did not exceed the potential injury threshold (0.14) in any of the 48 force conditions. Peak compressive strains exceeded the potential injury threshold (−0.20) in 3/48 conditions, all with maximum force magnitude applied in a non-routine location.
Conclusions:
With an intact cervical spine, even with application of twice the routine value of force magnitude, intervertebral motions during intubation did not exceed physiologically normal maximum values. However, under non-routine high force conditions, compressive strains exceeded potentially injurious values. In patients whose cords have less than normal tolerance to acute strain, compressive strains occurring with routine intubation forces may reach potentially injurious values.
Summary Statement:
This computational modeling study predicts that, during direct laryngoscopy with an intact cervical spine, high (twice normal) intubation force does not cause pathologic spine motion but can cause potentially injurious cord strain.
Introduction
Cervical spinal cord injury caused by tracheal intubation is a rare but catastrophic complication.1–3 Cervical cord injuries are not limited to patients who have unstable spines. In an American Society of Anesthesiologists Closed Claims study, most (28/37) cervical cord injury claims occurred in patients who had stable cervical spines.2 This Closed Claims study reported probable contributors to perioperative cervical cord injury included direct surgical complications (9/37), head/neck positioning (7/37), and airway management (4/37).2 Of the 4 patients in whom airway management was judged to be a probable contributor to cord injury, 2 patients had stable spines.2 The occurrence of intubation-related cervical cord injury in the presence of a stable cervical spine suggests intubation may cause cord injury by mechanisms not previously considered.
There are no clinical studies reporting unrestricted cervical spine motion during tracheal intubations in which intubations were more difficult and intubation forces were increased.4–6 Thus, we wondered, in the presence of an intact (stable) cervical spine, is it possible under uncommon, high-force, or otherwise abnormal intubation conditions that pathologic cervical spine motion could occur? In other words, are there tracheal intubation conditions in which cervical intervertebral motions can exceed physiologically normal maximum values?
When the cervical spine moves, the cervical spinal cord deforms. The cord stretches and contracts axially7 and thins and thickens transversely.8 Measures of strain quantify the extent of tissue deformation (e.g., change in length or width) in response to an applied stress (force/area=pressure). In animal models, high levels of cord strain cause acute and chronic spinal cord dysfunction and/or injury.9–14 Thus, we wondered, in the presence of an intact cervical spine, even if pathologic spine motion does not take place, are there tracheal intubation conditions in which potentially injurious cervical cord strain can occur?
The aim of this study was to answer the two questions posed above. To do so, we used a computational model of the human cervical spine and spinal cord to simulate tracheal intubation. We studied large variations in laryngoscope force application conditions (location, magnitude, and direction) to include practically any set of tracheal intubation conditions that could occur in clinical practice. Model outputs included cervical spine motions (intervertebral rotation and translation) and peak cervical cord tensile (stretch) and compressive strains occurring during intubation.
Materials and Methods
Background, Rationale, and Validation of the Finite Element Model
Finite element (FE) modeling is a computational simulation method used to predict the behaviors of complex three-dimensional structures. The basis of finite element modeling lies in dividing a complex structure into many smaller, simpler structures called elements so that the overall structural response to loading may be mathematically calculated. The response of each element is expressed in terms of a finite number of degrees of freedom at a set of points called nodes that connect each element to other adjacent elements. To model biological structures, FE models require accurate three-dimensional representations of the geometry (anatomy) of all structurally distinct components such as vertebrae, intervertebral discs, ligaments, etc. These models also require knowledge of the material properties of each component (e.g., elasticity) under all conditions under which the model will be tested.15 For more than 25 years, FE models of the human cervical spine have been used to predict spine motions that occur under routine or hazardous (e.g., high force) conditions. In addition, these models allow for characterization of processes and dynamics occurring inside the substance of the spine or cord that are impossible to directly measure, such as mechanical stress and strain.15
The model used in this study is of the complete human cervical spine (from the occiput [Oc] to C7) and cervical spinal cord.16 It consists of 196,984 elements, 237,635 nodes, and has 671,997 degrees of freedom. In a prior validation study, this model closely predicted intervertebral motions (Oc-C1 through C4-C5) measured during orotracheal intubation in living patients.16 It did so with intubations accomplished with both direct laryngoscopy (Macintosh) and videolaryngoscopy.16 Results of the current study provide additional evidence of the validity of this model; see Results. Specifically, under routine (Macintosh) intubation conditions, this model predicted 1–2 degrees of flexion at C5-C6 and C6-C7. Flexion below C5 during Macintosh intubations has been previously reported by Turkstra et al.17 Also, under routine conditions, this model predicted the occiput translates 1.4 mm posterior to C1, with progressively less posterior translation at C1-C2 and C2-C3, changing to anterior translation at C3-C4, with ≤ 1.0 mm of anterior translation in the remaining caudal segments. These predicted translations are compatible with translation values calculated from the clinical intubation data reported by Mentzelopoulos et al. (Oc-C1 = 1.0 mm, C1-C2 = 0.6 mm, C2-C3 = 0.5 mm, C3-C4 = 0.4 mm, and C4-C5 = 0.3 mm).18 Therefore, this model predicts cervical spine motions measured during routine intubations reported in three different clinical studies. In addition, in our prior validation study, this model closely predicted spine motions in cadavers with Type II Odontoid fractures during intubations performed with both conventional and videolaryngoscopy.16
For additional information about this model, including development, anatomy, material properties, convergence studies, software, execution time, and code availability see Supplemental Digital Content 1—Finite Element Model Development, Material Properties, Calculations, and Limitations. We followed the applicable EQUATOR reporting guidelines for simulation.19
Selection of Tracheal Intubation Force Characteristics and Defining Routine Conditions
Although laryngoscope force is not uniformly distributed along the blade, it can be represented biomechanically as being applied at a single point.20 Thus, laryngoscope blade contact force was modeled as being applied at a single point (location) having both magnitude (N) and direction (degrees), i.e., as a force vector.16 Intubation force was simulated as a force vector applied to the anterior surface of a selected cervical spine vertebral body. In a previous FE modeling study,16 using radiographic images and simultaneous laryngoscope force distribution measurements from a prior clinical study,20 the mean applied force location, magnitude, and direction for a routine intubation with a Macintosh blade were estimated to be the midpoint of the C3 vertebral body, 48.8 N, and 70° from the body’s coronal plane, respectively. This specific combination of laryngoscope force location, magnitude, and direction are hereafter referred to as routine conditions, denoting force conditions occurring during a routine direct (Macintosh) laryngoscopy and intubation.
As shown in fig. 1, laryngoscope force application location, magnitude, and direction were each varied over a range of values. Four laryngoscope force application locations were studied: the superior half of the anterior surface of the C2 vertebral body (C2SUP), the inferior half of the anterior surface of the C2 body (C2INF), the midpoint of the anterior surface of the C3 body (C3, routine location); and 4) the midpoint of the anterior surface of the C4 body (C4). The C2INF force application location corresponds to that observed with the Airtraq video-laryngoscope.16,20 Four intubation force magnitudes were studied: 24.4 N, 48.8 N (routine magnitude), 73.2 N, and 97.6 N, corresponding to 50%, 100%, 150%, and 200% of the routine force magnitude. In a study of patients who were predicted to be easy to intubate, Macintosh intubation force magnitude was 48.8 ± 15.8 N (mean ± SD), with the greatest individual patient force magnitude equal to 70.9 N.20 In a different intubation study, with the utilization of manual in-line stabilization (MILS), pressures applied by a Macintosh blade were two-fold greater than without the use of MILS.4 In a prior cadaver intubation study, Macintosh intubation force magnitude was 47.1 ± 20.5 N, with the greatest individual cadaver Macintosh force magnitude equaling 93.6 N.21 Thus, 97.6 N (twice the routine value) appears to approximate the maximum amount of force that anesthesiologists can apply with a conventional direct (Macintosh) laryngoscope. Finally, three laryngoscope force directions were studied: 50°, 70° (routine direction), and 90° from the body’s coronal plane. The 90° force direction corresponds to that observed with the Airtraq video-laryngoscope.16,20 Thus, in total, 48 simulations were conducted, consisting of all combinations of laryngoscope force application location (n=4), magnitude (n=4), and direction (n=3). Resultant spine motion and cord strain values represent quasi-static values corresponding to the maximum values occurring during tracheal intubation.
Fig.1.
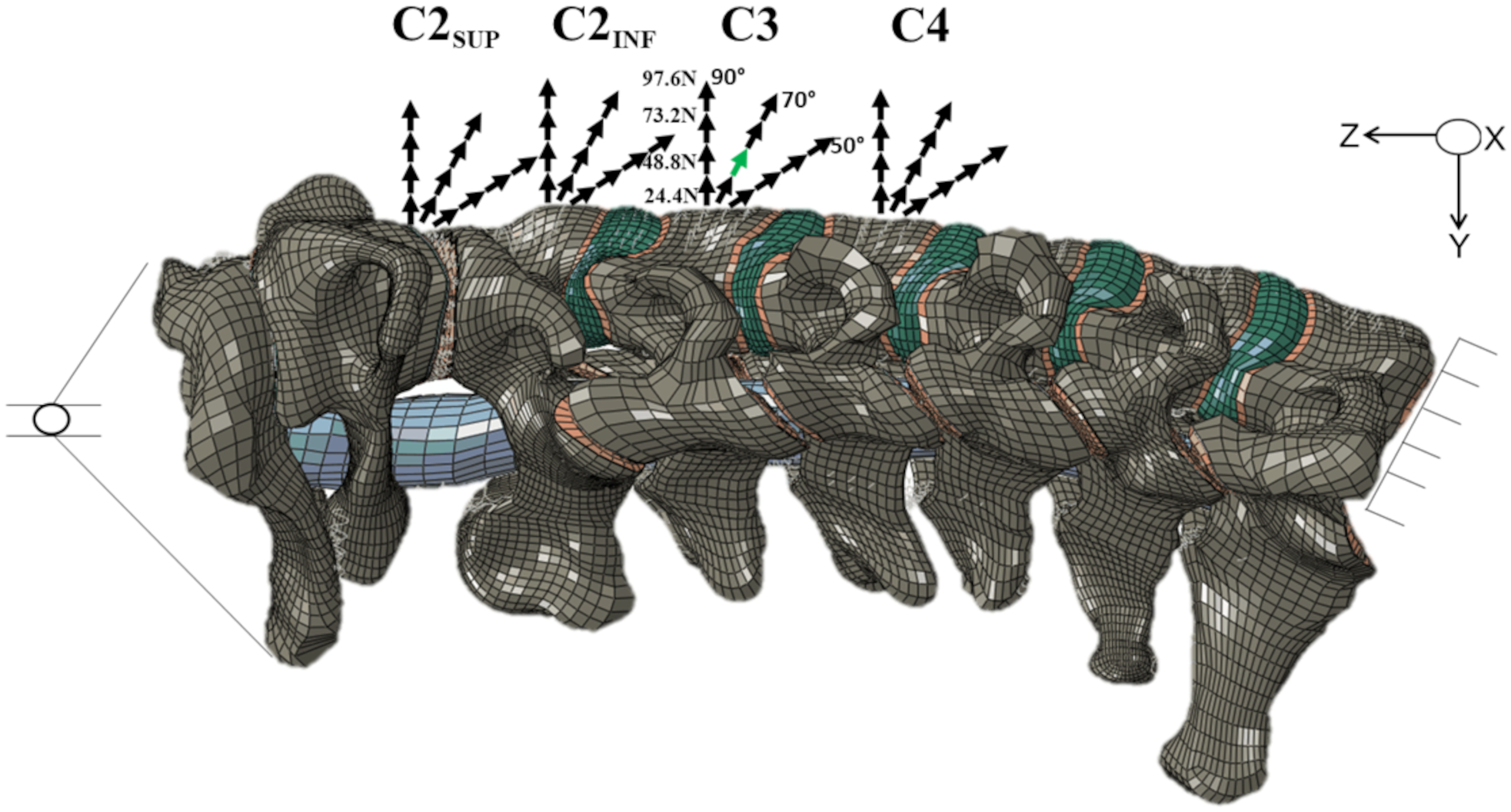
Finite element model of the human cervical spine and spinal cord, external sagittal view. For clarity, the caudal portion of the occiput (Oc) is shown without showing the skull. The spinal cord (blue cylinder) is seen within the spinal canal between Oc-C1 and C1-C2. The inferior surface of the C7 vertebral body was fixed in all directions. The occiput was allowed to rotate around the sagittal (X) axis in all simulations and translate in the axial (Z) direction. Four laryngoscope force application locations were studied: the superior half of the anterior surface of the C2 vertebral body (C2SUP), the inferior half of the anterior surface of the C2 body (C2INF), the midpoint of the anterior surface of the C3 body (routine location, shown in green), and the midpoint of the anterior surface of the C4 body. Four intubation force magnitudes were studied: 24.4 N, 48.8 N (routine force, shown in green), 73.2 N, and 97.6 N. Three laryngoscope force directions were studied: 50°, 70° (routine direction, shown in green), and 90° from the body’s coronal plane.
Measuring Cervical Spine Intervertebral Motion Characteristics
In all simulations, the occiput was allowed to rotate and translate cranially and caudally whereas the caudal surface of the C7 vertebral body was kinematically constrained to restrict all motion; see Discussion, Limitations. In all simulations, the cervical spine was considered to start at neutral position, with degrees of intervertebral rotation (flexion and extension) and anterior-posterior translation (subluxation) defined as zero. Segmental intervertebral rotation and translation at each of 7 intervertebral segments were calculated. Rotation was measured as the difference in rotation between reference nodes kinematically attached to adjacent vertebrae and was independent of translation. Intervertebral extension was represented by positive values and flexion by negative values. Translation was measured as the difference in anterior-posterior displacement of the centers of rotation of the two adjacent vertebrae. This method decreases the effect of intervertebral rotation on measures of translation. In a given intervertebral segment, translation of the cranial vertebral body posterior to the caudal vertebral body was defined as being posterior subluxation and is represented with positive values. Conversely, translation of the cranial vertebral body anterior to the caudal vertebral body of a segment was defined as anterior and is represented with negative values.
Measuring Cervical Spinal Cord Strain and Selection of Potentially Injurious Strain Thresholds
Because strain quantitates tissue deformation (e.g., change in length or width) as a ratio of the initial/final value of the parameter, strain is dimensionless. We utilized the logarithmic strain method to calculate strain, strain = ln(L/L0), where L is the final length and L0 is the initial length. Studies show accounting for strain in multiple simultaneous planes has a larger observed correlation with tissue injury than strain in any single plane.13,22 Thus, we used two strain measures that each incorporate the overall three-dimensional strain field: 1) maximum principal strain (tensile strain, analogous to stretch, represented by positive values); and 2) minimum principal strain (analogous to compression, represented by negative values); see Supplemental Digital Content 1—Finite Element Model Development, Material Properties, Calculations, and Limitations. In animal spinal cord injury models, these two strains had the largest observed correlations with tissue injury.13,14
Based on a recent experimental study of cervical cord injury in non-human primates,14 we defined two strain values as thresholds for potential cord injury. The maximum principal strains resulting in a 50% cord injury (ED50) measured histologically 14–17 weeks after insult were 0.26 to 0.31 for gray and white matter, respectively.14 In the same study, the ED50’s for minimum principal strains were −0.38 to −0.42 for gray and white matter, respectively. Because ED50 strain values are too great to use as clinical safety thresholds, we defined 50% of the ED50 values as a potentially injurious, specifically, 0.14 for maximum principal strain (stretch) and −0.20 for minimum principal strain (compression); see Discussion.
Statistical Analysis
Because model cervical spine anatomy was derived from a single adult human subject23 and mean material property data inputs were utilized to define the model, the model does not simulate the inherent variation across the human population. In addition, the model does not include random error from experimental measurements. The absence of these variations produces deterministic (i.e., single-valued) motion and strain values. Thus, model predictions for motion and strain are functionally equivalent to population mean values; see Discussion, Limitations. All values for cervical spine motions were rounded to a single decimal prior to analysis.
Results
Cervical Intervertebral Motion
Fig. 2A and 2B show the complete data set of predicted intervertebral rotations (extension and flexion) and anterior-posterior translations (subluxation) at the 7 cervical intervertebral segments, each under all (48) modeled tracheal intubation force conditions.
Fig. 2.
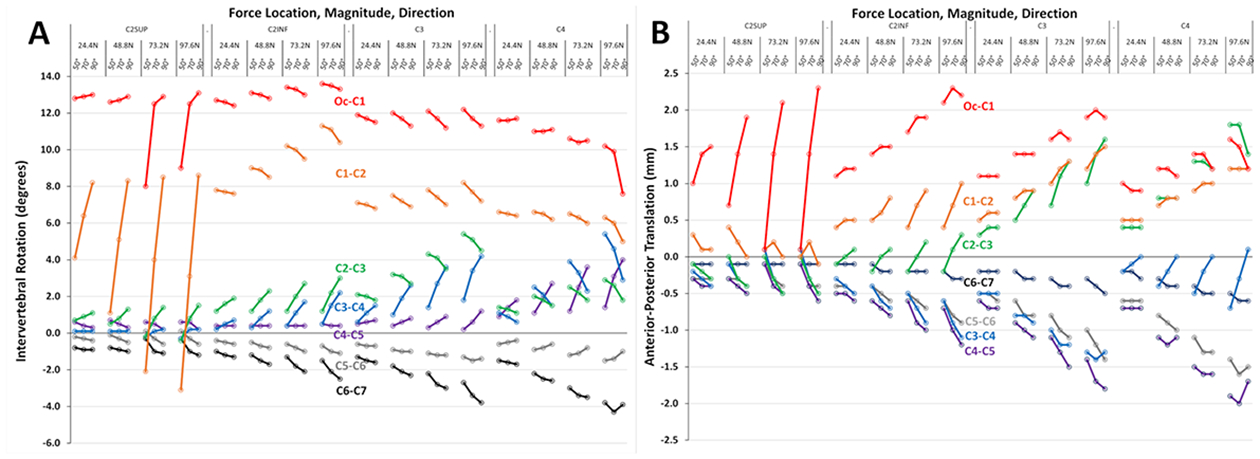
Segmental intervertebral rotation (A) and anterior-posterior translation (B) at each of seven cervical segments (Oc-C1 through C6-C7), each under 48 different intubation force conditions consisting of four locations (C2SUP, C2INF, C3, C4), four magnitudes (24.4 N, 48.8 N, 73.2 N, 97.6 N) and three directions (50°, 70°, 90°). The values for each segment are color coded (e.g., Oc-C1 is red, C1-C2 is orange, etc.). Positive rotation values indicate extension, negative rotation values indicate flexion. Positive translation values indicate the cranial vertebral body of the segment moves posterior to the caudal vertebral body, negative translation values indicate the cranial vertebral body moves anterior to the caudal vertebral body.
Table 122–28 summarizes model maximum values for intervertebral rotation and translation and the specific force conditions that resulted in these motions. Among the 14 combinations of motion (n=2; rotation and translation) and intervertebral segment (n=7), all maximum values occurred with the maximum force magnitude (97.6 N). Other intubation force characteristics (location, direction) causing maximum motions differed among motions and segments. To address our first question, table 1 also shows maximum physiologic values for intervertebral motion reported among 7 clinical voluntary range of motion studies.24–30 Maximum values for intervertebral rotation and translation predicted by the model did not meaningfully exceed physiologically normal maximum values measured during voluntary cervical flexion and extension; for additional details and discussion see Supplemental Digital Content 2—Clinical Studies of Voluntary Cervical Intervertebral Motion.
Table 1.
Intervertebral Rotation and Translation Predicted by the Model Under Maximum and Routine Intubation Force Conditions and Maximum Physiologically Normal Values Reported in the Literature
| Variable | Value | Intervertebral Segment | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Oc-C1 | C1-C2 | C2-C3 | C3-C4 | C4-C5 | C5-C6 | C6-C7 | ||||||
| Rotation (°) | Model Maximum | 13.6 | 11.3 | 5.4 | 5.4 | 4.0 | −1.5 | −4.3 | ||||
| Physiologic Maximum* | 14.2 | 8.3 | 9.3 | 11.3 | 13.3 | −9.7 | −12.5 | |||||
| Model Routine | 11.7 | 7.2 | 3.1 | 1.9 | 0.6 | −1.0 | −2.1 | |||||
| Translation (mm) | Model Maximum | 2.3 | 1.5 | 1.8 | −1.4 | −2.0 | −1.6 | −0.6 | ||||
| Physiologic Maximum* | 1.7 | 0.8 | 0.9 | −1.2 | −1.2 | −1.3 | −0.9 | |||||
| Model Routine | 1.4 | 0.9 | 0.7 | −0.8 | −1.0 | −0.8 | −0.3 | |||||
| Intubation Force Conditions: location, magnitude (N), direction (°) | Model Maximum Rotation | C2INF | C2INF | C3 | C4 | C4 | C3 | C4 | C4 | |||
| 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | |||||
| 50° | 50° | 50° | 50° | 90° | 70° | 50° | 70° | |||||
| Model Maximum Translation | C2SUP | C2INF | C3 | C4 | C4 | C3 | C4 | C4 | C4 | C4 | ||
| 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | 97.6 N | |||
| 90° | 70° | 90° | 50° | 70° | 70° | 70° | 70° | 70° | 90° | |||
| Model Routine | C3 | C3 | C3 | C3 | C3 | C3 | C3 | |||||
| 48.8 N | 48.8 N | 48.8 N | 48.8 N | 48.8 N | 48.8 N | 48.8 N | ||||||
| 70° | 70° | 70° | 70° | 70° | 70° | 70° | ||||||
Model rotation and translation values are analogous to group mean values. Physiologic maximum values are group mean values. For rotation, extension is represented with positive values and flexion is represented with negative values. For translation, translation of the superior vertebral body posterior to the inferior vertebral body is defined as posterior translation and is represented with positive values; translation of the superior vertebral body anterior to the inferior vertebral body is defined as anterior and is represented with negative values. See Methods for an explanation of intubation force conditions and notation. All force conditions are reported when there was more than one set of force conditions that resulted in equal maximum values for segmental motion.
Values are the greatest mean values reported among seven clinical voluntary range of motion studies.24–30 These studies and their results are reviewed and discussed in greater detail in Supplementary Digital Content 2—Clinical Studies of Voluntary Cervical Intervertebral Motion.
Table 1 also summarizes model values for rotation and translation under routine intubation conditions. Among the 7 segments, differences between maximum and routine values for rotation and translation were ≤ 3.5 degrees and ≤ 1.1 mm, respectively. Thus, predicted differences between maximum intervertebral motions during intubation and those occurring during a routine intubation are quantitatively small.
Cervical Cord Strain
Although our second aim pertained only to maximum (peak) values of strain present in any portion of the cord, the model predicted cord strain to be spatially heterogenous, with peak strains present in different regions of the cord depending on the location of applied force. Fig 3. shows the distribution of spinal cord strains at each of the four force application locations. Maximum principal (tensile) strain (stretch) was very low in most of the cord. However, there were foci of increased maximum principal strain in the anterior cord. In addition, there were smaller foci of greater (peak) tensile strain in the posterior cord at C1-C2 that was present at mid-C3 when force was applied at C4. Similarly, minimum principal strain (compression) was very low in most of the cord. A focus of increased (peak) compressive strain was present in the posterior cord at C1-C2 with the two most cephalad force application locations (C2SUP, C2INF), and was present at mid-C3 with the two most caudal force locations (C3, C4).
Fig 3.
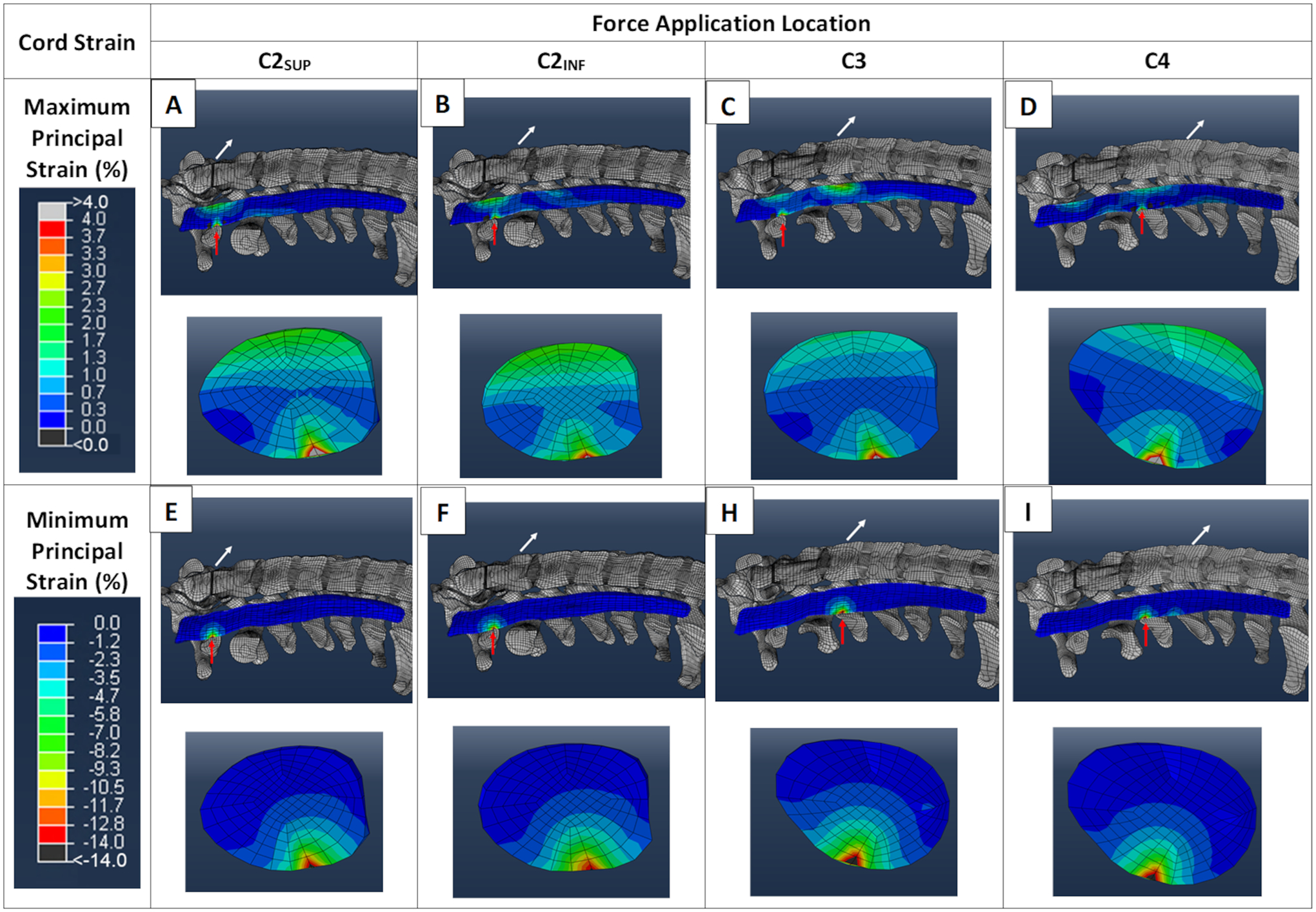
Cervical spinal cord strain distributions. Using routine values for intubation force magnitude (48.8 N) and direction (70°), the regional distribution of maximum principal strain (stretch) in sagittal and transverse sections of the cervical spinal cord at four force application locations are shown in panels A through D. In the sagittal views, the white arrows show the location and direction of the applied force and the red arrows show the location of peak cord strain. At each force location, the transverse view of the cord corresponds to the location of the peak cord strain (red arrow). Panels E through I show the regional distributions of minimum principal strain (compression), using the same conventions.
Specifically addressing our second aim, some tracheal intubation conditions did result in potentially injurious cord strains. Fig. 4 shows peak maximum and minimum principal strain under all (48) intubation force conditions. Peak maximum principal strain (stretch) did not exceed the potential injury threshold (0.14) in any modeled intubation force condition (0/48). Peak values for maximum principal strain were insensitive to force magnitude. In contrast, peak minimum principal strain (compression) exceeded the potential injury threshold (−0.20) in 3/48 conditions, all with force applied at C4 with the greatest force magnitude (97.6N). Peak values for minimum principal strain were sensitive to force magnitude; compressive strains increased markedly when force magnitude exceeded 24.4 N. Although peak compressive strains did not exceed the potential injury threshold when force was applied at the routine location (C3), compressive strains were close to the potential injury threshold with force magnitudes ≥ 48.8 N; see Discussion.
Fig. 4.
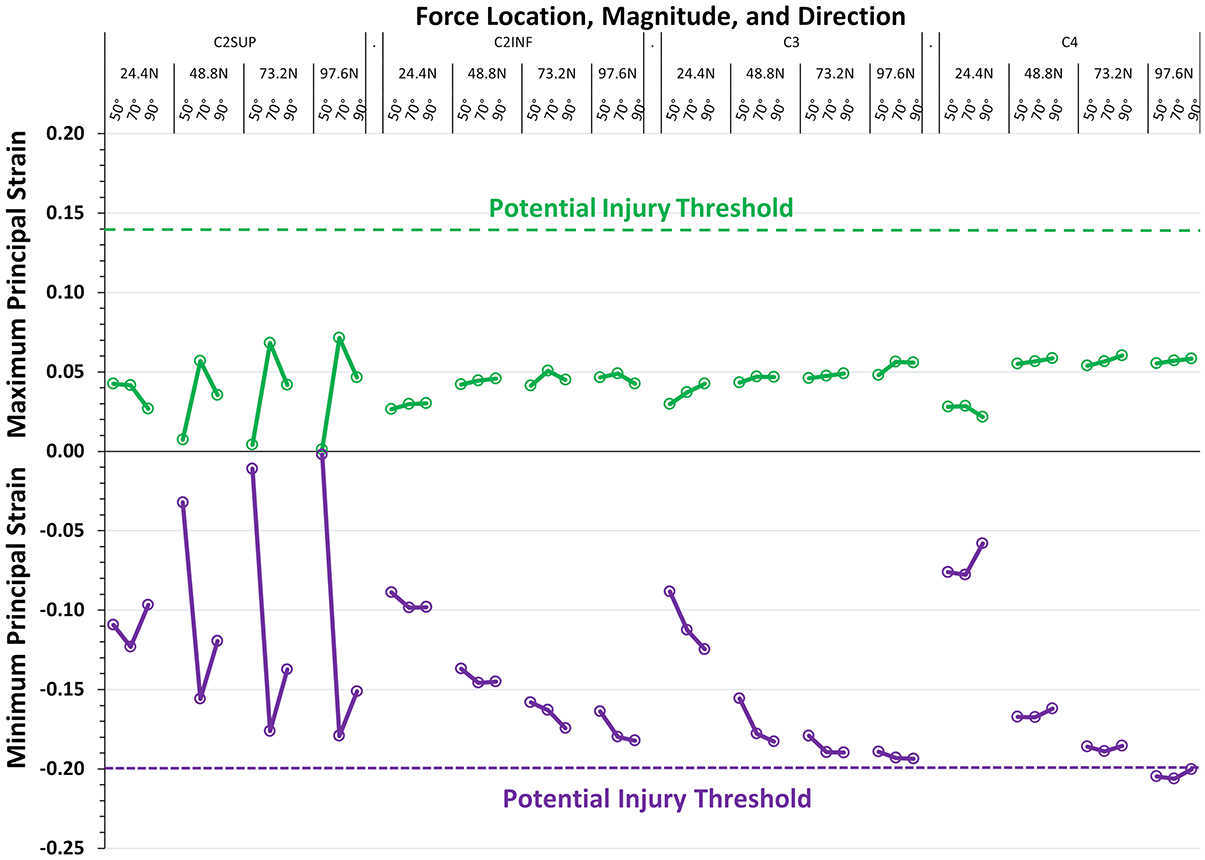
Peak spinal cord strain values as determined by intubation force location, magnitude, and direction. The figure shows the peak values of maximum principal strain (stretch, green points and lines) and minimum principal strain (compression, purple points and lines) present at any location in the cervical spinal cord under 48 different intubation force conditions consisting of four locations (C2SUP, C2INF, C3, C4), four magnitudes (24.4 N, 48.8 N, 73.2 N, 97.6 N) and three directions (50°, 70°, 90°). Potential cord injury thresholds are shown as color matched dashed lines. Three values of minimum principal strain exceed the potential injury threshold (−0.20), each with force applied at C4 with maximum force magnitude.
Discussion
Clinical Implications and Applications
In the presence of an intact (stable) spine, are there tracheal intubation conditions in which cervical intervertebral motions exceed physiologically normal maximum values? The model predicts the answer is no. Model predictions for intervertebral rotation (flexion/extension) and translation (subluxation) did not exceed the range of voluntary motion reported in the clinical studies. This was so even with the maximum modeled force magnitude, 97.6 N, which approximates the greatest amount of force anesthesiologists can apply with a conventional direct laryngoscope. In our models we included two intubation force locations that may, in fact, not be clinically achievable, one very cephalad (C2SUP), and one very caudad (C4). However, this only serves to reinforce the conclusion of this study. We modeled conditions that might truly be one in a million, and still it was practically impossible for tracheal intubation to cause an intact cervical spine to move beyond the maximum motions that occur voluntarily. This is the expected behavior of a stable cervical spine.
The second question was, in the presence of an intact cervical spine, are there tracheal intubation conditions in which potentially injurious cervical cord strains can occur? Importantly, for this second question, we obtained a different answer. The model predicted the answer is yes, conditionally. Notably, under force conditions approximating a routine intubation using a Macintosh blade, peak strains did not exceed estimated potential cord injury thresholds for maximum and minimum principal strains. This is an expected result because, if injurious cord strains occurred during routine direct laryngoscopy and intubation, intubation-related cervical cord injury would be commonplace, which it is not. In fact, even when intubation force magnitude was twice the routine value (97.6 N instead of 48.8 N), when force was applied at the routine (C3) location compressive strain did not exceed the potential injury threshold. Again, this is consistent with clinical experience because, even with a difficult intubation, cord injury is rare. However, when maximum force was applied in a location that was more caudal than is routine (i.e., force applied at C4), predicted compressive cord strains exceeded a potentially injurious value. Admittedly, it is difficult to imagine how, with any current laryngoscope, it would be helpful or even possible to apply such high force below the level of the glottis. Thus, in patients who have an intact cervical spine, it might appear to be practically impossible for the cervical cord to experience injurious strain during tracheal intubation. There is, however, one critically important caveat.
The caveat is that model predictions of whether or not injurious cord strains occur during tracheal intubation depend entirely on the levels of cord strain that cause injury. Strain values that cause cord injury in patients are not currently known. The potential strain injury thresholds used in this study are estimates; see Discussion, Limitations and Supplemental Content 1—Finite Element Model Development, Material Properties, Calculations, and Limitations. Logically, if a patient’s strain injury thresholds were less than our estimated injury thresholds (i.e., less than normal), strain-related cord injury could occur during routine intubation conditions. In other words, cord injury could occur even with normal intubation force and in the absence of pathologic cervical spine motion. In fact, there are several observations that suggest cervical cord injury does, in fact, occur in patients by this mechanism. First, in animal models, acute electrophysiologic responses (e.g., evoked potentials) serve as an indicator of neural sensitivity to acute cord strain.9,31 Second, in a study of 38 patients who had chronic cervical spondylotic myelopathy, spinal cord evoked potential (N13) amplitudes decreased when patients were placed in 20 degrees of head/neck extension.32 Decreased evoked potential amplitudes with extension were not associated with cervical spine stability but were associated with measures of pre-existing cervical cord compression.32 These observations suggest patients who have spondylotic myelopathy may have less tolerance to acute increases in cord strain, even in the absence of instability. Third, in a Closed Claims study, 11 of 37 patients who experienced perioperative cervical cord injury did so while undergoing a non-cervical spine procedure and with an apparently stable cervical spine.2 Most of these 11 patients had preoperatively unrecognized severe cervical spondylosis. Fourth, there are more than 20 case reports describing patients with severe cervical spondylosis and who, in the absence of a difficult intubation, suffered intraoperative cervical cord injury during non-cervical spine surgery;33–35 for additional references and discussion see Supplemental Digital Content 3—Case Reports of Perioperative Cervical Spinal Cord Injury in Patients with Cervical Spondylosis. Accordingly, we hypothesize patients who have severe cervical spondylosis have less tolerance to acute cord strain and, consequently, have greater potential to experience potentially injurious cord strain during an otherwise routine (normal force) intubation. Fig. 4 shows peak compressive strains increase markedly and approach the potential injury threshold when force magnitude exceeds 24.4 N, which is half the value applied during a routine intubation with a Macintosh blade. Thus, in patients who may have increased susceptibility to strain-related cord injury, we hypothesize low-force laryngoscopy20 may confer less risk of strain-related cervical cord injury.
Intubation-Related Cervical Cord Injury
The findings of this study suggest that the approach to preventing intubation-related cervical cord injury should be reconsidered. The model suggests cervical cord injury from tracheal intubation is not directly related to the motion of the cervical spine but, instead, by the resultant spinal cord deformation, i.e., strain. This mechanism of injury would apply regardless of whether the cervical spine is intact (stable) or injured (unstable). We suggest airway management of patients who have disease of the cervical spine or cord should no longer exclusively focus on minimizing cervical spine motion. Instead, an additional, more mechanistically oriented goal, should be to minimize cervical cord strain.
Limitations
As previously reported, when compared to patients, the current model appears to underestimate intubation-related extension at C3-C4 and C4-C5 by 2–3 degrees.16 This may be caused by the imposed kinematic constraint of the C7 vertebral body. Although the difference between observed and predicted motion is small at these two segments, we cannot estimate how much this difference might affect model values for cord strains in the more caudal regions of the cervical cord. In a future version of the model, inclusion of the first thoracic (T1) vertebral segment will permit C7-T1 motion, and this may increase sub-axial segmental motion.
Because model anatomy was derived from a single adult human subject, and because mean material property data were utilized to define the model, the lack of geometric and material property variation produces deterministic (i.e., single-valued) motion and strain values. Accordingly, the current model does not simulate the inherent variation across the human population but, instead, represents an anthropometrical mean, i.e., an “average” patient. In the future, to account for variation in geometry and material properties across the general population, probabilistic methods will be dovetailed with the current model. With probabilistic analyses, model parameters (anatomy, material properties) are not defined by a single value but are sampled from a distribution that represents the population’s variation and the model is solved many times to develop a distribution of output variables.36
The values used to definite potential strain injury thresholds—50% of ED50 values observed in non-human primates (see Methods)—are unavoidably speculative. In living humans, injurious cord strain values are not currently known. A recent magnetic resonance imaging study of 9 healthy volunteers reported in vivo maximum and minimum principal strains in sustained extension (without pain or symptoms) were approximately 0.12 and −0.14, respectively.37 Thus, potential strain injury thresholds used in our simulations (0.14 for maximum and −0.20 for minimum principal strains, respectively) were greater than cord strains that appear to be non-injurious in healthy asymptomatic patients. Thus, potential injury thresholds used in this study do not appear to be too low and, as a result, do not appear to greatly overestimate the potential for intubation-related cord injury.
The current model does not include an explicit representation of spinal cord gray and white matter. These tissues may38,39 or may not40 have different primary biomechanical properties and the rostral-caudal alignment of axonal fibers in the spinal cord white matter provides a direction-specific mechanical response.39 Gray matter may have lesser strain tolerances than white matter,10–12,14,41 although the difference is small (10–20%). Thus, spinal cord strain fields42,43 and regional (intra-cord) susceptibility to strain injury are certain to be more complex than are represented in the current version of our model. For additional discussion of model limitations see Supplemental Content 1—Finite Element Model Development, Material Properties, Calculations, and Limitations.
Conclusions
In the presence of an intact cervical spine, computational modeling predicted intervertebral motions during tracheal intubation did not exceed normal physiologic (voluntary) maximum values, even under high force conditions. In contrast, under non-routine high force conditions, the model predicted potentially injurious cervical cord strains could occur. In patients who have less than normal tolerance to acute cord strain (e.g., patients with cervical myelopathy), cord strains occurring during routine tracheal intubation conditions could approach potentially injurious values. In such patients, low force laryngoscopy may reduce the risk of intubation-related (i.e., strain-related) cervical cord injury.
Supplementary Material
Funding Statement:
This study was supported by the National Institutes of Health, Bethesda, Maryland (grant R01EB012048 to Drs. Puttlitz, Hindman, and Santoni). Additional support was provided by the Department of Mechanical Engineering, Colorado State University and by the Department of Anesthesia, The University of Iowa Roy J. and Lucille A. Carver College of Medicine.
Footnotes
Prior Presentations: Portions of this work were previously presented in abstract form:
Gadomski BC, Shetye SS, Hindman BJ, Santoni BG, Todd MM, Traynelis VC, Fontes RB, Puttlitz CM: The effect of cervical spine injury on intervertebral kinetics and spinal cord strain during direct laryngoscopy: A computation investigation. 61st Annual Meeting of the Orthopedic Research Society; Orlando, FL, March 5–8, 2016.
Gadomski BC, Hindman BJ, Santoni BG, Todd MM, Traynelis VC, Fontes RB, Puttlitz CM: Peak cervical spinal cord strain predictions are affected by the point of force application during direct laryngoscopy. International Anesthesia Research Society Annual Meeting; Washington DC, May 7, 2017.
Gadomski BC, Hindman BJ, Page M, Todd MM, Traynelis VC, Puttlitz CM: Changes in applied laryngoscope force affect peak spinal cord strain. International Anesthesia Research Society Annual Meeting; Montreal, Quebec, Canada, May 17–20, 2019.
Conflicts of Interest: From 2018 to the present, The National Institutes of Health and the Colorado Office of Economic Development and International Trade have provided ongoing support to Dr. Puttlitz. From 2018 to the present, the following entities provided external funding to both Dr. Gadomski and Dr. Puttlitz: Abbott (past), Acuitive (ongoing), Angiocrine (past), Anika Therapeutics, Inc. (past), Asahi Kasei Pharma (past), Auritec (past), Bioventus, Inc. (ongoing), CGBio (ongoing), Chap Med, Inc. (ongoing), Collagen Matrix, Inc. (past), Department of Defense (ongoing), DSM Biomedical (past), Elute, Inc. (past), Evoke Medical, LLC (ongoing), Hyalex Ortho, Inc. (ongoing), Ingeneron, Inc. (past), Intelligent Implants (past and ongoing), Magic Implants (ongoing), Miach Orthopaedics (ongoing), MiRus, LLC (ongoing), NeuroSigma (ongoing), Nushores Biosciences (ongoing), Organogenesis (past), Paragon 28 (past), Progenerative Medical (past), SI Tech (past), Smith & Nephew, Inc. (ongoing), Sparta Biopharma (ongoing), University of Arkansas, Little Rock (ongoing), University of Otago, Christchurch, New Zealand (past), Wright Medical (past), Zetagen Therapeutics, Inc. (ongoing). Drs. Hindman, Page, and Dexter have nothing to disclose.
Contributor Information
Benjamin C. Gadomski, Department of Mechanical Engineering, School of Biomedical Engineering, Orthopaedic Bioengineering Research Laboratory, Colorado State University, Fort Collins, CO, U.S.A.
Bradley J. Hindman, Department of Anesthesia, University of Iowa Roy J. and Lucille A. Carver College of Medicine, Iowa City, IA, U.S.A.
Mitchell I. Page, Department of Mechanical Engineering, School of Biomedical Engineering, Orthopaedic Bioengineering Research Laboratory, Colorado State University, Fort Collins, CO, U.S.A.
Franklin Dexter, Department of Anesthesia, University of Iowa Roy J. and Lucille A. Carver College of Medicine, Iowa City, IA, U.S.A.
Christian M. Puttlitz, Department of Mechanical Engineering, School of Biomedical Engineering, Orthopaedic Bioengineering Research Laboratory, Colorado State University, Fort Collins, CO, U.S.A.
References
- 1.Hastings RH, Kelley SD: Neurologic deterioration associated with airway management in a cervical spine-injured patient. Anesthesiology 1993; 78:580–3 [DOI] [PubMed] [Google Scholar]
- 2.Hindman BJ, Palecek JP, Posner KL, Traynelis VC, Lee LA, Sawin PD, Tredway TL, Todd MM, Domino KB: Cervical spinal cord, root, and bony spine injuries. A closed claims analysis. Anesthesiology 2011; 114:782–95 [DOI] [PubMed] [Google Scholar]
- 3.Oppenlander ME, Hsu FD, Bolton P, Theodore N: Catastrophic neurological complications of emergent endotracheal intubation: report of 2 cases. J Neurosurg Spine 2015; 22:454–8 [DOI] [PubMed] [Google Scholar]
- 4.Santoni BG Hindman BJ, Puttlitz CM, Weeks JB, Johnson N, Maktabi MA, Todd MM: Manual in-line stabilization increases pressures applied by the laryngoscope blade during direct laryngoscopy and orotracheal intubation. Anesthesiology 2009; 110:24–31 [DOI] [PubMed] [Google Scholar]
- 5.Hastings RH, Hon E, Nghiem C, Wahrenbrock EA: Force, torque, and stress relaxation with direct laryngoscopy. Anesth Analg 1996, 82:456–61 [DOI] [PubMed] [Google Scholar]
- 6.Cordovani D, Russell T, Wee W, Suen A, Cooper RM: Measurement of forces applied using a Macintosh direct laryngoscope compared with a Glidescope video laryngoscope in patients with predictors of difficult laryngoscopy. A randomized controlled trial. Eur J Anaesthesiol 2019; 36:221–6 [DOI] [PubMed] [Google Scholar]
- 7.Kuwazawa Y, Pope MH, Bashir W, Takahashi K, Smith FW: The length of the cervical cord; effects of postural changes in healthy volunteers using positional magnetic resonance imaging. (Phila Pa 1976) 2006; 31:E579–83 [DOI] [PubMed] [Google Scholar]
- 8.Muhle C, Wiskirchen J, Weinert D, Falliner A, Wesner F, Brinkmann G, Heller M: Biomechanical aspects of the subarachnoid space and cervical cord in healthy individuals examined with kinematic magnetic resonance imaging. (Phila Pa 1976) 1998; 23:556–67 [DOI] [PubMed] [Google Scholar]
- 9.Ouyang H, Sun W, Fu Y, Li J, Cheng J-X, Nauman E, Shi R: Compression induces acute demyelination and potassium channel exposure in spinal cord. J Neurotrauma 2010; 27:1109–20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Figley SA, Khosravi R, Legasto JM, Tseng Y-F, Fehlings MG: Characterization of vascular disruption and blood-spinal cord barrier permeability following traumatic spinal cord injury J. Neurotrauma 2014; 31:541–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Maikos JT, Qian Z, Metaxas D, Schreiber DI: Finite element analysis of spinal cord injury in the rat. J Neurotrauma 2008; 25:795–816 [DOI] [PubMed] [Google Scholar]
- 12.Russell CM, Choo AM, Tetzlaff W, Chung T-E, Oxland TR: Maximum principal strain correlates with spinal cord tissue damage in contusion and dislocation injuries in the rat cervical spine. J Neurotrauma 2012; 29:1574–85 [DOI] [PubMed] [Google Scholar]
- 13.Bhatnagar T, Liu J, Yung A, Cripton P, Kozlowski P, Tetzlaff W, Oxland T: Relating histopathology and mechanical strain in experimental contusion spinal injury in a rat model. J Neurotrauma 2016; 33:1685–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jannesar S, Salegio EA, Beattie MS, Bresnahan JC, Sparrey CJ: Correlating tissue mechanics and spinal cord injury: Patient-specific finite element models of unilateral cervical contusion spinal cord injury in non-human primates. J Neurotrauma 2021; 38:698–717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yoganandan N, Kumaresan S, Pintar FA: Biomechanics of the cervical spine Part 2. Cervical spine soft tissue responses and biomechanical modeling. Clin Biomech (Bristol, Avon) 2001; 16:1–27 [DOI] [PubMed] [Google Scholar]
- 16.Gadomski BC, Shetye SS, Hindman BJ, Dexter F, Santoni BG, Todd MM, Traynelis VC, From RP, Fontes RB, Puttlitz CM: Intubation Biomechanics: Validation of a finite element model of cervical spine motion during endotracheal intubation in stable and unstable conditions. J Neurosurg Spine 2018; 28:10–22 [DOI] [PubMed] [Google Scholar]
- 17.Turkstra TP, Eng M, Pelz DM, Hones PM: Cervical spine motion. A fluoroscopic comparison of the AirTraq laryngoscope versus the Macintosh laryngoscope. Anesthesiology 2009; 111:97–101 [DOI] [PubMed] [Google Scholar]
- 18.Mentzelopoulos SD, Tzoufi MJ, Papageorgiou EP: The disposition of the cervical spine and deformation of available cord space with conventional- and balloon laryngoscopy-guided laryngeal intubation: A comparative study. Anesth Analg 2001; 92:1331–36 [DOI] [PubMed] [Google Scholar]
- 19.Monks T, Currie CS, Onggo BS, Robinson S, Kunc M, Taylor SJ. Strengthening the reporting of empirical simulation studies: Introducing the STRESS guidelines. J Simul 2019; 13:55–67 [Google Scholar]
- 20.Hindman BJ, Santoni BG, Puttlitz CM, From RP, Todd MM: Intubation biomechanics: Laryngoscope force and cervical spine motion during intubation with Macintosh and Airtraq laryngoscopes. Anesthesiology 2014; 121:260–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hindman BJ, Fontes RB, From RP, Traynelis VC, Todd MM, Puttlitz CM, Santoni BG: Intubation biomechanics: laryngoscope force and cervical spine motion during intubation in cadavers—effect of severe distractive-flexion injury on C3–4 motion. J Neurosurg Spine 2016; 25:545–55 [DOI] [PubMed] [Google Scholar]
- 22.Galle B, Ouyang H, Shi R, Nauman E: Correlations between tissue-level stresses and strains and cellular damage within the guinea pig spinal cord white matter. J Biomechan 2007; 40:3029–33 [DOI] [PubMed] [Google Scholar]
- 23.Leahy PD: Assessment of the effects of ligamentous injury in the human cervical spine. Ph.D. Dissertation, Colorado State University, Fort Collins, CO, 2012. Available at https://mountainscholar.org/handle/10217/67466; accessed June 1, 2021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ordway NR, Seymour RJ, Donelson RG, Hojnowski LS, Edwards WT: Cervical flexion, extension, protrusion, and retraction. A radiographic segmental analysis. Spine (Phila Pa 1976) 1999; 24:240–47 [DOI] [PubMed] [Google Scholar]
- 25.Lin R-M, Tsai K-H, Chu L-P, Chang PQ: Characteristics of sagittal vertebral alignment in flexion determined by dynamic radiographs of the cervical spine. Spine (Phila Pa 1976) 2001; 26:256–61 [DOI] [PubMed] [Google Scholar]
- 26.Wu S-K, Kuo L-C, Lan H-C, Tsai W-W, Chen C-L, Su F-C: The quantitative measurements of the intervertebral angulation and translation during cervical flexion and extension. Eur Spine J 2007; 16:1435–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Anderst WJ, Lee JY, Donaldson WF III, Kang JD: Six-degrees of-freedom cervical spine range of motion during dynamic flexion-extension after single-level anterior arthrodesis. Comparison with asymptomatic control subjects. J Bone Joint Surg Am 2013; 95:497–506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Anderst WJ, Donaldson WF III, Lee JY, Kang JD: Three-dimensional intervertebral kinematics in the healthy young adult cervical spine during dynamic functional loading. J Biomech 2015; 48:1286–93 [DOI] [PubMed] [Google Scholar]
- 29.Parfenchuck TA, Bertrand SL, Powers MJ, Drvaric DM, Pueschel SM, Roberts JM.: Posterior occipitoatlantal hypermobility in Down syndrome: an analysis of 199 patients. J Ped Orthoped 1994; 14:304–8 [DOI] [PubMed] [Google Scholar]
- 30.Reitman CA, Mauro KM, Nguyen L, Ziegler JM, Hipp JA: Intervertebral motion between flexion and extension in asymptomatic individuals. Spine (Phila Pa 1976) 2004; 29:2832–43 [DOI] [PubMed] [Google Scholar]
- 31.Bain AC, Meaney DF: Tissue-level thresholds for axonal damage in an experimental model of central nervous system white matter injury. J Biomech Eng 2000; 122:615–22 [DOI] [PubMed] [Google Scholar]
- 32.Yu Z, Lin K, Chen J, Chen K-H, Guo W, Dai Y, Chen Y, Zou X, Peng X: Magnetic resonance imaging and dynamic X-ray’s correlations with dynamic electrophysiological findings in cervical spondylotic myelopathy: a retrospective cohort study. BMC Neurol 2020; 20:367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mercieri M, Paolini S, Mercieri A, De Blasi RA, Palmisani S, Pinto G, Arcioni R: Tetraplegia following parathyroidectomy in two long-term haemodialysis patients [Case Report]. Anaesthesia 2009; 64:1010–13 [DOI] [PubMed] [Google Scholar]
- 34.Kudo T, Sato Y, Kowatari K, Nitobe T, Hirota K: Postoperative transient tetraplegia in two patients caused by cervical spondylotic myelopathy. Anaesthesia 2011; 66:213–6 [DOI] [PubMed] [Google Scholar]
- 35.Mathkour M, McCormack E, Hanna J, Werner C, Skinner K, Borchardt JA, Dumont AS, Maulucci CM: Iatrogenic spinal cord injury with tetraplegia after an elective non-spine surgery with underlying undiagnosed cervical spondylotic myelopathy: Literature review and case report. Clin Neurol Neurosurg 2019; 187:105549. [DOI] [PubMed] [Google Scholar]
- 36.Easley SK, Pal S, Tomaszewski PR, Petrella AJ, Rullkoetter PJ, Laz PJ: Finite element-based probabilistic analysis tool for orthopaedic applications. Comput Methods Programs Biomed 2007; 85:32–40 [DOI] [PubMed] [Google Scholar]
- 37.Stoner KE, Abode-Iyamah KO, Mannotta VA, Howard MA III, Grosland NM: Measurement of in vivo spinal cord displacement and strain fields of healthy and myelopathic cervical spinal cord. J Neurosurg Spine 2019; 31:53–59 [DOI] [PubMed] [Google Scholar]
- 38.Ichihara K, Taguchi T, Shimada Y, Skauramoto I, Kawano S, Kawai S: Gray matter of the bovine cervical spinal cord is mechanically more rigid and fragile than white matter. J Neurotrauma 2001; 18:361–7 [DOI] [PubMed] [Google Scholar]
- 39.Koser DE, Moeendarbary E, Hanne J, Kuerten S, Franze K: CNS cell distribution and axon orientation determine local spinal cord mechanical properties. Biophys J 2015; 108:2137–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ozawa H, Matsumoto T, Ohashi T, Sato M, Kokubun S: Comparison of spinal cord gray matter and white matter softness: measurement by pipette aspiration method. J Neurosurg (Spine 2) 2001; 221–4 [DOI] [PubMed] [Google Scholar]
- 41.Maikos JT, Shreiber DI: Immediate damage to the blood-spinal cord barrier due to mechanical trauma. J Neurotrauma 2007; 24:492–507. [DOI] [PubMed] [Google Scholar]
- 42.Sparrey CJ, Manley GT, Keaveny TM: Effects of white, grey, and pia mater properties on tissue level stresses and strains in the compressed spinal cord. J Neurotrauma 2009; 26:585–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fournely M, Petit Y, Wagnac E, Evin M, Arnoux P-J: Effect of experimental, morphological and mechanical factors on the murine spinal cord subjected to transverse contusion: A finite element study. PLoS One 2020: 15(5): e0232975. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


