Abstract
Molecular dynamics (MD) simulations based on atomic models play an important role in the drug-discovery process to screen molecules, estimate binding free energies, and optimize lead compounds in chemical space. Accurate computations of thermodynamic and kinetic properties using MD simulations are highly dependent on the accuracy of the underlying atomic force field. In this context, going beyond nonpolarizable fixed-charge model by accounting explicitly for induced polarization is highly desirable. The CHARMM polarizable force field based on classical Drude oscillators, in which an auxiliary charged particle is attached via a harmonic spring to its parent nucleus, offers both a computationally convenient and rigorous framework to model explicitly induced electronic polarization in MD simulations. For any molecule of interest, electrostatic partial charges, atomic polarizabilities and Thole shielding factors, as well as bonded parameters can either be determined from ab initio calculations or ascribed from the knowledge-based library of the CHARMM Generalized force field (CGenFF). While this approach is fairly reliable in general, it is well understood that the overall accuracy of the models with respect to thermodynamic properties such as bulk density, enthalpies, and solvation free energies is particularly sensitive to the nonbonded Lennard-Jones (LJ) parameters. In the present study we systematically refined the set of LJ parameters for the atom types available in the Drude force field to best match the experimental thermodynamic properties for 416 small drug-like organic molecules. To further test the transferability of the optimized parameters, the hydration free energy of 372 molecules was computed. The calculations resulted in a small average error of 0.46 kcal/mol and a Pearson R of 0.9, representing a significant improvement over the additive GAFF force field in our previous study, where an average error of ~2 kcal/mol was obtained. Such an improvement is consistent with the ability of the polarizable Drude model to more accurately model interactions in different environments. The effort provides a roadmap for the global optimization of force field parameters using experimental data. It is hoped that the present effort will further the application of the Drude polarizable force field in molecular simulations including drug design and discovery.
Graphical Abstract
INTRODUCTION
Molecular dynamics (MD) simulation has been the workhorse to compute thermodynamic and kinetic properties of biological systems while gaining atomistic insights.1 More recent development in scalable free energy perturbation (FEP) calculations have been encouraging to improve the speed of free energy simulations.2–4 However, the accuracy of these simulations is also highly dependent on the accuracy of the force field used. A force field aims to represent the quantum mechanical (QM) Born-Oppenheimer (BO) potential energy surface using simple functional forms with multiple parameters such as harmonic potentials for bond and angle terms and cosine functions for the dihedral term. These simple functional forms are usually fitted to map to the QM surface and experimental observables.5–7 Given the simplicity of the potential energy functions it is of the utmost importance to properly parametrize the models to maximize the accuracy of the computed molecular properties.8
The construction and optimization of a force field is a complex and involved process. Generating an accurate force field applicable to a wide range of small molecules is even more challenging given the vastness of chemical space.9 While there is a finite number of amino acids and associated atom types for proteins, small organic molecules contain a much wider range of possibilities. Atom typing attempts to broadly define an atomic environment and serves as the basis for parameter assignment, though the quality of the assigned parameters need verification and careful revision. For instance, the CHARMM generalized force field (CGenFF) provides a penalty score to indicate problematic terms that need further refinement.10,11 To enable such refinement, we have previously established the General Automated Atomic Model Parameterization (GAAMP)12 and FFParam13 utilities to facilitate the parameters optimization of small molecules. Recent development in the application of SMARTS pattern to automatically detect and apply force field parameters is also useful to improve the acuracy of parameter assignement.14
The Drude polarizable force field is computationally efficient to model the polarization response of the electronic degrees of freedom, thereby providing a better physical representation of the molecular interactions than additive fixed-charge force fields.15–19 Because of its computational efficiency and ease of implementation,20–22 it has been widely used in the context of molecular dynamics simulations for various biologically important systems such as ion channels, lipids, proteins, and nucleic acids.23–28 Efforts towards developing parameters for the Drude model applicable towards drug design and discovery domain are actively underway.13 A recent advance is the application of machine learning to derive the partial charges in the context of the Drude polarizable force field.29 Our fully automated parameter refinement framework, GAAMP, optimizes the molecular properties and parameters in the context of both additive and polarizable force fields.12 GAAMP is an objective approach where the parameters are derived systematically using an algorithmic procedure. Indeed, the GAAMP framework is the only publicly available automated tool available to refine the Drude polarizable model going beyond the analogy-based approaches usually applied to assign the force field parameters to small organic molecules.30
GAAMP starts with molecular coordinates as input. The refinement process begins with accessing the initial guesses of the parameters based on analogy using traditional sources such as CGenFF,7 GAFF,6,31 or MATCH.32 Quantum mechanical (QM) calculations are carried out to successively refine the bond, angle, partial charge, and dihedral molecular mechanics (MM) parameters. The QM calculations involve optimizing geometry, computing electrostatic potential, (ESP) and scanning potential energy surfaces. These QM calculations provide target data to refine the MM parameters using gradient directed optimization techniques. The partial charge refinement is done in an environment aware manner where along with the ESP fitting, the interaction of hydrogen-bond donor and acceptor groups with water are taken into account during the refinement. Within GAAMP, a chi-squared objective is defined, analytical derivates are computed, and the MM parameters are refined by L-BFGS33,34 optimizer. The framework is applicable for the popular force fields such as GAFF and CGenFF. A webserver is also running at http://gaamp.lcrc.anl.gov to expose the GAAMP framework for the users to obtain refined force field parameters for their own small molecules. In the end, the resulting topology and parameters files contain simulation-ready data for molecular modeling and MD simulations.
The refinement of the LJ parameters is done separately from the GAAMP framework. Because of the limitations of the QM methodologies to model van der Waals interaction, these parameters are refined fitting directly to the experimentally measured liquid phase properties such as heat of vaporization, molecular volume, and hydration free energy.35 It should be noted that there have been several attempts in the past by various groups to optimize the force field parameters to better reproduce such experimental measurements. For example, Wang et al. refined nonbonded parameters using an automatic ForceBalance procedure,36,37 and Head-Gordon and coworkers adjusted the small molecule-water van der Waals interaction to fit the hydration free energies of small molecules encompassing all functional groups known in the proteins side chains and backbone.38,39 Our current work and past optimization of additive LJ parameters39 are inspired by these previous attempts with a hope of making the parameters globally applicable for diverse small drug-like organic molecules.
The LJ parameters assignment is dependent on the atom type. The type aims to define a chemical environment around an atom. This assignment is different, for example, compared to partial charge assignment that are atom specific. Atoms sharing similar atomic environment, such as hybridization state or proximity to a polar group, are represented with the same atom type sharing the same values of the LJ parameters. In this work, we have systematically refined the existing LJ parameters for the Drude polarizable force field for neutral small organic molecules using a diverse set of molecules in our training and validation data. In addition, we have also derived LJ parameters in the context of the Drude polarizable force field of several existing CGenFF atom types. We make use of experimental measurement of molecular volume and heat of vaporization of 416 molecules separated into a training set of 365 molecules, and a validation set of 51 molecules. We have systematically fit the LJ parameters on the training compounds encompassing wide range of atom types as described by the CGenFF assignment and test on the validation set. To ensure that the parameters are equally valuable for other molecular properties, we also computed the hydration free energies of 372 molecules for further validation. The resulting set of optimized LJ parameters expands the scope of the Drude force field and enhances its applicability for computer-aided drug design endeavors.
METHODS
The LJ optimization here was carried out in the context of CHARMM Drude polarizable force field. In the Drude force field, the explicit polarization is introduced by attaching a Drude particle to its heavy atom (nuclei) by a spring with a force constant of 500 kcal/mol/Å2.15 The Drude particle oscillates around the nuclei allowing the atomic dipoles to adjust in response to the surrounding electric field. The motion of the Drude is usually isotropic; however, the presence of electronegative atoms containing the lone pairs can break the isotropy.40 Similar to SCF calculation under the Born-Oppenheimer approximation, the Drude particle relaxation can be performed using the SCF style calculation where the position of the Drude is minimized with respect to the position of the nuclei. The SCF calculation is computationally expensive, so a small mass of 0.4 AMU is shifted from the atomic nucleus to the Drude particle, allowing the application of an extended Lagrangian based propagation in MD simulations.15,21 The popular MD packages such as NAMD,22 CHARMM,41 OpenMM,20 and GROMACS21 implement the extended Lagrangian propagation, including simulations on GPUs.
The functional form of the Drude force field is an extension of the additive potential energy function (equation 1) with small modification to the electrostatics terms (equation 3) and addition of the self-polarization term (equation 5).41
| (1) |
where Kb,Kθ, kω ku, b0, θ0, ω0 and u0 are the force constants and reference values for the bond, angle, improper, and Urey-Bradley terms. Kφ and φ0 are the force constant and phase angle for the dihedral terms. The electrostatic term is composed of the nuclei-nuclei, nuclei-Drudes, and Drudes-Drudes contributions to the electrostatic potential 18,42,43 as,
| (2) |
where i and j represent the index of atoms, q represents the partial charge on the atoms, r their positions and the subscript D indicates the Drude particles. The charge of the Drude particle is related to the polarizability as,
| (3) |
where is the force constant of the harmonic spring linking the Drude particle to the atomic nuclei, representing the self-polarization energy. The contribution to the electrostatic potential from the dipole-dipole interaction between the Drude-atom pairs separated by one or two covalent bonds (the 1–2 and 1–3 interactions) are screened using a Thole-like screening function44 as,
| (4) |
where the charge on the Drude particle, qD, is dependent on the isotropic atomic polarizability, , and the spring constant kD (equation 3). Partial charge of the nuclei, qA, is assigned to the attached Drude particle as qD = q – qA where q is the total partial charge of the nuclei and Drude particle. The electronic self polarization of the Drude is usually isotropic using a familiar harmonic potential Uself as,
| (5) |
where d represents the displacement of the Drude particle from its nuclei. To better represent the interactions of electronegative atoms in the molecule (N, O, S, Cl, Br, and I) with the environment, the self-polarization term is described anisotropically40 by expanding the isotropic force constant kD into a tensor KD having zero off-diagonal elements (equation 6).
| (6) |
where d1, d2, and d3 are the projections of the Drude-nuclei displacement vectors on the orthogonal axes determined by the local molecular frame of reference.
The remaining terms of the force field are identical to the CHARMM additive force field. The LJ parameter for pairs of atoms i and j are constructed using the Lorentz-Berthelot combination rule,45 and . In CHARMM, pair-specific LJ interaction parameters can be modified between the oxygen atom of a water and selected heavy atom of the solute using the NBFIX option. This functionality is useful to overcome the limitation of the Lorentz-Berthelot rule and has been applied to accurately reproduce the hydration free energies and correct folding of proteins.46–48 We have also applied this modification to the LJ interaction in this work to improve the accuracy of the calculated hydration free energies (HFE).
Before refining the LJ parameters, GAAMP algorithm was used to generate the electrostatic and dihedral parameters compatible with the CHARMM Drude Force Field initialized with parameters obtained from the CGenFF program.7 The available LJ parameters for the Drude force field were used during parametrization. GAAMP procedure starts with a structure file of the molecules in a pdb or a mol2 format. The parametrization for the Drude force field proceeds in 4 main steps: (1) Addition of Drude particles to the heavy atoms to generate initial topology and parameter files consistent with the Drude force field, (2) charge fitting using QM target data including ESP and specific interaction with water molecules, and (3) dihedral parameter fitting using QM target data. The charge fitting procedure is similar to RESP49 fitting but also takes advantage of the compound-water interactions.12,50 The partial charges are refitted for the compound that could undergo hydrogen bonding interaction by fitting to the minimum interaction energy and distance between the molecule and water at HF/6–31G* model chemistry without BSSE correction. The dihedral parameters are refitted after the charge refitting to have a consistent model. The geometry optimization and potential surface scans are done at the HF/6–31G* level of theory and the electrostatic potential (ESP) calculation is done using DFT at B3LYP/aug-cc-pVDZ level. As described previously, to fit the anisotropic polarization response of the electronic degrees of freedom, small positive perturbing test charges of 0.5 AMU are placed along the molecular surface resulting in multiple ESP potentials computed at various grid points. The multiple ESP data are then fitted to obtain the partial charges consistent with the Drude model.42 Gaussian 0951 software is used for the QM calculations to generate the target data for parameters optimization. Limited memory L-BFGS algorithm,33,34 available in NLOPT C++ library,52 is used to fit the parameters using the analytical or finite difference gradients obtained in the context of the chi-square objective function.
After refining the electrostatics and dihedral parameters, the LJ optimization process is initiated. The LJ parameters optimization procedure is framed as a minimization of objective function and driven by computing the analytical gradients of the objective function with respect to the LJ parameters. As described for the additive force field LJ optimization,39 the objective function is defined as,
| (7) |
where the sum runs over the molecules m in the training set, and are the computed and experimental molecular volumes respectively for a molecule m, and are the calculated and experimental heat of vaporization, respectively, for a molecule m, the and are the weights assigned to each molecular property. Equal weight for the molecular properties were used for this optimization. To compute the bulk properties, the liquid boxes from additive CGenFF simulations were obtained and Drude particles added to the non-hydrogen atoms followed by minimization and equilibration. The molecular volumes were calculated from the MD simulations as the average of the total volume of the liquid box divided by the number of molecules in the box as and the heat of vaporization were computed as,
| (8) |
where and are computed per molecule from the average of the potential energy in the gas and liquid phases, respectively. The derivative of the objective function with respect to the LJ parameter pi is given as,
| (9) |
where the derivative of a property of interest Q such as molecular volume or the heat of is expressed as,
| (10) |
As can be noticed, the first term in the equation 10 is non-zero only for a molecular property, such as the heat of vaporization in current optimization, that explicitly depend on the pi.
As indicated, experimental data are used to optimize the LJ parameters. A training data of 365 molecules with neat liquid properties were used and validation data of 51 molecules with neat liquid properties were held out. The molecules were curated from the prior publication of Mobley et al53 as well as National Institute of Science and Technology (NIST) database.54 The training and the validation data composed of aliphatic and polar molecules, which were carefully chosen to capture the diversity of atom types seen in drug like molecules. Since the parameters were optimized only using molecular volumes and the heat of vaporization, to test the transferability of the optimized parameters on a molecular property not explicitly in the objective function, hydration free energy (HFE) of the full set were computed and compared against the experimental measurements.
A gradient based optimizer L-BFGS33,34 algorithm was used for the LJ optimization. The optimization code is written in Bash, Python, and C++ and is also available together with the starting configurations of the solvent simulation boxes in GitHub (https://github.com/chetanrrk/LJOptimization). To compute the averages of molecular properties of each compound, a neat liquid box comprised of 200–400 molecules (volume ~ 38 × 38 × 38 Å3) was used and simulated for 2ns with MD under periodic boundary conditions with a time step of 1fs. The boxes were simulated under the constant pressure and temperature (NPT) using Langevin thermostat and piston.55 As prescribed in our previous study,17 the Drude particles were kept at 1K temperature with a hardwall of 0.2 Å and the non-hydrogen atoms at the experimental measurement temperature using the dual thermostat scheme. The long-range electrostatic interaction was computed using particle mesh Ewal (PME) summation56,57 with an Ewald splitting parameter of 0.34 Å−1, a grid spacing of 0.6 Å, and a sixth-order interpolation of the charge to the grid. The non-bonded van der Waals interactions were smoothly switched to zero between 10 to 12 Å and long-range correction as proposed by Shirts et al (LRC-MS) was applied.58 The SHAKE algorithm was used to constrain the bonds connecting a heavy atom to a hydrogen atom.59,60 All simulations were carried out using NAMD.
Optimization of the LJ parameters
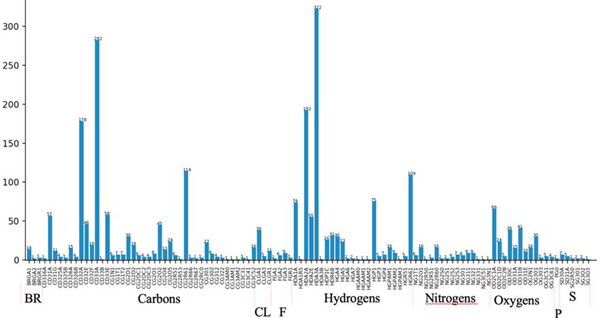
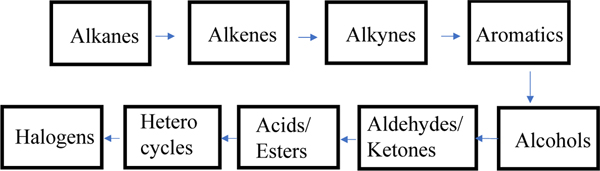
We seek to optimize a set of CGenFF atom types that is recurrent in drug-like small organic molecules (Figure 1). In total, 6 epochs of LJ optimization were carried out, with an epoch being defined as a stage when all training molecules are used during the optimization. The initial pass (epoch 0) through the training set was done to compute the initial liquid properties at their unoptimized LJ parameters. As shown in Figure 2, the optimization was carried out in batches during epoch 1. The atom types of the pure aliphatic molecules were optimized initially, followed by the optimization of the polar atom types. In each batch, about 10–20 iterations of L-BFGS algorithm were carried out. LJ parameters of atom types optimized in the previous batch were fixed on subsequent batches. The electrostatic and dihedral parameters were updated after the first epoch (epoch 1) for the molecules using GAAMP to be consistent with the optimized LJ parameters. Since the LJ parameters were stable after the first epoch, electrostatic and dihedral parameters were kept at their optimized value of the first epoch. After the completion of the initial LJ optimization on epoch 1, the atom types were then optimized in a concerted manner where all atom types were optimized simultaneously. The LJ parameters corresponding to the 84 Drude force field atom types were optimized in this work. Among these atom types, 56 atom types were already present in the Drude force field and 28 additional atom types were obtained from CGenFF and optimized in the context of the Drude force field.
Figure 1.
Coverage of CGenFF atom types by the current set of molecules. Broad range, ~70%, of the CGenFF atom types seen in drug-like small organic molecules are covered.
Figure 2.
Batch optimization workflow followed during epoch 1. Aliphatic atom types were optimized followed by aromatics and polar types. The arrow indicates the flow of optimized atom types to the next class to be optimized.
To test the transferability of the optimized parameters to other molecular properties not explicitly included in the objective function, the HFE of the molecules in the training set were calculated. Free energy perturbation (FEP) calculations were performed in CHARMM in the context of the Drude polarizable force field using the PERT module of CHARMM,61–64 as previously described. The molecules were solvated in a water box containing 250 SWM4 molecules using packmol software.65 The initial box was minimized and equilibrated. During the FEP, 11 windows were used for the electrostatic and 18 windows for the dispersion contribution calculations for both vacuum and solvated phases. A soft-core potential was used during the calculation of repulsive contribution during which the electrostatic and the dispersive interactions were turned off.66 For each window, the properties were averaged over 200 ps after an initial equilibration of 100 ps. The systems were simulated with PBC under conditions of constant pressure and constant temperature with PME. The aggregate data were post-processed using the weighted histogram analysis method (WHAM)67–69 for the dispersion and repulsion contributions and thermodynamic integration (TI)70,71 for the electrostatic contribution.
Optimization of the LJ parameters did not explicitly target the HFE property in the objective function. Initial results were calculated using an initial force field model corresponding to the optimized LJ parameters together with the standard Lorentz−Berthelot combination rule. To improve the performance, we examined the effect of a global scaling factor of the van der Waals interactions between atoms of a solute molecule and the oxygen atom of water introduced via the NBFIX functionality of the CHARMM parameter file.41 A similar procedure was used in our previous work.39 To determine the optimal scaling factor, equilibrium MD was launched for 2 ns with a timestep of 1 fs using the reference model (optimized LJ parameters and standard combination rule). The obtained equilibrium trajectories were then postprocessed with NBFIX based global scaling of the van der Waals between the solute and the oxygen atoms of water to obtain a reweighted HFE according to thermodynamic perturbation theory,
| (11) |
where represents the relative change in HFE, is the reference potential energy computed using the optimized LJ parameters with standard combination rule, and is perturbed potential energy with the van der Waals scaling factor . The scaling of the solute-water van der Waals dispersion can be expressed as a linear additive term,
| (12) |
which can be treated as a small perturbation on the HFE if is close to 1,72
| (13) |
On average, the calculated hydration free energies shift by about −2.4 kcal/mol with a factor , and by about −0.5 kcal/mol with a factor for the set of molecules examined here.
RESULTS AND DISCUSSION
The initial LJ parameters for 416 molecules were taken from the Drude force field if the particular atom type was available, or otherwise the parameters were obtained from the CGenFF previously tabulated values. For all compounds, the electrostatic parameters (charges, polarizabilities and Thole scale factors) as well as dihedrals parameters of each compound were fit targeting ab initio data using the GAAMP server.12 This resulted in a total of 84 atom types, each with two LJ parameters, to be optimized in order to best-match the bulk molecular properties according to the objective function given in equation 7.
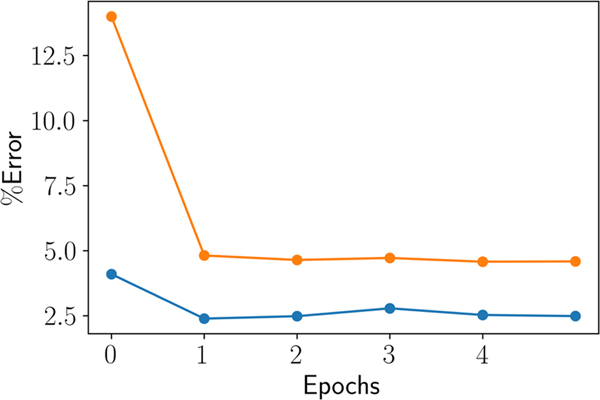
The L-BFGS algorithm coupled with the objective function and gradients was used to optimize the LJ parameters of 84 atom types. As shown in Figure 2, the initial epoch of optimization was carried out in stages, were the atom types found in pure aliphatic compounds were optimized first and the atom types found in other polar and non-polar functional groups were optimized later. After the initial epoch, all the atom types were optimized simultaneously. As seen in Figure 3, the optimization is remarkably efficient in improving the properties, with the molecular volume improving within the first two epochs by ~1.5%, and the heat of vaporization improving by ~9.5%. The initial unsigned average relative error over the molecular volumes was 4.1% and for the heats of vaporization it was 13.9%. After optimization, the unsigned average relative error on molecular volume and the heat of vaporization decreased to 2.4% and 4.6%, respectively. A total of 5 epochs of refinement were further carried out to better converge the parameters and liquid phase properties. A small fluctuation of less than 2% in the computed molecular properties toward later epochs is indicative of the convergence of the optimization.
Figure 3.
Progress made on liquid properties based on average percent absolute relative error during the training epochs. The orange line tracks the progress on the computed heat of vaporization and the blue line tracks the progress on the computed molecular volume.
Figure 4 shows the comparison against a hypothetical ideal fit (y=x) for both liquid properties. The liquid properties computed using the initial parameters clearly deviate more from the line of ideal fit whereas a close agreement to an ideal fit is obtained using the optimized LJ parameters. For molecular volumes computed using the initial LJ parameters, a linear fit with intercept set to zero had the slope of 0.996 and the Pearson R of 0.997. Using the optimized LJ parameter, the slope is comparable to the initial parameter of 1.01 and the Pearson R of 0.999. For the heat of vaporization computed using the initial LJ parameter, a linear fit with intercept set to zero has a slope of 1.1 and the Person R of 0.975. Using the optimized LJ parameter, a slope of 1.02 was obtained and the Person R improved to 0.997.
Figure 4.
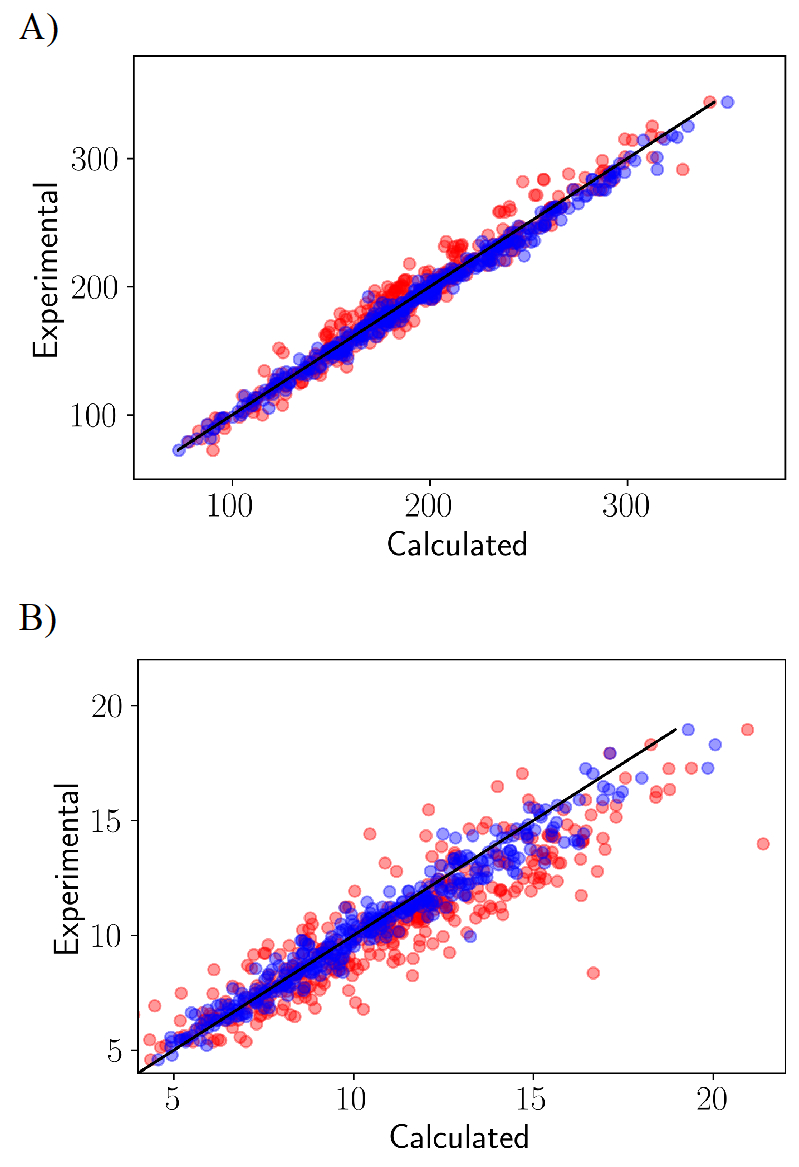
Liquid properties calculated for the training set of 365 molecules. The red and blue circles indicate properties computed using the initial and the final forcefields, respectively. (a) Molecular volumes in Å3 and (b) heats of vaporization in kcal/ mol. In black the ideal fit y=x line is shown.
A breakdown of the molecular properties computed using the optimized LJ parameters is given in Table 1 for the different classes of compounds. The errors in molecular volume for some classes, such as aromatics and alkynes, are as low as 1% whereas for polar groups, such as acids and ketones, they are as high as 3%. The errors in heat of vaporization are as low as 2% for the non-polar groups such as alkenes and aromatics and as high as 5.5 % for polar groups such as amides and nitros. Optimization of the atom types involving phosphorus atoms are particularly challenging. The initial average unsigned relative error on the heat of vaporization for the molecules containing phosphates are around 20% which is vastly improved to ~8% after optimization. Since this group is particular less populated containing just 2 molecules, more training molecules might be required to fully optimize these atom types, though experimental data for additional compounds is lacking.
Table 1.
Breakdown of the class specific unsigned average relative error on the training set computed using the optimized LJ parameters. The 2nd column contains the number of molecules used during training in each class, the 3rd column contains the error on the computed molecular volume, and the 4th column contains the error on the computed heat of vaporization (HVAP).
| Class | Number of Molecules | %Volume Error Final | %HVAP Error Final |
|---|---|---|---|
| Alkanes | 30 | 2.32 | 3.31 |
| Alkenes | 25 | 1.41 | 2.29 |
| Alkynes | 5 | 0.95 | 2.29 |
| Aromatics | 29 | 0.93 | 2.81 |
| Alcohols | 33 | 1.40 | 4.87 |
| Ketones | 23 | 3.51 | 2.77 |
| Ethers | 31 | 3.45 | 5.40 |
| Acids/Esters | 57 | 3.74 | 4.45 |
| Amides/Amines/Nitros | 79 | 2.14 | 5.88 |
| Sulfurs | 14 | 1.29 | 3.41 |
| Phosphorus | 2 | 1.526 | 8.467 |
| Halogens | 51 | 1.66 | 4.72 |
Figure 5 shows histograms of the error distributions for the molecular volumes and heats of vaporization, respectively. After optimization, a majority of the compounds have about 2.5% average unsigned relative error for the molecular volume and the overall average also close to 2.5%. The unsigned relative error is within 5% for the heats of vaporization with overall average also close to 5%. In fact, the optimization based on the Drude model shows slight improvement over our past LJ optimization based on the nonpolarizable GAFF model,39 where the average unsigned relative error on the heat of vaporization was around 6%. It should be noted that since the current optimization attempts to fit the LJ parameters globally and improve the average of the molecular properties, the properties of some molecules affect the overall performance of the parameter set, as seen towards the tail of the distribution. These are molecules containing exotic functional groups such as sulphones, phosphate, and some halogens in proximity of another polar functional groups. It is possible to reduce their errors further by defining additional specialized atom types. However, there is a risk of rapidly proliferating the atom types which would be inconsistent with the goal of this study to conduct the optimization that is globally applicable to a diverse set of molecules while using a conservative set of available atom types.
Figure 5.
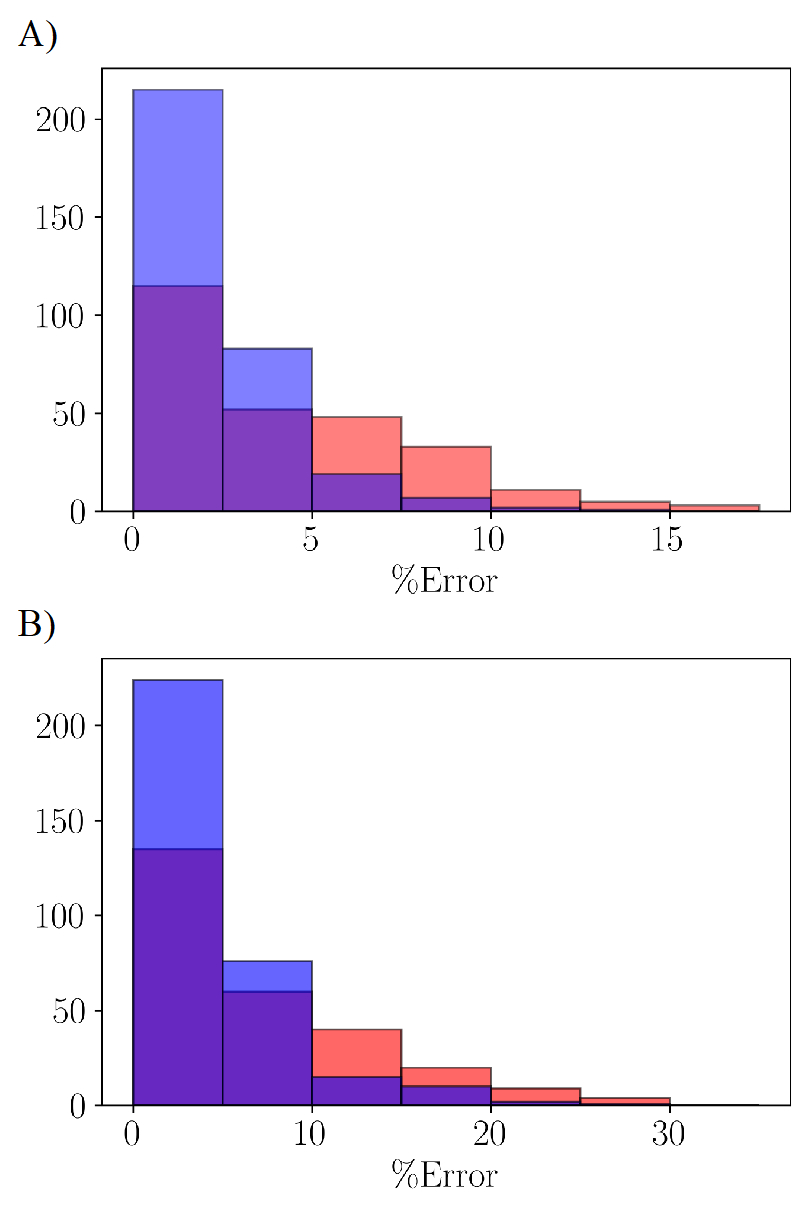
Distribution of the average unsigned relative error for the computed liquid properties on the training set computed on initial force field in red and optimized force field in blue for (a) the molecular volumes and (b) heats of vaporization.
For the majority of atom types, the optimized LJ parameters remained close to their initial values, taken from the CHARMM Drude force field or the CGenFF set. The average change in the Emin parameter was −0.01 kcal/mol, indicating a slight increase in the favorable LJ dispersion contributions. The average change in the Rmin parameter was 0.014 Å, indicating a slight but systematic increase in the radii. The average absolute change in the Emin parameter was 0.032 kcal/mol and the average absolute change in the Rmin parameter was 0.043 Å. As noted above, small perturbations to the LJ parameters were sufficient to improve a molecular property, especially the heat of vaporization which improved by around 9.5%. This vast improvement in the molecular properties with small changes in the LJ parameters also indicate the sensitivity of the properties towards the LJ parameters consistent with our prior LJ optimization39 using the GAFF based additive force field.
A more stringent test of the optimized LJ parameters is to apply the parameters to a set of molecules excluded from the training process. This validation of 51 molecules covering atom types of diverse functional groups were set aside in the training. As seen in Figure 6, the average percent absolute relative errors on the molecular volumes and heats of vaporization using the initial forcefield were 2.15% and 8.52% respectively. The error calculated using the optimized force field on the molecular volumes and heats of vaporization were 2.03% and 5.83% respectively. The RMSE on molecular volumes also improved from around 10 to 6 , and the RMSE on the heat of vaporization also improved from around 1.6 to 0.7 kcal/mol. For the molecular volumes, the slope of fit using the initial and the optimized force field were 0.99 each (both fit done with intercept at zero), and the Pearson’s R for the initial and the optimized forcefield were 0.99 as well. For the heat of vaporization, the slope of fit using the initial and the optimized force field were 0.92 and 0.96, respectively (both fit done with intercept at 0), and the Pearson’s R for the initial and the optimized forcefield were 0.94 and 0.98 respectively. As seen in the training set, the improvement in slopes and Pearson’s R upon optimization is also evident in the validation set. These errors and fits are consistent with the ones observed during the training, indicating the general transferability of the optimized LJ parameters to compounds not explicitly included in the training set.
Figure 6.
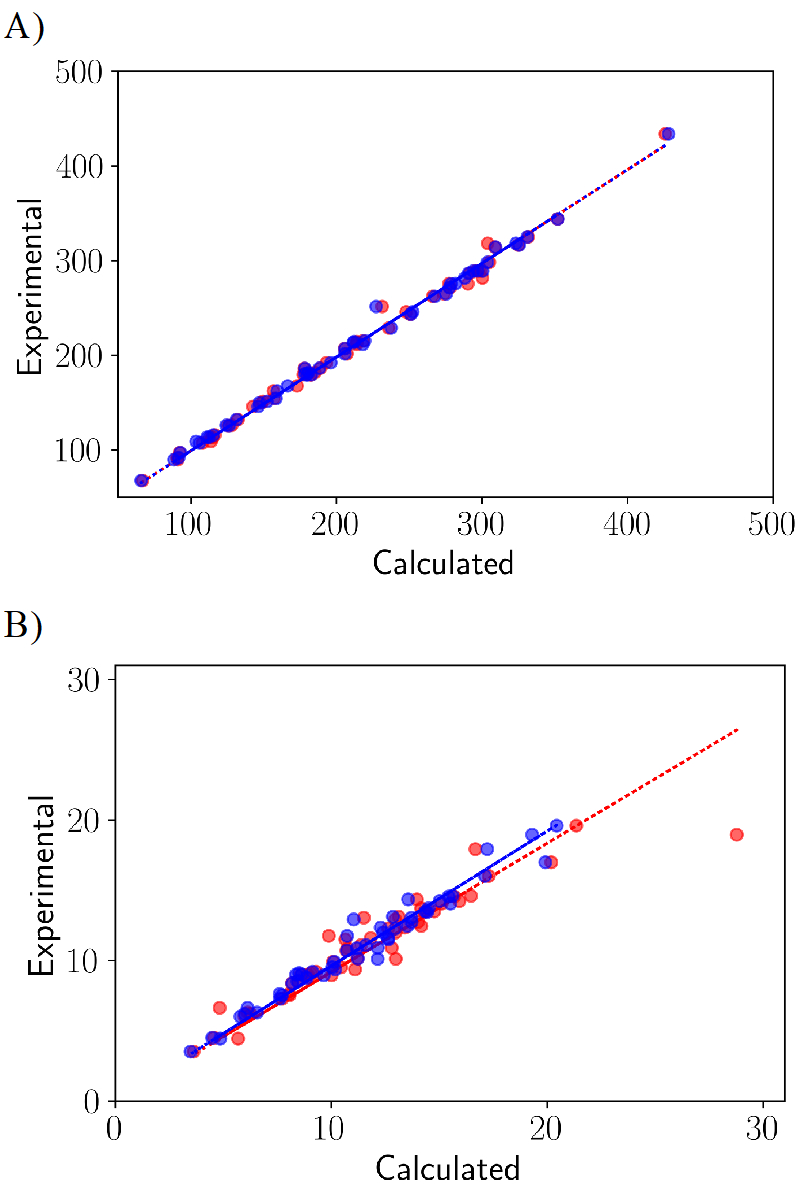
Linear fits on the set of 51 molecules training set molecules for (a) the molecular volumes in Å3 and (b) heats of vaporization in kcal/ mol. The red and blue circles show the comparison between initial and the optimized force field, respectively.
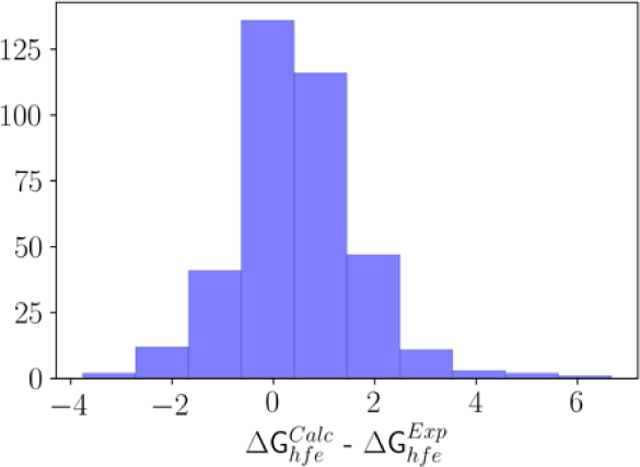
To further test the transferability of the optimized parameters on a property excluded from the objective function, HFE of the 372 molecules in the training set were computed using FEP. As seen in Figure 7, the overall trend with respect to the experimental measurement was good, yielding a linear best-fit with a slope of 0.81 and an intercept of 0.05 kcal/mol. The Pearson R is 0.9 and the average (signed) error is 0.46 kcal/mol, which is within statistical uncertainty. The mean absolute (unsigned) error is 0.95 kcal/mol. It is of interest to note that a systematic overestimation of the hydration free energy by ~2 kcal/mol was observed in our previous GAFF based LJ optimization.39 Such a systematic deviation in terms of the HFE was attributed to the overestimation of the dispersive interactions arising from the water model being used in the simulation. The issue was addressed using the NBFIX CHARMM utility by selectively scaling the LJ interaction between a molecule and the oxygen atoms of water by a factor of 1.115. Rescaling the Lennard-Jones well depth resulting from the Lorentz-Berthelot combination rule, by a factor γ=1.115 had reduced the average unsigned error of the HFE to 0.8 kcal/mol and the average signed error of 0.12 kcal/mol. To clarify the importance of this factor in the present study, the impact of rescaling the compound-water dispersion interaction was examined. Following a perturbative analysis, we find that a scaling factor γ=1.036 would reduce the average error of 0.5 kcal/mol to 0 kcal/mol. Since this scaling factor is very close to 1, we recommend to simply use the optimized LJ parameters together with the combination rule without further modification.
Figure 7.
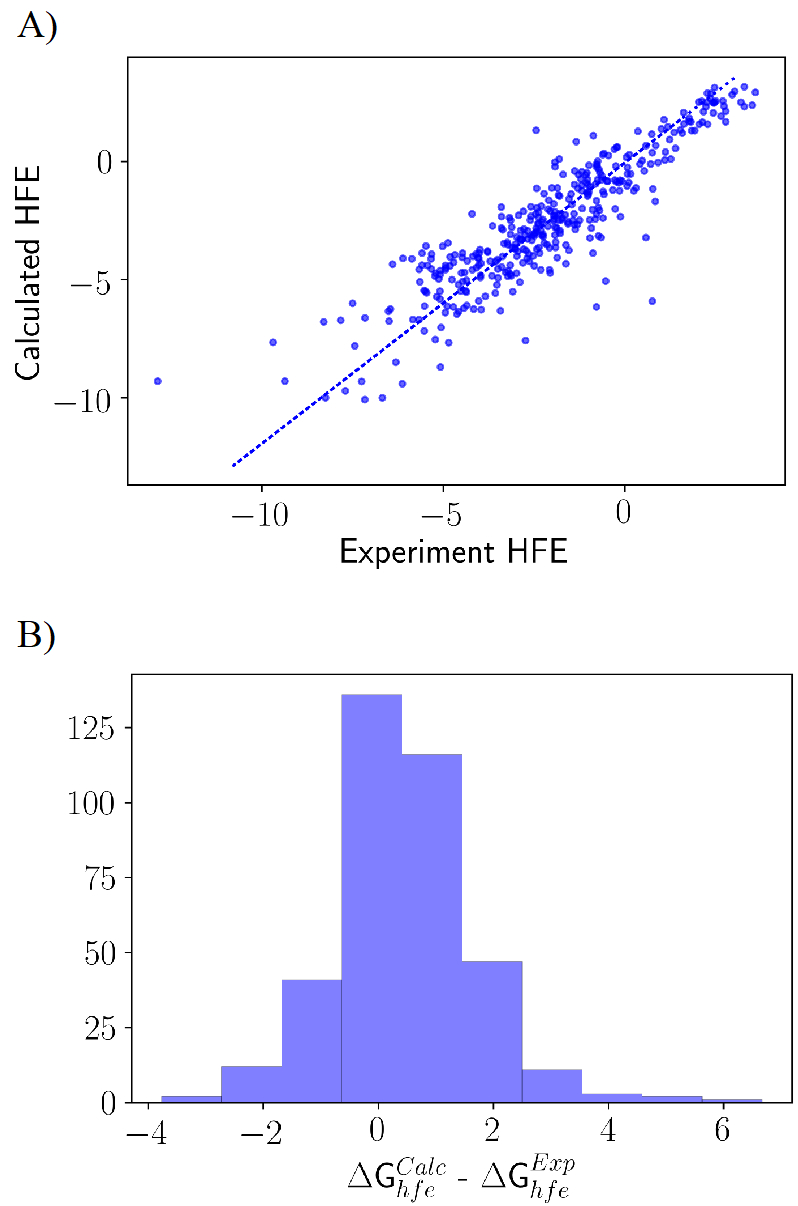
Validation of the optimized force field on the free energies of hydration (HFE) for 372 molecules. (a) Correlation plot showing the trend between experimental and computed HFE in kcal/mol using the optimized LJ. (b) Shows the distribution of the difference between the computed and the experimental HFE in kcal/mol.
CONCLUSION
Accurate force fields are critical for reliable computations of thermodynamic and kinetic properties. Optimization of force field parameters is a daunting challenge. While the bonded terms and electrostatic parameters can be fitted targeting QM data, the LJ optimization needs to be done by fitting directly to experimental measurements of molecular properties. We previously showed that significant improvement could be achieved in modeling the molecular properties in the context of additive forcefield starting from the GAFF LJ parameters.39 This current work built on the previous work to globally optimize the LJ parameters seen in drug-like small organic molecules but in the context of the CHARMM Drude force field.
It is important to be mindful of the number of optimized atom types given the total amount of data, although without additional experimental measurements it is not possible to use more extended training and test sets at this point. While one must avoid over-fitting the models with too many parameters, small drug-like organic molecules cover a wide range of chemistries and an insufficient number of atom types damages the accuracy of the final model. To balance these opposite goals, we aimed to be as parsimonious as possible in allowing the creation of additional atom types. As a comparison, the additive CGenFF model comprises LJ parameter for 28 atom types, while the LJ parameters for 56 atom types were globally optimized for the CHARMM Drude force field in the present effort. As a result of the optimization, the properties molecular volumes and heats of vaporization improved by 2%, and by > 9% overall, respectively. We showed that the parameters are transferable to molecules out of the training set with the average percent relative error on the test set for molecular volumes and heats of vaporization, being around 2% and 5.5% respectively. The LJ parameters were also shown to be transferable to compute HFE—a property that was not included in the optimization procedure. The fit obtained had a Pearson R of 0.9 and an average error of 0.46 kcal/mol. This represents a significant improvement over the additive GAFF force field in our previous study, where an average error of 2.0 kcal/mol was obtained. Such an improvement is consistent with the ability of the polarizable Drude model to more accurately model interactions in different environments, in contrast with optimized additive force fields that incorporate these effects into the fixed charge distribution and van der Waals parameters. The small remaining systematic error could be further reduced by introducing pair-specific LJ parameters (NBFIX terms in the syntax of the CHARMM parameter files) or by using a scaling factor γ=1.036 for the solute-solvent van der Waals dispersion interactions. Ideally, a complete polarizable force field model ought to account for all change in the interactions a molecule makes with its environment in different types of condensed phases. Systematic deviations of the HFE have been observed in other contexts,39,48,73 reflecting the inherent limitations of the LJ 6–12 potential and the standard Lorentz−Berthelot combination rule. A more accurate model could possibly be achieved with an alternate approach to treating the van der Waals interactions,74–76 or a different combination rule.77–79 These issues could be resolved through the use of pair-specific LJ parameters, while maintaining the simple form of the energy function as done in the present study, though in practice, the results obtained directly from the model are likely to have sufficient accuracy for most applications.
The Drude polarizable force field explicitly incorporates polarization in molecular mechanics-based modeling. It is also an attractive choice because of its ease of implementation since it can be coded as an extension of the additive force fields with slight modification to the electrostatic terms and addition of the self-term in the potential energy function. By globally optimizing the LJ parameters of small organic molecules and in the CGenFF context, we have extended the applicability of the Drude force field towards drug design and discovery applications. Future efforts shall expand on the present work by considering solvation free energy of molecules in a variety of solvents.
Supplementary Material
ACKNOWLEDGMENTS
We gratefully acknowledge the computing resources provided by the Laboratory Computing Resource Center at Argonne National Laboratory. This work is supported by National Institute of Health (NIH) via grant R01-GM072558 and R35-GM131710.
Footnotes
SUPPLEMENTARY MATERIAL
- feh.xlsx: Contains free energy of hydration (FEH) of molecules including their scientific name, experimental FEH, FEH computed with optimized LJ and standard combination rule, and FEH computed with optimized LJ and NBFIX based scaled combination rule.
- init_final_params.xlsx: Contains optimized atom types with initial and optimized Emin and Rmin.
- training.xlsx: Contains molecules used in training along with their names, molecular volumes (experimental and computed), and heat of vaporization (experimental and computed).
- testing.xlsx: Contains molecules used in testing along with their names, molecular volumes (experimental and computed), and heat of vaporization (experimental and computed).
REFERENCES
- (1).Karplus M; McCammon JA Molecular Dynamics Simulations of Biomolecules. Nat. Struct. Biol. 2002, 9 (9), 646–652. 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- (2).Chen H; Maia JDC; Radak BK; Hardy DJ; Cai W; Chipot C; Tajkhorshid E Boosting Free-Energy Perturbation Calculations with GPU-Accelerated NAMD. J. Chem. Inf. Model. 2020, 60 (11), 5301–5307. 10.1021/acs.jcim.0c00745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (3).Cournia Z; Allen B; Sherman W Relative Binding Free Energy Calculations in Drug Discovery: Recent Advances and Practical Considerations. J. Chem. Inf. Model. 2017, 57 (12), 2911–2937. 10.1021/acs.jcim.7b00564. [DOI] [PubMed] [Google Scholar]
- (4).Perez A; Morrone JA; Simmerling C; Dill KA Advances in Free-Energy-Based Simulations of Protein Folding and Ligand Binding. Curr. Opin. Struct. Biol. 2016, 36, 25–31. 10.1016/j.sbi.2015.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Mackerell ADJ Empirical Force Fields for Biological Macromolecules: Overview and Issues. J. Comput. Chem. 2004, 25 (13), 1584–1604. 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- (6).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- (7).Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; Mackerell ADJ CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31 (4), 671–690. 10.1002/jcc.21367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Rocklin GJ; Mobley DL; Dill KA Calculating the Sensitivity and Robustness of Binding Free Energy Calculations to Force Field Parameters. J. Chem. Theory Comput. 2013, 9 (7), 3072–3083. 10.1021/ct400315q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Dobson CM Chemical Space and Biology. Nature 2004, 432 (7019), 824–828. 10.1038/nature03192. [DOI] [PubMed] [Google Scholar]
- (10).Vanommeslaeghe K; MacKerell AD Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model. 2012, 52 (12), 3144–3154. 10.1021/ci300363c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Vanommeslaeghe K; Raman EP; MacKerell AD Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52 (12), 3155–3168. 10.1021/ci3003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (12).Huang L; Roux B Automated Force Field Parameterization for Nonpolarizable and Polarizable Atomic Models Based on Ab Initio Target Data. J. Chem. Theory Comput. 2013, 9 (8), 3543–3556. 10.1021/ct4003477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Kumar A; Yoluk O; MacKerell AD Jr. FFParam: Standalone Package for CHARMM Additive and Drude Polarizable Force Field Parametrization of Small Molecules. J. Comput. Chem. 2020, 41 (9), 958–970. 10.1002/jcc.26138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Mobley DL; Bannan CC; Rizzi A; Bayly CI; Chodera JD; Lim VT; Lim NM; Beauchamp KA; Slochower DR; Shirts MR; Gilson MK; Eastman PK Escaping Atom Types in Force Fields Using Direct Chemical Perception. J. Chem. Theory Comput. 2018, 14 (11), 6076–6092. 10.1021/acs.jctc.8b00640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (15).Lamoureux G; Roux B Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys. 2003, 119 (6), 3025–3039. 10.1063/1.1589749. [DOI] [Google Scholar]
- (16).Lamoureux G; MacKerell AD; Roux B A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J. Chem. Phys. 2003, 119 (10), 5185–5197. 10.1063/1.1598191. [DOI] [Google Scholar]
- (17).Rupakheti C; Lamoureux G; MacKerell AD; Roux B Statistical Mechanics of Polarizable Force Fields Based on Classical Drude Oscillators with Dynamical Propagation by the Dual-Thermostat Extended Lagrangian. J. Chem. Phys. 2020, 153 (11), 114108. 10.1063/5.0019987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Lemkul JA; Huang J; Roux B; MacKerell AD An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev. 2016, 116 (9), 4983–5013. 10.1021/acs.chemrev.5b00505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Lin F-Y; Huang J; Pandey P; Rupakheti C; Li J; Roux B; MacKerell AD Further Optimization and Validation of the Classical Drude Polarizable Protein Force Field. J. Chem. Theory Comput. 2020, 16 (5), 3221–3239. 10.1021/acs.jctc.0c00057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Huang J; Lemkul JA; Eastman PK; MacKerell AD Jr. Molecular Dynamics Simulations Using the Drude Polarizable Force Field on GPUs with OpenMM: Implementation, Validation, and Benchmarks. J. Comput. Chem. 2018, 39 (21), 1682–1689. 10.1002/jcc.25339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Lemkul JA; Roux B; van der Spoel D; MacKerell AD Jr. Implementation of Extended Lagrangian Dynamics in GROMACS for Polarizable Simulations Using the Classical Drude Oscillator Model. J. Comput. Chem. 2015, 36 (19), 1473–1479. 10.1002/jcc.23937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Jiang W; Hardy DJ; Phillips JC; Mackerell AD Jr; Schulten K; Roux B High-Performance Scalable Molecular Dynamics Simulations of a Polarizable Force Field Based on Classical Drude Oscillators in NAMD. J. Phys. Chem. Lett. 2011, 2 (2), 87–92. 10.1021/jz101461d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Chowdhary J; Harder E; Lopes PEM; Huang L; MacKerell AD; Roux B A Polarizable Force Field of Dipalmitoylphosphatidylcholine Based on the Classical Drude Model for Molecular Dynamics Simulations of Lipids. J. Phys. Chem. B 2013, 117 (31), 9142–9160. 10.1021/jp402860e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (24).Li H; Ngo V; Da Silva MC; Salahub DR; Callahan K; Roux B; Noskov SY Representation of Ion-Protein Interactions Using the Drude Polarizable Force-Field. J. Phys. Chem. B 2015, 119 (29), 9401–9416. 10.1021/jp510560k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Li H; Chowdhary J; Huang L; He X; MacKerell AD; Roux B Drude Polarizable Force Field for Molecular Dynamics Simulations of Saturated and Unsaturated Zwitterionic Lipids. J. Chem. Theory Comput. 2017, 13 (9), 4535–4552. 10.1021/acs.jctc.7b00262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (26).Lopes PEM; Huang J; Shim J; Luo Y; Li H; Roux B; MacKerell AD Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. J. Chem. Theory Comput. 2013, 9 (12), 5430–5449. 10.1021/ct400781b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Lemkul JA; MacKerell AD Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement Using Quantum Mechanical Base Stacking and Conformational Energetics. J. Chem. Theory Comput. 2017, 13 (5), 2053–2071. 10.1021/acs.jctc.7b00067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Lemkul JA; MacKerell AD Jr. Polarizable Force Field for RNA Based on the Classical Drude Oscillator. J. Comput. Chem. 2018, 39 (32), 2624–2646. 10.1002/jcc.25709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (29).Heid E; Fleck M; Chatterjee P; Schröder C; MacKerell AD Jr Toward Prediction of Electrostatic Parameters for Force Fields That Explicitly Treat Electronic Polarization. J. Chem. Theory Comput. 2019, 15 (4), 2460–2469. 10.1021/acs.jctc.8b01289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Huang LRB. GAAMP Web Server. 2013. [Google Scholar]
- (31).Wang J; Wang W; Kollman PA; Case DA Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graph. Model. 2006, 25 (2), 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- (32).Yesselman JD; Price DJ; Knight JL; Brooks CL 3rd. MATCH: An Atom-Typing Toolset for Molecular Mechanics Force Fields. J. Comput. Chem. 2012, 33 (2), 189–202. 10.1002/jcc.21963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Nocedal J Updating Quasi-Newton Matrices with Limited Storage. Math. Comput. 1980, 35 (151), 773–782. 10.2307/2006193. [DOI] [Google Scholar]
- (34).Liu DC; Nocedal J On the Limited Memory BFGS Method for Large Scale Optimization. Math. Program. 1989, 45 (1), 503–528. 10.1007/BF01589116. [DOI] [Google Scholar]
- (35).MacKerell AD; Karplus M Importance of Attractive van Der Waals Contribution in Empirical Energy Function Models for the Heat of Vaporization of Polar Liquids. J. Phys. Chem. 1991, 95 (26), 10559–10560. 10.1021/j100179a013. [DOI] [Google Scholar]
- (36).Wang J; Cieplak P; Li J; Cai Q; Hsieh M-J; Luo R; Duan Y Development of Polarizable Models for Molecular Mechanical Calculations. 4. van Der Waals Parametrization. J. Phys. Chem. B 2012, 116 (24), 7088–7101. 10.1021/jp3019759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (37).Wang L-P; Martinez TJ; Pande VS Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J. Phys. Chem. Lett. 2014, 5 (11), 1885–1891. 10.1021/jz500737m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (38).Nerenberg PS; Jo B; So C; Tripathy A; Head-Gordon T Optimizing Solute–Water van Der Waals Interactions To Reproduce Solvation Free Energies. J. Phys. Chem. B 2012, 116 (15), 4524–4534. 10.1021/jp2118373. [DOI] [PubMed] [Google Scholar]
- (39).Boulanger E; Huang L; Rupakheti C; MacKerell AD; Roux B Optimized Lennard-Jones Parameters for Druglike Small Molecules. J. Chem. Theory Comput. 2018, 14 (6), 3121–3131. 10.1021/acs.jctc.8b00172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (40).Harder E; Anisimov VM; Vorobyov IV; Lopes PEM; Noskov SY; MacKerell AD; Roux B Atomic Level Anisotropy in the Electrostatic Modeling of Lone Pairs for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory Comput. 2006, 2 (6), 1587–1597. 10.1021/ct600180x. [DOI] [PubMed] [Google Scholar]
- (41).Brooks BR; Brooks CL 3rd; Mackerell AD Jr; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30 (10), 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Anisimov VM; Lamoureux G; Vorobyov IV; Huang N; Roux B; MacKerell AD Determination of Electrostatic Parameters for a Polarizable Force Field Based on the Classical Drude Oscillator. J. Chem. Theory Comput. 2005, 1 (1), 153–168. 10.1021/ct049930p. [DOI] [PubMed] [Google Scholar]
- (43).Lin F-Y; MacKerell ADJ Force Fields for Small Molecules. Methods Mol. Biol. 2019, 2022, 21–54. 10.1007/978-1-4939-9608-7_2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (44).Thole BT Molecular Polarizabilities Calculated with a Modified Dipole Interaction. Chem. Phys. 1981, 59 (3), 341–350. 10.1016/0301-0104(81)85176-2. [DOI] [Google Scholar]
- (45).Allen MP; Tildesley DJ Computer Simulation of Liquids: Second Edition, 2nd ed.; Oxford University Press: Oxford, 2017. 10.1093/oso/9780198803195.001.0001. [DOI] [Google Scholar]
- (46).Baker CM; Lopes PEM; Zhu X; Roux B; MacKerell AD Accurate Calculation of Hydration Free Energies Using Pair-Specific Lennard-Jones Parameters in the CHARMM Drude Polarizable Force Field. J. Chem. Theory Comput. 2010, 6 (4), 1181–1198. 10.1021/ct9005773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (47).Best RB; Zheng W; Mittal J Balanced Protein–Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10 (11), 5113–5124. 10.1021/ct500569b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Piana S; Donchev AG; Robustelli P; Shaw DE Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B 2015, 119 (16), 5113–5123. 10.1021/jp508971m. [DOI] [PubMed] [Google Scholar]
- (49).Bayly CI; Cieplak P; Cornell W; Kollman PA A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97 (40), 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- (50).Foloppe N; MacKerell Alexander D, All-Atom J Empirical Force Field for Nucleic Acids: I. Parameter Optimization Based on Small Molecule and Condensed Phase Macromolecular Target Data. J. Comput. Chem. 2000, 21 (2), 86–104. . [DOI] [Google Scholar]
- (51).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Had M, and Gaussian DJF 09. (Gaussian, Inc., Wallingford CT, 2009) 2009. [Google Scholar]
- (52).Johnson SG The NLopt Nonlinear-Optimization Package. [Google Scholar]
- (53).Mobley DL; Bayly CI; Cooper MD; Shirts MR; Dill KA Small Molecule Hydration Free Energies in Explicit Solvent: An Extensive Test of Fixed-Charge Atomistic Simulations. J. Chem. Theory Comput. 2009, 5 (2), 350–358. 10.1021/ct800409d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (54).National Institute of Standards and Technology.
- (55).Feller SE; Zhang Y; Pastor RW; Brooks BR Constant Pressure Molecular Dynamics Simulation: The Langevin Piston Method. J. Chem. Phys. 1995, 103 (11), 4613–4621. 10.1063/1.470648. [DOI] [Google Scholar]
- (56).Essmann U; Perera L; Berkowitz ML; Darden T; Lee H; Pedersen LG A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103 (19), 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- (57).Darden T; York D; Pedersen L Particle Mesh Ewald: An N⋅log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98 (12), 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
- (58).Shirts MR; Mobley DL; Chodera JD; Pande VS Accurate and Efficient Corrections for Missing Dispersion Interactions in Molecular Simulations. J. Phys. Chem. B 2007, 111 (45), 13052–13063. 10.1021/jp0735987. [DOI] [PubMed] [Google Scholar]
- (59).Andersen HC Rattle: A “Velocity” Version of the Shake Algorithm for Molecular Dynamics Calculations. J. Comput. Phys. 1983, 52 (1), 24–34. 10.1016/0021-9991(83)90014-1. [DOI] [Google Scholar]
- (60).Miyamoto S; Kollman PA Settle: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Models. J. Comput. Chem. 1992, 13 (8), 952–962. 10.1002/jcc.540130805. [DOI] [Google Scholar]
- (61).Pearlman DA; Kollman PA The Lag between the Hamiltonian and the System Configuration in Free Energy Perturbation Calculations. J. Chem. Phys. 1989, 91 (12), 7831–7839. 10.1063/1.457251. [DOI] [Google Scholar]
- (62).Cieplak P; Bash P; Singh UC; Kollman PA A Theoretical Study of Tautomerism in the Gas Phase and Aqueous Solution: A Combined Use of State-of-the-Art Ab Initio Quantum Mechanics and Free Energy-Perturbation Methods. J. Am. Chem. Soc. 1987, 109 (21), 6283–6289. 10.1021/ja00255a010. [DOI] [Google Scholar]
- (63).Singh UC; Brown FK; Bash PA; Kollman PA An Approach to the Application of Free Energy Perturbation Methods Using Molecular Dynamics: Applications to the Transformations of Methanol .Fwdarw. Ethane, Oxonium .Fwdarw. Ammonium, Glycine .Fwdarw. Alanine, and Alanine .Fwdarw. Phenylalanine in Aqueou. J. Am. Chem. Soc. 1987, 109 (6), 1607–1614. 10.1021/ja00240a001. [DOI] [Google Scholar]
- (64).Zhu X; MacKerell ADJ Polarizable Empirical Force Field for Sulfur-Containing Compounds Based on the Classical Drude Oscillator Model. J. Comput. Chem. 2010, 31 (12), 2330–2341. 10.1002/jcc.21527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (65).Martínez L; Andrade R; Birgin EG; Martínez JM PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30 (13), 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- (66).Zacharias M; Straatsma TP; McCammon JA Separation‐shifted Scaling, a New Scaling Method for Lennard‐Jones Interactions in Thermodynamic Integration. J. Chem. Phys. 1994, 100 (12), 9025–9031. 10.1063/1.466707. [DOI] [Google Scholar]
- (67).Wang J; Deng Y; Roux B Absolute Binding Free Energy Calculations Using Molecular Dynamics Simulations with Restraining Potentials. Biophys. J. 2006, 91 (8), 2798–2814. 10.1529/biophysj.106.084301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (68).Souaille M; Roux B Extension to the Weighted Histogram Analysis Method: Combining Umbrella Sampling with Free Energy Calculations. Comput. Phys. Commun. 2001, 135 (1), 40–57. 10.1016/S0010-4655(00)00215-0. [DOI] [Google Scholar]
- (69).Kumar S; Rosenberg JM; Bouzida D; Swendsen RH; Kollman PA THE Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J. Comput. Chem. 1992, 13 (8), 1011–1021. 10.1002/jcc.540130812. [DOI] [Google Scholar]
- (70).Kirkwood JG Statistical Mechanics of Fluid Mixtures. \jcp 1935, 3 (5), 300–313. 10.1063/1.1749657. [DOI] [Google Scholar]
- (71).Frenkel D; Smit B Chapter 7 - Free Energy Calculations; Frenkel D, Smit BBT-UMS (Second E., Eds.; Academic Press: San Diego, 2002; pp 167–200. 10.1016/B978-012267351-1/50009-2. [DOI] [Google Scholar]
- (72).Deng Y; Roux B Hydration of Amino Acid Side Chains: Nonpolar and Electrostatic Contributions Calculated from Staged Molecular Dynamics Free Energy Simulations with Explicit Water Molecules. J. Phys. Chem. B 2004, 108 (42), 16567–16576. 10.1021/jp048502c. [DOI] [Google Scholar]
- (73).Best RB; Zheng W; Mittal J Correction to Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2015, 11 (4), 1978. 10.1021/acs.jctc.5b00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (74).Ponder JW; Wu C; Ren P; Pande VS; Chodera JD; Schnieders MJ; Haque I; Mobley DL; Lambrecht DS; DiStasio RA; Head-Gordon M; Clark GNI; Johnson ME; Head-Gordon T Current Status of the AMOEBA Polarizable Force Field. J. Phys. Chem. B 2010, 114 (8), 2549–2564. 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (75).Walters ET; Mohebifar M; Johnson ER; Rowley CN Evaluating the London Dispersion Coefficients of Protein Force Fields Using the Exchange-Hole Dipole Moment Model. J. Phys. Chem. B 2018, 122 (26), 6690–6701. 10.1021/acs.jpcb.8b02814. [DOI] [PubMed] [Google Scholar]
- (76).Mohebifar M; Johnson ER; Rowley CN Evaluating Force-Field London Dispersion Coefficients Using the Exchange-Hole Dipole Moment Model. J. Chem. Theory Comput. 2017, 13 (12), 6146–6157. 10.1021/acs.jctc.7b00522. [DOI] [PubMed] [Google Scholar]
- (77).Halgren TA The Representation of van Der Waals (VdW) Interactions in Molecular Mechanics Force Fields: Potential Form, Combination Rules, and VdW Parameters. J. Am. Chem. Soc. 1992, 114 (20), 7827–7843. 10.1021/ja00046a032. [DOI] [Google Scholar]
- (78).Waldman M; Hagler AT New Combining Rules for Rare Gas van Der Waals Parameters. J. Comput. Chem. 1993, 14 (9), 1077–1084. 10.1002/jcc.540140909. [DOI] [Google Scholar]
- (79).Kong CL Combining Rules for Intermolecular Potential Parameters. II. Rules for the Lennard‐Jones (12–6) Potential and the Morse Potential. J. Chem. Phys. 1973, 59 (5), 2464–2467. 10.1063/1.1680358. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.