Causal Inference in Studying the Long-Term Health Effects of Disasters: Challenges and Potential Solutions

Abstract

Two frequently encountered but underrecognized challenges for causal inference in studying the long-term health effects of disasters among survivors include 1) time-varying effects of disasters on a time-to-event outcome and 2) selection bias due to selective attrition. In this paper, we review approaches for overcoming these challenges and demonstrate application of the approaches to a real-world longitudinal data set of older adults who were directly affected by the 2011 Great East Japan Earthquake and Tsunami (n = 4,857). To illustrate the problem of time-varying effects of disasters, we examined the association between degree of damage due to the tsunami and all-cause mortality. We compared results from Cox regression analysis assuming proportional hazards with those derived using adjusted parametric survival curves allowing for time-varying hazard ratios. To illustrate the problem of selection bias, we examined the association between proximity to the coast (a proxy for housing damage from the tsunami) and depressive symptoms. We corrected for selection bias due to attrition in the 2 postdisaster follow-up surveys (conducted in 2013 and 2016) using multivariable adjustment, inverse probability of censoring weighting, and survivor average causal effect estimation. Our results demonstrate that analytical approaches which ignore time-varying effects on mortality and selection bias due to selective attrition may underestimate the long-term health effects of disasters.

Abbreviations

CI

confidence interval

IPCW

inverse probability of censoring weighting

IPTW

inverse probability of treatment weighting

JAGES

Japan Gerontological Evaluation Study

RR

risk ratio

SACE

survivor average causal effect

Major disasters not only cause immediate injury and loss of life but also appear to elevate the risk of long-term adverse physical and mental health outcomes among disaster survivors (1). Evidence on the lingering, long-term health sequelae of disaster exposure during the months and years following disasters has begun to accumulate (2–8). However, accurate assessment of long-term health consequences of a disaster among survivors is often hampered by major methodological challenges.

Socioeconomic and preexisting health problems can function as prior common causes of disaster vulnerability and later health problems, inducing confounding bias. For example, persons suffering from depression may be more likely to be victims of disaster (e.g., because they may be slower to evacuate ahead of a tsunami warning) (9). These same individuals may be at greater risk of illness after the disaster, regardless of their experience of disaster-related trauma (10). Adjustment for such confounding is particularly challenging in disaster epidemiology because researchers typically collect data after the disaster and do not have information on survivors predating the disaster. Several studies have taken advantage of “natural experiment” study designs, in which disasters affected participants in prospective cohort studies that were already in progress, thereby allowing for control of a rich set of predisaster information (4, 11, 12).

However, even with the availability of predisaster data with which to adjust for confounding, causal inference for the long-term effects of disasters remains challenging because of 2 additional and underrecognized causal inference challenges: 1) violation of the proportional hazards assumption due to time-varying effects of exposure on long-term health outcomes and 2) bias in estimating exposure-outcome associations due to selective attrition. In this article, we review each challenge and the existing methodologies for overcoming the problems. We then demonstrate the application of the methods to real-world data stemming from the 2011 Great East Japan Earthquake and Tsunami as motivating examples and discuss the implications for future studies.

CHALLENGE 1: ANALYSIS OF A TIME-TO-EVENT OUTCOME WHEN THE EFFECT OF AN EXPOSURE IS TIME-VARYING

The first challenge for causal inference emerges when the outcome of interest is the time to an event (e.g., death, onset of diseases). A common approach to the analysis of such outcomes adjusting for potential confounders is to use a Cox proportional hazards model and report a single hazard ratio as a measure of causal effect (13). However, the hazard ratio has been criticized as a flawed measure of causal effect (14–16), for 2 reasons.

The first reason is that a Cox proportional hazards model assumes that hazard ratios are constant over time, even though hazard ratios are time-varying for most situations in the real world. Assuming constant hazard ratios when assessing the long-term impacts of disaster exposure on the health of survivors ignores the fact that there are distinct postdisaster phases (e.g., the immediate postdisaster phase vs. the long-term recovery phase) during which traumatic disaster-related experiences may exert different adverse effects. When the hazard ratios are time-varying, the single hazard ratio estimate from a Cox model is a weighted average of the time-varying hazard ratios, which is often not informative since it is not intuitive and may mask significant changes in the pattern of effects over time (17).

The second reason is that estimating time-specific hazard ratios instead of assuming a constant hazard ratio is also problematic, because the time-specific hazard ratios do not have a causal interpretation due to selection bias. A hazard at a given time point is, by definition, the instantaneous probability density of event onset conditional on survival up to that time point. In examining the association between disaster-related damage and mortality, for instance, the probability of survival is lower in proportion to the scale of the disaster (18–21). Moreover, persons with baseline susceptibility to death (e.g., those with preexisting health problems) are less likely to survive up to any given time point. Thus, survival is a common effect (i.e., collider) of disaster damage and baseline health conditions and, if conditioned, induces selection bias (22). Although estimating a series of weighted averages of time-varying hazard ratios for increasingly longer periods of follow-up is a valid approach for examining time-varying effects while avoiding selection bias built into the time-specific hazard ratios, the approach allows estimation of exposure effects on the relative scale (i.e., hazard ratios) only.

Notably, the use of hazard ratios is problematic even in the absence of loss to follow-up or missing outcome data and resulting selection bias, which we discuss below in challenge 2.

Parametric survival curves with confounding adjustment

An alternative analytical approach for time-to-event outcomes is to estimate cumulative survival probabilities or cumulative incidence rates (i.e., risks, 1 − survival probabilities) at each time point instead of hazards and to plot survival curves. An advantage of this approach is that the survival curves allow us to visualize trajectories of absolute risks, which may be more intuitive and informative than a series of average hazard ratios (14). Moreover, the effects of an exposure can be computed on both the additive (i.e., cumulative incidence differences) and relative (i.e., cumulative incidence ratios) scales. Because these effect measures are not conditional on survival up to a certain time point, they are not susceptible to the same type of selection bias as time-specific hazard ratios.

The approach with which to parametrically estimate survival curves with confounding adjustment (a.k.a. causal survival analysis) is outlined by Hernán and Robins (16). In Figure 1 and Web Appendix 1 (available at https://doi.org/10.1093/aje/kwab064), we summarize the steps needed to adjust for confounding via standardization and obtain counterfactual survival curves that would have been observed if everyone had received a certain level of exposure. These counterfactual survival curves offer a full picture of the time-varying effects of the exposure. Although confounding adjustment can also be done via inverse probability of treatment weighting (IPTW), we will not focus on that approach in this article because estimation of inverse probability of treatment weights is complicated when the categorical exposure has 3 or more levels.

Figure 1.

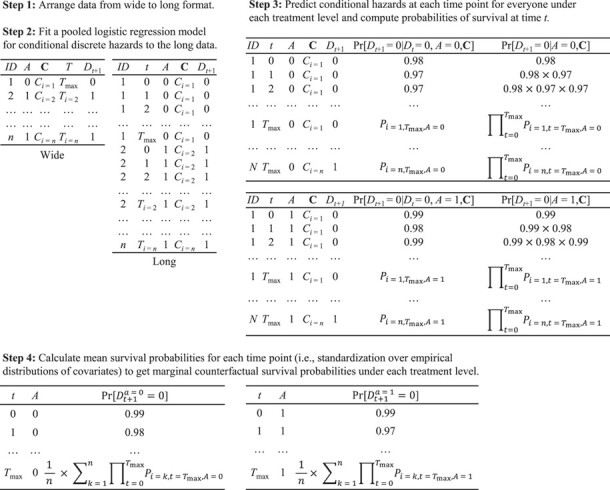
Estimation of parametric survival curves with confounding adjustment via standardization. A = exposure; C_i = a vector of covariates for individual i; T_i = time of death for individual i (follow-up ends at T_max because of administrative censoring); D_t = death by the end of follow-up; − conditional hazard of death for individual i at time t under treatment level A = a. In the “long” data created after step 1, person-time for each individual was separated into rows.

CHALLENGE 2: SELECTION BIAS DUE TO SELECTIVE ATTRITION

When evaluating long-term associations between disaster exposure and health, a common practice in disaster epidemiology is to 1) enroll survivors at a given time point (typically several months or years after the event), 2) measure health outcomes (e.g., depression) by means of surveys over the course of follow-up, and 3) analyze data only from individuals whose outcome was measured. However, associations from such analyses may not represent the causal effect of a disaster on health, even when the disaster exposure can be considered to have happened randomly.

By design, postdisaster health status cannot be ascertained for people who 1) were alive but chose not to participate in the survey (pattern 2 in Figure 2A) or 2) died before the time of the outcome assessment (pattern 3 in Figure 2A). Thus, analyzing only those survivors who participate in the follow-up wave is equivalent to conditioning on censoring due to death and study nonparticipation (represented by a box around censoring S = 0 of a directed acyclic graph in Figure 2B and Figure 2C). When exposure A (e.g., disaster-related experience) affects the probability of being censored and there is a common cause for censoring S and outcome Y, as illustrated by C in Figure 2B and C and U in Figure 2C, such conditioning on censoring status (i.e., a collider) would induce selection bias (22).

Figure 2.

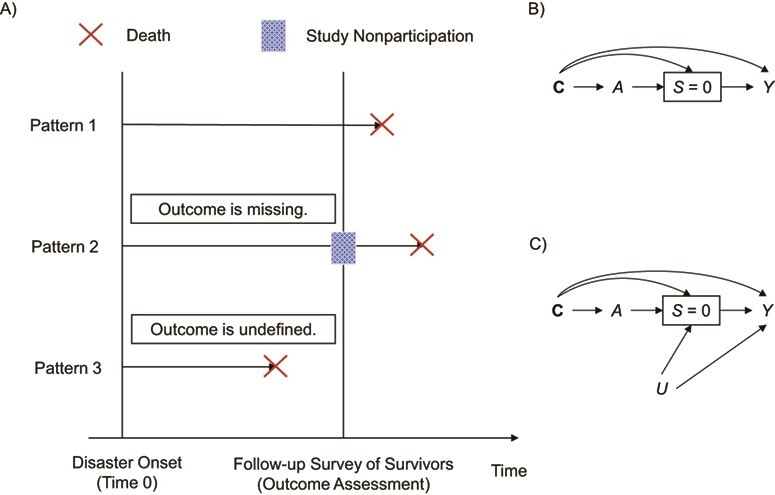
Illustration of selection bias due to selective attrition. A) Attrition by death and study nonparticipation in studies of the association between disasters and health outcomes, assessed in a follow-up survey of survivors. B) Directed acyclic graph where an association between an exposure A and an outcome Y is biased due to confounding by measured covariates C and selection bias of conditioning on no censoring, S = 0. C) Directed acyclic graph where an association between an exposure A and an outcome Y is biased due to confounding by measured covariates C and selection bias induced by C and U, both of which cause no censoring S = 0 and an outcome Y.

Selection bias due to selective attrition is particularly relevant in disaster epidemiology. For example, disaster-related damage, A, is likely to affect the probability of censoring, S, due to the effects of natural disasters on mortality discussed in challenge 1 or study nonparticipation due to acute mental health effects (depression and posttraumatic stress disorder) (18–21, 23, 24). Persons with predisaster health problems (e.g., depression) (C or U) may be at greater risk of poor health (Y) after the disaster and more likely to be censored (S = 1). Although the direction and magnitude of resulting selection bias depend on how the 2 causes of censoring (i.e., A and C/U) interact and cannot be known without a full understanding of the underlying selection mechanism, such selective attrition would often result in the underestimation of the true causal effect of disaster exposure (A) on health (Y) (22, 25, 26).

There are a few common approaches for dealing with the selection bias. These common approaches, if the necessary assumptions hold, estimate one of the 2 counterfactual estimands: 1) effects of disaster exposure on health that would have been observed if no one had been censored or 2) effect of the exposure in a subset of the population who would have been uncensored regardless of their exposure status. For each of the analytical methods we discuss, corresponding causal estimands, their interpretation, and underlying assumptions are shown in Table 1.

Table 1.

Analytical Methods for Dealing With Selection Bias Due to Selective Attrition by Death and Study Nonparticipation^a

Method	Causal Estimand	Interpretation	Assumptions b
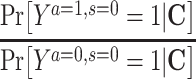
Multivariable adjustmentc		Risk of Y that would have been observed if everyone had been exposed to A and everyone had remained in the study divided by risk of Y if no one had been exposed to A and everyone had remained in the study conditional on C	No unmeasured common cause for an A-Y relationship (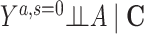) No unmeasured common cause for an S-Y relationship (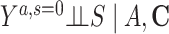) No model misspecification for the outcome (Y) model conditional on A and C
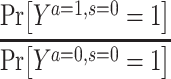
IPTW and IPCWc		Risk of Y that would have been observed if everyone had been exposed to A and everyone had remained in the study divided by risk of Y if no one had been exposed to A and everyone had remained in the study among the study population	No unmeasured common cause for an A-Y relationship (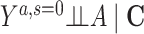) No unmeasured common cause for an S-Y relationship (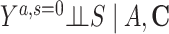) No model misspecification for the exposure (A) model conditional on C No model misspecification for death and attrition (S) conditional on A and C
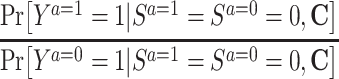
SACEd,e		Risk of Y that would have been observed if everyone had been exposed to A divided by risk of Y if no one had been exposed to A conditional on C in a study population subset of persons who would have remained in the study regardless of the exposure level	No unmeasured common cause for an A-Y relationship (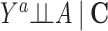) Cross-world exchangeability for an S-Y relationship (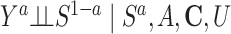) Linear association between U and Y conditional on A and C on the log scalef Linear association between U and S conditional on A and C on the logit scaleg No model misspecification for death and attrition (S) conditional on A and C A does not influence U conditional on Ch Location shift relationship between U and (A, C) given S = 0i

Abbreviations: IPCW, inverse probability of censoring weighting; IPTW, inverse probability of treatment weighting; SACE, survivor average causal effect.

^a  Y is a binary outcome, A is a binary exposure, S = 0 indicates that the person remained in the study (i.e., no censoring), C is a vector of covariates, U is an unmeasured common cause of an outcome and censoring, 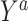is a potential outcome under exposure A = a, and 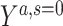is a potential outcome under exposure A = a and S = 0.

^b All approaches also assumed consistency and positivity.

^c Multivariable adjustment and inverse probability weights were based on conditional exchangeability, implied by the directed acyclic graph in Figure 2B.

^d Approach proposed by Tchetgen Tchetgen et al. (37). Assumptions for unmeasured confounder(s) U and model specification are also shown in the original article.

^e The SACE approach was based on conditional exchangeability, implied by the directed acyclic graph in Figure 2C.

^f The log-linear model for the outcome Y conditional on A, U, and C fitted to those who remained in the study (S = 0) was specified as follows: 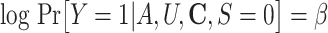, where 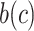is a flexible function of C.

^g The logistic model for the censoring S conditional on A, U, and C was specified as follows: 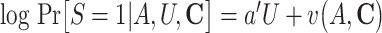, where .

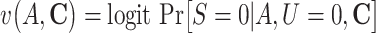^h Formally, this assumption is written as .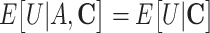

ⁱ Formally, the assumption states that the residual for U (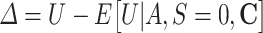) is independent of A and C given S = 0.

Effects if none of the survivors had been censored

The most common approach for dealing with selection bias is to estimate and compare counterfactual outcomes that would have been observed had no one been censored. Formally, this counterfactual estimand for a binary outcome Y and a binary exposure A on the risk ratio scale is defined by

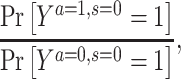where 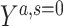represents the potential outcome under exposure 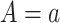and no censoring 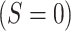. This counterfactual quantity, conditional on covariates or marginally, can be estimated via either multivariable-adjusted outcome regression or inverse probability of censoring weighting (IPCW). Both approaches are valid when a vector of measured covariates C suffices to remove all selection bias (i.e., block all open backdoor paths) due to prior common causes of exposure A and outcome Y and of the censoring variable S and the outcome Y (e.g., Figure 2B). The estimation procedure and the underlying assumptions for each analytical method are described in detail in Table 1 and Web Appendix 2. The causal estimands that multivariable-adjusted outcome regression and IPCW target would coincide when there is no effect-measure modification by the covariates C (i.e., the effect of an exposure is constant across levels of C).

Although these approaches can deal with selection bias, the resulting counterfactual estimand has been criticized because of conceptual problems with its interpretation. First, the interpretation of the estimand requires conceptualizing a hypothetical intervention that would eliminate censoring (27, 28). Since no realistic intervention could plausibly prevent all deaths and study nonparticipation resulting from disaster exposure, the causal estimand may not have a meaningful interpretation in practice. Second, the outcome for persons who died before the follow-up assessment is not simply missing (i.e., inadequate collection of information that could have been observed in principle) but is undefined, because the outcome that deceased individuals would have experienced is never known even with perfect data collection (pattern 3 in Figure 2A) (29, 30).

Survivor average causal effect

The second approach to addressing selection bias due to conditioning on posttreatment censoring is to estimate the effect of the exposure in a subset of the population who would have been uncensored regardless of their exposure status. Since the target population for inference is now restricted to people who never experience censoring, the problems with IPCW (i.e., conceptualizing hypothetical interventions that eliminate all censoring, as well as undefined outcomes for deceased individuals) are removed. This causal estimand is often called the survivor average causal effect (SACE), a form of the principal strata causal effect (31, 32). Formally, the SACE for a binary outcome Y and a binary exposure A on the risk ratio scale is defined by

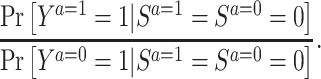Various approaches have been proposed for point estimates or bounds of the SACE under different identifiability assumptions (30, 33–38). In this article, we highlight a technique developed by Tchetgen Tchetgen et al. (37) using a 2-stage regression to obtain a point estimate of the SACE conditional on covariates. Specifically, we first fit a model for censoring conditional on the exposure and the covariates to compute conditional probabilities of being censored (S = 1); and then, in the second stage, we fit a model for the outcome Y conditional on the exposure, the same set of covariates as in the previous model, and the predicted probabilities of being censored as an additional covariate. We chose this method for its simplicity and robustness to unmeasured common causes for censoring and outcome (e.g., U in Figure 2C). The estimation procedure and underlying assumptions are described in detail in Table 1 and Web Appendix 3.

The conditional SACE and the causal estimand that the multivariable-adjusted outcome regression targets (i.e., the effect of an exposure had no one been censored conditional on covariates) will coincide if there are no unmeasured common causes for censoring and outcome (e.g., U in Figure 2C; see Web Appendix 4 for proof).

While the SACE is a useful estimand for avoiding selection bias, the approach has also been criticized because the “survivors” (i.e., people with 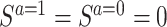) cannot be empirically identified, since the definition is based on counterfactuals, which we cannot observe in reality (15, 28).

MOTIVATING EXAMPLES

The Iwanuma Study

We illustrate application of the methods described above using a cohort of disaster survivors from the 2011 Great East Japan Earthquake and Tsunami, which struck the northeastern coast of Japan on March 11, 2011. Our analytical sample comprised residents of Iwanuma City in Miyagi Prefecture, located approximately 80 km (50 miles) west of the earthquake epicenter. Iwanuma was one of the field sites in a nationwide cohort study of Japanese adults aged 65 years or more, the Japan Gerontological Evaluation Study (JAGES), which was established 7 months prior to the disaster (39, 40). The tsunami killed 180 residents, damaged 5,542 houses, and inundated 48% of the land area in Iwanuma (see Web Figure 1) (41).

At baseline (August 2010), a census was conducted of all Iwanuma City residents aged 65 years or more (n = 8,576), and valid responses were obtained from a total of 4,957 residents (response rate = 57.8%). Two waves of follow-up surveys were conducted in the aftermath of the disaster: October 2013 (2.5 years after disaster onset) and November 2016 (5.5 years after disaster onset).

Notably, the Iwanuma Study has a rich set of information on the characteristics of the subjects predating the disaster. Thus, we were able to use the predisaster information to 1) examine the presence of selective attrition and adjust for resulting selection bias and 2) adjust for confounding by sociodemographic characteristics that were distributed differently across the levels of disaster damage.

The data underlying this article were provided by the JAGES investigators with permission. Data will be shared upon request to the corresponding author, with the permission of the JAGES investigators.

Example 1: Causal survival analysis

Question and problem.

We examined the effect of predisaster distance from the coast on all-cause mortality among survivors in the Iwanuma Study. We performed causal survival analysis to parametrically estimate survival curves adjusting for confounding via standardization.

Methods.

We used the data of all disaster survivors in the Iwanuma sample (n = 4,857) (see Web Figure 2 for selection of the analytical sample). Information on dates of death due to all causes was obtained through linkage to the national long-term care insurance database. The time to death or administrative censoring at the end of the 6-year follow-up period was available for everyone in the analytical sample; hence there was no loss to follow-up. Predisaster distance from the coast was categorized into 3 levels—<1,000 m, 1,000–3,000 m, and >3,000 m—as a proxy for complete home loss, major housing damage, and less severe damage, respectively (see Web Figure 3B). We adjusted for age, sex, depressive symptoms, self-rated health, education, household income, current smoking, current alcohol intake, and treatment for major diseases (including hypertension, stroke, diabetes, and dyslipidemia) prior to onset of the disaster.

We first performed conventional analyses for a time-to-event outcome including the Kaplan-Meier estimator and a Cox proportional hazards model. In pooled logistic regression of causal survival analysis, we modeled time as a quadratic function and included product terms between the exposure and time to allow time-varying hazard ratios. We estimated counterfactual survival curves as well as the trajectories of cumulative incidence differences and cumulative incidence ratios. Multiple imputation by chained equations (m = 20) was used to impute missing data on the covariates, assuming that the data were missing at random (42). Standard errors were obtained by bootstrapping with 1,000 replications.

Results.

Baseline demographic characteristics of the analytical sample are shown in Table 2 by level of exposure. People who lived closer to the coast (<1,000 m) were more likely to be older, depressed, and less educated, and they reported poorer self-rated health and lower household income than those who lived far from the coast (>3,000 m).

Table 2.

Baseline (2010) Sociodemographic Characteristics of the Analytical Sample Before the 2011 Earthquake and Mortality During the 6-Year Follow-up Period (2011–2017) According to Preexposure Residential Distance From the Coast, Iwanuma, Japan

			Distance From Coast
Characteristic	Total		>3,000 m		1,000–3,000 m		<1,000 m
	No.	%	No.	%	No.	%	No.	%
No. of participants	4,857	100.0	4,129	100.0	467	100.0	261	100.0
No. of deaths during follow-up period	806	16.7	650	15.7	95	20.3	61	23.4
Sex
Male	2,105	43.3	1,817	44.0	190	40.7	98	37.5
Female	2,752	56.7	2,312	55.0	277	59.3	163	62.5
Depression in 2010a
Mild or severe depression	1,444	29.7	1,222	29.6	133	28.5	89	34.1
No depression	2,682	55.2	2,302	55.8	253	54.2	127	48.7
Missing data	731	15.1	605	14.7	81	17.3	45	17.2
Self-rated health in 2010
Very good	538	11.1	445	10.8	57	12.2	36	13.8
Good	3,140	64.6	2,710	65.6	286	61.2	144	55.2
Bad	862	17.7	724	17.5	85	18.2	53	20.3
Very bad	227	4.7	180	4.4	26	5.6	21	8.0
Missing data	90	1.9	70	1.7	13	2.8	7	2.7
Duration of education in 2010, years
<6	123	2.5	95	2.3	13	2.8	15	5.7
6–9	1,634	33.6	1,260	30.5	240	51.4	134	51.3
10–12	1,938	39.9	1,767	42.8	122	26.1	49	18.8
≥13	916	18.9	846	20.5	54	11.6	16	6.1
Other	52	1.1	32	0.8	11	2.4	9	3.4
Missing data	194	4.0	129	3.1	27	5.8	38	14.6
Current smoking status in 2010
Nonsmoker	3,938	81.1	3,386	82.0	347	74.3	205	78.5
Smoker	496	10.2	410	9.9	63	13.5	23	8.8
Missing data	423	8.7	333	8.1	57	12.2	33	12.6
Current alcohol drinking status in 2010
Drinker	1,624	33.4	1,431	34.7	132	28.3	61	23.4
Nondrinker	3,114	64.1	2,611	63.2	316	67.7	187	71.6
Missing data	119	2.5	87	2.1	19	4.1	13	5.0
Current treatment for hypertension in 2010
No	2,729	56.2	2,326	56.3	252	54.0	151	57.9
Yes	2,001	41.2	1,710	41.4	194	41.5	97	37.2
Missing data	127	2.6	93	2.3	21	4.5	13	5.0
Current treatment for stroke in 2010
No	4,594	94.6	3,929	95.2	429	91.9	236	90.4
Yes	136	2.8	107	2.6	17	3.6	12	4.6
Missing data	127	2.6	93	2.3	21	4.5	13	5.0
Current treatment for diabetes in 2010
No	4,064	83.7	3,461	83.8	388	83.1	215	82.4
Yes	666	13.7	575	13.9	58	12.4	33	12.6
Missing data	127	2.6	93	2.3	21	4.5	13	5.0
Current treatment for dyslipidemia in 2010
No	4,274	88.0	3,638	88.1	399	85.4	237	90.8
Yes	456	9.4	398	9.6	47	10.1	11	4.2
Missing data	127	2.6	93	2.3	21	4.5	13	5.0
Age in 2010, yearsb	74.7 (6.97)		74.6 (6.79)		74.5 (7.38)		77.1 (8.40)
Equivalized household income in 2010 (10,000 yen)b,c	228 (147)		234 (148)		202 (140)		170 (126)
Missing data	977	20.1	791	19.2	103	22.1	83	31.8

^a Depression was defined as scoring 5 or more points on the Geriatric Depression Scale.

^b Values are expressed as mean (standard deviation).

^c Household income was divided by the square root of household size.

Table 3 shows hazard ratio estimates from the Cox models. After adjustment for confounding, living 1,000–3,000 m (vs. >3,000 m) from the coast was associated with a greater hazard of death (hazard ratio (HR) = 1.32, 95% confidence interval (CI): 1.06, 1.65), whereas there was no strong evidence of an association with mortality for persons who lived less than 1,000 m from the coast (HR = 1.22, 95% CI: 0.93, 1.61).

Table 3.

Association Between Pre-Earthquake Residential Distance From the Coast and Mortality in Cox Proportional Hazards Models, Iwanuma, Japan, 2010–2017

Distance From Coast in 2010, m	Crude		Confounder-Adjusted a
	HR	95% CI	HR	95% CI
>3,000	1.00	Referent	1.00	Referent
1,000–3,000	1.33	1.07, 1.65	1.32	1.06, 1.65
<1,000	1.59	1.23, 2.07	1.22	0.93, 1.61

Abbreviations: CI, confidence interval; HR, hazard ratio.

^a Adjusted for sex, age, depressive symptoms, self-rated health, education, household income, current smoking, current alcohol intake, and treatment for major diseases (including hypertension, stroke, diabetes, and dyslipidemia).

Figure 3 shows the results of causal survival analysis. Estimated parametric survival curves without confounding adjustment (Figure 3A) were identical to the nonparametric curves obtained via the Kaplan-Meier estimator (Web Figure 4), suggesting that our model specifications for conditional discrete hazards were appropriate. Figure 3B shows parametric survival curves after confounding adjustment via standardization. We observed that on the absolute scale, increasingly higher levels of the exposure (i.e., living closer to the coast before the disaster) were associated with higher mortality throughout the follow-up period (Figure 3C). After adjustment for confounding (Figure 3D), the risk of death was greater in the <1,000-m group (vs. >3,000 m) for the first 3 years (e.g., cumulative incidence difference at 36 months = 0.024 (95% CI: 0.001, 0.057). Results on the relative scale also showed similar trends before (Figure 3E) and after (Figure 3F) confounding adjustment (e.g., cumulative incidence ratio at 36 months = 1.33 (95% CI: 1.01, 1.79). However, at 48 months, the association for the <1,000-m group remained similar on the absolute scale (cumulative incidence difference = 0.023, 95% CI: −0.006, 0.055) but was attenuated on the relative scale (cumulative incidence ratio = 1.22, 95% CI: 0.94, 1.57). The associations became even less evident in the later period of follow-up. See Web Table 1 for estimates and confidence intervals.

Figure 3.

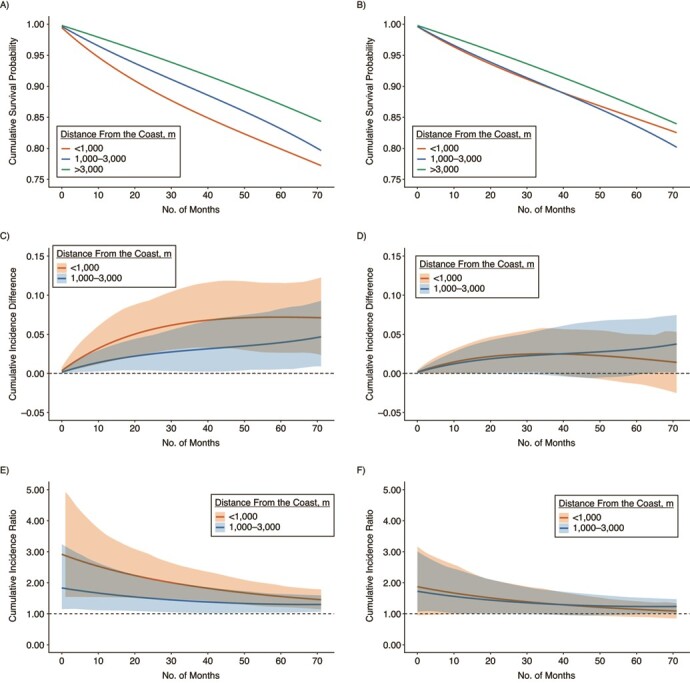
Parametric curves for mortality during the follow-up period (2011–2017) by predisaster distance from the coast among survivors of the 2011 earthquake in Iwanuma, Japan. A) Cumulative survival probability without confounding adjustment; B) cumulative survival probability with confounding adjustment; C) cumulative incidence difference without confounding adjustment; D) cumulative incidence difference with confounding adjustment; E) cumulative incidence ratio without confounding adjustment; F) cumulative incidence ratio with confounding adjustment. Panels A, C, and E (left column) show crude associations between predisaster distance from the coast and mortality. Panels B, D, and F (right column) show results adjusted for sex, age, depressive symptoms, self-rated health, education, household income, current smoking, current alcohol intake, and treatment for major diseases (including hypertension, stroke, diabetes, and dyslipidemia) via standardization. The 95% confidence intervals (shaded areas) were obtained via bootstrapping with 1,000 replications.

Discussion.

Our results indicate that using a Cox regression ignoring time-varying effects of disasters may result in the misleading conclusion that the degree of disaster damage (i.e., living less than 1,000 m from the coastline before the disaster vs. living at least 1,000 m away) did not have a causal effect on mortality over the 6-year follow-up period. Estimation of parametric survival curves adjusted for confounding is a more appropriate approach for assessing trajectories of the associations between a disaster exposure and risk of death. We demonstrated that living closer to the coast appeared to exert an adverse influence on the risk of mortality for at least the first 3 years after the disaster.

Example 2: Selection bias adjustment

Question and problem.

We examined the effect of disaster-related housing damage on depression in 2013 and 2016. Web Figure 5 shows the selection of the analytical sample. Among the disaster survivors (n = 4,857), the outcome of interest was measured only among people who survived up to and participated in the follow-up surveys in 2013 and 2016 (n = 3,567 for 2013 and n = 2,781 for 2016) and was censored for the rest. The severity of disaster-related damage is likely to be correlated with the probability of because of the disaster’s impacts on mortality during the immediate postdisaster phase and nonparticipation in follow-up surveys. In addition, censoring is likely to share common prior causes (e.g., predisaster health status) with depression assessed in 2013 and 2016. Thus, a naive analysis of people without missing outcome information would result in selection bias and underestimate the effect of disaster damage on depression.

Methods.

Our outcome was mild or severe depression, defined as scoring 5 points or higher on the validated Japanese short version of the Geriatric Depression Scale (43). For our exposure, as a proxy for housing damage due to the tsunami, we used the distance from each participant’s residential address and the coastline. As illustrated in Web Figure 1 and Web Figure 3A, people who lived closer to the coastline were more likely to experience inundation by the tsunami and property damage. We dichotomized the distance variable and created a binary indicator (<1,000 m and ≥1,000 m) representing distance from the coastline, because this demarcated the extent of inundation by the tsunami and thus correlated with complete home loss (see Web Figure 3B). In turn, previous evidence has documented that complete home loss was a unique predictor of increased depressive symptoms (44).

We compared 4 approaches to estimate the associations between predisaster distance from the coast and depression: 1) crude univariate Poisson regression, 2) multivariable-adjusted Poisson regression, 3) Poisson regression weighted by IPTW and IPCW, and 4) SACE estimation. Poisson regression was used because depression was common in our sample and odds ratios from logistic regression may not approximate risk ratios (45). Approaches 2–4 adjusted for age, sex, depressive symptoms, self-rated health, education, household income, and marital status prior to disaster onset. Multiple imputation by chained equations (m = 20) was used to impute missing data on covariates, assuming the data were missing at random (42). Standard errors were obtained by bootstrapping with 1,000 replications.

Results.

  Table 4 shows the prevalence of depression and baseline sociodemographic characteristics in the analytical samples (n = 3,567 for 2013 and n = 2,781 for 2016) and among persons who were censored. The prevalence of depression was 28.8% for 2013 and 22.7% for 2016. Compared with the analytical sample, people who died between the disaster onset and the follow-up surveys (n = 342 for 2013 and n = 740 for 2016) and people who were alive but did not participate in the follow-up surveys (n = 948 for 2013 and n = 1,336 for 2016) were more likely to have experienced severe damage (i.e., living less than 1,000 m from the coast before the disaster). Moreover, the censored individuals were more likely to be depressed, less educated, not married, and older compared with members of the analytical sample who remained in the study, and they reported poorer self-rated health.

Table 4.

Baseline Sociodemographic Characteristics of the Analytical Sample and Depression Outcomes by Censoring Status in 2013 and 2016, Iwanuma, Japan, 2010–2016

			2013						2016
					Censored						Censored
Characteristic	All Disaster Survivors		Not Censored		Died		Withdrew		Not Censored		Died		Withdrew
	No.	%	No.	%	No.	%	No.	%	No.	%	No.	%	No.	%
Total	4,857	100.0	3,567	100.0	342	100.0	948	100.0	2,781	100.0	740	100.0	1,336	100.0
Depression status in follow-up wavesa,b
Mild or severe depression	N/A		1,027	28.8	N/A		N/A		630	22.7	N/A		N/A
No depression	N/A		2,072	58.1	N/A		N/A		1,430	51.4	N/A		N/A
Missing data	N/A		468	13.1	N/A		N/A		721	25.9	N/A		N/A
Distance from home address to the coast in 2010, m
≥1,000			3,424	96.0	305	89.2	867	91.5	2,685	96.5	682	92.2	1,229	92.0
<1,000			143	4.0	37	10.8	81	8.5	96	3.5	58	7.8	107	8.0
Sex
Male	2,105	43.3	1,552	43.5	173	50.6	380	40.1	1,208	43.4	367	49.6	530	39.7
Female	2,752	56.7	2,015	56.5	169	49.4	567	59.9	1,573	56.6	373	50.4	806	60.3
Depression in 2010a
Mild or severe depression	1,444	29.7	984	27.6	140	40.9	320	33.8	730	26.2	300	40.5	414	31.0
No depression	2,682	55.2	2,090	58.6	136	39.8	456	48.1	1,703	61.2	298	40.3	681	51.0
Missing data	731	15.1	493	13.8	66	19.3	172	18.1	348	12.5	142	19.2	241	18.0
Self-rated health in 2010
Very good	538	11.1	423	11.9	23	6.7	92	9.7	347	12.5	50	6.8	141	10.6
Good	3,140	64.6	2,420	67.8	157	45.9	563	59.4	1,940	69.8	380	51.4	820	61.4
Bad	862	17.7	537	15.1	107	31.3	218	23.0	374	13.4	207	28.0	281	21.0
Very bad	27	4.7	121	3.4	51	14.9	55	5.8	71	2.6	89	12.0	67	5.0
Missing data	90	1.9	66	1.9	4	1.2	20	2.1	49	1.8	14	1.9	27	2.0
Duration of education in 2010, years
<6	123	2.5	47	1.3	26	7.6	50	5.3	25	0.9	55	7.4	43	3.2
6–9	1,634	33.6	1,183	33.2	121	35.4	330	34.8	866	31.1	269	36.4	499	37.4
10–12	1,938	39.9	1,486	41.7	114	33.3	338	35.7	1,214	43.7	244	33.0	480	35.9
≥13	916	18.9	713	20.0	43	12.6	160	16.9	596	21.4	102	13.8	218	16.3
Other	52	1.1	31	0.9	12	3.5	9	0.9	17	0.6	19	2.6	16	1.2
Missing data	194	4.0	107	3.0	26	7.6	61	6.4	63	2.3	51	6.9	80	6.0
Marital status in 2010
Not married	1,483	30.5	984	27.6	149	43.6	350	36.9	700	25.2	306	41.4	477	35.7
Married	3,173	65.3	2,460	69.0	170	49.7	543	57.3	1,999	71.9	391	52.8	783	58.6
Missing data	201	4.1	123	3.4	23	6.7	55	5.8	82	2.9	43	5.8	76	5.7
Age in 2010, yearsc	74.7 (6.97)		73.6 (6.29)		81.7 (7.95)		76.1 (7.32)		72.8 (5.73)		80.6 (7.60)		75.4 (6.99)
Equivalized household income in 2010 (10,000 yen)c,d	228 (147)		230 (142)		230 (171)		220 (157)		232 (138)		223 (154)		223 (161)
Missing data	977	20.1	656	18.4	79	23.1	242	25.5	458	16.5	182	24.6	337	25.2

Abbreviation: N/A, not applicable.

^a Depression was defined as scoring 5 or more points on the Geriatric Depression Scale.

^b Information on the prevalence of depression in 2013 and 2016 was available only for persons who were not censored in each wave.

^c Values are expressed as mean (standard deviation).

^d Household income was divided by the square root of household size.

Compared with those who lived far (≥1,000 m) from the coast before the disaster, persons who lived closer to the coast (<1,000 m) showed a greater risk of depression 2.5 years postdisaster (2013; Figure 4A) across all alternative analytical approaches. However, the SACE estimate (risk ratio (RR) = 1.94, 95% CI: 1.41, 2.50) was larger than the risk ratios from other approaches adjusting for confounding and selection bias (RR = 1.69 (95% CI: 1.33, 2.07) for the multivariable-adjusted regression; RR = 1.66 (95% CI: 1.21, 2.08) for IPTW and IPCW). In the second follow-up survey, conducted 5.5 years after the disaster (2016; Figure 4B), we did not find strong evidence of an association between distance from the coast and depression risk in the models with multivariable adjustment (RR = 1.34, 95% CI: 0.96, 1.68) or with IPTW and IPCW (RR = 1.21, 95% CI: 0.70, 1.69). By contrast, the SACE approach continued to show an elevated risk of depression in 2016 for persons living less than 1,000 m from the coast before the disaster (RR = 2.00, 95% CI: 1.21, 2.87).

Figure 4.

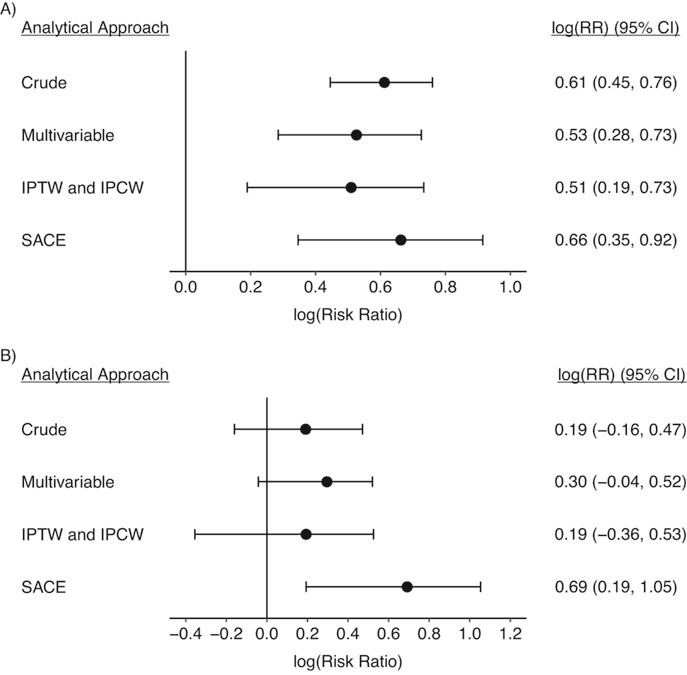
Risk ratio (RR) estimates for associations between pre-earthquake residential distance from the coast (<1,000 m vs. ≥1,000 m) and depression in 2013 (A) and 2016 (B) among survivors of the 2011 earthquake in Iwanuma, Japan, with or without selection bias adjustment. The crude model shows the univariate association between pre-earthquake distance from the coast and mild/severe depression in 2013 and 2016. Other models adjusted for potential confounding and selection bias by predisaster sociodemographic characteristics, including age, sex, Geriatric Depression Scale score, self-rated health, education, income, and marital status. In the survivor average causal effect (SACE) approach, results were further adjusted for selection bias due to unmeasured variable(s), which satisfies the conditions described in the paper by Tchetgen Tchetgen et al. (37). The 95% confidence intervals (CIs; bars) were obtained via bootstrapping with 1,000 replications. IPCW, inverse probability of censoring weighting; IPTW, inverse probability of treatment weighting.

Discussion.

We found that people who were censored before the follow-up surveys were more likely to have experienced severe disaster-related damage and to have characteristics that potentially put them at higher risk of depression. Moreover, the prevalence of depression was lower in the analytical sample for 2016—data collected with more attrition—than in the 2013 sample, which had less attrition, indicating that persons with preexisting depression may be selectively censored over time. The results from the descriptive analysis suggest that ignoring censoring would probably result in underestimation of the true causal effect.

The SACE estimate indicates that greater damage due to the tsunami is associated with elevated risk of depression even 5.5 years postdisaster in the subset of the population who would have remained in the study regardless of their exposure status. Such evidence for a long-term effect on depression was not observed when we estimated the effect of disaster exposure that would have been observed if no one had been censored, using multivariable adjustment or IPTW and IPCW. Since the estimate from multivariable adjustment would also have the same interpretation as the conditional SACE if there is no unmeasured common cause for censoring and outcome, the discrepancy in estimates is probably driven by the presence of additional selection bias that was adjusted for in the SACE estimation (37). Our findings underscore the importance of choosing the appropriate causal estimand and adjusting for selection bias in the presence of selective attrition over time.

ADDITIONAL CHALLENGES IN DISASTER EPIDEMIOLOGY

There are several other issues to consider that complicate causal inference in epidemiologic studies of the long-term health effects of disasters.

First, we have demonstrated how to parametrically estimate survival curves as well as trajectories of differences and ratios of cumulative incidence, or risk, as an alternative measure of causal effect. Although this approach for time-to-event outcomes has some advantages over estimating a series of average hazard ratios, both effect measures are averages of time-varying effects, and their interpretation is dependent on the length of follow-up. That is, both of the average effect measures become more likely to mask important time-varying effects as the duration of follow-up gets longer. Thus, the issue of time-varying effects merits attention even when methods other than Cox regression are used.

Second, some methods of “adjusting for” selection bias that we reviewed (IPCW and SACE) require information on the exposure and common causes for censoring and the outcome among both the censored and uncensored individuals. In the Iwanuma Study, we had a rich set of information on the predisaster characteristics of survivors to predict their probabilities of not being censored. If we only had information from persons who participated in the follow-up survey, such bias correction would not be feasible. Notably, even with the availability of predisaster information, had the relevant exposure been assessed in the follow-up survey (e.g., retrospective reporting of disaster-related traumatic experiences), it would not have been possible to calculate the probabilities of no censoring conditional on the exposure. This problem of misalignment of “time 0” (i.e., exposure assignment and measurement are separated in time) and the resulting selection bias is prevalent not only in disaster epidemiology but also in any observational studies of traumatic experiences, such as adverse childhood experiences (46). In such cases, where selection bias correction is infeasible, investigators could at least perform sensitivity analyses to simulate the range of causal effects by specifying plausible parameters representing the magnitude of potential selection bias (30, 47).

Third, there is no “silver bullet” causal estimand in the presence of censoring. The interpretation of the estimated causal effects after bias correction that we have discussed is either 1) the effect of an exposure that requires conceptualizing hypothetical interventions that eliminate all censoring (multivariable adjustment or IPCW) or 2) the effect of an exposure in a subset of the population that cannot be identified empirically (SACE). Neither of these estimands is particularly informative from a policy-making perspective (28). Methodologists have recently begun to develop alternative causal estimands in the presence of selection bias (27).

Lastly, studies assessing long-term impacts of disaster experiences are meaningful when the target of inference is disaster survivors. Thus, we excluded persons killed directly by the tsunami (n = 34; 0.7% of the baseline participants). Although our focus in this paper was on selective attrition due to postdisaster data collection, such exclusion may have induced selection bias.

In conclusion, we have illustrated 2 challenges for causal inference that are common in studies of long-term effects of disasters on the health of survivors, namely, analysis of time-to-event outcome data when the effect of an exposure varies over time and selection bias due to selective attrition. Using data from the 2011 Great East Japan Earthquake and Tsunami, we demonstrated that conventional analytical approaches which ignore these challenges underestimate the long-term health effects of the earthquake. Such bias may give rise to the misleading conclusion that disasters do not adversely affect the long-term health of survivors and misguided policies for supporting the well-being of survivors.