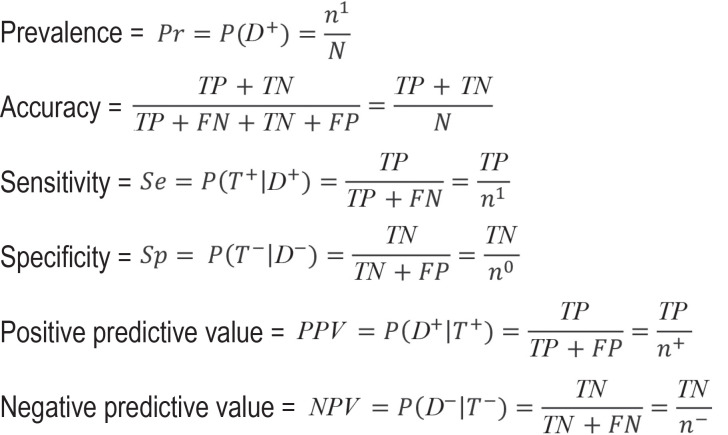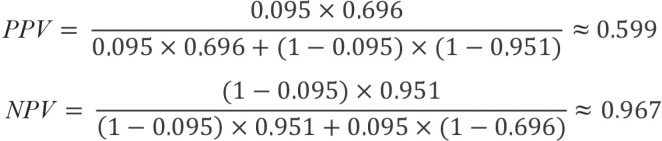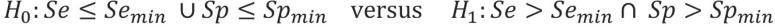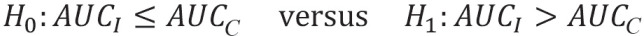Studies for the Evaluation of Diagnostic Tests

Abstract

Background

The accurate diagnosis of a disease is a prerequisite for its appropriate treatment. How well a medical test is able to correctly identify or rule out a target disease can be assessed by diagnostic accuracy studies.

Methods

The main statistical parameters that are derived from diagnostic accuracy studies, and their proper interpretation, will be presented here in the light of publications retrieved by a selective literature search, supplemented by the authors’ own experience. Aspects of study planning and the analysis of complex studies on diagnostic tests will also be discussed.

Results

In the usual case, the findings of a diagnostic accuracy study are presented in a 2 × 2 contingency table containing the number of true-positive, true-negative, false-positive, and true-positive test results. This information allows the calculation of various statistical parameters, of which the most important are the two pairs sensitivity/specificity and positive/negative predictive value. All of these parameters are quotients, with the number of true positive (resp. true negative) test results in the numerator; the denominator is, in the first pair, the total number of ill (resp. healthy) patients, and in the second pair, the total number of patients with a positive (resp. negative) test. The predictive values are the parameters of greatest interest to physicians and patients, but their main disadvantage is that they can easily be misinterpreted. We will also present the receiver operating characteristic (ROC) curve and the area under the curve (AUC) as additional important measures for the assessment of diagnostic tests. Further topics are discussed in the supplementary materials.

Conclusion

The statistical parameters used to assess diagnostic tests are primarily based on 2 × 2 contingency tables. These parameters must be interpreted with care in order to draw correct conclusions for use in medical practice.

cme plus

This article has been certified by the North Rhine Academy for Continuing Medical Education. Participation in the CME certification program is possible only over the internet: cme.aerzteblatt.de. The deadline for submission is 22 August 2022.

The diagnosis of a disease is the first step on the road to its treatment. The evaluation of the underlying diagnostic procedures is performed in what are referred to as diagnostic studies, which determine how well a diagnostic instrument, for example, a laboratory test, detects the presence of a disease.

The correct determination of the results of diagnostic tests is of central importance, since a positive result impacts not only the affected person, but—as in the SARS-CoV-2 pandemic—potentially also the social environment (1). In this context, the probability of the true presence of SARS-CoV-2 infection in patients that have tested positive is of particular importance—a probability that is also influenced by the increasing number of tests carried out in the population and by current infection rates (1, 2). Against this backdrop, it is crucial that physicians are able to correctly assess diagnostic parameters. However, misinterpretation of measured values of this kind is not new, irrespective of the test or disease, and the situation has not improved significantly over the years (3– 6).

Therefore, the aim of this paper is to present the various measures of accuracy of a diagnostic test and to describe the relationship between the measures in order that, after reading the article, the reader will be able to correctly interpret an individual test result.

Measures of diagnostic accuracy

In a first step, we present the diagnostic 2 × 2 contingency table and prevalence, followed by the most important parameters, sensitivity and specificity, as well as predictive values and accuracy. The equations of the empirical estimators are given in the Box, while in the text they are directly applied to an example. For diagnostic tests that yield a metric value or score rather than a binary result, we present the receiver operating characteristic (ROC) curve and the corresponding area under the curve (AUC). As a general rule, confidence intervals (CI) should also be given for all diagnostic parameters. For sensitivity, specificity, predictive values, and accuracy, we recommend logit confidence intervals, since these yield plausible results, most notably even when case numbers are small, and guarantee that the limits do not lie outside the [0;1] interval. For details, the reader is referred to the relevant literature (7, 8).

BOX.

Figure 10.

Abbreviations used:

n¹: Number of individuals with disease

n⁰: Number of individuals without disease

N: Total number of study participants

TP: Number of true-positive test results

TN: Number of true-negative test results

FN: Number of false-negative test results

FP: Number of false-positive test results

T ⁺: Positive result for the index test

T ^–: Negative result for the index test

D ⁺: True disease status “with disease”

D^–: True disease status “without disease”

Note: the empirical estimators are given in each case

Diagnostic 2 × 2 contingency table

When the test result is binary (positive versus negative), the results of a diagnostic study can be mapped in diagnostic 2 × 2 contingency tables (table 1). Since a diagnostic test generally yields a metric value or score as its result, a cut-off value needs to be defined in order to maintain the binary coding. The diagnostic test to be evaluated will be referred to hereafter as the index test. This contrasts with the so-called gold or reference standard, which defines the “true” disease state. These two terms are often used synonymously. However, since “gold standard” is often associated with an assumption of a perfect definition of the “true” disease status, a status that is not necessarily present in practice, we have chosen to use the term reference standard below. The most reliable method to determine true disease status should be chosen as the reference standard. This is often not feasible in routine practice, for example due to the fact that it is too invasive, expensive, or time-consuming, or since it can only be used after death. Based on the results of the index test (T⁺ [positive] versus T^– [negative]) and the reference standard (D¹ [with disease] versus D⁰ [without disease]), classification is made as true-positive (TP), true-negative (TN), false-positive (FP), or false-negative (FN). The respective row and column sums are given as n¹ and n⁰ for the number of people with the disease and those without the disease, respectively, and by n⁺ and n^– for the number of people that tested positive and negative, respectively. N relates to the total number of study participants.

Table 1. Diagnostic 2 x 2 contingency table as the result of a diagnostic study.

		Gold standard
		With disease D1	Without disease D0	Total
Index test T	Positive T+	TP	FP	n+
	Negative T–	FN	TN	n–
	Total	n1	n0	N

TP: true positive, FP: false positive, FN: false negative, TN: true negative

Example study

For illustrative purposes, this article uses the study conducted by Papoz et al., who evaluated HbA_1c as a screening marker for the diagnosis of type 2 diabetes (9). The oral glucose tolerance test (OGTT) was used as the corresponding reference standard procedure. An HbA_1c of 6.5 (among other parameters), which is currently used to diagnose type 2 diabetes, was used as the diagnostic cut-off value for the index test (10). This means that study participants in whom an HbA_1c of 6.5 or higher was measured were classified as positive. Table 2 shows the corresponding diagnostic 2 × 2 contingency table.

Table 2. Results of the study by Papoz et al. (9) on the HbA1c cut-off value of 6.5.

		Oral glucose tolerance test (OGTT)
		Type-2 diabetes D1	No type-2 diabetes D0	Total
Hemoglobin A1c(HbA 1c) T	Positive T+	78	24	102
	Negative T–	34	465	499
	Total	112	489	601

Prevalence

Prevalence plays a crucial role in the correct interpretation of test results. It denotes the proportion of individuals with disease in the studied collective and is calculated as the number of individuals with disease divided by the total number of study participants.

If we consider the study by Papoz et al. (9), we obtain the following estimated prevalence:

Figure

Figure 1.

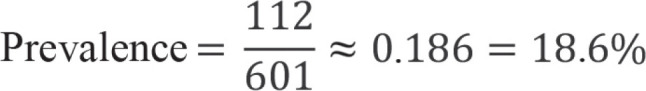
The 95% logit confidence interval (CI) is [15.7%; 21.9%].

Accuracy

Accuracy is calculated from the proportion of correct results (TN and TP) out of all test results:

Figure

Figure 2.

The 95% logit CI is [87.7%; 92.4%].

From this it follows that 90.3% of test results were correct. However, it is not possible to assess the proportion of incorrect results among individuals who did or did not have disease, which is why this parameter is generally not recommended.

Sensitivity and specificity

Sensitivity and specificity are the most important parameters in the development of tests. These two measures indicate the proportion of individuals with or without disease in whom a correct diagnosis was made. Sensitivity is calculated as the number of true-positive test results divided by the number of individuals with disease, while specificity is calculated as the number of true-negative test results divided by the number of persons without disease.

The following values are derived for the sensitivity and specificity of the example:

Figure

Figure 3.

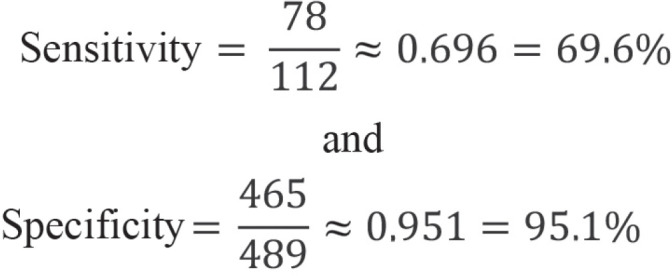
Thus, there is a 69.6% probability that the HbA_1c test will be positive if the investigated subject has type 2 diabetes (sensitivity). Conversely, the probability that the HbA_1c test will be negative is 95.1% if a study participant does not have type 2 diabetes (specificity). The 95% logit CIs for sensitivity and specificity are [60.5%; 77.4%] and [92.8%; 96.7%], respectively.

Predictive values

While sensitivity and specificity are the recommended parameters for diagnostic test development (11), they are not informative for the patient and physician in routine practice. The true disease status is not known outside the study since the reference standard is not determined. The interesting information here is the probability that the disease is present in the case of a positive test result and absent in the case of a negative test result. These conclusions can be drawn with the help of the predictive values. These are calculated as the number of true-positive test results divided by the number of positive test results (positive predictive value, PPV) and as the number of true-negative test results divided by the number of negative test results (negative predictive value, NPV). Therefore, these values are conditional probabilities. The PPV indicates the probability of the disease being present in the case of a positive test result, whereas the NPV indicates the probability of the disease not being present in the case of a negative test result.

The following values are obtained for the example:

Figure

Figure.

ROC curve in the study by Papoz et al. (9). The underlined value is the cut-off value with the highest Youden index.

Thus, in the case of a positive HbA_1c test result, the risk of suffering from type 2 diabetes is 76.5%. On the other hand, there is a 93.2% probability that type 2 diabetes is not present if the HbA_1c test result is negative. The corresponding 95% logit CIs are [67.3%; 83.7%] for the PPV and [90.6%; 95.1%] for the NPV. However, these results should be viewed with caution since predictive values, unlike sensitivity and specificity, depend on prevalence.

Receiver operating characteristic curve

Diagnostic studies often evaluate not only one cut-off value to classify test positives and negatives, but rather several in order to determine an optimal diagnostic threshold for clinical practice. This is associated with different pairs of sensitivities and specificities, which belong to the respective threshold under evaluation. Papoz et al. (9) investigated a total of five different HbA_1c cut-off values between 5.0 and 7.0. The corresponding sensitivity and specificity was determined for each of these values (table 3).

Table 3. Cut-off values evaluated by Papoz et al. (9)*.

HbA1c cut-off value	Sensitivity	Specificity	Youden index
5.0	111/112 = 99.1%	83/489 = 17.0%	0.161
5.5	110/112 = 98.2%	225/489 = 46.0%	0.442
6.0	100/112 = 89.3%	381/489 = 77.9%	0.672
6.5	78/112 = 69.6%	465/489 = 95.1%	0.647
7.0	60/112 = 53.7%	479/489 = 98.0%	0.517

* with corresponding sensitivities, specificities, and Youden index; HbA1c: hemoglobin A1c

The ROC curve was used to better depict the results of the study. Thus, for each cut-off value investigated, sensitivity is plotted on the y-axis and 1-specificity on the x-axis of a graph (figure).

One criterion to select a cut-off value is the Youden index. This is calculated as the sum of sensitivity and specificity in percentage points minus 100. The cut-off value with the highest Youden index is often considered to be optimal. In the example study, this would be 6.0 (underlined value on the Figure with a Youden index of 0.672, Table 3).

In its classical form, the Youden index assumes an equal weighting of sensitivity and specificity and, thus, also an equal weighting of false-positive and false-negative test results. However, for a screening test, sensitivity in particular should be high, whereas for a confirmatory test, specificity should be high. In order to determine optimal cut-off values for these types of diagnostic tests, it is recommended that a minimum required sensitivity and specificity be determined prior to starting the study. Alternatively, a weighted Youden index can be used, whereby sensitivity or specificity are given a higher weight.

In particular, sensitivity and specificity depend on the selected cut-off value (table 3). The higher the HbA_1c cut-off value, the greater the specificity, but the lower the sensitivity. This means, conversely, that any sensitivity can be achieved if a correspondingly low specificity is accepted and vice versa. For this reason, the European and US guidelines on diagnostic agents (European Medicines Agency, EMA [11], Food and Drug Administration, FDA [12]) recommend using sensitivity and specificity as primary endpoints.

Area under the curve

The area under the curve, the AUC, is suited to comparing the overall accuracy of one or more diagnostic tests. It indicates the probability that a person with disease has a higher test value than a person without disease, assuming high values indicate the presence of the disease.

For the example study, we obtain an AUC of 91.4%, meaning that there is a 91.4% probability that individuals with type 2 diabetes will have a higher HbA_1c than individuals without type 2 diabetes. The higher the AUC, the better the new diagnostic test discriminates between individuals with and individuals without disease. The maximum value for the AUC is 100%. If the AUC is 50%, the test is useless and comparable to the toss of a coin. AUC values below 50% mean that low rather than high values suggest that the disease is present.

Dependence of predictive values on prevalence

Predictive values, in contrast to sensitivity and specificity, depend on prevalence. This becomes apparent if we artificially modify the study results obtained by Papoz et al. (9), as in Table 4. These results might be obtained if the test is not used as a screening test in an at-risk population, but rather as a confirmatory test in individuals with suspected type 2 diabetes. To do this, we multiplied the number of individuals with type 2 diabetes (TP, FN, and n¹, respectively) by 10, but left the number of individuals without type 2 diabetes unchanged. This yields a prevalence of 69.9% and the following values:

Table 4. Artificially modified result of the study by Papoz et al. (9) on the HbA1c cut-off value of 6.5.

		Oral glucose tolerance test (OGTT)
		Type-2 diabetes (D1)	No type-2 diabetes (D0)	Total
Hemoglobin A1c(HbA 1c) T	Positive T+	780	24	804
	Negative T–	340	465	805
	Total	1120	489	1609

Figure

Figure 5.

Even after increasing the number of individuals with the disease, the sensitivity remains unchanged. However, the positive predictive value increases from 76.5% [67.3%; 83.7%] to 97.9% [96.6%; 98.7%], while the negative predictive value drops from 93.2% [90.6%; 95.1%] to 57.8% [54.4%; 61.2%]. The generally valid result becomes evident: sensitivity and specificity are independent of prevalence, but the predictive values are not. Therefore, when interpreting predictive values, the prevalence of the disease in the target population for which a new diagnostic test is intended to be used must be taken into consideration. If the study population is a representative sample of the target population and the study participants are appropriately selected, this is assured and the predictive values are interpretable. If study prevalence and target population prevalence do not match, predictive values can be determined by using Bayes’ theorem:

Figure

Figure 6.

Here, Se and Sp denote the sensitivity and specificity of the diagnostic test under evaluation, while Pr denotes the prevalence of the disease in the target population. Assuming a prevalence of type 2 diabetes of 18.6%, as found in the study by Papoz et al. (9), we obtain the following results:

Figure

Figure 7.

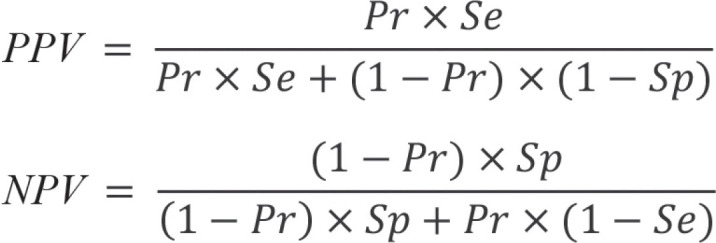
These are in agreement with the results determined on the basis of the 2 x 2 contigency table.

In order to the determine the predictive value for a different target population, the prevalence can be adjusted accordingly. If we assume that the predictive values of the HbA_1c test for screening type 2 diabetes are to be estimated in the entire German adult population, we would use the prevalence of type 2 diabetes in Germany, which was approximately 9.5% in 2015 (13):

Figure

Figure 8.

This means that any adult person in Germany with a positive HbA_1c test would have a 59.9% probability of developing type 2 diabetes, and if the test result was negative, a 96.9% probability of not developing type 2 diabetes. The positive predictive value in particular needs to be viewed critically, since it implies that of 100 individuals that test positive, only around 60 actually have diabetes. As such, one would expect approximately 40 false-positive test results, which may lead to unnecessary further diagnostic tests or treatment. One should also question in a critical manner whether the extrapolation of sensitivity and specificity from the study by Papoz et al. (9) is plausible. The assumption here is that sensitivity and specificity are the same in all scenarios. However, it is conceivable that a test could, for example, differentiate individuals with and without severe disease better than those with suspected disease and mild disease. Although sensitivity and specificity do not depend on prevalence, they do depend on disease pattern. It should additionally be noted that prevalence is also determined on the basis of studies, and thus associated with uncertainty. This needs to be taken into consideration when interpreting predictive values, and underscores the importance of confidence intervals.

Discussion

Diagnostic studies are the basis for the evaluation of diagnostic tests. As such, they form the bedrock of the resulting treatment or preventive measures. The correct interpretation of results obtained in these types of studies is vital in order to be able to evaluate the benefit of a new diagnostic procedure.

We have presented the most important parameters for the interpretation of diagnostic studies. These include sensitivity and specificity, which are primarily of interest from a study perspective, since they describe the accuracy of the diagnostic test under evaluation if the “true” disease status is known and are independent of prevalence. Predictive values, on the other hand, are of particular importance from a practical and clinical perspective. These indicate the probability that a disease is present or absent in the case of a positive or negative test result. As such, they reflect the situation in everyday clinical practice, but are dependent on disease prevalence, which needs to be taken into account when interpreting the values. Even a positive result using a test with extremely high sensitivity and specificity is highly likely to be a false-positive result if prevalence is very low

These parameters form the basis for the planning and analysis of more complex diagnostic studies (7, 14). An understanding of the measures used to evaluate a new diagnostic procedure and the critical interpretation of these measures are essential for the procedure’s practical evaluation and application.

The additional diagnostic parameters (diagnostic likelihood and odds ratios), as well as the further aspects of confirmatory diagnostic accuracy studies (for example, hypotheses and sample size determination), sources of bias, and study quality presented in the eMethods Section enable careful planning and a more differentiated evaluation of diagnostic studies.

Supplementary Material

eMethods Section

Diagnostic likelihood ratios

Diagnostic likelihood ratios (DLR) are parameters that combine sensitivity and specificity. They indicate how much more likely a positive test result (positive DLR) or a negative test result (negative DLR) is in a person with disease compared to a person without disease. DLRs can take values between 0 and infinity. If a positive or negative DLR takes the value 1, a positive or negative test result is just as likely in a person with disease as in a person without disease. In this case, the test would be of no use. The larger the positive DLR and the smaller the negative DLR, the better the test. In contrast to predictive values, diagnostic likelihood ratios do not depend on prevalence. One disadvantage, however, is that they cannot be calculated if sensitivity or specificity is 100% or 0%. For the example study, this yields:

Sample size determination

Also in a confirmatory diagnostic accuracy study, sample size determination should be performed in advance in order to avoid including too few or an unnecessarily high number of subjects in the study. Programs and formulas for sample size determination can be used to compare one rate with a fixed value or to compare two rates, in each case separately for sensitivity and specificity. However, it is important here to ensure that sufficient numbers of individuals with and individuals without disease are included and, at the same time, that the study population is representative of the target population. As a result, sample size determination is methodologically challenging, and the reader is referred to the literature for details (14, e2).

Statistical tests and confidence intervals

For the verification of hypotheses, statistical tests or confidence intervals can be used, whereby confidence intervals have the advantage of making it possible to assess the variability of the result in addition to assessing its significance. The α error does not need to be adjusted here. Thus, either the p-values are compared with α in each case or the two-sided (1-α) confidence intervals (when α = 5%, then 95%) are calculated.

When comparing the index test to the reference standard, the confidence interval is governed by whether the prespecified minimum value (AUC or sensitivity and specificity) is included in the confidence interval. If this is not the case, the null hypothesis cannot be rejected. If the index test is being compared with a comparator, the difference between groups with the corresponding confidence interval is calculated for the parameters (AUC, sensitivity, specificity) and the null hypothesis retained if the null (or non-inferiority margin) is included in the interval.

All tests and confidence intervals can be used to compare a rate to a fixed value or to compare two rates. However, when comparing a rate to a fixed value, one needs to bear in mind that rates (sensitivities and specificities) close to 1 are often obtained and, as such, some confidence intervals are more suitable than others. For extensive discussions and comparisons of the various intervals and tests, the reader is referred to Newcombe et al. (e3, e4).

In the case of a confirmatory diagnostic study, it is important to select a study design that is suited to the question being asked, as well as appropriate outcome measures. Furthermore, a clear definition of hypotheses and meticulous prior sample size determination are imperative. Statistical tests or confidence intervals can be used to analyze the data, whereby measures of accuracy should always be reported together with their corresponding confidence intervals.

Sources of bias and study quality

As in an intervention study, there are numerous sources of bias in a diagnostic accuracy study that can adversely impact the study‘s validity. Some sources of bias are the same as those in intervention studies, while others are specific to diagnostic accuracy studies. A list and description of the most important sources of bias are provided in the eTable, based on Zhou et al. (14, Table 3, 4).

The STARD statement is a suitable instrument to assess the quality of a diagnostic accuracy study (e5). It provides a checklist of items relating to the various sections of the article, allowing one to gain a good impression of study quality.

Outlook

The content provided so far can be used to plan, analyze, interpret, and assess the quality of diagnostic accuracy studies. However, since diagnostic studies are often more extensive in practice, a description of the associated methods would exceed the scope of this article. Instead, we will highlight potential special features, discuss these briefly, and refer the reader to the relevant literature.

Several investigators and factorial designs

The guidelines (11, 12) recommend involving at least two or, even better, more examiners for the evaluation of a subjective diagnostic test, for example, the interpretation of an X-ray. The investigators’ results are often aggregated prior to the analysis, for example, by means of a consensus or majority decision. However, this is strongly advised against since this approach can lead to biased results. Instead, the investigator should be included in the analysis as a fixed or random factor, depending on the selection of the investigator. For methods of factorial design analysis, the reader is referred to the further literature (7, 14, e6).

Multiple lesions and cluster data

For some diseases, there is no global diagnosis—instead, one can diagnose individual lesions, such as both eyes, different lobes of the liver, or multiple metastases. In such cases, the mistake is often made that lesions are regarded as independent, thereby leading to an incorrect assessment of variance in observations. An appropriate analysis would be possible using generalized linear (mixed) models, details of which can be found in the works by Pepe (7) and Rabe-Hesketh et al. (e6).

Study phases and randomized test-treatment studies

Much like the development of therapeutic agents, the development of diagnostic tests can also be subdivided into phases. After early studies aimed at technical evaluation come studies—often artificial case-control studies—to make an initial assessment of diagnostic accuracy. These are followed by confirmatory diagnostic accuracy studies in a representative setting. Since a correct diagnosis alone is of no benefit to a patient, the last step should be to compare, in a randomized approach, test strategies in what are referred to as test-treatment studies. Example studies include Oosterhuis et al. (e7), van den Berk et al. (e8), and Aviv (e9).

Here, for example, the index test is used in one group and the comparator in the other. Subsequently, all further decisions are made depending on the test result, with regard to, for example, further diagnostic investigations or the initiation, continuation, or discontinuation of treatment. Finally, the groups are compared in terms of a patient-relevant endpoint, such as mortality. For further information on the classification of randomized test-treatment trials into study phases, the reader is referred to the literature (7, 11, 14, e10– e12).

Adaptive designs

Although adaptive designs have long been established and frequently used in intervention studies, this approach has barely found its way into diagnostic studies. Under certain conditions, adaptive designs enable adjustments to be made during the course of the study, for example, early termination of the study or a change in the number of cases, without compromising the integrity of the study. Individual methodological articles, especially on group sequential procedures as a subgroup of adaptive designs, can be found, but virtually no examples of their application. For an overview of this topic, as well as concrete proposals for designs, the reader is referred to further studies (e2, e13– e16).

Meta-analyses

Meta-analyses of diagnostic studies differ from meta-analyses of intervention studies in that, according to the guideline recommendation, there are two primary endpoints (sensitivity and specificity) and, therefore, bivariate methods are mandatory. Thereby the dependence between sensitivity and specificity, induced by the selected cut-off value, must be taken into account.. The standard approaches can be found in the articles by Chu and Cole (e17), as well as Rutter and Gatsonis (e18). Information on more complicated analyses, for instance, when different or several cut-off values are used in individual studies, can be found, for example, in Biondi-Zoccai’s book dealing with all facets of meta-analyses of diagnostic accuracy studies (e19).

A number of aspects lead to the standard procedures no longer being adequate. In such cases, we recommend, in addition to the cited literature, involving a methodologist (for example, a statistician, biometrician, or epidemiologist).

Figure 9.

Questions on the article in issue 33/2021:

Studies for the Evaluation of Diagnostic Tests

The submission deadline is 22 August 2022. Only one answer is possible per question.

Please select the answer that is most appropriate.

Question 1

What should serve as the reference standard to construct a diagnostic 2 x 2 table?

1. The fastest diagnostic method

2. The most widely used diagnostic method

3. The diagnostic method in longest use

4. The most cost-effective diagnostic method

5. The most reliable diagnostic method

Question 2

How is the prevalence of a disease calculated?

1. The total number of study participants in the collective divided by the number of individuals with the disease

2. The number of positive test results divided by the total number of all test results

3. The number of true positive test results divided by the number of individuals that actually have the disease

4. The number of individuals with the disease divided by the total number of study participants in the collective

5. The total number of study participants in the collective divided by the number of positive test results

Question 3

How is the specificity of a diagnostic test calculated?

1. Difference between true-negative test results the and number of individuals without disease

2. Ratio of true-negative test results to the number of individuals without disease

3. Ratio of positive test results to the number of individuals with disease

4. Ratio of all negative test results to the number of individuals without disease

5. Difference between all positive test results and the number of individuals with disease

Question 4

Which area under the curve (AUC) of the receiver operating characteristic curve is considered to make the investigated diagnostic test unusable?

1. 50%

2. 65%

3. 75%

4. 90%

5. 100%

Question 5

Of a total of 2000 HbA_1c tests performed, 1200 are positive. However, 200 of these 1200 prove to be false-positive. What is the positive predictive value in this (hypothetical) case?

1. 60%

2. 62%

3. 70%

4. 83%

5. 86%

Question 6

How is the Youden index calculated?

1. The sum of percentage points for sensitivity and specificity minus 100

2. The ratio of percentage points for sensitivity and specificity minus 100

3. The product of percentage points for sensitivity and specificity divided by 100

4. The sum of percentage points for sensitivity and specificity divided by 100

5. The sum of percentage points for sensitivity and specificity multiplied by 100

Question 7

Which value depends on, among other factors, the prevalence of a disease?

1. Sensitivity

2. Specificity

3. The Youden index

4. The maximum Youden index

5. Positive predictive value

Question 8

What does the negative predictive value refer to?

1. The probability that a disease is not present when a test result is positive

2. The probability that a disease is present when a test result is negative

3. The probability that a disease is not present when a test result is negative

4. The probability of obtaining a positive test result when the disease is not present

5. The probability of obtaining a negative test result when the disease is present

Question 9

Which Youden index is often used to determine the optimal cut-off value of a diagnostic test?

1. The Youden index at which a specificity of 70% is reached

2. A Youden index of 0.5

3. The highest Youden index reached in the study

4. A Youden index of 0.7

5. The lowest Youden index reached in the study

Question 10

In the case of a positive screening test, which characteristic would you attach particular importance to when selecting a suitable confirmatory test?

1. Its sensitivity should be as high as possible

2. It should have similar specificity to the screening test

3. It should use the same sample material as the screening test

4. Its specificity should be as high as possible

5. It should enable faster evaluation than the screening test

Figure 11.

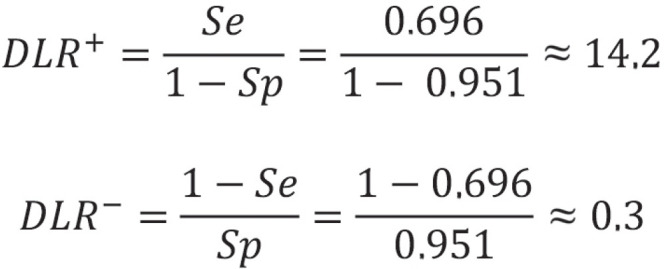
Thus, the likelihood for a positive test result in an individual with disease is 14.2 times higher than in an individual without disease. Conversely, a negative test result is only 0.3 times more likely for an individual with disease than for an individual without disease. The corresponding approximate 95% Wald confidence intervals (CI) comprise [9.43; 21.38] for DLR⁺ and [0.23; 2.46] for DLR^-.

Diagnostic odds ratios

Like diagnostic likelihood ratios (DLR), the diagnostic odds ratio (DOR) is another parameter that combines sensitivity and specificity. The DOR is the ratio of odds (chance) of a positive test result in an individual with disease to the odds of a positive test result in an individual without disease. As with the DLR, the range of possible values spans from 0 to infinity, and, likewise, a DOR of 1 is uninformative. The higher the DOR, the better the diagnostic test. Although the DOR does not depend on prevalence, it does have—like the DLR—a disadvantage in that it cannot be calculated at a sensitivity or specificity of 100% or 0%. The general equation for DOR is:

Figure 12.

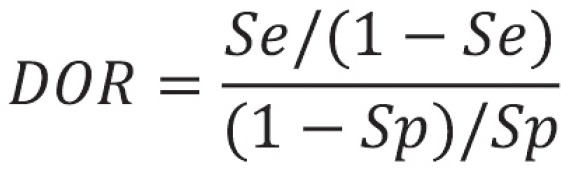
For the example study, the following value is obtained:

Figure 13.

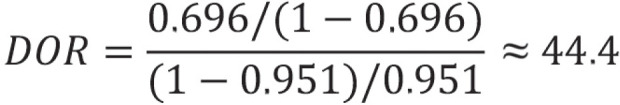
This result means that, with the test, the chance of a positive result in individuals with disease is 44.4 times greater than in individuals without disease.

Confirmatory diagnostic accuracy studies

Medicinal Products Act

Up until now, diagnostic tests that are used outside the body, known as in vitro tests, have not been approved, as is usual for drugs. These tests fall under the Medicinal Products Act (Medizinproduktegesetz, MPG; in the European context, medical device regulatory, MDR). To date, it was sufficient to demonstrate the safety of a product. However, with the amendment to the MDR, and thus also to the MPG, that comes into force in 2021, the benefit of the product may also need to be demonstrated depending on the risk category it is assigned. As such, confirmatory evidence of sufficient diagnostic accuracy will gain in importance.

Study design

In order to be able to assess the diagnostic accuracy of a test, both the index test and the reference standard need to be performed on the same person. If the test is to be compared with one or more tests, the recommendation is to perform all tests on all subjects, if practicable and ethically justifiable. Where this is not the case, the person receiving the index test and reference standard and the person receiving the comparison and reference standard should be randomized.

Endpoints

If no cut-off value has been defined as yet or the overall diagnostic accuracy is of interest, the area under the curve (AUC) should be selected as the primary outcome measure. If, on the other hand, a cut-off value has already been determined, the approval authorities recommend using sensitivity and specificity as co-primary endpoints (11, 12). “Co-primary” means that for a positive study, the null hypotheses regarding the two endpoints need to be rejected. As soon as one of the two hypotheses cannot be rejected, the study result is negative. As a result of this intersection–union test, no adjustment of the type 1 error (α) for multiplicity is needed. As such, the full α (in general fixed at 5% two-sided) may be used for the two individual hypotheses.

Due to the importance of predictive values on the one hand and their dependence on prevalence on the other, the recommendation is to consider them as the most important secondary endpoints.

Hypotheses

The hypotheses differ depending on whether the index test is compared with the reference standard or with a comparator test—using the gold standard as a reference. In the former case, the objective is to demonstrate a previously defined minimum accuracy (e1), while in the latter, the objective is to show superiority over the comparator, measured in each case by AUC or sensitivity and specificity. When comparing with a comparator in terms of sensitivity and specificity, it may also be a legitimate objective to show superiority in one endpoint and non-superiority in the other. Thus, if a more sensitive diabetes test is developed, one may accept the trade-off that it has comparable or slightly lower specificity.

For the comparison of the index test with the reference standard, the hypotheses for the AUC are accordingly:

Figure 14.

For sensitivity and specificity, they are defined as follows in this context:

Figure 15.

U means that at least one of the two null hypotheses holds, while ∩ means that both alternative hypotheses must hold.

For the comparison of the index test (I) with another test (C for comparison test), the hypotheses for the AUC are:

Figure 16.

For sensitivity and specificity, they are given here only for superiority, in the interests of simplification:

Figure 17.

eTable. Table listing and describing the various potential sources of bias, modified from (14).

Bias	Description
Selection bias	The study population is not representative of the target population.
Spectrum bias	The study population does not reflect the entire spectrum of patient and disease characteristics.
Imperfect gold standard bias	The reference or gold standard is not 100% correct.
Work-up bias	The results of the index test affect the further procedure required to arrive at the definitive diagnosis.
Incorporation bias	The results of the index test are incorporated (partially or fully) in the reference standard.
Verification bias	The reference standard is performed primarily in individuals with a positive or a negative test result.
Differential verification bias	A different reference standard is used for individuals with positive and negative test results.
Disease progression bias	The disease progresses between the time of the index test and the time of the reference standard.
Treatment paradox bias	Treatment that alters the disease status is carried out between the time of the index test and the time of the reference standard.
Test review bias	The index test is performed without adequate blinding to the result of the reference standard or comparator.
Diagnostic review bias	The reference standard is performed without adequate blinding to the result of the index test and/or comparator.
Reading order bias	When interpreting a test result (index or comparator), the investigator is influenced by their recollection of the other respective test result.
Context bias	The study prevalence differs significantly from the population prevalence, causing the investigator to arrive at a biased estimate.
Localization bias	A lesion is incorrectly classified as true-positive despite the fact that the investigator incorrectly localized the lesion.