Bayesian Multivariate Mixed-Effects Location Scale Modeling of Longitudinal Relations Among Affective Traits, States, and Physical Activity

Abstract

Intensive longitudinal studies and experience sampling methods are becoming more common in psychology. While they provide a unique opportunity to ask novel questions about within-person processes relating to personality, there is a lack of methods specifically built to characterize the interplay between traits and states. We thus introduce a Bayesian multivariate mixed-effects location scale model (M-MELSM). The formulation can simultaneously model both personality traits (the location) and states (the scale) for multivariate data common to personality research. Variables can be included to predict either (or both) the traits and states, in addition to estimating random effects therein. This provides correlations between location and scale random effects, both across and within each outcome, which allows for characterizing relations between any number of personality traits and the corresponding states. We take a fully Bayesian approach, not only to make estimation possible, but also because it provides the necessary information for use in psychological applications such as hypothesis testing. To illustrate the model we use data from 194 individuals that provided daily ratings of negative and positive affect, as well as their physical activity in the form of step counts over 100 consecutive days. We describe the fitted model, where we emphasize, with visualization, the richness of information provided by the M-MELSM. We demonstrate Bayesian hypothesis testing for the correlations between the random effects. We conclude by discussing limitations of the MELSM in general and extensions to the M-MELSM specifically for personality research.

The rise of intensive longitudinal studies and experience sampling methods provide a unique opportunity to ask novel questions about within-person processes relating to personality (Fleeson & Law, 2015; Vazire & Sherman, 2017). While personality research has traditionally focused on identifying trait like behavior, for example the degree to which an individual is agreeable, more recent work has broadened its focus to include states (Fleeson, 2001; P. Martin et al., 2002). That is, whether, as well as how much, individuals fluctuate in their thoughts, feelings, and behavior over time.

Research on within-person dynamics and short-term fluctuations in behavior has a long tradition in some areas of psychology, such as in the field of cognition (Salthouse, 2007), mood (Hepburn & Eysenck, 1989), and stress reactivity (Sliwinski et al., 2009). Note that the theoretical foundation behind these ideas extend to the realm of personality research. On the macro-time scale it is customary to assume stable personality traits, for example as shown empirically in Costa and McCrae (1988) and Cobb-Clark and Schurer (2012), which relates to an individual’s average for some personality trait. On the other hand, on the micro-time scale (e.g., day to day), we might observe substantial variability in these same personality traits (as reported in Fleeson, 2001). The focus here is on within-person variability, that is states, in relation to between-person differences in personality traits. More specifically, it is possible that time-varying predictors moderate the relation between person level traits and fluctuations therein. Of note, the focus is not only on explaining average, between person differences, but also on explaining the observed within-person variance in the respective trait over time or situations.

This conceptualization of personality builds upon a central idea that within-person, or intraindividual variability (IIV), is not regarded as reflecting mere measurement error but conveys systematic information (Cattell et al., 1947; Fiske & Rice, 1955; Horn, 1972; Ram & Gerstorf, 2009; Woodrow, 1932). IIV is commonly indexed by the individual-level standard deviation (iSD), wherein an important assumption is that it reflects other aspects of behavioral outcomes compared to individual levels or rates of change, such as, for example, individual means (iM). Fluctuations can also occur across situations and are often interpreted as carrying information about short-term adaptive processes, regulative mechanisms and the system’s vulnerability (Nesselroade, 1991; Röcke & Brose, 2013). Indeed, outside of personality research, IIV has been shown to predict cognitive decline, changes in general health and other important life outcomes. For example, IIV has been proposed as a potential marker for Alzheimer’s disease (Kälin et al., 2014) and even as a predictor of death (MacDonald et al., 2008).

The most common statistical approaches to extracting IIV rely on estimating the individual means (iMs) and individual standard deviations (iSDs) using a two-stage approach: In the first stage, the iMs are computed, for example, in a mixed effects model or from individual regressions, and the residuals are recorded. In the second stage, individual SDs are obtained from the residuals which are used in a separate model as either predictor or as the outcome (MacDonald et al., 2008). In the context of personality research this approach was recommended in Eid and Diener (1999) and was recently applied in Hardy and Segerstrom (2017) to characterize the relation between IIV in affect and health. However, this approach suffers from several drawbacks. It can result in unreliable estimates that are particularly sensitive to the number of measurement occasions (Estabrook et al., 2012; Wang & Grimm, 2012) and the underlying assumption of normality (Mestdagh et al., 2018; Wang et al., 2012). Moreover, separating iMs from iSDs assumes independence of means and variances, which seems unlikely in most applications, and it results in biased variance estimates (Leckie et al., 2014; Rast & Ferrer, 2018).

One aim of the present work is to introduce a Bayesian mixed-effects location scale (MELSM; Hedeker et al., 2012; Kapur et al., 2015; Rast et al., 2012; Williams et al., 2019) for personality research. The MELSM simultaneously estimates sub-models to both personality traits (location) and states (scale) and it accounts for all the underlying co-variances among the individual difference parameters in both sub-models. This not only overcomes limitations of the two-stage approach, but as we show below, opens the door for rigorously answering novel questions about intraindividual variation in personality. It is also important to realize that in the standard MELSM, IIV is predicted by at least a fixed intercept and a random effect. In the current application, we include time-varying person-level variables to account for daily variations in the within-person variance – a situation that can not be investigated in multi-stage models, as iSD describes the overall variation of a person across time. As such, while multi-stage models and MELSM focus on the same element, the within person variance, they typically serve different purposes.

The MELSM has been introduced to the field of psychology about a decade ago by Hedeker et al. (2008) and since then it has been extended to different applications such as longitudinal (Rast & Ferrer, 2018) or hierarchical settings (Brunton-Smith et al., 2017; Li & Hedeker, 2012), to multiple hierarchical levels (Li & Hedeker, 2012) and different estimation methods (Kapur et al., 2015; Lin et al., 2018; Rast et al., 2012). A number of simulation based studies investigated the quality of its parameter estimates in terms of bias, efficiency and coverage but also in comparison with standard mixed effects models (Leckie et al., 2014; Walters et al., 2018). Overall, and unsurprisingly, the MELSM yields unbiased estimates when scale effects are present compared to standard mixed effects models (Leckie et al., 2014). In the same work, Leckie et al. (2014) showed that in simple cases with only one random location and scale intercept, the MELSM parameters can be recovered with relatively few data points per person. That is, medium sized variance parameters can be recovered with N = 250 and as few as 10 repeated measurements. Similarly, Leckie (2014) was able to recover all parameters in another simulation study with 50 schools and 25 students per school. Moreover, MELSMs will lead to less overall shrinkage as the error variance is not assumed fixed but varying within- and between-persons (Williams, Mulder, et al., 2020) and the standard errors will be more efficient as the heteroskedasticity is modeled directly (Kapur et al., 2015). Recently, Walters et al. (2018) investigated the power to detect and predict MELSM parameters in longitudinal settings. The MELSM behaved consistent with “statistical power theory, in that, greater power was observed for designs with more individuals, more repeated occasions, greater proportions of variance available to be explained, and larger effect sizes” (p. 360). Similarly, Rast and Ferrer (2018, p. 768) concluded from a small-scale simulation, that “large correlations (r ≈ 40) were recoverable with approximately 75 participants and 75 repeated measurements while medium sized correlations (r ≈ .20) required up to 180 participants and 100 repeated measurements.” In a limited simulation study with N = 400 and 5 repeated measurement occasions on a Bayesian bivariate MELSM, Kapur et al. (2015) were able to recover all fixed and random effects and the large correlations (r = .5) among location and scales across both outcomes.

We are not the first to use a MELSM to study within-person variability in personality. For example, Hutteman et al. (2016) used a three-level MELSM to examine variability in personality states across different contexts. Separate models were fitted to several outcomes (e.g., self-esteem and expressive behaviors), with each predicted by aspects of the Big-Five inventory. In this paper we present a multivariate model, that is, a MELSM with two outcomes, to model states and traits given 100 daily measures for physical activity and (cross-)lagged autrogressive components in a sample of 194 individuals. To our knowledge, this is the most intensive sampling period that has been used to examine personality traits and states over time, which allows for answering fine grained questions not possible with relatively few observations collected from each individual. Specifically, we investigate the relation between individual differences in positive and negative affect both on average and in IIV conditional on physical activity. We employ Bayesian hypothesis testing to specifically evaluate correlations, or lack thereof (i.e., evidence for the null hypothesis), between individual (random) effects. Finally, our explicit aim is not to address a substantive question, as in Hutteman et al. (2016), but to introduce a general modeling framework that can facilitate the widespread adoption of the multivariate MELSM in personality research. This includes R code for estimating uni- and multivariate MELSM’s.

This work is organized as follows. Although our aim is to introduce the multivariate MESLM (M-MELSM), we first provide the rationale for investigating the relations between affect and physical activity. We then introduce the customary MELSM, after which we extend the notation to multivariate data structures. In this section, we also emphasize how this model can be used to answer novel questions in personality research, in addition to highlighting the advantages of the presented Bayesian approach. For example, to our knowledge, the full model cannot be estimated with classical methods (e.g., maximum likelihood; Hedeker & Nordgren, 2013). In the online supplement (https://osf.io/3bmdh/link) we present R code for the user-friendly package brims that was used to estimate the reported model (Bürkner, 2017b). The next section focuses on the fitted model, where we emphasize, with visualization, the richness of information that is provided by the Bayesian M-MELSM. We then demonstrate Bayesian hypothesis testing for the correlations between individual (random) effects in particular, as well as describing the inferences that this allows for in practical applications. We end by listing short-comings as well as possible extensions of the presented model in personality research.

Trait Affectivity and Intraindividual Variability

While it is customary, in the personality literature, to assess the relations between traditional personality traits and affectivity (Augustine & Larsen, 2015), for our purposes we focus exclusively on positive and negative affect (denoted PA and NA, respectively). The former is related to positive mood, including feelings of interest, excitement, and enthusiasm, whereas the latter is related to feelings of guilt, nervousness, and distress (Watson et al., 1988). There is a large body of literature on each construct, and in particular, on how they relate to the big five personality inventory (Hutteman et al., 2016; Yik & Russell, 2001). A well documented finding is that PA is related to extraversion and NA is related to neuroticism (Lucas et al., 2008; Wilson & Gullone, 1999; Wilt et al., 2012). Indeed, PA has been shown to load on the same factor as measures of extraversion (Watson et al., 1992). On the other hand, a second factor was identified that included indicators of NA and measures of neuroticism (Watson et al., 1992). However, contrary to reflecting the same construct, as argued in Watson et al. (1992), Burger and Caldwell (2000) demonstrated that trait PA was able to explain behavior after accounting for extraversion{the opposite was not the case.

Despite affect and personality typically being treated as related, but ultimately different concepts, it is important to note that the propensity toward, variability in, and trajectories of affective states across situations and time can be considered stable psychological traits (Eid & Diener, 1999; Fleeson, 2001). Indeed, the study of tendencies toward and consistencies in affective states across time and situations falls well within the purview of personality research. Moreover, there has been a substantial amount of work on trait affect and health related outcomes, with most of the focus on negative affective styles (Cohen & Pressman, 2005). For example, NA has been linked to cardiovascular disease (Kubzansky & Kawachi, 2000; Suls & Bunde, 2005), immune functioning (Kiecolt-Glaser et al., 2002), and stress reactivity (Chida & Hamer, 2008). On the other hand, there has been less focus on trait PA. The available evidence points toward an inverse relationships where higher trait levels of PA are associated to lower morbidity, as well as lower self reports of symptoms and pain (for a review see Cohen & Pressman, 2005).

As noted in Finch et al. (2012), a limitation of the above findings is that PA and NA are typically investigated in isolation of one another. That is, there are few examples that look into both simultaneously, and in particular, the relation between the two over time. This also applies to studies of intraindividual variability. The extant literature is relatively sparse, compared to trait affect, but has been linked to health (Hardy & Segerstrom, 2017) and aspects of personality (Kuppens et al., 2007; Timmermans et al., 2010). From a substantive perspective, we are, to the best of our knowledge, the first to consider temporal associations among PA and NA states. For example, although they were considered in Rast et al. (2012), our model captures the interplay between both by employing a multivariate (i.e., PA and NA are the dependent variables) mixed-effects location scale model. Furthermore, by considering PA and NA in the same model, this allows for investigating autoregressive effects on the intraindividual variability across and within the respective constructs. Given that the personality dynamics literature concerns itself with changes in state and trait distributions, over time and contexts, it is meaningful to assess how previous states and environmental inputs affect the consistencies in and tendencies toward other states. The multivariate MELSM indeed permits researchers to model such exogenous, autoregressive, and time-dependent effects on the entire distribution of states. In other words, the M-MELSM permits researchers fine-grained access to conditional trait density distributions, rather than merely marginal trait distributions. One can model how the distribution of states itself changes dynamically over time, and as functions of covariates (both the expected state, and variability therein). Finally, as an indirect marker of health (Paluska & Schwenk, 2000; Warburton et al., 2006), we predict each with physical activity measured with daily step counts. We include previous physical activity for two reasons: First, to build upon previous research relating affective states to physical health; second, to demonstrate how the characteristic distributions of personality states (Fleeson, 2001) can be modeled as a dynamic time-dependent process with situational inputs (Roberts, 2009). These substantive contributions are novel to the personality literature.

The Mixed-Effects Location Scale Model

To answer the previously described questions the employed model is necessarily complex. Thus, before describing the multivariate MELSM (M-MELSM), we first introduce a simpler, univariate MELSM. This makes the central idea behind the model clear, provides motivation for using it to study personality traits and states, and gives context for the proceeding applied example.

We begin with the standard linear mixed effects model with repeated measurement occasions on j = 1, 2,…, n, (occasions) – that is,

$$y_i=X_i\beta +Z_i{b}_i+{\epsilon }_i,$$ (1)

where y_i is a n_i × 1 vector of observations for the ith person, X_i is the n_i × m design matrix for the fixed effects of observations for the ith person. Here β is a m × 1 vector of fixed effect coefficients. The random effects are in the n_i × q matrix Z_i for observations in person i and b_i is the corresponding q × 1 vector with the random effects coefficients. These effects characterize a person’s mean response or location. In the context of personality, this would correspond to an individual’s personality trait as measured, for example, by the mean score over time if there is no predictor in the model. ε_i is a vector of errors specific to the ith person. In other words, this term corresponds to the fluctuations, or states, around the mean of the respective trait. It is customary to assume that the random effects are distributed as b_i ~ N(0, Φ), where Φ is a q × q covariance matrix for the random effects with the variances ${\sigma }_b^2$ and covariances σ_bb′ for b ≠ b. The errors are also assumed to be normally distributed with a mean of 0 and covariance of ${\sigma }_{\epsilon }^2\Psi$, where Ψ is a n_i × n_i matrix that can take different structures. For this work, we make the assumption that Ψ = I_n, wherein I_n is a n_i dimensional identity matrix – that is, the day to day states, or fluctuations around the mean, are assumed to be independent of one another. In these models the between-person variance is captured by ${\sigma }_b^2$, whereas the within-person variance is denoted by ${\sigma }_{\epsilon }^2$

Within-Person Variance

The mixed effects model assumes one value for the error variance ${\sigma }_{\epsilon }^2$, such that, in the context of personality, each individual is assumed to have the same state variance for a given trait. The two-stage approach attempts to overcome this by estimating iSDs for each person. The MELSM, instead, allows ${\sigma }_{\epsilon }^2$ to differ at the individual level – that is, ${\sigma }_{{\epsilon }_i}^2$. Additionally, we allow it to differ among j-time points to obtain ${\sigma }_{{\epsilon }_{ij}}^2$. Changes in ${\sigma }_{{\epsilon }_{ij}}^2$ are explained by the time-varying predictors included in the n_i × m matrix W_i for the fixed effects. The random effects matrix is then V_i (n_i × p; m ≥ p) which captures an individual’s variability. Bringing it together, with the inclusion of time-varying covariates, the within-person variance not only varies across persons but also across time given the following model:

$${\varphi }_i=\text{exp}(W_i\eta +V_i{t}_i).$$ (2)

Note that Equation 2 is for variances, and as such, the exponential function is used to ensure that the estimates are positive real values. ϕ_i is a n_i × 1 vector containing the error variances ${\sigma }_{{\epsilon }_{ij}}^2$ (i.e., the expected state variance for individual i at assessment j). The fixed effects are denoted with η and are analogous to β in Equation 1. That is, for an intercept and slope, η₀ is the average within-person variance in personality states and η₁ is the effect of some predictor (e.g., time) on the log scale. The individual deviations from these fixed effects are denoted by t₁ and are assumed to be normally distributed – that is, t₁ ~ N(0, Θ). Here Θ is a covariance matrix of dimensions p × p. Importantly, even with a personality trait that is constant over time, there could nonetheless be effects on the variance and individual variation therein. The MELSM allows for investigating this possibility. This has implications for the study of personality development (for example), in that the focus can be expanded beyond the mean trait level to also consider state variability over time: Do fluctuations in personality states diminish or increase as a function of an external variable across the lifespan? Or, is state variability relatively stable over time and could be considered a trait itself?

Motivating Example

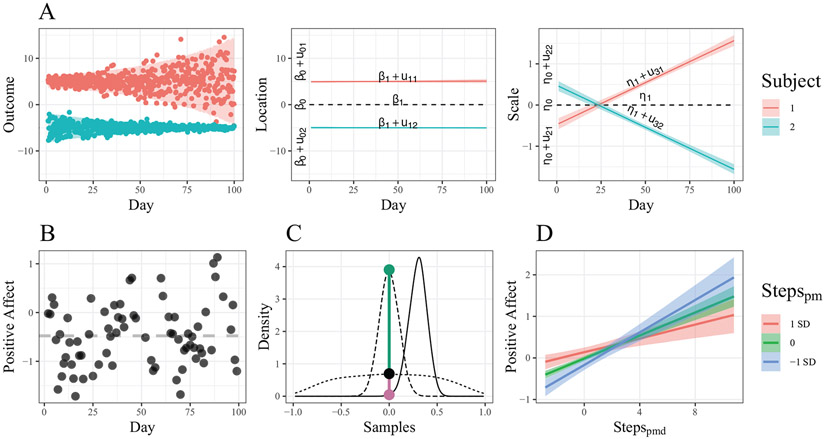
Figure 1 illustrates different possible outcomes from a MELSM. In this artificial example we discuss two individuals, each of which provided daily measurements over 100 days (represented as dots in Figure 1A, Panel 1). This hypothetical model is defined as

$$\begin{gathered} y_{ij}={\beta }_0+{\beta }_1\left({\text{Day}}_{ij}\right)+u_{0i}+u_{1i}\left({\text{Day}}_{ij}\right)+{\epsilon }_{ij}, \\ {\sigma }_{ij}^2=\text{exp}\left[{\eta }_0+{\eta }_1\left({\text{Day}}_{ij}\right)+u_{2i}+u_{3i}\left({\text{Day}}_{ij}\right)\right]. \end{gathered}$$ (3)

Figure 1.

(A) An example dataset consisting of raw observations for two individuals (Panel 1), with predicted locations (Panel 2) and log variances (Panel 3) from the MELSM. (B) A scatter plot of PA and Day for one subject. The gray line is the person’s mean. (C) Illustration of Savage-Dickey Bayes Factors for correlations when H₀ is supported (Green) and when H₁ is supported (Pink). The dotted line is the implied prior for correlations using the matrix-F distribution. The dashed line is a posterior distribution that favors the null hypothesis (BF₀₁ ≈ 5.69), whereas the solid line is a posterior distribution that supports the alternative hypothesis (BF₁₀ ≈ 15.40). (D) The interaction between mean number of steps and the deviation from the mean on PA. The effect of daily activity on PA is greater for those with less average activity.

This includes four fixed effects, the intercepts (β₀ and η₀) and slopes (β₁ and η₁), as well as individual deviations, the random intercepts (u_0i and u_2i) and random slopes (u_1i and u_3i). As is evident from Panel A, the individual represented by red dots seems to get more variable over time while the within-person variability for the individual represented by teal dots reduces over time. The location effects are captured in Figure 1A, Panel 2, where the black line, at day 0, is the fixed effect intercept β₀ – the average of these two individuals. Further, β₀ + u₀₁ would be the intercept for the first subject. In this example, there would be no effect of day (i.e., β₁ = 0) on the given trait, in addition to no individual variation therein ${\sigma }_{u1}^2=0$. The scale effects are provided in Figure 1A, Panel s. In reference to Equation 2, the fixed effect intercept η₀ is exp(0) = 1. Note that the random intercepts indicate that the individual variance differed on the first day of the study. Furthermore, while on average there is no change in variance over time (η₁ = 0), there are individual differences to consider. One person became more variable over time, whereas the other became less variable over the course of the study. Characterizing these effects, for both the location and scale, is the central idea behind the MELSM. This example illustrates how predictors can influence the location and the scale parameters differentially. In that sense, the MELSM seems ideally suited to capture traits and states simultaneously in one model while allowing a set of variables to predict both the location and scale parameters, and therefore, to model the changes in the trait density distribution (Fleeson, 2001).

A Multivariate Mixed-Effects Location Scale Model

Illustrative Data

We draw data from the iFit study, a research project on daily health behaviors and physical health outcomes. 193 participants were recruited from a commercial weight loss program as well as from the general population in Sacramento and Yolo counties in California, US. Their ages at recruitment ranged from 20 to 74 years (M = 40.72, SD = 12.38). Seventy-one percent of the participants were females. Sixty percent were white/Caucasian, 17% were Hispanic, 13% were Asian, and 6% were black/African Americans. Upon providing informed consent, participants completed a set of questionnaires containing demographic and other health-related information. They were then given a Fitbit Charge and were asked to wear it 24 hours a day for at least 100 days. The Fitbit Charge automatically tracked their physical activity in the form of daily step counts. In addition, every evening during the 100 days, participants received a link to an online survey which contained questions regarding their affect, stress, and food consumption. Daily affect was measured using the Positive and Negative Affect Scale (PANAS; Watson et al., 1988), which contained 10 items on positive affect (e.g., attentive, active, excited) and 10 items on negative affect (e.g., hostile, irritable, ashamed). All items were rated on a visual analogue scale from 1 (= not at all) to 100 (= extremely). The order of the items was randomized across days and persons to minimize carry-over effects. On average, the participants completed 82.46 daily surveys (Mdn = 93; SD = 22.65). Items were combined as sum scores which resulted in the two outcomes. Figure 1B depicts a scatter plot of PA across time for one subject of PA.

Propensity toward and stability in NA and PA can be understood as personality traits. Although affective states can vary considerably across time and situations, stable individual differences nevertheless exist across such contexts. The characteristics of the state density distributions can be understood as traits in and of themselves (Fleeson, 2001). Under reasonable definitions of personality traits, affective stabilities and propensities are therefore readily understood as personality traits (Roberts, 2009). Importantly, the illustrative data permit a fine-grained analysis of dynamic, time-dependent relationships between states and exogenous situational variables. In this particular example, we examine the effect of physical activity and previous affective states on current affective states and stability. Therefore, we model how personality states and stability can dynamically and interactively relate across time and behaviors.

Model Specification

The standard multivariate mixed model formulation is described in Maccallum et al. (1997) and Goldstein (2011). In that formulation the dependent variables are combined into one vector, and then dummy coded variables are introduced to “switch” on the respective outcome. This effectively allows for estimating a multivariate model with a univariate expression. While this is a common “trick” to overcome the limitations of standard software packages that only take univariate outcome vectors such as SAS’s proc mixed or R’s lme4, it is not necessary for matrix oriented programs such as Stan, and wrapper packages such as brms. Hence, the univariate MELSM can be extended easily to a multivariate model. While, so far, y was a n × 1 vector for one outcome variable, we can now represent the multivariate outcome in a n × k matrix Y = (y⁽¹⁾, …, y^(k)), where k is the number of dependent variables under consideration. Our dependent variables are PA and NA (k = 2), which are assumed to be random variables from a multivariate normal distribution with the mean vector μ_i = (μ_PAi, μ_NAi)′ and the k × k covariance matrix Σi – that is,

$$Y_i\sim \text{MVN}({\mu }_i,{\Sigma }_i).$$ (4)

Note that the residual variances and the covariance among PA and NA are captured in the diagonal and off-diagonal elements of Σ_i, respectively. In order to facilitate computation and the definition of priors, we re-expressed Σ_i, as τi $\Omega {\tau }_i^{\prime }$, where Κ is a 2 × 2 correlation matrix and τ_i is the 2 × 2 diagonal matrix of residual standard deviations diag (τ_i) = σ_i = (σ_PAi, σ_NAi)′. The assumed prior distribution for the correlations is

$$\Omega \sim \text{LKJcorr}(v=1),$$ (5)

where LKJcorr is the Lewandowski, Kurowicka, and Joe prior (Lewandowski et al., 2009). This distribution is governed by a single parameter ν. A value of one places a uniform prior over all correlation matrices. This results in a uniform (marginal) prior for the residual correlation that is between −1 and 1, assuming a 2 × 2 matrix. This formulation extends to any number of dependent variables.

Before defining the location and scale structure of the M-MELSM we need to decide on how to sensibly approach our time-varying predictors. As with any linear model, centering choices will, among other things, influence the magnitude and sign of correlations of the location and scale random effects. Generally, there are three options on how we can include these variables: uncentered, grand-mean centered, and person-mean centered (Wang & Maxwell, 2015). Uncentered predictors that are included at level 1 can be conceptualized as carrying two kinds of information. An average, between-person part for each individual, and a within-person fluctuation around that average. In the logic of multilevel models, we can separate these two sources of variation and place them in the corresponding levels: level 1 for the within-person fluctuation and level 2 for the between-person effect. As such, uncentered variables confound within- and between-person effects and potentially bias the results (Curran et al., 2012; Raudenbush & Bryk, 2002). This issue can not be resolved by grand-mean centering level 1 variables, as the within-person effect remains confounded with the between-person differences, and hence, only within-person centering can resolve this issue. A viable approach is to extract the person-mean from time-varying predictors and introduce it as a level 2 predictor while the centered within-person time-varying effects enter the model as a level 1 predictor (Curran & Bauer, 2011). In the case of autoregressive effects, the decision on whether or not to center is less clear. For example, Hamaker and Grasman (2015) noted that person-mean centering autoregressive effects can downward bias the within-person slope of the lagged parameter while no centering does not lead to bias in the level 1 parameter. However, once level 2 predictors are added, the person-mean centered autoregressive parameters fares better than the non-centered. For the current application, we chose to person-mean center all time-varying level 1 predictors, including the autoregressive predictors.

Location Model

We are primarily interested in the relation between affect and physical activity, including individual variation therein. For time series data, it is customary to include a lagged predictor. This not only accounts for the previous days rating, but in the present model, allows for investigating additional questions about longitudinal relations between PA and NA.

We now define the location sub-model for each person i and day j as

$$\begin{gathered} y_{ij}^{(k)}={\beta }_0^{(k)}+{\beta }_1^{(k)}\left({\text{Day}}_{ij}\right)+{\beta }_2^{(k)}({\text{PA}}_{\text{Lag1},ij}) \\ +{\beta }_3^{(k)}({\text{NA}}_{\text{Lag}1,ij})+{\beta }_4^{(k)}({\text{Steps}}_{\text{pm},i}) \\ +{\beta }_5^{(k)}({\text{Steps}}_{\text{pmd},ij}) \\ +{\beta }_6^{(k)}({\text{Steps}}_{\text{pm},i}\times {\text{Steps}}_{\text{pmd},ij})+u_{0i}^{(k)} \\ +u_{1i}^{(k)}\left({\text{Day}}_{ij}\right)+u_{2i}^{(k)}({\text{Steps}}_{\text{pmd},ij})+{\epsilon }_{ij}^{(k)}. \end{gathered}$$ (6)

k superscript denotes the column in the matrix Y and the column in the row vectors β that correspond to either PA or NA. Note that both outcomes were standardized to z scores across the whole sample. The predictors include the day elapsed since the beginning of the study (Day), each person’s PA and NA rating on the previous day (PA_Lag1 and NA_Lag1) and the count of daily steps taken. The daily step counts were separated into two components: Each person’s average step count across the study (Steps_pm) and each person’s daily deviation from its average mean (Steps_pmd). Note that, when dealing with time-varying variables and autoregressive components, it is important to separate between person level components from time-varying within-person components in order to minimize bias in the parameter estimates (Hamaker & Grasman, 2015; Wang & Maxwell, 2015). We also included the interaction (Steps_pm × Steps_pmd) to elucidate the interplay between deviations from their average level and their respective average. In other words, it could be that people who are relatively inactive (or active) may react more strongly to deviating from their daily routines. We also considered random intercepts (u_0i) that provide each person’s predicted affect on day 1, random slopes (u_1i) for Day that capture individual variation in affect over the course of the 100 days, as well as random slopes (u_2i) for the deviations from each person’s average step count.

Scale Model

The assumed scaled model is similar to that of the location, but with a slightly simplified random effects structure

$$\begin{gathered} {\sigma }_{ij}^{2(k)}=\text{exp}[{\eta }_0^{(k)}+{\eta }_1^{(k)}({\text{PA}}_{\text{Lag1},ij})\phantom{]} \\ +{\eta }_2^{(k)}({\text{NA}}_{\text{Lag}1,ij})+{\eta }_3^{(k)}({\text{Steps}}_{\text{pm},i}) \\ +{\eta }_4^{(k)}({\text{Steps}}_{\text{pmd},ij}) \\ +{\eta }_5^{(k)}({\text{Steps}}_{\text{pm},i}\times {\text{Steps}}_{\text{pmd},ij})+u_{3i}^{(k)} \\ +\phantom{[}{u}_{4i}^{(k)}({\text{Steps}}_{\text{pmd},ij})]. \end{gathered}$$ (7)

The predictors for the scale part are the same as in Equation 6. The rationale for including negative and positive affects comes from previous work. For example, negative affect has been shown to influence the variability of positive affect, for both the location (e.g. Röcke et al., 2009) and scale (e.g. Rast & Ferrer, 2018). The latter was in the context of dyadic interactions where the partners NA was used to predict the variance in the other partners PA on the same day. The present model extends this notion as it allows for assessing whether the previous days rating of PA or NA influences the following days fluctuation around their respective mean. The random effects in Equation 7 provide each person’s deviation from the overall variance at the beginning of the study (u_3i) and the random slopes (u_4i) capture individual departures from the average change in variability associated to daily changes in steps taken. The latter allows for answering whether deviations from the typical day explain variability in PA and NA and whether there are individual differences in these effects. Note that for both the location and scale fixed effects we assumed improper prior distributions. We acknowledge this is less than ideal but was done to simplify the model formulation. This is addressed further in the discussion.

Random Effects Variance Model

An important aspect of the present model is that it allows for estimating correlations between the random effects. Each outcome has five random effects in total, and rather than assume separate distributions for PA and NA, we instead estimate a 10 × 10 covariance matrix – that is,

$${\mathbf{u}}_i\sim N(0,\Theta ).$$ (8)

Here Θ contains the variances of the random effects of the location and the scale, as well as all covariances, for both PA and NA. We are particularly interested in the covariances, because they capture the interplay, within and between dependent variables, and among location and scale (random) effects. We thus used the matrix-F prior distribution for Θ which follows:

$$\Theta \sim F(v=10,\delta =6,B=0.4{\mathbf{I}}_{10}),$$ (9)

where B is a scale matrix and I₁₀ a 10 × 10 identity matrix. Technical details for this prior distribution can be found in found in Mulder and Raúl Pericchi (2018), with psychological applications provided in Williams and Mulder (2020) and Williams, Rast, et al. (2020). For the present purposes it suffices to note that the parameters (e.g., ν) were chosen to reflect a plausible effect size for the implied correlations (Figure 1C), which allows for Bayesian hypothesis testing. Further details are provided in the following section.

Hypothesis Testing

We test for the presence or absence of a correlation by comparing an equality constrained (null) hypothesis (H₀) versus an unconstrained hypothesis (H_u) – that is,

$$\begin{gathered} {\mathrm{H}}_0:{\rho }_{ij}=0,1\le i<j\le p, \\ {\mathrm{H}}_{\mathrm{u}}:{\rho }_{ij}\ne 0. \end{gathered}$$ (10)

Here 1 ≤ i < j ≤ p denotes the elements in the upper-triangular of the 10 × 10 matrix. To be clear, the unconstrained hypothesis is the prior distribution for ρ_ij. In this case, the hypotheses are nested which allows for using the Savage-Dickey ratio (Dickey, 1971; Wagenmakers et al., 2010). Furthermore, the present approach works directly with the correlations ρ_ij and the corresponding implied prior distribution derived from the matrix-F prior distribution. Thus, the hypothesis test in favor of the alternative hypothesis can be formulated as

$${\text{BF}}_{10}=\frac{p(\mathbf{Y}\mid {\mathrm{H}}_1)}{p(\mathbf{Y}\mid {\mathrm{H}}_0)}=\frac{p({\rho }_{ij}=0\mid {\mathrm{H}}_1)}{p({\rho }_{ij}=0\mid \mathbf{Y},{\mathrm{H}}_1)},$$ (11)

where H₁ is the unconstrained hypothesis. In words, by only considering H₁ with respect to ρ_ij, the Bayes factor can be computed as the unconstrained posterior density of ρ_ij evaluated at zero divided by the prior density also evaluated at zero (Mulder et al., 2012). Importantly, the Bayes factor provides relative evidence between each hypothesis under consideration. In the psychological literature, an analogous approach has been used for both correlations (Marsman & Wagenmakers, 2017; Wagenmakers et al., 2016) and partial correlations (Williams & Mulder, 2020). This requires computing the implied prior for ρ_ij from the matrix-F prior that is given in Equation 9. This is represented in Figure 1C, in addition to a hypothetical posterior distribution and the corresponding Bayes factor. In the results section (i.e., Correlations section), we follow the customary guidelines provided in Kass and Raftery (1995), wherein a Bayes factor greater than 3 is considered positive (relative) evidence for a given hypothesis.

Estimation and Software

The fitted model included four chains of 1,000 iterations each, excluding a warm-up period of the same size. This number of iterations provided a good quality of the parameter estimates in which the models converged with potential scale reduction factors $\widehat{R}$ smaller than 1.1 (Gelman, 2006). We summarize each posterior distribution with the mean, standard deviation, and a 90% equal-tailed credible interval (CI). Note that the equal tailed 90% CI has a lower and upper bound at the 5th and 95th percentile, respectively. If, for example, the lower bound exceeds zero, we can conclude that the posterior probability that a given parameter is larger than zero is ≥ 95%. At the same time, we can conclude that, with a probability if 90% the given parameter is within the lower and upper bound. We also report directional posterior probabilities greater than or less than zero in the text – that is, p(θ > 0∣Y, $\mathcal{M}$). This provides context to findings, for example to compare the magnitude of the respective effects between constructs. In a Bayesian framework these differences can be computed by simply subtracting the posterior distributions (Tables 1 and 2).

Table 1.

Fixed effects parameter estimates

	PA Location			NA Location
Parameter	M	SD	90% CI	M	SD	90% CI
β0	0.03	0.04	[−0.03, 0.10]	0.02	0.04	[−0.05, 0.09]
β1(Day) × 30	−0.04	0.01	[−0.06, −0.01]	−0.03	0.01	[−0.05, −0.01]
β2(PALag1)	0.30	0.01	[0.29, 0.32]	0.00	0.00	[−0.00, 0.01]
β3(NALag1)	0.03	0.01	[0.01, 0.04]	0.26	0.01	[0.24, 0.27]
β4(StepSpm)	0.15	0.07	[0.04, 0.25]	−0.04	0.07	[−0.16, 0.06]
β5(StepSpmd)	0.14	0.01	[0.12, 0.16]	−0.03	0.01	[−0.04, −0.02]
β6 (Stepspm × β5StepSpmd)	−0.06	0.02	[−0.09, −0.02]	0.01	0.01	[−0.01, 0.02]
	PA Scale			NA Scale
η0	−0.81	0.04	[−0.87, 0.75]	−0.90	0.04	[−0.97, 0.82]
η1(Day) × 30	0.02	0.01	[0.00, 0.04]	0.05	0.01	[0.03, 0.06]
η2(PALag1)	0.05	0.01	[0.03, 0.06]	0.20	0.01	[0.18, 0.22]
η3(NALag1)	−0.05	0.05	[−0.13, 0.04]	−0.01	0.07	[−0.13, 0.10]
η4(StepSpm)	−0.06	0.02	[−0.09, −0.04]	−0.08	0.03	[−0.13, −0.04]
η5(Stepspmd)	−0.01	0.02	[−0.05, 0.03]	0.04	0.05	[−0.04, 0.12]
Residual correlation	−.28	.01	[−.29, −.26]

Note. Entries are bolded if the 90% CI excludes zero, indicating that the sign can be discerned with ≥ 95% probability.

Table 2.

Random effects parameter estimates

	PA Location			NA Location
Parameter	M	SD	90% CI	M	SD	90% CI
Intercept SD($u_{0i}^k$)	0.59	0.03	[0.54, 0.65]	0.61	0.03	[0.57, 0.69]
Day SD($u_{1i}^k$)	0.01	0.00	[0.01, 0.01]	0.00	0.00	[0.00, 0.01]
Stepspmd SD($u_{2i}^k$)	0.16	0.01	[0.13, 0.18]	0.35	0.03	[0.31, 0.40]
	PA Scale			NA Scale
Intercept SD($u_{3i}^k$)	0.45	0.03	[0.41, 0.49]	0.63	0.03	[0.57, 0.69]
Stepspmd SD($u_{4i}^k$)	0.17	0.02	[0.14, 0.20]	0.35	0.03	[0.31, 0.40]

All computations were done in R version 3.5.2 (R Core Team, 2017). The model was fitted with the the package brms (Bürkner, 2017b), which serves as a front-end to the probabilistic programming language Stan (Stan Development Team, 2016). There are several advantages of the package brms. The model specification follows that of lme4 (Bates et al., 2015), although brms allows for fitting a much wider range of models. Additionally, there are several post-processing features for model checking and Bayesian hypothesis testing. There are also several tutorials describing brms, including for ordinal models (Bürkner & Vuorre, 2019), distributional regression (https://cran.r-project.org/web/packages/brms/vignettes/brms_distreg.html), and supporting code for an introductory Bayesian textbook on mixed models (https://osf.io/97t6w/). The Electronic Supplementary Material 1 (ESM) to this paper contains the annotated code and data used for running all analyses.

The M-MELSM model is very similar in nature to a multilevel SEM and, if autoregressive effects are included, to a dynamic SEM (Hamaker et al., 2018). The only difference between DSEM or MSEM in general is that the M-MELSM does not include a latent measurement model and the DSEM/MSEM typically does not include a model for the within-person residual variance component. However, both the M-MELSM and the DSEM/MSEM can be made equivalent: A M-MELSM can be made equivalent to a MSEM by including a latent measurement model (Martin & Rast, 2020) and the DSEM/MSEM can be expanded to include a submodel for the residual variance component (Hamaker et al., 2018; Nestler, 2020). As such, these models can be modeled by software that allows either Bayesian estimation or allows for customized maximum likelihood (ML) approaches such as marginal ML.

Results

Fixed Effects

Location

The fixed effects are reported in Table 1. The estimate of day was small and negative for both constructs, thus indicating a decrease in PA and NA over time on average. For PA both lagged predictors increased the reported rating, with a 100% posterior probability, on the following day. This was not the case for NA. Not only was ${\beta }_2^{(\text{NA})}$ (PA_Lag1) smaller than ${\beta }_3^{(\text{PA})}$ (NA_Lag1), with a 100% probability, but the former had (only) a 84% probability of increasing the rating of NA. For physical activity more steps, on average, was associated with higher levels of PA, whereas this was not observed for NA. Note that 90% CI for the difference included zero, which indicates the effect was not “significantly” different between constructs. On the other hand, the predictor Steps_pmd captured within-person differences from their daily average step count. Here, deviating positively from the average step count increased ratings of PA and decreased ratings of NA. The interaction for positive affect is displayed in Figure 1D. This reveals that individuals, who on average walked less than others, were also most responsive to deviating from their mean step count. In other words, for a relatively inactive person, walking more than their typical day was associated with higher ratings of PA, whereas active individuals were apparently less responsive to walking more on a given day.

Scale

The scale (i.e., intraindividual variability) fixed effects are also provided in Table 1. The lagged effects point toward some interesting findings, in that the previous days rating of PA and NA influenced fluctuations in the respective trait. That is, there was a positive relationship between within-person variance and yesterdays affective rating. However, the direction of these effects was perhaps counter intuitive: For each lagged effect, there was an increase in within-person variance. Note also that the largest lagged effect was ${\eta }_1^{\text{NA}}$ (NA_Lag1), wherein the others were smaller in magnitude with a 100% posterior probability. Furthermore, there was also a relation between each outcome and deviating from an individuals mean step count η₄(Steps_pmd). That is, if someone walked more than their respective average, this was associated with greater state stability.

Random Effects

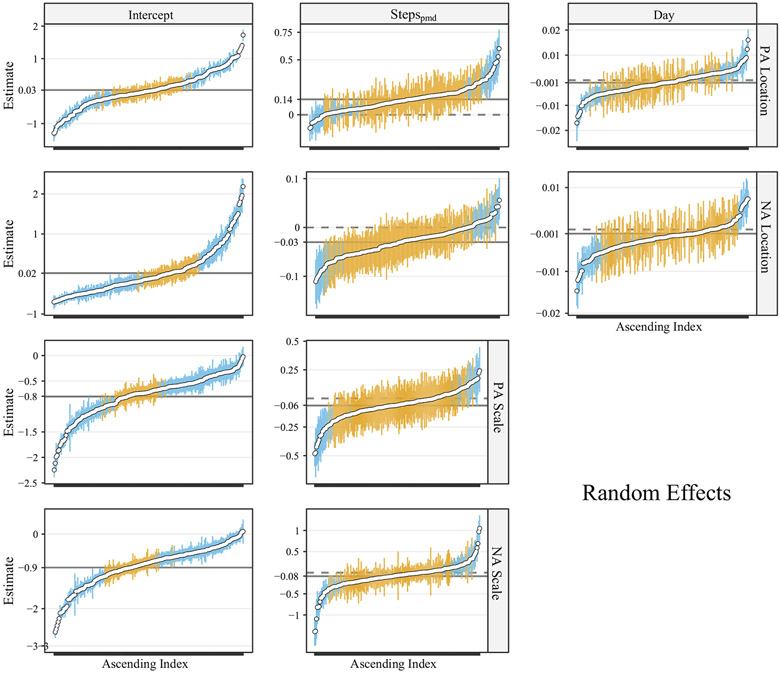
For the random effects we depart from customary approaches that focus on detecting non-zero variance components and instead take a more descriptive approach. They are plotted in Figure 2 and centered at the fixed effect value. The blue intervals correspond to 90% CIs that exclude the respective fixed effect. The corresponding standard deviations are provided in Table 2.

Figure 2.

Subject-specific posterior estimates and 90% intervals (in ascending order) for the intercepts and coefficients of the location and scale of both PA and NA. The solid line is the fixed effect, and the dashed line is zero. Intervals are blue if they exclude the fixed effect, and orange otherwise. Note that many individuals (blue) are inadequately described by the average effect, and several have effects in the opposite direction (in reference to the dashed lines).

Figure 2 reveals individual variation for each parameter, in that all had several people who differed from the fixed effect. The dotted line at zero can also be used as a reference point, for example to indicate how many individuals had a “significant” effect and/or in what direction. While there was an effect of day, for both constructs, it was not so simple as ratings decreasing over time (e.g., participants experiencing study fatigue). For positive affect in particular, 24% of the sample decreased in their rating, whereas 13% showed an increase in PA over time (an effect in the opposite direction). The effect of β5(Step_pmd) was more consistent across the sample. Here only one person showed an effect in the opposite direction, wherein deviating from their respective (average) step count reduced feelings of PA. Further, almost half of the sample showed a positive effect. Said another way, when a person took more steps than on their average day, this was associated with higher ratings of PA in 1 out of 2 individuals. A similar pattern was observed for NA.

We now discuss the scale random effects. Here the intercepts correspond to within-person variance at the beginning of the study. In reference to the fixed effect, η₀, there was considerable individual variation. That is, for both constructs, ≈ 75% of the individual effects differed from the fixed effect. The fixed effect of η₄(Step_pmd) indicated that taking more steps, than average, was related to stability in each construct. Importantly, this deserves some nuance because, in fact, there was an effect in the opposite direction for 6 (PA) and 15 (NA) participants. In other words, some people became more variable in their emotional states when they walked more than on average. These inferences are made possible by inspecting the individual (random) effects, and we encourage applied researcher to similarly go beyond significance testing of variance components (which was not pursued here).

It is straightforward to compare the posterior distributions – that is,$SD(u_{\mathrm{o}i}^{(\text{PA})})$ – $SD(u_{\mathrm{o}i}^{(\text{NA})})$. This allows for asking whether the random effects, for a particular construct, were more variable than the other (Table 2). When comparing the standard deviations of β₅(Step_pmd), SD(u_1i), this revealed that the random effects of NA were more variable than for PA (100% posterior probability). That is, individuals were more widely dispersed around the fixed effect estimate. A similar pattern was observed for the scale random effects standard deviations. Interestingly, at the beginning of the study, SD(u_3i), there was more variability in the within-person variance for NA. Here the probability was again 100%. This pattern also extended to η₄Step_pmd, where the random effects were again more variable for NA. Together, this points toward more individual variation in NA (the trait), in relation to physical activity, and also in the overall stability (or conversely instability) of the states.

Correlations

An additional advantage of the proposed model is that correlations between location and scale random effects can be estimated, as well as between constructs (due to the multivariate formulation). The full correlation matrix is provided in Table 3. The Bayes factors were computed on the logarithmic scale and are reported in the upper-triangular.

Table 3.

Random effects correlations

	μ			σ2		μ			σ2
	$u_{0i}^{(\text{PA})}$	$u_{1i}^{(\text{PA})}$	$u_{2i}^{(\text{PA})}$	$u_{3i}^{(\text{PA})}$	$u_{4i}^{(\text{PA})}$	$u_{0i}^{(\text{NA})}$	$u_{1i}^{(\text{NA})}$	$u_{2i}^{(\text{NA})}$	$u_{3i}^{(\text{NA})}$	$u_{4i}^{(\text{NA})}$
μ
$u_{0i}^{(\text{PA})}$		2.74	−0.81	7.77	3.07	1.09	−0.28	1.62	9.60	0.60
$u_{1i}^{(\text{PA})}$	−0.24†		−1.20	−1.83	−1.21	0.65	1.41	−1.16	− 1.10	−0.43
$u_{2i}^{(\text{PA})}$	−0.13	−0.10‡		3.17	2.13	−1.47	−0.93	6.63	−0.92	0.49
σ2
$u_{3i}^{(\text{PA})}$	−0.33†	−0.04‡	0.26†		−1.56	−0.26	−1.72	−0.58	35.15	−1.42
$u_{4i}^{(\text{PA})}$	−0.30†	−0.10‡	−0.34†	0.05‡		1.58	−1.49	−1.21	1.34	4.67
μ
$u_{0i}^{(\text{NA})}$	−0.18	0.19	−0.07‡	0.14	0.26†		4.58	0.15	20.92	−1.45
$u_{1i}^{(\text{NA})}$	0.15	−0.26†	0.13	0.05‡	−0.05‡	−0.35†		−0.93	−1.79	−1.69
$u_{2i}^{(\text{NA})}$	0.30†	0.04‡	−0.60†	−0.16	0.07‡	−0.29	−0.07		1.25	9.01
σ2
$u_{3i}^{(\text{NA})}$	−0.35†	0.10‡	0.12	0.58†	0.24†	0.47†	−0.04‡	−0.25†		−1.95
$u_{4i}^{(\text{NA})}$	−0.18	0.15	−0.20	0.08‡	0.38†	0.08‡	−0.04‡	0.55†	0.01‡

Note.

^†H₁ is supported.

^‡H₀ is supported.

Correlation estimates are provided below the diagonal, with corresponding logBF₁₀ values above the diagonal.

Location (μ parameters)

In the following we discuss some noteworthy correlations. For example, there was evidence for a negative correlation between both constructs in relation to deviating from their average daily step count (correlation among $u_2^{(\text{PA})}$ and $u_2^{(\text{NA})}$). Walking more than average was associated to higher PA and lower NA (r = −.60, BF₁₀ = 6.63). There was a positive relation between PA on day 1 (i.e., $u_{\mathrm{o}}^{(\text{PA})}$ the intercept) and ${\text{Steps}}_{\text{pmd}}^{(\text{NA})}$ ($u_2^{(\text{NA})}$), such that those with higher trait PA were less responsive to the effect physical activity on ratings of NA (r = .30, BF₁₀ = 1.62). On the other hand, when considering NA at Day 1 ($u_{\mathrm{o}}^{(\text{NA})}$) and ${\text{Step}}_{\text{pmd}}^{(\text{PA})}$ ($u_2^{(\text{PA})}$), there was evidence for the null hypothesis (r = −.07, BF₁₀ = −1.47) – that is, relative to the unconstrained hypothesis trait NA was not related to physical activity and PA.

Scale (σ² parameters)

There was a positive relation between constructs for within-person variance ($u_3^{(\text{PA})}$ and $u_3^{(\text{NA})}$) at the beginning of the study (r = .58, BF₁₀ = 35.15). In other words, individuals that fluctuated around their mean for one trait tended to also fluctuate around the mean of the other trait. Further, as described above, the fixed effect η₄(Steps_pmd) indicated that taking more steps, than average, reduced within-person variance for both constructs (Table 1). Accordingly, the random effects correlation between constructs was positive (r = .38, BF₁₀ = 4.67). This suggests that, when walking more than on a typical day, individuals who became more stable for PA also became more stable for NA. Note that this inference is made possible by the multivariate formulation (Equation 4, in addition to estimating the full covariance structure (see Random Effcts Variance Model section). When considering IIV at day 1 for PA, in relation to η₄(Steps_pmd) predicting both PA (r = .05, BF₁₀ = −1.56) and NA (r = .08, BF₁₀ = −1.42), there was evidence for the null hypothesis. In other words, more variable individuals were not more (or less) responsive to the dampening effect of physical activity on positive affect.

Location and Scale

A special feature of the MELSM are random effects correlations across the location and the scale. There were negative relations between the location of PA, at the beginning of the study, and within-person variance in both constructs. In other word, those who reported higher PA to begin with were also more stable in PA (r = −.33, BF₁₀ = 7.78) and NA (r = −0.35, BF₁₀ = 9.60). Conversely, the opposite was observed for NA, such that higher ratings of NA at day 1 were associated with more within-person variance in NA (r = .46, BF₁₀ = 20.92). Interestingly, those who had a larger effect for physical activity on ratings of PA were also more responsive to physical activity as it related to reducing fluctuations in PA (r = −.34, BF₁₀ = 2.14).

Discussion

In this paper, we extended the standard mixed-effects location scale model, by fitting two outcomes simultaneously, and allowing for individual variation therein. This model was conceptualized to address the goal of identifying and accounting for IIV in personality states. Intensive longitudinal modeling, with the goal of explaining constructs at both the mean and variance level, requires repeated trials and flexible methods that are able to capture changes within and differences between individuals, of which the M-MELSM is one such model. This approach can simultaneously model both the personality traits (the mean structure) and states (the variance structure) for multivariate data common to personality research. Moreover, variables can be included to predict either (or both) the traits and state IIV simultaneously. The model also provides random effects for both the location and the scale components, capturing the nature of individual differences therein. As a result, there are correlations between location and scale random effects, both across and within each outcome, which allows characterizing the interplay between personality traits and IIV therein.

Substantive Applications

In addition to affect, there are many applications where the M-MELSM may be fruitfully applied in personality research. For example, the model formulation seamlessly generalizes to any number of outcomes. This is ideal for personality assessment, in that traits can be modeled simultaneously (perhaps the Big-Five inventory). In this case, we anticipate the model will need fully informed priors for each parameter to ensure convergence. Note that prior distributions, in addition to serving as hypotheses, can also be used to constrain the parameter space (Gelman et al., 2017). This can improve the quality of estimates, reduce computation time, and allows for estimating complex models. Thus, the presented model provides a flexible approach that allows for asking novel research questions to elucidate both inter and intraindividual variability in personality traits.

Bayesian estimation has become more accessible and popular over the last years as it entered mainstream software packages. In fact, the models described here were fit with the R package brms which uses similar syntax as lme4 (Bürkner, 2017a). In our experience, brms is sufficiently flexible to fit most models in psychology, but Stan can be used directly if needed. For example, it is possible for another sub-model predicting the between-person variance (Rast & Ferrer, 2018). While Bayesian estimation techniques have become more widespread, the same can not be said about Bayesian inference. While a thorough discussion on that topic (e.g., on hypothesis testing) was beyond the scope of this work we illustrated some of the possibilities that Bayesian inference is able to offer. There are now several introductions for Bayesian inference specifically for psychological applications (Quintana & Williams, 2018). These are typically geared toward simpler models (e.g., t-test; Rouder et al., 2009), but the techniques can be used with the M-MELSM. We refer to Wagenmakers, Marsman, et al. (2018) and Wagenmakers, Love, et al. (2018), in addition to Wagenmakers et al. (2010) which is specifically about the Savage-Dickey ratio. Importantly, Bayes factors depend critically upon the prior distribution, which should ideally be informed by relevant theory. In the absence of precise theoretical predictions, it is common place to assume defaults (Rouder & Morey, 2012). In practice, when there is prior uncertainty, sensitivity analyses should be performed. They were not included in this work for simplicity. We refer to Carlsson et al. (2017), where the prior distributions were varied as a robustness check.

Limitations

There are notable limitations of this work. When the variances are of interest, it should be noted that their magnitude is also defined by the location of the average response. In other words, with bounded variables that are common in psychology, the variance will be a function of the person’s mean (Baird et al., 2006; Eid & Diener, 1999; Kalmijn & Veenhoven, 2005; Rouder et al., 2008). This problem is known in MELSM applications (Rast & Ferrer, 2018), but also applies to the M-MELSM. These effects could be of substantive interest, or dictated by aspects of the study design. This should be considered when making inference from the random effect correlations. Moreover, because our goal was to introduce a Bayesian M-MELSM to personality assessment, many choices were made for simplicity. For example, we did not provide an in-depth example of model checking, but note this is important in practical applications (see Gabry et al., 2019). Further, we discussed only those fixed effects in which the CI excluded zero, but evidence for the null hypothesis was not evaluated. In practical applications this would be possible by defining an informative prior and computing a Bayes factor or by defining a region of practical equivalence equivalence (ROPE; Kruschke, 2011). Importantly, for those effects not discussed, the reported estimates (Tables 1 and 2) can be used to infer which values are included in the CI (in addition to zero). Lastly, we assumed improper prior distributions for the fixed effects. This decision was again made to keep the model formulation concise, although in practice we would use (at minimum) weakly informative prior distributions (see Gelman, 2006; Gelman et al., 2008; Williams et al., 2018).

Conclusion and Outlook

The purpose of this paper was to present the M-MELSM as a flexible tool for personality assessment. Our proposed model is suited for the “Big-Two” of affect, as presented in this work, but can also be used more generally in personality research (e.g., the Big-Five). By focusing on the within-person variance, this approach opened up possibilities for modeling a component that is often disregarded as “noise” The application highlighted such possibilities and demonstrated that the residual variance may show systematic patterns that are important for understanding the interplay between personality traits and states. As such, these types of models open up the possibility to expand the focus beyond individual differences in traits but also include individual differences in states and their interplay. Especially this last feature, the relation among traits and states within and between individuals and their characterization holds the potential to substantially refine common psychological theories about the stability and fluctuations of traditional trait and state models.