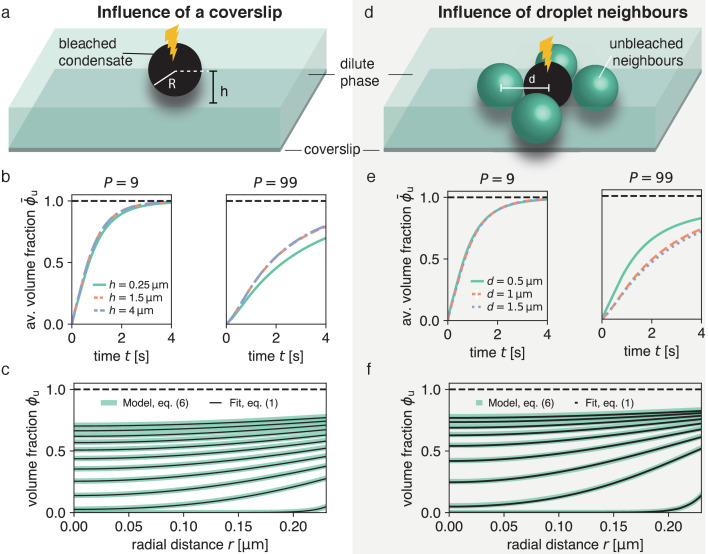
Figure 3. Impact of droplet environment on recovery dynamics.

(a) Sketch of a typical experimental set-up with a droplet above a passivated coverslip, where the droplet center has a distance $h>R$ to the coverslip. (b) Recovery of average unbleached volume fraction ${\displaystyle {\overline{\varphi }}_{\mathrm{u}}(t)=\int d^{3}r{\varphi }_{\mathrm{u}}(\mathit{r},t)\cdot 3/(4\pi R^3)}$ for different heights $h$ above the coverslip at different partition coefficients $P$. Results were obtained by solving Equation (6) using the finite element method and considering the geometries depicted in (a). For even larger $h$-values (e.g. no coverslip), results are approximately equal to the blue dashed line. (c) Using the method introduced in Figure 1 on the scenario with the largest influence of the coverslip (droplet sessile on coverslip) ${\displaystyle h=0.25\mu \mathrm{m}}$ in (a) results in an excellent fit and can reliably extract the input $D_{\mathrm{in}}$. (d) Sketch of neighboring droplets next to a bleached droplet. (e) Total recovery curves for finite element simulations of the geometry depicted in (d), for different distances between neighboring droplet centers, at different partition coefficients $P$. Note the strong dependence on the distance of neighboring droplets. For even larger $d$-values (e.g. no neighboring drops), results are approximately equal to the blue dashed line. (f) Same as (c) but for largest influence of neighboring droplets, that is ${\displaystyle d=0.5\mu \mathrm{m}}$, where there is no distance between bleached droplet and neighboring droplets.