Prediction of Visual Field Progression from OCT Structural Measures in Moderate to Advanced Glaucoma

Abstract

Purpose:

Test the hypothesis that visual field (VF) progression can be predicted from baseline and longitudinal optical coherence tomography (OCT) structural measures.

Design:

Prospective cohort study.

Methods:

104 eyes (104 patients) with ≥3 years of follow-up and ≥5 VF exams were enrolled. We defined VF progression based on pointwise linear regression on 24–2 VF (≥3 locations with slope ≤−1.0 dB/year and p<0.01). We used elastic net logistic regression (ENR) and machine learning (ML) to predict VF progression with demographics, baseline circumpapillary retinal nerve fiber layer (RNFL) and macular ganglion cell/inner plexiform layer (GCIPL) thickness and RNFL and GCIPL change rates at central 24 superpixels and 3 eccentricities 3.4°, 5.5° and 6.8° from fovea and hemimaculas. Areas-under-ROC curves (AUC) were used to compare models.

Results:

Average (SD) follow-up and VF exams were 4.5 (0.9) years and 8.7 (1.6), respectively. VF progression was detected in 23 eyes (22%). ENR selected rates of change of superotemporal RNFL sector and GCIPL change rates in five central superpixels and at 3.4° and 5.6° eccentricity as best predictor subset (AUC=0.79±0.12). Best ML predictors consisted of baseline superior hemimacular GCIPL thickness and GCIPL change rates at 3.4° eccentricity and three central superpixels (AUC=0.81±0.10). Models using GCIPL-only structural variables performed better than RNFL-only models.

Conclusions:

VF progression can be predicted with clinically relevant accuracy from baseline and longitudinal structural data. Further refinement of proposed models would assist clinicians with timely prediction of functional glaucoma progression and clinical decision-making.

Introduction

Timely detection of visual field (VF) progression is an essential task in the management of glaucoma, especially in the more advanced stages where the remaining retinal ganglion cell (RGC) reserve is small. ¹ However, by the time worsening trends or significant worsening of the VFs have been detected, restoration of already lost RGC function is unlikely. ² Therefore, prediction of future VF worsening based on baseline risk factors and structural information and evidence of structural change collected during follow-up may help prevent visually significant progression as therapeutic measures can potentially be applied before VF deterioration occurs.

Most predictive models in the literature have relied on standard statistical methods to predict rates of change or VF worsening based on binary criteria. ^3–5 However, the small number of study patients in relation to the large potential number of predictor variables can be a limiting factor for standard statistical techniques. Machine learning (ML) can combine features from different resources to identify disease markers. ^6–15 Some of these techniques have shown acceptable precision in glaucoma diagnosis. ^8,16,17 Such approaches have typically used single instrument-based optic disc or VF parameters for glaucoma diagnosis or prediction.

When a large number of variables are explored in prognostic models, collinearity among some variables of interest can influence the analysis. Penalized-regression models, such as elastic net logistic regression (ENR), provide a reasonable solution to this by shrinking the coefficient of less contributive variables toward zero. ^18,19 These statistical methods could be helpful when numerous clinical, structural, and functional data need to be combined in order to predict glaucoma progression. In one study on prediction of drug response in cancer, ENR was introduced as an effective tool for selecting the highest performing genomic and molecular features. ²⁰

The goal of this study is to use an array of baseline clinical and demographic variables, together with baseline and longitudinal structural parameters to predict VF deterioration in a cohort of glaucoma patients with advanced or central field damage at baseline. We explored and compared a statistical approach designed for best subset selection in this scenario, ENR, and machine learning methods due to the large number of predictors compared to the number of cases.

Methods

One hundred and four eyes from 104 patients from the Advanced Glaucoma Progression Study (AGPS) were selected for this study. The Advanced Glaucoma Progression Study is a longitudinal, prospective, observational study at the Stein Eye Institute, University of California Los Angeles (UCLA). The main goal of this study is to evaluate the role of central structural and functional measurements in detection of disease deterioration in eyes with advanced glaucoma. The current study was carried out in accordance with the tenets of the declaration of Helsinki and the Health Insurance Portability and Accountability Act (HIPAA) and was approved by the UCLA’s Human Research Protection Program.

The patient cohort consists of patients with glaucoma with clinical evidence of damage at the level of the optic disc and an associated VF defect on standard achromatic perimetry. One eye of each patient meeting the inclusion criteria was selected for further evaluation. If both eyes met the study criteria, the eye with worse mean deviation (MD) was selected to be enrolled. A VF defect was considered to be present if both of the following criteria were met: (1) Glaucoma Hemifield Test outside normal limits; and (2) four abnormal points with p <0.05 on the pattern deviation plot, both confirmed at least once. ²¹ Advanced glaucoma was defined in this study as VF mean deviation of −6.0 dB or worse, or evidence of central VF involvement, i.e., presence of ≥2 test locations with p <0.05 on the pattern deviation plot within the central 10° on 24–2 standard achromatic VFs confirmed at least once. This represents a group of glaucoma eyes that would be classified as having moderately to severe glaucoma. Patients must have had ≥3 years of follow-up and 5 or more 24–2 VF exams and macular and circumpapillary retinal nerve fiber layer (cp-RNFL) optical coherence tomography (OCT) images. The following baseline demographic data were also entered in the ENR and ML models: gender, race, age, intraocular pressure (IOP), central corneal thickness (CCT), axial length (AL) and baseline 24–2 VF MD and pattern standard deviation.

Macular and cp-RNFL imaging

Macular OCT imaging was performed with the Posterior Pole Algorithm of the Spectralis SD-OCT (Heidelberg Engineering®, Heidelberg, Germany). It acquires 61 horizontal B-scans each consisting of 768 A-scans and spanning a 30°×25° wide area parallel to the fovea-Bruch’s membrane opening axis. In order to decrease speckle noise and improve image quality, the B-scans are repeated 9–11 times. A built-in software, Glaucoma Module Premium Edition (GMPE) software, was used to segment individual macular layers. The segmentation accuracy was also checked manually and corrected as needed. Thickness measurements of individual macular layers are provided in an 8×8 grid of 64 superpixels, each 3°×3° in size. The macular outcome of interest in this study was the ganglion cell/inner plexiform layer (GCIPL). We estimated the rates of change of GCIPL in 24 central superpixels (the highlighted central superpixels in Figure 1) with univariate linear regression. Also, in order to decrease the possible contribution of noise when using superpixels, we grouped the superpixels into 3 circular clusters based on eccentricity (3.4°, 5.6° and 6.8° from fovea, or circles 1, 2 and 3, respectively; Figure 1) and superior and inferior hemimacular regions and estimated the corresponding rates of change. Circumpapillary retinal nerve fiber layer measurements were acquired with a single circular B-scan, consisting of 768 A-scans, 12° in diameter and centered on Bruch’s membrane opening centroid. Thickness of cp-RNFL is reported globally (G) and in the following sectors: superior temporal (ST), temporal (T), inferior temporal (IT), superior nasal (SN), nasal (N) and inferior nasal (IN). We estimated global and sectoral cp-RNFL rates of change with univariate linear regression.

Figure 1.

The Posterior Pole Algorithm of the Spectralis OCT provides an 8×8 array of 3°×3° superpixels within the central 24° of the macula.Only the central 24 superpixels were included in this study.Three circular clusters (circles 1, 2 and 3) were defined to account for the varying normative thickness vales and hence, the potentially different rates of change in the macula. The 3 circles were located at a distance of 3.4°, 5.6°, and 6.8° from fovea on average.

Visual field procedures and definition of progression

All patients underwent standard achromatic perimetry with the 24–2 Swedish Interactive Thresholding Algorithm (SITA) standard strategy on the Humphrey Field Analyzer (Carl Zeiss Meditec®, Dublin, CA). Eyes with false positive rate higher than 15% were excluded. We averaged the total deviation (TD) values of the central 12 locations on the 24–2 VF after converting them to Lambert scale to estimate the ‘central’ MD for the study eyes.Threshold sensitivity in 54 test locations were exported as xml data and pointwise linear regression (PLR) of threshold sensitivities over time was carried out. ^22,23 The definition for deterioration at each location was a rate of change ≤−1 dB/year with p <0.01. Presence of at least 3 deteriorating locations was required to call an eye progressing. ^22,24–28

Statistical methods

We performed ENR and ML analyses to identify structural and functional parameters that best predict worsening of VF at the end of the follow-up. In addition to the demographic and clinical factors mentioned above, we investigated the following variables in both approaches: global and sectoral baseline thickness and rates of change for cp-RNFL, and baseline thickness and rates of change of GCIPL in central 24 superpixels, 3 eccentricities, and superior and inferior hemimacular regions. The total number of variables explored were 54, 40, and 20 for the demographic and combined GCIPL and cp-RNFL models, only GCIPL models and only cp-RNFL models, respectively.

A. Elastic net regression

Given the large number of predictors of interest, i.e., baseline cp-RNFL and macular thickness measurements and rates of change along with clinical factors and the potential correlation between some of the explored predictors, ENR was used to identify the most parsimonious and relevant set of variables and address collinearity. ^29,30 Elastic net regression combines the properties of both lasso and ridge regression with regard to regularization of potential variable coefficients and is particularly useful when collinearity among predictors needs to be addressed. The ENR’s two major parameters α and λ were determined using 10-fold cross-validation after dividing the sample into training and validation subsets in 3 to 1 proportion. A multivariable logistic regression (MLR) with the 24–2 visual field progression as the dependent outcome (see above) was subsequently fit to assess the performance of the best subset of predictor variables identified with ENR. The area under the receiver characteristics curves (AUC) was subsequently calculated for each model. The ENR was performed through Glmnet package within the R programming language. ^31,32

B. Machine learning approach

We developed a framework to evaluate glaucoma prediction power of subsets of features using different machine learning schemes. We employed subset feature selection, ³³ which evaluates the worth of a subset of features by considering the individual glaucoma progression predictive ability of each feature along with the degree of redundancy among features. Feature selection has several advantages including better visualization, enhanced understanding of data, decreased computational complexity in terms of memory and time, avoidance of overfitting, and improved accuracy in most cases. ^34,35 More specifically, we generated different subsets of features along with different classifiers in an optimization framework and assessed their AUC in predicting VF progression. To generate subsets of features, we performed a greedy forward or backward search through the space of all clinical, demographic, and OCT subsets of parameters. We started with a random subset and then gradually added or removed features according to the increase or decrease in the prediction accuracy in terms of AUC. As a result, a subset of parameters that was highly predictive of glaucoma progression with low intercorrelation was identified. We investigated several machine learning models including Naïve Bayes, Random Forests, and Support Vector Machine (SVM) and selected the model with the highest AUC. More specifically, we used 5-fold cross-validation to evaluate the accuracy of each model. ³⁶ This approach involves randomly dividing the set of observations into five non-overlapping subsets, or folds, of approximately equal size. We trained the models using the combined four folds and tested the model using the remaining fold. ³⁷ We repeated this process five times and then averaged the results. As cross-validation stratifies the samples in generating the folds, all samples are eventually used in training and testing in separate non-overlapping folds iteratively until all folds are tested independently. Cross-validation minimizes the bias and generates a robust and dependable outcome through evaluating all samples, which is very effective particularly when dealing with relatively small datasets.

Results

One hundred and four eyes from 104 patients were enrolled in this study. Table 1 represents the baseline demographics and clinical characteristics of the study sample. The median (interquartile [IQR]) follow up time, number of visits, and mean (± standard deviation [SD]) baseline 24–2 VF MD were 3.8 (0.9) years, 8.7 (1.6), −8.4 (±5.5) dB, respectively. The average (±SD) MD of the central 12 locations on the 24–2 VF was –4.4 (±3.7) dB. Eighty-four out of 104 eyes had central loss defined as presence of at least 2 test locations flagged as having a p <0.05 on the pattern deviation plot. Based on the PLR criteria, 23 eyes (22%) were determined to be progressing. The mean (±SD) of GCIPL rates of change in the superior hemimacula for non-progressing and progressing eyes were −0.12 (±0.51) and −0.50 (±0.71) μm/year, respectively, p =0.02, t test); the corresponding numbers in the inferior hemimacula were −0.25 (±0.42) and −0.53 (±0.72) μm/year, respectively (p =0.08, t test).

Table 1.

Demographics and clinical characteristics of the study sample for the entire group and according to progression at final follow-up based on visual field progression.

Variable	All Eyes	Stable	Progressing	P value
Follow-up time (years)
Median	4.5	4.5	4.5	0.49
IQR	4.0–5.0	4.0–5.1	4.2–4.7
Age (years)
Mean (± SD)	67.3 (± 8.2)	66.6 (± 8)	69.1 (± 7.7)	0.19
Gender (%)
Female	66 (63.9%)	49 (60.5%)	16 (69.5%)	0.99
Male	38 (36.1%)	32 (39.5%)	7 (30.4%)	0.99
Race (%)
African American	12 (12.0%)	10 (12.3%)	2 (8.7%)	0.35
Asian	24 (22.2%)	19 (23.4%)	3 (13.0%)	0.70
Caucasian	56 (53.7%)	43 (53.0%)	14 (60.8%)	0.66
Hispanic	12 (12.0%)	9 (11.3%)	4 (17.5%)	0.47
Baseline IOP (mmHg)
Mean (± SD)	12.5 (± 3.7)	12.3 (± 3.7)	12.9 (± 3.7)	0.48
24–2 Baseline MD (dB)
Mean (± SD)	−8.4 (± 5.5)	−8.8 (± 6.2)	−7.5 (± 5.6)	0.35
24–2 Baseline PSD (dB)
Mean (± SD)	8.7 (± 4.3)	8.2 (± 3.7)	8.2 (± 3.5)	0.99
CCT (μm)
Mean (± SD)	533.3 (± 38.1)	534.4 (±38.6)	532.7(±38.1)	0.85
Baseline global cp-RNFL thickness (μm)
Mean (± SD)	62.9 (± 14.2)	62.8 (± 14.5)	62.3 (±13.2)	0.85
Baseline average GCIPL thickness (μm)
Mean (± SD)	56.7 (± 8.4)	56.5 (± 8.9)	56.5 (± 6.5)	0.97

IQR = interquartile range; SD = standard deviation; cp-RNFL = circumpapillary retinal nerve fiber layer; GCIPL = ganglion cell/inner plexiform layer; IOP = intraocular pressure; CCT = central corneal thickness; MD = mean deviation; PSD = pattern standard deviation.

When both macular GCIPL and cp-RNFL variables along with demographic and clinical data were entered into the logistic models, the best predictive subset of variables forecasting 24–2 VF progression based on ENR consisted of rates of change of cp-RNFL in the superior temporal sector and GCIPL rates of change in superpixels 2.5, 4.2, 4.3, 5.3 and 5.6 and at 3.4°, 5.6° eccentricities. The final AUC (± 95% confidence interval [CI]) for discriminating progressing vs. stable eyes was 0.79 (±0.12). We also applied ENR to select the best subset of parameters when demographic/clinical variables were combined with only GCIPL data or only cp-RNFL data. For the GCIPL only model, the best subset of variables selected were GCIPL rates of change within superpixels 2.5, 4.2, 4.3, 5.3 and 5.6 and at 3.4°, 5.6° eccentricities with AUC (±SD) of 0.78 (± 0.12) for predicting glaucoma progression. The model combining demographic/clinical variables with only cp-RNFL data failed to identify any significant variables for prediction of progression. Table 2 provides the results of multivariable logistic regression with the ENR approach for the 2 models mentioned above. Figure 2 shows the receiver operating characteristics (ROC) curves of the 2 models.±

Table 2.

Results of the multivariate logistic regression using the best subset of variables selected with elastic net regression. The elastic net approach allows selection of a parsimonious set of predictor variables that do not demonstrate significant collinearity.

Predictor	Coefficient
Combined GCIPL, cp-RNFL and clinical data
Rates of cp-RNFL change, superior temporal sector	−0.016
Rates of GCIPL change at 3.4° eccentricity	−0.030
Rates of GCIPL change at 5.6° eccentricity	−0.066
Rates of GCIPL change, superpixel 5.3	−0.040
Rates of GCIPL change, superpixel 5.6	−0.024
Rates of GCIPL change, superpixel 4.3	−0.008
Rates of GCIPL change, superpixel 4.2	−0.016
Rates of GCIPL change, superpixel 2.5	−0.010
Only GCIPL and clinical data
Rates of GCIPL change at 3.4° eccentricity	−0.008
Rates of GCIPL change at 5.6° eccentricity	−0.058
Rates of GCIPL change, superpixel 5.3	−0.050
Rates of GCIPL change, superpixel 5.6	−0.030
Rates of GCIPL change, superpixel 4.3	−0.007
Rates of GCIPL change, superpixel 4.2	−0.019
Rates of GCIPL change, superpixel 2.5	−0.008

SE = standard error; cp-RNFL = circumpapillary retinal nerve fiber layer; GCIPL = ganglion cell/inner plexiform layer.

Figure 2.

The receiver operating characteristiccurves (ROC) derived from elastic net logistic regression for 2 models using demographic/clinical data, ganglion cell complex-inner plexiform layer (GCIPL) and circumpapillary retinal nerve fiber layer (RNFL) variables (red curve) with area under ROC (AUC) of 0.78 and demographic/clinical data with only demographic/clinical information along with GCIPL variables (blue curve) (AUC =0.76). Note that the red curve is located higher than the blue curve at higher clinically more relevant specificities.

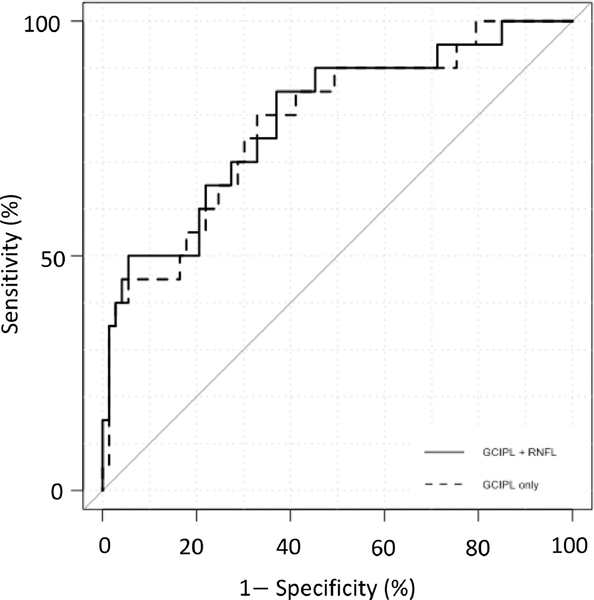
In the ML approach, baseline GCIPL thickness in the superior hemimacula and 3.4° eccentricity, rates of change of GCIPL at 3.4° eccentricity and superpixels 4.4, 5.4, 5.7, 7.4, and 7.5 along with AL were found to have the best performance for prediction of visual field progression with a Naïve Bayes classifier (AUC =0.81; 95% CI: 0.71–0.91) (Figure 3). The sensitivity and specificity of the final ML model were 66% and 85%, respectively. We also investigated several other machine learning classifiers including Random Forests and SVM; however, Naïve Bayes classifier was the best performing classifier on this subset of features and outperformed all the other classifiers. When the ML approach was applied to demographic/clinical data along with only GCIPL data, AL along with baseline GCIPL thickness in the superior hemimacula and 3.4° eccentricity, rates of change of GCIPL at 3.4° eccentricity and superpixels 4.4, 5.4, 5.7, 7.4 and 7.5 resulted in an AUC of 0.80 (95% CI: 0.69–0.91). When demographic/clinical data and only cp-RNFL data were used in the ML models, the best subset of parameters identified were AL, baseline RNFL thickness in the nasal superior sector and global RNFL rates of change and cp-RNFL change rates in the temporal and temporal superior sectors (AUC =0.61; 95% CI: 0.47–0.76). Table 3 summarizes the AUCs for various subsets used in the ENR and ML models.

Figure 3.

The receiver operating characteristic (ROC) curves derived from the Naïve Bayesian approach: when demographic/clinical variables were entered into the model along with circumpapillary retinal nerve fiber layer (cp-RNFL), and ganglion cell complex-inner plexiform layer (GCIPL) parameters an AUC of 0.81 was achieved (red curve); blue curve: clinical/demographic factors with only GCIPL variables (AUC =0.80), yellow curve, clinical/demographic factors with only cp-RNFL variables (AUC =0.61).

Table 3.

The area under the ROC curves for different combinations of demographic/clinical data and OCT parameters used in elastic net regression and machine learning approaches.

Predictive data	AUC	95% CI
Elastic net regression
Demographic/clinical + GCIPL + cp-RNFL	0.79	0.12
Demographic/clinical + GCIPL	0.78	0.12
Machine Learning applied on most discriminative subset of features
Demographic/clinical + GCIPL + cp-RNFL	0.81	0.10
Demographic/clinical + GCIPL	0.80	0.11
Demographic/clinical + cp-RNFL	0.61	0.15

CI = confidence interval; cp-RNFL = circumpapillary retinal nerve fiber layer; GCIPL = ganglion cell/inner plexiform layer.

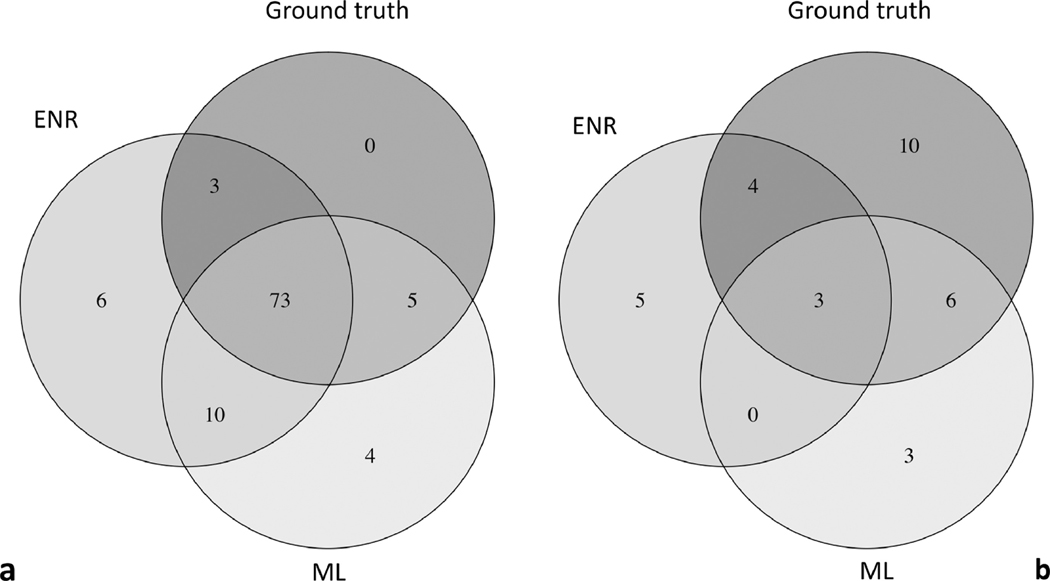
Figures 4a and 4b display Venn diagrams for agreement between ENR, ML model (both using the combined GCIPL and RNFL dataset), and the ground truth of progression based on PLR approach for stable and progressing eyes, respectively. While the agreement on progressing eyes was fair (Figure 4b), good agreement was observed on stable eyes (Figure 4a).

Figure 4.

Venn Diagrams demonstrate agreement of elastic net regression, machine learning and ground truth with regard to stability (a) or progression (b) of the 24–2 visual fields at final visit.

Discussion

We demonstrate the utility of structural measures including baseline measurements and rates of change of cp-RNFL and macular GCIPL thickness for predicting subsequent 24–2 VF progression based on both statistical (ENR) and machine learning approaches. We found that the best subset of parameters selected by ENR had a clinically relevant predictive performance for functional glaucoma progression (AUC =0.79). When cp-RNFL data were excluded, the performance of the best subset of variables only slightly decreased (AUC =0.78). The combination of demographic/clinical and cp-RNFL variables had the lowest performance. Similarly, with the ML approach, the best AUC was achieved with a Naïve Bayes classifier using all the demographic/clinical, GCIPL, and cp-RNFL data (AUC =0.81). Like logistic regression, the AUC for the prediction was almost as good when demographic/clinical data were combined with only GCIPL variables (AUC =0.80). When only cp-RNFL variables and demographic/clinical data were entered into the ML model, the model performance deteriorated (AUC =0.61).

The performance of either model (ENR or ML) with all the available demographic/clinical data and structural variables seems clinically relevant and is comparable or superior to the best predictor algorithms reported in the literature for forecasting glaucoma development or progression. The C statistic of the predictive model derived from the combined OHTS-EGPS database was 0.74 for predicting glaucoma progression during the initial 5-year period following patient enrollment. ³⁸In our study, enrolled eyes had moderate to advanced glaucoma damage at baseline; depending on the level of structural damage in cp-RNFL vs. inner macular layers, the prediction power of the specific outcomes explored may be different as the structural outcome of interest that has not reached measurement floor would provide better predictions of VF progression. ³⁹ In another study, De Moraes et al. reported good agreement between predicted and observed probability of progression based on their model with a C-index of 0.75. ³ The C-index has a similar interpretation as the AUC. Neither study utilized OCT data for prediction. Some studies considered OCT structural data for prediction of glaucoma progression. ^40–43 In the study by Sung et al., the authors found that changes in the average full macular thickness was significantly higher in the progressing group. ⁴³ We evaluated the utility of inner macular thickness measurements (specifically GCIPL where glaucoma damage is easier to detect) at the level of superpixels and 3 eccentricities. Schrems and colleagues evaluated cp-RNFL OCT thickness and neuroretinal rim measurements from confocal scanning laser ophthalmoscopy for predicting functional glaucoma progression; they reported that rates of cp-RNFL change within the temporal inferior sector was the best predictor of functional change; similarly, with only cp-RNFL thickness variables within the ML model, we found that rates of change of cp-RNFL within temporal and temporal inferior sectors were the best predictors. ⁴⁰ Our study is among the first ones to use both baseline and longitudinal cp-RNFL and GCIPL structural data for predicting VF progression using ENR and ML approaches.

Yousefi et al. found that an ML approach (unsupervised Gaussian mixture model with expectation maximization) was able to detect glaucomatous VF progression earlier than other methods such as global MD change, or region-wise or pointwise change. ⁴⁴ One of the advantages of the ML approach is the ability to select a smaller subset among multitude of parameters explored. The features (variables) with the highest Gini score in our study significantly improved the accuracy of the classifier compared to when all parameters were used. Traditional statistical methods such as logistic regression normally require much higher sample sizes given the large number of predicter variables investigated in this study. We used AUC values for assessing the performance of various ML and ENR model. Given the small number of progressing eyes, the sample is unbalanced and therefore, other measures such as confusion matrices could be misleading.

Daneshvar et al. recently reported the potential utility of baseline GCIPL and RNFL measures for prediction of subsequent glaucoma progression defined as worsening of 24–2 VFs based on event or trend criteria. ⁴⁵ In that study, thinner RNFL or GCIPL thickness at baseline significantly improved prediction of subsequent glaucoma progression. The study sample in the current investigation consisted of eyes with baseline central damage or moderate to advanced glaucoma; this group of eyes would be expected to show evidence of change on the macular OCT images. ^46–48 This fact partially explains the finding that GCIPL measures had a better performance than cp-RNFL measures for prediction of subsequent 24–2 VF progression. In advanced glaucoma, GCIPL reaches its measurement floor later than cp-RNFL. This could be another explanation for our finding that GCIPL was a better predictor of glaucoma progression based on 24–2 VFs than cp-RNFL in this group of patients with mostly moderate to advanced glaucoma. ⁴⁷ Rates of change of GCIPL in individual superpixels were among the variables providing prediction ability for glaucoma progression; most of the identified superpixels were centrally located. This is consistent with the regions of the macular cube demonstrating the fastest rates of change in a recent study by Rabiolo and colleagues. ⁴⁹ Rates of change of GCIPL at circles 1 and 2 for ENR and at circle 1 for ML approach were among the best subset of parameters for predicting glaucoma VF progression. This finding is in agreement with results reported by Mohammadzadeh et al. demonstrating that the average rates of GCIPL change on circles 1 and 2 had the highest correlation between with the corresponding regions of the central 10° VF. ⁵⁰

Kim and colleagues reported that older age, higher peak IOP and glaucoma surgery during follow-up were associated with higher rates of VF progression assessed with different methods. ⁵¹ In our study, neither of the approaches considered age a predictor of glaucoma progression. This is in contrast of some previous prognostic studies on glaucoma progression. ^52,53 The utility of IOP reduction for preventing glaucoma progression was proven by The Early Manifest Glaucoma Trial (EMGT). ⁵³ The patients in the current study were all under treatment during the study period; this could have expectedly masked the influence of IOP on disease progression as eyes at higher risk of progression would presumably have received more intensive treatment.

Use of ENR for prognostication of glaucoma progression is novel. A Japanese study implemented lasso regression for predicting glaucoma progression. ⁵⁴ The authors studied various regression models for predicting VF status from prior VF data and found that lasso regression was the most accurate method with the least prediction error. Elastic net regression is considered as hybrid of lasso and ridge regression approaches and the penalization method is also a mixture of those used by the 2 methods. It has been suggested that for datasets with highly correlated predictors, ENR can outperform lasso regression. ³⁰

We found modest agreement between ENR and ML approaches for prediction of progressing eyes. This could be explained by the fact that the models identified different parameters to provide predictions. Future studies will explore combining such models in order to provide better predictions of progressing eyes and higher sensitivity.

The findings of our study, once corroborated and validated in other cohorts, could be used to enhance prediction of visual field progression during the follow-up period, especially in eyes displaying macular damage at baseline. These eyes are at highest risk of losing central vision and becoming visually disabled with disease deterioration. A change in macular superpixels could potentially be a harbinger of subsequent visual field loss and could be considered with other clinical factors for decision making on optimization of therapeutic measures. The main limitations of our study are the relatively small sample size and the fairly small number of eyes that progressed during the follow-up period. This could have affected our ability to identify all predictor variables for functional progression and hence, the predictive ability of the model. Despite this, the predictive performance of the model was clinically relevant. Nevertheless, we used stratified subsets of eyes in both training and testing and employed cross-validation to assure both groups were represented in training and testing. Future studies on larger sample sizes and with longer follow-up times will be able to address the above limitations. Another limitation is that, although the study eyes had central glaucoma damage at baseline, functional progression was defined based on PLR on 24–2 VF test locations, rather than 10–2 VFs.

In conclusion, we demonstrate that functional glaucoma progression can be confirmed or predicted with baseline and longitudinal structural data with clinically relevant accuracy. Further refinement of our approaches could provide clinicians with a valuable tool for forecasting functional progression and clinical decision making in glaucoma.