Nonstatistical Photoinduced Processes in Gaseous Organic Molecules

Abstract

Processes that proceed in femtoseconds are usually referred to as being ultrafast, and they are investigated in experiments that involve laser pulses with femtosecond duration in so-called pump probe schemes, where a light pulse triggers a molecular process and a second light pulse interrogates the temporal evolution of the molecular population. The focus of this review is on the reactivity patterns that arise when energy is not equally distributed on all the available degrees of freedom as a consequence of the very short time scale in play and on how the localization of internal energy in a specific mode can be thought of as directing a process toward (or away from) a certain outcome. The nonstatistical aspects are illustrated with examples from photophysics and photochemistry for a range of organic molecules. The processes are initiated by a variety of nuclear motions that are all governed by the energy gradients in the Franck–Condon region. Essentially, the molecules will start to adapt to the new electronic environment on the excited state to eventually reach the equilibrium structure. It is this structural change that is enabling an ultrafast electronic transition in cases where the nuclear motion leads to a transition point with significant coupling between to electronic states and to ultrafast reaction if there is a coupling to a reactive mode at the transition point between the involved states. With the knowledge of the relation between electronic excitation and equilibrium structure, it is possible to predict how the nuclei move after excitation and often whether an ultrafast (and inherently nonstatistical) electronic transition or even a bond breakage will take place. In addition to the understanding of how nonstatistical photoinduced processes proceed from a given excited state, it has been found that randomization of the energy does not even always take place when the molecule takes part in processes that are normally considered statistical, such as for example nonradiative transitions between excited states. This means that energy can be localized in a specific degree of freedom on a state other than the one that is initially prepared. This is a finding that could kickoff the ultimate dream in applied photochemistry; namely light excitation that leads to the rupture of a specific bond.

1. Introduction

1.1. The Femtosecond Time Scale

Why femtoseconds? In essence because nuclei move on the femtosecond time-scale when a molecule vibrates.^1,2 Therefore, a comparable time resolution is required to make real-time observations. The vibrational period for molecular motion is determined by the (small) weight of the vibrating nuclei in combination with the potential energy function related to the molecular deformation. These parameters result in the molecular vibrational frequencies that are well-known from infrared absorption spectroscopy where the absorption of light is associated with the activation of a molecular motion. Absorptions range from 400 to 4000 cm^–1 for the most common and identifiable peaks in an IR spectrum. It is well-known that C–H stretches are in the 3000 cm^–1 range, that a C=O stretch lies around 1800 cm^–1, and that anything below 1000 cm^–1 are skeletal motions that usually involve the entire molecule for small organic systems or heavy atoms if such exists. If the 4000–400 cm^–1 wavenumber interval is converted into frequencies, the range is 129 THz to 12.9 THz which translates into around 8.3–83 fs. That essentially means that a carbonyl vibrational period takes 4000/1800 × 8.3 fs = 18.4 fs as illustrated in Figure 1.

Figure 1.

Illustration of why the femtosecond time scale is necessary to resolve atomic motion in molecules.

When discussing what are the advantages of being able to observe molecular motion in real-time, the attention is usually brought to the late 19th century controversy of whether a galloping horse at any point in time is hoovering with all four legs above the ground.³ Leland Stanford (of Stanford University) was a keen horseman and entered on the side those who supported the hoovering claim. Although most historians find it unsupported, the story goes that Stanford placed a 25000 USD (around 20 million in present day value) bet on the hoovering theory. The only acceptable proof was a photo series with a camera that is fast enough to capture the galloping horse in all stages of its galloping cycle. Stanford had not founded his university at the time but he was certainly already enthusiastically into technology and entered a collaboration with the, at the time famous photographer, Eadward Muybridge. He was to develop a camera with sufficient shutter speed to provide the answers that Stanford wanted. After declaring it impossible at first Muybridge took up the challenge: 4 years and 50000 USD later (significantly more than the bet) Muybridge had developed a camera with 2 ms resolution. The results of his efforts are shown in Figure 2, and it does indeed show that Stanford was on track–the galloping horse does indeed have all four legs hoovering above the ground during the ride.

Figure 2.

Galloping horse in Muybridge’ photography from a balmy June morning in 1878. Frame 3 clearly shows that the horse is flying. Courtesy of the Department of Special Collections, Stanford University Libraries.

If one were to capture the nuclear positions in different stages of the vibrational motion, an experiment with a temporal resolution on a comparable scale—that is, femtoseconds—would have to be in play. The Nobel Prize was awarded to Ahmed Zewail in 1999 for “his studies of transition states in chemical reactions using femtosecond spectroscopy”.² Zewail essentially defined the field of femtochemistry, and most of the early breakthroughs are his responsibility. Achieving finally the ability to handle the femtosecond time scale experimentally is what made Ahmed Zewail state that “science had beat the race against time”.²

The story of observing the flying horse is similar for studies of chemical reactions. The time scale for molecular vibrations is on the order of 10–100 fs, therefore the time it takes to actually break a bond is on that scale. Thus, all chemical bond ruptures take place on the femtosecond time scale. For photo- and thermally induced reactions alike there is, however, significant ambiguity in what happens prior to the actual breakage. That is, the details pertaining to the preceding nuclear motions and state-transitions are largely unknown and so are the potential prior involvement of electronic states other than the reactive one. Similar to the invention of the Muybridge camera, experimental femtosecond resolved methods have opened the window to this unchartered area in chemistry. The possibility of determining the nuclear motions and associated energy flow (vibrationally and electronically) is at our feet, and that is essentially what this review is about—an attempt to understand what are the energy flow patterns and associated nuclear motions in organic chemistry and what drives them.

1.2. Experimental Femtochemistry: How and Why?

Femtosecond resolved methods rely on pulsed lasers because they form the only possible platform for triggering a reaction on such a fast time scale. A starting time and an ending time that can be provided on the femtosecond time scale are required in order to generate femtosecond temporal resolution. Such well-defined time triggers can not be provided by neither electronics nor diffusion in play because both methods take place on the nano- to picosecond time scale. By the same token, the reliance on light pulses also means the processes under study have to be photoinduced and unimolecular as illustrated in Figure 3. A light pulse (the pump) starts the reaction, and a second light pulse (the probe) which has a well-defined time delay to the first interrogates the processes that the first pulse induced.

Figure 3.

A cartoon representation of the generation of a data point in a pump–probe experiment. A femtosecond pulse initiates a process, here the stretch of the Na–I bond. The system is exposed to a second pulse that records the intermediate structure–normally by inference from absorption measured in one form or another.

The femtosecond pulse and the processes that it induces are slightly more enigmatic than it appears at first, the main reason for this being the energy-time uncertainty relation which states that ΔΕ·Δt ≥ h/4π. This essentially means that for laser pulses with duration on the femtosecond time scale (Δt small) the corresponding ΔE has to be rather large. The way that this shows is that the pulse is polychromatic rather than monochromatic as is the case for a nonpulsed (continuous wave, CW) light source. Typically, a femtosecond pulse from a commercial laser system operating at 800 nm has a full width at half-maximum (fwhm) of around 20 nm which has the corollary that it is impossible to excite a single quantum state (eigenstate) but rather the excitation leads to an end state that is best described as a coherent superposition of (mostly vibrational) eigenstates. Such a superposition is referred to as a wave packet, and the femtosecond time-resolved experiments image its temporal evolution.⁴

This intrinsic property of femtosecond excitation is coincidentally exactly what ensures the possibility of observing a time dependent property following the excitation. In eq 1 the state ψ(t) is an example of a superposition of two stationary (vibrational) states. Equation 2 describes the evaluation of an observable property associated with the operator X.⁴

1

2

For the superposition, the complex conjugate does not cancel out as would be the case for the single quantum state where 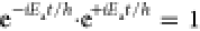. This renders the wave packet nonstationary, i.e., with a time dependence. Thus, what we are observing in femtosecond time-resolved experiments is the complex quantum phenomenon of a coherent superposition of vibrational eigenstates evolving in time. However, the quantum mechanical interpretation is usually aborted immediately and a classical vantage point where the molecules are perceived as marbles on a slide is normally adopted. That is, the way that the experiments are interpreted is based on an assessment of how the nuclei of the molecules would move in a given potential energy landscape. The principal factor is the steepness, i.e., the energy gradients, of the potentials involved and elaborate considerations of wave packets (and their complex quantum structures) are usually not taken into considerations. There is a good justification for the classical interpretation. A laser source emits photons that are uniform in all aspects (the source is coherent), and the molecules are initially in the same vibrational and electronic quantum states. This means that the ensemble of molecules when excited with broadband pulses can be perceived as the most classically behaving quantum state imaginable because all molecules essentially behave as one. There is an obvious conclusion to be drawn from this description pertaining to the entire set of vibrational motions, namely, that they are not excited all at once and that it seems unlikely for energy to flow between vibrations without a time lapse, or to put it in another way:

Energy is non-statistically distributed at the time of excitation and an unknown Δt after... Femtosecond resolution is essential in revealing the nuclear motions that are associated with randomization of the energy. The main hypothesis here is that the initial vibrational motion(s) are predetermining for the ultimate outcome of the excitation.⁵

Several observations indicate that there always seems to be an ultrafast mechanism for deactivation of an excited-state molecule. The most well-known example is probably Kashas’ rule which states that photoreactivity and light emission take place from the lowest-lying excited state.⁶ This indicates that the de-excitation to the lowest-lying excited state is significantly faster than bond breakage and emission. The most intriguing part is the mechanisms that are responsible for the deactivation from the time of wave packet generation to bond breakage, light emission, or heat exchange on (what is in 99% of all cases) the lowest lying excited state. It is fundamental questions such as these that make the femtosecond resolved experiments highly relevant in revealing systems where the ultrafast/initial deactivation aspects impact the ultimate outcome. The main limitation in experimental femtochemistry is that the reaction under study has to be light induced to be triggered on the femtosecond time scale and also it has to be unimolecular as diffusion is impossible to control with femtosecond precision. A possible exception is found in the (auto) photodetachment studies of transition states by Neumark.⁷ In addition, it is often challenging to convert (usually absorption) data into structure, but sometimes the coherence of an fs pulse, that is the fact that all photons act on a molecule in the same manner, is the saving grace as will be described below. Whether the resulting data and conclusions are representative of naturally occurring processes might be a different story. The sun, for example, does not exactly constitute a coherent pulsed light source.⁸ But experimental femtochemistry has nevertheless been employed in a vast number of studies that focus on solar cell materials.⁹ Here, for now, the focus is on small systems in the gas phase and without any immediate application beyond the advancement of science.

1.3. What is coherence and intramolecular vibrational redistribution (IVR)?

Zewail’s key papers on NaI and ICN truly highlighted the importance of being able to observe recurrences in the time-dependent data that result from an optical pump–probe experiment.^10,11 In the NaI case, the data unequivocally showed the real-time motion of two atoms connected by a chemical bond—a stretching motion that clearly leads to a transition back and forth between two distinct electronic states (Figure 4).²

Figure 4.

First ever set of experimental data to show molecular motion in real time, here for NaI. Reproduced from ref (12) with permission from AIP.

Since then, observations of oscillating signals that evolve on the femtosecond time scale have shown up in experimental studies of myriads of systems, and the underlying structural dynamics have been ascribed to a variety of processes that are more or less complex in nature.¹³⁻¹⁵ Particularly Scholes has put great effort in applying the concept of coherence in biological systems with focus on light harvesting systems.¹⁶⁻¹⁸ The common denominator in all the experiments, where the observable oscillates periodically, is that there is always something “extra” to be said about the nuclear motions involved in the photoinduced processes in those cases, especially when exposed to theoretical treatment.¹⁹ These considerations are not new and have been discussed in great detail in two very comprehensive reviews with roughly 300 references combined.^17,20 Oscillating signals are often referred to as being “coherent”. While this is in reality a mis-denomination, the oscillations are a result of nuclei moving coherently for each species in the molecular population and the recurring experimental signal assists in the interpretation of how.¹⁴ So essentially, what is being observed in that case is the real-time evolution of the wave packet that is generated by the absorption of a femtosecond laser pulse. For nuclei to be observed to move coherently via an oscillatory signal, the vibrational energy cannot be randomly distributed because if it was, the observable could not depend systematically on time and the temporal evolution of the signal would in essence be random. The process of distributing the vibrational energy to the vibrational states that were not included in the formation of the original wave packet is referred to as intramolecular vibrational redistribution (IVR); the time scale involved is debatable and strongly dependent on the system (primarily rigidity and symmetry), but the consensus is that >10 ps is not too far off.²¹ There have been reports of IVR that is slightly faster in a set of small amides in aqueous solution (4.9 ps for N-methylacetamide),²² and a simulation study even propose IVR that is concomitant with the electronic transition.²³ The latter has not be experimentally verified so altogether 10 ps is a good ballpark number. The concept of IVR is a fairly theoretical approach to experimental femtochemistry, but herein it is assumed that it is a sensible vantage point for the description of molecular dynamics. The presence of externally disturbing factors, such as, for example, solvation and diverging processes, may result in randomization of the energy and phases. As a result, it is less likely to observe an oscillatory signal from processes that are exposed to external perturbation. On a time scale faster than that of randomization of the energy and phases, it is usually envisioned that only a single or at least very few combinations of the molecular degrees of freedom are excited. These can give rise to a distinguishable change in the molecular structure as a function of time. Thus, with appropriate temporal and spatial resolution, one would be able to observe oscillatory signals and in principle be able to translate the observation into real-time structural information.

1.4. The State of the Art in Gas Phase Dynamics

Gas phase experiments have a significant advantage over condensed phase studies because the solvent–solute interactions can be neglected along with any intermolecular transfer of energy. This eases the interpretation quite significantly and restricts the dynamics to the isolated (single) molecule. The single molecule focus also enables a whole different level of precision of the computational methods that can be utilized. There is a large number of research groups around the world that are using femtolasers and vacuum chambers in their quest to unravel the molecular events that take place immediately after light absorption.²⁴⁻³⁰ As such, there is nothing new in conducting fs-resolved experiments in the gas phase; in fact the first studies were initiated at the time of the very first femtosecond lasers. The impact of a scientific study lies in the problem at hand—to a certain extent the method of choice is irrelevant so the use of femtosecond lasers is only considered a tool herein.

The general consensus is that there is too little systematics across the board of femtochemistry—many studies are conducted as isolated cases without an overall chemical context.^31,32 It has still to this day not been possible to establish the system that would enable prediction of the temporal evolution of molecular structure including the deformations that precedes bond breakage or electronic transitions. The number of research papers that present femtosecond resolved data is vast, and a simple web of science search on the term femto* gives 76 581 hits—whereas “ultrafast dynamics” results in around 23 000 hits. The unification of that body of data would require an intense data mining exercise at the epic proportions of artificial intelligence and machine learning combined. A breakthrough would potentially enable the realization of any photochemists dream—namely that of state- and site-selective photochemistry, all covered under the topic of control. This area of research was hot in the 1990s and has since then faded significantly probably because of the lack of real success.³³

The scattered nature of the overall body of femtochemistry data is a great offset for organic chemists who tend to use a systematic approach to chemistry which is based on the functional group. Already during a visit with the Stolow group in 2009 the concept of associating nuclear motion with a specific chromophore/excitation type was discussed. Stolow has since coined the term “dynamophore”.³⁴ In principle, only a limited number of transition classifications exist (Figure 5), and if they are localized at a functional group, the idea that the (localized) electronic environment will induce a specific nuclear motion (regardless of the surrounding molecular environment) is very sensible.

Figure 5.

Transitions that are possible in organic molecules. The classifications π, σ, and n correspond to traditional orbital classifications (n is a lonepair orbital).

There are a range of groups around the world who are central in the field of ultrafast dynamics of gaseous molecules. The groups of Bañares, Koch, Neumark, Stolow, Suzuki, Temps, Weber, and Zewail are (and in the latter case was) mostly responsible for the development in the field over that past decade with various in-house techniques to study gas phase dynamics. Each of the groups excel in their individual fields with methods that all rely on ionization of organic systems. Bañaras has focused on the preformation of organic radicals by fs pulses and the study of their dynamics with photoelectron spectroscopy. This has led to novel insight into the electronic states of open-shell systems.²⁴ Koch’s work pertains to the dynamics of organic molecules in He droplets.²⁵ Neumark has an entire range of focus areas, but particularly electron attachment/detachment spectroscopy is his trademark.²⁶ Stolow, Suzuki, and Weber all have a background in the group of Y. T. Lee and have (amongst many other things) been working on different distinct flavors of photoelectron spectroscopy since then.^27,30 Temps is using an ionizing probe to form charged species that are detected with a mass spectrometer, and Zewail does not need further introduction.^14,29 The field has grown with the advent of the free electron laser to encompass studies where it is possible to make use of direct structural determination of gaseous molecules with X-ray scattering, such as those by Minitti,³⁵ and to include the techniques that involve the time-resolved electron microscopy imaging techniques that were pioneered by Zewail.³⁶ The combined body of data clearly shows that the contemporary techniques are extremely comprehensive and the problems that have been approached span a very broad range of the molecules that are common in an organic chemistry context. The time resolution of stable commercially available laser systems is currently easily in the <25 fs range which does indeed enable the resolution of molecular motions in the fastest end of the spectrum (1800 cm^–1 corresponds to 18.4 fs). The insight and meticulous detail that are revealed in the combined body of research are extraordinary—it includes fascinating and impressive studies of the molecular motions that are involved prior to, and during, electronic transitions and/or bond breakages. From a bird’s eye perspective, it does seem like all of the studies represent individual problems—dots in the femtochemical space. We are short of one (or perhaps a few) unifying mechanism(s) that will enable us to connect these dots.

Within the past five years or so the scope of time-resolved studies has been expanded to include an even higher temporal resolution—namely the attosecond time-scale.³⁷ Since such pulses are 1000 times shorter than fs pulses, the spectral width is rather large. In fact, it is only X-rays that can accommodate a full wavelength cycle which means that attosecond pulses are of limited interest when it comes to more traditional photochemistry. The attosecond time scale is relevant to electronic transitions.³⁷ X-ray pulses are usefully employed as a probe because they provide a more direct route to structure.³⁸ As contemporary as the technique may be, it will not be dealt with further herein as the present focus is on structural (and not electronic) dynamics.

1.5. Bridging the Gaps: From Organic Photochemistry to Biology and beyond

The number of studies of fundamental photoinduced processes in organic molecules are vast. The actual overarching trends still remain to be derived as outlined above. As always, the organic chemist can explain almost everything but predict very little. The only really bullet-proof prediction of a relation between structure and ultrafast bond breakage arises in the cases of weak σ-bonds and thus low-lying σ* orbitals to which the initial excitation can take place. This is for example the case in halides where the carbon–halogen bond (R–X) normally undergoes a photoinduced rupture. With a direct excitation to a state where the energy decreases as a function of R–X bond length the initially generated wave packet will inevitably have most of its contribution in the R–X stretching mode. The reason is that the density of (R–X) vibrational states is very high because of the nonbounded nature of a repulsive surface. Thus, the molecular population will start to develop toward separated R· and ·X entities immediately after the excitation as fast as the bond can stretch, that is, in less than 20 fs (Figure 6).

Figure 6.

Excitation to a repulsive state simply makes the molecular population behave like a ball that rolls on a slide.

Essentially, this is an advanced way of stating what is obvious in the case of, for example, a marble that is placed on a slide; it will start rolling as soon as it is released. The main challenge in applied organic photochemistry is that to date there is no solid model for predicting how the state that is ultimately reactive is populated and what degrees of freedom are activated in the process. In almost all organic molecules of any real relevance the transfer of energy into to the bond(s) that ultimately breaks is the bottleneck. Once the relevant modes are activated the bond will break on the time scale of the molecular vibration that is descriptive of the reaction coordinate—that is, in femtoseconds.

Application of femtochemistry has been pronounced in trying to unravel the photodynamics and decay mechanisms of biomolecules.³⁹ As discussed in section 1.2, an obvious caveat in the application of fs laser-induced processes is whether processes that are induced by femtosecond pulses are representative of the photochemical processes that are induced by the sun or another incoherent light source. That is, whether, in reality, the experimental observations are consequences of the way that they are recorded. This is not a topic that anyone has debated in great detail—neither in the context of biology nor in studies of, for example, solar cell materials where the source of the radiation is the basis for the entire field. Brumer has discussed that some of the quantum effects that are found to be in play in biology may only be relevant in a lab setting and concluded that more work is needed.⁸ Thus, it is assumed herein that processes induced by femtosecond laser pulses are representative of those that are induced by stray photons from (for example) the sun. The primary focus has previously been on the nucleotides, nucleosides, and isolated DNA bases.⁴⁰⁻⁴³ In gas phase studies the isolated bases are those that have generated the most attention because they are the ones that most easily can be vaporized to generate the molecular beam that is needed to conduct gasphase fs resolved pump probe studies.⁴¹ The question is whether there are certain ultrafast phenomena that are responsible for the fundamental photochemical stability of the biological building blocks that have been evolutionarily selected through geological times.^39,40,44 They have survived periods of the earth’s history where the UV–C influx was significantly higher than it is today and where photoinduced rupture would have been a distinct deal breaker for their continued application in building organisms. It has been argued, on the basis of solid experimental proof, that the wave packet that is initially generated upon the excitation of biomolecules has a component that directs the molecule to a safe haven in an ultrafast manner before the energy can stray to destructive degrees of freedom.^41,42 This safe haven is a state where deactivation of the system can take place in a way so that the initial photon energy can be released as heat. Any gas phase study is inevitably a crude model of reality because the most important heat transfer mechanism in the condensed phase is via solvent–solute interactions. Although in large systems, such as those encountered in biology, the internal heat transfer would in principle transfer energy quanta larger than kT prior to interaction with the solvent. In the gas phase molecules are restricted to alternatives such as fluorescence or (preceded by intersystem crossing (ISC)) phosphorescence on the lowest-lying excited state or ultimately internal conversion to the ground state via internal conversion (IC) and subsequent very slow chemical processes (μs, ms, s, or even hours and days). This is illustrated in Figure 7.

Figure 7.

Jablonski diagram that shows the potential deactivation processes of an organic molecule that has been promoted to an excited state. The directed ISC still has to be experimentally verified. Radiative and reactive processes are left out.

Obviously, whatever path the molecular population is taking subsequent to excitation it will be a consequence of the underlying potential energy surface which again is directly determined by the molecular structure. There have been findings for several DNA-bases, for example, to show that topological points of particularly high IC (and ISC) propensity can be reached via the molecular motions that are activated immediately after excitation. Also, other biologically relevant entities, such as for example cyclic disulfides that are proxies for the S–S bond in peptides, have been shown to be “saved” by directed IC to the ground state where the excitation energy can be released as heat to avoid ultimate rupture of the labile S–S bond.⁴⁵ The question is whether this is always the case. So far all investigated molecules have an ultrafast deactivation pathway to the lowest-lying excited state triggered by “activation” of a specific molecular vibration. The observation forms the main common denominator of this review.

The hypothesis is that all processes are directed by the initial activation out of the Franck–Condon region and that the subsequent chain of events can be understood based on these very early nuclear motions that follow excitation. The intension is to explore the underlying reasons for this behavior.

2. Directionality of Internal Conversion

The Born–Oppenheimer approximation works under the assumption that electrons move much faster than nuclei and therefore light excitation places ground-state structures in a significantly changed electronic environment—often referred to as the Franck–Condon region on the excited-state potential energy surface.

2.1. The Motion out of the Franck–Condon Region

When the ground-state structure is exposed to the new electronic environment of the excited state, the nuclei will start to move to adapt to the new situation. This reorganization is often referred to as “the motion out of the Franck–Condon region”, a structural change that is indeed characteristic of the functional group in question. So the exploration of a range of functional organic molecules lead to novel insight on how molecules deactivate and on how the molecular structure determines the initial activation. This is the central idea behind the dynamophore concept.³⁴ The immediate thought is that the molecule will start to deform in the direction of the steepest descent out of the Franck–Condon region. These motions lead in all of the investigated cases to ultrafast deactivation. Several groups have approached the role of the direction of the nonadiabatic coupling vectors and their relation to the active modes from a theoretical perspective.⁴⁶⁻⁵⁰ The aim here is to verify the built-in directionality of the motion out of the Franck–Condon region toward an ultrafast electronic transition.

All molecules have a range of different electronically excited states, each with different excited-state minima. The most favorable structure on the n → 3s state of acetone for example differs significantly from that of the π–π* state. Therefore, the molecular motions that are in play to take the molecule out of the Franck–Condon region are different in the two cases. For the n → 3s state the (CH₃)₂C=O equilibrium geometry is pyramidal, so the motion that is activated immediately after the excitation is one that takes the molecule from a planar geometry to a pyramidal one. In the case of the π–π* state the structural change is a simple elongation of the C=O bond.^51,52 In some conjugated systems, the structural aspects lead to states that are “self-trapped” because of a specific planar structure along the chain.^53,54 Now, what matters is whether there is a possibility of an ultrafast transition along the initially activated trajectories. This seems to be the case for all of the systems under study, and perhaps even in general for all systems. The idea is illustrated in Figure 8.

Figure 8.

A cartoon showing how certain motions that are activated when the molecule is exiting the Franck–Condon region can lead to transition between two electronic surfaces. For acetone the electronic structure of the first excited state favors pyramidalization at the carbonyl. This motion directs the coupling whereas for example the carbonyl stretch does not leave room for exploration of the areas that are actively coupling two states.

2.2. Structure–Property Relationships

The first femtosecond time-resolved mass spectrometry study of aliphatic amines clearly showed that they provide an excellent venue for exploration of photophysics in general and for directed dynamics as a whole.^55,56 The transitions are bright, and responses from the excited states are excellent. The early studies of amines have led to a large body of work because of the easily accessible arena that they provide for gas phase studies.⁵⁷⁻⁶² This was exactly the same for acetone which used to be a calibration compound but turned out to be so much more than that. The electronic states of aliphatic amines are n→ (Rydberg orbital) in nature. A valence type σ → 3s state was also characterized close to the ionization threshold.⁵⁶ The amines for which the data were found to be the most easy to interpret are the tertiary ones (RN(R′′)R′′). The excited state manifold is by far the most clean without intervention from the N–H σ states that have been shown to alter the dynamics quite significantly.⁶³ The transitions in play are all involving the Rydberg orbitals so the resulting states are resembling a compact ionic core surrounded by a diffuse electron cloud as illustrated in Figure 9.

Figure 9.

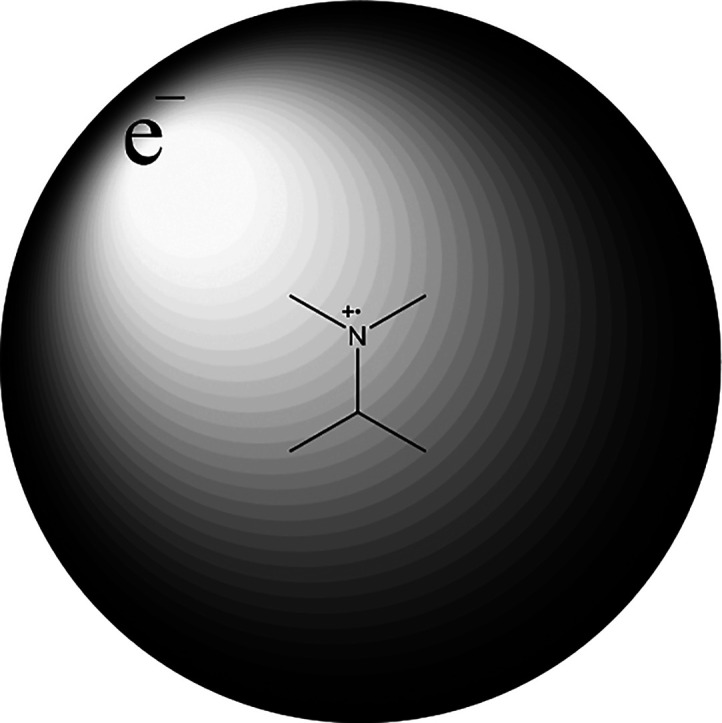
Illustration of what the electronic structure of a Rydberg state looks like with an ionic–radical cation–core.

The fact that the Rydberg states have the nature of a radical cation means that structure at the nitrogen is planar. Thus, the motion out of the Franck–Condon region is a planarization at the nitrogen in going from the tetrahedral structure to start off with to the planar structure at equilibrium. The result of a calculation that shows how the energy changes as a function of the planarization angle is shown in Figure 10, and it can be seen that it is steeply downhill toward the planar structure at the nitrogen.

Figure 10.

A TD-B3LYP/6-31+G(2df,p) calculation that shows the energy change as the structure becomes planar at the nitrogen. It can be seen that there is a drive toward a planar structure. Reproduced from ref (56) with permission from ACS.

The aliphatic amines have been exposed to a range of pump–probe schemes and the results all are in line with a pump excitation that populates the Rydberg manifold and a subsequent cascade of ultrafast internal conversion processes that finally populate the n → 3s state; fluorescence will ultimately take place from that state. A key hypothesis of this review is that the motions out of the Franck–Condon region are directing the IC to become ultrafast. Hence, the key question for the amine systems pertains to the involvement of the planarization/umbrella motion.⁶³⁻⁶⁵ Ever since the first paper on the ultrafast processes that are induced by 310 nm 100 fs pulses back in 2003,⁵⁶ there have been strong indications that this motion is key. The primary and secondary amines behave very differently to the tertiary amines. The reason is a combination of the N–H σ* states that become involved and the fact that hydrogen atoms move much faster than alkyl groups, which means that if the umbrella motion is determining for the internal conversion process, then the process will be significantly impacted by the substituents on nitrogen. To address the importance of the nitrogen substituents in greater detail, a few systems were designed so that the impact on the electronic environment is smallest but mass impact was largest. This is achieved with isotopic substitution that does not influence the electronic potential but simply changes the vibrational frequencies. The concept is illustrated in Figure 11.

Figure 11.

Three time-resolved mass spectrometry (TR-MS) data sets (200 nm pump, 267 nm probe) where the philosophy is to explore the variation in mass of the substituents that are involved in the umbrella motion. In all three approaches it is observed that the heavier the substituents slow down the motion. Reproduced from ref (65) with permission from Elsevier.

Starting from left it is observed how a systematic substitution at N influences the IC rate. It decreases by a factor of about five in going from RNH₂ to R₂NH to R₃N. In the middle, the mass of the N substituents is progressively increased from RNH₂ to RNHD to RND₂ and again the IC rate drops dramatically (lifetimes change from 158 to 789 fs). In the final part of Figure 11, the substitution pattern is modified from N(CH₃)₂ to N(CH₃)CD₃ to N(CD₃)₂ and here the impact is less dramatic, but still there is an observed change from 619 to 936 fs. This is taken as a clear indication that the umbrella motion is directing the IC in a matchmaking between the initial and receiver state. The computational results showed no direct electronic coupling between the states involved, and we therefore conclude that the coupling that results in a transition is mostly vibronic in nature.

To assess whether there are alternatives when the umbrellar motion is restricted the photophysics of ABCO was investigated. It turns out in a combined computational and VMI study that other degrees of freedom do become available when the pyramidalization is restricted and thus no longer represents the steepest descent out of the Franck–Condon region. Here, the C–N bonds become sufficiently weakned which enable a transition via a conical intersection in that coordinate. This alternative pathway is illustrated in Figure 12.

Figure 12.

CAS/NEVPT2 calculated change in potential energy with the N–C bond distance for a system where pyramidalization is not possible (ABCO). This motion becomes the IC trigger. Reproduced from ref (64) with permission from RSC.

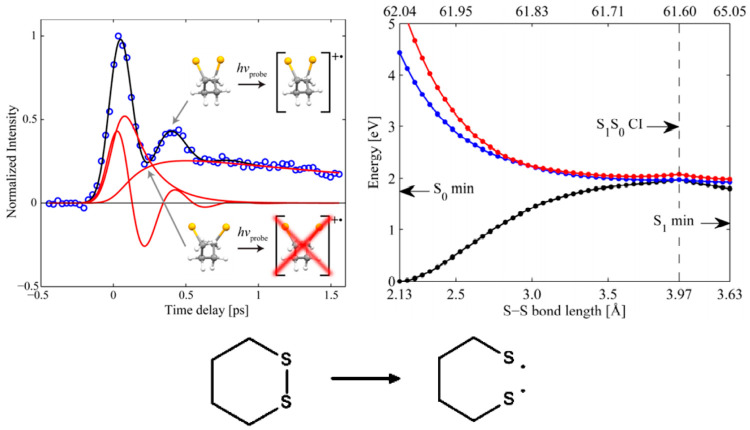
There are a range of systems that have been shown to undergo ultrafast internal conversion, and there is potentially an entire portfolio of directional trigger modes.⁶⁷ Understanding their impact will be the first step to establish structure–property relationships between molecular entities and photophysics. Even in some cases the ultrafast internal conversion can be the saving grace. The disulfide bridge is one of the central building blocks in nature, and it is an important factor in the determination of tertiary structure in proteins.⁶⁸ At first sight this does not agree very well with what else is known about the stability and particularly the photochemistry of disulfides. Already very early on, it was well recognized that disulfides, upon the absorption of light, cleave to form free radicals which take part in various chemical processes rather than reforming the S–S bond.⁶⁹ Time-resolved studies of the S–S bond breakage in linear systems showed that the rupture does indeed take place on the subpicosecond time scale.^70,71 An ultrafast S–S bond breakage does not speak in favor of the S–S bond as a key driver in determining protein structure because it simply would not have survived intense UV radiation since the beginning of time. So, what has saved the S–S structural element? We have found that it is the confinement that is built into the cyclic arrangement of the tertiary structure in proteins which induces a direction for the IC process.⁴⁵ We have focused on the photoinduced dynamics of dithiane (results in Figure 13), which is the smallest possible saturated cyclic structure containing an S–S bond that is stable enough to be exposed to ambient experimental conditions. The TR-MS results in Figure 13 show a decaying signal that is modulated by an oscillation where the period matches the oscillatory frequency of the sulfur atoms moving back and forth past each other to locate a crossing point to the ground state. It is the latter process that gives rise to the decay of the signal. From the crossing it is downhill all the way to the initial geometry that can then deactivate in a natural environment via the solvent molecules. It is worth noticing that lower wavelengths change the picture a little and leads to decomposition in the gas phase.⁷² A time-resolved X-ray study has shown that the time scale for decomposition at lower wavelengths is so long that the system is able to distribute the energy to the surrounding solvent medium. So even here the conclusions stand for what is a saving grace for the S–S bond to maintain its status as a key structural motif in biology.⁷³

Figure 13.

Time-resolved mass spectrometry (TR-MS) signal (left, m/z 55 from 284 nm pump/400 nm probe excitation) shows the decay that represents the S₁ → S₀ IC process. The signal is modulated by an oscillation that is a consequence of the changed ionization propensity as the sulfur atoms move past each other in a torsional motion. The potential energy change (right, SA-3-CAS(10,8)/6-31G(d,p)) when the S–S bond is stretched (and the carbon skeleton consequently twists) indicates that it is energetically favorable to reach the crossing point. Reproduced from ref (45) with permission from ACS.

It is noteworthy that the conclusions have been verified with slight modifications in an advanced MD study by Wann et al.⁷⁴ who also attempted an electron diffraction study of the process. However, due to challenges in handling dithiane it never reached maturity.

2.3. When Directionality Replaces Traditional Models for Internal Conversion Rates

There are well-established models rooted in statistical dynamics for the determination of IC rates and reaction kinetics in general, the most central ones being QET (quasi equilibrium theory) and RRKM (for reactivity) and Fermis Golden rule in the case of photophysics.^73,75 The latter gives the transition rate between states m and l in a very simple expression (eq 3) that involves a perturbation term (if the transition is induced) and the density of (vibrational) states in the transition region—the more receiver states the more probable the transition and thus the faster it will be.

3

A series of ketones (Figure 14) were exposed to that logic with the focus being on the S₂ to S₁ transition. The expectation is that the rate increases with the number of vibrational modes (i.e., receiver states). This, however, turns out not to be the case (Figure 14).

Figure 14.

Ketones under study with lifetimes from an exponential model in ps underneat.⁷⁶

Closer scrutiny of the TR-PES data for the ketones in Figure 15 shows a decaying signal modulated by an oscillation.⁷⁶ The period of this oscillation perfectly matches that of a puckering motion centered at the carbonyl and involving the neighboring carbons. An example is shown in Figure 15.

Figure 15.

Oscillatory signal from a time-resolved photoelectron spectroscopy experiment (200 nm pump/267 nm probe). High- and low energy refer to the flanks of the photoelectron peak associated with the S₂ state. The structures a-c are calculated at the EOM-CCSD/cc-pvtz level of theory. The torsional motion is primarily reflected in the twist of the front CH₂ in going from a to c. Reproduced from ref (76) with permission from John Wiley & Sons.

This result clearly shows that the driver in transiting the wave packet from S₂ to S₁ is a puckering motion centered at the carbonyl. It will have to be the only one activated; otherwise, it would not have appeared as a coherent contribution to the signal. With this in mind it is possible to make sense of the time constants in Figure 14. It can be seen that more strain in the vicinity of the carbonyl induces faster IC (shorter lifetime). This is in essence because a slower motion will enable more efficient coupling and thus a faster transition. The periods that are derived from the experimental signals are in line with this explanation. For cyclobutanone and 2-methylpentanone, the periods are 950 and 420 fs, respectively, and the time constants are 740 and 3470 fs. So, the more rigid and packed at the carbonyl, the longer the period and the shorter the lifetime. The idea is illustrated in Figure 16 in cartoon style—the characterization of the potential energy surface remains a work in progress, but the establishment of puckering mode as a driver for IC is robust.

Figure 16.

A cartoon illustration of how a slow ring-puckering leads to an efficient coupling between S₁ and S₂ and thus a faster transition between the states. The vibrational frequency ω and the energy difference ΔE determine the intersection point between the two excited states. These two parameters thereby determine how close the molecule can get to the intersection point and, thus, the rate of transition. The enlarged region shows two possible pathways: one statistical indicated by the dotted arrow and one directed transition through a conical intersection indicated by the dashed arrow. Reproduced from ref (76) with permission from John Wiley & Sons.

3. What Makes the Coherence Become Preserved from One State to Another?

Nonradiative transitions usually are considered to be statistical in nature. Models such as Fermi’s golden rule has traditionally been employed to account for transition rates between excited states.⁷⁷⁻⁷⁹ In standard Fermi-like systems, the available degrees of freedom are involved in a statistical manner, and the rate of internal conversion can largely be discussed in terms of the density of states available in the receiving state. Dating further back to the statistical models of Rice, Ramsberger, Kassel, and Marcus, it was essentially assumed that all degrees of freedom are involved prior to bond rupture and the RRKM theory is expressing the rate constant for a reaction as a ratio between the sum of (vibrational) states for the transition state and the density of states for the reactant.⁸⁰ The processes that are induced and interrogated with femtosecond laser pulses are prone to reveal nonstatistical aspects of photophysical and -chemical transformations. The entire discussion of directionality in the previous chapters provides examples of such nonstatistical processes on the initially activated electronic state. It would be groundbreakting to unequivocally show that some photophysical transitions involve the preservation of energy in a subset of the available degrees of freedom even after a transition between states. It was established above that the energy is located specifically in certain degrees of freedom for molecules that have been exposed to femtosecond laser excitation, but no remark was made as to the fate of the energy subsequent to e.g. internal conversion. Now, if this localization persists after transitions such as IC that are otherwise considered statistical in nature, the consequences of being able to form molecules that are vibrationally specifically excited by excitation to higher-lying electronic states would be significant. That could potentially lead to photoinduced bond selective chemistry.

The phenomenon of preservation is novel and to the best of my knowledge it was observed more or less simultaneously by our group, the Weber group, and the Chergui group.^62,81 Mukamel touched upon some of the potential experimental consequences in a comprehensive review.⁸² Peculiar results have been observed previously but never interpreted in terms preservation of a nonstatistical distribution of the internal energy.⁸³ Chergui showed that the initially activated mode in a rigid metal complex was still the only activated mode subsequent to a transition from one triplet state to another. In that case, the preservation was attributed to the rigidity of the system which prevents effective coupling of the vibrational levels.^81,84 In this case the preservation was shown indirectly. The first really clear-cut and unambiguous example of preservation was provided by Weber with his studies of N-methylmorpholine where excitation to the S₂ state leads to the activation of a planarization motion at the nitrogen; this motion persists at S₁.⁶² We have extended this study with the Weber group to show that preservation in this case clearly is due to symmetry restrictions in the coupling of the modes in between.⁸⁵ Moreover, we address systems where the pace of the transition plays a role to fully consolidate the concept of preservation.⁸⁶⁻⁸⁸ It is the combined body of data that we are to present here to show that preservation of energy in a specific degree of freedom (and potentially directionality) reaches far beyond the initially excited state.

3.1. Molecular Symmetry and Preservation of Coherence Following Internal Conversion

Using Fermi’s golden rule it can be concluded that systems with lower symmetry undergo internal conversion on faster time scales than analogous systems with higher orders of symmetry, simply due to the greater density of states that the system would be permitted to transition into; however, here it will be shown that by breaking the symmetry from one regioisomer to another, the behavior of the internal conversion changes from a nonstatistical, coherent process to a more statistical noncoherent process.⁸⁹ Weber found that the 200 nm excitation of N-methyl morpholine leads to the clear-cut formation of an n → 3p Rydberg state. Such transitions are usually bright and give rise to sharp peaks that are easy to distinguish (as imaged by photoelectron spectroscopy in Figure 17). The photoelectron pump–probe signature of N-methyl morpholine in Figure 17 shows a peak reflecting the initial population at around 0.7 eV and that the population in the lower-lying state appears after the time delay by which the initial state decays (around 200 fs). The signal to the right in Figure 17 clearly oscillates which is an unambiguous proof of localization of vibrational energy in a single (or at least a subset) of the available degrees of freedom. The period of the oscillation is 600 fs which very closely matches that of a planarization motion at N. This initial motion is expected because the Rydberg excited molecules are similar to radical cations in nature and these are known to be planar at N.⁵⁶ Thus, the tetrahedral initial structure at N will have to undergo an umbrella-type planarization motion to reach equilibrium. In order to assess whether the stringent conservation of energy in a specific degree of freedom is due to the symmetry of N-methyl morpholine, an unsymmetric molecule (N-methyl-isomorpholine) was synthesized and studied (left of Figure 17). Again, the molecule was initially excited to the n → 3p state to make it subsequently undergo an internal conversion to n → 3s. In this case no oscillation of the signal that can be attributed to the lower-lying state was observed.

Figure 17.

Time-resolved photoelectron spectra shown as contour plots (top) following 200 nm excitation of N-methylisomorpholine (left) and N-methylmorpholine (right) that are probed with 400 nm. To the right (N-methylmorpholine, the symmetric case) it can be seen that the signal which corresponds to the lower-lying state (n → 3s, lower kinetic energy of the outgoing electron) kicks in after the higher-lying state (n → 3p) is depleted and that the signal from the lower-lying state is oscillating (a transect is shown in the bottom to clearly indicate that the energy is located in a specific degree of freedom). Reproduced from ref (85) with permission from RSC.

The systems were studied computationally as well to investigate the explicit effects that are induced by the symmetry changes that are suspected to be responsible for the preservation of vibrational energy in a specific degree of freedom in the case of N-methylmorpholine and the dissipation in the isomorpholine. The results for the central potential energy surfaces and select orbitals along the reaction path are shown in Figure 18. A significant proportion of valence character was observed for the minima on the Rydberg states which led us to explore the methyl stretching coordinate as a contributing degree of freedom. It can be seen that symmetry enables the presence of a genuine transition point, a conical intersection, that facilitates transition from one electronic state to another without the necessity of vibrational energy transfer from one vibrational degree of freedom to another. This perfectly explains why, in the presence of such a topological feature, the vibrational energy remains localized in a single degree of freedom. On the other hand, for the nonsymmetrical system this possibility no longer exists and the transition from one state to another will involve vibronic coupling and randomization of the vibrational energy that was localized to begin with.

Figure 18.

Potential energy surfaces calculated at the TD-B3LYP/6-311++G(d,p) level of theory that show the presence of an easy point of transition—a conical intersection—in the case of the symmetric species (left) that will enable a fast transition from the highly lying states to the lower-lying ones in the case of N-methylmorpholine. The top shows the orbital change along CN stretch to illustrate how the n → σ*-state creeps in as an enabler for the transition. Reproduced from ref (85) with permission from RSC.

There are more examples of molecules where the vibrational energy has been preserved in the initially activated degree of freedom, all fascinating in each of their own right. The overarching theme is that the directionality that can be accomplished by localizing energy in a specific vibration can be induced in a high-energy state. The localization is then preserved on a lower-lying state. This is happening despite the involvement of an IC process which is usually considered a statistical bottleneck with involvement of all the available degrees of freedom. The fundamental and applied implications are significant. One example is that the observations show that the range of light sources to induce specific electronic transitions or even bond breakage will be much more diverse than considered hitherto. Also, the preservation concept will allow for utilization of a specific activation that is induced on a specific state to enable a particular activation—even if this particular degree of freedom does not lead to reactivity or to an electronic transition on the initial state. The mechanism differs in each of the individual cases that are discussed here. The internal conversion that allows for the preservation in N-methylmorpholine is enabled by symmetry because coupling to the remaining degrees of freedom is restricted by symmetry-section rules. In two other cases, azobenzene and dibromopropane, similar phenomena are in play.^86,87 For azobenzene, the driver is simply a very steep gradient that enables a transition which is too fast for coupling to the remaining degrees of freedom to occur. The case of DBP is similar to azobenzene. A steep gradient at the Franck–Condon region (induced by significantly different minimum structures at the initial state compared to the end state) drives the nuclei and initiates the key nuclear motion. In the case of DBP an electronic transition is only formally in play, but the concept remains the same because several electronic states are transected en route from the Franck–Condon region to the minimum geometry. The preservation of energy in a specific degree of freedom clearly is the kick off to bond selective chemistry—a topic that has been central since the very early days of femtochemistry.^33,90

4. Directionality in Photochemistry—Does the Ultrafast Bond Breakage Exist?

In this section the final aspect of femtochemistry is brought to light—the actual ultrafast breakage of a chemical bond and the pursuit of bond selective photochemistry. Unless the energy is located directly in a dissociative degree of freedom, there is little hope for the reaction in question to be ultrafast. Most organic systems of actual interest will be classified by the physical chemists as complex, meaning that any reaction will involve complex combinations of molecular vibrations. The photoinduced reactions of organic molecules will take place on a time scale which depends on the time it takes for the internal energy to dissipate across all the vibrational degrees of freedom. Underlying structural factors may direct this energy transfer, but in the absence of directionality the time scale for bond breakage will be determined by intramolecular redistribution of the internal energy. This is quite obviously even more pronounced in thermally induced processes where the possibility of exciting specific degrees of freedom is absent. Essentially, this means that reactions which are induced by ultrashort laser pulses and that do proceed on the femtosecond time scale are, in essence, bond specific. The main challenge is how to unambiguously predict what degrees of freedom are activated upon radiation. As for all of the other photoinduced and directed processes that have been presented herein, this question falls within the dynamophore category, where the ultimate goal is to be able to predict the nuclear motions and associated changes in electronic state and bonding environment by a sheer look at the molecular structure.³⁴ As much as the combined body of data presented in this review takes this aspiration one step closer to reality, we are still not quite there yet. The actual direct observations of ultrafast changes in bonding environment are limited, with the only clear-cut relation being a structural motif and an associated ultrafast bond breakage that is found for halides.⁹¹ In this case, the R–X bond is so sufficiently weak that the n → σ* state is low enough in energy to be accessed by a UV photon.⁹² For this state, the energy continuously decreases with the R–X distance and therefore the R–X bond stretching motion will become activated immediately after excitation to lead to R–X bond rupture on the time scale of the stretching period which essentially is less than 100 fs. That is much faster than the time scale for the internal energy to be redistributed to the remaining degrees of freedom.⁹³⁻⁹⁵ The most complex system where an ultrafast bond breakage has been observed unambiguously is in cyclohexadiene, i.e., in a small symmetric molecule where the reaction is a ring-opening (Figure 19).^35,96

Figure 19.

Ring opening reaction of cyclohexadiene that has been followed in real-time in a time-resolved X-ray study at the Stanford synchrotron facility. The product has been unambiguously identified by X-ray scattering and forms in a few hundreds of femtoseconds because of the continuous energy drop on the first excited state as the ring opens.

So, cyclohexadiene may be a special case that is driven to reaction according to the Woodward–Hoffmann selection rules that really are consequences of a continuously decreasing potential energy in the reactive degree of freedom. In this case the reactive mode is a combination of several modes—so a rather complex motion. There is a similar tendency observed in a range of sulpholenes that also have been shown to lose SO₂ in less than 200 fs and have been shown to give rise to stereochemistry that is in accordance with the symmetry selection rules of Woodward and Hoffmann (Figure 20).⁹⁷

Figure 20.

Ring-opening of sulfolene (shown with numbering) producing butadiene and SO₂ proceeds in either linear or nonlinear fashion to yield dis- or conrotatory products. In thermal reaction the disrotatory product is strongly favored, and is formed in >99.9% yield, while in the photochemical reaction the behavior is reversed, according to the Woodward–Hoffmann rules. Reproduced from ref (97) with permission from John Wiley & Sons.

The study of sulpholene also can be brought to illustrate another important point in discussion of the fundaments of the interactions between femtosecond laser pulses and materials; it does actually seem as if the outcome from a regular lamp and a femtosecond laser differs significantly with respect to both yield and stereochemistry.⁹⁷ This observation needs further exploration, but it is taken as an indication of directionality by the femtosecond pulse as being an important factor.

As much as the specific direction of energy can lead to ultrafast bond breakage by placing the energy right where it is needed, the same considerations can lead to diversion of energy to prevent bonds from breaking. Such phenomena have been argued to be in play for several key biologically active molecules. A mechanism for efficient direction AWAY from a reactive mode has for example been proposed for DNA in solution. Here, UV radiation by 267 nm involves a pathway where coupling to the surrounding bath molecules is responsible for ultrafast deactivation rather than direction toward decomposition.^41,42,44,98 In some cases, there really is a need to evoke the coupling mechanism to induce the desired reaction. This section tries to capture all the relevant aspects of bond breakage as a consequence of the interaction between femtosecond pulses and central organic chromophores.

4.1. Bond Breakage in Ketones and Other Carbonyl Compounds: The Classical Story of the Norrish Type-I Reaction

Ketones have attracted significant attention because of their well-known ability to undergo a light induced C–C simple bond rupture known as the Norrish Type-I reaction (depicted in Figure 21).

Figure 21.

Well-known Norrish Type-I reaction. A ketone loses an alkyl radical.

In addition to this known reactivity pattern, ketones, and in particular acetone, are extremely well-behaved molecules when it comes to gas phase experiments involving molecular beams, so it has been the to-go-to molecule for a benchmarking system and the literature from groups around the globe is vast with a range of different interpretations of the results.^99,100 As shown in this section there are certain excitations that lead to the induction of ultrafast internal conversions that are mediated by specific electronic transitions; herein, we reported on the S₂ state that is reached in cyclic ketones by a 200 nm pulse.^76,89 This excitation initiates a ring puckering motion that leads to a crossing with the S₁ state at which point the electronic transition can take place. If there is a coupling to a reactive mode at the crossing point, it will lead to the induction of an ultrafast bond breakage. This scenario is exactly what was encountered by excitation of ketones to higher-lying Rydberg states with two 310 nm photons; here, the motion that is activated to make the molecule adapt to the new electronic structure on the high-lying state is a pyramidalization at the carbonyl.⁵¹ It turns out, perhaps a bit fortuitously, that in this direction there is a coupling to a repulsive state where the crossing point involves a C–C stretching motion. In layman’s terms this means that the crossing point constitutes more than a simple point of transition; it is in fact an energetic funnel that transfers the internal energy not in random directions but rather into a specific mode that is ultimately dissociative—to put it in another way, the energy is placed right where it is needed for dissociation. This scenario is illustrated in Figure 22.

Figure 22.

Norrish Type-I ultrafast decomposition that is initiated in the highly excited manifold of states at a specific crossing point where there is a coupling to the reactive mode. Reproduced from ref (52) with permission from John Wiley & Sons.

As much as the ultrafast decomposion of the acetone (and the ketones in general) seems to be very wavelength specific and, admittedly, still needs to be verified by the experimental observation of the product radicals, the concept of having a coupling to a reactive mode at a crossing point is a prerequisite for the induction of ultrafast bond breakage. So in the search for specific functional groups that induce (direct) ultrafast bond breakage, it is key to understand the structure at the crossing point.

This concept of directionality in carbonyl compunds has been challenged in a study of amides (formamide and N-metyllformamide). These species are slightly more experimentally challenging because of their high boiling points. Also, it is well-known that their relevant electronic states are somewhat higher in energy so the molecules were exposed to 160 nm excitation. The results are indeed interpreted to conclude that amides do compose on the femtosecond time scale. This finding consolidates the induction of ultrafast bond breakage by the passing of a crossing point between electronic states where there is a coupling to a reactive mode.¹⁰¹

4.2. Presence and (Directed) Absence of Ultrafast Bond Breakage: The Saving Grace for Biologically Relevant Molecules

In the case of molecules where the potential energy curve is continuously decreasing in a reactive degree of freedom the associated bond breakage will proceed on the ultrafast time scale as long as the energy decrease proceeds beyond the van der Waals radii of the constituent fragments. The disulfide bond is known to be photochemically labile.⁶⁹ We have exposed the straight-chain diethylsulfide to 267 nm femtosecond laser pulses and found that the potential energy does indeed decrease beyond 3 Å (Figure 23).⁷⁰ The time-resolved signal does indeed show a decay of the disulfide population in less than 100 fs.

Figure 23.

Potential energy surface of the two lowest singlet excited states of diethyl disulfide calculated along the S–S reaction coordinate at the TD-B3LYP/6-31+G(2df,p)//CASSCF(10,8)/6-31+G(2df,p) level of theory. Reproduced from ref (70) with permission from Elsevier.

As much as the photoinduced decay of the straight-chain disulfides takes place in less than 100 fs, the disulfide structural motif is central in, for example, determining the tertiary structure in proteins.⁴⁵ In many ways, it is counterintuitive that the disulfide bond has survived the natural selection that has taken place throughout evolution because our planet has been swamped in damaging UV radiation to which a regular straight chain disulfide would not be stable. Dithiane is the simplest system that mimics a disulfide bond embedded in a more complex structure such as a protein. The molecule was discussed in section 2 with the focus directed toward internal conversion. For dithiane, the ends of the molecule are tied together to prevent it from flying apart. Thus, the energy only continuously decreases to a certain point (Figure 24). So, in essence there is a block that prevents the disulfide entity from total decay. This block enables the S-ends to vibrate back and forth past each other in a search for an exit channel which ultimately is provided by a crossing to the ground state. Subsequent to the transition, the photon energy is dissipated to the surroundings ensuring that the structural integrity of the disulfide unit is preserved and thus the role as biological building block is retained as shown in the cartoon in Figure 25.

Figure 24.

Potential energy surfaces of the two lowest singlet excited states of dithiane calculated at the SA-3-CAS(10,8)/6-31G(d,p) level of theory. The structures have been linearly interpolated in internal coordinates from the S₀ minimum to the S₀–S₁ point of transition and from the latter to the S₁ minimum. Reproduced from ref (45) with permission from ACS.

Figure 25.

General picture of how an S–S bond in a cyclic structure is deactivated. Subsequent to excitation the molecules stretch the S–S bond to start a torsional motion along the carbon backbone; this dynamical behavior makes the molecule visit the transition region where a strong interaction connects S₁ with S₀. Once on the ground state, the S–S bond is reformed. Reproduced from ref (45) with permission from ACS.

A similar situation arises in the case of the adenine containing nucleotides. Here, it was found that the species containing an adenine base result in decomposition patterns that do not comply with statistical models.⁴⁴ In this case computations have revealed the existence of a crossing point that dissipates the energy in a manner which is similar to what was found for the ketones and for the cyclic disulfide,⁴⁴ that is, a guidance of the internal energy away from the reactive modes by structural changes that lead toward the ground state. Again, the idea is shown as a cartoon in Figure 26. The common denominator here and the saving grace is that the ground state populates faster than the reactive modes can be populated because of the directional push that is induced by the favorable energy gradients.

Figure 26.

Ultrafast internal conversion from the first excited state to the ground state in adenine and its protonated form occurs by either activation of an N–H stretch or via ring puckering that leads to pyramidalization. The potential energy surface topology directs the internal energy in a nonstatistical manner. Reproduced from ref (44) with permission from John Wiley & Sons.

Similar mechanisms have been argued to be in play for other DNA related systems by for example Kohler, Barbatti, Gonzalez, and Keiding independently.^{42,98,102,103} Just as dithiane was argued to be a proxy for peptides, the combined body of data related to systems resembling DNA show how bond breakage can be prevented by directionality toward internal conversion to the ground state. The results are taken to indicate that certain structural motifs have been selected by nature because of their resilience to decomposition.

There is clear-cut evidence for the existence of the ultrafast bond breakage, but it has to involve a mechanism to ensure that the energy is located and stays in the reactive coordinate. This means that the process is directed and nonstatistical exactly as have been shown to be the case for the nonstatistical photophysical processes in section 2. The most obvious way to realize the localization of energy is when it continuously decreases as the reactive mode evolves. Such a scenario is usually referred to as involving a repulsive surface and is in play when halides are undergoing photoinduced processes involving σ* states. An alternative mechanism for deposition of energy involves a coupling to the reactive mode at the point of transition between two electronic states. By another token, ultrafast decomposition can be avoided if the reactive coordinate can be “defused” at the transition point to a lower-lying state—such as the ground state where energy then becomes randomized by dissipation to the solvent or by internal redistribution. Such a mechanism is the saving grace for a range of biomolecules and pose an argument for the natural evolutionary selection of species such as the nucleobases and disulfide bridges.

5. Conclusions, Outlook and Way Ahead

We have addressed the complexity of the interplay between nuclear dynamics, electronic transitions, and photoinduced bond breakage. The main lesson is that internal conversion in small polyatomic molecules is intimately related to the motion that is induced by the energy gradients in the Franck–Condon region. This essentially means that the subsequent processes are directed by the gradients for the (inevitably) nonstatistical events that take place on the femtosecond time scale. Specific nuclear motions are instrumental in directing a molecule toward configurations for which coupling to other electronic states is large and wherefrom population transfer can proceed. This is in turn why such processes are coined as being nonstatistical or nonergodic. Essentially, the observation of an oscillating signal in a femtosecond laser-induced process means that the nuclei are moving coherently and that any associated internal conversion is shorter than that of internal vibrational energy redistribution. A question still remains as to whether the nonergodicity is a molecular property or a function of the activation process. Especially the insight on dynamics at crossing points is central to the understanding of photoinduced reactions.

Different effects of the nonergodic behavior have been observed in the different molecular systems under investigation. We have reflected on the possibility of identifying the main parameters that determine the time scale for a given internal conversion process. In the Born–Oppenheimer approximation, it is ultimately the electronic structure that determines the potential energy surfaces which in turn determine the nuclear dynamics that take place, and one could therefore argue that this is the main parameter. From one perspective, the electronic structure defines the potential energy surfaces, but it is the nuclear dynamics that determine which parts of these surfaces are visited and thus the dynamics is of importance for electronic state transfer processes. A common trait of the molecular systems investigated in our work is the involvement of very few degrees of freedom in the nuclear dynamics that lead to internal conversion. The activation and frequency associated with these degrees of freedom, as well as energy release into them, ultimately determine on what time scale and to what extent the region of the potential energy surface with large coupling terms to other states is visited and thereby determine the time scale for internal conversion. This connection is evidenced by the significant effect of selective modification of these degrees of freedom on the rate of internal conversion observed in our work. The localization of the energy furthermore allows for a connection between nuclear dynamics and structural elements. In cycloketones, the main structural element of importance is the C–CO–C moiety, whereas in 1,2-dithiane it is the disulfide bond. In essence, simply from a consideration of molecular structure, the relative rates of internal conversion in related molecules can to some extent be predicted and impacted. When it comes to ultrafast bond breakage, there is a prerequisite for a continuously decreasing potential energy curve along the reactive degree of freedom, and if more than one state is involved, a coupling at the point of transition to a reactive mode has to be in play such as the one which is observed for ketones. So altogether, the work presented herein perhaps has not completely provided a full predictive roadmap, but at least we are a significant step closer to a predictive “dynamophore” scheme.

As much as the nonergodicity is a molecular property, we are still a step away from a link to processes that are initiated by light sources other than the femtosecond laser. The sun is incoherent and systems in solution are incoherent. As much as we have tried to transfer some of the gas phase consideration to problems in the condensed phase,^104−106 there is still a significant amount of work to be done to fully understand the nonstatistical and directionality aspects of solution-phase problems. The same appears to link processes that are induced by a femtosecond laser pulse and those that have their offspring in excitation by incoherent CW sources such as the sun. This would be an exciting direction to pursue going forward along with perhaps the development of direct methods for the observation of energy transfer in IR-pump/IR-probe schemes that will lead to controlled activation of a molecular degree of freedom followed by the direct observation of its temporal evolution. This would take femtochemistry one step closer to application in, for example, optimization of solar cell materials where a particularly favorable structural motif might reveal itself through the observation of the real-time nuclear motion that is induced by light absorption.

Biography

Dr. Solling is currently a Senior Research Scientist and the Program Lead of the Oilfield Chemicals program in the Center for Integrated Petroleum Research, College of Petroleum Engineering & Geoscience, King Fahd University of Petroleum and Minerals. Dr. Solling has a background in Physical Organic Chemistry as studied with ultrafast lasers, and interest that came from his postdoc years at Caltech under the guidance of late Professor Ahmed H. Zewail. After a three year position as a Researcher at Risø National Laboratories, Dr. Solling became Associate Professor (Organic Chemistry) at the University of Copenhagen and worked on ultrafast phenomena until he was appointed team lead at Maersk Oil Research and Technology Centre in Qatar. He returned to the University of Copenhagen as a Full Professor in 2016 to set up an educational specialization in Chemistry for the oil and gas sector. In 2018 he moved to the Kingdom of Saudi Arabia to be a part of CIPR.

The author declares no competing financial interest.