Abstract
In this report, the geometric and electronic properties and static and dynamic hyperpolarizabilities of alkali metal-doped C6O6Li6 organometallics are analyzed via density functional theory methods. The thermal stability of the considered complexes is examined through interaction energy (Eint) calculations. Doping of alkali metal derives diffuse excess electrons, which generate the electride characteristics in the respective systems (electrons@complexant, e–@M@C6O6Li6, M = Li, Na, and K). The electronic density shifting is also supported by natural bond orbital charge analysis. These electrides are further investigated for their nonlinear optical (NLO) responses through static and dynamic hyperpolarizability analyses. The potassium-doped C6O6Li6 (K@C6O6Li6) complex has high values of second- (βtot = 2.9 × 105 au) and third-order NLO responses (γtot = 1.6 × 108 au) along with a high refractive index at 1064 nm, indicating that the NLO response of the corresponding complex increases at a higher wavelength. UV–vis absorption analysis is used to confirm the electronic excitations, which occur from the metal toward C6O6Li6. We assume that these newly designed organometallic electrides can be used in optical and optoelectronic fields for achieving better second-harmonic-generation-based NLO materials.
1. Introduction
Interest in designing high-performance nonlinear optical (NLO) materials is growing rapidly due to their widespread applications in optical computing,1−3 optical communication,4,5 optical switching,6,7 optical logic functions,8,9 dynamic image processing,10,11 and many other optoelectronic fields.12−17 Recently, a unique class of compounds known as electrides having isolated excess electrons has garnered great interest from the chemical society.18−21 Due to this nontrivial electronic structure, they are easily polarizable and can serve as superior nonlinear optical materials.19,22,23 Electrides due to their certain interesting properties such as the ultralow work function, relatively high catalytic activity, high electronic mobility, and optical and anisotropic properties have great potential for various applications.24−28 In 1983, Dye and co-workers fabricated the first organic crystalline electride consisting of organic complexant cages in which alkali metals and electrons were trapped.29 Since then, various organic and inorganic electrides have been reported in literature, and their novel electronic structures have been investigated both computationally and experimentally.30−33
Johnson and co-workers performed density functional theory (DFT) investigation for describing the organic electronic structure of eight organic electrides and confirmed the presence of localized interstitial electrons and hence defined their electride properties.34 Kim et al. studied organic magnetic electrides in which they used maximally localized Wannier functions to identify the “cavity” electrons and the “empty atom” technique.35 Saha et al. prepared synthetically viable neutral [Mg4(DippHL)2]2–·2[K@CE]+ (CE = 18-crown-6 ether), containing four magnesium atoms and two Mg–Mg bonds, where the latter one act as an electride.36 Dale and Johnson also used the DFT method for reproducing the known antiferromagnetic behavior of organic electrides.24,37 Organic electrides are thermally less stable, so research is shifted toward the design and synthesis of thermally stable inorganic electrides.24,38,39 Hosono and co-workers synthesized the first room-temperature-stable inorganic electride Ca6Al7O16 (C12A7:2e–) via oxygen-reduction processes while starting from the mineral mayenite (12CaO·7Al2O3).40 Since then, C12A7:2e– has been used for ammonia synthesis41 and as an electron-injection barrier material.42 The discovery of C12A7:2e– has stimulated many new efforts to search for other inorganic electrides. Zhang et al. designed 33 hitherto unexpected structure prototypes of inorganic electrides through computer-assisted methods, in which 19 are not in the known structure databases.43 Boldyrev and co-workers studied electride-like features in the MgO crystal with the defect F-centers. Their calculations show that the corresponding electride-like cluster possesses a noticeably large first hyperpolarizability (βo = 5733 au).44 Wang et al. designed bipyramidal CaN3Ca by using quantum mechanical methods. They observed that these inorganic aromatic Robin–Day-type superalkali electrides have high sensitivity for use in multistate nonlinear optical switches.45 The design and synthesis of organic and inorganic electrides continues because of their applications in catalysis, metal-ion batteries, NLO materials, and so forth Recently, transition-metal-based organometallics have been reported to exhibit a better second-harmonic generation (SHG) response.46−49
From the literature, it has been revealed that introducing excess electrons into a molecule can remarkably enhance the first hyperpolarizability (βo).50,51 The first hyperpolarizability (βo) is the key factor which determines the presence of the NLO response in materials.52,53 Many studies have been conducted to investigate the first hyperpolarizability (βo) of different materials.54−56 Computational work on the electride-type structure of Mg4O3 showed that Mg4O3 has pronounced NLO properties because it exhibited a large value of hyperpolarizability, that is, βo = 5733.46 au.44 Meanwhile, the strategy of metal adsorption on isolated surfaces has been introduced in recent years to further enhance the NLO properties. In this regard, many computational chemists studied the effect of alkali metal doping on NLO responses. As we know, alkali metals have a low ionization energy, due to which they can easily donate electrons to the system and results in an increase of the electron number. Thus, the NLO response will be enhanced due to the increasing number of electrons.57−59 For example, the doping of inorganic Al12N12 nanocages into alkali metals narrowed the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap to a range of 0.49–0.71 eV. Furthermore, the value of hyperpolarizability (βo) is also increased, which resulted in a large NLO response.60,61
Various alkali metal-doped organic electrides have been reported in literature with a large NLO response. For example, the alkali-metal-doped organic complexes (Li@calix4pyrrole and Li+(calix4pyrrole)M–) have been reported by Yu and co-workers as effective NLO materials because of their high values of hyperpolarizability (ranging from 10,969 to 35,934 au).62 Similarly, alkali metal-doped organic fluorocarbon chains of H–(CF2–CH2)3–H with a high NLO response have been studied. Six different structures of Li atom-doped fluorocarbon complexes [Lin-H–(CF2–CH2)3–H (n= 1, 2] have been examined. Among them, the highest NLO response of 76,978 au was recorded.63 Recently, another electride Li+(C20H15Li5)e– modified by lithiation of the dodecahedron has been investigated computationally. In this electride, the C20 closed cage not only acts as a barrier for lithium ions but also has a negative inner electric field to stabilize the Li ion. Here, the excess electrons are released, which remain encapsulated in the Li5 cavity. Thus, Li+(C20H15Li5)e– exhibits a large value of hyperpolarizability (1.4 × 104 au) with potential for application in NLO materials.64 Mahmood and co-workers analyzed the organometallic C6O6 surface for the NLO response. They doped superalkalis on the C6O6 surface and achieved electride characteristics in their designed complexes with large hyperpolarizability.65 C6O6Li6 is obtained from lithium-ion batteries, as a result of redox reactions of electrodes. Cyclohexane is the precursor of this compound in lithium-ion batteries. Pure C6O6Li6 and alkali metal-doped C6O6Li6 are used here to study their NLO properties. We expect that the doped organometallics might show high values of induced dipole moment, polarizability, hyperpolarizability, and a high NLO response. The reason might be the increase in electronic density diffusion from the dopant to the surface or vice versa. Among alkali metals, lithium, sodium, and potassium are taken into account for doping on the C6O6Li6 organometallic surface, and their electronic and NLO properties are comparatively studied.
2. Results and Discussion
2.1. Geometries, Thermodynamic Stabilities, and Electride Characteristics of Alkali Metal (Li, Na, and K)-Doped C6O6Li6 Organometallics
The energy minimum structure of C6O6Li6 is shown in Figure 1, which is optimized at the ωb97XD/6-31+G(d,p) level of theory. It has a planar and star-like geometry having C–C, C–O, and O–Li bond lengths of 1.42, 1.38, and 1.79 Å, respectively. The alkali metal (Li, Na, and K)-doped M@C6O6Li6 complexes are also optimized at the same level of theory as shown in Figure 1. After optimizing the metal-doped organometallics, the bond lengths observed are 1.41, 1.37, and 1.81 Å for C–C, C–O, and C–Li, respectively. These minute changes in bond lengths confirm that structural integrity of the organometallic complex remains preserved after doping. The interaction distance of the Li metal from the center of ring is 1.95 Å, whereas for Na and K these are 2.46 and 2.80 Å, respectively. A monotonic trend of an increasing interaction distance, with an increase in the atomic number, from the center of the ring is observed, and this is similar to the already reported results.66 The interaction energy of the system reveals that the thermodynamic stability of any system that is highly exothermic in nature reflects a greater thermodynamic stability.67 The interaction energies of these alkali metal-doped M@C6O6Li6 complexes are given in Table 1. The Eint. values of Li@C6O6Li6, Na@ C6O6Li6, and K@C6O6Li6 organometallics are −27.11, −19.30, and −19.46 kcal mol–1, respectively. Among the three considered organometallics, the most stable one is the Li@C6O6Li6 complex due to the least interaction distance of Li with the complexant (vide supra) and hence a stronger interaction. The reason for the high thermal stability of Li-doped complexes is the low ionization potential and a smaller atomic size of the Li metal and thus is considered as the best adsorbing species on the C20 nanocage. The results are comparable to those of the work reported by Mahmood and co-workers on single and multiple alkali-doped C24 nanocages.66
Figure 1.
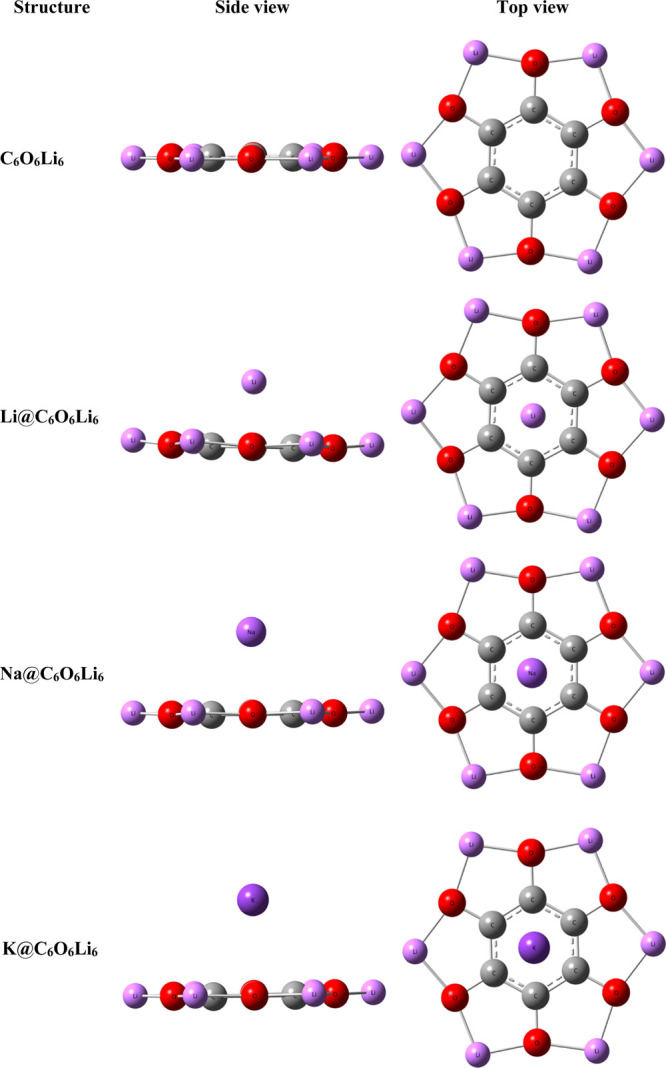
Side and top views of the optimized geometry of pristine C6O6Li6 and alkali metal (Li, Na, and K)-doped C6O6Li6 organometallics calculated at the ωB97XD/6-31+G(d,p) level.
Table 1. Smallest M-Ring Distance (dM-ring, M = Li, Na, and K); NBO Charges on Carbon (Qc), NBO Charges on Oxygen (Qo), and NBO Charges on Lithium (QLi) of the C6O6Li6 Nanocluster; NBO Charges on the Metal Dopant (QM, M = Li, Na, and K); Interaction Energies (Eint); and Vertical Ionization Energies (IEv).
| systems | dM-ring (Å) | QC (|e|) | Qo (|e|) | QLi (|e|) | QM (|e|) | Eint kcal mol–1 | IEv eV |
|---|---|---|---|---|---|---|---|
| C6O6Li6 | 0.176 | –1.122 | 0.947 | 4.39 | |||
| C6O6Li6–Li | 1.95 | 0.133 | –1.089 | 0.951 | 0.033 | –27.11 | 2.82 |
| C6O6Li6–Na | 2.46 | 0.147 | –1.099 | 0.952 | 0.007 | –19.30 | 3.03 |
| C6O6Li6–K | 2.80 | 0.154 | –1.106 | 0.951 | 0.015 | –19.46 | 2.73 |
To investigate the electride characteristics and electronic properties of M@C6O6Li6 organometallic complexes, Frontier molecular orbital analysis is performed. The energies of HOMOs, LUMOs, and the corresponding HOMO–LUMO (H–Lgap) energy gaps of pure C6O6Li6 and alkali metal-doped organometallics are presented in Table 2. The calculated energy gap (H–Lgap) of pure C6O6Li6 is 4.64 eV. The decoration of alkali metals on the surface resulted in a decrease of the corresponding H–Lgap (2.77–3.12 eV). The energies of the HOMO, LUMO, and the corresponding H–Lgap of the Li@C6O6Li6 complex are −2.73, 0.08, and 2.9 eV, respectively. For Na@C6O6Li6, the energies of the HOMO, LUMO, and H–Lgap are −3.03, 0.09, and 3.12 eV, respectively. Similarly, in the case of the K@C6O6Li6 complex, they are −2.73, 0.04, and 2.77 eV, respectively. The decreased H–L gaps reflect the conducting behavior of all newly designed organometallics.66 The decrease in H–Lgap is due to the formation of new HOMOs at high energy because of the presence of excess electrons. These excess electrons are introduced by electropositive alkali metals.68,69
Table 2. Dipole Moment (in Debye), Polarizability (αo), Static First Hyperpolarizability (βo), Vector-Based Static First Hyperpolarizability (βVec), Static Second Hyperpolarizability (γtot), Oscillator Strength (fo), Transition Energy (ΔE), the Variational Dipole Moment Z Component between the Ground and Crucial Excited States (Δμ), βZ under the Two-Level Model, the Energies of HOMO (EHOMO), the Energies LUMO (ELUMO), and the HOMO–LUMO Gaps (H–Lgap in eV)a.
| parameters | C6O6Li6 | C6O6Li6–Li | C6O6Li6–Na | C6O6Li6–K |
|---|---|---|---|---|
| μo (au) | 0.01 | 5.96 | 6.34 | 7.84 |
| αo (au) | 136 | 608 | 503 | 558 |
| *1βo (au) | 2.3 × 102 | 8.7 × 104 | 1.4 × 105 | 2.9 × 105 |
| *2βo (au) | 1.9 × 102 | 4.7 × 104 | 4.9 × 104 | 2.5 × 105 |
| βvec (au) | 4.13 | 8.4 × 104 | 8.3 × 103 | 2.7 × 105 |
| βHRS (au) | 1.60 | 3.8 × 104 | 2.9 × 105 | 8.4 × 103 |
| γtot (au) | 2.3 × 105 | 9.7 × 107 | 3.4 × 107 | 1.6 × 108 |
| fo | 0.20 | 0.22 | 0.11 | |
| sΔE (eV) | 2.39 | 1.45 | 1.59 | 1.02 |
| Δμ (Debye) | 0.01 | 0.11 | 5.35 | |
| βZ (au) | 1.1 × 103 | 4.3 × 103 | 1.2 × 105 | |
| EHOMO (eV) | –4.39 | –2.82 | –3.03 | –2.73 |
| ELUMO (eV) | 0.24 | 0.07 | 0.09 | 0.04 |
| H–Lgap (eV) | 4.63 | 2.89 | 3.12 | 2.77 |
*1βo (au) and *2βo (au) represent hyperpolarizability at the ωB97XD and LC-BLYP levels, respectively.
From the pictorial representation of isodensities of HOMOs of pure C6O6Li6 and alkali metal-doped organometallics (Figure 2), it is observed that the electronic density of HOMOs of the Li@C6O6Li6 and Na@C6O6Li6 organometallics mainly resides in empty space (does not shared by any atom), which proves their electride characteristics.65,70,71 The electride features of these both organometallics (Li@C6O6Li6 and Na@C6O6Li6) originate due to the presence of an intramolecular push–pull mechanism. The isolated C6O6Li6 molecule first pulls the valence s-shell electrons of the alkali metal to form an anion and then the resulting anion pushes these electrons to produce isolated excess electrons. In these newly designed electrides, the electronic density is present mainly near the alkali metal, which reflects the more contribution of alkali metal as compared to C6O6Li6. An exceptional behavior is observed for the K@C6O6Li6 complex, wherein the electronic density mainly resides over K, reflecting the simple excess electron system instead of the electride character.50,65
Figure 2.
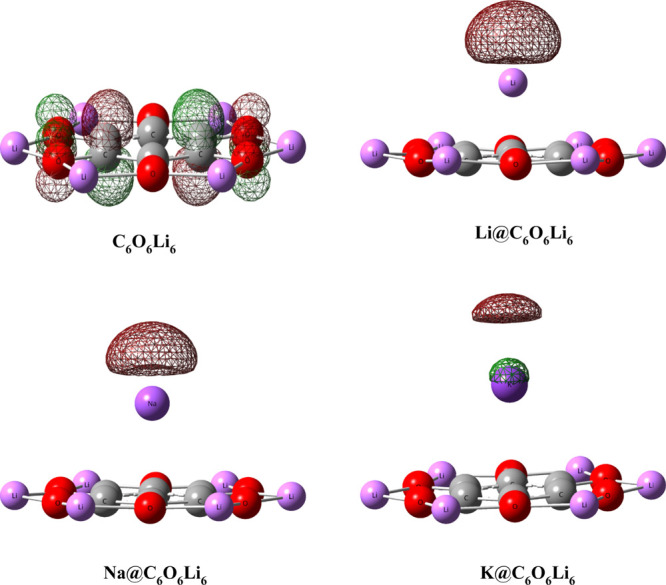
Graphical representation of HOMO of pristine C6O6Li6 and alkali metal-doped C6O6Li6 organometallics (isovalue = 0.05).
As the electrides contain a loosely bound electronic density, not belonging to any atom, the electronic stability is very important, which is directly related to the vertical ionization energies.43,72 Both electrides, Li@C6O6Li6 and Na@C6O6Li6, possess sufficiently high vertical ionization energies of 2.83 and 3.03 eV, respectively, which is indicative of their electronic stability.
Natural bond orbital (NBO) charge analysis revealed that the alkali metal is positively charged, whereas the negative charge on the complexant is increased. This indicates that charge is transferred from the metal to the C6O6Li6 ring. The average NBO charge on the Li atom (0.033 |e|) is comparatively higher than those of Na (0.007 |e|) and K (0.015 |e|) atoms. The reason for a higher charge on Li represents the ease in releasing electrons due to its smaller size and low ionization energy as observed by Biglari and co-workers.73 In all these organometallics, alkali metals donate the electronic density to the C6O6Li6 surface due to their low ionization energies compared to other metal atoms and are considered as the source of excess electrons for the generation of electride properties in the respective complexes.
2.2. Static and Dynamic Hyperpolarizability Analyses of Newly Designed Electrides for NLO Applications
2.2.1. Static Hyperpolarizability Analysis
All parameters, which are responsible for the effective NLO response of the newly designed organometallics (electrides), are given in Table 2. The dipole moment of isolated C6O6Li6 is 0.0 D due to its symmetry. However, the doping of alkali metals results in charge transfer, thus breaking the symmetry, which in turn increases the dipole moment. The dipole moments of Li@C6O6Li6, Na@C6O6Li6, and K@C6O6Li6 organometallic complexes are 5.96 D, 6.34 D, and 7.84 D, respectively. The monotonic trend of the increase in the dipole moment reflects the more charge separation of charges with an internuclear distance, going from Li to K, which is indicative of their possible linear and nonlinear optical potential, similar to the work of Cherepanov and co-workers.74 For investigation of the linear optical response, the mean static polarizabilities (αo) of newly designed electrides and the excess electron complex are investigated as well. αo of M@C6O6Li6 complexes is in the range of 503 to 608 au, which is very high as compared to that of the pure C6O6Li6 (136 au). The nonmonotonic trend of the increase in αo is observed as follows; Li@C6O6Li6 > K@C6O6Li6 > Na@C6O6Li6. The trend of polarization is governed by the charge transfer. More charge is transferred in the case of Li (0.033 |e|), followed by K (0.015 |e|), while less charge is shifted from the Na metal (0.007 |e|). Subsequently, this charge separation causes polarization changes in these organometallics.
Furthermore, the NLO response of alkali metal-doped M@C6O6Li6 (M = Li, Na, and K) complexes (electrides) is confirmed by computing their static first hyperpolarizabilities (βo) at the LC-BLYP and ωB97XD levels with a similar 6-311++G (2d,2p) basis set (Table 2). The βo value of the pristine system is relatively small (1.9 × 102 au at LC-BLYP and 2.3 × 102 au at ωB97XD). The βo values of the M@C6O6Li6 (M = Li, Na, and K) complexes (electrides) range from 4.7 × 104 to 2.5 × 105 au at the LC-BLYP level. At the ωB97XD level, the βo values of the M@C6O6Li6 (M = Li, Na, and K) complexes (electrides) range from 8.7 × 104 au to 2.9 × 105 au. Despite the small differences in their values with different functionals, the trend of hyperpolarizabilities is quite comparable. The similar values and the same trend of hyperpolarizability with both functionals are due to the same 1.00 fraction of nonlocal exchange. As a result of doping of alkali metals, a remarkable NLO response of M@C6O6Li6 electrides is observed and the static first hyperpolarizability (βo) is tremendously increased. βo values of the newly designed electrides and the excess electron system are in the range of 3.4 × 104 to 2.9 × 105 au. The highest βo is observed for K@C6O6Li6, that is, of 2.9 × 105 au, while the lowest value is computed for the Li@C6O6Li6 electride. The results revealed the monotonic increasing trend of βo, and it increases from Li@C6O6Li6 to K@C6O6Li6. This monotonic behavior of the designed electrides can be correlated with the vertical ionization potential, which is the major factor that affects the βo value. It increases with the decrease in vertical ionization energy.75−77 The K@C6O6Li6 complex has the lowest vertical ionization energy (−2.73 eV) among all organometallics (Na@C6O6Li6 = −2.73 eV and Li@C6O6Li6 = −2.73 eV), and exhibits the largest nonlinear optical response (2.9 × 105 au). To gain further insights into factors affecting the βo values of the designed electrides, we calculated the βz values by employing a two-level model using Multiwfn software.78 The βz values from the two-level model nicely correlate with our computed values of first hyperpolarizability (βo). From the two-level model, it can be observed that the crucial excitation energy is the dominant factor in determining the first hyperpolarizability values of the electrides. The crucial excitation energies of Li@C6O6Li6, Na@C6O6Li6, and K@C6O6Li6 are 1.45, 1.59, and 1.02 eV, respectively. Because (βo) is inversely proportional to the cube of crucial excitation energy, the βo value of K@C6O6Li6 is large, but the crucial excitation energy is low; on the other hand, the βo value of Li@C6O6Li6 is small, while the crucial excitation energy is large. An exceptional behavior is observed for Na@C6O6Li6, where the excitation energy is large (1.59 eV); however, βo for this complex is also high (1.4 × 105 au). Besides the excitation energy, βtot is directly proportional to Δμ. The trend in the values of Δμ is the same as that in the values of first static hyperpolarizability. It can be concluded that Δμ is a major factor, which influences the hyperpolarizability of the complexes (as shown in Table 2). The trend of increasing βo and Δμ is Li@C6O6Li6 (βo = 8.7 × 104 au and Δμ = 0.01 eV) < Na@C6O6Li6 (βo = 1.4 × 105 au and Δμ = 0.11 eV) < K@C6O6Li6 (βo = 2.9 × 105 au and Δμ = 5.35 eV).
βvec values of alkali metal-doped M@C6O6Li6 (M = Li, Na, and K) electrides are calculated and provided in Table 2. βvec is the projection of the first hyperpolarizability along the dipole moment vector and is a more reliable factor for predicting the NLO properties.79 Among all M@C6O6Li6 electrides, the dipole moment vector lies on the z-axis. The βvec values of Li@C6O6Li6, Na@C6O6Li6, and K@C6O6Li6 are 8.4 × 104, 8.3 × 103, and 2.7 × 105 au, respectively. It is observed that βvec values are very much comparable with the first hyperpolarizability (βo) results. The trend of increasing βvec value (2.7 × 105 au) for K@C6O6Li6 is almost similar to that of βo (2.9 × 105 au).
Hyper-Rayleigh scattering (HRS) is a very useful experimental technique for the direct measurement of the static hyperpolarizability values.75,80 βHRS values along with the depolarization ratio (DR) of all newly designed electrides and the diffuse excess electron system are calculated, and the values are given in Table 2. The observed trend of βHRS values is as follows; Na@C6O6Li6 (2.9 × 105 au) > Li@C6O6Li6 (3.8 × 104 au) > K@C6O6Li6 (8.4 × 103 au). The DR values of pure and alkali metal-doped organometallics, that is, Li@C6O6Li6, Na@C6O6Li6, and K@C6O6Li6, are 1.5, 3.1, and 3.4, respectively. βHRS depends on the polarization angle, and it is observed that pristine C6O6Li6 and the corresponding alkali metal-doped organometallics (Na@C6O6Li6 and K@C6O6Li6) are octupolar molecules with an octupolar contribution of Φ (βJ = 3) of 89.6, 58.8, and 56.6%, respectively.
2.2.2. Frequency-Dependent (Dynamic) Hyperpolarizability Analysis
For explaining the high accuracy of the results and gaining insights for the experimental utility, we computed the frequency-dependent first hyperpolarizability coefficients that include electro-optic Pockel’s effect (EOPE) with β(−ω;ω,0) and SHG of first hyperpolarizability with β(−2ω;ω,ω) at the routinely used laser wavelengths of 532 and 1064 nm, respectively. The detailed values are given in Table 3. The dynamic first hyperpolarizability parameters are always dependent on wavelengths. At 532 nm, the values of EOPE range from 2.6 × 104 to 7.3 × 105, and at 1064 nm of wavelength these are from 4.3 × 105 to 5.8 × 105 au. Both electrides, Li@C6O6Li6 and Na@C6O6Li6, have their maximum EOPE values at 532 and 1064 nm, respectively, indicating the resonant enhancement of these at respective wavelengths, while for K@C6O6Li6 the resonant enhancement occurs at 1064 nm (4.3 × 105 au). Similarly, β(−2ω;ω,ω) values reflecting the SHG response range from 1.7 × 104 to 6.5 × 105 au at a wavelength of 532 nm and range from 2.7 × 105 to 3.8 × 105 au at a wavelength of 1064 nm. At 532 nm, the highest SHG value has been computed for the Na@C6O6Li6 complex, while both Li@C6O6Li6 and K@C6O6Li6 organometallics have shown the strong SHG response at 1064 nm.
Table 3. Frequency-Dependent First Hyperpolarizability (β in au), Second Hyperpolarizability (γ in au), and the Nonlinear Refractive Index (n2 in cm2 W–1) of Designed Electrides (Complexes) M@C6O6Li6 (M = Li, Na, and K).
| parameters | frequency ω | C6O6Li6 | C6O6Li6–Li | C6O6Li6–Na | C6O6Li6–K |
|---|---|---|---|---|---|
| β(−ω,ω,0) (au) | 0.000 | 4.1 × 100 | 8.4 × 104 | 8.9 × 103 | 2.7 × 105 |
| 0.0428 (1064 nm) | 6.7 × 100 | 5.9 × 105 | 4.3 × 105 | 4.3 × 105 | |
| 0.856 (532 nm) | 1.0 × 103 | 3.5 × 105 | 7.3 × 105 | 2.6 × 104 | |
| β(−2ω,ω,ω) (au) | 0.000 | 4.1 × 100 | 8.4 × 104 | 8.9 × 103 | 2.7 × 105 |
| 0.0428 (1064 nm) | 7.4 × 101 | 3.0 × 105 | 3.8 × 105 | 2.7 × 105 | |
| 0.0856 (532 nm) | 3.5 × 103 | 9.3 × 104 | 6.5 × 105 | 1.7 × 104 | |
| γ(−ω;ω,0,0) (au) | 0.000 | 2.3 × 105 | 9.8 × 107 | 3.3 × 107 | 1.6 × 108 |
| 0.0428 (1064 nm) | 3.7 × 105 | 2.0 × 108 | 1.4 × 109 | 1.4 × 108 | |
| 0.0856 (532 nm) | 5.2 × 108 | 1.5 × 1011 | 1.3 × 109 | 3.5 × 106 | |
| γ(−2ω;ω,0,0) (au) | 0.000 | 2.3 × 105 | 9.8 × 107 | 3.3 × 107 | 1.6 × 108 |
| 0.0428 (1064 nm) | 1.5 × 107 | 1.5 × 109 | 3.8 × 108 | 4.7 × 107 | |
| 0.0856 (532 nm) | 5.0 × 107 | 5.9 × 1010 | 1.2 × 109 | 5.4 × 106 | |
| γDFWM (−ω;ω,−ω,ω) (au) | 0.0428 (1064 nm) | 3.4 × 107 | 3.6 × 109 | 1.5 × 1010 | 2.4 × 107 |
| 0.0856 (532 nm) | 6.1 × 1010 | 2.7 × 1013 | 6.4 × 1010 | 4.85 × 104 | |
| n2 (cm2 W–1) | 0.0428 (1064 nm) | 2.8 × 10–15 | 3.0 × 10–13 | 12.9 × 10–13 | 2.0 × 10–16 |
| 0.0856 (532 nm) | 5.1 × 10–12 | 2.2 × 10–12 | 5.3 × 10–13 | 4.0 × 10–19 |
2.2.3. Third-Order Nonlinear Optical Response
The third-order nonlinear optical response of the respective complexes was determined, and the dc-Kerr effect γ(−ω;ω,0,0), the electric field-induced SHG(ESHG), and the quadratic nonlinear refractive index of organometallics at 532 and 1064 nm were computed. The results emphasize that C6O6Li6 and Li@C6O6Li6 have the highest responses for the dc-Kerr effect γ(−ω;ω,0,0) at 532 nm; on the other hand, Na@C6O6Li6 and K@C6O6Li6 have their highest values at 1064 nm. It is reflected from the results that all organometallics except the K-doped complex have their highest values of the ESHG response at 532 nm. The remarkably high ESHG and the dc-Kerr effect γ(−ω;ω,0,0) values of C6O6Li6–K at high wavelengths indicate that the response of this organometallic complex can be enhanced by increasing the wavelength of incident light.
The four degenerate wave mixing values are calculated by using the second hyperpolarizability coefficients, then the nonlinear quadratic refractive index is calculated from γDWFM by using the equation shown below
| 1 |
The results of n2 are shown in Table 3. The quadratic nonlinear refractive index values of all doped organometallics are high at 532 nm, that is, 2.2 × 10–12 au (Li@C6O6Li6) and 5.3 × 10–13 au (Na@C6O6Li6), except for the potassium doped complex (K@C6O6Li6 = 2.0 × 10–16 au), which has a high value of quadratic nonlinear refractive index at 1064 nm. Among all these organometallics, the highest response has been observed for Li@C6O6Li6 at 532 nm, followed by a similar high response for Li@C6O6Li6 at a higher wavelength (1064 nm). Thus, we can predict that any variation in wavelength affects the response of a complex.
2.3. TD-DFT Calculations
NLO materials having high first hyperpolarizability are used in SHG for doubling of the frequency.67,81 Thus, these NLO materials (those that have high first hyperpolarizability) must have sufficient transparency in the laser beam UV region. For this purpose, UV–vis absorption analysis of the pure C6O6Li6 surface and doped organometallics was performed. Absorption spectroscopy calculations performed using the TD-DFT method also provides information about the absorption maxima (wavelength) of these NLO materials. None of these organometallics has shown absorption in the UV region and some part of the visible region (below 500 nm). Only the pure C6O6Li6 surface (λmax = 519 nm) shows absorption in these regions, as shown in Figure 3. After doping of the pure surface, the resultant-doped organometallics show a red shift to a large extent. The highest λmax value (1658 nm) is obtained for K@C6O6Li6, followed by Li@C6O6Li6 (λmax = 1438 nm), and the lowest λmax value (1188 nm) is observed for Na@C6O6Li6. A monotonic increase of the absorption maxima (wavelength) occurs with increasing atomic number of alkali metals in the dopant except for Na-doped organometallics. As the atomic size of K increases, more easily it can lose an electron to the surrounding species because the ionization potential is decreased. The Li atom has a small atomic size, so it can also shift the electronic density toward the surface. The obtained UV–vis results justify that the electronic excitation takes place in these organometallics. The HOMO–LUMO gaps are inversely proportional to the λmax values, which also clarified these results. The UV–vis spectra clearly illustrate the transparency of doped organometallics, which ought to be practically used for routine laser works. The proposed organometallics can be used as efficient NLO materials in the deep-UV region because of their full transparency in the deep-UV region (≤200 nm).
Figure 3.
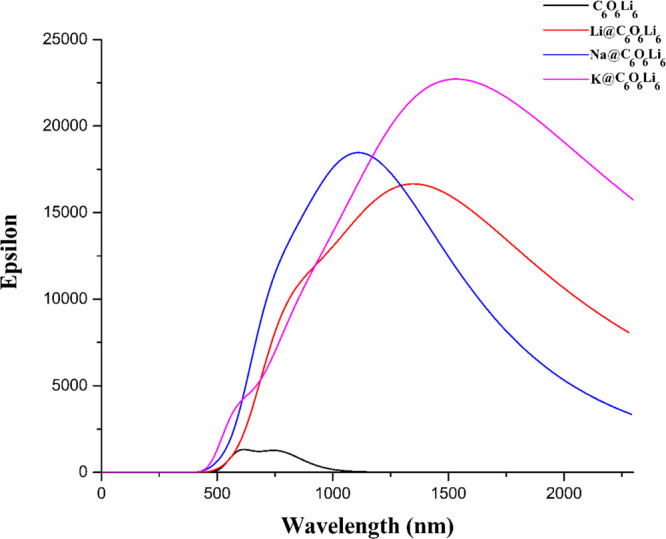
UV–vis spectra of pure and metal-doped M@C6O6Li6 (M = Li, Na, and K) organometallics.
3. Conclusions
In this study, we investigated the geometric, electronic, and optical properties and the NLO response of pure C6O6Li6 and alkali metal-doped C6O6Li6 organometallics. Thermal stabilities of the pure and doped organometallics are analyzed using interaction energy (Eint) calculations. Their electronic and FMO properties are also studied. The results illustrate that doping of a system with alkali metals increases the electronic density and enhances the electride character in the system via generating an excess electron system (electrons@complexant, e–@M@C6O6Li6, M = Li, Na, and K). The electronic density shifting is also supported by NBO charge analysis. These electrides are then investigated further for high NLO responses. The results revealed that the potassium-doped C6O6Li6 (K@C6O6Li6) complex has high values of first hyperpolarizability (βo = 2.9 × 105 au) and a third-order NLO response (γtot 1.6 × 108 au), along with a high refractive index at 1064 nm, implying that the NLO response will be increased by increasing the wavelength. From these results, it is believed that these newly designed organometallics can be used in optical and optoelectronic fields for achieving better SHGs based on their electride properties.
4. Computational Methodology
All calculations are performed using Gaussian 09,82 and the results are visualized by using GaussView 5.0.83 The geometries of pristine C6O6Li6 and alkali metal (Li, Na, and K)-doped C6O6Li6 complexes are optimized at the ωB97XD/6-31+G(d,p) level of theory.84−86 Frequency calculations are also performed to confirm that the optimized structures correspond to true minima on the potential energy surface (absence of imaginary frequency). Interaction energies for the alkali metal-doped C6O6Li6 organometallic complexes are calculated as follows
| 2 |
All other parameters, that is, electronic energy, interaction energy, vertical ionization energy, NBO charges, and HOMO–LUMO gaps have been calculated using the same ωB97XD functional with the 6-31+G(d,p) basis set.
The vertical ionization energy is calculated by using the formula
| 3 |
where E(X) is the energy of the neutral complex and E(X+) is the energy of the respective cation.
Parameters used for investigation of the linear optical response and nonlinear optical response include the polarizability (αo), first hyperpolarizability (βo), and second hyperpolarizability (γ). These parameters are calculated by using the LC-BLYP/6-311++G (2d,2p) and ωB97XD/6-311++G (2d,2p) levels of theory. LC-BLYP and ωb97XD are long-range-corrected functionals and have the correct 1.00 fraction of nonlocal exchange. They give more accurate results for noncovalent interactions30,87,88 and optical and nonlinear optical properties.71 The literature reveals several studies, which illustrate the reliability and validity of these functionals for the calculation of polarizability and hyperpolarizabilities.89−93 Pople’s 6-311++G (2d,2p) basis set is a suitable basis set with these functionals for the calculations of nonlinear optical properties and used in a number of recent works on nonlinear optical materials.94 Therefore, it is also selected in this study. The static polarizability (αo), static first hyperpolarizability (βo), and static second hyperpolarizability (γtot) are calculated through eqs 4, 5, and 7, respectively. Furthermore, frequency-dependent NLO responses are also calculated at wavelengths 532 and 1064 nm to obtain the results, which are predominantly required by the experimentalists. These frequency-dependent NLO responses are calculated in terms of the EOPE β(−ω,ω,0), electro-optical Kerr effect (EOKO) γ(−ω;ω,0,0), and SHG, that is, β(−2ω,ω,ω) and γ(−2ω,ω,ω,0).
| 4 |
| 5 |
The frequency-dependent first-order hyperpolarizability is estimated as follows
| 6 |
Static second hyperpolarizability (γ) can be calculated from the following equation
| 7 |
The frequency-dependent second-order hyperpolarizability is estimated as follows
| 8 |
where 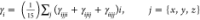
βvec is the projection of first hyperpolarizability on the dipole moment vector, which is as follows
| 9 |
Here, μi is the representation of the dipole moment in the direction of i, while |μ| is the total dipole moment of complexes, where βi = βiii (−2ω,ω,ω) + βijj (−2ω,ω,ω) + βikk (−2ω,ω,ω) for SHG and βi = βiii (−ω,ω,0) + βijj (−ω,ω,0) + βikk (−ω,ω,0) for EOPE.
HRS is calculated as follows
| 10 |
The two-level model is also applied to investigate the factors that affect the hyperpolarizability.
Acknowledgments
The author from the King Khalid University of Saudi Arabia extends his appreciation to the Deanship of Scientific Research in King Khalid University for supporting the work through project RGP.1/168/42. This study was also financially supported by the Higher Education Commission of Pakistan under a HEC indigenous fellowship to F.U. (315-19560-2PS3-146) and NRPU projects 3013 and 5309.
Author Contributions
⊥ S.W. and N.K. have equal contribution for the first authorship
The authors declare no competing financial interest.
References
- Cruzeiro E. Z.; Tiranov A.; Lavoie J.; Ferrier A.; Goldner P.; Gisin N.; Afzelius M. Efficient Optical Pumping Using Hyperfine Levels in 145 Nd3+ :Y2SiO5 and Its Application to Optical Storage. New J. Phys. 2018, 20, 053013. 10.1088/1367-2630/aabe3b. [DOI] [Google Scholar]
- Mande P.; Mathew E.; Chitrambalam S.; Joe I. H.; Sekar N. NLO Properties of 1, 4-Naphthoquinone, Juglone and Lawsone by DFT and Z-Scan Technique – A Detailed Study. Opt. Mater. 2017, 72, 549–558. 10.1016/j.optmat.2017.06.058. [DOI] [Google Scholar]
- Demkov A. A.; Bajaj C.; Ekerdt J. G.; Palmstrøm C. J.; Ben Yoo S. J. Materials for Emergent Silicon-Integrated Optical Computing. J. Appl. Phys. 2021, 130, 070907. 10.1063/5.0056441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karothu D. P.; Dushaq G.; Ahmed E.; Catalano L.; Polavaram S.; Ferreira R.; Li L.; Mohamed S.; Rasras M.; Naumov P. Mechanically Robust Amino Acid Crystals as Fiber-Optic Transducers and Wide Bandpass Filters for Optical Communication in the near-Infrared. Nat. Commun. 2021, 12, 1326. 10.1038/s41467-021-21324-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wada O. Femtosecond All-Optical Devices for Ultrafast Communication and Signal Processing. New J. Phys. 2004, 6, 183. 10.1088/1367-2630/6/1/183. [DOI] [Google Scholar]
- Hu X.; Jiang P.; Ding C.; Yang H.; Gong Q. Picosecond and Low-Power All-Optical Switching Based on an Organic Photonic-Bandgap Microcavity. Nat. Photonics 2008, 2, 185–189. 10.1038/nphoton.2007.299. [DOI] [Google Scholar]
- Hu Y.; Tong M.; Cheng X. a.; Zhang J.; Hao H.; You J.; Zheng X.; Jiang T. Bi2Se3 -Functionalized Metasurfaces for Ultrafast All-Optical Switching and Efficient Modulation of Terahertz Waves. ACS Photonics 2021, 8, 771–780. 10.1021/acsphotonics.0c01194. [DOI] [Google Scholar]
- Janjua M. R. S. A. Structure–Property Relationship and Systematic Study of a Series of Terpyridine Based Nonlinear Optical Compounds: DFT Computation of Interactive Design. J. Cluster Sci. 2019, 30, 45–51. 10.1007/s10876-018-1458-3. [DOI] [Google Scholar]
- Singh L.; Zhu G.; Mohan Kumar G.; Revathi D.; Pareek P. Numerical Simulation of All-Optical Logic Functions at Micrometer Scale by Using Plasmonic Metal-Insulator-Metal (MIM) Waveguides. Opt. Laser Technol. 2021, 135, 106697. 10.1016/j.optlastec.2020.106697. [DOI] [Google Scholar]
- Sathiya S.; Senthilkumar M.; Ramachandra Raja C. Crystal Growth, Hirshfeld Surface Analysis, DFT Study and Third Order NLO Studies of Thiourea 4 Dimethyl Aminobenzaldehyde. J. Mol. Struct. 2019, 1180, 81–88. 10.1016/j.molstruc.2018.11.067. [DOI] [Google Scholar]
- Wang N.; Zhang Y.; Zhang L. Dynamic Selection Network for Image Inpainting. IEEE Trans. Image Process. 2021, 30, 1784. 10.1109/TIP.2020.3048629. [DOI] [PubMed] [Google Scholar]
- Sreedharan R.; Ravi S.; Raghi K. R.; Kumar T. K. M.; Naseema K. Growth, Linear- Nonlinear Optical Studies and Quantum Chemistry Formalism on an Organic NLO Crystal for Opto-Electronic Applications: Experimental and Theoretical Approach. SN Appl. Sci. 2020, 2, 578. 10.1007/s42452-020-2360-9. [DOI] [Google Scholar]
- Dong J.-X.; Zhang H.-L. Azulene-Based Organic Functional Molecules for Optoelectronics. Chin. Chem. Lett. 2016, 27, 1097–1104. 10.1016/j.cclet.2016.05.005. [DOI] [Google Scholar]
- Islam N.; Pandith A. H. Optoelectronic and Nonlinear Optical Properties of Triarylamine Helicenes: A DFT Study. J. Mol. Model. 2014, 20, 2535. 10.1007/s00894-014-2535-7. [DOI] [PubMed] [Google Scholar]
- Hazim A.; Abduljalil H. M.; Hashim A. First Principles Calculations of Electronic, Structural and Optical Properties of (PMMA–ZrO2–Au) and (PMMA–Al2O3–Au) Nanocomposites for Optoelectronics Applications. Trans. Electr. Electron. Mater. 2021, 22, 185–203. 10.1007/s42341-020-00224-w. [DOI] [Google Scholar]
- Lay-Ekuakille A.; Massaro A.; Singh S. P.; Jablonski I.; Rahman M. Z. U.; Spano F. Optoelectronic and Nanosensors Detection Systems: A Review. IEEE Sens. J. 2021, 21, 12645–12653. 10.1109/JSEN.2021.3055750. [DOI] [Google Scholar]
- Ghosh D.; Sarkar K.; Devi P.; Kim K.-H.; Kumar P. Current and Future Perspectives of Carbon and Graphene Quantum Dots: From Synthesis to Strategy for Building Optoelectronic and Energy Devices. Renewable Sustainable Energy Rev. 2021, 135, 110391. 10.1016/j.rser.2020.110391. [DOI] [Google Scholar]
- Dale S. G.; Johnson E. R. Theoretical Descriptors of Electrides. J. Phys. Chem. A 2018, 122, 9371–9391. 10.1021/acs.jpca.8b08548. [DOI] [PubMed] [Google Scholar]
- Hosono H.; Kitano M. Advances in Materials and Applications of Inorganic Electrides. Chem. Rev. 2021, 121, 3121–3185. 10.1021/acs.chemrev.0c01071. [DOI] [PubMed] [Google Scholar]
- Nie S.; Bernevig B. A.; Wang Z. Sixfold Excitations in Electrides. Phys. Rev. Res. 2021, 3, L012028. 10.1103/PhysRevResearch.3.L012028. [DOI] [Google Scholar]
- Yang X.; Parrish K.; Li Y.-L.; Sa B.; Zhan H.; Zhu Q. Switchable Two-Dimensional Electrides: A First-Principles Study. Phys. Rev. B 2021, 103, 125103. 10.1103/PhysRevB.103.125103. [DOI] [Google Scholar]
- Garcia-Borràs M.; Solà M.; Luis J. M.; Kirtman B. Electronic and Vibrational Nonlinear Optical Properties of Five Representative Electrides. J. Chem. Theory Comput. 2012, 8, 2688–2697. 10.1021/ct300433q. [DOI] [PubMed] [Google Scholar]
- Ahsan A.; Khan S.; Gilani M. A.; Ayub K. Endohedral Metallofullerene Electrides of Ca12O12 with Remarkable Nonlinear Optical Response. RSC Adv. 2021, 11, 1569–1580. 10.1039/D0RA08571E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X.; Yang G. Recent Advances and Applications of Inorganic Electrides. J. Phys. Chem. Lett. 2020, 11, 3841–3852. 10.1021/acs.jpclett.0c00671. [DOI] [PubMed] [Google Scholar]
- Bai X.; Zha X.-H.; Qiao Y.; Qiu N.; Zhang Y.; Luo K.; He J.; Li Q.; Huang Q.; Francisco J. S.; Lin C.-T.; Du S. Two-Dimensional Semiconducting Lu2CT2 (T = F, OH) MXene with Low Work Function and High Carrier Mobility. Nanoscale 2020, 12, 3795–3802. 10.1039/C9NR10806H. [DOI] [PubMed] [Google Scholar]
- Cao Y.-D.; Sun Y.-H.; Shi S.-F.; Wang R.-M. Anisotropy of Two-Dimensional ReS2 and Advances in Its Device Application. Rare Met. 2021, 40, 3357–3374. 10.1007/s12598-021-01781-6. [DOI] [Google Scholar]
- Weber S.; Schäfer S.; Saccoccio M.; Seidel K.; Kohlmann H.; Gläser R.; Schunk S. A. Mayenite-Based Electride C12A7e- : An Innovative Synthetic Method via Plasma Arc Melting. Mater. Chem. Front. 2021, 5, 1301–1314. 10.1039/D0QM00688B. [DOI] [Google Scholar]
- Nie S.; Qian Y.; Gao J.; Fang Z.; Weng H.; Wang Z. Application of Topological Quantum Chemistry in Electrides. Phys. Rev. B 2021, 103, 205133. 10.1103/PhysRevB.103.205133. [DOI] [Google Scholar]
- Ellaboudy A.; Dye J. L.; Smith P. B. Cesium 18-Crown-6 Compounds. A Crystalline Ceside and a Crystalline Electride. J. Am. Chem. Soc. 1983, 105, 6490–6491. 10.1021/ja00359a022. [DOI] [Google Scholar]
- Khaliq F.; Mahmood T.; Ayub K.; Tabassum S.; Gilani M. A. Exploring Li4N and Li4O Superalkalis as Efficient Dopants for the Al12N12 Nanocage to Design High Performance Nonlinear Optical Materials with High Thermodynamic Stability. Polyhedron 2021, 200, 115145. 10.1016/j.poly.2021.115145. [DOI] [Google Scholar]
- Hu Q.; Tan R.; Li J.; Song W. Highly Conductive C12A7:E- Electride Nanoparticles as an Electron Donor Type Promoter to P25 for Enhancing Photocatalytic Hydrogen Evolution. J. Phys. Chem. Solids 2021, 149, 109810. 10.1016/j.jpcs.2020.109810. [DOI] [Google Scholar]
- Das P.; Chattaraj P. K.. Comparison Between Electride Characteristics of Li3@B40 and Li3@C60. Front. Chem. 2021, 9. DOI: 10.3389/fchem.2021.638581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y.; Zhang X.; Li R. [Ca24Al28O64 ]4+(4e– ) Are Directly and Quickly Synthesized by Self-reduction of C12H10Ca3O14 + Al2O3 without Any Reducing Agent. J. Am. Ceram. Soc. 2021, 104, 1641–1648. 10.1111/jace.17558. [DOI] [Google Scholar]
- Dale S. G.; Otero-de-la-Roza A.; Johnson E. R. Density-Functional Description of Electrides. Phys. Chem. Chem. Phys. 2014, 16, 14584–14593. 10.1039/C3CP55533J. [DOI] [PubMed] [Google Scholar]
- Kim T. J.; Yoon H.; Han M. J. Calculating Magnetic Interactions in Organic Electrides. Phys. Rev. B 2018, 97, 214431. 10.1103/PhysRevB.97.214431. [DOI] [Google Scholar]
- Saha R.; Das P.; Chattaraj P. K. A Complex Containing Four Magnesium Atoms and Two Mg-Mg Bonds Behaving as an Electride. Eur. J. Inorg. Chem. 2019, 4105–4111. 10.1002/ejic.201900813. [DOI] [Google Scholar]
- Dale S. G.; Johnson E. R. The Explicit Examination of the Magnetic States of Electrides. Phys. Chem. Chem. Phys. 2016, 18, 27326–27335. 10.1039/C6CP05345A. [DOI] [PubMed] [Google Scholar]
- Khan K.; Tareen A. k.; Khan U.; Nairan A.; Elshahat S.; Muhammad N.; Saeed M.; Yadav A.; Bibbò L.; Ouyang Z. Single Step Synthesis of Highly Conductive Room-Temperature Stable Cation-Substituted Mayenite Electride Target and Thin Film. Sci. Rep. 2019, 9, 4967. 10.1038/s41598-019-41512-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S. Y.; Hwang J.-Y.; Park J.; Nandadasa C. N.; Kim Y.; Bang J.; Lee K.; Lee K. H.; Zhang Y.; Ma Y.; Hosono H.; Lee Y. H.; Kim S.-G.; Kim S. W. Ferromagnetic Quasi-Atomic Electrons in Two-Dimensional Electride. Nat. Commun. 2020, 11, 1526. 10.1038/s41467-020-15253-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuishi S.; Toda Y.; Miyakawa M.; Hayashi K.; Kamiya T.; Hirano M.; Tanaka I.; Hosono H. High-Density Electron Anions in a Nanoporous Single Crystal: [Ca24Al28O64]4+(4e-). Science 2003, 301, 626–629. 10.1126/science.1083842. [DOI] [PubMed] [Google Scholar]
- Hayashi F.; Tomota Y.; Kitano M.; Toda Y.; Yokoyama T.; Hosono H. NH2– Dianion Entrapped in a Nanoporous 12CaO·7Al2O3 Crystal by Ammonothermal Treatment: Reaction Pathways, Dynamics, and Chemical Stability. J. Am. Chem. Soc. 2014, 136, 11698–11706. 10.1021/ja504185m. [DOI] [PubMed] [Google Scholar]
- Hosono H.; Kim J.; Toda Y.; Kamiya T.; Watanabe S. Transparent Amorphous Oxide Semiconductors for Organic Electronics: Application to Inverted OLEDs. Proc. Natl. Acad. Sci. U.S.A. 2017, 114, 233–238. 10.1073/pnas.1617186114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Wang H.; Wang Y.; Zhang L.; Ma Y. Computer-Assisted Inverse Design of Inorganic Electrides. Phys. Rev. X 2017, 7, 011017. 10.1103/PhysRevX.7.011017. [DOI] [Google Scholar]
- Kulichenko M.; Fedik N.; Bozhenko K. V.; Boldyrev A. I. Inorganic Molecular Electride Mg4O3 : Structure, Bonding, and Nonlinear Optical Properties. Chem.—Eur. J. 2019, 25, 5311–5315. 10.1002/chem.201806372. [DOI] [PubMed] [Google Scholar]
- Wang Y.-F.; Qin T.; Tang J.-M.; Liu Y.-J.; Xie M.; Li J.; Huang J.; Li Z.-R. Novel inorganic aromatic mixed-valent superalkali electride CaN3Ca: an alkaline-earth-based high-sensitivity multi-state nonlinear optical molecular switch. Phys. Chem. Chem. Phys. 2020, 22, 5985–5994. 10.1039/C9CP06848A. [DOI] [PubMed] [Google Scholar]
- Liyanage P. S.; de Silva R. M.; de Silva K. M. N. Nonlinear Optical (NLO) Properties of Novel Organometallic Complexes: High Accuracy Density Functional Theory (DFT) Calculations. J. Mol. Struct.: THEOCHEM 2003, 639, 195–201. 10.1016/j.theochem.2003.08.009. [DOI] [Google Scholar]
- de Silva I. C.; de Silva R. M.; Nalin de Silva K. M. Investigations of Nonlinear Optical (NLO) Properties of Fe, Ru and Os Organometallic Complexes Using High Accuracy Density Functional Theory (DFT) Calculations. J. Mol. Struct.: THEOCHEM 2005, 728, 141–145. 10.1016/j.theochem.2005.02.092. [DOI] [Google Scholar]
- Dairi M.; Elhorri A. M.; Tchouar N.; Boumedel H.; Azizi S. Theoretical Study by DFT of Organometallic Complexes Based on Metallocenes Active in NLO. J. Mol. Model. 2021, 27, 179. 10.1007/s00894-021-04797-y. [DOI] [PubMed] [Google Scholar]
- Taboukhat S.; Kichou N.; Fillaut J.-L.; Alévêque O.; Waszkowska K.; Zawadzka A.; El-Ghayoury A.; Migalska-Zalas A.; Sahraoui B. Transition Metals Induce Control of Enhanced NLO Properties of Functionalized Organometallic Complexes under Laser Modulations. Sci. Rep. 2020, 10, 15292. 10.1038/s41598-020-71769-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong R.-L.; Xu H.-L.; Li Z.-R.; Su Z.-M. Role of Excess Electrons in Nonlinear Optical Response. J. Phys. Chem. Lett. 2015, 6, 612–619. 10.1021/jz502588x. [DOI] [PubMed] [Google Scholar]
- Irshad S.; Ullah F.; Khan S.; Ludwig R.; Mahmood T.; Ayub K. First Row Transition Metals Decorated Boron Phosphide Nanoclusters as Nonlinear Optical Materials with High Thermodynamic Stability and Enhanced Electronic Properties; A Detailed Quantum Chemical Study. Opt. Laser Technol. 2021, 134, 106570. 10.1016/j.optlastec.2020.106570. [DOI] [Google Scholar]
- Mallah R. R.; Mohbiya D. R.; Sreenath M. C.; Chitrambalam S.; Joe I. H.; Sekar N. Fluorescent Meso-Benzyl Curcuminoid Boron Complex: Synthesis, Photophysics, DFT and NLO Study. Opt. Mater. 2018, 84, 786–794. 10.1016/j.optmat.2018.08.012. [DOI] [Google Scholar]
- Mejía-Hernández F. G.; Hernández-Ortíz O. J.; Muñoz-Pérez F. M.; Martínez-Pérez A. I.; Vázquez-García R. A.; Vera-Cárdenas E. E.; Ortega-Mendoza J. G.; Veloz-Rodríguez M. A.; Rueda-Soriano E.; Alemán-Ayala K. Mechanochemical Synthesis, Linear and Nonlinear Optical Properties of a New Oligophenyleneimine with Indole Terminal Moiety for Optoelectronic Application. J. Mater. Sci.: Mater. Electron. 2021, 32, 6283–6295. 10.1007/s10854-021-05344-4. [DOI] [Google Scholar]
- Ahsin A.; Ayub K. Oxacarbon superalkali C3X3Y3 (X = O, S and Y = Li, Na, K) clusters as excess electron compounds for remarkable static and dynamic NLO response. J. Mol. Graphics Modell. 2021, 106, 107922. 10.1016/j.jmgm.2021.107922. [DOI] [PubMed] [Google Scholar]
- Nazeer U.; Rasool N.; Mujahid A.; Mansha A.; Zubair M.; Kosar N.; Mahmood T.; Raza Shah A.; Shah S. A. A.; Zakaria Z. A.; Akhtar M. N. Selective Arylation of 2-Bromo-4-Chlorophenyl-2-Bromobutanoate via a Pd-Catalyzed Suzuki Cross-Coupling Reaction and Its Electronic and Non-Linear Optical (NLO) Properties via DFT Studies. Molecules 2020, 25, 3521. 10.3390/molecules25153521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Savithiri S.; Bharanidharan S.; Sugumar P.; Rajeevgandhi C.; Indhira M. Synthesis, spectral, stereochemical, biological, molecular docking and DFT studies of 3-alkyl/3,5-dialkyl-2r,6c-di(naphthyl)piperidin-4-one picrates derivatives. J. Mol. Struct. 2021, 1234, 130145. 10.1016/j.molstruc.2021.130145. [DOI] [Google Scholar]
- Liu Y.; Merinov B. V.; Goddard W. A. Origin of Low Sodium Capacity in Graphite and Generally Weak Substrate Binding of Na and Mg among Alkali and Alkaline Earth Metals. Proc. Natl. Acad. Sci. U.S.A. 2016, 113, 3735–3739. 10.1073/pnas.1602473113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sohail M.; Khaliq F.; Mahmood T.; Ayub K.; Tabassum S.; Gilani M. A. Influence of Bi-Alkali Metals Doping over Al12N12 Nanocage on Stability and Optoelectronic Properties: A DFT Investigation. Radiat. Phys. Chem. 2021, 184, 109457. 10.1016/j.radphyschem.2021.109457. [DOI] [Google Scholar]
- Hou N.; Wu Y.; Wu H. The Influence of Alkali Metals Interaction with Al/P-Substituted BN Nanosheets on Their Electronic and Nonlinear Optical Properties: A DFT Theoretical Study. ChemistrySelect 2019, 4, 1441–1447. 10.1002/slct.201803193. [DOI] [Google Scholar]
- Ayub K. Are Phosphide Nano-Cages Better than Nitride Nano-Cages? A Kinetic, Thermodynamic and Non-Linear Optical Properties Study of Alkali Metal Encapsulated X 12 Y 12 Nano-Cages. J. Mater. Chem. C 2016, 4, 10919–10934. 10.1039/C6TC04456E. [DOI] [Google Scholar]
- Shehzad R. A.; Iqbal J.; Ayub K.; Nawaz F.; Muhammad S.; Ayub A. R.; Iqbal S. Enhanced Linear and Nonlinear Optical Response of Superhalogen (Al7) Doped Graphitic Carbon Nitride (g-C3N4). Optik 2021, 226, 165923. 10.1016/j.ijleo.2020.165923. [DOI] [Google Scholar]
- Xu H.-L.; Wang F.-F.; Chen W.; Yu G.-T. The Complexant Shape Effect on First (Hyper)Polarizability of Alkalides Li+(NH2CH3)4 M – (M = Li, Na, and K). Int. J. Quantum Chem. 2011, 111, 3174–3183. 10.1002/qua.22613. [DOI] [Google Scholar]
- Song Y.-D.; Wang L.; Wu L.-M. How the Alkali Metal Atoms Affect Electronic Structure and the Nonlinear Optical Properties of C24N24 Nanocage. Optik 2017, 135, 139–152. 10.1016/j.ijleo.2017.01.096. [DOI] [Google Scholar]
- Teng Y.; Sheng Q.; Weng H.; Zhou Z.; Huang X.; Li Z.; Zhang T. Theoretical Study of a Novel Organic Electride with Large Nonlinear Optical Responses. Int. J. Quantum Chem. 2020, 120, e26235 10.1002/qua.26235. [DOI] [Google Scholar]
- Ullah F.; Ayub K.; Mahmood T. Remarkable Second and Third Order Nonlinear Optical Properties of Organometallic C6Li6 −M3O Electrides. New J. Chem. 2020, 44, 9822–9829. 10.1039/D0NJ01670E. [DOI] [Google Scholar]
- Kosar N.; Tahir H.; Ayub K.; Mahmood T. DFT Studies of Single and Multiple Alkali Metals Doped C24 Fullerene for Electronics and Nonlinear Optical Applications. J. Mol. Graphics Modell. 2021, 105, 107867. 10.1016/j.jmgm.2021.107867. [DOI] [PubMed] [Google Scholar]
- Kosar N.; Mahmood T.; Ayub K.; Tabassum S.; Arshad M.; Gilani M. A. Doping Superalkali on Zn12O12 Nanocage Constitutes a Superior Approach to Fabricate Stable and High-Performance Nonlinear Optical Materials. Opt. Laser Technol. 2019, 120, 105753. 10.1016/j.optlastec.2019.105753. [DOI] [Google Scholar]
- Chandiramouli R.; Srivastava A.; Nagarajan V. NO Adsorption Studies on Silicene Nanosheet: DFT Investigation. Appl. Surf. Sci. 2015, 351, 662–672. 10.1016/j.apsusc.2015.05.166. [DOI] [Google Scholar]
- Morisawa Y.; Tachibana S.; Ikehata A.; Yang T.; Ehara M.; Ozaki Y. Changes in the Electronic States of Low-Temperature Solid n-Tetradecane: Decrease in the HOMO-LUMO Gap. ACS Omega 2017, 2, 618–625. 10.1021/acsomega.6b00539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He H.-M.; Luis J. M.; Chen W.-H.; Yu D.; Li Y.; Wu D.; Sun W.-M.; Li Z.-R. Nonlinear Optical Response of Endohedral All-Metal Electride Cages 2e – Mg2+ (M@E12 ) 2–Ca2+ (M = Ni, Pd, and Pt; E = Ge, Sn, and Pb). J. Mater. Chem. C 2019, 7, 645–653. 10.1039/C8TC05647A. [DOI] [Google Scholar]
- Ullah F.; Kosar N.; Ayub K.; Mahmood T. Superalkalis as a Source of Diffuse Excess Electrons in Newly Designed Inorganic Electrides with Remarkable Nonlinear Response and Deep Ultraviolet Transparency: A DFT Study. Appl. Surf. Sci. 2019, 483, 1118–1128. 10.1016/j.apsusc.2019.04.042. [DOI] [Google Scholar]
- Bae S.; Espinosa-García W.; Kang Y. G.; Egawa N.; Lee J.; Kuwahata K.; Khazaei M.; Ohno K.; Kim Y. H.; Han M. J.; Hosono H.; Dalpian G. M.; Raebiger H. MXene Phase with C 3 Structure Unit: A Family of 2D Electrides. Adv. Funct. Mater. 2021, 31, 2100009. 10.1002/adfm.202100009. [DOI] [Google Scholar]
- Tahmasebi E.; Shakerzadeh E.; Biglari Z. Theoretical Assessment of the Electro-Optical Features of the Group III Nitrides (B12N12, Al12N12 and Ga12N12) and Group IV Carbides (C24, Si12C12 and Ge12C12) Nanoclusters Encapsulated with Alkali Metals (Li, Na and K). Appl. Surf. Sci. 2016, 363, 197–208. 10.1016/j.apsusc.2015.12.001. [DOI] [Google Scholar]
- Buldakov M. A.; Koryukina E. V.; Cherepanov V. N.; Kalugina Y. N. A Dipole-Moment Function of MeH Molecules (Me = Li, Na, K)). Russ. Phys. J. 2007, 50, 532–537. 10.1007/s11182-007-0080-x. [DOI] [Google Scholar]
- Li X.; Zhang Y.; Lu J. Remarkably Enhanced First Hyperpolarizability and Nonlinear Refractive Index of Novel Graphdiyne-Based Materials for Promising Optoelectronic Applications: A First-Principles Study. Appl. Surf. Sci. 2020, 512, 145544. 10.1016/j.apsusc.2020.145544. [DOI] [Google Scholar]
- Mondal A.; Hatua K.; Nandi P. K. Why Lithiation Results Large Enhancement of Second Hyperpolarizability of Delta Shaped Complexes M-C2H2 (M = Be, Mg and Ca)?. Chem. Phys. Lett. 2019, 720, 36–41. 10.1016/j.cplett.2019.01.055. [DOI] [Google Scholar]
- Li Z.-J.; Wang F.-F.; Li Z.-R.; Xu H.-L.; Huang X.-R.; Wu D.; Chen W.; Yu G.-T.; Gu F. L.; Aoki Y. Large Static First and Second Hyperpolarizabilities Dominated by Excess Electron Transition for Radical Ion Pair Salts M 2* + TCNQ*– (M = Li, Na, K). Phys. Chem. Chem. Phys. 2009, 11, 402–408. 10.1039/B809161G. [DOI] [PubMed] [Google Scholar]
- Lu T.; Chen F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Souza T. E.; Rosa I. M. L.; Legendre A. O.; Paschoal D.; Maia L. J. Q.; Dos Santos H. F.; Martins F. T.; Doriguetto A. C. Non-centrosymmetric crystals of newN-benzylideneaniline derivatives as potential materials for non-linear optics. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2015, 71, 416–426. 10.1107/S2052520615008859. [DOI] [PubMed] [Google Scholar]
- Campo J.; Wenseleers W.; Goovaerts E.; Szablewski M.; Cross G. H. Accurate Determination and Modeling of the Dispersion of the First Hyperpolarizability of an Efficient Zwitterionic Nonlinear Optical Chromophore by Tunable Wavelength Hyper-Rayleigh Scattering. J. Phys. Chem. C 2008, 112, 287–296. 10.1021/jp0758824. [DOI] [Google Scholar]
- Arun Kumar R.; Arivanandhan M.; Hayakawa Y. Recent Advances in Rare Earth-Based Borate Single Crystals: Potential Materials for Nonlinear Optical and Laser Applications. Prog. Cryst. Growth Charact. Mater. 2013, 59, 113–132. 10.1016/j.pcrysgrow.2013.07.001. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Normand R. K. J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.. Gaussian 09, Revision D.01; Gaussian, Inc: Wallingford CT, 2009.
- Dennington R.; Keith T.; Millam J.. GaussView, Version 5, 2009.
- Sajid H.; Khan S.; Ayub K.; Mahmood T. Effective Adsorption of A-Series Chemical Warfare Agents on Graphdiyne Nanoflake: A DFT Study. J. Mol. Model. 2021, 27, 117. 10.1007/s00894-021-04730-3. [DOI] [PubMed] [Google Scholar]
- Kosar N.; Ayub K.; Mahmood T. Surface Functionalization of Twisted Graphene C32H15 and C104H52 Derivatives with Alkalis and Superalkalis for NLO Response; a DFT Study. J. Mol. Graphics Modell. 2021, 102, 107794. 10.1016/j.jmgm.2020.107794. [DOI] [PubMed] [Google Scholar]
- Kosar N.; Tahir H.; Ayub K.; Gilani M. A.; Mahmood T. Theoretical Modification of C24 Fullerene with Single and Multiple Alkaline Earth Metal Atoms for Their Potential Use as NLO Materials. J. Phys. Chem. Solids 2021, 152, 109972. 10.1016/j.jpcs.2021.109972. [DOI] [Google Scholar]
- Sajid H.; Ullah F.; Khan S.; Ayub K.; Arshad M.; Mahmood T. Remarkable Static and Dynamic NLO Response of Alkali and Superalkali Doped Macrocyclic [Hexa-]Thiophene Complexes; a DFT Approach. RSC Adv. 2021, 11, 4118–4128. 10.1039/D0RA08099C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan P.; Mahmood T.; Ayub K.; Tabassum S.; Amjad Gilani M. Turning Diamondoids into Nonlinear Optical Materials by Alkali Metal Substitution: A DFT Investigation. Opt. Laser Technol. 2021, 142, 107231. 10.1016/j.optlastec.2021.107231. [DOI] [Google Scholar]
- Oviedo M. B.; Ilawe N. V.; Wong B. M. Polarizabilities of π-Conjugated Chains Revisited: Improved Results from Broken-Symmetry Range-Separated DFT and New CCSD(T) Benchmarks. J. Chem. Theory Comput. 2016, 12, 3593–3602. 10.1021/acs.jctc.6b00360. [DOI] [PubMed] [Google Scholar]
- Xu L.; Kumar A.; Wong B. M. Linear polarizabilities and second hyperpolarizabilities of streptocyanines: Results from broken-Symmetry DFT and new CCSD(T) benchmarks. J. Comput. Chem. 2018, 39, 2350–2359. 10.1002/jcc.25519. [DOI] [PubMed] [Google Scholar]
- Khan S.; Gilani M. A.; Munsif S.; Muhammad S.; Ludwig R.; Ayub K. Inorganic Electrides of Alkali Metal Doped Zn12O12 Nanocage with Excellent Nonlinear Optical Response. J. Mol. Graphics Modell. 2021, 106, 107935. 10.1016/j.jmgm.2021.107935. [DOI] [PubMed] [Google Scholar]
- Ahsan A.; Ayub K. Extremely Large Nonlinear Optical Response and Excellent Electronic Stability of True Alkaline Earthides Based on Hexaammine Complexant. J. Mol. Liq. 2020, 297, 111899. 10.1016/j.molliq.2019.111899. [DOI] [Google Scholar]
- Ahsan A.; Ayub K. Adamanzane Based Alkaline Earthides with Excellent Nonlinear Optical Response and Ultraviolet Transparency. Opt. Laser Technol. 2020, 129, 106298. 10.1016/j.optlastec.2020.106298. [DOI] [Google Scholar]
- Torrent-Sucarrat M.; Solà M.; Duran M.; Luis J. M.; Kirtman B. Basis Set and Electron Correlation Effects on Initial Convergence for Vibrational Nonlinear Optical Properties of Conjugated Organic Molecules. J. Chem. Phys. 2004, 120, 6346–6355. 10.1063/1.1667465. [DOI] [PubMed] [Google Scholar]


