Abstract

Vps34 is the only isoform of the PI3K family in fungi, making this protein an attractive target to develop new treatments against pathogenic fungi. The high structural similarity between the active sites of the human and fungal Vps34 makes repurposing of human Vps34 inhibitors an appealing strategy. Nonetheless, while some of the cross-reactive inhibitors might have the potential to treat fungal infections, a safer approach to prevent undesired side effects would be to identify molecules that specifically inhibit the fungal Vps34. This study presents the parameterization of four LIE models for estimating the binding free energy of Vps34–inhibitor complexes. Two models are parameterized using a multiparametric linear regression leaving one or more free parameters, while the other two are based on the LIE-D model. All of the models show good predictive capacity (R2 > 0.7, r > 0.85) and a low mean absolute error (MAE < 0.71 kcal/mol). The current study highlights the advantages of LIE-D-derived models when predicting the weight of the different contributions to the binding free energy. It is expected that this study will provide researchers with a valuable tool to identify new Vps34 inhibitors for relevant applications such as cancer treatment and the development of new antimicrobial agents.
Introduction
Phosphatidylinositol 3-kinase (PI3K) is an enzyme involved in growth, proliferation, motility, survival, and intracellular trafficking.1 Aberrations in its signaling pathway have been linked to many human diseases, including cancer, immune and neurological disorders, diabetes, and cardiovascular diseases.2 In this regard, significant efforts have been dedicated in the last decade to developing PI3K inhibitors for cancer treatment, with many of them currently in various stages of clinical studies. One of them, idelalisib, has obtained FDA approval.3
PI3K is a superfamily comprising eight isoforms divided into three classes, depending on their domain structure, the specificity toward their lipid substrate, and the accompanying regulatory subunit. All isoforms catalyze the phosphorylation of the inositol ring at position three, starting from different phosphorylation states of this substrate.1 Vertebrates such as humans and mice contain in their genome eight genes encoding the different isoforms of PI3K. In contrast, simple eukaryotic organisms such as fungi and plants have only the class III isoform.1 Vps34 (vacuolar protein sorting 34)—the only PI3K class III representative—plays a fundamental role in early and late endosome maturation, as well as macroautophagy.4
At present, there are only a handful of families of antifungal drugs, which in turn act on only a few molecular targets. The low number of novel antifungal drugs dramatically contrasts with the high number of reported disease cases produced by these microorganisms and the alarmingly increasing resistance to traditional antimycotic drugs developed by many common pathogenic fungal species.5
For several years, drug repurposing has been an attractive strategy for finding new uses for existing drugs.6 Various studies of this nature have been carried out in several Candida species with encouraging results.7,8 Additionally, similar studies related to the PI3K enzyme were performed in Trypanosoma cruzi.9 In this context, our group is investigating the potential of Vps34 as a therapeutic molecular target in fungi. We have recently tested in vitro a set of inhibitors of different isoforms of human PI3K in a few common pathogenic fungal species, such as Histoplasma capsulatum, Candida albicans, and Aspergillus fumigatus. Growth inhibitory activity in cell cultures was observed for several of these molecules, mainly in H. capsulatum. These inhibitors were selected based on structural analyses and docking simulations pointing to possible cross-reactivity with the fungal Vps34 (fVps34), whose binding site shares high sequence similarity with the binding site of human Vps34 (hVps34), as shown in Figure 1 for several fungi.
Figure 1.
Vps34 active site comparison between different pathogenic fungus species and human. Upper panel: differences between the active sites of H. capsulatum [homology model] (left) and hVps34 [PDB ID: 4UWH] (right). The protein is represented as a gray surface, while a representative ligand in hVps34 is shown as sticks. The two most significant mutations in the active site are shown in red and blue, respectively. Bottom panel: sequence alignment shows high conservation of the Vps34 active site region for several species of pathogenic fungi and the human enzyme. Positions directly involved in inhibitor binding are shown in bold, while those with a mutation in one or several fungi are colored in cyan.
While some of the cross-reactive inhibitors might have the potential to treat fungal infections, a safer approach to prevent undesired side effects would be to identify molecules that specifically inhibit fVps34. In this regard, the presence of a few amino acid differences in the fVps34 binding sites compared to the human enzyme makes designing selective fVps34 inhibitors an attractive project.10−12 To this end, having an effective method for a reliable in silico evaluation of candidate fVps34 inhibitors would be highly beneficial.
In previous studies, the MM-PB/GBSA method has been used to estimate the binding free energy of class I PI3K inhibitors.13−18 However, to our knowledge, no binding free-energy estimation method has been reported for Vps34–inhibitor complexes. In this study, we applied the linear interaction energy (LIE) method to calculate the binding free energy of Vps34–inhibitor complexes because of its efficiency, versatility, and low computational cost.19
LIE is a semiempirical method for absolute free-energy calculations developed by Åqvist et al.20 This method assumes a linear relationship between ΔGbind and the average differences of the van der Waals and electrostatic contributions for the protein-bound and protein-unbound ligand states, as calculated along with molecular dynamics (MD) simulations. The contributions are scaled with parameters denoted as α and β. In some LIE models, an independent term γ is also included as a compensation parameter (eq 1)21,22
| 1 |
where ΔVb-fvdW denotes the change in van der Waals interactions between the bound and the free states. The ΔVb-f and ΔVb-feleintra terms indicate the change in electrostatic interactions when the ligand is transferred from the solution (free state) into the solvated receptor binding site (bound state). It is worth noting that the electrostatic energy calculated from a force field and the solvation energy are coupled, so the solvation effect is explicitly considered when discussing the source of the energy contributions.
Thus far, several LIE models have been developed and applied to a vast number of systems for predicting protein–ligand affinities.21,23−26 Multiple parameterizations have been derived for LIE by fixing the scaling coefficients or leaving some or all free.21,23−29 Using a different strategy, the LIE-D model developed by Miranda and co-workers25 allows the calculation of specific parameters (namely, β and γ) for each protein–ligand system. This model uses a fixed value of α = 0.18, while the β parameter is determined for each ligand according to the E model of Almlöf et al.28 The γ parameter, on the other hand, is determined from a linear relationship between a parameter denoted as “D” and an optimal γ (γopt), aiming to reproduce the experimental energy for each protein–ligand complex (eq 2)
| 2 |
where m and n are the slope and intercept, respectively, and D corresponds to the balance (difference) between the electrostatic (polar) and van der Waals (nonpolar) contributions (eq 3)25
| 3 |
In this work, we parameterized four different LIE models to predict the binding free energies of Vps34–inhibitor complexes, taking advantage of the available experimental information, mainly for the human variant of this enzyme. As a result, we obtained a robust parameterization that can be applied in different scenarios. One of them is the development of new hVps34 inhibitors for cancer treatment. Another relevant application we are focused on is identifying fVps34 inhibitors with therapeutic potential for treating many long-neglected fungal infections.
Results and Discussion
Quality Assessment of the Vps34–Inhibitor Complexes Obtained by Docking
Our training data set comprises both crystallographic and modeled structures. The inclusion of complexes generated by docking was necessary because of two main reasons: (i) the relatively low number of crystallographic structures reported for hVps34 coupled to inhibitors and (ii) the high conservation of the chemical scaffolds and binding modes in the set of crystal inhibitors, which may bias the model.
To evaluate the reliability of our predictions, we carried out a re-docking of the ligands with a crystallographic structure. In all cases, AutoDock Vina reproduced the experimental pose with a maximum root-mean-square deviation (RMSD) of 1.1 Å (Table S1). For ligands without crystallographic structures in complex with hVps34, the predicted pose was validated against crystallographic complexes of hVps34 with ligands having the same chemical scaffold (Table S2) or against complexes of the same ligand with Vps34 from other species or other PI3K isoforms (Table S3). In all cases, the ligand was predicted in the same orientation as in the reference complex.
Additionally, we analyzed the evolution of each ligand in the MD simulation trajectory and the interaction profile. The average RMSD values for each ligand and its surrounding residues (within a 4 Å cutoff distance) throughout the MD simulations were <2 Å (Table S4), both for the crystallographic and docked complexes. The stability of the docked structures and their similar interaction profiles, as compared to the crystal complexes (Figures 2 andS1), indicate that the predicted binding modes are suitable for calculating binding free energies.
Figure 2.
Vps34–ligand contact profiles. The color (gray scale) boxes represent the contact frequency during the MD simulation for a given ligand–residue pair. Residues marked with (*) correspond to the following mutations in the 6I3U structure: F612A, L616N, I634L, M682L, and F684W.
Assessment of Derived LIE Models
To assess the performance of the derived models, we carried out an internal validation using a leave-one-out cross-validation (LOO-CV).30 The deviation of the calculated values from the experimental energy values was quantified using root-mean-square errors (RMSE), the mean absolute error (MAE) between predicted and experimental ΔGbind, and the standard deviation of the error (SDerror). Additionally, multiple determination (R2) and Pearson (r) coefficients were calculated (Table 1).
Table 1. Summary of the Results of the LIE Models Applied to Vps34c.
| model | MAE | SDerror | RMSE | R2 | r | E1d | E1.5e | E2f | Q2 | SPRESSLOO |
|---|---|---|---|---|---|---|---|---|---|---|
| LIE-Dm | 2.1 | 1.0 | 2.3 | –1.1g | 0.82 | 20 | 30 | 50 | ||
| LIEαβa | 0.6 | 0.5 | 0.8 | 0.76 | 0.87 | 85 | 95 | 100 | 0.69 | 0.20 |
| LIEβ = 0b | 0.7 | 0.6 | 0.8 | 0.70 | 0.84 | 70 | 90 | 100 | 0.68 | 0.19 |
| LIE-Dvps34 | 0.7 | 0.5 | 0.9 | 0.72 | 0.86 | 80 | 90 | 100 | 0.66 | 1.01 |
| LIE-Dvps34ni | 0.6 | 0.6 | 0.8 | 0.75 | 0.87 | 80 | 90 | 95 | 0.71 | 0.94 |
Parameters α = 0.51 and β = −0.07 determined by multiparametric regression minimizing the MAE value.
Parameters α = 0.57 and β = 0 determined by simple regression minimizing the MAE value.
MAE, SDerror, RMSE, and SPRESSLOO in kcal/mol.
Percentage of MAE values lower than 1 kcal/mol.
Percentage of MAE values lower than 1.5 kcal/mol.
Percentage of MAE values lower than 2 kcal/mol.
It is equivalent to R2 = 0, which means that the method does not correctly predict the energy values.
Interestingly, LIE-Dm ranks last in terms of the absolute errors but shows a good ranking power (r = 0.82) (Figure 3A). This result is remarkable considering that the Vps34 family has no representation in the training set used by Miranda et al.,25 thus denoting the robustness of the model and the potential applicability for estimating ΔGbind values.
Figure 3.
Scatter plot of experimental (ΔGexp) vs calculated (ΔGcalc) binding free energies for the 20 training data set complexes. (A) LIE-Dvps34: black circles, R2 = 0.72; LIE-Dvps34ni: gray triangles, R2 = 0.75; and LIE-Dm: empty squares, R2 = −1.1. (B) LIEαβ: empty circles, R2 = 0.76, and LIEβ = 0: black circles, R2 = 0.70.
The LIEαβ method was parameterized using a multiparametric regression model, leaving coefficients α and β freely adjustable to minimize the absolute error, obtaining α = 0.51 and β = −0.07. This model showed a good predictive capacity (R2 = 0.76) with a low RMSE (0.8 kcal/mol) and MAE = 0.6 ± 0.5 kcal/mol. In addition, it shows good ranking capabilities (r = 0.87) and relatively low error distributions of estimated energy (E1 = 85%, E1.5 = 95%, and E2 = 100%) (Figure 3B). The data overfitting evaluation (Q2 = 0.69 and SPRESSLOO = 0.2) further indicates a good performance. The negative value for the β parameter lacks physicochemical sense, and it is likely overfitting.27
We also parameterized a LIE model (LIEβ = 0) where β = 0 and α were freely adjustable. The derived α for this model was 0.57. This model shows slightly lower performance compared with LIEαβ, as well as the models derived from LIE-D (Table 1 and Figure 3B).
The LIE-D model was reparameterized by determining the D and γopt parameters for each complex in the data set (Table 2). The correlation between D and γopt showed a good linear fit for both the LIE-DVps34 (R2 = 0.90) and LIE-Dvps34ni (R2 = 0.91) models (Figure 4). In comparison with the LIEαβ (MAE = 0.6 ± 0.5 and RMSE = 0.8 kcal/mol) and LIEβ = 0 (MAE = 0.7 ± 0.6 and RMSE = 0.8 kcal/mol) models, LIE-DVps34 shows a small increase of the MAE (0.7 ± 0.5 kcal/mol) and RMSE (0.9 kcal/mol) values. This model, however, shows a good predictive capability (R2 = 0.72, r = 0.86, Q2 = 0.66, E1 = 80%, E1.5 = 90%, and E2 = 100%) (Figure 3A). Interestingly, the LIE-DVps34ni model has a low MAE (0.6 ± 0.6 kcal/mol) and RMSE values (RMSE = 0.8 kcal/mol). It also shows good ranking capabilities (r = 0.87) and the best overfit evaluation (Q2 = 0.71) among the four tested models (Table 1 and Figure 3A).
Table 2. Parameters of the LIE-D Models to Determine the Parameter γ.
| LIE-D model | slope (m) | intercept (n) | reference |
|---|---|---|---|
| LIE-Dm | –0.95 | –2.06 | Miranda et al.25 |
| LIE-DVps34 | –1.22 | –2.05 | this work |
| LIE-DVps34ni | –1.23 | –1.61 | this work |
Figure 4.
Linear fit between D parameter and γopt for derived LIE-D models. (A) LIE-Dvps34, R2 = 0.90, and (B) LIE-Dvps34ni, R2 = 0.91.
It is noteworthy that the obtained MAE and RMSE values for the adjusted LIE methods and reparameterized LIE-D models are all below 1 kcal/mol, which is the commonly accepted value for a binding free-energy estimation method to be considered accurate.31 In general, the four models—LIEαβ, LIEβ = 0, LIE-Dvps34, and LIE-Dvps34ni—showed a good performance. Therefore, all of them may be used to estimate the binding free energy of Vps34–inhibitor complexes. Nonetheless, the flexibility of the reparameterized LIE-D models, LIE-Dvps34 and LIE-Dvps34ni, and the possibility of calculating a system-dependent γ represents an advantage over the adjusted LIE methods, as evidenced below.
Understanding Vsp34–Inhibitor Complexes’ Energy Term Contributions
The analysis of the van der Waals and electrostatic contributions to binding affinities may help understand the molecular determinants for receptor–inhibitor interactions and, ultimately, guide a structure-based design of novel and selective inhibitors. The four LIE models show that nonpolar contributions are the most significant component of ΔGcalc (Table S5), reflecting the nonpolar nature of the ligands, which favors binding to the protein active site. Indeed, the contact profiles for most ligands show significant interactions with hydrophobic residues (PHE612, ILE634, TYR670, PHE684, ILE685, LEU750, ILE760), which interact with the adenosine base of ATP, the natural cofactor32 (Figures 2 andS1).
It is difficult to estimate the importance of polar and nonpolar contributions with LIE models adjusted by linear regression. In the LIEαβ model, a negative coefficient β = −0.07 is obtained probably due to overfitting. This value, although mathematically optimal, lacks physicochemical meaning. On the other hand, setting β = 0 does not significantly improve the results (Table 1), although the good performance shown by the LIEβ = 0 model reinforces the importance of the nonpolar contributions to ΔGbind. However, assuming a null contribution of the polar component to ΔGbind may bias the model, thus compromising its applicability for ligands of more polar nature.
Miranda and co-workers25 assessed the weight of polar and nonpolar contributions in their LIE-D model by substituting the parameter γ by eq 2 and grouping similar terms
| 4 |
| 5 |
| 6 |
| 7 |
where m and n are the slope and the intercept in the linear fit between D and γopt, respectively.
We consider, however, that this analysis is not adequate. When performing these substitutions (from eqs 4 to 7), the result tends to behave similarly to a linear regression leaving the parameters α′ and β′ free to adjust. The value of β′ changes sign around m = −1; thus, a negative value (β′ = −0.22 for LIE-DVps34 and β′ = −0.23 for LIE-DVps34ni) would be obtained (as for the LIEαβ model), which lacks physicochemical sense.
According to the original development of the LIE method, the coefficient scaling the electrostatic energy should not be used as a free parameter since small and even negative values can be obtained, thus leading to an incorrect interpretation of the electrostatic contribution.28 To avoid such problems, it makes more sense to consider γ as a compensation parameter related to the nonpolar component of the energy for the following reasons: (1) β ∼ 2α (since α = 0.18 and 0.37 ≤ β ≤ 0.43, as shown in Table S7), which a priori biases the contributions,21,33 and (2) desolvation of polar groups is energetically more expensive than desolvation of nonpolar groups.34−36
We have noticed that D and Polar are correlated; thus, the balance between contributions (parameter D) grows as the value of the polar term increases (Figure 5A). Although the R2 value for Polar vs γopt is lower (R2 = 0.80 for LIE-Dvps34 and R2 = 0.81 for LIE-Dvps34ni) (Figure 5B) than that obtained for D vs γopt (R2 = 0.9 for LIE-Dvps34 and R2 = 0.91 for LIE-Dvps34ni), we observed that the polar contribution has a strong influence on the γ value.
Figure 5.
Relationship between polar term and the D and γopt parameters. (A) Polar component (βΔVb-fele) vs D and (B) polar component (βΔVb-f) vs γopt.
Assuming that the nonpolar component of ΔGbind is αΔVb-fvdw + γ, we then obtain a more realistic representation of the contributions24 (Figure 6), based on both the βΔVb-f and βΔVb-fvdw values obtained from the MD simulation and the parameter β as determined for each ligand according to its chemical groups.
Figure 6.
Contributions to binding free energy of each Vps34–inhibitor complex using LIE-Dvps34. The striped bars represent the polar contribution (βΔVb-fele), the white bars represent the nonpolar contribution (αΔVb-f + γ), the gray bars represent ΔGcalc (eq 1), and the black bars represent ΔGexp (eq 10).
Advantages and Limitations of the Tailored LIE Method
In this study, we have parameterized several models of the LIE method to obtain an efficient tool for predicting the binding free energy of Vps34–inhibitor complexes. Overall, all models showed a good performance, however, those derived from LIE-D are more robust since they allow a more specific analysis of the contributions according to the nature of the ligand. Our training set, though, has a relatively small number of complexes and several inhibitors that share a common scaffold, which might limit the performance for chemically different ligands.
Nowadays, technology development has made applying more robust methodologies for calculating absolute binding free energy, such as free-energy perturbation or thermodynamic integration, more accessible. However, their computational cost remains extremely high as compared to endpoint free-energy estimation methods and requires computing resources that are not accessible to many research groups, especially in developing countries.37 A tailored method like the one we present here, with MAE values <1 kcal/mol and high computational efficiency, represents a valuable tool for high-throughput discovery of new inhibitors—in this case for Vps34, a relevant pharmaceutical target. Dozens or even hundreds of hits resulting from virtual screening may be evaluated in a short time (days/few weeks) using relatively modest computational resources. Moreover, with the LIE-D-derived models, it is possible to perform a linear decomposition of the contributions of ligand fragments, which constitutes an additional bonus for lead optimization. For instance, the methyl group in the morpholine moiety of the SAR405 ligand (PDB ID: 4OYS) has a net contribution of −0.5 kcal/mol, which explains its better binding affinity as compared to its parent inhibitor, SAR404 (Table S8). A similar decomposition scheme has been used in studying MurD ligase inhibition and molecular recognition.38
This study used the human Vps34 protein in complex with inhibitors to parameterize the LIE method. Although this parameterization can be used to design and discover new inhibitors of hVps34 against cancer, it can also be used on the homologous target in other species, particularly, in pathogenic fungi. Indeed, the different fungal Vps34 variants show only a few mutations in the active site as compared to their human counterpart (Figure 1); thus, both the active site topology and chemistry are conserved across all of these species, so the inhibitor binding mode should also be conserved. This high structural conservation strongly suggests that our parameterized LIE models should work as well for the fungal Vps34–inhibitor complexes.
Conclusions
We have obtained four LIE models specifically parameterized for Vps34, a relevant target in cancer and several pathogenic fungi. The four models showed a good performance in predicting ΔGbind values for our training set, with MAE and RMSE values <1.0 kcal/mol. The LIE-DVps34 and LIE-DVps34ni models allow deriving system-specific parameters and conducting a more unbiased analysis of the different energy contributions. Their low computational cost and satisfactory accuracy make both models valuable tools to identify new Vps34 inhibitors of the human enzyme and its orthologs in fungi and other pathogenic microorganisms.
Methods
Vps34–Inhibitor System Selection
Our data set was compiled from articles reporting molecules that inhibit human or mouse Vps34 (having identical active sites) in a specific way or spanning other PI3K isoforms. Vps34–inhibitor systems were selected based on the following criteria: (1) availability of a crystallographic structure for the Vps34–ligand system or a reference crystallographic structure with another PI3K isoform that could be confidently used as a template; (2) noncovalent protein–ligand interactions; (3) availability of experimental IC50 values; and (4) no bound cofactors. In the final data set, 40% (8 out of 20) of the Vps34–inhibitor complexes have a crystallographic structure, while the other 60% (12 out of 20) were obtained by docking (Table 3).
Table 3. 2D Structure of Ligands with N (Name) the Name Reported or PDB Code, S (Source) the Method for Obtaining the Vps34–Inhibitor Complex Structure, and the Reported IC50 Value.

The Ki values were determined from experimental IC50 constants using the Cheng–Prusoff equation3940,41
| 8 |
where IC50 is the reported IC50 value, [S] is the solute concentration used in the inhibition experiment, and KM is the Michaelis–Menten constant for the Vps34 enzyme.
Since most Vps34 inhibitors follow a competitive inhibition mechanism and assuming a [S] ∼ KM used in the experiments, then
| 9 |
and ΔGexp can be calculated as
| 10 |
where R is the gas constant (0.001987 kcal/(K mol)), T is the experimental temperature, and IC50 is the reported IC50 value. All of the selected compounds have IC50 in the 1–25 000 nM range, equivalent to −12.7 to −6.7 kcal/mol range in ΔGexp terms.
Docking Simulations
More than 250 crystallographic structures of the different PI3K isoforms are deposited in the Protein Data Bank (PDB),49,50 of which 24 correspond to Vps34. Structural alignment of hVps34–inhibitors complexes shows high conservation in the orientation of the bound ligands (Figure 7).
Figure 7.

Superposition of human Vps34 crystallographic structures used in this study. The protein is represented as gray cartoon, while the ligands are shown in salmon and sticks. PDB IDs: 4oys, 4ph4, 4uwf, 4uwg, 4uwh, 4uwk, 4uwl, and 6i3u.
The protonation state of the selected inhibitors was assigned using Chemaxon51 at the experimental pH value. We used the crystal structure of Vps34 from PDB entry 4uwh(42)(43−48) as a template to generate Vps34–inhibitor complexes by docking with AutoDock Vina.52 The whole docking process, including receptor and ligand preparation, search space definition, and running the calculation, was conducted with our graphical tool AMDock.53 We performed a re-docking process of the crystallographic structures to verify whether the docking engine can reliably predict the geometry of Vps34–inhibitor complexes. All ligands were randomized before docking. Since there is high conservation in the orientation and nature of the crystallographic ligands (Figure 7), the docking results were validated by comparing the resulting pose with the structural alignment shown in Figure 7, the crystallographic orientations of similar ligands, and interaction profiles. Structures in Figure 7 were aligned by superimposing the α carbons of a set of residues in secondary structures surrounding the binding site, chosen by visual inspection.
Molecular Dynamics Simulations
Ligands were parameterized with the general Amber force field (GAFF),54 and charges were calculated with the AM1-BCC55 semiempirical approximation using antechamber56 from AmberTools19.57 For each inhibitor complex, the protonation state of protein residues was determined using H++ (http://biophysics.cs.vt.edu/H++)58−60 at the pH value reported for the IC50 experimental determination. MD simulations were run for 20 ns using GROMACS 2018.361 and the Amber99SB33 force field, as reported by Miranda et al.25 Each Vps34–ligand complex was simulated in a dodecahedral box with 10 Å separation and explicit solvent using the TIP3P model.62 All systems were neutralized at a physiological concentration of 0.15 nM Na+/Cl–. All bonds were constricted using the LINCS algorithm,63 and energy minimization was performed using the steepest descent algorithm. Initially, we applied a restriction of 10 kcal/mol·Å2 to both the protein and the ligand, which were gradually heated for 100 ps to the reported experimental temperature, followed by 100 ps of equilibration. A Berendsen thermostat64 and coupling time of 0.1 ps for both solute and solvent were used. Next, we performed the Langevin dynamics production65 with an integration time step of 2 fs scheme to integrate the motion equations. For pressure control, a Parrinello–Rahman coupling algorithm66 with a time constant of 2.0 ps was used. Long-range electrostatic interactions were handled by the particle mesh Ewald (PME)67,68 summation with a Coulomb cutoff of 12 Å. The short-range van der Waals cutoff was set to 12 Å. Energies and atomic coordinates were stored every 10 ps for every system. For the unbound ligands, dynamics were performed following the protocol described for the protein–ligand complexes in a box of the same size as that of the respective complex. Considering that our training set contains complexes obtained by docking, we decided to consider the first 10 ns as an equilibration phase and then use the last 10 ns for energy calculations.
All trajectories were analyzed with Gromacs 2018.3.61 Periodic boundary conditions were removed and the protein–ligand heavy atoms in every MD frame were superimposed on the starting structure. Then, the RMSD values along the trajectory were calculated using the initial structure of the complex as a reference.
Derivation of LIE Models
Four LIE parameterizations were derived using the whole data set of Vps34–inhibitor complexes. The LIE-D method developed by Miranda et al.25 was used as a control. In this model, α = 0.18, β is calculated from model E of Almlöf et al.,28 and γ is estimated from eq 2.
In the first model (named LIEαβ), we set γ = 0 and left α and β freely adjustable. In the second variant (named LIEβ = 0), α was the only adjustable parameter while β = γ = 0. Lastly, we generated a new LIE-D model (denoted as LIE-DVps34) for Vps34–inhibitor systems, with the underlying assumption of a linear relationship between parameters D and γ proposed by Miranda et al.25 In this way, we recalculated D and γOpt for all of the systems, obtaining a linear equation that describes the best linear relationship between D and γOpt. In addition, we built a model (LIE-DVps34ni) omitting the intraligand electrostatic contribution in eq 1 to evaluate whether excluding this term affects the precision of the LIE-D model, as described by Miranda and co-workers.25
Calculations of the average energy component contributions, parameters β and γ, and graphical analyses were carried out using an in-house developed tool and Microsoft Excel. Contact frequencies during the MD simulation were calculated using GROMACS for all residues within 4 Å of the ligand.
Statistical Analysis
To quantify the predictive capacity of the different LIE models calculated in this study in relation to the experimental energy, we used the multiple determination coefficient (R2). This coefficient measures how well the model reproduces the experimental values (ΔGexp), according to the proportion of the total variation of the results explained by the model.
| 11 |
where SSE = ∑i(ΔGicalc – ΔGi)2 is the residual sum of squares and SST = ∑i(ΔGicalc – ⟨ΔGi⟩)2 is the total sum of squares. ΔGicalc and ΔGi are the calculated and experimental binding free energies for complex i, respectively.
To measure the precision of the models with respect to the experimental values, we have calculated the mean absolute error (MAE), the standard deviation of the error (SDerror), and the root-mean-square error (RMSE)
| 12 |
with ei = ΔGicalc – ΔGi
| 13 |
| 14 |
Data overfitting was assessed by the leave-one-out cross-validation (LOO-CV)30 in Microsoft Excel software. Optimization was carried out by leaving one protein–ligand complex out and using the resulting parameterization model to predict the ΔGbind from the left-out complex. This procedure was conducted for each one of the complexes in the training data set. The LOO-CV coefficient, Q2, assesses the predictivity of a model and is calculated as
| 15 |
where predictive residual sum of
squares (PRESS)
is PRESS = ∑j(ΔGjcalc – ΔGj)2. The ΔGjcalc value is calculated from an
optimized LIE model excluding complex j. Also, the
standard deviation for the cross-validation analysis (SPRESS) was
calculated as 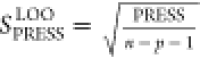 ,
where n = 20 is the number
of complexes in the data set and p is the number
of optimized parameters in the model (p = 2).
,
where n = 20 is the number
of complexes in the data set and p is the number
of optimized parameters in the model (p = 2).
Acknowledgments
This work was supported by the University of Medellin and Minciencias (grant 738-2016). M.E.V.-T. is an Eyes High Doctoral Recruitment (University of Calgary) and Alberta Graduate Student Scholarships recipient. Special thanks to the JetBrains company (https://www.jetbrains.com/) for granting a free open-source license to use their software.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c03582.
Representative structure (4 uwh) with the residues conserved in all of the interaction profiles; RMSD and standard deviation values for ligand atoms and residues within 4 Å of ligands during MD simulations; experimental ΔGbind values and energy contributions for all LIE models; calculation of FEP-derived β values; results from re-docking experiments; and energetic decomposition by fragments (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Foster F. M.; Traer C. J.; Abraham S. M.; Fry M. J. The Phosphoinositide (PI) 3-Kinase Family. J. Cell Sci. 2003, 116, 3037–3040. 10.1242/jcs.00609. [DOI] [PubMed] [Google Scholar]
- Chiu H.; Hopkins B. D.; Bagrodia S.; Cantley L. C.; Abraham R. T. The PI3K Pathway in Human Disease. Cell 2017, 170, 605–635. 10.1016/j.cell.2017.07.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J.; Nie J.; Ma X.; Wei Y.; Peng Y.; Wei X. Targeting PI3K in Cancer: Mechanisms and Advances in Clinical Trials. Mol. Cancer 2019, 18, 26 10.1186/s12943-019-0954-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Backer J. M. The Regulation and Function of Class III PI3Ks: Novel Roles for Vps34. Biochem. J. 2008, 410, 1–17. 10.1042/BJ20071427. [DOI] [PubMed] [Google Scholar]
- Scorzoni L.; de Paula e Silva A. C. A.; Marcos C. M.; Assato P. A.; de Melo W. C. M. A.; de Oliveira H. C.; Costa-Orlandi C. B.; Mendes-Giannini M. J. S.; Fusco-Almeida A. M. Antifungal Therapy: New Advances in the Understanding and Treatment of Mycosis. Frontiers in Microbiology. Front. Microbiol. 2017, 8, 36 10.3389/fmicb.2017.00036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pushpakom S.; Iorio F.; Eyers P. A.; Escott K. J.; Hopper S.; Wells A.; Doig A.; Guilliams T.; Latimer J.; McNamee C.; Norris A.; Sanseau P.; Cavalla D.; Pirmohamed M. Drug Repurposing: Progress, Challenges and Recommendations. Nat. Rev. Drug Discovery 2018, 8, 41–58. 10.1038/nrd.2018.168. [DOI] [PubMed] [Google Scholar]
- Miró-Canturri A.; Ayerbe-Algaba R.; Smani Y. Drug Repurposing for the Treatment of Bacterial and Fungal Infections. Front. Microbiol. 2019, 10, 41 10.3389/fmicb.2019.00041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stylianou M.; Kulesskiy E.; Lopes J. P.; Granlund M.; Wennerberg K.; Urban C. F. Antifungal Application of Nonantifungal Drugs. Antimicrob. Agents Chemother. 2014, 58, 1055–1062. 10.1128/AAC.01087-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braga M. V.; De Souza W. Effects of Protein Kinase and Phosphatidylinositol-3 Kinase Inhibitors on Growth and Ultrastructure of Trypanosoma cruzi. FEMS Microbiol. Lett. 2006, 256, 209–216. 10.1111/j.1574-6968.2006.00125.x. [DOI] [PubMed] [Google Scholar]
- Dali B.; Keita M.; Megnassan E.; Frecer V.; Miertus S. Insight into Selectivity of Peptidomimetic Inhibitors with Modified Statine Core for PlasmepsinII of Plasmodium falciparum over Human Cathepsin D. Chem. Biol. Drug Des. 2012, 79, 411–430. 10.1111/j.1747-0285.2011.01276.x. [DOI] [PubMed] [Google Scholar]
- Gierse J. K.; McDonald J. J.; Hauser S. D.; Rangwala S. H.; Koboldt C. M.; Seibert K. A Single Amino Acid Difference between Cyclooxygenase-1 (COX-1) and -2 (COX-2) Reverses the Selectivity of COX-2 Specific Inhibitors. J. Biol. Chem. 1996, 271, 15810–15814. 10.1074/jbc.271.26.15810. [DOI] [PubMed] [Google Scholar]
- Valiente P. A.; Batista P. R.; Pupo A.; Pons T.; Valencia A.; Pascutti P. G. Predicting Functional Residues in Plasmodium Falciparum Plasmepsins by Combining Sequence and Structural Analysis with Molecular Dynamics Simulations. Proteins: Struct., Funct., Bioinf.2 2008, 73, 440–457. 10.1002/prot.22068. [DOI] [PubMed] [Google Scholar]
- Yu M.; Gu Q.; Xu J. Discovering New PI3Kα Inhibitors with a Strategy of Combining Ligand-Based and Structure-Based Virtual Screening. J. Comput.-Aided Mol. Des. 2018, 32, 347–361. 10.1007/s10822-017-0092-8. [DOI] [PubMed] [Google Scholar]
- Zhu J.; Zhang H.; Yu L.; Sun H.; Chen Y.; Cai Y.; Li H.; Jin J. Computational Investigation of the Selectivity Mechanisms of PI3Kδ Inhibition with Marketed Idelalisib: Combined Molecular Dynamics Simulation and Free Energy Calculation. Struct. Chem. 2020, 32, 699–707. 10.1007/s11224-020-01643-4. [DOI] [Google Scholar]
- Li K.; Zhu J.; Xu L.; Jin J. Rational Design of Novel Phosphoinositide 3-Kinase Gamma (PI3K γ) Selective Inhibitors: A Computational Investigation Integrating 3D-QSAR, Molecular Docking and Molecular Dynamics Simulation. Chem. Biodiversity 2019, 16, e1900105 10.1002/cbdv.201900105. [DOI] [PubMed] [Google Scholar]
- Li Y.; Zhang J.; He D.; Liang Q.; Wang Y. Characterization of Molecular Recognition of Phosphoinositide-3-Kinase α Inhibitor through Molecular Dynamics Simulation. J. Mol. Model. 2012, 18, 1907–1916. 10.1007/s00894-011-1211-4. [DOI] [PubMed] [Google Scholar]
- Bian X.; Dong W.; Zhao Y.; Sun R.; Kong W.; Li Y. Definition of the Binding Mode of Phosphoinositide 3-Kinase α-Selective Inhibitor A-66S through Molecular Dynamics Simulation. J. Mol. Model. 2014, 20, 2166 10.1007/s00894-014-2166-z. [DOI] [PubMed] [Google Scholar]
- Wu F.; Hou X.; Luo H.; Zhou M.; Zhang W.; Ding Z.; Li R. Exploring the Selectivity of PI3Kα and MTOR Inhibitors by 3D-QSAR, Molecular Dynamics Simulations and MM/GBSA Binding Free Energy Decomposition. MedChemComm 2013, 4, 1482–1496. 10.1039/c3md00157a. [DOI] [Google Scholar]
- Genheden S.; Ryde U. Comparison of the Efficiency of the LIE and MM/GBSA Methods to Calculate Ligand-Binding Energies. J. Chem. Theory Comput. 2011, 7, 3768–3778. 10.1021/ct200163c. [DOI] [PubMed] [Google Scholar]
- Åqvist J.; Medina C.; Samuelsson J.-E. A New Method for Predicting Binding Affinity in Computer-Aided Drug Design. Protein Eng., Des. Sel. 1994, 7, 385–391. 10.1093/protein/7.3.385. [DOI] [PubMed] [Google Scholar]
- Aqvist J.; Marelius J. The Linear Interaction Energy Method for Predicting Ligand Binding Free Energies. Comb. Chem. High Throughput Screening 2001, 4, 613–626. 10.2174/1386207013330661. [DOI] [PubMed] [Google Scholar]
- Åqvist J.; Luzhkov V. B.; Brandsdal B. O. Ligand Binding Affinities from MD Simulations. Acc. Chem. Res. 2002, 35, 358–365. 10.1021/ar010014p. [DOI] [PubMed] [Google Scholar]
- van Dijk M.; ter Laak A. M.; Wichard J. D.; Capoferri L.; Vermeulen N. P. E.; Geerke D. P. Comprehensive and Automated Linear Interaction Energy Based Binding-Affinity Prediction for Multifarious Cytochrome P450 Aromatase Inhibitors. J. Chem. Inf. Model. 2017, 57, 2294–2308. 10.1021/acs.jcim.7b00222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valiente P. A.; Gil L A.; Batista P. R.; Caffarena E. R.; Pons T.; Pascutti P. G. New Parameterization Approaches of the LIE Method to Improve Free Energy Calculations of PlmII-Inhibitors Complexes. J. Comput. Chem. 2010, 31, 2723–2734. 10.1002/jcc.21566. [DOI] [PubMed] [Google Scholar]
- Miranda W. E.; Noskov S. Y.; Valiente P. A. Improving the LIE Method for Binding Free Energy Calculations of Protein-Ligand Complexes. J. Chem. Inf. Model. 2015, 55, 1867–1877. 10.1021/acs.jcim.5b00012. [DOI] [PubMed] [Google Scholar]
- Hao D.; He X.; Ji B.; Zhang S.; Wang J. How Well Does the Extended Linear Interaction Energy Method Perform in Accurate Binding Free Energy Calculations?. J. Chem. Inf. Model. 2020, 60, 6624–6633. 10.1021/acs.jcim.0c00934. [DOI] [PubMed] [Google Scholar]
- Rifai E. A.; van Dijk M.; Vermeulen N. P. E.; Yanuar A.; Geerke D. P. A Comparative Linear Interaction Energy and MM/PBSA Study on SIRT1–Ligand Binding Free Energy Calculation. J. Chem. Inf. Model. 2019, 59, 4018–4033. 10.1021/acs.jcim.9b00609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almlöf M.; Carlsson J.; Åqvist J. Improving the Accuracy of the Linear Interaction Energy Method for Solvation Free Energies. J. Chem. Theory Comput. 2007, 3, 2162–2175. 10.1021/ct700106b. [DOI] [PubMed] [Google Scholar]
- Poongavanam V.; Kongsted J. Binding Affinity Models for Falcipain Inhibition Based on the Linear Interaction Energy Method. J. Mol. Graphics Modell. 2016, 70, 236–245. 10.1016/j.jmgm.2016.06.008. [DOI] [PubMed] [Google Scholar]
- Webb G. I.; Sammut C.; Perlich C.; Horváth T.; Wrobel S.; Korb K. B.; Noble W. S.; Leslie C.; Lagoudakis M. G.; Quadrianto N.; Buntine W. L.; Quadrianto N.; Buntine W. L.; Getoor L.; Namata G.; Getoor L.; Han X. J. J.; Ting J.-A.; Vijayakumar S.; Schaal S.; Raedt L. De.. Leave-One-Out Cross-Validation. In Encyclopedia of Machine Learning, Springer, US, 2011; pp 600–601. [Google Scholar]
- Shirts M. R.; Mobley D. L.; Brown S. P.. Free-Energy Calculations in Structure-Based Drug Design. In Drug Design; Cambridge University Press, 2010; pp 61–86. [Google Scholar]
- Knight J. D. R.; Qian B.; Baker D.; Kothary R. Conservation, Variability and the Modeling of Active Protein Kinases. PLoS One 2007, 2, e982 10.1371/journal.pone.0000982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W.; Wang J.; Kollman P. A. What Determines the van Der Waals Coefficient? In the LIE (Linear Interaction Energy) Method to Estimate Binding Free Energies Using Molecular Dynamics Simulations?. Proteins Struct. Funct. Genet. 1999, 34, 395–402. . [DOI] [PubMed] [Google Scholar]
- Barratt E.; Bronowska A.; Vondrášek J.; Černý J.; Bingham R.; Phillips S.; Homans S. W. Thermodynamic Penalty Arising from Burial of a Ligand Polar Group Within a Hydrophobic Pocket of a Protein Receptor. J. Mol. Biol. 2006, 362, 994–1003. 10.1016/j.jmb.2006.07.067. [DOI] [PubMed] [Google Scholar]
- Kawasaki Y.; Freire E. Finding a Better Path to Drug Selectivity. Drug Discovery Today 2011, 16, 985–990. 10.1016/j.drudis.2011.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley D. L.; Dill K. A. Binding of Small-Molecule Ligands to Proteins: “What You See” Is Not Always “What You Get.”. Structure 2009, 17, 489–498. 10.1016/j.str.2009.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cournia Z.; Allen B. K.; Beuming T.; Pearlman D. A.; Radak B. K.; Sherman W. Rigorous Free Energy Simulations in Virtual Screening. J. Chem. Inf. Model. 2020, 60, 4153–4169. 10.1021/acs.jcim.0c00116. [DOI] [PubMed] [Google Scholar]
- Perdih A.; Wolber G.; Solmajer T. Molecular Dynamics Simulation and Linear Interaction Energy Study of D-Glu-Based Inhibitors of the MurD Ligase. J. Comput.-Aided Mol. Des. 2013, 27, 723–738. 10.1007/s10822-013-9673-3. [DOI] [PubMed] [Google Scholar]
- Y C.; WH P. Relationship between the Inhibition Constant (K1) and the Concentration of Inhibitor Which Causes 50 per Cent Inhibition (I50) of an Enzymatic Reaction. Biochem. Pharmacol. 1973, 22, 3099–3108. 10.1016/0006-2952(73)90196-2. [DOI] [PubMed] [Google Scholar]
- Ronan B.; Flamand O.; Vescovi L.; Dureuil C.; Durand L.; Fassy F.; Bachelot M. F.; Lamberton A.; Mathieu M.; Bertrand T.; Marquette J. P.; El-Ahmad Y.; Filoche-Romme B.; Schio L.; Garcia-Echeverria C.; Goulaouic H.; Pasquier B. A Highly Potent and Selective Vps34 Inhibitor Alters Vesicle Trafficking and Autophagy. Nat. Chem. Biol. 2014, 10, 1013–1019. 10.1038/nchembio.1681. [DOI] [PubMed] [Google Scholar]
- Dowdle W. E.; Nyfeler B.; Nagel J.; Elling R. A.; Liu S.; Triantafellow E.; Menon S.; Wang Z.; Honda A.; Pardee G.; Cantwell J.; Luu C.; Cornella-Taracido I.; Harrington E.; Fekkes P.; Lei H.; Fang Q.; Digan M. E.; Burdick D.; Powers A. F.; Helliwell S. B.; Daquin S.; Bastien J.; Wang H.; Wiederschain D.; Kuerth J.; Bergman P.; Schwalb D.; Thomas J.; Ugwonali S.; Harbinski F.; Tallarico J.; Wilson C. J.; Myer V. E.; Porter J. A.; Bussiere D. E.; Finan P. M.; Labow M. A.; Mao X.; Hamann L. G.; Manning B. D.; Valdez R. A.; Nicholson T.; Schirle M.; Knapp M. S.; Keaney E. P.; Murphy L. O. Selective VPS34 Inhibitor Blocks Autophagy and Uncovers a Role for NCOA4 in Ferritin Degradation and Iron Homeostasis in Vivo. Nat. Cell Biol. 2014, 16, 1069–1079. 10.1038/ncb3053. [DOI] [PubMed] [Google Scholar]
- Pasquier B.; El-Ahmad Y.; Filoche-Rommé B.; Dureuil C.; Fassy F.; Abecassis P. Y.; Mathieu M.; Bertrand T.; Benard T.; Barrière C.; El Batti S.; Letallec J. P.; Sonnefraud V.; Brollo M.; Delbarre L.; Loyau V.; Pilorge F.; Bertin L.; Richepin P.; Arigon J.; Labrosse J. R.; Clément J.; Durand F.; Combet R.; Perraut P.; Leroy V.; Gay F.; Lefrançois D.; Bretin F.; Marquette J. P.; Michot N.; Caron A.; Castell C.; Schio L.; McCort G.; Goulaouic H.; Garcia-Echeverria C.; Ronan B. Discovery of (2 S)-8-[(3 R)-3-Methylmorpholin-4-Yl]-1-(3-Methyl-2-Oxobutyl)-2-(Trifluoromethyl)-3,4-Dihydro-2 H -Pyrimido[1,2- a]Pyrimidin-6-One: A Novel Potent and Selective Inhibitor of Vps34 for the Treatment of Solid Tumors. J. Med. Chem. 2015, 58, 376–400. 10.1021/jm5013352. [DOI] [PubMed] [Google Scholar]
- Toledo-Sherman L.; Breccia P.; Cachope R.; Bate J. R.; Angulo-Herrera I.; Wishart G.; Matthews K. L.; Martin S. L.; Cox H. C.; Mcallister G.; Penrose S. D.; Vater H.; Esmieu W.; Van De Poël A.; Van De Bospoort R.; Strijbosch A.; Lamers M.; Leonard P.; Jarvis R. E.; Blackaby W.; Barnes K.; Eznarriaga M.; Dowler S.; Smith G. D.; Fischer D. F.; Lazari O.; Yates D.; Rose M.; Jang S. W.; Muñoz-Sanjuan I.; Dominguez C. Optimization of Potent and Selective Ataxia Telangiectasia-Mutated Inhibitors Suitable for a Proof-of-Concept Study in Huntington’s Disease Models. J. Med. Chem. 2019, 62, 2988–3008. 10.1021/acs.jmedchem.8b01819. [DOI] [PubMed] [Google Scholar]
- Certal V.; Carry J. C.; Halley F.; Virone-Oddos A.; Thompson F.; Filoche-Rommé B.; El-Ahmad Y.; Karlsson A.; Charrier V.; Delorme C.; Rak A.; Abecassis P. Y.; Amara C.; Vincent L.; Bonnevaux H.; Nicolas J. P.; Mathieu M.; Bertrand T.; Marquette J. P.; Michot N.; Benard T.; Perrin M. A.; Lemaitre O.; Guerif S.; Perron S.; Monget S.; Gruss-Leleu F.; Doerflinger G.; Guizani H.; Brollo M.; Delbarre L.; Bertin L.; Richepin P.; Loyau V.; Garcia-Echeverria C.; Lengauer C.; Schio L. Discovery and Optimization of Pyrimidone Indoline Amide PI3Kβ Inhibitors for the Treatment of Phosphatase and Tensin Homologue (PTEN)-Deficient Cancers. J. Med. Chem. 2014, 57, 903–920. 10.1021/jm401642q. [DOI] [PubMed] [Google Scholar]
- Burger M. T.; Pecchi S.; Wagman A.; Ni Z. J.; Knapp M.; Hendrickson T.; Atallah G.; Pfister K.; Zhang Y.; Bartulis S.; Frazier K.; Ng S.; Smith A.; Verhagen J.; Haznedar J.; Huh K.; Iwanowicz E.; Xin X.; Menezes D.; Merritt H.; Lee I.; Wiesmann M.; Kaufman S.; Crawford K.; Chin M.; Bussiere D.; Shoemaker K.; Zaror I.; Maira S. M.; Voliva C. F. Identification of NVP-BKM120 as a Potent, Selective, Orally Bioavailable Class i PI3 Kinase Inhibitor for Treating Cancer. ACS Med. Chem. Lett. 2011, 2, 774–779. 10.1021/ml200156t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller S.; Tavshanjian B.; Oleksy A.; Perisic O.; Houseman B. T.; Shokat K. M.; Williams R. L. Shaping Development of Autophagy Inhibitors with the Structure of the Lipid Kinase Vps34. Science 2010, 327, 1638–1642. 10.1126/science.1184429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bago R.; Malik N.; Munson M. J.; Prescott A. R.; Davies P.; Sommer E.; Shpiro N.; Ward R.; Cross D.; Ganley I. G.; Alessi D. R. Characterization of VPS34-IN1, a Selective Inhibitor of Vps34, Reveals That the Phosphatidylinositol 3-Phosphate-Binding SGK3 Protein Kinase Is a Downstream Target of Class III Phosphoinositide 3-Kinase. Biochem. J. 2014, 463, 413–427. 10.1042/BJ20140889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda A.; Harrington E.; Cornella-Taracido I.; Furet P.; Knapp M. S.; Glick M.; Triantafellow E.; Dowdle W. E.; Wiedershain D.; Maniara W.; Moore C.; Finan P. M.; Hamann L. G.; Firestone B.; Murphy L. O.; Keaney E. P. Potent, Selective, and Orally Bioavailable Inhibitors of VPS34 Provide Chemical Tools to Modulate Autophagy in Vivo. ACS Med. Chem. Lett. 2016, 7, 72–76. 10.1021/acsmedchemlett.5b00335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burley S. K.; Berman H. M.; Bhikadiya C.; Bi C.; Chen L.; Di Costanzo L.; Christie C.; Dalenberg K.; Duarte J. M.; Dutta S.; Feng Z.; Ghosh S.; Goodsell D. S.; Green R. K.; Guranović V.; Guzenko D.; Hudson B. P.; Kalro T.; Liang Y.; Lowe R.; Namkoong H.; Peisach E.; Periskova I.; Prlić A.; Randle C.; Rose A.; Rose P.; Sala R.; Sekharan M.; Shao C.; Tan L.; Tao Y. P.; Valasatava Y.; Voigt M.; Westbrook J.; Woo J.; Yang H.; Young J.; Zhuravleva M.; Zardecki C. RCSB Protein Data Bank: Biological Macromolecular Structures Enabling Research and Education in Fundamental Biology, Biomedicine, Biotechnology and Energy. Nucleic Acids Res. 2019, 47, D464–D474. 10.1093/nar/gky1004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marvin 20.21. ChemAxon. Http://Www.Chemaxon.Com. 2020. (Last accessed Dec 9, 2021).
- Trott O.; Olson A. J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2010, 31, 455–461. 10.1002/jcc.21334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdés-Tresanco M. S.; Valdés-Tresanco M. E.; Valiente P. A.; Moreno E. AMDock: A Versatile Graphical Tool for Assisting Molecular Docking with Autodock Vina and Autodock4. Biol. Direct 2020, 15, 12 10.1186/s13062-020-00267-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and Testing of a General Amber Force Field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: II. Parameterization and Validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Wang J.; Wang W.; Kollman P. A.; Case D. A. Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graphics Modell. 2006, 25, 247–260. 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- Case D. A.; Belfon K.; Ben-Shalom I. Y.; Brozell S. R.; Cerutti D. S.; Cheatham T. E. III; Cruzeiro V. W. D.; Darden T. A.; Duke R. E.; Giambasu G.; Gilson M. K.; Gohlke H.; Goetz A. W.; Harris R.; Izadi S.; Izmailov S. A.; Kasavajhala K.; Kovalenko P. A.. Amber 2018 and AmberTools 2019, University of California, San Francisco, 2019. [Google Scholar]
- Gordon J. C.; Myers J. B.; Folta T.; Shoja V.; Heath L. S.; Onufriev A. H++: A Server for Estimating PKas and Adding Missing Hydrogens to Macromolecules. Nucleic Acids Res. 2005, 33, W368–W371. 10.1093/nar/gki464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers J.; Grothaus G.; Narayanan S.; Onufriev A. A Simple Clustering Algorithm Can Be Accurate Enough for Use in Calculations of PKs in Macromolecules. Proteins: Struct., Funct., Bioinf. 2006, 63, 928–938. 10.1002/prot.20922. [DOI] [PubMed] [Google Scholar]
- Anandakrishnan R.; Aguilar B.; Onufriev A. V. H++ 3.0: Automating PK Prediction and the Preparation of Biomolecular Structures for Atomistic Molecular Modeling and Simulations. Nucleic Acids Res. 2012, 40, W537–W541. 10.1093/nar/gks375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindah E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
- Mark P.; Nilsson L. Structure and Dynamics of the TIP3P, SPC, and SPC/E Water Models at 298 K. J. Phys. Chem. A 2001, 105, 9954–9960. 10.1021/jp003020w. [DOI] [Google Scholar]
- Hess B.; Bekker H.; Berendsen H. J. C. C.; Fraaije J. G. E. M. E. M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. . [DOI] [Google Scholar]
- Berendsen H. J. C.; Postma J. P. M.; Van Gunsteren W. F.; Dinola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
- Van Gunsteren W. F.; Berendsen H. J. C. A Leap-Frog Algorithm for Stochastic Dynamics. Mol. Simul. 1988, 1, 173–185. 10.1080/08927028808080941. [DOI] [Google Scholar]
- Parrinello M.; Rahman A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. 10.1063/1.328693. [DOI] [Google Scholar]
- Essmann U.; Perera L.; Berkowitz M. L.; Darden T.; Lee H.; Pedersen L. G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. 10.1063/1.470117. [DOI] [Google Scholar]
- Darden T.; York D.; Pedersen L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. 10.1063/1.464397. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.








