Recombination rates in admixed individuals identified by ancestry-based inference

Abstract

Studies of recombination and how it varies depend crucially on accurate recombination maps. We propose a new approach for constructing high-resolution maps of relative recombination rates based on the observation of ancestry switch points among admixed individuals. We show the utility of this approach using simulations and by applying it to SNP genotype data from a sample of 2,565 African Americans and 299 African Caribbeans and detecting several hundred thousand recombination events. Comparison of the inferred map with high-resolution maps from non-admixed populations provides evidence of fine-scale differentiation in recombination rates between populations. Overall, the admixed map is well predicted by the average proportion of admixture and the recombination rate estimates from the source populations. The exceptions to this are in areas surrounding known large chromosomal structural variants, specifically inversions. These results suggest that outside of structurally variable regions, admixture does not substantially disrupt the factors controlling recombination rates in humans.

The extent to which patterns of recombination vary across human populations remains uncertain. Increasing evidence has suggested a high concordance between populations in large-scale recombination rates and more variation between populations in small-scale recombination rates^1-5. The lack of high-resolution genome-wide recombination maps for admixed individuals, such as African Americans, has limited the possibility of incorporating admixed populations in comparative analyses of recombination rates. The development of new genome-wide recombination maps is therefore an essential step for understanding recombination in admixed populations and enabling broader comparative analyses.

Generating new recombination maps has traditionally depended on observations of recombination events in pedigrees⁶. Large-scale applications of this approach have been limited to a few samples of European descent with unusually detailed genealogic data, such as samples from Iceland^7,8, Mormons from Utah⁹ and Hutterites¹⁰. For example, a recombination map based on inferences from about 15,000 meioses in the Icelandic pedigree genotyped with nearly 300,000 SNPs achieved a resolution of recombination rate variation down to the 10-kb scale⁸. In contrast, for non-European and admixed populations, such as African Americans, the best available pedigree-based maps use many fewer meioses and ~1,000 microsatellites or less^11,12.

Assessment of linkage disequilibrium (LD), or the non-random association of alleles on chromosomes, in unrelated individuals provides a second, more indirect means for inferring recombination rates in a population. The advent of high-density, genome-wide SNP data has enabled LD-based maps to achieve a resolution of about 1 kb^13,14 and has shown that recombination rates at such fine scales are dominated by recombination hotspots. Using LD-based maps in analyses of short target regions^1-4 and genome-wide SNP data⁵, comparisons between populations have documented some variation in small-scale recombination rates but very little variation in large-scale recombination rates. LD-based maps, however, conflate the effective population size and recombination rates, which complicates the interpretation of inter-population variation in recombination⁶. This conflation of the effective population size and recombination rate is particularly problematic in regions where recent natural selection has reduced the effective population size^6,15. In addition, care must be taken when applying LD-based approaches to recently admixed populations because these methods are based on population genetic models of populations at demographic equilibrium^1,16.

To address the need for genome-wide recombination maps in admixed samples, we report here an ancestry-switch–based method for constructing high-resolution genome-wide recombination maps. We used this method to infer a recombination map from genotypes at >570,000 SNPs in 2,864 admixed African-American and African Caribbean individuals. Because of the levels of admixture in this sample, we observed approximately 90 ancestry switch points per individual, each of which indicates the location of a recombination event in the history of the sample; thus, our map is based on roughly 250,000 unique recombination events. With the inferred map, we investigated whether there is evidence for population differentiation in recombination rates and to what extent admixture has a global and local effect on recombination patterns.

RESULTS

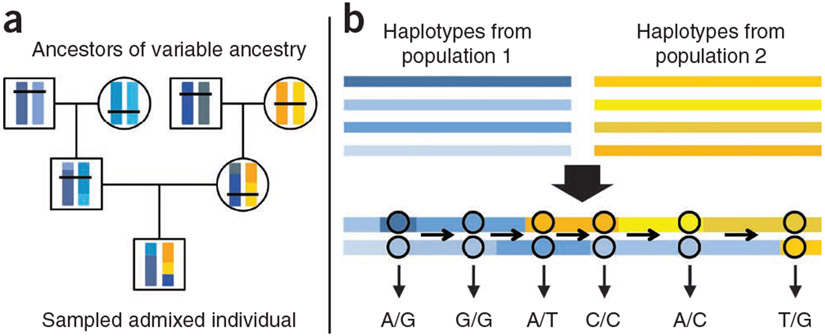
Recently admixed individuals derive their ancestors from two or more diverged populations, and thus, their chromosomes are mosaics of segments with different origins (Fig. 1). Switch points in ancestry along a chromosome mark locations where a recombination event occurred between ancestral chromosomes of different origins. In principle, ancestry switch-point events will be a random sample of all recombination events, and by tallying the location of such events across a large number of individuals, we can infer relative rates of recombination across the genome.

Figure 1.

Sketch of the haplotype-copying Hidden Markov model used to detect ancestry switch points. (a) Yellow and blue represent the chromosomal segments of different ancestry and the shades of each color represent different haplotypes from each ancestry. Recombination creates a mosaic of haplotypes regardless of origin but recombination events between haplotypes of different ancestries leave signatures that can be detected in descendant, admixed individuals. (b) The genotypes observed for such an individual form observed states of a Hidden Markov model in which underlying states are based on which haplotypes from a reference population each allele of the genotype is copied.

Our approach for identifying the locations of ancestry switch points is based on a previously developed Hidden Markov model (HMM) for admixture that matches chromosomal segments of admixed individuals to reference haplotypes from the ancestral populations¹⁷. To account for uncertainty in the locations of ancestry switch points, we implemented an algorithm to compute the probability of an ancestry switch between two markers conditional on an individual’s genotype data, and we based our inferences on these probabilities (Online Methods). Moreover, to pool evidence for recombination across individuals, we developed an empirical Bayes approach. Our method produced two estimators: (i) the individual-based estimator, ${\overline{c}}_{jk}^{(i)}$, of the number of switches between positions j and k in individual i; and (ii) the sample-wide estimator, r_jk, of the number of ancestry switch events in the history of the admixed sample between positions j and k.

Validation of the approach using simulations

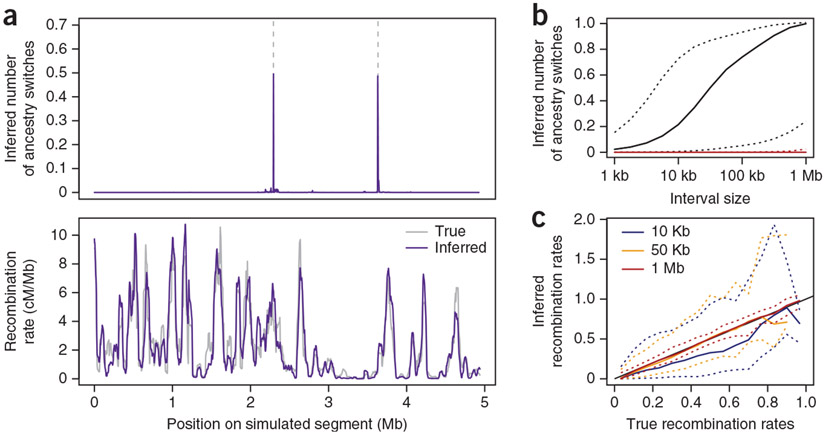
To investigate the resolution of this ancestry-switch approach, we tested our methods using a series of simulations of a simple model of African-American admixture with identical sample sizes and marker density to those found in our study sample. An example of the inferred number of ancestry switches from a random simulated segment from one individual is shown in Figure 2a.

Figure 2.

Sensitivity and specificity of inference. (a) Estimated number of switches (${\overline{c}}_{jk}^{(i)}$) between neighboring SNPs obtained for a simulated individual with two ancestry switches (vertical dashed lines). Below, the comparison at the 50-kb scale of the estimated rates (r_jk) and the underlying recombination map used to perform the simulations for this segment. Both maps are normalized to the same total rate. (b) The inferred number of switch points (${\overline{c}}_{jk}^{(i)}$) as function of the size of the interval between locations j and k. The black line represents the median for symmetric intervals around a single, isolated switch point. The red line represents the median for intervals with zero simulated switch points and which are located at least 1 Mb away from the closest switch point. Dashed lines mark the 2.5% and 97.5% quantiles. (c) Comparison of the inferred rates (r_jk) with the true rates across all segments at 10-kb (blue), 50-kb (orange) and 1-Mb (red) scales. The 2.5% and 97.5% quantiles are shown with dashed lines. All maps have been normalized to the same total rate for comparison.

To assess specificity, we investigated 50,000 randomly chosen locations more than 1 Mb away from the nearest switch point (Fig. 2b, red line). For more than 95% of those 1-Mb windows, the value of ${\overline{c}}_{jk}^{(i)}$ fell below 0.025, suggesting that the method produces little false evidence for ancestry switches where there are none. To assess sensitivity, we computed ${\overline{c}}_{jk}^{(i)}$ for symmetric intervals around isolated ancestry switch points (Fig. 2b, black line). If well calibrated, the method should find values of ${\overline{c}}_{jk}^{(i)}$ equal to 1 for these intervals. For intervals of 1 Mb around true switch points, we found the median ${\overline{c}}_{jk}^{(i)}$ to be approximately 1, and when we investigated at what scale the median ${\overline{c}}_{jk}^{(i)}=0.85$, we found it to be at roughly the 200-kb scale (Fig. 2b). These results suggest that our method resolves single switch points fairly well at the 200-kb scale and above.

For switch-points close to the ends of our simulated segments, we found a consistent bias downwards in the values of ${\overline{c}}_{jk}^{(i)}$ (Supplementary Fig. 1). This bias was to be expected, as it is only through analysis of several consecutive markers that evidence for a switch point can be derived. We thus did not attempt to infer recombination rates within 5 Mb of chromosome ends or centromeres (Supplementary Note). Finally, as with other methods for inferring recombinations, we observed a ‘multiple hits’ problem, such that if more than one switch point occurred within a 1-Mb interval, ${\overline{c}}_{jk}^{(i)}$ would typically be underestimated. For example, ${\overline{c}}_{jk}^{(i)}$ often takes values close to zero when the actual value is two or takes values close to one when the actual value is three (Supplementary Fig. 2). This problem is not evident if two switch points are spaced more than 1 Mb apart (Supplementary Fig. 1), and thus should not be a major problem for analysis of African-American samples, as simulations indicate the fraction of switch points with spacing <1 Mb is small when admixture has been recent (Supplementary Fig. 2). Nonetheless, we developed a refined estimator of recombination, r_jk, that corrects for the multiple hits problem and, more importantly, pools information across individuals in an empirical Bayes framework (Online Methods and Supplementary Fig. 3).

To assess how well the estimator r_jk performs at inferring recombination, we estimated maps of relative recombination rates from our simulated datasets and compared them to the ‘true’ maps we used to simulate the data. The correlation between the true and inferred rates was 0.99 at a 1-Mb scale, 0.90 at the 100-kb scale, 0.86 at the 50-kb scale and 0.71 at the 10-kb scale (Supplementary Fig. 3). Plots of the inferred versus true recombination rates (Fig. 2c) revealed that the map produces unbiased estimates of the rates at the 1-Mb and 50-kb scales, whereas at the smaller 10-kb scale there is evidence of a downward bias in the map. Based on these results, we focused the presentation of our results on the 1-Mb–scale map to represent large-scale recombination patterns and on the 50-kb–scale map to represent finer scales. Visual inspection of randomly chosen examples at the 50-kb scale (such as that shown in Fig. 2a) shows that the inferred map captures most of the major recombinational features that are found in the simulated map.

One potential drawback of either approach we took is a possible overestimation of recombination if a large number of switch points across individuals descended from the same ancestral event (that is, if switch points are inherited in an identical-by-descent manner in the sample). Using simulations, we found that under reasonable assumptions about the population size of African Americans and African Caribbeans, it would be rare for a given ancestry switch to be observed twice in our study sample (Supplementary Fig. 4).

Application to an African-American and African-Caribbean sample

We applied our approach to a study sample consisting of 2,565 African-American and 299 African-Caribbean individuals gathered from four studies (GeneSTAR¹⁸, GENOA^19,20, GRAAD^21-23 and SARP and CAG-CSGA²⁴; Supplementary Table 1). This sample has a mean African-ancestry coefficient of ~0.81 with a 95% quantile range of 0.54–0.96 (Supplementary Fig. 5), a broad range that is consistent with previous studies of African-American and African-Caribbean samples^25-28. We used as reference panels for the ancestral populations the HapMap YRI and HapMap CEU panels. Although neither of these panels is an exact representation of the ancestral populations of the admixed individuals in the sample used here, previous studies^17,25 and our own principal component analyses (Supplementary Fig. 6) suggest these two panels are reasonable proxies for the source populations.

We denote the map we generated as the ‘AfAdm’ map, and we compared this map to the recently published deCODE map based on Icelandic pedigrees as well as published LD-based maps for the HapMap CEU and YRI samples (labeled deCODE, HapMapYRI and HapMapCEU, respectively). When comparing the AfAdm map to the HapMap-based maps, there is the potential to overestimate the similarity between the maps because the HapMap samples served as the reference panels for our method. We investigated the potential magnitude of this effect through simulations and determined that by using a trimmed Pearson correlation coefficient, any possible bias as a result of shared data was minimized (Online Methods, Supplementary Note and Supplementary Fig. 7). Unless otherwise noted, all the correlations reported for scales <1 Mb are trimmed Pearson correlations.

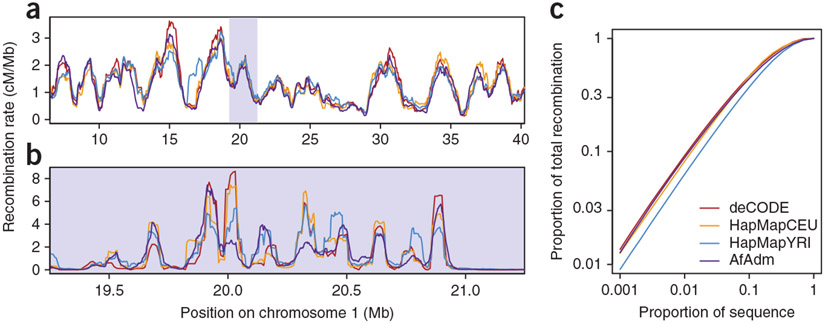
At the 1-Mb scale, we found a strong visual concordance and correlations greater than 0.9 among all the maps (Fig. 3a, Table 1 and see Supplementary Table 2 for additional scales). This degree of correlation suggests broad-scale similarity of the recombination maps across human populations, and that all three methods have the power to infer recombination maps well at this scale.

Figure 3.

Comparison of the African admixture-based map to existing maps. (a) Example of 1-Mb–scale map from 50 Mb of chromosome 1. (b) Example of 50-kb–scale map from the 2.5-Mb section of chromosome 1 indicated by the gray box in a. (c) Proportion of the total recombination in various proportions of sequence intervals at the 50-kb scale.

Table 1.

Correlations between recombination maps

	HapMap CEU	HapMap YRI	HapMap 80%:20%	deCODE	AfAdm
HapMap CEU	1.000	0.922	0.951	0.939	0.900
HapMap YRI	0.738	1.000	0.997	0.934	0.922
HapMap 80%:20%	0.844	0.985	1.000	0.948	0.929
Decode	0.789	0.734	0.788	1.000	0.924
AfAdm	0.611	0.697	0.712	0.666	1.000

We report Pearson correlations at the 1-Mb (above diagonal) and 50-kb (below diagonal) scales. See Supplementary Table 2 for additional scales.

At scales finer than 1 Mb, there was a more coarse correspondence between recombination maps (Fig. 3b, Table 1 and Supplementary Table 2). For example, at the 50-kb scale, the correlation of the AfAdm map with the HapMapCEU map is 0.611 and is 0.697 with the HapMapYRI map. The observed decay of correlation at smaller observation scales more likely reflects the impact of sampling error than drastic underlying recombination rate differences across samples. As evidence, we note the correlation between the deCODE and HapMapCEU maps is 0.789 at a 50-kb scale (Table 1) even though both maps are based on populations of northern European descent.

Investigation of what proportion of the genome contains the highest recombination rates provided further evidence for the general similarities between the maps. In the AfAdm map, we found that recombinations concentrate in a fraction of the sequence (recombination hotspots); for instance, at the 50-kb scale, 10% of the total recombinations accumulate in about 1.2% of the genomic sequence (Fig. 3c). This level of enrichment in the AfAdm map is similar to the level found in the HapMapCEU and the deCODE maps and is only slightly higher than in the HapMapYRI map (Fig. 3c). We note that because the inferred hottest fraction of the genome likely contains regions whose recombination rates have been overestimated by chance, the observed level of enrichment may be upwardly biased for each map in ways that depend on the sampling error specific to each map’s estimates.

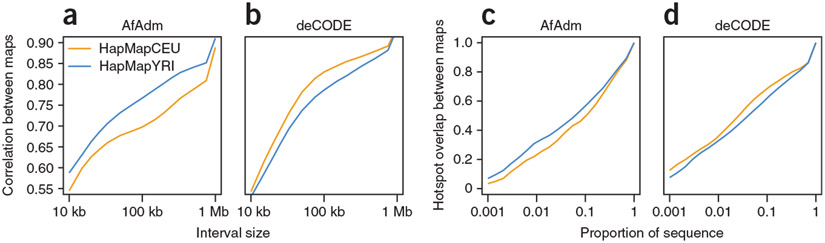
Despite the general similarity of all maps, there is evidence of subtle increases in similarity between recombination maps from more closely related populations. For example, the deCODE pedigree map correlates more strongly with the HapMapCEU map than the HapMapYRI map, whereas the AfAdm map correlates more strongly with the HapMapYRI map (Fig. 4a,b). We also observed this pattern when investigating recombination hotspot sharing (Fig. 4c,d). The overlap between AfAdm and HapMapYRI hotspots is significantly higher than the AfAdm overlap with HapMapCEU hotspots (0.32 compared to 0.23, P = 2 × 10⁻⁵ for hotspots defined as the 50-kb intervals with the top 1% largest rates). In contrast, deCODE hotspots overlap better with HapMapCEU hotspots (0.35 compared 0.32, P = 0.0297 on the same scale as used in the previous comparison).

Figure 4.

Population differences in recombination patterns. (a–d) Independent of scale, the AfAdm map correlates better (a) and shares more hotspots (c) with the HapMapYRI than the HapMapCEU map. In contrast, the deCODE map correlates better (b) and shares more hotspots (d) with the HapMapCEU than the HapMapYRI map. Hotspots are defined as the 50-kb intervals with the top 1% largest rates.

Further, the genome-wide European ancestry proportion of an individual in our sample is positively correlated with the fraction of switch points in that individual inferred to be in HapMapCEU hotspots (r = 0.102, P < 10⁻⁸) and negatively correlated with the fraction inferred to be in HapMapYRI hotspots (r = −0.122, P < 10⁻¹⁰). These results corroborate arguments that fine-scale recombination rate modifiers differ across populations and suggest that, because the ancestry in AfAdm individuals is predominantly African, our sample has recombination patterns that are more like the HapMapYRI population. Given these results, we attempted an admixture mapping approach to identify loci that would explain the usage of HapMapYRI as opposed to HapMapCEU hotspots. We did not identify any significant associations between hotspot usage and local ancestry (Supplementary Note), but this is likely due to a lack of power because of limited sample size and because of the limitation that the ancestry switches we observed took place across several generations on varied genotypic backgrounds.

Using a regression-based approach, we estimated what proportional weight would lead to the observed AfAdm rates if the rates are a weighted average of HapMapYRI and HapMapCEU rates. We estimated proportional weights of 0.79 at 50-kb, 0.75 at 100-kb and 0.68 at 1-Mb scales (Supplementary Fig. 8). For completely identical maps, the estimated proportional weight would be an equal weighting of each map, so the trending toward 0.5 observed here may be caused by the global similarity of the maps at larger scales (Supplementary Fig. 8). We note that this regression-based approach may be biased toward the map with the smaller sampling error. Given that the two HapMap maps were inferred with the same approach from samples of similar size, we did not expect large differences in sampling error between the maps. The results thus suggest that the AfAdm map can be coarsely approximated as an 80%:20% weighted average of the HapMapYRI and HapMapCEU maps. This weighting would be expected from the average ancestry coefficient in the sample (~80%:20% African:European ancestry).

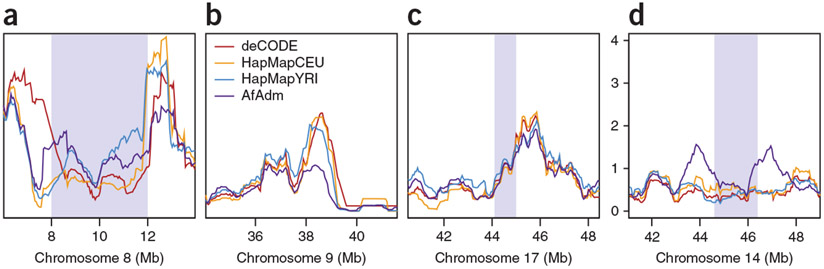
We next sought to identify intervals where the recombination rate differs from an 80%:20% average of the HapMapYRI and HapMapCEU maps. The region where the AfAdm map showed the strongest deficit in recombination when compared to the other maps lies at the centromeric end of a common inversion in 8p23.1 (at ~12 Mb on chromosome 8; Fig. 5a)^29,30. The same segment has been found, using coarser-scale microsatellite-based maps^11,12, to be the site of the largest map differences in the genome between Europeans and both Asians and African Americans. This inversion region is also characterized by several duplications and deletions^29-31, which may contribute to the complexity of the region, and we note that all three methods (pedigree, LD-based and admixture-based methods) gave differing estimates of recombination rates at the telomeric end of the inversion (at ~8 Mb on chromosome 8). This is not the only region with structural variation that appears to differ among the maps. Indeed, four out of the top five regions where the AfAdm map showed strong deficits in recombination contained large inversions (Table 2). An example of this is the region just outside the centromere on chromosome 9 (Fig. 5b), which harbors both a small inversion³² and large copy number variations (CNVs)³³. Large inversions do not, however, always affect rate estimates in the AfAdm map. For example, the 17q21.31 region harbors a large 900-kb inversion with a 20% frequency in Europeans that is rarely found in African samples³⁴, but the rate estimates in this region do not differ between the maps (Fig. 5c).

Figure 5.

Recombination rates in notable genomic locations. (a) The region with the largest deficit of the AfAdm map just outside the known inversion on chromosome 8p23.1–8p22 (gray). (b) The region with a large deficit of the AfAdm map on chromosome 9 near the boundary of multiple known polymorphic inversions. (c) The inversion on chromosome 17q21.31 (gray). (d) A region on chromosome 14 with an elevated average European-ancestry proportion (gray) framed by local peaks of recombination.

Table 2.

Regions for which the AfAdm map differs most from a 80%:20% average of the HapMapYRI and HapMapCEU maps. Regions where the AfAdm map has lower rate estimates are shown at top, followed by regions where the AfAdm map has higher rates.

Chr.	Positiona	Differenceb	Structural variations
8	11.4–13.3	−1.93	4.7-Mb inversion29,30
9	37.6–39.5	−1.04	36-kb inversion32/8-Mb CNV33
10	124.9–126.8	−1.00
16	21.7–23.5	−0.89	1.1-Mb inversion39
7	5.1–6.4	−0.87	1-Mb inversion39,41
22	24.5–26.9	1.42	500-kb CNV33,42,43
8	133.8–135.6	1.30
16	81.1–83.0	1.23	1-kb inversion41
22	34.8–36.5	1.23
14	45.9–47.6	1.20	1-Mb CNV42
8	7.2–9.1	1.10	4.7-Mb inversion29,30
18	22.1–23.7	1.04
3	51.4–54.3	1.03	45-kb inversion32,44
14	93.3–95.1	1.03	1-kb inversion45
14	43.2–44.9	1.03	1-Mb CNV46
2	59.8–63.3	1.03	2.9-Mb CNV33
15	67.6–68.9	0.99
5	30.6–32.2	0.99
14	50.9–52.1	0.97
16	64.0–65.4	0.97
6	16.1–18.4	0.96
10	72.5–74.0	0.94	36-kb inversion32/1.2-Mb CNV47
9	6.8–8.1	0.91
8	23.1–24.4	0.88	2.5-Mb CNV33
7	102.7–104.1	0.84

To identify the regions, we identified the top 1% of the intervals with the greatest difference between the AfAdm map and the HapMapYRI and HapMapCEU maps computed on 1-Mb intervals spaced every 50 kb. We joined intervals whose endpoints were not more than 1-Mb apart from each other, and we examined and present here only regions supported by at least five intervals. We omitted seven regions where visual inspection revealed that the difference was not caused by the AfAdm rate but rather by the HapMapYRi rate (Supplementary Table 3). The reported structural variations were observed in surveys of structural variations in random samples of European or African individuals and were not further than 1-Mb away from the focus regions. in addition, CNVs had to be at least 500 kb in length to be included, and we only report here the largest CNV in the region. The intervals before collapsing the data are shown in Supplementary Figure 10.

^aPosition in Mb.

^bLargest difference per region, given in cM. Negative values imply lower rates in the AfAdm map. Chr., chromosome; CNV, copy number variation.

Among the regions with the greatest elevation in recombination rates relative to an 80%:20% average of the HapMapYRI and HapMapCEU maps, the pattern observed here is more ambiguous; only 11 of the 27 such regions that we investigated harbor structural variations (Table 2 and Supplementary Table 3). We found the most strikingly elevated recombination rates in the major histocompatibility complex region (Supplementary Fig. 9), which is known to have high levels of genetic diversity and population differentiation³⁵. Using quartet families in a subset of the data, we found that this elevation in inferred ancestry switches is not concordant with family-based recombination rates (see the Discussion section, Supplementary Note and Supplementary Fig. 9). We also note two regions with large CNVs on chromosome 2 (Supplementary Fig. 10) and 14 (Fig. 5d), each consisting of two closely spaced peaks of elevated recombination rates flanking regions with an elevated level of European ancestry across individuals. In seven regions, the excess in recombination is caused by a particularly low rate in the HapMapYRI map (Supplementary Table 3). A possible explanation for such regions is selection specific to the Yoruban population, which can bias LD-based estimates of recombination downwards^6,15.

DISCUSSION

We have introduced a method for inferring recombination rates based on ancestry switch points. Simulations suggest that this method performs well for the sample size and SNP density of the data that we analyzed here. We obtained further support for the method by using it to infer a recombination map for African-American and African-Caribbean individuals (the AfAdm map); this map corresponds well to published maps from other populations while also permitting for the investigation of fine-scale recombination patterns in admixed populations. This ancestry-switch approach should be much less sensitive than LD-based methods to local distortions of LD caused by natural selection (for example, in selective sweep regions). In an ancestry-switch approach, such distortions would arise only when unusually strong selection has occurred in the typically brief period since admixture between ancestral populations. The approach also has an inherent efficiency in that the number of switch points observed per genotyped individual is relatively large. For example, in the African Americans and African Caribbeans sampled here, we observed roughly 90 switch points (recombination events) per genotyped individual (Supplementary Note) as opposed to the ~30 such events that are expected from genotyping multiple individuals in a pedigree to observe an informative meiosis.

A disadvantage of the ancestry-switch approach is that, like LD-based methods, it does not readily allow one to infer absolute recombination rates or to identify recombination events unique to individual parents. Hence, it is not an optimal approach for investigation of variation in recombination between individuals or sexes. Additionally, with the SNP markers considered here, the ancestry-switch method resolves events within individuals less precisely (roughly a 200-kb scale) than does direct investigation of dense SNP markers in pedigrees. The resolution of the ancestry-switch approach will improve by using variants that differ in frequency between the populations ancestral to admixed groups (Supplementary Fig. 11), and large-scale sequencing efforts are expected to identify more of such loci³⁶. With the current level of resolution, sampling error is clearly contributing to the observed differences and similarities between the maps we investigated. For example, we showed that the AfAdm map is more like the HapmapYRI map than the HapMapCEU map (Fig. 4), but we also found that the HapMapYRI map (and HapMapCEU map) correlated better with the deCODE map than the AfAdm map at the 1-Mb and 50-kb scales (Table 1). This pattern would be expected if recombination rates are fairly similar across populations and if the AfAdm map has a higher sampling error than the deCODE map, both of which are likely true. The AfAdm map is based on ~250,000 events resolved at a scale of roughly 200 kb each, whereas the deCODE map is based on ~600,000 events resolved to a scale of ~10 kb each. To circumvent this issue, we used comparisons of the HapMapYRI and HapMapCEU maps to the AfAdm map alone (Fig. 4a) and the deCODE map alone (Fig. 4b) to investigate population differences in recombination rates.

By comparing the AfAdm map to existing maps, we were able to make several observations: (i) there is evidence for subtle population differences in recombination rates between African and European populations, (ii) African-European admixed individuals appear to have recombination rates that are, on average, intermediate between the African and European rates, and (iii) the degree to which the rates are intermediate is predictable from the average ancestry coefficient (~80% African and ~20% European) in our sample. Further, in admixed individuals, recombinations appear to be concentrated at hotspots in a manner correlated with ancestry: individuals with more African ancestry have recombinations at hotspots found in the HapMapYRI map, and individuals with more European ancestry have recombinations at hotspots found in the HapMapCEU map. These observations are consistent with the differentiation between populations for fine-scale recombination rates^1-5 and with the European-African differentiation at PRDM9, the only known major locus affecting fine-scale recombination rates³⁷.

Because admixed individuals will often be heterozygous at recombination modifier loci for alleles from different ancestral populations, the mode of genetic action of modifier alleles that are differentiated between populations should mediate observed recombination patterns. For example, among known modifier loci, inversions suppress recombination in an underdominant fashion, and PRDM9 alleles may act additively³⁷. It is still unknown whether hotspot motifs that interact with PRDM9 are recessive or dominant, although its clear there are epistatic interactions between hotspot motif loci and PRDM9 (refs. 37,38). In our analysis, the AfAdm map appears as one would expect if the recombination phenotype were determined predominantly by additive factors: the AfAdm map has rates that, on average, are intermediate between the HapMapCEU and HapMapYRI rates and which are biased toward HapMapYRI rates in a proportion consistent with the average proportion of African ancestry in our sample. We speculate that the approximately additive behavior of small-scale recombination rates observed here is largely caused by the influence of PRDM9 acting additively³⁷ on hotspot motifs that may themselves have largely additive effects.

Many of the departures from additive expectations that we found fell near other regions known to be exceptional in the genome for containing large structural variations. In particular, most regions that showed strong deficits in recombination contain inversions. This observation suggests the capacity of polymorphic structural variation to disrupt local recombination rates may be enhanced in admixed individuals, perhaps by elevated heterozygosity. A caveat to these results is that SNP genotypes in regions of structural variation are less reliable and may confound rates estimated by recombination inference methods. In addition, rates may be biased in regions with long-range LD and/or high levels of diversity because HMMs are overly simplified models of such regions^39,40. We suspect rates in high-diversity regions will more likely be overestimates, as we confirmed in the major histocompatibility complex region (Supplementary Note and Supplementary Fig. 9).

For future applications, we note that the ancestry-switch method is extendible to three-way admixtures and thus can be applied to infer recombination maps in other settings, such as for admixed Latino individuals, who in some cases combine descent from Native-American, European and African ancestral populations. Admixture maps might be compared to LD-based maps to detect selective sweeps, much like how pedigree-based maps have recently been used¹⁵. Finally, given that the power of the ancestry-switch method is improved by sampling additional admixed individuals and that the density of available SNP markers is increasing, we speculate that an ancestry-switch approach will become an increasingly powerful, scalable tool for fine-scaled recombination analysis.

ONLINE METHODS

Samples and genotyping.

We inferred relative recombination rates from African-descendant admixed samples (predominantly African Americans) gathered from four independent projects: GeneSTAR¹⁸, GENOA^19,20, GRAAD^21-23, and SARP and CAG-CSGA²⁴. A detailed description of each sample is provided in the Supplementary Note. For the recombination rate inference, we excluded pedigree-related individuals and obtained a total of 2,864 unrelated African-American samples. GRAAD is unique in having 938 individuals sampled from the United States (from Baltimore, Maryland and Washington, DC), which we refer to as the GRAADi sample, and 299 individuals sampled from Barbados, which we refer to as the GRAADii sample. When we repeated this inference after excluding all GRAADii samples, the rate estimates were largely unchanged (the correlation between estimates without and without GRAADii samples were well above 99%, independent of scale; Supplementary Note and Supplementary Fig. 12).

The samples were typed on the Illumina Human1M-Duo (SARP and CAG-CSGA), Illumina Human 1Mv1C (GeneSTAR), Illumina Human650Y (GRAAD) and Affymetrix 6.0 (GENOA) platforms. Because they differ in the set of available SNPs and there are concerns about merging data, we took several steps to make sure to conservatively merge the data, in particular attempting to avoid allele strand flip issues (Supplementary Note and Supplementary Fig. 13).

Reference panels.

In line with previous reports²⁵, we found in exploratory principal component analysis plots that our admixed sample stratifies between the African (YRI) and European (CEU) populations from HapMap3 (Supplementary Fig. 6). In our analysis, we thus used 234 and 230 phased haplotypes from the CEU and YRI samples, respectively, available from the HapMap project (Supplementary Note).

Simulations for validation.

We generated a total of 120 Mb of data, consisting of 6-Mb segments randomly chosen from each of the chromosomes 1 through 20. For each of those segments, we simulated a model widely used in the population genetic literature for African Americans (for example, see refs. 48-50): a diploid, randomly mating population of 20,000 individuals followed forward in time for seven non-overlapping generations, where the first generation was 80% African and 20% European individuals. Recombination events were placed along the segments following a 50%:50% average of the HapMapCEU and HapMapYRI maps. Founder haplotypes were generated using MACS⁵¹ and assumed a demographic model previously proposed⁵², with recombination following the same map as used above. The resulting SNPs were sub-sampled to match the corresponding SNP densities among our samples and the frequency spectra of the CEU and YRI HapMap samples. We also selected 230 and 234 phased haplotypes randomly from the African and European samples, respectively, to serve as reference panels. For investigating reference panel bias, we inferred recombination maps from the pattern of LD present in the reference panels using LDhat¹⁶. See the Supplementary Note for more information.

Inference of ancestry switch points and relative recombination rates.

Our initial approach was based on summing the posterior mean number of ancestry switch events across individuals. For an interval on the chromosome between SNP markers j and k, define $c_{jk}^{(i)}$ as a variable that takes on the values 0, 1 or 2 depending on whether there is an ancestry switch on neither, one or both chromosomes between markers j and k. Given genotype data for individual i (D⁽ⁱ⁾), a set of reference haplotypes from two source populations (H) and admixture parameters (θ, for example, time since admixture), the posterior mean of $c_{jk}^{(i)}$, (that is, E[$c_{jk}^{(i)}\mid D^{(i)}$, H, θ], which we denote ${\overline{c}}_{jk}^{(i)}$) can be computed under probabilistic models of admixture. Here we developed algorithms for computing ${\overline{c}}_{jk}^{(i)}$ using the HMM-based models for admixture introduced in a previous study¹⁷ (Supplementary Note). Our first estimator of a relative recombination rate between markers j and k then is:

$${\overline{c}}_{jk}=\sum _{i=1}^N{\overline{c}}_{jk}^{(i)}$$

where N is the number of sampled individuals.

Although straightforward, this approach computes ${\overline{c}}_{jk}^{(i)}$ based only on information on that single individual, and as in many statistical inference problems, power can be gained by pooling information across individuals. In addition, this approach does not account for ‘multiple hits’. For example, if an even number of ancestry switch events takes place between markers j and k on both chromosomes, $c_{jk}^{(i)}$ will be 0, despite the unobserved ancestry switch events. By simulation, we found that both of these factors hinder this method from accurate inference in regions of high recombination.

To improve upon this method, we developed a post-processing step that reframes the inference in an empirical Bayes framework and corrects for the multiple hits problem. Define $s_{jk}^{(i)}$ as the number of switch events between markers j and k (which takes values in {0,1,2,3,…}). Because ${\overline{c}}_{jk}^{(i)}$ is a highly informative summary statistic of an individual’s genotype data, we can perform inference on $s_{jk}^{(i)}$ based on ${\overline{c}}_{jk}^{(i)}$ rather than the original data D. Specifically, we use Bayes Theorem to compute $E[s_{jk}^{(i)}\mid {\overline{c}}_{jk}^{(i)}]$ as

$$E(s_{jk}^{(i)}\mid {\overline{c}}_{jk}^{(i)})=\frac{{\sum }_{d=0}^{\infty }d\cdot p({\overline{c}}_{jk}^{(i)}\mid s_{jk}^{(i)}=d)\cdot p(s_{jk}^{(i)}=d)}{{\sum }_{d=0}^{\infty }p({\overline{c}}_{jk}^{(i)}\mid s_{jk}^{(i)}=d)\cdot p(s_{jk}^{(i)}=d)}.$$ (1)

The likelihood $p({\overline{c}}_{jk}^{(i)}\mid s_{jk}^{(i)}=d)$ is difficult to obtain analytically, and so we approximated its value using simulations (Supplementary Note). Pooling of information across individuals enters by an empirical Bayes approach in which we set the prior $p(s_{jk}^{(i)}=d)$ according to an initial estimator based on the same data. In this case, we set $p(s_{jk}^{(i)}=d)\propto {\overline{c}}_{jk}$ (Supplementary Note). The posterior expectation on the total number of switch points across all N individuals (S_jk) is then given by

$$r_{jk}=E[S_{jk}\mid c_{jk}^{(1)},\dots ,c_{jk}^{(N)}]=\sum _{i=1}^{N}E[s_{jk}^{(i)}\mid c_{jk}^{(i)}].$$ (2)

Although this approach does not detect recombination events between chromosomal segments of similar ancestry, the number of ancestry switch events is expected to be proportional to the recombination rate in the region, and so we use r_jk as a relative rate estimator of recombination.

Simulations show our empirical Bayes method results in substantially improved estimates of relative recombination rates (Supplementary Fig. 3), and hence, we present results only for the empirical Bayes approach.

The computations giving rise to the inferred r_jk require assumptions about several parameters of the HMM, such as the time since admixture and the population miscopying rate (Supplementary Note). The results shown are for a set of parameters previously suggested¹⁷ for African-American samples (Supplementary Table 4). We also investigated whether alternative parameters would result in improved performance, but found that the suggested parameters worked as well as or better than reasonable alternatives (Supplementary Note and Supplementary Fig. 14).

Accommodating disparate marker intervals and construction of recombination maps.

In the above presentation, we ignored that not all individuals have markers genotyped on the same intervals. To address this, if we are estimating recombination in an interval between markers at physical coordinates e and f, we take the convention of replacing ${\overline{c}}_{jk}^{(i)}$ with

$${\overline{c}}_{ef}^{(i)}=\sum _{j=1}^{L-1}{\alpha }_{ef,j}\cdot {\overline{c}}_{j(j+1)}^{(i)},$$ (3)

where the sum runs over all L markers typed in individual i, and α_ef,j is the proportional overlap between the interval [e, f] and the interval defined by markers j and j + 1 (that is, α_ef,j ∈ [0, 1]). This adjustment to ${\overline{c}}_{jk}^{(i)}$ is a form of linear interpolation.

We generated maps with constant interval sizes of 10 kb, 15 kb, 20 kb, 33 kb, 50 kb, 75 kb, 100 kb, 150 kb, 200 kb, 250 kb, 333 kb, 500 kb, 750 kb, 1 Mb and 3 Mb. Whereas we used non-overlapping intervals to compute all reported metrics (such as correlations), we used maps where the midpoints of the intervals were always shifted by 5% of the interval size to find intervals with largest differences between maps and for plotting. In addition, for plotting, we scaled the map so that the total length of our map corresponded to a rate of 1.04 cM/Mb (in line with the total length of the sex-averaged map from ref. 8). The inferred recombination maps are available on the Novembre group webpage (see URLs).

Comparison to existing recombination maps.

We compared the recombination map inferred from the African-American and African-Caribbean dataset to four existing, fine-scaled recombination maps. The HapMapCEU and HapMapYRI maps, two widely used maps based on patterns of LD in HapMap populations, were obtained from the IMPUTE website⁵³ (see URLs). We also downloaded the pedigree-based deCODE map⁸ (see URLs). For all these maps, we recomputed maps of various interval sizes matching those maps generated from our African-American samples by interpolation. Further, we discarded the first 5 Mb on each telomeric end of every chromosome and all centromeric locations (Supplementary Note). Intervals overlapping unsequenced regions of the human reference genome were discarded following previous studies⁸. Note that the intervals of our non-overlapping 10-kb map precisely match those of the deCODE map. Correlation figures between maps are based on Pearson’s correlation coefficients. To avoid bias when comparing published maps at scales below 1 Mb, we trimmed the 20% intervals with lowest estimated rates because we found the estimation errors of the LD maps and the switch-point–based map to be correlated at small scales (Supplementary Note and Supplementary Fig. 7).

Analsyis of AfAdm maps as a weighted average of the HapmapYRI and HapMapCEU maps.

Let A, Y and C represent the AfAdm, HapMapYRI and HapMapCEU rates within an interval. We fit a model in which A is a convex linear combination of the Y and C maps: A = aY + (1 − a)C. To estimate a, note that we can subtract C from both sides to obtain (A − C) = a(Y − C) and, hence, use a linear regression of (A − C) on (Y − C) to estimate a. For the regression approach to compare the AfAdm map with the HapMapCEU and HapMapYRI maps, we computed robust regressions with the rlm function in the MASS package in R.